Tight Security Analysis of 3-Round Key-Alternating Cipher with a Single Permutation

Abstract

The tight security bound of the KAC (Key-Alternating Cipher) construction whose round permutations are independent from each other has been well studied. Then a natural question is how the security bound will change when we use fewer permutations in a KAC construction. In CRYPTO 2014, Chen et al. proved that 2-round KAC with a single permutation (2KACSP) has the same security level as the classic one (i.e., 2-round KAC). But we still know little about the security bound of incompletely-independent KAC constructions with more than 2 rounds. In this paper, we will show that a similar result also holds for 3-round case. More concretely, we prove that 3-round KAC with a single permutation (3KACSP) is secure up to $\varTheta (2^{\frac{3n}{4}})$ queries, which also caps the security of 3-round KAC. To avoid the cumbersome graphical illustration used in Chen et al.’s work, a new representation is introduced to characterize the underlying combinatorial problem. Benefited from it, we can handle the knotty dependence in a modular way, and also show a plausible way to study the security of rKACSP. Technically, we abstract a type of problems capturing the intrinsic randomness of rKACSP construction, and then propose a high-level framework to handle such problems. Furthermore, our proof techniques show some evidence that for any r, rKACSP has the same security level as the classic r-round KAC in random permutation model.

1 Introduction

In provable-security setting, the construction of a practical cipher is often abstracted into a reasonable model with certain assumptions (e.g., the underlying primitives are random functions/permutations and independent from each other). Under those assumptions, we try to prove that the abstract construction is immune to all (known or unknown) attacks executed by an adversary with specific abilities. Then the provable-security results provide some heuristic support for the underlying design-criteria of the cipher, since the practical underlying primitives do not satisfy the assumptions in general.

As aforementioned, the provable-security results are closely related to the abstract assumptions. If the assumptions are closer to the actual implementations, then the corresponding results will be more persuasive. For example, most of the existing work reduces the security of SPN block ciphers to the classic KAC construction (see Eq. (2)), in which the underlying round permutations as well as the round keys are random and independent from each other. Unfortunately, most KAC-based practical ciphers use the same round function and generate the round keys from a shorter master-key (i.e., the underlying round permutations and round keys are not independent from each other at all). Thus, there is still a big gap between the existing provable-security results and the practical ciphers.

Opposite to the KAC construction with independent round permutations and round keys (i.e., the classic KAC construction), we refer to the one whose round permutations or round keys are not independent from each other as incompletely-independent KAC or KAC with dependence. It is well known that r-round KAC is $\varTheta (2^{\frac{r}{r+1}n})$-secure in the random permutation model [CS14, HT16]. To characterize the actual SPN block ciphers, we should abstract a natural KAC construction (with dependence) satisfying two requirements: all the round permutations are the same and the round keys are generated from a shorter master-key by a certain deterministic algorithm. Hence, the ultimate question is whether there exists such a r-round incompletely-independent KAC construction which can still achieve $\varTheta (2^{\frac{r}{r+1}n})$-security. In other words, we want to know whether the required randomness of KAC construction can be minimized without a significant loss of security.

Up to now, people know little about the incompletely-independent KAC constructions (even with very small number of rounds), since it becomes much more complicated when either the underlying round permutations or round keys are no longer independent. To our knowledge, the best work about the KAC with dependence was given by Chen et al. [CLL+18]. They proved that several types of 2-round KAC with dependence have almost the same security level as 2-round KAC construction. However, it is still open about the security of incompletely-independent KAC with more than 2 rounds in provable-security setting.

In this paper, we initiate the study on the incompletely-independent KAC with more than 2 rounds. Here, we mainly focus on a special class of KAC, in which all the round permutations are the same and the round keys are still independent from each other, and refer to it as KACSP construction. Given a permutation $P:\{0,1\}^n \rightarrow \{0,1\}^n$, as well as $r+1$ round keys $k_{0},\ldots ,k_{r}$, the r-round KACSP construction rKACSP$[P;k_0,\dots ,k_r]$ maps a message $x\in \{0,1\}^n$ to

$$\begin{aligned} k_{r}\oplus P\Big (k_{r-1}\oplus P\big (\cdots P( x \oplus k_{0})\cdots \big )\Big ). \end{aligned}$$

(1)

Before turning into the results, we review the related existing work on classic KAC and KAC with dependence, respectively.

KAC construction is the generalization of the Even-Mansour construction [EM97] over multiple rounds. As one of the most popular ways to construct a practical cipher, the KAC construction captures the high-level structure of many SPN block ciphers, such as AES [DR02], PRESENT [BKL+07], LED [GPPR11] and so on. Given r permutations $P_{1},\ldots ,P_{r}$:$\ \{0,1\}^n \rightarrow \{0,1\}^n$, as well as $r+1$ round keys $k_{0},\ldots ,k_{r}$, the r-round KAC construction rKAC[$P_{1},\ldots ,P_{r}$; $k_{0},\ldots ,k_{r}$] maps a message $x \in \{0,1\}^n$ to

$$\begin{aligned} k_{r}\oplus P_{r}\Big (k_{r-1}\oplus P_{r-1}\big (\cdots P_{1}( x \oplus k_{0})\cdots \big )\Big ). \end{aligned}$$

(2)

In the random permutation model, it was proved by Even and Mansour [EM97] that an adversary needs roughly $2^{\frac{n}{2}}$ queries to distinguish the 1-round KAC construction from a true random permutation. Their bound was matched by a distinguishing attack [Dae91] which needs about $2^{\frac{n}{2}}$ queries in total. Many years later, Bogdanov et al. [BKL+12] proved that r-round KAC is secure up to $2^{\frac{2n}{3}}$ queries and the result is tight for $r=2$ . Besides, they also conjectured that the security for r-round KAC should be $2^{\frac{rn}{r+1}}$ because of a simple generic attack. After that, Steinberger [Ste12] improved the bound to $2^{\frac{3n}{4}}$ queries for $r\ge 3$ by modifying the way to upper bound the statistical distance between two product distributions. In the same year, Lampe et al. [LPS12] used coupling techniques to show that $2^{\frac{rn}{r+1}}$ queries and $2^{\frac{rn}{r+2}}$ queries are needed for any nonadaptive and any adaptive adversary, respectively. The first asymptotically tight bound was proved by Chen et al. [CS14] through an elegant path-counting lemma. Recently, Hoang and Tessaro [HT16] refined the H-coefficient technique (named as the expectation method) and gave the first exact bound of KAC construction. At this point, the security bound of the classic KAC construction is solved perfectly.

The development in the field of incompletely-independent KAC is much slower, since it usually becomes very involved when the underlying components are no longer independent from each other. Dunkelman et al. [DKS12] initiated the study of minimizing 1-round KAC construction, and showed that several strictly simpler variants provide the same level of security. After that, the best work was given by Chen et al. [CLL+14] in CRYPTO 2014. They proved that several types of incompletely-independent 2-round KAC have almost the same security level as the classic one. The result even holds when only a single permutation and a n-bit master-key are used, where n is the length of a plaintext/ciphertext. In their work, a generalized sum-capture theorem¹ is used to upper bound the probability of bad transcripts. And the probability calculation related to good transcripts is reduced to a combinatorial problem. Using the similar techniques, Cogliati and Seurin [CS18] obtained the security bound of the single-permutation encrypted Davies-Meyer construction. Nevertheless, their work is still limited in the scope of 2-round constructions.

Recently, Dai et al. [DSST17] proved that the 5-round KAC with a non-idealized key-schedule is indifferentiable from an ideal cipher. The model employed in their work is however orthogonal to ours and hence the result is not directly comparable.

In this paper, we initiate the study on the incompletely-independent KAC with more than 2 rounds and give a tight security bound of 3KACSP construction. Our contributions are conceptually novel and mainly two-fold:

• 1. We prove the tight security bound $\varTheta (2^{\frac{3n}{4}})$ queries of 3KACSP, which is an open problem (proposed in [CLL+18]) for incompletely-independent KAC with more than 2 rounds. That is, we can use only one instead of three distinct permutations to construct 3-round KAC without a significant loss of security. Notably, our proof framework is general and theoretically workable for any rKACSP. Following the ideas of analyzing 3KACSP, we strongly believe that rKACSP is also $\varTheta (2^{\frac{r}{r+1}n})$-secure in random permutation model, provided that the input/output size n is sufficiently large.

• 2. We develop a lot of general techniques to handle the dependence. Firstly, a new representation (see Sect. 3.3) is introduced to circumvent the cumbersome graphical illustration used in [CLL+18]. Benefited from it, we can handle the underlying combinatorial problem in a natural and intuitive way. Secondly, we abstract a type of combinatorial problems (i.e., Problem 1) capturing the intrinsic randomness of rKACSP, and also propose a high-level framework (see Sect. 5.1) to solve such problems. To instantiate the framework, we introduce some useful notions such as Core, target-path, shared-edge, and so on (see Sect. 3.3). Combining with the methods for constructing multiple shared-edges, we solve successfully the key problem in 3KACSP (see Sect. 5.2). At last, we also develop some new tricks (see Section 6 in the full version of this paper [WYCD20]) which are crucial in analyzing rKACSP ($r \ge 3$). Such tricks are not needed in 2KACSP, since it is relatively simple and does not have much dependence to handle.

It is rather surprising that the randomness of a single random permutation can provide such high level of security. From our proof, we can know an important reason is that, the information obtained by adversary is actually not so much. For instance, assume that n is big enough and an adversary can make $\varTheta (2^{\frac{3n}{4}})$ queries to the random permutation, then the ratio of known points (i.e., roughly $2^{-\frac{n}{4}}$) is still very small. Furthermore, our work means a lot more than simply from 2 to 3, and we now show something new compared to Chen et al.’s work.

• 1. It is the first time to convert the analysis of rKACSP into a type of combinatorial problems, thus we can study the higher-round constructions in a modular way. To solve such problems, we propose a general counting framework, and also successfully instantiate it for a 3-round case which is much more involved than the 2-round cases.

• 2. An important discovery is that we can adapt the tricks used in 2KACSP to solve the corresponding subproblems in 3KACSP, by designing proper assigning-strategy and RoCs(Range of Candidates, see Notation 5). We believe that the similar properties also hold in the analysis of general rKACSP.

• 3. A very big challenge in rKACSP($r \ge 3$) is to combine all the subproblems together into a desired bound. We do not need to consider that problem in the case of 2KACSP, since there is only one 2-round case in it. As a result, we develop some useful techniques to handle the dependence between the subproblems. Particularly, the key-points as shown at the beginning of Section 6 in the full version [WYCD20] are also essential in rKACSP($r \ge 4$).

Combining all above findings together, we point out that a plausible way to analyze rKACSP is by induction, and what’s left is only to solve a single r-round case of Problem 1. That is, we actually reduce an extremely complex (maybe intractable) problem into a single combinatorial problem, which can be solved by our framework theoretically. From the view of induction, Chen et al. [CLL+18] proved the basis step, while we have done largely the non-trivial work of the inductive step. Besides the conceptually important results, the new notions and ideas used in our proof are rather general and not limited in the rKACSP setting. We hope that they can be applied to analyze more different cryptographic constructions with dependence.

We start in Sect. 2 by setting the basic notations, giving the necessary background on the H-coefficient technique, and showing some helpful lemmas. In Sect. 3, we state the main result of this paper and introduce the new representation used throughout the paper. After that, the main result is proved in Sect. 4 where we also illustrate the underlying combinatorial problem and give two technical lemmas. The core part is Sect. 5, where we propose the general framework and also show the high-level technical route to handle the key subproblem in 3KACSP. At last, we conclude and give some extra discussion in Sect. 6.

2 Preliminaries

2.1 Basic Notations

In this paper, we use capital letters such as $A,B,\dots$ to denote sets. If A is a finite set, then $|A|$ denotes the cardinality of A, and $\overline{A}$ denotes the complement of A in the universal set (which will be clear from the context). For a finite set S, we let $x\leftarrow _{\$}S$ denote the uniform sampling from S and assigning the value to x. Let A and B be two sets such that $|A|=|B|$, then we denote $Bjt(A \rightarrow B)$ as the set of all bijections from A to B. If g and h are two well-defined bijections, then let $g\circ h(x)=h\big (g(x)\big )$. Fix an integer $n\ge 1$, let $N=2^n$, $I_n=\{0,1\}^n$, and ${\mathcal {P}}_n$ be the set of all permutations on $\{0,1\}^n$, respectively. If two integers s, t satisfy $1\le s\le t$, then we will write $(t)_{s}=t(t-1) \cdots (t-s+1)$ and $(t)_0=1$ by convention.

Given $\mathcal {Q}=\{(x_1,y_1 ),\dots ,(x_q,y_q )\}$, where the $x_i$’s (resp. $y_i$’s) are pairwise distinct n-bit strings, as well as a permutation $P\in \mathcal {P}_n$, we say that the permutation P extends the set $\mathcal {Q}$, denoting $P\vdash \mathcal {Q}$, if $P(x_i)=y_i$ for $i=1,\dots ,q$. Let $X=\{x\in I_n:(x,y)\in \mathcal {Q}\}$ and $Y=\{y\in I_n: (x,y)\in \mathcal {Q}\}$. We call X and Y respectively the domain and range of the set $\mathcal {Q}$.

Definition 1

($\mathcal {Q'}$ is strongly-disjoint with $\mathcal {Q}$). Let $\mathcal {Q}=\{(x_1,y_1 ),\dots ,$$(x_m,y_m )\}$ and $\mathcal {Q'}=\{(x'_1,y'_1 ),\dots , (x'_n,y'_n )\}$. We denote X,Y,$X'$,$Y'$ as the domains and ranges of $\mathcal {Q}$ and $\mathcal {Q'}$, respectively. Then we say that $\pmb {\mathcal {Q'}}$ is strongly-disjoint with $\pmb {\mathcal {Q}}$ if and , and denote it as $\pmb {\mathcal {Q'} \perp \mathcal {Q}}$.

2.2 Indistinguishability Framework

We will focus on the provable-security analysis of block ciphers in random permutation model, which allows the adversary to get access to the underlying primitives of the block ciphers. Consider the rKACSP construction (see Eq. (1)), a distinguisher $\mathcal {D}$ can interact with a set of 2 permutation oracles on n bits that we denote as $(P_O,P_I)$. There are two worlds in terms of the instantiations of the 2 permutation oracles. If P is a random permutation and the round keys $\pmb {K}=(k_0, \dots ,k_r )$ are randomly chosen from $I_{(r+1)n}$, we refer to $(r\mathrm {KACSP}[P;\pmb {K}],P)$ as the “real” world. If E is a random permutation independent from P, we refer to (E, P) as the “ideal” world. We usually refer to the first permutation $P_O$ (instantiated by $r\mathrm {KACSP}[P;\pmb {K}]$ or E) as the outer permutation, and to permutation $P_I$ (instantiated by P) as the inner permutation. Given a certain number of the queries to the 2 permutation oracles, the distinguisher $\mathcal {D}$ should distinguish whether the “real” world or the “ideal” world it is interacting with. The distinguisher $\mathcal {D}$ is adaptive such that it can query both sides of each permutation oracle, and also can choose the next query based on the query results it received. There is no computational limit on the distinguisher, thus we can assume $wlog$ that the distinguisher is deterministic (with a priori query which maximizes its advantage) and never makes redundant queries (which means that it never repeats a query, nor makes a query $P_i (x)$ for $i\in \{I, O\}$, if it receives x as an answer of a previous query $P_i^{\,-1} (y)$, or vice-versa).

The distinguishing advantage of the adversary $\mathcal {D}$ is defined as

$$\begin{aligned} Adv(\mathcal {D})=\left| \mathrm {Pr}[\mathcal {D}^{r\mathrm {KACSP}[P;\pmb {K}],P}=1]- \mathrm {Pr}[\mathcal {D}^{E,P}=1] \right| , \end{aligned}$$

(3)

where the first probability is taken over the random choice of P and $\pmb {K}$, and the second probability is taken over the random choice of P and E. $\mathcal {D}^{(\cdot )}$ denotes that $\mathcal {D}$ can make both forward and backward queries to each permutation oracle according to the random permutation model described before.

For non-negative integers $q_e$ and $q_p$, we define the insecurity of rKACSP against any adaptive distinguisher (even with unbounded computational source) who can make at most $q_e$ queries to the outer permutation oracle (i.e., $P_O$) and $q_p$ queries to the inner permutation oracle (i.e., $P_I$) as

$$\begin{aligned} Adv_{r\mathrm {KACSP}}^{cca}(q_e,q_p )=\mathrm {max}_{\mathcal {D}}\ Adv(\mathcal {D}), \end{aligned}$$

(4)

where the maximum is taken over all distinguishers $\mathcal {D}$ making exactly $q_e$ queries to the outer permutation oracle and $q_p$ queries to the inner permutation oracle.

2.3 The H-Coefficient Method

H-coefficient method [Pat08, CS14] is a powerful framework to upper bound the advantage of $\mathcal {D}$ and has been used to prove a number of results. We record all interactions between the adaptive distinguisher $\mathcal {D}$ and the oracles as an ordered list of queries which is also called a transcript. Each query in a transcript has the form of $(i,b,z,z' )$, where $i\in \{I,O\}$ represents which permutation oracle being queried, b is a bit indicating whether this is a forward or backward query, z is the value queried and $z'$ is the corresponding answer. For a fixed distinguisher $\mathcal {D}$, a transcript is called attainable if exists a tuple of permutations $(P_O,P_I)\in {\mathcal {P}_n^{\,2}}$ such that the interactions among $\mathcal {D}$ and $(P_O,P_I)$ yield the transcript. Recall that the distinguisher $\mathcal {D}$ is deterministic and makes no redundant queries, thus we can convert a transcript into 2 following lists of directionless queries without loss of information

$$\begin{aligned} \mathcal {Q}_E&= \{(x_1,y_1 ),\dots ,(x_{q_e},y_{q_e } )\}, \\ \mathcal {Q}_P&= \{(u_1,v_1 ),\dots ,(u_{q_p },v_{q_p } )\}. \end{aligned}$$

We can reconstruct the transcript exactly through the 2 lists, since $\mathcal {D}$ is deterministic and each of its next action is determined by the previous oracle answers (which can be known from those lists) it has received. As a side note, the 2 lists contain the description of the deterministic distinguisher/algorithm $\mathcal {D}$ implicitly. Therefore, the above two representations of an attainable transcript are equivalent with regard to a fixed deterministic distinguisher $\mathcal {D}$. Based on Eq. (3), our goal is to know the values of the two probabilities. It can be verified that the first probability (i.e., the one related to the “real” world) is only determined by the number of coins which can produce the above 2 directionless lists, and the probability is irrelevant to the order of each query in the original transcript. Thus, it seems that the adaptivity of $\mathcal {D}$ is “dropped” (More details can be found in [CS14]). Through this conceptual transition, upper bounding the advantage of $\mathcal {D}$ is often reduced to certain probability problems. That is why the H-coefficient method works well in lots of provable-security problems, especially for an information-theoretic and adaptive adversary.

As what [CS14, CLL+18] did, we will also be generous with the distinguisher $\mathcal {D}$ by giving it the actual key $\pmb {K}=(k_0, \dots , k_r)$ when it is interacting with the “real” world or a dummy key $\pmb {K} \leftarrow _{\$} I_{(r+1)n}$ when it is interacting with the “ideal” world at the end of its interaction. This treatment is reasonable since it will only increase the advantage of $\mathcal {D}$. Hence, a transcript $\tau$ we consider actually is a tuple $(\mathcal {Q}_E,\mathcal {Q}_P,\pmb {K})$. We refer to $\widehat{\tau }=(\mathcal {Q}_E,\mathcal {Q}_P)$ as the permutation transcript of $\tau$ and say that a transcript $\tau$ is attainable if its corresponding permutation transcript $\widehat{\tau }$ is attainable. Let $\mathcal {T}$ denote the set of attainable transcripts. We denote $T_{re}$, resp. $T_{id}$, as the probability distribution of the transcript $\tau$ induced by the “real” world, resp. the “ideal” world. It should be pointed out that the two probability distributions depend on the distinguisher $\mathcal {D}$, since its description is embedded in the conversion between the aforementioned two representations. And we also use the same notation to denote the random variable distributed according to each distribution.

The H-coefficient method has lots of variants. In this paper, we will employ the standard “good versus bad” paradigm. More concretely, the set of attainable transcripts $\mathcal {T}$ is partitioned into a set of “good” transcripts $\mathcal {T}_1$ such that the probability to obtain some $\tau \in \mathcal {T}_1$ are close in the “real” world and in the “ideal” world, and a set of “bad” transcripts $\mathcal {T}_2$ such that the probability to obtain any $\tau \in \mathcal {T}_2$ is small in the “ideal” world. Finally, a well-known H-coefficient-type lemma is given as follows.

Lemma 1

(Lemma 1 of [CLL+18]). Fix a distinguisher $\mathcal {D}$. Let $\mathcal {T}=\mathcal {T}_1\sqcup \mathcal {T}_2$ be a partition of the set of attainable transcripts. Assume that there exists $\varepsilon _1$ such that for any $\tau \in \mathcal {T}_1$, one has

$$ \frac{\mathrm {Pr}[T_{re}=\tau ]}{\mathrm {Pr}[T_{id}=\tau ]}\ge 1-\varepsilon _1, $$

and that there exists $\varepsilon _2$ such that $\mathrm {Pr}[T_{id}\in \mathcal {T}_2 ]\le \varepsilon _2$. Then $Adv(\mathcal {D})\le \varepsilon _1+\varepsilon _2$.

2.4 A Useful Lemma

Lemma 2

(3KACSP version, Lemma 2 of [CLL+18]). Let $\tau =\big ( \mathcal {Q}_E, \mathcal {Q}_{P},\pmb {K}=(k_0,k_1,k_2,k_3)\big )\in \mathcal {T}$ be an attainable transcript. Let $p(\tau )=\mathrm {Pr} \big [ P \leftarrow _\$ \mathcal {P}_n: 3\mathrm {KACSP}[P;\pmb {K}] \vdash \mathcal {Q}_E \ \vert \ P \vdash \mathcal {Q}_{P} \big ]$. Then

$$\begin{aligned} \frac{\mathrm {Pr}[T_{re}=\tau ]}{\mathrm {Pr}[T_{id}=\tau ]}=(N)_{q_e}\cdot p(\tau ). \end{aligned}$$

Following Lemma 2, it is reduced to lower-bounding $p(\tau )$ if we want to determine the value of $\varepsilon _1$ in Lemma 1. In brief, $p(\tau )$ is the probability that $3\mathrm {KACSP}[P;\pmb {K}]$ extends $\mathcal {Q}_{E}$ when P is a random permutation extending $\mathcal {Q}_{P}$.

3 The Main Result and New Representation

3.1 3-Round KAC with a Single Permutation

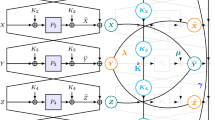
Let n be a positive integer, and let $P:I_n \rightarrow I_n$ be a permutation on $I_n$. On input $x \in I_n$ and round keys $\pmb {K}= (k_0, k_1, k_2, k_3) \in I_{4n}$, the block cipher 3KACSP returns $y= P\Big (P\big (P(x\oplus k_0 )\oplus k_1 \big )\oplus k_2 \Big )\oplus k_3$. See Fig. 1 for an illustration of the construction of 3KACSP.

Fig. 1.

Illustration of 3KACSP

3.2 Statement of the Result and Discussion

Since 3KACSP is a special case of 3-round KAC construction, its security is also capped by a distinguishing attack with $O(2^\frac{3n}{4})$ queries. We will show that the bound is tight by establishing the following theorem, which gives an asymptotical security bound of 3KACSP. Following the main theorem, we also give some comments. The proof of Theorem 1 can be found in Sect. 4, where we also illustrate the underlying combinatorial problem and give two technical lemmas.

Theorem 1

(Security Bound of 3KACSP). Consider the 3KACSP construction, in which the underlying round permutation P is uniformly random sampled from $\mathcal {P}_n$ and the round keys $\pmb {K}= (k_0, k_1, k_2, k_3)$ are uniformly random sampled from $I_{4n}$. Assume that $n\ge 32$ is sufficiently large, $\frac{28(q_e)^2}{N} \le q_p \le \frac{q_e}{5}$ and $2q_p+5q_e \le \frac{N}{2}$, then for any $6 \le t \le \frac{N^{1/2}}{8}$, the following upper bound holds:

$$\begin{aligned}&\qquad \qquad \quad Adv_{3\mathrm {KACSP}}^{cca} (q_e,q_p ) \le 98t \cdot \left( \frac{q_e}{N^{3/4}}\right) + 10t^2 \cdot \left( \frac{q_e}{N}\right) + \zeta (q_e),&\\&\text {where} \ \zeta (q_e) = \left\{ \begin{aligned}&\textstyle { \frac{32}{t^2},\ \quad \ \mathrm {if}\ q_e \le \frac{t}{6}N^{1/2} } \\&\textstyle { \frac{9N}{q_e^{\,2}}, \quad \ \mathrm {if}\ q_e \ge \frac{7t}{6}N^{1/2} } \end{aligned} \right. . \end{aligned}$$

Due to the special form of error term $\zeta (q_e)$, a single constant t cannot optimize the bound for all $q_e$’s simultaneously. The above result gives an upper bound for a range of $q_e$’s once t is chosen, thus different constants t will give different upper bounds for a fixed $q_e$. That is, for each $q_e$, we can make the error term $\zeta (q_e)$ be arbitrarily small by choosing a proper t, as long as the n is big enough. In general, we prefer to choose a small t to obtain the bound, since the first two terms in it are proportional to t. As an explanatory example, we next will show how to choose the constant t, assume that the threshold value of $\zeta (q_e)$ is set to 0.01.

Firstly, we should determine the range of $q_e$’s which are suitable for the minimum $t=6$. It is easy to verify that, for the range of big $q_e \ge 30N^{1/2}$, it must has $\zeta (q_e) \le 0.01$, since $\zeta (q_e)=\frac{9N}{q_e^2}$ for $q_e \ge 7N^{1/2}$ (when setting $t=6$). But for a small $q_e$ it needs a larger t, since we will use the function $\zeta (q_e)=\frac{32}{t^2}$ to obtain a desired $\zeta (q_e)$. For simplicity, we can set $t=60$ for each $q_e \le 10N^{1/2}$, because it has $\zeta (q_e)=\frac{32}{60^2} < 0.01$. Now what’s left is to choose a proper t for covering the remain range of $10N^{1/2}< q_e < 30N^{1/2}$. Using again the function $\zeta (q_e)=\frac{32}{t^2}$, we can crudely set $t=180$, which implies that $\zeta (q_e)=\frac{32}{180^2}< 0.001$ for all $q_e \le 30N^{1/2}$. As a side note, a slightly better choice is to choose $t=6c$ for $q_e=cN^{1/2}$, where $10< c < 30$.

From the above process, we obtain a concrete upper bound as follows.

It is easy to see that $t=6$ is available for almost all of the $q_e$’s (i.e., except the fraction of $\frac{30}{N^{1/2}}$). That is, the bound $Adv \le 588 \left( \frac{q_e}{N^{3/4}}\right) + 360 \left( \frac{q_e}{N}\right) + \frac{9N}{q_e^2}$ is suitable for almost $q_e$’s. We also stress here that Theorem 1 is an asymptotical result (for sufficiently large n) and we are not focusing on optimizing parameters. The point is that it actually shows that $\varOmega (N^{3/4})$ queries are needed to obtain a significant advantage against 3KACSP. Combining with the well-known matching attack, we conclude that the 3KACSP construction is $\varTheta (2^{\frac{3n}{4}})$-secure.

It should be pointed out that the deviation term $\zeta (q_e)$ and the assumption on $q_p$ in Theorem 1 are artifacts of our proof, and have no effect on the final result.

• 1. The $\zeta (q_e)$ is simply caused by the inaccuracy of Chebyshev’s Inequality (i.e., Lemma 5), rather than our proof methods nor the intrinsic flaws of 3KACSP. It is well-known that Chebyshev’s Inequality is rather coarse and there must exist a more accurate tail-inequality (e.g., Chenoff Bound). The $\zeta (q_e)$ and t will disappear, as long as a bit more accurate tail-inequality is applied during the computation of Eq. (95) in full version [WYCD20]. That is, just by replacing with a better tail-inequality, our proof techniques actually can obtain a concrete bound such like $Adv \le 98\left( \frac{q_e}{N^{3/4}}\right) +10\left( \frac{q_e}{N}\right)$, i.e., $t=1$ and $\zeta (q_e)=0$ in Theorem 1. But to our knowledge, there is no explicit expression of the moment generating function for a hypergeometric distribution, hence we now have no idea how to obtain a Chernoff-Type bound.

• 2. The assumption on $q_e$ and $q_p$ is determined by the assigning-strategy and all the RoCs (there are dozens in total) designed in the formal proof. It means that a better choice corresponds to a weaker assumption. Theoretically, there exist choices which can eliminate the assumption without changing our proof framework. However, optimizing such a choice is rather unrealistic, since it is extremely hard to find even one feasible solution (as provided in our formal proof).

In a word, our results and proof techniques are strong enough to show that 3KACSP is $\varTheta (N^{3/4})$-secure in random permutation model.

3.3 New Representation

In this subsection, we will propose a new representation which will be used throughout the paper. The representation improves our understanding of the underlying combinatorial problem, and is very helpful to handle the dependence caused by the single permutation. From our proof, it can be found that this new representation is natural to capture the intrinsic combinatorial problem, and the complicated graphical illustration used in [CLL+18] can also be avoided. More specifically, the new representation consists of several definitions.

Definition 2

(Directed-Edge). Let A denote a set and $\mathsf {a}, \mathsf {b} \in A$. If a permutation $\varPsi$ on A maps $\mathsf {a}$ to $\mathsf {b}$, then we denote it as $\mathsf {a} \xrightarrow {\varPsi } \mathsf {b}$ and say that there is a $\pmb {\varPsi }$-directed-edge (or simply directed-edge if $\varPsi$ is clear from the context) from $\mathsf {a}$ to $\mathsf {b}$. We also use $\mathsf {a} \xrightarrow {\varPsi } \mathsf {b}$ to denote the ordered query-answer pair $(\mathsf {a},\mathsf {b})$ of the permutation oracle $\varPsi$. That is, if we make queries $\varPsi (\mathsf {a})$ (resp. $\varPsi ^{-1}(\mathsf {b})$), then $\mathsf {b}$ (resp. $\mathsf {a}$) will be the answer.

For a directed-edge $\mathsf {a} \xrightarrow {\varPsi } \mathsf {b}$, we refer to $\mathsf {a}$ as the previous-point of $\mathsf {b}$ under $\varPsi$, and to $\mathsf {b}$ as the next-point of $\mathsf {a}$ under $\varPsi$, respectively. Naturally, the notation means that the next-point of $\mathsf {a}$ under $\varPsi$ is undefined, and the notation means that the previous-point of $\mathsf {b}$ under $\varPsi$ is undefined.

Definition 2 aims to view the binary relation under a permutation as a set of directed-edges. Consider a permutation $P \in \mathcal {P}_n$, the list of directionless queries $\mathcal {Q}_P= \{(u_1,v_1), \dots , (u_q,v_q) \}$ can be written as the set of P-directed-edges $\{u_1 \xrightarrow {P} v_1, \dots , u_q \xrightarrow {P} v_q \}$. From now on, we will not distinguish the two representations.

Definition 3

(Directed-Path and $\pmb {\mathsf {Core}}$). Let $\varphi [\cdot ]:\mathcal {P}_n\rightarrow \mathcal {P}_n$ be a block-cipher construction invoking one permutation $P\in \mathcal {P}_n$. Fix an attainable transcript $\tau = (\mathcal {Q}_E, \mathcal {Q}_P, \pmb {K})$, where $\mathcal {Q}_E$ and $\mathcal {Q}_P$ are the lists of directionless queries of the outer and inner permutation oracle, respectively.

For a specific $P \in \mathcal {P}_n$ and a string $\mathsf {a} \in I_n$, the steps related to P in the calculation of $\varphi [P](\mathsf {a})$ can be denoted as a chain of P-directed-edges and has the form of $\langle f(\mathsf {a}) \xrightarrow {P} \mathsf {a}_1,\dots , \mathsf {a}_m \xrightarrow {P} g^{-1}(\varphi [P](\mathsf {a})) \rangle$, where $f(\cdot )$ and $g(\cdot )$ are invertible operations before the first invocation of P and after the last invocation of P in the construction $\varphi [\cdot ]$, respectively.² We refer to such a chain as a $\pmb {\Big (\big ( \mathsf {a}, \varphi [P](\mathsf {a}) \big ), \varphi [P]\Big )}$-directed-path, where $\mathsf {a}$ and $\varphi [P](\mathsf {a})$ are called as the source and destination of the directed-path, respectively. We may simply say a directed-path for convenience, if all things are clear from the context.

Let $\mathcal {Q}_E=\{ (x_1,y_1 ),\dots ,(x_q,y_q ) \}$, where $x_i$’s (resp. $y_i$’s) are pairwise distinct n-bit strings. We say a permutation $P\in \mathcal {P}_n$ is $\varphi [\cdot ]$-correct with respect to $\mathcal {Q}_E$, if $\varphi [P] \vdash \mathcal {Q}_E$. That is, the $\varphi [P]$-directed-path starting from $x_i$ must end at $y_i$ (i.e., $y_i=\varphi [P](x_i)$) for a correct permutation P, where $i=1,\cdots ,q$. We refer to the set of P-directed-edges used in above q directed-paths as a $\varphi [P]$-$\mathsf {Core}$ with respect to $\mathcal {Q}_E$, and denote it as $\pmb {\mathsf {Core}(\varphi [P] \vdash \mathcal {Q}_E)}$. In addition, we use the notation $\mathsf {Core}(\varphi [\cdot ] \vdash \mathcal {Q}_E)$ to denote a certain $\varphi [P]$-$\mathsf {Core}$ in general. And we may simply say a $\mathsf {Core}$ for convenience, if $\varphi [\cdot ]$ and $\mathcal {Q}_E$ are clear from the context.

Definition 3 aims to highlight the steps related to P when calculating the value of $\varphi [P](a)$. In fact, the form of a directed-path is only determined by the construction $\varphi [\cdot ]$.³ That is, each $\big ((*,*),\varphi [P]\big )$-directed-path consists of m P-directed-edges, where m is the invoking number of P in the construction $\varphi [\cdot ]$. Thus, we often use the notation $\varphi [\cdot ]$-directed-path to denote a directed-path of the form in general. In addition, the calculation steps independent of P (e.g., the operations $f(\cdot )$ and $g(\cdot )$ in Definition 3) are always omitted, since we only care about the assignments of P. Of course, those omitted steps can still be inferred from the directed-path since they are deterministic. For instance, the calculation of $P\big ( P(x) \boxplus 1 \big )=y$ can be denoted as the directed-path $\langle x \xrightarrow {P} P(x), P(x)\boxplus 1 \xrightarrow {P} y \rangle$, in which the step from P(x) to $P(x) \boxplus 1$ is omitted but can still be known from it. Next, we will give an explanatory example for the above definitions.

Example 1

Let P denote a permutation on $\mathcal {Z}_5=\{0,1,2,3,4\}$, as well as $\mathcal {Q}_E=\{(0,4),(1,0)\}$, and $\varphi [P](x)=P\big ( P(x) \boxplus 1 \big )$, where $\boxplus$ represents the modulo-5 addition.

Case 1: If $P=\{0 \xrightarrow {P} 1, 1 \xrightarrow {P} 2, 2 \xrightarrow {P} 3, 3 \xrightarrow {P} 4, 4 \xrightarrow {P} 0\}$, then all directed-paths constructed by $\varphi [P]$ are $\langle 0 \xrightarrow {P} 1, 2 \xrightarrow {P} 3\rangle$, $\langle 1 \xrightarrow {P} 2, 3 \xrightarrow {P} 4\rangle$, $\langle 2 \xrightarrow {P} 3, 4 \xrightarrow {P} 0\rangle$, $\langle 3 \xrightarrow {P} 4, 0 \xrightarrow {P} 1\rangle$, and $\langle 4 \xrightarrow {P} 0, 1 \xrightarrow {P} 2\rangle$. That is, the permutation $\varphi [P]$ maps 0 to 3, 1 to 4, 2 to 0, 3 to 1 and 4 to 2, respectively. Obviously, the P is not $\varphi [\cdot ]$-correct with respect to $\mathcal {Q}_E$, since the $\varphi [P]$-directed-path $\langle 0 \xrightarrow {P} 1, 2 \xrightarrow {P} 3\rangle$ leads 0 to 3 which is inconsistent with the source-destination pair $(0,4) \in \mathcal {Q}_E$.

Case 2: If $P=\{ 0 \xrightarrow {P} 2, 1 \xrightarrow {P} 1, 2 \xrightarrow {P} 0, 3 \xrightarrow {P} 4, 4 \xrightarrow {P} 3\}$, then we have $\varphi [P] \vdash \mathcal {Q}_E$ because the directed-paths $\langle 0 \xrightarrow {P} 2, 3 \xrightarrow {P} 4\rangle$ and $\langle 1 \xrightarrow {P} 1, 2 \xrightarrow {P} 0\rangle$ lead 0 to 4 and 1 to 0, respectively. Also, we can know that $\mathsf {Core}(P)=\{0 \xrightarrow {P} 2, 1 \xrightarrow {P} 1, 2 \xrightarrow {P} 0, 3 \xrightarrow {P} 4 \}$, and thus $|\mathsf {Core}(P)| = 4$.

Case 3: If $P=\{ 0 \xrightarrow {P} 3, 1 \xrightarrow {P} 0, 2 \xrightarrow {P} 1, 3 \xrightarrow {P} 2, 4 \xrightarrow {P} 4\}$ , then it is easily to verify that $\varphi [P] \vdash \mathcal {Q}_E$, as well as $\mathsf {Core}(P)=\{ 0 \xrightarrow {P} 3, 1 \xrightarrow {P} 0, 4 \xrightarrow {P} 4\}$ and $|\mathsf {Core}(P)| = 3$.

Case 4: Similarly, if $P=\{ 0 \xrightarrow {P} 0, 1 \xrightarrow {P} 4, 2 \xrightarrow {P} 1, 3 \xrightarrow {P} 2, 4 \xrightarrow {P} 3 \}$, then $\varphi [P] \vdash \mathcal {Q}_E$. Furthermore, it has $\mathsf {Core}(P)=\{ 0 \xrightarrow {P} 0, 1 \xrightarrow {P} 4 \}$ and $|\mathsf {Core}(P)| = 2$.

Statement. For convenience, we will simply use the terms edge and path instead of directed-edge and directed-path, respectively. In addition, if $x_{\alpha }^{\beta }$ denotes the source of a path (where $\alpha$ and $\beta$ are some symbols), then the notation $y_{\alpha }^{\beta }$ always denotes the corresponding destination of the path and vice-versa, and the correspondence can be easily inferred from the context.

We have known that a path can be used to denote a complete calculation given the construction, source and P. In fact, we often confront an incomplete path whose source and destination are fixed, provided that the permutation P is partially defined.⁴ Namely, there are some edges missing in such a path. Particularly, we most interest in a special form of incomplete path which is called target-path.

Definition 4

(Target-Path). Assume that P is partially defined, then a $\pmb {\big ((\mathsf {a},\mathsf {b}),}$ $\pmb {\varphi [P]\big )}$-target-path is a $\varphi [\cdot ]$-path in which all the inner-nodes are undefined while the source $\mathsf {a}$ and the destination $\mathsf {b}$ are fixed. Thus, a target-path always has the form of⁵

$$ \langle \mathsf {a} \xrightarrow {P}\ \ ,\ \ \xrightarrow {P} \ \ , \cdots , \ \ \xrightarrow {P} \ \ , \ \ \xrightarrow {P} \mathsf {b} \rangle . $$

In essence, the proof of main result is reduced to the task of completing a group of target-paths (i.e., Problem 1). That is why we refer to such type of paths as target-paths. In general, it is convenient to consider a group of (target-)paths having the same form. Then, the notion of shared-edge can also be introduced naturally.

Definition 5

(Group of Paths and Shared-Edge). Fix a permutation P, which can be partially defined.

We call the paths $\big ((x_1,y_1),\varphi [P]\big )$-path, $\dots$, $\big ((x_q,y_q),\varphi [P]\big )$-path as a group of $\varphi [\cdot ]$-paths, and denote it as $\pmb {(\mathcal {Q}_E, \varphi [P])}$-paths, where $\mathcal {Q}_E = \{(x_1,y_1),\dots ,(x_q,y_q)\}$ is the set of source-destination pairs. Also, we may simply use the notation $\mathcal {Q}_E$-paths if $\varphi [P]$ is clear from the context.

Similarly, we call the target-paths $\big ((\mathsf {a}_1,\mathsf {b}_1),\varphi [P]\big )$-target-path, $\dots$, $\big ((\mathsf {a}_q,\mathsf {b}_q),$ $\varphi [P]\big )$-target-path as a group of $\varphi [\cdot ]$-target-paths, and denote it as $\pmb {(\mathcal {Q}, \varphi [P])}$-target-paths, where $\mathcal {Q} = \{(\mathsf {a}_1,\mathsf {b}_1),\dots ,(\mathsf {a}_q,\mathsf {b}_q)\}$ is the set of source-destination pairs.

If an edge is used in at least 2 different paths, then we refer to it as a shared-edge.

From now on, we can use Definition 5 to denote a group of (target-)paths conveniently. And it should be pointed out that the shared-edge is a key primitive in our proof, though the concept is rather simple and natural. Moreover, the notion of partial-P will be useful, since P is often partially defined.

Definition 6

(Partial-$\pmb {P}$ and Partially-Sample). Let P be a permutation on $I_n$, and let A be a subset of $I_n$. Then we refer to the set of edges $\{x_i \xrightarrow {P} P(x_i): x_i \in A \}$ as the partial- $\varvec{P}$ from A to P(A).

Let S and T be two sets of elements whose next-points and previous-points are undefined under P, respectively. If $|S|= |T|$, then we can sample randomly a bijection $f \leftarrow _\$ Bjt(S \rightarrow T)$ and define $x \xrightarrow {P} f(x)$ for each $x \in S$. We refer to the above process as sample partial-$\varvec{P}$ randomly from S to T, or $\varvec{P}$ is partially-sampled randomly from S to T.

It should be pointed out that a partial-P is a subset of P, and also a set of P-edges. Now let’s reconsider the sampling $P \leftarrow _\$ \mathcal {P}_n$ conditioned on $P \vdash \mathcal {Q}_P$, where $\mathcal {Q}_P=\{u_1 \xrightarrow {P} v_1,\dots ,u_q \xrightarrow {P} v_q \}$. If we denote $S=I_n\setminus \{u_1,\dots ,u_q \}$ and $T=I_n\setminus \{v_1,\dots ,v_q \}$, then the above sampling is equivalent to sample partial-P randomly from S to T. Furthermore, it is natural to view $\mathcal {Q}_P$ as the priori information of P. That is, we can fix the q edges of $\mathcal {Q}_P$ in advance, and then sample partial-P randomly from S to T.

4 Proof of Theorem 1

In this section, we will use the standard H-Coefficient method (i.e., Lemma 1) to prove our main result. That is, all attainable transcripts $\mathcal {T}$ should be partitioned into two disjoint parts: a set of “good” transcripts denoted as $\mathcal {T}_1$ and a set of “bad” transcripts denoted as $\mathcal {T}_2$. Determining the partition is often a subtle task, since it is intrinsically a trade-off between $\varepsilon _1$ and $\varepsilon _2$. If we add more conditions on good transcripts to make they have better property (i.e., with smaller $\varepsilon _1$), then the set of bad transcripts becomes larger accordingly (i.e., $\varepsilon _2$ becomes larger), or vice-versa.

Intuitively, the chance to obtain any $\tau \in \mathcal {T}_1$ in “real” world should be very close to the chance in “ideal” world, and it should be very rare to obtain any $\tau \in \mathcal {T}_2$ in the “ideal” world. For an attainable transcript $\tau =\big ( \mathcal {Q}_E, \mathcal {Q}_{P},\pmb {K}=(k_0,k_1,k_2,k_3)\big )$, we know that (from Lemma 2) the quotient of $\mathrm {Pr}[T_{re}=\tau ]$ and $\mathrm {Pr}[T_{id}=\tau ]$ is determined by the value of

$$\begin{aligned} p(\tau )=\mathrm {Pr} \big [ P \leftarrow _\$ \mathcal {P}_n: 3\mathrm {KACSP}[P;\pmb {K}] \vdash \mathcal {Q}_E \ \vert \ P \vdash \mathcal {Q}_{P} \big ]. \end{aligned}$$

(5)

That is, a transcript $\tau$ is whether “good” or not, can also be determined by the value of $p(\tau )$.

Therefore, we firstly illustrate the meaning of $p(\tau )$ through our new representation, and then give the definition of “bad” transcripts. In fact, it is also a good example to show that the knotty dependence can be sorted out if we use a proper representation. At the end of this section, we will prove Theorem 1 directly by combining two technical lemmas together.

4.1 Transcripts and $p(\tau )$

In this subsection, we firstly expound the meaning of $p(\tau )$ for a fixed transcript $\tau$, and then give the concrete definition of “bad” transcripts. To reduce the complexity of notations, we now rewrite the $p(\tau )$ into another equivalent form.

For an attainable transcript $\tau =(\mathcal {Q}_E, \mathcal {Q}_{P},\pmb {K})$, we modify the inner permutation P and its permutation transcript $\widehat{\tau }=(\mathcal {Q}_E, \mathcal {Q}_P)$ as follows:

$$\begin{aligned} P'&= P\oplus k_1, \\ \mathcal {Q'}\!_E&= \{(x\oplus k_0,y\oplus k_1\oplus k_3):(x,y)\in \mathcal {Q}_E\}, \\ \mathcal {Q'}\!_P&= \{(u,v\oplus k_1 ):(u,v)\in \mathcal {Q}_P\}. \end{aligned}$$

Let

$$\begin{aligned} X&= \{x'\in I_n:(x',y' )\in \mathcal {Q'}\!_E\},\ \ Y=\{y'\in I_n:(x',y' )\in \mathcal {Q'}\!_E\},\\ U&= \{u'\in I_n:(u',v' )\in \mathcal {Q'}\!_P\},\ \ V=\{v'\in I_n:(u',v' )\in \mathcal {Q'}\!_P\} \end{aligned}$$

denote the domains and the ranges of $\mathcal {Q'}\!_E$ and $\mathcal {Q'}\!_P$, respectively. Thus, $|\mathcal {Q}\!_E|=|\mathcal {Q'}\!_E|=|X|=|Y|=q_e$, and $|\mathcal {Q}\!_P|=|\mathcal {Q'}\!_P|=|U|=|V|=q_p$.

Accordingly, we also transform the 3KACSP construction into the 3KACSP$'$ construction (as shown in Fig. 2), i.e., $P' \circ P' \circ (\oplus k_1 \oplus k_2) \circ P'$. The above modification is reasonable, since we show the actual key used in 3KACSP after the distinguisher $\mathcal {D}$ finishing the query phase (i.e., after obtaining $\mathcal {Q}_E$ and $\mathcal {Q}_P$). Thus, it is simply a conceptual transformation and only the notations should be changed. That is, we can consider that the distinguisher $\mathcal {D}$ is querying the outer permutation and inner permutation oracles instantiated by 3KACSP$'$ and $P'$, respectively. Then the resulting transcript is $\tau '=(\mathcal {Q}'_E, \mathcal {Q}'_{P},\pmb {K})$. From now on, we will not distinguish the transcripts $\tau$ and $\tau '$, since they can transform from each other easily. Thus, we have

$$\begin{aligned} p(\tau )=p(\tau ')=\mathrm {Pr}[P'\leftarrow _\$ \mathcal {P}_n:\mathrm {3KACSP'}[P';\pmb {K}]\vdash \mathcal {Q}'_E \vert P'\vdash \mathcal {Q}'_P]. \end{aligned}$$

(6)

Fig. 2.

3KACSP$'$: a conceptual transformation of 3KACSP

Notation 1

(Abbreviation). Let A be a set of n-bit strings, and $\mathsf {a}$ be an element of A. From now on, we will abbreviate the expression $\mathsf {a}\oplus k_1\oplus k_2$ as $\mathsf {a}_\oplus$ for convenience. Similarly, we also denote that $A_\oplus =\{\mathsf {a}_\oplus : \mathsf {a} \in A\}$.

Next, we will show the underlying combinatorial problem of $p(\tau ')$ intuitively. Fix arbitrarily a transcript $\tau '=(\mathcal {Q}'_E, \mathcal {Q}'_{P},\pmb {K})$, the event $\mathrm {3KACSP'}[P';\pmb {K}]\vdash \mathcal {Q}'_E$ means that for each pair $(x',y') \in \mathcal {Q}'_E$, the 3KACSP$'$-path starting from $x'$ ends exactly at $y'$. A complete 3KACSP$'$-path consists of 3 $P'$-edges, and has the form of

$$\begin{aligned} \langle x' \xrightarrow {P'} *_1, *_1 \xrightarrow {P'} *_2, (*_2)_\oplus \xrightarrow {P'} y' \rangle , \end{aligned}$$

(7)

where $*_1$ and $*_2$ are the 2 inner-nodes should be assigned.

Before turning into the value of $p(\tau ')$, we consider a simpler case that as first. Since no edge of the $\mathcal {Q}'_E$-paths has been fixed in advance, our task is simply to complete all the $(\mathcal {Q}'_E, 3\text {KACSP}')$-target-paths, by sampling $P'$ uniformly random from $\mathcal {P}_n$. In fact, we will see that it is exactly the Problem 1 instantiated by $\varphi [P']=P' \circ P'_\oplus \circ P'$, $\mathcal {Q}_1=\mathcal {Q}'_E$, , and can be solved directly by a general framework⁶.

Unfortunately, it becomes much more complex when , since some 3KACSP$'$-target-paths will be “damaged”. More specifically, a path will turn into “some other construction”-target-path, when some edges in it are fixed by $\mathcal {Q}'_P$. We now give some intuition about those paths. Assume that $q_e$ and $q_p$ are $O(N^{3/4})$ and $\pmb {K}$ is uniformly random sampled from $I_{4n}$, then there are at most 4 types of paths. On average, there are O(1) paths containing 3 fixed edges. Similarly, we know that there exist $O(N^{1/4})$ (resp. $O(N^{1/2})$) paths whose 2 edges (resp. 1 edge) are fixed in advance. And there are $O(N^{3/4})$ paths containing no fixed edge (i.e., they are 3KACSP$'$-target-paths). It can be found that the circumstances are more involved than before, since the constructions of missing-edges are no longer uniform. In other words, there may exist several different constructions of target-paths to be completed. Thus, we should analyze each of the constructions and complete them in turns.

In fact, we judge a transcript $\tau '$ is whether “good” or not, according to the $\mathcal {Q'}\!_E$-paths and the edges fixed by $\mathcal {Q}'_{P}$. Firstly, a transcript will be classified into the set of “bad” transcripts, if there exists some $\mathcal {Q}'_E$-path containing 3 fixed edges. Otherwise, we should further study the circumstances of paths and fixed edges determined by the transcript. More specifically, for such a transcript, we can classify the $q_e$ paths between $\mathcal {Q'}\!_E$ into three groups (see Fig. 3 as an illustration) according to the number of fixed edges.

$\blacktriangleright$ Group-2. The paths containing 2 fixed edges belong to Group-2. More specifically, there are 3 subcases of such paths according to the position of fixed edges. Recall that U and V denote the domain and range of $\mathcal {Q'}\!_P$, respectively.

- Group-2.1: The paths whose first two edges are fixed. That is, Group-2.1 consists of the paths starting from the subset $X_{II} \subset X$, where

- Group-2.2: The paths whose last two edges are fixed. That is, Group-2.2 consists of the paths ending at the subset $Y_B \subset Y$, where

- Group-2.3: The paths whose first and third edges are fixed. That is, Group-2.3 consists of the paths starting from the subset $D_X\subset X$ to the corresponding $D_Y=\mathcal {Q'}\!_E(D_X)\subset Y$, where

Fig. 3.

Illustration of the missing-edges in $\mathcal {Q}'_E$-paths

Notation 2

(Group-2). We denote $|X_{II}|=\alpha _2$, $|Y_B|=\beta _2$, $|D_X|=|D_Y|=\gamma _2$, and $\delta _2=\alpha _2+\beta _2+\gamma _2$. Thus, Group-2 contains $\delta _2$ paths in total, where $\alpha _2$ paths belong to Group-2.1, $\beta _2$ paths belong to Group-2.2 and the other $\gamma _2$ paths belong to Group-2.3. For convenience, we assume wlog that $X_{II}=\{x_1,\dots ,x_{\alpha _2}\}$, $Y_B=\{y_{\alpha _2+1},\dots ,y_{\alpha _2+\beta _2}\}$, $D_X=\{x_{\alpha _2+\beta _2+1},\dots ,x_{\delta _2 }\}$ and $D_Y=\{y_{\alpha _2+\beta _2+1},\dots ,y_{\delta _2 }\}$.

$\blacktriangleright$ Group-1. The paths containing 1 fixed edge belong to Group-1. More specifically, there are 2 subcases of such paths according to the position of fixed edge. Recall that U and V denote the domain and range of $\mathcal {Q'}\!_P$, respectively.

- Group-1.1: The paths whose first edge is fixed. That is, Group-1.1 consists of the paths starting from the subset $X_I \subset X$, where

- Group-1.2: The paths whose third edge is fixed. That is, Group-1.2 consists of the paths ending at the subset $Y_A \subset Y$, where

Notation 3

(Group-1). We denote $|X_I|=\alpha _1$, $|Y_A|=\beta _1$ and $\delta _1=\alpha _1+\beta _1$. Namely, Group-1 contains $\delta _1$ paths in total, where $\alpha _1$ paths belong to Group-1.1 and the other $\beta _1$ paths belong to Group-1.2. For convenience, we assume wlog that $X_I=\{x_{\delta _2+1},\dots ,x_{\delta _2+\alpha _1}\}$ and $Y_A=\{y_{\delta _2+\alpha _1+1}, \dots ,y_{\delta _2+\delta _1}\}$.

$\blacktriangleright$ Group-0. Each path belongs to Group-0 contains no fixed edge.

Notation 4

(Group-0). We denote $\delta _0 = q_e - \delta _2 - \delta _1$. Thus, Group-0 contains $\delta _0$ paths in total. Let $X_0$ and $Y_0$ denote the sets of sources and destinations of Group-0, respectively. For convenience, we assume wlog that $X_0 = \{x_i: \delta _2 + \delta _1 + 1 \le i \le q_e\}$ and $Y_0 = \{y_i: \delta _2 + \delta _1 + 1 \le i \le q_e\}$.

For a fixed transcript $\tau '$, its circumstances of $\mathcal {Q}'_E$-paths and fixed edges can be illustrated as Fig. 3, where the missing-edges are the ones marked with a colored square. At this point, it is clear that $p(\tau ')$ (see Eq. (6)) represents the probability that, all missing-edges are filled by sampling $P'$ uniformly random from the set of permutations extending $\mathcal {Q}'_P$. Furthermore, the above problem becomes more straightforward if we use the notion of target-path (see Definition 4).

Definition 7

(Structure of Missing-Edges).

Let $E_2$ denote the event that the $\delta _2$ paths of Group-2 are completed (i.e., the $\delta _2$ missing-edges in Group-2 are filled).

Let $E_{11}$ denote the event that the $\big ( \mathcal {Q}'_{E_{11}}, \varphi _{11}[\cdot ] \big )$-target-paths are completed (i.e., the $2\alpha _1$ missing-edges in Group-1.1 are filled), where $\mathcal {Q}'_{E_{11}} = \big \{ \big (\mathcal {Q}'_P (x_i), y_i \big ): x_i \in X_I \big \} \text { and } \varphi _{11}[P']= P'_\oplus \circ P'$.

Let $E_{12}$ denote the event that the $\big ( \mathcal {Q}'_{E_{12}}, \varphi _{12}[\cdot ] \big )$-target-paths are completed (i.e., the $2\beta _1$ missing-edges in Group-1.2 are filled), where $\mathcal {Q}'_{E_{12}} = \big \{ \big (x_i, \mathcal {Q}'^{-1}_P(y_i) \big ): y_i \in Y_A \big \} \text { and } \varphi _{12}[P']= P' \circ P'_\oplus$.

Let $E_0$ denote the event that the $\big ( \mathcal {Q}'_{E_0}, \varphi _0[\cdot ] \big )$-target-paths are completed (i.e., the $3\delta _0$ missing-edges in Group-0 are filled), where $\mathcal {Q}'_{E_0} = \{ (x_i,y_i):x_i\in X_0\} \text { and } \varphi _{0}[P']= P' \circ P'_\oplus \circ P'$.

Immediately, we can know that

$$\begin{aligned} p(\tau ') = \mathrm {Pr}[P' \leftarrow _\$ \mathcal {P}_n: E_2 \wedge E_{11} \wedge E_{12} \wedge E_0 \vert P' \vdash \mathcal {Q}'_P]. \end{aligned}$$

(8)

Obviously, lower-bounding the value of $p(\tau ')$ is reduced to several subproblems which can be applied directly with the counting framework (proposed in Sect. 5.1). For a “good” transcript, we can successfully obtain an appropriate lower bound for each subproblem.⁷

Now, we will give the concrete definition of “bad”/“good” transcripts. From the formal proof, it will be seen that each attainable permutation transcript $\widehat{\tau }$ can be extended to a “good” transcript by adding a “good” key $\pmb {K}$. Thus, it is equivalent to study the properties of “bad”/“good” keys for a fixed permutation transcript $\widehat{\tau }$.

Definition 8

(Bad Transcripts and Bad Keys). Fix arbitrarily a permutation transcript $\widehat{\tau }=(\mathcal {Q}_E,\mathcal {Q}_P)$. If the extended transcript $\tau '=(\mathcal {Q}'_E,\mathcal {Q}'_P,\pmb {K})$ satisfies $\pmb {K} \in \mathrm {BadK} = \bigcup _{1 \le i \le 9} \mathrm {BadK}_i$, then we say the $\tau =(\mathcal {Q}_E,\mathcal {Q}_P,\pmb {K})$ is a “bad” transcript and the $\pmb {K}$ is a “bad” key for $\widehat{\tau }$. Otherwise, we say the $\tau$ is a “good” transcript and the $\pmb {K}$ is a “good” key for $\widehat{\tau }$. More specifically, the definitions of $\mathrm {BadK}_i$ $(1 \le i \le 9)$ are shown as follows.

where $S_i$ (resp. $T_i$) are the sets of n-bit strings whose next-points (resp. previous-points) are undefined when considering the subproblem related to $E_i$, for $i \in \{ 11, 12, 0 \}$.⁸

It should be pointed out that the conditions for “bad” keys are not designed only for the “real” world. In fact, all discussion in Sect. 4.1 depends only on the relation between permutation transcript $\widehat{\tau }$ and $\pmb {K}$ (which is dummy in the “ideal” world), and is irrelevant to which world we consider.

4.2 Two Technical Lemmas

In this subsection, we give two technical lemmas to upper-bound the values of $\varepsilon _1$ and $\varepsilon _2$ in Lemma 1, respectively. More specifically, Lemma 3 considers arbitrarily an attainable permutation transcript $\widehat{\tau }$, and lower-bounds the value of $\mathrm {Pr}[T_{re}=(\widehat{\tau },\pmb {K})])/(\mathrm {Pr}[T_{id}=(\widehat{\tau },\pmb {K})]$ for any “good” key $\pmb {K}$. This is the major task in our formal proof. And Lemma 4 upper-bounds the value of $\mathrm {Pr}[\pmb {K}\ \mathrm {is\ bad\ for\ }\widehat{\tau }]$ in “ideal” world, where $\widehat{\tau }$ can be any attainable permutation transcript.

Lemma 3

Consider the 3KACSP construction, and fix arbitrarily an attainable permutation transcript $\widehat{\tau }=(\mathcal {Q}_E,\mathcal {Q}_P)$, where $|\mathcal {Q}_E| = q_e$ and $|\mathcal {Q}_P| = q_p$. Assume that $n \ge 32$, $6 \le t \le \frac{N^{1/2}}{8}$, $\frac{28(q_e)^2}{N} \le q_p \le \frac{q_e}{5}$ and $2q_p+5q_e \le \frac{N}{2}$. Following the Definition 8, if $\pmb {K}$ is a good key for $\widehat{\tau }$, then we have the bound

$$\begin{aligned} \frac{\mathrm {Pr}[T_{re}=(\widehat{\tau }, \pmb {K})]}{\mathrm {Pr}[T_{id}=(\widehat{\tau }, \pmb {K})]} \ge 1 - 97t \cdot \left( \frac{q_e}{N^{3/4}}\right) - 10t^2 \cdot \left( \frac{q_e}{N}\right) - \zeta (q_e). \end{aligned}$$

From Lemma 2 and the Eq. (8), we know that

$$\begin{aligned} \frac{\mathrm {Pr}[T_{re}=(\widehat{\tau }, \pmb {K})]}{\mathrm {Pr}[T_{id}=(\widehat{\tau }, \pmb {K})]}&= (N)_{q_e} \cdot \mathrm {Pr}[P' \leftarrow _\$ \mathcal {P}_n: E_2 \wedge E_{11} \wedge E_{12} \wedge E_0 \vert P' \vdash \mathcal {Q}'_P] \nonumber \\&\ge (N)_{q_e} \cdot \mathrm {Pr}[P' \leftarrow _\$ \mathcal {P}_n: E_2 \wedge \widetilde{E_{11}} \wedge \widetilde{E_{12}} \wedge \widetilde{E_{0}} \vert P' \vdash \mathcal {Q}'_P] \nonumber \\&= (N)_{q_e} \nonumber \\&\times \mathrm {Pr}[P' \leftarrow _\$ \mathcal {P}_n: E_2 \vert P' \vdash \mathcal {Q}'_P] \end{aligned}$$

(9)

$$\begin{aligned}&\times \mathrm {Pr}[P' \leftarrow _\$ \mathcal {P}_n: \widetilde{E_{11}} \vert P' \vdash \mathcal {Q}'_P \wedge E_2] \end{aligned}$$

(10)

$$\begin{aligned}&\times \mathrm {Pr}[P' \leftarrow _\$ \mathcal {P}_n: \widetilde{E_{12}} \vert P' \vdash \mathcal {Q}'_P \wedge E_2 \wedge \widetilde{E_{11}}] \end{aligned}$$

(11)

$$\begin{aligned}&\times \mathrm {Pr}[P' \leftarrow _\$ \mathcal {P}_n: \widetilde{E_{0}} \vert P' \vdash \mathcal {Q}'_P \wedge E_2 \wedge \widetilde{E_{11}} \wedge \widetilde{E_{12}}], \end{aligned}$$

(12)

where $\widetilde{E_{11}}$ denotes the event $E_{11} \bigwedge \ |\mathsf {Core}(\varphi _{11}[P'] \vdash \mathcal {Q}'_{E_{11}})| \ge (2-\frac{1}{N^{1/4}})\alpha _1$, $\widetilde{E_{12}}$ denotes the event $E_{12} \bigwedge \ |\mathsf {Core}(\varphi _{12}[P'] \vdash \mathcal {Q}'_{E_{12}})| \ge (2-\frac{1}{N^{1/4}})\beta _1$, and $\widetilde{E_{0}}$ denotes the event $E_{0} \bigwedge \ |\mathsf {Core}(\varphi _{0}[P'] \vdash \mathcal {Q}'_{E_{0}})| \ge (3-\frac{2t}{N^{1/2}})\delta _0$.

We will see that it is easy to calculate the value of (9) when $\pmb {K}$ is a “good” key for $\widehat{\tau }$. Hence what’s left is to lower-bound the values of (10)–(12) for any “good” transcript, respectively. Intrinsically, the 3 probabilities belong to the same type of combinatorial problems (i.e., the Problem 1). That means we can view Eqs. (10)–(12) as a 2-round, 2-round and 3-round instantiation of Problem 1, respectively. Interestingly, we find that the techniques used in [CLL+18] can be tailored to obtain desired values of the 2-round cases. Nonetheless, our 2-round cases are more involved and there are some new non-trivial tasks should be solved. Furthermore, the 3-round case is a whole new challenge, and is much more difficult than the 2-round ones. To handle it, we introduce a general framework in Sect. 5, where we also give the high-level technical route.

However, knowing how to solve (9)–(12) individually is still far from enough. It is a very big challenge to combine all the lower bounds together to obtain an appropriate result, since those subproblems affect each other by sharing the same resource of permutation P. There are numerous technical specifics should be handled, and we defer the formal proof of Lemma 3 to Section 6 of the full version [WYCD20].

Lemma 4

Consider the “ideal” world, and fix arbitrarily an attainable permutation transcript $\widehat{\tau }=(\mathcal {Q}_E,\mathcal {Q}_P)$, where $|\mathcal {Q}_E| = q_e$ and $|\mathcal {Q}_P| = q_p$. Following the Definition 8, if $q_p \le \frac{q_e}{5}$, then it has

$$\begin{aligned} \mathrm {Pr}[\pmb {K} \leftarrow _{\$} I_{4n}: \pmb {K}\mathrm {\ is\ bad\ for\ }\widehat{\tau }] \le 6 \cdot \left( \frac{q_e}{N^{3/4}}\right) . \end{aligned}$$

The formal proof of Lemma 4 is deferred to Section 7 of the full version [WYCD20].

4.3 Concluding the Proof of Theorem 1

At this point,we are ready to complete the proof of Theorem 1. It can be inferred that $\varepsilon _1 = 97t \cdot \left( \frac{q_e}{N^{3/4}}\right) + 10t^2 \cdot \left( \frac{q_e}{N}\right) + \zeta (q_e)$ and $\varepsilon _2 = 6 \cdot \left( \frac{q_e}{N^{3/4}}\right)$ from Lemma 3 and Lemma 4, respectively. Following the H coefficient method and Lemma 1, we finally obtain

$$\begin{aligned} Adv^{cca}_{\mathrm {3KACSP}} (q_e,q_p)&\le \varepsilon _1 + \varepsilon _2&\\&\le 97t \cdot \left( \frac{q_e}{N^{3/4}}\right) + 10t^2 \cdot \left( \frac{q_e}{N}\right) + \zeta (q_e) + 6 \cdot \left( \frac{q_e}{N^{3/4}}\right)&\\&\le 98t \cdot \left( \frac{q_e}{N^{3/4}}\right) + 10t^2 \cdot \left( \frac{q_e}{N}\right) + \zeta (q_e),&\end{aligned}$$

where we use the fact that $t\ge 6$ for the last inequality.

5 A Type of Combinatorial Problem

It is known that the proof of Lemma 3 can be reduced to several subproblems having a similar form. In fact, the analysis of rKACSP can also be reduced to the same type of problems. That is a key perspective to simplify the task of studying the security of rKACSP.

In this section, we will only study how to solve such type of problems individually, while the tricks of balancing all the subproblems are deferred to the formal proof. More specifically, a general framework which can theoretically solve such problems is proposed. For the reason of space, we here only instantiate it for the 3-round case and the full version [WYCD20] also gives the 2-round instance as a warm-up.

First of all, the general definition of aforementioned problems is given as follows.

Problem 1

(Completing A Group of Target-Paths). Consider a group of $(\mathcal {Q}_1,\varphi [\cdot ])$-target-paths, where $\mathcal {Q}_1$ is the set of source-destination pairs. Let $\mathcal {Q}_2$ denote the set of fixed edges, and it has $\mathcal {Q}_1 \perp \mathcal {Q}_2$. Then, how to lower-bound the value of

$$\begin{aligned} p = \mathrm {Pr}[P \leftarrow _\$ \mathcal {P}_n: \varphi [P] \vdash \mathcal {Q}_1 \vert P \vdash \mathcal {Q}_2]. \end{aligned}$$

(13)

It should be pointed out that each target-path in the group has the same construction, and hence the same number of missing-edges. This number of missing-edges is the principal character of Problem 1. In addition, we do not care about the specific values of the source-destination pairs in $\mathcal {Q}_1$, as long as they satisfy some “good” properties and $\mathcal {Q}_1 \perp \mathcal {Q}_2$. More importantly, our work shows some evidence that, the problems with the same number of missing-edges can be solved by similar techniques.

Compared to Chen et al.’s ad-hoc work, our techniques stand in a higher level and unearth something more intrinsic. In a very high level, our method is reduced to constructing a certain number of shared-edges by assigning inner-nodes.

Statement. For simplicity, we assume that all edges defined in this section are well-defined and compatible from each other.

5.1 Counting Framework

In this subsection, we will study how to handle the Problem 1 with at least 2 missing-edges, since the case of 1 missing-edge is trivial. More specifically, a counting framework will be proposed based on the notions of Core (see Definition 3) and shared-edge (see Definition 5). Before that, we will give some intuition about the framework.

Let U and V denote the domain and range of $\mathcal {Q}_2$, respectively. Then, the sets $S= I_n \setminus U$ and $T= I_n \setminus V$ denote the sets of the strings whose next-points and previous-point are undefined, respectively. In fact, we will only use the edges from S to T to complete all the target-paths. Namely, the Cores we construct must be strongly-disjoint with $\mathcal {Q}_2$. The reason why we can still construct enough Cores is that, the number of known edges (i.e., $|\mathcal {Q}_2|$) is relatively rather small. For example, $|\mathcal {Q}_P|=O(N^{3/4})$ is far more smaller than N (i.e., roughly 1 out of $N^{1/4}$) when n is big enough.

Let $\mathcal {P}_C=\left\{ P \in \mathcal {P}_n: \varphi [P] \vdash \mathcal {Q}_1\ \wedge \ P \vdash \mathcal {Q}_2 \right\}$ denote the set of all correct permutations extending $\mathcal {Q}_2$, and $\mathcal {C}=\{\widetilde{C}: \widetilde{C}\ \perp \mathcal {Q}_2\ \bigwedge \ \exists \ P \in \mathcal {P}_C\ s.t.\ \widetilde{C} = \mathsf {Core}(\varphi [P] \vdash \mathcal {Q}_1) \}$ denote the set of all possible Cores strongly-disjoint with $\mathcal {Q}_2$. From the definition, we know that each correct permutation $P \in \mathcal {P}_C$ must determine a $\mathsf {Core}(\varphi [P] \vdash \mathcal {Q}_1)$. On the other side, for a specific $\widetilde{C}\in \mathcal {C}$, there exist exactly $(N-|\mathcal {Q}_2|-|\widetilde{C}|)!$ different correct permutations $P \in \mathcal {P}_C$ such that $\mathsf {Core}(\varphi [P] \vdash \mathcal {Q}_1) = \widetilde{C}$. That is because such P must contain the $|\mathcal {Q}_2|$ edges fixed in $\mathcal {Q}_2$ and the $|\widetilde{C}|$ edges fixed in $\widetilde{C}$, while the rest of edges can be defined freely. We can know that the above $(|\mathcal {Q}_2|+|\widetilde{C}|)$ edges are distinct and have no conflict, since it has $\widetilde{C}\ \perp \mathcal {Q}_2$. Additionally, it is easy to know that the size of the sample space is equal to $(N-|\mathcal {Q}_2|)!$, thus we have

$$\begin{aligned} 13&= \frac{|\mathcal {P}_C|}{(N-|\mathcal {Q}_2|)!} \nonumber \\&\ge \frac{\sum _{\widetilde{C}\in \mathcal {C}} \big |\{P \in \mathcal {P}_C : \mathsf {Core}(\varphi [P] \vdash \mathcal {Q}_1)=\widetilde{C}\} \big |}{(N-|\mathcal {Q}_2|)!} \nonumber \\&= \frac{\sum _{\widetilde{C}\in \mathcal {C}}(N-|\mathcal {Q}_2|-|\widetilde{C}|)!}{(N-|\mathcal {Q}_2|)!}\nonumber \\&= \frac{\sum _m \sum _{\widetilde{C}\in \mathcal {C}: |\widetilde{C}| =m} (N-|\mathcal {Q}_2|- m)!}{(N-|\mathcal {Q}_2|)!}\nonumber \\&= \sum _m\frac{\Big |\Big \{ \widetilde{C}\in \mathcal {C}: |\widetilde{C}| =m \Big \}\Big |}{(N-|\mathcal {Q}_2|)_m}. \end{aligned}$$

(14)

Intrinsically, we classify the correct permutations according to the cardinality of the corresponding Core. In fact, we only interest in the Cores strongly-disjoint with $\mathcal {Q}_2$, since they are easier to be counted. From Eq. (14), it is known that the value of p can be lower-bounded, if we can count the number of Cores with a specific cardinality and also know how to sum all the related terms up.

Based on the above intuition, a 4-step counting framework is proposed in Fig. 4. Roughly, the first 3 steps aim to lower-bound the number of Cores with a specific cardinality, and the last step will handle the calculation of a summation. As shown in Fig. 4, our first task is to instantiate the Problem 1 with specific parameters (i.e., Step 1). Then, we should propose an appropriate assigning strategy for constructing a specific number of shared-edges, and hence obtain the Cores with the specific cardinality (i.e., Step 2). Also, we should count the number of possible assignments which can be constructed from the above strategy (i.e., Step 3). Thus, we actually establish a lower bound for the number of Cores with a specific cardinality. At last, we should calculate a summation to obtain the final result (i.e., Step 4).

Fig. 4.

Illustration of the counting framework

5.2 The Key Subproblem in 3KACSP

In this subsection, we will instantiate the counting framework for the 3-round case to show how it works. For brevity, we here only give the high-level technical route, and all the details will be completed in the formal proof. First of all, we abstract the 3-round subproblem in 3KACSP as follows.

Problem 2

(A Problem with 3 Missing-Edges). Let $\mathcal {Q}_E = \{ (x_1,y_1), \dots , (x_q,y_q) \}$ be the set of source-destination pairs of $\varphi _2[\cdot ]$-target-paths, and $\mathcal {Q}_P = \{ (u_1,v_1), \dots , (u_p,v_p) \}$ be the set of known edges, where $\varphi _2[P] = P \circ P_\oplus \circ P$ and $\mathcal {Q}_P \perp \mathcal {Q}_E$. Then, how to lower-bound the value of

$$\begin{aligned} p_2&= \mathrm {Pr}[P \leftarrow _\$ \mathcal {P}_n: \varphi _2[P] \vdash \mathcal {Q}_E \vert P \vdash \mathcal {Q}_P]. \end{aligned}$$

(15)

Following the counting framework in Fig. 4, our first task is to make clear the group of target-paths (including the construction and source-destination pairs) and the set of fixed edges. Obviously, Problem 2 is exactly the Problem 1 instantiated by $\varphi [\cdot ] = \varphi _2[\cdot ]$, $\mathcal {Q}_1 = \mathcal {Q}_E$ and $\mathcal {Q}_2 = \mathcal {Q}_P$. We denote X and Y as the domain and range of $\mathcal {Q}_E$, respectively. And let $S=I_n \setminus \{ u_1,\dots ,u_p \}$ and $T=I_n \setminus \{v_1,\dots ,v_p\}$ denote the sets of strings whose next-points and previous-points are undefined, respectively. Then, it has $|S|=|T|=N-p$.

As shown in (16), there are 2 inner-nodes (i.e., $*_{i,1}$ and $*_{i,2}$) to be assigned in each $(\mathcal {Q}_E, \varphi _2[\cdot ])$-target-path. We refer to the 2 inner-nodes in such a target-path as $1^{st}$-inner-node and $2^{nd}$-inner-node, respectively. Since a well-defined assignment of all the inner-nodes (i.e., the tuple of $(*_{1,1},*_{1,2},\dots ,*_{q,1},*_{q,2})$) is equivalent to a $\mathsf {Core}(\varphi _2[\cdot ] \vdash \mathcal {Q}_E)$, we will not distinguish them from now on. Moreover, we will count the number of assignments of all the inner-nodes, to lower-bound the value of (15).

$$\begin{aligned} (\mathcal {Q}_E, \varphi _2[\cdot ])\text {-target-paths} \left\{ \begin{aligned}&\langle x_1 \xrightarrow {P} *_{1,1},\ *_{1,1} \xrightarrow {P} *_{1,2},\ (*_{1,2})_\oplus \xrightarrow {P} y_1 \rangle \\&\qquad \qquad \qquad \quad \ \dots \\&\langle x_q \xrightarrow {P} *_{q,1},\ *_{q,1} \xrightarrow {P} *_{q,2},\ (*_{q,2})_\oplus \xrightarrow {P} y_q \rangle \end{aligned} \right. \end{aligned}$$

(16)

In essence, constructing Cores with a specific cardinality is equivalent to constructing a specific number of shared-edges. Our goal is to construct Cores with $3q-k-h$ edges, where k and h are variables of positive integers. It means that $k+h$ shared-edges (each of them is used exactly in 2 paths) should be constructed. Naturally, we study 2 assigning methods for constructing such shared-edges at first, and then use them to save k edges and h edges, respectively. In addition, we also need to know how to construct the edges, which are used exclusively in only 1 target-path (i.e., the ones are not shared-edges).

Definition 9

(Exclusive-Element). We say an inner-node is assigned by an exclusive-element, if it not creates any new shared-edge at this moment. In this paper, we always use a notation related to w (e.g., $w_i$) to denote an exclusive-element.

Consider the $(\mathcal {Q}_E, \varphi _2[\cdot ])$-target-paths in (16), we will only focus on the shared-edge involved exactly in 2 paths (i.e., each such shared-edge will save 1 edge). It is easy to verify that a shared-edge is established once a $1^{st}$-inner-node is assigned by an element from X or Y. Similarly, a shared-edge is also established once a $2^{nd}$-inner-node is assigned by an element from $X_\oplus$ or Y. Therefore, for constructing a shared-edge, we choose a target-path at first, and then assign a proper value to its $1^{st}$-inner-node or $2^{nd}$-inner-node. In either case, the chosen value determines the other path sharing an edge with the former one. To distinguish them, we refer to the later determined target-path as a negative-path (denoted as $path^-$), since it is determined passively by the assigning. Accordingly, we call the former path as a positive-path (denoted as $path^+$).

Next, we will further interpret the above process. Since both of the 2 inner-nodes can be used to establish shared-edges, we discuss the 2 cases separately. At first, we will show how to construct shared-edges by assigning $1^{st}$-inner-nodes.

$\blacktriangleright$ $\pmb {1^{st}}$-Inner-Node. In fact, we will construct exactly 1 shared-edge for each $path^+$. That is, the $2^{nd}$-inner-node of a $path^+$ must be assigned by an exclusive-element. According to the position of the shared-edge(s) in $path^-$, there are 3 cases as follows.

• Case 1: Fix a target-path from x to y as the $path^+$ at first. If we assign $\ddot{x} \in X$ as its $1^{st}$-inner-node (i.e., the one with box), then the target-path from $\ddot{x}$ to $\ddot{y}$ becomes the corresponding $path^-$ whose first edge (i.e., the bold one) is the shared-edge. That is, the $1^{st}$-inner-node (i.e., the underline one) in $path^-$ must be the same exclusive-element (i.e., w) as the $2^{nd}$-inner-node in $path^+$. Additionally, if $\ddot{y}$ is not assigned to the $1^{st}$- nor $2^{nd}$- inner-node of any target-path, then we can assign an exclusive-element (i.e., $\widetilde{w}$) to the $2^{nd}$-inner-node of $path^-$. As a result, we obtain a Type$^{1a}$ sharing-gadget (as shown in (17)) containing 2 paths, 1 shared-edge and 2 exclusive-elements. And we refer to the 2 paths as a Type$^{1a}$-$path^+$ and a Type$^{1a}$-$path^-$, respectively.

  $$\begin{aligned} \begin{aligned} Type {^{1a}\quad \ } \\ sharing-gadget \end{aligned} \left\{ \begin{aligned}&\langle x\, \xrightarrow {P}\, \boxed {\ddot{x}},\ \varvec{ \ddot{x}\xrightarrow {P} w},\ w_\oplus \xrightarrow {P} y \rangle \qquad (path^+) \\&\langle \varvec{ \ddot{x} \xrightarrow {P}\underline{w} },\ \ w \xrightarrow {P} \widetilde{w},\ \ \widetilde{w}_\oplus \xrightarrow {P} \ddot{y} \rangle \qquad (path^-) \end{aligned} \right. \end{aligned}$$

  (17)

• Case 2: Fix a target-path from x to y as the $path^+$ at first. If we assign $\ddot{y} \in Y$ as its $1^{st}$-inner-node (i.e., the one with box), then the target-path from $\ddot{x}$ to $\ddot{y}$ becomes the corresponding $path^-$ whose third edge (i.e., the bold one) is the shared-edge. That is, the $2^{th}$-inner-node (i.e., the underline one) in $path^-$ must be assigned by $x_\oplus$. Additionally, if $\ddot{x}$ is not assigned to the $1^{st}$-inner-node of any target-path and $\ddot{x}_\oplus$ is not assigned to the $2^{nd}$-inner-node of any target-path, then we can assign an exclusive-element (i.e., $\widetilde{w}$) to the $1^{st}$-inner-node of $path^-$. As a result, we obtain a Type$^{1b}$ sharing-gadget (as shown in (18)) containing 2 paths, 1 shared-edge and 2 exclusive-elements. And we refer to the 2 paths as a Type$^{1b}$-$path^+$ and a Type$^{1b}$-$path^-$, respectively.

  $$\begin{aligned} \begin{aligned} Type {^{1b}\quad \ } \\ sharing-gadget \end{aligned} \left\{ \begin{aligned}&\langle \varvec{ x \xrightarrow {P} \boxed {\ddot{y}} },\ \ddot{y}\xrightarrow {P} w,\ w_\oplus \xrightarrow {P}\, y \rangle \qquad (path^+) \\&\langle \ddot{x}\, \xrightarrow {P} \widetilde{w},\ \ \widetilde{w} \xrightarrow {P} \underline{x_\oplus },\ \ \varvec{ x\xrightarrow {P} \ddot{y} } \rangle \qquad (path^-) \end{aligned} \right. \end{aligned}$$

  (18)

• Case 3: Interestingly, a $path^-$ can share edges with 2 different $paths^+$ simultaneously. Fix the target-path from $x_1$ to $y_1$ as $path^+_1$, and fix the target-path from $x_2$ to $y_2$ as $path^+_2$. If we assign $\ddot{x}$ (resp. $\ddot{y}$) as the $1^{st}$-inner-node of $path^+_1$ (resp. $path^+_2$) (i.e., the ones with box), then the target-path from $\ddot{x}$ to $\ddot{y}$ becomes the $path^-$ of $path^+_1$ and $path^+_2$ simultaneously. That is, the $1^{st}$-inner-node in $path^-$ must be the same exclusive-element (i.e., w) as the $2^{nd}$-inner-node in $path^+_1$, and the $2^{nd}$-inner-node in $path^-$ must be assigned by $(x_2)_\oplus$. As a result, we obtain a Type$^{1c}$ sharing-gadget (as shown in (19)) containing 3 paths, 2 shared-edge and 2 exclusive-elements. And we refer to the 3 paths as a Type$^{1c}$-$path^+_1$, a Type$^{1c}$-$path^+_2$ and a Type$^{1c}$-$path^-$, respectively.

  $$\begin{aligned} \begin{aligned} Type {^{1c}\quad \ } \\ sharing-gadget \end{aligned} \left\{ \begin{aligned}&\langle x_1\, \xrightarrow {P}\, \boxed {\ddot{x}} ,\ \varvec{\ddot{x}\xrightarrow {P} w},\ \ \ \ \ w_\oplus \xrightarrow {P} y_1 \rangle \qquad (path^+_1) \\&\langle \varvec{ x_2 \xrightarrow {P} \boxed {\ddot{y} }},\ \ddot{y}\, \xrightarrow {P} \widetilde{w},\ \ \ \ \ \,\widetilde{w}_\oplus \xrightarrow {P} y_2 \rangle \qquad (path^+_2) \\&\langle \varvec{\ddot{x}\,\ \xrightarrow {P} \underline{w}},\ \ w \xrightarrow {P} \underline{(x_2)_\oplus },\ \varvec{x_2\xrightarrow {P}\, \ddot{y} } \rangle \qquad (path^-) \end{aligned} \right. \end{aligned}$$

  (19)

At this point, we have known how to construct a shared-edge for a $path^+$ by assigning its $1^{st}$-inner-node. Naturally, we can establish k such shared-edges if k $paths^+$ are considered. It is easy to verify that the following Method 1 actually establishes k shared-edges for the involved $paths^+$ and $paths^-$.⁹

We can see that Method 1 allows the $paths^-$ to be a mixture of Type$^{1a}$-, Type$^{1b}$- and Type$^{1c}$- $paths^-$. This is a key point to obtain an appropriate lower bound in our proof, since it enlarge the number of candidates for $paths^-$ (i.e., roughly double the one involved in 2-round case¹⁰). It should be pointed out that the number of $paths^-$ is determined by the $1^{st}$-inner-nodes of the k $paths^+$, and is not necessarily equal to k. In a sense, the k $paths^+$ with their $1^{st}$-inner-nodes determine almost “everything” about the involved $paths^+$ and $paths^-$.

$\blacktriangleright$ $\pmb {2^{nd}}$-Inner-Node. It is similar to construct a shared-edge by assigning the $2^{nd}$-inner-node of a $path^+$. We will also construct exactly 1 shared-edge for each $path^+$. That is, the $1^{st}$-inner-node of a $path^+$ must be assigned by an exclusive-element. According to the position of the shared-edge(s) in $path^-$, there are also 3 cases. For reason of the space, we omit the explanation here, and defer the details to the corresponding part of full version [WYCD20].

• Case 1:

  $$\begin{aligned} \begin{aligned} Type {^{2a}\quad \ } \\ sharing-gadget \end{aligned} \left\{ \begin{aligned}&\langle x\, \xrightarrow {P} w,\ w \xrightarrow {P} \boxed {\ddot{x}_\oplus },\ \ \varvec{\ddot{x}\xrightarrow {P} y} \rangle \qquad (path^+) \\&\langle \varvec{ \ddot{x} \xrightarrow {P} \underline{y} },\ \, y\xrightarrow {P}\, \widetilde{w},\ \ \ \, \widetilde{w}_\oplus \xrightarrow {P}\, \ddot{y} \rangle \qquad (path^-) \end{aligned} \right. \end{aligned}$$

  (20)

• Case 2:

  $$\begin{aligned} \begin{aligned} Type {^{2b}\quad \ } \\ sharing-gadget \end{aligned} \left\{ \begin{aligned}&\langle x \xrightarrow {P} w,\ \varvec{w \xrightarrow {P}\boxed {\ddot{y}}},\ \ddot{y}_\oplus \xrightarrow {P}\, y \rangle \qquad (path^+) \\&\langle \ddot{x} \xrightarrow {P} \widetilde{w},\ \widetilde{w} \, \xrightarrow {P} \underline{w_\oplus },\ \ \varvec{ w \xrightarrow {P} \ddot{y} } \rangle \qquad (path^-) \end{aligned} \right. \end{aligned}$$

  (21)

• Case 3:

  $$\begin{aligned} \begin{aligned} Type {^{2c}\quad \ } \\ sharing-gadget \end{aligned} \left\{ \begin{aligned}&\langle x_1 \xrightarrow {P} w,\ \ \, w \xrightarrow {P} \boxed {\ddot{x}_\oplus },\ \ \ \, \varvec{\ddot{x} \xrightarrow {P} y_1} \rangle \qquad (path^+_1) \\&\langle x_2 \xrightarrow {P} \widetilde{w},\ \ \varvec{\widetilde{w} \xrightarrow {P} \boxed {\ddot{y}}}, \ (\ddot{y})_\oplus \xrightarrow {P}\ y_2 \rangle \qquad (path^+_2) \\&\langle \varvec{\ddot{x}\, \xrightarrow {P} \underline{y_1}},\ y_1 \xrightarrow {P} \underline{\widetilde{w}_\oplus },\ \ \ \ \, \varvec{\widetilde{w} \xrightarrow {P}\ \, \ddot{y} } \rangle \qquad (path^-) \end{aligned} \right. \end{aligned}$$

  (22)

At this point, we have known how to construct a shared-edge for a $path^+$ by assigning its $2^{nd}$-inner-node. Naturally, we can establish h such shared-edges if h $paths^+$ are considered. It is easy to verify that the following Method 2 actually establishes h shared-edges for the involved $paths^+$ and $paths^-$.

Similarly, the number of $paths^-$ is determined by the $2^{nd}$-inner-nodes of the h $paths^+$, and is not necessarily equal to h. In a sense, the h $paths^+$ with their $2^{nd}$-inner-nodes determine almost “everything” about the involved $paths^+$ and $paths^-$.

Combing the Method 1 and Method 2, we propose the assigning strategy for constructing a Core with $3q-k-h$ edges. As shown in Fig. 5, Step 1 (resp. Step 2) establishes k (resp. h) shared-edges, and Step 3 produces no shared-edge. In brief, we fix k $paths^+$ and their $1^{st}$-inner-nodes firstly, then other h $paths^+$ and their $2^{nd}$-inner-nodes. At last, we assign all the undefined inner-nodes with proper exclusive-elements.

Fig. 5.

Assigning strategy for constructing a $\mathsf {Core}(\varphi _2[\cdot ] \vdash \mathcal {Q}_E)$ with $3q-k-h$ edges

Intrinsically, the assigning strategy consists of several samplings such as the $paths^+$, $paths^-$, and so on. To lower-bound the number of Cores constructed by Fig. 5, we should know how many elements can be chosen for each sampling. For convenience, we introduce the notation RoC to denote the range of candidates for a sampling.

Notation 5

(Range of Candidates). Let A denote a finite set to be sampled, then we write RoC(A) as a set of elements which can be chosen into A.

That is, we should determine the size of each RoC to count the number of possible assignments. The analysis is rather cumbersome, and we defer it to the formal proof. Here, we can just assume that the lower bound of the number of Cores with $3q-k-h$ edges is given as follows.

$$\begin{aligned} \# \mathsf {Cores}_{3q-k-h} \ge LB(k,h), \end{aligned}$$

(23)

where $\# \mathsf {Cores}_{3q-k-h}$ denotes the number of Cores with $3q-k-h$ edges, and LB(k, h) is a function of k and h.

At this point, we are ready to calculate a lower bound of (15). Since $|S|=|T|=N-p$, and from the Eq. (14) and (23), we finally obtain that

where $MHyp_{N,a,b,c}$ is a multivariate hypergeometric distribution random variable. It can be seen that a tail inequality (i.e., Lemma 5) and a combinatorial inequality (i.e., Lemma 6) will be used during the calculation.

Lemma 5

(Chebyshev’s Inequality). Let $X\sim Hyp_{N,a,b}$ be a hypergeometric distribution random variable, that is, $\mathrm {Pr}[X=k]=\frac{{b\atopwithdelims ()k}{N-b\atopwithdelims ()a-k}}{{N\atopwithdelims ()a}}=\frac{(a)_k(b)_k(N-b)_{a-k}}{k!(N)_a}$. Then we have

$$\begin{aligned} \mathrm {Pr}[X>\lambda ]\le \frac{ab(N-a)(N-b)}{(\lambda N-ab)^2 \, (N-1)}. \end{aligned}$$

(24)

Lemma 6

Let N, a, b, c, d be positive integers such that $c\,+\,d=2b$ and $2a\,+\,2b\le N$. Then

$$\begin{aligned} \frac{(N)_a\, (N-2b)_a}{(N-c)_a\, (N-d)_a} \times \frac{(N-\frac{b}{2})_a}{(N-b)_a}\ge 1-\frac{8ab^3}{N^3}. \end{aligned}$$

(25)

6 Conclusion and Discussion

The practical block-ciphers often iterate the same round function and use a key-schedule algorithm to produce round-keys, while there are a few theoretical results supporting such designing philosophy. Particularly, only a little provable-security work considers the dependence between components, since it always becomes very complicated.

In this paper, we study a family of KAC construction with dependence, and finally prove that 3KACSP construction has the same security level as the classic 3KAC construction. It means that the randomness of one random permutation and a random 4n-bit string is enough to make the 3KAC construction achieve the ideal security. To our knowledge, it is the first time to obtain a tight bound about an incompletely-independent KAC construction with more than 2 rounds.

Besides the tight security analysis of 3KACSP, our most valuable contributions are the insights into the general rKACSP. Before our work, there is no proof method handling the knotty dependence in a high level. Compared to Chen et al.’s techniques, ours are more general and highly modular so that they can be easily generalized. More concretely, we abstract a type of combinatorial problems capturing the intrinsic randomness of rKACSP construction. To solve such problems, we also propose a general counting framework and successfully apply it to the cases with 2 and 3 missing-edges. Following the proof ideas in this work, we give some intuition on the analysis of rKACSP.

Intuitively, when handling a “good” transcript, the paths between $\mathcal {Q}_E$ can be classified into r groups according to the number of fixed edges. Similar to 3KACSP, we denote the Group-i as the group of paths whose i edges are fixed by $\mathcal {Q}_P$, where $0 \le i \le r-1$. The subproblem of completing the paths in Group-i can be instantiated by Problem 1 with $r - i$ missing-edges. Inspired by the analysis of 3KACSP, the tricks used in $(r-i)$KACSP can be tailored to solve the corresponding subproblems related to Group-i, where $1 \le i \le r-2$. By induction, what’s left is only to solve a single r-round instance of Problem 1. Our counting framework, as well as the notions of shared-edges and assigning strategy can still work, but the circumstances of analysis would be very complicated.

To our conjecture, rKACSP construction is also $\varTheta (2^{\frac{r}{r+1}n})$-secure in the random permutation model, which is a well-known result for classic rKAC construction.

Conjecture 1

Consider the rKACSP construction (see Eq. (1)), if P is a random permutation, as well as the round keys $\pmb {K} = (k_0, \dots , k_r)$ are random and independent from each other, then rKACSP is $\varTheta \left( 2^{\frac{r}{r+1}n}\right)$-secure in the random permutation model.

In fact, the bottleneck of pushing our work to higher-round case is simply the computational power. Following our ideas, the technical roadmap for analyzing rKACSP is rather clear, and one can solve it given sufficient energy. Honestly, we consider that the complexity of proof specifics will increase very fast (maybe exponentially) so that the proof may not be explicitly written out, but we strongly believe that Conjecture 1 is intrinsically correct. If the conjecture is true, then it is exactly a powerful support for the aforementioned broadly-used designing philosophy. Moreover, the proof complexity may just reveal the reason why there often exist gaps between the practical and theoretical results.

Currently, our results only apply when the round keys are random and independent from each other. Thus, it is unknown that whether we can reduce the randomness of round keys without a significant loss of security. Another challenging open problem is of course to generalize our results to larger number of rounds. In addition, the new representation and counting framework are rather generic, therefore we hope that they can be used in more scenarios.