Abstract
Reducing the rounds of interaction in secure multiparty computation (MPC) protocols has been the topic of study of many works. One popular approach to reduce rounds is to construct round compression compilers. A round compression compiler is one that takes a highly interactive protocol and transforms it into a protocol with far fewer rounds. The design of round compression compilers has traditionally focused on preserving the security properties of the underlying protocol and in particular, not much attention has been given towards preserving their computational and communication efficiency. Indeed, the recent round compression compilers that yield round-optimal MPC protocols incur large computational and communication overhead.
In this work, we initiate the study of efficiency-preserving round compression compilers, i.e. compilers that translate the efficiency benefits of the underlying highly interactive protocols to the fewer round setting. Focusing on the honest majority setting (with near-optimal corruption threshold \(\frac{1}{2} - \varepsilon \), for any \(\varepsilon > 0\)), we devise a new compiler that yields two round (i.e., round optimal) semi-honest MPC with similar communication efficiency as the underlying (arbitrary round) protocol. By applying our compiler on the most efficient known MPC protocols, we obtain a two-round semi-honest protocol based on one-way functions, with total communication (and per-party computation) cost \(\widetilde{O}(s+n^4)\) – a significant improvement over prior two-round protocols with cost \(\widetilde{O}(n^\tau s+n^{\tau +1}d)\), where \(\tau \ge 2\), s is the size of the circuit computing the function and d the corresponding depth. Our result can also be extended to handle malicious adversaries, either using stronger assumptions in the public key infrastructure (PKI) model, or in the plain model using an extra round.
An artifact of our approach is that the resultant protocol is “unbalanced” in the amount of computation performed by different parties. We give evidence that this is necessary in our setting. Our impossibility result makes novel use of the “MPC-in-the-head" paradigm which has typically been used to demonstrate feasibility results.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Understanding the minimal rounds of interaction required to carry out a cryptographic task has been the subject of extensive study over the past few decades. While ad-hoc techniques are often used to obtain low round complexity solutions, a more systematic approach adopted in the literature is to build a round compression compiler. As the name suggests, a round compression compiler transforms a highly interactive protocol into one with far fewer rounds. The celebrated compiler of Fiat and Shamir [22] is one such example that transforms a public-coin interactive proof system into a non-interactive one (in the random oracle model).
Recently, a sequence of works have designed round compression compilers to resolve major open problems in cryptography. For instance, the recent result on non-interactive zero knowledge proofs for NP from learning with errors was designed by instantiating the Fiat-Shamir methodology [11, 38]. In the context of secure multiparty computation (MPC) [6, 12, 29, 40] – the focus of this work – a recent sequence of exciting works devised novel round compression compilers to construct round-optimal MPC protocols based on minimal assumptions [1,2,3,4, 7, 24, 25].
Rounds vs Computation in MPC. In this work, we continue the study of round compression in MPC. Starting from [5], round compression in MPC has been extensively studied over the years in a variety of models. Traditionally, most works have focused on devising compilers that preserve the security properties of the underlying protocol. However, not much emphasis has been placed on preserving the computational and communication efficiency.
Indeed, the recent round compression compilers that yield round-optimal MPC [1,2,3,4, 7, 24, 25] incur a large overhead in computation and communication. Some of these compilers work in the setting where a majority of parties are allowed to be dishonest, while others require a majority of the parties to be honest. In this work, we focus on the latter setting, referred to as honest majority. In this setting, consider an arbitrary round MPC protocol with total computational work \(W=W(n,s)\), where n denotes the number of parties executing the protocol and s denotes the size of the circuit implementing the function being computed. Then, applying the compilers of [1,2,3,4, 24] on such a protocol yields a two round protocol with total communication and per-party computation \(\widetilde{O}(n^\tau \cdot W)\), where \(\tau \ge 2\), ignoring multiplicative factors in security parameter. Plugging in the most efficient known multi-round MPC protocols [15, 16, 26] with total cost \(\widetilde{O}(s+ nd)\) (where d is the circuit depth), we obtain a two round protocol with significantly worse total communication (and per-party computation) \(\widetilde{O}(n^\tau s+n^{\tau +1}d)\).
The above state of affairs raises the question: does round compression necessarily require high computational and communication cost? If not, can we design efficiency-preserving round compression compilers for MPC that preserve both the security as well as the computational and communication efficiency of the underlying protocol?
1.1 Our Results
We study efficiency-preserving round compression compilers for MPC. As a first step in this direction, we narrow our focus on the honest majority setting.
Our main result stated below holds with respect to semi-honest adversaries. Later, we also discuss extensions to the case of malicious adversaries.
Theorem 1 (Informal)
Let n be the number of parties and let \(\lambda \) be the security parameter, such that n is polynomially related to \(\lambda \). Assuming one-way functions, there is a round compression compiler that transforms a semi-honest secure MPC protocol \(\varPi \) for any n-party functionality \(\mathcal {F}\) into a two-round semi-honest secure protocol \(\varPi '\) for \(\mathcal {F}\) with the following properties:
-
If \(\varPi \) tolerates corruption threshold \(\varepsilon \), then \(\varPi '\) tolerates \(\varepsilon '\), for arbitrary constants \(\varepsilon '< \varepsilon < \frac{1}{2}\).
-
If the total computation cost of \(\varPi \) is \(W=W(n,s)\), where s is the circuit size representation of \(\mathcal {F}\), then the amortized per-party computation cost and total communication cost of \(\varPi '\) is
$$ \tilde{O}\left( (W(\log ^2(n),s)+n^4)\right) , $$where the \(\widetilde{O}\) notation suppresses polynomial factors in \(\lambda \) and polylog factors in n.
To handle smaller values of n, we can use a hybrid mode of compilation: if n is small, simply use existing compilers; for larger values of n, one should use our compiler.
Comparison with Prior Work. Our compiler performs significantly better than previous compilers [1, 3, 4] that yield two-round protocols with total communication and per-party computation cost of \(\tilde{O}(n^\tau W(n,s))\), where \(\tau \ge 2\). All of these existing two round compilers [1, 3, 4] rely on the following high level ideaFootnote 1- they view the entire computation done in the underlying protocol as a circuit and then require all the parties to communicate at least one-bit for each gate in this circuit, with every other party over pair-wise private channels in the first round. This adds a multiplicative overhead of at least \(n^2\) in the complexity of the resulting protocol. Infact, the exact overhead in these compilers might even be more than \(n^2\), because these are not the only messages that the parties compute and send in those compilers. However, for comparison, it suffices for us to use a conservative approximation, i.e., \(\tau \ge 2\).
On the other hand, by applying our compiler on the most asymptotically efficient MPC protocols [15, 16, 26] with total computation cost \(W(n,s)=\widetilde{O}(s+nd)\), we obtain a two-round protocol with total communication and per-party computation cost \(\tilde{O}(s+n^4)\). In contrast, applying previous compilers on the same protocols yields two-round protocols with total communication and per-party computation cost \(\tilde{O}(n^\tau \cdot s+n^{\tau +1}d)\), where \(\tau >2\).
Extensions. With suitable modifications to the above compiler, we can obtain additional results that achieve different tradeoffs, both in the case of semi-honest and malicious adversaries.
-
Semi-honest: The above compiler can be easily modified such that the total (as opposed to amortized per-party) computation cost is \(\widetilde{O}(W(\log ^2(n),s) + n^4)\), at the cost of increasing a round of interaction.Footnote 2
-
Malicious: The above compiler can also be easily modified to work against malicious adversaries, yielding either two round protocols in the PKI model assuming verifiable random functions [37], or three round protocols in the plain model without additional assumptions. Both these protocols achieve the standard notion of security with abort, assuming that the underlying protocol also achieves the same security.
Impossibility of Balanced Protocols. Our compiler utilizes a committee-based approach which has been used in many prior works in the larger round setting. A caveat of this approach is that it results in unbalanced protocols where a small subset of parties (namely, the committee members) perform much of the “heavy” computation, while other parties only do “light” computation. Furthermore, this approach also yields a sub-optimal corruption threshold (i.e., \(n>2t+1\), where t is the number of corrupted parties). In view of this, we investigate whether this is inherent.
We give evidence that our approach is “tight” by showing that there exists some functionality for which there does not exist a balanced constant round (even insecure) MPC protocol with total computational cost \(\widetilde{O}(s)\). In contrast, our compiler yields an unbalanced constant-round secure MPC protocol with roughly the same total cost (ignoring additive terms).
1.2 Our Techniques
In this section we describe the main ideas underlying our results. In Sect. 1.2.1 we give an overview of our techniques for designing efficiency-preserving round-compression compilers. Later, in Sect. 1.2.2, we describe ideas for proving impossibility of balanced constant-round MPC protocols with total computation cost \(\tilde{O}(s)\). Throughout this section we assume \(\tau \ge 2\), and is hereby omitted for clarity of exposition.
1.2.1 Efficiency-Preservation via Committees
We now proceed to describe the techniques used in our compiler. At a high-level, we devise a two step approach:
-
Step 1: Special Two Round MPC. First, given a potentially highly interactive MPC protocol with total computational work \(W=W(n,s)\), where s is the size of the circuit and n is the number of parties, we apply a round-compression compiler to obtain a special two round protocol with some specific structural properties. The total computational complexity of this special MPC is proportional to \(\tilde{O}(n^\tau \cdot W)\).Footnote 3 Even though it does not achieve our desired efficiency, its structural properties are crucially used in the second step.
-
Step 2: Efficiency Boost. We then leverage the structural properties of the special two round MPC to transform it into a new protocol with the same round complexity, but improved asymptotic computational and communication complexity.
We postpone the discussion on the structural properties required from the two round protocol. Instead, we first focus on Step 2; the efficiency boosting transformation would then guide us towards identifying these structural properties.
Starting Ideas for Efficiency Boost. We first focus on the semi-honest setting, and defer the malicious case to later. Given a special two-round MPC, our starting idea for improving its efficiency is to use the classical committee-based approach, where the bulk of the computation is “delegated” to a small committee of parties, while the remaining parties do very little work.
More specifically, the main idea in a committee-based approach is to first elect a “small” committee, while ensuring that a majority of the parties in the committee are honest and letting these elected parties run the actual protocol. Since the parties not elected to the committee are no longer doing any work, we need a mechanism to allow these parties to transfer their inputs to the committee members. To ensure privacy of their inputs, the parties who are not elected in the committee, secret-share their inputs amongst the committee members. The elected committee then runs an MPC computing a modified functionality \(\mathcal {F}'\), that collects all the secret shares of all the non-elected parties, reconstructs their inputs, and computed the original function \(\mathcal {F}\). Unlike the original function \(\mathcal {F}\), \(\mathcal {F}'\) requires inputs from only the elected committee members, which as described above, also implicitly contains the remaining parties’ inputs. Since the cost of the computation is dominated by the number of parties involved in the “heavy” computation, it suffices to use a committee of size poly-logarithmic in the total number of parties to yield non-trivial savings in the total cost.
In order to prevent an adversary from corrupting a majority of the members in the committee, it is important to choose the committee at random. This means that the identities of the committee members are unknown to all parties at the start of the protocol; instead, we must implement a committee election mechanism during the protocol execution. Let \(\varPi \) be the two-round protocol obtained by applying the round-compression compiler in the first step. Now, applying the committee-based approach over \(\varPi \), we get the following five round protocol \(\varPi '\):
-
1.
Round 1. Each party tosses an appropriately biased coin to decide whether or not it will be in the committee and reveals the result to all other parties.
-
2.
Round 2. The parties that are not part of the committee secret share their inputs amongst the committee members.
-
3.
Round 3. The committee members compute and send their first round messages in \(\pi \).
-
4.
Round 4. The committee members compute and send their second round messages in \(\pi \).
-
5.
Round 5. The committee members reconstruct the output and then send the output to all other parties.
Since the bulk of the computation is performed by the committee members, the amortized per-party computation in \(\varPi '\) depends only on \(\mathsf {polylog}(n)\) as opposed to  . The main problem however, is that \(\varPi '\) requires five rounds, while we seek a two round protocol.
. The main problem however, is that \(\varPi '\) requires five rounds, while we seek a two round protocol.
Committee-Based Approach in Two-Rounds. Towards obtaining a two round protocol, we start with the observation that if protocol \(\varPi \) allows for public reconstruction of output based on the transcript of the last round, then Rounds 4 and 5 of \(\varPi '\) can be parallelized. Indeed, this property is satisfied by the protocol output by our compiler in Step 1Footnote 4 and is also true for other recent round-compression compilers [2, 7, 25]. While this yields a saving of one round, it is not clear how to proceed further. Indeed, to obtain a two-round protocol, the task of electing a committee and sharing of inputs by the remaining parties must be parallelized with the computation done by the committee members using \(\varPi \). In other words, Rounds 1, 2 and 3 must seemingly be executed in the first round of \(\varPi '\), and Round 4 in the second round. This, however, raises some fundamental challenges:
-
1.
Challenge 1: Sharing of Inputs. If the committee election happens in parallel with input sharing, the non-committee members (henceforth referred to as the clients) would not know the identities of the committee members (henceforth referred to as the servers) at the time of distributing their inputs. How can the clients secret share their inputs with the servers, without knowing their identities? It seems like there is no way to get around this, which means that the servers must start their computation without knowing their “entire input”. But parallelizing committee election and input sharing is crucial both for the correctness and security. Indeed, in any two round MPC protocol, the private inputs of all parties must be “fixed” in the first round to prevent input resetting attacks [32].
-
2.
Challenge 2: Blind Computation. All known two-round honest majority MPC protocols based on minimal assumptions [1,2,3,4, 24] necessarily rely on the use of private channels in the first round. Since the committee election and computation must happen simultaneously, it is not clear how the servers would exchange private channel messages in the first round without knowing each other’s identities. It seems like we require the servers to start their computation “in the blind”.
To address these two challenges, we require some structural properties from \(\varPi \). We now describe them.
Special Two Round MPC. We require the following two structural properties from the special two round MPC in Step 1:
-
1.
Decomposability: The first round messages of each party in a special two round MPC protocol can be decomposed into: (i) “light” messages that depend on the input but whose computational complexity is independent of \(W\), and (ii) “heavy” messages that are independent of the input but whose computational complexity may depend on \(W\). The light and heavy messages may share common randomness.
-
2.
Independence: The private channel messages in a special two round MPC protocol should be independent of the inputs of the parties.
At a first glance, these properties may seem quite unconventional and strong. Indeed, our main technical contribution is in identifying these rather unconventional and specific structural properties of two-round protocols and then leveraging these properties for efficiency gains in the setting of two rounds. In particular, as we describe below, the decomposability property, with additional delegation of computation techniques, is used to address Challenge 1 and the independence property is used to address Challenge 2. Moreover, as we discuss later, these properties can, in fact, be achieved generically.
Solving Challenge 1. Towards explaining our main ideas, let us first consider a simpler scenario where \(\varPi \) only consists of broadcast channel messages (we deal with private channel messages later while addressing challenge 2). As noted earlier, the main issue in parallelizing input distribution and committee election is that the servers cannot know their entire input in the first round, yet the first round messages of the protocol must fix the inputs of all the parties. Moreover, the second round messages of all parties can also depend on the entire first round transcript (which in turn must depend on the inputs).
To address these problems, a natural starting idea is to require the clients to aid the servers in the computation of the first and second round messages of \(\varPi \) while still achieving the desired efficiency. Let us first focus on the second round messages of \(\varPi \); specifically, that of a particular server (say) \(S_i\). Our first idea is to run a separate helper protocol involving all parties (servers and clients) to help compute the second round messages of \(S_i\). This helper protocol can take the input shares from all clients and the randomness from all servers to first internally compute the first round messages of all servers and then compute and output the second round message of \(S_i\). A naive implementation of this approach, however, runs into an obvious problem: since the per-party complexity for computing second round messages of the servers in \(\varPi \) is \(\tilde{O}(n^\tau \cdot W)\), the size of the functionality implemented by the helper protocol, and thereby the per-party computation performed by the clients, also has the same total complexity of \(\tilde{O}(n^\tau \cdot W)\).
Towards addressing this problem, we first use a delegation of computation approach implemented via garbled circuits and a modified two-round helper protocol as follows:
-
We require the server \(S_i\) to garble and send its second round next-message function of \(\varPi \) in the second round of \(\varPi '\). This circuit takes as input the entire first round transcript of \(\varPi \) and computes, and outputs, \(S_i\)’s second round messages in \(\varPi \).
-
The input wire labels for this garbled circuit are computed via a modified two-round helper protocol for a specific functionality. This functionality takes as input, secret-shares from the clients and randomness used to compute the first round messages from the servers. It also takes as input all of the garbled circuit input wire labels from \(S_i\). It internally computes the first round message of all servers and then selects and outputs the corresponding input wire labels.
Thus far we have ignored the first round messages and an observant reader may notice that this solution still does not suffice; indeed, since the size of the first round messages in \(\varPi \) is also proportional to \(\tilde{O}(n^\tau \cdot W)\), the clients still need to spend the same computational effort.
Our main conceptual idea to overcome this problem is to leverage the decomposability property of special MPC. Recall that the decomposability property requires that in the first round, each party sends computationally light messages depend on its input and computationally heavy messages that are independent of its input. We leverage this property as follows: we require the servers to compute (on their own) and send the heavy messages in the first round, which can then be hardwired in the circuit that \(S_i\) garbles in the second round. The helper protocol involving all parties is now only required to compute the input wire labels corresponding to the light messages, as opposed to the entire first round messages, which is efficient. Moreover, this also ensures that the inputs of all parties are indeed fixed in the first round, which is necessary for security.
Finally, we remark that if the light messages in \(\varPi \) can be computed using a degree-1 computation over the parties’ inputs, then we can use lightweight protocols such as [36] (satisfying security with abort) for quadratic functionalities to further reduce the work done by clients. We later show that our compiler from Step 1 achieves this property as well.
Solving Challenge 2. While so far we have only considered the simplified setting of broadcast-only protocols, in reality, our protocol \(\varPi \) from the first step (necessarily) consists of both the broadcast and P2P messages. As described earlier, this creates the challenge that the servers cannot send P2P messages to each other in the first round without knowing their identities. Since the computation must start in the first round itself, we need a mechanism for “computing in the blind”.
We implement such a mechanism by allowing the servers to encrypt their private channel messages and broadcasting them in the first round and then enabling others to somehow compute on these encrypted messages. To help compute on the encrypted messages, we again utilize a delegation of computation approach:
-
Each server garbles a circuit that takes the decryption key as input and decrypts the corresponding first round encrypted message that was intended for it and computes its second round message.
-
Wire labels corresponding to the decryption key are computed via a helper protocol involving all properties, similar to the solution to the previous challenge. Since the helper protocol is only responsible for computing labels corresponding to the decryption keys, the total work done by the parties (especially clients) in this helper protocol does not depend upon the complexity of the next-message functions of the parties in \(\varPi \).
An observant reader, however, may notice that this approach fails completely, if the P2P messages in \(\varPi \) were dependent on the input. Indeed, since the servers do not have access to their entire input in the first round, it is unclear how they would compute and encrypt these messages in such a case.
Our next conceptual idea to overcome this problem is to leverage the independence property of special MPC. Recall that this property requires all of the private channel messages in \(\varPi \) to be independent of the inputs. Given this property, the above solution already works.
Realizing Special Two Round MPC. Recall that a special two-round MPC must satisfy the following requirements:
-
1.
Structural Properties: It must satisfy the decomposability and independence properties defined earlier.
-
2.
Complexity: The total communication complexity of the special MPC must be \(\tilde{O}(n^\tau \cdot W)\). (As discussed earlier, the key requirement here is the linear dependence on W, whereas the exact multiplicative dependence on n is less important since this special MPC is only executed by \(\mathsf {polylog}(n)\)-sized) committee of parties.)
We address each of these requirements separately. There is a surprisingly simple approach for achieving the structural properties generically. Specifically, we show that any two-round protocol \(\pi \) with the delayed-function propertyFootnote 5 can be made to achieve these structural properties without affecting its asymptotic efficiency. The idea is to have each party \(P_i\) sample a random mask \(r_i\) for its input \(x_i\), and broadcast \(x_i\oplus r_i\) in the first round. Additionally, the parties run \(\pi \) on a modified functionality \(f'_{x_1\oplus r_i,\ldots ,x_n\oplus r_n}\) that has \(x_1\oplus r_i,\ldots ,x_n\oplus r_n\) hardwired in its description, such that
where f is the original functionality. It is easy to see that because of this simple modification, the first round messages of party \(P_i\) in the modified protocol \(\varPi \) can now be decomposed into a “light” message \(x_i\oplus r_i\) that depends on its input and “heavy” messages which correspond to its first round messages in \(\pi \). Moreover, because of the delayed-function property of \(\pi \), these “heavy” first round messages in \(\varPi \) are independent of their actual inputs. This already achieves decomposability. With regards to independence property, we first note that the above transformation already ensures that the first round private channel messages in \(\varPi \) are independent of the parties’ inputs. However, their second round private channel messages may still depend on their inputs. Towards this, we observe that any two-round protocol that makes use of private channel messages in the second round can be modified into one that only uses broadcast channel messages in the second round. This can be done by letting the parties exchange one-time pads with each other in the first round, and then broadcasting their second round messages encrypted under these one-time pads. With this modification, we can also achieve independence.
Since the above approach works generically with any protocol that satisfies the delayed-function property, it can also be applied to a delayed-function variant of [1, 3, 4]. We note that while [1] already satisfies the delayed function property, the two-round compilers of [3, 4] do not. A simple modification to this construction can yield two-round protocols with delayed-function property without compromising its efficiency. We refer the reader to the full version for details on this modification.
Moreover, when applied to an interactive protocol with total computation W, the compilers of [1, 3, 4] already yield two-round protocols with total communication at least \(\tilde{O}(n^\tau \cdot W)\). Hence, in summary, either of the recent two-round protocols [1, 3, 4] in the honest majority setting, with the above modifications, can be used to obtain a two-round special MPC with all of the required properties.
Summary (so far). Putting the above solutions together, we now obtain a two-round semi-honest protocol that achieves total communication complexity \(\tilde{O}(W(\mathsf {polylog}(n),s)+n^4)\)Footnote 6 and total computation complexity \(\tilde{O}(nW(\mathsf {polylog}(n),s)+n^5)\) if we elect a committee of size \(\mathsf {polylog}(n)\). The computation complexity is higher than the communication complexity. This is because in order to reconstruct the output, all the parties must locally compute on all the second round messages of all parties, which adds a multiplicative overhead of n to the computation complexity. We note that we are limited to this computation complexity in two rounds, since we do not know of any two round compilers with better and more efficient output reconstruction algorithms. However, if we add another round such that only one of the parties the output at the second round and broadcasts it to others in the third round, we can get optimal computational efficiency.Footnote 7
Handling Malicious Adversaries. The above approach only works against semi-honest adversaries. For the malicious setting, we need to start with a malicious special two round MPC protocol. We are now faced with the following additional issues in the malicious setting:
-
1.
Input Consistency. Recall that in the semi-honest protocol proposed above, the servers are required to use the same randomness as input in multiple sub-protocols: (1) for computing its “heavy” first round messages in \(\varPi \) and (2) in the helper protocol for computing its “light” first round messages. Since the light messages depend on the inputs of clients, if a malicious server does not use the input randomness consistently in the two sub-protocols, it could potentially change the input share of an honest client.
-
2.
Malicious Secure Committee Election. Our naive way of doing a committee election where the parties can randomly elect themselves to be in the committee, clearly does not work in the malicious setting. A corrupt party can always elect it self to be in the committee.
Towards describing our solution to the first problem, let us first address why simply compiling a maliciously secure protocol \(\varPi \) with the compiler described above is not sufficient. Recall that in general, a maliciously secure protocol cannot prevent adversarial parties from choosing their inputs arbitrarily. However, in the above compiler, since the underlying (maliciously secure) protocol \(\varPi \) is only run amongst the committee members and their inputs also contain input shares of the honest clients, we cannot afford to let them choose their entire input arbitrarily.
To prevent this, we make use of one-time message authentication codes (  s). The honest clients compute a
s). The honest clients compute a  over each of their input shares. For the
over each of their input shares. For the  ’s to be verified, they must be checked, and hence require the key. However, providing a (potentially corrupt) server with the MAC key defeats the purpose, since there is no longer any security. Therefore, for each input share, we shall create
’s to be verified, they must be checked, and hence require the key. However, providing a (potentially corrupt) server with the MAC key defeats the purpose, since there is no longer any security. Therefore, for each input share, we shall create  s with each of the server keys, i.e., one corresponding to each server. These keys are sent to the respective servers, while the input share and all the corresponding
s with each of the server keys, i.e., one corresponding to each server. These keys are sent to the respective servers, while the input share and all the corresponding  tags are sent only to the designated server. The functionality computed by the protocol \(\varPi \) is modified to first check if for each input share that it gets as input, all its corresponding
tags are sent only to the designated server. The functionality computed by the protocol \(\varPi \) is modified to first check if for each input share that it gets as input, all its corresponding  s are valid. As long as there is an honest party, for which the adversary does not have access to the key, it cannot create a mauled tag that will verify with that key. We use the helper protocols exactly as described earlier with the only exception that now instead of just their input shares, the clients also communicate these
s are valid. As long as there is an honest party, for which the adversary does not have access to the key, it cannot create a mauled tag that will verify with that key. We use the helper protocols exactly as described earlier with the only exception that now instead of just their input shares, the clients also communicate these  s and
s and  keys to the servers via the helper protocol.
keys to the servers via the helper protocol.
To implement a maliciously secure committee election protocol, we use the following standard techniques:
-
Using VRFs: We use the strategy from Algorand [27] based on verifiable random functions (VRFs) [37]. This is implemented in the reusableFootnote 8 correlated randomness model where the adversarial corruption may happen after the setup. We note that since VRFs are known from non-interactive witness indistinguishability proofs (NIWIs)[8, 30], we get a resulting maliciously secure two-round protocol in the correlated randomness model based on NIWI, whose communication complexity is \(\tilde{O}(W(\mathsf {polylog}(n),s)+n^{\tau +4})\) and total computation complexity is \(\tilde{O}(nW(\mathsf {polylog}(n),s)+n^{\tau +5})\).Footnote 9
-
Feige’s Lightest Bin Protocol [21]: This gives a statistically secure committee election protocol. However each party learns whether or not it is in the committee only at the end of this protocol, so it adds another round at the start of the two-round protocol. As a result we get a three-round maliciously secure protocol in the plain model, whose communication complexity is \(\tilde{O}(W(\mathsf {polylog}(n),s)+n^{\tau +4})\) and total computation complexity is \(\tilde{O}(nW(\mathsf {polylog}(n),s)+n^{\tau +5})\).
Comparison with Existing Maliciously Secure Compilers: By applying our compiler on the most asymptotically efficient MPC protocols [15, 16, 26] with total computation cost \(W(n,s)=\widetilde{O}(s+nd)\), we obtain a two-round protocol with total communication and per-party computation cost \(\tilde{O}(s+n^{\tau +4})\). In contrast, applying previous maliciously secure compilers on the same protocols yields two-round protocols with total communication and per-party computation cost \(\tilde{O}(n^\tau \cdot s+n^{\tau +1}d+n^{\tau +2})\), where \(\tau >2\).
1.2.2 Impossibility of Balanced Protocols
While our approach gives an efficiency preserving compiler in 3 rounds, a drawback of our compiler is that it yields unbalanced protocols with sub-optimal corruption threshold of \(t<n/2\). This is a consequence of our committee-based approach. Next, we provide some evidence towards the fact that a committee-based approach is necessary. In particular, we show that it is impossible to obtain a constant round MPC protocol with equal division of labor, where the total work done by parties is \(\tilde{O}(|C|)\), where |C| is the size of the circuit implementing the functionality. We show this impossibility using the player emulation methodology [13, 33, 35]. To the best of our knowledge, this is the first time that this paradigm is used for proving a negative result.
Let us assume that there exists an \(r-\)round MPC protocol \(\varPi \), where the total work done by each party is approximately \(\tilde{O}(|C|)/n\), where r is some constant. In other words, the size (and depth) of the circuit implementing the next-message function of each party is \(\tilde{O}(|C|)/n\). In every round, we can recursively use protocol \(\varPi \) to implement the next-message function of each party. The total number of rounds in the resulting protocol is \(r^2\), while the total work done by each party in each round is still \(\tilde{O}(|C|)/n\), it can now be computed using n-parallel circuits each of depth \(\tilde{O}(|C|)/n^2\).
If we repeat this approach of recursively replacing the next-message function of each party in each round with an execution of \(\varPi \) for k iterations, we get a protocol with \(r^k\) rounds where in each round, the next message function of each party can be computed using a circuit of depth \(\tilde{O}(|C|)/n^k\). Let k, c be constants such that \(\tilde{O}(|C|)/n^k=c\). In each round the total computation done by the parties can be viewed as an execution of n-parallel circuits, each of depth at most c. Overall, the total work done by the parties in the final protocol, can be viewed as an execution of \(n-\)parallel circuits, each of depth at most \(c\cdot r^k=O(1)\).
This approach can be used to reduce any arbitrary-depth circuit C into a constant-depth circuit, which is a contradiction since we know that functions like parity are not computable in constant depth.
1.3 Related Work
The study of multiparty computation was initiated in the seminal works of [6, 12, 29, 40]. Beaver et al. [5] initiated the study of constant round protocols in the honest majority setting. Subsequently, there has been extensive work in the study of constant round protocols, resulting in round optimal protocols both in the honest majority and dishonest majority settings [1,2,3,4, 7, 23,24,25].
Further, the design of efficient protocols have been studied in both the computational and information theoretic settings [9, 14,15,16,17,18, 20, 34, 39, 41]. Some of these results [15, 16] achieve optimal computational and communication complexity of \(\tilde{O}(s)\). Similar to us, their results also have an additive factors which are polynomial in both the security parameter and number of parties.
Committee based techniques have been used primarily in the context of scalable computation, where the goal is to build secure computation protocols that scale well with a large number of parties. Of these, the works of [9, 10, 19, 39, 41] seek to reduce computational and communication complexity work in the large round setting. See [39] and the references therein for for a detailed survey of the use of committee based techniques in the context of scalable computation. To the best of our knowledge no prior works apply committee based approaches in the two round setting. This is perhaps unsurprising given the recency of the two round protocols based on standard assumptions.
1.4 Full Version
Due to space constraints, preliminaries, details of the proofs, and complexity calculations have been omitted from this manuscript, and can be found in the full version of the paper.
2 Two-Round Efficiency Preserving Compiler in the Client-Server Model
In order to describe our compiler in a manner that easily extends to the malicious setting, we will present our solution in two steps, spread across Sects. 2 and 3. In this section, we construct a maliciously secure efficiency preserving, round compression compiler in the Client-Server model.
Recall that in the client-server model, every party is designated to be either a client or a server, and is additionally aware of the roles of all the other parties. The clients share their inputs among all the servers (servers may additionally have inputs), who in turn do the computation and broadcast the result. Later in Sect. 3, we will show how this protocol in the client-server model can be extended to obtain an efficiency preserving compiler in the plain model, namely, where the parties do not have any pre-designated roles assigned to them.
The rest of this section is organized as follows. First, we present a two-round special MPC with some specific structural properties in Sect. 2.1. Then in Sect. 2.2, we make use of the properties of this protocol to present a two-round, maliciously secure, efficiency preserving compiler in the client server model.
2.1 Special Two-Round MPC
As discussed in the technical overview, given an interactive protocol with total computation work W, as a starting step, we need to transform it into a two-round special MPC protocol that satisfies the following properties:
-
1.
Decomposability: The first round messages of each party in \(\varPi \) can be decomposed into “light” messages that depend on the input but not \(W\), and “heavy” messages that depend on \(W\) but not on the input; however they may share common randomness.
-
2.
Independence: The private channel messages in \(\varPi \) are independent of the inputs.
-
3.
Complexity: The total computation complexity of the resulting protocol should only be linearly dependent on W.
We state the following lemma proven in the full version of our paper.
Lemma 1
Let  be the security parameter. There is a round compression compiler that transforms a maliciously (and semi-honest, resp.) secure MPC protocol \(\pi \) for any n-party functionality \(\mathcal {F}\) into a two-round maliciously (and semi-honest, resp) secure protocol \(\varPi \) for \(\mathcal {F}\) with the following properties:
be the security parameter. There is a round compression compiler that transforms a maliciously (and semi-honest, resp.) secure MPC protocol \(\pi \) for any n-party functionality \(\mathcal {F}\) into a two-round maliciously (and semi-honest, resp) secure protocol \(\varPi \) for \(\mathcal {F}\) with the following properties:
-
1.
If \(\pi \) tolerates corruption threshold \(\epsilon \), then \(\varPi \) tolerates \(\epsilon '\), for arbitrary constants \(\epsilon '<\epsilon <1/2\).
-
2.
If the computational cost of \(\pi \) is \(W=W(n,s)\), where s is the circuit size representation of \(\mathcal {F}\), then the amortized per-party computational cost of \(\varPi \) is \(O(n^\tau W)\) and the per-party communication cost of \(\varPi \) is \(O(n^{\tau -1}W)\).
-
3.
Each party in \(\varPi \) sends messages over both private channels and a broadcast channel in the first round. While in the second round, each party only sends messages over a broadcast channel.
-
4.
Each party \(P_i\) in \(\varPi \) broadcasts its masked input \((x_i\oplus \gamma _i)\) in the first round, where \(x_i\) is its input and \(\gamma _i\) is a random value. The rest of its first round broadcast messages are independent of its input but may depend on \(r_i\).
-
5.
The private channel message of each party \(P_i\) in \(\varPi \) is independent of its input \(x_i\) but may depend on \(r_i\).
Remark 1
We note that we consider the computation of functions represented by circuits consisting of AND, OR and NOT gates.
2.2 From Special MPC to Efficiency Preserving Compiler in the Client-Server Model
Now that we have a two-round protocol \(\varPi \) with the desired structural properties from Lemma 1, we use it to present a two-round maliciously secure, efficiency preserving compiler in the client-server model. Since our protocol works in the client server model, for ease of presentation we use indices with different fonts for referring to specific servers and clients:  for
for
 (double-struck) and
(double-struck) and  for
for
 (bold).
(bold).
Protocol Overview. At a high level, given  servers and
servers and  clients, where
clients, where  , the semi-honest protocol works as follows. Each client generates
, the semi-honest protocol works as follows. Each client generates  additive secret shares of its input - one for each server. The servers then engage in a single execution of the two round protocol \(\varPi \) to compute the function. As mentioned in the introduction, this doesn’t work directly and requires servers delegating their second round computation to a garbled circuit. The corresponding keys for the circuit are computed by a two round helper protocol \(\varPi _{\mathsf {help}}\) that all parties participate in.
additive secret shares of its input - one for each server. The servers then engage in a single execution of the two round protocol \(\varPi \) to compute the function. As mentioned in the introduction, this doesn’t work directly and requires servers delegating their second round computation to a garbled circuit. The corresponding keys for the circuit are computed by a two round helper protocol \(\varPi _{\mathsf {help}}\) that all parties participate in.
For security against malicious adversaries, we must prevent a malicious server from modifying the input shares of an honest client and make use of one-time message authentication codes ( s) to enforce consistency checks. So, in addition to secret sharing their inputs, the clients compute
s) to enforce consistency checks. So, in addition to secret sharing their inputs, the clients compute 
 ’s on each of their shares using a different
’s on each of their shares using a different  key. The functionality computed by the protocol \(\varPi \) first checks if inputs and their corresponding
key. The functionality computed by the protocol \(\varPi \) first checks if inputs and their corresponding  s are valid. Only if this check succeeds, does it start computing on them. We use the helper protocol \(\varPi _{\mathsf {help}}\) exactly as described earlier with the only addition that now instead of just their input shares, the clients also communicate these
s are valid. Only if this check succeeds, does it start computing on them. We use the helper protocol \(\varPi _{\mathsf {help}}\) exactly as described earlier with the only addition that now instead of just their input shares, the clients also communicate these  s and
s and  keys to the servers via the helper protocol.
keys to the servers via the helper protocol.
Formally, we prove the following theorem. In this theorem we also enlist additional properties achieved by our resulting protocol. These properties are crucially used by our compiler in Sect. 3 to obtain an efficiency preserving compiler in the plain model. We refer the reader to Sect. 3 for a detailed discussion on the relevance of these properties.
Theorem 2
Let n be the number of parties and  be the security parameter. Assuming one-way functions, there is a round compression compiler that transforms a maliciously (and semi-honest, resp.) secure MPC protocol \(\varPi \) for any n-input functionality \(\mathcal {F}\) into a two-round maliciously (and semi-honestly, resp.) secure protocol \(\varPhi \) for \(\mathcal {F}\) in the client-server model with the following properties:
be the security parameter. Assuming one-way functions, there is a round compression compiler that transforms a maliciously (and semi-honest, resp.) secure MPC protocol \(\varPi \) for any n-input functionality \(\mathcal {F}\) into a two-round maliciously (and semi-honestly, resp.) secure protocol \(\varPhi \) for \(\mathcal {F}\) in the client-server model with the following properties:
-
1.
Let
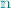 be the number of servers and
be the number of servers and  be the number of clients. If the computational cost of \(\pi \) is \(W=W(n,s)\), where s is the circuit size representation of \(\mathcal {F}\), then the amortized per-party computational cost and total communication of maliciously (and semi-honest, resp.) secure protocol \(\varPhi \) is
be the number of clients. If the computational cost of \(\pi \) is \(W=W(n,s)\), where s is the circuit size representation of \(\mathcal {F}\), then the amortized per-party computational cost and total communication of maliciously (and semi-honest, resp.) secure protocol \(\varPhi \) is 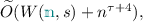 (and
(and 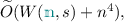 resp.), where the \(\widetilde{O}\) notation suppresses suppresses polynomial factors in \(\lambda \) and
resp.), where the \(\widetilde{O}\) notation suppresses suppresses polynomial factors in \(\lambda \) and  .
. -
2.
If \(\pi \) tolerates corruption threshold \(\epsilon \), then \(\varPhi \) tolerates \(\epsilon '\), for arbitrary constants \(\epsilon '<\epsilon <1/2\) corruptions in the server set and \(\epsilon \) corruptions in the client set.
-
3.
Each party can send messages over both private channels and a broadcast channel in the first round in \(\varPhi \). While in the second round, each party only sends messages over a broadcast channel.
-
4.
The private channel messages sent by clients in \(\varPhi \) are independent of the role (client/server) of the receiving party in the protocol.
-
5.
The total length of messages sent by all clients is
 in the semi-honest case and
in the semi-honest case and  in the malicious case.
in the malicious case. -
6.
The private channel messages sent by servers in \(\varPhi \) can be divided into messages that are independent of the role (client/server) of the receiving party and ones that are specifically intended for other server parties.
-
7.
The total length of messages sent by all servers in \(\varPhi \) is
 in the semi-honest case and
in the semi-honest case and  in the malicious case.
in the malicious case.
We now give a constructive proof of Theorem 2 using the protocol described below.
2.2.1 Construction
We start by establishing some notations that will be used throughout this section.
Notations. We use various underlying protocols for different functionalities in our construction. We use \(\varPi _{X}\) to denote the underlying protocol used for computing functionality \(\mathcal {F}_X\). The \(r^{\text {th}}\) next message function of protocol \(\varPi _X\) is denoted by \(\varPi _X^r\). We use multiple instantiations of these underlying protocols. In the \(r^{th}\) round of the \(y^{\text {th}}\) instantiation of \(\varPi _X\), we use  to the message that server i sends to client j and
to the message that server i sends to client j and  denotes the message that it broadcasts.
denotes the message that it broadcasts.  denotes the input of server i in the \(y^{\text {th}}\) instantiation of \(\varPi _X\). Often times, we replace some indices in the above notations with symbols such as
denotes the input of server i in the \(y^{\text {th}}\) instantiation of \(\varPi _X\). Often times, we replace some indices in the above notations with symbols such as  or \(*\) to denote a set. For instance
or \(*\) to denote a set. For instance  . Similarly,
. Similarly,  is used to denote all servers and \(*\) is used for referring to all clients and all parties respective. The collection of labels (of a garbled circuit) are denoted as
is used to denote all servers and \(*\) is used for referring to all clients and all parties respective. The collection of labels (of a garbled circuit) are denoted as  . Projection of a string of \(c \in \lbrace 0,1,\perp \rbrace ^L\) is defined as \(\mathsf {Projection}(c,\overline{\mathsf {lab}})=\lbrace \mathsf {lab}_{i,c[i]} \rbrace _{i \in [L]}\), where \(\mathsf {lab}_{i,\perp }\) is defined to be \(\perp \). The output of \(\mathsf {Projection}\) is treated as a string. For convenience, we also specify that \(\perp \) under the XOR operation remains unchanged. Specifically,
. Projection of a string of \(c \in \lbrace 0,1,\perp \rbrace ^L\) is defined as \(\mathsf {Projection}(c,\overline{\mathsf {lab}})=\lbrace \mathsf {lab}_{i,c[i]} \rbrace _{i \in [L]}\), where \(\mathsf {lab}_{i,\perp }\) is defined to be \(\perp \). The output of \(\mathsf {Projection}\) is treated as a string. For convenience, we also specify that \(\perp \) under the XOR operation remains unchanged. Specifically,  . Wherever necessary, we augment the protocol description with comments denoted as
. Wherever necessary, we augment the protocol description with comments denoted as
 .
.
Next, we list the building blocks used in our construction.
Building Blocks. The main primitives required in this construction for computing an n-input functionality \(\mathcal {F}\) are the following:
-
1.
An unconditionally secure message authentication scheme
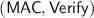 .
. -
2.
A two-round protocol \(\varPi _\mathsf {aug}\) [4] for
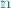 parties output by the compiler in Lemma 1, for the function \(\mathcal {F}_\mathsf {aug}\) defined in Fig. 1. \(\mathcal {F}_\mathsf {aug}\) takes inputs from n parties, and parses each input as: (1)its own input; (2) input shares (from parties not involved in the computation of \(\mathcal {F}'\)); (3) MAC tags for each share; (4) MAC keys to verify tags.Footnote 10 Upon aggregation the functionality checks if all the MAC tags verify. If the verification succeeds, input shares are used to reconstruct inputs of the parties not involved in the computation. Output the result on evaluating \(\mathcal {F}\) on the inputs (both parties’ own and reconstructed).
parties output by the compiler in Lemma 1, for the function \(\mathcal {F}_\mathsf {aug}\) defined in Fig. 1. \(\mathcal {F}_\mathsf {aug}\) takes inputs from n parties, and parses each input as: (1)its own input; (2) input shares (from parties not involved in the computation of \(\mathcal {F}'\)); (3) MAC tags for each share; (4) MAC keys to verify tags.Footnote 10 Upon aggregation the functionality checks if all the MAC tags verify. If the verification succeeds, input shares are used to reconstruct inputs of the parties not involved in the computation. Output the result on evaluating \(\mathcal {F}\) on the inputs (both parties’ own and reconstructed). -
3.
A Garbled Circuit scheme \(\textsf {GC}=\left\{ \mathsf {Gen}, \mathsf {Garb},\mathsf {Eval}\right\} \) based on one-way functions.
-
4.
A two-round maliciously secure honest majority protocol [4] \(\varPi _{\mathsf {help}}\) computing function \(\mathcal {F}_{\mathsf {help}}\), which helps the client select labels, of a garbled circuit, corresponding to its input share (Fig. 2). \(\mathcal {F}_{\mathsf {help}}\) separates out its participants into two sets, clients and servers. In addition, it designates two special parties: client
 , and server
, and server 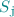 .
. 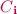 provides input
provides input  , and
, and  provides input
provides input  . Additionally, all servers (including
. Additionally, all servers (including 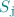 ) provide as input labels to a garbled circuit. The other clients do not have any inputs. The functionality outputs to all parties the projection of the labels corresponding to
) provide as input labels to a garbled circuit. The other clients do not have any inputs. The functionality outputs to all parties the projection of the labels corresponding to  . Since the parties have asymmetric roles, the next message function of this protocol additionally takes one of these labels as input \((\mathsf {sen},\mathsf {rec},\mathsf {lrec},\mathsf {hel})\) to specify the exact role of the party.
. Since the parties have asymmetric roles, the next message function of this protocol additionally takes one of these labels as input \((\mathsf {sen},\mathsf {rec},\mathsf {lrec},\mathsf {hel})\) to specify the exact role of the party.
Remark 2
Throughout this work, B will be used to denote broadcast messages.
Protocol. For each  , server
, server  has input
has input  and for each
and for each  , client
, client  has input
has input  . For simplicity we assume that each these inputs are of length 1. Our protocol easily extends to the setting with longer inputs. We assume that every party samples a sufficiently long random string at the start of the protocol, which is used appropriately throughout the protocol. Therefore we remove the randomness from protocol description and assume that it is implicit in all the algorithms used in the protocol.
. For simplicity we assume that each these inputs are of length 1. Our protocol easily extends to the setting with longer inputs. We assume that every party samples a sufficiently long random string at the start of the protocol, which is used appropriately throughout the protocol. Therefore we remove the randomness from protocol description and assume that it is implicit in all the algorithms used in the protocol.

The security proof of the protocol can be found in the full version.
Semi Honest Protocol. We note that for the semi-honest variant of the above protocol, the MAC checks are no longer needed. Therefore, \(\mathcal {F}_{\mathsf {help}}\) can be simplified. The rest of the protocol remains the same, except that we can instantiate the underlying protocols used in this protocol with their semi-honest variants.
Complexity. Note that there are  instances of \(\varPi _{\mathsf {help}}\). Given that \(\varPi _{\mathsf {help}}\) implements a quadratic functionality, the resulting circuit computed by each instance has size
instances of \(\varPi _{\mathsf {help}}\). Given that \(\varPi _{\mathsf {help}}\) implements a quadratic functionality, the resulting circuit computed by each instance has size  . Also, each instance is run by all n parties. Importantly, the circuit size is independent of s, size of circuit representing the underlying protocol. There is also a single instance of \(\varPi _\mathsf {aug}\) computing a circuit of size s with
. Also, each instance is run by all n parties. Importantly, the circuit size is independent of s, size of circuit representing the underlying protocol. There is also a single instance of \(\varPi _\mathsf {aug}\) computing a circuit of size s with  parties. From the described properties of the underlying protocols, this gives us a protocol with the desired complexity. The details of the exact calculations are presented in the full version.
parties. From the described properties of the underlying protocols, this gives us a protocol with the desired complexity. The details of the exact calculations are presented in the full version.
3 Efficiency Preserving Compiler in the Plain Model
In this section we go from the compiler in the client-server model in Sect. 2 to present our main result, namely an efficient two-round compiler in the plain model. Formally we prove the following theorem.
Theorem 3
Let n be the number of parties and \(\lambda \) be the security parameter, such that n is polynomially related to \(\lambda \) and let k be set to \(\log ^2(n)\).
-
1.
Assuming one-way functions, there is a round compression compiler that transforms a semi-honest MPC protocol \(\pi \) for any n-party functionality \(\mathcal {F}\) into a two-round semi-honest protocol \(\varPi '\) for \(\mathcal {F}\) with the following properties:
-
(a)
If \(\pi \) tolerates corruption threshold \(\varepsilon \), then \(\varPi '\) tolerates \(\varepsilon '\), for arbitrary constants \(\varepsilon '< \varepsilon < \frac{1}{2}\).
-
(b)
If the computational cost of \(\pi \) is \(W=W(n,s)\), where s is the circuit size representation of \(\mathcal {F}\), then the amortized per-party computational cost and total communication cost of \(\varPi '\) is \( O\left( (W(k,s+kn)+n^4\lambda ^2)\cdot \lambda \cdot k^3\right) . \) We will denote this by \(\widetilde{O}(W(k,s+kn)k^{\tau -2} + n^4)\), where the \(\widetilde{O}\) notation suppresses polynomial factors in k and \(\lambda \). For most known protocols, the additive term in the circuit size (kn) will be suppressed by the additive term of \(n^4\) simplifying the expression to \(\widetilde{O}(W(k,s) + n^4)\).
-
(a)
-
2.
Assuming one-way functions, there is a round compression compiler that transforms a maliciously secure MPC protocol \(\pi \) for any n-party functionality \(\mathcal {F}\) into a three-round maliciously secure protocol \(\varPi '\) for \(\mathcal {F}\) that satisfies properties 1(a) and amortized per-party computational cost \(\widetilde{O}(W(k,s) + n^{\tau +4})\).
-
3.
Assuming NIWIs, there is a round compression compiler that transforms a maliciously secure MPC protocol \(\pi \) for any n-party functionality \(\mathcal {F}\) into a two-round maliciously secure protocol \(\varPi '\) in the reusable correlated randomness setup model for \(\mathcal {F}\) that satisfies properties 1(a) and amortized per-party computational cost \(\widetilde{O}(W(k,s) + n^{\tau +4})\).
Overview. We now present an overview of the compiler that builds on the protocol output by the compiler from Sect. 2 (Theorem 2) in the client-server model to get a compiler in the plain model. Along the way, we shall discuss the relevant properties used from Theorem 2. We shall do this in two steps.
-
1.
Phase One: Compile the protocol in Sect. 2 to a protocol in the \(\mathcal {F}_{\textsf {election}}\)-hybrid model. In this model, at the start of the protocol, each party receives a bit from \(\mathcal {F}_{\textsf {election}}\) indicating whether it is in the committee. The functionality \(\mathcal {F}_{\textsf {election}}\) is described in Fig. 4.
-
2.
Phase Two: Instantiate \(\mathcal {F}_{\textsf {election}}\) based on the desired security properties of the final protocol.
The main challenge in going from the client-server model to the plain model is that parties are no longer aware of the roles of the other parties, i.e. which parties are clients and which are servers. To get around this issue, we will leverage the fact that \(\mathcal {F}_{\textsf {election}}\) guarantees that every party knows whether it is a server, but doesn’t know its index in the server set.
Since the party doesn’t know its role (index) in the server (resp. client) set, it computes messages assuming all  (resp.
(resp.  ) roles. At the end of the first round, when all parties are aware of the elected committee based on the messages sent, the irrelevant messages are discarded. But a problem with this approach is that the protocol involves private messages, which require knowledge of the recipient’s role. Based on the properties listed in Theorem 2 from Sect. 2, we can divide the private messages into two categories which are handled differently:
) roles. At the end of the first round, when all parties are aware of the elected committee based on the messages sent, the irrelevant messages are discarded. But a problem with this approach is that the protocol involves private messages, which require knowledge of the recipient’s role. Based on the properties listed in Theorem 2 from Sect. 2, we can divide the private messages into two categories which are handled differently:
Private Message Independent of the Role of the Receiving Party. This is the case for all private messages sent by the clients, and some of the private messages sent by the servers. This is an easy setting to handle since these messages can be sent privately without the need to know the recipient’s role.
Private Message Intended for the Parties in the Server Set. This is of concern only to parties that are elected into the committee. Since a party is not aware of other elected parties, these messages cannot be sent privately. Instead, the party masks these messages, and broadcasts the masked messages. But we want the designated party to receive the mask, and unmask the message to proceed with the computation. We seem to be back where we started, but we use a solution similar to Sect. 2, where the second round computation of the server parties are delegated to a garbled circuit. Now, the party generating the mask initiates a helper protocol that will enable the appropriate party’s garbled circuit to receive the mask, thereby allowing to proceed with the computation. To ensure there is no complexity blow-up by involving all parties, we make sure that the size of the computation involving all parties is independent of the underlying circuit. This is easily done by utilizing a pseudo-random generator (PRG) to generate the masks.
The relevance of the other properties listed in Theorem 2 is in the efficiency of the resultant protocol.
3.1 Phase One: \(\mathcal {F}_{\textsf {election}}\)-hybrid Model
In this section, we shall perform the first step of our compilation. Namely, we shall compile the protocol in Sect. 2 from the client-server model to a protocol in the \(\mathcal {F}_{\textsf {election}}\)-hybrid model. To differentiate from the client-server models, we shall refer to parties “elected” to be in the server set to be a part of a committee.
Building Blocks. The main primitives required in this construction are the following:
-
1.
The two-round protocol \(\varPi _{f_\mathsf {c\text {-}s}}\) from Sect. 2 in the client-server model. For this section, we shall use the following notation to refer to the first round messages of \(\varPi _{f_\mathsf {c\text {-}s}}\). There are special first round messagesFootnote 11 that are privately sent among the servers, these will be denoted by an additional
 :
:  indicates the special message sent from server indexed by
indicates the special message sent from server indexed by 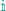 to the server indexed by
to the server indexed by 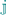 . Other messages are denoted as previous sections with \(\mathtt {M}_{f_\mathsf {c\text {-}s}}^1[i,j]\) indicating a message from party i to j (with appropriate font to differentiate between clients and severs). Broadcast messages correspondingly defined. Additionally, as before, we group messages corresponding clients (
. Other messages are denoted as previous sections with \(\mathtt {M}_{f_\mathsf {c\text {-}s}}^1[i,j]\) indicating a message from party i to j (with appropriate font to differentiate between clients and severs). Broadcast messages correspondingly defined. Additionally, as before, we group messages corresponding clients ( ), servers (
), servers ( ) or all parties (\(*\)).
) or all parties (\(*\)). -
2.
A Garbled Circuit scheme \(\textsf {GC}=\left\{ \mathsf {Gen}, \mathsf {Garb},\mathsf {Eval}\right\} \).
-
3.
A two-round maliciously secure honest majority protocol \({\varPi _{\mathsf {mOT}}}\) computing function \(\mathcal {F}_{\mathsf {mOT}} \) described in Fig. 5. \(\mathcal {F}_{\mathsf {mOT}} \) is similar to a multi-party variant of oblivious transfer. There are two designated parties, sender (\(\mathsf {sen}\)) and receiver (\(\mathsf {rec}\)) with inputs b and \((x_0,x_1)\) respectively, while all other parties are referred to as helper (\(\mathsf {hel}\)) parties. \(\mathcal {F}_{\mathsf {mOT}} \) outputs \(x_b\) to all the parties. Our protocol will use multiple instance of the \({\varPi _{\mathsf {mOT}}}\) protocol, which is indexed by indices corresponding to (sender, receiver).
-
4.
A pseudo-random generator
 .
.
As explained earlier, prior to sending the first round messages, a party is only aware if it is in the committee, but not its role (index) in the committee (or outside). In our protocol, depending on whether party \(P_i\) is in the committee (resp. outside), \(P_i\) computes the first round message for every possible role in the committee (resp. outside). The index of the sender in the protocol message is thus denoted by  (resp.
(resp.  ) to indicate \(P_i\)’s message for role
) to indicate \(P_i\)’s message for role  in the committee (resp. role
in the committee (resp. role  outside).
outside).
Although no party is aware of the roles of the other parties at the start of the first round of the protocol, there is an implicit mapping from the set of all parties to the corresponding role in the committee (or outside).  (resp.
(resp.  ) denotes this mapping. At the end of the first round, all parties will be able to locally compute both the mappings and discard the relevant messages. We shall also abuse notation slightly and use
) denotes this mapping. At the end of the first round, all parties will be able to locally compute both the mappings and discard the relevant messages. We shall also abuse notation slightly and use  and
and  to denote the corresponding sets.
to denote the corresponding sets.
Protocol. Let \(\mathcal {P}= \lbrace P_1, \cdots , P_n\rbrace \) be the set of parties in the protocol and let the corresponding inputs be \(x_1,\cdots ,x_n\). We now give a formal description of the protocol in the \(\mathcal {F}_{\textsf {election}}\)-hybrid model. We assume parties sample appropriate random strings in the protocol description.

The security proof of the protocol can be found in the full version of the paper.
Complexity. Note that there are  instances of \({\varPi _{\mathsf {mOT}}}\), where the sender has inputs of length
instances of \({\varPi _{\mathsf {mOT}}}\), where the sender has inputs of length  , while the receiver has inputs of length
, while the receiver has inputs of length  . Given that \({\varPi _{\mathsf {mOT}}}\) implements a quadratic functionality, the resulting circuit computed by each instance has size
. Given that \({\varPi _{\mathsf {mOT}}}\) implements a quadratic functionality, the resulting circuit computed by each instance has size  . Also, each instance is run by all n parties. Importantly, the circuit size is independent of s, size of circuit representing the underlying protocol. There is an additional overhead of parties not knowing their own role in the committee. Finally, there is a single instance of \(\varPi _{f_\mathsf {c\text {-}s}}\) computed by all parties. The cost then follows from the properties of the underlying protocols and the details are presented in the full version.
. Also, each instance is run by all n parties. Importantly, the circuit size is independent of s, size of circuit representing the underlying protocol. There is an additional overhead of parties not knowing their own role in the committee. Finally, there is a single instance of \(\varPi _{f_\mathsf {c\text {-}s}}\) computed by all parties. The cost then follows from the properties of the underlying protocols and the details are presented in the full version.
3.2 Phase Two
We can now complete the description of our compiler by instantiating the randomized functionality \(\mathcal {F}_{\textsf {election}}\) used in the protocol described in the \(\mathcal {F}_{\textsf {election}}\)-hybrid model. We consider three different settings, which will lead to corresponding results. The settings are (a) semi-honest; (b) malicious in the reusable correlated randomness model; (c) malicious in the plain model.
Semi-honest. For the semi-honest setting, the protocol idea is simple: every party tosses appropriately biased coins to determine if it is in the committee. The only thing left to do is to determine the right parameters so that we have a committee with poly-logarithmic size and honest majority. This is a non-interactive process, and the resultant protocol is given below. The committee size will be \((1-\delta )\cdot k\), where \(\delta \) is any non-zero constant.
-
Round 1. Each party does the following:
-
Toss a coin that outputs 1 with probability \(p = \frac{k}{n}\). If output 1, it assumes it is a part of the committee and computes the messages
-
If it is in the committee, pick an element
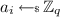 , from an exponentially sized field
, from an exponentially sized field 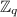 . This is to pick the relative position within the committee and trim the committee if needed.
. This is to pick the relative position within the committee and trim the committee if needed. -
All parties compute the client messages, and the parties that assumed they were in the committee additionally compute server messages. This is because the committee might be larger than the final size, and a party make not make it to the final committee.
-
Only parties that assumed they were in the committee broadcast their \(a_i\) value.
-
-
Round 2. On receiving the first round messages, each party knows both (a) which parties are in the committee; and (b) the relative roles of each party in the committee. This follows from picking the committee to be the ordered set of first \((1-\delta )\cdot k\) parties based on their broadcast \(a_i\). It then executed the rest of the protocol appropriately.
Since each party independently samples coins to determine if it is in the committee, the expected party size is k. If we set \(k=\Omega (\log ^2(n))\), from the Chernoff bound, other than with negligible probability, the size of the committee is \(>(1-\delta )\log ^2(n)\), and thus will not end up with a smaller committee. By a similar argument, it is easy to see that other than with negligible probability, honest majority is maintained in the committee. This gives us a resultant two round semi-honest protocol in the plain model.
Lemma 2
Assuming the that the fraction of adversarial parties are bounded by \( \left( \frac{1}{2} - \epsilon \right) \) for some \(\epsilon > 0\), our constructed protocol is a two round semi-honest protocol.
Remark 3
While our protocol is proven in the malicious setting, we instantiate the underlying protocols with their corresponding semi-honest versions. The semi-honest versions also satisfy Lemma 1.
The security of the protocol follows from the composition theorem for semi-honest protocols [28].
Malicious in the Reusable Correlated Randomness Model. We consider the setting of the reusable correlated randomness model, where the trusted set up can select the public and private keys for a verifiable random function (VRF)[37]. We then follow the same strategy of selecting a committee as done in Algorand [27]. While they select committees by weight, we set the weights for each party to be identical (say 1).
Specifically, the trusted parties select public/private key pairs  for each party i, and a random seed. Additionally, a threshold \(\tau \) is picked based on the required size of the committee.
for each party i, and a random seed. Additionally, a threshold \(\tau \) is picked based on the required size of the committee.
-
Round 1. Each party receives the public key for all parties, and a public/private key pair
 unique to it. It then evaluates the VRF to determine if it is in the committee. It then computes the first round messages of the Phase one protocol, and also broadcasts the messages indicating it is in the committee.
unique to it. It then evaluates the VRF to determine if it is in the committee. It then computes the first round messages of the Phase one protocol, and also broadcasts the messages indicating it is in the committee. -
Round 2. Compute the second round messages of the Phase one protocol.
We allow the adversary to adaptively pick the parties it corrupts having seen only the public keys for all parties and the private keys for the parties it has corrupted thus far.
As stated in [27], we have the following two properties. Given a random seed, VRF outputs a pseudorandom value. Hence the parties are randomly picked into the committee. An adversary that does not know the secret key  for party i cannot guess if i was chosen at all (more precisely, the adversary cannot guess any better than just by randomly guessing).
for party i cannot guess if i was chosen at all (more precisely, the adversary cannot guess any better than just by randomly guessing).
This lets us allow the adversary to adaptively corrupt parties based on the public keys, seed and the secret keys of the parties it has corrupted thus far. This would give us a two round protocol, maliciously secure against an adaptive adversary in the presence of trusted set up.
Lemma 3
Assuming the that the fraction of adversarial parties are bounded by \( \left( \frac{1}{2} - \epsilon \right) \) for some \(\epsilon > 0\), our constructed protocol is a two round protocol in the trusted set up model secure against malicious adversaries.
We note that the best known constructions for VRFs are based on non-interactive witness indistinguishable proofs (NIWIs) [8, 30], which are in turn known from the assumption of bilinear maps [31].
Malicious in the Plain Model. In the malicious setting, we cannot let the parties locally sample coins. Instead, we run Feige’s lightest bin protocol [21] to determine the committee. The protocol gives a method of selecting a committee of approximately k parties for a given parameter k. It is a single round protocol, where the parties broadcast their choice of a random bin in the set \(\left[ \frac{n}{k}\right] \). This adds an additional round to the start of the protocol.
-
Round 1. Every party broadcasts a random bin in the set \(\left[ \frac{n}{\log ^2(n)}\right] \).
-
Round 2. Each party knows whether they are in the committee based on the received broadcast, by picking the \((1-\delta )\cdot k\) lightest bins. In fact at the end of this round, we get a stronger property that every party is aware of the role of every party in the protocol, i.e. whether a given party is in the committee. Now each party can compute first round messages of the protocol from Phase one.
-
Round 3. Each party computes second round messages of the protocol from Phase one.
The following lemma from [21] is relevant to us.
Lemma 4
([21]). For \(k=\log ^2 n\), if the number of corrupted parties is \(\beta n\), for any constant \(\delta >0\), other than with negligible probability in n, the size of the committee \(\mathcal {C}\) will be elected such that:
-
Bound on Size: \((1-\beta - \delta ) \log ^2 n \le |\mathcal {C}| \le \log ^2 n\);
-
Honest Parties in Committee: # honest parties in the committee is \(\ge ((1-\beta - \delta ) \log ^2 n)\).
In our setting, \(\beta < \left( \frac{1}{2} - \epsilon \right) \), which guarantees an honest majority in the committee. This gives us a resultant three round maliciously secure protocol in the plain model.
Lemma 5
Assuming the that the fraction of adversarial parties are bounded by \( \left( \frac{1}{2} - \epsilon \right) \) for some \(\epsilon > 0\), our constructed protocol is a three round protocol secure against malicious adversaries.
The security of the protocol follows from the sequential composition theorem [28].
Remark 4
We note that both \(\mathcal {F}_{\mathsf {help}}\) and \(\mathcal {F}_{\mathsf {mOT}} \) resemble the multiparty homomorphic OT (M-OT) functionality described in [1]. These functionalities can be seen as special cases of the M-OT functionality, but we’ve described them separately for ease of notation.
4 Impossibility Result
In this section we prove our impossibility result showing that our committee based approaches are inherent to the results we achieve.
Theorem 4
There exists an n-party function \(\mathcal {F}\), such that there does not exist an n-party, r-round balanced scalable (possibly insecure) MPC protocol, where each party does asymptotically equal amount of work, computing a circuit C of size s, where r is some constant, and the protocol can be represented by a circuit of size \(\tilde{O}(s)\) defined over the basis \(\{\mathrm {AND},\mathrm {OR},\mathrm {NOT}\}\).
Proof
We make a novel use of the “MPC in the head” paradigm [35] to prove this theorem.
Let us assume for contradiction that for every n-party functionality \(\mathcal {F}\), there exists an r-round scalable MPC protocol \(\varPi \) computing \(\mathcal {F}\), where r is a constant and each party can be represented as a circuit over the basis \(\{\mathrm {AND},\mathrm {OR},\mathrm {NOT}\}\) of size \(\tilde{O}(s)/n\). Let \(\varPi .\mathsf {NMF}{i,j}\) be the next-message function of party i (for each \(i\in [n]\)) in round j (for each \(j\in [r]\)). Since r is a constant, the size of the circuit implementing the next-message function of each party \(i\in [n]\) in each round \(j\in [r]\) is
Hence, depth of each next message function \(|\varPi .\mathsf {NMF}_{i,j}|_d=\tilde{O}(s)/{n}\).
Base Step. We now modify \(\varPi \) to \(\varPi _1\) as follows: for each \(i\in [n],~j\in [r]\), we execute MPC protocol \(\varPi \) (let us denote this execution by \(\varPi _{1,i,j}\)) to implement \(\varPi .\mathsf {NMF}_{i,j}\). The size of the circuit implementing the next-message function of each party \(i'\in [n]\) in each round \(j'\in [r]\) of this sub-protocol \(\varPi _{1,i,j}\) is
Hence, depth of each next message function in each sub-protocol \(|{\varPi _{1,i,j}}.\mathsf {NMF}_{i',j'}|_d=\tilde{O}(s)/{n^2}\).
The total number of rounds in the resulting protocol \(\varPi _1\) is \(r^2\) and in each round \(j'\in [r^2]\), the next message function of each party \(i'\in [n]\) is
where \(j=j'\mod r\). Note that since this is a parallel composition of n circuits, each of depth \(\tilde{O}(s)/{n^2}\), the depth of each next message function in the modified protocol \(\varPi _1=\tilde{O}(s)/{n^2}\).
Let p be a constant such that \(\tilde{O}(s)/n^p\) is some constant c. Now for each \(k\in \{2,\ldots ,p-1\}\), we perform the following recursion step.
Recursion Step. We modify the \(r^k\)-round protocol \(\varPi _{k-1}\) to obtain \(\varPi _k\) as follows: for each \(i\in [n],~j\in [r^{k}]\), we execute MPC protocol \(\varPi \) (let us denote this execution by \(\varPi _{k,i,j}\)) to implement \({\varPi _{k-1}}.\mathsf {NMF}_{i,j}\). Similar to before, the depth of the circuit implementing the next-message function of each party \(i'\in [n]\) in each round \(j'\in [r]\) of this sub-protocol \(\varPi _{k,i,j}\) is
The total number of rounds in the resulting protocol \(\varPi _1\) is \(r^2\) and in each round \(j'\in [r^{k+1}]\), the next message function of each party \(i'\in [n]\) is
where \(j=j'\mod r\). Again since this is a parallel composition of n circuits, each of depth \(\tilde{O}(s)/{n^{k+1}}\), the depth of each next message function in the resulting modified protocol \(\varPi _1=\tilde{O}(s)/{n^{k+1}}\).
Protocol \(\varPi _{p-1}\). The depth of the next message function of each party in each round, in the final \(r^{p}\)-round protocol \(\varPi _{p-1}\) is
Thus the final modified protocol \(\varPi _{p-1}\) can be viewed as a circuit of depth \((c\times \text { No. of rounds })=c\cdot r^p=O(1)\). Moreover, the size of this circuit is \(\mathrm {poly}(s)\).
This means that every n-party functionality \(\mathcal {F}\) representable by a polynomial-sized circuit, also admits a constant-depth polynomial-sized circuit over the basis \(\{\mathrm {AND},\mathrm {OR},\mathrm {NOT}\}\) and thus is in \(\mathsf {AC}^0\). However note that there are functions like parity and majority that are not in \(\mathsf {AC}^0\). Therefore, this is a clear contradiction.
Notes
- 1.
- 2.
If there are only a constant number of parties that are recipients of the output, then the resultant protocol from Theorem 1 already achieves this result.
- 3.
While special MPC with total computation proportional to \(\tilde{O}(n^\tau \cdot W)\) can be constructed (as we discuss later), the second step of our approach is actually less sensitive to the exact asymptotic complexity of special MPC. In particular, the exact dependence on n is not very important as long the total computation in special MPC has only linear dependence on W.
- 4.
- 5.
At a high level, a two-round MPC protocol satisfies the delayed-function property if the first round messages of the honest parties are computed independent of the functionality, but may depend on the size of the circuit implementing the functionality.
- 6.
For this technical overview, some details of the protocol are omitted. The resultant protocol incurs an additive term of \(n^4\), which is elaborate upon in the technical section.
- 7.
Alternatively, if the number of parties computing the output are already a constant, then even the two round protocol achieves optimal computation.
- 8.
A simpler solution using non-reusable correlated randomness can be obtained using regular digital signatures which are known from one-way functions.
- 9.
As for the semi-honest setting, the additive term will be elaborated upon in the technical sections.
- 10.
The MAC keys correspond to tags held by other parites.
- 11.
This will correspond to the messages whose size depend on the size of the circuit being computed.
References
Ananth, P., Choudhuri, A.R., Goel, A., Jain, A.: Round-optimal secure multiparty computation with honest majority. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018. LNCS, vol. 10992, pp. 395–424. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_14
Ananth, P., Choudhuri, A.R., Goel, A., Jain, A.: Two round information-theoretic MPC with malicious security. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 532–561. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_19
Applebaum, B., Brakerski, Z., Tsabary, R.: Perfect secure computation in two rounds. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11239, pp. 152–174. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_6
Applebaum, B., Brakerski, Z., Tsabary, R.: Degree 2 is complete for the round-complexity of malicious MPC. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019. LNCS, vol. 11477, pp. 504–531. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17656-3_18
Beaver, D., Micali, S., Rogaway, P.: The round complexity of secure protocols (extended abstract). In: 22nd ACM STOC, pp. 503–513. ACM Press, May 1990. https://doi.org/10.1145/100216.100287
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation (extended abstract). In: 20th ACM STOC, pp. 1–10. ACM Press, May 1988. https://doi.org/10.1145/62212.62213
Benhamouda, F., Lin, H.: k-round multiparty computation from k-round oblivious transfer via Garbled interactive circuits. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 500–532. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_17
Bitansky, N.: Verifiable random functions from non-interactive witness-indistinguishable proofs. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. Lecture Notes in Computer Science, vol. 10678, pp. 567–594. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_19
Boyle, E., Chung, K.-M., Pass, R.: Large-scale secure computation: multi-party computation for (Parallel) RAM programs. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. Lecture Notes in Computer Science, vol. 9216, pp. 742–762. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_36
Boyle, E., Goldwasser, S., Tessaro, S.: Communication locality in secure multi-party computation. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 356–376. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_21
Canetti, R., et al.: Fiat-Shamir: from practice to theory. In: STOC (2019)
Chaum, D., Crépeau, C., Damgård, I.: Multiparty unconditionally secure protocols (extended abstract). In: 20th ACM STOC, pp. 11–19. ACM Press, May 1988. https://doi.org/10.1145/62212.62214
Cohen, G., Damgård, I.B., Ishai, Y., Kölker, J., Miltersen, P.B., Raz, R., Rothblum, R.D.: Efficient multiparty protocols via log-depth threshold formulae. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 185–202. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_11
Damgård, I., Ishai, Y.: Scalable secure multiparty computation. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 501–520. Springer, Heidelberg, August 2006. https://doi.org/10.1007/11818175_30
Damgård, I., Ishai, Y., Krøigaard, M.: Perfectly secure multiparty computation and the computational overhead of cryptography. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 445–465. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_23
Damgård, I., Ishai, Y., Krøigaard, M., Nielsen, J.B., Smith, A.: Scalable multiparty computation with nearly optimal work and resilience. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 241–261. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_14
Damgård, I., Nielsen, J.B.: Scalable and unconditionally secure multiparty computation. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 572–590. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-74143-5_32
Dani, V., King, V., Movahedi, M., Saia, J.: Brief announcement: breaking the O(nm) bit barrier, secure multiparty computation with a static adversary. In: ACM Symposium on Principles of Distributed Computing, PODC 2012, 16–18 July 2012, Funchal, Madeira, Portugal, pp. 227–228 (2012)
Dani, V., King, V., Movahedi, M., Saia, J.: Quorums quicken queries: efficient asynchronous secure multiparty computation. In: Chatterjee, M., Cao, J., Kothapalli, K., Rajsbaum, S. (eds.) ICDCN 2014. LNCS, vol. 8314, pp. 242–256. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-45249-9_16
Dani, V., King, V., Movahedi, M., Saia, J., Zamani, M.: Secure multi-party computation in large networks. Distrib. Comput. 30(3), 193–229 (2017)
Feige, U.: Noncryptographic selection protocols. In: 40th FOCS, pp. 142–153. IEEE Computer Society Press, October 1999. https://doi.org/10.1109/SFFCS.1999.814586
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg, August 1987. https://doi.org/10.1007/3-540-47721-7_12
Garg, S., Gentry, C., Halevi, S., Raykova, M.: Two-round secure MPC from indistinguishability obfuscation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 74–94. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_4
Garg, S., Ishai, Y., Srinivasan, A.: Two-round MPC: information-theoretic and black-box. In: Beimel, A., Dziembowski, S. (eds.) TCC 2018. LNCS, vol. 11239, pp. 123–151. Springer, Cham (2018). https://doi.org/10.1007/978-3-030-03807-6_5
Garg, S., Srinivasan, A.: Two-round multiparty secure computation from minimal assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 468–499. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_16
Genkin, D., Ishai, Y., Polychroniadou, A.: Efficient multi-party computation: from passive to active security via secure SIMD circuits. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 721–741. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_35
Gilad, Y., Hemo, R., Micali, S., Vlachos, G., Zeldovich, N.: Algorand: scaling byzantine agreements for cryptocurrencies. In: Proceedings of the 26th Symposium on Operating Systems Principles, 28–31 October 2017, Shanghai, China, pp. 51–68 (2017)
Goldreich, O.: The Foundations of Cryptography, vol. 2, Basic Applications. Cambridge University Press, Cambridge (2004)
Goldreich, O., Micali, S., Wigderson, A.: How to play any mental game or a completeness theorem for protocols with honest majority. In: Aho, A. (ed.) 19th ACM STOC, pp. 218–229. ACM Press, May 1987. https://doi.org/10.1145/28395.28420
Goyal, R., Hohenberger, S., Koppula, V., Waters, B.: A generic approach to constructing and proving verifiable random functions. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10678, pp. 537–566. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70503-3_18
Groth, J., Ostrovsky, R., Sahai, A.: New techniques for noninteractive zero-knowledge. J. ACM 59(3), 11:1–11:35 (2012)
Halevi, S., Lindell, Y., Pinkas, B.: Secure computation on the web: computing without simultaneous interaction. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 132–150. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-22792-9_8
Hirt, M., Maurer, U.: Player simulation and general adversary structures in perfect multiparty computation. J. Cryptol. 13(1), 31–60 (2000)
Hirt, M., Nielsen, J.B.: Robust multiparty computation with linear communication complexity. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 463–482. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_28
Ishai, Y., Kushilevitz, E., Ostrovsky, R., Sahai, A.: Zero-knowledge proofs from secure multiparty computation. SIAM J. Comput. 39(3), 1121–1152 (2009)
Ishai, Y., Kushilevitz, E., Paskin, A.: Secure multiparty computation with minimal interaction. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 577–594. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_31
Micali, S., Rabin, M.O., Vadhan, S.P.: Verifiable random functions. In: 40th FOCS, pp. 120–130. IEEE Computer Society Press, October 1999. https://doi.org/10.1109/SFFCS.1999.814584
Peikert, C., Shiehian, S.: Noninteractive zero knowledge for NP from (plain) learning with errors. Tech. rep., Cryptology ePrint Archive Report 2019/158 (2019). https://eprint.iacr.org/2019/158
Saia, J., Zamani, M.: Recent results in scalable multi-party computation. In: SOFSEM 2015: Proceedings of the Theory and Practice of Computer Science - 41st International Conference on Current Trends in Theory and Practice of Computer Science, 24–29 January 2015, Pec pod Sněžkou, Czech Republic, pp. 24–44 (2015)
Yao, A.C.C.: How to generate and exchange secrets. In: 27th Annual Symposium on Foundations of Computer Science, pp. 162–167. IEEE (1986)
Zamani, M., Movahedi, M., Saia, J.: Millions of millionaires: multiparty computation in large networks. IACR Cryptol. ePrint Arch. 2014, 149 (2014). https://eprint.iacr.org/2014/149
Acknowledgments
Arka Rai Choudhuri, Aarushi Goel and Abhishek Jain are supported in part by DARPA/ARL Safeware Grant W911NF-15-C-0213, NSF CNS-1814919, NSF CAREER 1942789, Samsung Global Research Outreach award and Johns Hopkins University Catalyst award. Arka Rai Choudhuri is also supported by NSF Grants CNS-1908181, CNS-1414023, and the Office of Naval Research Grant N00014-19-1-2294. Aarushi Goel is also supported in part by NSF Grants CNS-1653110 and CNS-1801479 and the Office of Naval Research under contract N00014-19-1-2292.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Ananth, P., Choudhuri, A.R., Goel, A., Jain, A. (2020). Towards Efficiency-Preserving Round Compression in MPC. In: Moriai, S., Wang, H. (eds) Advances in Cryptology – ASIACRYPT 2020. ASIACRYPT 2020. Lecture Notes in Computer Science(), vol 12493. Springer, Cham. https://doi.org/10.1007/978-3-030-64840-4_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-64840-4_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-64839-8
Online ISBN: 978-3-030-64840-4
eBook Packages: Computer ScienceComputer Science (R0)





 be the number of servers and
be the number of servers and  be the number of clients. If the computational cost of
be the number of clients. If the computational cost of 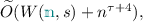 (and
(and 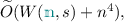 resp.), where the
resp.), where the  .
. in the semi-honest case and
in the semi-honest case and  in the malicious case.
in the malicious case. in the semi-honest case and
in the semi-honest case and  in the malicious case.
in the malicious case.

 .
. parties output by the compiler in Lemma
parties output by the compiler in Lemma  , and server
, and server 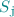 .
. 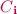 provides input
provides input  , and
, and  provides input
provides input  . Additionally, all servers (including
. Additionally, all servers (including 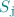 ) provide as input labels to a garbled circuit. The other clients do not have any inputs. The functionality outputs to all parties the projection of the labels corresponding to
) provide as input labels to a garbled circuit. The other clients do not have any inputs. The functionality outputs to all parties the projection of the labels corresponding to  . Since the parties have asymmetric roles, the next message function of this protocol additionally takes one of these labels as input
. Since the parties have asymmetric roles, the next message function of this protocol additionally takes one of these labels as input 

 :
:  indicates the special message sent from server indexed by
indicates the special message sent from server indexed by  to the server indexed by
to the server indexed by  . Other messages are denoted as previous sections with
. Other messages are denoted as previous sections with  ), servers (
), servers ( ) or all parties (
) or all parties ( .
.

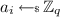 , from an exponentially sized field
, from an exponentially sized field 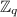 . This is to pick the relative position within the committee and trim the committee if needed.
. This is to pick the relative position within the committee and trim the committee if needed. unique to it. It then evaluates the VRF to determine if it is in the committee. It then computes the first round messages of the Phase one protocol, and also broadcasts the messages indicating it is in the committee.
unique to it. It then evaluates the VRF to determine if it is in the committee. It then computes the first round messages of the Phase one protocol, and also broadcasts the messages indicating it is in the committee.