Abstract
Threshold Private Set Intersection (PSI) allows multiple parties to compute the intersection of their input sets if and only if the intersection is larger than \(n-t\), where n is the size of each set and t is some threshold. The main appeal of this primitive is that, in contrast to standard PSI, known upper-bounds on the communication complexity only depend on the threshold t and not on the sizes of the input sets. Current threshold PSI protocols split themselves into two components: A Cardinality Testing phase, where parties decide if the intersection is larger than some threshold; and a PSI phase, where the intersection is computed. The main source of inefficiency of threshold PSI is the former part.
In this work, we present a new Cardinality Testing protocol that allows N parties to check if the intersection of their input sets is larger than \(n-t\). The protocol incurs in \(\tilde{ \mathcal {O}} (Nt^2)\) communication complexity. We thus obtain a Threshold PSI scheme for N parties with communication complexity \(\tilde{\mathcal {O}}(Nt^2)\).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
It is a slightly different problem from the one we solve in this work. Here, we want to disclosure the intersection \(\cap _{i=1}^N S_i\) if \(|\cap _{i=1}^N S_i|\ge n-t\), which is denoted as
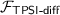 in [1].
in [1]. - 2.
Given this, we conclude that the communication complexity of the threshold PSI protocol of [17] is dominated by this Cardinality Testing protocol.
- 3.
We need a bit-conversion protocol such as [37] to convert between binary circuits and algebra operations.
- 4.
We actually need to randomize the polynomials in the numerator to guarantee correctness, that is, we need to multiply each term in the numerator by a uniformly chosen element. This is in contrast with the two-party setting where correctness holds even without randomizing the numerator. However, we omit this step for simplicity.
- 5.
- 6.
This is important to us since, in the threshols PSI setting, \(t\ll n\) where t is the threshold and n is the set size. Kiltz et al. solve linear algebra problems via minimal polynomials, and use adaptors between garbled circuits and additive homomorphic encryption to reduce round complexity. In this work, we extend Kiltz’s protocol to the multiparty case without using garbled circuits (otherwise the circuit size would depend on number of parties) while preserving the same communication complexity for each party (\(\mathcal {O}(t^2)\)).
- 7.
We will assume the message space of Paillier’s cryptosystem as a field as also mentioned in [24].
- 8.
We refer the reader to [7] for a detailed explanation of the framework.
- 9.
A support set is a set of pairs (x, y).
- 10.
Note that this is the linear system that we need to solve in order to perform rational interpolation [28].
- 11.
The polynomial multiplication can be expressed as matrix multiplication.
- 12.
In the case that only \(Q(\alpha _i)=0\), use a different tagged pair
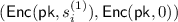 , and this can be noticed by the party who owns polynomial Q(x). In our PSI setting, it is party \(\mathsf {P}_1\).
, and this can be noticed by the party who owns polynomial Q(x). In our PSI setting, it is party \(\mathsf {P}_1\). - 13.
Here, \(\mathcal {F}_\mathsf {SDT}\) has shared functionality \(\mathcal {F}_\mathsf {Gen}\).
- 14.
From now on, we always assume that PKE and TPKE used in this work fulfill this property, unless stated otherwise.
References
Badrinarayanan, S., Miao, P., Raghuraman, S., Rindal, P.: Multi-party threshold private set intersection with sublinear communication. In: PKC 2021 (2021)
Berke, A., Bakker, M., Vepakomma, P., Larson, K., Pentland, A.S.: Assessing disease exposure risk with location data: a proposal for cryptographic preservation of privacy (2020). https://arxiv.org/abs/2003.14412
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_3
Boneh, D., Goh, E.-J., Nissim, K.: Evaluating 2-DNF formulas on ciphertexts. In: Kilian, J. (ed.) TCC 2005. LNCS, vol. 3378, pp. 325–341. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-30576-7_18
Bouman, N.J., de Vreede, N.: New protocols for secure linear algebra: pivoting-free elimination and fast block-recursive matrix decomposition. IACR Cryptology ePrint Archive 2018/703 (2018)
Branco, P., Döttling, N., Pu, S.: Multiparty cardinality testing for threshold private set intersection. Cryptology ePrint Archive, Report 2020/1307 (2020). https://eprint.iacr.org/2020/1307
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: 42nd Annual Symposium on Foundations of Computer Science, Las Vegas, NV, USA, 14–17 October 2001, pp. 136–145. IEEE Computer Society Press. https://doi.org/10.1109/SFCS.2001.959888
Canetti, R., Dodis, Y., Pass, R., Walfish, S.: Universally composable security with global setup. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 61–85. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_4
Cramer, R., Damgård, I.: Secure distributed linear algebra in a constant number of rounds. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 119–136. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_7
Cramer, R., Damgård, I., Nielsen, J.B.: Multiparty computation from threshold homomorphic encryption. In: Pfitzmann, B. (ed.) EUROCRYPT 2001. LNCS, vol. 2045, pp. 280–300. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44987-6_18
Dachman-Soled, D., Malkin, T., Raykova, M., Yung, M.: Efficient robust private set intersection. In: Abdalla, M., Pointcheval, D., Fouque, P.-A., Vergnaud, D. (eds.) ACNS 2009. LNCS, vol. 5536, pp. 125–142. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01957-9_8
De Cristofaro, E., Kim, J., Tsudik, G.: Linear-complexity private set intersection protocols secure in malicious model. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 213–231. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_13
Dong, C., Chen, L., Wen, Z.: When private set intersection meets big data: an efficient and scalable protocol. In: Sadeghi, A.R., Gligor, V.D., Yung, M. (eds.) ACM CCS 2013: 20th Conference on Computer and Communications Security, Berlin, Germany, 4–8 November 2013, pp. 789–800. ACM Press (2013). https://doi.org/10.1145/2508859.2516701
Elgamal, T.: A public key cryptosystem and a signature scheme based on discrete logarithms. IEEE Trans. Inf. Theory 31(4), 469–472 (1985)
Freedman, M.J., Nissim, K., Pinkas, B.: Efficient private matching and set intersection. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 1–19. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_1
Ghosh, S., Nilges, T.: An algebraic approach to maliciously secure private set intersection. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part III. LNCS, vol. 11478, pp. 154–185. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_6
Ghosh, S., Simkin, M.: The communication complexity of threshold private set intersection. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part II. LNCS, vol. 11693, pp. 3–29. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26951-7_1
Ghosh, S., Simkin, M.: The communication complexity of threshold private set intersection. Cryptology ePrint Archive, Report 2019/175 (2019). https://eprint.iacr.org/2019/175
Grigorescu, E., Jung, K., Rubinfeld, R.: A local decision test for sparse polynomials. Inf. Process. Lett. 110(20), 898–901 (2010). https://doi.org/10.1016/j.ipl.2010.07.012
Hallgren, P., Orlandi, C., Sabelfeld, A.: Privatepool: privacy-preserving ridesharing. In: 2017 IEEE 30th Computer Security Foundations Symposium (CSF), pp. 276–291 (2017)
Hazay, C., Venkitasubramaniam, M.: Scalable multi-party private set-intersection. In: Fehr, S. (ed.) PKC 2017, Part I. LNCS, vol. 10174, pp. 175–203. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54365-8_8
Ion, M., Kreuter, B., Nergiz, E., Patel, S., Saxena, S., Seth, K., Shanahan, D., Yung, M.: Private intersection-sum protocol with applications to attributing aggregate ad conversions. Cryptology ePrint Archive, Report 2017/738 (2017). http://eprint.iacr.org/2017/738
Kaltofen, E., David Saunders, B.: On Wiedemann’s method of solving sparse linear systems. In: Mattson, H.F., Mora, T., Rao, T.R.N. (eds.) AAECC 1991. LNCS, vol. 539, pp. 29–38. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-54522-0_93
Kiltz, E., Mohassel, P., Weinreb, E., Franklin, M.: Secure linear algebra using linearly recurrent sequences. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 291–310. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_16
Kissner, L., Song, D.: Privacy-preserving set operations. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 241–257. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_15
Kolesnikov, V., Kumaresan, R., Rosulek, M., Trieu, N.: Efficient batched oblivious PRF with applications to private set intersection. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S. (eds.) ACM CCS 2016: 23rd Conference on Computer and Communications Security, Vienna, Austria, 24–28 October 2016, pp. 818–829. ACM Press (2016). https://doi.org/10.1145/2976749.2978381
Meadows, C.: A more efficient cryptographic matchmaking protocol for use in the absence of a continuously available third party. In: 1986 IEEE Symposium on Security and Privacy, pp. 134–134 (1986)
Minsky, Y., Trachtenberg, A., Zippel, R.: Set reconciliation with nearly optimal communication complexity. IEEE Trans. Inf. Theory 49(9), 2213–2218 (2003). https://doi.org/10.1109/TIT.2003.815784
Nissim, K., Weinreb, E.: Communication efficient secure linear algebra. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 522–541. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_27
Paillier, P.: Public-key cryptosystems based on composite degree residuosity classes. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 223–238. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_16
Pinkas, B., Rosulek, M., Trieu, N., Yanai, A.: SpOT-light: lightweight private set intersection from sparse OT extension. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part III. LNCS, vol. 11694, pp. 401–431. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_13
Pinkas, B., Schneider, T., Segev, G., Zohner, M.: Phasing: private set intersection using permutation-based hashing. In: Jung, J., Holz, T. (eds.) USENIX Security 2015: 24th USENIX Security Symposium, Washington, DC, USA, 12–14 August 2015, pp. 515–530. USENIX Association (2015)
Pinkas, B., Schneider, T., Weinert, C., Wieder, U.: Efficient circuit-based PSI via cuckoo hashing. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part III. LNCS, vol. 10822, pp. 125–157. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78372-7_5
Pinkas, B., Schneider, T., Zohner, M.: Faster private set intersection based on OT extension. In: Fu, K., Jung, J. (eds.) USENIX Security 2014: 23rd USENIX Security Symposium, San Diego, CA, USA, 20–22 August 2014, pp. 797–812. USENIX Association (2014)
Rindal, P., Rosulek, M.: Improved private set intersection against malicious adversaries. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part I. LNCS, vol. 10210, pp. 235–259. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_9
Rindal, P., Rosulek, M.: Malicious-secure private set intersection via dual execution. In: Thuraisingham, B.M., Evans, D., Malkin, T., Xu, D. (eds.) ACM CCS 2017: 24th Conference on Computer and Communications Security, Dallas, TX, USA, 31 October–2 November 2017, pp. 1229–1242. ACM Press (2017). https://doi.org/10.1145/3133956.3134044
Schoenmakers, B., Tuyls, P.: Efficient binary conversion for Paillier encrypted values. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 522–537. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_31
Acknowledgment
Pedro Branco: Part of this work was done while the author was at CISPA. The author is supported by DP-PMI and FCT (Portugal) through the grant PD/BD/135181/2017. This work is supported by Security and Quantum Information Group of Instituto de Telecomunicações, by the Fundaçõo para a Ciência e a Tecnologia (FCT) through national funds, by FEDER, COMPETE 2020, and by Regional Operational Program of Lisbon, under UIDB/50008/2020.
Nico Döttling: Part of this work was done while visiting Simons Institute, Berkeley, California. This work is partially funded by the Helmholtz Association within the project “Trustworthy Federated Data Analytics” (TFDA) (funding number ZT-I-OO1 4).
Sihang Pu: Part of this work was done while visiting Simons Institute, Berkeley, California.
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Appendices
A Preliminaries Cont’d
1.1 A.1 Threshold Public-Key Encryption
In this work, we will use Public-Key Encryption schemes and a variant of it: Threshold Public-key Encryption. We now define Threshold Public-key Encryption. Such schemes can be instantiated from several hardness assumptions such as DDH, DCR or pairing-based assumptions [21].
Definition 3
(Threshold Public-Key Encryption). A Threshold Public-Key Encryption (TPKE) scheme is defined by the following algorithms:
-
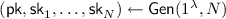 takes as input a security parameter. It outputs a public key
takes as input a security parameter. It outputs a public key 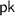 and N secret keys
and N secret keys  .
. -
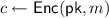 takes as input a public key
takes as input a public key 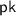 and a message \(m\in \{0,1\}^*\). It outputs a ciphertext c.
and a message \(m\in \{0,1\}^*\). It outputs a ciphertext c. -
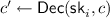 takes as input one of the secret keys
takes as input one of the secret keys 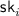 and a ciphertext. It outputs a share decryption \(c'\) of c.
and a ciphertext. It outputs a share decryption \(c'\) of c.
Correctness. For any \(N\in \mathbb {N}\) and any permutation \(\pi :[N]\rightarrow [N]\), we have that

where  .
.
IND-CPA Security. For any \(N\in \mathbb {N}\), any permutation \(\pi :[N]\rightarrow [N]\) and any adversary \(\mathcal {A}\), we require that

for any \(k<N\).
Additive Homomorphism. We also assume that the TPKE (or plain PKE) is homomorphic for additive operation.Footnote 14 That is, for all  , we can define two groups \((\mathcal {M},\oplus ),(\mathcal {C},\otimes )\) such that, given two ciphertexts
, we can define two groups \((\mathcal {M},\oplus ),(\mathcal {C},\otimes )\) such that, given two ciphertexts  and
and  , we require that
, we require that

By abuse of notation, we usually denote the operations of \(\mathcal {M}\) and \(\mathcal {C}\) as \(+\).
1.2 A.2 Linear Algebra
We first introduce minimal polynomials of a sequence and of a matrix. Then we present how they can be used to solve linear algebra related problems.
Minimal Polynomial of a Matrix. The minimal polynomial of a sequence \(\mathfrak {a}\) is the least degree polynomial m such that \(\langle m\rangle = Ann (\mathfrak a)\) where \( Ann (\mathfrak a)\) is the annihilator ideal of \(\mathfrak a\) (that is, the ideal such that every element f of \( Ann (\mathfrak a)\) satisfies \(f\cdot \mathfrak a=0\)).
Lemma 6
(Lemma 3 in [24]). Let \(\mathbf {A}\in \mathbb {F}^{n\times n}\) and let \(m_\mathbf {A}\) be the minimal polynomial of matrix \(\mathbf {A}\). For  , we have \(m_\mathbf {A}= m_{\mathfrak {a}'}\) with probability at least \(1-2\deg (m_\mathbf {A})/|\mathbb {F}|\), where \(\mathfrak {a}'=(\mathbf {u}^{\mathsf {T}} \mathbf {A}^i \mathbf {v})_{i\in \mathbb {N}}\). Moreover, \(m_{\mathfrak {a}'}\) can be calculated using a Boolean circuit of size \(\mathcal {O}(nk\log n\log k\log \log k)\) where \(k=\log |\mathbb {F}|\).
, we have \(m_\mathbf {A}= m_{\mathfrak {a}'}\) with probability at least \(1-2\deg (m_\mathbf {A})/|\mathbb {F}|\), where \(\mathfrak {a}'=(\mathbf {u}^{\mathsf {T}} \mathbf {A}^i \mathbf {v})_{i\in \mathbb {N}}\). Moreover, \(m_{\mathfrak {a}'}\) can be calculated using a Boolean circuit of size \(\mathcal {O}(nk\log n\log k\log \log k)\) where \(k=\log |\mathbb {F}|\).
Compute the Rank of a Matrix and Solve a Linear System
Lemma 7
([23]). Let \(\mathbf {A}\in \mathbb {F}^{n\times n}\) of (unknown) rank r. Let \(\mathbf {U}\) and \(\mathbf {L}\) be randomly chosen unit upper triangular and lower triangular Toeplitz matrices in \(\mathbb {F}^{n\times n}\), and let \(\mathbf {B}=\mathbf {U}\mathbf {A}\mathbf {L}\). Let us denote the \(i\times i\) leading principal of \(\mathbf {B}\) by \(\mathbf {B}_i\). The probability that \(\det (\mathbf {B}_i) \ne 0\) for all \(1\le i\le r\) is greater than \(1-n^2/|\mathbb {F}|\).
Lemma 8
([23]). Let \(\mathbf {B}\in \mathbb {F}^{n\times n}\) with leading invertible principals up to \(\mathbf {B}_r\) where r is the (unknown) rank of \(\mathbf {B}\). Let \(\mathbf {X}\) be a randomly chosen diagonal matrix in \(\mathbb {F}^{n\times n}\). Then, \(r = \deg (m_{\mathbf {X}\mathbf {B}})-1\) with probability greater than \(1-n^2/|\mathbb {F}|\).
B Oblivious Linear Algebra
1.1 B.1 Oblivious Matrix Multiplication
Protocol. The following Protocol 4 allows several parties to jointly compute the (encrypted) product of two encrypted matrices. Note that the protocol can also be used to compute the encryption of the product of two encrypted values in \(\mathbb {F}\).

Analysis. We proceed to the analysis of the protocol described above.
Lemma 9
(Correctness). The protocol \(\mathsf {secMult}\) is correct.
Proof
The correctness is straightforward. \(\Box \)
Lemma 10
(Security). The protocol \(\mathsf {secMult}\) securely EUC-realizes \(\mathcal {F}_{\mathsf {OMM}}\) with shared ideal functionality \(\mathcal {F}_\mathsf {Gen}\) against semi-honest adversaries corrupting up to \(N-1\) parties, given that \(\mathsf {TPKE}\) is IND-CPA.
Proof
(Sketch). Assume that the adversary corrupts \(N-k\) parties. The simulator takes the inputs from these parties and send them to the ideal functionality. Upon receiving the encrypted value  , it simulates the protocol as the honest parties would do.
, it simulates the protocol as the honest parties would do.
We now prove that no set of at most \(N-1\) colluding parties can extract information about \(\mathbf {M}_l,\mathbf {M}_r\). First, observe that any set of \(N-1\) parties cannot extract any information about encrypted values that are not decrypted during the protocol (because there is always a missing secret key share) given that \(\mathsf {TPKE}\) is IND-CPA. Second, we analyze the matrix \(\mathbf {M}_l'\) (which is decrypted during the protocol). We have that \(\mathbf {M}_l'=\mathbf {M}_l+\sum _j \mathbf {R}_l^{(j)}\). Hence, there is always at least one matrix \(\mathbf {R}_l^{(\ell )}\) which is unknown to the adversary and that perfectly hides the matrix \(\mathbf {M}_l\) (the same happens \(\mathbf {M}_r'\). \(\Box \)
Complexity. The communication complexity of the protocol is dominated by the messages carrying the (encrypted) matrix. Hence, assuming a broadcast channel between the parties, the protocol has communication complexity of \(\mathcal {O}(Nt^2)\) where t is the size of the input matrices and N the number of parties involved in the protocol.
1.2 B.2 Compute the Rank of a Matrix
Protocol. We present this protocol in the full version of this paper in [6].
Complexity. Each party broadcasts \(\mathcal {O}(t^2k\log t)\) bits of information, where \(k=\log | \mathbb {F}|\). To see this, note that the communication of the protocol is dominated by the computation of the circuit that computes the degree of \(\mathfrak {a}\) and this can be implemented with communication cost of \(\mathcal {O}(t^2k\log t)\) [24]. Assuming a broadcast channel, the communication complexity is \(\tilde{\mathcal {O}}(Nt^2)\).
1.3 B.3 Invert a Matrix
In this section, we present and analyze a protocol that allows N parties to invert an encrypted matrix. In this setting, each of the N parties holds a secret share of a public key  of a TPKE. Given an encrypted matrix, they want to compute an encryption of the inverse of this matrix.
of a TPKE. Given an encrypted matrix, they want to compute an encryption of the inverse of this matrix.
Ideal Functionality. The ideal functionality of oblivious rank computation is defined below.

Protocol. This protocol allows N parties to jointly compute the encryption of the inverse of a matrix, given that this matrix is non-singular. Please refer to the full version of this paper in [6] to see details.
Analysis. The proofs of the following lemmas follow the same lines as the proofs in the analysis of \(\mathsf {secMult}\) protocol. We state the lemmas but omit the proofs for briefness.
Lemma 11
The protocol \(\mathsf {secInv}\) is correct.
Lemma 12
The protocol \(\mathsf {secInv}\) securely EUC-realizes \(\mathcal {F}_\mathsf {OInv}\) with shared ideal functionality \(\mathcal {F}_\mathsf {Gen}\) against semi-honest adversaries corrupting up to \(N-1\) parties, given that \(\mathsf {TPKE}\) is IND-CPA.
Complexity. Each party broadcasts \(\mathcal {O}(t^2)\) bits of information. The communication complexity of the protocol is \(\mathcal {O}(Nt^2)\), assuming a broadcast channel.
1.4 B.4 Secure Unary Representation
Following [24], we present a protocol that allows to securely compute the unary representation of a matrix.
Ideal Functionality. The ideal functionality for Secure Unary Representation is given below.

Protocol. A protocol for secure unary representation can be implemented with the help of a binary-conversion protocol [37]. That is, given  , all parties jointly compute
, all parties jointly compute  , where \(\delta _i=1\), if \(i\le r\), and \(\delta _i=0\) otherwise, via a Boolean circuit (which can be securely implemented based on Paillier cryptosystem).
, where \(\delta _i=1\), if \(i\le r\), and \(\delta _i=0\) otherwise, via a Boolean circuit (which can be securely implemented based on Paillier cryptosystem).
Communication Complexity. We can calculate the result using a Boolean circuit of size \(O(r\log t)\), thus the communication complexity is \(O(Nr\log t)\).
1.5 B.5 Solve a Linear System
Protocol. We now present the Protocol 5 that allows multiple parties to solve an encrypted linear system. In the following, we assume that the system has at least one solution (note that this can be guaranteed using the \(\mathsf {secRank}\) protocol).

Lemma 13
(Correctness). The protocol \(\mathsf {secLS}\) is correct.
Proof
The proof follows directly from [23, 24]. \(\Box \)
Lemma 14
The protocol \(\mathsf {secLS}\) securely EUC-realizes \(\mathcal {F}_\mathsf {OLS}\) with shared ideal functionality \(\mathcal {F}_\mathsf {Gen}\) in the \((\mathcal {F}_\mathsf {ORank},\mathcal {F}_\mathsf {OInv},\mathcal {F}_\mathsf {SUR})\)-hybrid model against semi-honest adversaries corrupting up to \(N-1\) parties, given that \(\mathsf {TPKE}\) is IND-CPA.
Communication Complexity. Each party broadcasts \(\mathcal {O}(t^2k\log t)\) bits of information where \(k=|\mathbb {F}|\). The total communication complexity is \(\tilde{\mathcal {O}}(t^2)\).
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Branco, P., Döttling, N., Pu, S. (2021). Multiparty Cardinality Testing for Threshold Private Intersection. In: Garay, J.A. (eds) Public-Key Cryptography – PKC 2021. PKC 2021. Lecture Notes in Computer Science(), vol 12711. Springer, Cham. https://doi.org/10.1007/978-3-030-75248-4_2
Download citation
DOI: https://doi.org/10.1007/978-3-030-75248-4_2
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-75247-7
Online ISBN: 978-3-030-75248-4
eBook Packages: Computer ScienceComputer Science (R0)


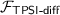 in [
in [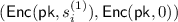 , and this can be noticed by the party who owns polynomial Q(x). In our PSI setting, it is party
, and this can be noticed by the party who owns polynomial Q(x). In our PSI setting, it is party 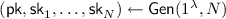 takes as input a security parameter. It outputs a public key
takes as input a security parameter. It outputs a public key  and N secret keys
and N secret keys  .
.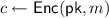 takes as input a public key
takes as input a public key 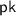 and a message
and a message 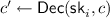 takes as input one of the secret keys
takes as input one of the secret keys 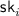 and a ciphertext. It outputs a share decryption
and a ciphertext. It outputs a share decryption 