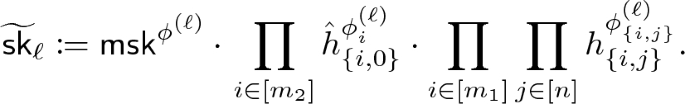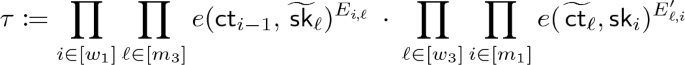Abstract
Attribute-based encryption (ABE) is a cryptographic primitive which supports fine-grained access control on encrypted data, making it an appealing building block for many applications. Pair encodings (Attrapadung, EUROCRYPT 2014) are simple primitives that can be used for constructing fully secure ABE schemes associated to a predicate relative to the encoding. We propose a generic transformation that takes any pair encoding scheme (PES) for a predicate \(P\) and produces a PES for its negated predicate \(\bar{P}\). This construction finally solves a problem that was open since 2015. Our techniques bring new insight to the expressivity and generality of PES and can be of independent interest. We also provide, to the best of our knowledge, the first pair encoding scheme for negated doubly spatial encryption (obtained with our transformation) and explore several other consequences of our results.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In fact, it is known that predicate encodings are a subclass of pair encodings [3].
- 2.
In some literature, the number of non-lone ciphertext variables is defined as \(w_1{+}1\), since the special variable \(s_0\) is treated separately. Observe that our vector of non-lone variables ranges from \(s_0\) to \(s_{w_1{-}1}\), this is for the sake of notation in further sections.
- 3.
Recall that
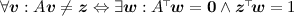 for all compatible A and \(\varvec{z}\).
for all compatible A and \(\varvec{z}\). - 4.
That way, the witness of non-reconstructability can be used as the linear combination for decryption (reconstructability) in the negated encoding and vice versa: the solution for reconstructability can be used as the witness of security in the negated encoding.
- 5.
An easy way of arguing that this is w.l.o.g. is to apply the generic dual transformation defined in [10] twice. (Note that the dual operation is an involution and a double application of it would preserve the original predicate.).
- 6.
Recall that we are assuming, without loss of generality, that the first polynomial produced by \(\mathsf{EncKey}\) is \(\alpha + r_1b_1\) and that \(\alpha \) does not appear anywhere else.
- 7.
To see why, set the matrices in Lemma 2 to
 ,
,  , for \(i \in [n]\) and
, for \(i \in [n]\) and 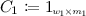 ,
,  for \(j \in [2,n]\). Also,
for \(j \in [2,n]\). Also,  and
and 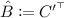 .
. - 8.
Spatial encryption is already a quite powerful predicate, that generalizes hierarchical identity-based encryption (HIBE).
- 9.
Before applying the transformation, we rename \(b_0 \mapsto t\), \(b_{d{+}1} \mapsto u\), \(b_{d{+}2} \mapsto v\). After the transformation, the two new common variables are named \(b_0\) and w respectively.
- 10.
We denote by coCFL the class of languages whose complement is context-free.
- 11.
See the ABE compiler from PES described in Appendix B.2.
References
Agrawal, S., Chase, M.: A study of pair encodings: predicate encryption in prime order groups. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016, Part II. LNCS, vol. 9563, pp. 259–288. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49099-0_10
Agrawal, S., Chase, M.: Simplifying design and analysis of complex predicate encryption schemes. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part I. LNCS, vol. 10210, pp. 627–656. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_22
Ambrona, M., Barthe, G., Schmidt, B.: Generic transformations of predicate encodings: constructions and applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 36–66. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_2
Attrapadung, N.: Dual system encryption via doubly selective security: framework, fully secure functional encryption for regular languages, and more. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 557–577. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_31
Attrapadung, N.: Dual system encryption framework in prime-order groups via computational pair encodings. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016, Part II. LNCS, vol. 10032, pp. 591–623. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_20
Attrapadung, N.: Unbounded dynamic predicate compositions in attribute-based encryption. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part I. LNCS, vol. 11476, pp. 34–67. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_2
Attrapadung, N., Imai, H.: Dual-policy attribute based encryption. In: Abdalla, M., Pointcheval, D., Fouque, P.-A., Vergnaud, D. (eds.) ACNS 2009. LNCS, vol. 5536, pp. 168–185. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-01957-9_11
Attrapadung, N., Libert, B.: Functional encryption for inner product: achieving constant-size ciphertexts with adaptive security or support for negation. In: Nguyen, P.Q., Pointcheval, D. (eds.) PKC 2010. LNCS, vol. 6056, pp. 384–402. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13013-7_23
Attrapadung, N., Tomida, J.: Unbounded dynamic predicate compositions in ABE from standard assumptions. In: Moriai, S., Wang, H. (eds.) ASIACRYPT 2020, Part III. LNCS, vol. 12493, pp. 405–436. Springer, Cham (2020). https://doi.org/10.1007/978-3-030-64840-4_14
Attrapadung, N., Yamada, S.: Duality in ABE: converting attribute based encryption for dual predicate and dual policy via computational encodings. In: Nyberg, K. (ed.) CT-RSA 2015. LNCS, vol. 9048, pp. 87–105. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16715-2_5
Beimel, A.: Secret-sharing schemes: a survey. In: Chee, Y.M., et al. (eds.) IWCC 2011. LNCS, vol. 6639, pp. 11–46. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20901-7_2
Boneh, D., Boyen, X.: Efficient selective identity-based encryption without random oracles. J. Cryptol. 24(4), 659–693 (2011)
Boneh, D., Hamburg, M.: Generalized identity based and broadcast encryption schemes. In: Pieprzyk, J. (ed.) ASIACRYPT 2008. LNCS, vol. 5350, pp. 455–470. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-89255-7_28
Chatterjee, S., Mukherjee, S., Pandit, T.: CCA-secure predicate encryption from pair encoding in prime order groups: generic and efficient. In: Patra, A., Smart, N.P. (eds.) INDOCRYPT 2017. LNCS, vol. 10698, pp. 85–106. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-71667-1_5
Chen, J., Gay, R., Wee, H.: Improved dual system ABE in prime-order groups via predicate encodings. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part II. LNCS, vol. 9057, pp. 595–624. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_20
Chen, J., Wee, H.: Fully, (almost) tightly secure IBE and dual system groups. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part II. LNCS, vol. 8043, pp. 435–460. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_25
Chen, J., Wee, H.: Dual system groups and its applications – compact HIBE and more. Cryptology ePrint Archive, Report 2014/265 (2014). http://eprint.iacr.org/2014/265
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 545–554. ACM Press, June 2013
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: Juels, A., Wright, R.N., De Capitani di Vimercati, S. (eds.) ACM CCS 2006, pp. 89–98. ACM Press, October/November 2006. Available as Cryptology ePrint Archive Report 2006/309
Hamburg, M.: Spatial encryption. Cryptology ePrint Archive, Report 2011/389 (2011). http://eprint.iacr.org/2011/389
Hopcroft, J.E., Ullman, J.D.: Introduction to Automata Theory, Languages and Computation. Addison-Wesley, Boston (1979)
Karchmer, M., Wigderson, A.: On span programs. In: Proceedings of Structures in Complexity Theory, pp. 102–111 (1993)
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_9
Kim, J., Susilo, W., Guo, F., Au, M.H.: A tag based encoding: an efficient encoding for predicate encryption in prime order groups. In: Zikas, V., De Prisco, R. (eds.) SCN 2016. LNCS, vol. 9841, pp. 3–22. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-44618-9_1
Lewko, A., Waters, B.: New techniques for dual system encryption and fully secure HIBE with short ciphertexts. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 455–479. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_27
Lewko, A., Waters, B.: Unbounded HIBE and attribute-based encryption. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 547–567. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20465-4_30
Lewko, A.B., Waters, B.: New proof methods for attribute-based encryption: achieving full security through selective techniques. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 180–198. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_12
Ostrovsky, R., Sahai, A., Waters, B.: Attribute-based encryption with non-monotonic access structures. In: Ning, P., De Capitani di Vimercati, S., Syverson, P.F. (eds.) ACM CCS 2007, pp. 195–203. ACM Press, October 2007
Rouselakis, Y., Waters, B.: Practical constructions and new proof methods for large universe attribute-based encryption. In: Sadeghi, A.-R., Gligor, V.D., Yung, M. (eds.) ACM CCS 2013, pp. 463–474. ACM Press, November 2013
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_5
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_36
Waters, B.: Functional encryption for regular languages. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 218–235. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_14
Wee, H.: Dual system encryption via predicate encodings. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 616–637. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_26
Acknowledgment
I would like to express my sincere gratitude to Nuttapong Attrapadung, for very fruitful discussions at the early stages of this project, and for pointing out that the transformation described herein would lead to an encoding for negated doubly spatial encryption. I would also like to thank Mehdi Tibouchi, for his help with the formulation of Lemma 1, which led to a simple proof for Lemma 2; and Elena Gutiérrez, for her advice on automata theory, and for all her feedback. Finally, I would like to thank the anonymous reviewers of PKC 2021, for their valuable time and multiple suggestions.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Pair Encoding for Negated Doubly Spatial Encryption
1.1 A.1 Building the Encoding
A direct application of our negated transformation (Fig. 1) to the encoding for doubly spatial encryption from [4] (after minor modifications so that it satisfies our structural constraints) leads to the encoding from Fig. 3. This encoding can be simplified, as the following reasoning shows that not all the polynomials are needed for reconstructability.
The only way to get polynomial \(s_0r_1b_0\) (and consequently \(\alpha s_0\)) as a linear combination of polynomials from \(L = \varvec{s} \otimes \varvec{k} \,\cup \, \varvec{c} \otimes \varvec{r}\) is through the two first polynomials in the key (multiplied by \(s_0\)): \(s_0r_1b_0 + s_0r_1w\) and \(s_0r_1b_0 + s_0r_1t\). For that, we need to express monomial \(s_0r_1w\) or monomial \(s_0r_1t\) as a linear combination of other polynomials in L. The former is impossible to obtain (since monomial \(s_0r_1w\) does not appear in any other polynomial in L). The latter can be achieved only through polynomial \(r_1s_0t - r_1\hat{s}_1 \in L\). Again, that requires to arrive at polynomial \(r_1\hat{s}_1\), which is present only in \(r_1s_1v - r_1\hat{s}_1\). Furthermore, \(r_1s_1v\) can only be (additionally) found in \(s_1r_1v + s_1\hat{r}_1\). However, \(s_1\hat{r}_1\) is present in several polynomials in L, namely: \(s_1r_2u + s_1\hat{r}_1\) and \(s_1(Y_j\hat{\varvec{r}}' + r_2b_{j} + \hat{r}_1 {y}_j)_{j \in [d]}\). The former contains a monomial, \(s_1r_2u\), that only additionally appears in \(r_2s_1u - r_2\hat{s}_2\), but \(r_2\hat{s}_2\) is only present in polynomials \(r_2(X_j\hat{\varvec{s}}' - s_1 b_{j} + \hat{s}_2 {x}_j)_{j \in [d]}\). Consequently, reconstructability will be possible if there exist coefficients \(\beta _j\) and \(\gamma _j\) for all \(j \in [0,d]\) such that:

Considering the different monomials in both sides of the equation, we deduce:

Consequently, reconstructability is possible if there exist coefficients \(\beta _j\) for all \(j \in [d]\) such that:

But this is equivalent to \(\varvec{y}-\varvec{x} \notin \mathrm{span}(Y) \cup \mathrm{span}(X)\) (see Lemma 1) which holds if and only if the predicate is true, as needed.
All the polynomials in the key and the ciphertext which have not been used for reconstructability can be eliminated. Figure 2 describes the resulting encoding after this simplification.
1.2 A.2 Arguing Security
Our Theorem 2 guarantees that the encoding from Fig. 3 is secure. Note that removing polynomials cannot change security (only spoil reconstructability), so the simpler scheme presented in the main body (Fig. 2) must also be secure. Nevertheless, we provide an independent proof of its security, for the sake of completeness.
Proof
(Security of the encoding from Fig. 2). Assume the predicate is false, i.e., the affine spaces \(\varvec{x} + \mathrm{span}(X)\) and \(\varvec{y} + \mathrm{span}(Y)\) intersect. Let \(\varvec{z} \in \mathbb {Z}_N^{d}\) be a vector in their intersection and let \(\varvec{z_x} \in \mathbb {Z}_N^{\ell }\) and \(\varvec{z_y} \in \mathbb {Z}_N^{\ell '}\) be such that:
Observe that all the polynomials in \(\mathsf{EncKey}(N,(\varvec{y},Y))\) and \(\mathsf{EncCt}(N, (\varvec{x},X))\) (see Fig. 2) evaluate to zero on the following substitution:
but polynomial \(\alpha s_0\) evaluates to \(-1\) (\(\ne 0\)). As explained in Example 1, this is an evidence of the security of the encoding.
B Additional Definitions
1.1 B.1 Security of Attribute-Based Encryption
An ABE scheme is adaptively secure if there exists a negligible \(\epsilon \) such that for all PPT adversaries \(\mathcal{A}\), and all sufficiently large \(\lambda \in \mathbb {N}\), \(\mathsf{Adv}_{\mathcal{A}}^\mathsf{ABE}(\lambda ) < \epsilon (\lambda )\), where:

where the advantage is defined to be zero if some of the queries y made by \(\mathcal{A}\) to the \(\mathsf{KeyGen}\) oracle violates the condition \(P(x^\star ,y) = 0\).
1.2 B.2 Attribute-Based Encryption from Pair Encodings
In order to explain how to build attribute-based encryption from pair encodings, we need to introduce the notion of dual system groups (DSG) [2, 16, 17], since the compilers from pair encodings into ABE [1, 5] rely on DSG in a black-box way.
Dual System Groups
A dual system group is a tuple of six efficiently computable algorithms:
-
\(\mathsf{SampP}(1^\lambda , 1^n)\): on input the security parameter and an integer n, outputs public parameters \(\mathsf {pp}\) and secret parameters \(\mathsf {sp}\) such that:
- \(\circ \):
-
The public parameters, \(\mathsf {pp}\), include a triple of abelian groups \((\mathsf{G},\mathsf{H},\mathsf{G}_{\mathsf{t}})\) (that are \(\mathbb {Z}_p\)-modules for some \(\lambda \)-bits prime p), a non-degenerate bilinear map \(e : \mathsf{G}\times \mathsf{H}\rightarrow \mathsf{G}_{\mathsf{t}}\), an homomorphism \(\mu \) (defined over \(\mathsf{H}\)) and additional parameters required by \(\mathsf{SampP}\) and \(\mathsf{SampH}\).
- \(\circ \):
-
Given \(\mathsf {pp}\), it is possible to uniformly sample to \(\mathsf{H}\).
- \(\circ \):
-
The secret parameters, \(\mathsf {sp}\), include a distinguished element \(h^* \in \mathsf{H}\) (different from the unit) and additional parameters required by
 and
and  .
.
-
\(\mathsf{SampG}(\mathsf {pp})\) and
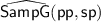 output an element from \(\mathsf{G}^{n{+}1}\).
output an element from \(\mathsf{G}^{n{+}1}\). -
\(\mathsf{SampH}(\mathsf {pp})\) and
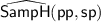 output an element from \(\mathsf{H}^{n{+}1}\).
output an element from \(\mathsf{H}^{n{+}1}\). -
\(\mathsf{SampGT}\) is a function defined from \(\mathrm{Im}(\mu )\) to \(\mathsf{G}_{\mathsf{t}}\).
Additional conditions are required for correctness and security:
-
projective: For all public parameters, \(\mathsf {pp}\), every \(h \in \mathsf{H}\) and all coin tosses \(\sigma \), it holds \(\mathsf{SampGT}(\mu (h); \sigma ) = e(g_0, h)\), where \((g_0, g_1,\dots ,g_n) \leftarrow \mathsf{SampG}(\mathsf {pp}; r)\).
-
associative: Let \((g_0,g_1,\dots ,g_n) \leftarrow \mathsf{SampG}(\mathsf {pp})\), \((h_0,h_1,\dots ,h_n) \leftarrow \mathsf{SampH}(\mathsf {pp})\), it holds \(e(g_0, h_i) = e(g_i, h_0)\) for every \(i \in [n]\).
-
\(\mathsf{H}\)-subgroup: \(\mathsf{SampH}(\mathsf {pp})\) is the uniform distribution over a subgroup of \(\mathsf{H}^{n{+}1}\).
-
orthogonality: \(h^* \in \mathrm{Kernel}(\mu )\).
-
non-degeneracy: For every \((h_0,h_1,\dots ,h_n) \leftarrow \mathsf{SampH}(\mathsf {pp})\), \(h^* \in \langle h_0 \rangle \). Furthermore, for every
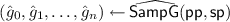 ,
, 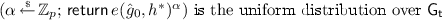 .
. -
left-subgroup indistinguishability: \((\mathsf {pp},\, \varvec{g}) \approx _{c}(\mathsf {pp},\, \varvec{g}{\cdot } \varvec{\hat{g}})\).
-
right-subgroup indistinguishability: \((\mathsf {pp},\, h^*,\, \varvec{g} {\cdot } \varvec{\hat{g}},\, \varvec{h}) \approx _{c}(\mathsf {pp},\, h^*,\, \varvec{g} {\cdot } \varvec{\hat{g}},\, \varvec{h} {\cdot } \varvec{\hat{h}})\).
-
parameter-hiding: \((\mathsf {pp},\, h^*,\, \varvec{\hat{g}},\, \varvec{\hat{h}}) \equiv (\mathsf {pp},\, h^*,\, \varvec{\hat{g}}{\cdot }\varvec{\hat{g}'},\, \varvec{\hat{h}}{\cdot }\varvec{\hat{h}'})\).
Where, \(\approx _{c}\) denotes a distinguishing probability upper-bounded by a negligible function on \(\lambda \) and, for any \(n \in \mathbb {N}\), the above elements are sampled as:

for  .
.
Remark. Observe that we have presented the version of dual system groups defined in [15]. Other works consider slightly different conditions (e.g., the non-degeneracy of [1]). However, the widely used instantiation of DSG from k-lin given in [15] also satisfies the properties of those variations.
ABE from Pair Encodings
Given a pair encoding scheme \(\{\mathsf{Param}, \mathsf{EncKey}, \mathsf{EncCt}, \mathsf{Pair}\}\) (see Definition 2) for a predicate family \(P_{\kappa } : \mathcal{X}_{\kappa } \times \mathcal{Y}_{\kappa } \rightarrow \{0,1\}\) indexed by \(\kappa = (N,\mathsf{par})\) (let \(\lambda = |N|\)), an attribute-based encryption scheme can be constructed as follows:
-
\(\mathsf{Setup}(1^\lambda ,\mathcal{X}_{\kappa },\mathcal{Y}_{\kappa })\): let \(n \leftarrow \mathsf{Param}(\mathsf{par})\) and run the DSG generation algorithm \(\mathsf{SampP}(1^\lambda , 1^n)\) to obtain \(\mathsf {pp}\) and \(\mathsf {sp}\). Let
 and
and  . Output \((\mathsf {mpk}, \mathsf {msk})\).
. Output \((\mathsf {mpk}, \mathsf {msk})\). -
\(\mathsf{Enc}(\mathsf {mpk}, x)\): run \(\mathsf{EncCt}(N,x)\) to obtain polynomials \(\varvec{c}_x(\varvec{s},\varvec{\hat{s}},\varvec{b})\). For every \(\ell \in [w_3]\), let the \(\ell \)-th polynomial in \(\varvec{c}_x\) be
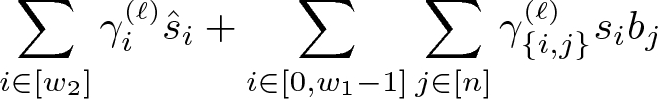
for some coefficients
 and
and 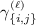 in \(\mathbb {Z}_p\). Now, run \(\mathsf{SampG}\) to produce $$\begin{aligned} (\hat{g}_{\{i,0\}}, \hat{g}_{\{i,1\}},\dots ,\hat{g}_{\{i,n\}})&\leftarrow \mathsf{SampG}(\mathsf {pp}) \qquad \text { for }i \in [w_2] \\ (g_{\{i,0\}}, g_{\{i,1\}},\dots ,g_{\{i,n\}})&\leftarrow \mathsf{SampG}(\mathsf {pp}) \qquad \text { for }i \in [0,w_1{-}1] \\ (g_{\{0,0\}}, g_{\{0,1\}},\dots ,g_{\{0,n\}})&\leftarrow \mathsf{SampG}(\mathsf {pp}; \sigma ) \end{aligned}$$
in \(\mathbb {Z}_p\). Now, run \(\mathsf{SampG}\) to produce $$\begin{aligned} (\hat{g}_{\{i,0\}}, \hat{g}_{\{i,1\}},\dots ,\hat{g}_{\{i,n\}})&\leftarrow \mathsf{SampG}(\mathsf {pp}) \qquad \text { for }i \in [w_2] \\ (g_{\{i,0\}}, g_{\{i,1\}},\dots ,g_{\{i,n\}})&\leftarrow \mathsf{SampG}(\mathsf {pp}) \qquad \text { for }i \in [0,w_1{-}1] \\ (g_{\{0,0\}}, g_{\{0,1\}},\dots ,g_{\{0,n\}})&\leftarrow \mathsf{SampG}(\mathsf {pp}; \sigma ) \end{aligned}$$Observe that we have made explicit the coin tosses, \(\sigma \), used in the last sampling. Setup
 and define the symmetric encryption key as
and define the symmetric encryption key as 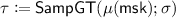 , where
, where  for every \(i \in [0,w_1{-}1]\); and for every \(\ell \in [w_3]\),
for every \(i \in [0,w_1{-}1]\); and for every \(\ell \in [w_3]\), 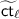 is computed as
is computed as 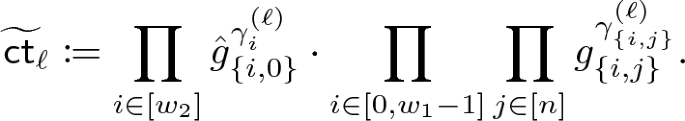
Output \((\mathsf {ct}_x, \tau )\).
-
\(\mathsf{KeyGen}(\mathsf {msk},y)\): run \(\mathsf{EncKey}(N,y)\) to obtain polynomials \(\varvec{k}_y(\varvec{r},\varvec{\hat{r}},\varvec{b})\). For every \(\ell \in [m_3]\), let the \(\ell \)-th polynomial in \(\varvec{k}_y\) be
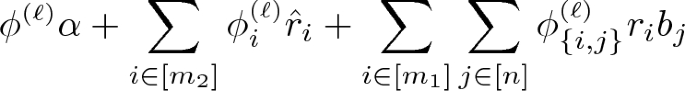
for some coefficients
 ,
,  and
and  in \(\mathbb {Z}_p\). Now, run \(\mathsf{SampH}\) to produce $$\begin{aligned} (\hat{h}_{\{i,0\}}, \hat{h}_{\{i,1\}},\dots ,\hat{h}_{\{i,n\}})&\leftarrow \mathsf{SampH}(\mathsf {pp}) \qquad \text { for }i \in [m_2] \\ (h_{\{i,0\}}, h_{\{i,1\}},\dots ,h_{\{i,n\}})&\leftarrow \mathsf{SampH}(\mathsf {pp}) \qquad \text { for }i \in [m_1] \end{aligned}$$
in \(\mathbb {Z}_p\). Now, run \(\mathsf{SampH}\) to produce $$\begin{aligned} (\hat{h}_{\{i,0\}}, \hat{h}_{\{i,1\}},\dots ,\hat{h}_{\{i,n\}})&\leftarrow \mathsf{SampH}(\mathsf {pp}) \qquad \text { for }i \in [m_2] \\ (h_{\{i,0\}}, h_{\{i,1\}},\dots ,h_{\{i,n\}})&\leftarrow \mathsf{SampH}(\mathsf {pp}) \qquad \text { for }i \in [m_1] \end{aligned}$$Define the secret key as
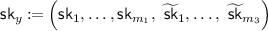 , where
, where  for every \(i \in [m_1]\); and for every \(\ell \in [m_3]\),
for every \(i \in [m_1]\); and for every \(\ell \in [m_3]\),  is computed as
is computed as 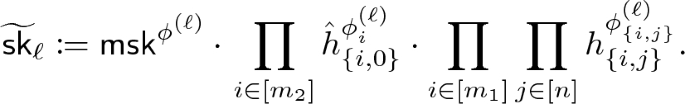
Output \(\mathsf {sk}_y\).
-
\(\mathsf{Dec}(\mathsf {mpk},\mathsf {sk}_y,\mathsf {ct}_x,x)\): run \(\mathsf{Pair}(N,x,y)\) to obtain matrices \(E, E'\) (note that y is assumed to be extractable from \(\mathsf {sk}_y\), whereas x is explicitly included as an input to \(\mathsf{Dec}\)). Define:
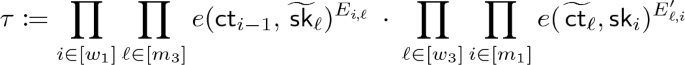
Output the symmetric encryption key \(\tau \).
Rights and permissions
Copyright information
© 2021 International Association for Cryptologic Research
About this paper
Cite this paper
Ambrona, M. (2021). Generic Negation of Pair Encodings. In: Garay, J.A. (eds) Public-Key Cryptography – PKC 2021. PKC 2021. Lecture Notes in Computer Science(), vol 12711. Springer, Cham. https://doi.org/10.1007/978-3-030-75248-4_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-75248-4_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-75247-7
Online ISBN: 978-3-030-75248-4
eBook Packages: Computer ScienceComputer Science (R0)


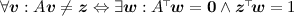 for all compatible A and
for all compatible A and  ,
,  , for
, for 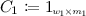 ,
,  for
for  and
and 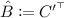 .
.
 and
and  .
.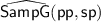 output an element from
output an element from 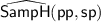 output an element from
output an element from 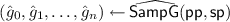 ,
, 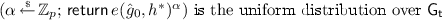 .
. and
and  . Output
. Output 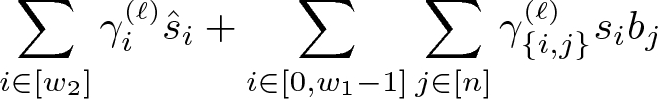
 and
and 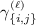 in
in  and define the symmetric encryption key as
and define the symmetric encryption key as 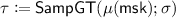 , where
, where  for every
for every 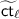 is computed as
is computed as 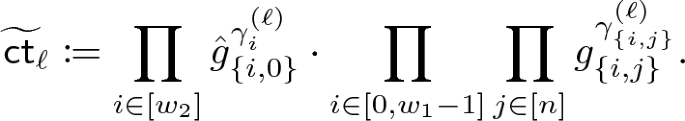
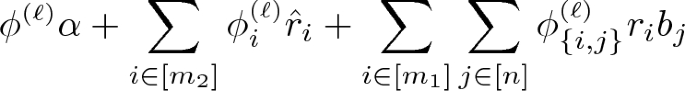
 ,
,  and
and  in
in 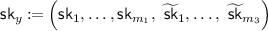 , where
, where  for every
for every  is computed as
is computed as