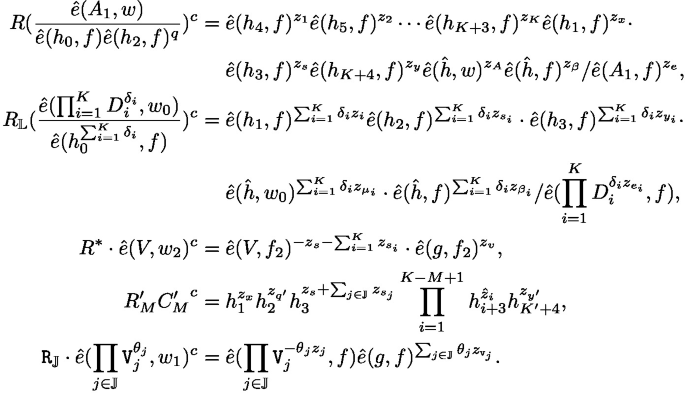Scored Anonymous Credentials

Abstract

Securely maintaining “credits” of users judging their behavior in past authenticated sessions is vital to encourage user participation, but doing it over anonymous credentials is non-trivial, especially when users would avoid claiming negative credit and escape from blocklisting. Prevalent designs impose an authentication cost linear in the blocklist size or a stringent requirement of sequential and timely judgment of each session without retrospective adjustment, as a single unjudged session curbs the authentication of all users. We propose scored anonymous credentials, a new design storing a number of active sessions with volatile scores downgradable before finalized. Sessions can be judged in any order and at varying times without affecting all users. Any backlog of unjudged sessions only affects the users behind them. We achieve efficiency and flexibility using verifiable shuffle, which is hardly used in existing anonymous blocklisting/reputation enforcement systems.

Sherman Chow is supported in part by the General Research Funds (CUHK 14210621 and 14209918), University Grants Committee, Hong Kong, and is also grateful for their recognition in granting the Early Career Award on “Accountable Privacy in Online Communication” (CUHK 439713). We thank Kin-Ying Yu for inspiration from his Ph.D. thesis, and Russell Lai and reviewers for their helpful comments.

Appendices

A Batch BBS+ Signature

The original ZKP for a BBS+ signature [6] is performed as follows.

Protocol $\mathbb {P}_\textsf{Sig}$. It allows a prover to prove that it knows a signature $\sigma = (A, e, y)$ on blocks of messages $(x_1, \ldots , x_\ell )$ without revealing the signature nor the messages.

• 1. The prover randomly generates $r_A \in \mathbb {Z}_p$, sets $\beta = r_A e$, and sends $A_1 = A \hat{h}^{r_A}, A_2 = h_1^{r_A}$ to the verifier along with the following proof $\varPi$:

  $$\begin{aligned} \textsf{PoK}\left\{ \begin{aligned} (\{x_i\}_{i \in [1, \ell ]},&e, y, r_A, \beta ):\\ (A_2 = h_1^{r_A})&\wedge (1 = A_2^{-e} h_1^{\beta })~\wedge \\ \frac{\hat{e}(A_1, w )}{ \hat{e}(h_0, f)}&= \hat{e}(h_1, f)^{x_1} \cdots \hat{e}(h_\ell , f)^{x_\ell } \cdot \hat{e}(h_{\ell + 1}, f)^y \cdot \\&~~~~ \hat{e}(\hat{h}, w)^{r_A} \cdot \hat{e}(\hat{h}, f)^{\beta } / \hat{e}(A_1, f)^e \end{aligned} \right\} . \end{aligned}$$

• 2. Upon receiving $(A_1, A_2, \varPi )$, the verifier outputs 1 if proof $\varPi$ is valid.

Details such as its construction can be found in [6].

Batch BBS+ Signatures. We construct batch BBS+ (B-BBS+) featuring a batch verification algorithm for BBS+ signatures and its zero-knowledge version. Without loss of generality, we illustrate with two-message blocks $(s_1, m_1) \in \mathbb {Z}_p^2$ (suffices for SAC). The signature $(A_1 = (h_0 h_1^{s_1} h_2^{m_1} h_{3}^{y_1})^{\frac{1}{\gamma +e_1}}, e_1, y_1)$ can be verified by:

$$ \hat{e}(A_1, wf^{e_1}) = \hat{e}(h_0 h_1^{s_1} h_2^{m_1} h_{3}^{y_1}, f). $$

For $i \in [1, K]$, let $(A_i,e_i,y_i)$ be the signature on $(s_i, m_i)$. To batch verify, pick $(\delta _1, \ldots , \delta _K)$ as a random vector of $\ell _b$-bit elements from $\mathbb {Z}_p$ and test if:

$$\begin{aligned}&\hat{e}(\prod _{i=1}^K A_i^{\delta _i}, w) \cdot \hat{e}(\prod _{i=1}^K A_i^{e_i \delta _i}, f) = \hat{e}(h_0^{ \sum _{i=1}^K \delta _i } \cdot h_1^{ \sum _{i=1}^K s_i \delta _i } \cdot h_2^{ \sum _{i=1}^K m_i \delta _i } \cdot h_{3}^{ \sum _{i=1}^K y_i \delta _i}, f). \end{aligned}$$

which takes 2 pairings, $2K + 4$ exponentiations in $\mathbb {G}_1$, and $2K + 2$ multiplications in $\mathbb {G}_1$. Since 1 pairing takes roughly the time of 5 exponentiations, and non-batch verifications take 2K pairings, 4K exponentiations in $\mathbb {G}_1$, and 4K multiplications in $\mathbb {G}_1$ for K signatures, the batch verification speeds up by $4.5\times$ for large K.

Theorem 1

For security level $\ell _b$, the above algorithm is a batch verifier for BBS+ signatures with the probability of accepting an invalid signature being $2^{-\ell _b}$.

The batching technique for BBS+ basically follows from [31][Theorem 3.2]. BBS+ signature is weakly secure in the standard model under the q-SDH assumption [6]. Below is the batched zero-knowledge proof $\mathbb {P}_\textsf{Bvfy}$ for B-BBS+.

Protocol $\mathbb {P}_\textsf{Bvfy}$. It allows proving the knowledge of K signatures $\sigma _i = (A_i,e_i,y_i)$ on messages $(s_i, m_i)$ for $i \in [1, K]$.

• 1. Let $\delta _i$ be an $\ell _b$-bit element picked by the verifier in $\mathbb {Z}_p$. The prover randomly generates $\mu _i \in \mathbb {Z}_p$, computes $B_i = h_1^{\mu _i}, D_i = A_i \hat{h}^{\mu _i}$, $\iota _i = \mu _i e_i$, and sends $B_i, D_i$ to the verifier along with the proof $\varPi$:

  $$\begin{aligned} \textsf{PoK}\left\{ \begin{aligned}&(\{s_i, m_i, \mu _i, e_i, y_i, \iota _i \}_{i \in [1, K]} ):\\&\bigwedge _{i=1}^K \big (B_i = h_1^{\mu _i} \wedge 1 = B_i^{-e_i} h_1^{\iota _i } \big ) ~\wedge \\&\begin{aligned} \frac{\hat{e}(\prod _{i=1}^K D_i^{\delta _i}, w)}{\hat{e}(h_0^{\sum _{i=1}^K \delta _i}, f)} =&\hat{e}(h_1, f)^{\sum _{i=1}^K \delta _i s_i} \cdot \hat{e}(h_2, f)^{\sum _{i=1}^K \delta _i m_i} \cdot \\&\hat{e}(h_{3}, f)^{\sum _{i=1}^K \delta _i y_i} \cdot \hat{e}(\hat{h}, w)^{\sum _{i=1}^K \delta _i \mu _i} \cdot \\&\hat{e}(\hat{h}, f)^{\sum _{i=1}^K \delta _i \iota _i} / \hat{e}(\prod _{i=1}^K D_i^{\delta _i e_i}, f) \end{aligned} \end{aligned} \right\} . \end{aligned}$$

• 2. Upon $((B_1, D_1), \ldots , (B_K, D_K), \varPi )$, the verifier outputs 1 if proof $\varPi$ is valid.

B Alternative for Zero-Knowledge Argument of a Shuffle

Let $C_i = \mathcal {E}_{\textsf{pk}}(M_i; \rho _i)$ for $i \in [1,N]$, a ciphertext created from encrypting message $M_i$ under public key $\textsf{pk}$ using randomness $\rho _i$. Homomorphic encryption allows simple multiplications of encrypted $M_i$ and $M_j$ without decrypting it first via simple multiplication of ciphertexts: $\mathcal {E}_{\textsf{pk}}(M_i; \rho _i)\mathcal {E}_{\textsf{pk}}(M_j; \rho _j) = \mathcal {E}_{\textsf{pk}}(M_iM_j; \rho _i + \rho _j)$. There are efficient zero-knowledge arguments for showing a shuffling of ciphertexts produced by homomorphic encryption, i.e., for all $i \in [N]$, decrypting $C'_i$ is the same as decrypting $C_{\pi (i)}$, where $\pi : [N] \rightarrow [N]$ is the permutation.

We review a recent scheme by Bayer and Groth [9]. The first step is to commit to permutation $\pi$. The prover receives a challenge x and commits to $x^{\pi (1)}, \ldots x^{\pi (N)}$. The prover will give an argument of knowledge of openings of the commitments to permutations of $1, \ldots , N$ and $x^1, \ldots , x^N$. The prover demonstrates that the same permutation has been used in both cases using random challenges y and z. By using the homomorphic properties of the commitment, the prover can compute commitments to $d_1 -z = y\pi (1)+x^{\pi (1)}-z, \ldots , d_N -z = y\pi (N)+x^{\pi (N)}-z$, in a verifiable manner, then uses a product argument to show:

$$ \prod _{i=1}^N (d_i - z) = \prod _{i=1}^N (y i + x^i - z). $$

These are two identical degree-N polynomials in z (with the roots permuted). By Schwartz-Zippel lemma, the prover has a negligible chance over the choice of z of making a convincing argument unless there is a permutation $\pi$ such that $d_i = y \pi (i) + x^{\pi (i)}$ for $i \in [1,N]$. Furthermore, there is negligible probability over the choice of y of this being true unless the first commitment contains $\pi (i)$ and the second commitment contains $x^{\pi (i)}$ for $i \in [1,N]$.

The prover has commitments to $x^{\pi (i)}$ and uses the multi-exponentiation argument to show there exists a $\rho$ such that

$$ \prod _{i=1}^N C_i^{x^i} = \mathcal {E}_{\textsf{pk}}(1;\rho ) \prod _{i=1}^N C_i^{x^{\pi (i)}}. $$

Since the encryption $\mathcal {E}$ is homomorphic, the verifier can deduce that $\prod _{i=1}^N M_i^{x^i} = \prod _{i=1}^N M_i^{x^{\pi (i)}}$ for some permutation $\pi$. Since x is a random challenge chosen by the verifier, we have a correct shuffle with overwhelming probability.

Depending on the implementation, there is a trade-off between the round complexity, communication complexity, and the computation time of the users and the SP [9]. In principle, we can apply any zero-knowledge arguments of a shuffle. For efficiency, we will require the shuffle and the commitments (to session identifiers) to be in the same group. For our construction, we can use the homomorphic ElGamal encryption of a message M with $\textsf{pk}= (h, u)$ is $(M u^\rho , h^\rho )$, which fits with Bayer-Groth’s argument [9]. Since decryption is not needed in our case, we can encode a ticket t by $M = h^t$, and only include the first part of the ciphertext. It is easy to see that it preserves the homomorphic property.

C Authentication using Batch-BBS+ and Range Proof

The signature-based range proof can be constant-size if the threshold score $s_\textsf{th}$ and the maximum score $s_{\textsf{max}}$ is short, e.g., $\ell _b$-bit integers for $\ell _b = 10$. Let $g \in \mathbb {G}_1$, $u \in \mathbb {G}_1$ (for the shuffle), and $f_2 \in \mathbb {G}_2$ be generators. The SP picks a random $\alpha \in \mathbb {Z}_p$, and computes $w_2 = f_2^\alpha$. The SP puts BB signatures $Y_j = g^{\frac{1}{\alpha + j}}$ for all $j \in [s_\textsf{th}, s_{\textsf{max}}]$ in the public parameters. (One can instead apply Bulletproofs [14].)

• 1. Let $\sigma _{\textsf{A}} = (A, e, y)$ be the credential on attributes $\textsf{A}= (x, q, s, \{t_1, \ldots , t_K\})$. Let $\mathbb {J}$ be a set of $M = |\mathbb {J}|$ indexes where $t_j \in \mathbb {T}$ for all $j \in \mathbb {J}$. The user sends the parameters K, M, and q to the SP. The SP returns a new identifier $t'$.

• 2. The SP randomly picks $\delta _1, \ldots , \delta _K$, $\zeta _i, \iota _i$ for $i \in [1, K - M]$ and $\ell _b$-bits numbers $\{\theta _j\}_{j \in \mathbb {J}}$ and sends to the user.

• 3. The user picks $r_A, r_t, r_e, r_\beta , r_x, r_s, r_1, \ldots$, $r_K$ in $\mathbb {Z}_p$, computes $\beta = r_A e$ and:

  $$\begin{aligned} A_1&= A \hat{h}^{r_A}, ~ A_2 = h_1^{r_A}, ~ T_1 = h_1^{r_{t}}, ~~T_2 = A_2^{-r_e} h_1^{r_{\beta }},\\ R_x&= g^{r_x}, ~~~ R_s = g^{r_s}, ~~ R_{1} = g^{r_1}, \ldots , R_K = g^{r_K},\\ R&= \hat{e}(h_1, f)^{r_x} \cdot \hat{e}(h_3, f)^{r_s} \cdot \hat{e}(h_4, f)^{r_1} \cdots \hat{e}(h_\ell , f)^{r_K} \cdot \\&~~~~ \hat{e}(h_{\ell + 1}, f)^{r_y} \cdot \hat{e}(\hat{h}, w)^{r_{t}} \cdot \hat{e}(\hat{h}, f)^{r_{\beta }} / \hat{e}(A_1, f)^{r_e}. \end{aligned}$$

  For $i \in [1, K]$, let $(A_i, e_i, y_i)$ be the B-BBS+ signature for ticket $t_i$ and score $s_{i}$ in $\mathbb {L}$. The user randomly picks $\mu _i, r_{s_i}, r_{\mu _i}, r_{\beta _i}$ in $\mathbb {Z}_p$, and computes

  $$\begin{aligned} \beta _i&= \mu _i e_i, ~ {D}_{i} = A_i \hat{h}^{\mu _{i}}, ~ B_{i} = h_1^{\mu _i}, \quad S_i = g^{r_{s_i}}, \bar{T}_i = h_1^{r_{\mu _i}}, ~~\bar{W}_i = B_i^{-r_{e_i}} h_1^{r_{\beta _i}}, \\ {R}_{\mathbb {L}}&= \hat{e}(h_1, f)^{\sum _{i=1}^K \delta _i r_i} \cdot \hat{e}(h_2, f)^{\sum _{i=1}^K \delta _i r_{s_i}} \hat{e}(h_3, f)^{\sum _{i=1}^K \delta _i r_{y_i}} \cdot \hat{e}(\hat{h}, w_0)^{\sum _{i=1}^K \delta _i r_{\mu _i}} \\&~~~~ \hat{e}(\hat{h}, f)^{\sum _{i=1}^K \delta _i r_{\beta _i}} / \hat{e}(\prod _{i=1}^K D_i^{ \delta _i r_{e_i}}, f). \end{aligned}$$

  Let $s^* = s + \sum _{i=1}^K s_{i}$. The user computes a range proof of $s^*$ with $v, r_v \in \mathbb {Z}_p$:

  $$\begin{aligned} V&= Y_{s^*}^{v}, \quad R^* = \hat{e}( V, f_2)^{-r_s - \sum _{i=1}^K r_{s_i}} \cdot \hat{e}(g,f_2)^{r_v}. \end{aligned}$$

  For all $j \in \mathbb {J}$, the user randomly picks $\texttt{v}_j, r_{\texttt{v}_j}$ in $\mathbb {Z}_p$ and computes:

  $$\begin{aligned} \texttt{V}_j&= {\hat{\sigma }}_{j}^{\texttt{v}_j}, \quad \texttt{R}_{\mathbb {J}} = \hat{e}(\prod _{j \in \mathbb {J}} \texttt{V}_j^{-\theta _j r_j},f) \cdot \hat{e}(g,f)^{\sum _{j \in \mathbb {J}} \theta _j r_{\texttt{v}_j}}. \end{aligned}$$

  The user runs $\textsf{Redeem}(\mathbb {U}\cup \{t'\}, \mathbb {T}, K')$ as follows. Suppose w.l.o.g. $\mathbb {U}= \{t_1, \ldots , t_K\}$ and $\mathbb {T}= \{t_{K - M + 1}, \ldots , t_K\}$. So $\mathbb {J} = \{K - M + 1, \ldots , K\}$. Suppose $\mathbb {U}' = \{t'_1, \ldots , t'_{K'-1}, t'\}$ is selected where $t'_i = t_i$ for $i \in [1, K - M]$, $t'_{K - M + 1} = t'$, and $t'_i$ is a random element in $\mathbb {L}_{\texttt{D}}$, $i \in [K - M + 2, K']$. The user computes $s' = \sum _{j \in \mathbb {J}} s_j$, and the encryption for tickets $t'_1, \ldots t'_{K - M + 1}$, by randomly picking $\rho _i \in \mathbb {Z}_p$ for $i \in [1, K - M + 1]$ and setting $\hat{C}_{i,1} = g^{t'_i} u^{\rho _i}, \hat{C}_{2} = g^{\sum _{i=1}^{K - M + 1} \zeta _i \rho _i}$. The user picks a permutation $\pi : [K'] \rightarrow [K']$. Let $\hat{t}_i = t'_{\pi (i)}$ for $i \in [1, K - M + 1]$. The user also computes the homomorphic encryption by randomly picking $\rho '_i \in \mathbb {Z}_p$ and setting $\hat{C}'_{i,1} = g^{\hat{t}_i} u^{\rho '_i}, \hat{C}'_{2} = g^{\sum _{i=1}^{K - M + 1} \iota _i \rho '_i}$. For updating the credential, the user randomly picks $\hat{r}_1, \ldots , \hat{r}_{K - M}$ and sets:

  $$\begin{aligned} C'_M&= h_1^x h_2^{q'} h_3^{s + s'} h_4^{\hat{t}_1} \cdots h_{K - M+4}^{\hat{t}_{K - M + 1}} h_{K'+4}^{y'},\\ R'_M&= h_1^{r_x} h_2^{r_{q'}} h_3^{r_s+ \sum _{j\in \mathbb {J}} r_{s_j}} h_4^{\hat{r}_1} \cdots h_{K - M+4}^{\hat{r}_{K - M + 1}} h_{K'+4}^{r_{y'}},\\ \hat{R}_1&= g^{\hat{r}_1}, \quad \ldots , \quad \hat{R}_{K - M + 1} = g^{\hat{r}_{K - M + 1}} \end{aligned}$$

  and sends SP set $\mathbb {J}$, dummies $(t'_{K - M + 2}, \ldots , t'_{K'-1})$, and the commitments:

  $A_1, A_2, T_1, T_2, R_x, R_s, R_1, \ldots , R_K, R$, $\{D_i, B_i, S_i, \bar{T}_i, \bar{W}_i\}_{i \in [1, K]}, {R}_{\mathbb {L}}, V, R^*$,

  $\{\texttt{V}_j\}_{j\in \mathbb {J}}, \texttt{R}_{\mathbb {J}}$, $\{ \hat{C}_{i,1}, \hat{C}'_{i,1}, \hat{R}_i \}_{i \in [1, K - M + 1]}, \hat{C}_{2}, \hat{C}'_{2}$, $C'_M, R'_M$. The user can now perform the ZK argument for shuffling $\hat{C}_{i,1}, \hat{C}_{2}$ to $\hat{C}'_{i,1}, \hat{C}'_{2}$. Details can be found in [9].

• 4. If $(t'_{K - M + 2}, \ldots , t'_{K'-1})$ are dummies, the SP returns challenge $c \in \mathbb {Z}_p$.

• 5. The user computes and sends the following with q to the SP:

  $$\begin{aligned} z_x&= r_x + c x,&z_s&= r_s + cs,&z_{A}&= r_{t} + c r_A,\\ z_e&= r_e + c e,&z_v&= r_v + cv,&z_{q'}&= r_{q'} +cq', \\ z_{\beta }&= r_{\beta } + c r_A e,&z_{y'}&= r_{y'} + c y',&z_y&= r_y + cy.\\ \hbox {For }&i \in [1, K], \\ z_i&= r_i + c t_i,&z_{s_i}&= r_{s_i} + c s_i,&z_{y_i}&= r_{y_i} + cy_i,\\ z_{e_i}&= r_{e_i} + c e_i,&z_{\mu _i}&= r_{\mu _i} + c \mu _i,&z_{\beta _i}&= r_{\beta _i} + c \mu _i \beta _i.\\ \hbox {For }&j \in \mathbb {J},&z_{\texttt{v}_j}&= r_{\texttt{v}_j} + c \texttt{v}_j.\\ \hbox {For }&l \in [1, K - M],&\hat{z}_l&=\hat{r}_l + c \hat{t}_l. \end{aligned}$$

• 6. The SP checks if $T_1 A_2^c = h_1^{z_A}$, $T_2 = A_2^{-z_e} h_1^{z_{\beta }}$,

  

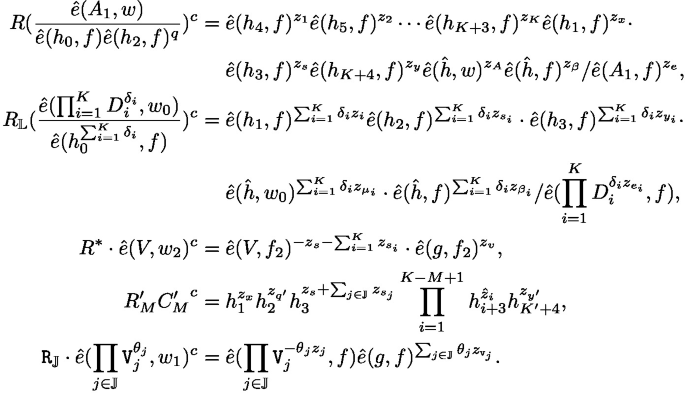
  It checks $\bar{T}_i B_i^c = h_1^{z_{\mu _i}}$, $\bar{W}_i = B_i^{-z_{e_i}} h_1^{z_{\beta _i}}$ for $i \in [1, K]$ and the zero-knowledge argument for the shuffling [9]. The SP computes: $A' = (h_0 C'_M h_{K - M+5}^{t'_{K - M + 2}} \cdots h_{K' + 2}^{t'_{K'-1}} h_{K'+3}^{t'_{K'}} h_{K'+4}^{y''})^{\frac{1}{e'+\gamma }}$ for random $e', y'' \in \mathbb {Z}_p$, and sends $(A',e',y'')$ to the user. The SP then adds the entry $(t', 0, \sigma , \emptyset )$ to list $\mathbb {T}$, where $\sigma = (A, e, y)$ is the B-BBS+ signature with $A = (h_0 h_1^{t'} h_3^y)^{\frac{1}{\gamma + e}}$ for some random $e, y \in \mathbb {Z}_p$.

• 7. The user gets $\sigma '_{\textsf{A}} = (A', e'$, $y' + y'')$ and updates its attributes to $\textsf{A}' = (x, q', s + s'$, $\{\hat{t}_1, \ldots , \hat{t}_{K - M + 1}, t'_{K - M + 2}, \ldots , t'_{K'}\})$.

D Security

1.1 D.1 Simulation-Based Model

We use the simulation-based security definition following the literature [4, 45]. We consider a security game where an environment $\mathcal {E}$, which can schedule the invocation of the functionalities of SAC at its wish, is asked whether it is interacting with the real world or the ideal world. In the real world, all honest players communicate as specified in the protocol description. In the ideal world, the same players also follow the protocol except that they interact via a trusted party $\mathcal {T}$, responsible for handling all the inputs and outputs for them. The adversary $\mathcal {A}$ in the real world takes control of some of the players and can communicate arbitrarily with environment $\mathcal {E}$. But $\mathcal {A}$ does not know the communications between honest parties and the origin of messages received by $\mathcal {A}$.

Roughly, SAC is secure if, for any probabilistic polynomial time (PPT) algorithms $\mathcal {A}$ and $\mathcal {E}$, there exists another algorithm $\mathcal {S}$, which has black-box access to $\mathcal {A}$, controlling the same players in the ideal world as $\mathcal {A}$ does in the real world, such that $\mathcal {E}$ cannot distinguish if it is interacting with $\mathcal {A}$ or $\mathcal {S}$. In other words, it also cannot distinguish between the real world and the ideal world. We first specify the functionalities of SAC in the real world and the ideal world, respectively:

• 1. Setup. The system starts when $\mathcal {E}$ specifies the set of honest and dishonest users and the SP (static model).

  • Real World. The SP generates $(\textsf{pp}, \textsf{sk})$ and gives $\textsf{pp}$ to all players.

  • Ideal World. The trusted party $\mathcal {T}$ initializes a database that stores the registration and authentication transcripts of all users. It also keeps track of the attributes of each user, and the public parameter $\textsf{pp}$, which contains the status/score of each session.

• 2. Registration. $\mathcal {E}$ asks user i to register with the SP.

  • Real World. User i registers with the SP, and both parties output individually the output of this interaction to $\mathcal {E}$. If user i has already been registered, the honest SP will reject the request. Similarly, an honest  user discards the credential from the SP if it has successfully registered before.

  • Ideal World. User i sends a registration request to $\mathcal {T}$, who informs the SP about the request and whether user i has obtained a credential before. $\mathcal {T}$ forwards the decision of the SP to user i. The user and the SP individually send the output of this interaction to $\mathcal {E}$. If the SP accepts the request and user i has not registered before, $\mathcal {T}$ stores this transcript in its database.

• 3. Authentication. $\mathcal {E}$ asks user i to authenticate and redeem some sessions.

  • Real World. User i authenticates with the SP w.r.t. the access policy f like a threshold score $s_\textsf{th}$ and redeems the scores of sessions specified by $\mathcal {E}$. Both user i and the SP pass the local output of this interaction to $\mathcal {E}$.

  • Ideal World. User i sends an authentication request to $\mathcal {T}$, who checks according to $\textsf{pp}$ whether the user i satisfies the authentication condition. In more detail, $\mathcal {T}$ maintains a database of the current and past tickets for each user, where the score of a user should match with the current $\textsf{pp}$. $\mathcal {T}$ informs the SP that some anonymous user wants to authenticate and whether the user satisfies the authentication condition. The SP replies with a new session identifier t or reject to $\mathcal {T}$, and $\mathcal {T}$ forwards it to user i. If the authentication is successful, $\mathcal {T}$ removes the redeemed sessions ($\mathbb {T}$ specified by the user) from the user’s attributes and updates its score. It also adds an entry for the active session t with score 0 to the database, and stores t as one of the user’s session identifiers. The user and the SP individually send the output of this interaction and t (if not reject) to $\mathcal {E}$.

• 4. Update. $\mathcal {E}$ asks the SP to update the score s to, or finalize, a session t.

  • Real World. The SP runs the update algorithm as instructed by $\mathcal {E}$.

  • Ideal World. $\mathcal {T}$ updates its database accordingly as instructed by $\mathcal {E}$.

In the ideal world, all sessions are anonymous and unlinkable from the SP’s view, and $\mathcal {T}$ verifies whether the authenticating user satisfies the authentication condition. These capture completeness, anonymity, and soundness.

Definition 2

Let $\textbf{Real}_{\mathcal {E},\mathcal {A}}(\lambda )$ (resp. $\textbf{Ideal}_{\mathcal {E},\mathcal {S}}(\lambda )$) be the probability that $\mathcal {E}$ outputs 1 when it runs in the real world (resp. ideal world) with adversary $\mathcal {A}$ (resp. $\mathcal {S}$ having black-box accesses to $\mathcal {A}$). SAC is secure if, for all PPT algorithms, $|\textbf{Real}_{\mathcal {E},\mathcal {A}}(\lambda ) - \textbf{Ideal}_{\mathcal {E},\mathcal {S}}(\lambda )|$ is negligible in $\lambda$.

1.2 D.2 Proof

Theorem 2

Our scheme is secure if the BBS+ and weak BB signatures are existentially unforgeable, and the range proof, set membership proof, zero-knowledge argument of shuffling, $\mathbb {P}_\textsf{Iss}$, $\mathbb {P}_\textsf{Sig}$, $\mathbb {P}_\textsf{Set}$, and ZKPoK protocols are secure.

We describe how to construct $\mathcal {S}$ in detail, except with the details of the underlying building blocks omitted (e.g., how to extract what $\mathcal {S}$ needs from the ZKPoK). Firstly, $\mathcal {S}$ maintains a list of credentials issued to $\mathcal {A}$ during the life span of the system. $\mathcal {S}$ also acts as an ideal-world adversary to the trusted party $\mathcal {T}$. $\mathcal {S}$ simply forwards any messages between $\mathcal {E}$ and $\mathcal {A}$. We consider two cases for $\mathcal {S}$:

Case 1: The SP is honest:

• 1. Setup. $\mathcal {S}$ generates $(\textsf{pp}, \textsf{sk})$ and sends $\textsf{pp}$ to $\mathcal {A}$.

• 2. Registration. $\mathcal {S}$ acts as a dishonest user i (in the ideal world) to $\mathcal {T}$ and an honest SP to $\mathcal {A}$ as a dishonest user in the real world. Using the knowledge extractor of the ZKPoK protocol, $\mathcal {S}$ extracts the value of x from $\mathcal {A}$. This value will be used to identify the dishonest user i. $\mathcal {S}$ sends the request to $\mathcal {T}$ on behalf of the user i. If $\mathcal {T}$ replies accept, $\mathcal {S}$ issues the credential to $\mathcal {A}$ and also stores that credential.

• 3. Authentication. $\mathcal {S}$ acts as a dishonest user i to $\mathcal {T}$ and an honest SP to $\mathcal {A}$. $\mathcal {S}$ extracts and uses the value x during authentication to determine user i. Two worlds are indistinguishable except in the rare events below:

  • During registration, $\mathcal {S}$ fails to extract x from $\mathcal {A}$. This happens with negligible probability by the soundness property of $\mathbb {P}_\textsf{Iss}$.

  • During a successful authentication, $\mathcal {S}$ fails to extract x from $\mathcal {A}$. This happens with negligible probability by the soundness property of $\mathbb {P}_\textsf{Sig}$.

  • There exists a successful authentication from $\mathcal {A}$ such that $\mathcal {S}$ outputs accept on behalf of an honest SP, but $\mathcal {T}$ indicates the authenticating user does not satisfy the policy.

  The last case implies that $\mathcal {A}$ successfully did one of the following:

  • forged a credential on attributes that has never been issued,

  • obtained a credential on attributes with a ticket that is neither originated from the past version of the credential nor any dummy sessions,

  • created one fake proof in authentication.

  All these happen with negligible probability due to the following:

  • BBS+ signatures are existentially unforgeable and $\mathbb {P}_\textsf{Sig}$ is sound,

  • the set membership proof is sound,

  • the argument of shuffling is (computationally) sound, and

  • the zero-knowledge proof is sound.

  Since $\mathcal {S}$ may need to run the extractor of the ZKPoK protocol, we require that the registration and authentications are run sequentially. A similar restriction also applies to PEREA, BLACR, and PERM.

Case 2: The SP is dishonest:

• 1. Setup. $\mathcal {S}$ is given $\textsf{pp}$ by $\mathcal {A}$.

• 2. Registration. $\mathcal {S}$ acts as a dishonest SP to $\mathcal {T}$ (in the ideal world) and an honest user i to $\mathcal {A}$. When $\mathcal {T}$ requests registration for user i, $\mathcal {S}$ runs the registration protocol with $\mathcal {A}$ using the simulator of $\mathbb {P}_\textsf{Iss}$. If $\mathcal {S}$ does not obtain a valid credential from $\mathcal {A}$, then $\mathcal {S}$ replies reject to $\mathcal {T}$.

• 3. Authentication. $\mathcal {S}$ acts as a dishonest SP to $\mathcal {T}$ and an honest user to $\mathcal {A}$. When $\mathcal {T}$ requests authentication for an anonymous user, $\mathcal {S}$ runs the authentication protocol with $\mathcal {A}$. If $\mathcal {T}$ proceeds and satisfies the authentication policy, $\mathcal {S}$ uses the simulator of the ZKPoKs and shuffling protocol to simulate the view of $\mathcal {A}$ using the random number q. If $\mathcal {A}$ rejects, $\mathcal {S}$ replies reject to $\mathcal {T}$.

The simulation provided to $\mathcal {A}$ is correct due to the zero-knowledge property of the ZKPoK protocols and shuffling protocol and the hiding property of the commitment scheme. The behavior of $\mathcal {S}$ in the ideal world is the same as that of $\mathcal {A}$ in the real world.