Abstract
Nested timed automata (NeTAs), proposed by Li et al. are a pushdown system whose stack symbols are timed automata (TAs). With this formal models, we can model and analyze complex real-time frameworks with recursive context switches. The reachability problem of NeTAs is proved to be decidable, via encoding NeTAs to dense timed pushdown automata (DTPDAs). This paper gives a forward algorithm for reachability problem of NeTAs, by dividing the problem into two phases and integrating these two corresponding results. One phase is the reachability checking for the stack contents (i.e. TAs) and another is the state reachability problem for the TAs nested in an NeTA. The algorithm neglects time accumulation during context switches and thus an over-approximation of the original problem. As the result, the algorithm gains soundness in the sense that there exists one corresponding timed trace in the NeTA when the approximation has a timed trace to the state in less time-complexity.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
Li, G., Cai, X., Ogawa, M., Yuen, S.: Nested timed automata. In: Braberman, V., Fribourg, L. (eds.) FORMATS 2013. LNCS, vol. 8053, pp. 168–182. Springer, Heidelberg (2013)
Abdulla, P.A., Atig, M.F., Stenman, J.: Dense-Timed pushdown automata. In: Proceedings of the 27th Annual IEEE Symposium on Logic in Computer Science (LICS’12). IEEE Computer Society (2012), pp. 35–44 (2012)
Alur, R., Dill, D.L.: A theory of timed automata. Theor. Comput.Sci. 126, 183–235 (1994)
Henzinger, T.A., Nicollin, X., Sifakis, J., Yovine, S.: Symbolic model checking for real-time systems. Inf. Comput. 111, 193–244 (1994)
Larsen, K.G., Pettersson, P., Yi, W.: Uppaal in a nutshell. Int. J. Softw. Tools Technol. Transfer 1, 134–152 (1997)
Bengtsson, J.E., Yi, W.: Timed automata: semantics, algorithms and tools. In: Desel, J., Reisig, W., Rozenberg, G. (eds.) Lectures on Concurrency and Petri Nets. LNCS, vol. 3098, pp. 87–124. Springer, Heidelberg (2004)
Schwoon, S.: Model-checking pushdown system. Ph.D. thesis, Technical University of Munich (2000)
Bouyer, P., Dufourd, C., Fleury, E., Petit, A.: Updatable timed automata. Theor. Comput. Sci. 321, 291–345 (2004)
Bouyer, P.: Forward analysis of updatable timed automata. Formal Methods Syst. Design 24, 281–320 (2004)
Ausmees, K.: Zone-based reachability analysis of dense-timed pushdown automata. Student thesis, IT 12 034, Department of Information Technology, Uppsala University (2012)
Trivedi, A., Wojtczak, D.: Recursive timed automata. In: Bouajjani, A., Chin, W.-N. (eds.) ATVA 2010. LNCS, vol. 6252, pp. 306–324. Springer, Heidelberg (2010)
Acknowledgment
The authors thank Prof. Mizuhito Ogawa for fruitful discussions on the research. This research is supported by the National Nature Science Foundation of China (61100052, 61472240, 91318301, 61261130589), JSPS Kakenhi Grant-in-Aid for Scientific Research(B) (25280023) and Challenging Exploratory Research(26540026).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A An Algorithm for State Reachability Problem of TAs
An algorithm based on the notion of region is given in the following. In order to better describe the algorithm, we need to introduce some definitions first.
Let \(C\) be the maximal clock constant appearing in the TA. Given a clock valuation \(\nu \) over a set of clock \(X=\{x_1,\ldots ,x_n\}\),and a time \(t\in \mathbb {R}^{\ge 0}\), \((\nu +t)(x)\) is redefined by \(\nu (x)+t\) if \(\nu (x)+t \le C\) and otherwise any non-integral value \(C'\) whose integral part is \(C\). A function \(isInt(x)\) is defined by \(1\) if \(\nu (x)\) is an integer and 0 otherwise, determining whether the value of a given clock is integer or not. A vector \(\mathbf {H}(\nu )\),which characterizes integral properties of a clock valuation \(\nu \), is defined by \((isInt(x_1),\ldots ,isInt(x_n))\).
For any time interval \(I \in \mathcal {I}\) that appears in the TA, we bound it in the following way: \(I_b=\{ r | r \in I \wedge r \le C' \}\). Without confusion, any interval mentioned in the following is bounded.
Definition 13
(Region Equivalence). For a real number \(d\), let \(\{d\}\) denote the fractional part of \(d\), and \(\lfloor d \rfloor \) denote its integer part. We say, two clock valuations \(\nu _1,\nu _2\) are region-equivalent, denoted \(\nu _1\sim {}\nu _2\), if and only if
-
1. for all \(x\), either \(\lfloor \nu _1(x) \rfloor = \lfloor \nu _2(x) \rfloor \) or both \(\nu _1(x)>C\) and \(\nu _2(x)>C\),
-
2. for all \(x\), if \(\nu _1(x) \le C\) then \(\{ \nu _1(x) \}=0\) iff \(\{ \nu _2(x) \}=0\) and,
-
3. for all \(x,y\) if \(\nu _1(x) \le C\) and \(\nu _1(y)\le {} C\) then \(\{ \nu _1(x) \} \le \{ \nu _1(y) \}\) iff \(\{ \nu _2(x) \} \le \{ \nu _2(y) \}\).
The equivalence class \([\nu _1]\) induced by \(\sim \) is called a region, where \([\nu _1]\) represent all clock valuations that is region-equivalent to \(\nu _1\).
A symbolic state of TA is a pair \(\langle q,R \rangle \) representing a set of states of the TA, where \(p\) is a location and \(R\) is a region. A symbolic transition describes all the possible concrete transitions from the set of states.
Definition 14
Given a region \(R\), we define its direct successor: \(R^{\uparrow }=\{\nu +t|\nu \in R \wedge \mathbf {H}(\nu +t)=\mathop {\min }_{t'}\mathbf {H}(\nu +t') \ne \mathbf {H}(\nu )\}\), where \(t, t' \in \mathbb {R}^{\ge 0}\). We define \(R(x) \models I\) if \(\forall \nu \in R,\nu (x) \in I\), and \(I_x(R)=\{ [\nu [x\leftarrow {}r]] | \nu \in R \wedge r \in I \}\), where \(x \in X\) is a clock and \(I\) is a time interval. Let \(\rightsquigarrow \) denote the symbolic transition relation over symbolic states defined by the following rules:
-
\(\langle q,R \rangle \rightsquigarrow \langle q,R^{\uparrow } \rangle \)
-
\(\langle q,R \rangle \rightsquigarrow \langle q',R \rangle \), if \(q \xrightarrow {\varepsilon } q'\)
-
\(\langle q,R \rangle \rightsquigarrow \langle q',R \rangle \), if \(q \xrightarrow {x \in I?} q'\) and \(R \models I\)
-
\(\forall R' \in I_x(R), \langle q,R \rangle \rightsquigarrow \langle q',R' \rangle \), if \(q \xrightarrow {x \leftarrow I} q'\)
With the above definitions, we give a reachability algorithm for diagonal-free TAs. In Algorithm 4, we use a boolean variable \(flag\) to indicate whether the corresponding location is reached from \(p\) or not.

Remark 4
Algorithm 4 is based on region, which could be computational expensive. Although it could be optimized by using the well-known zone technique, it does not improve its theoretical complexity.
B An Algorithm for \(\mathcal {P}\)-Automaton from PDS
The following is an effective algorithm for constructing \(\mathcal {P}\)-automaton from a PDS, which is taken from [7].

With out of generality,we assume that \(A\) has no transition leading to an initial state. For Algorithm 5, the input is a pushdown system \(\mathcal {P}=(P,\varGamma ,\varDelta ,c_0)\) and an automaton \(\mathcal {A}\) accepting \(c_0\), and the output is an automaton \(\mathcal {A}_{post*}\) with \(\varepsilon \)-moves that accept all reachable configurations of \(\mathcal {P}\). In Algorithm 5, \(\mathcal {A}_{post*}\) is obtained from \(\mathcal {A}\) in two phases:
-
1.
For each \((p',\gamma ')\) satisfying that \(\mathcal {P}\) contains at least one rule of the form \(\langle p,\gamma \rangle \hookrightarrow \langle p',\gamma '\gamma \rangle \), add a new state \(q_{p',\gamma '}\).
-
2.
Add new transitions to \(A\) according to the following saturation rules:
-
If \(\langle p,\gamma \rangle \hookrightarrow \langle p',\varepsilon \rangle \) and \(p \xrightarrow {\gamma }^* q\) in the current automaton, add a transition \((p',\varepsilon ,q)\).
-
If \(\langle p,\gamma \rangle \hookrightarrow \langle p',\gamma ' \rangle \) and \(p \xrightarrow {\gamma }^* q\) in the current automaton, add a transition \((p',\gamma ',q)\).
-
If \(\langle p, \gamma \rangle \hookrightarrow \langle p', \gamma '\gamma '' \rangle \) and \(p \xrightarrow {\gamma }^* q\) in the current automaton, first add \((p',\gamma ',q_{p',\gamma '})\) and then \((q_{p',\gamma '},\gamma '',q)\).
-
C A Proof of the Lemma 1
Proof
Since \(\langle \mathcal {A}_i,p \rangle \mapsto \langle \mathcal {A}_j,q \rangle \), by Definition 9, there exists two configurations \(c\) and \(c'\), such that \(c_0=\langle \mathcal {A}_0,q_0(\mathcal {A}_0),\nu _\mathbf{0}\rangle \longrightarrow ^* c=\langle \mathcal {A}_{i},p,\nu \rangle \cdots \longrightarrow ^* c'=\langle \mathcal {A}_{j}, q, \nu ' \rangle \cdots \), where \(\nu ,\nu '\) are clock valuations over \(X(\mathcal {A}_i)\) and \(X(\mathcal {A}_j)\) respectively.
-
1.
Obviously, by the definition of reachability problem of NeTAs, \( \langle \mathcal {A}_i,p \rangle \mapsto \langle \mathcal {A}_j, q \rangle \) implies both of TAs, \(\mathcal {A}_i\) and \(\mathcal {A}_j\), must appear at the top of stack. Since \(\mathcal {A}_{post*}\) can recognize all reachable configurations from initial configuration \(c_0=\langle \bullet ,\mathcal {A}_0 \rangle \), there must be 2 transitions \(s_0 \xrightarrow {\mathcal {A}_i} s_1\) and \(s_0 \xrightarrow {\mathcal {A}_i} s_1\), where \(s_1,s_2 \in Q(\mathcal {A}_{post*})\).
-
2.
By contradiction. Assume property 2 don’t hold. With out loss of generosity, assume \((\mathcal {A}_i, q_0(\mathcal {A}_i)) \nrightarrow ^* (\mathcal {A}_i, p)\). This implies the control location \(p\) of TA \(\mathcal {A}_i\) can never be reached . Furthermore, \(\langle \mathcal {A}_i, p \rangle \) can never appear at the top of stack, which contradicts the fact \(c_0=\langle \mathcal {A}_0,q_0(\mathcal {A}_0),\nu _\mathbf{0}\rangle \longrightarrow ^* c=\langle \mathcal {A}_{i},p,\nu \rangle \cdots \). Hence, property 2 must hold.
-
3.
If \(i = j = k\), then it’s trivial that
 due to the reflexive of
due to the reflexive of  and \(\rightsquigarrow \). If not this case, consider expanding the reachable path \(c=\langle \mathcal {A}_{i},p,\nu \rangle \cdots \longrightarrow ^* c'=\langle \mathcal {A}_{j}, q, \nu ' \rangle \cdots \). Since we focus on the TAs’ reachability, we ignore the internal location change and timing behaviours of TAs. The reachable path can be transformed to a transition sequence \(\omega _0=\langle \mathcal {A}_{k_0}(i.e. \mathcal {A}_i)\rangle \cdots \xrightarrow {\phi _0} \omega _1 = \langle \mathcal {A}_{k_1} \rangle \cdots \xrightarrow {\phi _1} \cdots \xrightarrow {\phi _{n-1}} \omega _{n}=\langle \mathcal {A}_{k_n}(i.e. \mathcal {A}_j) \rangle \cdots \), where \(\omega _k\) represent stack word and \(\phi _k \in \{ push,pop,internal \}\), for \(0 \le k < n\). Noticed that some reachable paths have useless “segment”. If there exist \(0 \le a < b \le n\), such that \(\omega _a=\langle \mathcal {A}_{k_a} \rangle \cdots \xrightarrow {\phi _a} \cdots \xrightarrow {\phi _{b-1}} \omega _{k_b}=\langle \mathcal {A}_{k_b} \rangle \cdots \) and \(\omega _{a} = \omega _{b}\), the partial transition sequence is useless “segment”. It can be replaced with \(\omega _{a}\), keeping its original reachability. Assume the new transition sequence replaced all useless “segment” is \(\omega _0=\langle \mathcal {A}_{k_0}(i.e. \mathcal {A}_i) \rangle \cdots \xrightarrow {\phi _0} \omega _1 = \langle \mathcal {A}_{k_1} \rangle \cdots \xrightarrow {\phi _1} \cdots \xrightarrow {\phi _{m-1}} \omega _{m}=\langle \mathcal {A}_{k_m}(i.e. \mathcal {A}_j) \rangle \cdots \), where for \(0 \le i,j \le m\), \(\omega _i \ne \omega _j\). Notice the fact that for the new transition sequence there exists some \(0 \le k \le m-1\) such that:
and \(\rightsquigarrow \). If not this case, consider expanding the reachable path \(c=\langle \mathcal {A}_{i},p,\nu \rangle \cdots \longrightarrow ^* c'=\langle \mathcal {A}_{j}, q, \nu ' \rangle \cdots \). Since we focus on the TAs’ reachability, we ignore the internal location change and timing behaviours of TAs. The reachable path can be transformed to a transition sequence \(\omega _0=\langle \mathcal {A}_{k_0}(i.e. \mathcal {A}_i)\rangle \cdots \xrightarrow {\phi _0} \omega _1 = \langle \mathcal {A}_{k_1} \rangle \cdots \xrightarrow {\phi _1} \cdots \xrightarrow {\phi _{n-1}} \omega _{n}=\langle \mathcal {A}_{k_n}(i.e. \mathcal {A}_j) \rangle \cdots \), where \(\omega _k\) represent stack word and \(\phi _k \in \{ push,pop,internal \}\), for \(0 \le k < n\). Noticed that some reachable paths have useless “segment”. If there exist \(0 \le a < b \le n\), such that \(\omega _a=\langle \mathcal {A}_{k_a} \rangle \cdots \xrightarrow {\phi _a} \cdots \xrightarrow {\phi _{b-1}} \omega _{k_b}=\langle \mathcal {A}_{k_b} \rangle \cdots \) and \(\omega _{a} = \omega _{b}\), the partial transition sequence is useless “segment”. It can be replaced with \(\omega _{a}\), keeping its original reachability. Assume the new transition sequence replaced all useless “segment” is \(\omega _0=\langle \mathcal {A}_{k_0}(i.e. \mathcal {A}_i) \rangle \cdots \xrightarrow {\phi _0} \omega _1 = \langle \mathcal {A}_{k_1} \rangle \cdots \xrightarrow {\phi _1} \cdots \xrightarrow {\phi _{m-1}} \omega _{m}=\langle \mathcal {A}_{k_m}(i.e. \mathcal {A}_j) \rangle \cdots \), where for \(0 \le i,j \le m\), \(\omega _i \ne \omega _j\). Notice the fact that for the new transition sequence there exists some \(0 \le k \le m-1\) such that:-
for \(0 \le t \le k\), \(\phi _{t}\in \{ pop,internal \}\);
-
for \(k+1 \le t \le m-1\), \(\phi _t \in \{ push, internal\}\).
By the definition of \(\rightsquigarrow \) and
 , we have
, we have  .
. -
-
4.
if \(\mathcal {A}_i \rightsquigarrow \mathcal {A}_j\) don’t hold, there must be some \(k\) such that
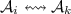 , and \(k \ne i\). This implies the fact that when the top symbol of stack is \(\mathcal {A}_i\), it must be either popped out through “pop” transition or replaced with another TA through “internal” transition. In either way, \(\mathcal {A}_i\) muse reach one of its final locations;otherwise, it cannot be popped or replaced by the semantics of TAs. Therefore, \(\exists q_f \in F(\mathcal {A}_i)\) s.t. \((\mathcal {A}_i,p) \rightarrow ^* (\mathcal {A}_i,q_f)\).
, and \(k \ne i\). This implies the fact that when the top symbol of stack is \(\mathcal {A}_i\), it must be either popped out through “pop” transition or replaced with another TA through “internal” transition. In either way, \(\mathcal {A}_i\) muse reach one of its final locations;otherwise, it cannot be popped or replaced by the semantics of TAs. Therefore, \(\exists q_f \in F(\mathcal {A}_i)\) s.t. \((\mathcal {A}_i,p) \rightarrow ^* (\mathcal {A}_i,q_f)\).
D A Proof of the Lemma 2
Proof
The main idea is to construct a reachable path of \(\langle \mathcal {A}_i, p \rangle \mapsto \langle \mathcal {A}_j, q \rangle \) from the above 4 properties. Due to the first property, \((s_0,\mathcal {A}_i,s_1) \in \rightarrow (\mathcal {A}_{post*})\) implies \(\mathcal {A}_i\) can appear at the top of stack. We can construct a reachable path of \(c_0=\langle \mathcal {A}_0, q_0(\mathcal {A}_0), \nu _\mathbf{0} \rangle \rightarrow ^* c_1=\langle \mathcal {A}_i, q_0(\mathcal {A}_i), \nu _\mathbf{0} \rangle \cdots \) through all kinds of operations but \({{\varvec{Pop}}}\) operation. Besides, configuration \(c_1\) in the form \(c_1=\langle \mathcal {A}_{k_0},p_{k_0},\nu _{k_0} \rangle \langle \mathcal {A}_{k_1},p_{k_1},\nu _{k_1} \rangle \cdots \langle \mathcal {A}_{k_n},p_{k_n},\nu _{k_n} \rangle \),where for \(0 \le i \le n, \mathcal {A}_{k_i} \in T(\mathcal {N}), p_{k_i} \in Q(\mathcal {A}_{k_i})\) and \(\nu _{k_i}\) is a clock valuation over \(X(\mathcal {A}_{k_i})\), should satisfy the requirement that for \(0 \le i \le n\), if \(\exists p_f \in F(\mathcal {A}_{k_i})~s.t.~ (\mathcal {A}_{k_i},q_0(\mathcal {A}_{k_i})) \rightarrow ^* (\mathcal {A}_{k_i},p_f)\), then \(p_{k_i}=p_f\). Note we can always do this, because when transferring to \(c_1\) each time one TA is pushed into the stack, we can always check if topmost symbol in stack can reach one of its final locations. If so, wait until it reach one of its final locations. With second property, \((\mathcal {A}_i,q_0(\mathcal {A}_i)) \rightarrow ^* (\mathcal {A}_i,p)\) implies \(c_1=\langle \mathcal {A}_i, q_0(\mathcal {A}_i), \nu _\mathbf{0} \rangle \cdots \rightarrow ^* c_2=\langle \mathcal {A}_i, p, \nu \rangle \cdots \), where \(\nu \) is a clock valuation over \(X(\mathcal {A}_i)\). Note the transitions from \(c_1\) to \(c_2\) involve only progress transition and intra-action of TA \(\mathcal {A}_i\). Next we consider two different cases.
-
1.
if \(\mathcal {A}_i \rightsquigarrow \mathcal {A}_j\) holds, when the topmost symbol in stack is \(\mathcal {A}_i\), we can always make the topmost symbol be \(\mathcal {A}_j\) through all kinds of operations except \(Pop\) operation. Hence, \(c_2=\langle \mathcal {A}_i, p, \nu \rangle \cdots \rightarrow ^* c_3=\langle \mathcal {A}_j, q_0(\mathcal {A}_j), \nu _\mathbf{0} \rangle \cdots \). Note in the process of transferring to \(c_3\), the symbols below topmost symbol \(\mathcal {A}_i\) are still there and their locations are not changed.
-
2.
if \(\mathcal {A}_i \rightsquigarrow \mathcal {A}_j\) doesn’t hold, there exist a \(k\), \(k \ne i\) s.t.
 , where \(\mathcal {A}_k \in T(\mathcal {N})\). By the definition of
, where \(\mathcal {A}_k \in T(\mathcal {N})\). By the definition of  and the specific requirement for \(c_1\), we have \(c_2=\langle \mathcal {A}_i, p, \nu \rangle \cdots \rightarrow ^* c_4=\langle \mathcal {A}_k, q_0(\mathcal {A}_k), \nu \rangle \cdots \) through only \(pop\) and \(internal\) operations. Note, due to the fourth property, \(\mathcal {A}_i\) can reach one of its final locations and can be popped out or replaced. For \(\mathcal {A}_k \rightsquigarrow \mathcal {A}_j\), similarly we have \(c_4=\langle \mathcal {A}_k, q_0(\mathcal {A}_k), \nu \rangle \cdots \rightarrow ^* c_5=\langle \mathcal {A}_j, q_0(\mathcal {A}_j), \nu \rangle \cdots \) through all kinds of operations except \(Pop\) operation.
and the specific requirement for \(c_1\), we have \(c_2=\langle \mathcal {A}_i, p, \nu \rangle \cdots \rightarrow ^* c_4=\langle \mathcal {A}_k, q_0(\mathcal {A}_k), \nu \rangle \cdots \) through only \(pop\) and \(internal\) operations. Note, due to the fourth property, \(\mathcal {A}_i\) can reach one of its final locations and can be popped out or replaced. For \(\mathcal {A}_k \rightsquigarrow \mathcal {A}_j\), similarly we have \(c_4=\langle \mathcal {A}_k, q_0(\mathcal {A}_k), \nu \rangle \cdots \rightarrow ^* c_5=\langle \mathcal {A}_j, q_0(\mathcal {A}_j), \nu \rangle \cdots \) through all kinds of operations except \(Pop\) operation.
In general, in both cases we have \(c_0 \rightarrow ^* c_2=\langle \mathcal {A}_i,p,\nu \rangle \cdots \rightarrow ^* c_6 = \langle \mathcal {A}_j,q_0(\mathcal {A}_j),\nu _\mathbf{0} \rangle \cdots \). By second property, we have \(c_6=\langle \mathcal {A}_j,q_0(\mathcal {A}_j),\nu _\mathbf{0} \rangle \cdots \rightarrow ^* \langle \mathcal {A}_j,q,\nu ' \rangle \cdots \), where \(\nu '\) is a clock valuation over \(X(\mathcal {A}_j)\). Since \(c_0 \rightarrow ^* c_2=\langle \mathcal {A}_i,p,\nu \rangle \cdots \rightarrow ^* \langle \mathcal {A}_j,q,\nu ' \rangle \cdots \), \(\langle \mathcal {A}_i, p \rangle \mapsto \langle \mathcal {A}_j, q \rangle \) holds.
Rights and permissions
Copyright information
© 2015 Springer International Publishing Switzerland
About this paper
Cite this paper
Wen, Y., Li, G., Yuen, S. (2015). An Over-Approximation Forward Analysis for Nested Timed Automata. In: Liu, S., Duan, Z. (eds) Structured Object-Oriented Formal Language and Method. SOFL+MSVL 2014. Lecture Notes in Computer Science(), vol 8979. Springer, Cham. https://doi.org/10.1007/978-3-319-17404-4_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-17404-4_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-17403-7
Online ISBN: 978-3-319-17404-4
eBook Packages: Computer ScienceComputer Science (R0)


 due to the reflexive of
due to the reflexive of  and
and  , we have
, we have  .
.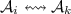 , and
, and  , where
, where  and the specific requirement for
and the specific requirement for