Skip to main content
SpringerLink
Log in
Book cover

International Conference on Interactive Theorem Proving

ITP 2015: Interactive Theorem Proving pp 170–186Cite as

Proof-Producing Reflection for HOL

With an Application to Model Polymorphism

  • Conference paper
  • First Online:

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 9236))

Abstract

We present a reflection principle of the form “If \(\ulcorner \varphi \urcorner \) is provable, then \(\varphi \)” implemented in the HOL4 theorem prover, assuming the existence of a large cardinal. We use the large-cardinal assumption to construct a model of HOL within HOL, and show how to ensure \(\varphi \) has the same meaning both inside and outside of this model. Soundness of HOL implies that if \(\ulcorner \varphi \urcorner \) is provable, then it is true in this model, and hence \(\varphi \) holds. We additionally show how this reflection principle can be extended, assuming an infinite hierarchy of large cardinals, to implement model polymorphism, a technique designed for verifying systems with self-replacement functionality.

This is a preview of subscription content, log in via an institution.

Chapter
USD   29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD   39.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD   54.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Learn about institutional subscriptions

Notes

  1. 1.

    \(\ulcorner \varphi \urcorner \) refers to \(\varphi \) as a syntactic object, represented e.g. by its Gödel number or by an abstract syntax tree.

  2. 2.

    Including, as in Gordon [9], polymorphism (type variables and polymorphic constants) and defined constants and type operators.

  3. 3.

    This is akin to working within an Isabelle [23] locale which fixes \(\mu \) and \({ {mem}}\) and assumes \(\mathsf{is\_set\_theory }\;{ {mem}}\). (We assume infinity only when necessary).

  4. 4.

    The abstract syntax here is the inner HOL rendition of our example term. \(\mathsf{Bool }\) and \(\mathsf{Fun }\;{ {a}}\;{ {b}}\) are abbreviations for \(\mathsf{Tyapp }\;{\text {``bool''}}\;\mathsf{[\,] }\) and \(\mathsf{Tyapp }\;{\text {``fun''}}\;[{ {a}};\;{ {b}}]\).

  5. 5.

    To understand the three turnstiles: \(\vdash \) denotes provability in outer HOL (and applies to the whole formula), infix |- denotes provability in inner HOL, and infix \(\models \) states that a sequent is valid according to the semantics of inner HOL.

  6. 6.

    To be pedantic, \(\mathsf{to\_inner }\) also depends on the pervasive \({ {mem}}\) relation of the set theory.

  7. 7.

    We follow the convention of treating predicates in outer HOL as sets. To be clear \(\mathcal {U}({:}\alpha )\) is a term of type 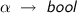, and \(\left\{ \right. {}{ {a}}\;|{}\;{ {a}}\;\mathsf{\lessdot }\;{ {x}}\left. \right\} {}\) is a term of type . These sets-as-predicates are distinct from the Zermelo sets, i.e., the terms of type \(\mu \).

  8. 8.

    Also known as indefinite choice, the Hilbert choice principle in HOL provides a constant \((\mathsf{\varepsilon {} })\), usually written as a binder, together with the axiom \((\mathsf{\exists \,{} }{ {x}}.\;{ {P}}\;{ {x}})\;\mathsf{\Rightarrow {} }\;{ {P}}\;(\mathsf{\varepsilon {} }{ {x}}.\;{ {P}}\;{ {x}})\) which holds for any predicate \({ {P}}\).

  9. 9.

    \(\mathsf{Num }\) is an abbreviation for \(\mathsf{Tyapp }\;{\text {``num''}}\;\mathsf{[\,] }\).

  10. 10.

    When a new constant or type operator is defined, theorems produced by the definition are considered axioms of the resulting theory. The other source of axioms is new-axiom updates, which we do not support since they are not sound in general.

  11. 11.

    Any valuation would do for this input since it has no free type or term variables.

  12. 12.

    Our proof constructs a potentially slightly different model of inner HOL for each value of t; this is, roughly, the origin of the term model polymorphism.

References

  1. Allen, S.F., Constable, R.L., Howe, D.J., Aitken, W.E.: The semantics of reflected proof. In: Proceedings of the LICS, pp. 95–105, IEEE Computer Society (1990)

    Google Scholar 

  2. Dybjer, P., Setzer, A.: A finite axiomatization of inductive-recursive definitions. In: Girard, J.-Y. (ed.) TLCA 1999. LNCS, vol. 1581, pp. 129–146. Springer, Heidelberg (1999)

    Chapter  Google Scholar 

  3. Fallenstein, B., Soares, N.: Vingean reflection. Technical report, Machine Intelligence Research Institute, Berkeley, CA (2015)

    Google Scholar 

  4. Feferman, S.: Transfinite recursive progressions of axiomatic theories. J. Symb. Log. 27(3), 259–316 (1962)

    Article  MathSciNet  Google Scholar 

  5. Franzén, T.: Transfinite progressions: a second look at completeness. B. Symb. Log. 10(3), 367–389 (2004). http://www.math.ucla.edu/~asl/bsl/1003/1003-003.ps

  6. Gödel, K.: Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I. Monatshefte fr Mathematik und Physik 38(1), 173–198 (1931)

    Article  Google Scholar 

  7. Gonthier, G.: The four colour theorem: engineering of a formal proof. In: Kapur, D. (ed.) ASCM 2007. LNCS (LNAI), vol. 5081, pp. 333–333. Springer, Heidelberg (2008)

    Chapter  Google Scholar 

  8. Gonthier, G., Mahboubi, A.: An introduction to small scale reflection in Coq. J. Form. Reasoning 3(2), 95–152 (2010)

    MATH  MathSciNet  Google Scholar 

  9. Gordon, M.: From LCF to HOL: a short history. In: Plotkin, G.D., Stirling, C., Tofte, M. (eds.) Proof, Language, and Interaction, Essays in Honour of Robin Milner, pp. 169–186. The MIT Press, Cambridge (2000)

    Google Scholar 

  10. Harrison, J.: Metatheory and reflection in theorem proving: A survey and critique. Technical report CRC-053, SRI, Cambridge, UK (1995). http://www.cl.cam.ac.uk/~jrh13/papers/reflect.dvi.gz

  11. Harrison, J.: Towards self-verification of HOL Light. In: Furbach, U., Shankar, N. (eds.) IJCAR 2006. LNCS (LNAI), vol. 4130, pp. 177–191. Springer, Heidelberg (2006)

    Chapter  Google Scholar 

  12. Harrison, J.: HOL Light: an overview. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 60–66. Springer, Heidelberg (2009)

    Chapter  Google Scholar 

  13. Jech, T.: Set Theory. The Third Millenium Edition, Revised and Expanded. Springer Monographs in Mathematics. Springer, Heidelberg (2003)

    Google Scholar 

  14. Klein, G., Gamboa, R. (eds.): Interactive Theorem Proving. Springer, Heidelberg (2014)

    MATH  Google Scholar 

  15. Kumar, R., Arthan, R., Myreen, M.O., Owens, S.: HOL with definitions: semantics, soundness, and a verified implementation. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 308–324. Springer, Heidelberg (2014)

    Google Scholar 

  16. Kumar, R., Arthan, R., Myreen, M.O., Owens, S.: Self-formalisation of higher-order logic. J. Autom. Reasoning (2015), submitted. Preprint at https://cakeml.org

  17. Mohamed, O.A., Muñoz, C.A., Tahar, S. (eds.): Theorem Proving in Higher Order Logics. Springer, Heidelberg (2008)

    MATH  Google Scholar 

  18. Myreen, M.O., Davis, J.: The reflective Milawa theorem prover is sound - (down to the machine code that runs it). In: Klein and Gamboa [14], pp. 421–436

    Google Scholar 

  19. Myreen, M.O., Owens, S.: Proof-producing translation of higher-order logic into pure and stateful ML. J. Funct. Program. 24(2–3), 284–315 (2014)

    Article  MATH  MathSciNet  Google Scholar 

  20. Norrish, M., Huffman, B.: Ordinals in HOL: transfinite arithmetic up to (and beyond) \(\omega _{1}\). In: Blazy, S., Paulin-Mohring, C., Pichardie, D. (eds.) ITP 2013. LNCS, vol. 7998, pp. 133–146. Springer, Heidelberg (2013)

    Chapter  Google Scholar 

  21. Slind, K., Norrish, M.: A brief overview of HOL4. In: Mohamed et al. [17], pp. 28–32

    Google Scholar 

  22. Turing, A.M.: Systems of logic based on ordinals. Proc. LMS 2(1), 161–228 (1939)

    MathSciNet  Google Scholar 

  23. Wenzel, M., Paulson, L.C., Nipkow, T.: The Isabelle framework. In: Mohamed et al. [17], pp. 33–38

    Google Scholar 

Download references

Acknowledgements

We thank Magnus Myreen for feedback on a draft of this paper. We also thank the anonymous reviewers for their helpful criticism.

Author information

Authors and Affiliations

  1. Machine Intelligence Research Institute, Berkeley, USA

    Benja Fallenstein

  2. Computer Laboratory, University of Cambridge, Cambridge, UK

    Ramana Kumar

Authors
  1. Benja Fallenstein
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ramana Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ramana Kumar .

Editor information

Editors and Affiliations

  1. Department of Informatics, King's College London, London, United Kingdom

    Christian Urban

  2. PLA University of Science and Technology, Nanjing, China

    Xingyuan Zhang

Rights and permissions

Reprints and permissions

Copyright information

© 2015 Springer International Publishing Switzerland

About this paper

Cite this paper

Fallenstein, B., Kumar, R. (2015). Proof-Producing Reflection for HOL. In: Urban, C., Zhang, X. (eds) Interactive Theorem Proving. ITP 2015. Lecture Notes in Computer Science(), vol 9236. Springer, Cham. https://doi.org/10.1007/978-3-319-22102-1_11

Download citation

  • DOI: https://doi.org/10.1007/978-3-319-22102-1_11

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-319-22101-4

  • Online ISBN: 978-3-319-22102-1

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

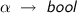Policies and ethics

Search

Navigation