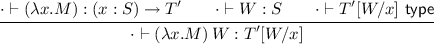A Delta for Hybrid Type Checking

Abstract

A hybrid type checker defers parts of the type checking to run time. At compile time, the checker attempts to statically verify as many subtyping constraints as possible. Constraints that cannot be proved by the static checker, are reified as run-time casts in an intermediate language, which is a variant of the blame calculus.

The goal of this work is to simplify casts in the intermediate blame calculus by exploiting context information. To this end, we develop a coercion calculus that corresponds to the blame calculus via a pair of translations and we define the formal framework to simplify these coercions. We give a concrete instance of the calculus and demonstrate that simplification can be regarded as a synthesis problem.

A Proofs

1.1 A.1 Preservation for $\lambda _{hb}$

Proof of Proposition 2

Induction on the derivation of $M \longrightarrow N$.

Case $(\lambda x.M)\,W \longrightarrow M[W/x]$.

• 1. Inversion of $\cdot \vdash (\lambda x.M)\,W : T$ yields the next two items

• 2.

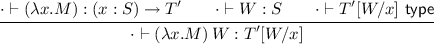
• 3. $\cdot \vdash T'[W/x] \le T$

• 4. Inversion on the first premise of Item 2 yields the next two items

• 5. $x:S' \vdash M : T''$

• 6. $\cdot \vdash (x:S') \rightarrow T'' \le (x:S) \rightarrow T'$ which implies $\cdot \vdash S \le S'$ and $x:S \vdash T'' \le ~T'$

• 7. From Items 5 and 6 and the premise $\cdot \vdash W : S$ in Item 2, the substitution lemma yields $\cdot \vdash M[W/x] : T''[W/x]$

• 8. From Item 6 and substitution, we obtain $\cdot \vdash T''[W/x] \le T'[W/x]$

• 9. Item 3, transitivity of subtyping, and subsumption yield $\cdot \vdash M[W/x] : T$

Case $\lceil m\rceil +\lceil n\rceil \longrightarrow \lceil m+n\rceil$.

• 1. Inversion of $\cdot \vdash \lceil m\rceil +\lceil n\rceil : T$ yields the following three items

• 2. $\cdot \vdash z \,{:}\, \mathsf {int} \{ \exists xy.z=x+y \wedge P\wedge Q\} \le T$

• 3. $\cdot \vdash \lceil m\rceil : x \,{:}\, \mathsf {int} \{ P\}$ where $\cdot \vdash x \,{:}\, \mathsf {int} \{ x=m\} \le x \,{:}\, \mathsf {int} \{ P\}$

• 4. $\cdot \vdash \lceil n\rceil : y \,{:}\, \mathsf {int} \{ Q\}$ where $\cdot \vdash y \,{:}\, \mathsf {int} \{ y=n\} \le y \,{:}\, \mathsf {int} \{ Q\}$

• 5. Hence, $x=m \supset P$ and $y=n \supset Q$

• 6. Now $\cdot \vdash \lceil m+n\rceil : z \,{:}\, \mathsf {int} \{ z=m+n\}$

• 7. The predicate is equivalent to $\exists xy. z=x+y \wedge x=m \wedge y=n$.

• 8. By Item 5, the predicate in Item 7 implies $\exists xy. z=x+y \wedge P\wedge Q$

• 9. Taking Items 6, 7, 8, and 2 and applying subsumption yields $\cdot \vdash \lceil m+n\rceil : T$

Case .

• 1. Inversion applied to $\cdot \vdash \lceil m\rceil : x \,{:}\, B \{ P\}\Rightarrow x \,{:}\, B \{ Q\}: T$ yields

• 2. $\cdot \vdash x \,{:}\, B \{ Q\}\le T$ and

• 3. $\cdot \vdash \lceil m\rceil : x \,{:}\, B \{ P\}$ and

• 4. $\models Q[m/x]$

• 5. For the reduct, $\cdot \vdash \lceil m\rceil : x \,{:}\, B \{ x = m\}$

• 6. Since $\models Q[m/x]$, we have $\models \forall x. x=m \wedge Q$, which establishes the subtyping $\cdot \vdash x \,{:}\, B \{ x = m\} \le x \,{:}\, B \{ Q\}$

• 7. The claim follows by subsumption with Item 2.

Case .

• 1. Applying inversion to $\cdot \vdash (V : (x:S) \rightarrow T \Rightarrow (x:S') \rightarrow T')\, W : T'[W/x]$ yields the following items

• 2. $\cdot \vdash (V : (x:S) \rightarrow T \Rightarrow (x:S') \rightarrow T') : (x:S') \rightarrow T'$

• 3. $\cdot \vdash W : S'$

• 4. $\cdot \vdash T'[W/x]$

• 5. Inverting the premise of Cast-Arg-Base, we further obtain

• 6. $S = x \,{:}\, B \{ P\}$

• 7. $S' = x \,{:}\, B \{ P\}'$

• 8. $\models {P}'[W/x]$

• 9. From Item 3 and 6, we obtain $\models P[W/x]$

• 10. Applying inversion to Item 2, we obtain

• 11. $\cdot \vdash V : (x:S) \rightarrow T$ and

• 12. $\lfloor (x:S) \rightarrow T\rfloor = \lfloor (x:S') \rightarrow T'\rfloor$

• 13. Using Item 9, we obtain $\cdot \vdash W : S$ (with an intermediate subsumption step)

• 14. Hence $\cdot \vdash T[W/x]$ and $\cdot \vdash V\, W : T[W/x]$

• 15. We conclude that $\cdot \vdash (V\, W : (T \Rightarrow T')[W/x]) : T'[W/x]$

Case .

• 1. From the premise, we know that $\lfloor S'\rfloor = \lfloor S\rfloor = G \rightarrow G'$

• 2. Applying inversion to $\cdot \vdash (V : (x:S) \rightarrow T \Rightarrow (x:S') \rightarrow T')\, W : T_0$ yields

• 3. $T_0 = T'[W/x]$

• 4. $\cdot \vdash W: S'$

• 5. $\cdot \vdash (V : (x:S) \rightarrow T \Rightarrow (x:S') \rightarrow T') : (x:S') \rightarrow T'$

• 6. From Item 1 and 3, we obtain $T_0 = T'[W/x] = T'$ and, in fact, $T'[N/x] = T'$ and $T[N/x]=T$, for any N, because all free variables in types are restricted to base types.

• 7. Inversion of Item 5 yields the following

• 8. $\cdot \vdash V : (x:S) \rightarrow T$ and

• 9. $\lfloor (x:S) \rightarrow T\rfloor = \lfloor (x:S') \rightarrow T'\rfloor$

• 10. From Item 5, we conclude $\cdot \vdash (W : S' \Rightarrow S) : S$

• 11. From Item 10 and 8, we obtain $\cdot \vdash (V\, (W : S' \Rightarrow S)) : T[(W : S' \Rightarrow S)/x]$, where Item 6 assures us that $T[(W : S' \Rightarrow S)/x] = T$ is well-formed.

• 12. We conclude that $\cdot \vdash (V\, (W : S' \Rightarrow S) : (T \Rightarrow T')) : T'$ where $T' = T'[W/x] = T_0$ by Item 6.

Case reduction in context: immediate by application of the inductive hypothesis.     $\square$

1.2 A.2 Preservation for $\lambda _{hc}$

Proof of Proposition 2

; cases for $\lambda _{hc}$. We just state the additional inductive cases for the reductions involving coercions.

Case .

• 1. From $\cdot \vdash \lceil m\rceil \langle x.R\rangle : T$ (wlog, we omit inversion of a potential outermost application of the subsumption rule) we obtain the following two items

• 2. $\cdot \vdash \lceil m\rceil : S$

• 3. $\cdot \vdash {x.R} \,{:}{:}\, S \Longrightarrow T$

• 4. Inversion of Item 2 yields $\cdot \vdash x \,{:}\, B \{ x=m\} \le S$

• 5. Hence, $S = x \,{:}\, B \{ P\}$ for some $P$ such that $\forall x. x=m \supset P$

• 6. Inversion of Item 3 yields $T = x \,{:}\, B \{ Q\}$ such that $\forall x:B. P\supset (Q\Leftrightarrow R)$.

• 7. Since $\models R[m/x]$, we obtain that $\forall x. x=m \supset P\wedge R$ and thus $\forall x. x=m \supset Q$ by Item 6.

• 8. Hence, $\cdot \vdash \lceil m\rceil : T = x \,{:}\, B \{ Q\}$ by subsumption.

Case .

• 1. From the premise, we obtain

• 2. $k = x.R$ and

• 3. $\models R[W/x]$.

• 4. Applying inversion to $\cdot \vdash (V \langle (x:k) \rightarrow d\rangle )\, W : T_0$ yields

• 5. $\cdot \vdash (V \langle (x:k) \rightarrow d\rangle ) : (x:S') \rightarrow T'$

• 6. $\cdot \vdash W : S'$

• 7. $\cdot \vdash T_0$ where $T_0 = T'[W/x]$

• 8. Inversion of Item 5 yields

• 9. $\cdot \vdash (x:k) \rightarrow d \,{:}{:}\, (x:S) \rightarrow T \Longrightarrow (x:S') \rightarrow T'$

• 10. $\cdot \vdash V : (x:S) \rightarrow T$

• 11. From Item 9, we obtain by inversion

• 12. $\cdot \vdash k \,{:}{:}\, S' \Longrightarrow S$ and

• 13. $x : S \vdash d \,{:}{:}\, T \Longrightarrow T'$.

• 14. Hence, $S = x \,{:}\, B \{ P\}$ and $S' = x \,{:}\, B \{ P\}'$

• 15. Using Item 3, $\cdot \vdash W: S$

• 16. Hence $\cdot \vdash (V\, W) : T[W/x]$

• 17. By substitution on Item 13: $\cdot \vdash d[W/x] \,{:}{:}\, T[W/x] \Longrightarrow T'[W/x]$

• 18. Hence $\cdot \vdash (V\, W) \langle d[W/x]\rangle : T'[W/x]$

• 1. From the premise, we obtain that $k = (x':k') \rightarrow d'$ a function coercion.

• 2. By inversion on $\cdot \vdash (V \langle (x:k) \rightarrow d\rangle )\, W : T_0$ we obtain

• 3. $\cdot \vdash (V \langle (x:k) \rightarrow d\rangle ) : (x:S') \rightarrow T'$

• 4. $\cdot \vdash W : S'$

• 5. $\cdot \vdash T_0$ where $T_0 = T'[W/x]$

• 6. Further inversion on Item 3 yields

• 7. $\cdot \vdash V : (x:S) \rightarrow T$ and

• 8. $\cdot \vdash (x:k) \rightarrow d \,{:}{:}\, (x:S) \rightarrow T \Longrightarrow (x:S') \rightarrow T'$

• 9. By inversion $\cdot \vdash k \,{:}{:}\, S' \Longrightarrow S$ and $x:S \vdash d \,{:}{:}\, T \Longrightarrow T'$

• 10. By the premise, we know that $\lfloor S\rfloor = G\rightarrow G'$

• 11. Hence x does not occur free in T, $T'$, and d

• 12. Hence $\cdot \vdash \,{:}{:}\, T \Longrightarrow T'$

• 13. Thus $\cdot \vdash W \langle k\rangle : S$ (using Item 9)

• 14. By Item 11, $\cdot \vdash T[W \langle k\rangle /x]$ because $T[W \langle k\rangle /x] = T$

• 15. Hence $\cdot \vdash V (W \langle k\rangle ) : T$

• 16. We conclude $\cdot \vdash (V (W \langle k\rangle )) \langle d\rangle : T'$     $\square$