Morse Chain Complex from Forman Gradient in 3D with $\mathbb {Z}_2$ Coefficients

Abstract

A Forman gradient V on a cell complex $\varGamma$ enables efficient computation of the homology of $\varGamma$: the Morse chain complex defined by critical cells of V and their connection through gradient V-paths is equivalent to the homology of chain complex defined by cells of $\varGamma$ and the immediate boundary relation between them.

We propose an algorithm that computes the boundary operator of the Morse chain complex associated with Forman gradient V defined on a regular cell 3-complex $\varGamma$. The algorithm computes the boundary operator with coefficients in $\mathbb {Z}_2$, and encodes it in the form of the boundary matrix. Our algorithm is incremental: as it progresses through a filtration of $\varGamma$ induced by V, it computes the boundary operator for each critical cell reached in the filtration order.

1 Introduction

Available scientific data sets are of increasing quantity and quality, thus generating the need for efficient computational methods for the topological analysis of shapes represented as such complexes and of functions defined on them.

Forman theory has been established as a versatile and widely applied tool in many research fields, such as computational topology, computer graphics, scientific visualization, molecular shape analysis, and geometric modeling [1, 2, 7–9, 11, 13]. To be able to exploit its theoretical results, starting from a scalar field f given on the vertices of a regular cell complex $\varGamma$, a Forman gradient V is defined on $\varGamma$. Many algorithms that construct such gradient have been proposed, and the connection between critical points of scalar field f and critical cells of the associated Forman gradient V has been established in 2D [9] and 3D [13].

The Morse chain complex $\mathcal{M}$ of a Forman gradient V on a cell complex $\varGamma$ enables the calculation of its (persistent) homology [4, 12]. The chain groups of $\mathcal{M}$ are defined by the critical k-cells of V and the boundary operator is defined through gradient V-paths connecting them.

We propose here an iterative algorithm, which computes the boundary operator $\partial _\mathcal{M}$ and boundary matrices $B_k$ with coefficients in $\mathbb Z_2$ from a Forman gradient V on a regular 3-complex $\varGamma$ in $\mathbb R^3$. The algorithm updates the Morse chain complex at each step of the Forman gradient traversal. Thus, it produces the Morse chain complex not only for the given cell complex $\varGamma$, but also for each subcomplex $F_i$ in a (non -unique) filtration $\emptyset =F_0\subseteq F_1\subseteq ... \subseteq F_M=\varGamma$ induced by V.

In Sect. 2 we give some basic notions on Forman theory. In Sect. 3 we describe our algorithm for computing the Morse chain complex $\mathcal{M}$. In Sect. 4 we summarize the paper with a brief discussion.

2 Background Notions

We review some basic notions on Forman gradient and on the associated Morse chain complex. We focus on regular cell 3-complexes. Recall that a cell d-complex in $\mathbb R^m$ is a finite set $\varGamma$ of cells in $\mathbb R^m$ such that (i) the cells in $\varGamma$ are pairwise disjoint, and (ii) for each cell $a\in \varGamma$, the boundary of a is a disjoint union of cells in $\varGamma$. The maximum of dimensions of cells in $\varGamma$ is d. A complex is constructed inductively by starting from a discrete set of points and attaching discs of nondecreasing dimension along their boundaries. Each attaching map is continuous, homeomorphic on the interior of discs, and maps the boundary of the disc to a union of lower-dimensional discs. A complex is regular if each attaching map is a homeomorphism. The immediate boundary of a k-cell a in $\varGamma$ is composed of $(k-1)$-cells incident to a (called faces of a). The set of k-cells in $\varGamma$ is denoted as $\varGamma _k$. The total number of cells in $\varGamma$ is denoted as n.

2.1 Forman Gradient

A discrete vector field V on a regular cell complex $\varGamma$ is a collection of pairs (a, b), such that

• a is a k-cell, and b is a $(k+1)$-cell of $\varGamma$,

• a is a face of b (denoted as $a<b$), and

• each cell in $\varGamma$ is in at most one pair of V.

Thus, V can be seen as a mapping $V : \varGamma \rightarrow \varGamma \cup \{\emptyset \}$. If $(a,b)\in V$, then $V(a)=b$, and (from the third condition of the previous definition) $V(b)=\emptyset$.

A V-path is a sequence $a_1, b_1, a_2, b_2,...,a_{r+1}$ of k-cells $a_i$ and $(k+1)$-cells $b_j$, $i=1,..,r+1$, $j=1,..,r$, such that $(a_i,b_i)\in V$, $b_i>a_{i+1}$, and $a_i\ne a_{i+1}$. V-path $a_1, b_1,...,a_{r+1}$, $r > 0$, is closed if $a_{r+1}=a_{1}$. Sequence $a_1$ is a stationary V-path.

A discrete vector field V is called a Forman (discrete) gradient if and only if there are no closed V-paths in V. A critical cell of V of index k is a k-cell c which does not appear in any pair of V. In other words, a cell c is critical if $V(c)=\emptyset$, and $c\notin Im V$. We denote as C the set of critical cells, and as $C_k$ the set of critical k-cells.

Fig. 1.

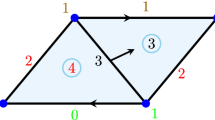
Forman gradient (a) $V_1$ and (b) $V_2$ defined on a complex $\varGamma$ with one 3-cell, four triangles, six edges and four vertices (a solid tetrahedron). Arrows indicate the pairing between cells (green for vertices and edges, blue for edges and faces, red for faces and 3-cells). (Color figure online)

In Fig. 1, two Forman gradients $V_1$ and $V_2$ are illustrated. The pairing between a k-cell a and a $(k+1)$-cell b is indicated by an arrow starting at a and pointing towards b. Both gradients $V_1$ and $V_2$ have two critical vertices (labeled 1 and 2) and one critical edge (labeled c). Gradient $V_ 2$ has also one critical face (labeled D) and one critical 3-cell (labeled v).

2.2 Morse Chain Complex

The homology of cell complex $\varGamma$ with $\mathbb Z_2$ coefficients can be computed as the homology of the chain complex with chain groups defined by the k-cells in $\varGamma$, and the boundary operator defined for each k-cell a in $\varGamma$ as the set of all $(k-1)$-cells in its immediate boundary. The homology of $\varGamma$ is equivalent to the homology of the Morse chain complex $\mathcal{M}$ induced by a Forman gradient V on $\varGamma$ [5]. The chain groups of $\mathcal{M}$ are defined by the critical cells of V, and the boundary operator $\partial _\mathcal{M}$ is defined by the parity of gradient V-paths connecting them: a critical $(k-1)$-cell c is in the boundary $\partial _\mathcal{M} (d)$ of critical k-cell d in the Morse chain complex $\mathcal{M}$ if there is an odd number of V-paths connecting some $(k-1)$-cell incident to d in $\varGamma$ to c, i.e., for $d\in C_k$

$$\partial _\mathcal{M} (d)=\sum _{\begin{array}{c} c\in {C}_{k-1} \\ there\,is\,an\,odd\,number\,of\,{ V}-paths \\ starting\,at\,a\,cell \,e\,\in \,\varGamma _{k-1},\,e<d,\, and\,ending\,at \,c \end{array}} c$$

Complex $\mathcal M$ has fewer cells than complex $\varGamma$, implying that homology computation on $\mathcal M$ requires less time than homology computation on $\varGamma$, if the boundary operator $\partial _\mathcal{M}$ can be computed efficiently. In the next section, we propose an iterative algorithm that computes this boundary operator and the boundary matrices $B_k$ of the Morse chain complex $\mathcal{M}$, not only for $\varGamma$, but also for subcomplexes $F_i$ of $\varGamma$ in a filtration induced by the topological order defined by Forman gradient V.

3 Extraction Algorithm

The input of the algorithm is a regular cell 3-complex $\varGamma$ in $\mathbb R^3$, endowed with a Forman gradient V. The gradient V induces a filtration $\emptyset =F_0\subset F_1\subset .. \subset F_M=\varGamma$ of $\varGamma$, which is computed in the preprocessing step of the algorithm. In the main loop of the algorithm, the boundary operator $\partial _\mathcal{M}$ on the Morse chain complex $\mathcal{M}$ is computed iteratively, while traversing a filtration induced by V. In the post processing step, boundary matrices $B_k$, $1\le k\le 3$, are constructed from boundary operator $\partial _\mathcal{M}$.

Recall that a cell complex is regular if all the attaching maps are homeomorphisms, i.e., if there are no identifications on the boundaries of attached cells. We are interested in computing the boundary operator $\partial _\mathcal{M}$ of the associated Morse chain complex $\mathcal{M}$ and the boundary matrices $B_k$, $1\le k\le 3$, with coefficients in $\mathbb Z_2$. Thus, there is no need to consider the orientation of cells: the incidence coefficient between incident cells of consecutive dimension in $\varGamma$ is equal to 1. Most complexes used in shape modeling, computer graphics, or image processing, such as cubical and simplicial complexes, are regular.

3.1 Filtration

A Forman gradient V on a cell complex $\varGamma$ can be encoded in a directed acyclic graph (DAG) $G=(N,A)$. Each node in N corresponds either to a critical cell of V, or to a pair of cells in V, i.e., $N= \{\{c\} : c\in C\}\cup \{\{a,b\} : (a,b)\in V\}$. There is an arc in A connecting node $m_1\in N$ to node $m_2\in N$ if a cell in node $m_2$ is in the boundary of a cell in node $m_1$.

The DAG G encodes a partial order on the set N of nodes, which can be extended to a (non-unique) total order, called topological order of the DAG [3]. When the nodes in N are sorted in ascending topological order as $m_1\le m_2\le ... \le m_M$, then no cell in $\varGamma$ comes before any cell in its boundary.

Each subsequence $m_1$, .. $m_i$ corresponds to a subcomplex $F_i$ of $\varGamma$. The topological order induces the filtration $\emptyset =F_0\subseteq F_1\subseteq ... \subseteq F_M=\varGamma$ of $\varGamma$, where each $F_i$, $1\le i\le M$, is obtained from $F_{i-1}$ by adding to it the cells in $m_i$. Thus

• $F_i=F_{i-1}\cup \{c\}$, where c is a critical cell of V, or

• $F_i=F_{i-1}\cup \{a,b\}$ where $(a,b)\in V$.

For the Forman gradient $V_1$ illustrated in Fig. 1(a), one possible topological order is e.g.

$$\{\{1\},\{2\},\{3,a\},\{4,b\},\{c\},\{d,A\},\{e,B\},\{f,C\},\{D,v\}\}.$$

For Forman gradient $V_2$ in Fig. 1(b), one possible topological order is

$$\{\{1\},\{2\},\{3,a\},\{4,b\},\{c\},\{d,A\},\{e,B\},\{f,C\},\{D\},\{v\}\}.$$

The corresponding filtrations of complex $\varGamma$ are illustrated in Fig. 2.

Fig. 2.

(a)–(h) The common subcomplexes in the filtrations induced by the topological order of Forman gradients $V_1$ and $V_2$ illustrated in Fig. 1, and the updates of sets Conn and $\partial _\mathcal{M}$ performed by the extraction algorithm. (i) The final complex obtained by adding the paired face D and 3-cell v to the complex illustrated in (h) and the last step of the extraction algorithm for Forman gradient $V_1$ illustrated in Fig. 1(a). (j) and (k) The final complex obtained by adding critical face D and critical 3-cell v to the complex in (h) and the last steps of the extraction algorithm for Forman gradient $V_2$ illustrated in Fig. 1(b)

3.2 Boundary Operator

For each critical edge c, $\partial _\mathcal{M} (c)$ is either empty, or it consists of two distinct critical vertices. As the gradient lines connecting critical vertices and edges never split, they can be extracted by tracing the Forman gradient V starting from the endpoints of each critical edge c until critical vertices are reached. If the two reached critical vertices are distinct, then there is a unique gradient path from c to each of them, and they both belong to $\partial _\mathcal{M} (c)$. Otherwise, if the same critical vertex is reached from both endpoints of c, then it is reached through two distinct gradient paths from c, and $\partial _\mathcal{M} (c)$ is empty.

Dually, gradient lines connecting critical 3-cells and faces never merge, and can be extracted by backtracking V starting from critical faces until critical 3-cells are reached. Each critical face d belongs to $\partial _\mathcal{M} (v)$ of two distinct critical 3-cells, or it does not belong to $\partial _\mathcal{M} (v)$ for any critical 3-cell v, depending on whether the two reached critical 3-cells are distinct or the same, respectively. Thus, boundary operator for critical edges and critical 3-cells (and boundary matrices $B_1$ and $B_3$) can be computed directly from V in a straightforward fashion. For completeness, we will include their computation in the algorithm through the same technique used for the computation of boundary operator for faces (and boundary matrix $B_2$).

The interesting and challenging part of the algorithm is the extraction of boundary operator for critical faces in the Morse chain complex, and we describe this part of the algorithm in greater detail. The algorithm is iterative. It traverses the cells of the complex in ascending order determined by the Forman gradient V and the induced filtration F and updates two sets (Conn and $\partial _\mathcal{M}$) associated with relevant edges and faces.

The edges that contribute to boundary operator for faces are critical edges and edges that are paired with a face, while the edges paired with a vertex do not contribute to it. The faces that contribute to boundary operator for critical faces are critical faces of V, and those that are paired with an edge. The latter will be processed at the same step of the algorithm as the edge they are paired with. The algorithm stores for each current reached edge a the set Conn(a) of all critical edges c that can be reached from a following the Forman gradient V, through an odd number of gradient V-paths.

If a is a critical edge, then the only critical edge that can be reached from a is a itself, through a unique stationary path of length 0 ($Conn(a)=\{a\}$). This unique path from a to a consists of a only.

If edge a is paired with some face b in V, then each V-path starting at a is of the form a, b, e, ..., where e is an edge incident to face b in $\varGamma$. The only critical edges that can be reached from a are those that can be reached from some of the edges e. In other words, the set of all gradient V-paths that start at edge a and connect edge a to some critical edge can be obtained by adding edge a and face b at the beginning of each gradient V-path that starts at some edge e incident to face b in $\varGamma$ and ends at some critical edge. Such edges e are those that are not paired with a vertex in V: they are either critical edges, or edges that are paired with some face in V. The information contained in the edges e in the boundary of b is propagated to edge a. If a critical edge c cannot be reached through a V-path from some edge e incident to face b in $\varGamma$, then it cannot be reached from edge a, and it does not belong to Conn(a). If c can be reached through a V-path from some edge e incident to b in $\varGamma$, then the total number of V-paths from a to c that pass through e is equal to the total number of V-paths from e to c. This is due to the fact that there is exactly one V-path from a to e: it is the path a, b, e. The total number of paths from a to c (mod 2), i.e., the parity of the number of such paths, is equal to the sum (mod 2) of the number of paths from some edge e incident to face b in $\varGamma$ to c. The sum is taken over all edges e. Thus, the set Conn(a) of all critical edges that can be reached from edge a through an odd number of V-paths can be obtained as the symmetric difference of sets Conn(e) over all edges e incident to face b in $\varGamma$.

When a critical face d is reached by the algorithm, critical edges c in the sets Conn(e) associated with the edges e incident to critical face d in $\varGamma$ are used to compute the boundary operator $\partial _\mathcal{M} (d)$. With the similar reasoning as above, we conclude that $\partial _\mathcal{M} (d)$ can be obtained as the symmetric difference of sets Conn(e) over all edges e incident to d in $\varGamma$.

We give a more formal pseudo-code-like description of the algorithm, and we illustrate its steps in Fig. 2. At step i, i.e., when complex $F_i$ is reached in the filtration F, the following actions are performed depending on $D_i=F_i-F_{i-1}$:

$\mathbf {D_i=\{c\}, c\in C_0}$

• set $Conn(c)=\{c\}$

For example, after the addition of critical vertex 1 to empty complex $F_0$, the set Conn(1) of critical vertices that are connected to critical vertex 1 through an odd number of gradient V-paths contains only vertex 1 (see Fig. 2(a)), and similarly for critical vertex 2 (Fig. 2(b)).

$\mathbf {D_i=\{a,b\}, (a,b)\in V, a\in \Gamma _0, b\in \Gamma _1}$

• set $Conn(a)=Conn(a_1)$, where $a_1$ is the other endpoint of edge b

• set $Conn(b)=\emptyset$

For example, when vertex 3 and edge a (that are paired in V) are reached and added to the complex, the set Conn(3) of critical vertices connected to vertex 3 contains critical vertex 1 (see Fig. 2(c)). Similarly, when vertex 4 and edge b are added, the set Conn(4) contains critical vertex 1 (Fig. 2(d)). The sets Conn(a) and Conn(b) are empty.

$\mathbf {D_i=\{c\}, c\in C_1}$

• set $Conn(c)=\{c\}$, $\partial _\mathcal{M} (c)=\emptyset$

• for each of the two vertices v incident to c in $\varGamma$ do $\partial _\mathcal{M} (c)=\partial _\mathcal{M} (c) \triangle Conn(v)$

For example, the two vertices incident to critical edge c in $\varGamma$ are 2 and 4. Since $Conn(2)=\{2\}$, $Conn(4)=\{1\}$ and $1\ne 2$, the boundary $\partial _\mathcal{M} (c)$ of c contains critical vertices 1 and 2. The set Conn(c) of critical edges that are connected to c contains only edge c (see Fig. 2(e)).

$\mathbf {D_i=\{a,b\}, (a,b)\in V, a\in \Gamma _1, b\in \Gamma _2}$

• set $Conn(a)=\emptyset$

• for each edge e incident to face b in $\varGamma$ do $Conn(a)=Conn(a)\triangle Conn(e)$

• set $Conn(b)=\emptyset$

For example, there are no critical edges in the set Conn(d) of edge d paired with face A in V, because the other two edges a and b incident to face A in $\varGamma$ are paired with a vertex in V: no critical edge can be reached from edge d through V (see Fig. 2(f)). The set Conn(e) for edge e paired with face B in V contains critical edge c, because c is incident to face B in $\varGamma$, and the remaining edge b incident to A is paired with a vertex (Fig. 2(g)). The set Conn(f) for edge f paired with face C contains critical edge c, because the other two edges incident to face C in $\varGamma$ are a and e. Edge a is paired with a vertex ($Conn(a)=\emptyset$) and $Conn(e)=\{c\}$ (Fig. 2(h)).

$\mathbf {D_i=\{a,b\}, (a,b)\in V, a\in \Gamma _2, b\in \Gamma _3}$

• set $Conn(a)=\emptyset$

• for each face f incident to 3-cell b in $\varGamma$ do $Conn(a)=Conn(a)\triangle Conn(f)$

For example, $Conn(D)=\emptyset$, because each of the remaining faces A, B and C incident to 3-cell v in $\varGamma$ is paired with an edge, and hence no critical face is connected to any of them through $V_1$ (see Fig. 2(i)).

$\mathbf {D_i=\{d\}, d\in C_2}$

• set $Conn(d)=\{d\}$

• set $\partial _\mathcal{M} (d)=\emptyset$

• for each edge e incident to d in $\varGamma$ do $\partial _\mathcal{M} (d)=\partial _\mathcal{M} (d)\triangle Conn(e)$

For example, $\partial _\mathcal{M} (D)=\emptyset$, because there are two gradient paths starting at an edge incident to D in $\varGamma$ and ending at c: one starts at edge f, and the other at edge c (see Fig. 2(j)).

$\mathbf {D_i=\{v\}, c\in C_3}$

• set $\partial _\mathcal{M} (v)=\emptyset$

• for each face f incident to v in $\varGamma$ do $\partial _\mathcal{M} (v)=\partial _\mathcal{M} (v)\triangle Conn(f)$

For example, $\partial _\mathcal{M} (v)=\{D\}$, since there is one gradient path from a face incident to 3-cell v in $\varGamma$ to critical face D: it is the stationary path D (see Fig. 2(k)).

3.3 Boundary Matrices

There is a 1-1 correspondence between rows in $B_k$ and critical $(k-1)$-cells of V, and between columns of $B_k$ and critical k-cells of V. Boundary matrices are computed from the boundary operator in a straightforward manner.

For the 2-complex $\varGamma _1$ and the Forman gradient illustrated in Fig. 2(i), the computed boundary matrices are

$$ \begin{array}{ccc} B_1=\left[ \begin{array}{c} 1 \\ 1 \end{array} \right]&\text{ and }&B_2=\left[ \begin{array}{c} 0 \end{array} \right] . \end{array} $$

The rows of matrix $B_1$ correspond to critical vertices 1 and 2, respectively, and the column corresponds to critical edge c.

The row of matrix $B_2$ corresponds to critical edge c and the column corresponds to critical face D.

For the 3-complex $\varGamma$ and Forman gradient $V_1$ illustrated in Fig. 1(a) and in Fig. 2(j), the (only nontrivial) boundary matrix is

$$ \begin{array}{c} B_1=\left[ \begin{array}{c} 1 \\ 1 \end{array} \right] . \end{array} $$

For the 3-complex $\varGamma$ and Forman gradient $V_2$ in Figs. 1(b) and 2(k), the boundary matrices are

$$ \begin{array}{cccc} B_1=\left[ \begin{array}{c} 1 \\ 1 \end{array} \right] \quad&B_2=\left[ \begin{array}{c} 0 \end{array} \right]&\text{ and }&B_3=\left[ \begin{array}{c} 1 \end{array} \right] . \end{array} $$

The row of matrix $B_3$ corresponds to critical face D and the column corresponds to critical 3-cell v.

3.4 Analysis

The preprocessing step of the proposed algorithm finds a topological order in the DAG $G=(N,A)$ induced by Forman gradient V on the complex $\varGamma$. The number |N| of nodes in N is in O(n), where n is the total number of cells in $\varGamma$. The number |A| of arcs in A in a DAG is at most $|N|\cdot |N-1|/2$. Thus, |A| is in $O(n^2)$. Kahn’s algorithm finds a topological order of the nodes in N in time $O(|N|+|A|)=O(n^2)$ [3].

If $\varGamma$ is a cubical complex, then each k-cell has a constant number of $(k-1)$-cells in its immediate boundary (six for 3-cells, four for edges and two for edges). Thus, the number |A| of arcs in A is in O(n), and the preprocessing step takes O(n) time in the worst case.

Proposition 1

The proposed algorithm correctly extracts the boundary operator $\partial _\mathcal{M}$ and boundary matrices $B_k$ from the Forman gradient V on a regular 3D cell complex $\varGamma$.

Proof

We need to show that the extracted boundary operator $\partial _\mathcal{M}$ is correct and does not depend on the filtration order. The algorithm maintains the following invariant: if the sets Conn and $\partial _\mathcal{M}$ are correct for complex $F_{i-1}$, then the application of the corresponding step of the algorithm produces the correct sets Conn and $\partial _\mathcal{M}$ for complex $F_i$, $1\le i\le n$. This follows from the discussion in Sect. 3.2, and the fact that the initial complex $F_0$ is empty. Thus, for each sub complex $F_i$, the algorithm computes the correct sets Conn and $\partial _\mathcal{M}$. The last complex in every filtration induced by some topological order is $\varGamma$, implying that the output of the algorithm is correct and independent of the filtration order.

Proposition 2

The time cost of the extraction algorithm is in O(nhc), where h is the maximum cardinality of the set of cells forming the immediate boundary of cells in $\varGamma$ and c is the total number of critical cells of V.

Proof

The algorithm iterates over the filtration induced by V, and the number of complexes $F_i$ in the filtration is in O(n). The time cost for each step of the algorithm depends on the set $D_i$, and can be broken in two parts. The first consists of initialization of sets Conn and/or $\partial _\mathcal{M}$, which can be done in constant time. The second part is due to loop through O(h) $(k-1)$-cells incident to the processed k-cell (critical k-cell c if $D_i=\{c\}$, $c\in C_k$, or higher-dimensional cell b if $D_i=\{(a,b)\}$, $(a,b)\in V$), and the computation of symmetric difference of O(h) sets each containing O(c) elements.

If $\varGamma$ is a cubical 3-complex, then h is constant ($h=6$), and the extraction algorithm runs in time $O(nc)=O(n^2)$ (the total number of critical cells of V may be linear in the total number of cells in $\varGamma$).

The alternative algorithms for the extraction of Morse chain complex with $\mathbb Z_2$ coefficients have been proposed in [6, 13]. Both algorithms first construct a Forman gradient on a (cubical) cell 3-complex $\varGamma$, and then the Morse chain complex induced by it.

For each critical k-cell d of V, the algorithm in [13] follows all gradient paths that start at d using a breadth first search, and counts those that connect d to another critical $(k-1)$-cell c. First, the $(k-1)$-cells incident to d in $\varGamma$ that are paired with some k-cell in V are enqueued. Then, for each $(k-1)$ cell a in the queue that is paired with a k-cell b in V, each non-critical $(k-1)$-cell e that is incident to b in $\varGamma$ and that is paired with a k-cell in V is enqueued and subsequently processed by the algorithm. The gradient paths connecting edges and faces may (branch and) merge, causing the possible multiple traversal of cells: when processing a critical k-cell d, each $(k-1)$-cell e that can be reached from d through a V-path may be enqueued and processed multiple times.

The algorithm in [6] improves on the previous one by not allowing this multiple traversal. It first extracts all $(k-1)$-cells that can be reached from a critical k-cell d by traversing Forman gradient V and deleting the visited cells, thus preventing the multiple traversal of cells. Then, from each critical $(k-1)$ cell c that can be reached from d, V-paths connecting d and c are backtracked and their number is counted (mod 2). The reported computational complexity of algorithms in [13] and [6] is in $O(n^2)$ and O(cn), respectively.

Both algorithms in [13] and [6] compute the boundary operator $\partial _\mathcal{M}$ and boundary matrices for the given cubical 3-complex $\varGamma$ with the Forman gradient V. Unlike ours, these algorithms do not adapt straightforwardly to the computation of the same boundary information for all intermediate complexes in a filtration induced by V.

4 Conclusions

We have presented an iterative algorithm that extracts the boundary operator $\partial _\mathcal{M}$ and boundary matrices $B_k$, $k=1,2,3$ for homology computation over $\mathbb Z_2$ of the Morse chain complex $\mathcal{M}$ of a regular 3D cell complex $\varGamma$ endowed with a Forman gradient V. The algorithm progresses through a filtration of $\varGamma$ induced by V, and computes this data not only of the Morse chain complex of $\varGamma$ but also of each of the subcomplexes in the filtration of $\varGamma$.

Our present work includes the extension of the algorithm presented here to computation of boundary operator and boundary matrices with coefficients in $\mathbb Z$ for cell complexes in arbitrary dimension. We are also developing a specialization of the extraction algorithm to cubical complexes. The structure of cubical complexes allows for implicit encoding of its cells, which can be accessed through their combinatorial coordinates [10]. We will utilize this encoding for efficient implementation of the extraction algorithm. We plan to investigate the computation of persistent homology of $\varGamma$ using the extracted boundary matrices.