Abstract
Local businesses and retail stores are a crucial part of local economy. Local governments design policies for facilitating the growth of these businesses that can consequently have positive externalities on the local community. However, many times these policies have completely opposite from the expected results (e.g., free curb parking instead of helping businesses has been illustrated to actually hurt them due to the small turnover per spot). Hence, it is important to evaluate the outcome of such policies in order to provide educated decisions for the future. In the era of social and ubiquitous computing, mobile social media, such as Foursquare, form a platform that can help towards this goal. Data from these platforms capture semantic information of human mobility from which we can distill the potential economic activities taking place. In this paper we focus on street fairs (e.g., arts festivals) and evaluate their ability to boost economic activities in their vicinity. In particular, we collected data from Foursquare for the three month period between June 2015 and August 2015 from the city of Pittsburgh. During this period several street fairs took place. Using these events as our case study we analyzed the data utilizing propensity score matching and a quasi-experimental technique inspired by the difference-in-differences method. Our results indicate that street fairs provide positive externalities to nearby businesses. We further analyzed the spatial reach of this impact and we find that it can extend up to 0.6 miles from the epicenter of the event.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
A healthy local business sector is important for the prosperity of the surrounding community. City governments design policies and community organizations take actions that aim in boosting the growth of such businesses. This growth can have rippling positive externalities, such as, reducing local unemployment rates, keeping the local economy aliveFootnote 1 and facilitating regional resilience to name just a few. These are even more important during periods of economic crises and recession, similar to the recent one in 2008 that US is just getting itself out of.
However, these efforts might not have the results expected. For example, many local governments during the “Small Business Saturday” (last Saturday of November) offer free curb parking. The rationale behind this policy is to give incentives to city dwellers (i.e., reduced trip cost to the business) to shop locally. However, the outcome is in many cases radically different. The underpricing of curb parking creates latent incentives for drivers to keep their cars parked for longer than normal periods of times. This leads to low turnover per parking spot and hence, ultimately to fewer number of customers in the local stores [22]. Therefore it is crucial to evaluate the efficiency of similar interventions. Knowing what boosts the local economy and what not, can allow the involved parties to make educated decisions for their future actions and ultimately lead to urban intelligence through data-driven decisions and policy making. In this study we are interested in a specific question and in particular, we are studying a research hypothesis related with the impact of street fairs on neighboring local businesses.
The golden standard for evaluating public policies is randomized experiments. However, in many cases designing and running the experiment is impossible from a practical point of view. Hence, quasi-experimental techniques [21] have been developed to analyze observational data in such a way that resembles a field experiment. To complicate things more with respect to our specific research hypothesis, evaluating the economic impact of street fairs requires access to the appropriate revenue data. While a city government office can obtain access to information such as sales tax revenue, local business advocates and citizens organizations will certainly face obstacles in obtaining such kind of data. This type of information is not part of the Open Data released by local governments and are accessible (if at all) in a very limited form through pay-per-request APIs (e.g., http://zip-tax.com/pricing). This lack of transparency can be compensated to a certain extend by utilizing information from social networks and social media. While similar types of data can potentially suffer from well-documented biases (e.g., demographic biases), they form an open platform that can be easily accessed and analyzed by citizens themselves to facilitate further investigation of issues, leading to a grassroots approach to urban governance.
In our case, given that we do not have actual revenue data for the businesses in the area of Pittsburgh as aforementioned, we collect Foursquare check-ins from the city of Pittsburgh over a three-month period (June-August 2015) and evaluate the effect of summer street fairs on local economy. The check-in information can serve as a proxy - even though not perfect - for the revenue \(\rho \) generated [24]. We would like to emphasize here that, our study aims in evaluating the impact of street fairs on the brick-and-mortar stores that are adjacent to the event location and not that on the participating entities – which is expected to be positive in order for them to participate.
In order to analyze our data we rely on two quasi-experimental techniques. First, an increase in the check-ins for the venues near the street fair does not necessarily mean that this was due to the event. One or more control areas need to be used for comparison. However, our data are not generated through a randomized experiment but they are purely observational. For our analysis, this essentially means that we cannot assume that the area hosting a street fair event is chosen at random. Consequently, we cannot assume that the areas that do not host street fairs exhibit the same characteristics with respect to unobserved confounding features and hence, we cannot compare the revenue in the treated area with any untreated area. For overcoming this problem, we rely on quasi-experimental design techniques that identify appropriate control areas. In particular, we rely on propensity score matching [20], adopted in our setting by utilizing expert domain knowledge, in order to pick a set of matched areas \(\mathcal {A}_m\) with the treated area \(\alpha \) that will serve as our control subjects. Second, once the matched areas for comparison are chosen, we adopt the difference-in-differences method [3] in our setting in order to quantify the impact of the street fairs on local businesses. In a nutshell, the difference-in-differences is a regression model that examines the average change of the treatment group once the treatment has been applied and compares it with the control group. The implicit assumption is that this difference would be zero if the treatment had not been applied. We elaborate further on these two methods in the following section.
The main contributions of our work can be summarized as follows:
-
We provide quantifiable evidence that support the positive impact of street fairs on local businesses.
-
We show how social media data - despite their potential biases - can be useful to public policy makers and local governments since they are transparent, accessible and are able to provide good evidence when analyzed properly.
Scope of our work: While in the current study we are focusing on the effect of street fairs on local businesses the method can be applied in a variety of scenarios that include an external event/stimulant. For example, one can use our framework to quantify the effect of short-term road closures and/or constructions on the local economy. This is especially important during the bidding phase of a construction project since these effects should be included in the calculation of liquidated damages [9]. However, they are not currently included since there is not a framework to estimate this effect.
Roadmap: In the following section we present our method. We then describe our experimental setup and results, while we further discuss the limitations of our study. Finally, we discuss relevant to our work studies and conclude our study.
2 Analytical Methods
Let us denote the total volume of revenue within area \(\alpha \) at day \(t\) with \(\rho _{t,\alpha }\). Furthermore, \(\mathcal {T}_{\alpha }\) is the set of days that a street fair took place within area \(\alpha \). The trending of \(\rho _{t,\alpha }\) by itself cannot reveal anything with respect to the contribution of the street fair at the revenue generated in area \(\alpha \). Hence, in order to account for various confounding factors and other externalities we will need to get a “baseline” for comparison. When experimental design and implementation is possible this happens with random assignment of the treatment (in our case the street fair) to the experimental subjects. However, in our case this is not possible and hence, we rely on matching techniques and more specifically we use propensity score matching. Matching techniques provide us with the ability to analyze observational data in a way that mimics some of the particular characteristics of a randomized trial. In particular, we choose a matched, with area \(\alpha \), neighborhood, say, \(\alpha _m\), to analyze and compare the corresponding revenues generated.
Our analysis is inspired by the difference-in-differences method [3]. In brief, we compare the daily revenue differences between the area with the street fair and the corresponding matched area(s) both during the period of the street fairs as well as during the period without any street fair. The comparison with the matched area(s) - that are exposed to the same externalities - accounts for various confounding factors that can affect revenues, and hence, any observed difference can be attributed to the treatment, i.e., the street fairs in our case. In what follows, we describe in detail the building blocks of our analysis, i.e., propensity score matching and difference-in-differences.
2.1 Propensity Score Matching
Propensity score matching can be used to reduce (or even eliminate) the effect of confounding variables on the analysis of observational data. To reiterate propensity score matching allows an analysis in a way that mimics a randomized trial. In our own context, the treatment of interest is whether or not there is a street fair in neighborhood i. The propensity score of each (untreated) instance (i.e., every untreated neighborhood) represents the probability of this instance to be treated, conditional on a set of confounding variables. In a real randomized experiment, the instances are randomly assigned to the treatment and control groups. This ensures (given sufficiently large number of instances) that on average the two groups will only differ with respect to the reception of the treatment. In the case of observational data, the treatment is not randomly assigned but usually the “treated” instances are chosen due to some specific characteristics (i.e., the confounding factors). Therefore, in order to identify an appropriate control group we need to calculate the probability of the untreated instances obtaining the treatment.
In order to calculate the propensity scores, i.e., the conditional probabilities of the instances receiving the treatment, we employ a logistic regression model similar to [1]. In particular, given a feature vector \(\varvec{Z}\) that is formed by a set of neighborhood characteristics (i.e., the confounding factors) we estimate the following conditional probability:
where \(b_i\) is a binary indicator variable, which takes the value 1 if area i is treated and 0 otherwise. In our case, \(\varvec{Z}_i\) includes three types of features for every type of establishment \(T\) that exists in neighborhood i that captures (a) the fraction of type \(T\) venues in i, as well as, (b) the fraction of the revenue (check-ins in our case) within \(\alpha \) that was generated by venues of type \(T\). Finally, for every business venue type, we use (c) the “stickiness” of the users in this type as an additional feature. The “stickiness” is defined as the ratio between the total number of check-ins in the corresponding category over the number of unique users that generated these check-ins.
After training the aforementioned logistic regression model, we estimate the probability from Eq. (1) for all neighborhood instances \(i\in \mathcal {N}\) (both treated and untreated), where \(\mathcal {N}\) is the set of areas/neighborhoods. Then we match the treated neighborhood \(\alpha \), with:
Essentially, this means that area \(\alpha _m\) is the one that has the closest probability of hosting a street fair to that of area \(\alpha \), under the assumption that the only features that affect the decision are the ones captured by the observable confounding variable vector \(\varvec{Z}\).
In many scenarios (such as in our case study) we might only have one treated area \(\alpha \), i.e., only one area has hosted a street fair. In this case, evaluating Eq. (2) is trivial, since, the minimum is observed for the area i for which the vector distance \(d(\varvec{Z}_i,\varvec{Z}_{\alpha })\) is minimized. Simply put, the matched area \(\alpha _m\) is the one whose feature vector \(\varvec{Z}_{\alpha _m}\) is closer to that of the treated area \(\varvec{Z}_{\alpha }\). We would like to emphasize here that, there might be other, unobserved, factors that lead to the choice of an area for a street fair. This is a limitation of the quasi-experimental techniques in general and propensity score matching can only account for observable confounders \(\varvec{Z}\).
One way we propose to use in order to alleviate some of the potential problems associated with the aforementioned limitation is to initialize the matching process with expert knowledge. In particular, the matched area \(\alpha _{m}\) can be chosen using expert knowledge (e.g., urban planners in our case). The benefit of this approach is that the domain expert is - implicitly or explicitly - considering various (potentially unobserved) confounders simultaneously. We can then use the expert matching as a “seed” for matching more than one neighborhoods to \(\alpha \) using the propensity scores.
In particular, with \(\pi _{m,e}\) being the propensity score of the (domain expert) matched area \(\alpha _{m,e}\), we can pick the following set of matched areas:
Essentially, as per Eq. (3), the set \(\mathcal {A}_m\) includes neighborhoods that have propensity scores that are closer to the score of the treated area (within a tolerance factor \(\epsilon \)) as compared to the expert matched area. Once set \(\mathcal {A}_m\) is obtained we can analyze the corresponding revenues generated using the difference-in-differences method described in what follows.
2.2 Difference-in-Differences
The difference in differences (DD) method [3] is a quasi-experimental technique that aims in identifying the effect of an intervention using observational data. DD requires observations obtained in different points in time, e.g., \(t_1\) and \(t_2\) (\(t_1<t_2\)), for both the control (e.g., \(y_{m,1}\) and \(y_{m,2}\)) and the treatment (e.g., \(y_{\tau ,1}\) and \(y_{\tau ,2}\)) groups. The treatment group is exposed to the intervention only during \(t_2\). The difference between \(y_{\tau ,2}\) and \(y_{m,2}\) does not only include the effect of the intervention but it also includes other “intrinsic” differences between the two groups. The latter can be captured by their difference during time \(t_1\), i.e., \(y_{\tau ,1} - y_{m,1}\), where the treatment group has not been exposed to the intervention. The DD estimate is then:
If \(\delta _{\tau ,m}>0\) (\(\delta _{\tau ,m}<0\)), then the treatment has a positive (negative) impact on \(y\), while if \(\delta _{\tau ,m}=0\) there is not any impact from the intervention. Eq. (4) captures the impact of the intervention assuming that both the treatment and control follow a parallel trend. In particular, in order for the conclusions drawn from a difference-in-differences analysis to be reliable, the parallel trend assumption needs to hold. This assumption essentially states that the average change in the control group represents the counterfactual change expected in the treatment group if there was no treatment. Simply put, if there was not any treatment applied, we would have: \((y_{\tau ,2} - y_{m,2}) = (y_{\tau ,1} - y_{m,1})\), that is, the two groups would have a stable difference. This assumption is crucial for the conclusions from a difference-in-differences analysis to hold and is many times overlooked when the method is applied.
The exactly same estimate for the DD can be formally derived through a linear regression that models the dependent variable \(y\). In particular, we have the following model:
where \(y_{ilt}\) is the dependent variable for instance i (at time t and location l), \(\alpha _l\) and \(\beta _t\) are binary variables that capture the fixed effects of location and time respectively, \(D_{lt}\) is a dummy variable that represents the treatment status (i.e., \(D_{lt} = \alpha _l\cdot \beta _t\)) and \(\epsilon _{ilt}\) is the associated error term. The coefficient \(\delta \) captures the effect of the intervention on the dependent variable \(y\). It is then straightforward to show that the DD estimate \(\hat{\delta }\) is exactly Eq. (4). In particular, if \(\overline{y}_{lt}\) is the sample mean of \(y_{ilt}\) and \(\overline{\epsilon }_{lt}\) is the sample mean of \(\epsilon _{ilt}\), and using Eq. (5) we have:
Taking expectations and considering the i.i.d. assumptions for the errors for the ordinary least squares we further get:
Given that the dummy variable D is equal to 1 only when \(l=1\) and \(t=1\) (i.e., for the treatment group after the intervention), we finally get for the DD estimator:
which is essentially the same as Eq. (4). Therefore, one can estimate the DD using either of the Eq. (4) or (5). Figure 1 further visualizes the estimation process. The control and treatment subjects in our setting are urban neighborhoods. Treated subjects includes neighborhoods that host street fairs.
2.3 Hypothesis Development
Having introduced our basic methodology we are ready to formally state the research hypotheses that are the focus of our study. In particular, we will examine the following two hypotheses.
Hypothesis 1
[Street fairs impact on local businesses]: Street fair events lead to an increase in customer visitations for nearby business venues.
Hypothesis 2
[Spatial impact of street fairs]: The impact of street fairs on the customer visitations is geographically contained in a very small area.
In order to support or reject Hypotheses 1 and 2 we will rely on data we collected from Foursquare described in the next section, utilizing the difference-in-differences method described in Sect. 2.2. We will further examine contextual dependencies, i.e., whether specific types of business venues benefit more than others.
3 Experimental Setup and Results
In this section we will present the dataset we collected, as well as, the setup for our analysis. We will then present our results and finally, we will discuss the implications and the limitations of our analysis.
3.1 Dataset
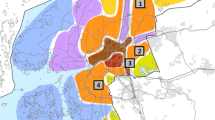
For the purposes of our study we collected time-series data using Foursquare’s venue public API. We queried daily all Foursquare venues in Pittsburgh for the three-month period between 06/01/2015 - 08/30/2015. This period includes six street fairs/eventsFootnote 2 that took place at a specific neighborhood in the city of Pittsburgh (see the street marked with red in Fig. 2).
Our time-series data include information with respect to the number of check-ins \(c_{v}[t]\) that have been generated in venue \(v\) during day \(t\). To reiterate, given the fact that we do not have actual revenue data for the businesses in Pittsburgh we rely on the check-in information as a proxy for the corresponding revenue of venue \(v\), \(\rho _{v}[t]\). This information will allow us to build the aggregate volume daily check-ins \(c_{\alpha }\) within area \(\alpha \), i.e., \(c_{\alpha }[t] = \sum _{v\in \alpha }c_{v}[t]\). Every area is defined as a circle of radius \(r\) centered at the centroid of the neighborhood under consideration. In our experiments, we examine various values for r in order to explore the spatial distribution of the impact.
We have also collected meta-data information. In particular, Foursquare associates each venue \(v\) with a type/category \(T\) (e.g., restaurant, school etc.). This classification is hierarchical and at the top level of the hierarchy there were 9 categories at the time of data collection. In order to obtain the feature vector \(\varvec{Z}\), we use the top-level categories and hence \(\varvec{Z}\) includes 21 features (2 for each category and 3 for the stickiness of each type of business venue). Our final dataset includes 27,263 venues in the city of Pittsburgh, where 21.53 % (5,869) are business venues (i.e., Nightlife Spots, Food and Shops & Services). There are in total 32,501 check-ins in our dataset, among which 44.46 % were generated in business venues.
3.2 Experimental Setup
In our study we consider a single area \(\alpha \) that has hosted street fairs during our data collection period. This area is a small business center, with a number of restaurants, cafes, retail stores (e.g., clothing stores, galleries etc.) and services (e.g., bank branches). The treated area is also accessible through public transportation, Pittsburgh’s shared bike system as well as through private vehicle with parking facilities nearby. We (initially) perform the matching process based on the expertise Footnote 3 of local urban planners. Based on their recommendations we choose another small business area, with a similar urban form and accessibility patterns not very far from the treated area (approximately 2 miles away - green area in Fig. 2). We have further used Eq. (3) to build a set of matched areas. More specifically, we first pick 2,000 random points in the city of Pittsburgh and create a neighborhood of radius 0.3 miles around this point. We further eliminate areas with less than 60 venues. We consequently obtain the matched area set \(\mathcal {A}_m\) using Eq. (3) with \(\epsilon = 0\) and we filter out overlapping matched neighborhoods, in order to remove possible dependencies in our datasets originating from the overlapping regions. In particular, when k matched areas overlap we only keep the final matched set the area with a propensity score matching closest to the treated area. We would like to emphasize here that we have examined different values for the radius of the control neighborhood area selection and the tolerance factor \(\epsilon \) and the results obtained were very similar.
3.3 Results
The metric of interest for our analysis is the mean number of daily check-ins in area \(\alpha \), denoted with \(y_{\alpha }\). For every area \(\alpha \) we compute the average number of daily check-ins during the treatment period, \(y_{\alpha ,\mathcal {T}_{\alpha }}\), as well as, during the days with no street fair, \(y_{\alpha ,\mathcal {T}_{\alpha }^c}\), where \(\mathcal {T}_{\alpha }^c\), represents the complement of \(\mathcal {T}_{\alpha }\), i.e., the set of days in our dataset where no street fair took place in \(\alpha \). With this setting the difference-in-differences coefficient is equal to 4.95 (p-value < 0.001). Simply put, there are 5 more check-ins every day with a fair in area \(\alpha \) on average. This corresponds to an almost 100 % increase in the check-ins in the area, since the average daily check-ins for the days with no event is 5.3.
As mentioned in Sect. 2.2 one of the crucial assumptions for the difference-in-differences to provide robust results is the parallel trend assumption. Typically the way that has been followed in the literature for verifying this assumption is to calculate the difference-in-differences coefficient for periods that the treatment has not been applied [16, 17]. Hence, for the days that in reality no street fair occurred we randomly assign pseudo-treatments in order to calculate a null coefficient \(\delta \). Figure 3 depicts the distribution of the corresponding coefficients obtained from 100 randomizations. As we can see the mass of the distribution is concentrated around \(\delta = 0\), while the 95 % confidence interval is \([-0.42, 0.37]\). Hence, we cannot reject the hypothesis that the null coefficient \(\delta \) is actually 0, hence, verifying the parallel trend assumption needed for the difference-in-differences method.
We also want to examine the spatial extent of this impact, i.e., how the impact decays with space. For this, we compute the difference-in-differences coefficient for zones of different radius around the treated area making sure that there is not any overlap with control areas. In particular, we examine zones of [0, 0.1], [0.1, 0.3], [0.3, 0.6] miles. Our results are depicted in Fig. 4 where as we can see there is a clear decreasing trend of the impact. In fact, the coefficient for the range [0.1, 0.3] miles is much smaller, and equal to 0.89 (p-value < 0.1), while going further away from the area of the event (i.e., [0.3, 0.6] miles) the effect is practically eliminated (\(\delta _{[0.3,0.6]}=0.33\), p-value = 0.61). These results indicate - as one might have expected - that the impact of a street fair event is highly localized within a very small area around the epicenter of the event.
We further examine the impact of each event individually, i.e., we consider a single day treatment. Table 1 presents our results. As we can see every event contributes to the overall local business sector a positive increase to the check-ins, which can further be translated to increase foot traffic and revenue. The only exception is the Vintage GP Car show. Compared to the other events, this attracts a very specific part of the population - i.e., car-lovers - and this might have affected its overall impact.
Our analysis until now has considered all of the business venues together regardless of their type. This essentially captures the aggregate impact of the street fair in the neighborhood. However, we would like to decompose this effect in order to understand better what type of establishments benefit from the fairs. In particular, we compute the difference-in-differences regression coefficient for the three different types of business venues our dataset contains. Figure 5 depicts our results, where the 95 % confidence interval of the estimated coefficients is also presented. As we can see shopping venues are the ones that benefit the most from the street fairs, while nightlife and food establishment exhibit a much (but significant and positive) lower coefficient \(\delta \). However, one crucial point here is that the coefficient provides the cumulative - additional to the counterfactual - check-ins recorded in all venues of the specific type. Hence, if a specific venue type is overrepresented in the area the estimated DD coefficient might be inflated Footnote 4. In order to avoid similar issues, we can normalize the obtained coefficients from the regression model by the number of venues for every establishment type. In particular, the number of shop, nightlife and food venues in the treated area are 60, 13 and 25 respectively. Therefore, the normalized coefficients for the shop and nightlife are practically equal (0.066 and 0.061 respectively). However, the food venues still have a much smaller normalized coefficient, that is, 0.014.
Overall, we can say that our results support the two research hypotheses put forth in Sect. 2.3. In particular, street fairs have a positive impact on nearby businesses as captured by the check-ins on Foursquare and the difference-in-differences method. Furthermore, this impact is highly concentrated in the areas around the street fair (i.e., 0.1, 0.2 miles) and drops extremely fast as we move further away.
3.4 Discussion and Limitations
One of the main critics that studies relying on social media get is that of the potential demographic biases that the data include. This is certainly true and is one of our study’s limitation as well. Nevertheless, location-based social media is a very good, and accessible, proxy for the economic activities in urban areas. Certainly there will be noise in the obtained signal, but this information is valuable for providing supporting (or not) evidence in a variety of research hypotheses similar to ours. For example, similar datasets have been used to study urban gentrification, deprivation, emotions in a city [7, 11, 23] etc.
In our difference-in-differences regression model we included fixed time and location effects. One might argue that we should also control for the day of the week. However, this is not necessary since the null regression model essentially shows us that the different days of the week will exhibit the same “trending” on average (of course the absolute values of the check-ins will be different). To verify this we run the regression model by adding an independent variable that captures the day of the week. Our results for the various zones around the treated neighborhood are presented in Table 2.
As we can see even when controlling for the day of the week the impact is strong and significant. In fact, when controlling for the day of the week the impact appears to be significant even for distances beyond the 0.1 miles. Nevertheless, the impact itself is weak (i.e., the coefficient is small). Furthermore, even though it appears that the further zone has a stronger effect, the 95 % confidence intervals for the two coefficients overlap, and hence, we cannot confidently support the presence of a trend.
4 Related Work
In this section we briefly discuss related methodological literature as well as literature relevant to the specific application domain.
Quasi-experimental methodologies: The gold standard for evaluating the impact of a policy is a field experiment. However, when it comes to public policy many times this is not possible for a variety of reasons. In this case we need to rely on quasi-experimental techniques [21] in order to quantify the potential impact. Quasi-experimental designs allows to control the assignment to the treatment condition, but using some criterion different than random assignment as in field experiments.
There are various techniques that can be used depending on the type of observational data one has. For example, the difference-in-differences method [3] compares the average change over time in the outcome variable for the treatment group to the average change over time for the control group. One of the major problems when applying this method is the parallel trend assumption, that is, that the two groups exhibit the same temporal trend on their averages without the treatment. Regression discontinuity [12] is another technique that can be used to quantify the effects of treatments that are assigned by a threshold. The key idea is that observations lying very closely on either side of the threshold while differing in the reception of the treatment, they are equal for all practical purposes. Hence, their treatment assignment mimics that of a randomized control trial. It should be clear that not all quasi-experimental designs are applicable in all scenarios (for example regression discontinuity cannot be applied in our setting), while there can be settings were no method is applicable. A nice survey of various quasi-experimental techniques can be found in [10].
Local businesses and urban economy: Small shops and businesses are the backbone of local economy and quantifying the effect of external events and policies on their prosperity is of utmost importance. Given the absence of large scale data, most of the existing studies have been based on survey data. For instance, a survey research conducted by Lee et al. [14] during the 2002 World Cup identified that the event-related tourists yielded much higher expenditure as compared to regular tourists, indicating that such mega-events could have a positive economic impact for local businesses. As another example, a report from a Toronto-based think tank has identified the positive impact that bike lanes have on the revenue of local businesses despite the fact that business owners systematically underestimate it [2]. In a similar direction, based on merchant and pedestrian surveys in Toronto’s Annex Neighborhood, the “Clean Air Partnership” [5] recommended reallocating a curb parking lane to bike lanes, since this is likely to increase commercial activity. A recent study further showed that the installation of shared bike system can lead to an increase of the housing property values [17]. Moreover, in a briefing paper DeShazo et al. [6] using a survey conducted over a small sample of businesses quantified the effect of CicLAvia on local businesses. CicLAviaFootnote 5 is a car-free event that happens once every year in various areas in Los Angeles. Furthermore, anecdotal hard evidence from Seattle [18] show that increasing the price of curb parking can be beneficial to restaurants and local businesses mainly due to the increased turnover of each parking spot [22].
During the last years, and driven by the proliferation and availability of geo-tagged social media data, there has been a surge of studies on business analytics. For instance, Qu and Zhang [19] proposed a framework that extends traditional trade area analysis and incorporates location data of mobile users. Their framework can answer crucial questions in retail management such as “where are the customers of a business coming from?”. As another example, Karamshuk et al. [13] proposed a machine learning framework to predict the optimal placement for retail stores, where they extracted two types of features from a Foursquare check-in dataset. Furthermore, these platforms can serve as mobile “yellow pages” with business reviews that can influence customer choices and business revenue. For example, Luca [15] has identified a causal impact of Yelp ratings on restaurant demand using the regression discontinuity framework. Closer to our study, Georgiev et al. [8] using data collected from Foursquare study the impact of the 2012 Olympic Games on the businesses in London, while Zhang et al. [24] quantify the effectiveness of special deals offered through location-based services as an affordable advertisement for local businesses.
To the best of our knowledge no one has examined the impact of street fairs on the adjacent businesses, even though local authorities expect this policy to have a positive outcome for businessesFootnote 6. Studies that examine the economic effects of special events/festivals exist (e.g., [4]) but their focus is slightly different, focusing on the participating entities/kiosks themselves. On the contrary, our study is focused on the “network” effects a street fair can have for the nearby businesses.
5 Conclusions and Future Work
In this study we have used social media data and quasi-experimental techniques to evaluate the effect of street fairs on the local business sector. In particular, we have adopted quasi-experimental techniques, i.e., difference-in-differences, and synthesized them with domain expert knowledge. We consequently applied our method on street fairs and outdoors arts festivals that took place on a specific neighborhood in the city of Pittsburgh as a case study. Our results indicate that similar street fairs can boost local businesses and stimulate and contribute to a healthy local economy. Similar approaches can be used to evaluate the impact of different interventions (e.g., installation of new transportation modes, alterations on the street network etc.).
Of course, our specific case study exhibits limitations with respect to the available data as we elaborated earlier. In particular, while check-in information is intuitively a good proxy for the underlying revenues, demographic biases can provide us with a skewed view of the exact magnitude of the impact. Nevertheless, similar analysis can provide advocate citizens’ organizations with a case for further scrutiny of any public policy in place. Social media data are “readily” available and accessible (at least most of the times) and can provide the basis for grassroots innovation in the space of policy evaluation. In the future we plan in examining other potential sources (e.g., sales tax data) and analyze information from other cities as well, in order to obtain a cross-city comparison with respect to street fairs and their impact on local economy. Furthermore, even though we have verified the parallel trend assumption, the increase in the check-ins (revenues) in the treated area might be partly attributed to a decrease in the rest of the areas. This interaction between neighborhoods is extremely interesting and can potentially be captured and analyzed through a network between the urban areas. Finally, the long-term effect of these events is also important. In particular, even though the street fair can potentially increase the revenues during its lifetime, does it have the ability to create new clientele for the area? We will further explore these points in our future work.
Notes
- 1.
As per the New Economics Foundation “local purchases are twice as efficient in terms of keeping the local economy alive”.
- 2.
- 3.
We have consulted with urban planners familiar with the city of Pittsburgh.
- 4.
Note here that, this is not an issue when we applied the difference-in-differences at the level of a neighborhood. In that case, we were interested in the total additional check-ins in the neighborhood as compared to the counterfactual. Hence, if a control area had a different number of venues this would not impact the results.
- 5.
- 6.
E.g., http://tinyurl.com/zdved39.
References
Aral, S., Muchnik, L., Sundararajan, A.: Distinguishing influence-based contagion from homophily-driven diffusion in dynamic networks. Proc. Nat. Acad. Sci. 106(51), 21544–21549 (2009)
Arancibia, D.: Cycling economies: economic impact of bike lanes. Report. Toronto Cycling, Think and Do Tank (2012)
Ashenfelter, O., Card, D.: Using the longitudinal structure of earnings to estimate the effect of training programs. Rev. Econ. Stat. 67(4), 648–660 (1985)
Carter, R.D., Zieren, J.W.: Festivals that say cha-ching! measuring the economic impact of festivalst. In: Main Street Now (2012)
CleanAir-Partnership: Bike lanes, on-street parking and business. Report (2009)
DeShazo, J., Callahan, C., Brozen, M., Heimsath, B.: Economic impacts of ciclavia: study finds gains to local businesses. In: Briefing Paper - UCLA Luscin School of Public Fairs (2013)
Gallegos, L., Lerman, K., Huang, A., Garcia, D.: Geography of emotion: where in a city are people happier? In: WWW (2016)
Georgiev, P., Noulas, A., Mascolo, C.: Where businesses thrive: predicting the impact of the olympic games on local retailers through location-based services data. In: AAAI ICWSM (2014)
Goetz, C.J., Scott, R.E.: Liquidated damages, penalties and the just compensation principle: some notes on an enforcement model and a theory of efficient breach. Columbia Law Rev. 77(4), 554–594 (1977)
Harris, A.D., McGregor, J.C., Perencevich, E.N., Furuno, J.P., Zhu, J., Peterson, D.E., Finkelstein, J.: The use and interpretation of quasi-experimental studies in medical informatics. J. Am. Med. Inform. Assoc. 13(1), 16–23 (2006)
Hristova, D., Williams, M., Musolesi, M., Panzarasa, P., Mascolo, C.: Measuring urban social diversity using interconnected geo-social networks. In: ACM WWW (2016)
Imbens, G., Lemieux, T.: Regression discontinuity designs: a guide to practice. Working Paper 13039, National Bureau of Economic Research, April 2007
Karamshuk, D., Noulas, A., Scellato, S., Nicosia, V., Mascolo, C.: Geo-spotting: mining online location-based services for optimal retail store placement. In: ACM SIGKDD (2013)
Lee, C.K., Taylor, T.: Critical reflections on the economic impact assessment of a mega-event: the case of 2002 FIFA world cup. Tourism Manag. 26(4), 595–603 (2005)
Luca, M.: Reviews, reputation, and revenue: The case of yelp. com. Technical report, Harvard Business School (2011)
Mora, R., Reggio, I.: Treatment effect identification using alternative parallel assumptions (2012)
Pelechrinis, K., Kokkodis, M., Lappas, T.: On the value of shared bike systems in urban environments: evidence from the real estate market. Available at SSRN (2015)
de Place, E.: Are parking meters boosting business? http://daily.sightline.org/2012/03/28/is-metered-parking-boosting-business/
Qu, Y., Zhang, J.: Trade area analysis using user generated mobile location data. In: ACM WWW (2013)
Rosenbaum, P.R., Rubin, D.B.: The central role of the propensity score in observational studies for causal effects. Biometrika 70(1), 41–55 (1983)
Shadish, W.R., Cook, T.D., Campbell, D.T.: Experimental and Quasi-Experimental Designs for Generalized Causal Inference. Cengage Learning, Belmont (2001)
Shoup, D.: The High Cost of Free Parking. American Planning Association, Chicago (2011)
Venerandi, A., Quattrone, G., Capra, L., Quercia, D., Saez-Trumper, D.: Measuring urban deprivation from user generated content. In: ACM CSCW. pp. 254–264 (2015)
Zhang, K., Pelechrinis, K., Lappas, T.: Analyzing and modeling special offer campaigns in location-based social networks. In: AAAI ICWSM (2015)
Acknowledgments
We would like to thank Bob Gradeck from the University Center of Urban & Social Sciences, for his suggestions on matching the treated area in our case study.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer International Publishing AG
About this paper
Cite this paper
Zhang, K., Pelechrinis, K. (2016). Do Street Fairs Boost Local Businesses? A Quasi-Experimental Analysis Using Social Network Data. In: Berendt, B., et al. Machine Learning and Knowledge Discovery in Databases. ECML PKDD 2016. Lecture Notes in Computer Science(), vol 9853. Springer, Cham. https://doi.org/10.1007/978-3-319-46131-1_22
Download citation
DOI: https://doi.org/10.1007/978-3-319-46131-1_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-46130-4
Online ISBN: 978-3-319-46131-1
eBook Packages: Computer ScienceComputer Science (R0)