Keywords

1 Introduction

The accurate diagnosis of neurodegenerative diseases is a prerequisite to apply efficient treatment strategies, insofar as available, or recruit homogeneous study cohorts [6]. Many studies have shown that visually assessed criteria and a battery of quantitative features extracted from brain magnetic resonance imaging (MRI) have the potential to discriminate between different types of dementia [2]. Most published studies that address this classification problem assume a complete data set in the sense that all features are available for all samples. In practice this assumption does not hold as certain examinations might have been missed due to high measurement cost or missing patient consent [13]. However, many discriminative classifiers, such as SVMs, require training and testing data where a full set of features is available for every sample.

A common strategy to account for unavailable features is the removal of incomplete samples from the study cohort [13, 14]. However, the exclusion of data does not only reduce statistical power, but is also of ethical concern as acquired subject data remains unused. Other proposed approaches rely on feature imputation, such as replacing a missing feature with the feature’s mean, or model-based feature estimation using Gaussian Mixture Models (GMMs) [7, 11, 12, 14]. In so-called “hot-deck” imputation missing features are replaced by those of similar complete samples [14]. Feature imputation can also be considered as a matrix completion problem [3, 13] or tackled with genetic algorithms and neural networks [1, 11]. Care needs to be taken when features are not missing at random to avoid the introduction of bias [7, 15]. The performance of imputation approaches is ideally assessed by both the feature error and the classification accuracy on the imputed features. The latter is usually the main objective [7, 15].

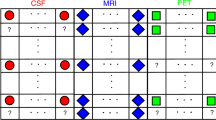
In this paper, we adapt the recently developed Latent Tree (LT) structure learningFootnote 1 [9] to estimate missing features before applying a discriminative classifier. The proposed approach is applicable to the two common scenarios where features are missing in (1) the testing data or (2) both in the training and testing data. The basic idea of the approach is summarised in Fig. 1. LT learns a hierarchical model of latent variables and thus is able to discover a hidden dependence structure within the features. In contrast, GMMs assume that all features depend on a single latent variable. LTs can thus exploits the learned structure to provide more accurate estimates of missing features. In comparison to other LT learning methods [5, 8], the approach of [9] poses less restrictions on the features (distribution, tree structure) while allowing for an efficient optimisation.

The main contributions of this paper are (a) formulation of the LT model to be trainable on incomplete data; (b) feature imputation using LTs and subsequent combination with a discriminative classifier (SVM); (c) evaluation on a novel dementia cohort for the differential diagnosis of five dementia types under missing features; (d) proof of concept that LTs are suitable to detect candidate outlier samples within the data set.

Fig. 1.
figure 1

A data model is trained using the mean (blue), GMMs (orange) or LTs (yellow) to complete missing data (red). The trained models are employed to estimate missing features in the training/testing data. A discriminative classifier (e.g. SVM) is then trained and employed for testing on samples with the complete feature set available.

Full size image

In Sect. 2, we describe a LT model that can handle missing data. In Sect. 3 we compare its performance to a baseline mean imputation and the widely used GMM estimation.

2 Method

This work addresses the classification problem of inferring the disease condition state \(\mathbf {y}\) from M features \(\mathbf {X}=\{\mathbf {x}_{1},...,\mathbf {x}_{M}\}\), while only an observed subset of the features \(\mathbf {O}\subseteq \mathbf {X}\) is available. Each feature \(\mathbf {x}_{m}\) (\(m\in \{1,...,M\}\)) can either be continuous (for attributes like structural volumes) or categorical with the number of states \(K_{m}\) (for attributes like gender). Which features are observed, i.e. the composition of \(\mathbf {O}\), varies between samples and is unknown a-priori for the testing data. Since any feature might be missing in any of the samples, it is not possible to find a subset of features that is observed for all samples. Only in case of complete data (i.e. \(\mathbf {O}=\mathbf {X}\)), we can use any of the established classification methods (in this work we use SVM). Thus we propose to complete the partial data \(\mathbf {O}\rightarrow \mathbf {X}\) first using LT and then classify \(\mathbf {X}\rightarrow \mathbf {y}\) using SVM.

Let the unobserved set of features be \(\mathbf {U}=\mathbf {X}{\setminus }\mathbf {O}\). We proceed by training LT to model the density \(p(\mathbf {X})\), i.e. we treat each \(\mathbf {x}_{m}\) as a random variable. During testing, the observed features \(\mathbf {O}\) are completed by inferring the unseen features \(\mathbf {U}\) using the maximum likelihood solution \(\mathbf {u}_{m}^{\text {pred}}=\arg \max _{\mathbf {u}_{m}}p(\mathbf {u}_{m}|\mathbf {O})\) for each \(\mathbf {u}_{m}\in \mathbf {U}\). Once all features are completed, we can proceed with established classification methods to obtain \(\mathbf {y}\).

2.1 Latent Trees (LT)

LT specifies a graphical model to represent the distribution \(p(\mathbf {X})\), by introducing additional latent random variables \(\mathbf {H}=\{\mathbf {h}_{1},...,\mathbf {h}_{L}\}\). Each node of the graphical model corresponds to a single variable from \(\mathbf {X}\cup \mathbf {H}\) and edges correspond to conditional probability distributions. In order to keep inference tractable, the graph structure is limited to a tree. All \(\mathbf {x}_{m}\) are leaves of the tree and the distribution of each node \(\mathbf {x}_{m}\) or \(\mathbf {h}_{l}\) is conditioned on its parent \(\mathbf {h}_{P(m)}\) or \(\mathbf {h}_{P(l)}\), respectively (\(l\in \{1,...,L\}\)). The tree structure is learned from data and represented by the function P(.), which assigns the parent to each node or the empty set \(\emptyset \) if the node is a root. For discrete observed nodes and hidden nodes \(\mathbf {h}_{l}\), the conditional distribution is categorical:

$$\begin{aligned} \textstyle p(\mathbf {h}_{l}|\mathbf {h}_{P(l)}=k)=\text {Cat}(\mathbf {h}_{l};\varvec{\mu }_{k,l}), \end{aligned}$$
(1)

Here \(k\in \{1,...,K\}\), \(\text {Cat}(\mathbf {h};\varvec{\mu })\) is a categorical distribution over \(\mathbf {h}\in \{1,...,K\}\) with the parameter \(\varvec{\mu }\in \mathbb {R}^{K}\) , \(\varvec{\mu }(k)\ge 0\) and \(\sum _{k}\varvec{\mu }(k)=1\). For observed nodes K is determined by the feature type (cf. Sect. 3.1) and for all hidden nodes K is set to \(K^\text {hid}\). The conditional distribution is Gaussian for continuous observed nodes \(\mathbf {x}_{m}\):

$$\begin{aligned} \textstyle p(\mathbf {x}_{m}|\mathbf {h}_{P(m)}=k)=\mathcal {N}(\mathbf {x}_{m};\mu _{k,m},\sigma _{k,m}^{2}), \end{aligned}$$
(2)

Here \(\mathcal {N}(\mathbf {x};\mu ,\sigma ^{2})\) is a Gaussian distribution over \(\mathbf {x}\in \mathbb {R}\) with mean \(\mu \in \mathbb {R}\) and variance \(\sigma ^{2}\in \mathbb {R}^{+}\). The tree root \(\mathbf {h}_{r}\) has no parent and therefore is not conditioned on another node, which means that the distribution is a prior: \(p(\mathbf {h}_{r}|\mathbf {h}_{P(r)})=p(\mathbf {h}_{r}|\emptyset )=\text {Cat}(\mathbf {h}_{r};\varvec{\mu }_{r})\). Then the joint distribution of the whole tree is

$$\begin{aligned} \textstyle p(\mathbf {X},\mathbf {H})=\prod _{m,l}p(\mathbf {x}_{m}|\mathbf {h}_{P(m)})p(\mathbf {h}_{l}|\mathbf {h}_{P(l)}) \end{aligned}$$
(3)

Given N datapoints \(\mathbf {X}^{(1)},...,\mathbf {X}^{(N)}\), the marginal log-likelihood of the complete data is

$$\begin{aligned} \textstyle \mathcal {L}=\sum _{n}\ln p(\mathbf {X}^{(n)})=\sum _{n}\ln \sum _{\mathbf {H}}p(\mathbf {X}^{(n)},\mathbf {H}) \end{aligned}$$
(4)

LT training optimises \(\mathcal {L}\) on the training data by applying a structural EM procedure, that iteratively optimises the tree structure and the parameters of the conditional probability distributions, for details see [9]. An example tree structure is shown in Fig. 2.

Fig. 2.
figure 2

Example LT and GMM structure for four feature variables \(\mathbf {x}_{1},...,\mathbf {x}_{4}\). Here, LT has learned three latent variables, whereas GMM always includes only a single latent variable. The rightmost edges are labeled with the conditional probability distributions.

Full size image

The application of LT in this work differs from [9] in three ways: (1) we use LT to predict features and not to classify the disease target (for this we use SVM), (2) we adapt LT to handle missing features rather than noisy features that have been replaced by a random value, and (3) we deal with missing features during both the training and testing stages of the model. In contrast, [9] only induces noisy features in the test data.

2.2 Handling of Missing Data

LT (and GMM) handle missing variables \(\mathbf {U}\) by treating them as latent variables (equivalent to \(\mathbf {H}\)) and derive \(p(\mathbf {u}_{m}|\mathbf {O})\) during inference. For predicting the missing variables, the maximum likelihood estimate is obtained as specified in Sect. 2. Since the parameter and structure learning algorithms only depend on the posterior marginal distributions obtained from inference, it is sufficient for the LT algorithm to deal with missing variables at the inference step. Treating missing values \(\mathbf {U}^{(n)}\) as latent variables leads to the modified log-likelihood optimisation target

$$\begin{aligned} \textstyle \mathcal {L}=\sum _{n}\ln \sum _{\mathbf {H},\mathbf {U}^{(n)}}p(\mathbf {O}^{(n)},\mathbf {U}^{(n)},\mathbf {H}) \end{aligned}$$
(5)

In the complete data case (i.e. \(\mathbf {O}^{(n)}=\mathbf {X}^{(n)}\) and \(\mathbf {U}^{(n)}=\emptyset , \forall n\)) Eq. 5 is equivalent to Eq. 4.

3 Experiments

3.1 Data and Setup

We study a total of 491 patientsFootnote 2 from the Amsterdam Dementia Cohort who had visited the Alzheimer center of the VU University Medical Center. Images were acquired on MRI scanners at the field strengths 1, 1.5 or 3 T. All patients underwent a standardised work-up including a lumbar puncture and a battery of neurological and neuropsychological markers. Patients were subsequently diagnosed in a multidisciplinary consensus meeting in 5 categories: subjective cognitive decline (SCD), Alzheimer’s Dementia (AD), Frontotemporal-Lobe Dementia (FTD), Dementia with Lewy Bodies (DLB) and Vascular Dementia (VaD) according to standardised criteria. A detailed description of the data and the employed clinical disease criteria can be found in [10]. A brief overview and the distribution of the data is summarised in Table 1. For our experiments we consider 31 features in total, which are grouped in two sets: The first set (VIS) contains 13 biomarkers assessed during the clinical visit, and the second set (IMG) includes 18 features automatically derived from the MRI scans. In detail, the sets contain:

  • VIS: Age, Gender (Categorical variable: K = 2), Verhage 7-point scale for education (K = 7), years of education (YoE), mini-mental state examination (MMSE), Amyloid-\(\beta _{42}\), ApoE4 genotype (K = 5), Fazekas Score (K = 4), presence of lacunes in basal ganglia (K = 2), presence of infarcts (K = 2), 3 manually assessed atrophy measures (K=5, for left/right medial temporal lobe and global cortex)

  • IMG: 15 unnormalised volume measures (left/right/total HC, l/r Amy, l/r Ent, l/r inf lat Vent, l/r lat Vent, 3rd/4th Vent, l/r WM), 3 vascular burden measures (WM hyper-intensities total/adj., lacunar infarcts volume)

Table 1. Overview over patient data with reference diagnosis and age.
Full size table

The data contains dependencies between features (e.g. between structural volumes), which LT is able to encode to enable an improved imputation.

All experiments were evaluated with five repetitions (to account for random model initialisation) of five configurations (to account for randomly removed features) of a 10-fold cross-validation (CV), leading to 250 evaluations in total. Paired, two-sided Student’s t-tests were calculated on the results of the five configurations averaged over the five repetitions. Significant differences between LT/GMM and mean imputation (\(p<0.05^m/0.001^{M}\)) or between LT and GMM \((^g/^{G})\) are indicated respectively.

For the 5-class classification problem we employ libSVM [4] (linear, cost = 0.1) and calculate the balanced accuracy as bACC = \(\frac{1}{5} \sum _\text {rows} \frac{M_{r,r}}{\sum _\text {columns} M_{r, c}}\) from the confusion matrix \(\mathbf {M}\). Here, features were normalised (zero-mean, unit-variance) based on the respective training data. The model parameter \(K^\text {hid}\in [2;20]\) was chosen for \(\epsilon ^\text {test}\) = 0.5 (cf. Sect. 3.2) and set to the optimum value of \(K^\text {hid}=16\) for GMM and \(K^\text {hid}=5\) for LT. We compare LT with the baseline methods (1) mean imputation (Mean) and (2) GMM.

3.2 Predicting Missing Features

In a first experiment we investigate the performance of LTs to predict missing features. We simulated missing features by randomly removing a fraction \(\epsilon ^\text {test}\) of features of the testing data. The random selection of features to remove is applied per sample, i.e. each sample now includes different features. We measure the prediction error with respect to the true value of the removed features (\(\mathbf {u}^\text {true}_{n,m}\)) by the normalised root mean squared error (NRMSE). The NRMSE is calculated for each feature \(\mathbf {x}_{m}\) over all N samples as NRMSE\(_{m}\) = \( \sqrt{\frac{1}{N}\sum _{n} (\tilde{\mathbf {u}}^\text {true}_{n,m} - \tilde{\mathbf {u}}^\text {pred}_{n,m} )^2 }\), where \(\tilde{\mathbf {u}}_{n,m}=(\mathbf {u}_{n,m}-\mu ^\text {all}_m)/\sigma ^\text {all}_m\) denotes feature m of sample n normalised by the feature statistics \((\mu ^\text {all}_m,\sigma ^\text {all}_m)\) calculated on the whole dataset. The NRMSE is an error measure relative to the standard deviation \(\sigma ^\text {all}_m\) of each feature. E.g. an NRMSE of 0.5 means that the expected prediction error is 50 % of \(\sigma ^\text {all}_m\). For selected features the NRMSE is summarised in Table 2. The prediction error with respect to \(\epsilon ^\text {test}\) is illustrated in Fig. 3. LT significantly improves feature imputation as compared to mean replacement and GMMs. The advantage of LT reduces with increasing \(\epsilon ^\text {test}\) as not sufficient information remains to leverage the learned structure.

Table 2. Prediction error as \(\sigma ^\text {all}_m \times \) NRMSE\(_m\) of selected features using mean, GMM or LT for feature completion with 20/50/70 % missing features in testing data.
Full size table

3.3 Disease Classification

We explored the effect of improved feature imputation on classification accuracy. We simulated missing features as in Sect. 3.2, but now either in the testing set \(\epsilon ^\text {test}\) or in all available data \(\epsilon ^\text {all}\). Classification results and NRMSE for varying \(\epsilon ^\text {test}\) are shown in Fig. 3 for mean, GMM and LT feature imputation. All approaches yield 68 % accuracy on complete data and drop to 20 % when all features are missing, equivalent to a random guess of five classes. For an increasing \(\epsilon ^\text {test}\) the NRMSE approaches 1, which means that the standard deviation of the error becomes equivalent to \(\sigma ^\text {all}_m\) of the respective feature. Classification accuracies for varying \(\epsilon ^\text {test}\) and \(\epsilon ^\text {all}\) are shown in Table 3. With 50 % of the features missing in both training and testing data, LT imputation still allows a high accuracy of 56.6 % (58.6 % if trained on complete data). The SVM model can better account for mean replacement during testing when it is also trained on mean-replaced data. This leads to a 8 % increase at \(\epsilon ^\text {all}\) = 50 % in comparison to clean training data, even outperforming GMM. LT consistently outperforms both reference methods.

Table 3. Balanced accuracy [%] with missing features in testing data (left) or in all data (middle) and the confusion matrix corresponding to \(\epsilon ^\text {all}\) = 0 % (right).
Full size table
Fig. 3.
figure 3

Classification accuracy (bACC, left) and prediction error (NRMSE, right) for an increasing factor of missing features in testing data for compared methods.

Full size image
Fig. 4.
figure 4

Performance for detecting outlier samples after swapping two random features within 50 % of the testing samples (intra-sample swaps).

Full size image

3.4 Application: Detection of Samples with Inconsistent Features

The LT model allows the calculation of \(\mathcal {L}\) (Eq. 5), which measures the likelihood that a given sample belongs to the distribution of the trained model. This is used to detect samples that contain inconsistent features. We suggest to calculate \(\mathcal {L}\) for all samples in the training data to estimate \(\mu ^\mathcal {L}_\text {train}\) and \(\sigma ^\mathcal {L}_\text {train}\). We then calculate the Z-score for each testing sample as a measure for how well a sample fits the training distribution. Specifically we classify each sample n as outlier if \((\mathcal {L}_n - \mu ^\mathcal {L}_\text {train}){/} \sigma ^\mathcal {L}_\text {train} \le Z_\text {Limit}\).

To investigate the applicability of this approach we simulated erroneous samples by swapping two random features within 50 % of the testing samples (intra-sample swaps). This simulates the common human error of inserting values in the wrong data field. Then we employed the proposed method to detect the samples with swapped features. The results are summarised in Fig. 4. Balanced accuracies are high (around 80 %) for a wide range of possible thresholds \(Z_\text {Limit}\) and consistently higher using the LT model as compared to the reference GMM model. A high AUC \(\approx \)87 % (GMM AUC \(\approx \)83 %) confirms the feasibility to detect outlier candidates. Note that there is an upper bound to the possible accuracy as feature swapping might lead to valid samples (e.g. swapping left and right hippocampal volumes), which are consistent with the training distribution.

4 Conclusion

We have shown that LT is a powerful model to incorporate incomplete data for differential dementia diagnosis. The generative nature of LT allows the classification of arbitrary, a-priori unknown targets and substantially boosts the performance of discriminative classifiers under missing data. LT can reveal candidate outlier samples and is superior to the comparison data imputation strategies in all conducted experiments. An open source implementation of LT is available (cf. Sect. 1).