Detecting Ellipses in Elongated Shapes Using the Thickness Profile

Abstract

This paper presents a method that detects elliptical parts of a given elongated shape. For this purpose, first, the shape is represented by its skeleton. In case of branches, the skeleton is partitioned into a set of lines/curves. Second, the ellipse parameters are estimated using the thickness profile along each line/curve, and the properties of its first and second derivatives. The proposed method requires no prior information about the model, number of ellipses and their parameter values. The detected ellipses are then used in our second proposed approach for ellipse-based shape description. It can be applied for analysing motion and deformation of biological objects like roots, worms, and diatoms.

A. Gabdulkhakova—Supported by the Austrian Agency for International Cooperation in Education and Research (OeAD) within the OeAD Sonderstipendien program, financed by the Vienna PhD School of Informatics.

1 Introduction

The advantages of modelling the structure of the shape with ellipses cover various aspects. Human perceptual system interprets the significant parts of the shape or the rigid parts of articulated objects with the ellipses [10]. Also the ellipsoids and super quadrics provide a strong cue about the orientation of anisotropic phenomena [11]. Indeed, the major axis of the ellipse, when interpreted as an orientation, becomes useful for judging the motion direction or for constraining the motion of articulated parts of the object [29]. The eccentricity of the ellipse, $\varepsilon$, characterizes its elongation, and is estimated as $(\sqrt{a^2 - b^2})/a$, where a and b are the lengths of the semi-major and semi-minor axes of the ellipse respectively. It can be applied for analysis of deformations like shrinking and stretching. Tuning the ellipse elongation along its orientation can be used to enhance the traditional skeletonization algorithms for the problem of representing the intersection of two straight lines (or, alternatively, a cross), compare cases (a) and (d) in Fig. 1. Another advantage of using ellipses refers back to the paper of Rosenfeld [23]. He defines the ribbon-like shapes that can be represented given a spine and a generator (disc or line segment). There are also algorithms that use ellipse as the generator [27]. To the best of our knowledge the ellipse was not assumed as a unified generator that can degenerate into a disc ($\varepsilon =0$) and/or into a line segment ($\varepsilon =1$). On one side, this provides a smooth transition between the rectangular parts of the object that have different properties, compare Fig. 1, cases (b) and (e). On the other side, symmetric shapes with a high positive curvature can be represented by a single spine instead of a branched skeleton, compare Fig. 1, cases (c) and (f).

Fig. 1.

Advantages of using ellipses as a generator for improving the skeletonization in case of intersection of two straight lines [(a) and (d)]; a union of two distinct rectangles [(b) and (e)]; a shape with a high positive curvature [(c) and (f)]. Blue indicates a type of generator, and the skeleton is shown in pink. (Color figure online)

The goal of this paper is twofold: (1) detect elliptical parts of the given elongated shape, and (2) describe its structure with ellipses and their degenerations (line segments and discs). Existing approaches for ellipse detection either try to minimize the deviation between a single ellipse and the given shape (based on Least-Squares [8, 19]), or require an information about a number of ellipses and their parameters (based on Hough Transform [4, 22] and Gaussian Mixture Models [14]). In contrast, the proposed method does not have the above constraints. Taking the skeleton of the shape, we, first, decompose it into a set of simple lines/curves w.r.t. branches. Then, for each line/curve we analyse its thickness profile and detect the parameters of ellipses. To obtain invariance to deformation, we find the ellipses on the flattened version of the shape, while preserving the mapping to the original shape [1, 13].

The remaining of the paper is structured as follows. Section 2 discusses the state-of-the art in the area of ellipse detection. Then we explain the proposed methods for ellipse detection and shape description in Sects. 3 and 4 respectively. Specific algorithms and the related research are directly described in the corresponding subsections. In Sect. 5 we provide the experimental results, and give the final remarks in Sect. 6.

2 Related Work

Wong et al. [28] distinguished three major categories of approaches that aim at finding ellipses: (1) based on Least-Squares (LS), (2) based on voting scheme, (3) uncategorized (statistical, heuristic, and hybrid techniques).

LS approaches minimize the deviation between the computed ellipse points and the original set of points [8, 19]. The disadvantage of the standard LS method is that it finds only a single ellipse and is sensitive to noise and outliers. Voting scheme based methods mainly operate with the Hough Transform (HT) [4, 16, 20, 22, 24]. Ellipse has five parameters - orientation, length of the semi-major axis a, length of the semi-minor axis b, coordinates of a center x and y. The complexity of searching a combination of these parameters is high - $O(n^5)$, where n is the number of input points [7]. In order to optimize the computation and reduce the complexity of the parameter space, the ellipse-specific properties are used (symmetry, tangents, locus, edge grouping, etc.). The hybrid method by Cicconet et al. [5] combines LS and HT within a single system. The disadvantage lies in specifying parameters for the HT, such as the maximum number of ellipses, range of semi-major and semi-minor axes lengths. Another group of methods uses the statistical techniques like Gaussian Mixture Models (GMM) [14, 29], or RANdom SAmple Consensus (RANSAC) [18]. The limitation of this idea is that the elliptical model of the shape should be given a priori.

3 Thickness-Based Ellipse Detection (TED)

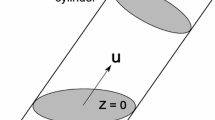
The TED algorithm aims at finding the parameters of ellipse according to the thickness profile along the skeleton of the shape, or, in case of branches, along the lines/curves that form a skeleton. The finest detection is achieved on the symmetric shape that satisfies the following criterion. Consider a symmetric 2D shape, S1, in a Cartesian XY plane. Its major symmetry axis coincides with the abscissa. Rotate S1 about the abscissa (Fig. 2(a)), project the resultant 3D volume (Fig. 2(b)) orthogonally w.r.t. the original XY plane (Fig. 2(c)). The criterion requires the original shape S1 to be identical to the resultant projection S2. In general, the present work aims at the above type of symmetric shapes and/or at their combination. To emphasize the fact that points of the skeleton are equidistant from the opposite borders of the shape, we will also refer to it as a symmetry axis.

Fig. 2.

Description of the target shape: (a) original shape S1 (b) 3D volume, which is obtained by rotating S1 about X-axis (c) projection of the 3D volume onto the XY plane - S2. For the target shape, S1 is identical to S2.

The pipeline of the proposed TED contains three algorithmic steps: Step 1 - skeletonization, Step 2 - computation of the thickness profile along the skeleton, Step 3 - ellipse parameter estimation w.r.t. the thickness profile. When the shape is deformed, the algorithm has an additional step of flattening the shape after skeletonization. In the scopes of this paper we will call this modification as a Straightened TED, or S-TED.

3.1 Skeletonization

Numerous skeletonization techniques exist. The majority of them refers to the concept of Medial Axis Transformation (MAT), introduced by Blum [3]. The underlying principle is to fit the circles of maximum radii inside the shape and sequentially connect their centres. The resultant representation does not contain the ridges of the contour, as opposed to grass-fire skeleton [3] and the Distance Transform (DT) [26]. By the definition, DT is an operator that yields a distance-valued image by assigning to each pixel of the given binary image its distance to the nearest background pixel.

Another group of methods evolves from Voronoi diagrams [21]. The idea is to use the boundary points of the shape in order to produce the Voronoi tesselation. After that the skeleton is obtained as the set of points and of the Voronoi diagram that belongs to the given shape.

The last approach within this overview is homotopic thinning [9] (a recent survey on skeletonization was conducted by Saha et al. [25]). It iteratively peels the surface of the object, while preserving topology. The result is a one-pixel-thick skeleton.

In general, all the above approaches suffer from noise. This impact is reflected by spurious branches that do not correspond to the essential parts of the shape.

3.2 Shape Flattening

One way to flatten the shape is to compute the curvature along the symmetry axis. Starting at the origin, the points of the symmetry axis are sequentially translated towards the alignment direction [12]. Such an approach has a high computational cost, and fails on the spiral shapes.

Our idea is to transform the Cartesian coordinates of each point of the shape in image space to the object-specific space. For this purpose we use Straightened Curved Planar Reformation (CPR) [13]. It takes longitudinal values along one axis and latitudinal values along the other axis.

The longitudinal axis reflects the length of the main axis of the object. One of the two end points is used as the origin. The values range from 0 to N, where N equals the number of points that form the axis. The latitudinal axis reflects the thickness of the object for each point along the longitudinal axis. The advantages of the above method include (1) the stability to deformations (excluding crossing), (2) the invariance to affine transformations, (3) the reconstruction of the straightened representation of the shape without an additional computation. The method can be extended to 3D case.

3.3 Thickness Profile

Given a symmetry axis of the object, SA, a position function, $pos:\mathbb {R_+}~\rightarrow ~\mathbb {R}^2$, associates the point $P=(x,y) \in SA$ to the arc length s between the point P and the origin. In this context, thickness profile, $f:~\mathbb {R}\rightarrow ~\mathbb {R_+}~$, is a 1D function of arc length s along SA that returns the thickness of the object at pos(s):

$$\begin{aligned} {\small {f(s)=\{lthick(pos(s))|s\in [0,\ldots ,length(SA)]\}}} \end{aligned}$$

(1)

By lthick we denote a distance metric which defines the local thickness of the object at the point P. This metric is chosen such that it satisfies the requirements of the particular problem. Indeed, in TED algorithm, the target objects have a straight symmetry axis, and are rotated such that this axis is parallel to abscissa. Let us assume that local thickness equals the width of a cut taken along the normal at the given skeletal point. Then, lthick can be defined as a double value of a chamfer DT [26] with a City-Block metric at this skeletal point. The reason is that (1) in this problem statement, the City-Block metric provides a better thickness estimation than the Euclidean metric since having a 4-neighbourhood, (2) as opposed to computing the number of the shape points corresponding to each cut along the skeleton, chamfer DT is less sensitive to noise and local perturbations, (3) chamfer DT has a linear time complexity.

In S-TED algorithm lthick can be defined by latitudinal values along the flattened shape. Computing the latitudinal values with the normals to the symmetry axis is sensitive to noise. The linear LS algorithm enables to reduce the impact of such local perturbations. Also, the algorithm enables to build a hierarchy of ellipses by smoothing the thickness profile with the Gaussian filter. Starting at a fine level with many ellipses that correspond to every local perturbation (in case of a noisy data), and finishing at a coarse level that represents the whole shape with a single ellipse.

In literature also exist another thickness-estimation algorithms, such as [6], that may improve the performance. Though, comparison of various distance metrics for thickness was not the goal of the present paper.

3.4 Ellipse Parameter Estimation

The idea of detecting the parameters of ellipse is derived from the properties of the thickness change along the elongated shape. The centre of an ellipse-candidate corresponds to the position of the local maximum (C in Fig. 3), and/or to the position of the bending point ($C_1$, $C_2$ in Fig. 3). The local minimum corresponds to some point on the ellipse-candidate ($P_1$, $P_2$ in Fig. 4).

Position of the Ellipse Centre. The algorithm for detecting the centres of ellipses is described in relation to three possible configurations of the target shapes: (1) a single ellipse, (2) a union of multiple ellipses, and (3) a union of multiple ellipses with a smooth transition.

Single ellipse. Thickness profile of a single ellipse monotonically increases to the length of the semi-minor axis, b, and then monotonically decreases. Thus, the position of the ellipse centre is exactly at the local maximum of the thickness profile. Indeed, consider the canonical ellipse representation (see Fig. 4). Its centre is at the origin, $O=(0,0)$, minor and major axes are correspondingly collinear with the ordinate and abscissa. The canonical ellipse equation is:

$$\begin{aligned} \frac{x^2}{a^2}+\frac{y^2}{b^2}=1, \text {where } P=(x,y) \text { is a point on the ellipse.} \end{aligned}$$

(2)

Substituting x with s, and assuming that $y=\pm f(s)$ w.r.t. Eq. 1 gives:

$$\begin{aligned} \begin{aligned}&\frac{s^2}{a^2}+\frac{f^2(s)}{b^2}=1 \Rightarrow f^2(s) = \frac{b^2}{a^2}(a^2-s^2) \Rightarrow 2f(s)f'(s)=\frac{b^2}{a^2}(-2s) \\&f'(s)=0, a\ne 0, b\ne 0 \Rightarrow s=a, x=0 \end{aligned} \end{aligned}$$

(3)

Fig. 3.

Example of multiple ellipses with smooth transitions. The positions of the centres are detected w.r.t. to the local maximum at the point C, and the bending points - $C_1$ and $C_2$.

Since dealing with the discrete space, $f'(s)$ is approximated by the differences between the neighbouring points of the profile. Therefore, local maximum is the point, where $f'(s)$ changes from positive to zero/negative value.

Multiple ellipses. In general, a union of multiple ellipses along the symmetry axis results in multiple local maxima. So, the positions of the centres are found w.r.t. $f'(s)$ as for the single ellipse. Specific case is the union of two identical ellipses with the common major or minor axis - there is only one local maximum, and, thus, one detected ellipse. Another issue is the union of two ellipses of different sizes, that overlap along the minor axis of the smaller ellipse. For the small ellipse, the local maximum cannot be detected, since the sign of the derivative does not change. This case is discussed in the next paragraph. For the complete enclosure case, estimation of the ellipse centre positions w.r.t. the local maxima is possible, if performed for each object separately.

Multiple ellipses with smooth transitions. Consider a shape that consists of ellipses and smooth transitions between them which cover at most a half of each ellipse (see Fig. 3). In this case, the ellipse centre positions $C_1$ and $C_2$ w.r.t. the local maxima cannot be estimated. At these points, the sign of $f'(s)$ stays the same, but its value is changing by $\varDelta$ while connecting two different monotonic functions. As a result, there is a Dirac function like peak at $f''(s)$ with a negative $\varDelta$ amplitude at the corresponding positions. We call $C_1$ and $C_2$ bending points.

The algorithm for detecting bending points has 2 steps. First, we find the set of the peak-candidates by comparing the ratio between the maximum and median values of the $f''(s)$. This is done, in order to eliminate the impact of noise. As opposed to mean, median is not distorted by the maximum values.

In the second step we fit ellipses inside the peak-candidates, and compute their eccentricities using the equation $(\sqrt{a^2 - b^2})/a$. For the Dirac function like peaks this ratio converges to 1.

The Lengths of the Semi-major and Semi-minor Axes. Let us consider that pos(C) = $(x_C,y_C)$ is the center of the ellipse-candidate, $pos(P_1)$ = $(x_{P_1},y_{P_1})$ and $pos(P_2)$ = $(x_{P_2},y_{P_2})$ are the points on it, detected as the closest local minima to C (Fig. 4). Then the length of the minor axis b equals:

$$\begin{aligned} b=f(C) \end{aligned}$$

(4)

The length of the semi-major axis a is then computed w.r.t. the thickness profile (see Fig. 4) and implicit ellipse representation:

$$\begin{aligned} \frac{(P_{i}-C)^2}{a^2}+\frac{(f(P_{i})-0)^2}{b^2}=1 \Rightarrow a=\underset{1 \le i \le 2}{\arg \min }{\frac{|P_{i}-C|}{\sqrt{1-\frac{f^2(P_{i})}{b^2}}}} \end{aligned}$$

(5)

Fig. 4.

Estimation of the ellipse parameters. C is the ellipse centre (found as the local maximum); $P_1$ and $P_2$ are some points on the ellipse (found as local minima). Two ellipse candidates are computed w.r.t. $P_1$, $P_2$ and the implicit ellipse representation.

3.5 Complexity of the Algorithms

TED contains 3 algorithmic steps. Step 1 - skeletonization of the shape using the chamfer DT - O(n), where n is the number of shape points. Next, in Step 2, the thickness profile is computed by taking the maximum DT value along the skeleton. The complexity remains O(n). Step 3 - finding the local extrema and the bending points has a linear complexity. Since the above steps are performed sequentially, the resultant complexity equals O(n).

S-TED contains shape flattening in addition to Step 1. The complexity of this procedure is O(n), where n is the number of shape points. Steps 2–3 are identical to those described in TED. Therefore, the overall complexity of the S-TED is O(n). In contrast, the approach proposed by Cicconet et al. [5] has a higher complexity of $O(m \cdot n^2)$, where n is the number of shape contour points, and m is the number of ellipses.

4 Shape Description

Given a shape as a single ellipse, or a union of multiple ellipses along the symmetry axis, the shape description contains a set of detected ellipses. Given a shape as a union of smoothly connected ellipses, the shape description contains a set of detected ellipses and line segments. The centres of these line segments correspond to the points of the skeleton that connect the neighbouring ellipses. The length of each line segment equals to the corresponding local shape thickness.

Our approach enables to describe the shapes which parts have a high positive curvature. If function f(s) at some point P changes from concave to convex, or vice versa, then P is a point of inflection. In this case the sign of $f''(s)$ should change from positive to zero/negative value or from negative to zero/positive value. In contrast, axial representations with a single generator are not able to handle the shape with round ends and high positive curvature [23].

5 Experiments and Discussion

The performance of TED and S-TED was compared to the state-of-the-art approach of Cicconet et al. [5]. As opposed to standard LS-based methods [5, 8, 19] can detect multiple overlapping ellipses, and does not require an a priori model, in contrast to GMM-based methods [14, 29]. As reported, [5] outperformed the algorithm of Prasad et al. [22], which in turn showed better results than [2, 15, 17, 18, 20].

The test dataset contains 80 synthetic images of one and two ellipses, 500 by 500 pixels. As discussed with the authors [5], the test shapes closely resemble ellipses, and contain boundary points of each ellipse. For the proposed method we use the union of binary masks of these ellipses. With the reference to the target shape definition, there are 8 classes of possible configurations, 10 images each (see Table 2). For a single ellipse: (1) different degree of elongation (a varies from 40 to 200 pixels, b - from 4 to 40 pixels), (2) rotation, (3) distortion with a white Gaussian noise, (4) distortion with a "sinusoidal" noise¹. For two ellipses: (5) a union of ellipses of the same size, (6) a union of ellipses of the different sizes, (7) ellipses with mutually orthogonal major axes, and (8) configurations that approximate an articulated motion. Since targeting the elongated shapes without holes, having more than two ellipses will not reveal additional test cases. The quantitative comparison was performed in Precision/Recall manner, as described in [5] (see Table 1, Ellipse Detection).

Table 1. Interpretation of Precision/Recall methods w.r.t. the experiment type

Table 2. On the left: the results of TED and S-TED as compared to Cicconet et al. [5]. On the right: the examples of ellipse configurations w.r.t. 8 classes, and examples of the input data for the compared algorithms.

Table 3. The results of shape reconstruction as tested on a diatom dataset.

The experimental results² are summarized in Table 2. The proposed detection of the ellipse parameters relies on $f'(s)$ and $f''(s)$. So, both TED and S-TED are sensitive to perturbations, and on a single ellipse their Recall rate worsens under the noise impact. Applying Gaussian function, $G(n)=\frac{1}{\sigma \sqrt{2\pi }}e^{-0.5(n/\sigma )^{2}}$, to the thickness profile enables to decrease the impact of noise, and achieve the highest Precision and Recall rates for TED ($\sigma = 5, n = 15$, and $L = 30$). Here n is the size of the Gaussian window, $\sigma$ - a standard deviation, L is the number of smoothing iterations. The method of Cicconet et al. [5] assumes the number of ellipses to be given a priori. As a result, it demonstrates a high Precision rate on a single ellipse, as well as on two ellipses (always 1). Though, the Recall rates are lower as compared to TED and S-TED, and decrease sufficiently (from the minimum of 0.6 for a single ellipse to the minimum of 0.15 for two ellipses).

The quality of the shape reconstruction from the proposed shape description was tested on a part of a diatom dataset³, that contains 357 real images. Figure 5 shows the main steps of processing a diatom image: segmentation (b), shape description (c), and shape reconstruction (d). Elliptical parts of the diatoms were detected w.r.t. TED algorithm. We performed the evaluation using the Precision/Recall method (as described in Table 1, Shape Description), and achieved the results as shown in Table 3.

Fig. 5.

Example of the shape description and reconstruction of a diatom: (a) original image, (b) binary shape of the diatom, (c) shape description that includes detected ellipses (in yellow) and line segments (in blue), (d) reconstructed shape (Color figure online)

6 Conclusion and Future Work

The paper presents a novel approach that finds the parameters of ellipses by tracking the thickness change along the symmetry axis. The shape does not have to be a combination of fine ellipses. The proposed method enables to build a hierarchy of ellipse-based descriptions by smoothing the thickness profile with the Gaussian filter. The presented shape description approach has a high recoverability rate. In future we plan to use it for motion, growth and deformation analysis of the biological objects like roots, worms, and diatoms. A hierarchy of descriptions will enable to describe the motion at multiple levels of abstraction: from local movements of the parts to global behaviour of the entire object.