Bent Functions in $\mathcal C$ and $\mathcal D$ Outside the Completed Maiorana-McFarland Class

Abstract

Two new classes of bent functions derived from the Maiorana-McFarland ($\mathcal {M}$) class, so-called ${\mathcal {C}}$ and ${\mathcal {D}}$, were introduced by Carlet [2] two decades ago. However, apart from the subclass ${\mathcal {D}}_0$, some explicit construction methods for these functions were not provided in [2]. Assuming the possibility of specifying a bent function f that belongs to one of these two classes (apart from ${\mathcal {D}}_0$), the most important issue is then to determine whether f is still contained in the known primary classes or lies outside their completed versions. In this article we partially solve this question by providing sufficient conditions on the permutation and related characteristic function (used to define f in these classes) so that f is provably outside the completed $\mathcal {M}$ class. To give some existence results, we employ recent results in [12] where some instances of bent functions in ${\mathcal {C}}$ were identified by providing specific permutations and related characteristic functions. More precisely, using our sufficient conditions that apply to both ${\mathcal {C}}$ and ${\mathcal {D}}$, it is shown that these identified classes of ${\mathcal {C}}$ functions described in [12] do not belong to the completed $\mathcal {M}$ class, whereas the question (which is more difficult) whether these functions are also outside the completed partial spread class remains open. We also propose some generic methods for specifying bent functions in ${\mathcal {D}}$ outside the completed Maiorana-McFarland class.

Appendix

Proof of Theorem 2 :

Proof

Let $a^{(1)}, b^{(1)}, a^{(2)}, b^{(2)}\in {{\mathbb F}}_2^{n}$. We prove that f does not belong to $\mathcal {M}^{\#}$, by using Lemma 1. We need to show that there does not exist an $(\frac{n}{2})$-dimensional subspace V such that

$$D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f=0,$$

for any $(a^{(1)}, a^{(2)}),$ $(b^{(1)}, b^{(2)})\in V$.

The second derivative of f with respect to a and b can be written as,

$$\begin{aligned}&D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x) \nonumber \\= & {} x\cdot \left( D_{a^{(2)}}D_{b^{(2)}}\pi (y)\right) \oplus a^{(1)}\cdot D_{b^{(2)}}\pi (y\oplus a^{(2)}) \nonumber \\&\oplus b^{(1)} \cdot D_{a^{(2)}}\pi (y\oplus b^{(2)})\oplus D_{a}D_{b}1_{E_1}(x)1_{E_2}(y) \nonumber \\= & {} x\cdot \left( D_{a^{(2)}}D_{b^{(2)}}\pi (y)\right) \oplus a^{(1)}\cdot D_{b^{(2)}}\pi (y\oplus a^{(2)}) \oplus b^{(1)} \cdot D_{a^{(2)}}\pi (y\oplus b^{(2)}) \\&\oplus 1_{E_1}(x)D_{a^{(2)}}D_{b^{(2)}}1_{E_2}(y) \oplus 1_{E_2}(y\oplus a^{(2)} )D_{a^{(1)}}1_{E_1}(x) \nonumber \\&\oplus 1_{E_2}(y\oplus b^{(2)} )D_{b^{(1)}}1_{E_1}(x)\oplus 1_{E_2}(y\oplus a^{(2)}\oplus b^{(2)} )D_{a^{(1)}\oplus b^{(1)}}1_{E_1}(x).\nonumber \end{aligned}$$

(6)

We denote the set $\{(x,0_{n})\mid x\in {{\mathbb F}}_2^{n}\}$ by $\varDelta$, and consider two cases $V= \varDelta$ and $V \ne \varDelta$.

• 1. For $V=\varDelta$, we can find two vectors $(a^{(1)}, 0_{n}),(b^{(1)}, 0_{n}) \in \varDelta$ such that

  $$ D_{a^{(1)}}D_{b^{(1)}}1_{E_1}(x)\ne 0 $$

  since $\dim (E_1)\ge 2$. Further, we have

  $$\begin{aligned} D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x)= & {} 1_{E_2}(y )(D_{a^{(1)}}1_{E_1}(x) \oplus D_{b^{(1)}}1_{E_1}(x) \\&\oplus D_{a^{(1)}\oplus b^{(1)}}1_{E_1}(x))\\&=1_{E_2}(y)D_{a^{(1)}}D_{b^{(1)}}1_{E_1}(x)\ne 0. \end{aligned}$$

• 2. For $V\ne \varDelta$, we split the proof into three cases depending on the cardinality of $V\cap \varDelta$. We set $V=\left\{ (v_1^{(1)},v_2^{(1)}),(v_1^{(2)},v_2^{(2)}),\ldots , (v_1^{(2^{n})},v_2^{(2^{n})}\right\}$,

  • (a) For $|V\cap \varDelta |= 1$, we have $v_2^{(i)}\ne v_2^{(j)}$ for any $i\ne j$. If there exist two vectors $v_2^{(i_1)}, v_2^{(j_1)}$ such that $v_2^{(i_1)}=v_2^{(j_1)}$ , then $v_1^{(i_1)}= v_1^{(j_1)}$, (or $(v_1^{(i_1)}\oplus v_1^{(j_1)},0_{n} )\in V\cap \varDelta$), that is, $(v_1^{(i_1)},v_2^{(i_1)})= (v_1^{(j_1)},v_2^{(j_1)})$. Further, $|\{v_2^{(1)}, v_2^{(2)}, \ldots , v_2^{(2^{n})} \}|=|V|= 2^{n}$, that is, $\{ v_2^{(1)},$ $v_2^{(2)},\ldots , v_2^{(2^{n})}\}={{\mathbb F}}_2^{n}$ (here, if $v_2^{(i_1)}=v_2^{(i_2)}$, they are called one element). Thus, we can find two vectors $a,b\in V$ such that

    $$ D_{a^{(2)}}D_{b^{(2)}}1_{E_2}(y)\ne 0$$

    since $\dim (E_2)\ge 2$.

    Now, there are four cases to be considered.

    • i. If $a^{(1)}=b^{(1)}=0_n$, from (6), we have

      $$\begin{aligned}&D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x) \nonumber \\= & {} x\cdot \left( D_{a^{(2)}}D_{b^{(2)}}\pi (y)\right) \oplus 1_{E_1}(x)D_{a^{(2)}}D_{b^{(2)}}1_{E_2}(y)\ne 0 \end{aligned}$$

      (7)

      since $\dim (E_1){+}\dim (E_2)=n$ and $\dim (E_2)\ge 2$, that is, $\deg (1_{E_1}(x))\ge 2$.

    • ii. If $a^{(1)}=0_n, b^{(1)}\ne 0_n$, from (6), we have

      

      We know $\dim (E_1){+}\dim (E_2)=n$ and $\dim (E_2)\ge 2$, thus $\deg (1_{E_1}(x))\ge 2$. Further, $\deg (1_{E_1}(x))>\deg (D_{b^{(1)}}1_{E_1}(x))$. Thus, we have

      $$D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x)\ne 0.$$

    • iii. If $a^{(1)}\ne 0_n, b^{(1)}= 0_n$, from (6), we have

      

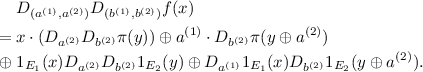      (8)

      We know $\dim (E_1){+}\dim (E_2)=n$ and $\dim (E_2)\ge 2$, thus $\deg (1_{E_1}(x))\ge 2$. Further, $\deg (1_{E_1}(x))>\deg (D_{a^{(1)}}1_{E_1}(x))$. Thus, we have

      $$D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x)\ne 0.$$

    • iv. If $a^{(1)}\ne 0_n, b^{(1)}\ne 0_n$, from (6), we have

      $$D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x)\ne 0.$$

      Since $\dim (E_1){+}\dim (E_2)=n$ and $\dim (E_2)\ge 2$, then $\deg (1_{E_1}(x))\ge 2$. Furthermore, $\deg (1_{E_1}(x))>\deg (D_{b^{(1)}}1_{E_1}(x))$, $\deg (1_{E_1}(x))>$ $\deg (D_{a^{(1)}}1_{E_1}(x))$ and $\deg (1_{E_1}(x))>\deg (D_{a^{(1)}\oplus b^{(1)}}1_{E_1}(x))$.

    Hence, we have

    $$D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x)\ne 0$$

    for $|V\cap \varDelta |= 1$.

  • (b) For $|V\cap \varDelta |= 2$, without loss of generality, let $(a^{(1)},0_{n}) \in V\cap \varDelta$, $a^{(1)} \ne 0_{n}$.

    We know $\{ v_2^{(1)},$ $v_2^{(2)},\ldots , v_2^{(2^{n})}\}$ is a subspace of ${{\mathbb F}}_2^{n}$ which is denoted by $\mathcal {V'}$. We first prove $\dim (\mathcal {V'})=n-1$ by showing that $|\{v_2^{(1)}, v_2^{(2)}, \ldots , v_2^{(2^{n})} \}|= 2^{n-1}$, where we only count distinct vectors (e.g. if $v_2^{(i_1)}=v_2^{(i_2)}$ only one vector is counted). If $|\{v_2^{(1)}, v_2^{(2)}, \ldots , v_2^{(2^{n})} \}|$ $=2^{n}$, then it is clear that V is not a subspace. If $|\{v_2^{(1)}, v_2^{(2)}, \ldots , v_2^{(2^{n})} \}|< 2^{n-1}$, there must exist three vectors $v_2^{(i_1)}=v_2^{(i_2)}=v_2^{(i_3)}$, where $i_1\ne i_2 \ne i_3$. Thus, we will have $(v_1^{(i_1)},v_2^{(i_1)})\oplus (v_1^{(i_2)},v_2^{(i_2)}) \in V\cap \varDelta$, $(v_1^{(i_1)},v_2^{(i_1)})\oplus (v_1^{(i_3)},v_2^{(i_3)}) \in V\cap \varDelta$ and $(v_1^{(i_3)},v_2^{(i_3)})\oplus (v_1^{(i_2)},v_2^{(i_2)}) \in V\cap \varDelta$, which contradicts the fact that $|V\cap \varDelta |= 2$. We now show that $|E_2\cap \mathcal {V'}|\ge 1$ by using a well-known fact that

    $$\dim (E_2\cap \mathcal {V'})= \dim (E_2){+}\dim (\mathcal {V'})-\dim (E_2\boxplus \mathcal {V'}),$$

    where $E_2\boxplus \mathcal {V'}=\{\alpha \oplus \beta |\alpha \in E_2, \beta \in \mathcal {V'} \}$. Since by assumption $\dim (E_2)\ge 2$ and we have shown that $\dim (\mathcal {V'})=n-1$, then $\dim (E_2\cap \mathcal {V'})\ge 1.$ We now choose one vector $b^{(2)}$ from $(\mathcal {V'}\cap E_2)\backslash \{0_{n}\}$, then $b^{(2)}\ne 0_{n}$ and $1_{E_2}(y)=1_{E_2}(y\oplus b^{(2)} )$ (since $b^{(2)}\in E_2$). Set $b=(b^{(1)},b^{(2)})\in V$. From (6), we have

    

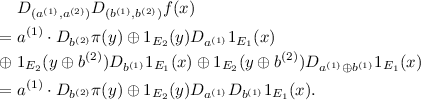    (9)

    Now, there are three cases to be considered. If $D_{a^{(1)}}D_{b^{(1)}}1_{E_1}(x)\ne ~ const.$ or $D_{a^{(1)}}D_{b^{(1)}}1_{E_1}(x)=0$, then it is clear that

    $$D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x)\ne 0$$

    since $\pi$ has no nonzero linear structure and $b^{(2)}\ne 0_{n}$.

    If $D_{a^{(1)}}D_{b^{(1)}}1_{E_1}(x)=1$, then it is clear that

    $$D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x)=a^{(1)}\cdot D_{b^{(2)}}\pi (y)\oplus 1_{E_2}(y)\ne 0$$

    since $\deg (\pi )\le n-\dim (E_2 )$, that is, $\deg (a^{(1)}\cdot D_{b^{(2)}}\pi (y))<n-\dim (E_2)=\deg (1_{E_2}(y))$.

  • (c) For $|V\cap \varDelta |> 2$ (i.e., $|V\cap \varDelta |\ge 4$ ), without loss of generality, let $a=(a^{(1)},0_{n}) (\ne 0_{2n})\in V\cap \varDelta$. Here, there are two cases to be considered.

    • i. If there exists one vector $v=(0_n, v_2)\in V{\setminus }\{0_{2n}\}$, then we set $b=v$. Further, using that $b^{(1)}=0_n$, we have

      $$\begin{aligned} D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x) = a^{(1)}\cdot D_{b^{(2)}}\pi (y) \oplus D_{ b^{(2)}}1_{E_2}(y )D_{a^{(1)}}1_{E_1}(x). \end{aligned}$$

      If $D_{a^{(1)}}1_{E_1}(x)\ne ~ constant$ or $D_{a^{(1)}}1_{E_1}(x)=0$, then again

      $$D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x)\ne 0,$$

      since $\pi$ has no nonzero linear structure.

      We now show that $D_{a^{(1)}}1_{E_1}(x)= 1$ is impossible. We have that $D_{ a^{(1)}}1_{E_1}(x )=0$ if $a^{(1)}\in E_1$, or alternatively if $a^{(1)}\notin E_1$

      $$\deg (D_{ a^{(1)}}1_{E_1}(x ))=n-\dim (E_1 )-1,$$

      since $E_1\cup (a^{(1)}\oplus E_1)$ is a subspace of dimension $\dim (E_1 )+1$. Since $n-\dim (E_1 )-1>0$ and by assumption $\dim (E_1)<n-1$, we have $D_{a^{(1)}}1_{E_1}(x)\ne 1$.

    • ii. Let $v=(v_1,v_2) \in V{\setminus }\{0_{2n}\}$. If we always have $v=(v_1,v_2)$ such that $v_1\ne 0_n$ for every $v_2\ne 0_n$, then we set $b=v\in V{\setminus }\{0_{2n}\}$ such that $v_2\ne 0_n$. Further, we have

      $$\begin{aligned}&D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x) = a^{(1)}\cdot D_{b^{(2)}}\pi (y) \oplus 1_{E_2}(y)D_{a^{(1)}}1_{E_1}(x) \nonumber \\&\oplus 1_{E_2}(y\oplus b^{(2)} )D_{b^{(1)}}1_{E_1}(x)\oplus 1_{E_2}(y\oplus b^{(2)} )D_{a^{(1)}\oplus b^{(1)}}1_{E_1}(x)\nonumber \\&= a^{(1)}\cdot D_{b^{(2)}}\pi (y) \oplus 1_{E_2}(y)D_{a^{(1)}}1_{E_1}(x) \\&\oplus 1_{E_2}(y\oplus b^{(2)} )D_{a^{(1)}}1_{E_1}(x\oplus b^{(1)}).\nonumber \end{aligned}$$

      (10)

      There are two cases to be considered. If $b^{(2)}\in E_2$, then we have

      $$\begin{aligned} D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x)= & {} a^{(1)}\cdot D_{b^{(2)}}\pi (y) \oplus 1_{E_2}(y)(D_{a^{(1)}}1_{E_1}(x) \\&\oplus D_{a^{(1)}}1_{E_1}(x\oplus b^{(1)}))\ne 0, \end{aligned}$$

      since $\deg ( 1_{E_2}(y))>\deg (a^{(1)}\cdot D_{b^{(2)}}\pi (y))$. If $b^{(2)}\notin E_2$, then we have three cases to be considered.

      • A. For $a^{(1)}\in E_1$ we have

        $$D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x) =a^{(1)}\cdot D_{b^{(2)}}\pi (y)\ne 0.$$

      • B. For $a^{(1)}\notin E_1, b^{(1)}\in E_1$ we have

        $$\begin{aligned} D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x)= & {} a^{(1)}\cdot D_{b^{(2)}}\pi (y) \\&\oplus D_{b^{(2)}}1_{E_2}(y) D_{a^{(1)}}1_{E_1}(x)\ne 0, \end{aligned}$$

        since $D_{a^{(1)}}1_{E_1}(x)\ne ~ constant$.

      • C. For $a^{(1)}\notin E_1, b^{(1)}\notin E_1$ we have

        $$\begin{aligned} D_{(a^{(1)}, a^{(2)})}D_{(b^{(1)}, b^{(2)})}f(x)= & {} a^{(1)}\cdot D_{b^{(2)}}\pi (y) \\&\oplus D_{b^{(2)}}1_{E_2}(y)D_{a^{(1)}}1_{E_1}(x) \\&\oplus 1_{E_2}(y\oplus b^{(2)} )D_{a^{(1)}}D_{b^{(1)}}1_{E_1}(x)\ne 0, \end{aligned}$$

        since $D_{a^{(1)}}1_{E_1}(x)\ne ~ constant$ and furthermore $\deg (D_{a^{(1)}}1_{E_1}(x))$ $>\deg (D_{a^{(1)}}D_{b^{(1)}}1_{E_1}(x))$.

Combining items 1 and 2, we deduce that f does not belong to ${M}^{\#}$.   $\square$