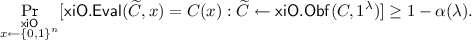On Removing Graded Encodings from Functional Encryption

Abstract

Functional encryption (FE) has emerged as an outstanding concept. By now, we know that beyond the immediate application to computation over encrypted data, variants with succinct ciphertexts are so powerful that they yield the full might of indistinguishability obfuscation (IO). Understanding how, and under which assumptions, such succinct schemes can be constructed has become a grand challenge of current research in cryptography. Whereas the first schemes were based themselves on IO, recent progress has produced constructions based on constant-degree graded encodings. Still, our comprehension of such graded encodings remains limited, as the instantiations given so far have exhibited different vulnerabilities.

Our main result is that, assuming LWE, black-box constructions of sufficiently succinct FE schemes from constant-degree graded encodings can be transformed to rely on a much better-understood object — bilinear groups. In particular, under an über assumption on bilinear groups, such constructions imply IO in the plain model. The result demonstrates that the exact level of ciphertext succinctness of FE schemes is of major importance. In particular, we draw a fine line between known FE constructions from constant-degree graded encodings, which just fall short of the required succinctness, and the holy grail of basing IO on better-understood assumptions.

In the heart of our result, are new techniques for removing ideal graded encoding oracles from FE constructions. Complementing the result, for weaker ideal models, namely the generic group model and the random oracle model, we show a transformation from collusion-resistant FE in either of the two models directly to FE (and IO) in the plain model, without assuming bilinear groups.

N. Bitansky—Supported by NSF Grants CNS-1350619 and CNS-1414119, and the Defense Advanced Research Projects Agency (DARPA) and the U.S. Army Research Office under contracts W911NF-15-C-0226. Part of this research was done while visiting Tel Aviv University and supported by the Leona M. & Harry B. Helmsley Charitable Trust and Check Point Institute for Information Security.

H. Lin—Partially supported by NSF grants CNS-1528178 and CNS-1514526.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Functional Encryption (FE) is a fascinating object. It enables fine-grained control of encrypted data, by allowing users to learn only specific functions of the data. This ability is captured trough the notion of function keys. A function key $\textsf {SK}_{f}$, associated with a function f, allows to partially decrypt a ciphertext ${\textsf {CT}}_{x}$ encrypting an input x in a way that reveals f(x) and nothing else.

A salient aspect of FE schemes is their ciphertext succinctness. Focusing on the setting of (indistinguishability-based) single-key FE where only one function key $\mathsf {SK}_{f}$ is supported, we say that an FE scheme is weakly succinct if the ciphertext size scales sub-linearly in the size of the circuit f; namely,¹

$$ |{\mathsf {CT}}_{x}| \le |f|^{\gamma } \cdot \mathrm {poly}(|x|),\qquad \text {for some constant } \, {compression \, factor} \, \gamma <1. $$

While non-succinct single-key FE schemes (where we allow the size of ciphertexts to grow polynomially with |f|) are equivalent to public-key encryption (or just one-way functions, in the secret-key setting) [28, 41], weakly succinct schemes are already known to be extremely strong. In particular, subexponentially-secure weakly-succinct FE for functions in NC $^{1}$ implies indistinguishability obfuscation (IO) [1, 6, 11], and has far reaching implications in cryptography and beyond (e.g., [7, 10, 18, 23, 24, 42]).²

Thus, understanding how, and under which assumptions, weakly-succinct FE can be constructed has become a central question in cryptographic research. While schemes for Boolean functions in NC $^{1}$ have been constructed from LWE [27], the existence of such FE scheme for non-Boolean functions (which is required for the above strong implications) is still not well-founded, and has been the subject of a substantial body of work. The first construction of general purpose FE that achieves the required succinctness relied itself on IO [24]. Subsequent constructions were based on the algebraic framework of multilinear graded encodings [22]. Roughly speaking, this framework extends the traditional concept of encoding in the exponent in groups. It allows encoding values in a field (or ring), evaluating polynomials of a certain bounded degree d over the encoded values, and testing whether the result is zero.

Based on graded encodings of polynomial degree Garg, Gentry, Halevi, and Zhandry [25] constructed unbounded-collusion FE, which in turn is known to lead to weakly succinct FE [2, 11]. Starting from the work of Lin [31], several works [3, 32, 35] have shown that assuming also pseudorandom generators with constant locality, weakly-succinct FE can be constructed based on constant-degree graded encodings under simple assumptions like asymmetric DDH. However, these constructions require constant degree $d \ge 5$.

Despite extensive efforts, our understanding of graded encodings of any degree larger than two is quite limited. Known instantiations are all based on little-understood lattice problems, and have exhibited different vulnerabilities [15, 20,21,22, 38]. In contrast, bilinear group encodings [14, 29], akin to degree-2 graded encodings, have essentially different instantiations based on elliptic curve groups, which are by now quite well understood and considered standard. Bridging the gap between degree 2 and degree $d>2$ is a great challenge.

Our Main Result in a Nutshell: Size Matters. We show that the exact level of succinctness in FE schemes has a major impact on the latter challenge. Roughly speaking, we prove that black-box constructions [40] of weakly-succinct FE from degree-d graded encodings, with compression factor ${\gamma < \frac{1}{d}}$, can be transformed to rely only on bilinear groups. Specifically, assuming LWE³ and for any constant $\varepsilon$, starting from $\frac{1}{d+\varepsilon }$-succinct FE in the ideal degree-d graded encoding model, we construct weakly-succinct FE in the ideal bilinear model.

The ideal graded encoding model generalizes the classical generic-group model [43]. In this model, the construction as well as the adversary perform all graded encoding operations through an ideal oracle, without access to an explicit representation of encoded elements. Having this ideal model as a starting point allows capturing a large class of constructions and assumptions, as it models perfectly secure graded encodings. Indeed, the FE schemes in [3, 31, 32, 35] can be constructed and proven secure in this model.

The resulting construction from ideal bilinear encodings can further be instantiated in the plain model using existing bilinear groups, and proven secure under an über assumption on bilinear groups [13, 16]. In particular, assuming also subexponential-security, it implies IO in the plain model.

How Close are We to IO from Bilinear Maps? Existing weakly-succinct FE schemes in the ideal constant-degree model [3, 31, 32, 35] have a compression factor $\gamma = C/d$, for some absolute constant $C>1$. Thus, our result draws a fine line that separates known FE constructions based on constant-degree graded encodings and constructions that would already take us to the promised land of IO based on much better-understood mathematical objects. Crossing this line may very well require a new set of techniques. Indeed, one may also interpret our result as a negative one, which puts a barrier on black-box constructions of FE from graded encodings.

Discussion: Black-Box vs Non-Black-Box Constructions. For IO schemes (rather than FE), a combination of recent works [12, 39] demonstrates that black-box constructions from constant-degree graded encodings are already very powerful. They show that any IO construction relative to a constant-degree oracle can be converted to a construction in the plain model (under standard assumptions, like DDH). Since weakly-succinct FE schemes imply IO, we may be lead to think that weakly-succinct black-box constructions of FE from constant-degree graded encodings would already imply IO in the plain model from standard assumptions. Interestingly, this is not the case.

The crucial point is that the known transformations from FE to IO [1, 11] are non-black-box, they use the code of the underlying FE scheme, and thus do not relativize with respect to graded encoding oracle. That is, we do not know how to move from an FE scheme based on graded encodings to an IO scheme that uses graded encodings in a black-box way. Indeed, if there existed such a black-box transformation between FE and IO, then combining [12, 31, 35, 36, 39], IO in the plain model could be constructed from standard assumptions.

Instead, we show how to directly remove constant-degree oracles from FE. Our transformation relies on new techniques that are rather different than those used in the above works for removing such oracles from IO.

1.1 Our Results in More Detail

We now describe our results in further detail. We start by describing the ideal graded encoding model and the ideal bilinear encoding model more precisely.

The Ideal Graded Encoding Model. A graded encoding [22] is an encoding scheme for elements of some field.⁴ The encoding supports a restricted set of homomorphic operations that allow one to evaluate certain polynomials over the encoded field elements and test whether these polynomials evaluate to zero or not. Every field element is encoded with respect to a label (sometimes called the level of the encoding). For a given sequence of encodings, their labels control which polynomials are valid and can be evaluated over the encodings. The degree of the graded encoding is the maximal degree of a polynomial that is valid with respect to any sequence of labels.

In the ideal graded encoding model, explicit encodings are replaced by access to an oracle that records the encoded field elements and provides an interface to perform operations over the elements. Different formalizations of such ideal graded encoding oracles exist in the literature (e.g. [4, 5, 17, 39]) and differ in details. In this work, we follow the model of Pass and shelat in [39].

The ideal graded encoding oracle $\mathcal {M}$ is specified by a field $\mathbb {F}$ and a validity predicate V operating on a polynomial and labels taken from a set ${\mathbb {L}}$. The oracle $\mathcal {M}= (\mathbb {F}, V)$ provides two functions — encoding and zero-testing.

 

Encoding: :

Given a field element $\xi \in \mathbb {F}$ and a label $\ell \in {\mathbb {L}}$ the oracle $\mathcal {M}$ samples a sufficiently long random string $r$ to create a handle $h= (r,\ell )$. It records the pair $(h, \xi )$ associating the handle with the encoded field element.

Zero-testing: :

a query to $\mathcal {M}$ consists of a polynomial p and a sequence of handles $h_1, \cdots , h_m$ where $h_i$ encodes the field elements $\xi _{i}$ relative to label $\ell _i$. $\mathcal {M}$ tests if the polynomial and the labels satisfy the validity predicate and whether the polynomial vanishes on the corresponding field elements. That is, $\mathcal {M}$ returns true if and only if $V(p,\ell _1, \cdots \ell _m) = \mathtt{{true}}$ and $p(\xi _1, \cdots \xi _m) = 0$.

 

Like in [39], we restrict attention to well-formed validity predicates. For such predicates, a polynomial p is valid with respect to labels $\ell _1, \cdots , \ell _m$, if and only if every monomial $\varPhi$ in p is valid with respect to the labels of the handles that $\varPhi$ acts on. Indeed, existing graded encodings all consider validity predicates that are well-formed.⁵

The Ideal Bilinear Encoding Model. The ideal bilinear encoding model corresponds to the ideal graded encoding model where valid polynomials are of degree at most two. We note that in the ideal graded encoding model described above, encoding is a randomized operation. In particular, encoding the same element and label $(\xi ,\ell )$ twice gives back two different handles. In contrast, traditional instantiations of the ideal bilinear encoding model are based on bilinear pairing groups (such as elliptic curve groups) where the encoding is a deterministic function. We can naturally capture such instantiations, by augmenting the ideal bilinear encoding model to use a unique handle for every pair of field element and label (as done for instance in [4, 35, 44]).

The Main Result. Our main result concerns FE schemes in the ideal graded encoding model. In such FE schemes, all algorithms (setup, key derivation, encryption, and decryption), as well as all adversaries against the scheme, have access to a graded encoding oracle $\mathcal {M}$. We show:

Theorem 1

(Informal). Assume the hardness of LWE. For any constants $d\in \mathbb {N}$ and $\gamma \le \frac{1}{d}$, any $\gamma$-succinct secret-key FE scheme for $\mathbf P /\mathbf{poly }$, in the ideal degree-d graded encoding model, can be transformed into a weakly-succinct public-key FE scheme for $\mathbf P /\mathbf{poly }$ in the ideal bilinear encoding model.

IO in the Plain Model under an Über Assumption. Our main transformation results in a weakly-succinct public-key FE scheme in the ideal bilinear encoding model. By instantiating the ideal bilinear encoding oracle with concrete bilinear pairing groups, we get a corresponding FE scheme in the plain model. For security to hold, we make an über assumption [13] on the bilinear groups. An über assumption essentially says that two encoded sequences of elements in the plain model can be distinguished only if they are also distinguishable in the ideal model. There are no known attacks on the über security of existing instantiations of bilinear pairing groups.

Since weakly-succinct public-key FE with subexponential security in the plain model implies IO we deduce the following corollary

Corollary 1

(Informal). Assume subexponential hardness of LWE and bilinear groups with subexponential über security. For any constants $d\in \mathbb {N},\gamma < \frac{1}{d}$, any subexponentially-secure, $\gamma$-succinct, secret-key FE for $\mathbf P /\mathbf{poly }$ in the ideal degree-d graded encoding model, can be transformed into an IO scheme for $\mathbf P /\mathbf{poly }$ in the plain model.

FE in Weaker Ideal Models. We also consider FE schemes in ideal models that are weaker than the ideal bilinear encoding model. Specifically, we consider the generic-group model (that corresponds to the ideal degree-1 graded encoding model) and the random-oracle model. We give transformations from FE in these models directly to FE in the plain model without relying on bilinear encodings.

In the transformation given by Theorem 1, from the ideal constant-degree graded encoding model to the ideal bilinear encoding model, we considered the notion of single-key weakly succinct FE. In contrast, our transformations from the generic-group model and the random-oracle model to the plain model require that we start with a stronger notion of collusion-resistant FE. Collusion-resistance requires security in the presence of an unbounded number of functional keys. Crucially, ciphertexts are required not to grow with the number of keys (but are allowed to grow polynomially in the size of the evaluated functions).

Collusion-resistant FE is known to imply weakly-succinct FE through a black-box transformation [2, 11]. In the converse direction, only a non-black-box transformation is known [26, 30], and therefore we cannot apply it to ideal model constructions of FE.

Theorem 2

(Informal). Assume the hardness of LWE. Any collusion-resistant secret-key FE scheme in the generic-group model, or in the random-oracle model, can be transformed into a collusion-resistant public-key FE scheme in the plain model.

1.2 Our Techniques

We next give an overview of the main ideas behind our degree-reduction transformation given by Theorem 1.

Can We Adopt Techniques from IO? As already mentioned, we do not know how to transform FE schemes into IO schemes in a black-box way. Thus, we cannot rely directly on existing results that remove ideal oracles from IO [39]. Furthermore, trying to import ideas from these results in the IO setting to the setting of FE encounters some inherent difficulties, which we now explain.

Roughly speaking, removing ideal oracles from IO is done as follows. Starting with a scheme in an ideal oracle model, we let the obfuscator emulate the oracle by itself and publish, together with the obfuscated circuit, some partial view of the self-emulated oracle. This partial view is on one hand, sufficient to preserve the functionality of the obfuscated circuit on most inputs, and on the other hand, does not compromise security. The partial view is obtained by evaluating the obfuscation on many random inputs (consistently with the self-emulated oracle), observing how evaluation interacts with the oracle, and performing a certain learning process. Arguing that the published partial view does not compromise security crucially relies on the fact that evaluating the obfuscated program is a public procedure that does not share any secret state with the obfuscator.

The setting of FE, however, is somewhat more complicated. Here rather than an evaluator we have a decryptor that given a function key $\mathsf {SK}_{f}$ and ciphertext ${\mathsf {CT}}$ encrypting x, should be able to compute f(x). In contrast to the evaluator in obfuscation, the state of the decryptor is not publicly samplable. Indeed, generating function keys $\mathsf {SK}_{f}$ for different functions requires knowing a master secret key. Accordingly, it is not clear how to follow the same approach as before.

XIO instead of IO. Nevertheless, we observe that there is a way to reduce the problem to a setting much more similar to IO. Specifically, there exists [9] a black-box transformation from FE to a weaker version of IO called XIO. XIO [33], which stands for exponentially-efficient IO, allows the obfuscation and evaluation algorithms to run in exponential time $2^{O(n)}$ in the input size n, and only requires that the size of an obfuscation $\widetilde{{C}}$ of a circuit C is slightly subexponenetial in n:

$$ |\widetilde{{C}}| \le 2^{\gamma n} \cdot \mathrm {poly}(|C|) \qquad \text {for some constant}\, compression \, factor~\gamma <1. $$

Despite this inherent inefficiency, [33] show that XIO for logarithmic-size inputs implies IO assuming subexponential hardness of LWE. A natural direction is thus to try and apply the techniques used to remove oracles from IO to remove the same oracles also from XIO; indeed, if this can be done, such oracles can also be removed from FE, due to the black-box transformation between the two.

This, again, does not work as is. The issue is that the transformations removing degree-d graded encoding oracle from IO may blow up the size of the original obfuscation from $|\widetilde{{C}}|$ in the oracle model to roughly $|\widetilde{{C}}|^{2d}$ in the plain model. However, the known black-box construction of XIO from FE [9] is not sufficiently compressing to account for this blowup. Even starting from FE with great compression, say $\gamma _{\tiny \text{ FE }} < d^{-10}$, the resulting XIO has a much worst compression factor $\gamma _{\tiny \text{ XIO }} > 1/2$. In particular, composing the two would result in a useless plain model obfuscation of exponential size $2^{n \cdot d}$.

Motivating our Solution. To understand our solution, let us first describe an over-simplified candidate transformation for reducing XIO with constant-degree graded encoding oracles to XIO with degree-1 oracles (akin to the generic-group model). This transformation will suffer from the same size blowup of the transformations mentioned above.

For simplicity of exposition, we first restrict attention to XIO schemes with the following simple structure:

• Any obfuscated circuit $\widetilde{{C}}$ consists of a set of handles $h_1,\dots ,h_m$ corresponding to field elements $\xi _1,\dots ,\xi _m$ encoded during obfuscation, under certain labels $\ell _1,\dots ,\ell _m$.

• Evaluation on any given input x consists of performing valid zero-tests over the above handles, which are given by degree-d polynomials $p_1,\dots ,p_k$.

A simple idea to reduce the degree-d oracle to a linear oracle is to change the obfuscation algorithm so that it computes ahead of time the field elements $\xi _{\varPhi }$ corresponding to all valid degree-d monomials $\varPhi (\xi _1,\dots ,\xi _m) = \prod _{i\in [d]}\xi _{j_i}$. Then, rather than using the degree-d oracle, it uses the linear oracle to encode the field elements $\xi _\varPhi$, and publishes the corresponding handles $\left\{ h_{\varPhi }\right\} _{\varPhi }$. Evaluation is done in a straight forward manner by writing any zero-test polynomial p of degree d as a linear function in the corresponding monomials

$$\begin{aligned} p(\xi _1, \cdots , \xi _m) = \sum _{\varPhi } \alpha _\varPhi \varPhi (\xi _1,\dots ,\xi _m), \end{aligned}$$

and making the corresponding zero-test query $L_p(\left\{ h_\varPhi \right\} ) := \sum _{\varPhi } \alpha _\varPhi h_\varPhi$ to the linear oracle.

Indeed, the transformation blows up the size of the obfuscated circuit from roughly m, the number of encodings in the original obfuscation, to $m^d$, the number of all possible monomials. While such a polynomial blowup is acceptable in the context of IO, for XIO with compression $d^{-1}\le \gamma < 1$, it is devastating.

Key Idea: XIO in Decomposable Form. To overcome the above difficulty, we observe that the known black-box construction of XIO from FE [9] has certain structural properties that we can exploit. At a very high level, it can be decomposed into smaller pieces, so that instead of computing all monomials over all the encodings created during obfuscation, we only need to consider a much smaller subset of monomials. In this subset, each monomial only depends on a few small pieces, and thus only on few encodings.

To be more concrete, we next give a high-level account of this construction. To convey the idea in a simple setting of parameters, let us assume that we have at our disposal an FE scheme that support an unbounded number of keys, rather than a single key scheme, with the guarantee that the size of ciphertexts does not grow with the number of keys. In this case, the XIO scheme in [9] works as follows:

• To obfuscate a circuit C with n input bits, the scheme publishes a collection of function keys $\left\{ \mathsf {SK}_{D_\tau }\right\} _\tau$ for circuits $D_\tau$, indexed by prefixes $\tau \in \{0,1\}^{n/2}$ (will be specified shortly), and a collection of ciphertexts $\left\{ {\mathsf {CT}}_{\rho \Vert C}\right\} _\rho$, each encrypting the circuit C and a suffix $\rho \in \{0,1\}^{n/2}$.

• Decrypting a ciphertext ${\mathsf {CT}}_{\rho \Vert C}$ with key $\mathsf {SK}_{D_\tau }$ reveals $D_\tau (\rho \Vert C) := C(\tau ,\rho )$.

The obfuscated circuit indeed has slightly subexponential size. It contains:

• $2^{n/2}$ function keys $\mathsf {SK}_{D_\tau }$, each of size $\mathrm {poly}(|C|)$,

• $2^{n/2}$ ciphertexts ${\mathsf {CT}}_{\rho \Vert C}$, each of size $\mathrm {poly}(|C|)$.

Going back to the ideal graded-encoding model, the FE key generation and encryption algorithms use the ideal oracle to encode elements. Therefore, generating the obfuscation involves generating a set of k encodings $\varvec{h}_{\tau } = \left\{ h_{\tau ,i}\right\} _{i\in [k]}$ for each secret key $\mathsf {SK}_{D_\tau }$ and a set of k encodings $\varvec{h}_{\rho } = \left\{ h_{\rho ,i}\right\} _{i\in [k]}$ for each ciphertext ${\mathsf {CT}}_{\rho \Vert C}$, for some $k=\mathrm {poly}(|C|)$. The crucial point is that now, evaluating the obfuscation on a given input $(\tau ,\rho )$ only involves the two small sets of encodings $\varvec{h}_{\tau },\varvec{h}_{\rho }$. In particular, any zero-test made by the decryption algorithm is a polynomial defined only over the underlying field elements $\varvec{\xi }_{\tau } = \left\{ \xi _{\tau ,i}\right\} _{i\in [k]}$ and $\varvec{\xi }_{\rho } = \left\{ \xi _{\rho ,i}\right\} _{i\in [k]}$.

This gives rise to the following degree reduction strategy. In the obfuscation, rather then precomputing all monomials in all encodings as before, we precompute only the monomials corresponding to the different pieces $\left\{ \varPhi (\varvec{\xi }_{\rho })\right\} _{\rho ,\varPhi }, \left\{ \varPhi (\varvec{\xi }_{\tau })\right\} _{\tau ,\varPhi }$. Now, rather than representing zero-tests made by the decryption algorithm as linear polynomials in these monomials, they can be represented as quadratic polynomials

$$\begin{aligned} p(\varvec{\xi }_{\tau },\varvec{\xi }_{\rho }) = Q_p\left( \left\{ \varPhi (\varvec{\xi }_{\tau })\right\} _{\varPhi }, \left\{ \varPhi (\varvec{\xi }_{\rho })\right\} _{\varPhi }\right) . \end{aligned}$$

To support such quadratic zero tests, we resort to bilinear groups. We use the bilinear encoding oracle to encode the values $\left\{ \varPhi (\varvec{\xi }_{\rho })\right\} _{\rho ,\varPhi }, \left\{ \varPhi (\varvec{\xi }_{\tau })\right\} _{\tau ,\varPhi }$, and publish the corresponding handles $\left\{ h_{\tau ,\varPhi }\right\} _{\tau ,\varPhi },\left\{ h_{\rho ,\varPhi }\right\} _{\rho ,\varPhi }$. Evaluation is done in a straight forward manner by testing the quadratic polynomial $Q_p$.

The key gain of this construction is that now the blowup is tolerable. Now, each set of k encodings, blows up to $k^d$, which is acceptable since $k=\mathrm {poly}(|C|)$ is small (and not proportional to the size of the entire obfuscation as before, which is exponential in n). In the body, we formulate a general product form property for XIO schemes, which can be used as the starting point of the above-described transformation; we further show that single-key FE schemes with $\frac{1}{d+\varepsilon }$-succinctness implies such XIO schemes.

A Closer Look. The above exposition is oversimplified. To actually fulfill our strategy, we need to overcome two main challenges.

Challenge 1: Explicit Handles. The core idea described above assumes that the obfuscation is simply given as an explicit list of handles, which may not be the case starting from an arbitrary FE scheme. In particular, the obfuscator may use the oracle $\mathcal {M}$ to produce a set of encodings, but not output them explicitly; indeed, it can output an arbitrary string. In this case, we can no longer apply the degree reduction technique, since we do not know which encodings are actually contained in the obfuscation. Naïvely publishing all monomials in all field elements ever encoded by the obfuscator may be insecure — some of these encodings, which are never explicitly included in the obfuscation, may leak information.

To handle XIO schemes constructed from general FE schemes, we need a way to make any “implicit” handles explicit, without compromising security. Our idea is to learn the significant handles that would later suffice for evaluation on most inputs, and publish them explicitly. This idea is inspired by [19, 36, 39] and their observation (already mentioned above) that in obfuscation, the evaluator’s view, including all the handles it sees, is publicly and efficiently samplable.

Roughly speaking, the learning process involves evaluating the obfuscated circuit on many random inputs and making explicit all handles involved in these evaluations. When doing this naïvely, the number of such test evaluations required to guarantee reasonable correctness is proportional to the number of elements encoded by the obfuscator. This would result in a quadratic overhead in the size of the obfuscation, which would again completely foil XIO compression. Avoiding the blowup requires a somewhat more sophisticated learning process that once again exploits the local structure of the construction in [9].

The scheme resulting from the above learning process is only approximately correct — the obfuscation with explicit handles errs on say $10\%$ of the inputs. We show that even such approximate XIO is sufficient for obtaining FE and IO in the plain model (this step is described later in this overview).

Challenge 2: Invalid Monomials. Another main challenge is that it may be insecure to publish encodings of all the monomials $\left\{ \varPhi (\varvec{\xi }_{\rho })\right\} _{\rho ,\varPhi }$, $\left\{ \varPhi (\varvec{\xi }_{\tau })\right\} _{\tau ,\varPhi }$. The problem is that some products $\varPhi (\varvec{\xi }_{\rho })\cdot \varPhi '(\varvec{\xi }_{\tau })$ may result in monomials that would have been invalid in the degree-d ideal model. For example, $\varPhi (\varvec{\xi }_{\rho })$ could correspond to a degree-$(d-2)$ monomial $\varPhi$. In the degree-d ideal model, it would only be possible to multiply such a monomial by degree-2 monomials $\varPhi '(\varvec{\xi }_{\tau })$, and zero test. In the the described new scheme, however, it can multiply monomials $\varPhi '(\varvec{\xi }_{\tau })$ of degree 3, or even d, which might compromise security.

Our solution proceeds in two steps. First, we show how to properly preserve validity by going to a more structured model of bilinear encodings that generalizes asymmetric bilinear groups. In this model, every encoding contains one of many labels and only pairs of encodings with valid labels can be multiplied. We then encode the monomials $\left\{ \varPhi (\varvec{\xi }_{\rho })\right\} _{\rho ,\varPhi }$, $\left\{ \varPhi (\varvec{\xi }_{\tau })\right\} _{\tau ,\varPhi }$ with appropriate labels that preserve the information regarding the original set of labels. This guarantees that the set of monomials that can be zero-tested in this model corresponds exactly to the set of valid monomials in the constant-degree graded encoding model we started from.

Second, we show how to transform any construction in this (more structured) ideal model into one in the standard ideal bilinear encoding model (corresponding to symmetric bilinear maps). At a very high-level, we develop a “secret-key transformation” from asymmetric bilinear groups to symmetric bilinear groups. The transformation allows anyone in the possession of a secret key to translate encodings in the asymmetric setting to new encodings in the symmetric setting in a manner that enforces the asymmetric structure.

From Approximately-Correct XIO back to FE. After applying all the above steps, we obtain an approximately-correct XIO scheme in the ideal bilinear encoding model. The only remaining step is going from such an XIO scheme back to FE. The work of [34] showed how to construct FE from XIO with perfect correctness, assuming in addition LWE. We modify their transformation to construct FE starting directly from approximately-correct XIO. This is done using appropriate Error Correcting Codes to accommodate for the correctness errors from XIO.⁶ The transformation uses XIO as a black-box, and can thus be performed in the ideal bilinear model.

Putting It All Together. Putting all pieces together, we finally obtain our transformation from $\frac{1}{d+\varepsilon }$-succinct FE in the constant-degree graded encoding model to weakly-succinct FE in the bilinear encoding model. To recap the structure of the transformation:

• 1. Start with a $\frac{1}{d+\varepsilon }$-succinct (single-key) FE in the ideal constant-degree graded encoding model.

• 2. Transform it into an XIO scheme in the ideal constant-degree graded encoding model satisfying an appropriate decomposition property (which we call product form).

• 3. Transform it into an approximate XIO scheme in the ideal bilinear encoding model.

• 4. Use the resulting approximate XIO scheme and LWE to get a weakly-succinct FE (still, in the ideal bilinear encoding model).

Instantiating the oracle in bilinear groups with über security gives a corresponding construction in the plain model.

Organization. In Sect. 2, we define (oracle-aided) XIO, and introduce the constant-degree oracles considered in this work. In Sect. 3, we show how to transform XIO, in a certain product form, relative to constant-degree oracles to approximate XIO relative to symmetric bilinear oracles. In Sect. 4, we explain how to move from approximate XIO and LWE, to IO. Due to the space limit, some of the details and proofs are omitted. These can be found in the full version of this paper [8], where we additionally describe how to remove generic-group oracles and random oracles from unbounded collusion FE schemes.

2 Preliminaries

2.1 XIO

We next formally define the notion of exponentially-efficient indistinguishability obfuscation (XIO) for any collection of circuit classes $\varvec{\mathcal {C}}\subseteq \mathbf P ^{\log }/\mathbf{poly }$, where $\mathbf P ^{\log }/\mathbf{poly }$ is the collection of all classes of polynomial-size circuits with logarithmic size input. The definition extends the one in [33] by considering also approximate correctness.

Definition 1

( $\mathbf P ^{\log }/\mathbf{poly }$ ). The collection $\mathbf P ^{\log }/\mathbf{poly }$ includes all classes $\mathcal {C}= \left\{ \mathcal {C}_\lambda \right\}$ for which there exists a constant $c=c(\mathcal {C})$, such that the input of any circuit $C\in \mathcal {C}_\lambda$ is bounded by $c\log \lambda$ and the size of C is bounded by $\lambda ^c$.

Definition 2

(XIO [33]). A pair of algorithms $\mathsf {xiO}=(\mathsf {xiO.Obf},\mathsf {xiO.Eval})$ is an exponentially-efficient indistinguishability obfuscator (XIO) for a collection of circuit classes $\varvec{\mathcal {C}}=\left\{ \mathcal {C}=\left\{ \mathcal {C}_\lambda \right\} \right\} \subseteq \mathbf P ^{\log }/\mathbf{poly }$ if it satisfies:

• Functionality: for any $\mathcal {C}\in \varvec{\mathcal {C}}$, security parameter $\lambda \in \mathbb {N}$, and $C \in \mathcal {C}_\lambda$ with input size $n$,

  

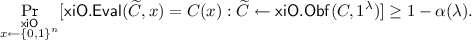
  We say that $\mathsf {xiO.Obf}$ is correct if $\alpha (\lambda )\le \mathrm {negl}(\lambda )$ and approximately-correct if $\alpha (\lambda )\le 1/100$.

• Non-trivial Efficiency: there exists a constant $\gamma <1$ and a fixed polynomial $\mathrm {poly}(\cdot )$, depending on the collection $\varvec{\mathcal {C}}$ (but not on any specific class $\mathcal {C}\in \varvec{\mathcal {C}}$), such that for any class $\mathcal {C}\in \varvec{\mathcal {C}}$ security parameter $\lambda \in \mathbb {N}$, circuit $C \in \mathcal {C}_\lambda$ with input length $n$, and input $x\in \{0,1\}^n$ the running time of both $\mathsf {xiO.Obf}(C,1^\lambda )$ and $\mathsf {xiO.Eval}(\widetilde{{C}},x)$ is at most $\mathrm {poly}(2^n,\lambda ,|C|)$ and the size of the obfuscated circuit $\widetilde{{C}}$ is at most $2^{n\gamma }\cdot \mathrm {poly}(|C|,\lambda )$. We call $\gamma$ the compression factor, and say that the scheme is $\gamma$-compressing.

• Indistinguishability: for any $\mathcal {C}=\left\{ \mathcal {C}_\lambda \right\} \in \varvec{\mathcal {C}}$ and polynomial-size distinguisher $\mathcal {D}$, there exists a negligible function $\mu (\cdot )$ such that the following holds: for all security parameters $\lambda \in \mathbb {N}$, for any pair of circuits $C_0, C_1 \in \mathcal {C}_\lambda$ of the same size and such that $C_0(x) = C_1(x)$ for all inputs x,

  $$\begin{aligned} \left| \Pr \big [\mathcal {D}(\mathsf {xiO.Obf}(C_0,1^\lambda ))= 1\big ] - \Pr \big [\mathcal {D}(\mathsf {xiO.Obf}(C_1,1^\lambda ))= 1\big ] \right| \le \mu (\lambda ). \end{aligned}$$

  We further say that $\mathsf {xiO.Obf}$ is $\delta$-secure, for some concrete negligible function $\delta (\cdot )$, if for all polynomial-size distinguishers the above indistinguishability gap $\mu (\lambda )$ is smaller than $\delta (\lambda )^{\varOmega (1)}$.

Remark 1

(Logarithmic Input). Indeed, for XIO to be useful, we must restrict attention to circuit collections $\varvec{\mathcal {C}}\subseteq \mathbf P ^{\log }/\mathbf{poly }$. This ensures that obfuscation and evaluation are computable in time $2^{O(n)}=\mathrm {poly}(\lambda )$.

Remark 2

(Probabilistic $\mathsf {xiO.Eval}$ ). Above, we allow the evaluation algorithm $\mathsf {xiO.Eval}$ to be probabilistic. Throughout most of the paper, we restrict attention to deterministic evaluation algorithms. This typically will simplify exposition and is without loss of generality.

XIO with an Oracle. We say that an XIO scheme $\mathsf {xiO}=(\mathsf {xiO.Obf},\mathsf {xiO.Eval})$ is constructed relative to an oracle $\mathcal {O}$ if the corresponding algorithms, as well as the adversary, may access the oracle $\mathcal {O}$. Namely, the obfuscation algorithm $\mathsf {xiO.Obf}^{\mathcal {O}}(C,1^\lambda )$ and the evaluation algorithm $\mathsf {xiO.Eval}^{\mathcal {O}}(\widetilde{{C}},x)$ are given oracle access to $\mathcal {O}$. In the security definition, the adversarial distinguisher $\mathcal {D}^{\mathcal {O}}$ also gets access to the oracle.

2.2 The Ideal Graded Encoding Model

The ideal graded-encoding model we consider is inspired by previous generic group and ideal graded-encoding models [5, 17, 37, 43] and is closest to the model of Pass and Shelat [39]. As in [39], we consider well-formed predicates that are determined by the validity of monomials.

Definition 3

(Well-Formed Validity Predicate). $V$ is well-formed if for any $d\in \mathbb {N}$ and degree-d polynomial $V(p,\ell _1,\dots ,\ell _m) = \bigwedge _{i\le d, j_1,\dots ,j_i \in [m],\ \rho _{j_1,\dots ,j_i}\ne 0} V(\left\{ \ell _{j_1},\dots ,\ell _{j_i}\right\} )$; namely, p is valid relative to the labels $\ell _1,\dots ,\ell _m$ if every monomial of p is valid relative to the corresponding multi-set of labels $\left\{ \ell _{j_1},\dots ,\ell _{j_i}\right\}$.

We additionally consider the following decomposability requirement.

Definition 4

(Decomposable Validity Predicate). $V$ is decomposable if it is well-formed and there exist a projection function $\varPi$ and a two-input predicate $V_\varPi$ satisfying: For every two multisets $A = \left\{ \ell _{1,1},\dots ,\ell _{1,k_1}\right\}$ and $B = \left\{ \ell _{2,1},\dots ,\ell _{2,k_2}\right\}$ of labels, the validity of their union is given by⁷

$$V(A \uplus B) = V_\varPi (\varPi (A), \varPi (B)).$$

The arity of a decomposable predicate $V$ is

$$\begin{aligned} \mathsf {Arity}(V) := \max _A \left| \left\{ \varPi (B)\ : \ V_\varPi (\varPi (A), \varPi (B)) = 1 \ \right\} \right| ; \end{aligned}$$

namely, it is the maximum number of projections $\varPi (B)$ that satisfy the validity predicate together with any given projection $\varPi (A)$, where A and B are multisets of labels.

Intuitively, a decomposable validity predicate has the property that any two different pairs of multi-sets $(A, B) \ne (A', B')$ share the same validity decision if they have the same projection $(\varPi (A), \varPi (B)) = (\varPi (A'), \varPi (B'))$. In other words, any information about the multi-sets beyond their projection does not matter. In the literature, all known ideal graded encoding models consider decomposable validity predicates with arity bounded by the degree (or even less). For instance, in set-based graded encodings, the labels correspond to subsets of some fixed universe $\mathbb {U}$, and a set of labels is valid if the sets are disjoint and $\biguplus S_i = \mathbb {U}$. Therefore, we can define the projection of any $A=\left\{ S_1,\dots ,S_i\right\}$ to be $\varPi (A)=\biguplus S_i$ (or $\bot$ if the sets are not disjoint), in which case the arity is exactly one (indeed, for any $\varPi (A)$ only $\mathbb {U}\setminus \varPi (A)$ may satisfy the induced validity predicate).

We now formally define the ideal graded encoding model.

Definition 5

(Ideal Graded Encoding Oracle). The oracle $\mathcal {M}_{\mathbb {F},V}$ is a stateful oracle, parameterized by a field $\mathbb {F}$ and a validity predicate $V$. The oracle answers queries of two forms:

• 1. Encoding Queries: Given a field element $\xi \in \mathbb {F}$ and label $\ell$, the oracle samples a uniformly random string $r\leftarrow \{0,1\}^{\log |\mathbb {F}|}$, returns the handle $h=(r,\ell )$, and stores $(h,\xi )$.

• 2. Zero-Test Queries: Given a polynomial $p\in \mathbb {F}[v_1,\dots ,v_m]$, and handles $h_1,\dots ,h_m$, the oracle does the following:

  • For each $i\in [m]$, obtains a tuple $(h_i,\xi _i)$ from the stored list. If no such tuple exists, stops and returns $\mathtt{{false}}$.

  • From each $h_i=(r_i,\ell _i)$, obtains $\ell _i$, and checks that $V(p,\ell _1,\dots ,\ell _m)=\mathtt{{true}}$ to verify the query is valid and if not, returns $\mathtt{{false}}$.

  • Performs a zero test, returning true if $p(\xi _1,\dots ,\xi _m)=0$ and falseotherwise.

An ideal graded encoding oracle $\mathcal {M}= \left\{ \mathcal {M}_{\mathbb {F}_\lambda ,V_\lambda }\right\}$ is a collection of oracles $\mathcal {M}_{\mathbb {F}_\lambda ,V_\lambda }$, one for each $\lambda \in \mathbb {N}$, where $|\mathbb {F}|=2^{\varTheta (\lambda )}$.

The oracle $\mathcal {M}$ is said to be degree-d, if for every polynomial p of degree $\deg (p)>d$, and any label vector $\varvec{\ell }$, $V(p,\varvec{\ell }) =\mathtt{{false}}$. We say that an oracle $\mathcal {M}$ is decomposable if it has a decomposable validity predicate with bounded polynomial arity $\mathrm {poly}(\lambda )$.

Remark 3

In some previous models (e.g., [39]), the ability to make encoding queries is further restricted. The above definition does not enforce any such restrictions. The results in this paper are presented in a public encoding model, which allows anyone to encode at any time. Our results on removing generic group oracle and random oracle from FE schemes can be extended to the model of private encodings, and the same holds for our results on reducing the degree of graded encoding oracles (Sect. 3), under certain mild assumptions. See the full version [8] for more details.

3 Reducing Constant-Degree Oracles to Bilinear Oracles

We show that any XIO scheme with a constant-degree decomposable ideal oracle can be transformed into an approximately-correct one with an ideal symmetric bilinear oracle (analogous to symmetric bilinear groups), provided that the XIO scheme is in a certain product form. We start by defining formally the notion of XIO in product form and of a symmetric bilinear oracle.

Definition 6

(Product Collection). $\mathcal {X}=\left\{ \mathcal {X}_n\right\} _{n\in \mathbb {N}},\mathcal {Y}=\left\{ \mathcal {Y}_n\right\} _{n\in \mathbb {N}}$ are said to be a product collection if:

• 1. Equal-Size Partition: For any $X,X' \in \mathcal {X}_n$ and $Y,Y' \in \mathcal {Y}_n$:

  $$ |X|=|X'|, X\cap X' = \emptyset \qquad |Y|=|Y'|, Y\cap Y' = \emptyset , $$

• 2. Product Form: let $\varvec{X}_n= \biguplus _{X\in \mathcal {X}_n} X, \varvec{Y}_n= \biguplus _{Y\in \mathcal {Y}_n} Y$ then the input space $\{0,1\}^n$ factors:

  $$ \{0,1\}^n\cong \varvec{X}_n\times \varvec{Y}_n. $$

Definition 7

(XIO in Product Form). We say that an XIO scheme $\mathsf {xiO}= (\mathsf {xiO.Obf}^{\mathcal {O}},\mathsf {xiO.Eval}^{\mathcal {O}})$, relative to oracle $\mathcal {O}$, for a collection of circuit classes $\varvec{\mathcal {C}}$, is in $(\mathcal {X},\mathcal {Y})$-product form for a product collection $(\mathcal {X},\mathcal {Y})$ if:

• The obfuscation algorithm $\mathsf {xiO.Obf}^{\mathcal {O}}$ factors into two algorithms $(\mathsf {xiO.Obf}_\mathcal {X}^{\mathcal {O}}, \mathsf {xiO.Obf}_\mathcal {Y}^{\mathcal {O}})$, such that for any circuit $C\in \varvec{\mathcal {C}}$, $\mathsf {xiO.Obf}^{\mathcal {O}}(C,1^\lambda ;r)$, outputs

  $$\begin{aligned} \left( \left\{ \widetilde{{C}}_X \leftarrow \mathsf {xiO.Obf}_\mathcal {X}^{\mathcal {O}}(C,X,1^\lambda ;r)\right\} _{X\in \mathcal {X}_n},\left\{ \widetilde{{C}}_Y \leftarrow \mathsf {xiO.Obf}_\mathcal {Y}^{\mathcal {O}}(C,Y,1^\lambda ;r)\right\} _{Y\in \mathcal {Y}_n}\right) , \end{aligned}$$

  and all executions may use joint randomness r.

• There is an evaluation algorithm $\mathsf {xiO.Eval}_{\mathcal {X},\mathcal {Y}}^{\mathcal {O}}$ such that for any $(X,Y)\in \mathcal {X}_n\times \mathcal {Y}_n$,

  $$ \mathsf {xiO.Eval}_{\mathcal {X},\mathcal {Y}}^{\mathcal {O}}(\widetilde{{C}}_{X},\widetilde{{C}}_{Y}) = \left( \mathsf {xiO.Eval}^{\mathcal {O}}(\widetilde{{C}},(x,y))\right) _{(x,y)\in X\times Y}. $$

Corresponding notation:

• We denote by $q_{o}^\mathcal {X}=q_{o}^\mathcal {X}(C,\lambda )$ the maximal total size $\sum _{Q\in \mathbf {Q}_o^X}{|Q|}$ of all oracle queries $\mathbf {Q}_o^X=\left\{ Q\right\}$ made by $\mathsf {xiO.Obf}_\mathcal {X}^{\mathcal {O}}(C,X,1^\lambda )$ when obfuscating an $n$-bit input circuit $C\in \varvec{\mathcal {C}}$ for any $X\in \mathcal {X}_n$. Symmetrically, we denote by $q_{o}^\mathcal {Y}=q_{o}^\mathcal {Y}(C,\lambda )$ the bound on the total size $\sum _{Q\in \mathbf {Q}_o^Y}{|Q|}$ of oracle queries $\mathbf {Q}_o^Y=\left\{ Q\right\}$ made by $\mathsf {xiO.Obf}_\mathcal {Y}^{\mathcal {O}}(C,Y,1^\lambda )$ for any $Y\in \mathcal {Y}_n$.

Definition 8

(Symmetric Bilinear Oracle). The symmetric Bilinear Oracle $\mathcal {B}^2 = \left\{ \mathcal {B}^2_{\mathbb {F}_\lambda ,V}\right\}$ is a special case of the ideal graded encoding oracle, where the validity predicate $V$ is of degree two and is defined over a single label $\ell _\mathcal {B}$. That is, $V(L)=\mathtt{{true}}$ for a multiset of labels L, if and only if $L\subseteq \left\{ \ell _\mathcal {B},\ell _\mathcal {B}\right\}$.

We now state the main theorem of this section.

Theorem 3

Let $\mathsf {xiO}= (\mathsf {xiO.Obf}^{\mathcal {M}},\mathsf {xiO.Eval}^{\mathcal {M}})$ be an $\mathsf {xiO.Obf}$ scheme, relative to a degree-d decomposable ideal graded encoding oracle $\mathcal {M}$, for a collection of circuit classes $\varvec{\mathcal {C}}$ that is in $(\mathcal {X},\mathcal {Y})$-product form, for some product collection $(\mathcal {X},\mathcal {Y})$. Further assume that for some constant $\gamma < 1$,

$$\begin{aligned}&|\mathcal {X}_n|\cdot \left( q_{o}^\mathcal {X}\cdot \min \left( q_{o}^\mathcal {X},|\mathcal {Y}_n|\cdot \log q_{o}^\mathcal {X}\right) \right) ^d+ |\mathcal {Y}_n|\cdot \left( q_{o}^\mathcal {Y}\cdot \min \left( q_{o}^\mathcal {Y},|\mathcal {X}_n|\cdot \log q_{o}^\mathcal {Y}\right) \right) ^d\\&\le 2^{\gamma n}\cdot \mathrm {poly}(|C|,\lambda ). \end{aligned}$$

Then $\mathsf {xiO}$ can be converted into an approximately-correct scheme $\mathsf {xiO}^\star$ relative to the symmetric bilinear oracle $\mathcal {B}^2$.

Remark 4

A slightly easier to parse version of the above condition, with some loss in parameters, is that $|\mathcal {X}_n|\cdot \left( q_{o}^\mathcal {X}\right) ^{2d}+ |\mathcal {Y}_n|\cdot \left( q_{o}^\mathcal {Y}\right) ^{2d} \le 2^{\gamma n}\cdot \mathrm {poly}(|C|,\lambda ).$

Remark 5

Our ideal symmetric bilinear oracle captures symmetric bilinear pairing groups, but with two small gaps: Our oracle generates randomized encodings (following the Pass-shelat model) whereas bilinear pairing groups have unique encodings (of the form $g^a$), and our oracle does not support homomorphic opeartions whereas bilinear paring groups do. These differences are not consequential. In the full version of this paper [8], we show how to instantiate the transformed XIO schemes produced by the above theorem using concrete bilinear pairing groups.

Without Loss of Generality. Throughout this section, we make the following assumptions without loss of generality.

• Obfuscator only encodes: The XIO obfuscation algorithm only performs encoding queries and does not perform any zero tests. This is without loss of generality, as the obfuscator knows the field elements and labels underlying any generated handle (it encoded them itself), so zero-tests can be internally simulated.

• Evaluator and adversary only zero-test: The XIO evaluation algorithm as well as the adversary only perform zero tests and do not encode any elements themselves. Indeed, encoding of any $(\xi ,\ell )$ can be internally simulated by sampling a corresponding handle $\widetilde{h}$. Then, whenever a zero-test $(p, h_1,\dots , h_m, \widetilde{h}_1,\dots ,\widetilde{h}_{\widetilde{m}})$ includes such self-simulated handles $\widetilde{h}_i$, it is translated to a new zero test that does not include such handles, by hardwiring the required field elements into the polynomial p.

3.1 Step 1: Explicit Handles

In this section, we show how to transform any XIO in product form relative to an ideal degree-d oracle (not necessarily decomposable) into one where all handles required for evaluation are given explicitly (also in product form). We start by defining the notion of explicit handles in product form and then state and describe the transformation.

Definition 9

(Explicit Handles in Product Form). An XIO scheme $\mathsf {xiO}= (\mathsf {xiO.Obf}^{\mathcal {M}},\mathsf {xiO.Eval}^{\mathcal {M}})$, relative to an ideal graded encoding oracle, for a collection of circuit classes $\varvec{\mathcal {C}}$, is said to have explicit handles in $(\mathcal {X},\mathcal {Y})$-product form, for a product collection $(\mathcal {X},\mathcal {Y})$, if the obfuscation and evaluation algorithms satisfy the following structural requirement:

• The algorithm $\mathsf {xiO.Obf}^{\mathcal {M}}(C,1^\lambda )$ outputs $\widetilde{{C}} = \left( \widetilde{{Z}},\{\widetilde{{H}}_X\}_{X\in \mathcal {X}_n}, \{\widetilde{{H}}_Y\}_{Y\in \mathcal {Y}_n}\right)$, where each $\widetilde{{H}}_X$ and $\widetilde{{H}}_\mathcal {Y}$ are sets of handles generated by the oracle $\mathcal {M}$ during obfuscation, and $\widetilde{{Z}}$ is arbitrary auxiliary information.

• All true zero-test queries $(p,h_1,\dots ,h_m)$ — that is, zero-test queries that evaluate to $\mathtt{{true}}$ — made by the evaluation algorithm $\mathsf {xiO.Eval}^{\mathcal {M}}\left( \widetilde{{C}},(x,y)\right)$ are such that for all $j\in [m]$, $h_j\in \widetilde{{H}}_{X} \cup \widetilde{{H}}_{Y}$, where $(X,Y)\in \mathcal {X}_n\times \mathcal {Y}_n$ are the (unique) sets such that $(x,y)\in X\times Y$.

Corresponding notation:

• We denote by $q_{h}^\mathcal {X}=q_{h}^\mathcal {X}(C,\lambda )$ the bound $\max _{X\in \mathcal {X}_n}|\widetilde{{H}}_X|$ on the maximum size of the set of explicit handles corresponding to any $X\in \mathcal {X}_n$. We denote by $q_{h}^\mathcal {Y}=q_{h}^\mathcal {Y}(C,\lambda )$ the bound on $\max _{Y\in \mathcal {Y}_n}|\widetilde{{H}}_Y|$.

We show that any $\mathsf {xiO.Obf}$ scheme relative to an ideal graded encoding oracle that is in product form can be turned into one that has explicit handles in product form, but is approximately correct.

Lemma 1

Let $\mathsf {xiO}= (\mathsf {xiO.Obf}^{\mathcal {M}},\mathsf {xiO.Eval}^{\mathcal {M}})$ be an $\mathsf {xiO.Obf}$ scheme, relative to an ideal graded encoding oracle $\mathcal {M}$, for a collection of circuit classes $\varvec{\mathcal {C}}$, that is in $(\mathcal {X},\mathcal {Y})$-product form, for some product collection $(\mathcal {X},\mathcal {Y})$. Then $\mathsf {xiO}$ can be converted into a new approximately-correct scheme $\mathsf {xiO}^\star$ with explicit handles in $(\mathcal {X},\mathcal {Y})$-product form (relative to the same oracle $\mathcal {M}$).

Furthermore, the size of the explicit handle sets are bounded as follows

$$\begin{aligned} q_{h}^{\mathcal {X}} \le O\left( q_{o}^\mathcal {X}\right) \cdot \min \left( q_{o}^\mathcal {X},|\mathcal {Y}_n|\cdot \log q_{o}^\mathcal {X}\right) ,\ q_{h}^{\mathcal {Y}} \le O\left( q_{o}^\mathcal {Y}\right) \cdot \min \left( q_{o}^\mathcal {Y},|\mathcal {X}_n|\cdot \log q_{o}^\mathcal {Y}\right) . \end{aligned}$$

Our New XiO Scheme with Explicit Handles. We now describe the new obfuscator $\mathsf {xiO}$. We assume w.l.o.g that $q_{o}^\mathcal {X}\ge q_{o}^\mathcal {Y}$ (otherwise, the obfuscator reverses the roles of $\mathcal {X},\mathcal {Y}$).

The Obfuscator $\mathsf {xiO^\star .Obf}$ : Given a circuit $C\in \varvec{\mathcal {C}}$ with input size $n$, and security parameter $1^\lambda$, $\mathsf {xiO^\star .Obf}^{\mathcal {M}}(C,1^\lambda )$ does the following:

• Obfuscate: Emulate the obfuscator $\mathsf {xiO.Obf}^{\mathcal {M}}(C,1^\lambda )$ to obtain

  $$\left( \{\widetilde{{C}}_X \leftarrow \mathsf {xiO.Obf}_\mathcal {X}^{\mathcal {M}}(C,X,1^\lambda )\}_{X\in \mathcal {X}_n}, \{\widetilde{{C}}_Y\leftarrow \mathsf {xiO.Obf}_\mathcal {Y}^{\mathcal {M}}(C,Y, 1^\lambda )\}_{Y\in \mathcal {Y}_n}\right) .$$

  For each $X\in \mathcal {X}_n$ store a list $L_X$ of all tuples $(h,\xi )$ such that $\mathsf {xiO.Obf}_\mathcal {X}^{\mathcal {M}}(C,X, 1^\lambda )$ requested the oracle $\mathcal {M}$ to encode $(\xi ,\ell )$ and obtained back a handle $h=(r,\ell )$. Store a similar list $L_Y$ for each execution $\mathsf {xiO.Obf}_\mathcal {Y}^{\mathcal {M}}(C,Y,1^\lambda )$.

• Learn Heavy Handles for $\mathcal {X}_n$ : for each $X\in \mathcal {X}_n$, let $\widetilde{{H}}_X=\emptyset$.

  For $i \in \left\{ 1, \dots , K_\mathcal {X}= \min \left( 400q_{o}^\mathcal {X},|\mathcal {Y}_n|\cdot \log \left( 400q_{o}^\mathcal {X}\right) \right) \right\}$ do:

  • Sample a random $Y_i\leftarrow \mathcal {Y}_n$.

  • Emulate $\mathsf {xiO.Eval}^{(\cdot )}_{\mathcal {X},\mathcal {Y}}(\widetilde{{C}}_{X},\widetilde{{C}}_{Y_{i}})$. To answer zero-test queries, emulate $\mathcal {M}$ using the lists $(L_{X},L_{Y_{i}})$ constructed during the obfuscation phase.

  • In the process, for every zero-test query $(p,h_1,\dots ,h_m)$, if $\mathcal {M}(p,h_1,\dots , h_m)=\mathtt{{true}}$, namely it is a valid zero test and the answer is indeed zero, add $h_1,\dots ,h_m$ to $\widetilde{{H}}_X$.

  Store the resulting $\widetilde{{H}}_X$.

• Learn Remaining Handles for $\mathcal {Y}_n$ : for each $Y\in \mathcal {Y}_n$, let $\widetilde{{H}}_Y=\emptyset$.

  For $i \in \left\{ 1, \dots , K_\mathcal {Y}= \min \left( 200q_{o}^\mathcal {Y},|\mathcal {X}_n|\cdot \log \left( 200q_{o}^\mathcal {Y}\right) \right) \right\}$ do the following:

  • Sample a random $X_i\leftarrow \mathcal {X}_n$, and let $\widetilde{{H}}_{X_{i},Y} = \emptyset$.

  • Emulate $\mathsf {xiO.Eval}^{(\cdot )}_{\mathcal {X},\mathcal {Y}}(\widetilde{{C}}_{X_{i}},\widetilde{{C}}_{Y})$. To answer zero-test queries, emulate $\mathcal {M}$ using the lists $(L_{X_{i}},L_{Y})$ constructed during the obfuscation phase.

  • In the process, for every zero-test query $(p,h_1,\dots ,h_m)$, if $\mathcal {M}(p,h_1,\dots , h_m)=\mathtt{{true}}$, namely it is a valid zero test and the answer is indeed zero, add $h_1,\dots ,h_m$ to $\widetilde{{H}}_{X_{i},Y}$.

  • Remove from $\widetilde{{H}}_{X_{i},Y}$ all handles in $\widetilde{{H}}_{X_{i}}$.

  • If $|\widetilde{{H}}_{X_{i},Y}| \le q_{o}^\mathcal {Y}(C,\lambda )$, add $\widetilde{{H}}_{X_{i},Y}$ to $\widetilde{{H}}_Y$. Otherwise discard $\widetilde{{H}}_{X_{i},Y}$.

  Store the resulting $\widetilde{{H}}_Y$.

• Output:

  $$\widetilde{{C}}^\star = (\widetilde{{Z}},\{\widetilde{{H}}_X\}_{X\in \mathcal {X}_n}, \{\widetilde{{H}}_Y\}_{ Y\in \mathcal {Y}_n}), \text { where }\widetilde{{Z}} = (\{\widetilde{{C}}_X\}_{X\in \mathcal {X}_n},\{\widetilde{{C}}_Y\}_{Y\in \mathcal {Y}_n}).$$

The Evaluator $\mathsf {xiO^\star .Eval}$ : Given an obfuscation $\widetilde{{C}}^\star = (\widetilde{{C}},\{\widetilde{{H}}_X\}_{X\in \mathcal {X}_n}, \{\widetilde{{H}}_Y\}_{ Y\in \mathcal {Y}_n})$, $(x,y)\in \varvec{X}_n\times \varvec{Y}_n$, $\mathsf {xiO^\star .Eval}^{\mathcal {M}}(\widetilde{{C}}^\star ,(x,y))$ does the following:

• Let $(X,Y)\in \mathcal {X}_n\times \mathcal {Y}_n$ be the (unique) sets such that $(x,y)\in X\times Y$.

• Emulate $\mathsf {xiO.Eval}^{(\cdot )}_{\mathcal {X},\mathcal {Y}}(\widetilde{{C}}_{X},\widetilde{{C}}_{Y})$.

• Whenever $\mathsf {xiO.Eval}$ makes a zero-test query $(p,h_1,\dots ,h_m)$:

  • If for some i, $h_i\notin \widetilde{{H}}_{X} \cup \widetilde{{H}}_{Y}$, answer $\mathtt{{false}}$.

  • Forward any other zero-test to the oracle $\mathcal {M}$ and return its answer.

In the full version [8], we show that the new obfuscator is approximately correct, secure, and efficient as stated in Lemma 1.

3.2 Step 2: From Constant-Degree to Degree Two

We show that any XIO scheme with explicit handles in product form, relative to a degree-d decomposable ideal oracle (for arbitrary $d=O(1)$), can be transformed into one relative to a degree-2 decomposable ideal oracle. The resulting degree-2 oracle is defined with respect to a validity predicate $V^2$ related to the validity predicate $V^d$ of the degree-d oracle we start with.

Intuitively, this model can be seen as an extension of the standard asymmetric bilinear maps, where instead of two base groups we may have more. That is, instead of two asymmetric base-groups $G_1,G_2$ where $(g_1^a,g_2^b)\in G_1\times G_2$ can be mapped to $e(g_1,g_2)^{ab}$ in the target group $G_T$, we possibly have a larger number of groups $G_1,\dots ,G_n$ and a collection of valid mappings $\{e_k:G_{i_{k}}\times G_{j_{k}}\rightarrow G_T\}$, which may be a strict subset of all possible bilinear maps.

Lemma 2

Let $\mathsf {xiO}=(\mathsf {xiO.Obf}^{(\cdot )},\mathsf {xiO.Eval}^{(\cdot )})$ be an XIO scheme, for a collection of circuit classes $\varvec{\mathcal {C}}$, defined relative to a degree-d decomposable ideal oracle $\mathcal {M}^d=\{\mathcal {M}^d_{\mathbb {F}_\lambda ,V_\lambda }\}$, with explicit handles in $(\mathcal {X},\mathcal {Y})$-product form, for some product collection $(\mathcal {X},\mathcal {Y})$. Assume further that for some constant $\gamma <1$,

$$ |\mathcal {X}_n|\cdot \left( q_{h}^{\mathcal {X}}\right) ^d+ |\mathcal {Y}_n|\cdot \left( q_{h}^{\mathcal {Y}}\right) ^d\le 2^{\gamma n}\cdot \mathrm {poly}(|C|,\lambda ). $$

Then $\mathsf {xiO}$ can be converted to a new scheme $\mathsf {xiO}^\star$, also with explicit handles in $(\mathcal {X},\mathcal {Y})$-product form, relative to a degree-2 decomposable oracle $\mathcal {M}^2$.

We now present our new XiO scheme relative to a degree-2 decomposable oracle; see the full version for its analysis.

The New XiO Scheme Relative to a Degree-2 Oracle $\mathcal {M}^2$ . In what follows, let $\mathsf {xiO}=(\mathsf {xiO.Obf}^{(\cdot )},\mathsf {xiO.Eval}^{(\cdot )})$ be an XIO scheme with explicit handles in product form, defined relative to a degree-d decomposable ideal oracle $\mathcal {M}^d=\{\mathcal {M}^d_{\mathbb {F}_\lambda ,V_\lambda }\}$. We describe a new scheme $\mathsf {xiO}^\star =(\mathsf {xiO^\star .Obf}^{(\cdot )},\mathsf {xiO^\star .Eval}^{(\cdot )})$ (also, with explicit handles in product form) defined relative to a degree-2 decomposable ideal oracle $\mathcal {M}^2=\{\mathcal {M}^2_{\mathbb {F}_\lambda ,V^{\star }_\lambda }\}$.

The Obfuscator $\mathsf {xiO^\star .Obf}$ : Given a circuit $C\in \varvec{\mathcal {C}}$ with input size $n$, and security parameter $1^\lambda$, and oracle access to $\mathcal {M}^2$, $\mathsf {xiO^\star .Obf}^{\mathcal {M}^2}(C,1^\lambda )$ does as follows:

• Emulate Obfuscation:

  • Emulate $\mathsf {xiO.Obf}^{\mathcal {M}^d}(C,1^\lambda )$.

  • Throughout the emulation, emulate the oracle $\mathcal {M}^d$, storing a list $L=\left\{ (h,\xi )\right\}$ of encoded element-label pairs $(\xi ,\ell )$ and corresponding handles $h=(r,\ell )$.

  • Obtain the obfuscation $(\widetilde{{Z}},\{\widetilde{{H}}_X \}_{X\in \mathcal {X}_n}, \{\widetilde{{H}}_X\}_{ Y\in \mathcal {Y}_n})$.

• Encode Monomials:

  • For each $X\in \mathcal {X}_n$:

    • 1. Retrieve $\widetilde{{H}}_X = (h_1,\dots ,h_m)$ and the corresponding field elements and labels $(\xi _1,\ell _1),\dots ,(\xi _m,\ell _m)$ from the stored list L.

    • 2. For every formal monomial $\varPhi (v_1,\dots ,v_m) = v_{i_1}\dots v_{i_j}$, where $j\le d$ and $i_1,\dots ,i_j \in [m]$, compute

      $$ \varPhi (\varvec{\xi }) := \xi _{i_1}\cdots \xi _{i_j},\ \varPhi (\varvec{\ell }) := \left\{ \ell _{i_1},\dots ,\ell _{i_j}\right\} ,\ \varPhi (\varvec{h}) := \left\{ h_{i_1},\dots ,h_{i_j}\right\} . $$

      (For simplicity of notation, we overload $\varPhi$ to describe different functions when acting on field elements, labels, and handles.) Then, request $\mathcal {M}^2$ to encode the field element and label $(\xi ^{\star }_{X,\varPhi },\ell ^\star _{X,\varPhi }):=(\varPhi (\varvec{\xi }),\varPhi (\varvec{\ell }))$, and obtain a handle $h^{\star }_{X,\varPhi }$.

    • 3. Store $\widetilde{{H}}^{\star }_X = \left\{ (h^{\star }_{X,\varPhi },\varPhi (\varvec{h}))\right\} _{\varPhi }$

  • For each $Y\in \mathcal {Y}_n$:

    • 1. Symmetrically perform the above two steps with respect to $\widetilde{{H}}_Y$ (instead of $\widetilde{{H}}_X$).

    • 2. Store $\widetilde{{H}}^{\star }_Y = \left\{ (h^{\star }_{Y,\varPhi },\varPhi (\varvec{h}))\right\} _{\varPhi }$.

• Output:

  $$\widetilde{{C}}^\star = (\widetilde{{C}},\{\widetilde{{H}}^{\star }_X\}_{X\in \mathcal {X}_n}, \{\widetilde{{H}}^{\star }_Y\}_{ Y\in \mathcal {Y}_n}), \text { where } \widetilde{{C}} := (\widetilde{{Z}},\{\widetilde{{H}}_X\}_{X}, \{\widetilde{{H}}_Y\}_{ Y}).$$

The Evaluator $\mathsf {xiO^\star .Eval}$ : Given an obfuscation $\widetilde{{C}}^\star = (\widetilde{{C}},\{\widetilde{{H}}^{\star }_X \}_{X\in \mathcal {X}_n}$,

$\{\widetilde{{H}}^{\star }_Y\}_{ Y\in \mathcal {Y}_n})$, input $(x,y)\in \varvec{X}_n\times \varvec{Y}_n$, and oracle $\mathcal {M}^2$, $\mathsf {xiO^\star .Eval}^{\mathcal {M}^2}(\widetilde{{C}}^\star ,(x,y))$ does the following:

• Emulate $\mathsf {xiO.Eval}^{\mathcal {M}^d}(\widetilde{{C}},(x,y))$.

• Emulate any zero-test query $(p,h_1,\dots ,h_m)$ it makes to $\mathcal {M}^d$ as follows:

  • 1. Parse $\widetilde{{C}} = (\widetilde{{Z}},\{\widetilde{{H}}_X\}_{X\in \mathcal {X}_n}, \{\widetilde{{H}}_Y\}_{ Y\in \mathcal {Y}_n})$.

  • 2. Let $(X,Y) \in \mathcal {X}_n\times \mathcal {Y}_n$ be the (unique) sets such that $(x,y)\in X\times Y$. Retrieve $\widetilde{{H}}_X,\widetilde{{H}}_Y$.

  • 3. Split $\varvec{h}= (h_1,\dots ,h_m)$ into two verctors of handles $\varvec{h}_X \subseteq \widetilde{{H}}_X$ and $\varvec{h}_Y \subseteq \widetilde{{H}}_Y$. (Such a partition always exists, by the guarantee of explicit handles in product form.)

  • 4. Viewing $p(\varvec{h})$ as a formal polynomial in variables $\varvec{h}$, factor it as

    $$p(\varvec{h}) = \sum _i \gamma _i \varPhi _{i}(\varvec{h}) = \sum _i \gamma _i \varPhi _{X,i}(\varvec{h}_X)\varPhi _{Y,i}(\varvec{h}_Y),$$

    where $\gamma _i\in \mathbb {F}\setminus \left\{ 0\right\}$ are the coefficients, and each monomial $\varPhi _i(\varvec{h})$ is factored into $\varPhi _{X,i}(\varvec{h}_X)\cdot \varPhi _{Y,i}(\varvec{h}_Y)$.

  • 5. Translate $\left\{ \varPhi _{X,i}(\varvec{h}_X), \varPhi _{Y,i}(\varvec{h}_Y)\right\} _i$ into handles $\{h^{\star }_{X,i},h^{\star }_{Y,i}\}_i$ by locating $(h^{\star }_{X,i},\varPhi _{X,i}(\varvec{h}_X)) \in \widetilde{{H}}^{\star }_X$ and $(h^{\star }_{Y,i},\varPhi _{Y,i}(\varvec{h}_Y)) \in \widetilde{{H}}^{\star }_Y$.

  • 6. Consider the degree-2 formal polynomial:

    $$p^\star (\varvec{h}^\star )=\sum _i \gamma _i h^{\star }_{X,i} h^{\star }_{Y,i}.$$

  • 7. Make the zero-test $(p^\star ,\varvec{h}^\star )$ to the oracle $\mathcal {M}^2$ and return the result.

Labels and Validity Predicate $V^2$ of Oracle $\mathcal {M}^2$ . Note that labels with respect to $\mathcal {M}^2$ are subsets of the label set of $\mathcal {M}$. Let $V^d$ be the decomposable validity predicate associated with $\mathcal {M}^d$. We define a new validity predicate of degree 2, which is also decomposable. For this purpose, we need to define $V^2$ for labels corresponding to bilinear monomials given by a multi-set $\left\{ \ell ^\star _1,\ell ^\star _2\right\}$. For all other multi-sets L (with cardinality larger than 2), $V^2(L)=\mathtt{{false}}$, capturing that this is a degree 2-predicate.

The validity predicate $V^2(\left\{ \ell ^\star _1,\ell ^\star _2\right\} )$ is computed as follows:

• Parse $\ell ^\star _1$ and $\ell ^\star _2$ as as two multi-sets $\left\{ \ell _{1,1},\dots ,\ell _{1,k_1}\right\} ,\left\{ \ell _{2,1},\dots ,\ell _{2,k_2}\right\}$.

• Apply the original predicate to the disjoint union multi-set:

  $$V^2(\left\{ \ell ^\star _1,\ell ^\star _2\right\} ) := V^d(\ell ^\star _1 \uplus \ell ^\star _2) = V^d(\left\{ \ell _{1,1},\dots ,\ell _{1,k_1}\right\} \uplus \left\{ \ell _{2,1},\dots ,\ell _{2,k_2}\right\} ).$$

Recall that the fact that $V^d$ is decomposable means that there exist a projection function $\varPi ^d$ and predicate $V^d_\varPi$, such that, for every two multi-sets $\ell ^\star _1, \ell ^\star _2$, $V^d(\ell ^\star _1 \uplus \ell ^\star _2) = V^d_\varPi (\varPi ^d(\ell ^\star _1), \varPi ^d(\ell ^\star _2))$. We show that $V^2$ is also decomposable, by defining its corresponding projection function $\varPi ^2$ and predicate $V^2_\varPi$, and showing that on input two multisets $A= \{\ell ^\star _i\}_{i}$ and $B= \{\ell ^\star _j\}_{j}$, $V^2(A \uplus B) = V^2_\varPi (\varPi ^2(A), \varPi ^2(B))$. The projection function $\varPi ^2$ on input a multiset A computes: $\varPi ^2(A) = \left( |A|, \varPi ^d(\uplus _{\ell ^\star \in A} \ell ^\star )\right)$. The predicate $V^2_\varPi$ on input two multisets A, B outputs $\mathtt{{false}}$ if $|A| +|B| > 2$. Otherwise, if A, B contain exactly two labels $\ell ^\star _1, \ell ^\star _2$, the predicate computes:

$$\begin{aligned} V^2_\varPi (\varPi ^2(A), \varPi ^2(B))= & {} V^d( \varPi ^d(\uplus _{\ell ^\star \in A} \ell ^\star ), \varPi ^d(\uplus _{\ell ^\star \in B} \ell ^\star ))\\= & {} V^d( (\uplus _{\ell ^\star \in A} \ell ^\star ) \uplus (\uplus _{\ell ^\star \in B} \ell ^\star )) = V^d(\ell ^\star _1 \uplus \ell ^\star _2) = V^2(A \uplus B) \end{aligned}$$

Therefore $V^2$ is decomposable. Moreover, it is easy to see that the arity of $V^2$ is exactly that of $V^d$, which is bounded by a fixed polynomial.

3.3 Step 3: Asymmetric Oracles to Symmetric Oracles

We show that any XIO scheme with explicit handles relative to the oracle $\mathcal {M}^2$ can be converted to a scheme relative to a symmetric bilinear oracle $\mathcal {B}^2$ (also with explicit handles). This model is analogous to the symmetric bilinear pairing groups where there is a single base group G with a bilinear map $e:G\times G\rightarrow G_T$ (Definition 8). The transformation will incur a certain blowup depending on the arity of the oracle $\mathcal {M}^2$, which is a bounded polynomial.

Lemma 3

Let $\mathsf {xiO}=(\mathsf {xiO.Obf}^{(\cdot )},\mathsf {xiO.Eval}^{(\cdot )})$ be an XIO scheme, for a collection of circuit classes $\varvec{\mathcal {C}}$, defined relative to the (asymmetric) decomposable oracle $\mathcal {M}^2$, with explicit handles in $(\mathcal {X},\mathcal {Y})$-product form, for some product collection $(\mathcal {X},\mathcal {Y})$. Then $\mathsf {xiO}$ can be converted to a new scheme $\mathsf {xiO}^\star$ relative to the (symmetric) oracle $\mathcal {B}^2$, also with explicit handles in $(\mathcal {X},\mathcal {Y})$-product form.

Towards the lemma, we show a transformation that reduces the oracle $\mathcal {M}^2$ to a symmetric bilinear oracle $\mathcal {B}^2$. In the full version [8], we use this transformation to convert any XiO scheme relative to $\mathcal {M}^2$ to one relative to $\mathcal {B}^2$.

Reducing Oracle $\mathcal {M}^2$ to Oracle $\mathcal {B}^2$ . The transformation consists of a recoding process $\mathcal {E}$ that takes a secret key K, and an arbitrary encoding query of the form $(\xi ,\ell )$ to $\mathcal {M}^2$, and transforms it into a set of new encoding queries $(\xi ^{\star }_1,\ell _\mathcal {B}),\dots ,(\xi ^{\star }_k,\ell _\mathcal {B})$ which it gives $\mathcal {B}^2$ (all with respect to the unique label $\ell _\mathcal {B}$). $\mathcal {E}$ then outputs a handle $\varvec{h}$ representing $(\xi ,\ell )$ consisting of a list of handles $\varvec{h}= (h^{\star }_1,\dots ,h^{\star }_k)$ generated by $\mathcal {B}^2$ for $\xi ^{\star }_1,\dots ,\xi ^{\star }_k$.

The encoder $\mathcal {E}$ is associated with a (public) decoder $\mathcal {D}$. The decoder $\mathcal {D}$ is given as input a zero-test query $(p,\varvec{h}_1,\dots ,\varvec{h}_m)$ for $\mathcal {M}^2$ to be evaluated over underlying field elements $\varvec{\xi }=(\xi _1,\dots ,\xi _m)$, and now represented by $\varvec{\xi }^\star =(\xi ^{\star }_{1,1},\dots ,\xi ^{\star }_{1,k},\dots ,\xi ^{\star }_{m,1},\dots ,\xi ^{\star }_{m,k})$ encoded in $\mathcal {B}^2$ with handles $\varvec{h}^\star =(h^{\star }_{1,1},\dots ,h^{\star }_{1,k},\dots , h^{\star }_{m,1},\dots ,h^{\star }_{m,k})$. The decoder then translates it into a new zero-test query $(p^\star ,\varvec{h}^\star )$ and submits it to $\mathcal {B}^2$, with the guarantee that if the zero test is valid with respect to the validity predicate $V$ associated with $\mathcal {M}^d$, then $p(\varvec{\xi }) = p^\star (\varvec{\xi }^\star )$, and otherwise, $p^\star (\varvec{\xi }^\star )$ evaluates to non-zero with overwhelming probability.

We next turn to a more formal description of the transformation. In what follows, let $V$ be an arbitrary degree-2 decomposable validity predicate, defined over pairs of labels $(\ell ,\ell ') \in {\mathbb {L}}\times {\mathbb {L}}$ from a label set ${\mathbb {L}}$, and associated with projection function $\varPi$ and predicate $V_\varPi$ with bounded arity $\mathsf {Arity}(V_\varPi )\le \mathrm {poly}(\lambda )$.

Secret Encoding Key. The secret key K consists of random invertible field elements $\eta _\ell ,\varphi _\ell \leftarrow \mathbb {F}\setminus \left\{ 0\right\}$ for each label $\ell \in {\mathbb {L}}$, and random invertible field elements $\alpha _\pi ,\beta _\pi ,\gamma _\pi ,\delta _\pi \leftarrow \mathbb {F}\setminus \left\{ 0\right\}$ for every $\pi$ in the corresponding set of projections $\varGamma = \left\{ \varPi (\left\{ \ell \right\} )\ :\ \ell \in \ {\mathbb {L}}\right\}$.

Remark 6

(Lazy Secret-Key Sampling). Note that the total number of labels and their projection could be superpolynomial, making the secret key superpolynomial in length. To deal with such cases, the recoder uses lazy sampling to sample the above random invertible elements only when needed and keeps a record of all sampled elements. As we argue below, the total number of random invertible elements to be sampled is polynomial in the number of tuples $(\xi , \ell )$ to be recoded. For simplicity of exposition, we describe the procedure with respect to a key consisting of all possible random invertible elements.

Recoding. Given the secret key K and $(\xi ,\ell ) \in \mathbb {F}\times {\mathbb {L}}$, the encoder $\mathcal {E}^{\mathcal {B}^2}((\xi ,\ell ),K)$ does the following:

• Samples two secret shares $\xi _{L},\xi _{R}$ at random from $\mathbb {F}$ subject to $\xi _{L}+\xi _{R}=\xi$.

• Let $\pi = \varPi (\left\{ \ell \right\} )$ be the projection of $\left\{ \ell \right\}$. Generates the field elements:

  $$\varvec{\xi }^\star _\circ :=\left( \xi ^{\star }_{\circ ,\alpha ,L} = \alpha _\pi \cdot \xi _{L},\ \xi ^{\star }_{\circ ,\beta ,R} = \beta _\pi \cdot \xi _{R},\ \xi ^{\star }_{\circ ,\gamma ,L} = \gamma _\pi \cdot \xi _{L},\ \xi ^{\star }_{\circ ,\delta ,R} = \delta _\pi \cdot \xi _{R}\right) . $$

• Let $\mathsf {match}(\pi ) = \left\{ \pi '\ : \ V_\varPi (\pi , \pi ')=\mathtt{{true}} \right\}$ be the set of projections that evaluates to $\mathtt{{true}}$ with $\pi$. (For every $\pi '\in \mathsf {match}(\pi )$, and every $\ell '$, such that, $\pi ' = \varPi (\left\{ \ell '\right\} )$, it holds that $V(\left\{ \ell , \ell '\right\} ) = \mathtt{{true}}$.)

  For each $\pi ' \in \mathsf {match}(\pi )$, generates the field elements:

  $$\begin{aligned} \varvec{\xi }^\star _{\pi '} :=\Big (\xi ^{\star }_{\pi ',\frac{1}{\alpha },L} = \frac{1}{\alpha _{\pi }} \cdot \xi _{ L},&\qquad \xi ^{\star }_{\pi ',\frac{1}{\beta },L} = \frac{1}{\beta _{\pi }} \cdot \xi _{ L},\qquad \\&\xi ^{\star }_{\pi ',\frac{1}{\gamma },R} = \frac{1}{\gamma _{\pi }} \cdot \xi _{ R},\qquad \xi ^{\star }_{\pi ',\frac{1}{\delta },R} = \frac{1}{\delta _{\pi }} \cdot \xi _{ R}\Big ). \end{aligned}$$

• If $V\left( \left\{ \ell \right\} \right) =\mathtt{{true}}$, generates field elements

  $$ \varvec{\xi }^\star _{\vartriangle } :=\left( \xi ^{\star }_{\vartriangle ,\eta ,L} = \eta _\ell \cdot \xi _{L},\qquad \xi ^{\star }_{\vartriangle ,\frac{1}{\eta }} = \frac{1}{\eta _\ell },\qquad \xi ^{\star }_{\vartriangle ,\varphi ,R} = \varphi _\ell \cdot \xi _{R},\qquad \xi ^{\star }_{\vartriangle ,\frac{1}{\varphi }} = \frac{1}{\varphi _\ell } \right) , $$

• Asks $\mathcal {B}^2$ to encode (with respect to the unique label $\ell _\mathcal {B}$) the field elements $\varvec{\xi }^\star _\circ ,\left( \varvec{\xi }^\star _{\pi '}\right) _{\pi ' \in \mathsf {match}(\pi )}, \varvec{\xi }^\star _{\vartriangle }$ generated above, obtaining corressponding handles

  $$\varvec{h}^\star =\left( \varvec{h}^\star _\circ ,\left( \varvec{h}^\star _{\pi '}\right) _{\pi '\in \mathsf {match}(\pi )},\varvec{h}^\star _{\vartriangle } \right) .$$

• Outputs handles $\varvec{h}^\star$.

We argue that when $V$ has bounded $\mathrm {poly}(\lambda )$ arity, the size of the new encoding $\varvec{h}^\star$ is bounded by $\mathrm {poly}(\lambda )$. This is because, $\varvec{h}^\star _\circ$ and $\varvec{h}^\star _\vartriangle$ each consists of 4 encodings, while $\left( \varvec{h}^\star _{\pi '}\right) _{\pi '\in \mathsf {match}(\pi )}$ consists of $O(|\mathsf {match}(\pi )|) =$ Arity($V_{\varPi }$) $\le \mathrm {poly}(\lambda )$.

Decoding. Given a degree-2 polynomial p and handles $(\varvec{h}_1^\star ,\dots ,\varvec{h}_m^\star )$, where $\varvec{h}_i^\star = \varvec{h}_{i,\circ }^\star ,\left( \varvec{h}^\star _{i,\pi '}\right) _{\pi '\in \mathsf {match}(\pi )},\varvec{h}_{i,\vartriangle }^\star$ the decoder $\mathcal {D}^{\mathcal {B}^2}(p,\varvec{h}_1^\star ,\dots ,\varvec{h}_m^\star )$:

• Writes p as a formal polynomial

  $$ p(\varvec{h}_1^\star ,\dots ,\varvec{h}_m^\star ) = \sigma + \sum _{k}\rho _{k}\varvec{h}_k^\star + \sum _{i \le j}\rho _{i,j}\varvec{h}_i^\star \varvec{h}_j^\star . $$

• If for any monomial $\varvec{h}^\star _k$ in p, $V(\left\{ \ell _k\right\} ) = \mathtt{{false}}$, or for any monomial $\varvec{h}^\star _i\varvec{h}_j^\star$, $V(\left\{ \ell _i, \ell _j\right\} ) = \mathtt{{false}}$, return false. Otherwise, continue.

• Generates a new degree-2 formal polynomial

  $$\begin{aligned}&p^\star (\varvec{h}^\star ) = \sigma + \sum _{k} \rho _{k}\cdot \left( h^{\star }_{k, \vartriangle , \eta ,L}h^{\star }_{k, \vartriangle , \frac{1}{\eta }}+h^{\star }_{k, \vartriangle , \varphi ,R}h^{\star }_{k, \vartriangle , \frac{1}{\varphi }}\right) +\\&\sum _{i\le j} \rho _{i,j}\ \cdot \left( h^{\star }_{i, \circ , \alpha ,L}h^{\star }_{j, \pi _i,\frac{1}{\alpha },L} + h^{\star }_{i, \circ , \gamma ,L}h^{\star }_{j, \pi _i,\frac{1}{\gamma },R} + h^{\star }_{i, \circ , \beta ,R} h^{\star }_{j, \pi _i,\frac{1}{\beta },L} + h^{\star }_{i, \circ , \delta ,R}h^{\star }_{j, \pi _i,\frac{1}{\delta },R} \right) . \end{aligned}$$

• It submits to $\mathcal {B}^2$ the zero test $(p^\star ,\varvec{h}^\star )$ and returns the result.

3.4 Putting It All Together

We conclude the proof of Theorem 3.

Proof

(of Theorem 3 ). To obtain $\mathsf {xiO}^\star$, we apply to $\mathsf {xiO}$ Lemmas 1, 2, 3.

• Lemma 1 turns $\mathsf {xiO}$ into an approximately-correct XIO scheme $\mathsf {xiO}_1$ with explicit handles, relative to the same degree-d decomposable oracle $\mathcal {M}^d$ that $\mathsf {xiO}$ uses.

• Lemma 2 turns $\mathsf {xiO}_1$ into an approximately-correct XiO scheme $\mathsf {xiO}_2$ with explicit handles, relative to an asymmetric bilinear oracle $\mathcal {M}^2$ that is also decomposable.

• Lemma 3 turns $\mathsf {xiO}_2$ into an approximately-correct XiO scheme $\mathsf {xiO}_3$ with explicit handles, relative to a symmetric bilinear oracle $\mathcal {B}^2$.

The final XiO scheme $\mathsf {xiO}_3$ is exactly the new XiO scheme $\mathsf {xiO}^\star$. By composing the three lemmas, we have that $\mathsf {xiO}^\star$ is approximately correct and secure. The only thing to argue that $\mathsf {xiO}^\star$ is also weakly succinct. Note that the obfuscated circuits of $\mathsf {xiO}^\star$ have the form

$$\begin{aligned} \widetilde{C} = \left( \widetilde{Z}, \{\widetilde{H}_X\}, \{\widetilde{H}_Y\},\ \{\widetilde{H}^\star _X\}, \{\widetilde{H}^\star _Y\}, \ \{\widetilde{H}'_X\}, \{\widetilde{H}'_Y\} \right) \end{aligned}$$

where $\widetilde{Z}$ is an obufscated circuit of the original scheme $\mathsf {xiO}$, $\widetilde{H}_X$ and $\widetilde{H}_Y$ are the sets of explicit handles of $\mathcal {M}^d$ added by Lemma 1, $\widetilde{H}^\star _X$ and $\widetilde{H}^\star _Y$ are the encodings of monomials of $\mathcal {M}^2$ added by Lemma 2, $\widetilde{H}'_X$ and $\widetilde{H}'_Y$ are the re-encodings of $\mathcal {B}^2$ added by Lemma 3. By the three lemmas and the fact that the original scheme $\mathsf {xiO}$ is $\gamma ^\star$-compressing and satisfies the efficiency requirement stated in Theorem 3, we have,

for some $\gamma '<1$. Thus,the new XIO scheme is weakly succinct.

4 From (Approximate) XIO and LWE to FE

We describe at a high-level how to use approximate XIO to construct 1-key weakly succinct FE for $\mathbf P /\mathbf{poly }$, assuming LWE. The formal transformation can be found in the full version of this paper [8].

Theorem 4

Assuming LWE with subexponential modulus-to-noise ratio and the existence of an approximate XIO scheme for $\mathbf P ^{\log }/\mathbf{poly }$, there exists a single-key weakly-succinct FE scheme $\mathsf {FE}$ for $\mathbf P /\mathbf{poly }$.

A Failed Attempt. Lin, Pass, Seth and Telang [33] showed a transformation from correct XIO for $\mathbf P ^{\log }/\mathbf{poly }$ to IO for $\mathbf P /\mathbf{poly }$, assuming LWE.⁸ Previously, Bitansky and Vaikuntanathan [12] showed how to make any approximately correct IO correct (assuming, say, LWE). Thus, to prove the above theorem, a natural idea is to amplify the correctness of approximate XIO to obtain correct XIO by [12], and then invoke the transformation of [33]. This approach turns out to completely fail. Indeed, the [12] transformation only works for classes of circuits that are expressive enough; in particular, it relies on the ability of circuits in the class to process encrypted inputs, which must inherently be of super-logarithmic length in the security parameter. However, XIO for such circuit classes, which lie outside of $\mathbf P ^{\log }/\mathbf{poly }$, is inefficient (see Remark 1).

Instead, we show how to modify the transformation of [33], based on error-correcting codes, so that, it works directly with approximate XIO. Below, we briefly review the [33] transformation and describe our key ideas.

Review of the [33] Transformation. Goldwassar et al. [27] constructed, from LWE with subexponential modulus-to-noise ratio, a fully succinct, public-key, single-key, FE scheme for Boolean NC $^1$ circuits; namely, the encryption circuit of their scheme has size $\mathrm {poly}(n,\lambda )$, where n is the message length.

Starting from such an FE scheme bFE for Boolean circuits, the first observation in [33] is as follows: To construct an FE scheme, $\mathsf {FE}$ for any (possibly non-Boolean) circuit C, one can use bFE to issue a key for the corresponding Boolean circuit B that produces one output bit at a time, that is, $B(m,i) = \left( C(m)\right) _i$. Then to enable evaluating the circuit C, it suffices to publish a list of bFE ciphertexts encrypting all pairs (m, i). This, however, leads to a scheme with encryption time linear in the length of the output (as it needs to produce a ciphertext for every output bit), and is not weakly succinct. The key idea in [33] is using XIO to generate the list of encrypted pairs (m, i). Namely, obfuscate a circuit that given as input i, outputs the encryption of (m, i), where randomness is derived with a pseudorandom function. Since XIO achieves “sublinear compression”, the resulting FE scheme is now weakly succinct for all of NC $^1$, including circuits with non-Boolean output.

Our Approach. The basic idea behind replacing XIO with approximate XIO is to use good error-correcting codes to allow recovering the output of a given function even if some of the encryptions (m, i) are faulty. Specifically, we make the following modification to the transformation of [33]. Instead of deriving a key for the Boolean function $B(m,i) = \left( C(m)\right) _i$, which computes the i-th bit of the circuit’s output, we consider the function $B^\star (m,i) = \left( \mathsf {ECC}(C(m))\right) _i$ that outputs the i-th bit of an error-corrected version of this output. As before, we use XIO to to generate the list of encryptions (m, i), only that now, with approximate XIO, some of these encryptions may be faulty. Nevertheless, we can still recover $\left( \mathsf {ECC}(C(m))\right) _i$ for a large enough fraction of indices i, and can thus correct, and obtain C(m). By using codes with constant rate, and a linear-size constant-depth encoding circuit, we can show that this transformation achieves the required compression.