One-Shot Verifiable Encryption from Lattices

Abstract

Verifiable encryption allows one to prove properties about encrypted data and is an important building block in the design of cryptographic protocols, e.g., group signatures, key escrow, fair exchange protocols, etc. Existing lattice-based verifiable encryption schemes, and even just proofs of knowledge of the encrypted data, require parallel composition of proofs to reduce the soundness error, resulting in proof sizes that are only truly practical when amortized over a large number of ciphertexts.

In this paper, we present a new construction of a verifiable encryption scheme, based on the hardness of the Ring-LWE problem in the random-oracle model, for short solutions to linear equations over polynomial rings. Our scheme is “one-shot”, in the sense that a single instance of the proof already has negligible soundness error, yielding compact proofs even for individual ciphertexts. Whereas verifiable encryption usually guarantees that decryption can recover a witness for the original language, we relax this requirement to decrypt a witness of a related but extended language. This relaxation is sufficient for many applications and we illustrate this with example usages of our scheme in key escrow and verifiably encrypted signatures.

One of the interesting aspects of our construction is that the decryption algorithm is probabilistic and uses the proof as input (rather than using only the ciphertext). The decryption time for honestly-generated ciphertexts only depends on the security parameter, while the expected running time for decrypting an adversarially-generated ciphertext is directly related to the number of random-oracle queries of the adversary who created it. This property suffices in most practical scenarios, especially in situations where the ciphertext proof is part of an interactive protocol, where the decryptor is substantially more powerful than the adversary, or where adversaries can be otherwise discouraged to submit malformed ciphertexts.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Lattice cryptography has matured to the point where the general belief is that any primitive that can be constructed from any other assumption can also be constructed based on a lattice assumption. The main question that remains is how efficient (in a practical, rather than asymptotic, sense) one can make the lattice-based constructions. A primitive that has been getting a lot of recent attention is a “proof of plaintext knowledge.”

In a proof of plaintext knowledge, a prover who has a message $\mu$ produces a ciphertext $t =\mathsf {Enc}(\mu )$ and a zero-knowledge proof of knowledge $\pi$ showing that he knows the value of $\mathsf {Dec}( t )$. Proving knowledge of the value of $\mathsf {Dec}( t )$ is usually the same as proving that $t$ is a correctly formed ciphertext along with proving the knowledge of $\mu$ that was used to construct it.

By itself, a proof of plaintext knowledge is not particularly useful, and it is almost always used as a part of a primitive known as a verifiable encryption scheme. In such a scheme, there is a relation $R_L$ and a language

$$ L= \{x~:~ \exists w \text { s.t. } R_L(x,w)=1\}.$$

Thus the value w is a witness to the fact that x is in the language $L$. The relation $R_L$ and the element x are public, while the prover possesses the secret witness w. He then produces an encryption $t =\mathsf {Enc}(w)$ as well as a zero-knowledge proof of knowledge $\pi$ of the value $w=\mathsf {Dec}( t )$ and that w satisfies $R_L(x,w)=1$. Verifiable encryption can therefore also be seen as an extractable non-interactive zero-knowledge proof. It is a building block for many primitives, e.g.,

• group signatures [CvH91], where a group manager hands distinct signing keys to all users, using which they can anonymously sign messages. A trusted opener is able to trace back a signature to the identity of the signer. A common construction [CL06] is to let users verifiably encrypt their identity under the opener’s public key together with a proof that they know a signature by the group manager on the same identity.

• key escrow protocols [YY98, PS00], where users encrypt their decryption key under the public key of a trusted escrow authority. Using verifiable encryption, communication partners or network providers can check that the ciphertext indeed encrypts the user’s decryption key, and not some bogus data.

• optimistic fair exchange protocols [ASW00, BDM98], where two parties can fairly exchange secrets by, in a first step, proving that they encrypted their respective secrets under the public key of a trusted authority, who can later be called upon to recover the secret in case one of the parties aborts the protocol early;

• verifiable secret sharing, where one dealer sends verifiably encrypted shares of a secret to a set of parties, and proves to an external third party that the ciphertexts contain actual shares of the secret.

1.1 Proofs of Plaintext Knowledge from Lattices – Prior Work

If one uses a lattice-based encryption scheme based on LWE or Ring-LWE, then the encryption of a message m satisfies the linear relation $\mathbf{A}\begin{bmatrix} \mathbf{r} \\ m \end{bmatrix}=\mathbf{t} \,\mathrm{mod}\,q.$ There are several known techniques to prove that the ciphertext $\mathbf{t}$ is well-formed and one knows the message m. One technique is adapting Stern’s protocol based on permutations [Ste93] to lattice-based schemes [LNSW13]. This approach is unfortunately very impractical due to the fact that each round of the protocol has soundness error 2 / 3 (and therefore needs to be repeated 192 times to achieve 128-bit security). Furthermore, if proving relations where the secret has coefficients of size k, the size of the proof increases by a factor of $\log {k}$ [LNSW13]. This makes schemes using Stern’s protocol unsuitable for most practical applications.

Another approach is to use the “Fiat-Shamir with Aborts” zero-knowledge proof technique from [Lyu09, Lyu12] with 0 / 1 challenges. This also has the problem of having soundness error 1 / 2 and needing to be repeated 128 times for 128-bit security. This approach, however, is more algebraic than Stern’s proof of knowledge and it was shown to admit several improvements. If one uses a Ring-LWE encryption scheme, then it was shown in [BCK+14] how the soundness error can be reduced to 1 / (2n), where n is the dimension of the ring being used (typically 1024 or 2048). For 128-bit security, one then only needs to run the protocol around a dozen times. A scenario where the Fiat-Shamir with Aborts technique leads to truly practical protocols is when one wants to simultaneously do many proofs of plaintext knowledge. If one then considers the amortized cost of the proof of knowledge, then the number of iterations is only a small constant (approaches 2 as the number of instances increases) per proof [DPSZ12, BDLN16, CD16].

Despite having received considerable attention in the literature, there seems to be no satisfactory solution for the most natural scenario where the prover has a single instance to prove and would like to do it in “one shot”—that is, without repeating a protocol to amplify soundness. It is therefore conceivable that lattice-based encryption schemes are not compatible with efficient proofs of plaintext knowledge, which would make all the applications much less efficient than their number theoretic counterparts.

1.2 Proofs of Plaintext Knowledge – Our Results

In this work, we introduce a very efficient “one-shot” protocol for proving plaintext knowledge. The caveat is that the running time of the decryption algorithm depends on the running time of the prover. More precisely, our decryption algorithm is randomized in that it tries to decrypt ciphertexts that are “close” to the one provided by the prover. And we show that the expected number of decryption tries our decryptor needs is within a small factor (essentially 1) of the number of random oracle queries that the prover makes while constructing the proof of knowledge $\pi$. If q is the number of queries made by the prover, then Markov’s inequality implies that the probability that the decryptor will need more than $\alpha \cdot q$ decryption tries is less than $1/\alpha$. If the prover is honest, though, then the decryptor will succeed from the first try.

While tying the decryption time to the adversary’s running time is unusual, this should be acceptable in many scenarios. Apart from creating out-of-band incentives such as fines to prevent cheating, there are also technical ways to limit the power of the adversary. If the protocol in which the proof of knowledge is being used is interactive, then the verifier can send the prover a fresh salt during every interaction that has to be included in the cryptographic hash function (modeled as a random oracle) and require that the prover performs the proof within a certain small amount of time. Thus the adversary will have a limited time-frame during which he can make queries to the random oracle (because each new salt in essence creates a new random oracle). The decryption algorithm, on the other hand, is almost always off-line and is therefore allowed more time. In non-interactive settings, the prover can be required to use a salt from a public “randomness beacon” (such as one provided by NIST) at the time the proof was created.

In our scheme, the verification algorithm uses one random oracle query and the decryption algorithm uses none. Thus another simple way of preventing an adversary from using too many random oracle queries during encryption would be to artificially make the computational complexity of computing the hash function high (e.g. by iterating SHA-256 some number of times to produce one output). This has the effect of significantly slowing down a cheating prover, while keeping the decryption time exactly the same.

We also show that, if one wishes, one can upper-bound the running time of the decryptor by making the protocol “k-shot” rather than one shot. In this scenario, the length of the proof of knowledge would go up by a factor k, but one could bound the decryption algorithm’s running time to $k\cdot 2^{\lambda /k}$ for $\lambda$-bit security.

1.3 Verifiable Encryption Schemes – Our Results

We build upon our proof of plaintext knowledge to construct a verifiable encryption scheme that is adapted to be used as a building block for lattice constructions. The relations that are most common in lattice cryptography are those of the form

$$\begin{aligned} \mathbf{B}\mathbf{m}=\mathbf{u}\,\mathrm{mod}\,p \end{aligned}$$

(1)

where $\mathbf{B}$ is a matrix over some ring, $\mathbf{m}$ is a vector with small coefficients, and $\mathbf{u}$ is the product of $\mathbf{B}\mathbf{m}$ modulo p. For example, in (Ring)-LWE encryption $\mathbf{B},\mathbf{u}$ is the public key and $\mathbf{m}$ is the secret key. In full domain hash signatures, $\mathbf{B}$ is the public key, $\mathbf{m}$ is the signature, and $\mathbf{u}=\mathsf {H}(\mu )$ is derived from the message $\mu$. Giving a verifiable encryption scheme for such relations is a main building block for many of the protocols listed in the introduction.

While verifiable encryption would normally guarantee that decrypting a valid ciphertext yields a witness satisfying (1), our construction relaxes this guarantee to only yield a witness $(\overline{\mathbf{m}},\overline{\mathrm{c}})$ with small coefficients satisfying

$$\begin{aligned} \mathbf{B}\overline{\mathbf{m}}=\overline{\mathrm{c}}\mathbf{u}\,\mathrm{mod}\,p. \end{aligned}$$

(2)

This relaxation actually turns out to be sufficient for many applications of verifiable encryption. Lattice schemes can often be slightly augmented to allow for relations of the form (2) to be “useful” whenever those of the form (1) are. We will see this in the two examples provided in Sect. 6.

Notice also how it appears as if the decryption and the proof of knowledge are disjoint. Indeed, the proof of knowledge $\pi$ may prove the existence of some witness $(\overline{\mathbf{m}},\overline{\mathrm{c}})$, whereas the decryption algorithm may obtain a completely different witness $(\overline{\mathbf{m}}',\overline{\mathrm{c}}')$. But in addition to still being sufficient for many applications, there is also a connection between the two tuples that is actually crucial to our construction – we have that

$$\overline{\mathbf{m}}/\overline{\mathrm{c}} = \overline{\mathbf{m}}'/\overline{\mathrm{c}}'\,\mathrm{mod}\,\, p.$$

While this property is not needed in many applications, the presence of this relationship may be useful when constructing group signatures or other primitives where it is important that the decryption recovers some specific attribute of the prover rather than just a witness to a relation.

1.4 Paper Organization

We present the Ring-LWE encryption scheme and the non-interactive “Fiat-Shamir with Aborts” zero-knowledge proof protocol in Sects. 2.5 and 2.6. Slight variations of these two primitives are used throughout our constructions.

We then present the definitions of our relaxed version of verifiable encryption in Sect. 3.1, and describe all the elements of the scheme in Sect. 3.2. In Sect. 7, we give some example instantiations for the proofs of plaintext knowledge and verifiable encryption schemes. The proof of plaintext knowledge scheme requires 9 KB for the ciphertext and 9 KB for the proof. This is quite efficient since this ciphertext is only around 4 times larger than a regular Ring-LWE ciphertext.

The efficiency of the verifiable encryption scheme is mostly affected by the size of the modulus p and the witness $\mathbf{m}$ in the relation. The larger these values, the larger the proofs and ciphertexts will be. The sample instantiations in Sect. 7 are meant to support the two sample applications in Sect. 6, where we describe how our relaxed verifiable encryption scheme can be used to build key escrow schemes and verifiably encrypted signatures. In Sects. 4 and 5 we describe two variants of our schemes, the former trading longer ciphertexts for bounded decryption time, the latter adding simulatability under chosen-ciphertext to the scheme.¹

2 Preliminaries

For a set S, we write to mean that a is chosen uniformly at random from S. If D is a distribution, then signifies that a is randomly chosen according to the distribution D. The assignment operator $a\leftarrow b$ signifies that a gets assigned the value b. We will also sometimes write column vectors of the form $\begin{bmatrix} a_1 \\ \ldots \\ a_k\end{bmatrix}$ as $[~a_1~;~\ldots ~;~a_k~].$

2.1 The Ring $\mathbb {Z}[\mathrm{x}]/(\mathrm{x}^n+1).$

Consider the ring $R=\mathbb {Z}[\mathrm{x}]/(\mathrm{x}^n+1)$ and $R_q=\mathbb {Z}_q[\mathrm{x}]/(\mathrm{x}^n+1)$ where n is a power of 2 integer and q is some prime. The elements of the latter ring are polynomials of degree at most $n-1$ with coefficients between $-(q-1)/2$ and $(q-1)/2$ (for the ring R, there is no restriction on the sizes of coefficients). All definitions that follow apply both to R and $R_q$. We will denote elements of $\mathbb {Z}$ and of R by lower-case letters, elements of vectors in $R^k$ by bold lower-case letters, and of matrices in $R^{k\times l}$ by bold upper-case letters.

We will define the $\ell _1$, $\ell _2$, and $\ell _\infty$ lengths of an element $\mathrm{a}=\sum \limits _{i=0}^{n-1}a_i\mathrm{x}^i\in R$ as

$$\Vert \mathrm{a}\Vert _1=\sum \limits _{i=0}^{n-1}|a_i|,\,\,\,\,\,\Vert \mathrm{a}\Vert =\sqrt{\sum _{i=0}^{n-1}a_i^2}\,\,\,\,\text { and }\,\,\,\,\,\Vert \mathrm{a}\Vert _\infty = \max _i(|a_i|)$$

respectively.² For k-dimensional vectors $\mathbf{a}=[~\mathrm{a}_1~|~\ldots ~|~\mathrm{a}_k~]\in R^k$, we write $\Vert \mathbf{a}\Vert _1=\Vert \mathrm{a}_1\Vert _1+\ldots +\Vert \mathrm{a}_k\Vert _1$, $\Vert \mathbf{a}\Vert =\sqrt{\Vert \mathrm{a}_1\Vert ^2+\ldots +\Vert \mathrm{a}_k\Vert ^2}$ and $\Vert \mathbf{a}\Vert _\infty =\max _i\Vert \mathrm{a}_i\Vert _\infty$. We will denote by $S_i$ (respectively $S^k_i$), the set of elements of R (resp. of $R^k$) whose $\ell _\infty$ length is at most i.

It is not hard to check that for any two polynomials $\mathrm{a},\mathrm{b}\in R$, we have $\Vert \mathrm{a}\mathrm{b}\Vert _\infty \le \Vert \mathrm{a}\Vert _1\cdot \Vert \mathrm{b}\Vert _\infty$ and $\Vert \mathrm{a}\mathrm{b}\Vert _\infty \le \Vert \mathrm{a}\Vert \cdot \Vert \mathrm{b}\Vert$. Similarly for $\mathbf{a},\mathbf{b}\in R^k$, we have the same inequalities on the $\ell _\infty$ norms of their inner products: that is, $\Vert \mathbf{a}\cdot \mathbf{b}\Vert _\infty \le \Vert \mathbf{a}\Vert _1\cdot \Vert \mathbf{b}\Vert _\infty$ and $\Vert \mathbf{a}\cdot \mathbf{b}\Vert _\infty \le \Vert \mathbf{a}\Vert \cdot \Vert \mathbf{b}\Vert$.

2.2 Special Properties of $\mathbb {Z}_q[\mathrm{x}]/(\mathrm{x}^n+1)$

The algebraic properties of the ring $R_q=Z_q[\mathrm{x}]/(\mathrm{x}^n+1)$, where n is a power of 2, depend on the prime q. For efficiency, one often takes $q=1\,\mathrm{mod}\,(2n)$, which results in the polynomial $\mathrm{x}^n+1$ splitting into n linear factors modulo q. Operations within the ring can then be performed extremely efficiently using the number theory transform. On the other hand, one sometimes wants the ring to be “almost a field”. In particular, it is sometimes desirable for the ring to have many invertible elements. While there do not exist q that will make $R_q$ a field, using $q=3 \,\mathrm{mod}\,8$ (as first suggested in [SSTX09]) has the effect that $\mathrm{x}^n+1$ factors into two irreducible polynomials of degree n / 2 and so the ring $R_q$ contains $q^n-2q^{n/2}+1$ invertible elements. By the Chinese Remainder theorem, it is also easy to see that all elements of degree less than n / 2 are invertible.

We have not seen this used in previous works, but it turns out that setting $q=5 \,\mathrm{mod}\,\, 8$ may be even more convenient. Modulo such a q, the polynomial $\mathrm{x}^n+1$ also factors into two irreducible polynomials of degree n / 2. And in addition to all elements of degree less than n / 2 being invertible, one can also show that all elements (of degree up to n) with small coefficients are invertible as well. We present the proof of this statement in Lemma 2.2. To the best of our knowledge, this lemma was first proven in an unpublished manuscript of Lyubashevsky and Xagawa.

Lemma 2.1

([LN86], special case of Theorem 3.35, p. 88). Let $q= 5(\,\mathrm{mod}\,\,8)$ be prime and r be an integer such that $r^2=-1(\,\mathrm{mod}\,\,q)$. Then for all positive integers $\kappa$, the polynomials $\mathrm{x}^{2^{\kappa }}-r$ and $\mathrm{x}^{2^{\kappa }}+r$ are irreducible over $\mathbb {Z}_q[\mathrm{x}]$. And in particular, the complete factorization into irreducibles over $\mathbb {Z}_q[\mathrm{x}]$ of the polynomial $\mathrm{x}^{2^{\kappa +1}}+1$ is $\mathrm{x}^{2^{\kappa +1}}+1=(\mathrm{x}^{2^{\kappa }}-r)(\mathrm{x}^{2^{\kappa }}+r)\,\mathrm{mod}\,q$.

Lemma 2.2

Let $R_q=\mathbb {Z}_q[\mathrm{x}]/(x^n+1)$ where $n>1$ is a power of 2 and q is a prime congruent to $5(\,\mathrm{mod}\,\,8)$. This ring has exactly $2q^{n/2}-1$ elements without an inverse. Moreover, every non-zero polynomial $\mathrm{a}$ in $R_q$ with $\Vert \mathrm{a}\Vert _\infty <\sqrt{q/2}$ has an inverse.

Proof

In all that follows, the reduction modulo q will be implicit. By Lemma 2.1, $\mathrm{x}^n+1=(\mathrm{x}^{n/2}-r)(\mathrm{x}^{n/2}+r)$ where $r^2=-1$ and $\mathrm{x}^{n/2}\pm r$ are irreducible. Any element $\mathrm{a}\in R_q$ can be written as $\mathrm{a}=\mathrm{a}_0+\mathrm{x}^{n/2}\mathrm{a}_1,$ where $\mathrm{a}_0,\mathrm{a}_1$ are polynomials in $\mathbb {Z}[\mathrm{x}]$ of degree less than n / 2. Then the Chinese remainder decomposition of $\mathrm{a}$ is

$$CRT(\mathrm{a})=(\mathrm{a}\,\mathrm{mod}\,(\mathrm{x}^{n/2}-r),\mathrm{a}\,\mathrm{mod}\,(\mathrm{x}^{n/2}+r))=(\mathrm{a}_0+r\mathrm{a}_1,\mathrm{a}_0-r\mathrm{a}_1).$$

If $\mathrm{a}$ is not invertible, it means that either $\mathrm{a}_0+r\mathrm{a}_1=\mathrm{0}$ or $\mathrm{a}_0-r\mathrm{a}_1=\mathrm{0}$. If $\mathrm{a}_1=\mathrm{0}$, then $\mathrm{a}_0=\mathrm{0}$ and $\mathrm{a}$ is the zero polynomial. If $\mathrm{a}_1\ne \mathrm{0}$, then some coefficient of $\mathrm{a}_0$, say $\alpha _0$, must be equal to $\pm r \alpha _1$, where $\alpha _1$ is a non-zero coefficient of $\mathrm{a}_1$. Therefore we have $\alpha _0^2=(\pm r\alpha _1)^2=-\alpha _1^2$. In other words, $\alpha _0^2+\alpha _1^2=0$. But since we assumed that $|\alpha _0|,|\alpha _1|<\sqrt{q/2}$, this is not possible, and thus proves the second part of the lemma by contradiction. The first part of the lemma follows from the fact that CRT is a bijection and all the elements without an inverse must be $\mathrm{0}$ modulo at least one of $\mathrm{x}^{n/2}\pm r$.    $\square$

2.3 Lattices and the Discrete Gaussian Distribution

A full-rank integer lattice $\varLambda$ of dimension n is an additive subgroup of $\mathbb {Z}^n$ that is generated by some basis $\mathbf{B}=[\mathbf{b}_1~|~\ldots ~|~\mathbf{b}_n]\in \mathbb {Z}^{n\times n}$ of linearly-independent vectors. If a basis $\mathbf{B}$ is a generator for a lattice $\varLambda$, we will write $\mathcal {L}(\mathbf{B})=\varLambda$.

For a matrix $\mathbf{A}\in \mathbb {Z}^{n\times m}$, we define

$$\begin{aligned} \mathcal {L}^\perp (\mathbf{A})=\{\mathbf{y}\in \mathbb {Z}^m~:~\mathbf{A}\mathbf{y}=\mathrm{0}\,\mathrm{mod}\,q\}. \end{aligned}$$

(3)

It’s easy to see that $\mathcal {L}^\perp (\mathbf{A})$ is a full-rank lattice of dimension m.

For a full-rank integer lattice $\varLambda$, we define the discrete Gaussian distribution for any $\mathbf{v}\in \varLambda$, and 0 on all other points in space.

For the special case of $\varLambda =\mathbb {Z}^m$, we know that

which implies that for $t=6$, the probability that any coefficient of $\mathbf{s}$ is greater than $6\sigma$ is less than $m\cdot 2^{-25}$.

2.4 Polynomial Lattices and Sampling over the Ring R

In this paper, rather than working over the ring $\mathbb {Z}_q$ (with the usual addition and multiplication operation modulo q), we will be working over the ring $R=\mathbb {Z}_q[\mathrm{x}]/(\mathrm{x}^n+1)$ with the usual addition and multiplication operations modulo q and $x^n+1$. Analogously to (3), for a vector $\mathbf{A}\in R^{1\times m}$, a lattice $\mathcal {L}^\perp (\mathbf{A})$ can be defined as

$$\mathcal {L}^\perp {(\mathbf{A})}=\{\mathrm{y}\in \left( \mathbb {Z}[\mathrm{x}]/(\mathrm{x}^n+1)\right) ^m : \mathbf{A}\mathrm{y}=\mathrm{0}\,\mathrm{mod}\,q\}.$$

Note that while it is an m-dimensional lattice over $\mathbb {Z}[\mathrm{x}]/(\mathrm{x}^n+1)$, it is really an nm-dimensional lattice over $\mathbb {Z}$.

If we want to generate a discrete Gaussian sample over $\mathbb {Z}[\mathrm{x}]/(\mathrm{x}^n+1)$, we can simply generate it over $\mathbb {Z}^n$ and then map into $\mathbb {Z}[\mathrm{x}]/(\mathrm{x}^n+1)$ using the obvious embedding of coordinates into coefficients of the polynomials. We will slightly abuse notation and write to mean that $\mathrm{y}$ is generated according to $D_{\mathbb {Z}^n,\mathrm{0},\sigma }$ and then interpreted as an element of R. Similarly, we write to mean that $\mathrm{z}$ is generated according to $D_{\mathbb {Z}^{ln},\mathrm{0},\sigma }$ and then gets interpreted as l polynomials $\mathrm{y}_i$.

2.5 Ring-LWE Encryption Scheme

We recall the Ring-LWE encryption scheme from [LPR13]. For simplicity, we take the distribution of the secret keys and the randomness to be uniformly-random elements with $\ell _\infty$ norm 1. The secret keys are chosen as and the public keys are and $\mathrm{t}\leftarrow \mathrm{a}\mathrm{s}_1+\mathrm{s}_2$. There is also a public parameter $p>2$, which is a positive integer. To encrypt a message $\mathrm{m}\in {R{_p}}$, the encryptor chooses and outputs $(\mathrm{v},\mathrm{w})$ where $\mathrm{v}\leftarrow p(\mathrm{a}\mathrm{r}+\mathrm{e})$ and $\mathrm{w}\leftarrow p(\mathrm{t}\mathrm{r}+\mathrm{e}')+\mathrm{m}$. The decryption procedure computes

$$\begin{aligned} \mathrm{w}-{\mathrm{v}\mathrm{s}{_1}}\,\mathrm{mod}\,q\,\mathrm{mod}\,p=p(\mathrm{r}\mathrm{s}_2+\mathrm{e}'-{\mathrm{e}\mathrm{s}{_1}})+\mathrm{m}\,\mathrm{mod}\,p=\mathrm{m}, \end{aligned}$$

(4)

where the last equality holds in the case that $\Vert p(\mathrm{r}\mathrm{s}_{2}+\mathrm{e}'-\mathrm{e}\mathrm{s}_1)+\mathrm{m}\Vert _\infty <q/2$.

From the above equations, we see that the encryption of a plaintext $\mathrm{m}$ under public keys $\mathrm{a},\mathrm{t}$ is a ciphertext $\mathrm{v},\mathrm{w}$ satisfying the equation

$$\begin{aligned} \begin{bmatrix}\mathrm{v}\\ \mathrm{w}\end{bmatrix}=\begin{bmatrix} p\mathrm{a}~|~p~|~\mathrm{0}~|~\mathrm{0}~\\ p\mathrm{t}~|~\mathrm{0}~|~p~|~\mathrm{1}~\\ \end{bmatrix} \begin{bmatrix} \mathrm{r}\\ \mathrm{e}\\ \mathrm{e}'\\ \mathrm{m}\end{bmatrix}\,\mathrm{mod}\,q, \end{aligned}$$

(5)

Extending this, the encryption of k messages $\mathrm{m}_1,\ldots ,\mathrm{m}_k$ under the same public key $\mathrm{a},\mathrm{t}$ satisfies the following relation:

(6)

which we will write in abbreviated form as

$$\begin{aligned} \begin{bmatrix} p\mathrm{a}\mathbf{I}_k&p\mathbf{I}_k&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k} \\ p\mathrm{t}\mathbf{I}_k&\mathrm{0}^{k\times k}&p\mathbf{I}_k&\mathbf{I}_k\\ \end{bmatrix} \begin{bmatrix} \mathbf{r}\\ \mathbf{e}\\ \mathbf{e'}\\ \mathbf{m} \end{bmatrix}= \begin{bmatrix} \mathbf{v}\\ \mathbf{w} \end{bmatrix} \,\mathrm{mod}\,q, \end{aligned}$$

(7)

where $\mathbf{I}_k$ corresponds to an identity matrix of dimension k and $\mathrm{0}^{\ell \times k}$ corresponds to an $\ell \times k$ matrix of all zeroes. The decryption procedure is then simply the vector analogy of (4), i.e.

$$\mathbf{m}=\mathbf{w}-\mathbf{v}\mathrm{s}_1\,\mathrm{mod}\,q\,\mathrm{mod}\,p.$$

2.6 “Fiat-Shamir with Aborts” Proofs of Knowledge of Linear Relations

In [Lyu09, Lyu12], Lyubashevsky introduced a technique for constructing practical digital signatures (in the random oracle model) based on the hardness of lattice problems. At the heart of the construction is a zero-knowledge proof of knowledge that, given an $\mathbf{s}\in R^k$ satisfying the relation

$$\begin{aligned} \mathbf{A}\mathbf{s}=\mathbf{t}\,\mathrm{mod}\,q, \end{aligned}$$

(8)

proves the knowledge of low-norm $\bar{\mathbf{s}}$ and $\bar{\mathrm{c}}$ that satisfy

$$\mathbf{A}\bar{\mathbf{s}}=\bar{\mathrm{c}}\mathbf{t}\,\mathrm{mod}\,q.$$

The idea in [Lyu09, Lyu12] was to construct a $\varSigma$-protocol with the main twist being that the prover does not always output the result. In particular, the protocols use rejection sampling to tailor the distribution so that it does not depend on the secret $\mathbf{s}$. This rejection sampling can be done by making the resulting distribution uniform in a box (as in [Lyu09]), or the more efficient approach in [Lyu12] of making it a discrete Gaussian. The interactive protocol is then converted to a non-interactive one in the random-oracle model [BR93] using the Fiat-Shamir technique [FS86]. This combined technique is sometimes referred to as “Fiat-Shamir with Aborts”.

A variation of the signing protocol from [Lyu12] is given in Algorithm 1. It was shown in that work that the output $\mathbf{z}$ is distributed according to $D_{R^k,0,\sigma }$. In particular, the rejection sampling stem on line 4 has the effect that the distribution of $\mathbf{z}$ is independent of the secret vector $\mathbf{s}$ (and the challenge $\mathrm{c}$). This algorithm is therefore honest-verifier zero knowledge since a simulator can simply output and program $\mathrm{c}=\mathsf {H}(\mathbf{A},\mathbf{t},\mathbf{A}\mathbf{z}-\mathbf{t}\mathrm{c}\,\mathrm{mod}\,\mathbf{q})$.³ We also make the observation that one does not need to use the same modulus q for every row of the relation in (8). One can instead use a different modulus for each row, and we represent this in the protocol by a vector $\mathbf{q}$ – having different moduli is crucial to the application in this paper.

We also need simulation soundness [Sah99], meaning that an adversary cannot create proofs of incorrect statements, even after seeing simulated proofs of incorrect statements. Faust et al. [FKMV12] showed that Fiat-Shamir proofs are simulation-sound if the underlying three-move protocol is honest-verifier zero-knowledge and has “quasi-unique responses”, meaning that an adversary cannot create two accepting transcripts that are different only in the response value. For our proof system, this translates into finding $\mathbf{z} \ne \mathbf{z'}$ such that $\mathbf{A}\mathbf{z} = \mathbf{A}\mathbf{z}'\,\mathrm{mod}\,q$ be hard. Finding such $\mathbf{z},\mathbf{z}'$ would imply that $\mathbf{A}(\mathbf{z}-\mathbf{z}')=0\,\mathrm{mod}\,q$ where $\mathbf{A}$ is the matrix in Eq. 7. Thus, there is either a non-zero tuple $(\mathrm{y}_1,\mathrm{y}_2)\in R_q$ with $l_\infty$ norm less than $12\sigma$ such that $\mathrm{a}\mathrm{y}_1+p\mathrm{y}_2=0\,\mathrm{mod}\,q$ or $p\mathrm{y}_1+\mathrm{y}_2=0\,\mathrm{mod}\,q$. In our applications $p>12\sigma$ and $12\sigma p+12\sigma <q$, which implies that the second equality is not possible. Also, for most of the parameter sets (see the table in Sect. 7), $(24\sigma )^2<q$, and therefore a standard probabilistic argument can be used to show that for all $\mathrm{y}_1,\mathrm{y}_2$ of norm less than $12\sigma$,

Thus for almost all $\mathrm{a}$, there will not be a short solution $(\mathrm{y}_1,\mathrm{y}_2)$ that satisfies $\mathrm{a}\mathrm{y}_1+p\mathrm{y}_2=0$.

If $(24\sigma )^2 > q$, then the probabilistic argument no longer applies, but then finding such $(\mathrm{y}_1,\mathrm{y}_2)$ gives a solution to Ring-SIS [LM06] problem for a random $\mathrm{a}$, which is a computationally hard problem when the norm of $\mathrm{y}_i$ is small-enough with relation to q (which it is in all applications).

3 One-Shot Verifiable Encryption for Linear Relations from Ring-LWE

We follow Camenisch and Shoup [CS03] in defining verifiable encryption as encrypting a witness for a member of a language. The class of languages that we’ll be looking at will be the linear relations of short vectors in a ring. While Camenisch and Shoup defined soundness by requiring that decryption of a valid ciphertext always recovers a valid witness, we will only achieve a relaxed property that recovers a witness for a related “extended” language that includes the original language. As we will see in Sect. 6, however, this weaker property suffices for many practical applications of verifiable encryption.

3.1 Definition of Relaxed Verifiable Encryption

We relax Camenisch and Shoup’s [CS03] definitions for verifiable encryption in two ways. First, as mentioned above, and analogous to relaxed knowledge extraction for proofs of knowledge [CKY09], the encryption algorithm encrypts a witness w for a member x of a language $L$, but soundness only guarantees that decryption of a valid ciphertext returns a witness $\bar{w}$ of an extented language $\bar{L}$ instead of $L$. Second, rather than looking at verifiable encryption as a combination of a standard public-key encryption scheme with an associated proof system, we consider encryption and proof as a single algorithm, producing a verifiable ciphertext that includes the proof. This generalization allows for more efficient schemes, in particular our construction that speeds up decryption using information from the proof.

Let $L\subseteq \{0,1\}^*$ be a language with witness relation $R_L$, i.e., $x \in L$ iff there exists a witness w such that $(x,w) \in R_L$. Let $\bar{L}$ with witness relation $R_{\bar{L}}$ be an extension of $L$, meaning that $L\subseteq \bar{L}$ and $R_L\subseteq R_{\bar{L}}$. For our language of linear relations over short vectors, we will consider the language $L$ with relation

$$ R_L= \{((\mathbf{B},\mathbf{u}), (\mathbf{m},1)) \in (R_p^{\ell \times k} \times R_p^\ell ) \times (R_p^k \times R_p) \;:\; \mathbf{B}\mathbf{m} = \mathbf{u} \,\mathrm{mod}\,p \;\wedge \mathbf{m} \in S_\gamma ^k \} $$

and the extended language $\bar{L}$ with relation

where $\bar{\mathcal {C}} = \{\mathrm{c}-\mathrm{c}' \;:\; \mathrm{c},\mathrm{c}' \in \mathcal {C}\}$ for $\mathcal {C}=\{\mathrm{c}\in R: \Vert \mathrm{c}\Vert _\infty =1, \Vert \mathrm{c}\Vert _1\le 36\}$ and other parameters are described in Algorithm 3.

A relaxed verifiable encryption scheme for languages $L,\bar{L}$ is a tuple of algorithms $(\mathsf {Kg}, \mathsf {Enc}, \mathsf {V}, \mathsf {Dec})$ where the key generation algorithm $\mathsf {Kg}(1^ \lambda )$ returns a public and secret key $( pk , sk )$; the encryption algorithm $\mathsf {Enc}( pk ,x,w)$ returns a verifiable ciphertext $t$ that encrypts the witness w of language member $x \in L$; the verification algorithm $\mathsf {V}( pk , x, t )$ returns 1 or 0 indicating whether $t$ encrypts a witness for x; the decryption algorithm $\mathsf {Dec}( sk , x, t )$ returns a witness $\bar{w}$ or a failure symbol $\bot$. We will focus on the case where the ciphertext $t$ includes a Fiat-Shamir proof of a $\varSigma$-protocol, where the proof $\pi = ( cmt , c , rsp )$ consists of a commitment $cmt$, a challenge $c = \mathsf {H}( pk , x, t , cmt , \ldots )$ generated through a random oracle $\mathsf {H}$, and a response $rsp$. We require that the algorithms satisfy the following adapted properties from [CS03]:  

Correctness.:

Correctness requires that $\mathsf {Dec}( sk ,x,\mathsf {Enc}( pk ,x,w))=w$ with probability one for all $(x,w) \in R_L$ and all key pairs .

Completeness.:

For all $(x,w) \in R_L$ and all key pairs , $\mathsf {V}( pk ,x,\mathsf {Enc}( pk ,x,w))=1$ with probability one.

Soundness.:

Soundness requires that a ciphertext with a valid proof for $x \in L$ can with overwhelming probability be decrypted to a valid witness $\bar{w}$ such that $(x,\bar{w}) \in R_{\bar{L}}$, i.e., the following probability is negligible:

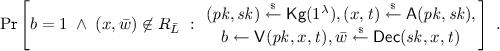
Simulatability.:

There exists a simulator $\mathsf {Sim}$ such that no adversary $\mathsf {A}$ can distinguish real from simulated ciphertexts, i.e., the following advantage of $\mathsf {A}$ is negligible:

 

3.2 Construction

Given a linear relation

$$\begin{aligned} \mathbf{B}\mathbf{m}=\mathbf{u}\,\mathrm{mod}\,p, \end{aligned}$$

(9)

for a matrix $\mathbf{B}\in R_p^{\ell \times k}$, our goal is to produce a ciphertext and a proof that the decryption of this ciphertext is $(\overline{\mathbf{m}},\overline{\mathrm{c}})$ that satisfies the relation

$$\begin{aligned} \mathbf{B}\overline{\mathbf{m}}=\mathbf{u}\overline{\mathrm{c}}\,\mathrm{mod}\,p. \end{aligned}$$

(10)

Key generation. Key pairs are generated as for the Ring-LWE encryption scheme from Sect. 2.5, i.e., by choosing and computing and $\mathrm{t}\leftarrow \mathrm{a}\mathrm{s}_1+\mathrm{s}_2$. The public key is $pk = (\mathrm{a},\mathrm{t},p,q)$, where p is the same value as the modulus that we are proving our linear relation over. The secret key is $sk =\mathrm{s}_1$.

Encryption and verification. The prover encrypts a witness $w = \mathbf{m}$ for language member $x = (\mathbf{B},\mathbf{u})$ satisfying (9) with randomness as in (7). The prover then concatenates this with (9) to form the relation below:

$$\begin{aligned} \begin{bmatrix} p\mathrm{a}\mathbf{I}_k&p\mathbf{I}_k&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k} \\ p\mathrm{t}\mathbf{I}_k&\mathrm{0}^{k\times k}&p\mathbf{I}_k&\mathbf{I}_k\\ \mathrm{0}^{\ell \times k}&\mathrm{0}^{\ell \times k}&\mathrm{0}^{\ell \times k}&\mathbf{B}\end{bmatrix}\begin{bmatrix} \mathbf{r}\\ \mathbf{e}\\ \mathbf{e'}\\ \mathbf{m} \end{bmatrix}= \begin{bmatrix} \mathbf{v}\\ \mathbf{w}\\ \mathbf{u} \end{bmatrix} \begin{matrix} \,\mathrm{mod}\,q\\ \,\mathrm{mod}\,q\\ \,\mathrm{mod}\,p \end{matrix} \end{aligned}$$

(11)

As discussed, there is no practical proof of knowledge for the above relation, and so the prover instead uses the “Fiat-Shamir with Aborts” approach from Sect. 2.6 to construct a proof of knowledge $\pi$ of low-weight $\overline{\mathbf{r}},\overline{\mathbf{e}},\overline{\mathbf{e}}',\overline{\mathbf{m}},$ and $\overline{\mathrm{c}}$ that satisfy

$$\begin{aligned} \begin{bmatrix} p\mathrm{a}\mathbf{I}_k&p\mathbf{I}_k&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k} \\ p\mathrm{t}\mathbf{I}_k&\mathrm{0}^{k\times k}&p\mathbf{I}_k&\mathbf{I}_k\\ \mathrm{0}^{\ell \times k}&\mathrm{0}^{\ell \times k}&\mathrm{0}^{\ell \times k}&\mathbf{B}\end{bmatrix}\begin{bmatrix} \overline{\mathbf{r}}\\ \overline{\mathbf{e}}\\ \overline{\mathbf{e}}'\\ \overline{\mathbf{m}} \end{bmatrix}= \overline{\mathrm{c}} \begin{bmatrix} \mathbf{v}\\ \mathbf{w}\\ \mathbf{u} \end{bmatrix} \begin{matrix} \,\mathrm{mod}\,q\\ \,\mathrm{mod}\,q\\ \,\mathrm{mod}\,p \end{matrix} \end{aligned}$$

(12)

This procedure and the corresponding verification is presented in Algorithms 3 and 4.

Decryption. The main result of our work is showing that, when given the ciphertext $t = (\mathbf{v},\mathbf{w},\mathrm{c},\mathbf{z})$, the decryptor can recover some $(\overline{\mathbf{m}}, \overline{\mathrm{c}})$ that satisfies (10). Because the proof of knowledge $(\mathrm{c},\mathbf{z})$ does not imply that $\begin{bmatrix} \mathbf{v}\\ \mathbf{w}\end{bmatrix}$ is a valid Ring-LWE ciphertext, we cannot simply use the Ring-LWE decryption algorithm from (4).

Instead, the intuition is to guess a value for $\overline{\mathrm{c}}$ and then attempt to decrypt the ciphertext $\overline{\mathrm{c}}\begin{bmatrix} \mathbf{v}\\ \mathbf{w}\end{bmatrix} \,\mathrm{mod}\,q$ in hopes of recovering $\overline{\mathbf{m}}$. The problem with this straightforward approach is that the decryption algorithm will always return something, and so one needs a way to decide whether this decryption is something valid or just garbage. In Lemma 3.1, we show that if the parameters of the Ring-LWE encryption scheme are set in a particular way, then the decryptor can test whether a particular ciphertext $\overline{\mathrm{c}}\begin{bmatrix} \mathbf{v}\\ \mathbf{w}\end{bmatrix} \,\mathrm{mod}\,q$ is “valid”, and for any $\overline{\mathrm{c}}$ and $\overline{\mathrm{c}}'$ that lead to valid ciphertexts decrypting to $\overline{\mathbf{m}}$ and $\overline{\mathbf{m}}'$, respectively, we have the equality

$$\begin{aligned} \overline{\mathbf{m}}/\overline{\mathrm{c}} = \overline{\mathbf{m}}'/\overline{\mathrm{c}}'\,\mathrm{mod}\,p \end{aligned}$$

(13)

The implication of the above equation is that once the decryptor decrypts some pair $(\overline{\mathbf{m}}',\overline{\mathrm{c}}')$, it is a valid solution to (10). This is because the proof of knowledge $\pi$ proves knowledge of some $(\overline{\mathbf{m}},\overline{\mathrm{c}})$ that satisfies $\mathbf{B}\overline{\mathbf{m}}=\overline{\mathrm{c}}\mathbf{u}\,\mathrm{mod}\,p$, or equivalently $\mathbf{B}\overline{\mathbf{\mathrm{m}}}/\overline{\mathrm{c}}=\mathbf{u}\,\mathrm{mod}\,p$. Equation (13) then implies that

$$\mathbf{B}\overline{\mathbf{m}}'=\overline{\mathrm{c}}'\mathbf{u}\,\mathrm{mod}\,p.$$

The second issue is how to find a valid $\overline{\mathrm{c}}$. In particular, if we would like the proof of knowledge to be “one-shot”, then the challenge space should be exponentially large, and so it is impractical to simply try all the possible $\overline{\mathrm{c}}$ (of which there are actually even more than in the challenge space). We show in Lemma 3.2, however, that the decryptor can try random $\overline{\mathrm{c}}$ (there is some relation between $\pi$ and which $\bar{\mathrm{c}}$ should be tried), and then the expected number of tries is essentially the number of random oracle queries that the prover makes when constructing $\pi$, where the probability is taken over the randomness of the random oracle (modeled as a random function) and the coins of the decryptor. Algorithm 5 is the decryption algorithm that guesses a random $\mathrm{c}'$ from $\mathcal {C}$, constructs $\overline{\mathrm{c}}=\mathrm{c}-\mathrm{c}'$, where $\mathrm{c}$ is part of the proof $\pi$, and then checks whether $\overline{\mathrm{c}}\begin{bmatrix} \mathbf{v}\\ \mathbf{w}\end{bmatrix} \,\mathrm{mod}\,q$ is a valid ciphertext (actually k valid ciphertexts because the plaintext $\mathbf{m}$ is encrypted as k independent plaintexts). If it is, then it decrypts it, and otherwise it guesses a new random $\mathrm{c}'$.

If the prover is honest, then of course $\begin{bmatrix}\mathbf{v}\\ \mathbf{w}\end{bmatrix}$ will already be a valid ciphertext, and then it’s not hard to see that any $\overline{\mathrm{c}}$ will result in a valid decryption (or the decryptor can try $\overline{\mathrm{c}}=1$ first). On the other hand, what Lemma 3.2 roughly implies is that if the prover can only query the random oracle a few times, then the decryptor will also expect to recover a solution to (10) within a few queries.

In Sect. 4, we propose a modification to our protocol that still retains the relation between the number of random-oracle queries the prover makes and the expected number of decryption tries that the decryptor needs, but also puts an upper-bound on the decryption time. The idea is to reduce the space of challenges in the zero-knowledge proof from, say, $2^{128}$ down to $2^{32}$ and then doing the proof in parallel 4 times. This increases the proof size by a factor of 4, but upperbounds the number of decryptions tries to $4\cdot 2^{32}$. One can of course adjust the trade-off between the decryption-time upper bound and the size of the proof to suit the particular scenario. This is the main advantage of this parallelized protocol over the earlier idea in [BCK+14]. In the latter scheme, the size of the challenge space could not be varied – if one were working over the ring $\mathbb {Z}[\mathrm{x}]/(\mathrm{x}^n+1)$, then the challenge space was exactly $2n+1$.

3.3 Interlude: Proofs of Plaintext Knowledge

One can see proofs of plaintext knowledge as a verifiable encryption scheme without a relation, or where the relation is trivially satisfied. In our case, one could consider the scheme from the previous section with $\mathbf{B}$ and $\mathbf{u}$ being 0, or simply the row(s) containing $\mathbf{B}$ and $\mathbf{u}$ not being present in relation (11).

The soundness requirement that a valid ciphertext must decrypt to a valid witness obviously makes no sense if the relation is trivial. Instead, soundness for a proof of plaintext knowledge requires that decryption returns the same value as can be extracted from the proof of knowledge. Our randomized decryption algorithm as described in Algorithm 5 does not satisfy such a requirement, as it potentially returns a different pair $(\overline{\mathbf{m}},\overline{\mathrm{c}})$ at each execution. However, because of the property that $\overline{\mathbf{m}}/\overline{\mathrm{c}} = \overline{\mathbf{m}}'/\overline{\mathrm{c}}' \,\mathrm{mod}\,p$ for any $(\overline{\mathbf{m}},\overline{\mathrm{c}}), (\overline{\mathbf{m}}',\overline{\mathrm{c}}')$ returned by the decryption algorithm, we can make the decryption deterministic by letting it return $\overline{\mathbf{m}}/\overline{\mathrm{c}} \,\mathrm{mod}\,p$. Because this unique value can also be extracted from the proof, this turns our verifiable encryption scheme into a proof of plaintext knowledge.

3.4 Correctness and Security

Soundness. We first show the soundness property of our relaxed verifiable encryption scheme by showing that decryption of a valid ciphertext, if it finishes, yields a witness from $R_{\bar{L}}$. In Sect. 3.5, we prove that the expected running time of the decryption algorithm is proportional to the number of random-oracle queries made by the adversary who created the ciphertext.

If an adversary $\mathcal {A}$ who is trying to break the soundness of the scheme outputs a ciphertext $t = (\mathbf{v}, \mathbf{w}, \mathrm{c}, \mathbf{z})$ that is valid for $x = (\mathbf{B},\mathbf{u})$, then by the verification procedure described in Algorithm 4 we have that $\Vert \mathbf{z}\Vert _\infty \le 6\cdot \sigma$ and

$$\begin{aligned} \mathrm{c}= \mathsf {H}\left( \mathbf{B}', \begin{bmatrix} \mathbf{v}\\ \mathbf{w}\\ \mathbf{u} \end{bmatrix},\mathbf{B}' \mathbf{z}-\mathrm{c}\begin{bmatrix}\mathbf{v}\\ \mathbf{w} \\ \mathbf{u}\end{bmatrix} \begin{matrix} \,\mathrm{mod}\,q\\ \,\mathrm{mod}\,q\\ \,\mathrm{mod}\,p \end{matrix} \right) ~ \end{aligned}$$

(14)

where

$$\begin{aligned} \mathbf{B}'=\begin{bmatrix} p\mathrm{a}\mathbf{I}_k&p\mathbf{I}_k&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k} \\ p\mathrm{t}\mathbf{I}_k&\mathrm{0}^{k\times k}&p\mathbf{I}_k&\mathbf{I}_k\\ \mathrm{0}^{\ell \times k}&\mathrm{0}^{\ell \times k}&\mathrm{0}^{\ell \times k}&\mathbf{B}\end{bmatrix}. \end{aligned}$$

(15)

Let $\mathbf{A}$ denote the first argument of the above random-oracle query and $\mathbf{y}$ the last, i.e., the above equation can be rewritten as $\mathrm{c}= \mathsf {H}(\mathbf{A}, [\; \mathbf{v} \;;\; \mathbf{w} \;;\; \mathbf{u} \;] , \mathbf{y})$.

With overwhelming probability, there exists a second challenge $\mathrm{c}' \in \mathcal {C}\setminus \{\mathrm{c}\}$ for which there exists a vector $\mathbf{z'}$ with $\Vert \mathbf{z'}\Vert _\infty \le 6\cdot \sigma$ and $\mathbf{y} = \mathbf{A}\mathbf{z'} - \mathrm{c}' [\; \mathbf{v} \;;\; \mathbf{w} \;;\; \mathbf{u} \;]$. Indeed, if $\mathrm{c}$ were the only such challenge, then at the moment of making the above random-oracle query, $\mathsf {A}$ would have had probability $1/|\mathcal {C}|$ of hitting the only challenge $\mathrm{c}$ for which a valid proof exists. The probability that $\mathsf {A}$ outputs a proof for which only one such challenge $\mathrm{c}$ exists is therefore at most ${ q _\mathsf {H}}/|\mathcal {C}|$.

So with overwhelming probability such $\mathrm{c}',\mathbf{z'}$ does exist, and we have that $\mathbf{y} = \mathbf{A}\mathbf{z} - \mathrm{c}[\; \mathbf{v} \;;\; \mathbf{w} \;;\; \mathbf{u} \;] = \mathbf{A}\mathbf{z'} - \mathrm{c}' [\; \mathbf{v} \;;\; \mathbf{w} \;;\; \mathbf{u} \;]$ with $\Vert \mathbf{z}\Vert _\infty \le 6\cdot \sigma$ and $\Vert \mathbf{z'}\Vert _\infty \le 6\cdot \sigma$. Hence, letting $\bar{\mathrm{c}} = \mathrm{c}-\mathrm{c}'$ and $\mathbf{\bar{z}} = \mathbf{z'} - \mathbf{z} = [~\bar{\mathbf{r}}~;~\bar{\mathbf{e}}~;~\bar{\mathbf{e}}'~;~\bar{\mathbf{m}}\;]$, we have that $\mathbf{A}\mathbf{\bar{z}} = \bar{\mathrm{c}} [\; \mathbf{v} \;;\; \mathbf{w} \;;\; \mathbf{u} \;]$ with $\Vert \mathbf{\bar{z}}\Vert _\infty \le 12\cdot \sigma$.

By choosing the scheme parameters appropriately, e.g., such that $(36 p + 12) \sigma < q/2C$, one can satisfy the preconditions of the following crucial lemma that shows that for any $(\mathbf{\bar{m}}',\bar{\mathrm{c}}')$ returned by the decryption algorithm, we have that $\mathbf{\bar{m}}'/\bar{\mathrm{c}}' = \mathbf{\bar{m}}/\bar{\mathrm{c}}$, and, because $\mathbf{B}\mathbf{\bar{m}} = \bar{\mathrm{c}} \mathbf{u}$, that $\mathbf{B}\mathbf{\bar{m}}' = \bar{\mathrm{c}}' \mathbf{u}$.

Lemma 3.1

Let $(\mathrm{a},\mathrm{t},p,q)$ and $(\mathrm{s}_1,\mathrm{s}_2)$ be generated keys as in Sect. 3.2. If for given $\mathrm{v},\mathrm{w}\in R_q$ there exist $\overline{\mathrm{r}},\overline{\mathrm{e}},\overline{\mathrm{e}}',\overline{\mathrm{m}},\overline{\mathrm{c}}$ such that

$$\begin{bmatrix} p\mathrm{a}~|~p~|~\mathrm{0}~|~\mathrm{0}~\\ p\mathrm{t}~|~\mathrm{0}~|~p~|~\mathrm{1}~\\ \end{bmatrix} \begin{bmatrix} \overline{\mathrm{r}}\\ \overline{\mathrm{e}}\\ \overline{\mathrm{e}}'\\ \overline{\mathrm{m}} \end{bmatrix}=\overline{\mathrm{c}}\begin{bmatrix}\mathrm{v}\\ \mathrm{w}\end{bmatrix}\,\mathrm{mod}\,q$$

and

$$\begin{aligned} \Vert p(\overline{\mathrm{r}}\mathrm{s}_2+\overline{\mathrm{e}}'-\overline{\mathrm{e}}\mathrm{s}_1)+\overline{\mathrm{m}}\Vert _\infty <q /2C \end{aligned}$$

(16)

where $C=\max \limits _{\overline{\mathrm{c}}\in \overline{\mathcal {C}}}\Vert \overline{\mathrm{c}}\Vert _1=\max \limits _{\mathrm{c},\mathrm{c}'\in \mathcal {C}}\Vert \mathrm{c}-\mathrm{c}'\Vert _1$, then

• 1. $\Vert (\mathrm{w}-\mathrm{v}\mathrm{s}_1)\overline{\mathrm{c}}\,\mathrm{mod}\,q\Vert _\infty <q/2C$

• 2. For any $\overline{\mathrm{c}}'\in \overline{\mathcal {C}}$ for which $\Vert (\mathrm{w}-\mathrm{v}\mathrm{s}_1)\overline{\mathrm{c}}'\,\mathrm{mod}\,q\Vert _\infty <q/2C$,

  $$(\mathrm{w}-\mathrm{v}\mathrm{s}_1)\overline{\mathrm{c}}'\,\mathrm{mod}\,q/\overline{\mathrm{c}}'\,\mathrm{mod}\,p= \overline{\mathrm{m}}/\overline{\mathrm{c}}\,\mathrm{mod}\,p.$$

   $\square$

Proof

To prove the first part, we note that by the definition of Ring-LWE decryption,

$$(\mathrm{w}-\mathrm{v}\mathrm{s}_1)\overline{\mathrm{c}}\,\mathrm{mod}\,q = p(\overline{\mathrm{r}}\mathrm{s}_2+\overline{\mathrm{e}}'-\overline{\mathrm{e}}\mathrm{s}_1)+\overline{\mathrm{m}},$$

which has $\ell _\infty$ length less than ${\frac{q}{2C}}$ by the hypothesis of the lemma.

To prove the second part, we first note that

$$\begin{aligned} (\mathrm{w}-\mathrm{v}\mathrm{s}_1)\overline{\mathrm{c}}\overline{\mathrm{c}}'\,\mathrm{mod}\,q \bmod p= & {} (p(\overline{\mathrm{r}}\mathrm{s}_2+\overline{\mathrm{e}}'-\overline{\mathrm{e}}\mathrm{s}_1)+\overline{\mathrm{m}})\overline{\mathrm{c}}'\,\mathrm{mod}\,q\bmod p \nonumber \\= & {} \overline{\mathrm{m}}\overline{\mathrm{c}}'\,\mathrm{mod}\,p. \end{aligned}$$

(17)

Then we can write

$$\begin{aligned} ((\mathrm{w}-\mathrm{v}\mathrm{s}_1)\overline{\mathrm{c}}'\,\mathrm{mod}\,q)\,/\, \overline{\mathrm{c}}'\,\mathrm{mod}\,p&= ((\mathrm{w}-\mathrm{v}\mathrm{s}_1)\overline{\mathrm{c}}'\,\mathrm{mod}\,q) \cdot \overline{\mathrm{c}} / (\overline{\mathrm{c}}\overline{\mathrm{c}}') \,\mathrm{mod}\,p \\&=((\mathrm{w}-\mathrm{v}\mathrm{s}_1)\overline{\mathrm{c}}\overline{\mathrm{c}}'\,\mathrm{mod}\,q) /(\overline{\mathrm{c}}\overline{\mathrm{c}}')\,\mathrm{mod}\,p\\&=\overline{\mathrm{m}}\overline{\mathrm{c}}'/(\overline{\mathrm{c}}\overline{\mathrm{c}}')\,\mathrm{mod}\,p = \overline{\mathrm{m}}/\overline{\mathrm{c}}\,\mathrm{mod}\,p \end{aligned}$$

The first equality is an identity, the second equality holds since $\Vert (\mathrm{w}-\mathrm{v}\mathrm{s}_1)\overline{\mathrm{c}}'\,\mathrm{mod}\,q\Vert _\infty <{\frac{q}{2C}}$ and therefore multiplication by $\overline{\mathrm{c}}$ does not cause a reduction modulo q. The third equality follows from (17).    $\square$

By checking that $\Vert (\mathrm{w}-\mathrm{v}\mathrm{s}_1)\overline{\mathrm{c}}\,\mathrm{mod}\,q\Vert _\infty <q/2C$ in line 6 of the $\mathsf {Dec}$ algorithm, we ensure that the condition of the second part of Lemma 3.1 is satisfied for decryption, so that the value $(\bar{\mathbf{m}}' (\mathbf{w} - \mathbf{v}\mathrm{s}_1)\overline{\mathrm{c}}'\,\mathrm{mod}\,q\bmod p, \overline{\mathrm{c}}')$ is indeed a witness for $(\mathbf{B},\mathbf{u}) \in \bar{L}$. This proves the soundness of our scheme.

Correctness. Correctness is straightforward because a valid encryption (see (5)) satisfies the preconditions of Lemma 3.1 with $[\;\bar{\mathbf{r}} \;;\; \bar{\mathbf{e}} \;;\; \bar{\mathbf{e}}' \;;\; \bar{\mathbf{m}}\;] = [\; \mathbf{r} \;;\; \mathbf{e} \;;\; \mathbf{e}' \;;\; \mathbf{m}\;]$ and $\bar{\mathrm{c}}=1$; and it’s clear that $\Vert p(\mathbf{r}\mathrm{s}_2+\mathbf{e}'-\mathbf{e}\mathrm{s}_1)+\mathbf{m} \Vert _\infty \le \Vert p(\bar{\mathbf{r}}\mathrm{s}_2+\bar{\mathbf{e}}'-\bar{\mathbf{e}} \mathrm{s}_1)+\bar{\mathbf{m}}\Vert _\infty$.

Completeness. Completeness follows from the completeness of the proof system of Sect. 2.6.

Simulatability. The simulator $\mathsf {Sim}$ creates a Ring-LWE encryption $[\;\mathbf{v} \;;\; \mathbf{w} \;]$ of $\mathbf{m}=1$ using the scheme of Sect. 2.5 and runs the zero-knowledge simulator for the proof system of Sect. 2.6 to create a valid-looking proof $(\mathrm{c},\mathbf{z})$ for $(\mathbf{B},\mathbf{u})$. The indistinguishability from the real proof follows from the IND-CPA security of Ring-LWE encryption and the zero-knowledge property of the proof system.

3.5 Decryption Running Time

Even though the running time of the decryption algorithm is unbounded in principle, we show that its expected running time is proportional to the number of times that the adversary queries the random oracle. More precisely, we show that if an adversary uses ${ q _\mathsf {H}}$ random-oracle queries to construct a ciphertext, then the probability that the decryption algorithm requires more than $\alpha \cdot { q _\mathsf {H}}$ iterations is less than $1/\alpha$.

We prove the above information-theoretic statement for any adversary $\mathcal {A}$, and we can therefore limit the analysis to deterministic adversaries, since the coins that maximize the adversary’s success can always be hardwired into its code.

Lemma 3.2

For a given key pair $( pk , sk ) \in \mathsf {Kg}(1^ \lambda )$, consider the following experiment with an adversary $\mathcal {A}$:

Let $\widehat{H}$ be the random coins of the function $\mathsf {H}$ (when it is modeled as a random function) and $\widehat{D}$ be the random coins of the Decryption algorithm $\mathsf {Dec}$. Let T be the number of loop iterations in the execution of $\mathsf {Dec}$ (see Algorithm 5 lines 2–10) until it produces its output $\bar{w}$. Then there is an event G, such that for all algorithms $\mathcal {A}$ that make at most $q_\mathsf {H}-1$ queries to $\mathsf {H}$, all key pairs $( pk , sk )$, and any positive integer f, it holds that

• 1. $\mathop {\mathrm {Exp}}_{{\widehat{H}},{\widehat{D}}}[~T~|~G~]\le \left( 1+{\frac{1}{f}}\right) \cdot q_\mathsf {H}.$

• 2. $\Pr _{{\widehat{H}},{\widehat{D}}}[\lnot G]\le q_\mathsf {H}\cdot f/|\mathcal {C}|$

By Markov’s inequality and optimization over f, this implies that for any positive $\alpha$,

Proof

For a given public key $pk$, language member $x = (\mathbf{B},\mathbf{u})$, and valid ciphertext $t = (\mathbf{v},\mathbf{w}, \mathrm{c}, \mathbf{z})$, let $\mathbf{A}$ and $\mathbf{y}$ be the matrix and vector in the verification algorithm (Algorithm 4) so that $c = \mathsf {H}(\mathbf{A}, [\; \mathbf{v} \;;\; \mathbf{w} \;;\; \mathbf{u}\;], \mathbf{y})$ and $\mathbf{y} = \mathbf{A}\mathbf{z} - \mathrm{c}[\; \mathbf{v} \;;\; \mathbf{w} \;;\; \mathbf{u}\;]$. Let $\mathcal {G}_{ t }$ be the set of “good” challenges $\mathrm{c}'$ for which a valid zero-knowledge proof response $\mathbf{z}'$ exists, i.e.,

$$ \mathcal {G}_{ t } \;=\; \{\mathrm{c}' \in \mathcal {C}\;:\; \exists \; \mathbf{z}' : \mathbf{y} = \mathbf{A}\mathbf{z}' - \mathrm{c}' [\; \mathbf{v} \;;\; \mathbf{w} \;;\; \mathbf{u} \;] \wedge \Vert \mathbf{z}'\Vert _\infty \le 6 \sigma \}~. $$

Let G be the “good” event that the adversary $\mathcal {A}$ produces a ciphertext $t$ (for the decryption algorithm) with $|\mathcal {G}_ t | > f$. Let $\widehat{D}$ denote the coins of the decryption algorithm $\mathsf {Dec}$ and let $\widehat{H}$ denote the coins determining the random oracle $\mathsf {H}$. For any ciphertext t, the probability over $\widehat{D}$ that one particular iteration of $\mathsf {Dec}$ decrypts successfully, i.e., hits a good challenge $c' \in \mathcal {G}_{ t } \setminus \{c\}$, is ${\frac{|\mathcal {G}_ t |-1}{|\mathcal {C}|}}.$ We therefore have that the expected number of iterations for a ciphertext $t$ is

$$ \mathop {\mathrm {Exp}}_{\widehat{D}}[~T~|~ \mathcal {A}^\mathsf {H}\text { outputs } t~]={\frac{|\mathcal {C}|}{|\mathcal {G}_ t |-1}} $$

and therefore, conditioned on the event G, that

$$\begin{aligned} \mathop {\mathrm {Exp}}_{\widehat{D}}[~T~|~ \mathcal {A}^\mathsf {H}\text { outputs } t \;\wedge \; G~] \le {\frac{|\mathcal {C}|}{f}}~. \end{aligned}$$

(18)

Below, when we say that “$\mathcal {A}^\mathsf {H}$ outputs $t _i$”, we mean that $\mathcal {A}^\mathsf {H}$ outputs a language member $x = (\mathbf{B}, \mathbf{u})$ and a ciphertext $t = (\mathbf{v}, \mathbf{w}, \mathrm{c}, \mathbf{z})$ such that $\mathcal {A}$’s i-th random-oracle query is

$$ \mathrm{c}= \mathsf {H}\left( \mathbf{B}', \begin{bmatrix} \mathbf{v}\\ \mathbf{w}\\ \mathbf{u} \end{bmatrix},\mathbf{B}' \mathbf{z}-\mathrm{c}\begin{bmatrix}\mathbf{v}\\ \mathbf{w} \\ \mathbf{u}\end{bmatrix} \begin{matrix} \,\mathrm{mod}\,q\\ \,\mathrm{mod}\,q\\ \,\mathrm{mod}\,p \end{matrix} \right) ~, $$

where $\mathbf{B}'$ is the matrix defined in (15). Also, for any adversary making at most ${ q _\mathsf {H}}-1$ queries, there exists an adversary making at most ${ q _\mathsf {H}}$ queries that include the above query; we consider the latter adversary $\mathcal {A}$ in the rest of the analysis.

Because we are conditioning on the event G, we can assume without loss of generality that $\mathcal {A}$ only makes random-oracle queries for ciphertexts $t _i$ with $|\mathcal {G}_{ t _i}|> f$. (It is easy to see that for any $\mathcal {A}$ that does not obey these rules, there exists an adversary $\mathcal {A}'$ producing the same output that does.) We now have that

$$\begin{aligned} \mathop {\mathrm {Exp}}_{\widehat{H},\widehat{D}}[~T~|~G~] = \sum _{i=1}^{q_\mathsf {H}} \Pr _{\widehat{H}}[\mathcal {A}^\mathsf {H}\text { outputs } t _i ~|~ G~] \cdot \mathop {\mathrm {Exp}}_{\widehat{D}}[~T~|~ \mathcal {A}^\mathsf {H}\text { outputs } t _i\;\wedge \; G~] \end{aligned}$$

(19)

The above is true because

$$\begin{aligned} \sum _{i=1}^{q_\mathsf {H}}&\Pr _{\widehat{H}}[\mathcal {A}^\mathsf {H}\text { outputs } t _i ~|~ G~] \cdot \mathop {\mathrm {Exp}}_{\widehat{D}}[~T~|~ \mathcal {A}^\mathsf {H}\text { outputs } t _i\;\wedge \; G~]\\&=\sum _{i=1}^{q_\mathsf {H}} \Pr _{\widehat{H}}[\mathcal {A}^\mathsf {H}\text { outputs } t _i ~|~ G~] \cdot \sum _{j\in \mathbb {Z}^+}\Pr _{\widehat{D}}[~T=j~|~\mathcal {A}^\mathsf {H}\text { outputs } t _i\;\wedge \; G~]\cdot j\\&=\sum _{j\in \mathbb {Z}^+}j \cdot \sum _{i=1}^{q_\mathsf {H}}\Pr _{\widehat{H},\widehat{D}}[~T=j~ \wedge \mathcal {A}^\mathsf {H}\text { outputs } t _i~|~G~]\\&=\sum _{j\in \mathbb {Z}^+}j\cdot \Pr _{\widehat{D},\widehat{H}}[~T=j~|~G~]\\&=\mathop {\mathrm {Exp}}_{\widehat{H},\widehat{D}}[~T~|~G~] \end{aligned}$$

For each random-oracle query that $\mathcal {A}$ makes for a ciphertext $t _i$ (all the ciphertexts need not be distinct), the probability that $\mathcal {A}$ can output $t _i$ (over the randomness $\widehat{H}$) is at most the probability that the output of the random-oracle query is in $\mathcal {G}_{ t _i}$, because otherwise no valid response $\mathbf{z}$ exists. Thus each $t _i$ has the probability of being output at most $|\mathcal {G}_{ t _i}|/|\mathcal {C}|$, regardless of the strategy of the adversary. Plugging this and (18) into (19), we obtain

(20)

By applying Markov’s inequality, we have that for any positive $\beta$,

(21)

It is furthermore easy to see that

Plugging this and (20) into (21) and letting $\beta = \alpha \cdot q_\mathsf {H}$ yields

To minimize this expression, we set $f=\left\lceil \sqrt{\frac{|\mathcal {C}|}{\alpha q{_\mathsf {H}}}}\right\rceil$, which gives us the claim in the Lemma.    $\square$

4 Multi-shot Verifiable Encryption – Construction with a Bounded Decryption Time

If one would like to put a limit on how much computational time decryption takes in the worst case, then the idea is to reduce the size of the challenge space and repeat the proof-of-knowledge protocol from Algorithm 3 in parallel $\alpha$ times using the standard approach. This protocol is described in Algorithm 6. The verification procedure simply checks if all the $\alpha$ copies are verified correctly.

One can show that with probability approximately $1-|\mathcal {C}|^{-\alpha }$, there will be at least one $\overline{\mathrm{c}}$ for which $\overline{\mathrm{c}}\begin{bmatrix} \mathbf{v} \\ \mathbf{w}\end{bmatrix}$ is a valid ciphertext satisfying Lemma 3.1, and so one simply needs to find it (and check its validity) analogously to the way $\overline{\mathrm{c}}\begin{bmatrix} \mathbf{v} \\ \mathbf{w}\end{bmatrix}$ was found in Algorithm 5. The main difference is that the challenge space is no longer exponentially large, and so one can search through all the $\overline{\mathrm{c}}=\mathrm{c}^{(i)}-\mathrm{c}'$ in time $\alpha \cdot |\mathcal {C}|$. This procedure is described in Algorithm 8. If one wants to also maintain the relationship between the number of random oracle queries of the prover to the number of decryption tries, one could “dovetail” between Algorithm 8 which systematically goes through all $\mathrm{c}' \in \mathcal {C}$ with one that randomly guesses them at random.

The trade-off between having the decryption running time be upper-bounded by $\alpha \cdot |\mathcal {C}|$ is that the proof of knowledge is now approximately $\alpha$ times larger.

5 Chosen-Ciphertext Security

Many applications require a verifiable ciphertext to hide the encrypted witness, even when the adversary has access to decryptions of other ciphertexts. As a natural analog of indistinguishability under chosen-ciphertext attack (IND-CCA) for standard public-key encryption schemes, we define chosen-ciphertext simulatability and describe a construction that satisfies it.

Our construction essentially follows the Naor-Yung paradigm [NY90] where the sender encrypts the message twice under different public keys and adds a non-interactive zero-knowledge (NIZK) proof that both ciphertexts encrypt the same message. Naor and Yung only proved their approach secure under non-adaptive chosen-ciphertext (CCA1), but Sahai [Sah99] later showed that if the NIZK proof is simulation-sound, then the resulting encryption scheme is secure against adaptive chosen-ciphertext (CCA2) attacks. Faust et al. [FKMV12] showed that Fiat-Shamir proofs are simulation-sound in the random-oracle model if the underlying proof system has quasi-unique responses.

Furthermore, because the verifiable encryption scheme for a CPA-secure encryption scheme already includes a NIZK, this conversion from CPA to CCA2 security is rather cheap, increasing the size of the proof and ciphertext by factors less than 2 (see (22)).

Chosen-ciphertext simulatability. We say that a relaxed verifiable encryption scheme $(\mathsf {Kg}, \mathsf {Enc}, \mathsf {V}, \mathsf {Dec})$ is chosen-ciphertext simulatable when there exists a simulator $\mathsf {Sim}$ such that the following advantage is negligible for all PPT adversaries $\mathsf {A}$:

where $\mathsf {A}$ is not allowed to query its $\mathsf {Dec}$ oracle on the challenge ciphertext $t _b$. In the random-oracle model, $\mathsf {Sim}$ can additionally program the random oracle.

Construction. The receiver generates a Ring-LWE key pair by choosing the secrets $\mathrm{s}_1,\mathrm{s}'_1,\mathrm{s}_2,\mathrm{s}'_2 \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}S_1$ and $\mathrm{a}\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}R$, and computing $\mathrm{t}_1 \leftarrow \mathrm{a}\mathrm{s}_1+\mathrm{s}_2$ and $\mathrm{t}_1 \leftarrow \mathrm{a}\mathrm{s}'_1+\mathrm{s}'_2$. The public key is $pk = (\mathrm{a},\mathrm{t}_1,\mathrm{t}_2,p,q)$, where p is modulus for proving the linear relation. The secret key is $sk = \mathrm{s}_1$.

The sender encrypts a witness $w = \mathbf{m}$ for language member $x = (\mathbf{B},\mathbf{u})$ by choosing randomness $(\mathbf{r}_1, \mathbf{e}_1, \mathbf{e}'_1, \mathbf{r}_2, \mathbf{e}_2, \mathbf{e}'_2) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}S_1^{6k}$, computing

$$\begin{aligned} \begin{bmatrix} p\mathrm{a}\mathbf{I}_k&p\mathbf{I}_k&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k} \\ p\mathrm{t}_1\mathbf{I}_k&\mathrm{0}^{k\times k}&p\mathbf{I}_k&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathbf{I}_k\\ \mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&p\mathrm{a}\mathbf{I}_k&p\mathbf{I}_k&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k} \\ \mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&p\mathrm{t}_2\mathbf{I}_k&\mathrm{0}^{k\times k}&p\mathbf{I}_k&\mathbf{I}_k \end{bmatrix}\begin{bmatrix} \mathbf{r}_1\\ \mathbf{e}_1\\ \mathbf{e}'_1\\ \mathbf{r}_2\\ \mathbf{e}_2\\ \mathbf{e}'_2\\ \mathbf{m} \end{bmatrix}= \begin{bmatrix} \mathbf{v}_1\\ \mathbf{w}_1\\ \mathbf{v}_2\\ \mathbf{w}_2 \end{bmatrix} \begin{matrix} \,\mathrm{mod}\,q\\ \,\mathrm{mod}\,q\\ \,\mathrm{mod}\,q \\ \,\mathrm{mod}\,q \end{matrix} \end{aligned}$$

(22)

and concatenating a proof $(\mathrm{c}, \mathbf{z})$ using the relaxed NIZK proof system of Sect. 2.6 for the language element:

$$\begin{aligned} \begin{bmatrix} p\mathrm{a}\mathbf{I}_k&p\mathbf{I}_k&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k} \\ p\mathrm{t}_1\mathbf{I}_k&\mathrm{0}^{k\times k}&p\mathbf{I}_k&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathbf{I}_k\\ \mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&p\mathrm{a}\mathbf{I}_k&p\mathbf{I}_k&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k} \\ \mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&\mathrm{0}^{k\times k}&p\mathrm{t}_2\mathbf{I}_k&\mathrm{0}^{k\times k}&p\mathbf{I}_k&\mathbf{I}_k \\ \mathrm{0}^{\ell \times k}&\mathrm{0}^{\ell \times k}&\mathrm{0}^{\ell \times k}&\mathrm{0}^{\ell \times k}&\mathrm{0}^{\ell \times k}&\mathrm{0}^{\ell \times k}&\mathbf{B}\end{bmatrix}\begin{bmatrix} \mathbf{r}_1\\ \mathbf{e}_1\\ \mathbf{e}'_1\\ \mathbf{r}_2\\ \mathbf{e}_2\\ \mathbf{e}'_2\\ \mathbf{m} \end{bmatrix}= \begin{bmatrix} \mathbf{v}_1\\ \mathbf{w}_1\\ \mathbf{v}_2\\ \mathbf{w}_2\\ \mathbf{u} \end{bmatrix} \begin{matrix} \,\mathrm{mod}\,q\\ \,\mathrm{mod}\,q\\ \,\mathrm{mod}\,q\\ \,\mathrm{mod}\,p \end{matrix}~. \end{aligned}$$

(23)

Verification of a ciphertext $(\mathbf{v}_1, \mathbf{w}_1, \mathbf{v}_2, \mathbf{w}_2, \mathrm{c}, \mathbf{z})$ is done by verifying the zero-knowledge proof $(\mathrm{c},\mathbf{z})$ for the language element (23). Decryption works exactly as in Algorithm 5, using $\mathbf{w}_1$ instead of $\mathbf{w}$.

Security. Correctness, completeness, and soundness all hold under the same assumptions as the CPA-secure scheme in Sect. 3.4. The following theorem states the chosen-ciphertext simulatability of the scheme. The proof can be found in the full version.

Theorem 5.1

If the Ring-LWE encryption scheme is IND-CPA secure and the relaxed NIZK proof system is unbounded non-interactive zero-knowledge and unbounded simulation-sound, then the above construction is chosen-ciphertext simulatable.

6 Applications

6.1 Key Escrow for Ring-LWE Encryption

A verifiable escrow scheme for decryption keys [YY98, PS00] allows a key owner to encrypt his private decryption key under the public key of a trusted authority so that anyone can check that the ciphertext is indeed an encryption of the private key corresponding to the owner’s public key, but only the trusted authority can actually recover the private key. Intuitively, the owner is giving a proof that all messages sent to his public key can also be decrypted by the trusted third party. Note that a key escrow scheme cannot prevent parties from communicating securely, because even when forced to use escrowed keys, the parties can choose to double-encrypt messages under a non-escrowed key, or apply steganography to hide the fact that they are communicating altogether. The goal, therefore, is rather to prevent “dishonest” usage of public-key infrastructures, e.g., by using it to certify non-escrowed keys.

We show how our verifiable encryption scheme can be used to verifiably escrow Ring-LWE decryption keys. While, due to our relaxation of verifiable encryption, we cannot guarantee that the trusted authority recovers the actual decryption key, we show that whatever he recovers suffices to decrypt messages encrypted under the corresponding public key.

Let the authority have a Ring-LWE public key $\mathrm{t}= \mathrm{a}\mathrm{s}_1 + \mathrm{s}_2 \,\mathrm{mod}\,q$ as described in Sect. 2.5. Users also have Ring-LWE encryption keys, but in $R_p$ instead of $R_q$. Meaning, a secret key is a pair $(\mathrm{m}_1,\mathrm{m}_2) \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}S_1^2$, while the public key is $\mathrm{u}= \mathrm{b}\mathrm{m}_1 + \mathrm{m}_2 \,\mathrm{mod}\,p$ for $\mathrm{b}\mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}R_p$ together with a prime $p' < p$. Encryption and decryption work as in regular Ring-LWE, i.e., the sender chooses $\mathrm{r},\mathrm{e},\mathrm{e}' \mathop {\leftarrow }\limits ^{{\scriptscriptstyle \$}}S_1$ and computes

$$\begin{aligned} \begin{array}{rcl} \mathrm{v}&{} = &{} p'(\mathrm{b}\mathrm{r}+ \mathrm{e}) \,\mathrm{mod}\,p \\ \mathrm{w}&{} = &{} p'(\mathrm{u}\mathrm{r}+ \mathrm{e}') + \mu \,\mathrm{mod}\,p~. \end{array} \end{aligned}$$

(24)

To decrypt, the receiver computes $\mu \leftarrow \mathrm{w}- \mathrm{v}\mathrm{s}_1 \,\mathrm{mod}\,p \,\mathrm{mod}\,p'$.

To escrow his decryption key, the key owner creates a verifiable encryption of his secret key $\mathbf{m} = [\; \mathrm{m}_1 \;;\; \mathrm{m}_2 \;]$ using our scheme from Sect. 3.2 under the authority’s public $\mathrm{t}$ with a proof that $\mathbf{m}$ is a witness for the relation

$$ [\; \mathrm{b}\;\; 1 \;] \begin{bmatrix}\mathrm{m}_1 \\ \mathrm{m}_2 \end{bmatrix} \;=\; \mathrm{u}\,\mathrm{mod}\,p~. $$

The soundness property of our relaxed verifiable encryption scheme guarantees that the authority can decrypt a witness $(\bar{\mathbf{m}},\bar{\mathrm{c}})$ such that

$$ \mathrm{b}\bar{\mathrm{m}}_1 + \bar{\mathrm{m}}_2 \;=\; \bar{\mathrm{c}} \mathrm{u}\,\mathrm{mod}\,p~. $$

The authority can decrypt an honestly generated ciphertext of the form (24) by computing

from which $\mu$ can be recovered by reducing modulo $p'$ and then dividing by $\bar{\mathrm{c}}$ modulo $p'$ (note that it is important that $p'$ is chosen such that all differences of challenges in the challenge space are invertible), as long as the parameters are chosen such that $\Vert p'(\bar{\mathrm{m}}_2\mathrm{r}+ \bar{\mathrm{c}} \mathrm{e}' - \mathrm{e}\bar{\mathrm{m}}_1)+\bar{\mathrm{c}}\mu \Vert _\infty <p/2$.

6.2 Verifiably Encrypted Signatures

Suppose two parties want to engage in a contract together and exchange signatures on the agreed contract. Neither of the parties wants to be the first to send his signature, however, fearing that the other party may not reciprocate and hold the first party liable to the conditions in the contract, without being held liable himself. Fair signature exchange protocols [ASW00, BDM98] ensure that no party can obtain a significant advantage over the other party by aborting the protocol early.

Verifiably encrypted signatures [ASW00, BDM98, BGLS03] are an important tool to build optimistic fair exchange protocols. The first party initially sends his signature encrypted under the key of a trusted adjudicator such that the other party can verify that the ciphertext indeed contains a valid signature on the agreed contract, but cannot recover the signature itself. The second party responds by sending his signature, after which the first party also sends over his signature. In case the first party refuses to send his signature in the last step, the second party can contact the adjudicator to have the encrypted signature from the first decrypted.

We show how our relaxed verifiable encryption scheme can be used to build verifiably encrypted signatures for the ring-based variant of Gentry-Peikert-Vaikuntanathan (Ring-GPV) signature scheme [GPV08] based on the hardness of the Ring-SIS or NTRU problems [SS11, DLP14]. Here, the signer’s public key is a polynomial $\mathrm{b}\in R_p$, while the secret key is a trapdoor allowing to find, for a given $\mathrm{u}\in R_p$, short polynomials $\mathrm{m}_1,\mathrm{m}_2$ such that $\mathrm{b}\mathrm{m}_1 + \mathrm{m}_2 = \mathrm{u}$. A signature on a message $\mu$ in the usual scheme is a short vector $(\mathrm{m}_1, \mathrm{m}_2)$ such that $\mathrm{b}\mathrm{m}_1 + \mathrm{m}_2 = \mathsf {H}(\mu ) \,\mathrm{mod}\,p$, where $\mathsf {H}: \{0,1\}^* \rightarrow R_p$ is a random oracle. It is easy to show, however, that the scheme remains secure if one relaxes the verification algorithm to accept any tuple of short polynomials $(\mathrm{m}_1,\mathrm{m}_2,\mathrm{c})$ such that $\mathrm{b}\mathrm{m}_1 + \mathrm{m}_2 = \mathrm{c}\mathsf {H}(\mu ) \,\mathrm{mod}\,p$.

In the usual security proof, when the adversary produces a forgery, $\mathrm{b}\mathrm{m}_1 + \mathrm{m}_2 = \mathsf {H}(\mu ) \,\mathrm{mod}\,p$, the simulator already possesses another equality $\mathrm{b}\mathrm{m}_1' + \mathrm{m}_2' = \mathsf {H}(\mu ) \,\mathrm{mod}\,p$, and thus obtains a solution to Ring-SIS as $\mathrm{b}(\mathrm{m}_1-\mathrm{m}_1') + (\mathrm{m}_2-\mathrm{m}_2') =0 \,\mathrm{mod}\,p$. If, on the other hand, the adversary produces a forgery $\mathrm{b}\mathrm{m}_1 + \mathrm{m}_2 = \mathrm{c}\mathsf {H}(\mu ) \,\mathrm{mod}\,p$, then the simulator can obtain the equation $\mathrm{b}(\mathrm{c}\mathrm{m}_1-\mathrm{m}_1') + (\mathrm{c}\mathrm{m}_2-\mathrm{m}_2') =0 \,\mathrm{mod}\,p$, which is still a (slightly longer) solution to Ring-SIS.

For this modified signature scheme that we build a verifiably encrypted signature scheme using our CCA-secure relaxed verifiable encryption scheme from Sect. 5. Namely, to encrypt an honest signature $(\mathrm{m}_1,\mathrm{m}_2,1)$ under the adjudicator’s public key, one encrypts the witness $\mathbf{m} = [\; \mathrm{m}_1 \;;\; \mathrm{m}_2 \;]$ with the encryption scheme from Sect. 5 while proving that $[\; \mathrm{b}\;\; 1 \;] \; \mathbf{m} = \mathsf {H}(\mu ) \,\mathrm{mod}\,p$. When the adjudicator decrypts the signature, it recovers $(\bar{\mathbf{m}},\bar{\mathrm{c}})$ such that $[\; \mathrm{b}\;\; 1 \;] \; \bar{\mathbf{m}} = \bar{\mathrm{c}}\mathsf {H}(\mu ) \,\mathrm{mod}\,p$, which is also a valid signature on $\mu$. Unforgeability follows from the unforgeability of the relaxed Ring-GPV scheme, while the security against extraction follows from the security of Ring-LWE encryption.

6.3 Other Applications

One of the most prominent applications of verifiable encryption is in group signatures [CvH91], where group members can sign anonymously in name of the entire group, but their anonymity can be lifted by a dedicated opening authority. A common construction paradigm [CL06, BCK+14] is to let a user’s signing key consist of a signature by the group manager on the user’s identity. To sign a message, the user encrypts his identity under the public key of the opener and creates a NIZK proof of knowledge of a valid signature for the encrypted identity. To recover the identity of the signer, the opener simply decrypts the ciphertext included in the signature.

Our verifiable encryption scheme could be very useful to group signatures in principle, what is missing is a practical signature scheme where the message $\mathbf{m}$ and the signature $\mathbf{s}$ are short vectors for which the verification equation can be expressed as a linear relation $\mathbf{B}\begin{bmatrix} \mathbf{m} \\ \mathbf{s}\end{bmatrix} = \mathbf{u}$.

Table 1. Sample parameter sets for the verifiable encryption scheme

7 Concrete Parameters

In this section we give some sample concrete instantiations of proofs of plaintext knowledge and verifiable encryption schemes (see Table 1). We express the security of each scheme in terms of the “gamma factor” from [GN08]. Values of 1.01 can be broken today, 1.007 seem to be fairly secure (conjectured at least 80-bits), and those less than 1.005 are believed to require more than $2^{128}$ time even for quantum computers. There have been some other attacks considered (e.g. in [ADPS16]), but those require as much memory as time, and are at this point not as useful in practice as variations of lattice-reduction attacks based on LLL (e.g. [CN11]). It is of course possible that attacks that are currently impractical can be made more practical, and at that point the concrete parameters (for all lattice-based schemes) would have to be adjusted. But the ratio between parameter sizes for verifiable encryption and regular encryption (and zero-knowledge authentication) should remain the same. One caveat would be if the algorithms for “overstretched” NTRU would become applicable to Ring-LWE. It was recently shown that when the modulus in NTRU is larger than the secrets by a sub-exponential (i.e. $2^{O(\sqrt{d})},$ where d is the lattice dimension) factor, then the NTRU problem becomes easy [ABD16, CJL16, KF16]. This is in contrast to LWE and Ring-LWE, for which efficient algorithms are only known in the case that the modulus is $2^{\omega (d)}$). If these attacks are transferred to the Ring-LWE setting, then this would have implications toward all constructions (e.g. those in this paper, most FHE schemes based on Ring-LWE, etc.) in which the secrets are significantly smaller than the modulus.

Our schemes are instantiated from the Ring-LWE cryptosystem where we take the secret and error parameters to be from the set $\{-1,0,1\}$. While the worst-case to average-case hardness of Ring-LWE (and LWE) was only proven with larger parameters [Reg09, LPR13], there haven’t been any weaknesses found when constructing public-key encryption schemes with smaller errors. In particular, the part of the NTRU cryptosystem [HPS98] that is based on the Ring-LWE assumption has never been attacked due to having secret and error vectors having coefficients from the set $\{-1,0,1\}$. The most practical attacks is still to rewrite the Ring-LWE instance as a lattice problem and apply lattice reduction.

For all the parameter sets, we analyze the hardness of recovering the vector $[\mathbf{r};~\mathbf{e};~\mathbf{e'};~\mathbf{m}]$ in (11). In column I, we give parameters for a proof of plaintext knowledge where there is no message $\mathbf{m}$. The exact parameters for verifiable encryption will of course depend on the parameters of the relation in (9). In columns II and III, we give the parameters that are large enough to instantiate the two example cases in Sect. 6. All the parameters are as defined in Algorithm 3 with the value of q is taken so as to satisfy (16) in the statement of Lemma 3.1 which is required for the decryption algorithm to function correctly. We point out that in the application to key escrow, there is also an encryption in the key escrow itself. But because that encryption works over modulus p, which is smaller than q, the hardness of breaking it is at least as hard as breaking the verifiable encryption scheme.