Privacy-Preserving Data Mining for Distributed Medical Scenarios

Abstract

In this paper, we consider the application of data mining methods in medical contexts, wherein the data to be analysed (e.g. records from different patients) is distributed among multiple clinical parties. Although inference procedures could provide meaningful medical information (such as optimal clustering of the subjects), each party is forbidden to disclose its local dataset to a centralized location, due to privacy concerns over sensible portions of the dataset. To this end, we propose a general framework enabling the parties involved to perform (in a decentralized fashion) any data mining procedure relying solely on the Euclidean distance among patterns, including kernel methods, spectral clustering, and so on. Specifically, the problem is recast as a decentralized matrix completion problem, whose proposed solution does not require the presence of a centralized coordinator, and full privacy of the original data can be ensured by the use of different strategies, including random multiplicative updates for secure computation of distances. Experimental results support our proposal as an efficient tool for performing clustering and classification in distributed medical contexts. As an example, on the known Pima Indians Diabetes dataset, we obtain a Rand-Index for clustering of 0.52 against 0.54 of the (unfeasible) centralized solution, while on the Parkinson speech database we increase from 0.45 to 0.50.

1 Introduction

Health care and biomedicine are two of the most prolific areas for the application of data mining methods [15], with successful implementations ranging from clustering of patients to rule extraction for expert systems, automatic diagnosis, and many others. In this paper, we are concerned with one particular aspect of medical scenarios, which hinders the use of standard machine learning techniques in practice. Specifically, many medical databases are distributed in nature [13], i.e. different parties may possess separate records on the process to be analysed. As an example, consider the problem of training a classifier to perform automatic diagnosis of a specific disorder (e.g. a cancer), starting from a set of standardized medical measurements. In this case, different hospitals have access to historical training data relative to disjoint patients, and it would be highly beneficial to collect these separate sources in order to train an effective classifier. At the same time, however, releasing medical data to a centralized location (to perform training) generally goes against a number of privacy concerns on sensible information, being subject to privacy attacks even if identifiers are removed before releasing it [2]. So the question becomes, is it possible to perform inference in a decentralized fashion (i.e., without the need for a central coordinator), and without requiring the exchange of training data?

In the literature, this is known as the problem of ‘distributed machine learning’, and many algorithms have been proposed to train specific classes of neural networks models, subject to the constraints detailed above. These include algorithms for distributed training of support vector machines (SVMs) [4, 9], random-weights networks [10, 11], kernel ridge regression [7], and many others, also considering computing energy constraints [1]. Our aim in this paper is instead more general, and starts from the known fact that a large number of learning techniques depend on the input data only through the computation of pairwise Euclidean distances among points. Examples of methods belonging to this category include kernel algorithms (e.g. SVMs), spectral clustering, k-means, and many others. Thus, instead of solving the original distributed learning problem, we can focus on the equivalent problem of completing in a distributed fashion the full matrix of Euclidean distances (EDM). Recasting the problem in this way allows us to leverage over a large number of works on matrix completion and EDM completion [6], especially in the distributed setting [3].

Particularly, we consider a distributed gradient-descent algorithm to this end, originally proposed for SVM inference over networks [3]. The proposed algorithm consists of two iterative steps, which are performed locally by every party (agent) in the network. First, each agent performs a single gradient descent step with respect to a locally defined cost function. Then, the new estimate of the EDM is averaged with respect to the estimates of other agents connected to it, and the process is repeated until convergence. Due to the way in which information is propagated, this kind of iterative techniques go under the general name of ‘diffusion’ strategies [8]. Additionally, we reduce the computational complexity by the exploitation of the specific structure of the EDM, by operating on a suitable factorization of the original matrix.

Once all the agents have access to the global estimate of the EDM, many data mining techniques can be applied directly (e.g. spectral clustering [14]), or by simple in-network operations (e.g. SVMs), as we discuss subsequently. Additionally, if there is the need of applying more than one technique, the same estimate can be reused for all of them, making the framework particularly useful whenever data must be used in an ‘exploratory’ fashion, without a particular predefined objective in mind. In order to show the applicability of the framework, we present experimental results for clustering of three well-known medical databases, showing that the solutions obtained are comparable to that of a fully centralized implementation.

The rest of the paper is organized as follows. In Sect. 12.2 we provide our algorithm for EDM completion. Since this requires the exchange of a small portion of the dataset, we present in the subsequent section two efficient methods to ensure privacy preservation. Then, a set of experimental evaluations are provided in Sect. 12.4, followed by some concluding remarks in Sect. 12.5.

2 Proposed Framework

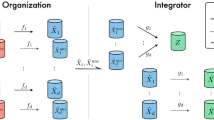
Consider the application of a data mining procedure on a dataset of N examples $S = \left( \mathbf {x}_i \right) _{i=1}^N \in \mathbb {R}^d$, e.g. vectors to be suitably clustered. In a supervised setting, they can also be supplemented by additional labels. We assume that the dataset S is not available on a centralized location. Instead, it is partitioned over L agents (e.g. hospitals), such that the kth agent has access to a dataset $S_k$ and $\bigcup _{k=1}^L S_k = S$. For generality, we can fully describe the connectivity between the agents in the form of an $L \times L$ connectivity matrix $\mathbf {C}$, where $C_{ij} \ne 0$ if and only if agents i and j are connected. In this paper, we assume that the network is connected (i.e., every agent can be reached from any other agent with a finite number of steps), and undirected (i.e., $\mathbf {C}$ is symmetric). Based on what we stated previously, we also assume that no coordinating entity is available, and communication is possible only if two agents are directly connected.

Suppose that the data mining procedure depends on the inputs $\mathbf {x}_i$ only through the computation of Euclidean distances among them (such as in the case of kernel methods). In this case, the overall distributed data mining procedure can be recast as the distributed computation of the Euclidean distance matrix (EDM) $\mathbf {E}$, where $E_{ij} = \left\| \mathbf {x}_i - \mathbf {x}_j \right\| _{2}$. For unsupervised problems, knowledge of this matrix is generally enough to solve the overall problem. In the supervised case, we would instead be left with a distributed optimization problem where only labels are distributed, which can be solved efficiently (see [3] for a fuller treatment on this aspect). To formalize this equivalent problem, we note that with a proper rearrangement of patterns, the global EDM $\mathbf {E}$ can always be expressed as:

$$\begin{aligned} \mathbf {E} = \begin{bmatrix} \mathbf {E}_1&?&?\\ ?&\ddots&? \\ ?&?&\mathbf {E}_L \end{bmatrix} \,, \end{aligned}$$

(12.1)

where $\mathbf {E}_k$ denotes the EDM computed only from the patterns in $S_k$. This structure implies that the sampling set is not random, and makes non-trivial the problem of completing $\mathbf {E}$ solely from the knowledge of the local matrices. At the opposite, the idea of exchanging the entire local datasets between nodes is unfeasible because of the amount of data which would need to be shared. Starting from these considerations, based on [3] we propose the following distributed procedure:

• 1. Patterns exchange: every agent exchanges a fraction p of the available $S_k$ with its neighbours. This is necessary so that the agents can increase the number of known entries in their local matrices. How to ensure privacy in this step is described in the following section.

• 2. Local EDM computation: each agent computes, using its original dataset and the data received from its neighbours, an incomplete approximation $\hat{\mathbf {E}}_k\in \mathbb {R}^{N\times N}$ of the real EDM matrix $\mathbf {E}$.

• 3. Entries exchange: the agents exchange a sample of their local EDMs $\hat{\mathbf {E}}_k$ with their neighbours (similarly to step 1).

• 4. Distributed EDM completion: the agents complete the estimate $\tilde{\mathbf {E}}$ of the global EDM using the strategy detailed next.

To formalize this last step, define a local matrix $\varvec{\varOmega }_k$ as:

$$\begin{aligned} \varvec{\varOmega }_k = {\left\{ \begin{array}{ll} 1 &{} \text { if } \hat{E}_{ij} \ne 0 \\ 0 &{} \text { otherwise } \end{array}\right. }. \end{aligned}$$

(12.2)

We aim at finding a matrix ${\tilde{\mathbf E}}$ such that the following (joint) cost function is minimized:

$$\begin{aligned} \min _{{\tilde{\mathbf E}} \in \text {EDM}(N)} \sum _{k=1}^L J_k({\tilde{\mathbf E}}) = \sum _{k=1}^L \left\| \varvec{\varOmega }_k \circ \left( \hat{\mathbf {E}}_k - {\tilde{\mathbf E}} \right) \right\| _{F}^2 \,, \end{aligned}$$

(12.3)

where $\circ$ denotes the Hadamard product, and $\text {EDM}(N)$ is the set of EDMs of size $N \times N$. To solve problem (12.3) in a fully decentralized fashion, we use the algorithm introduced in [3], which in turn derives from the framework of diffusion adaptation (DA) for optimization [8] and on previous works on EDM completion [6]. In particular, we approximate the objective function in Eq. (12.3) by:

$$\begin{aligned} J_k(\mathbf {V}) = \left\| \varvec{\varOmega }_k \circ \left[ \hat{\mathbf {E}}_k - \kappa \left( \mathbf {VV}^{\text {T}}\right) \right] \right\| _{\text {F}}^2\; k=1,\ldots ,L\;, \end{aligned}$$

(12.4)

where $\kappa (\cdot )$ is the Schoenberg mapping, which maps every positive semidefinite (PSD) matrix to an EDM, given by:

$$\begin{aligned} \kappa (\mathbf {E}) = \text {diag}(\mathbf {E})\mathbf {1}^{\text {T}} + \mathbf {1}\text {diag}(\mathbf {E})^{\text {T}} - 2\mathbf {E} \,, \end{aligned}$$

(12.5)

such that $\text {diag}(\mathbf {E})$ extracts the main diagonal of $\mathbf {E}$ as a column vector, and we also exploits the known fact that any PSD matrix $\mathbf {D}$ with rank r admits a factorization $\{ \mathbf {D}= \mathbf {VV}^\text {T} \}$, where $\mathbf {V}\in \mathbb {R}_{*}^{N\times r}=\{\mathbf {V}\in \mathbb {R}^{N\times r}:\;\det {(\mathbf {V}^{\text {T}}\mathbf {V})}\ne 0\}$. This allows to strongly reduce the computational cost of our algorithm, as the objective function is now formulated only in terms of the low-rank factor $\mathbf {V}$. The diffusion gradient descent for the distributed completion of the EDM is then defined by an alternation of updating and diffusion equations in the form of [3]:

• 1. Initialization: All the agents initialize the local matrices $\mathbf {V}_k$ as random $N\times r$ matrices.

• 2. Update of V: At time n, the kth agent updates the local matrix $\mathbf {V}_k$ using a gradient descent step with respect to its local cost function:

  $$\begin{aligned} \tilde{\mathbf {V}}_k\left[ n+1 \right]&= \mathbf {V}_k[n] - \eta _k[n] \nabla _{\mathbf {V}_k} J_k(\mathbf {V}) \,. \end{aligned}$$

  (12.6)

  where $\eta _k\left[ n\right]$ is a positive step-size. It is straightforward to show that the gradient of the cost function is given by:

  $$\begin{aligned} \nabla _{\mathbf {V}_k} J_k(\mathbf {V})&= \kappa ^* \Bigl \{ \varvec{\varOmega }_k \circ \Bigr . \nonumber \\&\Bigl . \circ \left( \kappa \left( \mathbf {V}_k\left[ n\right] \mathbf {V}_k^{\text {T}}\left[ n \right] \right) -\hat{\mathbf {E}}_k \right) \Bigr \} \mathbf {V}_k\left[ n\right] \,, \end{aligned}$$

  (12.7)

  where $\kappa ^*(\mathbf {A}) = 2\left[ \text {diag}\left( \mathbf {A}1\right] -\mathbf {A}\right)$ is the adjoint operator of $\kappa (\cdot )$.

• 3. Diffusion: In order to propagate information over the network, the updated matrices are combined according to the mixing weights $\mathbf {C} \in \mathbb {R}^{L \times L}$:

  $$\begin{aligned} \mathbf {V}_k\left[ n+1 \right] = \sum _{i=1}^L C_{ki}\tilde{\mathbf {V}}_i\left[ n+1 \right] . \end{aligned}$$

  (12.8)

  where $C_{ki} > 0$ if and only if agents k and i are connected, in order to send information only through neighbours.

The above process is repeated for a maximum of T iterations to ensure convergence (see [8] for a general introduction on DA algorithms).

3 Techniques for Privacy Preservation

The algorithm in the previous section is extremely general, but its efficient implementation requires the distributed computation of a small subset of distances (step 1 in the algorithm). In this section, we show two techniques which are able to preserve privacy (i.e., avoid the exchange of the original data), during this phase. The first is the random projection-based technique developed in [5]. Suppose that both agents agree on a projection matrix $\mathbf {R} \in \mathbb {R}^{m \times d}$, with $m < d$, such that each entry $R_{ij}$ is independent and chosen from a normal distribution with mean zero and variance $\sigma ^2$. We have the following lemma:

Lemma 1

Given two input patterns $\mathbf {x}_i, \mathbf {x}_j$, and the respective projections:

$$\begin{aligned} \mathbf {u}_i = \frac{1}{\sqrt{m}\sigma }\mathbf {R}\mathbf {x}_i \text {, and } \mathbf {u}_j = \frac{1}{\sqrt{m}\sigma }\mathbf {R}\mathbf {x}_j \,, \end{aligned}$$

(12.9)

we have that:

$$\begin{aligned} \mathbb {E}\left\{ \mathbf {u}_i^T\mathbf {u}_j \right\} = \mathbf {x}_i^T\mathbf {x}_j \,. \end{aligned}$$

(12.10)

Proof

See [5, Lemma 5.2].

In light of Lemma 1, exchanging the projected patterns instead of the original ones allows to preserve, on average, their inner product. A thorough investigation on the privacy-preservation guarantees of this protocol can be found in [5]. Additionally, we can observe that this protocol provides a reduction on the communication requirements of the application, since it effectively reduces the dimensionality of the patterns to be exchanged by a factor m / d.

The second technique is the k-anonymity presented in [12]. In this case, we assume that the pattern $\mathbf {x}_i$ is composed by both quasi-identifier fields (e.g., age) and sensible fields (e.g., diagnosis). We say that a dataset is k-anonymous if, for any pattern, there exist at least $k-1$ other patterns with the same quasi-identifiers. It is possible to preserve k-anonymity by performing what is called “generalization” on the dataset [12], wherein the quasi-identifiers are binned in a set of Q predefined bins, and only the information on the corresponding bins is included in the dataset. Different values for Q correspond to different privacy values for k, with an inverse relation [12]. In this paper, we only wish to analyse the influence of this operation on our framework. For this reason, we choose to perform generalization artificially on the full dataset, while a decentralized implementation would require a sophisticated procedure going outside the scope of the paper.

4 Experimental Results

4.1 Experimental Setup

In this section, we evaluate the performance of the proposed algorithm for decentralized spectral clustering [14] with the privacy-preserving protocols described in Sect. 12.3. Note that spectral clustering can be achieved directly with the use of the EDM, so no additional distributed step is necessary after completing the matrix. We consider three different (medical) public datasets available on the UCI repository,¹ a schematic description of which is given in Table 12.1. The number of attributes is always greater than three and depends on the specific features of the dataset. In all cases, for clustering the optimal solution is known beforehand for testing purpose. Below we add some additional information on each dataset.

• Pima Indians Diabetes Dataset: It is a classification dataset composed by 768 instances. The task is to identify whenever the tests are positive for diabetes or negative. Eight attributes are used for this purpose.

• Breast Cancer Wisconsin Dataset: It is a binary classification dataset of 569 instances composed by 32 attributes. The features describe the characteristics of the cell nuclei present in the image. The task is to identify the correct diagnosis (M = malignant, B = benign).

• Parkinson Speech Dataset: The dataset contains data of 20 Parkinson’s Disease patients (PD) and 20 healthy subjects for which multiple types of sound recording are taken. Globally 1040 instances composed by 26 attributes are used to identify the correct type of sound recording (6 in total).

Table 12.1 Detailed description of each dataset

Five different runs of simulation are performed for each dataset which is preventively normalized between $-1$ and 1 before the experiments and randomly partitioned among the agents. A network of 7 agents is considered, where every pair of nodes is connected with a fixed probability $p=0.5$ according to the so-called “Erdos-Rènyi model”. The only requirement is that the graph is connected. We compare the following strategies:

• Centralized: this simulates the case where a dataset is collected beforehand on a centralized location (for comparison).

• No-privacy: the dataset is used with no privacy protocol applied to the data;

• Randomization protocol: the privacy of the data in step 1 is preserved by computing the distance on the projected patterns according to (12.9); parameter d is chosen in $k = \left[ 2, \ldots , 8\right]$ to minimize RMSE;

• K-anonymity: the privacy of the data is preserved by generalization on the quasi-identifiers of the dataset. We use 4 bins for each quasi-identifier.

All experiments are carried out using MATLAB R2013b on a machine with Intel Core i5 processor with a CPU @ 3.00 GHz with 16 GB of RAM. All parameters of the algorithms are set according to [3].

Table 12.2 Experimental results for the randomization. We show the average and the standard deviation of the indexes. Best results for each algorithm are highlighted in bold

4.2 Results and Discussion

We begin by evaluating the results of the framework with the randomization procedure. Three quality indexes are computed for both the privacy-preserving protocols and the privacy-free algorithm, namely the Rand Index, the Falks-Mallows index (F-M Index) and the F-measure. All of the indexes range in $\left[ 0,1\right]$, with 1 indicating a perfect correlation between the true label of the cluster and the output of the clustering algorithm, and 0 the perfect negative correlation. In Table 12.2 we report the mean and the standard deviation of each quality index averaged over 10 k-means evaluations and over the different agents in the distributed case. The best result for each index is highlighted in bold. The results of the three approaches are reasonably aligned; for all of the datasets they are very similar and in some cases the algorithm with privacy-preservation outperforms the traditional one. For evaluating the k-anonymity, we use the Pima Indians Diabetes Dataset described in Sect. 12.4, where the first and the eighth feature, that are respectively the number of pregnancies and the age of the subject, are used as quasi-identifiers. In Table 12.3 we computed the three quality indexes for the k-anonymity protocol, the randomization and the no-privacy transformation strategy. As shown in Table 12.3, we can obtain a comparable performance with respect to the privacy-free algorithm, additionally in the k-anonymity protocol the results are even better.

5 Conclusion

In this paper, we presented a general framework for performing distributed data mining procedures on medical scenarios. The algorithms rely on the distributed computation of a matrix of distances, which is obtained via an innovative gradient descent procedure. Preliminary results on a clustering application show the feasibility of the approach, which is able to reach almost-optimal performance with respect to a fully centralized implementation. Additionally, we have investigated two different techniques allowing to preserve privacy even during the exchange of patterns among agents. Future research direction will involve designing more efficient procedures for the distributed computation of the EDM, together with an analysis of the different customizations of the framework for multiple algorithms.

Table 12.3 Experimental results for the k-anonymity. We show the average and the standard deviation of the F-Index, Rand Index, F-M Index for the Randomization, k-anonimity and privacy-free protocols. Best results for each algorithm are highlighted in bold