Fault Attack on Supersingular Isogeny Cryptosystems

Abstract

We present the first fault attack on cryptosystems based on supersingular isogenies. During the computation of the auxiliary points, the attack aims to change the base point to a random point on the curve via a fault injection. We will show that this would reveal the secret isogeny with one successful perturbation with high probability. We will exhibit the attack by placing it against signature schemes and key-exchange protocols with validations in place. Our paper therefore demonstrates the need to incorporate checks in implementations of the cryptosystem.

A Signature Schemes in Detail

1.1 A.1 Digital Signature Scheme

The signature scheme has three steps: key generation, signing and verifying.

• Set-up and key generation: Fix a prime p of the form $p=\ell _A^{e_A}\cdot \ell _B^{e_B}\cdot f\pm 1$ where $\ell _A$ and $\ell _B$ are small distinct primes, f is a small cofactor and $e_A$ and $e_B$ are positive integers such that $\ell _A^{e_A}\approx \ell _B^{e_B}$. Now fix an elliptic curve E over $\mathbb {F}_{p^2}$. Next, let $t=0.5\lfloor \log _2 p\rfloor$ and fix a hash function $H:\{0,1\}^{*}\rightarrow \{0,1\}^{t}$.

  The signer picks a random element $S\in E[\ell _A^{e_A}]$ with order $\ell _A^{e_A}$ and computes $\phi :E\rightarrow E/\langle S\rangle =E_S$. The signer then generates a basis $\{P_B,Q_B\}$ for $E[\ell _B^{e_B}]$, and computes and publishes the tuple

  $$\begin{aligned} (E,P_B,Q_B,E_S,\phi (P_B),\phi (Q_B)) \end{aligned}$$

  as the public key.

• Signing: The signer needs to produce t challenges. So for each $i=1,\dots ,t$, choose random elements $r_{1,i},r_{2,i}\in \mathbb {Z}/\ell _B^{e_B}\mathbb {Z}$ such that not both are divisible by $\ell _B$ and computes the points

  $$\begin{aligned} R_i&=[r_{1,i}]P_B+[r_{2,i}]Q_B,\\ T_i&=[r_{1,i}]\phi (P_B)+[r_{2,i}]\phi (Q_B) \end{aligned}$$

  and the isogenies

  $$\begin{aligned} \psi _i:E&\rightarrow E/\langle R_i\rangle = E_{R_i},\\ \phi _i':E_S&\rightarrow E_S/\langle T_i\rangle = E_{T_i}. \end{aligned}$$

  Given a message m, the signer computes

  $$\begin{aligned} h=H\left( m,E_{R_1},\dots ,E_{R_t},E_{T_1},\dots ,E_{T_t}\right) . \end{aligned}$$

  The bit-string of h would serve as the sequence of challenge bits. If the i-th bit of h is 0, the signer sets $z_i=(R_i,\phi (R_i))$ ². If the i-th bit of h is 1, the signer sets $z_i=\psi _i(S)$. The signature would then be the tuple

  $$\begin{aligned} (h,z_1,z_2,\dots ,z_{t}). \end{aligned}$$

• Verifying: To verify the signature, the verifier would use the output of the hash as the challenge bits and use the same verification procedure as seen in Sect. 2.2 to verify each $z_i$ as the response to the challenge bits.

1.2 A.2 Undeniable Signature Scheme

This signature scheme has three steps: key generation, signing and verifying. The last step is split into confirmation or disavowal.

• Set-up and key generation: Fix a hash function $H:\{0,1\}^{*}\rightarrow \mathbb {Z}$. Fix a prime p of the form $p=\ell _A^{e_A}\cdot \ell _M^{e_M}\cdot \ell _C^{e_C}\cdot f\pm 1$ and fix a supersingular elliptic curve E over $\mathbb {F}_{p^2}$. Now pick bases $\{P_A,Q_A\}$, $\{P_M,Q_M\}$ and $\{P_C,Q_C\}$ for the $\ell _A^{e_A}$, $\ell _M^{e_M}$ and $\ell _C^{e_C}$-torsion points respectively. The signer then randomly picks elements $a_1,a_2\in \mathbb {Z}/\ell _A^{e_A}\mathbb {Z}$ not both divisible by $\ell _A$, computes the subgroup $G_A=\langle [a_1]P_A+[a_2]Q_A\rangle$ and uses Vélu’s formula to compute $E_A=E/G_A$ and the isogeny $\phi _A:E\rightarrow E_A$. The signer computes the image of $P_C$ and $Q_C$ under this isogeny and publishes the tuple $(E_A,\phi _A(P_C),\phi _A(Q_C))$.

• Signing: Given a message M, the signer computes the hash $h=H(M)$ and the subgroup $G_M=P_M+[h]Q_M$. Next, the signer computes the following isogenies:

  • $\phi _M:E\rightarrow E_M=E/G_M$

  • $\phi _{M,AM}:E_M\rightarrow E_{AM}=E/\phi _M(G_A)$

  • $\phi _{A,AM}:E_A\rightarrow E_{AM}=E/\phi _A(G_M)$

  The signature then consists of the tuple

  $$\begin{aligned} \left( E_{AM},\phi _{M,AM}(\phi _M(P_C)), \phi _{M,AM}(\phi _M(Q_C))\right) . \end{aligned}$$

• Verification: Since this is an undeniable signature scheme, there are two components to this: the confirmation protocol and the disavowal protocol. In the former protocol, given the signature

  $$\begin{aligned} \left( E_{AM},\phi _{M,AM}(\phi _M(P_C)), \phi _{M,AM}(\phi _M(Q_C))\right) , \end{aligned}$$

  the objective is to confirm $E_{AM}$. In the latter, given the signature $(E_F,F_P,F_Q)$, the objective is to disavow the signature.

  • Confirmation:

    • 1. The signer picks random elements $c_1,c_2\in \mathbb {Z}/\ell _C^{e_C}\mathbb {Z}$ not both divisible by $\ell _C$, computes the subgroup $G_C=\langle [c_1]P_C+[c_2]Q_C\rangle$ and computes

      

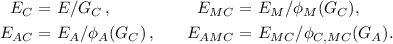
    • 2. The signer publishes $(E_C,E_{AC},E_{MC}, E_{AMC},\phi _C(P_M)+[h]\phi _C(Q_M))$.

    • 3. The verifier randomly selects $b\in \{0,1\}$.

      • If $b=0$: the signer outputs $\ker \phi _C$. The verifier then computes $\phi _C$, $\phi _{M,MC}$, $\phi _{A,AC}$ and $\phi _{F}:E_F\rightarrow E_{FC}$ and checks that each isogeny maps between the curves in the commitment. The verifier also computes $\phi _{C,MC}$ and checks that it matches the commitment.

      • If $b=1$: the signer outputs $\ker \phi _{C,AC}$ and the verifier then computes $\phi _{MC,AMC}$, $\phi _{AC,AMC}$ and checks that $E_{AMC}$ is the codomain.

  • Disavowal: The disavowal step is almost exactly the same as the confirmation step with the exception in the last step where if $b=0$, the verifier would see that $E_{FC}\not \cong E_{AMC}$ (Fig. 4).

Fig. 4.

Commutative diagrams generated during protocol