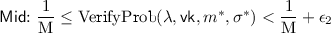Abstract
A signature scheme consists of a setup, signing and verification algorithms. In most existing works, the verification algorithm is assumed to be deterministic. However, there could be signature schemes where the verification algorithm is randomized. In this work, we study signature schemes with randomized verification. Our results can be summarized as follows.
First, we present a security definition for signature schemes with randomized verification. The standard EUFCMA notion of security for signature schemes with deterministic verification is very restrictive when we consider randomized verification. Therefore, we propose a new security definition called \(\chi \)-EUFCMA which captures a broad class of signature schemes with randomized verification.
Next, we analyse the security of Naor’s transformation from Identity Based Encryption to signature schemes. Such a transformation results in a scheme with randomized verification. We show that this transformation can be proven \(\chi \)-EUFCMA secure by choosing \(\chi \) appropriately.
Finally, we show how a scheme with randomized verification can be generically transformed to one with deterministic verification.
S. Hohenberger—Supported by the National Science Foundation (NSF) CNS-1228443 and CNS-1414023, the Office of Naval Research under contract N00014-14-1-0333, and a Microsoft Faculty Fellowship.
B. Waters—Supported by NSF CNS-1228599 and CNS-1414082, DARPA SafeWare, Microsoft Faculty Fellowship, and Packard Foundation Fellowship.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Digital signatures [6] are one of the central primitives of modern cryptography, both as an application, and as a building block for other primitives. A signature scheme consists of three algorithms: a setup algorithm that outputs a secret signing key and a public verification key, a signing algorithm that computes signatures on messages using the signing key, and a verification algorithm that uses the verification key to check if a signature corresponding to a message is valid. Clearly, the setup algorithm must be probabilistic. The signing algorithm can be transformed to a deterministic one by using a pseudorandom function (PRF). In such a transformation, a PRF key can be included as part of the secret key, and to sign a message, this PRF key can be used to generate the randomness for the signing algorithm. However, such a transformation cannot be applied to the verification algorithm, since verification is public.
Indeed, as noted by [8], “no generic transformation outside the random oracle model is known that makes the verification deterministic”. As a result, when describing or using signatures, the verification algorithm is often implicitly or explicitly assumed to be deterministic. This is especially true for works which use signatures as part of a larger protocol. Moreover, in certain applications [8, 9], it is important for the verification algorithm to be deterministic. This assumption regarding the determinism of the verification algorithm is often justified by the fact that most existing schemes have deterministic verification.
At the same time there are circumstances where a signature construction with a randomized verification will naturally arise. The most popular one is the transformation from identity based encryption (IBE) schemes to digital signatures suggested by Naor (sketched in [2]). This transformation, popularly referred to as Naor transformation, can be described as follows. The signing key consists of the IBE master secret key and the verification key is the IBE public key. To sign a message m, the signing algorithm generates an IBE secret key corresponding to the identity m. This signature can be verified by first choosing a random message x from the IBE message space, encrypting x for identity m and checking if the secret key can decrypt this ciphertext correctly. We would like to point out that the random coins used by verification algorithm consists of the IBE message x and the randomness required to encrypt x.Footnote 1
The signature schemes derived from IBE schemes have some nice properties (for instance shorter signatures) as compared to the traditional signature schemes. Fortunately, for many IBE schemes, there are naturally derived signature schemes where the verification is deterministic. Boneh, Lynn and Shacham showed how to modify the Boneh-Franklin IBE scheme to get a signature scheme with deterministic verification [3]. Waters, in [10], showed an IBE scheme in the standard model, and then showed how it can be modified to get a signature scheme with deterministic verification. However, such signature scheme counterparts with deterministic verification do not exist for all IBE schemes. For example, the dual system based Waters IBE scheme [11] did not give an immediate signature with deterministic verification, and the generic Naor transformation was the only known approach. More generally, in future, there could be signature schemes with desirable properties, but where the verification algorithm is randomized.
Our Goals and Contributions. With this motivation, we explore a broad notion of signature schemes with randomized verification. We note that a few different works have considered randomized verification with varying degrees of formality (e.g., [7, 8, 11]). The main contributions of our work can be summarized as follows. First, we propose a formal security definition for signature schemes with randomized verification security. This security notion, called \(\chi \)-Existential Unforgeability under Chosen Message Attack (\(\chi \)-EUFCMA) security, captures a broad class of signature schemes with randomized verification. Next, we give a formal proof of Naor’s IBE to signatures transformation. The proof of Naor transformation also illustrates the importance of our proposed security definition. Third, we show how to amplify the security of a \(\chi \)-EUFCMA secure scheme. Finally, we show generic transformations from a signature scheme with randomized verification to one with deterministic verification. Each of these contributions is described in more detail below.
Defining a broad notion of security for signature schemes with randomized verification. Our first goal is to define a broad notion of security for signature schemes with randomized verification. Intuitively, a signature scheme is said to be secure if no polynomial time adversary can produce a forgery that gets verified with non-negligible probability. For deterministic verification, this can be easily captured via a security game [6] between a challenger and an adversary, where the adversary can query for polynomially many signatures, and eventually, must output a forgery \(\sigma ^{*}\) on a fresh (unqueried) message \(m^{*}\). The adversary wins if the verification algorithm accepts \(\sigma ^{*}\) as a signature on message \(m^{*}\), and we want that no polynomial time adversary wins with non-negligible probability.
Now one can achieve a standard notion of security for randomized verification if we just take the same game and make the attacker’s success probability be over the coins of the challenger’s verification algorithms (as well as the other coins in the game). While this is the most natural extension of the security to randomized verification, there are signature schemes that do not meet this definition, yet still offer some meaningful notion of security. Looking ahead, signature schemes that arise from the Naor transformation applied to IBE schemes with small message space does not satisfy this strong notion but still provide some type of security that we would like to be able to formally capture.
In order to capture a broad class of signature schemes with randomized verification, we introduce a weaker notion called \(\chi \)-EUFCMA security. In this security game, the adversary receives a verification key from the challenger. It is allowed to make polynomially many signature queries, and must finally output a forgery \(\sigma ^{*}\) on message \(m^{*}\) (not queried during the signature query phase). Informally, a signature scheme is said to be \(\chi \)-EUFCMA secure if for any forgery \(\sigma ^{*}\) on message \(m^{*}\) produced by a polynomially bounded adversary, the fraction of random coins that accept \(\sigma ^{*}\), \(m^{*}\) is at most \(\chi \). Ideally, we would want \(\chi = 0\) (or negligible in the security parameter). However, as we will show below, this is not possible to achieve for certain Naor transformed signature schemes.
Naor Transformation for IBE schemes with small message spaces. For simplicity, let us consider the Naor transformation from IBE schemes with one bit message space (for example the Cocks IBE scheme [4]). Here, the adversary can send a malformed signature such that the adversary wins the game, but the signature-to-IBE reduction algorithm has 0 advantage. In more detail, consider an adversary that, with probability 1/2, outputs a valid IBE key \(\sigma ^*\) for ID \(m^*\), and with probability 1/2, outputs a malformed IBE key \(\sigma ^*\) for \(m^*\). This malformed key always outputs the incorrect decryption of the ciphertext. Such an adversary would break the signature scheme security, but if a reduction algorithm uses such a forgery directly to break the IBE security, then it has advantage 0. To get around this problem, we use a counting technique which is inspired by the artificial abort technique introduced by Waters [10]. The main idea behind Waters’ artificial abort was to reduce the dependence between the event in which adversary wins and the one where simulation aborts. However, we require a technique which could efficiently test whether the forgery (i.e. IBE key) is malformed or not. To this end, the reduction algorithm runs the IBE decryption multiple times, each time on freshly generated ciphertext, and counts the number of correct decryptions. This helps the reduction in estimating whether the key is malformed or not. If the key is malformed, then the reduction algorithm simply aborts, otherwise it uses the forgery to break IBE security. The analysis is similar to that in [10].
The above issue with small message space IBE schemes was also noted by the work of Cui et al. [5]. They outlined a sketch of proof for large message spaces. However, even in the case of large message spaces, the issue of artificial abort needs to be addressed (although, unlike the small message case, the reduction algorithm does not suffer a loss in the winning advantage).
Amplifying the soundness from \(\chi = 1 - 1/\mathsf {poly}(\cdot )\) to \(\chi = 0\) . Next, we show how to amplify the soundness from \(\chi = 1 - 1/\mathsf {poly}(\lambda )\) to \(\chi = 0\). Such a problem closely resembles that of transforming weak OWFs to strong OWFs. Therefore, the direct product amplification technique [12] could be used. So, if the verification algorithm is run sufficiently many times, each time with fresh randomness, and the signature is accepted only if all verifications succeed, then we could achieve \(\chi = 0\)-EUFCMA security.
Derandomizing the verification algorithm. Finally, we show how to transform any \(\chi = 0\)-EUFCMA secure signature scheme with randomized verification algorithm to a signature scheme with deterministic verification. We show two such transformations, one in the random oracle model (ROM), and another in the standard model. The transformation in the random oracle model is fairly straightforward. Here, the verification algorithm uses a hash function H which will be modeled as a random oracle in the proof. To verify a signature \(\sigma \) on message m, the verification algorithm computes \(r = H(m,\sigma )\) and uses r as the randomness for the verification. To prove security, we first model the hash function H as a random oracle. Suppose there exists an attacker on this modified signature scheme. After the hash function is replaced with a random oracle, the attacker’s forgery can be directly used as a forgery for the original \(\chi = 0\)-EUFCMA secure signature scheme. Here, note that it is crucial that the starting signature scheme with randomized verification is \(\chi = 0\)-EUFCMA secure, else the adversary’s forgery may not be useful for the reduction as it will not translate to a forgery for the original signature scheme.
In our standard model transformation, the setup algorithm chooses a sufficiently large number of random strings \(r_1, \ldots , r_{\ell }\) and includes them as part of the public verification key. The verification algorithm uses each of these strings as its randomness, and checks if \(m, \sigma \) verify in all cases. If so, it outputs 1, else it outputs 0. For security, suppose the adversary \(\mathcal {A}\) sends a message \(m^{*}\) and a forgery \(\sigma ^{*}\) such that the verification algorithm accepts \(m^{*}, \sigma ^{*}\) when using \(r_1, \ldots , r_{\ell }\) as the random strings. The reduction algorithm simply forwards \(m^{*}, \sigma ^{*}\) as a forgery to the original signature scheme’s challenger. To compute the winning probability of the reduction algorithm, we need to consider the case when the adversary \(\mathcal {A}\) wins, but the reduction algorithm does not. This, in particular, can happen if the set of ‘bad’ random strings that result in \((m^{*}, \sigma ^{*})\) being accepted is a negligible fraction of the total number of random strings. Suppose there exists a message \(m^{*}\) and forgery \(\sigma ^{*}\) such that the number of ‘bad’ randomness strings that cause the verification algorithm to accept \(m^{*}, \sigma ^{*}\) is a negligible fraction of the total number of randomness strings, and all strings \(r_1, \ldots , r_{\ell } \) are in the bad set. We argue that since \(r_1, \ldots , r_{\ell } \) are chosen uniformly at random, and since \(\ell \) is a suitably large polynomial in the security parameter, this probability is negligible in the security parameter.
Conclusions. Many times in cryptography and security there is a concept that is thought to be well understood, but has never been rigorously proven or explored. Often when such an exploration takes place some new twists or facts will be discovered. In this case when we first decided to dig into the IBE to signature transformation we had an initial expectation that there would be a lossless connection from IBE to signatures. We actually were surprised that our initial attempts did not work out and that an artificial abort type mechanism was required for the small message spaces. Besides formally proving the IBE to signature transformation, we also show how to derandomize any signature scheme with randomized verification, both in the random oracle model as well as the standard model.
2 Definitions and Preliminaries
2.1 Signature Schemes with Deterministic Verification
A signature scheme \(\mathcal {S}= (\textsf {Setup}_{\mathrm {Det}}, \textsf {Sign}_{\mathrm {Det}}, \textsf {Verify}_{\mathrm {Det}})\) with message space \(\mathcal {M}\) consists of three algorithms, as follows:
-
1.
\(\textsf {Setup}_{\mathrm {Det}}(1^{\lambda })\) is a randomized algorithm that takes security parameter \(\lambda \) as input and returns a pair of keys \((\mathsf {sk}, \mathsf {vk})\), where \(\mathsf {sk}\) is the signing key and \(\mathsf {vk}\) is the verification key.
-
2.
\(\textsf {Sign}_{\mathrm {Det}}(\mathsf {sk}, m)\) is a possibly randomized algorithm that takes as input the signing key \(\mathsf {sk}\), and a message m, and returns a signature \(\sigma \).
-
3.
\(\textsf {Verify}_{\mathrm {Det}}(\mathsf {vk}, m, \sigma )\) is a determistic algorithm that takes as input the verification key \(\mathsf {vk}\), a message m, and a signature \(\sigma \), and outputs 1 (accepts) if verification succeeds, and 0 (rejects) otherwise.
Definition 1
A pair of polynomial time algorithms \((\textsf {Setup}_{\mathrm {Det}}, \textsf {Sign}_{\mathrm {Det}}, \textsf {Verify}_{\mathrm {Det}})\) is a EUFCMA secure signature scheme if it satisfies the following conditions
-
1.
(Correctness) For all \(\lambda \in \mathbb {N}\), \(m \in \mathcal {M}\),
$$ \Pr \left[ \textsf {Verify}_{\mathrm {Det}}(\mathsf {vk}, m, \sigma ) = 1:\ \begin{array}{cl} (\mathsf {sk}, \mathsf {vk}) \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Setup}_{\mathrm {Det}}(1^{\lambda })\\ \sigma \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Sign}_{\mathrm {Det}}(\mathsf {sk}, m) \end{array} \right] = 1. $$ -
2.
(Security) For every PPT attacker \(\mathcal {A}\) there exists a negligible function \(\text {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(\mathsf {Adv}^\mathrm{EUFCMA}_\mathcal {A}(\lambda ) \le \text {negl}(\lambda )\), where advantage of \(\mathcal {A}\) is defined as
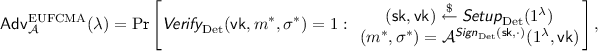
and \(\mathcal {A}\) should never have queried \(m^{*}\) to \(\textsf {Sign}_{\mathrm {Det}}\) oracle.
2.2 Identity-Based Encryption
An Identity-Based Encryption (IBE) scheme \(\mathcal {E}= (\textsf {Setup}_\mathrm{IBE}, \textsf {KeyGen}_\mathrm{IBE}, \textsf {Enc}_\mathrm{IBE}, \textsf {Dec}_\mathrm{IBE})\) with message space \(\mathcal {M}_\mathrm{IBE}\) and identity space \(\mathcal {I}\) consists of the following polynomial time algorithms:
-
1.
\(\textsf {Setup}_\mathrm{IBE}(1^\lambda )\) is a randomized polynomial time algorithm that takes security parameter \(\lambda \) as input and returns \((\mathsf {pp}, \mathsf {msk})\), where \(\mathsf {pp}\) are public parameters and \(\mathsf {msk}\) is the master secret key.
-
2.
\(\textsf {KeyGen}_\mathrm{IBE}(\mathsf {pp}, \mathsf {msk}, \mathsf {ID})\) is a randomized polynomial time algorithm that takes as inputs the public parameters \(\mathsf {pp}\), the master secret key \(\mathsf {msk}\), and an identity \(\mathsf {ID}\) and returns a secret key \(\mathsf {sk}_{\mathsf {ID}}\) for \(\mathsf {ID}\).
-
3.
\(\textsf {Enc}_\mathrm{IBE}(\mathsf {pp}, m, \mathsf {ID})\) is a randomized polynomial time algorithm that takes as inputs the public parameters \(\mathsf {pp}\), a message m, and an identity \(\mathsf {ID}\) and returns a ciphertext \(\mathsf {ct}\).
-
4.
\(\textsf {Dec}_\mathrm{IBE}(\mathsf {pp}, \mathsf {sk}_{\mathsf {ID}}, \mathsf {ct})\) is an polynomial time algorithm that takes as inputs the public parameters \(\mathsf {pp}\), a secret key \(\mathsf {sk}_{\mathsf {ID}}\), and a ciphertext \(\mathsf {ct}\) and returns a message m or \(\bot \).
Definition 2
A pair of polynomial time algorithms \((\textsf {Setup}_\mathrm{IBE}, \textsf {KeyGen}_\mathrm{IBE}, \textsf {Enc}_\mathrm{IBE}, \textsf {Dec}_\mathrm{IBE})\) is an adaptively-secure IBE scheme if it satisfies the following conditions
-
1.
(Correctness) For all \(\lambda \in \mathbb {N}\), \(m \in \mathcal {M}_\mathrm{IBE}\), \(\mathsf {ID}\in \mathcal {I}\),
$$ \Pr \left[ \textsf {Dec}_\mathrm{IBE}(\mathsf {pp}, \mathsf {sk}_{\mathsf {ID}}, \mathsf {ct}) = m:\ \begin{array}{cl} (\mathsf {pp}, \mathsf {msk}) \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Setup}_\mathrm{IBE}(1^{\lambda })\\ \mathsf {sk}_{\mathsf {ID}} \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {KeyGen}_\mathrm{IBE}(\mathsf {pp}, \mathsf {msk}, \mathsf {ID})\\ \mathsf {ct}\mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Enc}_\mathrm{IBE}(\mathsf {pp}, m, \mathsf {ID}) \end{array} \right] = 1. $$ -
2.
(Security) For every PPT attacker \(\mathcal {A}= (\mathcal {A}_0, \mathcal {A}_1)\) there exists a negligible function \(\text {negl}(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(\mathsf {Adv}^\mathrm{IBE}_\mathcal {A}(\lambda ) \le \text {negl}(\lambda )\), where advantage of \(\mathcal {A}\) is defined as
$$ \left| \Pr \left[ \mathcal {A}_1^{\mathcal {O}_{\mathsf {ID}^{*}}}(\mathsf {st}, \mathsf {ct}_b)\ = b : \ \begin{array}{cl} (\mathsf {pp}, \mathsf {msk}) \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Setup}_\mathrm{IBE}(1^{\lambda });\quad b \mathop {\leftarrow }\limits ^{\scriptstyle \$}\{0,1\}\\ (\mathsf {ID}^{*}, m_0^{*}, m_1^{*}, \mathsf {st}) = \mathcal {A}_0^{\mathcal {O}}(1^{\lambda }, \mathsf {pp})\\ \mathsf {ct}_b \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Enc}_\mathrm{IBE}(\mathsf {pp}, m^{*}_b, \mathsf {ID}^{*}) \end{array} \right] - \dfrac{1}{2} \right| , $$Here oracle \(\mathcal {O}\) behaves same as \(\textsf {KeyGen}_\mathrm{IBE}(\mathsf {pp}, \mathsf {msk}, \cdot )\), \(\mathcal {A}\) should not have queried \(\mathcal {O}\) for \(\mathsf {ID}^{*}\) in the pre-challenge phase, and \(\mathcal {O}_{\mathsf {ID}^{*}}\) behaves same as \(\mathcal {O}\), except on input \(\mathsf {ID}^{*}\) it outputs \(\perp \).
3 Signatures Schemes with Randomized Verification
In traditional signature schemes (as defined in Sect. 2.1), the verification algorithm is assumed to be deterministic. However, in certain scenarios, it might be useful to consider verification algorithms that are randomized. In this section, we propose a EUFCMA equivalent definition that captures a broad class of signature schemes with randomized verification. Let \(\chi \) be a fixed parameter. Intuitively, a signature scheme with randomized verification is said to be \(\chi \) secure if any forgery produced by a PPT adversary is accepted by the verification algorithm with probability at most \(\chi \). For example, if \(\chi =1/2\), then in the security game, the adversary first gets the verification key, then queries for q signatures, and finally sends a forgery \(\sigma ^*\) on message \(m^*\). The scheme is \(\chi \) secure if \((\sigma ^*, m^*) \) is accepted by the verification algorithm with probability at most 1/2.
More formally, a randomized verification signature scheme \(\mathcal {S}_\mathrm{RV} = (\textsf {Setup}_{\mathrm {RV}}\), \(\textsf {Sign}_{\mathrm {RV}}\), \(\textsf {Verify}_{\mathrm {RV}})\) with message space \(\mathcal {M}(\lambda )\) and verification coin space \(\mathcal {R}(\lambda )\) consists of three algorithms, as follows:
-
1.
\(\textsf {Setup}_{\mathrm {RV}}(1^{\lambda })\) is a randomized polynomial time algorithm that takes security parameter \(\lambda \) as input and returns a pair of keys \((\mathsf {sk}, \mathsf {vk})\), where \(\mathsf {sk}\) is the signing key and \(\mathsf {vk}\) is the verification key.
-
2.
\(\textsf {Sign}_{\mathrm {RV}}(\mathsf {sk}, m)\) is a possibly randomized polynomial time algorithm that takes as input the signing key \(\mathsf {sk}\), and a message m, and returns a signature \(\sigma \).
-
3.
\(\textsf {Verify}_{\mathrm {RV}}(\mathsf {vk}, m, \sigma ; r)\) is a randomized polynomial time algorithm that takes as input the verification key \(\mathsf {vk}\), a message m, and a signature \(\sigma \). It also uses random coins \(r \in \mathcal {R}\), and outputs 1 (accepts) if verification succeeds, and 0 (rejects) otherwise.
Successful Verification Probability. We define a function over the tuple \((\lambda , \mathsf {vk}, m, \sigma )\) for a randomized verification signature scheme which captures the fraction of message-signature pairs \((m, \sigma )\) which get verified under verification key \(\mathsf {vk}\) as follows.
In our security proofs, we will use the notation \(\mathcal {R}_{m,\sigma }\) to denote the set \(\left\{ r \in \mathcal {R} : \textsf {Verify}_{\mathrm {RV}}(\mathsf {vk}, m, \sigma ; r) = 1\right\} \).
Definition 3
A pair of polynomial time algorithms \((\textsf {Setup}_{\mathrm {RV}}, \textsf {Sign}_{\mathrm {RV}}, \textsf {Verify}_{\mathrm {RV}})\) is a \(\chi (\lambda )\)-EUFCMA secure signature scheme with randomized verification if it satisfies the following conditions
-
1.
(Correctness) For all \(\lambda \in \mathbb {N}\), \(m \in \mathcal {M}\), \(r \in \mathcal {R}\),
$$ \Pr \left[ \textsf {Verify}_{\mathrm {RV}}(\mathsf {vk}, m, \sigma ; r) = 1:\ \begin{array}{cl} (\mathsf {sk}, \mathsf {vk}) \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Setup}_{\mathrm {RV}}(1^{\lambda })\\ \sigma \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Sign}_{\mathrm {RV}}(\mathsf {sk}, m) \end{array} \right] = 1. $$ -
2.
(Security) For every PPT attacker \(\mathcal {A}\) there exists negligible functions \(\text {negl}_1(\cdot )\) and \(\text {negl}_2(\cdot )\) such that for all \(\lambda \in \mathbb {N}\), \(\mathsf {Adv}^\mathrm{RV}_\mathcal {A}(\lambda ) \le \text {negl}_1(\lambda )\), where advantage of \(\mathcal {A}\) is defined as

and \(\mathcal {A}\) should never have queried \(m^{*}\) to \(\textsf {Sign}_{\mathrm {RV}}\) oracle.
4 Signature Scheme with Randomized Verification from IBE: Naor’s Transformation
In this section, we construct signature schemes with randomized verification from IBE schemes using Naor’s transformation. Naor suggested a generic method to construct signature schemes from IBE schemes, and a sketch of this transformation was given in [1]. At a high level, this transformation can be described as follows. The message space of the signature scheme is the identity space of the IBE scheme. To generate the signing key/verification key, the setup algorithm runs the IBE setup algorithm to compute an IBE public key/master secret key pair. The public key is set to be the verification key, while the master secret key is the signing key. To sign a message m, the signing algorithm generates a secret key corresponding to identity m. The verification algorithm chooses a uniformly random message x, encrypts it using the verification key for identity m. It then decrypts the encryption using the signature, and checks if the decryption is correct.
Intuitively, it appears that this signature scheme should be secure if the underlying IBE scheme is secure. However, there are certain subtleties, especially when the message space of the IBE scheme is small (see Sect. 1 for more details).
4.1 Construction
Let \(\mathcal {E}= (\textsf {Setup}_\mathrm{IBE}, \textsf {KeyGen}_\mathrm{IBE}, \textsf {Enc}_\mathrm{IBE}, \textsf {Dec}_\mathrm{IBE})\) be an IBE scheme with message space \(\mathcal {M}_\mathrm{IBE}\) and ID space \(\mathcal {I}\). We define a randomized verification signature scheme \(\mathcal {S}_\mathrm{RV} = (\textsf {Setup}_{\mathrm {RV}}, \textsf {Sign}_{\mathrm {RV}}, \textsf {Verify}_{\mathrm {RV}})\) with message space \(\mathcal {M}= \mathcal {I}\) as follows:
-
1.
\(\textsf {Setup}_{\mathrm {RV}}(1^\lambda )\): It computes \((\mathsf {pp}, \mathsf {msk}) \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Setup}_\mathrm{IBE}(1^\lambda )\) and returns \((\mathsf {sk}_\mathrm{RV}, \mathsf {vk}_\mathrm{RV})\) where \(\mathsf {sk}_\mathrm{RV} = \mathsf {msk}\) and \(\mathsf {vk}_\mathrm{RV} = \mathsf {pp}\).
-
2.
\(\textsf {Sign}_{\mathrm {RV}}(\mathsf {sk}_\mathrm{RV}, m)\): Let \(\mathsf {vk}_\mathrm{RV} = \mathsf {pp}\), \(\mathsf {sk}_\mathrm{RV} = \mathsf {msk}\), and \(m = \mathsf {ID}\). It computes \(\mathsf {sk}_{\mathsf {ID}} \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {KeyGen}_\mathrm{IBE}(\mathsf {pp}, \mathsf {msk}, \mathsf {ID})\) and returns \(\sigma = \mathsf {sk}_{\mathsf {ID}}\).
-
3.
\(\textsf {Verify}_{\mathrm {RV}}(\mathsf {vk}_\mathrm{RV}, m, \sigma ; r)\): Let \(\mathsf {vk}_\mathrm{RV} = \mathsf {pp}\), \(m = \mathsf {ID}\), \(\sigma = \mathsf {sk}_{\mathsf {ID}}\), and \(r = d || r'\). It computes \(\mathsf {ct}= \textsf {Enc}_\mathrm{IBE}(\mathsf {pp}, d, \mathsf {ID})\) passing \(r'\) as the random coins to \(\textsf {Enc}_\mathrm{IBE}\). It outputs 1 if \(\textsf {Dec}_\mathrm{IBE}(\mathsf {pp}, \mathsf {sk}_{\mathsf {ID}}, \mathsf {ct}) = d\) and 0 otherwise.
4.2 Correctness and Security
Theorem 1
If \(\mathcal {E}= (\textsf {Setup}_\mathrm{IBE}, \textsf {KeyGen}_\mathrm{IBE}, \textsf {Enc}_\mathrm{IBE}, \textsf {Dec}_\mathrm{IBE})\) is an adaptively-secure IBE scheme (Definition 2) with message space \(\mathcal {M}_\mathrm{IBE}\) such that \(|\mathcal {M}_\mathrm{IBE}| = \mathrm M\), then above construction forms a \(1/\mathrm M\)-secure randomized verification signature scheme as per Definition 3.
Proof
It is straightforward to verify the correctness as it follows directly from the correctness of IBE scheme. To prove \(1/\mathrm M\)-EUFCMA security, consider a PPT adversary \(\mathcal {A}\) that wins the \(1/\mathrm M\)-EUFCMA security game described in Definition 3 with non-negligible advantage \(\epsilon _1\). This could be equivalently stated as that with probability \(\epsilon _2\), \(\mathcal {A}\) outputs \((m^{*}, \sigma ^{*})\) such that \(\mathrm {VerifyProb}(\lambda , \mathsf {vk}, m^{*}, \sigma ^{*}) > 1/\mathrm M+ \epsilon _2\) where \(\epsilon _1\) and \(\epsilon _2\) are non-negligible functions in \(\lambda \). We construct a reduction algorithm \(\mathcal {B}\) that acts as the challenger in the randomized verification signature security game and is the attacker in the adaptive IBE security game. We define algorithm \(\mathcal {B}\) as follows:
-
1.
The IBE challenger computes \((\mathsf {msk}, \mathsf {pp}) \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Setup}_\mathrm{IBE}(1^{\lambda })\) and sends \(\mathsf {pp}\) to the IBE attacker \(\mathcal {B}\).
-
2.
\(\mathcal {B}\) sets \(\mathsf {vk}= \mathsf {pp}\) and sends \(\mathsf {vk}\) as the verification key to adversary \(\mathcal {A}\).
-
3.
Attacker \(\mathcal {A}\) submits signature queries on a polynomial number of messages \(m_i\). On each message, \(\mathcal {B}\) sets \(\mathsf {ID}_i = m_i\) and sends a secret key query for identity \(\mathsf {ID}_i\) to the IBE challenger. \(\mathcal {B}\) receives \(\mathsf {sk}_{\mathsf {ID}_i}\) and sends \(\sigma _i = \mathsf {sk}_{\mathsf {ID}_i}\) to attacker \(\mathcal {A}\) as the signature for \(m_i\).
-
4.
Attacker \(\mathcal {A}\) submits a forgery \((m^{*}, \sigma ^{*})\) to \(\mathcal {B}\) where \(m^{*}\not = m_i\) for any queried \(m_i\).
-
5.
\(\mathcal {B}\) sets \(\mathsf {ID}^* = m^*\) and chooses \(d_0^*, d_1^* \mathop {\leftarrow }\limits ^{\scriptstyle \$}\mathcal {M}_\mathrm{IBE}\) uniformly at random such that \(d_0^* \ne d_1^*\). \(\mathcal {B}\) sends \(\mathsf {ID}^*\) as the challenge identity and \(d_0^*, d_1^*\) as the challenge messages to the IBE challenger. The IBE challenger chooses \(b \mathop {\leftarrow }\limits ^{\scriptstyle \$}\{0,1\}\) and sends the challenge ciphertext \(\mathsf {ct}^* \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Enc}_\mathrm{IBE}(\mathsf {pp}, d_b^*, \mathsf {ID}^*)\) to \(\mathcal {B}\).
-
6.
\(\mathcal {B}\) runs \(\textsf {Verify}_{\mathrm {RV}}(\mathsf {vk}, m^*, \sigma ^*; r)\) q times, where \(q = O(\lambda \cdot \epsilon _2^{-2})\) and \(r \mathop {\leftarrow }\limits ^{\scriptstyle \$}\mathcal {R}\) is freshly chosen for each run. Note that q is a polynomial when \(\epsilon _2\) is non-negligible. Let \(\mathsf {count}\) be the number of times \(\textsf {Verify}_{\mathrm {RV}}\) outputs 1. If \(\mathsf {count}< q \left( 1/\mathrm M+ \epsilon _2/2 \right) \), \(\mathcal {B}\) aborts and chooses \(b' \mathop {\leftarrow }\limits ^{\scriptstyle \$}\{0,1\}\) at random as its guess. If \(\mathsf {count}\ge q \left( 1/\mathrm M+ \epsilon _2/2 \right) \), \(\mathcal {B}\) computes \(d' = \textsf {Dec}_\mathrm{IBE}(\mathsf {pp}, \sigma ^*, \mathsf {ct}^*)\). If \(d' = d_0^*\), then \(\mathcal {B}\) sets \(b' = 0\). If \(d' = d_1^{*}\), \(\mathcal {B}\) sets \(b' = 1\). Otherwise, \(d'\) is a non-challenge message or \(\bot \), so \(\mathcal {B}\) guesses \(b' \mathop {\leftarrow }\limits ^{\scriptstyle \$}\{0,1\}\) uniformly at random and sends \(b'\) to IBE challenger as its guess.
We claim that \(\mathcal {B}\) wins the IBE security game with non-negligible probability. To prove our claim, we define the following events:
-
\(\mathsf {Abort}\):
 .
. -
\(\mathsf {Bad}\):

-
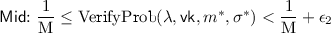
-

We say that \(\mathcal {B}\) aborts when event \(\mathsf {Abort}\) occurs and it chooses a random bit \(b' \mathop {\leftarrow }\limits ^{\scriptstyle \$}\{0,1\}\) as its guess. Events \(\mathsf {Bad}, \mathsf {Mid},\) and \(\mathsf {Good}\) quantify the successful verification probability of the forgery \((m^*, \sigma ^*)\) that \(\mathcal {A}\) produces. Event \(\mathsf {Bad}\) signifies that \((m^*, \sigma ^*)\) verifies with probability no greater than \(\chi = 1/\mathrm M\). Event \(\mathsf {Good}\) is the case when the forgery produced by \(\mathcal {A}\) verifies with non-negligible advantage over \(\chi = 1/\mathrm M\). Then, event \(\mathsf {Mid}\) represents the case in between \(\mathsf {Bad}\) and \(\mathsf {Good}\) such that \(\mathsf {Bad}, \mathsf {Mid},\) and \(\mathsf {Good}\) are mutually exclusive events.
The intuition behind running \(\textsf {Verify}_{\mathrm {RV}}\) q times independently is to make sure that the reduction does not use the forgery whenever \(\mathcal {A}\) provides a forgery that does worse than random guessing (of the encrypted message). This becomes necessary when we try to visualize the IBE message space to be very small. For instance, consider the scenario where \(\mathcal {A}\) can win with advantage 1 in the randomized verification signature security game, but instead of always outputting a correct forgery it creates a bad forgery almost half the time. Therefore, if \(\mathcal {B}\) directly uses the forgery to decrypt the challenge ciphertext which contains only one bit, then half the time it would be using a correct forgery and decrypting the challenge correctly, while at other times it would be decrypting incorrectly, and thus \(\mathcal {B}\)’s advantage in a direct reduction would be zero despite \(\mathcal {A}\)’s non-negligible advantage. Therefore, we want \(\mathcal {B}\) to accept the forgery and not abort only if \(\mathcal {A}\) produces a forgery such that verification succeeds with non-negligible probability over \(1/\mathrm M\). We provide a sketch of how these events relate to the probability that \(\mathcal {B}\) wins as follows.
We know that \(\Pr [\mathsf {Good}] = \epsilon _1\). Using Chernoff bound, we can show that \(\Pr [\; \mathsf {Abort}\mid \mathsf {Good}\; ] \le \text {negl}(\lambda )\), where \(\text {negl}(\cdot )\) is a negligible function. Therefore, \(\Pr [\; \overline{\mathsf {Abort}}\ \wedge \ \mathsf {Good}\; ] \ge \epsilon _1 - \text {negl}(\lambda )\). Similarly, we can show that \(\Pr [\; \overline{\mathsf {Abort}}\ \wedge \ \mathsf {Bad}\; ] \le \text {negl}(\lambda )\).
As described before, we want \(\mathcal {B}\) to have non-negligible advantage in the IBE security game when \(\mathcal {A}\) submits a forgery with high verification probability i.e. in event \(\mathsf {Good}\). Also we show that if the forgery submitted by \(\mathcal {A}\) is verifies with at least \(1/\mathrm M\) probability i.e. event \(\mathsf {Mid}\), then \(\mathcal {B}\) still wins the IBE security game with probability at least 1/2. We consider the following three mutually exclusive events describing a particular run of \(\textsf {Dec}_\mathrm{IBE}\) on challenge ciphertext \(\mathsf {ct}^*\) given that \(\mathcal {B}\) does not abort:
-
1.
\(\mathsf {Win}\): \(\textsf {Dec}_\mathrm{IBE}\) outputs the challenge message \(d_b^*\).
-
2.
\(\mathsf {Lose}\): \(\textsf {Dec}_\mathrm{IBE}\) outputs the incorrect challenge message \(d_{1-b}^*\).
-
3.
\(\mathsf {Split}\): \(\textsf {Dec}_\mathrm{IBE}\) outputs a non-challenge message or \(\bot \)
Note that \(\mathcal {B}\) wins with probability 1 in event \(\mathsf {Win}\), probability 0 in event \(\mathsf {Lose}\), and probability 1/2 in event \(\mathsf {Split}\). We use these different cases to analyze the probability the \(\mathcal {B}\) wins in the event \(\overline{\mathsf {Abort}}\).
Claim 1
\(\Pr [\; b=b^\prime \mid \overline{\mathsf {Abort}} \wedge \mathsf {Good}\; ] \ge \dfrac{\epsilon _2}{4} + \dfrac{1}{2}\)
Proof
Let \(p = \Pr [\;\mathsf {Win}\mid \overline{\mathsf {Abort}} \wedge \mathsf {Good}\;] \ge 1/\mathrm M+ \epsilon _2/2\) since in event \(\mathsf {Good}\), \(\mathrm {VerifyProb}(\lambda , \mathsf {vk}, m^*, \sigma ^*) \ge 1/\mathrm M+ \epsilon _2/2\). Then, \(\Pr [\;\mathsf {Split}\mid \overline{\mathsf {Abort}} \wedge \mathsf {Good}\;] \ge (1-p) \cdot \left( 1 - 1/(\mathrm M- 1)\right) \) since the challenge messages were chosen uniformly at random from \(\mathcal {M}_\mathrm{IBE}\).

Claim 2
\(\Pr [\; b=b^\prime \mid \overline{\mathsf {Abort}} \wedge \mathsf {Mid}\;] \ge \dfrac{1}{2}\)
Proof
The proof of the claim is the same as Claim 1 where  . Therefore, we get that
. Therefore, we get that  .
.
Now we can complete our analysis of the winning probability of the reduction algorithm \(\mathcal {B}\) in the IBE security game.

Thus,  , which is non-negligible if \(\epsilon _1\) and \(\epsilon _2\) are non-negligible.
, which is non-negligible if \(\epsilon _1\) and \(\epsilon _2\) are non-negligible.
We conclude that if \(\mathcal {E}\) is an adaptively-secure IBE scheme, then our construction is a  -secure randomized verification signature scheme.
-secure randomized verification signature scheme.
5 Amplifying Soundness
Ideally we would want from a randomized verification signature scheme that \(\chi = 0\), which could be equivalently stated as that the forgery does not get verified with non-negligible probability. However not all constructions could be provably \(\chi = 0\) secure, therefore we show a generic transformation from \(\chi = 1 - 1/p\) to \(\chi = 0\), where p is a polynomial in the security parameter \(\lambda \).
5.1 Construction
Let \(\mathcal {S}' = (\mathsf {Setup}', \mathsf {Sign}', \mathsf {Verify}')\) be a \(\chi = 1 - 1/p\) secure randomized verification signature scheme with message space \(\mathcal {M}'\) and verification coin space \(\mathcal {R}'\). We construct a \(\chi = 0\) secure randomized verification signature scheme as follows:
-
1.
\(\textsf {Setup}_{\mathrm {RV}}(1^\lambda )\): It computes \((\mathsf {sk}', \mathsf {vk}') \mathop {\leftarrow }\limits ^{\scriptstyle \$}\mathsf {Setup}'(1^\lambda )\) and returns \((\mathsf {sk}, \mathsf {vk})\) where \(\mathsf {sk}= \mathsf {sk}'\) and \(\mathsf {vk}= \mathsf {vk}'\).
-
2.
\(\textsf {Sign}_{\mathrm {RV}}(\mathsf {sk}, m)\): Let \(\mathsf {sk}= \mathsf {sk}'\). It computes \(\sigma \mathop {\leftarrow }\limits ^{\scriptstyle \$}\mathsf {Sign}'(\mathsf {sk}', m)\) and outputs \(\sigma \) as the signature.
-
3.
\(\textsf {Verify}_{\mathrm {RV}}(\mathsf {vk}, m, \sigma ; r)\): Let \(\mathsf {vk}= \mathsf {vk}'\), \(n = \varOmega (p \lambda )\), and \(r = (r_1, \ldots , r_n) \in (\mathcal {R}')^n\). For all \(i \in [n]\), it runs \(\mathsf {Verify}'(\mathsf {vk}', m, \sigma ; r_i)\). It outputs 1 if all n verifications output 1, and 0 otherwise.
5.2 Correctness and Security
Theorem 2
If \(\mathcal {S}' = (\mathsf {Setup}', \mathsf {Sign}', \mathsf {Verify}')\) be a \(\chi = (1 - 1/p)\)-EUFCMA secure signature scheme (Definition 3) with message space \(\mathcal {M}'\) and verification coin space \(\mathcal {R}'\), then above construction forms a \(\chi = 0\)-EUFCMA secure signature scheme as per Definition 3 with message space \(\mathcal {M}'\) and verification coin space \((\mathcal {R}')^n\), where \(n = \varOmega (p \lambda )\) and p is a polynomial in \(\lambda \).
Proof
It is straightforward to verify the correctness as it follows directly from the correctness of underlying randomized verification signature scheme. The proof of soundness amplification is the standard direct product amplification [12]. For completeness, we sketch the argument below.
Let \(\mathcal {R}^{*} = \left\{ r \in \mathcal {R}' : \mathsf {Verify}'(\mathsf {vk}', m^{*}, \sigma ^{*}; r) = 1\right\} \) denote the set of random coins on which verifier accepts the forgery \((m^{*}, \sigma ^{*})\). Since, \(\mathcal {S}'\) is \(\chi = 1 - 1/p\) secure, we know that \(\mathrm {VerifyProb}{(\lambda , \mathsf {vk}', m^{*}, \sigma ^{*})} \le 1 - 1/p + \mu '\) with all but negligible probability, where \(\mu '\) is a negligible function in \(\lambda \). Therefore, we can write that with all but negligible probability \(\left| \mathcal {R}^{*}\right| \le (1 - 1 / p + \mu ') \left| \mathcal {R}'\right| \). After amplification, \(\textsf {Verify}_{\mathrm {RV}}\) runs \(\mathsf {Verify}'\) on n uniformly random coins from \(\mathcal {R}'\), thus set of random coins in \((\mathcal {R}')^n\) on which \(\textsf {Verify}_{\mathrm {RV}}\) accepts the forgery \((m^{*}, \sigma ^{*})\) is \((\mathcal {R}^{*})^n\). So, substituting \(n = \varOmega (p \lambda )\), we can write that with all but negligible probability,
Therefore, we can conclude that if \(\mathcal {S}'\) is a \(\chi = (1 - 1/p)\)-EUFCMA secure randomized verification signature scheme, then \(\mathcal {S}\) is a \(\chi = 0\)-EUFCMA secure randomized verification signature scheme, where p is a polynomial in \(\lambda \).
6 Derandomizing Verification in the Random Oracle Model
In this section, we show how to generically transform a signature scheme with randomized verification to a signature scheme with deterministic verification in the Random Oracle Model (ROM). Consider any \(\chi =0\)-secure signature scheme with randomized verification.Footnote 2 Let \(\ell \) denote the number of random bits used by the verification algorithm. To make the verification algorithm deterministic, we will use a hash function H that maps (message, signature) pairs to \(\ell \) bit strings. The deterministic verification algorithm takes as input a signature \(\sigma \), message m, computes \(H(\sigma , m)\), and uses this as the randomness. For our security proof, the hash function H is modeled as a random oracle.
Let \(\mathcal {S}_\mathrm{RV} = (\textsf {Setup}_{\mathrm {RV}}, \textsf {Sign}_{\mathrm {RV}}, \textsf {Verify}_{\mathrm {RV}})\) be a \(\chi = 0\) secure randomized verification signature scheme with message space \(\mathcal {M}(\cdot )\), signature space \(\varSigma (\cdot )\) and verification coin space \(\mathcal {R}(\cdot )\). We construct a deterministic verification signature scheme with identical message and signature space:
-
1.
\(\textsf {Setup}_{\mathrm {Det}}(1^\lambda )\): It computes \((\mathsf {sk}_\mathrm{RV}, \mathsf {vk}_\mathrm{RV}) \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Setup}_{\mathrm {RV}}(1^\lambda )\) and returns \((\mathsf {sk}, \mathsf {vk}) = (\mathsf {sk}_\mathrm{RV}, \mathsf {vk}_\mathrm{RV})\).
-
2.
\(\textsf {Sign}_{\mathrm {Det}}(\mathsf {sk}, m)\): Let \(\mathsf {sk}= \mathsf {sk}_\mathrm{RV}\). It computes \(\sigma \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Sign}_{\mathrm {RV}}(\mathsf {sk}_\mathrm{RV}, m)\) and outputs \(\sigma \) as the signature.
-
3.
\(\textsf {Verify}_{\mathrm {Det}}(\mathsf {vk}, m, \sigma )\): Let \(\mathsf {vk}= \mathsf {vk}_\mathrm{RV}\) and \(r = H(m, \sigma )\). It outputs \(\textsf {Verify}_{\mathrm {RV}}(\mathsf {vk}_\mathrm{RV}, m, \sigma ; r)\).
Theorem 3
If \(\mathcal {S}_\mathrm{RV} = (\textsf {Setup}_{\mathrm {RV}}, \textsf {Sign}_{\mathrm {RV}}, \textsf {Verify}_{\mathrm {RV}})\) be a \(\chi = 0\)-EUFCMA secure randomized verification signature scheme (Definition 3) with message space \(\mathcal {M}(\cdot )\), signature space \(\varSigma (\cdot )\) and verification coin space \(\mathcal {R}(\cdot )\), then above construction forms a EUFCMA secure deterministic verification signature scheme as per Definition 1 with message space \(\mathcal {M}(\cdot )\) and signature space \(\varSigma (\cdot )\).
Proof
It is straightforward to verify the correctness as it follows directly from the correctness of underlying randomized verification signature scheme. For proving security in the random oracle model, we will assume the hash function H is modeled as a random oracle. Let q denote the number of queries made by the adversary to the random oracle. Without loss of generality, we can assume that the forgery \((m^*, \sigma ^*)\) is one of the q queries.
We can directly reduce an attack on our deterministic verification scheme construction to an attack on \(\mathcal {S}_\mathrm{RV}\). Our reduction algorithm \(\mathcal {B}\) will receive a verification key \(\mathsf {vk}_\mathrm{RV}\) from \(\mathcal {S}_\mathrm{RV}\) challenger. It forwards \(\mathsf {vk}_\mathrm{RV}\) to \(\mathcal {A}\). \(\mathcal {B}\) relays all signature queries made by \(\mathcal {A}\) to \(\mathcal {S}_\mathrm{RV}\) challenger. For answering hash queries \(\mathcal {B}\) maintains a lookup table, and for each new query \((m, \sigma )\) it chooses a uniformly random coin from \(\mathcal {R}\). Finally, when \(\mathcal {A}\) submits the forgery \((m^*, \sigma ^*)\), \(\mathcal {B}\) forwards it to the challenger.
Suppose \(\mathcal {A}\) wins with probability \(\epsilon _1\), and let \(\mathcal {R}^* = \mathcal {R}_{m^*,\sigma ^*}\).

Now, note that  . This is because for each of the random oracle queries, the response is a uniformly random element in \(\mathcal {R}\). As a result, using union bound, \(\Pr [\exists \text { RO query } (m_i, \sigma _i) \text { such that }| \mathcal {R}_{m_i, \sigma _i}|/|\mathcal {R}| \le \text {negl}(\lambda ) \text { and } H(m_i, \sigma _i) \in \mathcal {R}_{m_i, \sigma _i} ] \le q\cdot \text {negl}(\lambda )\).
. This is because for each of the random oracle queries, the response is a uniformly random element in \(\mathcal {R}\). As a result, using union bound, \(\Pr [\exists \text { RO query } (m_i, \sigma _i) \text { such that }| \mathcal {R}_{m_i, \sigma _i}|/|\mathcal {R}| \le \text {negl}(\lambda ) \text { and } H(m_i, \sigma _i) \in \mathcal {R}_{m_i, \sigma _i} ] \le q\cdot \text {negl}(\lambda )\).
Therefore, \(\Pr [\mathcal {B}\text { wins}] = \Pr [\mathcal {A}\text { outputs } (m^*, \sigma ^*) \text { and } |\mathcal {R}^*|/|\mathcal {R}| \ge 1/\mathsf {poly}(\lambda )] \ge \epsilon _1 - \text {negl}(\lambda )\).
7 Derandomizing Verification in the Standard Model
In this section, we present a transformation from a \(\chi = 0\)-EUFCMA secure signature scheme with randomized verification to one that has a deterministic verification algorithm, and prove it EUFCMA secure in the standard model. At a high level, the transformed scheme can be described as follows. The verification key consists of n uniformly random strings \(r_1, \ldots , r_n\) from \(\mathcal {R}\), where n is bounded by a sufficiently large polynomial in the security parameter. These random strings are then used by the verification algorithm to check if \(\sigma \) is a valid signature for message m. Note that the random strings \(r_1, \ldots , r_n\) used during verification are chosen during Setup and kept as part of the verification key. At first sight, it might appear that, since the random strings are fixed during setup, the reduction to the underlying verification scheme will not go through because now the adversary’s forgery may depend on the random coins used to verify. However, this is not the case because the underlying randomized verification signature scheme satisfies \(\chi = 0\)-EUFCMA security, therefore taking a union bound over all possible message-signature pairs we could rule out this case as if n is sufficiently large, then the probability that some bad message-signature pair gets verified using all \(r_1, \ldots , r_n\) (independently) is negligible. Below we describe the transformation.
Let \(\mathcal {S}_\mathrm{RV} = (\textsf {Setup}_{\mathrm {RV}}, \textsf {Sign}_{\mathrm {RV}}, \textsf {Verify}_{\mathrm {RV}})\) be a \(\chi = 0\)-EUFCMA secure randomized verification signature scheme with message space \(\mathcal {M}(\cdot )\), signature space \(\varSigma (\cdot )\) and verification coin space \(\mathcal {R}(\cdot )\). We construct a deterministic verification signature scheme with identical message and signature space:
-
1.
\(\textsf {Setup}_{\mathrm {Det}}(1^\lambda )\): The setup algorithm first chooses \((\mathsf {sk}_\mathrm{RV}, \mathsf {vk}_\mathrm{RV}) \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Setup}_{\mathrm {RV}}(1^\lambda )\). Next, it sets \(\mathsf {sk}= \mathsf {sk}_\mathrm{RV}\), \(n = \varOmega \left( \ \log (|\mathcal {M}| \cdot |\varSigma |)\ \right) \), and chooses n coins \(\left\{ r_1, \ldots , r_n\right\} \) where \(r_i \mathop {\leftarrow }\limits ^{\scriptstyle \$}\mathcal {R}\) for \(i\le n\). The verification key \(\mathsf {vk}\) consists of \((\mathsf {vk}_\mathrm{RV}, \{r_1, \ldots , r_n\})\).
-
2.
\(\textsf {Sign}_{\mathrm {Det}}(\mathsf {sk}, m)\): Let \(\mathsf {sk}= \mathsf {sk}_\mathrm{RV}\). The signing algorithm computes \(\sigma \mathop {\leftarrow }\limits ^{\scriptstyle \$}\textsf {Sign}_{\mathrm {RV}}(\mathsf {sk}_\mathrm{RV}, m)\) and outputs \(\sigma \) as the signature.
-
3.
\(\textsf {Verify}_{\mathrm {Det}}(\mathsf {vk}, m, \sigma )\): Let \(\mathsf {vk}= (\mathsf {vk}_\mathrm{RV}, \left\{ r_1, \ldots , r_n\right\} )\). The verification algorithm checks if \(\textsf {Verify}_{\mathrm {RV}}(\mathsf {vk}_\mathrm{RV}, m, \sigma ; r_i) =1\) for all \(i\le n\). If so, it outputs 1, else it outputs 0.
Theorem 4
Let \(\mathcal {S}_\mathrm{RV} = (\textsf {Setup}_{\mathrm {RV}}, \textsf {Sign}_{\mathrm {RV}}, \textsf {Verify}_{\mathrm {RV}})\) be a \(\chi = 0\)-EUFCMA secure randomized verification signature scheme (Definition 3) with message space \(\mathcal {M}(\cdot )\), signature space \(\varSigma (\cdot )\) and verification coin space \(\mathcal {R}(\cdot )\). The above construction forms a EUFCMA secure deterministic verification signature scheme as per Definition 1 with message space \(\mathcal {M}(\cdot )\) and signature space \(\varSigma (\cdot )\).
Proof
It is straightforward to verify the correctness as it follows directly from the correctness of underlying randomized verification signature scheme. To formally describe our reduction we distinguish between two types of forgers that an attacker \(\mathcal {A}\) can emulate. Let \(\mathcal {R}_{m^{*}, \sigma ^{*}} = \left\{ r \in \mathcal {R}: \textsf {Verify}_{\mathrm {RV}}(\mathsf {vk}_\mathrm{RV}, m^{*}, \sigma ^{*}; r) = 1\right\} \) denote the set of random coins on which verifier accepts the forgery \((m^{*}, \sigma ^{*})\). We distinguish between two types of forgers as follows:
Type 1 forger: \(\mathcal {A}\) with non-negligible probability, outputs a forgery \((m^{*}, \sigma ^{*})\) such that \(|\mathcal {R}_{m^{*}, \sigma ^{*}}| / |\mathcal {R}|\) is non-negligible in \(\lambda \).
Type 2 forger: \(\mathcal {A}\) with non-negligible probability, outputs a forgery \((m^{*}, \sigma ^{*})\) such that \(|\mathcal {R}_{m^{*}, \sigma ^{*}}| / |\mathcal {R}|\) is negligible in \(\lambda \).
Claim 3
If \(\mathcal {A}\) emulates a Type 1 forger, then there exists a reduction algorithm \(\mathcal {B}\) that breaks \(\chi = 0\)-EUFCMA security of randomized verification signature scheme \(\mathcal {S}_\mathrm{RV}\).
Proof
In case of type 1 forgery, we can directly reduce an attack on our deterministic verification scheme construction to an attack on \(\mathcal {S}_\mathrm{RV}\). Our reduction algorithm \(\mathcal {B}\) will receive a verification key \(\mathsf {vk}_\mathrm{RV}\) from \(\mathcal {S}_\mathrm{RV}\) challenger. It chooses n coins \(\left\{ r_1, \ldots , r_n\right\} \mathop {\leftarrow }\limits ^{\scriptstyle \$}\mathcal {R}^n\) and forwards \((\mathsf {vk}_\mathrm{RV}, \left\{ r_1, \ldots , r_n\right\} )\) to \(\mathcal {A}\). \(\mathcal {A}\) relays all signature queries made by \(\mathcal {A}\) to \(\mathcal {S}_\mathrm{RV}\) challenger. By assumption, \(|\mathcal {R}_{m^{*}, \sigma ^{*}}| / |\mathcal {R}|\) is non-negligible for a type 1 forger, thus \(\mathrm {VerifyProb}(\lambda , \mathsf {vk}_\mathrm{RV}, m^{*}, \sigma ^{*}) = |\mathcal {R}_{m^{*}, \sigma ^{*}}| / |\mathcal {R}|\) is also non-negligible. Hence, if \(\mathcal {A}\) emulates a type 1 forger, then it also breaks \(\chi = 0\)-EUFCMA security of randomized verification signature scheme \(\mathcal {S}_\mathrm{RV}\).
Claim 4
If \(\mathcal {A}\) emulates a Type 2 forger, then it does not break \(\chi = 0\)-EUFCMA security of randomized verification signature scheme \(\mathcal {S}_\mathrm{RV}\) with all but negligible probability.
Proof
In case of type 2 forgery, we show that if we set \(n = \varOmega \left( \ \log (|\mathcal {M}| \cdot |\varSigma |)\ \right) \),Footnote 3 then (with all but negligible probability) there does not exists any \((m, \sigma )\) pair such that \(\left\{ r_1, \ldots , r_n\right\} \subseteq \mathcal {R}_{m, \sigma }\) and \(|\mathcal {R}_{m, \sigma }| / |\mathcal {R}|\) is negligible. Let \(\mathsf {Bad}\) denote the set of \((m, \sigma )\) pairs such that \(|\mathcal {R}_{m, \sigma }| / |\mathcal {R}|\) is negligible, and \(R_{\max } = \underset{(m, \sigma ) \in \mathsf {Bad}}{\max } |\mathcal {R}_{m, \sigma }|\). The proof follows from union bound over all such \((m, \sigma )\) pairs in \(\mathsf {Bad}\). First, observe that
where \(\mu '\) is a negligible function. Using union bound, we can write that
Since we set \(n = \varOmega \left( \ \log (|\mathcal {M}| \cdot |\varSigma |)\ \right) \), the above expression is negligible in \(\lambda \). Therefore, no type 2 forger can win with non-negligible probability over random choice of n verification coins.
Therefore, reduction algorithm \(\mathcal {B}\) always guesses \(\mathcal {A}\) to be a Type 1 forger and plays the standard reduction.
Notes
- 1.
In this work we define take the “Naor transformation” to be how it was originally described in the Boneh-Franklin [2] paper. We empahsize that in this case there is a single message x that is encrypted and tested for verification.
- 2.
In the previous section, we showed how to amplify the security from \(\chi = 1-1/\mathsf {poly}(\lambda )\) to \(\chi =0\). Therefore, our starting point in the transformation will be a randomized verification signature scheme with \(\chi = 0\).
- 3.
Setting \(n = \varOmega \left( \ \log (|\mathcal {M}| \cdot |\varSigma |) / \log (1 / \mu ')\ \right) \) is sufficient where \(\mu '\) is a negligible function that depends upon the parameters of the randomized verification scheme.
References
Boneh, D., Franklin, M.: Identity-based encryption from the weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_13
Boneh, D., Franklin, M.K.: Identity-based encryption from the weil pairing. SIAM J. Comput. 32(3), 586–615 (2003)
Boneh, D., Lynn, B., Shacham, H.: Short signatures from the Weil pairing. J. Cryptol. 17(4), 297–319 (2004)
Cocks, C.: An identity based encryption scheme based on quadratic residues. In: Honary, B. (ed.) Cryptography and Coding 2001. LNCS, vol. 2260, pp. 360–363. Springer, Heidelberg (2001). doi:10.1007/3-540-45325-3_32
Cui, Y., Fujisaki, E., Hanaoka, G., Imai, H., Zhang, R.: Formal security treatments for IBE-to-signature transformation: relations among security notions. IEICE Trans. 92–A(1), 53–66 (2009)
Goldwasser, S., Micali, S., Rivest, R.L.: A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. 17(2), 281–308 (1988)
Naor, M.: On cryptographic assumptions and challenges. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 96–109. Springer, Heidelberg (2003). doi:10.1007/978-3-540-45146-4_6
Schröder, D., Unruh, D.: Security of blind signatures revisited. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 662–679. Springer, Heidelberg (2012). doi:10.1007/978-3-642-30057-8_39
Unruh, D.: Everlasting multi-party computation. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 380–397. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_22
Waters, B.: Efficient identity-based encryption without random oracles. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 114–127. Springer, Heidelberg (2005). doi:10.1007/11426639_7
Waters, B.: Dual system encryption: realizing fully secure IBE and HIBE under simple assumptions. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 619–636. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03356-8_36
Yao, A.C.: Theory and application of trapdoor functions. In: Proceedings of the 23rd Annual Symposium on Foundations of Computer Science, SFCS 1982, pp. 80–91 (1982). http://dx.doi.org/10.1109/SFCS.1982.95
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Freitag, C. et al. (2017). Signature Schemes with Randomized Verification. In: Gollmann, D., Miyaji, A., Kikuchi, H. (eds) Applied Cryptography and Network Security. ACNS 2017. Lecture Notes in Computer Science(), vol 10355. Springer, Cham. https://doi.org/10.1007/978-3-319-61204-1_19
Download citation
DOI: https://doi.org/10.1007/978-3-319-61204-1_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-61203-4
Online ISBN: 978-3-319-61204-1
eBook Packages: Computer ScienceComputer Science (R0)





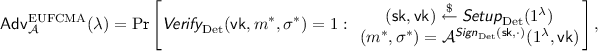

 .
.