Abstract
Interactive program synthesizers enable a user to communicate his/her intent via input-output examples. Unfortunately, such synthesizers only guarantee that the synthesized program is correct on the provided examples. A user that wishes to guarantee correctness for all possible inputs has to manually inspect the synthesized program, an error-prone and challenging task.
We present a novel synthesis framework that communicates only through (abstract) examples and guarantees that the synthesized program is correct on all inputs. The main idea is to use abstract examples—a new form of examples that represent a potentially unbounded set of concrete examples. An abstract example captures how part of the input space is mapped to corresponding outputs by the synthesized program. Our framework uses a generalization algorithm to compute abstract examples which are then presented to the user. The user can accept an abstract example, or provide a counterexample in which case the synthesizer will explore a different program. When the user accepts a set of abstract examples that covers the entire input space, the synthesis process is completed.
We have implemented our approach and we experimentally show that our synthesizer communicates with the user effectively by presenting on average 3 abstract examples until the user rejects false candidate programs. Further, we show that a synthesizer that prunes the program space based on the abstract examples reduces the overall number of required concrete examples in up to 96% of the cases.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
We address the problem of interactive synthesis, where a user and synthesizer interact to generate a program that captures the user’s intent. Interactive synthesis enables users to express their intent by providing the synthesizer with input-output examples. Unfortunately, such synthesizers only guarantee that the synthesized program is correct on the provided examples. A user that wishes to guarantee correctness for all possible inputs has to manually inspect the synthesized program, an error-prone and challenging task.
Motivating Example. Eli Gold is a crisis manager at a respected law firm that due to a crisis has to meet all office members personally. After setting up times and storing the meeting times in an Excel spreadsheet (Fig. 1), Eli wants to send emails with a personal message notifying each member the time of the meeting. He starts typing the messages in Excel. While typing the third message, Flash Fill [21] (a PBE synthesizer integrated in Excel) synthesizes a program and creates messages for all members on the list.
At first glance, Flash Fill seems to have learned the correct program. However, careful inspection reveals that instead of the desired “Hi” greeting, the message’s first word is an “H” followed by the second letter of the person’s first name. This demonstrates the importance of inspecting the synthesis result before relying on it to handle additional examples (e.g., lines 4–6 in the Excel spreadsheet).
Goal. In this work, we wish to ensure correctness of the synthesized program on all inputs, while still interacting with the user through examples.
Existing Techniques. Interactive synthesis with correctness guarantees can be viewed as a special case of exact learning [10], where a learner (the synthesizer) and a teacher (the user) interact to find the target concept known to the teacher. In exact learning, the learner interacts with the teacher by asking two kinds of questions: (i) membership questions, where the learner asks for the output of a given input, and (ii) validation questions, where the learner asks whether a hypothesis (a synthesized program) is correct and if not, asks for a counterexample.
The popular counterexample-guided inductive synthesis (CEGIS) [41] approach can be viewed as an instance of exact learning where the teacher is realized as a verifier with a formal specification (rather than a user). The formal specification provides an efficient way to answer validation questions automatically. Using validation questions ensures correctness on all inputs, but requires a formal specification of the user intent, a specification which often does not exist.
In contrast, in programming by example (PBE), the user provides a set of input-output examples which correspond to membership questions (and answers). Classical PBE approaches (e.g., [5, 29, 33]) do not use any validation questions, and never present the synthesized program to the user. These techniques tradeoff exactness for ease of interaction with an end-user. In terms of correctness, they only guarantee that the synthesized program is consistent with the user-provided examples. Other techniques (e.g., [26]) obtain correctness but make additional assumptions (see Sect. 6).
Relying solely on membership questions is limited in its ability to ensure correctness. Without validation queries or additional assumptions on the program space, correctness is only guaranteed if the entire input space is covered by membership questions (examples). When the input space is finite, this is usually impractical. When the input space is infinite, asking membership questions about all inputs is clearly impossible.
Our Approach. We present a novel interactive synthesis framework that communicates with a user only through abstract membership queries—asking the user whether an abstract example of the current candidate program should be accepted or rejected—and guarantees that the synthesized program is correct on all inputs. Abstract examples are a new form of examples that represent a potentially unbounded set of concrete examples of a candidate program. Abstract examples are natural for a user to understand and inspect (similarly to examples), and at the same time enable validation of the synthesis result without enumerating all concrete examples (which is only possible for a finite domain, and even then is often prohibitively expensive). In fact, an abstract membership question can also be viewed as a partial validation question. Instead of presenting the user with a program and asking him/her to determine whether it is correct or not (a validation question), we present an abstract example, which describes (declaratively) how the candidate program transforms part of the input space. In this way, abstract examples allow us to perform exact synthesis without a predefined specification.
Throughout the synthesis process, as the synthesizer explores the space of candidate programs to find the one that matches the user intent, the synthesizer presents to the user abstract examples of candidate programs. The user can accept an abstract example, or provide a counterexample in which case the synthesizer will explore a different candidate program. If the user accepts an abstract example, he/she confirms the behavior of the candidate program on part of the input space. That is, the synthesizer learns the desired behavior for an unbounded number of concrete inputs. Thus, it can prune every program that does not meet the confirmed abstract example. This pruning is correct even if later the candidate program is rejected by another abstract example. Generally, pruning based on an abstract example removes more programs than pruning based on a concrete example. Thus, our synthesizer is likely to converge faster to the target program compared to the current alternative (see Sect. 5). When the user accepts a set of abstract examples that covers the entire input space, our synthesizer returns the corresponding candidate program and the synthesis process is completed.
A key ingredient of our synthesizer is a generalization algorithm, called L-SEP. L-SEP takes a concrete example and a candidate program, and generalizes the example to a maximally general abstract example consistent with the candidate program. To illustrate, consider our motivating example, and assume the candidate program is the one synthesized by Flash Fill (that returns “H” followed by the second letter of the person’s first name, etc.) and the initial concrete example is the first member on the list (i.e., Diane). Our generalization algorithm produces the following abstract example:

This example describes the program behavior on the cells at columns A, B, and C, for the case where the string at cell A has at least two characters, denoted by \(a_0\) and \(a_1\), followed by a string sequence of an arbitrary size (including 0), denoted by \(A_2\). For such inputs, the example describes the output as a sequence consisting of: (i) the string “H” followed by \(a_1\), (ii) the entire string at A followed by a comma, (iii) the string: “please come to my office at”, (iv) the string at C, and (v) the string: “. -EG”.
This abstract example is presented to the user. The user rejects it and provides a concrete counterexample (e.g., line 4 in the Excel spreadsheet). Thus, the synthesizer prunes the space of candidate programs and generates a new candidate program. Eventually, the synthesizer generates the target program (as a candidate program), and our synthesizer presents the following abstract example:

This time, the user accepts it. Since this abstract example covers the entire input space, the synthesizer infers that this program captures the user intent on all inputs and returns it. In general, covering the input space may require multiple abstract examples.
We have implemented our synthesizer and experimentally evaluated it on two domains: strings and bit vectors. Results indicate that our synthesizer can communicate with the user effectively by presenting on average 3 abstract examples until the user rejects false candidate programs (on our most challenging benchmark, consisting of programs that require a large number of examples to differentiate them from the other programs). Further, results show that pruning the program space based on the abstract examples reduces the overall number of required concrete examples in up to 96% of the cases.
Main Contributions. The main contributions of this paper are:
-
A new notion of abstract examples, which capture a (potentially unbounded) set of concrete examples, and a realization via a language inspired by regular expressions (Sect. 2).
-
A generalization algorithm for learning a maximally generalizing abstract example from a concrete example and a candidate program (Sect. 3).
-
A novel synthesis framework that communicates only through abstract examples and guarantees that the synthesized program is correct on all inputs (Sect. 4).
-
An implementation and experimental evaluation that shows that our synthesizer requires few abstract examples to reject false programs, and that it reduces the number of concrete examples required to find the target program (Sect. 5).
2 Abstract Specifications and Sequence Expressions
In this section, we define the key terms pertaining to abstract examples. We then present a special class of abstract examples for programs that manipulate strings. For simplicity’s sake, from here on we assume that programs take one input. This is not a limitation as multiple inputs (or outputs) can be joined with a predefined delimiter (e.g., the inputs in the motivating example can be considered as one string separated by spaces).
2.1 Abstract Examples
Program Semantics. The semantics of a program P is a function over a domain D: \({[\![{P} ]\!]}:D\rightarrow D\). We equate \({[\![{P} ]\!]}\) with its input-output pair set: \(\{ (in, {[\![{P} ]\!]}(in)) \mid in \in D\}\).
Abstract Examples. An abstract example ae defines a set \({[\![{ae} ]\!]} \subseteq D \times D\), which represents a partial function: if \((in, out_1), (in, out_2) \in {[\![{ae} ]\!]}\), then \(out_1 = out_2\). An abstract example ae is an abstract example for program P if \({[\![{ae} ]\!]} \subseteq {[\![{P} ]\!]}\). We define the domain of ae to be \(dom(ae)=\{in \in D \mid \exists out.\ (in, out)\in {[\![{ae} ]\!]}\}\).
Abstract Example Specifications. An abstract example specification of P is a set of abstract examples A for P such that \(\bigcup _{ae \in A} dom(ae) = D\). Note that A need not be finite and the example domains need not be disjoint.
2.2 Sequence Expressions
In this work, we focus on programs that manipulate strings, i.e., \(D = \varSigma ^*\) for a finite alphabet \(\varSigma \). Thus, it is desirable to represent abstract examples as expressions that represent collections of concrete strings and can be readily interpreted by humans. A prominent candidate for this goal is regular expressions, which are widely used to succinctly represent a set of strings. However, regular expressions are restricted to constant symbols (from \(\varSigma \)). Thus, they cannot relate outputs to inputs, which is desirable when describing partial functions (abstract examples). To obtain this property, we introduce a new language, Sequence Expressions (SE), that extends regular expressions with the ability to relate the outputs to their inputs via shared variables. We begin this section with a reminder of regular expressions, and then introduce the two types of sequence expressions: input SEs, for describing inputs, and output SEs, for describing outputs.
Regular Expressions (RE). The set of regular languages over a finite alphabet \(\varSigma \) is the minimal set containing \(\epsilon , \sigma _1,...,\sigma _{|\varSigma |}\) that is closed under concatenation, union, and Kleene star. A regular expression r is a text representation of a regular language over the symbols in \(\varSigma \) and the operators \(\cdot , | ,^*\) (concatenation, or, and Kleene star).
Input SE Syntax. Figure 2(a) shows the grammar of input SEs. Compared to RE, SEs are extended with three kinds of variables that later help to relate the output to the input:
-
Character variables, denoted
 , used to denote an arbitrary letter from \(\varSigma \).
, used to denote an arbitrary letter from \(\varSigma \). -
Sequence variables, denoted \(X\in \mathbf {X}\), used to denote a sequence of arbitrary size.
-
Star variables, denoted
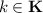 , used instead of the Kleene star to indicate the number of consecutive repeating occurrences of a symbol. For example, \(0^k\) has the same meaning as the RE \(0^*\).
, used instead of the Kleene star to indicate the number of consecutive repeating occurrences of a symbol. For example, \(0^k\) has the same meaning as the RE \(0^*\).
To eliminate ambiguity, in our examples we underline letters from \(\varSigma \). For example, \(xX\underline{\text {a}}\) represents the set of words that have at least two letters and end with an a (a \(\in \varSigma \)).
We limit each variable (i.e., \(x,X,k\)) to appear at most once at an input SE. We also limit the use of a Kleene star to single letters from the alphabet. Also, since the goal of each SE is to describe a single behavior of the program, we exclude the ‘or’ operator. Instead, we extend the grammar to enable to express ‘or’ to some extent via predefined predicates that put constraints on the variables. We denote these predicates by \(R \in \mathcal {R}\), and their meaning (i.e., the set of words that satisfy them) by \({[\![{R} ]\!]} \subseteq \varSigma ^*\). We note that we do not impose restrictions on the set \(\mathcal {R}\), however our algorithm relies on an SMT-solver, and thus predicates in \(\mathcal {R}\) have to be encodable as formulas.
Some examples for predicates and their meaning are: \({[\![{\text {num}} ]\!]}=\{w \in \varSigma ^*\mid w \text { consists of digits only}\}\), \({[\![{\text {anum}} ]\!]}=\{w \in \varSigma ^*\mid w \text { consists of letters and digits only}\}\), \({[\![{\text {del}} ]\!]}=\{., \backslash t,;\}\), \({[\![{\text {no}\_\text {del}} ]\!]} =\varSigma ^* \setminus {[\![{\text {del}} ]\!]}\). We assume that the predicate satisfied by any string, \(\textit{T}\), (where \({[\![{T} ]\!]}=\varSigma ^*\)) is always in \(\mathcal {R}\). We abbreviate \({x}_{\textit{T}}\), \({X}_{\textit{T}}\) to \(x,X\). In the following, we refer to these as atomic constructs: \(\sigma , {x}_{R}, {X}_{R}, \sigma ^k\). Given an input SE se we denote by \(\mathbf {x}_{se}\), \(\mathbf {X}_{se}\), and \(\mathbf {K}_{se}\) the set of variables in se.
Input SE Semantics. To define the semantics, we first define interpretations of an SE, which depend on assignments. An assignment env for an input SE se maps every \(x\in \mathbf {x}_{se}\) to a letter in \(\varSigma \), every \(X\in \mathbf {X}_{se}\) to a sequence in \(\varSigma ^*\), and every \(k\in \mathbf {K}_{se}\) to a natural number (including 0). We denote by \(env[se]\) the sequence over \(\varSigma \) obtained by substituting the variables with their interpretations. Formally: (i) \(env[\epsilon ] = \epsilon \) (ii) \(env[\sigma ] = \sigma \) (iii) \(env[x_R] = env(x)\) (iv) \(env[X_R] = env(X)\) (v) \(env[\sigma ^k] =\sigma ^{env(k)}\) (vi) \(env[ S_1\cdot S_2] = env[S_1] \cdot env[S_2]\) (where \(\cdot \) denotes string concatenation). An assignment is valid if for every \({x}_R\) and \({X}_R\) in se, \(env(x),env(X)\in {[\![{R} ]\!]}\). In the following we always refer to valid assignments.
The semantics of an input SE se, denoted by \({[\![{se} ]\!]}\), is the set of strings obtained by the set of all valid assignments, i.e. \({[\![{se} ]\!]} = \{ s \in \varSigma ^* \mid \exists env.\ env[se] = s \}\). For example, \({[\![{\sigma } ]\!]} = \{\sigma \}\), \({[\![{x} ]\!]} = \varSigma \), \({[\![{X} ]\!]}=\varSigma ^*\), and \({[\![{\sigma ^k} ]\!]}=\{\epsilon , \sigma , \sigma \sigma ,...\}\).
Output SE. Figure 2(b) shows the grammar of output SEs. Output SEs are defined with respect to an input SE and they can only refer to its variables. Formally, given an input SE se, an output SE over se is restricted to variables in \(\mathbf {x}_{se}\), \(\mathbf {X}_{se}\), and \(\mathbf {K}_{se}\). Unlike input SEs, an output SE is allowed to have multiple occurrences of the same variable, and variables are not constrained by predicates. In addition, output SEs can express invocations of unary functions over the variables. Namely, the grammar is extended by \(f(x)\) and \(f(X)\), where \(x \in \mathbf {x}_{se}\) and \(X \in \mathbf {X}_{se}\), and \(f : \varSigma \rightarrow \varSigma ^*\) is a function.
An interpretation of an output SE is defined with respect to an assignment, similarly to the interpretation of an input SE. We extend the interpretation definition for the functions as follows:  and if \(env(X) = \sigma _1 \cdots \sigma _n\) then \(env[f(X)] = f(\sigma _1) \cdots f(\sigma _n)\), i.e., \(env[f(X)]\) is the concatenation of the results of invoking f on the characters of the interpretation of X. (If \(env(X) = \epsilon \), \(env[f(X)] = \epsilon \).)
and if \(env(X) = \sigma _1 \cdots \sigma _n\) then \(env[f(X)] = f(\sigma _1) \cdots f(\sigma _n)\), i.e., \(env[f(X)]\) is the concatenation of the results of invoking f on the characters of the interpretation of X. (If \(env(X) = \epsilon \), \(env[f(X)] = \epsilon \).)
Input-Output SE Pairs. An input-output SE (interchangeably, an SE pair) is a pair \(io = se_{in} \rightarrow se_{out}\) consisting of an input SE, \(se_{in}\), and an output SE, \(se_{out}\), defined over \(se_{in}\). Given \(io = se_{in} \rightarrow se_{out}\), we denote \(in(io)=se_{in}\) and \(out(io)=se_{out}\). The semantics of io is the set of pairs: \({[\![{io} ]\!]} = \{ (s_{in}, s_{out}) \in \varSigma ^*\times \varSigma ^*\mid \exists env.\ s_{in} = env[in(io)] \wedge s_{out} = env[out(io)] \}\). The domain of io is \(dom(io) = {[\![{in(ae)} ]\!]}\).
Example. An input-output SE for the pattern of column D based on columns A, B in Fig. 1 is:

where \(x_0\) is a character variable, \(X_1\) and \(X_2\) are sequence variables and \({\_ }\) denotes a column delimiter (taken from \(\varSigma \)). The predicate no_del is satisfied by words that do not contain a delimiter. The semantics of this SE pair is the set of all word pairs whose first element is a string consisting of a first name, a delimiter, and a last name, and the second element is the email address which is the sequence of the first letter of the first name in lower case, a dot, the lower-cased last name, and the suffix “@lockhart-gardner.com”.
2.3 Sequence Expressions as Abstract Examples
SE pairs provide an intuitive mean to describe relation between outputs to inputs. In this work, we focus on learning abstract examples that can be described with SE pairs. For simplicity’s sake, in the following we ignore predicates and functions (i.e., \(\mathcal {R},\mathcal {F}\)). Our definitions and algorithms can be easily extended to arbitrary (but finite) sets \(\mathcal {R}\) and \(\mathcal {F}\).
We say that an input-output SE is an abstract example if \({[\![{io} ]\!]}\) describes a partial function. Note that in general, an SE pair is not necessarily an abstract example. For example, the pair \(io_{XY} = XY \rightarrow XaY\), can be interpreted to (bbb, babb) (by \(env_1 = \{X \mapsto b, Y \mapsto bb\}\)) and (bbb, bbab) (by \(env_2 = \{X \mapsto bb, Y \mapsto b\}\)). Thus, \({[\![{io_{XY}} ]\!]}\) is not a partial function and hence not an abstract example.
Given a program P, we say that an input-output SE is an abstract example for P if \({[\![{io} ]\!]} \subseteq {[\![{P} ]\!]}\). Since \({[\![{P} ]\!]}\) is a function, this requirement subsumes the requirement of abstract example. Given an input SE \(se_{in}\), we say that an output SE \(se_{out}\) over \(se_{in}\) is a completion of \(se_{in}\) for P if \(se_{in}\rightarrow se_{out}\) is an abstract example for P.
Example. We next exemplify how SEs can provide an abstract example specification to describe a program behavior. Assume a user has a list of first names and middle names (space delimited), some are only initials, and he/she wants to create a greeting message of the form “Dear <name>”. The name in the greeting is the first string if it is identified as a name, i.e., has at least two letters; otherwise, the name is the entire string. For example: (i) Adam \(\rightarrow \) Dear Adam, (ii) Adam R. \(\rightarrow \) Dear Adam, (iii) A. Robert \(\rightarrow \) Dear A. Robert (iv) A.R. \(\rightarrow \) Dear A.R.. In this example, we assume the predicate set contains the predicates \(\mathcal {R}=\{T, \text {name},\text {other}\}\), where \({[\![{\text {name}} ]\!]}=\{A,a,...,Z,z\}^+ \setminus \{A,a,...,Z,z\}\),  . An abstract example specification is: (i) \(X_{0_{\text {name}}}\rightarrow \underline{\text {Dear }}X_0\) (ii)
. An abstract example specification is: (i) \(X_{0_{\text {name}}}\rightarrow \underline{\text {Dear }}X_0\) (ii)  (iii) \(X_{0_{\text {other}}}\rightarrow \underline{\text {Dear }}X_0\) (iv)
(iii) \(X_{0_{\text {other}}}\rightarrow \underline{\text {Dear }}X_0\) (iv)  .
.
Discussion. While SEs can capture many program behaviors, they have limitations. One limitation is that an SE can only describe relations between output characters to input characters, but not among input characters. For example, it cannot capture inputs that are palindromes or inputs of the form XX (e.g., abab). This limitation arises because we chose input SEs to be (a subset of) regular expressions, which cannot capture such languages. Also, tasks that are not string manipulations are likely to have a specification that contains (many) trivial abstract examples (i.e., concrete input-output examples). For example, consider a program that takes two digits and returns their multiplication. Some abstract examples describing it are \(X\ 1\rightarrow X\) and \(1\ X \rightarrow X\). However, the specification also contains \(9\ 2\rightarrow 18\), \(9\ 3\rightarrow 27,...,9\ 9\rightarrow 81\). Also, an abstract example specification consists of a set of independent abstract examples, with no particular order. As a result, describing if-else rules requires encoding the negation of the “if” condition explicitly in order to obtain the same case splitting as an if-else structure.
Generalization Order. We next define a partial order between SEs that are abstract examples. This order is leveraged by our algorithm in the next section. We call this order the generalization order and if an abstract example is greater than another one, we say it is more general or abstract. We begin with defining a partial order \(\preceq \) on the atomic constructs of SEs, as follows:

where \(\sigma \in \varSigma \), \(x\in \mathbf {x}\), \(X \in \mathbf {X}\) and \(k \in \mathbf {K}\).
We say that an input SE \(se'\) is more general than se, \(se \preceq se'\), if its atomic constructs are pointwise more general than the atomic constructs of se. Namely, for \(se = a_1 \cdots a_n\) and \(se' = a_1' \cdots a_n'\) (where \(a_i\) and \(a_i'\) are atomic constructs), \(se \preceq se'\) if for every \(1 \le i \le n\), \(a_i \preceq a_i'\). If \(se \preceq se' \wedge se \ne se'\), we write \(se \prec se'\). For example, \(\underline{\text {abc}} \prec \underline{\text {a}}b^k\underline{\text {c}} \prec xYZ\). In addition, we define that for any atomic construct a, \(a \not \preceq \epsilon \) and \(\epsilon \not \preceq a\). The generalization order implies the following:
Lemma 1
Let \(se,se'\) be two input SEs. If \(se \preceq se'\), then \({[\![{se} ]\!]} \subseteq {[\![{se'} ]\!]}\).
The proof follows directly from the definition of \(\preceq \) and the semantics of an input SE. Note that the converse does not necessarily hold. For example, \({[\![{XY} ]\!]} = {[\![{Z} ]\!]}\), but \(XY \not \preceq Z\) and \(Z \not \preceq XY\). In fact, \(\preceq \) may only relate SEs of the same length. In practice, we partly support generalizations beyond \(\preceq \) (see Sect. 3).
The generalization order of input SEs induces a generalization order on input-output SEs: \(io \preceq io'\) if \(in(io) \preceq in(io')\). If io and \(io'\) are abstract examples for the same program P, this implies that \({[\![{io} ]\!]} \subseteq {[\![{io'} ]\!]}\). Moreover, in that case \({[\![{io} ]\!]} \subseteq {[\![{io'} ]\!]}\) if and only if \({[\![{in(io)} ]\!]} \subseteq {[\![{in(io')} ]\!]}\). This observation enables our algorithm to focus on generalizing the input SE instead of generalizing the pair as a whole.
3 An Algorithm for Learning Abstract Examples
In this section, we describe L-SEP, our algorithm for automatically Learning an SE Pair. This pair is an abstract example for a given program and it generalizes a given concrete example. In Sect. 4, we will use L-SEP repeatedly in order to generate an abstract example specification.
L-SEP (Algorithm 1) takes as input a program P (e.g., the program Flash Fill learned) and a (concrete) input in (e.g., Diane). These two define the initial SE to start with: \((in, {[\![{P} ]\!]}(in))\) (namely, the concrete example). The algorithm outputs an input-output SE, \(io = s_{in} \rightarrow s_{out}\), such that \((in, {[\![{P} ]\!]}(in)) \in {[\![{io} ]\!]} \subseteq {[\![{P} ]\!]}\). Namely, io generalizes (or abstracts) the concrete example and is consistent with P. L-SEP’s goal is to find an io that is maximal with respect to \(\preceq \).
The high-level operation of L-SEP is as follows. First, it sets \(io=in \rightarrow {[\![{P} ]\!]}(in)\). Then, it gradually generalizes io while this results in pairs that are abstract examples for P. The main insight of L-SEP is that instead of generalizing io as a whole, it generalizes the input SE, in(io), and then checks whether there is a completion of in(io) for P, namely an output SE over in(io) such that the resulting pair is an abstract example for P. This is justified by the property that \(io \preceq io'\) if and only if \(in(io) \preceq in(io')\).
3.1 Input Generalization
We now explain the pseudo code of L-SEP. After initializing io by setting \(s_{in} = in\) and \(s_{out} = {[\![{P} ]\!]}(in)\), L-SEP stores in InCands the set of candidates generalizing \(s_{in}\) (which are the input components of io’s generalizations). Then, a loop attempts to generalize \(s_{in}\) as long as \(InCand \ne \emptyset \). Each iteration picks a minimal element from InCands, \(s_{in}'\), which is a candidate to generalize \(s_{in}\). To determine if \(s_{in}'\) can generalize \(s_{in}\), findCompletion is called. If it succeeds, it returns \(s_{out}'\) such that \(s_{in}'\rightarrow s_{out}'\) is an abstract example for P. If it fails, \(\bot \) is returned. Either way, the search space, InCands, is pruned: if the generalization succeeds, then the candidates are pruned to those generalizing \(s_{in}'\); otherwise, to those except the ones generalizing \(s_{in}'\). If the generalization succeeds, \(s_{in}\) and \(s_{out}\) are updated to \(s_{in}'\) and \(s_{out}'\).
Our next lemma states that if findCompletion returns \(\bot \), pruning InCands does not remove input SE that have a completion for P. The lemma guarantees that L-SEP cannot miss abstract examples for P because of this pruning.

Lemma 2
If \(s_{in}'' \succeq s_{in}'\) and \(s_{in}'\) has no completion for P, \(s_{in}''\) has no completion for P.
Proof
(sketch). We prove by induction on the number of generalization steps required to get from \(s_{in}'\) to \(s_{in}''\). Base is trivial. Assume the last generalization step is to replace \(a_i'\) in \(s_{in'}\) with \(a_i''\) in \(s_{in}''\). If \(s_{in}''\) has a completion \(s_{out}''\) for P, then substitute \(a_{i}''\) in \(s_{out}''\) by \(a_i'\) to obtain a completion for \(s_{in}'\). However, this contradicts our assumption. \(\square \)
InCands. For ease of presentation, L-SEP defines InCand as the set of all generalizations of in that remain to be checked, where initially it contains all generalizations. However, the size of this set is exponential in the length of in, and thus practically, L-SEP does not maintain it explicitly. Instead, it maintains two sets: MinCands, which records the minimal generalizations of the current candidate \(s_{in}\) that remain to be checked, and Pruned, which records the minimal generalizations that were overruled (and hence none of their generalizations need to be inspected). Technically, in Line 2 and Line 8 L-SEP initializes MinCands based on the current candidate \(s_{in}\) by computing all of its minimal generalizations. In Line 10 it removes from MinCand the generalization that was last checked and failed, and also records this generalization in Pruned to indicate that none of its generalizations needs to be inspected. Pruned is used immediately after initializing MinCand in Line 8 to remove from MinCands any generalization that generalizes a member of Pruned – this efficiently implements the update of InCands in Line 10. Using this representation of InCands we can now establish:
Lemma 3
The number of iterations of L-SEP is \(O(|in|^2 \cdot |\mathcal {R}|^2)\).
Proof
The number of iterations is at most the maximal size of MinCands multiplied by the number of initializations of MinCands based on a new candidate \(s_{in}\) in Line 8. The size of MinCands computed based on some \(s_{in}\) is at most \(|in|\cdot (|\mathcal {R}|+1)\). This follows since a minimal generalization of \(s_{in}\) differs from \(s_{in}\) in a single construct that is more general than the corresponding construct in \(s_{in}\) (with respect to the partial order of constructs). The number of initializations of MinCands at Line 8 is bounded by the longest (possible) chain of generalizations. This follows because each such initialization is triggered by the update of \(s_{in}\) to a more general SE. Since the longest chain of generalizations is at most \(|in|\cdot (|\mathcal {R}|+1)\), the number of iterations is \(O(|in|^2 \cdot |\mathcal {R}|^2)\). \(\square \)
Lemma 3 implies that MinCands and Pruned provide a polynomial representation of InCands (even though the latter is exponential). Further, the use of these sets enables L-SEP to run in polynomial time because they provide a quadratic bound on the number of iterations, and because findCompletion is also polynomial, as we shortly prove.
Picking a Minimal Generalization. We now discuss how L-SEP picks a minimal generalization of \(s_{in}\) in Line 4. One option is to arbitrarily pick a minimal generalization. However, this greedy approach may result in a sub-optimal maximal generalization, namely a maximal generalization that concretizes to fewer concrete inputs than some other possible maximal generalization. On the other hand, to obtain an optimal generalization, all generalizations that have a completion have to be computed and only then the best one can be picked by comparing the number of concretizations. Unfortunately, this approach results in an exponential time complexity and is thus impractical. Instead, our implementation of L-SEP takes an intermediate approach: it considers all minimal generalizations that have a completion and picks one that concretizes to a maximal number of inputs. To avoid counting the number of inputs (which may be computationally expensive), our implementation employs the following heuristic. It syntactically compares the generalizations by comparing the construct in each of them that is not in \(s_{in}\) (i.e., where generalization took place). It then picks the generalization whose construct is maximal with respect to the order: \(X>\sigma ^k>x\). If there are generalized constructs incomparable w.r.t. this order (e.g., \(\sigma _1^k\) vs. \(\sigma _2^k\)), one is picked arbitrarily.
3.2 Completion
findCompletion (Algorithm 2) takes P and an input generalization \(s_{in}'\) and returns a completion of \(s_{in}'\) for P, if exists; or \(\bot \), otherwise.
Unlike input SEs, the fact that a certain candidate \(s_{out}''\) is not a completion of \(s_{in}'\) for P, does not imply that its generalizations are also not completions of \(s_{in}'\). Thus, a pruning similar to the one of L-SEP may result in missing completions. To exemplify this, consider a program P whose abstract example specification is \(\{xX \rightarrow \underline{\text {b}}X\}\). Assume that while L-SEP looks for a completion for \(s_{in}' = \underline{\text {a}}x\) it considers \(s_{out}'=\underline{\text {ba}}\), which is not a completion. Pruning SEs that are more general than \(s_{out}'\), will result in pruning the completion \(\underline{\text {b}}x\). Likewise, pruning elements that are more specific than a candidate that is not a completion may result in pruning completions.

Since the former pruning cannot be used to search the output SE, findCompletion searches differently. Its search involves attempts to gradually construct a completion \(s_{out}'\) construct-by-construct. If an attempt fails, it backtracks and attempts a different construction. This is implemented via the recursive function findOutputPrefix. At each step, a current prefix \(s_{out}^{pref}\) (initially \(\epsilon \)) is extended with a single atomic construct sym (i.e., \(\sigma , x, X, {\sigma ^k}\)). Then, it checks whether the current extended construction is partially consistent with P (Line 7). If the check fails, this extended prefix is discarded, thereby pruning its extensions from the search space. Otherwise, the extended prefix is attempted to be further extended. We next define partial consistency.
Definition 1
An SE pair \(s_{in}' \rightarrow s_{out}^{pref}\) is partially consistent with P if for every assignment \(env\), \(env[s_{out}^{pref}]\) is a prefix of \({[\![{P} ]\!]}(env[s_{in}'])\).
When \(s_{in}'\) is clear from the context, we say that \(s_{out}^{pref}\) is partially consistent with P.
By the semantics definition, a pair \(s_{in}' \rightarrow s_{out}^{pref}\) is partially consistent with P if and only if \({[\![{s_{in}' \rightarrow s_{out}^{pref}} ]\!]} \subseteq \{(in,o_p) \mid \exists o_s\in \varSigma ^*. (in,o_p \cdot o_s)\in {[\![{P} ]\!]}\}\) (which is the check of line 7). Partial consistency is a necessary condition (albeit not sufficient) for \({s_{out}^{pref} \cdot sym}\) to be a prefix of a completion \(s_{out}'\). Thus, if \(s_{out}^{pref} \cdot sym\) is not partially consistent, there is no need to check its extensions. Note that even if a certain prefix \(s_{out}^{pref}\cdot sym\) is partially consistent, it may be that this prefix cannot be further extended (namely, the suffixes cannot be realized by an SE). In this case, this prefix will be discarded in later iterations and \(s_{out}^{pref}\) will be attempted to be extended differently. This extension process terminates when an extension results in a completion, in which case it is returned, or when all extensions fail, in which case \(\bot \) is returned.
Lemma 4
The recursion depth of Algorithm 2 is bounded by the length of \({[\![{P} ]\!]}(in)\).
Proof
Denote by n the length of \({[\![{P} ]\!]}(in)\). Assume to the contrary that the recursion depth exceeds n. Namely, the current prefix, \(s_{out}^{pref}\), is strictly longer than n. We show that in this case, the partial consistency check is guaranteed to fail. To this end, we show an assignment \(env\) to \(s_{in}'\) such that \(env[s_{out}^{pref}]\) is not a prefix of \({[\![{P} ]\!]}(env[s_{in}'])\). Consider the assignment \(env\) that maps each variable in \(s_{in}'\) to its original value in in (namely, \(env[s_{in}']=in\)). This assignment maps each variable to exactly one letter. By our assumption, the length of \(env[s_{out}^{pref}]\) is greater than n. Thus, \(env[s_{out}^{pref}]\) (of length \(>n\)) cannot be a prefix of \({[\![{P} ]\!]}(in)\) (of length n). \(\square \)
3.3 Guarantees
Lemmas 3 and 4 ensure that both the input generalization and the completion algorithms terminate in polynomial time. Thus, the overall runtime of L-SEP is polynomial. Finally, we discuss the guarantees of these algorithms.
Lemma 5
findCompletion is sound and complete: if it returns \(s_{out}'\), then \(s_{out}'\) is a completion of \(s_{in}'\) for P, and if it returns \(\bot \), then \(s_{in}'\) has no completion for P.
Soundness follows since findOutputPrefix returns \(s_{out}'\) only after validating that \({[\![{s_{in}' \rightarrow s_{out}'} ]\!]}\subseteq {[\![{P} ]\!]}\). Completeness follows since \(s_{out}'\) is gradually constructed and every possible extension is examined.
Lemma 6
L-SEP is sound and complete: for every (in, out) pair, an SE pair is returned, and if L-SEP returns an SE pair, then it is an abstract example for P.
Soundness is guaranteed from findCompletion. Completeness follows since even if all generalizations fail, L-SEP returns the concrete example as an SE pair.
Theorem 1
L-SEP returns an abstract example io for P such that \((in, {[\![{P} ]\!]}(in)) \in {[\![{io} ]\!]}\) and io is maximal w.r.t. \(\preceq \).
This follows from Lemmas 2 and 5, and since L-SEP terminates only when InCands is empty (i.e., when there are no more input generalizations to explore).
We note that in our implementation, findCompletion runs heuristics instead of the expensive backtracking. In this case, maximality is no longer guaranteed.
3.4 Running Example
We next exemplify L-SEP on the (shortened) example from the introduction, where we start from a concrete example \(in= \text {Diane}\) and we wish to obtain the abstract example  . L-SEP starts with: \(s_{in}=\underline{\text {Diane}}\) and \(s_{out}=\underline{\text {Hi Diane}}\). It then picks a minimal candidate that generalizes \(s_{in}\). A minimal candidate differs from \(s_{in}\) in one atomic construct in some position i. By \(\preceq \), if \(s_{in}[i]=\sigma \), then \(s_{in}'[i]\) is \(x\) or \(\sigma ^k\).
. L-SEP starts with: \(s_{in}=\underline{\text {Diane}}\) and \(s_{out}=\underline{\text {Hi Diane}}\). It then picks a minimal candidate that generalizes \(s_{in}\). A minimal candidate differs from \(s_{in}\) in one atomic construct in some position i. By \(\preceq \), if \(s_{in}[i]=\sigma \), then \(s_{in}'[i]\) is \(x\) or \(\sigma ^k\).
Assume that L-SEP first tests this minimal candidate: \(s_{in}' = \text {D}^{k_0}\underline{\text {iane}}\). To test it, L-SEP calls findCompletion to look for a completion. The completion is defined over \(s_{in}'\) and in particular can use the variable \(k_0\). Then, findCompletion invokes findOutputPrefix(P, \(\text {D}^{k_0}\underline{\text {iane}}\), \(\epsilon \)). In the first call of findOutputPrefix, all extensions of the current prefix, \(\epsilon \), except for \(\underline{\text {H}}\), fail in the partial consistency check. This follows since the output of P always starts with an ‘H’ (and not, e.g., with ‘\(\text {H}^{k_0}\)’). Thus, a recursive call is invoked (only) for the output SE prefix \(\underline{\text {H}}\). In this call, all extensions (i.e., \(\underline{\text {H}}\sigma \) or \(\underline{\text {H}}\sigma ^{k_0}\)) fail. For example, \(\underline{\text {Hi}}\) fails since the output prefix is not always “Hi” (e.g., P(DDiane) = HD DDiane. Since the prefix \(\underline{\text {H}}\) cannot be extended further, \(\bot \) is returned. This indicates that the input generalization \(s_{in}' = \text {D}^{k_0}\underline{\text {iane}}\) fails. Thus, L-SEP removes from InCands all generalizations whose first construct generalizes \(\text {D}^{k_0}\).
L-SEP then tests another minimal generalization: \(s_{in}' = x_0\underline{\text {iane}}\). It then calls findCompletion (which can use \(x_0\)). As before, (only) the prefix SE \(\underline{\text {H}}\) is found partially consistent. Next, a second call attempts to extend \(\underline{\text {H}}\). This time, the extension \(\underline{\text {Hi}}\) succeeds because for all interpretations of \(x_0\underline{\text {iane}}\), the output prefix is “Hi”. The recursion continues, until obtaining and returning the completion \(\underline{\text {Hi }}x_0\underline{\text {iane}}\).
When L-SEP learns that \(s_{in}'\) is a feasible generalization, it updates \(s_{in}\) and \(s_{out}\), and prunes InCands to candidates generalizing \(x_0\underline{\text {iane}}\) (for example, InCands contains \(x_0 x_1\underline{\text {ane}}\)). Eventually, \(s_{in}\) is generalized to \(s_{in}' = x_0 x_1 X_2 X_3 X_4\) with the completion  . In a postprocessing step (performed when L-SEP is done), \(X_2 X_3 X_4\) is simplified to Y, resulting in the abstract example
. In a postprocessing step (performed when L-SEP is done), \(X_2 X_3 X_4\) is simplified to Y, resulting in the abstract example  . Note that the last “generalization” is no longer according to \(\preceq \).
. Note that the last “generalization” is no longer according to \(\preceq \).
4 Synthesis with Abstract Examples
In this section, we present our framework for synthesis with abstract examples. We assume the existence of an oracle \(\mathcal {O}\) (e.g., a user) that has fixed a target program \(P_{tar}\). Our framework is parameterized with a synthesizer \(\mathcal {S}\) that takes concrete or abstract examples and returns a consistent program. Note that the guarantee to finally output a program equivalent to \(P_{tar}\) is the responsibility of our framework, and not \(\mathcal {S}\). Nonetheless, candidate programs are provided by \(\mathcal {S}\).
Goal. The goal of our framework is to learn a program equivalent to the target program. Note that this is different from the traditional goal of PBE synthesizers, which learn a program that agrees with the target program at least on the observed inputs. More formally, our goal is to learn a program \(P'\) such that \({[\![{P_{tar}} ]\!]}={[\![{P'} ]\!]}\), whereas PBE synthesizers that are given a set of input-output examples \(E\subseteq D \times D\) can only guarantee to output a program \(P''\) such that \({[\![{P_{tar}} ]\!]}\cap E={[\![{P''} ]\!]}\cap E\).
Interaction Model. We assume that the oracle \(\mathcal {O}\) can accept abstract examples or reject them and provide a counterexample. If the oracle accepts an abstract example io, then \({[\![{io} ]\!]}\subseteq {[\![{P_{tar}} ]\!]}\). If it returns a counterexample \(cex = (in',out')\), then (i) \((in',out')\in {[\![{P_{tar}} ]\!]}\), (ii) \((in',out')\notin {[\![{io} ]\!]}\), and (iii) \(in'\in {[\![{in(io)} ]\!]}\).
Operation. Our framework (Algorithm 3) takes an initial (nonempty) set of input-output examples \(E \subseteq D\times D\). This set may be extended during the execution. The algorithm consists of two loops: an outer one that searches for a candidate program and an inner one that computes abstract examples for a given candidate program. The inner loop terminates when one of the abstract examples is rejected (in which case a new iteration of the outer loop begins) or when the input space is covered (in which case the candidate program is returned along with the abstract example specification).
The framework begins with initializing A to the empty set. This set accumulates abstract examples that eventually form an abstract example specification of \(P_{tar}\). Then the outer loop begins (Lines 2–10). Each iteration starts by asking the synthesizer for a program P consistent with the current set of concrete examples in E and abstract examples in A. Then, the inner loop begins (Lines 4–9). At each inner iteration, an input in is picked and  is invoked. When an abstract example io is returned, it is presented to the oracle. If the oracle provides a counterexample \(cex = (in',out')\), then \({[\![{P} ]\!]}\ne {[\![{P_{tar}} ]\!]}\) (see Lemma 7). In this case, E is extended with cex, and a new outer iteration begins. If the oracle accepts the abstract example, io, the abstract example is added to A (since it is an abstract example for \(P_{tar}\)). Conceptually, the synthesizer extends its set of examples with more examples (potentially an infinite number). This (potentially) enables faster convergence to \(P_{tar}\) (in case additional outer iterations are needed). If the inner loop terminates without encountering counterexamples, then A covers the input domain D. At this point it is guaranteed that \({[\![{P} ]\!]}={[\![{P_{tar}} ]\!]}\) (see Theorem 2). Thus, P is returned, along with the abstract example specification A. Note that A has already been validated and need not be inspected again.
is invoked. When an abstract example io is returned, it is presented to the oracle. If the oracle provides a counterexample \(cex = (in',out')\), then \({[\![{P} ]\!]}\ne {[\![{P_{tar}} ]\!]}\) (see Lemma 7). In this case, E is extended with cex, and a new outer iteration begins. If the oracle accepts the abstract example, io, the abstract example is added to A (since it is an abstract example for \(P_{tar}\)). Conceptually, the synthesizer extends its set of examples with more examples (potentially an infinite number). This (potentially) enables faster convergence to \(P_{tar}\) (in case additional outer iterations are needed). If the inner loop terminates without encountering counterexamples, then A covers the input domain D. At this point it is guaranteed that \({[\![{P} ]\!]}={[\![{P_{tar}} ]\!]}\) (see Theorem 2). Thus, P is returned, along with the abstract example specification A. Note that A has already been validated and need not be inspected again.
We remark that although abstract examples can help the synthesizer to converge faster to the target program, still the convergence speed (and the number of counterexamples required to converge) depends on the synthesizer (which is a parameter to our framework) and not on L-SEP or our synthesis framework.
Lemma 7
If \(\mathcal {O}(io) = (in', out')\) (\(\ne \bot \)), then \({[\![{P} ]\!]}\ne {[\![{P_{tar}} ]\!]}\).
Proof
From the oracle properties \((in',out')\in {[\![{P_{tar}} ]\!]}\), \((in',out')\notin {[\![{io} ]\!]}\), and \(in'\in {[\![{in(io)} ]\!]}\). Thus, there exists \(out''\ne out'\) such that \((in',out'')\in {[\![{io} ]\!]}\). Since by construction, \({[\![{io} ]\!]} \subseteq {[\![{P} ]\!]}\), it follows that \((in',out'')\in {[\![{P} ]\!]}\). Thus, \({[\![{P} ]\!]}\ne {[\![{P_{tar}} ]\!]}\). \(\square \)

Theorem 2
Upon termination, Algorithm 3 returns a program P s.t. \({[\![{P} ]\!]} = {[\![{P_{tar}} ]\!]}\).
Proof
Upon termination, for every \(in\in D\) there exists \(io \in A\) s.t. \(in \in {[\![{in(io)} ]\!]}\). By construction \({[\![{io} ]\!]}\subseteq {[\![{P} ]\!]}\), thus \((in, {[\![{P} ]\!]}(in)) \in {[\![{io} ]\!]}\). By the oracle properties, \({[\![{io} ]\!]}\subseteq {[\![{P_{tar}} ]\!]}\), thus \((in, {[\![{P_{tar}} ]\!]}(in)) \in {[\![{io} ]\!]}\). Altogether, \({[\![{P} ]\!]}(in) = {[\![{P_{tar}} ]\!]}(in)\). \(\square \)
We emphasize that the interaction with the oracle (user) is only after obtaining both a candidate program and an abstract example, and the goal of the interaction is to determine whether the candidate program is correct. If the user rejects an abstract example, it means he/she rejects the candidate program, in which case the PBE synthesizer \(\mathcal {S}\) looks for a new candidate program. In particular, the interaction goal is not to confirm the correctness of the abstract examples – L-SEP always returns (without any interaction) a correct generalization with respect to the candidate program.
Example. We next exemplify our synthesis framework in the bit vector domain. We consider a program space \(\mathcal {P}\) defined inductively as follows. The identity function and all constant functions are in \(\mathcal {P}\). For every \(op\in \{\text {Not}, \text {Neg}\}\) and \(P \in \mathcal {P}\), \(op(P)\in \mathcal {P}\), and for every \(op\in \{ \text {AND}, \text {OR}, \text {+}, {-}, \text {SHL}, \text {XOR}, \text {ASHR}\}\) and \(P_1,P_2\in \mathcal {P}\), \(op(P_1,P_2)\in \mathcal {P}\). We assume a naïve synthesizer that enumerates the program space by considering programs of increasing size and returning the first program consistent with the examples. In this setting, we consider the task of flipping the rightmost 0 bit, e.g., \(10101\rightarrow 10111\) (taken from the SyGuS competition [3]). While this task is quite intuitive to explain through examples, phrasing it as a logical formula is cumbersome. Assume a user provides to Algorithm 3 the set of examples \(E=\{(10101,10111)\}\). Table 1 shows the execution steps taken by our synthesis framework: E shows the current set of examples, P(x) shows the candidate program synthesized by the naïve synthesizer, Abstract Examples shows the abstract examples computed by L-SEP and Counterexample? is either No if the user accepts the current abstract example (to its left) or a pair of input-output example contradicting the current abstract example. In this example, L-SEP uses the set of functions \(\mathcal {F}=\{f_\textit{neg}\}\) in the output SE, where \(f_\textit{neg}(0)=1,f_\textit{neg}(1) =0\), and we abbreviate \(f_\textit{neg}(y)\) with \(\bar{y}\). Further, since the bit vector domain consists of vectors of a fixed size (namely, \(\varSigma ^n\) for a fixed n instead of \(\varSigma ^*\)), the SE’s semantics in this domain is defined as the suffixes of size n of its (normal) interpretation. Formally, \({[\![{se} ]\!]}_n = \{ s \in \varSigma ^n \mid \exists env.\ s \text { is a suffix of }env[se] \}\). The semantics of an input-output SE is defined similarly. In the example, the first couple of programs are eliminated immediately by the user, whereas the third program is eliminated only after showing the third abstract example describing it. This enables the synthesizer to prune a significant portion of the search space. Note that since abstract examples are interpreted over fixed sized vectors (as explained above), the last abstract example covers the input space: if \(k=n\), the input is \(\overbrace{11...1}^{\text {n times}}\); if \(k=0\), the input takes the form of \(b_0...b_{n-1}0\) (where the \(b_i\)-s are bits); and if \(0<k<n\), the input takes the form of \(b_0...b_{n-k-1}01^k\).
Leveraging Counterexamples for Learning Abstract Examples. A limitation of L-SEP is that it only generalizes the existing characters of the concrete input. For example, consider a candidate program generated by \(\mathcal {S}\) that returns the first and last character of the string, which can be summarized by the abstract example \(x_0X_1x_2 \rightarrow x_0x_2\). If, in the process of generating an abstract example specification for the candidate program, the first example provided by Algorithm 3 to L-SEP for generalization is ab, then it is generalized to \(x_0x_1 \rightarrow x_0x_1\). On the other hand, if the first example is acb, then it is generalized to \(x_0X_1x_2\rightarrow x_0x_1\), whose domain is a strict superset of the former’s domain. This exemplifies that some inputs may provide better generalizations than others. Although eventually our framework will learn the better generalizations, if Algorithm 3 starts from the less generalizing examples, then the termination of our framework is delayed, and unnecessary questions are presented to the oracle (in our example, it will present \(x_0x_1 \rightarrow x_0x_1\), and then \(x_0X_1x_2 \rightarrow x_0x_2\), which are both accepted, but the former perhaps could be avoided). We believe that the way to avoid this is by picking “good” examples. We leave the question of how to identify them to future work, but note that if the oracle is assumed to provide “good” examples (e.g., representative) then Line 5 can be changed to first look for an uncovered input in E.
5 Evaluation
In this section, we discuss our implementation and evaluate L-SEP and our synthesis framework. We evaluate our algorithms in two domains: strings and bit vectors (of size 8). The former domain is suitable for end users, as targeted by approaches like Flash Fill or learning regular expressions. The latter domain is of interest to the synthesis community (evident by the SyGuS competition [3]). We begin with our implementation and then discuss the experiments. All experiments ran on a Sony Vaio PC with Intel(R) Core(TM) i7-3612QM processor and 8 GB RAM.
5.1 Implementation
We implemented our algorithms in Java. We next provide the main details.
Program Spaces. The program space we consider for bit vectors is the one defined in the example at the end of Sect. 4.
The program space \(\mathcal {P}\) we consider for the string domain is defined inductively as follows. The identity function and all constant functions are in \(\mathcal {P}\). For every \(P_1, P_2\in \mathcal {P}\), \(concat(P_1,P_2)\in \mathcal {P}\).
For \(P\in \mathcal {P}\) and integers \(i_1,i_2\), \(Extract(P,i_1,i_2)\in \mathcal {P}\). For \(P_1,P_2\in \mathcal {P}\), and a condition e over string programs and integer symbols, \(ITE(e,P_1,P_2)\in \mathcal {P}\).
SE Spaces. In the bit vector domain we consider \(\mathcal {F}=\{f_{neg}\}\) where \(f_{neg}(b)=1-b\).
FindCompletion. To answer the containment queries (Lines 3 and 7), we use the Z3 SMT-solver [15]. To this end, we encode the candidate program P and the SEs as formulas.
Roughly speaking, an SE is encoded as a conjunction of sequence predicates, each encodes a single atomic construct. A sequence predicate extends the equality predicate with a start position and is denoted by \(t_1\overset{i}{=}t_2\). An interpretation \(d_1,d_2\) for \(t_1,t_2\) satisfies \(t_1{\overset{i}{=}}t_2\) if starting from the \(i^{th}\) character of \(d_1\) the next \(|d_2|\) characters are equal to \(d_2\). The term \(t_1\) is either a unique variable \(t_{in}\), representing the input (for input SEs), or \(P(t_{in})\) (for output SEs). The term \(t_2\) can be (i) \(\sigma \) (a letter from \(\varSigma \)), (ii) \(\sigma ^k\) where k is a star variable, or (iii) a character or sequence variable. For example, \(X_0\underline{\text {a}}b^{k_2}x_3\) is encoded as: \(t_{in} {\overset{0}{=}} X_0 \wedge t_{in} {\overset{|X_0|}{=}}a \wedge (\forall i. 1 + |X_0| \le i < 1 + |X_0| +k_2 \rightarrow t_{in} {\overset{i}{=}}b) \wedge t_{in} {\overset{1+|X_0|+k_2}{=}}x_3\). Note that the positions can be a function of the variables. In the string domain, the formulas are encoded in the string theory (except for i and \(k_2\) that are integers). In the bit vector domain, entities are encoded as bit vectors and \(\overset{i}{=}\) is implemented with masks.
Synthesis Framework. To check whether A covers the input domain and obtain an uncovered input in if not, we encode the abstract examples in A as formulas. We then check whether one of the concrete examples from E does not satisfy any of these formulas. If so, it is taken as in. Otherwise, we check if there is another input that does not satisfy the formulas, and if so it is taken as in; otherwise the input domain is covered.
Synthesizer. Our synthesizer is a naïve one that enumerates the program space by considering programs of increasing size and returning the first program consistent with the examples. Technically, we check consistency by submitting the formula \(P(in)=out\) to an SMT-solver for every \((in,out)\in E\). Likewise, P is checked to be consistent with the abstract examples by encoding them as formulas and testing whether they imply P. More sophisticated PBE synthesizers, such as Flash-Fill, can in many cases be extended to handle abstract examples in a straight-forward way.
5.2 Synthesis Framework Evaluation
In this section, we evaluate our synthesis framework on the bit vector domain. We consider three experimental questions: (1) Do abstract examples reduce the number of concrete examples required from the user? (2) Do abstract examples enable better pruning for the synthesizer? (3) How many abstract examples are presented to the user before he/she rejects a program? To answer these questions, we compare our synthesis framework (denoted AE) to a baseline that implements the current popular alternative (e.g., [41]) that guarantees that a synthesized program is correct. The baseline acts as follows. It looks for the first program that is consistent with the provided examples and then asks the oracle whether this program is correct. The oracle checks whether there is an input for which the synthesized program and the target program return different outputs. If so, the oracle provides this input and its correct output to the synthesizer, which in turn looks for a new program. If there is no such input, the oracle reports success, and the synthesis completes. We assume a knowledgable user (oracle), implemented by an SMT-solver, which is oblivious to whether the program is easy for a human to understand, making the comparison especially challenging.
Benchmarks. We consider three benchmarks, B(4), B(6), and B(8), each consists of 50 programs. A program is in B(n) if baseline required at least n examples to find it. To find such programs, we randomly select programs of size 4, for each we execute baseline (to find it), and if it required at least n examples, we add it to B(n) and execute our synthesis framework (AE) to find the same (or an equivalent) program.
Consistency of Examples. The convergence of these algorithms highly depends on the examples the oracle provides. To guarantee a fair comparison, we make sure that the same examples are presented to both algorithms whenever possible. To this end, we use a cache that stores the examples observed by the baseline. When our algorithm asks the oracle for an example, it first looks for an example in the cache. Only if none meets its requirements, it can ask (an SMT-solver) for a new concrete example.
Results. Table 2 summarizes the results. It reports the following:
-
#Concrete examples: the average number of concrete examples the oracle provided, which is also the number of candidate programs.
-
Spec-final: the average size of the final abstract example specification (after removing implied abstract examples).
-
#AE-intermediate: the average number of abstract examples shown to the user before he/she rejected the corresponding candidate program.
-
%Better/equal/worse than baseline: the percentage of all programs in the benchmark that required fewer/same/more (concrete) examples than the baseline.
We note that we observed that the time to generate a single abstract example is a few seconds (\(\approx 6\) s).
Results indicate that our synthesis framework (AE), which prunes the program space based on the abstract examples, improves the baseline in terms of the examples the user needs to provide. This becomes more significant as the number of examples required increases: AE improves the baseline on B(4) by 22%, on B(6) by 30%, and on B(8) by 37%. Moreover, in each benchmark AE performed worse than the baseline only in a single case – and the common case was that it performed better (in B(8), AE performed better on all cases except two).
Figure 3 provides a detailed evidence on the improvement: it shows for each experiment (the x-axis) the number of concrete examples each algorithm required (the y-axis). The figure illustrates that the improvement can be significant. For example, in the \(47^{th}\) experiment, AE reduced the number of examples from 17 to 7.
The number of concrete examples is also the number of candidate programs generated by the synthesizer. Thus, the lower number of examples indicates that the abstract examples improve the pruning of the program space. Namely, abstract examples help the overall synthesis to converge faster to the target program.
5.3 Abstract Example Specification Evaluation
In this section, we evaluate our generalization algorithm, L-SEP, in the string domain and check how well it succeeds in learning small specifications. To this end, we fix a program and a concrete example to start with and run L-SEP. We repeat this with uncovered inputs until the set of abstract examples covers the string domain. We then check how many abstract examples were computed.
The programs we considered are related to the motivating example. For each program, we run five experiments. Each experiment uses a different Excel row (lawyer) as the first concrete example. We note that our implementation assumes that the names and meeting times are non-empty strings and are space-delimited. Table 3 reports the programs and the average number of abstract examples. Results indicate that the average number of abstract examples required to describe the entire string domain is low.
6 Related Work
In this section, we survey the work closely related to ours.
Learning Specifications. Learning regular languages from examples has been extensively studied in the computational learning theory, under different models: (i) identification in the limit (Gold [20]), (ii) query learning (Angluin [4]), and (iii) PAC learning (Valiant [44]). Our setting is closest to Angluin’s setting that defines a teacher-student model and two types of queries: membership (concrete examples) and equivalence (validation). The literature has many results for this setting, including learning automata, context-free grammars, and regular expressions (see [37]). In the context of learning regular expressions, current algorithms impose restrictions on the target regular expression. For example, [9] allows at most one union operator, [27] prevents unions and allows loops up to depth 2 , [17] assumes that input samples are finite and Kleene stars are not nested, and [6] assumes that expressions consist of chains that have at most one occurrence of every symbol. In contrast, we learn an extended form of regular expressions but we also impose some restrictions. In the context of learning specifications, [43] learns specifications for programs in the form of logical formulas, which are not intuitive for most users. Symbolic transducers [8, 45] describe input-output specifications, but these are more natural to describe functions over streams than input manipulations.
Least General Generalization. L-SEP takes the approach of least general generalization to compute an abstract example. The approach of least general generalization was first introduced by Plotkin [32] that pioneered inductive logic programming and showed how to generalize formulas. This approach was later used to synthesize programs from examples in a PBE setting [31, 35]. In contrast, we use this approach not to learn the low-level program, but the high-level specification in the form of abstract examples.
Pre/Post-condition Inference. Learning specifications is related to finding the weakest pre-conditions, strongest post-conditions, and inductive invariants [12, 13, 16, 19, 24, 36]. Current inference approaches are mostly for program analysis and aim to learn the conditions under which a bad behavior cannot occur. Our goal is different: we learn the (good and bad) behaviors of the program and present it through a high-level language.
Applications of Regular Expressions. There are many applications of regular expressions, for example in data filtering (e.g., [46]), learning XML files’ schemes (DTD) (e.g., [6, 17]), and program boosting (e.g., [11]). All of these learn expressions that are consistent with the provided examples and have no guarantee on the target expression. In contrast, we learn expressions that precisely capture program specifications.
Synthesis. Program synthesis has drawn a lot of attention over the last decade, and especially in the setting of synthesis from examples, known as PBE (e.g., [1, 5, 14, 18, 21,22,23, 25, 28,29,30, 33, 34, 38, 39, 47]). Commonly, PBE algorithms synthesize programs consistent with the examples, which may not capture the user intent. However, some works guarantee to output the target program. For example, CEGIS [41] learns a program via equivalence queries, and oracle-based synthesis [26] assumes that the program space is finite, which allows them to guarantee correctness by exploring all distinguishing inputs (i.e., without validation queries). Synthesis has also been studied in a setting where a specification and the program’s syntax are given and the goal is to find a program over this syntax meeting the specification (e.g., [2, 7, 40, 42]).
7 Conclusion
We presented a novel synthesizer that interacts with the user via abstract examples and is guaranteed to return a program that is correct on all inputs. The main idea is to use abstract examples to describe a program behavior on multiple concrete inputs. To that end, we showed L-SEP, an algorithm that generates maximal abstract examples. L-SEP enables our synthesizer to describe candidate programs’ behavior through abstract examples. We implemented our synthesizer and experimentally showed that it required few abstract examples to reject false candidates and reduced the overall number of concrete examples required.
References
Albarghouthi, A., Gulwani, S., Kincaid, Z.: Recursive program synthesis. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 934–950. Springer, Heidelberg (2013). doi:10.1007/978-3-642-39799-8_67
Alur, R., Bodik, R., Juniwal, G., Martin, M.M.K., Raghothaman, M., Seshia, S.A., Singh, R., Solar-Lezama, A., Torlak, E., Udupa, A.: Syntax-guided synthesis. In: FMCAD 2013 (2013)
Alur, R., Fisman, D., Singh, R., Solar-Lezama, A.: SyGuS-Comp 2016: results and analysis. In: SYNT@CAV 2016 (2016)
Angluin, D.: Queries and concept learning. Mach. Learn. 2(4), 319–342 (1988)
Barowy, D.W., Gulwani, S., Hart, T., Zorn, B.: FlashRelate: extracting relational data from semi-structured spreadsheets using examples. In: PLDI 2015 (2015)
Bex, G.J., Neven, F., Schwentick, T., Tuyls, K.: Inference of concise DTDs from XML data. In: VLDB 2006 (2006)
Bornholt, J., Torlak, E., Grossman, D., Ceze, L.: Optimizing synthesis with metasketches. In: POPL 2016 (2016)
Botinčan, M., Babić, D.: Sigma*: symbolic learning of input-output specifications. In: POPL 2013, pp. 443–456 (2013)
Brāzma, A., Čerāns, K.: Efficient learning of regular expressions from good examples. In: Arikawa, S., Jantke, K.P. (eds.) AII/ALT -1994. LNCS, vol. 872, pp. 76–90. Springer, Heidelberg (1994). doi:10.1007/3-540-58520-6_55
Bshouty, N.H.: Exact learning from membership queries: some techniques, results and new directions. In: Jain, S., Munos, R., Stephan, F., Zeugmann, T. (eds.) ALT 2013. LNCS, vol. 8139, pp. 33–52. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40935-6_4
Cochran, R.A., D’Antoni, L., Livshits, B., Molnar, D., Veanes, M.: Program boosting: program synthesis via crowd-sourcing. In: POPL 2015 (2015)
Cousot, P., Cousot, R., Fähndrich, M., Logozzo, F.: Automatic inference of necessary preconditions. In: Giacobazzi, R., Berdine, J., Mastroeni, I. (eds.) VMCAI 2013. LNCS, vol. 7737, pp. 128–148. Springer, Heidelberg (2013). doi:10.1007/978-3-642-35873-9_10
Cousot, P., Cousot, R., Logozzo, F.: Precondition inference from intermittent assertions and application to contracts on collections. In: Jhala, R., Schmidt, D. (eds.) VMCAI 2011. LNCS, vol. 6538, pp. 150–168. Springer, Heidelberg (2011). doi:10.1007/978-3-642-18275-4_12
Das Sarma, A., Parameswaran, A., Garcia-Molina, H., Widom, J.: Synthesizing view definitions from data. In: ICDT 2010 (2010)
De Moura, L., Bjørner, N.: Z3: an efficient SMT solver. In: Ramakrishnan, C.R., Rehof, J. (eds.) TACAS 2008. LNCS, vol. 4963, pp. 337–340. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78800-3_24
Dijkstra, E.W.: Guarded commands, nondeterminacy and formal derivation of programs. Commun. ACM 18(8), 453–457 (1975)
Fernau, H.: Algorithms for learning regular expressions from positive data. Inf. Comput. 207, 521–541 (2009)
Feser, J.K., Chaudhuri, S., Dillig, I.: Synthesizing data structure transformations from input-output examples. In: PLDI 2015 (2015)
Garg, P., Löding, C., Madhusudan, P., Neider, D.: ICE: a robust framework for learning invariants. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 69–87. Springer, Cham (2014). doi:10.1007/978-3-319-08867-9_5
Gold, E.M.: Language identification in the limit. Inf. Control 10(5), 447–474 (1967)
Gulwani, S.: Automating string processing in spreadsheets using input-output examples. In: POPL 2011 (2011)
Gulwani, S.: Dimensions in program synthesis. In: PPDP 2010 (2010)
Gulwani, S., Harris, W.R., Singh, R.: Spreadsheet data manipulation using examples. Commun. ACM 55(8), 97–105 (2012)
Gulwani, S., Tiwari, A.: Computing procedure summaries for interprocedural analysis. In: Nicola, R. (ed.) ESOP 2007. LNCS, vol. 4421, pp. 253–267. Springer, Heidelberg (2007). doi:10.1007/978-3-540-71316-6_18
Harris, W.R., Gulwani, S.: Spreadsheet table transformations from examples. In: PLDI 2011 (2011)
Jha, S., Gulwani, S., Seshia, S.A., Tiwari, A.: Oracle-guided component-based program synthesis. In: ICSE 2010 (2010)
Kinber, E.: Learning regular expressions from representative examples and membership queries. In: Sempere, J.M., García, P. (eds.) ICGI 2010. LNCS, vol. 6339, pp. 94–108. Springer, Heidelberg (2010). doi:10.1007/978-3-642-15488-1_9
Lau, T.A., Wolfman, S.A., Domingos, P., Weld, D.S.: Programming by demonstration using version space algebra. Mach. Learn. 53, 111–156 (2003)
Le, V., Gulwani, S.: Flashextract: a framework for data extraction by examples. In: PLDI 2014 (2014)
Menon, A.K., Tamuz, O., Gulwani, S., Lampson, B.W., Kalai, A.: A machine learning framework for programming by example. In: ICML 2013 (2013)
Muggleton, S., Feng, C.: Efficient induction of logic programs. In: First Conference on Algorithmic Learning Theory, pp. 368–381 (1990)
Plotkin, G.D.: A note on inductive generalization. Mach. Intell. 5, 153–163 (1970)
Polozov, O., Gulwani, S.: Flashmeta: a framework for inductive program synthesis. In: OOPSLA 2015 (2015)
Raychev, V., Bielik, P., Vechev, M., Krause, A.: Learning programs from noisy data. In: POPL 2016 (2016)
Raza, M., Gulwani, S., Milic-Frayling, N.: Programming by example using least general generalizations. In: AAAI 2014 (2014)
Rival, X.: Understanding the origin of alarms in Astrée. In: Hankin, C., Siveroni, I. (eds.) SAS 2005. LNCS, vol. 3672, pp. 303–319. Springer, Heidelberg (2005). doi:10.1007/11547662_21
Sakakibara, Y.: Recent advances of grammatical inference. Theor. Comput. Sci. 185(1), 15–45 (1997)
Singh, R., Gulwani, S.: Learning semantic string transformations from examples. In: VLDB 2012 (2012)
Singh, R., Gulwani, S.: Transforming spreadsheet data types using examples. In: POPL 2016 (2016)
Singh, R., Solar-Lezama, A.: Synthesizing data structure manipulations from storyboards. In: ESEC/FSE 2011 (2011)
Solar-Lezama, A.: Program Synthesis by Sketching. ProQuest, Ann Arbor (2008)
Solar-Lezama, A., Jones, C.G., Bodik, R.: Sketching concurrent data structures. In: PLDI 2008 (2008)
Tripakis, S., Lickly, B., Henzinger, T.A., Lee, E.A.: A theory of synchronous relational interfaces. ACM Trans. Program. Lang. Syst. 33(4), 14 (2011)
Valiant, L.G.: A theory of the learnable. Commun. ACM 27(11), 1134–1142 (1984)
Veanes, M., Hooimeijer, P., Livshits, B., Molnar, D., Bjorner, N.: Symbolic finite state transducers: algorithms and applications. In: POPL 2012 (2012)
Wang, X., Gulwani, S., Singh, R.: Fidex: filtering spreadsheet data using examples. In: OOPSLA 2016 (2016)
Yessenov, K., Tulsiani, S., Menon, A.K., Miller, R.C., Gulwani, S., Lampson, B.W., Kalai, A.: A colorful approach to text processing by example. In: UIST 2013 (2013)
Acknowledgements
The research leading to these results has received funding from the European Union, Seventh Framework Programme (FP7) under grant agreement n\(^o\) 908126, as well as from Len Blavatnik and the Blavatnik Family foundation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer International Publishing AG
About this paper
Cite this paper
Drachsler-Cohen, D., Shoham, S., Yahav, E. (2017). Synthesis with Abstract Examples. In: Majumdar, R., Kunčak, V. (eds) Computer Aided Verification. CAV 2017. Lecture Notes in Computer Science(), vol 10426. Springer, Cham. https://doi.org/10.1007/978-3-319-63387-9_13
Download citation
DOI: https://doi.org/10.1007/978-3-319-63387-9_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-63386-2
Online ISBN: 978-3-319-63387-9
eBook Packages: Computer ScienceComputer Science (R0)






 , used to denote an arbitrary letter from
, used to denote an arbitrary letter from 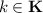 , used instead of the Kleene star to indicate the number of consecutive repeating occurrences of a symbol. For example,
, used instead of the Kleene star to indicate the number of consecutive repeating occurrences of a symbol. For example, 
