Groupwise Registration of MR Brain Images Containing Tumors via Spatially Constrained Low-Rank Based Image Recovery

Abstract

We propose a new low-rank based image recovery method and embed it into an existing Groupwise Image Registration (GIR) framework to achieve accurate GIR of Magnetic Resonance (MR) brain images containing tumors. In our method, brain tumor regions in the input images are recovered with population-consistent normal brain appearance to produce low-rank images. The GIR framework is then applied to the tumor-free low-rank images. With no influence from the brain tumor, accurate GIR can be achieved. Unlike conventional low-rank based image recovery methods, a spatial constraint is added to the low-rank framework in our method, by which the quality of the resulting low-rank images can be improved. Particularly, the low-rank images produced by our method contain both effectively recovered brain tumor regions and well-preserved normal brain regions of input images, which are two key factors for accurate GIR. By contrast, in conventional low-rank based image recovery methods, these two factors are mutually exclusive and a good balance is difficult to achieve. Synthetic and real MR brain images are used to evaluate our method. The results show that based on our method, image recovery quality and GIR accuracy are improved in comparison to the state-of-the-art method.

1 Introduction

Groupwise Image Registration (GIR) plays an important role in the study of the brain, such as for brain atlas construction [1] and brain parcellation [2]. The objective of GIR is to establish spatial correspondences between input images, which assumes that for any part of an image, corresponding parts in other images can be found. However, this assumption only holds for normal brain images, and for images that contain brain tumors, there is no spatial correspondence for the brain tumor. Therefore, for most existing GIR methods [3, 4], they suffer from the problem that if the input brain images contain tumors, the GIR accuracy is usually unsatisfactory.

To solve this problem, many solutions have been proposed. One well-known approach is Cost Function Masking (CFM) [5]. The basic idea of CFM is to identify pathological brain regions (e.g., brain tumors) and mask them in the cost function of image registration, so that registration is driven by normal brain regions. Different from the CFM method, the pathology simulation method [6] synthesizes pathological regions in a normal brain image to create an image that is similar to the patient’s image and therefore a typical image registration algorithm can be adopted for registering these images. Recently, an interesting method has been proposed in [7]. It adopts an image recovery method based on Low Rank plus Sparse matrix Decomposition (LRSD) [8] to decompose input images into low-rank images and residual error. Since brain tumors do not manifest in consistent location and appearance in populations, brain tumor regions are recovered with population-consistent normal brain appearance to produce low-rank images. The difference between the input images and the low-rank images is the residual error. An existing GIR framework is then applied to the tumor-free low-rank images. With no influence from the brain tumor, accurate GIR can be achieved.

In conventional low-rank based image recovery methods including LRSD, the low-rank images are produced under two constraints: the low-rank constraint and the residual error constraint. To achieve effective brain tumor region recovery where brain tumors are unperceivable in the low-rank images, the residual error constraint is weakened to allow large residual error. However, by doing this, normal brain regions of input images could be seriously distorted in the low-rank images. Figure 1 shows two original Magnetic Resonance (MR) brain images containing tumors and the corresponding low-rank images obtained by LRSD under a gradually weakened residual error constraint (from left to right). As the residual error constraint becomes weaker, the brain tumors are faded but the normal brain regions are blurred and closely resemble each other in the corresponding low-rank images, despite initially being different. It is known that the low-rank images should have both effectively recovered brain tumor regions and well-preserved normal brain regions of input images, which are two key factors for accurate GIR. However, these two factors are mutually exclusive, and it is difficult to achieve a good balance using conventional low-rank based image recovery methods.

Fig. 1.

Two original MR brain images containing tumors (leftmost) and their corresponding low-rank images obtained by using different levels of residual error constraint. From left to right, the residual error constraint is gradually weakened.

Inspired by recent work in computer vision [9], in this paper, we propose a new low-rank based image recovery method and embed it into an existing GIR framework to achieve accurate GIR of MR brain images containing tumors. In our method, a spatial constraint is added to the low-rank framework to produce high quality low-rank images which contain both effectively recovered brain tumor regions and well-preserved normal brain regions of input images. Moreover, the existing GIR framework via our method is capable of handling MR brain images containing tumors, and more accurate GIR can be achieved in comparison to the state-of-the-art GIR method.

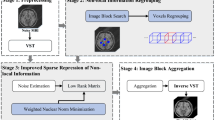
2 Method

By default, input images are 3D MR brain images and presented by a matrix $\varvec{D} = \left[ {\varvec{I}_{1} , \ldots ,\varvec{I}_{n} } \right] \in R^{m \times n}$ where $m$ is the total voxel number of each image and $n$ is the number of input images. All input images have been spatially normalized to a standard space defined by MNI152 [10] using affine transformation, and image intensity has been normalized using histogram matching.

In conventional low-rank based image recovery methods e.g., LRSD, the matrix $\varvec{D}$ of input images is decomposed into low-rank images $\varvec{B} = \left[ {\varvec{B}_{1} , \ldots ,\varvec{B}_{n} } \right] \in R^{m \times n}$ and residual error $\varvec{S} = \varvec{D} - \varvec{B} = \left[ {\varvec{S}_{1} , \ldots ,\varvec{S}_{n} } \right] \in R^{m \times n}$ using

$$ \mathop {min}\limits_{{\varvec{B},\varvec{S}}} \left( {\left\| \varvec{S} \right\|_{1} + \lambda \left\| \varvec{B} \right\|_{ *} } \right), {\text{s}}.{\text{t}}.\,\varvec{D} = \varvec{B} + \varvec{S}, $$

(1)

where $\left\| \varvec{B} \right\|_{*}$ is the nuclear norm which is the sum of the singular values of $\varvec{B}$, and $\left\| \varvec{S} \right\|_{1}$ is the L1 norm of $\varvec{S}$. Since brain tumors usually have no inter-subject consistency in location and image appearance, brain tumor regions are recovered by population-consistent normal brain appearance to satisfy the low-rank constraint. Furthermore, the inter-subject anatomical variability of the normal brain region is also reduced under the low-rank constraint. Therefore, the residual error $\varvec{S}$ comes from both the brain tumor region and normal brain region. To achieve effective brain tumor region recovery, the residual error constraint is weakened to allow large residual error in the brain tumor region. However, by doing this, the residual error in the normal brain region is also encouraged to be large, causing the normal brain regions of input images be seriously distorted in the low-rank images, as shown in Fig. 1. To make the low-rank images contain both effectively recovered brain tumor regions and well-preserved normal brain regions of input images, different residual error constraints for the brain tumor region and normal brain region should be applied. Therefore, we propose to divide the residual error $\varvec{S}$ into two parts: one is the residual error in the brain tumor region and the other is in the normal brain region. The former residual error is allowed and the latter one is restricted in the low-rank framework.

2.1 The Spatial Constraint

We first introduce an indicative matrix $\varvec{C} \in R^{m \times n}$ containing the indication for each residual error element in $\varvec{S}$. $\varvec{C}_{ij} = 1$ indicates that element $\varvec{S}_{ij}$ at i-th row and j-th column of $\varvec{S}$ belongs to the brain tumor region, while $\varvec{C}_{ij} = 0$ means $\varvec{S}_{ij}$ belongs to the normal brain region. The spatial constraint is then defined as an energy function:

$$ E_{spatial} = \mathop \sum \limits_{1 \le i \le m;1 \le j \le n} \varvec{P}_{ij} \cdot \varvec{C}_{ij} + \alpha \mathop \sum \limits_{1 \le i,k \le m;1 \le j \le n} \varvec{W}_{ij,kj} \left| {\varvec{C}_{ij} - \varvec{C}_{kj} } \right|, $$

(2)

where $\varvec{P} \in R^{m \times n}$ contains the probabilities of residual error elements that belong to the normal brain region. For each residual error element $\varvec{S}_{ij}$, the corresponding $\varvec{P}_{ij} = \left\{ {\begin{array}{*{20}l} {\frac{1}{n}\mathop \sum \nolimits_{1 \le l \le n} T_{\mu } \left( {\left| { \varvec{S}_{il} } \right|} \right), } \hfill & {\rm if} \left|{ \varvec{S}_{ij}} \right| > \mu \hfill \\ {1,} \hfill & {\rm otherwise} \hfill \\ \end{array} } \right.$, where $T_{\mu } \left( {\left| { \varvec{S}_{il} } \right|} \right) = \left\{ {\begin{array}{*{20}l} {1, } \hfill & {\rm if} \left| { \varvec{S}_{il} } \right| > \mu \hfill \\ {0, } \hfill & {\rm otherwise} \hfill \\ \end{array} } \right.$ is a thresholding function, and the threshold $\mu$ in this paper is set to the average value of all the absolute non-zero values in $\varvec{S}$. The definition of $\varvec{P}$ is based on the assumption that brain tumors have inconsistent locations across subjects and large corresponding absolute residual error. Particularly, if $\varvec{S}_{ij}$ has a small absolute value i.e., $\left| { \varvec{S}_{ij} } \right| \le \mu$, it is considered to be in the normal brain region i.e., $\varvec{P}_{ij} = 1$. If $\varvec{S}_{ij}$ has a large absolute value i.e.,$\left| { \varvec{S}_{ij} } \right| > \mu$, probability of $\varvec{S}_{ij}$ in the normal brain region is proportional to the frequency that residual error elements at the same position of other columns of $\varvec{S}$ i.e., $\varvec{S}_{il} , 1 \le l \le n$ have larger absolute values, as large residual error caused by inter-subject variability in the normal brain region has large coincidence to present at the same spatial location. $\varvec{W} \in R^{{\left( {m \times n} \right) \times \left( {m \times n} \right)}}$ is an adjacent matrix and its element $\varvec{W}_{ij,kj} = 1$ in Eq. (2) means that element $\varvec{S}_{ij}$ is adjacent to element $\varvec{S}_{kj}$, otherwise $\varvec{W}_{ij,kj} = 0$. In this paper, adjacent elements are restricted within a $3 \times 3 \times 3$ voxel range in the same column of $\varvec{S}$. $\alpha$ in Eq. (2) is a weighting factor.

2.2 Spatially Constrained Low-Rank Based Image Recovery

The energy function of the spatial constraint is added to the low-rank framework [9] to achieve Spatially COnstrained LOw-rank based image Recovery (SCOLOR):

$$ \mathop {\hbox{min} }\limits_{{\varvec{B},\varvec{C}}} \left\| {\left( {1 - \varvec{C}} \right) \odot \left( {\varvec{D} - \varvec{B}} \right)} \right\|_{F}^{2} + \beta \left\| \varvec{B} \right\|_{ *} + \gamma E_{spatial} $$

(3)

where $1 \in R^{m \times n} , 1_{ij} \; = \;1,$ $\left\| {\left( {1 - \varvec{C}} \right) \odot \left( {\varvec{D} - \varvec{B}} \right)} \right\|_{F}^{2}$ is the Frobenius norm which considers the residual error in the normal brain region only. $\beta$ and $\gamma$ are weighting factors. An effective algorithm is derived to solve Eq. (3), which carries out the following two steps iteratively: (1) Solving $\varvec{B}$ while fixing $\varvec{ C}$, and Eq. (3) then becomes

$$ \mathop {\hbox{min} }\limits_{\varvec{B}} \left\| {\left( {1 - \varvec{C}} \right) \odot \left( {\varvec{D} - \varvec{B}} \right)} \right\|_{F}^{2} + \beta \left\| \varvec{B} \right\|_{ *} $$

(4)

which is a well-known matrix completion problem and can be solved by the soft impute method [11]; (2) Solving $\varvec{C}$ while $\varvec{B}$ is fixed, then Eq. (3) becomes,

$$ \mathop {\hbox{min} }\limits_{\varvec{C}} \mathop \sum \limits_{{\begin{array}{*{20}c} {1 \le i \le m,} \\ {1 \le j \le n} \\ \end{array} }} (\gamma \varvec{P}_{ij} - \left( {\varvec{D}_{ij} - \varvec{B}_{ij} } \right)^{2} )\varvec{C}_{ij} + \alpha \gamma \mathop \sum \limits_{{\begin{array}{*{20}c} {1 \le i,k \le m,} \\ {1 \le j \le n} \\ \end{array} }} \varvec{W}_{ij,kj} \left| {\varvec{C}_{ij} - \varvec{C}_{kj} } \right| + c, $$

(5)

where $c$ is a constant value. This problem can be solved using the graph cut method [12]. The algorithm iteratively repeats the above two steps until convergence i.e., $\varvec{ B}$ and $\varvec{C}$ are unchanged. It is worth noting that for simplicity and fast convergent speed, $\varvec{P}$ is calculated in the first iteration and is fixed throughout the whole iterations. Since the objective function decreases in each step, and the objective of Eq. (3) has a low bound, the convergence of the above algorithm is always guaranteed.

We embed SCOLOR into an existing GIR framework to achieve accurate GIR of MR brain images containing tumors. Most existing GIR frameworks can be used here. In this paper, we choose the GIR framework used in [7]. This GIR framework is proposed by Joshi et al. [1], and in [7] it is extended with a low-rank based image recovery method LRSD to perform GIR of pathological MR brain images (denoted as GIR-LRSD). GIR-LRSD works in an iterative manner. In each iteration, low-rank images $\varvec{B}^{iter} = \left[ {\varvec{B}_{1}^{iter} , \ldots ,\varvec{B}_{n}^{iter} } \right]$ are produced from $\varvec{D}^{iter} = \left[ {\varvec{I}_{1}^{iter} , \ldots ,\varvec{I}_{n}^{iter} } \right]$ using LRSD, and the template image $\varvec{I}_{t}^{iter} = \frac{1}{n}\mathop \sum \nolimits_{i = 1}^{n} \varvec{B}_{i}^{iter} .$ To avoid accumulation error in the composing of deformation fields through the iteration, each low-rank image in $\varvec{B}^{iter}$ is first transformed back to the original image space and then registered to $\varvec{I}_{t}^{iter}$. The resulting deformation fields in the current iteration $\varvec{\varPhi}_{i}^{iter} ,i = 1,..,n$ are applied to original input images $\varvec{D}^{0} = \left[ {\varvec{I}_{1}^{0} , \ldots ,\varvec{I}_{n}^{0} } \right]$ to produce the input images $\varvec{D}^{iter + 1} = \left[ {\varvec{I}_{1}^{0} \circ\varvec{\varPhi}_{1}^{iter} , \ldots ,\varvec{I}_{n}^{0} \circ\varvec{\varPhi}_{n}^{iter} } \right]$ for the next iteration. The iteration repeats until convergence. We replace LRSD in GIR-LRSD with SCOLOR, and the new GIR method is denoted as GIR-SCOLOR.

3 Results

We compare SCOLOR and GIR-SCOLOR with LRSD and GIR-LRSD. Evaluation focuses on image recovery quality and GIR accuracy. Two kinds of image datasets are used in the experiment. Dataset I is based on 40 T1-weighted MR brain images from a public database LPBA40 [13]. Each image in LPBA40 contains a normal brain and has a corresponding label image of 54 manually segmented brain regions. To create dataset I, real tumors segmented from other MR brain images are added into the images in LPBA40. Figure 2(a) shows some examples of dataset I. Dataset II has 28 T1-weighted MR brain images randomly selected from a public database BRATS2015 [14], and each image contains a real tumor. Figure 2(b) shows some images in dataset II. In the preprocessing step, both datasets are normalized to MNI152 [10] by affine transformation, and image intensity is normalized using histogram matching.

Fig. 2.

Examples of dataset I (a) and dataset II (b).

LRSD has a parameter $\uplambda$ in Eq. (1) and SCOLOR has parameters $\alpha$, $\beta$ and $\gamma$ in Eqs. (3–5). $\uplambda$ in LRSD plays the same role as $\beta$ in SCOLOR and their values are set manually based on the input image dataset. $\alpha$ and $\gamma$ are set to 1.0 and 0.5 by default.

3.1 Evaluation of Dataset I

Figure 3(a) shows two original images in dataset I and the corresponding low-rank images using LRSD ($\uplambda = 300$) and SCOLOR ($\beta = 30$, 5 iterations). It can be found that brain tumor regions and normal brain regions are better recovered and preserved by SCOLOR than LRSD as marked by red arrows. Image recovery quality is quantified by calculating the recovery error ratio for the 40 low-rank images produced by LRSD and SCOLOR, respectively. For the $i$-th image, the recovery error ratio is defined as $e_{i} = \frac{{\mathop \sum \nolimits_{{x \in\Omega _{i} }} \left| {\varvec{I}_{i}^{tf} \left( x \right) - \varvec{B}_{i} \left( x \right)} \right|}}{{\mathop \sum \nolimits_{{x \in\Omega _{i} }} \varvec{I}_{i}^{tf} \left( x \right)}}$ where $\Omega _{i}$ is the whole region of the $i$-th image, $\varvec{I}_{i}^{tf}$ stands for the $i$-th ground truth of tumor-free image and $\varvec{B}_{i}$ is the corresponding low-rank image produced by LRSD or SCOLOR. The average recovery error ratios of LRSD and SCOLOR are 0.087 ($\sigma = 0.008)$ and 0.047 ($\sigma =$ 0.004). The p value of the Wilcoxon signed rank test on the 40 recovery error ratios of LRSD and SCOLOR is 3.569 $\times 10^{ - 8}$ i.e., SCOLOR produces better low-rank images than LRSD with statistical significance.

Fig. 3.

(a) Examples of original images in dataset I and corresponding low-rank images using LRSD and SCOLOR. Brain tumor regions and normal brain regions are better recovered and preserved by SCOLOR than LRSD as marked by red arrows. (b) Average Dice indexes of GIR results of dataset I after each iteration of GIR-LRSD and GIR-SCOLOR.

GIR accuracy is quantified by the Dice index [15] which calculates the overlap of each brain region between each pair of registered images. Specifically, the resulting deformation fields of GIR-LRSD and GIR-SCOLOR are applied to the corresponding label images. The Dice index of each brain region between each pair of the deformed label images is calculated by $Q_{ij}^{l} = \frac{{2\left| {\Omega _{i}^{l} \cap\Omega _{j}^{l} } \right|}}{{\left| {\Omega _{i}^{l} } \right| + \left| {\Omega _{j}^{l} } \right|}}, l = 1,..,54;i,j = 1, \ldots ,40,i < j$ where $\left| {\Omega _{i}^{l} } \right|$ and $\left| {\Omega _{j}^{l} } \right|$ are the volumes of the l-th brain region in the $i$-th and $j$-th deformed label images respectively. Then we can obtain a summary measure between each pair of the deformed label images $Q_{ij}^{{}} = \mathop \sum \nolimits_{l = 1}^{54} \frac{{\left| {\Omega _{i}^{l} } \right|}}{{\left| {\Omega _{i} } \right|}}Q_{ij}^{l} ,$ where $\left| {\Omega _{i} } \right| = \mathop \sum \nolimits_{l = 1}^{54} \left| {\Omega _{i}^{l} } \right|$. GIR-LRSD and GIR-SCOLOR work in an iterative manner, so the accuracy of the GIR result after each iteration is evaluated. Figure 3(b) shows the average Dice index of 780 pairs of deformed label images warped by the deformation fields produced after each iteration of GIR-LRSD and GIR-SCOLOR, respectively. For both GIR methods, 6 iterations are performed. The p value of Wilcoxon signed rank test on the 780 Dice indexes after the final iteration of GIR-LRSD and GIR-SCOLOR is $1.7 \times 10^{ - 129}$, which further indicates that GIR-SCOLOR achieves better GIR performance with statistical significance.

3.2 Evaluation of Dataset II

Figure 4(a) shows two original images in dataset II and the corresponding low-rank images using LRSD ($\uplambda = 300$) and SCOLOR ($\beta = 30$, 5 iterations). It can be found that the low-rank images of SCOLOR contain higher quality of recovered brain tumor regions and better preserved normal brain regions than LRSD, especially on the regions marked by red arrows. Dataset II does not have the ground truth of tumor-free images, so the recovery error ratio cannot be calculated. GIR accuracy is quantified by calculating the entropy at every voxel position (except image background) across the input original images warped by the deformation fields obtained by GIR-LRSD and GIR-SCOLOR. More accurate GIR results should have lower entropy. The evaluation result of average entropies after each iteration of GIR-LRSD and GIR-SCOLOR is shown in Fig. 4(b). For both GIR-LRSD and GIR-SCOLOR, 7 iterations are needed.

Fig. 4.

(a) Examples of original images in dataset II and corresponding low-rank images using LRSD and SCOLOR. SCOLOR produces higher quality of recovered brain tumor regions and better preserved normal brain regions than LRSD as marked by red arrows. (b) Average entropies of warped original images of dataset II using deformation fields resulting from GIR-LRSD and GIR-SCOLOR after each iteration.

4 Conclusion

We proposed a new low-rank based image recovery method named SCOLOR and embedded it into an existing GIR framework to achieve accurate GIR of MR brain images containing tumors. Different from conventional low-rank based image recovery methods, a spatial constraint is added to the low-rank framework. Based on the spatial constraint, the residual error in the brain tumor region and normal brain region can be treated separately in the low-rank framework. Therefore, brain tumor regions are effectively recovered and normal brain regions of input images are well preserved in the resulting low-rank images. In the experiment, SCOLOR and GIR-SCOLOR were compared with LRSD and GIR-LRSD using both synthetic and real MR brain images. Evaluation results showed that SCOLOR can produce higher quality low-rank images than LRSD, and more accurate GIR of MR brain images containing tumors can be achieved using GIR-SCOLOR in comparison to GIR-LRSD. It is worth noting that GIR-SCOLOR is applicable to other pathological brain images which share the same properties of the brain tumor. For future work, more characteristics of the brain tumor will be used to define the spatial constraint e.g., brain tumors usually locate asymmetric in the brain. Furthermore, we hope to set the parameters in SCOLOR automatically.