Large Families of “Grey” Arrays with Perfect Auto-Correlation and Optimal Cross-Correlation

Abstract

Digital watermarking applications have a voracious demand for large sets of distinct 2D arrays of variable size that possess both strong auto-correlation and weak cross-correlation. We use the discrete Finite Radon Transform to construct “perfect” $p \times p$ arrays, for p any prime. Here the array elements are comprised of the integers $\{0,\pm 1,+2\}$. Each array exhibits perfect periodic auto-correlation, having peak correlation value $p^2$, with all off-peak values being exactly zero. Each array, by design, contains just $3(p-1)/2$ zero elements, the minimum number possible when using this “grey” alphabet. The grey alphabet and the low number of zero elements maximises the efficiency with which these perfect arrays can be embedded into discrete data. The most useful aspect of this work is that large families of such arrays can be constructed. Here the family size, M, is given by $M = p^2-1$. Each of the $M(M-1)/2$ intra-family periodic cross-correlations is guaranteed to have one of the three lowest possible merit factors for arrays with this alphabet. The merit factors here are given by $v^2/(p^2-v^2)$, for $v = 2$, 3 and 4. Whilst the strength of the auto-correlation rises with array size p as $p^2$, the strength of the many (order $p^4$) cross-correlations between all M family members falls as $1/p^2$.

1 Introduction

We are motivated by the many watermarking applications, like [2, 7, 8], for which one needs large families of arrays that have both low off-peak auto-correlation and cross-correlation. For example, to provide watermark tags for each frame of a 5 min YouTube 120 fps video requires about 36,000 arrays. If all of these tags are unique and have a low cross-correlation, it is possible to easily isolate and verify any individual frame within a 5 min sequence. A family comprised of 39,600 perfect arrays, each of size $199 \times 199$, would suffice for such an application.

The cross-correlation between functions f and g is given by

$$\begin{aligned} C_{fg}(s) = f \otimes g = \sum f(s) \cdot g(s-r) \end{aligned}$$

(1)

where r, a shift variable, is taken over all coordinates of g, and s covers the domain of f. Auto-correlation corresponds to the case where $f = g$. Perfect arrays have periodic auto-correlation with constant off-peak values. For a $p \times p$ array, the peak is $p^2$ with zero elsewhere (or $p^2 -1$ peak and $-1$ elsewhere), and cross-correlation between all family members have only $\pm p$ values.

Previous work [11] used the Finite Radon Transform (FRT) to construct $p \times p$ pseudo-noise arrays in families of size $M = p$ (where p is a $4N-1$ prime) that had optimal periodic auto-correlation and cross-correlation, that meet the Welch correlation bounds [12]. These families of (Legendre) arrays have an alphabet of a single zero element with the remainder being equal numbers of $\pm 1$ elements. “Grey” versions of these array families were also constructed that have integer alphabets (with integer values ranging between $\pm \sqrt{p}$). Recovery of a “grey” array, A, embedded in “grey” data, B, can be advantageous, as $A \otimes (A+B) \approx 2A \otimes A$ if we choose to embed A in those parts of B where $A \approx B$.

Subsequent work [10] extended the size of these array families (M) to multiples of p, typically $M \approx 3p$. This was done by blending the original array family with distinct arrays either derived from the original array auto-correlations, or with new arrays, also built using the FRT, but with their families generated using different (but equivalent) Hadamard matrices. The only concession made when extending the family size beyond p is that the strength of each cross-correlation now lies in a range of statistically predictable values, at or just above the lowest possible levels.

Further extension of the size of a family of arrays well beyond p is difficult as it is hard to constrain the range of cross-correlation values. The rapidity of this rise is, in part, due to the depth of the array alphabet. A binary array (or any array with mostly $\pm 1$ values) has only so many combinations that can simultaneously sustain high auto- and low cross-correlation. The “grey” versions of the $p \times p$ Legendre arrays constructed in [11] can support a much larger and more diverse range of well-correlated structures. The combinatorial diversity of grey perfect arrays also makes them significantly more secure and resistant to hacking.

However, the balance theorem ensures that the sum of the array values dictates the sum over all correlation values [3]. This ensures that alphabets spanning a wide range of greys also require a rapid increase in the number of zero elements in those perfect arrays (see Sect. 5). The number of zero elements in a perfect-correlation array increases with the square of the values of the non-zero elements. Arrays containing a large number of zero elements have reduced operational efficiency, as the zero terms “change nothing” when embedded into any local data.

For these reasons, we have investigated construction of perfect $p \times p$ arrays with a restricted grey alphabet of just $\{0, \pm 1, +2\}$. We introduce a minimal number, $(p-1)/2$, of elements having value $+2$, thus requiring $3(p-1)/2$ zero terms in each array. The balance of these array values (always a clear majority) are either $\pm 1$. The presence of a relatively few extra zeroes reduces the efficiency of these arrays, by $\mathcal {O}(1/p)$, but this becomes less significant for large p. Very large numbers of such arrays can be made, where each array contains a fixed proportion of each grey element. We can then select large families of arrays, where the intra-family array cross-correlations are restricted to the lowest possible levels.

Section 2 reviews the important link between the correlations of arrays and the correlations between projection of those arrays. This link permits the construction of 2D perfect arrays from 1D perfect projections. Section 3 reviews the Finite Radon Transform, a discrete projection scheme whose inverse back-projection permits exact reconstruction of any $p \times p$ set from $p+1$ discrete projections, for p prime. Section 4 reviews the use of affine transforms as a means to produce many distinct variants of a perfect array that retain the original array and correlation properties. Section 5 introduces a method to construct perfect arrays with a fixed “grey” alphabet and tightly bounded cross-correlation values. It then shows how to assemble a large family of such arrays. Section 6 presents some results for example array families. Ways to improve this technique and future work are highlighted in Sect. 7.

2 Projection Preserves Moments and Correlations

The central slice theorem [1] states that projected views of a distribution preserve the Fourier transform of the distribution. This is the main result underlying image reconstruction methods for computed tomography. As a corollary of the central slice theorem, moments and correlations of a distribution are also preserved under projection. This means, for example, that the auto-correlation of the projected view of some object is equal to the same projected view of the full object auto-correlation [4, 6]. The projections of any distribution inherit that distribution’s correlation properties.

We use this result in reverse to construct arrays with any desired correlation properties. For example, we assemble a set of 1D projections, each having perfect auto-correlation. We then reconstruct from that set a 2D object that inherits their perfect auto-correlation [10, 11].

The cross-correlation $C_{fg}$ between function f and g is defined in Eq. (1). Correlations are termed periodic where the sum of the products of overlapped functions is taken over cyclic boundary conditions and termed aperiodic when zeroes extend the function boundaries. Auto-correlation is the case where $f = g$. The correlation results as presented here are for periodic arrays. In practice, the aperiodic correlation results are more relevant. However, there the boundary conditions are usually not zero, but depend on the values of the data in which the arrays are embedded.

3 Using 1D FRT Projections to Build 2D Arrays

We exploit the correlation-preserving property of projections as given in Sect. 2. The discrete Finite Radon Transform [5] is used to provide a unique and exact reconstruction of any 2D $p \times p$ object from its $p+1$ 1D projected views. Here p must be prime to ensure the (cyclically wrapped) projections are uncoupled, as each projection fully tiles a $p \times p$ array, exactly once, at all positions, in a distinct pattern.

Projection R(t, m) of an image I(x, y) starts from translate t, $0 \le t < p$. Usually t is defined as one of the pixels along the top row of a $p \times p$ image. Each 1D projection is comprised of p parallel rays, where each ray sums p pixel values in I(x, y) that are located at p steps beginning from t, each step being m pixels across and one pixel down, wrapping periodically around the ray as required, where $0 \le m \le p$. Projections 0 and p are column and row sums of I(x, y), respectively.

$$\begin{aligned} R(t,m) = \sum I(\langle t + my \rangle _p,y) \end{aligned}$$

(2)

where $\langle j \rangle _p$ means j modulus p. Back-projecting each of the $p+1$ 1D projections across a zeroed $p \times p$ array at the complemented angles ($m' = p-m$) and normalising the result recovers, exactly, the 2D data that was projected.

4 Affine Transforms Preserve Correlations

Just as discrete projection preserves correlation, so too does affine transformation. For example, a 2D affine transformation (reversibly) maps each pixel (x, y) of a prime $p \times p$ 2D image to a new location $(x',y')$. Under matrix multiplication in homogeneous coordinates (modulus p):

$$\begin{aligned} \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} a&b&e \\ c&d&f \\ 0&0&1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \end{aligned}$$

where the values, $0 \le {a,b,c,d,e,f} < p$, are arbitrary integer transform coefficients, provided only that the upper matrix [a b;  c d] has non-zero determinant (modulus p).

The coefficients e and f serve as a discrete translation vector; hence we always set these to 0, as simple translations of an array exhibit the same (periodic) correlations. When [a b;  c d] = [j $-i;$ i j], the affine transform rotates the array by the discrete angle i:j, when [a b;  c d] = [j i;  i j], the affine transform skews the array by vector i:j.

With 4 arbitrary affine transform coefficients, a single $13 \times 13$ perfect array A thus has $12^4$ distinct affine variations, each of which has perfect correlation, since the original A is perfect. The very many cross-correlations between these arrays will vary from being optimally low through to many cases where the transformed array is a cyclic shift of A (equivalent under periodic correlations). For watermarking applications, sign changed, reflected or transposed arrays should be avoided.

For $p \times p$ arrays, we know in advance the exact set of angles i:j that correspond to the complete set of $p+1$ discrete projections of the FRT for a $p \times p$ array [9]. If we avoid the simple axial rotations 1:0 ($90^\circ$) and 0:1 ($0^\circ$), we can, without redundancy, rotate each original array A by affine coefficients i:j to obtain up to $p-3$ distinct copies $A'$ of each A, whilst preserving the original correlation properties. Affine skews for angles $\pm 1$:1 are skipped, because they yield a zero determinant. Similarly, for all $p = 4n+1$ primes, there is one set of degenerate rotations $\pm i$:j (and $\pm j$:i) that are skipped, for the case $i^2+ j^2 = p^2$, which also has zero determinant [9].

5 Construction of a Family of Perfect Arrays with Alphabet $\{0,\pm 1, +2\}$

In this section, we detail the construction of families of perfect $p \times p$ arrays using the alphabet $\{-1,0,+1,+2\}$. The FRT is employed to construct perfect arrays using distinct cyclic shifts. Affine rotations can then be used to extend the size of the array family.

5.1 Array Construction

Discrete 1D “delta” functions (or unit impulses) of length p, for example [1 0 0 0 0 0 0], can be used to create the $p+1$ FRT projections (as done in [11]). A delta function has a perfect 1D auto-correlation, hence so too will any 2D array reconstructed from these 1D delta projections by applying the FRT inverse transform.

We want to minimise the number of zeroes in the 2D array reconstructed from these projections. This requires that the 1D rays back-projected from each view angle ($m_{1}$) must intersect with the rays from other angles ($m_{2}$) at as many distinct array positions as possible. This condition can be achieved by judicious adjustment of the (circular) phase shift of each delta function, for example from [1 0 0 0 0 0 0] to something like [0 0 0 1 0 0 0].

In the FRT, each ray (m, t) is back-projected [5] as the line that passes through the image points (x, y), where

$$\begin{aligned} x = -my+t. \end{aligned}$$

(3)

We want to ensure that the delta impulse from projection $m_{1}$ intersects with the delta impulse from projection $m_{2}$ at a distinct point $(x_{12},y_{12})$ for each pair $m_{1}$, $m_{2}$. We assign

$$\begin{aligned} t = 1/m \end{aligned}$$

(4)

for $1 \le m \le p-1$, and substitute into (3) so the rays for projections $m_{1}$ and $m_{2}$ have

$$\begin{aligned}&x_{12} = -m_{1}y_{12} + \frac{1}{m_{1}} = -m_{2}y_{12} + \frac{1}{m_{2}} \\&y_{12}(m_{2}-m_{1}) = \frac{1}{m_{2}} - \frac{1}{m_{1}} = \frac{-(m_{2}-m_{1})}{m_{1}m_{2}} \end{aligned}$$

which intersects at $(x_{12},y_{12}) = \left( \frac{1}{m_{1}} + \frac{1}{m_{2}}, \frac{-1}{m_{1}m_{2}} \right)$. Alternatively, we can assign

$$\begin{aligned} t = m^2 \end{aligned}$$

(5)

for $1 \le m \le p-1$, and substitute into (3) so the rays $m_{1}$ and $m_{2}$ have

$$\begin{aligned}&x_{12} = -m_{1}y_{12} + m_{1}^2 = -m_{2}y_{12} + m_{2}^2 \\&y_{12}(m_{2}-m_{1}) = m_{2}^2-m_{1}^2 = (m_{2}-m_{1})(m_{2}+m_{1}) \\&y = m_{1}+m_{2} \text { and } x = -m_{1}m_{2} \end{aligned}$$

which intersects at $(x_{12},y_{12}) = \left( -m_{1}m_{2}, m_{1}+m_{2} \right)$.

Fig. 1.

FRT projection matrices for a 2D array built from 1D phase shifted delta functions, for $p = 7$, (a) $t = 1/m$, (b) $t = m^2$. The pseudo-orthogonality of these phase shifts is shown on the right via the matrix product of their 2D FRT arrays

Assigning projection m to have cyclic shift $t = 1/m$ or $t = m^2$ imposes a strong symmetry on the FRT matrix, as each projection m has a negative counterpart $m' = p-m = -m$, and then $m_{2} = m'_{2}$, and $1/m = -1/m'$. The “near-orthogonality” of these shift assignments is evident in the “pseudo-Hadamard” constructed from the $p \times p$ matrix product of the shifted delta functions of the FRT, B, with the shifted impulses of its transpose, shown as $B *B^T$, in Fig. 1 (a) for $t = 1/m$ and (b) for $t = m^2$. We use the term near-orthogonal to reference the fact that there are few non-zero elements that lie off the diagonal of $B *B^T$.

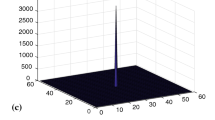
Typical arrays reconstructed from FRT’s that are built using delta functions where the phase-shift t for projection m are given by $t = 1/m$ are shown in Fig. 2a and for $t = m^2$ in Fig. 2b. Note that these perfect $p \times p$ arrays all have sum = p. All arrays made this way will have the same histograms: for the 49 elements in each $7 \times 7$ array, 18 elements have value $-1$, 9 are zero, 19 are $+1$ and 3 are $+2$ elements, giving sum = 7.

We extend the size of the array families by computing FRT matrices with shifts, t, that are linear multiples of (4, 5), modulus p, which then undergo many affine rotations and skews. Combining these operations can produce some duplicated arrays. Although every distinct FRT set corresponds to a unique array, some scaled mapping of the FRT variables m and t can be degenerate. For example, the FRT of the transpose of a $p \times p$ array, $B^T(m,t)$, can be obtained from shuffling the FRT of the original array, B(m, t), by $m' = 1/m$ and $t' = -t/m$ (as the transpose maps projection angle x:y to y:x). The shifts of Eq. (4) are thus very close to a transpose operation. Similar structural overlaps in reconstructed arrays can result from axial rotations or symmetric reflections.

Fig. 2.

$7 \times 7$ arrays reconstructed from (a) FRT $B_{a}$ from Fig. 1 (a). (b) $B_{b}$ from Fig. 1 (b). (c) The auto-correlation for arrays (a) and (b) is perfect. (d) The cross-correlation between (a) and (b) has type $L_{2}$. This example shows the strongest cross we accept.

We assign frequencies k, l, m and n to the occurrence of grey elements $-1$, 0, $+1$ and $+2$ respectively in any $p \times p$ array. The FRT translates, t, arrange the $(p-1)$ projections to have distinct intersections as pairs, yielding $(p-1)/2$ elements with value $+2$ in the final array, thus fixing $n = (p-1)/2$. The sum over all $p^2$ elements of a $p \times p$ array is then

$$\begin{aligned} -1 \cdot k + 0 \cdot l +1 \cdot m + 2 \cdot (p-1)/2 = p. \end{aligned}$$

(6)

The sum of the array auto-correlation values, by the balance theorem [3], means

$$\begin{aligned} (-1)^2 \cdot k + (0)^2 \cdot l + (+1)^2 \cdot m + (+2)^2 \cdot (p-1)/2 = p^2. \end{aligned}$$

(7)

From (6), $m-k=1$ and from (7), $m+k=p^2-2p+2$, giving $m=(p-1)^2/2$, $k=m+1$ and $l=3(p-1)/2$. Any $p \times p$ array (with p prime) made using the FRT with these values of t will have a fixed histogram for its element values, $-1$ through $+2$, as [$(p-1)^2/2$, $3(p-1)/2$, $(p-1)^2/2+ 1$, $(p-1)/2$].

The fixed histogram of element values permits quantification of the merit factors for the periodic cross-correlation of these arrays. The merit factor (MF) is defined as the square of the peak correlation value divided by the sum of all $p^2-1$ off-peak values. Perfect arrays are, by definition, spectrally flat. All cross-correlations between pairs of spectrally flat arrays are also spectrally flat by the convolution theorem, and hence those cross-correlations are also perfect arrays themselves.

The lowest possible maximum value of any cross-correlation is $\pm 1 \cdot 2 = \pm 2$ (it cannot be $\pm 1$, as one of the 2’s will line up at least once with the majority of $\pm 1$ terms). The sum of all array terms squared is always $p^2$, hence $L_{0}$, the lowest possible MF value, is given by $L_{0} = 2^2/(p^2-2^2) = 4/(p^2-4)$.

The next level possible cross level, $L_{1}$, corresponds to a maximum cross-correlation sum of 3, giving $L_{1} = 3^2/(p^2-3^2)$. The next possible level has cross-correlation value = 4, thus $L_{2} = 16/(p^2-16)$. The next level $L_{3} = (p-1)^2/(2p-1)$, corresponds to arrays where all the ones line up, and finally $L_{4} = p^2/0 = \infty$, when the two arrays are identical (and the cross becomes a perfect auto-correlation).

Here $L_{0}$, $L_{1}$, $L_{2}$, $L_{3}$ and $L_{4}$ are the only possible periodic cross-correlation values between these arrays when built using symmetric 1D projections, for any array size p. For $p=7$, $L_{3}$ corresponds to a peak cross value of $p-1 = 6$. A correlation peak value of 5 is not possible for a cross between these arrays. However we can construct different arrays (that require an asymmetric set of cyclic shifts for different projections m in the FRT) to give an alphabet $\{0,\pm 1,2,5\}$. This array, for $p = 7$, contains 27 zeroes, compared to just 9 zeroes for the arrays with alphabet $\{0,\pm 1,2\}$. These “asymmetrically made” grey arrays also, of course, still retain perfect auto-correlations.

Note the merit factors $L_{0}$, $L_{1}$ and $L_{2}$ are all $< 1$ for any prime $p > 5$, while $L_{3}$ denotes a strong cross-correlation with MF of order p / 2 and $L_{4}$ means the two arrays are a perfect match. When selecting arrays to build an extended family, we restrict the choice of arrays to be only those that yield cross-correlations of $L_{0}$, $L_{1}$ or $L_{2}$, preferably choosing the sets of arrays that have a larger fraction of crosses being either $L_{0}$ or $L_{1}$.

5.2 Building Array Families

To construct a family of arrays, a set $A_1$ of $p-1$ seed arrays is made using the FRT with delta functions as 1D projections. Each array is made using (4) and a distinct cyclic shift $t = \alpha /m$, for $1 \le \alpha \le p-1$. A second set $A_2$ of $p-1$ seed arrays is made using (5) and cyclic shifts $t = \alpha m^2$, again for $1 \le \alpha \le p-1$. The translates chosen for the remaining FRT projections, for $m = 0$ and p in set $A_1$, can be fixed independently of the assigned shifts necessary for the $(p-1)$ paired intersecting rays. If the $m = 0$ and p rays are all set to $t = 0$, the arrays $A_2$ are the transpose of the arrays in $A_1$, listed in reverse order. A free choice is possible in the assignments of parameter t for the perpendicular rays $m = 0$ and $m = p$ when constructing the arrays for set $A_1$. This permits several distinct perfect $A_1$ families to be constructed whilst using the same pairing rules that fix the array histogram.

The sets $A_1$ and $A_2$ are pooled to form $A_P$. The seed family $A_P$ is then affine rotated by a selection of the FRT projection angles i:j for that prime p to produce array family $A_R$. The seed family $A_P$ is skewed by selected valid skew vectors to form array family $A_S$. The two families $A_R$ and $A_S$ are then pooled to form a (large) family $A_T$. Any duplicate copies of arrays formed by matched affine transformations are removed. Each array in $A_T$ has perfect periodic auto-correlation. All intra-family correlations for $A_T$ are checked and those pairings that produce correlation values $L_{3}$ and $L_{4}$ are discarded from $A_T$ to produce the final optimal family A.

This method of pooling rotated and skewed arrays ensures all valid possible variants of $A_1$ and $A_2$ are produced. The final thinned set A then is always comprised of $p^2-1$ arrays. There are also many different ways to thin and discard pairs of arrays from $A_T$ to select the final family A. We select arrays with the most favourable distribution of cross-correlation values $L_{0}$, $L_{1}$ and $L_{2}$ that best suit a given application.

6 Results

Table 1 presents example results for families of $p \times p$ arrays where $p =$ 7, 23 and 43 with family sizes 48, 528 and 1848, respectively. In each case, all auto-correlations within each family are perfect, having peak values of 49, 529 and 1849 respectively. The merit factor (MF) for any intra-family periodic cross-correlations is either $L_{0}$, $L_{1}$ or $L_{2}$, having the values as listed. The relative frequencies of the $L_{0}$, $L_{1}$ or $L_{2}$ occurrences are given to highlight the distribution of cross-correlation values between all family members.

The family of arrays for $p = 23$ is generated as follows: each of the initial seed sets $A_1$ and $A_2$ contains $p-1 = 22$ perfect arrays. Each of these $23 \times 23$ arrays contains 529 elements; 242 elements being $-1$, 33 zeroes, 243 $+1$ elements and 11 $+2$ values. Their periodic auto-correlation peak $= 529$, with all off-peak entries $= 0$. Each of the 231 cross-correlations between the 22 arrays in $A_1$ (and also between all $A_2$ members) has the minimal MF $L_{0} = 0.00762$.

Set $A_P = (A_1+A_2)$ has 44 distinct arrays. Affine rotation of the set $A_P$, by 11 FRT angles, produces 484 more perfect arrays, 396 of which are distinct (duplicate free). When $A_P$ is skewed by 10 FRT angles, another 440 perfect arrays are produced, of which 308 are duplicate-free. The resulting $396+308+44 = 748$, $23 \times 23$ arrays are pooled as set $A_T$. $A_T$ is checked for cross-correlations, from which 220 arrays, whose crosses give an $\text {MF} > 1$, are discarded, leaving the final family A of $748-220 = 528$ perfect arrays. Two different families of 528 arrays were selected from $A_T$, each has a slightly different distribution of cross-correlations over the same low cross-correlation merit factors.

Table 1. Cross-correlation values and their relative frequencies for two sets.

Table 1 shows that the MF for the bulk of the intra-family cross-correlation values are mainly of type $L_{1}$, but that selecting arrays in different ways can, at least marginally, alter the proportion of $L_{0}$, $L_{1}$ and $L_{2}$ results. However, the $p = 7$ case shows that it is possible to select different families of arrays from $A_T$ that favour the production of more $L_{0}$ crosses and that minimise the number of $L_{2}$ crosses.

7 Conclusions and Further Work

The families of $p \times p$ arrays constructed here have perfect auto-correlation with guaranteed low cross-correlation values between all family members. These arrays have a restricted grey alphabet (elements of $\{0,\pm 1, +2\}$) with a small number, $3(p-1)/2$, of zero elements. This makes them highly efficient and secure when embedded as watermarks. The fixed frequency of array element values permits selection of $p^2-1$ family members that have cross-correlation values with just three of the lowest possible merit factors, $\text {MF} = v^2/(p^2-v^2)$, for $v = 2$, 3 and 4.

The size of $A_T$ needs to be kept small to avoid excessive computation to do the cross-correlation checks required to remove arrays that have MF $> 1$. If $A_T$ has size M, $M(M-1)/2$ crosses of size $p \times p$ need to be checked. However, pooling $A_T$ to be too small may also restrict the range of distinct or partially overlapped solution sets A that can be selected from $A_T$. It may be possible to define a set of affine rotations and skews to directly produce a final set A without computing the larger intermediate set $A_T$.

At present, we select the final A arrays by deleting of one of each pair of arrays in $A_T$ that has MF $> 1$. The order of these deletions can be done in several different ways. This selection and deletion process could be organised more strategically.

The FRT can be adapted to reconstruct higher dimensional arrays from 1D projections. The technique developed here can then be extended to produce families of nD arrays.

We have yet to examine perfect arrays over other, larger alphabets, even in 2D, to see if the merit factors of their cross-correlations can also be fixed algebraically.