A Convexity Measure for Gray-Scale Images Based on hv-Convexity

Abstract

There are several measures for the convexity of digital images that extend the basic binary decision of the classic geometrical convexity. Some algorithms measure the convexity of a binary image using intensity profiles from horizontal and vertical directions. In this paper, we generalize the idea of binary, directional convexity and evaluate the proposed algorithm on gray-scale images. Furthermore, instead of a single convexity value, a vector can be formed using our approach, which provides a more prominent feature for various applications, such as computer vision, classification, retrieval, or medical image processing. The proposed feature can also be used locally on image parts, which makes that applicable as a shape descriptor.

The research was supported by the NKFIH OTKA [grant number K112998].

1 Introduction

Convexity is a widely studied and applied shape descriptor in image analysis and classification. On digital shapes, there are various measures that approximate the continuous convexity, like area based [6, 19, 20] and boundary-based ones [22]. It shall be noted that many convexity measures produce continuous output [15, 17, 18], unlike the classic, geometrical approach, which gives a binary decision whether or not the observed shape is convex.

In case of digital images, directional convexity is a common alternative for the convexity for continuous shapes, due to the pixel-based representation of the image. Mostly horizontal and vertical convexity is used (shortly, hv-convexity), which means that the convexity measure is defined by the aggregation of the convexity degree along horizontal and vertical sweeping lines. The property of hv-convexity is deeply studied in Binary Tomography [14], where one problem in focus is to reconstruct binary images (matrices) from their row and column sums according to geometrical constraints. Several reconstruction methods utilize the preliminary information of hv-convexity about the binary image to be reconstructed [3, 8, 11]. Enforcing compactness of the image to reconstruct can also result in binary images which are (almost) hv-convex [12]. In [21] the authors introduced a measure of directional convexity and proved it to be useful in binary tomographic reconstruction. However, they also showed that a 2D extension of this measure is not straightforward [2]. Later, immediate 2D convexity measures were also proposed in [1, 9], while in [5] an upgrade of the measure of [2] was published.

The aim of this paper is to generalize the directional convexity measure from binary to gray-scale images, that can be used with existing binary convexity measures [1, 5, 21]. The structure of the paper is the following. In Sect. 2 we describe the proposed gray-scale convexity measure. In Sect. 3 we present experimental results. Section 4 is for the conclusion.

2 The Proposed Gray-Scale Convexity Measure

2.1 Preliminaries

A digital image M is a matrix having m rows and n columns (where $m,n\in \mathbb {N}$). Numbering of rows and columns start with 1 from top to bottom and left to right, respectively. If M is a digital image then $M^T$ is the image we get by interchanging the rows and columns of M. Let $I=\{i_0,\dots , i_l\}$ be the set of possible intensity values of the image such that $i_k<i_{k+1}$ ($k=0,\dots ,l-1$) and $M(r,c) \in I$ denote the intensity value corresponding to the position (r, c). A typical choice is $I=\{ 0,\dots ,255\}$ (8-bit images) or $I=\{ 0,\dots ,65535\}$ (16-bit images).

For binary images $I=\{ 0,1\}$. In this case, a run of object (background) points within a row or column is a sequence of consecutive pixels, all of them being object (resp. background) points, such that it cannot be expanded by further neighboring pixels of the same color. Obviously, each row and column of the image can be expressed by an alternating sequence of object and background runs. The length of an arbitrary run a will be denoted by |a|.

2.2 Measure of hv-Convexity for Binary Images

Originally, we follow the idea of hv-convexity measuring on binary images in [5] which is a modified version of [2]. According to that paper, first, the convexity defect $\varphi ^{bin}_h (r)$ for each row $r=1,\dots , m$ is calculated in the following way (bin stands for “binary”).

Let R be the pixel sequence of an arbitrary row. To compute the non-convexity of R, we split it into a list of object and background runs. If the first or last run is a background run then we omit them. Thus the rest of the row can be encoded as $R=b_1w_1b_2w_2\dots w_{n-1}b_n$, where each $b_i$ is an object run ($i=1,\dots , n$) and each $w_i$ ($i=1,\dots , n-1$) is a background run.

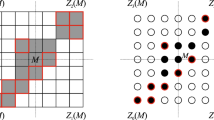
Let $O_R$ be the ordered set of object runs in row r, i.e., $O_R = \{b_1, b_2, \dots , b_n\}$. The sum of object pixels in R is $N_R = |b_1|+|b_2|+\dots +|b_n|$. Now, let $b_i, b_j\in O_R$ such that $i<j$. We select one random point from both, say, the k-th from left in $b_i$ denoted by $b_{i_k}$ and the l-th from left in $b_j$ denoted by $b_{j_l}$. The section connecting these two points is characterized by the non-convexity measure, which value depends on the number of background pixels between $b_i$ and $b_j$. Let $W_{i,j}=\sum _{l=i}^{j-1}|w_l|$, $B_{i,j}=\sum _{l=i+1}^{j-1}|b_l|$ and $d_{i_k,j_l}$ denote the distance of the two chosen points. This distance is partially made up of the points of $b_i$ to the right of $b_{i_k}$, the points of $b_j$ to the left of $b_{j_l}$. There are, $\vert b_i \vert - k +1$ and l such points (including the chosen points, too), respectively. Additionally, the section contains the $W_{i,j}$ background points, and further object point runs ($B_{i,j}$), if $j>i+1$. That is, $d_{i_k,j_l} = \vert b_i \vert - k + 1 + W_{i,j} + B_{i,j} + l$ (Fig. 1 illustrates the calculation). The normalized non-convexity measure for this section is

$$\begin{aligned} \frac{W_{i,j}}{d_{i_k,j_l}}\ , \end{aligned}$$

(1)

and the cumulated non-convexity of R is

$$\begin{aligned} \frac{\sum _{b_i, b_j \in O_R, i<j} \sum _{k=1}^{\vert b_i \vert } \sum _{l=1}^{\vert b_j \vert } \frac{W_{i,j}}{d_{i_k,j_l}}}{C_r}\ , \end{aligned}$$

(2)

where $C_r$ is the number of combinations to select the two object points from different object point runs, computed as

$$\begin{aligned} C_r = \left( \begin{array}{c}N_R\\ 2\end{array}\right) - \sum _{b \in O_R} \left( \begin{array}{c}\vert b \vert \\ 2\end{array}\right) \ . \end{aligned}$$

(3)

Fig. 1.

Calculation of the non-convexity between two object points from different object runs, proposed in [5].

The horizontal convexity of M is defined as

$$\begin{aligned} \varPsi ^{bin}_h (M) = 1-\frac{\sum _{r=1}^m \varphi ^{bin}_h (r)}{m}\ . \end{aligned}$$

(4)

The vertical convexity $\varPsi ^{bin}_v(M)$ can be calculated analogously by the observation that $\varPsi ^{bin}_v(M)=\varPsi ^{bin}_h(M^T)$. Finally, the hv-convexity is the algebraic mean of the horizontal and vertical convexity, i.e.,

$$\begin{aligned} \varPsi ^{bin}_{hv}(M)=\frac{\varPsi ^{bin}_h(M)+\varPsi ^{bin}_h(M^T)}{2}\ . \end{aligned}$$

(5)

2.3 Extension of the Convexity Measure to Gray-Scale Images

The aforementioned approach only measures convexity of binary images, since we need to define sequences of object and background pixels. In most cases, binarization is solved by thresholding (for example, with Otsu’s method [16]), which leads to loss of information. To overcome this, we propose to aggregate the convexity using all possible thresholds. Let T(M, t) denote the binary image we get by thresholding M at level t. For the continuous case, convexity is computed as

$$\begin{aligned} \varPsi _{hv}(M) = \frac{1}{i_l - i_0}\int _{i_0}^{i_l} \varPsi ^{bin}_{hv}(T(M,t)) dt\ . \end{aligned}$$

(6)

This calculation theoretically takes infinite time, however, it collapses to a factor of $\mathcal {O}(|I|)$ when the input is quantized. Assuming that the image is in the positive intensity range, convexity is computed as

$$\begin{aligned} \varPsi _{hv}(M) = \frac{1}{|I|}\sum _{t=i_0}^{i_l} \varPsi ^{bin}_{hv}(T(M,t))\ . \end{aligned}$$

(7)

The aforementioned approach calculates the convexity of the same binary image multiple times if the intensity value t does not occur within the original one. Exploiting this, the calculation of T(M, t) is only necessary where $t \in J$ with $J=\{j_0,j_1,\dots , j_{|J|-1}\}\subseteq I$ being the ordered set of distinct intensity values of I. For the sake of technical simplicity we assume that the maximal element $i_l$ of I is always contained in J even if it is not present in the image. Each $\varPsi ^{bin}_{hv}(T(M,t))$ can be assigned a weight, reflecting how many times we could have calculated that. Let W(t) be a weight corresponding to t. We perform thresholding at all intensity levels of J and aggregate the results of binary convexity measures (Algorithm 1) as

$$\begin{aligned} \varPsi _{hv}(M)= \frac{1}{|I|} \sum _{t=0}^{|J|-1} \varPsi ^{bin}_{hv}(T(M, j_t)) W(t)\ \end{aligned}$$

(8)

with

$$\begin{aligned} W(t)= {\left\{ \begin{array}{ll} j_0+1 &{}\text { if }t=0 \\ j_t-j_{t-1} &{}\text { otherwise} \end{array}\right. }\ . \end{aligned}$$

(9)

The weight values W(t) would be 1 for all t input, if all intensities occur in the image within the full intensity range. For an other example, if $I=\{0,1,2,3,4\}$ and the ordered set of intensities in the image is $J=\{0, 1, 4\}$, then the corresponding weights are $\{1, 1, 3\}$. It shall be noted that the sum of weights is always equal to the size of the intensity range in which the image is represented.

3 Evaluation and Experiments

Our first experiment is about to show the basic difference between the original binary convexity [5] and the proposed one. In Fig. 2, binary thresholding leads to the same result for both squares. On the other hand, the proposed algorithm forms the weighted sum of thresholds on all occurring gray levels, and can differentiate between the two images. It gives a convexity value of 0.8940 for the gray-scale image and 0.5975 to its binarized version.

Fig. 2.

Images of two empty square objects and their corresponding convexity values. The gray square is intuitively more “full”, which attribute is also supported by the proposed gray-scale convexity value.

We also examined the proposed algorithm on a real gray-scale image (Fig. 3). We thresholded the image at 50% of the intensity range, produced another image using 16 quantization levels, and finally, measured the hv-convexity of the original 8-bit image. According to this example, the quantization levels may be reduced for 8-bit images in order to achieve faster run-time of the algorithm, however, that only gives an approximation of the original convexity.

Fig. 3.

The proposed approach on a real 8-bit image.

It shall be noted that not only a scalar value can be derived from this approach. If desired, the convexity values can be used for each occurring intensity (Figs. 4 and 5). Thus, two vectors can be formed for each image, one containing the convexity values for each threshold level, and another with the corresponding weights. Both vectors have the same length (the number of distinct intensities of the source image). Those vectors can also be computed locally on image parts, which renders them applicable as a shape descriptor for computer vision, classification and object recognition.

Fig. 4.

Convexity values for the 8-bit real image (represented in Fig. 3) and its 16-level quantized version w.r.t. threshold level. The vector of individual convexities may give a more prominent feature for classification tasks than a single convexity value.

Fig. 5.

The thresholded versions of the image represented on Fig. 3, quantized to 16 levels, and its corresponding values of h-, v-, and hv-convexity.

The proposed generalization of the binary convexity measure has the same behavior w.r.t. rotation and scale invariance than the original convexity measure we generalize. While this paper only evaluates the convexity measure of [5], the proposed idea can be used with other binary convexity measures as well [1].

4 Conclusion

In this paper, we presented a gray-scale generalization of an hv-convexity measure for binary images. Using this approach, the loss of information at the thresholding step is avoided, while all existing convexity measures that work on binary images [1, 2, 5] can be adapted to work on gray-scale images, too. Having only a few distinct intensity levels in an image, the calculation can be performed rapidly. If less precise calculation is acceptable and speed is more desired, intensity levels of the image may be further quantized.

The descriptor can be also computed locally to an image part, therefore it may also be used as an additional shape descriptor in applications, such as computer vision, classification, object recognition, image retrieval, or medical image processing. A further perspective is to use the single gray-scale convexity measure as prior information in multivalued discrete tomography. The reconstruction of multicolor images (i.e., containing at least 3 different gray intensity values) is in general an NP-hard problem, however, for certain image classes and/or with appropriate heuristics it can be effectively solved [4, 7, 10, 13]. It needs a further investigation whether gray-level convexity measures can also facilitate such kind of reconstruction problems.