Abstract
Non-malleable commitments are a central cryptographic primitive that guarantee security against man-in-the-middle adversaries, and their exact round complexity has been a subject of great interest. Pass (TCC 2013, CC 2016) proved that non-malleable commitments with respect to commitment are impossible to construct in less than three rounds, via black-box reductions to polynomial hardness assumptions. Obtaining a matching positive result has remained an open problem so far.
While three-round constructions of non-malleable commitments have been achieved, beginning with the work of Goyal, Pandey and Richelson (STOC 2016), current constructions require super-polynomial assumptions.
In this work, we settle the question of whether three-round non-malleable commitments can be based on polynomial hardness assumptions. We give constructions based on polynomial hardness of ZAPs, as well as one out of DDH/QR/\(N^{th}\) residuosity. Our protocols also satisfy concurrent non-malleability.
The full version of this paper is available at http://eprint.iacr.org/2017/734.
Research supported in part by the UCLA Dissertation Year Fellowship 2017–18. Research also supported in part from a DARPA/ARL SAFEWARE award, NSF Frontier Award 1413955, NSF grants 1619348, 1228984, 1136174, and 1065276, BSF grant 2012378. This material is based upon work supported by the Defense Advanced Research Projects Agency through the ARL under Contract W911NF-15-C-0205. The views expressed are those of the authors and do not reflect the official policy or position of the Department of Defense, the National Science Foundation, or the U.S. Government.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Non-malleable commitments are a fundamental primitive in cryptography, that help prevent man-in-the-middle attacks. A man-in-the-middle (MIM) adversary participates simultaneously in multiple protocol executions, using information obtained in one execution to breach security of the other execution. To counter such adversaries, the notion of non-malleable commitments was introduced in a seminal work of Dolev et al. [7]. From their inception, non-malleable commitments have been instrumental to building various several important non-malleable protocols, including but not limited to non-malleable proof systems and round-efficient constructions of secure multi-party computation.
A commitment scheme is a protocol between a committer \({\mathcal C} \) and receiver \({\mathcal R} \), where the committer has an input message m. Both parties engage in an interactive probabilistic commitment protocol, and the receiver’s view at the end of this phase is denoted by \(\mathsf{com}(m)\). Later in a opening phase, the committer and receiver interact again to generate a transcript, that allows the receiver to verify whether the message m was actually committed to, during the commit phase. A cryptographic commitment must be binding, that is, with high probability over the randomness of the experiment, no probabilistic polynomial time committer can claim to have used a different message \(m' \ne m\) in the commit phase. In short, the commitment cannot be later opened to any message \(m' \ne m\). A commitment must also be hiding, that is, for any pair of messages \((m, m')\), the distributions \(\mathsf{com}(m)\) and \(\mathsf{com}(m')\) should be computationally indistinguishable. Very roughly, a commitment scheme is non-malleable if for every message m, no MIM adversary, intercepting a commitment protocol \(\mathsf{com}(m)\) and modifying every message sent during this protocol arbitrarily, is able to efficiently generate a commitment to a message \(\tilde{m}\) related to the original message m.
Round Complexity. The study of the round complexity of non-malleable commitments has been the subject of a vast body of research over the past 25 years. The original construction of non-malleable commitments of [7] was conceptually simple, but it required logarithmically many rounds. Subsequently, Barak [2], Pass [20], and Pass and Rosen [22] constructed constant-round protocols relying on non-black box techniques. Pass and Wee [23], Wee [24], Goyal [9], Lin and Pass [17] and Goyal et al. [11] then gave several round-optimized constant-round black-box constructions of non-malleable commitments based on various sub-exponential or polynomial hardness assumptions.
More recently, there has been noteworthy progress in understanding the exact amount of interaction necessary for non-malleable commitments. Pass [21] showed an impossibility for constructing non-malleable commitments using 2 rounds of communication or less, via a black-box reduction to any “standard” polynomial intractability assumption. Goyal et al. [13] constructed four round non-malleable commitments in the standard model based on the existence of one-way functions. Even more recently, Goyal et al. [12] constructed three round non-malleable commitments (matching the lower bound of [21]) using quasi-polynomially hard injective one-way functions, by exploiting properties of non-malleable codes. Ciampi et al. [5] showed how to bootstrap the result of [12] to obtain concurrent non-malleable commitments in three rounds assuming sub-exponential one-way functions. In fact, in the sub-exponential hardness regime, Khurana and Sahai [16] and concurrently Lin et al. [18] showed how to achieve two-round non-malleable commitments from DDH and from time-lock puzzles, respectively. Subsequently, [1] used these to obtain various concurrently secure protocols in two or three rounds. All these works use complexity leveraging and therefore must inherently rely on super-polynomial hardness. This state of affairs begs the following fundamental question:
“Can we construct round optimal non-malleable commitments from polynomial assumptions?”
We answer this question in the affirmative, by giving an explicit construction of three-round non-malleable commitments, based on polynomial hardness of any one out of the Decisional Diffie-Hellman, Quadratic Residuosity or \(N^{th}\) residuosity assumptions. We additionally assume ZAPs, which can be built from trapdoor permutations [8], the decisional linear assumption on bilinear maps [14] or indistinguishability obfuscation together with one-way functions [4]. Our construction additionally satisfies concurrent (many-many) non-malleability.
Informal Theorem 1
Assuming polynomial DDH or QR or \(N^{th}\)-residuosity, and ZAPs, there exist three-round concurrent non-malleable commitments.
Related Work. Goyal et al. [10] recently constructed two-round non-malleable commitments with respect to opening, secure against synchronizing adversaries, from polynomial hardness of injective one-way functions. Their result is incomparable to ours because they achieve a weaker notion of security (non-malleability with respect to opening), in two rounds, but against only synchronizing adversaries.
2 Technical Overview
We now describe the key technical roadblocks that arise in constructing non-malleable commitments from polynomial hardness, and illustrate how we overcome these hurdles.
As we already explained, proving non-malleability requires arguing that the value committed by a man-in-the-middle adversary remain independent of the value committed by an honest committer. This seems to inherently require extraction (as also implicit in [21]): a reduction must successfully extract the value committed by the MIM and use this value to contradict an assumption. However, current constructions of non-malleable commitments in three rounds based on polynomial assumptions [12] suffer from a problem known as over-extraction. That is, they admit extractors which suffer from the following undesirable issue: the extractor may sometimes extract a valid value from the MIM even though the MIM committed to an invalid value. Non-malleable commitments built using such extractors suffer from “selective abort”: a man-in-the-middle can choose to commit to invalid values depending upon the value in the honest commitment, and an over-extracting reduction may never even be able to detect such attacks.
Non-synchronizing adversaries. Let us begin by considering a non-synchronizing man-in-the-middle (MIM) adversary that interacts with an honest committer \({\mathcal C} \) in a left session, then tries to maul this message and commit to a related message when interacting with an honest receiver \({\mathcal R} \) in a different (right) session. By non-synchronizing, we mean that this MIM completes the entire left execution before beginning the right session. Known protocols for achieving weaker notions of non-malleability from polynomial hardness (these include the three-round sub-protocol without the ZK argument from [13] which we will denote by \(\varPi \), and the basic three-round protocol from [12] which we will denote by \(\varPi '\)) do not achieve non-malleability with respect to commitment, even in this restricted settingFootnote 1.
On the other hand, any extractable commitment is non-malleable in this restricted setting of non-synchronizing adversaries. The reason is simple: Suppose a non-synchronizing MIM managed to successfully maul the honest commitment. For a fixed transcript of the honest commitment, a reduction can rewind the MIM and use the extractor of the commitment scheme to extract the value committed by the MIM. If this value is related to the value within the honest commitment, this can directly be used to contradict hiding of the honestly generated commitment.
The main technical goal of this paper is to find a way to bootstrap the basic schemes \(\varPi , \varPi '\) to obtain non-malleability against general synchronizing and non-synchronizing adversaries, while only relying on polynomial hardness.
Barrier I: Over-Extraction. A natural starting point, then, is to add extractability to the schemes \(\varPi , \varPi '\), by using some variant of an AoK of committed values, and within three rounds.
We cannot rely on witness indistinguishable (WI) arguments of knowledge, since arguing hiding of the scheme would require allowing a committer to commit to two witnesses to invoke WI security. Moreover, all existing constructions of WI arguments with black-box proofs, involve a parallel repetition of constant-soundness arguments. Now, a malicious committer could commit to two different witnesses: and use one witness in some parallel executions of the WI argument, and a different witness in some others. In this situation, even though the commitment may be invalid, one cannot guarantee that an extractor will detect the invalidity of the commitment, and over-extraction is possible. This is a known problem with 3 round protocols based on one-one one-way functions.
On the other hand, very recently, new protocols have been constructed in situations unrelated to non-malleability, that do not suffer from over-extraction [15]. Assuming polynomial hardness of DDH or Quadratic Residuosity or \(N^{th}\) residuosity, [15] demonstrated how to achieve arguments of knowledge in three rounds, that do not over-extract and have a “weak” ZK propertyFootnote 2.
However, the protocols of [15] guarantee privacy only when proving statements that are chosen from a distribution, by a prover, exclusively in the third round. On the other hand, both schemes \(\varPi , \varPi '\), and in fact most general non-malleable commitment schemes follow a commit-challenge-response structure, where cryptography is necessarily used in the first round. Thus, the statement being proved is already fully/partially decided in the first round, which are incompatible withthe kind of statements that [15] allows proofs for. Thus ideally, we would either like to inject non-malleability into the scheme of [15], or we would like to give an argument of knowledge of the message committed in the first round of \(\varPi , \varPi '\), that doesn’t overextract. The protocols of [15] are unlikely to directly help us achieve these objectives, because of their restriction to proving messages generated in the third round. However, before describing how we solve this problem, we describe another technical barrier.
Barrier II: Composing Non-Malleability with Extraction. Many state-of-the-art protocols for non-malleable commitments admit black-box proofs of security. Naturally then, security reductions for these protocols must rely on rewinding the adversary in order to prove non-malleability. This makes these protocols notoriously hard to compose with other primitives that rely on rewinding. More specifically, it is necessary to ensure that the knowledge extractor for the extractable commitment does not interfere with the rewinding strategies used in the proof of non-malleability, and vice-versa.
A relatively straightforward technique to get around this difficulty, used in [9, 11, 13, 17] is to arrange the protocol such that the non-malleable component and the argument of knowledge appear in completely different rounds and do not overlap. A more challenging method that does not add rounds, that is also used in prior work [13], is to use “bounded-rewinding-secure” WIAoK’s while making careful changes to the non-malleable commitment scheme.
Our Solution: First Attempt. Our first technical idea is to turn the problem of incompatibility between non-malleability and arguments of knowledge on its head, and try to use the same commitments to both argue non-malleability and perform knowledge-extraction. In other words, the only extractable primitive that we rely on will be a non-malleable commitment scheme. This is explained in more detail below.
In the following, we will rely on non-malleable commitments with a weak extraction property. Very roughly, we will require the existence of a probabilistic “over”-extractor \({\mathcal E} \) parameterized by error \(\epsilon \) (we will usually think of \(\epsilon \) as being inverse-polynomial). We will require given a PPT (synchronizing) man-in-the-middle adversary and a transcript of an execution between the MIM and honest committer, \({\mathcal E} \) “extracts” a value v such that if the value committed by the MIM in the transcript is valid, then it equals v except with probability \(\epsilon \). Furthermore, the extractor \({\mathcal E} \) does not rewind the honest execution. As noted in [9, 12], this already guarantees a flavor of non-malleability: since it is possible to extract the value from the MIM while maintaining hiding of the honest commitment. The weak extraction property is satisfied, even in the one-many setting (where the MIM participates in multiple right executions) by the protocol \(\varPi \). In the one-one setting, this property is satisfied by \(\varPi '\).
We note that a non-malleable commitment satisfying the weak extraction property is not an extractable commitment (and in particular, need not be non-malleable with respect to commitment), because \({\mathcal E} \) is allowed to output a valid value even when the MIM committed to an incorrect/invalid value in the transcript. Thus, a MIM may cheat for example, by generating a commitment to an invalid value when the honest commitment is to 0, and to a valid value when the honest commitment is to 1: and the extractor \({\mathcal E} \) may fail to observe the difference. On the other hand, in order to achieve non-malleability with respect to commitment, we will have to solve this problem and know when incorrectly extracted a valid value even though the MIM committed to an invalid value.
Now in order to gain confidence in the correctness of the value we extract, our scheme will have the committer generate two non-malleable commitments in parallel, and give a WI argument that one of the two was correctly constructed. This argument will satisfy a specific type of security under rewinding, and can be constructed based on ZAPs and DDH in three rounds via [15]. For the purposes of this overview, even though we don’t actually require a non-interactive proof, assume that we use a non-interactive witness indistinguishable proof, NIWI [3, 14]. Let \(\phi _1\) denote the protocol that results from committing to the message twice using the non-malleable commitment scheme \(\varPi \), and giving a NIWI proof that one of the two was correctly computed.
This partial solution still leaves scope for over-extraction: how can we be sure that the extractor does not output any valid value even when a malicious committer could be committing to two different values within the non-malleable commitments and using both witnesses for the WI?
Second Attempt. Since protocol \(\phi _1\) also suffers from over-extraction, it may seem like we made no progress at all. However, note that the same protocol can be easily modified to a WIAoK (witness indistinguishable argument of knowledge): by committing to a witness twice using \(\varPi \) and proving via NIWI that one of the two non-malleable commitments is a valid commitment to a witness. Let us call the resulting protocol \(\phi _2\). At a high level, the protocol \(\phi _2\) has the following properties:
-
Knowledge Extraction. \(\phi _2\) is an argument of knowledge (which suffers from over-extraction).
-
Non-malleability. Weak non-malleability of \(\varPi \) implies a limited form of non-malleability of the protocol \(\phi _2\).
Third Attempt. In order to prevent over-extraction, we will need to force any prover that generates a proof according to \(\phi _2\) to use a unique witness in \(\phi _2\). We will now try to rely on three round “weak” zero-knowledge arguments of [15], which are secure when used to prove cryptographic statements chosen by the prover in the last round. These arguments also retain a limited type of security under rewinding, which will help ensure that rewinding for extraction from the non-malleable commitment does not interfere with simulation security.
Assume again, for the purposes of this overview, that these arguments satisfy the standard notion of simulation for zero-knowledge, except that the statement to be proved, must be chosen in the last round. Let us denote them by \(\mathsf {wzk}\).
We will now use \(\mathsf {wzk}\) to set up a trapdoor for \(\phi _2\). This trapdoor will include a statistically binding commitment \(c_1\) using a non-interactive statistically binding commitment scheme \(\mathsf{com}\), and a \(\mathsf {wzk}\) argument that \(c_1\) was generated correctly as a commitment to 1. The trapdoor statement will be that \(c_1\) is a commitment to 0. This trapdoor statement will serve as the ‘other’ witness for \(\phi _2\).
Given these building blocks, our actual commitment scheme \(\phi \) will have the following structure:
-
Trapdoor: The committer will generate commitment \(c_1\) to 1, via \(\mathsf{com}\) in the third round. In parallel, the committer will prove via \(\mathsf {wzk}\), that \(c_1\) was correctly generated as a commitment to 1.
-
Actual Commitment: The committer will also generate commitment c to input message m, via \(\mathsf{com}\), only in the third round. In parallel the committer will also run scheme \(\phi _2\), proving that either c was correctly generated, or that \(c_1\) was generated as a commitment to 0.
Note that the protocol \(\phi _2\) as described is not delayed-input: the non-malleable commitment \(\varPi \) requires an input (that is, the witness) in the first round, whereas the witness for the statement is only decided in the third round. However, suffices to use one-time pads to get this delayed-input property from \(\phi _2\), by using the two non-malleable commitments within \(\phi _2\) to commit to random values \(r_1, r_2\) and then sending in the last round, the messages \(r_1 \oplus w, r_2 \oplus w\).
A simple (informal) description that captures the essence of our final protocol, \(\phi \), is in Fig. 1. The scheme \(\phi \) is opened up into its components: two non-malleable commitments and a WI argument. This scheme can be shown to be computationally hiding by the privacy properties of \(\phi \), \(\mathsf {wzk}\) and \(\mathsf{com}\).
Extraction. We first argue that the scheme in Fig. 1 is an extractable commitment. We already discussed that there exists a knowledge extractor for \(\phi _2\) that extracts at least one out of \(\gamma _1, \gamma _2\): which can then be used to extract the randomness r via \(z_1, z_2\). All we need to argue is that this extractor does not over-extract. However, soundness of \(\mathsf {wzk}\) already forces a computational committer to set \(c_1\) as a commitment to 1, which means that there remains only one randomness (the randomness used for committing to m), that the committer can use in order to generate \(z_1\) or \(z_2\) in the WI. Extractability of this scheme is already enough to guarantee security against non-synchronizing adversaries, even if such adversaries simultaneously participate in several parallel executions.
Non-malleability. Now, we need to argue that the resulting scheme is concurrent non-malleable with respect to commitment, when instantiated with \(\varPi \) from [13], or is non-malleable with respect to commitment when instantiated with \(\varPi '\) from [12]. Since \(\varPi \) helps us obtain a more general result, we restrict the rest of this overview to only consider the scheme \(\varPi \).
At a very high level, the system \(\phi _2\) behaves like a non-malleable witness indistinguishable argument of knowledge. Like we already discussed, only relying on the witness indistinguishability of \(\phi _2\) gives rise to issues such as over-extraction. It is here that the weak zero-knowledge argument helps: soundness of the weak ZK argument ensures that any PPT MIM adversary interacting with the honest committer, can generate \(c_1\) as a commitment to 0 with only negligible probability. Thus, such a MIM is “forced” to use as witness, the actual randomness used to generate a commitment to his value, and will therefore will never commit to an invalid value.
However, while formally arguing non-malleability, some subtle technical issues arise that require careful analysis. For instance, the distinguisher-dependent simulation strategy of weak ZK if used naively, only guarantees that the view of the distinguisher remains indistinguishable under simulation. However, while arguing non-malleability, it is imperative to ensure that not just the view, but the joint distribution of the view and the value committed by the MIM remains indistinguishable under simulation. It is here that the over-extraction property of \(\varPi \) helps: in hybrids where we must argue non-malleability while also performing distinguisher-dependent simulation, we will use the extractor that is guaranteed by the weak non-malleability of \(\varPi \), to extract the value committed by the MIM without having to rewind the left non-malleable commitment. This helps us guarantee that the joint distribution of the view and values committed by the MIM remains indistinguishable under simulation.
Our actual protocol is formalized in Sect. 4 and is identical to the protocol described above, except the following modification: For technical reasons, in our actual protocol, instead of masking the randomness \(r'\) with \(\gamma \), we mask it with \(\mathsf {PRF}(\gamma , \alpha )\) for randomly chosen \(\alpha \). The committer must also send \(\alpha \) to the receiver. This is for similar reasons as [15]: the simulator for \(\mathsf {wzk}\) sends many third protocol messages for the same fixed transcript of the first two messages, and we require security to hold even in this setting.
On Rewinding Techniques in the Proof. The weak ZK protocol of [15] that we use in this work, relies on the simulator rewinding the distinguisher. Because of this, our actual proof of security relies on two sequential rewindings within a three round protocol: one which rewinds to the end of the first round, and helps extract values committed in the MIM executions, and the second that rewinds to the end of the second round, in order to simulate the argument with respect to a distinguisher. This requires careful indistinguishability arguments that take such sequential rewindings into account, and can also be found in Sect. 4. We believe that the careful use of two sets of rewindings within a three-round protocol is another novel contribution of this work, and may be of independent interest.
In Sect. 3, we recall preliminaries and definitions, and in Sect. 4, we describe our construction and provide a proof of non-malleability.
3 Preliminaries
We first recall some preliminaries that will be useful in our constructions.
3.1 Proofs and Arguments
Definition 1
(Delayed-Input Distributional \(\epsilon \) -Weak Zero Knowledge) [15]. An interactive argument (P, V) for a language L is said to be delayed-input distributional \(\epsilon \)-weak zero knowledge if for every efficiently samplable distribution \(({\mathcal X} _{{n}},{\mathcal W} _{{n}})\) on \(R_L\), i.e., \(\mathsf {Supp}({\mathcal X} _{{n}},{\mathcal W} _{{n}}) = \{(x,w):x\in L\cap {{\{0,1\}}} ^{{n}},w\in R_L(x)\}\), every non-adaptive PPT verifier \(V^*\), every \(z \in {{\{0,1\}}} ^*\), every PPT distinguisher \({\mathcal D} \), and every \(\epsilon = 1/{\mathsf {poly}} ({{n}})\), there exists a simulator \({\mathcal S} \) that runs in time \({\mathsf {poly}} ({{n}},\epsilon )\) such that:
where the probability is over the random choices of (x, w) as well as the random coins of the parties.
Definition 2
(Weak Resettable Delayed-Input Distributional \(\epsilon \)
-Weak Zero Knowledge) [15]. A three round delayed-input interactive argument (P, V) for a language L is said to be weak resettable distributional weak zero-knowledge, if for every efficiently samplable distribution \(({\mathcal X} _{{n}},{\mathcal W} _{{n}})\) on \(R_L\), i.e., \(\mathsf {Supp}({\mathcal X} _{{n}},{\mathcal W} _{{n}}) = \{(x,w):x\in L\cap {{\{0,1\}}} ^{{n}},w\in R_L(x)\}\), every non-adaptive PPT verifier \(V^*\), every \(z \in {{\{0,1\}}} ^*\), every PPT distinguisher \({\mathcal D} \), and every \(\epsilon = 1/{\mathsf {poly}} ({{n}})\), there exists a simulator \({\mathcal S} \) that runs in time \({\mathsf {poly}} ({{n}},\epsilon )\) and generates a simulated proof for instance  , such that over the randomness of sampling \((x, w) \leftarrow ({\mathcal X} _{{n}}, {\mathcal W} _{{n}})\), \(\Pr [b' = b] \le \frac{1}{2} + \epsilon (n) + {\mathsf {negl}} ({{n}})\) in the following experiment, where the challenger C plays the role of the prover:
, such that over the randomness of sampling \((x, w) \leftarrow ({\mathcal X} _{{n}}, {\mathcal W} _{{n}})\), \(\Pr [b' = b] \le \frac{1}{2} + \epsilon (n) + {\mathsf {negl}} ({{n}})\) in the following experiment, where the challenger C plays the role of the prover:
-
At the beginning, \((C, V^*)\) receive the size of the instance, \(V^*\) receives auxiliary input z, and they execute the first 2 rounds. Let us denote these messages by \(\tau _1, \tau _2\).
-
Next, \((C, V^*)\) run \(poly({{n}})\) executions, with the same fixed first message \(\tau _1\), but different second messages chosen potentially maliciously by \(V^*\). In each execution, C picks a fresh sample \((x, w) \leftarrow ({\mathcal X} _{{n}}, {\mathcal W} _{{n}})\), and generates a proof for it according to honest verifier strategy.
-
Next, C samples bit
 and if \(b = 0\), for
and if \(b = 0\), for 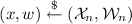 it generates an honest proof with first two messages \(\tau _1, \tau _2\), else if \(b = 1\), for
it generates an honest proof with first two messages \(\tau _1, \tau _2\), else if \(b = 1\), for 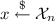 it generates a simulated proof with first two messages \(\tau _1, \tau _2\) using simulator \({\mathcal S} \) that has oracle access to \(V^*, {\mathcal D} \).
it generates a simulated proof with first two messages \(\tau _1, \tau _2\) using simulator \({\mathcal S} \) that has oracle access to \(V^*, {\mathcal D} \). -
Finally, \(V^*\) sends its view to a distinguisher \({\mathcal D} \) that outputs b.
Imported Theorem 1
[15]. Assuming DDH/QR/\(N^{th}\) residuosity, along with ZAPs, there exist three-message arguments that satisfy delayed-input weak resettable distributional \(\epsilon \)-weak zero knowledge/strong WI. In our protocols, we will always use weak zero-knowledge/strong witness-indistinguishable arguments in the “delayed-input” setting, that is, to prove statements that are chosen by the prover only in the third round of the execution.
Definition 3
(Resettable Reusable WI Argument). We say that a two-message delayed-input interactive argument (P, V) for a language L is resettable reusable witness indistinguisable, if for every PPT verifier \(V^*\), every \(z \in {{\{0,1\}}} ^*\), \(\Pr [b = b'] \le \frac{1}{2} + {\mathsf {negl}} (n)\) in the following experiment, where we denote the first round message function by \(m_1 = \mathsf {wi} _1(r_1)\) and the second round message function by \(\mathsf {wi} _2 (x, w, m_1, r_2)\).
The challenger samples  . \(V^*\) (with auxiliary input z) specifies \((m_1^1, x^1, w_1^1, w_2^1)\) where \(w_1^1, w_2^1\) are (not necessarily distinct) witnesses for \(x^1\). \(V^*\) then obtains second round message \(\mathsf {wi} _2 (x^1, w_b^1, m_1^1, r)\) generated with uniform randomness r. Next, the adversary specifies arbitrary \((m_1^2, x^2, w_1^2, w_2^2)\), and obtains second round message \(\mathsf {wi} _2 (x^2, w_b^2, m_1^2, r)\). This continues \(m(n) = {\mathsf {poly}} (n)\) times for a-priori unbounded m, and finally \(V^*\) outputs b.
. \(V^*\) (with auxiliary input z) specifies \((m_1^1, x^1, w_1^1, w_2^1)\) where \(w_1^1, w_2^1\) are (not necessarily distinct) witnesses for \(x^1\). \(V^*\) then obtains second round message \(\mathsf {wi} _2 (x^1, w_b^1, m_1^1, r)\) generated with uniform randomness r. Next, the adversary specifies arbitrary \((m_1^2, x^2, w_1^2, w_2^2)\), and obtains second round message \(\mathsf {wi} _2 (x^2, w_b^2, m_1^2, r)\). This continues \(m(n) = {\mathsf {poly}} (n)\) times for a-priori unbounded m, and finally \(V^*\) outputs b.
Remark 1
Note that ZAPs (more generally, any two-message WI) can be modified to obtain resettable reusable WI, by having the prover apply a PRF on the verifier message and the instance to compute randomness for the proof. This allows to argue, via a hybrid argument, that fresh randomness can be used for each proof, and therefore perform a hybrid argument so that each proof remains WI. In our construction, we will use resettable reusable ZAPs.
3.2 Non-malleable Commitments
Throughout this paper, we will use \({{n}} \) to denote the security parameter, and \({\mathsf {negl}} ({{n}})\) to denote any function that is asymptotically smaller than \(\frac{1}{{\mathsf {poly}} ({{n}})}\) for any polynomial \({\mathsf {poly}} (\cdot )\). We will use PPT to describe a probabilistic polynomial time machine. We will also use the words “rounds” and “messages” interchangeably.
We follow the definition of non-malleable commitments introduced by Pass and Rosen [22] and further refined by Lin et al. [19] and Goyal [9] (which in turn build on the original definition of [7]). In the real interaction, there is a man-in-the-middle adversary MIM interacting with a committer \({\mathcal C} \) (where \({\mathcal C} \) commits to value v) in the left session, and interacting with receiver \({\mathcal R} \) in the right session. Prior to the interaction, the value v is given to C as local input. MIM receives an auxiliary input z, which might contain a-priori information about v. Let \({\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} \) denote a random variable that describes the value \(\widetilde{\mathsf {val}}\) committed by the MIM in the right session, jointly with the view of the MIM in the full experiment. In the simulated experiment, a simulator \({\mathcal S} \) directly interacts with \({\mathcal R} \). Let \({\mathsf{Sim}_{\langle C, R\rangle }(1^{{n}},z)} \) denote the random variable describing the value \(\widetilde{\mathsf {val}} \) committed to by \({\mathcal S} \) and the output view of \({\mathcal S} \). If the tags in the left and right interaction are equal, the value \(\widetilde{\mathsf {val}} \) committed in the right interaction, is defined to be \(\bot \) in both experiments.
Definition 4
(Non-malleable Commitments w.r.t. Commitment). A commitment scheme \(\langle C, R \rangle \) is said to be non-malleable if for every PPT MIM, there exists an expected PPT simulator \({\mathcal S} \) such that the following ensembles are computationally indistinguishable:
The setting of concurrent non-malleability considers an adversary that participates in multiple sessions with an honest committer, acting as receiver. The adversary simultaneously participates in multiple sessions with an honest receiver, acting as committer. In the left sessions, the MIM interacts with honest committer(s) obtaining commitments to values \(m_1, m_2, \ldots m_{{\mathsf {poly}} (n)}\) (say, from distribution \(\mathsf {val}\) using tags \(t_1, t_2, t_{{\mathsf {poly}} (n)}\) of its choice. In the right session, \({\mathcal A}\) interacts with \({\mathcal R} \) attempting to commit to a sequence of related values \(\tilde{m}_1, \ldots \tilde{m}_{{\mathsf {poly}} (n)}\) again using identities \(\tilde{t}_1, \ldots \tilde{t}_{{\mathsf {poly}} (n)}\). If any of the right commitments are invalid, or undefined, their value is set to \(\bot \). For any i such that \(\tilde{t}_i = t_j\) for some j, set \(\tilde{m}_i\) (the value committed using that tag) to \(\bot \). Let \({\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} \) denote a random variable that describes the values \(\widetilde{\mathsf {val}}\) committed by the MIM in the right sessions, jointly with the view of the MIM in the full experiment, when the \(\mathsf {value}\) is the joint distribution of values committed in the left sessions. In a simulated execution, there is an expected polynomial time simulator that interacts with the MIM and generates a distribution \(\mathsf{Sim}\) consisting of the views and values committed by the MIM. Then, the definitions of concurrent non-malleable commitment scheme w.r.t. commitment, replacement and opening are defined as above.
Definition 5
(Concurrent Non-malleable Commitments w.r.t. Commitment). A commitment scheme \(\langle C, R \rangle \) is said to be concurrently non-malleable if for every PPT MIM, there exists an expected PPT simulator \({\mathcal S} \) such that the ensembles \(\mathsf {real}\) and \(\mathsf {sim}\) defined above are indistinguishable.
Definition 6
(One-Many Weak Non-malleable Commitments against Synchronizing Adversaries). A statistically binding commitment scheme \(\langle C, R \rangle \) is said to be one-many weak non-malleable against synchronizing adversaries, if there exists a probabilistic “over”-extractor \({\mathcal E} \) parameterized by \(\epsilon \), that given a PPT synchronizing MIM which participates in one left session and \(p = {\mathsf {poly}} ({{n}})\) right sessions, and given only the transcript of a main-thread interaction \(\tau \) where the MIM interacts with an honest committer and honest receiver, together with oracle access to the MIM, outputs a set of values \(v_1, v_2, \ldots v_p\) in time \({\mathsf {poly}} ({{n}}, \frac{1}{\epsilon })\). These values are such that:
-
For any \(j \in [p]\), if the \(j^{th}\) commitment in \(\tau \) is a commitment to a valid message \(m_j\), then \(v_j = m_j\) over the randomness of the extractor and the transcript, except with probability \(\frac{\epsilon }{p}\).
-
For any \(j \in [p]\), if the \(j^{th}\) commitment in \(\tau \) is a commitment to some invalid message (which we will denote by \(\bot \)), then \(v_j\) need not necessarily be \(\bot \).
Remark 2
By the union bound, the values output by the extractor are correct for all p sessions in which the MIM committed to valid messages in the transcript \(\tau \), except with probability \(\epsilon \).
This formalization helps us to abstract out the exact properties satisfied by existing three-round schemes based on polynomial assumptions, which we can rely on for our bootstrapping protocol. We note that this is an alternative way of formalizing the requirement of “security against non-aborting adversaries” from [6]. When invoking the security of non-malleable commitments in our proof, the adversary will always be forced (via appropriate proofs) to not generate a commitment to \(\bot \), except with negligible probability.
Instantiating one-many weak non-malleable commitments. The three-round sub-protocol in the non-malleable commitment scheme from [13] (their basic construction without the zero-knowledge argument of knowledge), based on injective one-way functions, is a one-many weak non-malleable commitment according to Definition 6. On the other hand, the basic protocol of [12] based on injective one-way functions, that is only secure against synchronous adversaries, is a one-one weak non-malleable commitment scheme against synchronizing adversaries according to Definition 6.
4 Non-malleable Commitments w.r.t. Commitment
In this section, we describe a round-preserving way to transform one-many weak non-malleable commitments against synchronous adversaries, to (one-many) non-malleable commitments with respect to commitment. Our construction of three round non-malleable commitments is described in Fig. 2.
4.1 Proof of Security
We begin by proving that the scheme is statistically binding and computationally hiding. We note that computational hiding is in fact, implied by non-malleability: therefore as a warm up, we sketch the proof of hiding via a sequence of hybrid experiments without giving formal reductions. In Theorem 1, we prove formally that not only is the view of a receiver indistinguishable between these hybrids, in fact, the joint distribution of the view and values committed by a MIM interacting with an honest committer remains indistinguishable between these hybrids.
Lemma 1
The protocol in Fig. 2 is a statistically binding, computationally hiding, commitment scheme.
Proof
(Sketch). The statistical binding property follows directly from statistical hiding property of the underlying commitment scheme \(\mathsf{com}(\cdot )\).
The computational hiding property follows from the hiding of \(\mathsf{com}\) and \(\mathsf {nmc} \), the weak zero-knowledge property of \(\mathsf {wzk}\), and the witness indistinguishability of \(\mathsf {wi}\). Here, we sketch a proof of computational hiding. Note that computational hiding is implied by non-malleability, therefore the proof of Theorem 1 can also be treated as a formal proof of hiding of the commitment scheme \(\phi \). Let \(\langle {\mathcal C} _\phi (m;r), {\mathcal R} \rangle \) denote an execution where the committer uses input message m and randomness R. We prove that the view of any malicious receiver \({\mathcal R} ^*\), that is, \({\mathsf {view}} _{{\mathcal R} ^*}\langle {\mathcal C} _\phi (m_0;r), {\mathcal R} ^* \rangle \approx _c {\mathsf {view}} _{{\mathcal R} ^*}\langle {\mathcal C} _\phi (m_1;r), {\mathcal R} ^* \rangle \) for all \(m_0, m_1\), via the following sequence of hybrid experiments:
\(\mathsf{{Hybrid}}_{m_0}\): This hybrid corresponds to an interaction of \({\mathcal C} \) and \({\mathcal R} ^*\) where \({\mathcal C} \) uses input message \(m_0\), that is, the output is \({\mathsf {view}} _{{\mathcal R} ^*}\langle {\mathcal C} _\phi (m_0;r), {\mathcal R} ^* \rangle \).
\(\mathsf{{Hybrid}}_1\): In this hybrid, the challenger behaves identically to \(\mathsf{{Hybrid}}_{m_0}\), except that it generates \(\mathsf {nmc} ^2\) as a non-malleable commitment to a different randomness \(\gamma _{2}'\) than the (uniform) randomness \(\gamma _2\) used to compute \(\delta _{2}\). This hybrid is indistinguishable from \(\mathsf{{Hybrid}}_0\) because of the hiding of \(\varPi \).
\(\mathsf{{Hybrid}}_{2, {\mathcal D}}\): In this hybrid, the challenger behaves identically to \(\mathsf{{Hybrid}}_1\), except that it outputs the transcript of an execution where the \(\mathsf {wzk}\) argument is simulatedFootnote 3. The challenger uses the simulation strategy of the weak zero-knowledge argument \(\mathsf {wzk}\), which executes the last message of the protocol multiple times, and learns the \(\mathsf {wzk}\) challenge based on the distinguisher’s output. However, the challenger continues to commit to \(m_0\) while generating a simulated \(\mathsf {wzk}\) argument. By the simulation security of \(\mathsf {wzk}\), for any distinguisher \({\mathcal D} \) and any inverse polynomial \(\epsilon \), there exists a polynomial time distinguisher-dependent simulator/challenger such that \(\mathsf{{Hybrid}}_{2,{\mathcal D}}\) is \(\epsilon \)-indistinguishable from \(\mathsf{{Hybrid}}_1\).
\(\mathsf{{Hybrid}}_{3,{\mathcal D}}\): In this hybrid, the challenger behaves identically to \(\mathsf{{Hybrid}}_{2, {\mathcal D}}\), except that it sets \(c_1 = \mathsf{com}(0;\widehat{r})\) for some randomness \(\widehat{r}\), in the main thread. Note that this is possible because the challenger is generating a simulated proof in the output transcript. This hybrid is indistinguishable from \(\mathsf{{Hybrid}}_{2, {\mathcal D}}\) by the computational hiding property of \(\mathsf{com}\).
\(\mathsf{{Hybrid}}_{4, {\mathcal D}}\): In this hybrid, the challenger behaves identically to \(\mathsf{{Hybrid}}_{3, {\mathcal D}}\) except that in the output transcript, it sets \(\delta _{2} = \mathsf {PRF}(\gamma _{2}, \alpha _{2}) \oplus \widehat{r}\) where \(\widehat{r}\) is the randomness used to generate \(c_1 = \mathsf{com}(0;\widehat{r})\). Note that the committer is committing to a different value \(\gamma '_{2}\) in the protocol \(\varPi ^{2}\), thus the key \(\gamma _{2}\) does not appear anywhere in the rest of the protocol. Therefore, this hybrid is indistinguishable from \(\mathsf{{Hybrid}}_{3, {\mathcal D}}\) by the security of the PRF.
\(\mathsf{{Hybrid}}_{5, {\mathcal D}}\): In this hybrid, the challenger behaves identically to \(\mathsf{{Hybrid}}_{4, {\mathcal D}}\) except that in all transcripts, it sets \(\mathsf {nmc} ^{2}\) as a non-malleable commitment to the same randomness \(\gamma _{2}'\) that is used to compute \(\delta _{2}\). This hybrid essentially “reverts” the cheating performed in \(\mathsf{{Hybrid}}_{1}\). Indistinguishability of this hybrid follows because of the hiding of \(\varPi ^2\).
Note that the transcript output by the challenger in this experiment is such that \(\varPi ^1\) is a valid non-malleable commitment to \(\gamma _1\) with randomness \(r_1\) AND \(r = \mathsf {PRF}(\gamma _1, \alpha _1) \oplus \delta _1\) such that \(c = \mathsf{com}(m;r)\). Additionally, \(\varPi ^{2}\) is a valid non-malleable commitment to \(\gamma _2\) with randomness \(r_2\) AND \(\widehat{r} = \mathsf {PRF}(\gamma _2, \alpha _2) \oplus \delta _2\) such that \(c_1 = \mathsf{com}(0;\widehat{r})\).
\(\mathsf{{Hybrid}}_{6, {\mathcal D}}\): In this hybrid, the challenger behaves the same was as \(\mathsf{{Hybrid}}_{5, {\mathcal D}}\), except that it uses the second witness, \((r_2, \gamma _2)\), to generate the argument \(\mathsf {wi}\) in the output transcript. This hybrid is indistinguishable from \(\mathsf{{Hybrid}}_{5, {\mathcal D}}\) by the reusable witness-indistinguishability of \(\mathsf {wi}\), that is, witness indistinguishability in the setting where multiple proofs are provided for different statements, using the same first two messages transcript.
\(\mathsf{{Hybrid}}_{7, {\mathcal D}}\): In this hybrid, the challenger behaves the same way as \(\mathsf{{Hybrid}}_{6, {\mathcal D}}\), except that it uses the second witness, \(r_2, \gamma _2\), to generate the arguments \(\mathsf {wi}\) all the “lookahead executions” of the simulation strategy, as well as in the output transcript. That is, in every message that the challenger ever sends, it uses the second witness instead of the first. This hybrid is indistinguishable from \(\mathsf{{Hybrid}}_{6, {\mathcal D}}\) by the reusable witness-indistinguishability of \(\mathsf {wi}\).
\(\mathsf{{Hybrid}}_{8, {\mathcal D}}\): In this hybrid, the challenger behaves the same way as \(\mathsf{{Hybrid}}_{7, {\mathcal D}}\), except that in all transcripts, it sets \(\mathsf {nmc} ^{1}\) as a non-malleable commitment to a different randomness \(\gamma _{1}'\) than the one used to compute \(\delta _{1}\). The view of a malicious receiver in this hybrid is indistinguishable from \(\mathsf{{Hybrid}}_{7, {\mathcal D}}\) by the hiding of the non-malleable commitment \(\varPi ^1\).
\(\mathsf{{Hybrid}}_{9, {\mathcal D}}\): In this hybrid, the challenger behaves the same way as \(\mathsf{{Hybrid}}_{8, {\mathcal D}}\), except that in the output transcript, it sets  , instead of setting \(\delta _1 = \mathsf {PRF}(\gamma _{1}, \alpha _1) \oplus r\). Note that the committer is committing to a different value \(\gamma '_{1}\) in the protocol \(\varPi ^{1}\), thus the key \(\gamma _{1}\) does not appear in the rest of the protocol. Therefore, this hybrid is indistinguishable from \(\mathsf{{Hybrid}}_{8, {\mathcal D}}\) by PRF security.
, instead of setting \(\delta _1 = \mathsf {PRF}(\gamma _{1}, \alpha _1) \oplus r\). Note that the committer is committing to a different value \(\gamma '_{1}\) in the protocol \(\varPi ^{1}\), thus the key \(\gamma _{1}\) does not appear in the rest of the protocol. Therefore, this hybrid is indistinguishable from \(\mathsf{{Hybrid}}_{8, {\mathcal D}}\) by PRF security.
\(\mathsf{{Hybrid}}_{10, {\mathcal D}}\): In this hybrid, the challenger behaves the same way as \(\mathsf{{Hybrid}}_{10, {\mathcal D}}\) except that it replaces \(\mathsf{com}(m_0; r)\) with \(\mathsf{com}(m_1;r)\) in the output transcript. Note that at this point, r is not used anywhere else in the protocol, and hence the commitment can be obtained externally. This hybrid is indistinguishable from \(\mathsf{{Hybrid}}_{9, {\mathcal D}}\) by computational hiding of the non-interactive commitment.
At this point, we have successfully indistinguishably switched to an experiment where the commitment is generated to message \(m_1\) instead of \(m_0\) in the main transcript output by the challenger. Computational hiding follows by repeating the above hybrids in reverse order, until in \(\mathsf{{Hybrid}}_{m_1}\), the challenger generates an honest commitment to message \(m_1\). This completes the proof of hiding, and we now prove that the scheme \(\phi \) is an extractable commitment.
Lemma 2
There exists a PPT extractor \({\mathcal E} \) that given oracle access to any committer \({\mathcal C} ^*\), and a valid commitment transcript \(\tau \) generated by \({\mathcal C} ^*\) participating in an execution of \(\phi \) with an honest receiver \({\mathcal R} \), outputs the value committed by \({\mathcal C} ^*\) in \(\tau \), with probability \(1 - {\mathsf {negl}} (n)\) over the randomness of \({\mathcal R} \) and \({\mathcal E} \).
Proof
For any accepting commitment transcript generated by a committer, with probability \(1 - {\mathsf {negl}} (n)\), because of adaptive soundness of \(\mathsf {wi}\), the \(i^{th}\) extractable commitment is generated as a valid extractable commitment to randomness \(r_i\), such that \(\mathsf {PRF}(r_i, a_i) \oplus x_i\) yields a valid witness for \(\mathsf {wi}\), for some \(i \in \{1, 2\}\). Furthermore, by soundness of \(\mathsf {wzk}\), \(c_1\) is a commitment to 1, and by statistical binding of \(\mathsf{com}\), \(c_1\) cannot be a commitment to 0. Thus, the only possible valid witness in \(\mathsf {wi}\), with overwhelming probability, must necessarily be a witness for c, which is the actual commitment to the message.
We now argue that this witness can be extracted by a polynomial time extractor. This follows roughly because of the (over)-extraction property of \(\varPi \) and the soundness of \(\mathsf {wi}\), similar to [15]. Specifically, we consider a committer that generates an accepting transcript with probability \(\frac{1}{{\mathsf {poly}} (n)}\). Then, within \({{n}} \cdot {\mathsf {poly}} ({{n}})\) rewindings, such a committer generates an expected \({{n}} \) accepting transcripts. Moreover, with overwhelming probability at least \(\sqrt{{{n}}}\) of the accepting transcripts (in the lookahead threads) generate a valid commitment using scheme \(\varPi \) for the same index i as the main thread. This allows for extraction of randomness r from the over-extracting commitment \(\varPi ^i\). Next, the extractor checks the extracted value r against c to ensure that r is the correct randomness that was used to compute c. Note that this scheme does not suffer from over-extraction, since by the soundness of \(\mathsf {wzk}\) and \(\mathsf {wi}\), a malicious committer is always forced to use the unique witness corresponding to the commitment c. Furthermore, an extractor can extract with error at most \(\epsilon \) by running in time \({\mathsf {poly}} (1/\epsilon )\).
Next, we directly prove concurrent non-malleability of the resulting scheme when instantiated with the basic protocol \(\varPi \) from [13]. The scheme can also be instantiated with the protocol from [12], to yield one-one non-malleability.
Theorem 1
The protocol \(\phi \) in Fig. 2, when instantiated with the one-many weak non-malleable commitment \(\varPi \) from [13], is a concurrent non-malleable commitment with respect to commitment according to Definition 5.
Proof
We first note that it suffices to argue non-malleability against one-many adversaries, that participate in one left session and polynomial right sessions. By [19], security against such adversaries already implies concurrent non-malleability. Suppose the MIM opens \(p = {\mathsf {poly}} (n)\) sessions on the right.
The proof of non-malleability against non-synchronizing adversaries, that complete the left session before opening right sessions, follows directly because \(\phi \) is an extractable commitment, by Lemma 2. In other words, given a non-synchronizing MIM adversary, there exists a reduction that runs an extractor to extract the value committed by the MIM from the right execution(s) by rewinding the adversary, and uses the view jointly with the values extracted from such a malleating adversary to directly break hiding of the commitment in the left execution. Because of the non-synchronizing scheduling, the reduction can rewind the MIM’s commitment and run the extractor of Lemma 2 without rewinding the honest commitment at all. This leads to a contradiction, ruling out the existence of any PPT MIM adversary that successfully mauls the honest commitment.
It remains to argue non-malleability in the fully synchronizing setting (these arguments directly combine to argue security against adversaries that are synchronizing in some executions and non-synchronizing in others). We do this via a sequence of hybrid experiments, relying on the non-malleability of \(\varPi \), along with various properties of other primitives used in the protocol. These hybrids are all parameterized by an inverse polynomial error parameter \(\epsilon \), and sometimes require the challenger to run in time \({\mathsf {poly}} (n, \frac{1}{\epsilon })\). Later, we will set \(\epsilon \) to be significantly smaller than the advantage of any distinguisher between \({\mathsf{MIM}_{\langle C, R\rangle }(V_1,z)} \) and \({\mathsf{MIM}_{\langle C, R\rangle }(V_2,z)} \) (but \(\epsilon \) will still be some inverse polynomial \(\frac{1}{{\mathsf {poly}} (\cdot )})\), thereby proving the lemma. We will use \(\widetilde{a}\) to denote message a sent in the right execution, and a message a sent during the left execution will just be denoted by a.
Overview of Hybrid Experiments. Before describing the hybrid arguments in detail, we provide an overview. The sequence of experiments follows the same pattern as the proof of hiding, except that we now argue about the joint distribution of the view and values committed by the MIM. Whenever the challenger rewinds and generates lookahead threads to learn \(\gamma \) or to simulate the weak ZK, the challenger always generates multiple lookahead threads where half commit to value \(V_1\) and half to \(V_2\) (this is possible since the message is decided in the last round), and combines information extracted using both \(V_1, V_2\), like [15].
In the following hybrids, the challenger will never generate simulated \(\mathsf {wzk}\) proofs in any rewinding execution. The \(\mathsf {wzk}\) proof will be carefully simulated only in the main transcript (in some of the hybrids). Thus, by soundness of the \(\mathsf {wi}\), the MIM will always commit to the witness for the commitment, by correctly generating a non-malleable commitment to at least one of the \(\gamma \) values, in any rewinding execution. Therefore, a rewinding extractor will correctly extract at least one \(\gamma \) value committed by the MIM, with high probability. Furthermore, when relying on the extractor of the non-malleable commitment scheme, we will again generate a transcript for the extractor that does not contain any simulated proofs – therefore, this extractor is guaranteed to correctly extract at least one of the \(\gamma \) values committed by the MIM.
\(\mathsf{{Hybrid}}_{V_1}\): The output of the first experiment, \(\mathsf{{Hybrid}}_{V_1}\) corresponds to the joint distribution of the view and values committed by the MIM on input an honest commitment to value \(V_1\).
\(\mathsf{{Hybrid}}_1\): In the first hybrid, the challenger changes the left execution by first sampling \((\gamma _2, \gamma '_2)\) independently and uniformly at random. The value committed using the second non-malleable commitment \(\varPi ^2\) is \(\gamma '_2\), while the third message \(\delta _2 = \mathsf {PRF}(\gamma _2, \alpha _2) \oplus r\) is computed honestly using a different \(\gamma _2\). At this point, we invoke soundness of the \(\mathsf {wi}\) and \(\mathsf {wzk}\) to argue that the MIM must commit to at least one valid \(\widetilde{\gamma }_i^1\) or \(\widetilde{\gamma }_i^2\) in the main execution, for every \(i \in [p(n)]\). Therefore, we can invoke the extractor for \(\varPi ^2\), to extract the joint distribution of the values committed by the man-in-the-middle (MIM) in all right executions.
By the property of the non-malleable commitment, when the MIM commits to a valid value in the main execution, such an extractor will successfully extract at least one of the committed values \(\widetilde{\gamma }_i^1\) or \(\widetilde{\gamma }_i^2\) from the \(i^{th}\) right interaction, for all \(i \in [p(n)]\). Because of soundness of \(\mathsf {wi}\) and \(\mathsf {wzk}\), this extracted value will directly help recover the message committed by the MIM in this interaction. Since this extractor operates without rewinding the left execution, if the joint distribution of the view and values changes from \(\mathsf{{Hybrid}}_0\) to \(\mathsf{{Hybrid}}_1\), we obtain a contradiction to the hiding of \(\varPi \).
\(\mathsf{{Hybrid}}_2\): In the next hybrid, the challenger modifies the left execution by generating an output view where the left execution contains a simulated weak ZK argument. When applied naively, the simulation guarantee is that the view of the MIM remains indistinguishable when provided a transcript with a simulated proof. However, there are no guarantees about the MIM’s committed values.
In order to ensure that the joint distribution of committed values remains indistinguishable, we modify the input to the distinguisher-dependent simulator. That is, we modify the experiment so that, the challenger first rewinds the MIM and extracts the joint distribution of values \(\widetilde{\gamma }\) committed by the MIM. Here, we rely on the fact that \(\varPi \) is stand-alone extractable (with over-extraction). Note that once extracted, these \(\widetilde{\gamma }\)’s can be used to extract the messages committed by the MIM in any transcript with the same fixed first two messages, with overwhelming probability. The only situation in which the \(\widetilde{\gamma }_i^b\) extracted for some execution i does not help recover the message committed by the MIM from transcript \(\tau \) with the same fixed first message, is if the MIM uses a different witness \(\widetilde{\gamma }_i^{1-b}\) in \(\tau \) and uses \(\widetilde{\gamma }_i^b\) in all the rewinding executions. However, this event occurs only with probability at most \({\mathsf {negl}} (n)\).
Upon extracting these values, with the same fixed first message, the challenger begins running the simulation strategy of weak ZK to output a main transcript with a simulated proof. That is, the challenger uses the \(\widetilde{\gamma }\)’s to extract the joint distribution of the values committed by the MIM from any right execution, and runs the distinguisher-dependent simulator on a distinguisher that obtains the joint distribution of the view output by the MIM, together with these extracted values. Now, by the guarantee of distinguisher-dependent simulation, we have that the joint distribution remains indistinguishable between \(\mathsf{{Hybrid}}_1\) and \(\mathsf{{Hybrid}}_2\). In our actual reduction, we require a special type of weak resettable security of the weak ZK. Additional details are in the formal proof.
\(\mathsf{{Hybrid}}_3\): In the next hybrid, the output transcript generated in the left execution, consists of a commitment \(c_1 = \mathsf{com}(0; \widehat{r})\) with uniform randomness \(\widehat{r}\), instead of \(c_1\) being a commitment to 1. This is allowed because the weak ZK proof is being simulated by this point. The joint distribution of the view and values committed do not change in this hybrid, because \(c_1\) is non-interactive, and thus can be replaced in the main transcript, while rewinding the MIM and extracting the joint distribution of the values committed by the MIM in all right executions.
\(\mathsf{{Hybrid}}_4\): In this next hybrid, the challenger sets \(\delta _2 = \mathsf {PRF}(\gamma _2, \alpha _2) \oplus \widehat{r}\) (instead of \(\mathsf {PRF}(\gamma _2, \alpha _2) \oplus r\)), where \(\widehat{r}\) is the randomness used to generate \(c_1\). Since the PRF key \(\gamma _2\) does not appear elsewhere in the protocol, the joint distribution of the view and values committed do not change in this hybrid. This is \(\delta _2\) can be replaced in the main transcript, while rewinding the MIM and extracting the joint distribution of the values committed by the MIM in all right executions.
\(\mathsf{{Hybrid}}_5\): In this next hybrid, the challenger changes the non-malleable commitment \(\varPi ^2\) to commit to the same randomness \(\gamma _2\), that is used to compute \(\delta _2\) in all threads (instead of committing to a different \(\gamma _2'\)). In order to argue indistinguishability of the view and committed values, we now rely on the non-malleability of \(\varPi ^2\). The challenger runs the extractor for \(\varPi ^2\) on a transcript that contains honestly generated \(\mathsf {wzk}\) proofs: again by soundness, at least one of the \(\widetilde{\gamma }\) values committed by the MIM in every execution is a valid commitment in the main thread. Thus, the extractor outputs this value. Next, the challenger uses this extracted value to recover the joint distribution of messages from transcripts generated by the MIM. This helps the challenger generate an output transcript with a simulated \(\mathsf {wzk}\) proof, such that the joint distribution of the view of the MIM and values committed remains indistinguishable.
Note that in this experiment, even though the left execution is rewound to generate lookahead threads for distinguisher-dependent simulation, this rewinding happens after the first two rounds have been fixed. Thus, the non-malleable commitment used in the left execution is never rewound, and can be obtained externally. If the joint distribution of view and values output by the extractor for \(\varPi \) changes in this hybrid, then this contradicts hiding of \(\varPi \). The argument of indistinguishability again requires a specific ordering to generate the lookahead threads for extracting the MIM’s committed values, and the lookahead threads for simulation. Additional details can be found in the formal proof.
\(\mathsf{{Hybrid}}_6, \mathsf{{Hybrid}}_7\): By the end of these hybrids, the challenger will behave the same way as \(\mathsf{{Hybrid}}_5\), except that it will use the second witness \(\gamma _2\) in all executions (in the main as well as lookahead threads). For the main thread, for which the witness is switched in \(\mathsf{{Hybrid}}_6\), the challenger will use witness \(\gamma _2, \widehat{r}, \delta _2, c_1\) to compute the \(\mathsf {wi}\). In the rewinding threads, for which the witness is switched in \(\mathsf{{Hybrid}}_7\), the challenger will use witness \(\gamma _2, r, \delta _2, c\). The joint distribution of the view and value extracted remains indistinguishable because of the reusable resettable security of \(\mathsf {wi}\) allows for switching the witness even when multiple proofs are given in the main as well as rewinding executions.
\(\mathsf{{Hybrid}}_8\): In this hybrid, the challenger sets \(\varPi ^1\) as a non-malleable commitment to a different independently uniform randomness \(\gamma _1'\), than the randomness \(\gamma \) that is used to compute \(\delta _1\) in all executions. The joint distribution of view and values committed by the MIM remains indistinguishable by the non-malleability of \(\varPi \). The proof follows in a similar manner as of the indistinguishability of \(\mathsf{{Hybrid}}_5\).
\(\mathsf{{Hybrid}}_9\): In this hybrid, the challenger behaves similar to the previous hybrid except setting \(\delta _1\) to uniformly at random, only in the output transcript. Since the key \(\gamma _1\) no longer appears elsewhere in the protocol, indistinguishability of the view and committed values follows by security of the \(\mathsf {PRF}\).
\(\mathsf{{Hybrid}}_{10:}\) In this hybrid, the challenger behaves similar to the previous hybrid, except in the output transcript, it sets c as a commitment to value \(V_2\) instead of to value \(V_1\). This is allowed because the randomness used to compute c in the output transcript is not used elsewhere in the protocol. Indistinguishability of the view and values committed by the MIM in this execution, follows by hiding of the non-interactive commitment c.
At this point, the main transcript consists of a commitment to \(V_2\) instead of to \(V_1\), while the lookahead transcripts are generated using both \(V_1\) and \(V_2\). Now, following the same sequence of hybrids in reverse order, we get to a hybrid experiment where the challenger generates an honest commitment to \(V_2\) in the left execution. Thus, the joint distribution of the view and values committed by the MIM remains indistinguishable between when the left commitment is to \(V_1\), versus to \(V_2\), which is the guarantee required by the definition of non-malleability.
Hybrid Experiments. We now formally describe the hybrid arguments that we use to prove non-malleability.
\(\mathsf{{Hybrid}}_{V_1}\): This hybrid corresponds to an interaction of the challenger and the MIM where the challenger uses input message \(V_1\) in the honest interaction. Let \({\mathsf{MIM}_{\langle C, R\rangle }(V_1,z)} \) denote the joint distribution of the view and values committed by the MIM in this interaction.
\(\mathsf{{Hybrid}}_1\): In this hybrid, the challenger behaves identically to \(\mathsf{{Hybrid}}_{V_1}\), except that it generates \(\varPi ^2\) as a non-malleable commitment to a different randomness \(\gamma '_{2}\) chosen uniformly and independently at at random, from the randomness \(\gamma _2\) that was used to compute \(\delta _{2}\). Let \({\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_1}\) denote the joint distribution of the view and values committed by the MIM in this interaction, in all the right sessions.
Lemma 3
For any PPT distinguisher \({\mathcal D} \) with auxiliary information z, \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }(V_1,z)}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_1}) = 1]|\) \(\le \epsilon + {\mathsf {negl}} ({{n}}).\)
Proof
The proof of this lemma follows via a reduction to the weak non-malleability of the scheme \(\varPi \). More specifically, given a distinguisher \({\mathcal D} \) that distinguishes \({\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_1}\) and \({\mathsf{MIM}_{\langle C, R\rangle }(V_1,z)} \), we construct an adversary \({\mathcal A} ^{\mathcal D} \) against the weak one-many non-malleability of \(\varPi \) according to Definition 6.
The adversary \({\mathcal A} \) participates in the experiment exactly as \(\mathsf{{Hybrid}}_{V_1}\), except that it samples  and submits these to an external challenger. It obtains externally, the messages of \(\varPi ^2\), which are either a non-malleable commitment to \(\gamma _2\) or to \(\gamma '_2\). It complete the third message of the protocol using \(\gamma _2\) to compute \(\delta _2\).
and submits these to an external challenger. It obtains externally, the messages of \(\varPi ^2\), which are either a non-malleable commitment to \(\gamma _2\) or to \(\gamma '_2\). It complete the third message of the protocol using \(\gamma _2\) to compute \(\delta _2\).
By the weak non-malleability of \(\varPi \), there exists an extractor that runs in time \({\mathsf {poly}} (\frac{1}{\epsilon })\) and extracts the values committed by the MIM in all the non-malleable commitments for all \(j \in [p]\), without rewinding the honest execution. Further, this extractor has the property that it only extracts an incorrect value if the MIM is committing to \(\bot \) in the main thread in the honest execution, except with error \(\epsilon \).
However, in both \(\mathsf{{Hybrid}}_{V_1}\) and \(\mathsf{{Hybrid}}_1\), by the soundness of \(\mathsf {wi}\), the adversary is guaranteed to generate at least one out of the two non-malleable commitments (to \(\widetilde{\gamma }_1\) or \(\widetilde{\gamma }_2\)) from each session, correctly in any execution, except with probability \({\mathsf {negl}} (n)\). Moreover, by soundness of \(\mathsf {wzk}\), the extracted value from at least one of the non-malleable commitments generated by the MIM in each session, will correspond to a witness for the commitment c, and therefore directly help recover the value committed by the MIM in each right session.
\({\mathcal A} \) then samples a random main thread execution, and then just runs this extractor to extract the values \(\{\widetilde{\gamma }_i^1, \widetilde{\gamma }_i^2\}_{i \in [{{n}} ]}\) committed by the MIM, and by soundness of \(\mathsf {wi}\) and \(\mathsf {wzk}\), at least one is correctly extracted. Depending upon whether the challenge non-malleable commitment is to \(\gamma _2\) or \(\gamma _2'\), the joint distribution of the view and value extracted by \({\mathcal A} \) corresponds to either \({\mathsf{MIM}_{\langle C, R\rangle }(V_1,z)} \) or \({\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_1}\).
Therefore, if the joint distribution of the view and the values committed by the MIM changes by more than \(\epsilon \) between these executions, it can be used to contradict the one-many weak non-malleability of \(\varPi \). Thus, if
This gives a contradiction, thus the distributions are indistinguishable upto \(\epsilon \) error.
We note that in \(\mathsf{{Hybrid}}_1\), soundness of the \(\mathsf {wi}\) and \(\mathsf {wzk}\) arguments in the left as well as right interactions is still maintained, thus a rewinding extractor always successfully extracts the value committed by the MIM.
\(\mathsf{{Hybrid}}_{2, {\mathcal D}}\): In this hybrid, the challenger behaves similarly to \(\mathsf{{Hybrid}}_1\), except that it outputs the transcript of an execution where the distinguisher-dependent weak zero-knowledge protocol \(\mathsf {wzk}\) is simulated as follows. For simplicity of exposition, we add some clearly demarcated analysis to the description of the experiment.
-
1.
Run the execution until the MIM sends the first message for the right execution. With fixed first messages, \(\phi _1\) and \(\widetilde{\phi }_1^j\) for \(j \in [p]\), run the rest of the protocol as follows.
-
2.
Send second messages \(\widetilde{\phi }_2^j\) for the right interactions, and wait for the MIM’s response \({\phi }_2\). These will correspond to the first and second messages for the main transcript.
-
3.
With first two messages fixed as above, generate a lookahead thread as follows: send the third message on behalf of the honest party, computed as a commitment to \(V_1\) honestly as in \(\mathsf{{Hybrid}}_1\) (this is later also repeated for \(V_2\)). Let \(\{ \widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j \}_{j \in [p]}\) denote the joint distribution of values committed by the MIM in this execution. If the MIM produced an invalid transcript, abort. Otherwise, continue.
-
4.
With the same fixed first messages, \(\phi _1\) and \(\widetilde{\phi }_1^j\) for \(j \in [p]\), rewind the MIM \((1/\epsilon ^2)\) times sending various second round challenge messages to the MIM on behalf of honest receiver. When the MIM sends a challenge for the left (honest) execution, complete the transcript as an honest commitment to \(V_1\) (this is later also repeated for \(V_2\)), and wait for the MIM’s response.
Use these rewinding executions to extract the value committed in at least one (or both) of the non-malleable commitments \(\{ \widehat{\gamma }_1^j, \widehat{\gamma }_2^j \}_{j \in [p]}\) provided by the MIM adversary, for each session.
Analysis. Whenever the MIM completes a right execution (that is, it does not generate any invalid messages), by soundness of the WI and the weak ZK argument, we have that with probability at least \(1 - {\mathsf {negl}} (n)\), at least one of the non-malleable commitments were generated correctly in each execution. Thus, by the same argument as used in the Lemma 3, with overwhelming probability, the extractor runs in time \({\mathsf {poly}} (\frac{1}{\epsilon ^2})\) and correctly extracts at least one of the values committed by the MIM using the non-malleable commitment in all executions, except with error at most \(\epsilon ^2\).
-
5.
Repeat Steps 3 and 4, \(\frac{1}{\epsilon ^4}\) times for both \(V_1\) and \(V_2\), and compute the union of extracted values (by checking whenever a value was correctly extracted). For each right session \(j \in [p]\), denote the values extracted by the challenger by \(\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\).
Analysis. At the end of this step, at least one value must be correctly extracted for every right session, except with total failure probability at most \(\epsilon ^2\). Moreover, if for any right execution the extractor successfully extracted only one value, then by a Markov argument, the MIM will continue to use the same value as witness for the \(\mathsf {wi}\) in all lookahead executions that we will create for distinguisher-dependent simulation, except with probability at most \({\epsilon ^2}\) (otherwise, if the MIM used a different value as witness for the \(\mathsf {wi}\), then that value would also be extracted with significant probability). Therefore, \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\) can be used to recover the value committed by the MIM from any transcript generated by the MIM with fixed first two messages \(\phi _1, \widetilde{\phi }_1^{j}, \phi _2, \widetilde{\phi }_2^j\), except with failure probability \({\epsilon ^2}\).Footnote 4
-
6.
After completing the previous step, with the first message transcript fixed, go back and again fix first two messages \(\phi _1, \widetilde{\phi }_1^j, \widetilde{\phi }_2^j, \phi _2\). These will now remain fixed for the rest of the experiment. Since these same first two round messages were in fact fixed at the start of the protocol, by the weak resettable weak ZK property of \(\mathsf {wzk}\), the simulation security of \(\mathsf {wzk}\) holds with respect to the partial transcript \((\phi _1, \phi _2, \widetilde{\phi }_1^j, \widetilde{\phi }_2^j)\).
In particular, weak resettable security implies that indistinguishability between real and simulated view must hold even against a distinguisher that performed the rewindings in the previous step and obtained \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\). Note that these values \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\) can now be used to extract the message committed in the string c by the MIM from any transcript generated by the MIM with fixed first two messages, except with error at most \({\epsilon }^2 + {\mathsf {negl}} ({{n}})\).
-
7.
Next, run the distinguisher-dependent simulation strategy \({\mathcal S} \) of the weak zero-knowledge argument, with error \({\epsilon }^2\), on the distinguisher \({\mathcal D} '\) constructed as follows. \({\mathcal D} '\) is given the view of the MIM, together with auxiliary information \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\). On input the view of the MIM, it uses this information to extract the value committed by the MIM from all its executions. It then runs the distinguisher \({\mathcal D} \) on the joint distribution of the view and the extracted values and mirrors the output of \({\mathcal D} \).
Recall, that the distinguisher-dependent simulation strategy \({\mathcal S} \) of [15] generates several different third messages (corresponding to the same fixed messages \((\phi _1, \phi _2, \widetilde{\phi }_1^j, \widetilde{\phi }_2^j)\)), while sampling fresh \(\alpha _1, \alpha _2\) each time. Also note that the output transcript still contains a commitment to \(V_1\), and is infact identical to \(\mathsf{{Hybrid}}_1\) except that it contains a simulated \(\mathsf {wzk}\) argument.
Let \({\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{2, {\mathcal D}}}\) denote the joint distribution of the view and value committed by the MIM when interacting with an honest committer in this hybrid.
Lemma 4
For any PPT distinguisher \({\mathcal D} \) with auxiliary information z, \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{2, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_1}) = 1]| \le \epsilon + {\mathsf {negl}} ({{n}}).\)
Proof
This claim follows by the weak resettable security of distinguisher-dependent simulation: since \({\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{2,{\mathcal D}}}\) is the result of executing distinguisher-dependent simulation against distinguisher \({\mathcal D} '\), which itself runs the distinguisher \({\mathcal D} \) on \({\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{1}}\). Note that the weak resettable security experiment for distinguisher-dependent simulation allows the adversary to obtain, in addition to a real/simulated main transcript, several “lookahead” transcripts, where all lookahead transcripts contain honestly generated proofs, that may all use the same first message of the argument.
In other words, we consider a reduction that first fixes the first two messages of the honest and MIM execution corresponding to the main thread. Next, it generates multiple lookahead threads, as allowed by the security experiment of weak resettable \(\mathsf {wzk}\), using these threads to extract the values \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\) committed by the MIM. In all these lookahead threads, the challenger generates all messages on its own according to \(\mathsf{{Hybrid}}_1\), except that it obtains the honestly generated \(\mathsf {wzk}\) proofs for these threads externally from a challenger for weak resettable weak ZK.
Finally, the challenger flips a bit b, and if \(b = 0\), it outputs an honestly generated weak ZK argument for the main transcript. On the other hand, if \(b = 1\), it outputs a simulated argument (with error at most \(\epsilon \)), while simulating the output of distinguisher \({\mathcal D} \) on input the view and values extracted from the MIM. The reduction obtains this proof from the challenger and uses it to complete the main transcript. Because of correctness of extracted values argued in the analysis above, we note that if \(b = 0\), the experiment corresponds to running \({\mathcal D} \) on \({\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{1, {\mathcal D}}}\) and if \(b = 1\), the experiment corresponds to running the distinguisher \({\mathcal D} \) on \({\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{2, {\mathcal D}}}\). Thus, if \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{2, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_1}) = 1]| > \epsilon + {\mathsf {negl}} ({{n}})\), this gives a distinguisher against the weak resettable simulation security of the weak ZK argument according to Definition 2, which is a contradiction.
\(\mathsf{{Hybrid}}_{3,{\mathcal D}}\): In this hybrid, the challenger behaves identically to \(\mathsf{{Hybrid}}_{2, {\mathcal D}}\), except that it sets \(c_1 = \mathsf{com}(0;\widehat{r})\) by picking uniform randomness \(\widehat{r}\), in the main transcript (instead of generating \(c_1\) as a commitment to 1). Note that this is possible because the challenger is generating a simulated proof in the output transcript, for the fact that \(c_1\) is a commitment to 1. Let \({\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{3, {\mathcal D}}}\) denote the joint distribution of the view and values committed by the MIM when interacting with the challenger in this hybrid.
Lemma 5
For any PPT distinguisher \({\mathcal D} \) with auxiliary information z, \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{2, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{3, {\mathcal D}}}) = 1]| \le {\mathsf {negl}} ({{n}}).\)
Proof
This hybrid is indistinguishable from \(\mathsf{{Hybrid}}_2\) by the computational hiding property of the non-interactive commitment scheme \(\mathsf{com}\). More formally, consider a reduction \({\mathcal R} \) that behaves identically to \(\mathsf{{Hybrid}}_{2, {\mathcal D}}\), first extracting \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\). Next, it obtains the commitment \(c_1\) (only for the main thread and not for any of the rewinding executions), externally, as either a commitment to 0 or a commitment to 1, and uses this to complete the main transcript. It then uses the extracted values \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\) to recover the values committed by the MIM in the main transcript. It outputs the joint distribution of the transcript and the values committed by the MIM to distinguisher \({\mathcal D} \). Then given a distinguisher \({\mathcal D} \) where: \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{2, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{3, {\mathcal D}}}) = 1]| \ge \frac{1}{{\mathsf {poly}} ({{n}})}\), the reduction mirrors the output of this distinguisher such that:
This is a contradiction to the hiding of \(\mathsf{com}\).
\(\mathsf{{Hybrid}}_{4, {\mathcal D}}\): In this hybrid, the challenger behaves identically to \(\mathsf{{Hybrid}}_{3, {\mathcal D}}\) except that in the output transcript, it sets \(\delta _{2} = \mathsf {PRF}(\gamma _{2}, \alpha _{2}) \oplus \widehat{r}\) where \(\widehat{r}\) is the randomness used to generate \(c_1 = \mathsf{com}(0;\widehat{r})\). Note that the committer is using PRF key \(\gamma '_{2}\) in the protocol \(\varPi ^{2}\), thus the key \(\gamma _{2}\) does not appear anywhere else in the rest of the protocol.
Let \({\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{4, {\mathcal D}}}\) denote the joint distribution of the view and value committed by the MIM when interacting with an honest committer in this hybrid.
Lemma 6
For any PPT distinguisher \({\mathcal D} \) with auxiliary information z, \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{4, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{3, {\mathcal D}}}) = 1] \le {\mathsf {negl}} ({{n}}).\)
Proof
This hybrid is indistinguishable from \(\mathsf{{Hybrid}}_{3, {\mathcal D}}\) by the security of the PRF. More formally, consider a reduction \({\mathcal R} \) that behaves identically to \(\mathsf{{Hybrid}}_{3, {\mathcal D}}\) except that for all lookahead (recall that the distinguisher is rewound several times) threads, it samples fresh \(\alpha _2\) each time and obtains \(\mathsf {PRF}(\gamma _{2}, \alpha _{2}) \oplus \widehat{r}\) externally from a PRF challenger.
Then, for the main thread it obtains the value \(\delta _{2}\) externally as either \(\mathsf {PRF}(\gamma _{2}, \alpha _{2}) \oplus \widehat{r}\), or \(\mathsf {PRF}(\gamma _{2}, \alpha _{2}) \oplus r\), where r is the randomness used generate commitment c in the left execution, and \(\widehat{r}\) is the randomness used to generate commitment \(c_1\). It uses the externally obtained \(\delta _2\) to complete the main transcript. It then uses the extracted values \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\) to obtain the values committed by the MIM in the main transcript. It outputs the joint distribution of the transcript and the values committed by the MIM to distinguisher \({\mathcal D} \).
Given a distinguisher \({\mathcal D} \) where \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{4, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{3, {\mathcal D}}}) = 1]| \ge \frac{1}{{\mathsf {poly}} ({{n}})}\), the reduction can mirror the output of this distinguisher to directly contradict the security of the PRF.
\(\mathsf{{Hybrid}}_{5, {\mathcal D}}\): In this hybrid, the challenger behaves identically to \(\mathsf{{Hybrid}}_{4, {\mathcal D}}\) except that it sets \(\varPi ^{2}\) as a non-malleable commitment to the same randomness \(\gamma _{2}\) that is used to compute \(\delta _{2}\), for all executions.
This hybrid essentially “reverts” the changes performed in \(\mathsf{{Hybrid}}_{1}\). Note that the challenger in this hybrid, first extracts the values committed via the non-malleable commitments provided by the MIM, and then rewinds the distinguisher multiple times – however, the first two messages of the protocol are fixed at the time of rewinding the distinguisher. In particular, for fixed \(\mathsf {nmc} _1^{2}\) and \(\mathsf {nmc} _2^{2}\), the challenger gives the same response \(\mathsf {nmc} _3^{2}\) for all the third messages it generates while/before simulating \(\mathsf {wzk}\) argument.
Since the main thread transcript output in this hybrid consists of a simulated proof, indistinguishability of this hybrid is the most interesting to argue. We prove that it follows by the weak non-malleability of \(\varPi ^2\). It is important, for the proof of non-malleability to go through, that the witness used by the prover in the proof of WI in this hybrid, is always the randomness used to compute \(\varPi ^1\) and never the randomness used to compute \(\varPi ^2\) – because the messages of \(\varPi ^2\) will be obtained externally. Moreover, recall that the proof of non-malleability of the weak non-malleable commitment scheme \(\varPi \) requires a simulator-extractor to “cheat” in the scheme \(\varPi ^2 \) in rewinding executions.
Note that the challenger in this hybrid, fixes the first two rounds for the output transcript. Then, with the same fixed first round, it attempts to extract the values \((\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j)\) committed by the MIM in the non-malleable commitments in all right sessions. After extraction, it rewinds the distinguisher multiple times – at this point the first two messages of the protocol are again the first two rounds that were fixed prior to extraction. Note that the transcript output by the challenger in this experiment is such that \(\varPi ^1\) is a valid non-malleable commitment to \(\gamma _1\) with randomness \(r_1\) AND \(r = \mathsf {PRF}(\gamma _1, \alpha _1) \oplus \delta _1\) such that \(c = \mathsf{com}(m;r)\) (and this is the witness used in \(\mathsf {wi}\)). Additionally, \(\varPi ^{2}\) is also a valid non-malleable commitment to \(\gamma _2\) with randomness \(r_2\) AND \(\widehat{r} = \mathsf {PRF}(\gamma _2, \alpha _2) \oplus \delta _2\) such that \(c_1 = \mathsf{com}(0;\widehat{r})\). However, the witness used in \(\mathsf {wi} \) is always \(\varPi ^1\).
Let \({\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{5, {\mathcal D}}}\) denote the joint distribution of the view and value committed by the MIM when interacting with an honest committer in this hybrid.
Lemma 7
For any PPT distinguisher \({\mathcal D} \) with auxiliary information z, \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{5, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{4, {\mathcal D}}}) = 1]| \le 3\epsilon + {\mathsf {negl}} ({{n}}).\)
Proof
Recall that the challenger strategy in both \(\mathsf{{Hybrid}}_{5, {\mathcal D}}\) and \(\mathsf{{Hybrid}}_{4, {\mathcal D}}\) is as follows: The challenger first generates and fixes the first two messages of the main transcript \(\phi _1, \widetilde{\phi }_1^j, \widetilde{\phi }_2^j, {\phi }_2\). It then rewinds the MIM multiple times with the same fixed first message but different second round messages, to extract \(\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\) for all \(j \in [n]\). Finally, it runs the distinguisher-dependent simulation strategy with partial transcript \(\phi _1, \widetilde{\phi }_1^j, \widetilde{\phi }_2^j, {\phi }_2\) to output a main transcript with a simulated proof.
The main difference between \(\mathsf{{Hybrid}}_{4, {\mathcal D}}\) and \(\mathsf{{Hybrid}}_{5, {\mathcal D}}\) is that the committer commits to \(\gamma '_2\) using \(\varPi ^2\) in \(\mathsf{{Hybrid}}_{4, {\mathcal D}}\), and uses a different \(\gamma _2\) for the rest of the protocol, whereas in \(\mathsf{{Hybrid}}_{5, {\mathcal D}}\), \(\gamma '_2 = \gamma _2\). However, both hybrids involve the challenger rewinding the MIM (and consequently rewinding the left session) several times in order to extract \(\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\) for \(j \in [n]\). In this rewinding situation, invoking weak one-malleability of \(\varPi ^2\) requires care.
Our first observation is that by the weak non-malleability of \(\varPi \), there exists an extractor that runs in time \({\mathsf {poly}} (\frac{1}{\epsilon })\) and extracts the values committed by the MIM in all the non-malleable commitments for all \(j \in [p]\), without rewinding the left execution. The reduction to one-many weak non-malleability of \(\varPi \) uses this extractor and proceeds as follows:
-
1.
The reduction begins by fixing the first two messages in the left and right executions in the main thread. For these messages, it obtains an externally generated non-malleable commitment to either \(\gamma _2' = \gamma _2\) or \(\gamma _2'\) chosen uniformly at random independent of \(\gamma _2\). The former corresponds to \(\mathsf{{Hybrid}}_{5, {\mathcal D}}\) and the latter to \(\mathsf{{Hybrid}}_{4, {\mathcal D}}\).
Instead of rewinding the MIM providing honestly generated transcripts in the left interaction as is done in \(\mathsf{{Hybrid}}_{5, {\mathcal D}}\) and \(\mathsf{{Hybrid}}_{4, {\mathcal D}}\), we will now consider two sub-hybrids, \(\mathsf{{Hybrid}}_{4, a, {\mathcal D}}\) and \(\mathsf{{Hybrid}}_{5, a, {\mathcal D}}\) where the reduction uses the extractor \({\mathcal E} \) for the non-malleable commitment to extract the values committed by the MIM without rewinding the left interaction. We will show that the view and values extracted from these sub-hybrids will remain identical to the view and value extracted via rewinding in \(\mathsf{{Hybrid}}_{4, {\mathcal D}}\) and \(\mathsf{{Hybrid}}_{5, {\mathcal D}}\), respectively. This will essentially follow because of correctness of extractor \({\mathcal E} \), and because of soundness of \(\mathsf {wi}\) and \(\mathsf {wzk}\) in the interactions from which extraction occurs. We will also directly give a reduction proving that the joint distribution of the views and values extracted must be indistinguishable between these sub-hybrids.
-
2.
Recall that \({\mathcal E} \) extracts the values committed by the MIM in a main transcript, without rewinding the messages sent in the non-malleable commitment in the left interaction (the extractor \({\mathcal E} \) may still rewind the MIM, only in all such rewindings it will not need to rewind the left non-malleable commitment, indeed it will suffice to generate “fake” third round messages for the non-malleable commitment to \(\gamma _2\) – please refer to [13] for details on the extraction procedure). It is important to note that the \(\mathsf {wzk}\) simulation strategy requires that the MIM’s committed values be extracted first, therefore we cannot generate a simulated \(\mathsf {wzk}\) argument without first extracting all values \(\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\) committed by the MIM.
-
3.
Thus, in sub-hybrids \(\mathsf{{Hybrid}}_{i, a, {\mathcal D}}\) for \(i \in \{4, 5\}\), the challenger just runs extractor \({\mathcal E} \) to extract the values \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [n]}\), instead of rewinding the left execution. \({\mathcal E} \) extracts the value committed in a main transcript without rewinding the left execution. Thus, first the challenger generates a special main transcript for the extractor \({\mathcal E} \) as follows. It generates \(\phi _1, \widetilde{\phi }_1^j, \widetilde{\phi }_2^j, {\phi }_2\) the same way as \(\mathsf{{Hybrid}}_{4, {\mathcal D}}\), and then completes the third message by generating an honest commitment to \(V_1\) (also repeated with \(V_2\)), that is, giving an honestly generated \(\mathsf {wzk}\) argument and using \(\gamma _1\) as witness for the \(\mathsf {wi}\) Footnote 5. It waits for the MIM to generate the third messages for the right executions, and now feeds the transcript of the interaction to \({\mathcal E} \) (if the MIM aborts, the challenger just repeats again with the same fixed first two messages, \({\mathsf {poly}} (1/\epsilon )\) times). Whenever \({\mathcal E} \) requests to rewind the MIM, the challenger rewinds the MIM, except that it obtains the messages for the left commitment \(\varPi ^2\) in all rewinding executions from \({\mathcal E} \). Further, recall that \({\mathcal E} \) has the property that it only extracts an incorrect value when the MIM is committing to \(\bot \) in the honest execution, except with error \(\epsilon \), however, this is not true except with probability \(1 - {\mathsf {negl}} (n)\), by soundness of \(\mathsf {wi}\) and \(\mathsf {wzk}\). The MIM waits for \({\mathcal E} \) to output the extracted values \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}\). Next, the MIM repeats this again (\(\epsilon ^4\) times, with same fixed first two messages, waiting for the extractor to output (potentially different) extracted values. Finally the challenger uses the union of these extracted values to complete the rest of the experiment according to \(\mathsf{{Hybrid}}_{4, {\mathcal D}}\).
Claim. The joint distribution of the views and values committed by the MIM remain indistinguishable (with error at most \(\epsilon + {\mathsf {negl}} (n)\)) between \({\mathsf{{Hybrid}}_{i, {\mathcal D}}}\) and \({\mathsf{{Hybrid}}_{i, a,{\mathcal D}}}\) for \(i \in \{4, 5\}\).
Proof. Note that the special main transcript provided to \({\mathcal E} \) to facilitate extraction in the sub-hybrids, is distributed identically to the transcripts provided in the lookahead executions for extraction in \({\mathsf{{Hybrid}}_{4, {\mathcal D}}}\) and \({\mathsf{{Hybrid}}_{5, {\mathcal D}}}\). Additionally, in all these executions, the challenger always provides honestly generated proofs, thus the soundness of \(\mathsf {wi}\) and \(\mathsf {wzk}\) provided by the MIM is guaranteed in all these executions. Therefore, the adversary is guaranteed to generate at least one out of the two non-malleable commitments from each session correctly in any non-aborting execution, except with probability \({\mathsf {negl}} (n)\).
Moreover, by soundness of \(\mathsf {wzk}\), the extracted value from at least one of the non-malleable commitments generated by the MIM in the \(j^{th}\) session, will correspond to a witness for the commitment to \(\widetilde{\gamma }^1_j\) or \(\widetilde{\gamma }^2_j\), directly allowing to recover the message committed by the MIM in each non-aborting right session (if only one \(\widetilde{\gamma }_j\) was extracted, w.h.p. the MIM continues to use the same witness). By correctness of extraction from \({\mathcal E} \) and because of soundness of \(\mathsf {wi} \) and \(\mathsf {wzk}\) in all rewinding executions as well as the special main execution, the joint distribution of views and value extracted via rewinding in \(\mathsf{{Hybrid}}_{i, {\mathcal D}}\) is \(\epsilon \)-indistinguishable from the distribution when \({\mathcal A} \) extracts using \({\mathcal E} \) in \(\mathsf{{Hybrid}}_{i, a, {\mathcal D}}\) for \(i \in \{4, 5\}\).
-
4.
Next, keeping the first two messages of the transcript \(\tau \) fixed, the challenger outputs a main transcript with a simulated weak ZK argument, where the simulation strategy runs on the distinguisher that obtains input the view of the MIM as well as the value extracted in the previous step, in a similar manner to \(\mathsf{{Hybrid}}_{4, {\mathcal D}}\).
If the joint distribution of the view and values committed by the MIM between \(\mathsf{{Hybrid}}_{4, a, {\mathcal D}}\) and \(\mathsf{{Hybrid}}_{5, a, {\mathcal D}}\) are more than \(\epsilon \)-distinguishable, there exists a reduction to the hiding of the non-malleable commitment \(\varPi ^2\), which obtains the messages of \(\varPi ^2\) externally to generate the first two round messages. In response to the MIM’s challenge for the left execution, it obtains the third message of \(\varPi ^2\) externally, and uses it to generate the special main transcript for \({\mathcal E} \). Next, it runs the extractor \({\mathcal E} \), which does not need to rewind \(\varPi ^2\) in the left execution. Once it obtains \(\{\widetilde{\gamma }^1_j, \widetilde{\gamma }^2_j\}_{j \in [p]}\) from \({\mathcal E} \), it proceeds to run the distinguisher-dependent simulation strategy. In this step, since the first two messages for the main transcript have already been fixed, the challenger can use the same third message \(\varPi _2^{3}\) that it obtained externally, to complete the second non-malleable commitment in the left execution, in all third messages it generates in order to simulate the \(\mathsf {wzk}\) argument by rewinding the distinguisher.
Therefore, if the joint distribution of the view and the values committed by the MIM changes by more than \(\epsilon \) between \(\mathsf{{Hybrid}}_{4, a, {\mathcal D}}\) and \(\mathsf{{Hybrid}}_{5, a, {\mathcal D}}\), it can be used directly to contradict the hiding of \(\varPi ^2\). That is, if \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{5, a, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{4, a, {\mathcal D}}}) = 1]| \ge \epsilon + \frac{1}{{\mathsf {poly}}}({{n}}),\)
This gives a contradiction, thus the distributions \(\mathsf{{Hybrid}}_{4, {\mathcal D}}\) and \(\mathsf{{Hybrid}}_{5, {\mathcal D}}\) are indistinguishable upto at most \(3\epsilon \)-error.
\(\mathsf{{Hybrid}}_{6, {\mathcal D}}\): In this hybrid, the challenger behaves the same way as \(\mathsf{{Hybrid}}_{5, {\mathcal D}}\), except that it uses the second witness, \(r_2, \gamma _2\), to generate the witness-indistinguishable argument \(\mathsf {wi}\) in the output transcript.
Lemma 8
For any PPT distinguisher \({\mathcal D} \) with auxiliary information z, \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{6, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{5, {\mathcal D}}}) = 1]| \le \epsilon + {\mathsf {negl}} ({{n}}).\)
Proof
The proof of this lemma relies on the reusable resettable witness indistinguishability of \(\mathsf {wi}\).
The reduction \({\mathcal R} \) samples all messages for the experiment according to \(\mathsf{{Hybrid}}_{5, D}\), except that it obtains WI proofs for all lookahead (rewinding) executions externally from the challenger, by providing the first witness to the challenger. In this experiment, note that some executions rewind the MIM to the end of the first round, thus proofs for these executions are provided with respect to new verifier messages generated by the MIM. Some other executions (corresponding to weak ZK simulation strategy) rewind the MIM to the end of the second round: thus different statements are proved in these executions, corresponding to the same verifier message from the MIM, that is fixed before the end of the second round. Thus, this experiment exactly corresponds to the security game of resettable reusable WI.
For the main/output transcript generated during distinguisher-dependent simulation, \({\mathcal R} \) samples all messages except the WI proof according to \(\mathsf{{Hybrid}}_{5, D}\). Note that the statement being proved in this transcript has two valid witnesses, \(w_1\) = (\(r_1, \gamma _1\) randomness r and commitment c) and \(w_2\) = (\(r_2, \gamma _2\), randomness \(\widehat{r}\) and commitment \(c_1\)), which are sampled by the reduction \({\mathcal R} \). \({\mathcal R} \) forwards the verifier message \(\mathsf {wi}_1\) to the challenger, together with both witnesses, and obtains \(\mathsf {wi}_2\) that is generated using either witness \(w_1\) or \(w_2\). The reduction uses this externally generated proof to complete the experiment. If \(w_1\) was used, the experiment is identical to \(\mathsf{{Hybrid}}_{5, D}\), otherwise it is identical to \(\mathsf{{Hybrid}}_{6, D}\).
Note that in the experiment, \({\mathcal R} \) behaves according to \(\mathsf{{Hybrid}}_{5, {\mathcal D}}\) or \(\mathsf{{Hybrid}}_{6, {\mathcal D}}\): that is, it first extracts \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\). It then uses the extracted values \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\) to obtain the values committed by the MIM in the main transcript. It outputs the joint distribution of the transcript and the values committed by the MIM to distinguisher \({\mathcal D} \). Given a distinguisher \({\mathcal D} \) where \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{6, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{5, {\mathcal D}}}) = 1]| \ge \frac{1}{{\mathsf {poly}} ({{n}})}\), the reduction mirrors the output of this distinguisher to directly contradict the security of \(\mathsf {wi}\). Thus, the joint distribution in this hybrid is indistinguishable from \(\mathsf{{Hybrid}}_{5, {\mathcal D}}\) by the resettable reusable witness-indistinguishability of \(\mathsf {wi}\).
\(\mathsf{{Hybrid}}_{7, {\mathcal D}}\): In this hybrid, the challenger behaves the same way as \(\mathsf{{Hybrid}}_{6, {\mathcal D}}\), except that it uses the second witness, \(r_2, \gamma _2\), to generate the witness-indistinguishable arguments \(\mathsf {wi}\) in all the lookahead executions. That is, in every message sent by the challenger, it uses the second witness instead of the first. This hybrid is indistinguishable from \(\mathsf{{Hybrid}}_{6, {\mathcal D}}\) by the resettable reusable witness-indistinguishability of \(\mathsf {wi}\).
Lemma 9
For any PPT distinguisher \({\mathcal D} \) with auxiliary information z, \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{7, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{6, {\mathcal D}}}) = 1]| \le {\mathsf {negl}} ({{n}}).\)
Proof
The proof of this lemma follows similarly to that of Lemma 8, by relying on the resettable reusable witness-indistinguishability of \(\mathsf {wi}\). In this experiment, note that some executions rewind the MIM to the end of the first round, thus proofs for these executions are provided with respect to new verifier messages generated by the MIM. Some other executions (corresponding to weak ZK simulation strategy) rewind the MIM to the end of the second round: thus different statements are proved in these executions, corresponding to the same verifier message from the MIM, that is fixed before the end of the second round. This experiment exactly corresponds to the security game of resettable reusable WI.
That is, the reduction obtains WI proofs externally from the challenger by providing both witnesses \(w_1 = (r_1, \gamma _1\), randomness r and commitment c) and \(w_2 = (r_2, \gamma _2\), randomness r and commitment c). The challenger sends proofs that are all generated either using witness \(w_1\) or all using witness \(w_2\). The reduction completes the rest of the protocol according to \(\mathsf{{Hybrid}}_{6, D}\), except using the externally generated proofs in the left execution. If the challenger used witness \(w_1\), the game corresponds to \(\mathsf{{Hybrid}}_{6, D}\) otherwise it corresponds to \(\mathsf{{Hybrid}}_{7, D}\).
Note that in the experiment, R behaves according to \(\mathsf{{Hybrid}}_{6, {\mathcal D}}\) or \(\mathsf{{Hybrid}}_{7, {\mathcal D}}\): that is, it first extracts \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\). It then uses the extracted values \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\) to obtain the values committed by the MIM in the main transcript. It outputs the joint distribution of the transcript and the values committed by the MIM to distinguisher \({\mathcal D} \). Given a distinguisher \({\mathcal D} \) where \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{7, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{6, {\mathcal D}}}) = 1]| \ge \frac{1}{{\mathsf {poly}} ({{n}})}\), the reduction mirrors the output of this distinguisher to directly contradict the resettable reusable security of \(\mathsf {wi}\).
We note that the changes made in \(\mathsf{{Hybrid}}_{7, {\mathcal D}}\) and \(\mathsf{{Hybrid}}_{6, {\mathcal D}}\) can be collapsed into a single hybrid experiment relying on resettable reusable security of WI, however we keep them separate for additional clarity – since the witness used in the main transcript refers to \(\varPi ^2\) and the randomness for \(c_1 = \mathsf{com}(0;\widehat{r})\) while the witness used in the lookahead transcripts refer to \(\varPi ^2\) and the randomness for \(c = \mathsf{com}(V_1; r)\). At this point, the value \(\gamma _1\) committed using the first non-malleable commitment \(\varPi ^1\) is not used as a witness in any of the WI proofs.
\(\mathsf{{Hybrid}}_{8, {\mathcal D}}\): In this hybrid, the challenger behaves the same way as \(\mathsf{{Hybrid}}_{7, {\mathcal D}}\), except that in all transcripts, it sets \(\varPi ^{1}\) as a non-malleable commitment to a different randomness \(\gamma _{1}'\) than the one used to compute \(\delta _{1}\).
Lemma 10
For any PPT distinguisher \({\mathcal D} \) with auxiliary information z, \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{8, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{7, {\mathcal D}}}) = 1]| \le \epsilon + {\mathsf {negl}} ({{n}}).\)
Proof
The proof of this lemma is exactly the same as that of Lemma 7. The joint distribution of the view and value committed by a malicious receiver in \(\mathsf{{Hybrid}}_{8, {\mathcal D}}\) is \(\epsilon \)-indistinguishable from \(\mathsf{{Hybrid}}_{7, {\mathcal D}}\) by the non-malleability of the commitment \(\varPi ^1\).
\(\mathsf{{Hybrid}}_{9, {\mathcal D}}\): In this hybrid, the challenger behaves the same way as \(\mathsf{{Hybrid}}_{8, {\mathcal D}}\), except that in the output transcript, it sets  , instead of setting \(\delta _1 = \mathsf {PRF}(\gamma _{1}, \alpha _1) \oplus r\). Note that the committer is using PRF key \(\gamma '_{1}\) in the protocol \(\varPi ^{1}\), thus the key \(\gamma _{1}\) does not appear in the rest of the protocol.
, instead of setting \(\delta _1 = \mathsf {PRF}(\gamma _{1}, \alpha _1) \oplus r\). Note that the committer is using PRF key \(\gamma '_{1}\) in the protocol \(\varPi ^{1}\), thus the key \(\gamma _{1}\) does not appear in the rest of the protocol.
Lemma 11
For any PPT distinguisher \({\mathcal D} \) with auxiliary information z, \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{9, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{8, {\mathcal D}}}) = 1]| \le {\mathsf {negl}} ({{n}}).\)
Proof
The proof of this lemma is the same as that of Lemma 6, by relying on the security of the \(\mathsf {PRF}\).
\(\mathsf{{Hybrid}}_{10, {\mathcal D}}\): In this hybrid, the challenger behaves the same way as \(\mathsf{{Hybrid}}_{9, {\mathcal D}}\) except that it replaces \(c = \mathsf{com}(V_1; r)\) with \(c = \mathsf{com}(V_2;r)\) in the output transcript. Note that in this transcript, the randomness r is not used elsewhere in the protocol.
Lemma 12
For any PPT distinguisher \({\mathcal D} \) with auxiliary information z, \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{10, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{9, {\mathcal D}}}) = 1]| \le {\mathsf {negl}} ({{n}}).\)
Proof
This hybrid is indistinguishable from \(\mathsf{{Hybrid}}_{9, {\mathcal D}}\) because of computational hiding of the non-interactive commitment scheme \(\mathsf{com}\). More formally, consider a reduction \({\mathcal R} \) that behaves identical to \(\mathsf{{Hybrid}}_{9, {\mathcal D}}\) except that it obtains the commitment c (only for the main thread and not for any of the lookahead threads), externally, as either a commitment to \(V_1\) or a commitment to \(V_2\). This is allowed because by the end of \(\mathsf{{Hybrid}}_{9, {\mathcal D}}\), the randomness used to generate this commitment is not used anywhere else in the protocol.
Note that in the experiment, the reduction it first extracts \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\). It then uses the extracted values \(\{\widetilde{\gamma }_1^j, \widetilde{\gamma }_2^j\}_{j \in [p]}\) to obtain the values committed by the MIM in the main transcript. It outputs the joint distribution of the transcript and the values committed by the MIM to distinguisher \({\mathcal D} \). Then given distinguisher \({\mathcal D} \) where \(|\Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{9, {\mathcal D}}}) = 1] - \Pr [{\mathcal D} (z, {\mathsf{MIM}_{\langle C, R\rangle }({\mathsf {value}},z)} _{\mathsf{{Hybrid}}_{10, {\mathcal D}}}) = 1]| \ge \frac{1}{{\mathsf {poly}} ({{n}})}\), The reduction mirrors the output of this distinguisher such that:
This is a contradiction to the hiding of \(\mathsf{com}\).
At this point, we have successfully switched (with distinguishing advantage at most \(\varTheta (\epsilon ) + {\mathsf {negl}} (n)\)) to an experiment where the commitment is generated to message \(V_2\) instead of \(V_1\) in the transcript output by the challenger. However, note that the \(\mathsf {wzk}\) argument is still being simulated in this hybrid. Also note that throughout these hybrids, lookahead threads for extraction will be generated according to both values \(V_1\) and \(V_2\). Non-malleability follows by repeating the above hybrids in reverse order, until in \(\mathsf{{Hybrid}}_{V_2}\), the challenger generates an honest commitment to message \(V_2\)m and. setting \(n \epsilon \) to be less than the distinguishing advantage of the given distinguisher \({\mathcal D} \) to arrive at a contradiction. By invoking [19], this completes the proof of concurrent non-malleability.
Notes
- 1.
The basic protocol from [12] however, does achieve non-malleability against synchronous adversaries.
- 2.
Very roughly, this means that for every (malicious) PPT verifier and distinguisher \({\mathcal D} \), there exists a distinguisher-dependent simulator \(\mathsf {Sim}_{{\mathcal D}}\), that can generate a simulated proof.
- 3.
Note that in all hybrid experiments, we will actually use the extended simulation strategy of the weak ZK argument \(\mathsf {wzk}\) as described in [15]– that is used for strong witness indistinguishability, and where the simulator takes into account both messages \(m_0\) and \(m_1\) during simulation.
- 4.
Please refer to the full version for exact calculations and additional details.
- 5.
Note that the actual transcript that is output by the experiment must contain a simulated \(\mathsf {wzk}\) argument: the transcript with the honest \(\mathsf {wzk}\) argument is only generated to facilitate extraction.
References
Badrinarayanan, S., Goyal, V., Jain, A., Khurana, D., Sahai, A.: Round optimal concurrent MPC via strong simulation. IACR Cryptology ePrint Archive 2017, 597 (2017). http://eprint.iacr.org/2017/597
Barak, B.: Constant-round coin-tossing with a man in the middle or realizing the shared random string model. In: FOCS 2002, pp. 345–355 (2002)
Barak, B., Ong, S.J., Vadhan, S.P.: Derandomization in cryptography. SIAM J. Comput. 37(2), 380–400 (2007). http://dx.doi.org/10.1137/050641958
Bitansky, N., Paneth, O.: ZAPs and non-interactive witness indistinguishability from indistinguishability obfuscation. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 401–427. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_16
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I.: Concurrent non-malleable commitments (and more) in 3 rounds. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 270–299. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_10
Ciampi, M., Ostrovsky, R., Siniscalchi, L., Visconti, I.: Four-round concurrent non-malleable commitments from one-way functions. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 127–157. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_5
Dolev, D., Dwork, C., Naor, M.: Non-malleable cryptography (extended abstract). In: STOC 1991 (1991)
Dwork, C., Naor, M.: Zaps and their applications. SIAM J. Comput. 36(6), 1513–1543 (2007). https://doi.org/10.1137/S0097539703426817
Goyal, V.: Constant round non-malleable protocols using one-way functions. In: STOC 2011, pp. 695–704. ACM (2011)
Goyal, V., Khurana, D., Sahai, A.: Breaking the three round barrier for non-malleable commitments. In: FOCS (2016)
Goyal, V., Lee, C.K., Ostrovsky, R., Visconti, I.: Constructing non-malleable commitments: a black-box approach. In: FOCS (2012)
Goyal, V., Pandey, O., Richelson, S.: Textbook non-malleable commitments. In: Wichs, D., Mansour, Y. (eds.) Proceedings of the 48th Annual ACM SIGACT Symposium on Theory of Computing, STOC 2016, Cambridge, MA, USA, 18–21 June 2016, pp. 1128–1141. ACM (2016)
Goyal, V., Richelson, S., Rosen, A., Vald, M.: An algebraic approach to non-malleability. In: FOCS 2014, pp. 41–50 (2014)
Groth, J., Ostrovsky, R., Sahai, A.: New techniques for noninteractive zero-knowledge. J. ACM 59(3), 11:1–11:35 (2012). http://doi.acm.org/10.1145/2220357.2220358
Jain, A., Kalai, Y.T., Khurana, D., Rothblum, R.: Distinguisher-dependent simulation in two rounds and its applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10402, pp. 158–189. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_6
Khurana, D., Sahai, A.: How to achieve non-malleability in one or two rounds. Electronic Colloquium on Computational Complexity (ECCC) 24, Report no. 100 (2017). https://eccc.weizmann.ac.il/report/2017/100
Lin, H., Pass, R.: Constant-round non-malleable commitments from any one-way function. In: STOC 2011, pp. 705–714 (2011)
Lin, H., Pass, R., Soni, P.: Two-round and non-interactive concurrent non-malleable commitments from time-lock puzzles. Cryptology ePrint Archive, Report 2017/273 (2017). http://eprint.iacr.org/2017/273
Lin, H., Pass, R., Venkitasubramaniam, M.: Concurrent non-malleable commitments from any one-way function. In: Canetti, R. (ed.) TCC 2008. LNCS, vol. 4948, pp. 571–588. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78524-8_31
Pass, R.: Bounded-concurrent secure multi-party computation with a dishonest majority. In: Proceedings of the 36th Annual ACM Symposium on Theory of Computing, STOC 2004, pp. 232–241 (2004)
Pass, R.: Unprovable security of perfect NIZK and non-interactive non-malleable commitments. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 334–354. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_19
Pass, R., Rosen, A.: New and improved constructions of non-malleable cryptographic protocols. In: STOC 2005, pp. 533–542 (2005)
Pass, R., Wee, H.: Black-box constructions of two-party protocols from one-way functions. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 403–418. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_24
Wee, H.: Black-box, round-efficient secure computation via non-malleability amplification. In: Proceedings of the 51th Annual IEEE Symposium on Foundations of Computer Science, pp. 531–540 (2010)
Acknowledgements
We are extremely grateful to Vipul Goyal for helpful discussions about the properties of the protocol in [13], Yael Kalai for several useful discussions regarding [15] and Amit Sahai for very valuable feedback about this writeup. We also thank the anonymous reviewers of TCC 2017 for their useful comments.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Khurana, D. (2017). Round Optimal Concurrent Non-malleability from Polynomial Hardness. In: Kalai, Y., Reyzin, L. (eds) Theory of Cryptography. TCC 2017. Lecture Notes in Computer Science(), vol 10678. Springer, Cham. https://doi.org/10.1007/978-3-319-70503-3_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-70503-3_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70502-6
Online ISBN: 978-3-319-70503-3
eBook Packages: Computer ScienceComputer Science (R0)



 and if
and if 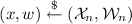 it generates an honest proof with first two messages
it generates an honest proof with first two messages 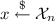 it generates a simulated proof with first two messages
it generates a simulated proof with first two messages 
