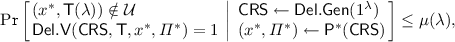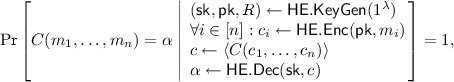On Zero-Testable Homomorphic Encryption and Publicly Verifiable Non-interactive Arguments

Abstract

We define and study zero-testable homomorphic encryption (ZTHE) – a semantically secure, somewhat homomorphic encryption scheme equipped with a weak zero test that can identify trivial zeros. These are ciphertexts that result from homomorphically evaluating an arithmetic circuit computing the zero polynomial over the integers. This is a relaxation of the (strong) zero test provided by the notion of graded encodings, which identifies all encodings of zero.

We show that ZTHE can suffice for powerful applications. Based on any ZTHE scheme that satisfies the additional properties of correctness on adversarial ciphertexts and multi-key homomorphism, we construct publicly verifiable non-interactive arguments for delegating computation. Such arguments were previously constructed from indistinguishability obfuscation or based on so-called knowledge assumptions. The arguments we construct are adaptively sound, based on an efficiently falsifiable assumption, and only make black-box use of the underlying cryptographic primitives.

We also show that a ZTHE scheme that is sufficient for our application can be constructed based on an efficiently-falsifiable assumption over so-called “clean” graded encodings.

This work subsumes an earlier report posted on the Cryptology ePrint Archive [PR14]. The current version features new results and addresses correctness issues with the earlier report.

O. Paneth—Research supported in part by NSF Grants CNS-1350619, CNS-1414119 and CNS-1413920, by the Defense Advanced Research Projects Agency (DARPA) and the U.S. Army Research Office under contracts W911NF-15-C-0226 and W911NF-15-C-0236 and by Simons Investigator Award Agreement Dated 6-5-12.

1 Introduction

Recent breakthroughs in the study of fully homomorphic encryption [Gen09] and program obfuscation [GGH+13b] have revolutionized the foundations of cryptography. Fully homomorphic encryption (FHE) allows arbitrary polynomial-time computations to be performed “homomorphically” on encrypted data, while ensuring that semantic security is maintained and nothing about the data can be learned. While this powerful security guarantee enables important applications, other scenarios require more fine-grained control: allowing some information about the data to be exposed, while other information remains hidden. Multilinear maps [BS02] and graded encodings [GGH13a] are basic building blocks that have proven to be incredibly useful in such scenarios. Intuitively, a graded encoding scheme is a somewhat homomorphic encryption, supporting homomorphic evaluation of low-degree algebraic computations, with an additional capability: an efficient zero test procedure that publicly identifies encodings of zero. Graded encodings cannot be semantically secure: the zero test procedure leaks partial information on the encoded elements. Nevertheless, other information can remain hidden (in particular, inverting the encoding might still be hard). This balance between functionality and security makes the notion of graded encoding incredibly useful for computing on encrypted data, with applications such as indistinguishability obfuscation and functional encryption [GGH+13b, GGHZ16].

While homomorphic encryption can by based on the Learning with Errors assumption [BV11, GSW13], the situation for graded encodings is less clear. Analyzing the security of existing candidates and designing new ones are central challenges [GGH13a, CLT15, GGH15, CHL+15, HJ16, MSZ16, GMM+16].

Zero-testable homomorphic encryption. In this work we define and study a new relaxation of graded encodings that we call zero-testable (somewhat) homomorphic encryption (ZTHE). A ZTHE is a semantically secure somewhat homomorphic encryption scheme equipped with a weak zero test that can only identify trivial zeros. These are ciphertexts that result from homomorphically evaluating an arithmetic circuit computing the zero polynomial over $\mathbb {Z}$. The weak zero test should accept such trivial zeros, but reject ciphertexts that encrypt non-zero values.

Importantly, an efficient weak zero test poses no contradiction to semantic security, since it does not allow to distinguish between encryptions of two different values. Given a ciphertext $c$ it is possible to homomorphically evaluate a circuit $P$ on $c$ and test if the result is a trivial zero. However, this does not give any information on the value encrypted in $c$, since the zero test only required to pass if $P$ vanishes on all values. Intuitively, the zero test is giving information on the evaluated computation $P$ rather then on the ciphertext $c$. Indeed, semantic security implies that if $P$ only vanishes on some values, then even if the evaluated ciphertext encrypts zero it will not pass the weak zero test (except with negligible probability). Otherwise, the zero test would have revealed information on the original encrypted evaluation point.

From ZTHE to delegation. The main technical result in this work demonstrates that ZTHE can suffice for powerful applications. Based on any ZTHE scheme that satisfies the additional properties of correctness on adversarial ciphertexts and multi-key homomorphism (we elaborate on these additional properties below), we construct publicly verifiable non-interactive arguments for delegating computation. Such arguments were previously constructed from indistinguishability obfuscation or based on so-called knowledge assumptions. Our construction follows a new approach and has important properties, such as adaptive soundness, reduction to an efficiently falsifiable assumption, and black-box use of the underlying cryptographic primitives. We note that the additional properties we assume (adversarial correctness and multi-key homomorphism) make ZTHE incomparable to “vanilla” graded encodings: the weak zero test assumption is more relaxed than the strong zero test of graded encodings schemes, but we require a stronger correctness property (namely correctness on adversarially generated ciphertexts).

ZTHE Candidate. We study the feasibility of constructing ZTHE. First, we observe that several existing somewhat homomorphic encryption schemes [Gen09, vDGHV10] admit a simple weak zero test. These schemes, however, do not satisfy the additional properties required for our non-interactive arguments. We construct ZTHE that is sufficient for our application based on an efficiently-falsifiable assumption over graded encodings with strong properties such as adversarial correctness. Our construction cannot be instantiated based on the existing graded encoding candidates (so-called “clean” graded encodings [Zim15, LV16] do guarantee these stronger properties). We leave the question of ZTHE instantiations as an important open problem and hope it will lead to new and improved deletion protocols based on weaker assumptions, as well as other applications.

Organization. In the rest of this introduction we elaborate on our results and techniques. Section 1.1 gives background on non-interactive arguments and discusses our main technical result, a construction of non-interactive arguments from ZTHE. In Sect. 1.2 we present our results in more detail. The construction of non-interactive arguments from ZTHE is described in Sect. 1.3. The construction of ZTHE from graded encodings is described in Sect. 1.4.

1.1 Non-interactive Arguments

Background. The power of efficiently verifiable proof systems is a foundational issue in the study of computation. A central goal is constructing proof systems that can be used by a powerful prover to convince a weak verifier of the correctness of a complex computational statement, usually framed as proving membership of an input $x$ in a language $\mathcal {L}$. Beyond its foundational importance in the theory of computation, this question has real-world applications, such as delegating computation. In this setting, a powerful server (playing the role of the prover) can run a complex computation for a much weaker client (playing the role of the verifier), and provide a proof of the output’s correctness.

A similar question was raised by Babai, Lund, Fortnow and Szegedy [BFLS91] in the PCP setting. Kilian [Kil92] and Micali [Mic94] gave the first candidate scheme for delegating computation. The question re-emerged in the theoretical literature in the work of Goldwasser, Kalai and Rothblum [GKR08], and became the focus of a rich body of research spanning theory and systems. See the recent survey by Walfish and Blumberg [WB13].

A “holy grail” for delegating computations is fully non-interactive proofs, comprised of a single message sent from the prover to the verifier with unconditional soundness, as in classic NP or Merlin-Arthur proofs. Unfortunately, there are serious barriers to constructing such proofs for delegating general deterministic computations (in particular, they imply Merlin-Arthur speedups for deterministic computations). Thus, a body of research has focused on computationally sound proofs in the common reference string model, where:

• 1. Soundness is only required to hold against efficient cheating provers. Computationally sound proof systems are commonly called argument systems.

• 2. There is a (public) common reference string (CRS), generated in advance by a trusted authority (or the verifier herself). This CRS can be used (repeatedly) by different parties to verify proofs. The prover and the verifier both have access to the CRS, but neither has access to the secret coins used to generate the CRS.

We focus on non-interactive argument systems for polynomial-time computations, where the verifier should be super-efficient (nearly-linear in the input length), and the honest prover should run in polynomial time. Non-interactive arguments are especially attractive for delegating computation, as any untrusted server can simply use the CRS to generate proofs and send them off (non-interactively and asynchronously), to be verified at the clients’ convenience. We refer to such a system as a publicly verifiable non-interactive argument for delegating computation. For the remainder of this work, we use the term non-interactive argument as shorthand.

Prior works on non-interactive arguments. In his seminal work, Micali [Mic94] gave the first construction of non-interactive arguments in the random oracle model. However, instantiating random oracle model constructions in a provably secure way is notoriously difficult, and often impossible [CGH04, GW11]. A rich body of research has aimed to construct non-interactive arguments in the plain model led to a variety of beautiful constructions based on strong cryptographic assumptions.

One line of works based non-interactive arguments on non-falsifiable¹ knowledge assumptions such as the knowledge of exponent assumption in bilinear groups [Gro10, Lip12, DFH12, GGPR13, BCI+13, BCCT13]. A recent sequence of works [SW14, BGL+15, CHJV14, KLW14] show how to base non-interactive arguments on indistinguishability obfuscation (IO). Based on standard assumptions such as somewhat-homomorphic encryption or private information retrieval schemes, the works of [KRR13, KRR14, BHK16] achieve the weaker notion of designated-verifier arguments. These are two-message arguments where, in the first message, the verifier samples the CRS and sends it to the prover. The secret coins used to sample the CRS are required to verify the proof sent in the second message.

This work. Our main technical result is a construction of non-interactive arguments from any ZTHE with the additional properties mentioned above (see Sect. 1.2). Our construction follows a different approach from previous works and leverages ideas and techniques that were previously used only in the context of designated-verifier arguments [KRR14, BHK16], such as efficient probabilistically checkable proofs and no-signaling soundness. As a result, our non-interactive arguments have some notable advantages compared to previous works:

• Efficiently falsifiable assumptions. Our arguments are based on the semantic security of the underlying ZTHE - an efficiently falsifiable assumption. Moreover, in our candidate construction of ZTHE from graded encodings, we further base semantic security of the ZTHE on a simple and efficiently falsifiable assumption on the graded encodings. Taken together, we can base soundness of the argument system on a falsifiable assumption on graded encodings.

  In contrast, the constructions of publicly verifiable non-interactive argument are based on assumptions that are not efficiently falsifiable. IO was recently constructed from simpler primitives such as multi-linear maps or functional encryption. However, these construction involve a sub-exponential security loss. While many applications of IO can be based directly on polynomially secure functional encryption, currently non-interactive arguments still require the full power of IO. For more information on this line of work, see [GPSZ17] and references therein.

  We note that for any particular non-interactive argument candidate, the assumption that the candidate is secure is efficiently falsifiable. Therefore, our focus will be on falsifiable assumptions that are elementary and natural compared to the tautological assumption that the candidate is secure.

• Adaptive soundness. The soundness of our non-interactive arguments is adaptive: it holds even when the statement proven is chosen as a function of the CRS. Adaptive soundness is required in many applications, and it is especially important in settings where the CRS is set “once and for all”.

  We note that any sound argument can be turned into an adaptively sound one via “complexity leveraging”. However, this reduction incurs an exponential loss in security, and therefore cannot be based on efficiently falsifiable assumptions.

• Black-box construction. In contrast to all previous construction of non-interactive arguments, our construction makes only black-box use of the underlying cryptographic primitives.² Understanding the feasibility and limitation of black-box constructions in cryptography is the subject of a rich body of work motivated both by theoretical interest as well as efficiency considerations.

1.2 Our Results in More Details

In this section we present our results in more details. We start by describing the basic notion of zero testable homomorphic encryption and the additional properties we consider.

Zero-testable homomorphic encryption. A homomorphic encryption is a semantically secure public key encryption equipped with a public evaluation algorithm that adds, subtracts and multiplies values homomorphically “under the encryption”. We focus on somewhat homomorphic encryption that only supports homomorphic evaluation of polynomial-size arithmetic circuits of logarithmic degree. That is, of degree $c\cdot \log \lambda$ for any constant c, where $\lambda$ is the security parameter. We require that ciphertexts are succinct: their size is bounded by some fixed polynomial in $\lambda$ that is independent of c.

A zero-testable somewhat homomorphic encryption (ZTHE) has an additional zero test procedure that takes a ciphertext and tests if it is a trivial zero. In more detail, we consider the homomorphic evaluation of a circuit $P$ over freshly encrypted ciphertexts $c_1,\dots ,c_n$, resulting in the evaluated ciphertext $c$. If the polynomial computed by $P$ is identically zero over $\mathbb {Z}$, then we require that $c$ passes the zero test. We also require that a ciphertext $c'$ that decrypts to a non-zero value does not pass the zero-test. If $c$ decrypts to zero, but it is not a trivial zero, we make no requirement on the outcome of the zero test. However, as discussed above, it follows from the semantic security of the encryption that such a ciphertext should not pass the zero test. Moreover, we note that even if $P$ vanishes on all boolean inputs, but it is not identically zero as a polynomial over $\mathbb {Z}$, we still expect the zero test to fail. Otherwise, the zero test can be used to efficiently decide the satisfiability of $P$.

We further study the following additional properties of ZTHE, which we use in our construction of non-interactive arguments:

Multi-key evaluation. In multi-key homomorphic encryption, introduced by López-Alt et al. [LTV12], homomorphic computation can be executed over ciphertexts encrypted under different keys. To ensure semantic security, decrypting the result requires all secret keys. We use ZTHE for three keys. That is, it is possible to homomorphically compute over ciphertexts encrypted under at most three different keys, and to run a weak zero test on the result. Importantly, a system can generate ciphertext under an unbounded number of keys and any three of them can be combined in a homomorphic computation. The encryption may also use shared public parameters to generate all keys.

Correctness for adversarially generated ciphertexts. We require that an efficient adversary, given the public key, cannot generate a pair of ciphertexts that result in an evaluation error. A pair of ciphertexts $c_1,c_2$ cause an evaluation error if computing a homomorphic operation $\star$ over $c_1,c_2$ and decrypting the evaluated ciphertext $c$ give a different result than decrypting $c_1$ and $c_2$ and computing $\star$ on the decrypted values. If $c_1$ and $c_2$ are generated honestly, this follows from the standard correctness guarantee of the encryption. However, we require correctness even when the ciphertext are not generated honestly. Note that the zero test is only required to accept honest ciphertexts that are trivially zero. However, even a malformed ciphertext that decrypts to a non-zero value should make the zero test reject.

In known constructions of somewhat homomorphic encryption, there exist invalid ciphertexts that do not represent an encryption of any value. To account for such candidates, we allow the decryption algorithm to fail. If $c_1$ or $c_2$ are invalid (fail to decrypt) we require that the evaluated ciphertext $c$ is invalid as well. If both $c_1$ and $c_2$ are valid, we require that $c$ is either invalid or it decrypts to the correct value.

Theorem 1.1

(Informal). Assuming a 3-key zero-testable somewhat homomorphic encryption scheme with correctness for adversarially-generated ciphertexts, there exists an adaptively-secure publicly-verifiable non-interactive argument for delegating all polynomial time computations. The non-interactive argument uses the encryption scheme as a black box.

Instantiations: discussion. We observe that existing constructions of somewhat homomorphic encryption, such as the ones in [Gen09, vDGHV10], already support zero testing: simply test if the ciphertext is zero in the ring of ciphertexts. More generally, in any encryption scheme where ciphertexts are elements of some ring, and the homomorphic operations on ciphertext identify with the ciphertext-ring operations, every trivial zero is represented by the zero of the ciphertext ring. While these construction satisfy the weak zero test requirement, they do not seem to support the additional properties stated above.

Following the observations in [LTV12, GHV10, HRSV11], any homomorphic encryption scheme that supports homomorphic computations of sufficiently large degree can be generically modified to satisfy both multi-key evaluation for a constant number of keys and correctness for adversarially generated ciphertexts. This transformation, however, may not preserve the weak zero test property. Roughly speaking, the generic transformation is based on the idea of bootstrapping [Gen09], where the evaluated circuit is modified to include the decryption circuit of the scheme itself. Now, even if we evaluate a circuit computing the zero polynomial, the modified circuit, which now runs the scheme’s decryption circuit, will not be identically zero.

We show that ZTHE satisfying both additional properties can be constructed from graded encodings with additional properties described below.

Graded encoding. A graded encoding is an encoding scheme for elements of a ring. We consider a symmetric graded encoding that supports homomorphic computations of bounded degree $\varDelta$. The encoding scheme also features a (strong) zero test that identifies encodings of zero (even non-trivial ones). In Sect. 1.4 we describe the interface of a graded encoding scheme in more detail.

We consider graded encodings that satisfy a simple and natural decisional assumption.

Assumption 1.2

(Informal). Given encoded coefficients $\alpha _0,\dots ,\alpha _\varDelta$ of a random degree $\varDelta$ polynomial, it is hard to distinguish an encoding of a root from an encoding of a random element.

Intuitively, this problem should be hard since testing if the given encoding is a root requires a homomorphic computation of degree $\varDelta +1$.

To reduce the semantic security of the ZTHE to the above assumption on the graded encoding, we need the graded encodings to support a re-randomization operation. Intuitively, re-randomizing an encoding results in a new encoding of the same value that is otherwise independent of the original encodings. As in many other applications of graded encoding (for example [GLSW15]), the re-randomization operation is only needed in the reduction and not in the construction. We note that it is possible to avoid the use of randomization, but this requires making a more complicated and less natural (though still efficiently falsifiable) hardness assumption.

Correctness for adversarially generated encodings. In order to construct a ZTHE scheme with correctness for adversarially generated ciphertexts we need to require that the graded encoding themselves have correctness for adversarially generated ciphertexts. This is a non-standard requirement for graded encoding schemes, and it is not required in other applications such as obfuscation (where all encodings are generated by an honest party).

The correctness requirement for adversarially generated encodings is somewhat stronger than in the context of encryption. We require that it is hard to find a pair of valid encodings such that a homomorphic operation on them results in an invalid encoding. In order to support “noisy” candidates, where such an evaluation error always occurs after a large enough number of homomorphic evaluations, we also consider a relaxed requirement. Intuitively, it should be possible to publicly test that the level of noise in an adversarially generated encoding is low. If we determine that an encoding has low noise, it should support a large number of homomorphic operation without an error.

Theorem 1.3

(Informal). Assuming a graded encoding scheme satisfying Assumption 1.2, there exists a O(1)-key zero-testable somewhat homomorphic encryption scheme. Moreover, if the graded encoding scheme is correct for adversarially generated encodings, then the encryption scheme is correct for adversarially generated ciphertexts.

Instantiations: discussion. The existing constructions of graded encodings [GGH13a, CLT15, GGH15] that support re-randomization do not satisfy our hardness assumption [GGH13a, CHL+15, HJ16]. We don’t know if in existing constructions of graded encodings it is possible to publicly test for low noise level. One potential strategy to implement such a test would be to combine the re-randomization and zero test operations. We note that so-called “clean” graded encoding schemes (see for example [Zim15, LV16]), where every element has a unique encoding, trivially satisfy correctness for adversarially generated encodings, and support re-randomization.

1.3 Non-interactive Arguments from Zero-Testable Homomorphic Encryption

Our construction is based on ideas developed in the context of designated-verifier arguments.

Designated-verifier arguments. Aiello et al. [ABOR00] suggested the following approach to constructing designated verifier arguments: The prover computes a probabilistically checkable proof (PCP) for the statement. The verifier’s message contains PCP queries, encrypted using an FHE scheme, where each query is encrypted under a different key. The prover computes the PCP answers homomorphically, and the verifier decrypts and verifies the answers. The hope was that since a cheating prover couldn’t tailor its answer to one query depending on other queries’s values, the argument would inherit the PCP’s soundness. Dwork et al. [DLN+04, DNR16] showed obstacles to proving this construction’s soundness. Nonetheless, Kalai, Raz and Rothblum [KRR14] proved that when the underlying PCP satisfies a strong notion of soundness called no-signaling soundness, the suggested arguments are in fact sound.

Leaking information on queries: a failed attempt. A naive attempt to turn the above designated-verifier protocol into a publicly verifiable non-interactive argument would be to place the verifier’s encrypted queries in the CRS, and provide some leakage on encrypted queries that allows verifying the evaluated answers, but (somehow) does not compromise the soundness of the protocol. We argue, however, that any such leakage must (inherently) compromise soundness. A cheating prover can begin with an accepting PCP proof, changing it into a rejecting proof one symbol at a time. By observing which of the intermediate proofs makes the verifier reject, the prover can recover the encrypted queries and break soundness.

Our approach: intuition. Our protocol follows the blueprint described above: the CRS contains encrypted queries, and the prover homomorphically evaluates the PCP and sends the evaluated queries as the proof. However, to make the proof publicly verifiable we do not leak any information about the encrypted queries or their answers. The main idea is to encrypt the queries with a ZTHE. By executing a sequence of homomorphic evaluations and zero tests on the evaluated ciphertexts in the proof, the verifier learns information about the PCP proof computed by the prover, which is sufficient to verify its validity.

Next we elaborate on this idea. We start by giving some background on the PCP system we use.

The BFLS PCP. The PCP of Babai et al. [BFLS91] proves that a given computation accepts its input. The tableau of the computation is translated into a multi-variate low-degree polynomial $P_0$ and the PCP proof contains all the evaluations of $P_0$ over some finite field. Testing the validity of the tableau is reduced to testing that $P_0$ is indeed a low-degree polynomial and that it vanishes on all boolean inputs. The proof that $P_0$ vanishes on all boolean inputs is based on the well-known sum-check protocol. The sum-check proof contains auxiliary polynomials $P_1,\dots ,P_m$ and the verifier tests that these polynomials satisfy some local low-degree relations of the form $R(P_i,P_{i+1}) \equiv 0$. These tests are carried out by probing the polynomials on a small number of random inputs and testing that the relations are satisfied.

A sketch of our protocol. As described above, the CRS contains encryptions $c_1,\dots ,c_m$ that specify queries to the PCP. Each triplet $c_j,c_k,c_\ell$ specifies an evaluation point for the polynomials $P_1,\dots ,P_m$. For every such triplet, and for every polynomial $P_i$, the proof contains the homomorphically evaluated answer $d_i = P_i(c_j,c_k,c_\ell )$. To verify the relation $R(P_i,P_{i+1}) \equiv 0$, the verifier homomorphically evaluates $R(d_i,d_{i+1})$ and tests that the evaluation results in a trivial zero. Since the different queries are encrypted under different keys, we use a multi-key homomorphic encryption scheme. While the CRS contains encryptions under $m$ different keys, the verifier only computes homomorphically on three keys at a time, therefore we only need 3-key homomorphism.

The proof strategy. Intuitively, if the prover is cheating and $R(P_i,P_{i+1}) \not \equiv 0$ it follows from sematic security that the verifier’s zero test fails. Alas, this intuition is fundamentally flawed. A cheating prover may not derive its answers by homomorphically evaluating the low degree polynomials $P_1,\dots ,P_m$, or any other polynomial for that matter. Our actual proof strategy is inspired by that of Kalai, Raz and Rothblum [KRR14] and consists of the following steps.

• 1. Since the encryption is semantically secure, the prover’s answers are no-signaling, meaning that the decrypted answer to one query gives no information on the other queries values.

• 2. In the BFLS PCP, it is possible to reconstruct any small subset of entries L of the computation’s tableau based on PCP values in some small set of locations q(L). We show that our proof satisfies the following local soundness guarantee: if the verifier’s encrypted queries include the locations q(L) and if the verifier accepts the prover’s encrypted answers then the reconstructed subset of the tableau is locally consistent. That is, it obeys the computation’s local constrains. To show that this is the case even when the prover sends malformed answers we use the fact that the encryption scheme is correct for adversarially generated ciphertext.

• 3. By the semantic security of encrypted queries, and by the fact that the protocol is publicly verifiable, we deduce that if the verifier accepts the answers to any queries encrypted in the CRS (say the all-0 queries), it would also accept the answers to the to queries q(L), for every subset L.

• 4. It follows that we can turn any convincing prover in our protocol into an algorithm that samples local assignments for any subset L of the computation’s tableau that are guaranteed to be both no-signaling and locally consistent.

• 5. Based on the augmented circuit technique of [KRR14], we show how to use such a local-assignment generator to reconstruct a complete and valid tableau.

We note that our soundness proof is significantly simpler than that of [KRR14]. In particular we only use a striped down version of the BFLS PCP without any low-degree tests, and we do not argue that this PCP has no-signaling soundness. Intuitively, what enables this simplification is that in the publicly-verifiable setting we can move from local consistency for one subset to local consistency on all subsets using semantic security (see Step 3 above) and without using global properties of the PCP.

Proving adaptive soundness presents additional challenges. To argue adaptive soundness, we use ideas inspired by the recent work of Brakerski et al. [BHK16], who constructed an adaptively sound arguments in the designated-verifier setting. Roughly, they show how to reconstruct a tableau from any local-assignment generator that can chose the statement adaptively as a function of the subset L.

On the notion of local-assignment generator. The augmented circuit technique as well as the technique of reconstructing the computation’s tableau by reading subsets that are no-signaling and locally-consistent originates from the analysis of [KRR14]. The notion of local-assignment generator and the generic transformation from a local-assignment generator to global soundness first appeared in an earlier version of this work [PR14]. Since then the local-assignment generator abstraction played a key role in achieving stronger designated-verifier arguments for RAM computations [KP16] and Batch-NP computations [BHK16], as well as in achieving adaptive soundness [BHK16]. In the current version of this work we use the adaptive local-assignment generator of [BHK16].

1.4 Zero-Testable Homomorphic Encryption from Graded Encodings

We start by describing the interface of a graded encoding scheme in more details. The scheme has public parameters that define a ring $R$ and a maximal degree $\varDelta$. The scheme encodes elements in $R$ and supports homomorphic computations up to degree $\varDelta$. Every encoding has a level. Freshly generated encodings are of level 1 and level-$\delta$ encodings are the result of a degree-$\delta$ homomorphic computation. We also refer to the elements of $R$ as level-0 encoding. Following the standard formulation of graded encodings, we do not assume that the ring $R$ is public. Instead, there is a public interface for sampling random level-0 encodings and evaluating the ring operations. We also assume that the public parameters include encodings of the constants 0 and 1 in every level.

The graded encoding supports a (strong) zero test that can publicly identify encodings of zero in any level. It also supports a re-randomization operation that, given an encoding, generates a new random encoding of the same element. For example, re-randomizing an encoding can be used to hide the homomorphic computation that generated it.

The ZTHE scheme. We construct multi-key ZTHE from graded encoding as follows. The scheme’s public parameters are the parameters of a graded encoding scheme with degree bound $\varDelta$. The secret key is a random ring element $t\in R$ and the corresponding public key is a level-1 encoding of $t$.

An encryption $c$ of a message $m\in \{0,1\}$ is given by a random degree-$\varDelta$ univariate polynomial $P$ such that $P(t) = m$. The ciphertext $c$ consists of level-1 encodings of the $\varDelta +1$ coefficients $\alpha _0,\dots ,\alpha _\varDelta$ of $P$. The semantic security of this encryption follows from Assumption 1.2 that states that even given the public key encoding of $t$, the encodings in $c$ are indistinguishable from encodings of random elements, independent of $m$.

Encryption. We need to sample such an encryption using only the public parameters and the public key encoding of $t$. A naive approach would be to sample all the coefficients of $P$ except for the free coefficient $\alpha _0$ randomly and then homomorphically compute an encoding of $\alpha _0$. However, this would result in an encoding in level $\varDelta$ instead of level 1. Instead we can sample all the coefficients of $P$ as linear functions of $t$. We sample random ring elements $r_1,\dots ,r_\varDelta$ and homomorphically compute encodings of the coefficients

$$ \alpha _0 = m- r_1\cdot t,\quad \dots \quad , \alpha _i = r_i - r_{i+1}\cdot t,\quad \dots \quad , \alpha _\varDelta = r_\varDelta . $$

Note that $\alpha _0,\dots ,\alpha _\varDelta$ are indeed random subject to $\sum {\alpha _i\cdot t^i} = m$. Finally, we re-randomize the encoded coefficient to hide the process in which they where sampled (which depends on $m$).

We note that the re-randomization operation is only used during encryption. In our non-interactive argument the ZTHE encryption procedure is only used to generate the CRS and in the security proof. As noted above, we could avoid the use of re-randomization at the cost of making a more complicated assumption on the graded encoding that implies the CPA security of our encryption scheme in the secret key setting.

Same-Key homomorphic evaluation. Let $c_1$ and $c_2$ be ciphertexts encrypting messages $m_1$ and $m_2$ respectively under the same secret key $t$. Let $P_1$ and $P_2$ be the polynomials encoded by $c_1$ and $c_2$, where

$$ P_1(t) = m_1,\quad P_2(t) = m_2. $$

To evaluate a homomorphic operation $\star \in \left\{ +,-,\times \right\}$ we homomorphically compute the encoded coefficients of the polynomial $P_1 \star P_2$. Correctness follows since

$$ (P_1 \star P_2)(t) = P_1(t)\star P_1(t) = m_1\star m_2. $$

For addition and subtraction, the homomorphic computation of the new coefficients is a linear operation (over the input coefficients), and the degree of the resulting polynomial is the maximal degree of the two input polynomials. For multiplication, we homomorphically compute a convolution of the input coefficients, and the degree of the resulting polynomial is the sum of the degrees of the input polynomials. Thus, the evaluation of a degree-$\delta$ homomorphic computation yields coefficients that are encoded in level-$\delta$ of the graded encoding scheme, and the resulting (univariate) polynomial has degree $(\delta \cdot \varDelta )$. It follows that the encryption supports degree-$\varDelta$ homomorphic computations, before the level of encoded coefficient exceeds the degree bound.

Multi-key homomorphic evaluation. To compute a homomorphic operation $\star$ over ciphertexts $c_1,c_2$ encrypted under different secret keys $t_1,t_2$, we homomorphically compute the coefficients of the bivariate polynomial $P(x,y) \equiv P_1(x)\star P_2(y)$, where $P_1$ and $P_2$ are the polynomials encoded by $c_1$ and $c_2$ respectively. In general, a homomorphic computation involving ciphertexts under $d$ different keys will result in a ciphertext encoding a $d$-variate polynomial. Since the number of coefficients grows exponentially with $d$, we only support homomorphic computation involving a constant number of keys.

Decryption. To decrypt a ciphertext $c$, we homomorphically evaluate the polynomial $P$ it encodes on the secret key $t$. Since the secret key is a level-0 encoding, this homomorphic evaluation does not exceed the degree bound $\varDelta$. We then use the graded encoding zero test to compare the evaluated encoding to an encoding of 0 or of 1. If none of the tests succeed decryption fails.

Note that in homomorphic evaluation, the algebraic operation on the plaintexts are evaluated over the ring $R$. However, since our decryption only obtains an encoding of the plaintext, we can only decrypt messages in $\{0,1\}$ (or more generally, messages taken from a small plaintext space). This is analogous to the behaviour of the additively-homomorphic ElGamal encryption and other schemes [BGN05]. Such decryption is sufficient for our application, where we evaluate arithmetic circuits (over $\mathbb {Z}$) whose outputs are expected to be boolean.

Zero Test. A ciphertext $c$ that results from a homomorphic evaluation of a polynomial that is identically zero always encodes a polynomial $P\equiv 0$. We can test this by using the zero test procedure of the graded encoding, testing that all the encoded coefficient of $P$ are zero. It is also the case that a ciphertext that passes the zero test must encode a polynomial $P\equiv 0$ and therefore it must decrypt to zero.

Correctness for adversarially generated ciphertexts. If the graded encoding scheme is correct even on adversarially generated encodings, we inherit this strong correctness guarantee also for the ciphertext. Note, however, that even a ciphertext that consists of valid encodings may encode a polynomial $P$ such that $P(t) \notin \{0,1\}$, and therefore fail to decrypt. To deal with this case, we consider an alternative decryption algorithm that is inefficient and can decrypt any value in $R$. The correctness requirement for adversarially generated ciphertexts is therefore defined with respect to this inefficient decryption procedure. The weaker correctness requirement suffices for proving the computational soundness of the non-interactive argument, even though it considers an inefficient decryption algorithm: once the correctness requirement is guaranteed, the remainder of the soundness proof is information theoretic.

1.5 Organization

The definition of non-interactive arguments and other preliminaries are given in Sect. 2. In Sect. 3 we define the notion of ZTHE and the additional properties we use. Section 4 describes the construction of non-interactive argument from ZTHE. The analysis of the non-interactive argument and the construction of ZTHE from graded encodings appear in the full version of this work.

2 Preliminaries

For a sequence $\mathbf{x }= \left( x_1,\dots ,x_n\right)$, we denote by $\mathbf{x }_{-i}$ the sequence with the i-th elements removed

$$ \mathbf{x }_{-i} = \left( x_1,\dots ,x_{i-1},x_{i+1},x_n\right) . $$

For a pair of sequences $\mathbf{x }= \left( x_1,\dots ,x_n\right)$ and $\mathbf{y }= \left( y_1,\dots ,y_{n'}\right)$ we denote by $\mathbf{x }\,|\,\mathbf{y }$ the concatenated sequence

$$ \mathbf{x }\,|\,\mathbf{y }= \left( x_1,\dots ,x_n,y_1,\dots ,y_{n'}\right) . $$

2.1 Arithmetic Circuits

We consider arithmetic circuits with binary addition, subtraction and multiplication gates. We only allow use of the constants $\{0,1\}$.

Degree. For an arithmetic circuit $C$, the degree (resp. total degree) of $C$ is the individual (resp. total) degree of the formal polynomial computed by $C$. A  degree-1 circuit is said to be multi-linear.

Equivalence. An arithmetic circuit $C$ is said to be identically zero (denoted by $C\equiv 0$) if the formal polynomial computed by $C$ is identically zero over $\mathbb {Z}$. Two arithmetic circuits $C_1,C_2$ are said to be equivalent (denoted by $C_1 \equiv C_2$) if $C_1 - C_2 \equiv 0$.

Computing boolean functions. An arithmetic circuit $C$ is said to compute a boolean function $f$ if $C$ agrees with $f$ when evaluated over $\mathbb {Z}$. That is, if $f$ takes $n$ inputs, then for every $x\in \{0,1\}^n$ we have that $f(x)=C(x)$ when $C$ is evaluated over $\mathbb {Z}$.

Fact 2.1

Let $C_1$ and $C_2$ be arithmetic circuits with $n$ inputs wires computing boolean functions $f_1$ and $f_2$ respectively.

• 1. The circuit $1- C_1$ computes the boolean function $1-f_1$.

• 2. The circuit $C_1\cdot C_2$ computes the boolean function $f_1\cdot f_2$.

• 3. If for every $x\in \{0,1\}^n$, at most one of the values $C_1(x)$ and $C_2(x)$ is non-zero, then the circuit $C_1+C_2$ computes the boolean function $f_1+f_2$.

Circuit restrictions. Let $C$ be an arithmetic circuit with $n$ inputs wires and individual degree $\delta$. For $i \in [n]$ let ${\left. C\right| }_{i,0},\dots ,{\left. C\right| }_{i,\delta }$ be the arithmetic circuits with $n-1$ inputs wires and individual degree $\delta$ such that

$$\begin{aligned} C(x_1,\dots ,x_n) \equiv \sum _{j\in [0,\delta ]}{{\left. C\right| }_{i,j}(x_1,\dots ,x_{i-1},x_{i+1},\dots ,x_n)\cdot x_i^j}. \end{aligned}$$

(1)

For $j>\delta$ let ${\left. C\right| }_{i,j}$ denote the identically 0 circuit.

Fact 2.2

There is an procedure that given an arithmetic circuit $C$ with $n$ inputs wires and individual degree $\delta$ and given an index $i \in [n]$ computes ${\left. C\right| }_{i,0},\dots ,{\left. C\right| }_{i,\delta }$ in time $\mathrm {poly}(|C|, \delta )$.

2.2 Multi-linear Extension

A multi-linear extension of a boolean function $f$ is a multi-linear arithmetic circuit $C$ computing $f$. Next we describe a multi-linear extension circuit of an arbitrary boolean function $f$.

Let $\beta _n$ be the multi-linear arithmetic circuit with $2n$ inputs computing the boolean identity function. That is, for every $\mathbf{x },\mathbf{y }\in \{0,1\}^n$, $\beta _n(\mathbf{x },\mathbf{y }) = 1$ if and only if $\mathbf{x }= \mathbf{y }$. The arithmetic circuit $\beta _n$ is given by the expression

$$\begin{aligned} \beta _n(x_1,\dots ,x_n,y_1,\dots ,y_n) = \prod _{i\in [n]}{x_iy_i + (1-x_i)(1-y_i)}. \end{aligned}$$

(2)

We sometimes omit the subscript $n$ when it is clear from the context.

The multi-linear extension of a boolean function $f$ with $n$ inputs is given by the arithmetic circuit

$$\begin{aligned} C(\mathbf{x }) = \sum _{\mathbf{y }\in \{0,1\}^n}{\beta _n(\mathbf{x },\mathbf{y }) \cdot f(\mathbf{y })}. \end{aligned}$$

(3)

Since for every $\mathbf{x }\in \{0,1\}^n$ there exist only one value of $\mathbf{y }\in \{0,1\}^n$ such that $\beta _n(\mathbf{x },\mathbf{y }) \ne 0$, it follows by Fact 2.1 that $C$ computes the boolean function $f$.

2.3 Publicly-Verifiable Non-interactive Arguments

In this section we define publicly verifiable non-interactive arguments.

Let $\mathcal {U}$ be the universal language such that $(x,\mathsf {T}) \in \mathcal {U}$ for $x= (M,y)$ if and only if the Turing machine $M$ accepts the input $y$ within at most $\mathsf {T}$ steps.

Syntax. A publicly verifiable non-interactive argument scheme for the universal language $\mathcal {U}$ consists of PPT algorithms $(\mathsf {Del.Gen},\mathsf {Del.P},\mathsf {Del.V})$ with the following syntax.

• $\mathsf {Del.Gen}$ : Given the security parameter $1^\lambda$, outputs a common reference string $\mathsf {CRS}$.

• $\mathsf {Del.P}$ : Given the common reference string, a time bound $1^\mathsf {T}$ in unary representation and an instance $x\in \{0,1\}^*$, outputs a proof $\varPi$.

• $\mathsf {Del.V}$ : Given the common reference string, a time bound $\mathsf {T}$ in binary representation, an instance $x\in \{0,1\}^*$ and a proof $\varPi$, outputs a bit.

Definition 2.1

A publicly verifiable non-interactive argument scheme $(\mathsf {Del.Gen},\mathsf {Del.P},\mathsf {Del.V})$ for the universal language $\mathcal {U}$ satisfies the following requirements

• Completeness: For every $\lambda \in {\mathbb {N}}$ and every $(x,\mathsf {T}) \in \mathcal {U}$

  

• Efficiency: In the above (honest) experiment the size of the proof $\varPi$ is $\mathrm {poly}(\lambda ,\log \mathsf {T})$. The running time of $\mathsf {Del.V}$ is $|x|\cdot \mathrm {poly}(|\mathsf {CRS}|,|\varPi |,\log \mathsf {T})$.

• Adaptive Soundness: For every polynomial $\mathsf {T}$ and for every poly-size cheating prover ${\mathsf {P}^*}$ there exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$

  

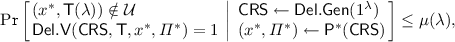
3 Zero-Testable Homomorphic Encryption

In this section we define the notion of zero-testable homomorphic encryption. We also define a multi-key variant [LTV12].

3.1 Homomorphic Encryption

We start by recalling the notion of homomorphic encryption.

Syntax. A homomorphic encryption scheme consists of PPT algorithms

$$ \left( \mathsf {HE.KeyGen},\mathsf {HE.Enc},\mathsf {HE.Dec},\mathsf {HE.Eval}\right) $$

with the following syntax.

• $\mathsf {HE.KeyGen}$ : Given the security parameter $1^\lambda$, outputs a secret key $\mathsf {sk}$, a public key $\mathsf {pk}$ and a description of a ring $R$.

• $\mathsf {HE.Enc}$ : Given the public key $\mathsf {pk}$ and a message $m\in \{0,1\}$, outputs a ciphertext $c$.

• $\mathsf {HE.Dec}$ : Given the secret key $\mathsf {sk}$ and a ciphertext $c$, outputs a ring element $\alpha \in R$ or a special symbol $\bot$.

• $\mathsf {HE.Eval}$ : Given e public key $\mathsf {pk}$, an operation $\star \in \left\{ +,-,\times \right\}$, and a pair of ciphertexts $c_1,c_2$, outputs a ciphertext $c$ or a special symbol $\bot$.

Evaluating circuits. Some formulations of homomorphic encryption only consider an evaluation algorithm for circuits and not individual gates. By explicitly requiring that the evaluation is performed gate by gate, we ensure correctness for a “multi-hop” evaluation [GHV10] where ciphertexts that result from a homomorphic computation support further homomorphic operations.

Homomorphic evaluation of an arithmetic circuit $C$ is implemented by iteratively applying the basic evaluation algorithm $\mathsf {HE.Eval}$ for every gate in $C$. This process is described formally below.

We only consider arithmetic circuits containing constants from $\{0,1\}$, which can be evaluated over any ring. When evaluating a gate that takes a constant $b\in \{0,1\}$ we do not generate a fresh random encryption of $b$. Instead, we assume that the public key includes ciphertexts $\hat{0}$ and $\hat{1}$ of 0 and 1 respectively. This evaluation strategy guarantees that all occurrences of a constant in $C$ are replaced with the same ciphertext. This will be crucial later when we introduce the notion of zero-testable homomorphic encryption.

For an arithmetic circuit $C$, and ciphertexts $\left( c_1,\dots ,c_n\right)$ encrypted under public key $\mathsf {pk}$ we denote by $\left\langle C\left( c_1,\dots ,c_n\right) \right\rangle$ the evaluated ciphertext $c$ computed as follows.

• If $C$ is the constant 0 then $c= \hat{0}$.

• If $C$ is the constant 1 then $c= \hat{1}$.

• If $C$ is the i-th input wire then $c= c_i$.

• If $C$ is of the form $C= C_1 \star C_2$ then

  $$ c= \mathsf {HE.Eval}\left( \mathsf {pk},\star ,\left( \left\langle C_1\left( c_1,\dots ,c_n\right) \right\rangle ,\left\langle C_2\left( c_1,\dots ,c_n\right) \right\rangle \right) \right) . $$

Definition 3.1

(Homomorphic Encryption). Let $\mathcal{C}= \left\{ \mathcal{C}_\lambda \right\} _{\lambda \in {\mathbb {N}}}$ be an ensemble of circuits. A homomorphic encryption scheme $(\mathsf {HE.KeyGen},\mathsf {HE.Enc},$ $\mathsf {HE.Dec},\mathsf {HE.Eval})$ for $\mathcal{C}$ satisfies the following requirements.

• Correctness: For every $\lambda \in {\mathbb {N}}$, every $C\in \mathcal{C}_\lambda$ with $n$ inputs wires, and every $m_1,\dots ,m_n\in \{0,1\}$

  

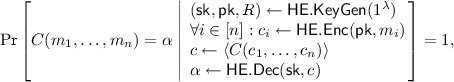
  where $C$ is evaluated over $R$.

• Compactness: There exists a polynomial $L$ such that in the above honest experiment $|c| \le L(\lambda )$ (independently of $|C|$).

• Semantic Security: For every poly-size adversary $\mathsf {Adv}$ there exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$

  

Definition 3.2

(Somewhat Homomorphic Encryption). For $B,\varDelta \in {\mathbb {N}}$ let $\mathcal{C}_{B,\varDelta }$ be the set of arithmetic circuits of size at most $B$ and total degree at most $\varDelta$. Let $B= B(\lambda ),\varDelta = \varDelta (\lambda )$ be polynomially bounded functions. A homomorphic encryption scheme is $(B,\varDelta )$-somewhat homomorphic if it satisfies Definition 3.1 for the circuit ensemble $\left\{ \mathcal{C}_{B(\lambda ),\varDelta (\lambda )}\right\} _{\lambda \in {\mathbb {N}}}$. A scheme is $\varDelta$-somewhat homomorphic if it is $(B,\varDelta )$-somewhat homomorphic for every polynomial $B$.

3.2 Correctness for Adversarial Ciphertexts

We formulate an additional correctness requirement that considers evaluation of adversatively generated ciphertexts. Informally, we require that an efficient adversary cannot generate a pair of ciphertexts that cause en evaluation error. A homomorphic evaluation $\left\langle c_1\star c_2\right\rangle$ is erroneous if the following two experiments have different outputs

• 1. Homomorphically evaluate $\left\langle c_1\star c_2\right\rangle$ and output the decryption of the evaluated ciphertext.

• 2. Decrypt $c_1,c_s$. If one of the ciphertexts fails to decrypt (decryption output $\bot$), then output $\bot$. Otherwise output the evaluation of $\star$ on the decrypted elements.

Many existing homomorphic encryption candidates only support a polynomially bounded number of homomorphic operations before the noise in the ciphertexts becomes too large and causes an evaluation error. Therefore, in such candidates, ciphertexts that cause en evaluation error are easy to generate. To support candidate of this nature we allow the output of the first experiment above to be $\bot$ even if the output of the second experiment is different than $\bot$.

• Correctness for Adversarial Ciphertexts: For every poly-size adversary $\mathsf {Adv}$ there exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$ and for every operation $\star \in \left\{ +,-,\times \right\}$

  

  where in the probability above, if $\alpha _1,\alpha _2\in R$, the expression $\alpha _1 \star \alpha _2$ is evaluated over $R$. If either $\alpha _1 = \bot$ or $\alpha _1 = \bot$ then $\alpha _1 \star \alpha _2 = \bot$.

3.3 Zero Test

A zero test for a homomorphic encryption scheme is a PPT algorithm $\mathsf {HE.ZT}$ that can identify trivial encryptions of 0. These are ciphertexts that result from homomorphically evaluating an arithmetic circuit that is identically zero. We additionally require that the zero test never incorrectly identifies encryptions of non-zero values. This holds even for adversatively generated ciphertexts.

Given the public key $\mathsf {pk}$ and a ciphertext $c$, the zero test $\mathsf {HE.ZT}$ outputs a bit. The zero test satisfies the following requirements.

• Zero-Test Completeness: For every $\lambda \in {\mathbb {N}}$, every $C\in \mathcal{C}_\lambda$ with $n$ inputs wires such that $C$ is identically zero, and every $m_1,\dots ,m_n\in \{0,1\}$

  

• Zero-Test Soundness: For every poly-size adversary $\mathsf {Adv}$ there exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$

  

3.4 Weak Decryption

We define a relaxation of homomorphic encryption where

• The decryption procedure $\mathsf {HE.Dec}$ is not required to be PPT.

• Instead we require that there exists a weak decryption procedure $\mathsf {HE.WeakDec}$ which is PPT but does not decrypt messages outside $\{0,1\}$.

• The weak decryption result should be consistent with the inefficient decryption result even for adversarially generated ciphertexts.

The encryption scheme we construct from graded encodings will only satisfy this relaxation which is sufficient for our application.

Given the secret key $\mathsf {sk}$ and a ciphertext $c$, the weak decryption procedure $\mathsf {HE.WeakDec}$ outputs a message $m\in \{0,1\}$ or a special symbol $\bot$. The weak decryption procedure satisfies the following requirement.

• Weak Decryption: For every poly-size adversary $\mathsf {Adv}$ there exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$

  

  where in the above probability, $\alpha ' = \alpha$ if $\alpha \in \{0,1\}$ and $\alpha '=\bot$ otherwise.

3.5 Multi-key Zero-Testable Homomorphic Encryption

In this section we define a multi-key variant of homomorphic encryption that also satisfies the other requirements defined above. In multi-key homomorphic encryption, introduced by López-Alt et al. [LTV12] homomorphic computation can be executed over ciphertexts encrypted under $d$ different keys. To ensure semantic security, decrypting the result requires all secret keys. Importantly, a system can generate ciphertext under an unbounded number of keys and any $d$ of them can be combined in a homomorphic computation. We assume that the number of different keys $d$ is constant. We also allow for common public parameters used to generate all keys.

Syntax. A $d$-key zero-testable homomorphic encryption scheme consists of PPT algorithms

$$\left( \mathsf {MHE.ParamGen},\mathsf {MHE.KeyGen},\mathsf {MHE.Enc},\mathsf {MHE.WeakDec},\mathsf {MHE.Eval},\mathsf {MHE.ZT}\right) $$

and an unbounded algorithm $\mathsf {MHE.Dec}$ with the following syntax.

• $\mathsf {MHE.ParamGen}$ : Given the security parameter $1^\lambda$, outputs public parameters $\mathsf {pp}$ and a description of a ring $R$.

• $\mathsf {MHE.KeyGen}$ : Given the public parameters $\mathsf {pp}$, outputs a secret key $\mathsf {sk}$ and a public key $\mathsf {pk}$.

• $\mathsf {MHE.Enc}$ : Given public parameters $\mathsf {pp}$, a public key $\mathsf {pk}$ and a message $m\in \{0,1\}$, outputs a ciphertext $c$.

• $\mathsf {MHE.Dec}$ : Given public parameters $\mathsf {pp}$, $d$ secret keys $\mathsf {sk}_1,\dots ,\mathsf {sk}_d$ and a ciphertext $c$, outputs a ring element $\alpha \in R$ or a special symbol $\bot$.

• $\mathsf {MHE.WeakDec}$ : Given public parameters $\mathsf {pp}$, $d$ secret keys $\mathsf {sk}_1,\dots ,\mathsf {sk}_d$ and a ciphertext $c$, outputs a message $m\in \{0,1\}$ or a special symbol $\bot$.

• $\mathsf {MHE.Eval}$ : Given public parameters $\mathsf {pp}$, a pair of public keys $\mathsf {pk}_1,\mathsf {pk}_2$, an operation $\star \in \left\{ +,-,\times \right\}$ and a pair $c_1,c_2$, outputs a ciphertext $c$ or a special symbol $\bot$.

• $\mathsf {MHE.ZT}$ : Given public parameters $\mathsf {pp}$, $d$ public keys $\mathsf {pk}_1,\dots ,\mathsf {pk}_d$ and a ciphertext $c$, outputs a bit.

Remark 3.1

(Superfluous keys). The decryption and zero test algorithms take $d$ keys, even if the input ciphertext results from a computation involving less keys. We assume without loss of generality that adding superfluous keys does not affect the procedures functionality.

Definition 3.3

(Multi-key Zero-Testable Homomorphic Encryption). Let $\mathcal{C}= \left\{ \mathcal{C}_\lambda \right\} _{\lambda \in {\mathbb {N}}}$ be an ensemble of circuits. A $d$-key zero-testable homomorphic encryption scheme

$$ (\mathsf {MHE.ParamGen},\mathsf {MHE.KeyGen},\mathsf {MHE.Enc},\mathsf {MHE.Dec},\mathsf {MHE.WeakDec},$$

$$\mathsf {MHE.Eval},\mathsf {MHE.ZT}) $$

for $\mathcal{C}$ satisfies the following requirements.

• Correctness: There exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$, every $C\in \mathcal{C}_\lambda$ with $n$ inputs wires, every $m_1,\dots ,m_n\in \{0,1\}$ and every indices $j_1,\dots ,j_n\in [d]$

  

  where $C$ is evaluated over $R$.

• Compactness: There exists a polynomial $L$ (that may depend on $d$) such that in the above honest experiment $|c| \le L(\lambda )$ (independently of $|C|$).

• Correctness for Adversarial Ciphertexts: For every poly-size adversary $\mathsf {Adv}$ there exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$ and for every operation $\star \in \left\{ +,-,\times \right\}$

  

  where in the probability above, if $\alpha _1,\alpha _2\in R$, the expression $\alpha _1 \star \alpha _2$ is evaluated over $R$. If either $\alpha _1 = \bot$ or $\alpha _1 = \bot$ then $\alpha _1 \star \alpha _2 = \bot$.

• Zero Test Completeness: There exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$, every $C\in \mathcal{C}_\lambda$ with $n$ inputs wires that is identically zero, every $m_1,\dots ,m_n\in \{0,1\}$, and every indices $j_1,\dots ,j_n\in [d]$

  

• Zero-Test Soundness: For every poly-size adversary $\mathsf {Adv}$ there exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$

  

• Weak Decryption: For every poly-size adversary $\mathsf {Adv}$ there exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$

  

  where in the above probability, $\alpha ' = \alpha$ if $\alpha \in \{0,1\}$ and $\alpha '=\bot$ otherwise.

• Semantic Security: For every poly-size adversary $\mathsf {Adv}$ there exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$

  

4 A Non-interactive Argument

This section describes our publicly-verifiable non-interactive arguments. We start with an overview of the construction.

4.1 Overview

We construct a non-interactive argument system for the universal language $\mathcal {U}$. Given an instance $x= (M,y) \in \{0,1\}^n$ and a time bound $\mathsf {T}$ the verifier wants to ascertain that $(x,\mathsf {T}) \in \mathcal {U}$, that is, that the Turing machine $M$ accepts the input $y$ within $\mathsf {T}$ steps. The protocol should be adaptively sound: even an adaptive cheating prover, who first sees the CRS and then picks an instance $(x,\mathsf {T}) \notin \mathcal {U}$ adaptively, should not be able to generate am accepting proof.

In the protocol, the prover and verifier translate the instance $(x,\mathsf {T})$ into a 3CNF formula $\varphi$ over $\mathrm {poly}(n,\mathsf {T})$ variables, which is satisfiable if and only if $(x,\mathsf {T}) \in \mathcal {U}$. $\varphi$ has a “short” implicit description via an arithmetic circuit $\varPhi$ of small size and degree that, given the labels of three literals, determines whether their disjunction is a clause in $\varphi$. Note that given $\varphi$, the formula $\varPhi$ and the original instance $(x,\mathsf {T})$ can be efficiently reconstructed. More over, if $(x,\mathsf {T})\in \mathcal {U}$, a satisfying assignment for $\varphi$ can be efficiently computed. With this formula in mind, the argument system has two main ingredients:

Ingredient 1: the core protocol. The first ingredient is a publicly-verifiable non-interactive “core protocol”. The prover in the core protocol is presented with a CRS, a circuit $\varPhi$ describing a 3CNF $\varphi$ (as above), and a satisfying assignment $\sigma$ to $\varphi$. It generates a proof $\varPi$ that will convince the verifier that the 3CNF described by $\varPhi$ is satisfiable.

The core protocol has a relaxed soundness property: it is not guaranteed that an adaptive cheating prover ${\mathsf {P}^*}$ cannot generate a circuit $\varPhi$ describing an unsatisfiable 3CNF together with a proof $\varPi ^*$ that makes the verifier accept. Rather, the soundness guarantee is that any adaptive cheating prover for the core protocol can be used to derive a no-signalling adaptive local assignment generator $\mathsf {Assign}$. The adaptive assignment generator $\mathsf {Assign}$ is a randomized algorithm that gets as input a small set $S$ of variables, and outputs a pair $(\varPhi ,\sigma )$, where $\sigma : S\rightarrow \{0,1\}$ is a local assignment to the variables in $S$. The algorithm $\mathsf {Assign}$ satisfies the following properties:

• 1. No-signalling. Given a set $S$ of variables, $\mathsf {Assign}$ outputs a pair $(\varPhi ,\sigma )$. Intuitively, the joint distribution of $\varPhi$ and the values assigned to any subset of the variables in $S$ are independent of the other variables in $S$. More precisely, for every two sets of variables $S_1, S_2$ both containing a subset $T$, the distributions obtained by executing $\mathsf {Assign}$ on $S_1$ and on $S_2$ to obtain $(\varPhi ,\sigma )$, and then restricting $\sigma$ to the variables in $T$, are computationally indistinguishable.

• 2. Adaptive local soundness. We consider an execution of the cheating prover ${\mathsf {P}^*}$ in the core protocol that generates a pair $(\varPhi ,\varPi ^*)$. Additively, for every small subset $S$ of variables, we consider an execution of $\mathsf {Assign}$ on the set $S$ that generates a pair $(\varPhi ',\sigma ')$. We require that $\varPhi '$ is indistinguishable from $\varPhi$, and moreover, if the proof $\varPi ^*$ is accepting, then the assignment $\sigma '$ is locally-consistent with the 3CNF $\varphi '$ described by $\varPhi '$. We say that the assignment $\sigma ':S\rightarrow \{0,1\}$ is locally-consistent with $\varphi '$ if $\sigma '$ satisfies all clauses of $\varphi '$ that are comprised entirely of variables in $S$.

  In particular, we have that if ${\mathsf {P}^*}$ has a noticeable probability of generating a pair $(\varPhi ,\varPi ^*)$ such that $\varPhi$ describes an unsatisfiable 3CNF, but the verifier accepts $\varPi ^*$. Then for every small subset $S$ of variables, running $\mathsf {Assign}$ on the set $S$ has a noticeable probability of producing a pair $(\varPhi ',\sigma ')$ where $\varPhi '$ describes an unsatisfiable 3CNF $\varphi '$, but $\sigma$ is a locally-consistent with $\varPhi '$.

Some remarks are in order. First, we note that the relaxed soundness property has a flavor of “knowledge extraction”: while we do not claim that any cheating prover for the core protocol must “know” a satisfying assignment to the 3CNF (indeed, the 3CNF might not be satisfiable, in which case no such assignment exists), a cheating prover can be used to generate “locally consistent” assignments on any set of variables. This extraction property is slightly more involved because it is concerned with adaptive cheating provers: the 3CNF is not fixed in advance. Rather, an adaptive cheating prover for the core protocol can be used to adaptively generate, given a set $S$ of variables, an unsatisfiable 3CNF together with a locally-consistent assignment for those variables in $S$. The distribution of 3CNFs generated by the core protocol cheating prover (together with the bit indicating whether the verifier accepts the jointly-generated proof) is computationally indistinguishable from the distribution of 3CNFs generated by the assignment generator (together with the bit indicating whether the jointly-generated assignment is locally satisfiable). We note further that the no-signalling property implies that for any two sets $S$ and $S'$, the distributions of the circuit $\varPhi$ generated by $\mathsf {Assign}$ are themselves computationally indistinguishable.

While the core protocol’s soundness guarantee is robust to adaptive provers, it is weak in the sense that it only guarantees local consistency of the assignment generator. Even for a fixed 3CNF (let alone for an adaptively-generated one) the existence of no-signalling locally-consistent assignments does not imply that the 3CNF is satisfiable! As in prior works, we provide a “circuit-augmentation” procedure that encodes a Turing Machine computation as a 3CNF with a particular structure. The existence of a (no-signalling) locally-consistent assignment generator for the augmented 3CNF guarantees that the Turing Machine accepts its input. Here too, we need to take care to handle adaptive adversaries. This is the second main ingredient of our delegation protocol.

Ingredient 2: adaptive augmented circuit. To build an adaptively-sound delegation protocol we need an adaptive variant of the augmented circuit construction from [KRR14]. We describe this as a circuit-augmentation algorithm that transforms an instance $(x,\mathsf {T})$ for $\mathcal {U}$ into an arithmetic circuit $\varPhi$ of small size and degree, which describes a 3CNF $\varphi$. The 3CNF $\varphi$ should be satisfiable if and only if $(x,\mathsf {T}) \in \mathcal {U}$. This property alone, of course, is not sufficient, since the core protocol does not prove the 3CNF’s global satisfiability. Prior work showed a transformation where if $(x,\mathsf {T}) \notin \mathcal {U}$, then it is not possible to generate even locally-consistent assignments in a no-signalling manner. Since we want an adaptively-sound delegation protocol, we need an even stronger property: let $\mathsf {Assign}$ be a no-signalling adaptive assignment generator as above. We assume that $\mathsf {Assign}$ generates the circuit $\varPhi$ by applying the adaptive circuit-augmentation procedure to an instance $(x,\mathsf {T})$. Then for some small set $S^*$ of variables the probability that $(x,\mathsf {T}) \notin \mathcal {U}$ but $\mathsf {Assign}$ generates a locally-consistent assignment for $S^*$ is negligible. The transformation and its proof are based on [KRR14, PR14, BHK16].

There is a (slight) gap between the soundness we consider in the augmented-circuit transformation and in the core protocol: the core protocol is simply concerned with 3CNFs described by small circuits. The augmented-circuit transformation, on the other hand, considers (and relies on) the procedure used to derive these 3CNFs from a computation described by a Turing Machine. This gap makes the presentation of the core protocol considerably simpler and more modular (in particular, there is no need to consider Turing Machines in the core protocol). We bridge the gap by noting that the augmentation procedure $\mathsf {Aug}$ is easy to invert: given a circuit $\varPhi$, it is easy to recover the instance $(x,\mathsf {T})$ from which it was derived (or to output $\perp$ if $\varPhi$ is not an output of $\mathsf {Aug}$). This allows us to argue that for two computationally indistinguishable distributions on $\varPhi$, if the first distribution is over outputs of $\mathsf {Aug}$, then the second must be over such outputs too (except with negligible probability). Moreover, given a circuit $\varPhi$ produced by $\mathsf {Aug}$, we can determine whether it describes a satisfiable 3CNF by recovering the original instance for $\mathcal {U}$ and testing (in polynomial time) whether the Turing Machine accepts or rejects.

Putting it together. To derive a delegation protocol, we use the core protocol’s CRS. Given an instance $(x,\mathsf {T})$, the prover and verifier both use the augmented-circuit transformation to derive $\varPhi$ and execute the core protocol on $\varPhi$. A prover ${\mathsf {P}^*}$ that cheats with noticeable probability can be used to derive a no-signalling adaptive local assignment generator $\mathsf {Assign}^*$. By the core protocol’s soundness we conclude that for every set $S$ of variables, with noticeable probability $\mathsf {Assign}^*$ generates pairs $(\varPhi ,\sigma )$ where $\varPhi$ describes an unsatisfiable 3CNF, but $\sigma$ is locally consistent. Moreover, $\varPhi$ is derived by running the augmented circuit construction on an instance $(x,\mathsf {T}) \notin \mathcal {U}$ (this is true for the execution of the core protocol, by computational indistinguishability it holds also for the outputs of $\mathsf {Assign}^*$). However, the the augmented circuit construction guarantees that no such assignment generator exists, leading to a contradiction.

Organization. We define adaptive no-signalling local assignment generators in Sect. 4.2. The core protocol is given in Sect. 4.3. The properties of the augmented-circuit transformation are discussed in Sect. 4.4. The analysis of the core protocol, the augmented-circuit transformation, and the full delegation protocol appear in the full version of this work.

4.2 Adaptive No-Signaling Local-Assignment Generator

Before stating the properties of the core protocol, we introduce some notation and formalize the notion of an adaptive no-signaling local-assignment generator.

Succinct formula representation ${\mathcal {I}_\varphi }$ . Let $\varphi$ be a 3CNF boolean formula with variables $\alpha _1,\dots ,\alpha _B$. Let $B= 2^m$ and identify the indices in $[B]$ with strings in $\{0,1\}^m$. We define a boolean indicator function ${\mathcal {I}_\varphi }:\{0,1\}^{3m+3} \rightarrow \{0,1\}$ of $\varphi$ as follows. For every indices $\mathbf u _1,\mathbf u _2,\mathbf u _3 \in \{0,1\}^m$ and for every bits $b_1,b_2,b_3 \in \{0,1\}^3$, we have that

$$ {\mathcal {I}_\varphi }(\mathbf u _1,\mathbf u _2,\mathbf u _3,b_1,b_2,b_3)=1, $$

if and only if $\varphi$ contains the clause:

$$ (\alpha _\mathbf{u _1} = b_1)\vee (\alpha _\mathbf{u _2} = b_2)\vee (\alpha _\mathbf{u _3} = b_3). $$

The locally consistency verifier $\mathsf {V}_{\mathsf {local}}$ . We denote by $\mathsf {V}_{\mathsf {local}}$ the verification algorithm for local assignments to $\varphi$. The algorithm is given as input

• An arithmetic circuit $\varPhi$ computing a boolean function with $3m+ 3$ inputs (we think of $\varPhi$ as computing the indicator function ${\mathcal {I}_\varphi }$ for some formula $\varphi$).

• A partial assignments $\sigma :S\rightarrow \{0,1\}$ for a set $S\subseteq \{0,1\}^m$.

$\mathsf {V}_{\mathsf {local}}(\varPhi ,\sigma )$ accepts if an only if the assignment $\sigma$ is locally consistent with the formula described by $\varPhi$. That is, for every $\mathbf u _1,\mathbf u _2,\mathbf u _3 \in S$ and every $b_1,b_2,b_3 \in \{0,1\}$

$$ \varPhi (\mathbf u _1,\mathbf u _2,\mathbf u _3,b_1,b_2,b_3)=1 \quad \Rightarrow \quad (\sigma (\mathbf u _1) = b_1)\vee (\sigma (\mathbf u _2) = b_2)\vee (\sigma (\mathbf u _3) = b_3). $$

Adaptive local-assignment generator. Let $Q= Q(\lambda ),B= B(\lambda )$ be functions and let $B= 2^m$. An adaptive $Q$-local-assignment generator $\mathsf {Assign}$ for $B$-variate formulas is a probabilistic algorithm with the following syntax: given the the security parameter $1^\lambda$ and a set of indices $S\subseteq \{0,1\}^m$ of size at most $Q$, $\mathsf {Assign}$ outputs

• An arithmetic circuit $\varPhi$ computing a boolean function with $3m+ 3$ inputs.

• A partial assignment $\sigma :S\rightarrow \{0,1\}$.

We define a no-signaling adaptive local-assignment generator

Definition 4.1

(No-Signaling Adaptive Local-Assignment Generator). A $Q$-local-assignment generator $\mathsf {Assign}$ for $B=2^{m}$-variate formulas is (computationally) no-signalling if for every polynomial-size distinguisher $D$ there exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$ and every subsets $S\subseteq S' \subseteq \{0,1\}^m$ of size at most $Q$

$$ \left| \mathop {\text {Pr}}\limits _{\left( \varPhi ,\sigma \right) \leftarrow \mathsf {Assign}(1^\lambda ,S)}\left[ D(\varPhi ,\sigma (S))=1\right] - \mathop {\text {Pr}}\limits _{\left( \varPhi ,\sigma '\right) \leftarrow \mathsf {Assign}(1^\lambda ,S')}\left[ D(\varPhi ,\sigma '(S))=1\right] \right| $$

$$\le \mu (\lambda ). $$

4.3 The Core Protocol

In this section we describe the syntax and the properties of the core delegation protocol. The protocol itself is given in Sect. 4.3.

Syntax. Let $\varDelta = \varDelta (\lambda )$ be a polynomially bounded function. The core protocol with degree bound $\varDelta$ consists of PPT algorithms $(\mathsf {Core.Gen},\mathsf {Core.P},\mathsf {Core.V})$ with the following syntax. Let $\varphi$ be a $B$-variate 3CNF boolean formula where $B= 2^m$ and let $\varPhi$ be an arithmetic circuit of total degree $\delta \le \varDelta$ computing the function ${\mathcal {I}_\varphi }$.

• $\mathsf {Core.Gen}$ : Given the security parameter $1^\lambda$ and a locality parameter $1^Q$ outputs a common reference string $\mathsf {CRS}$.

• $\mathsf {Core.P}$ : Given the common reference string $\mathsf {CRS}$, the circuit $\varPhi$ and an assignment $\sigma :\{0,1\}^m\rightarrow \{0,1\}$, outputs a proof $\varPi$.

• $\mathsf {Core.V}$ : Given the common reference string $\mathsf {CRS}$, the circuit $\varPhi$ and the proof $\varPi$ outputs a bit.

The protocol satisfies the following requirements.

Completeness. For every security parameter $\lambda \in {\mathbb {N}}$, every 3CNF boolean formula $\varphi$ with $B$ variables, every satisfying assignment $\sigma$, every arithmetic circuit $\varPhi$ of individual degree $\delta \le \varDelta$ computing the function ${\mathcal {I}_\varphi }$, and every locality parameter $Q\in [B]$

Efficiency. There exists a polynomial $L$ such that in the above honest experiment $|\varPi | \le L(\lambda )\cdot Q\cdot \delta$ where $\delta$ is the individual degree of the circuit $\varPhi$. Additionally the verifier’s running time is bounded by $L(|\mathsf {CRS}|)\cdot (|\varPhi |+ |\varPi |)$.

No-Signaling adaptive local soundness. For every polynomially bounded functions $Q= Q(\lambda ),B= B(\lambda )$ there exists an algorithm $\mathsf {Assign}$ such that for every poly-size cheating prover ${\mathsf {P}^*}$ the following holds

• $\mathsf {Assign}^{\mathsf {P}^*}$ is a no-signaling adaptive $Q$-local-assignment generator for $B$-variate formulas.

• For every polynomial-size distinguisher $D$ there exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$, letting $B= 2^m$, for every set of indices $S\subseteq \{0,1\}^m$ of size at most $Q$

  

Construction. Let $\varDelta = \varDelta (\lambda )$ be the function bounding the total degree of the circuit $\varPhi$. The core protocol makes use of a 3-key zero-testable $2\varDelta$-somewhat homomorphic encryption scheme

$$ (\mathsf {MHE.ParamGen},\mathsf {MHE.KeyGen},\mathsf {MHE.Enc},\mathsf {MHE.Dec},\mathsf {MHE.WeakDec},$$

$$\mathsf {MHE.Eval},\mathsf {MHE.ZT}). $$

The CRS generator. The CRS generation algorithm $\mathsf {Core.Gen}$ is given as input the security parameter $1^\lambda$ and a locality parameter $1^Q$. It outputs a common reference string $\mathsf {CRS}$ as follows.

• 1. Sample public parameters for the encryption scheme

  $$ (\mathsf {pp},R) \leftarrow \mathsf {MHE.ParamGen}(1^\lambda ). $$

• 2. For every $q\in [Q]$, generate a key pair

  $$ (\mathsf {sk}^q,\mathsf {pk}^q) \leftarrow \mathsf {MHE.KeyGen}(\mathsf {pp}), $$

  and $\lambda$ encryptions of 0

  $$ \left\{ c^q_i \leftarrow \mathsf {MHE.Enc}(\mathsf {pp},\mathsf {pk}^q,0)\right\} _{i \in [\lambda ]}. $$

• 3. Output a reference string containing the public parameters and all the public keys and ciphers

  $$ \mathsf {CRS}= \left( \mathsf {pp}, \left\{ \mathsf {pk}^q, (c^q_1,\dots ,c^q_\lambda )\right\} _{q\in [Q]}\right) . $$

The prover. The prover algorithm $\mathsf {Core.P}$ is given as input

• The common reference string

  $$ \mathsf {CRS}= \left( \mathsf {pp}, \left\{ \mathsf {pk}^q, (c^q_1,\dots ,c^q_\lambda )\right\} _{q\in [Q]}\right) . $$

• An (individual) degree $\delta$ arithmetic circuit $\varPhi$ computing a boolean function with $3m+ 3$ inputs.

• An assignment $\sigma :\{0,1\}^m\rightarrow \{0,1\}$.

We start by introducing some notation.

• 1. For every query $q\in [Q]$, let $\mathbf c ^q= \left( c^q_1,\dots ,c^q_m\right)$. We refer to the ciphertext vector $\mathbf c ^q$ as an encryption of the $q$-th CRS index (in an honestly generated CRS the index value is always $0^m$).

• 2. Let $\varSigma$ be a multi-linear extension of $\sigma$ (See Sect. 2.2).

• 3. For every triplet of bits $\mathbf b = (b_1,b_2,b_3) \in \{0,1\}^3$ let ${P}^\mathbf{b }_{0}$ be the degree $\delta +1$ arithmetic circuit taking $3m$ inputs

  $$\begin{aligned} P^\mathbf{b }_{0}(\mathbf{x }_{1},\mathbf{x }_{2},\mathbf{x }_{3}) = \varPhi (\mathbf{x }_{1},\mathbf{x }_{2},\mathbf{x }_{3},\mathbf b )\cdot \prod _{k \in [3]}\left( 1- \beta (b_k,\varSigma (\mathbf{x }_k)) \right) . \end{aligned}$$

  (4)

  (See Sect. 2.2 for the definition of the circuit $\beta$.)

• 4. For every $i \in [3m]$, let ${P}^\mathbf{b }_{i}$ be the linearization of the first i variables of the circuit ${P}^\mathbf{b }_{0}$. That is, ${P}^\mathbf{b }_{i}$ is the following arithmetic circuit taking $3m$ inputs which is multilinear in its first i variables, and of degree at most $\delta +1$ in its other variables.

  $$\begin{aligned} {P}^\mathbf{b }_{i}(x_1,\dots ,x_{3m}) = \sum _{y_1,\dots y_i \in \{0,1\}}{\beta (y_1,\dots y_i,x_1,\dots x_i)\cdot {P}^\mathbf{b }_{0}(y_1,\dots ,y_i,x_{i+1},\dots ,x_{3m})}. \end{aligned}$$

  (5)

$\mathsf {Core.P}$ outputs a proof $\varPi$ as follows.

• 1. For every $q\in [Q]$ obtain an encryption of the assignment $\varSigma$ evaluated on the $q$-th CRS index. That is, homomorphically obtain the ciphertext $d^q= \left\langle \varSigma \left( \mathbf c ^q\right) \right\rangle$.

• 2. For every triplet of bits $\mathbf b \in \{0,1\}^3$, triplet of queries $\mathbf q = \left( q_1,q_2,q_3\right) \in [Q]^3$, and $i \in [3m]$ obtain the encrypted coefficients of the circuit ${P}^\mathbf{b }_{i-1}$ evaluated on the CRS indices $\mathbf q$ and restricted to its i-th input variable (see Sect. 2.1). Since the individual degree of ${P}^\mathbf{b }_{i-1}$ is at most $\delta + 1$, the restricted polynomial will have at most $\delta + 2$ coefficients. That is, homomorphically obtain the sequence of $\delta + 2$ ciphertexts $\mathbf e ^\mathbf{q ,\mathbf b }_{i-1}$

  $$ \mathbf e ^\mathbf{q ,\mathbf b }_{i-1} = \left( \left\langle {\left. {P}^\mathbf{b }_{i-1}\right| }_{i,j}\left( \left( \mathbf c ^{q_1}\,|\,\mathbf c ^{q_2}\,|\,\mathbf c ^{q_3}\right) _{-i}\right) \right\rangle \right) _{j\in [0,\delta +1]}. $$

• 3. Output a proof $\varPi$ that contains all the ciphertexts

  $$ \varPi = \left( \left\{ d^q\right\} _{q\in [Q]},\quad \left\{ \mathbf e ^\mathbf{q ,\mathbf b }_{i-1}\right\} _\mathbf{b \in \{0,1\}^3, \mathbf q \in [Q]^3, i \in [3m]}\right) . $$

The verifier. The verifier algorithm $\mathsf {Core.V}$ is given as input

• The common reference string

  $$ \mathsf {CRS}= \left( \mathsf {pp}, \left\{ \mathsf {pk}^q, (c^q_1,\dots ,c^q_\lambda )\right\} _{q\in [Q]}\right) . $$

• A degree $\delta$ arithmetic circuit $\varPhi$ computing a boolean function with $3m+ 3$ inputs.

• An proof

  $$ \varPi = \left( \left\{ d^q\right\} _{q\in [Q]},\quad \left\{ \mathbf e ^\mathbf{q ,\mathbf b }_{i-1}\right\} _\mathbf{b \in \{0,1\}^3, \mathbf q \in [Q]^3, i \in [3m]}\right) . $$

$\mathsf {Core.V}$ performs the following tests for every triplet of bits $\mathbf b = (b_1,b_2,b_3)\in \{0,1\}^3$ and triplet of queries $\mathbf q = \left( q_1,q_2,q_3\right) \in [Q]^3$. $\mathsf {Core.V}$ accepts only if all tests pass.

First, $\mathsf {Core.V}$ homomorphically evaluates the following ciphertexts

• Let ${{\tilde{P}}}^\mathbf{b }$ be the following arithmetic circuit taking $3m+ 3$ inputs

  $$\begin{aligned} {{\tilde{P}}}^\mathbf{b }(\mathbf{x }_1,\mathbf{x }_2,\mathbf{x }_3, y_1, y_3, y_3) = \varPhi (\mathbf{x }_1,\mathbf{x }_2,\mathbf{x }_3,\mathbf b )\cdot \prod _{k \in [3]}\left( {1- \beta (b_k,y_k)}\right) . \end{aligned}$$

  (6)

  Evaluate the ciphertext

  $$ f'_0 = \left\langle {{\tilde{P}}}^\mathbf{b }\left( \mathbf c ^{q_1},\mathbf c ^{q_2},\mathbf c ^{q_3},d^{q_1},d^{q_2},d^{q_3}\right) \right\rangle . $$

• Let $F$ be the following arithmetic circuit taking $\delta + 3$ inputs

  $$\begin{aligned} F(x,y_0,\dots ,y_{\delta +1}) = \sum _{j\in [0,\delta +1]}{y_{j}\cdot x^j}. \end{aligned}$$

  (7)

  For $i \in [3m]$, evaluate the ciphertext $f_{i-1}$ that encrypts the evaluation of the univariate polynomial with encrypted coefficient $\mathbf e ^\mathbf{q ,\mathbf b }_{i-1}$ on the i-th input bit of the concatenated CRS indices $\mathbf q$. Recall that $\mathbf e ^\mathbf{q ,\mathbf b }_{i-1}$ are supposedly the encrypted coefficients of the circuit ${P}^\mathbf{b }_{i-1}$ evaluated on the CRS indices $\mathbf q$ and restricted to its i-th input variable. Therefore, $f_{i-1}$ is suppose to encrypt the evaluation of ${P}^\mathbf{b }_{i-1}$ on the CRS indices $\mathbf q$.

  $$ f_{i-1} = \left\langle F\left( \left( \mathbf c ^{q_1}\,|\,\mathbf c ^{q_2}\,|\,\mathbf c ^{q_3}\right) _i , \mathbf e ^\mathbf{q ,\mathbf b }_{i-1}\right) \right\rangle . $$

• Let $F'$ be the following arithmetic circuit taking $\delta + 3$ inputs

  $$ F'(x,y_0,\dots ,y_{\delta +1}) = \sum _{z\in \{0,1\}}{\beta (z,x)\cdot F(z,y_0,\dots ,y_{\delta +1})}. $$

  For $i \in [3m]$, evaluate the ciphertext $f'_{i}$ that encrypts the linearization of the univariate polynomial with encrypted coefficient $\mathbf e ^\mathbf{q ,\mathbf b }_{i-1}$ evaluated on the on the i-th input bit of the concatenated CRS indices $\mathbf q$. Therefore, $f_{i-1}$ is suppose to encrypt the evaluation of the circuit ${P}^\mathbf{b }_{i-1}$ with its i-th variable linearized on the CRS indices $\mathbf q$.

  $$ f'_{i} = \left\langle F'\left( \left( \mathbf c ^{q_1}\,|\,\mathbf c ^{q_2}\,|\,\mathbf c ^{q_3}\right) _i , \mathbf e ^\mathbf{q ,\mathbf b }_{i-1}\right) \right\rangle . $$

• Let $f_{3m} = \hat{0}$.

  For every $i \in [0,3m]$, $\mathsf {Core.V}$ tests that

  $$ \mathsf {MHE.ZT}\left( \mathsf {pp},\left( \mathsf {pk}^{q_1},\mathsf {pk}^{q_2},\mathsf {pk}^{q_3}\right) ,\left\langle f_{i} - f'_{i}\right\rangle \right) = 1. $$

4.4 The Augmented Circuit

Syntax. Let $\mathcal {U}$ be the universal language (see Sect. 2.3). The augmented-circuit transformation consists of deterministic polynomial time algorithms $(\mathsf {Aug},\mathsf {Aug}^{-1},\mathsf {Trans})$ with the following syntax.

• $\mathsf {Aug}$ : the circuit-augmentation procedure takes as input an instance $x= (M,y)$ and a time bound $\mathsf {T}$ for $\mathcal {U}$. It outputs an arithmetic circuit $\varPhi$ computing the indicator function ${\mathcal {I}_\varphi }$ of the “augmented formula” $\varphi$ (see Sect. 4.2)). We say that $\varPhi$ represents $\varphi$.

• $\mathsf {Aug}^{-1}$ : the inversion procedure takes as input an arithmetic circuit $\varPhi$. It either outputs $(x,\mathsf {T})$ or fails and outputs $\bot$.

• $\mathsf {Trans}$ : the assignment generation procedure takes as input an instance $x$ and a time bound $\mathsf {T}$ for $\mathcal {U}$. It outputs an assignment $\sigma$ for $\varphi$.

These procedures satisfy the following properties:

Efficiency. For $x\in \{0,1\}^n$

• $\mathsf {Aug}(x,\mathsf {T})$ runs in time $n\cdot \mathrm {polylog}(\mathsf {T})$ and outputs an arithmetic circuit $\varPhi$ such that

  • $\varPhi$ is of size $n\cdot \mathrm {polylog}(\mathsf {T})$.

  • $\varPhi$ is of total degree $\delta = \delta (n,\mathsf {T}) = \mathrm {polylog}(n,\mathsf {T})$.

  • $\varPhi$ represents a formula $\varphi$ on $B= B(n,\mathsf {T})=\mathrm {poly}(n,\mathsf {T})$ variables.

• $\mathsf {Aug}(x,\mathsf {T})$ and $\mathsf {Aug}^{-1}(\varPhi )$ run in time $n\cdot \mathrm {polylog}(\mathsf {T})$.

• $\mathsf {Trans}(x,\mathsf {T})$ runs in time $\mathrm {poly}(n,\mathsf {T})$.

Inversion. For every $(x,\mathsf {T}) \in \{0,1\}^*$

$$ \mathsf {Aug}^{-1}(\mathsf {Aug}(x,\mathsf {T}))=(x,\mathsf {T}). $$

Completeness. For every $(x,\mathsf {T})\in \mathcal {U}$, $\mathsf {Trans}(x,\mathsf {T})$ outputs a satisfying assignment $\sigma$ for the formula $\varphi$ represented by the output of $\mathsf {Aug}(x,\mathsf {T})$.

Soundness. At a high level, the soundness guarantees that there does not exist an adaptive no-signalling local-assignment generator (see Sect. 4.2) that for every small set of indices $S$ generates a circuit $\varPhi = \mathsf {Aug}(x,\mathsf {T})$, such that $(x,\mathsf {T})\notin \mathcal {U}$, together with partial assignment $\sigma :S\rightarrow \{0,1\}$ that is locally consistent with the formula represented by $\varPhi$.

Lemma 4.1

(Augmented Circuit Soundness). There exists a function $Q=\mathrm {polylog}(\lambda )$ such that for every polynomially bounded function $B= B(\lambda )$, and every polynomial-time no-signaling $Q$-local-assignment generator $\mathsf {Assign}$ for $B$-variate formulas there exists a negligible function $\mu$ such that for every $\lambda \in {\mathbb {N}}$, letting $B= 2^m$, there exists a set $S^* \subseteq \{0,1\}^m$ of size at most $Q$ such that