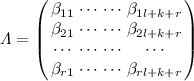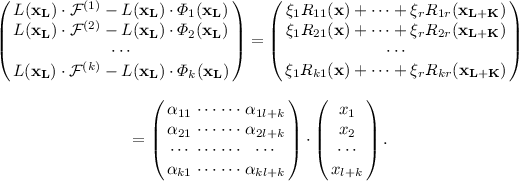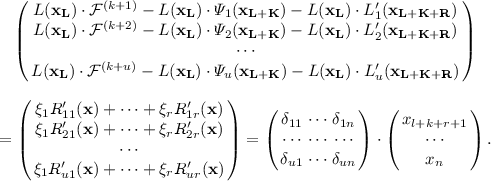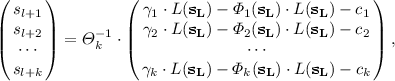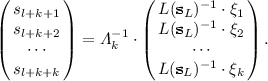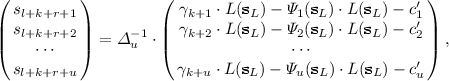1 Introduction

Online banking, e-commerce, mobile communication, and cloud computing depend fundamentally on the security of the underlying cryptographic algorithms. Public-key cryptography (PKC) is particularly crucial since they provide digital signatures and establish secure communication without requiring in-person meetings. In 1996, Shor [49] proposed a quantum algorithm that solves the integer factorization problem and the discrete logarithm problem in finite fields and on elliptic curves in polynomial time. Thus, the existence of a sufficiently large quantum computer would be a real-world threat to break RSA, Diffie-Hellman key exchange, DSA and ECDSA the most widely used PKC in practice. There are four well-known classes of cryptographic primitives that are believed to remain secure in the presence of a quantum computer: code-based cryptography (McEliece encryption [37]), lattice-based cryptography (NTRU [30]), hash-based cryptography (Merkle’s hash-tree signatures [38]), and multivariate quadratic (MQ) cryptography (HFEv- [40], UOV [33]). These cryptographic primitives have been resist classical and quantum cryptanalysis which has inspired widespread confidence in their suitability as a post-quantum primitive.

MQ-PKC is based on the hardness of solving large systems of multivariate quadratic equations, called MQ-problem which is known to be NP-complete. To construct MQ-PKC, it needs a way to hide a trapdoor. In MQ-PKC, a public key is a system of multivariate quadratic polynomials and a trapdoor is hidden in secret affine layers using the ASA (affine-substitution-affine) structure. A long-standing challenge is to design PKC based on symmetric cipher components which are similar to those used in mainstream block ciphers such as AES. Solving this appealing but difficult challenge would not only increase the diversity in PKC, but might also help reducing the considerable performance gap between PKC and symmetric cryptography. One of the directions was to design public-key schemes from symmetric components. A typical symmetric cipher is built from layers of affine transformations (A) and S-boxes (S). This has been the mainstream of MQ-PKC. The security of the ASA structure relies on the hardness of the isomorphism-of-polynomials (IP) problem [40].

Several new ideas to build MQ-schemes from symmetric cipher components were recently introduced by Biryukov et al. [10] at Asiacrypt 2014. They used the so-called ASASA structure: combining two quadratic mappings S by interleaving random affine layers A. With quadratic S layers, the overall scheme has degree 4, so the polynomial description provided by the public key remains of reasonable size. This is very similar to the 2R scheme by Patarin and Goubin [43], which is broken by several attacks [8, 18], including a powerful decomposition attack [25]. At Crypto 2015 and Asiacrypt 2015, Biryukov et al.’s two public-key encryption schemes are broken by key recovery attacks [27, 39].

Since the first MQ-encryption scheme was proposed by Imai and Matsumoto [36], a number of MQ-schemes in this MQ + IP paradigm have been proposed, i.e., these MQ-schemes are not solely based on the MQ-Problem, but also on some variants of the IP problem. Most of the MQ-schemes have been broken due to the uncertainty of the IP problem. There are only two exceptions from the MQ-IP paradigm: HFEv- variants [42, 45] and Unbalanced Oil-and-Vinegar (UOV) variants [16, 33] as signature schemes. MQ-schemes require simplicity of operations (matrices and vectors) and small fields avoid multiple-precision arithmetic. So, they require only modest computational resources, which makes them attractive for the use on low cost devices such as smart cards [11, 12]. In particular, MQ-signature schemes in the MQ + IP paradigm are superior to other competitors in terms of performance and signature size. Despite these advantages, MQ-schemes in the MQ + IP paradigm has two main problems: (i) it has relatively large key sizes and (ii) all the schemes in the MQ + IP paradigm have been proposed with actual parameters for practical, but they have no security reduction to the hardness of the MQ-problem. The reason for this is that they require a hidden structure which relies on the hardness of the IP problem. Moreover, cryptanalysis results of many MQ-schemes have shown that the IP-problem relies on the MinRank problem [14, 24].

In the last years, a few researchers started designing provably secure MQ-schemes based on the hardness of random instances of the MQ-problem. At PKC 2012, Huang et al. [31] proposed a public-key encryption scheme with a security reduction to the hardness of solving a set of quadratic equations whose coefficients of highest degree are chosen according to a discrete Gaussian distributions. The other terms are chosen uniformly at random. Such a problem is a variant of the classical problem of solving a system of non-linear equations (PoSSo, PoSSo problem with degree 2 equations is the MQ-problem), which is known to be hard for random systems. They claimed that their variant is not easier than solving the PoSSo problem for random instances. At PKC 2014, Albrecht et al. [2] showed that Huang et al.’s new problem is reduced to an easy instance of the Learning With Errors problem. They concluded that one cannot find parameters for a secure and practical scheme: a public-key of at least 1.03 GB is required to achieve 80-bit security against the simplest of their attacks.

Another approach is to construction of an MQ-signature scheme from an identification scheme (IDS) based on the MQ-problem via the Fiat-Shamir transform. The resulting scheme [1] obtained from Sakumoto et al.’s IDS based on the MQ-problem [47] via the Fiat-Shamir transform is the first provably secure MQ-signature scheme, which solely relies on the MQ-problem. Recently, Chen et al. [13] implemented the resulting signature scheme, MQDSS in [1]. MQDSS solves the problem of large key sizes of MQ-PKC by removing the dependence of the IP-problem, but loses the most significant advantages of MQ-ones, fast performance and short signature size. Like this, the history of the design of public-key schemes show that the stronger security arguments the larger performance gap. Therefore, it still remains an open problem to design a practical MQ-signature scheme with a security reduction to the MQ-problem.

For most practical purposes, one still requires a signature scheme that is sufficiently fast and has a short signature size. There have been several attempts to design MQ-signature schemes with higher performance. Gligoroski et al. [28] proposed an MQ-signature scheme, MQQ-SIG, based on multivariate quadratic quasigroups (MQQ). MQQ-SIG is the shortest secret key among MQ-ones and the fastest in signing among known signature schemes, but it requires a huge public key which is about 5.7 times and 12,336 times larger than that of Rainbow and ECDSA, respectively. At PKC 2015, Faugère et al. [23] mounted polynomial-time key-recovery attacks on all known constructions based on MQQ. They broke an MQQ-SIG instance of an 80-bit security level in less than 2 days. An enhanced version of the Tame Triangular System scheme (enTTS) [15, 52] uses very sparse polynomials which make enTTS very efficient in terms of secret key size and signing time, but its public key size is much bigger than other MQ-ones. In this paper, we provide a solution to the two problems of MQ-schemes in the MQ + IP paradigm by proposing a existential unforgeable MQ-signature scheme with a highly optimized practicability for both performance and signature size.

Our Contributions. We propose a new MQ-signature scheme, ELSA, with faster performance and shorter secret key.

  • A New Signature Scheme. Our signature scheme is based on a hidden layer of quadratic equations. This method makes it possible to remove the use of the Gaussian elimination by reducing the complexity of signing from \(\mathcal{O}(n^3)\) to \(\mathcal{O}(n^2)\). It plays an important role in dramatically reducing the secret key size and computational cost in signing.

  • High Speed for Both Signing and Verification. Our scheme is the fastest public-key signature scheme for both signing and verification among the state-of-the-art signature schemes including classical ones and Post-Quantum ones. We implement our scheme for a secure and optimal parameter at a 128-bit security level. Signing of ELSA is about 3.2 times and hundreds of times faster than that of Rainbow and MQDSS, respectively. Also, signing and verification of ELSA is about 17.2 times and 2.3 times faster than those of BLISS-BI, respectively, and signature size of BLISS-BI is about 8.9 times larger than that of ELSA, where BLISS-BI is currently the most efficient lattice-based signature scheme.

  • Shorter Secret Key Size. Compared to Rainbow, the secret key size of ELSA has reduced by a factor of 88% maintaining the same public key size. Compared to enTTS, the public key size of ELSA have reduced by a factor of 40%.

  • Existential Unforgeability. We prove existential unforgeability of ELSA against an adaptive chosen-message attack under the hardness of the MQ-problem induced by a public key of ELSA with a specific parameter set in the random oracle model.

Organization. The rest of the paper is organized as follows. In Sect. 2, we propose a new MQ-signature scheme, ELSA. In Sect. 3, we analyze the security of our scheme against all known attacks. In Sect. 4, we give a security proof of ELSA under the hardness of the MQ-problem in the random oracle model. We evaluate performance of our scheme for a secure and optimal parameter at the 128-bit security level and compare it to the state-of-the-art signature schemes in Sect. 5. We conclude in Sect. 6.

2 A New MQ-Signature Scheme

Here, we propose a new MQ-signature scheme based on a hidden layer of quadratic equations.

Let \(\mathbb F_q\) be a finite field with elements q. A multivariate quadratic system \(\mathcal{P}=(\mathcal{P}^{(1)}, \cdots , \mathcal{P}^{(m)})\) of m equations in n variables is defined by

$$\begin{aligned} \mathcal{P}^{(k)}(x_1, \cdots , x_n)= \sum _{i=1}^n \sum _{j=i}^n p_{ij}^{(k)} x_{i}x_{j} + \sum _{i=1}^n p_i^{(k)} x_i+ p_0^{(k)}, \end{aligned}$$

for \(k=1, \cdots , m\), and \(p_{ij}^{(k)}\), \(p_i^{(k)}\), \(p_0^{(k)} \in _R \mathbb F_q\). The main idea for the construction of MQ-signature schemes is to choose a system \(\mathcal{F}: \mathbb F_q^n \rightarrow \mathbb F_q^m\) of m quadratic polynomials in n variables which can be easily inverted. We call \(\mathcal{F}\) a central map. After that one chooses two affine or linear invertible maps S: \( \mathbb F_q^m \rightarrow \mathbb F_q^m\) and T: \( \mathbb F_q^n \rightarrow \mathbb F_q^n\) to hide the structure of the central map \(\mathcal{F}\) in the public key. A public key is the composed quadratic map \(\mathcal{P}=S \circ \mathcal{F} \circ T\) which is supposed to be hardly distinguishable from a random system and therefore be difficult to invert. The secret key consists of \((S, \mathcal{F}, T)\) which allows to invert \(\mathcal{P}\).

2.1 Our Construction

To construct a new central map for an MQ-signature scheme, we need to define the following four index sets as

$$\begin{aligned} L=\{1, \cdots , l\}, \ K=\{l+1, \cdots , l+k\}, \ R=\{l+k+1, \cdots , l+k+r\}, \end{aligned}$$
$$\begin{aligned} U=\{l+k+r+1, \cdots , l+k+r+u\}, \end{aligned}$$

where \(|L|=l, |K|=k, |R|=r\), and \(|U|=u\). A central map is a multivariate quadratic system \(\mathcal{F}=(\mathcal{F}^{(1)}, \cdots , \mathcal{F}^{(m)})\) of m equations and n variables defined by

$$\begin{aligned} \begin{aligned}&{\left\{ \begin{array}{ll} \begin{aligned} \mathcal{F}^{(1)}(\mathbf{x}) &{}=L_1(\mathbf{x_{L+K+R}})R_{11}(\mathbf{x_{L+K}})+ \cdots + L_r(\mathbf{x_{L+K+R}})R_{1r}(\mathbf{x_{L+K}})+\varPhi _1(\mathbf{x_L}),\\ &{}\vdots \\ \mathcal{F}^{(k)}(\mathbf{x}) &{}=L_1(\mathbf{x_{L+K+R}})R_{k1}(\mathbf{x_{L+K}})+ \cdots + L_r(\mathbf{x_{L+K+R}})R_{kr}(\mathbf{x_{L+K}})+\varPhi _k(\mathbf{x_L}),\\ \end{aligned} \end{array}\right. } \\ \\&{\left\{ \begin{array}{ll} \begin{aligned} \mathcal{F}^{(k+1)}(\mathbf{x}) &{}=L_1(\mathbf{x_{L+K+R}})R_{11}'(\mathbf{x})+ \cdots + L_r(\mathbf{x_{L+K+R}})R_{1r}'(\mathbf{x})+\varPsi _1(\mathbf{x_{L+K}})+L_1'(\mathbf{x_{L+K+R}}), \\ &{}\vdots \\ \mathcal{F}^{(k+u)}(\mathbf{x}) &{}=L_1(\mathbf{x_{L+K+R}})R_{u1}'(\mathbf{x})+ \cdots + L_r(\mathbf{x_{L+K+R}})R_{ul}'(\mathbf{x})+\varPsi _u(\mathbf{x_{L+K}})+L_u'(\mathbf{x_{L+K+R}}),\\ \end{aligned} \end{array}\right. } \end{aligned} \end{aligned}$$

where \(\mathbf{x_L}=(x_1, \cdots , x_l)\), \(\mathbf{x_{L+K}}=(x_1, \cdots , x_{l+k})\), \(\mathbf{x_{L+K+R}}=(x_1, \cdots , x_{l+k+r})\), \(\mathbf{x}=(x_1, \cdots , x_n)\), \(m=k+u\) and \(n=l+r+m\). We call \(\mathcal{F}^{(i)}\) for \(i=1, \cdots , k\) and \(\mathcal{F}^{(i)}\) for \(i=k+1, \cdots , k+u\) polynomials in the first layer and the second layer, respectively.

How to Define \(L_i\), \(R_{ij}\) and \(R_{ij}'\) .

  • To define \(L_i\), it needs to construct a hidden layer \(\mathcal L\) of quadratic equations. \(L_i\) is a linear equation in variables \((x_1, \cdots , x_{l+k+r})\) for \(i=1, \cdots , r\). We define a system of r quadratic equations as

    $$\begin{aligned} \mathcal{L}: {\left\{ \begin{array}{ll} \begin{aligned} L(\mathbf{x_L})&{}L_1(\mathbf{x_{L+K+R}})=\xi _1,\\ &{}\vdots \\ L(\mathbf{x_L})&{}L_r(\mathbf{x_{L+K+R}})=\xi _r,\\ \end{aligned} \end{array}\right. } \end{aligned}$$

    where L is a linear equation in variables \((x_1, \cdots , x_l)\) and \(\xi _i \in \mathbb F_q^*\). We choose random \(\beta _{ij}\) for \(i=1, \cdots , r\) and \(j=1, \cdots , l+k+r\) such that an \(r \times r\) submatrix matrix \(\varLambda _{r}=\left( \begin{array}{cccc} \beta _{1l+k+1} &{} \cdots &{} \cdots &{} \beta _{1l+k+r} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ \beta _{rl+k+1} &{} \cdots &{} \cdots &{} \beta _{rl+k+r} \\ \end{array} \right) \) of an \(r \times (l+k+r)\) matrix \(\varLambda \) is invertible, where

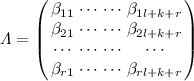
    figure a

    is a coefficient matrix of \((L_1, \cdots , L_r)\).

  • \(\varPhi _i\) is a quadratic equation in variables \((x_1, \cdots , x_l)\) for \(i=1, \cdots , k\) defined by \(\varPhi _i=\sum _{j=1}^l\sum _{t=j}^{l} \varphi _{j,t}^i x_jx_t\), for \(\varphi _{j,t}^i \in _R \mathbb F_q\).

  • \(R_{ij}\) is a linear equation in variables \((x_1, \cdots , x_{l+k})\) for \(i=1, \cdots , k\) and \(j=1, \cdots , r\) such that a \(k \times k\) submatrix matrix \(\varTheta _k=\left( \begin{array}{cccc} \alpha _{1l+1} &{} \cdots &{} \cdots &{} \alpha _{1l+k} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ \alpha _{kl+1} &{} \cdots &{} \cdots &{} \alpha _{kl+k} \\ \end{array} \right) \) of a \(k \times (l+k)\) matrix \(\varTheta \) is invertible, where \(\varTheta \) is a coefficient matrix of \((L(\mathbf{x_L}) \cdot \mathcal{F}^{(1)}-L(\mathbf{x_L}) \cdot \varPhi _1(\mathbf{x_{L}}), \cdots , L(\mathbf{x_L}) \cdot \mathcal{F}^{(k)}-L(\mathbf{x_L}) \cdot \varPhi _k(\mathbf{x_{L}}))\) such that

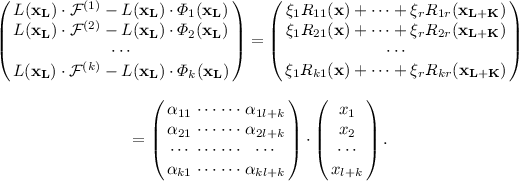
    figure b

  • \(\varPsi _i\) is a sparse polynomial in variables \((x_1, \cdots , x_{l+k})\) for \(i=k+1, \cdots , k+u\) defined by

    $$\begin{aligned} \varPsi _i=\sum _{j=1}^{l+k}\psi _{i,j} x_j x_{(i+j-1)(\text {mod } l+k)+1} \end{aligned}$$

    where \(\psi _{i, j} \in _R \mathbb F_q\) so that the symmetric matrix of the quadratic part of each \(\varPsi _i\) has rank \(l+k\) and any crossterms in \(\varPsi _i\) for all \(i=k+1, \cdots , k+u\) don’t overlap.

  • \(L_i'\) is a linear equation in variables \((x_1, \cdots , x_{l+k+r})\) for \(i=1, \cdots , u\) defined by \(L_i'=\sum _{j=1}^{l+k+r}\nu _j^ix_j\), where \(\nu _j^i \in _R \mathbb F_q\).

  • \(R_{ij}'\) is a linear equation in variables \((x_{l+k+r+1}, \cdots , x_n)\) for \(i=1, \cdots , u\) and \(j=1, \cdots , r\). We choose \(R_{ij}'\) such that a \(u \times u\) submatrix \(\varDelta _u=\left( \begin{array}{ccc} \delta _{1l+k+r+1} &{} \cdots &{} \delta _{1n} \\ \cdots &{} \cdots &{} \cdots \\ \delta _{ul+k+r+1} &{} \cdots &{} \delta _{un} \\ \end{array} \right) \) of a \(u \times n\) matrix \(\varDelta =\left( \begin{array}{ccc} \delta _{11} &{} \cdots &{} \delta _{1n} \\ \cdots &{} \cdots &{} \cdots \\ \delta _{u1} &{} \cdots &{} \delta _{un} \\ \end{array} \right) \) is invertible, where \(\varDelta \) is a coefficient matrix of \((L(\mathbf{x_L}) \cdot \mathcal{F}^{(k+1)}-L(\mathbf{x_L}) \cdot \varPsi _1(\mathbf{x_{L+K}})-L(\mathbf{x_L}) \cdot L_1'(\mathbf{x_{L+K+R}}), \cdots , L(\mathbf{x_L}) \cdot \mathcal{F}^{(k+u)}-L(\mathbf{x_L}) \cdot \varPsi _u(\mathbf{x_{L+K}})-L(\mathbf{x_L}) \cdot L_u'(\mathbf{x_{L+K+R}}))\) such that

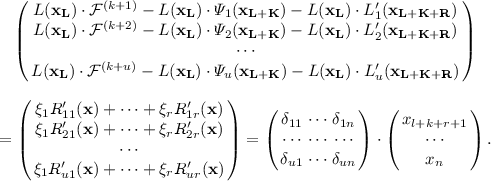
    figure c

  • From this construction, we store only \((\mathbf{L}, \mathbf{L'}, \varPhi , \varPsi ^S, {\varTheta _k}^{-1}, {\varLambda _r}^{-1}, {\varDelta _u}^{-1})\) for \(\mathcal F\) instead of all the coefficients of \(\mathcal F\), where \(\mathbf{L}=\{L, \xi _i\}_{i=1}^r\), \(\mathbf{L'}=\{L_i'\}_{i=1}^{l+k+r}\), \(\varPhi =\{\varPhi _i\}_{i=1}^k\) and \(\varPsi ^S=\{\varPsi _i\}_{i=1}^u\).

How to Invert the Central Map. Given \(\gamma =(\gamma _1, \cdots , \gamma _m)\), to compute \(\mathcal{F}^{-1}(\gamma )=\mathbf{s}\), i.e., to find \(\mathbf{s}\) such that \(\mathcal{F}(\mathbf{x})=\gamma \), do the followings:

  • In the first layer, compute \(L(\mathbf{x_L}) \cdot \mathcal{F}^{(i)}=L(\mathbf{x_L}) \cdot \gamma _i\) for \(i=1, \cdots , k\) by getting a linear system of k equations with \(l+k\) variables as

    $$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \xi _1R_{11}(\mathbf{x_{L+K}})+ \cdots + &{}\xi _l R_{1r}(\mathbf{x_{L+K}})=\gamma _1 \cdot L(\mathbf{x_L})-\varPhi _1(\mathbf{x_L}) \cdot L(\mathbf{x_L}), \\ &{}\vdots \\ \xi _1R_{k1}(\mathbf{x_{L+K}})+ \cdots +&{} \xi _r R_{kr}(\mathbf{x_{L+K}})=\gamma _k \cdot L(\mathbf{x_L})-\varPhi _k(\mathbf{x_L}) \cdot L(\mathbf{x_L}).\\ \end{aligned} \end{array}\right. } \end{aligned}$$

    • Choose a random Vinegar vector \(\mathbf{s_L}=(s_1, \cdots , s_l) \in \mathbb F_q^l\). If \(L(\mathbf{s}_L)=0\) then choose another random Vinegar vector. Plug \(\mathbf{s_L}\) into the above linear system by getting a new linear system of k equations with k variables.

    • Solve the linear system by computing

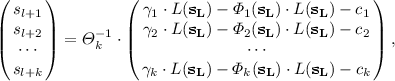
      figure d

      where \(c_j\) is a constant derived from the linear equation \(\xi _1R_{j1}(\mathbf{x_{L+K}})+ \cdots + \xi _l R_{jr}(\mathbf{x_{L+K}})\) for \(j=1, \cdots , k\).

  • In the hidden layer, plug \(\mathbf{s_{L+K}}=(s_1, \ldots , s_{l+k})\) into a quadratic system \(\mathcal L\) by getting a linear system of r equations with r variables as

    $$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} L_1(\mathbf{s_{L+K}}, x_{l+k+1}, \cdots , x_{l+k+r})&{}=L(\mathbf{s}_L)^{-1} \cdot \xi _1, \\ &{}\vdots \\ L_r(\mathbf{s_{L+K}}, x_{l+k+1}, \cdots , x_{l+k+r})&{}=L(\mathbf{s}_L)^{-1} \cdot \xi _k, \\ \end{aligned} \end{array}\right. } \end{aligned}$$

    where \(L(\mathbf{s}_L) \ne 0\). Get a solution \((s_{l+k+1}, \cdots , s_{l+k+r})\) by computing

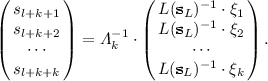
    figure e

  • In the second layer, compute \(L(\mathbf{x_L}) \cdot \mathcal{F}^{(i)}=L(\mathbf{x_L}) \cdot \gamma _i\) for \(i=k+1, \cdots , k+u\) getting a linear system of u equations with \(l+k+r+u\) variables as

    $$\begin{aligned} {\left\{ \begin{array}{ll} \begin{aligned} \xi _1R_{11}'(\mathbf{x})+ \cdots +&{} \xi _l R_{1r}'(\mathbf{x})= \gamma _{k+1} \cdot L(\mathbf{x}_L)-\varPsi _1(\mathbf{x}_L) \cdot L(\mathbf{x}_L)-L_1'(\mathbf{x_{L+K+R}}) \cdot L(\mathbf{x}_L),\\ \xi _1R_{21}'(\mathbf{x})+ \cdots +&{} \xi _l R_{2r}'(\mathbf{x})= \gamma _{k+2} \cdot L(\mathbf{x}_L)-\varPsi _2(\mathbf{x}_L) \cdot L(\mathbf{x}_L)-L_2'(\mathbf{x_{L+K+R}}) \cdot L(\mathbf{x}_L),\\ &{}\cdots \\ \xi _1R_{u1}'(\mathbf{x})+ \cdots +&{} \xi _l R_{ur}'(\mathbf{x})= \gamma _{k+u} \cdot L(\mathbf{x}_L)-\varPsi _u(\mathbf{x}_L) \cdot L(\mathbf{x}_L)-L_u'(\mathbf{x_{L+K+R}}) \cdot L(\mathbf{x}_L), \\ \end{aligned} \end{array}\right. } \end{aligned}$$

    and plug \(\mathbf{s_{L+K+R}}=(s_1, \cdots , s_{l+k+r})\) into the linear system getting a linear system of u equations with u variables. Get a solution \((s_{l+k+r+1}, \cdots , s_{l+k+r+u})\) by computing

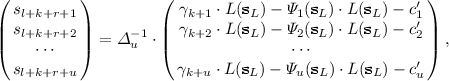
    figure f

    where \(c_i'\) is a constant of the linear equation \(\xi _1R_{i1}'(\mathbf{s_{L+K}}, \mathbf{x}_R)+ \cdots + \xi _r R_{ir}'(\mathbf{s_{L+K}}, \mathbf{x}_R)\) for \(i=1, \cdots , u\).

  • Finally, we get a solution \((s_1, \cdots , s_n)\) of \(\mathcal{F}(\mathbf{x})=\gamma \) by performing only three matrix multiplications and computation of quadratic terms without using the Gaussian elimination.

Now, we construct a new MQ-signature scheme based on this central map.

\(\blacksquare \) ELSA (Efficient Layered Signature Scheme).

  • KeyGen \((1^{\lambda }).\) For a security parameter \(\lambda \), generate a public/secret key pair \({<}PK, SK{>}={<}\mathcal{P}, (\widetilde{S}, \widetilde{T}, \mathcal{F}=(\mathbf{L}, \mathbf{L'}, \varPhi , \varPsi ^S, \widetilde{\varTheta _r}, \widetilde{\varLambda _k}, \widetilde{\varDelta _u})){>}\) as

    • – Choose randomly two affine maps \(\widetilde{S}\) and \(\widetilde{T}\). If neither \(\widetilde{S}\) nor \(\widetilde{T}\) is invertible then choose again, where \(\widetilde{X}=X^{-1}\).

    • – Choose randomly \(\mathbf{L}, \varPhi , \varPsi ^S, \widetilde{\varTheta _r}, \widetilde{\varLambda _r}\) and \(\widetilde{\varDelta _u}\), where \(\mathbf{L}=\{L, \xi _i\}_{i=1}^{r}\), \(\mathbf{L'}=\{L_i'\}_{i=1}^{u}\), \(\varPhi =\{\varPhi _i\}_{i=1}^k\) and \(\varPsi ^S=\{\varPsi _i\}_{i=1}^u\) satisfy all the conditions described above. If neither \(\widetilde{\varTheta _r}\), \(\widetilde{\varLambda _k}\) nor \(\widetilde{\varDelta _u}\) is invertible then choose again.

    • Compute \(\mathcal{P}\) from \(\mathcal{P}=S \circ \mathcal{F} \circ T\).

  • Sign(\(SK, \texttt {m}).\) Given a message \(\mathtt {m}\),

    • – Compute \(h(\texttt {m})\) and \(\widetilde{S}(h(\texttt {m}))=\gamma \), where \(\gamma =(\gamma _1, \cdots , \gamma _m)\).

    • – Compute \(\mathbf s\) such that \(\mathcal{F}^{-1}(\gamma )=\mathbf{s}\), i.e., \(\mathcal{F}(\mathbf{s})=\gamma \) as the above. Then \(\mathbf{s}=(s_1, \cdots , s_n)\) is a solution of \(F(\mathbf{x})=\gamma \).

    • – Compute \(\widetilde{T}(\mathbf{s})=\sigma \). Then \(\sigma \) is a signature of \(\mathtt{m}\).

  • Verify \((PK, \mathtt{m}, \sigma )\). Given a signature \(\sigma \) on \(\mathtt{m}\) and a public key \(\mathcal{P}\), check \(\mathcal{P}(\sigma )=h(\mathtt{m})\). If it holds, accept \(\sigma \), otherwise, reject it.

Remark

1. We now explain how the public key and secret key sizes of ELSA are calculated. The public key requires \(\displaystyle \frac{m(n+1)(n+2)}{2}\) field elements as their coefficients. The secret maps S and T require \(m(m+1)\) and \(n(n+1)\) field elements, respectively. It requires \((l+r+l+1)\) field elements for \(\mathbf L\), \(u(l+k+r+1)\) field elements for \(\mathbf L'\), \(\displaystyle \frac{k(l+1)(l+2)}{2}\) field elements for \(\varPhi \), \(u(l+k)\) field elements for \(\varPsi ^S\), \(k^2\) field elements for \(\widetilde{\varTheta _k}\), \(r^2\) field elements for \(\widetilde{\varLambda _k}\) and \(u^2\) field elements for \(\widetilde{\varDelta _u}\). Thus, the secret key requires \(n(n+1)+m(m+1)+\displaystyle \frac{k(l+1)(l+2)}{2}+u(2l+2k+r+1)+(k^2+r^2+u^2)+(l+r+1)\) field elements.

2. UOV and Rainbow requires the use of Gaussian elimination for solving linear systems in signing. In these schemes, the majority of computational cost for signing count for that of the Gaussian elimination. In ELSA, only three matrix multiplications using \({\varTheta _r}^{-1}, {\varLambda _k}^{-1}, {\varDelta _u}^{-1}\) are required for solving the resulting linear systems in signing without using the Gaussian elimination. So, it achieves \(\mathcal{O}(n^2)\) complexity in signing instead of \(\mathcal{O}(n^3)\).

3 Security Analysis of ELSA

The security of all MQ-schemes in the MQ + IP paradigm is not only based on the MQ-Problem, but also on some variant of the Isomorphism of Polynomials (IP) problem. Furthermore, layered MQ-schemes require the hardness of the MinRank problem. These underlying problems are defined as follows:

  • Polynomial System Solving (PoSSo) Problem: Given a system \(\mathcal{P}=(\mathcal{P}^{(1)}, \cdots , \mathcal{P}^{(m)})\) of m nonlinear polynomials defined over \(\mathbb F_q\) with degree of d in variables \((x_1, \cdots , x_n)\) and \(\mathbf{y}=(y_1, \cdots , y_m) \in \mathbb F_q^m\), find \(\mathbf{x'}=(x_1', \cdots , x_n') \in \mathbb F_q^n\) such that \(\mathcal{P}(\mathbf{x'})\!=\!\mathbf{y}\), i.e., \(\mathcal{P}^{(1)}(x_1', \cdots , x_n')\!=\!y_1, \cdots , \mathcal{P}^{(m)}(x_1', \cdots , x_n')\!=\!y_m\).

  • EIP (Extended Isomorphism of Polynomials) Problem: Given a nonlinear multivariate system \(\mathcal P\) such that \(\mathcal{P}=S \circ \mathcal{F} \circ T\) for linear or affine maps S and T, and \(\mathcal F\) belonging to a special class of nonlinear polynomial system \(\mathcal C\), find a decomposition of \(\mathcal P\) such that \(\mathcal{P}=S' \circ \mathcal{F}' \circ T'\) for linear or affine maps \(S'\) and \(T'\), and \(\mathcal{F}' \in \mathcal{C}\).

  • MinRank Problem: Let \(m, n, r, k \in \mathbb N\) and \(r, m < n\). The MinRank(r) problem is, given \((M_1, \cdots , M_l) \in \mathbb F_q^{m \times n}\), find a non-zero k-tuple \((\lambda _1, \cdots , \lambda _k) \in \mathbb F_q^k\) such that \(Rank(\sum _{i=1}^k \lambda _i M_i) \le r\).

The PoSSo problem is proven to be NP-complete [26]. For efficiency, MQ-PKC restrict to quadratic polynomials. The PoSSo problem with all polynomials \((P^{(1)}, \cdots , P^{(m)})\) of degree 2 is called the MQ-Problem for multivariate quadratic. The IP problem was first described by Patarin at Eurocrypt’96 [40], there is not much known about the difficulty of the IP problem in contrast to the MQ-problem. The problem of finding a low rank linear combination of matrices was originally introduced in [48] as one of the natural questions in linear algebra, and the authors proved its NP-completeness.

A feature of MQ-PKC in the MQ + IP paradigm is that there exist a large number of different secret keys for a given public key [51]. Informally, suppose that \({<}\mathcal{P}, (S, \mathcal{F}, T){>}\) is a public/secret key pair of an MQ-PKC, we call \((S', \mathcal{F}', T')\) is an equivalent key of \((S, \mathcal{F}, T)\) if \(\mathcal{P}=S \circ \mathcal{F} \circ T=S' \circ \mathcal{F}' \circ T'\), where \(S'\) and \(T'\) are invertible affine maps, and \(\mathcal{F}'\) preserves all zero coefficients of \(\mathcal F\). The concept of equivalent keys plays a major role in the cryptanalysis of MQ-schemes. If an attacker finds any of the equivalent keys then he can forge a signature. Thus, the attacker wants to find an equivalent key with the simplest structure. Known attacks of MQ-schemes be divided into the following two classes:

  • Direct Attack. Given a public key \(\mathcal P\) and \(\mathbf{y} \in \mathbb F_q^m\), find a solution \(\mathbf{x} \in \mathbb F_q^n\) of \(\mathcal{P}(\mathbf{x})=\mathbf{y}\).

  • Key Recovery Attack (KRA). Given \(\mathcal{P}=S \circ \mathcal{F} \circ T\), find equivalent keys of \((S, \mathcal{F}, T)\):

    • – KRAs using equivalent keys and good keys,

    • – Rank-based KRAs to find linear combinations associated matrices at some given rank, to find nontrivial invariant subspaces of linear combinations associated matrices and so on: MinRank attack, HighRank attack, Kipnis-Shamir attack.

3.1 Direct Attacks

Direct attacks use equation solvers like XL and Gröbner basis algorithms such as Buchberger, F4 and F5 for solving the MQ-problem. Complexity of the MQ-Problem is determined by that of the HybridF5 (HF5) algorithm [7]. The basic idea is to guess some of the variables to create overdetermined systems before applying Faugère’s F5 algorithm [22]. When doing so, one has to run the F5 algorithm several times to find a solution of the original system. When guessing k variables over \(\mathbb F_q\), this number is given by \(q^k\). The complexity of solving a semi-regular (random) system of m quadratic equations in n variables over \(\mathbb F_q\) by HF5 can be estimated as

$$\begin{aligned} C_{HF5}(q, m, n)=min_{k \ge 0} \ q^k \cdot \mathcal{O} \left( \left( m \cdot {{n-k+d_{reg}-1}\atopwithdelims (){d_{reg}}}\right) ^\omega \right) , \end{aligned}$$

where the degree of regularity \(d_{reg}\) is the index of the first non-positive coefficient in the \(S_{m,n}=\displaystyle \frac{(1-z^{2})^m}{(1-z)^{n}}\) and \(2 \le \omega \le 3\) is the linear algebra constant of solving a linear system. The internal equations used by HF5 are very sparse and thus \(\omega =2\) can be used to obtain a lower bound on the complexity. If we really want to break a scheme, we either calculate the correct \(\alpha \) or use \(\omega =2.8\) as an upper bound [50].

Using HF5 algorithm (\(\omega =2\)), we summarize the lower bounds of the numbers of equations (m) for solving determined systems defined over \(\mathbb F_{2^8}\) required to achieve given security levels in Table 1.

Table 1. Lower bounds of the numbers of quadratic equations for determined systems over \(\mathbb F_{2^8}\) at each security level.
Full size table

3.2 Replacement Attacks

Our central map has a special feature for inverting: each central polynomial uses a linear combination of the products of two lines and additional quadratic terms. This feature and hidden quadratic systems make it possible to remove the use of the Gaussian elimination resulting in the reduction of signing cost and secret key size. In particular, \(L_i\) for \(i=1, \cdots , r\) are used in all the central polynomials \(\mathcal{F}^{(i)}\) for \(i=1, \cdots , k+u\). Thus, one can replace \(L_i\) with a new variable via an appropriate changing of variables. More precisely, one can replace \(L_i(\mathbf{x_{L+K+R}})\) with \(y_{l+k+i}\) for \(i=1, \cdots , r\) and \(x_j\) with \(y_j\) for \(j=1, \cdots , l+k, l+k+r+1, \cdots , l+k+r+u\). Then one gets a new central map, \(\overline{\mathcal{F}}=(\overline{\mathcal{F}}^{(1)}, \cdots , \overline{\mathcal{F}}^{(m)})\) in the new variables \((y_1, \cdots , y_n)\) as

$$\begin{aligned} \begin{aligned}&{\left\{ \begin{array}{ll} \begin{aligned} \widehat{\mathcal{F}}^{(1)}(\mathbf{y}) &{}=y_{l+k+1}R_{11}(\mathbf{y_{L+K}})+ \cdots + y_{l+k+r}R_{1r}(\mathbf{y_{L+K}})+\varPhi _1(\mathbf{y_L}),\\ &{}\vdots \\ \widehat{\mathcal{F}}^{(k)}(\mathbf{y}) &{}=y_{l+k+1}R_{k1}(\mathbf{y_{L+K}})+ \cdots + y_{l+k+r}R_{kr}(\mathbf{y_{L+K}})+\varPhi _k(\mathbf{y_L}),\\ \end{aligned} \end{array}\right. } \\ \\&{\left\{ \begin{array}{ll} \begin{aligned} \widehat{\mathcal{F}}^{(k+1)}(\mathbf{y}) &{}=y_{l+k+1}R_{11}'(\mathbf{y})+ \cdots + y_{l+k+r}R_{1r}'(\mathbf{y})+\varPsi _1(\mathbf{y_{L+K}})+\overline{L_1}(\mathbf{y_{L+K+R}}), \\ &{}\vdots \\ \widehat{\mathcal{F}}^{(k+u)}(\mathbf{y}) &{}=y_{l+k+1}R_{u1}'(\mathbf{y})+ \cdots + y_{l+k+r}R_{ur}'(\mathbf{y})+\varPsi _u(\mathbf{y_{L+K}})+\overline{L_u}(\mathbf{y_{L+K+R}}),\\ \end{aligned} \end{array}\right. } \end{aligned} \end{aligned}$$

where \(\mathbf{y_L}\!=\!(y_1, \cdots , y_l)\), \(\mathbf{y_{L+K}}\!=\!(y_1, \cdots , y_{l+k})\) and \(\mathbf{y_{L+K+R}}\!=\!(y_1, \cdots , y_{l+k+r})\). Then the public key can be written as

$$\begin{aligned} \mathcal{P}=S \circ (\mathcal{F} \circ T_R) \circ ( T_R^{-1} \circ T)=S \circ \overline{\mathcal{F}} \circ \overline{T}, \end{aligned}$$

where \(\overline{\mathcal{F}}=\mathcal{F} \circ T_R\), \(\overline{T}=T_R^{-1} \circ T\) and \(T_R\) is an invertible map defined by

figure g

where \(I_{L+K}\) and \(I_U\) are an \((l+k) \times (l+k)\)-identity matrix and a \(u \times u\)-identity matrix, respectively. In this case, we can consider the public key \(\mathcal{P}=S \circ \overline{\mathcal{F}} \circ \overline{T}\) with the secret key \((S, \overline{\mathcal{F}}, \overline{T})\) since \(\overline{\mathcal{F}}\) is still invertible with the same way as in §2.1. We provide security analysis of ELSA against all attacks with respect to these two types of secret keys \((S, \mathcal{F}, T)\) and \((S, \overline{\mathcal{F}}, \overline{T})\) for the public key \(\mathcal{P}\).

3.3 Key Recovery Attacks

In 2008, Ding et al. [17] presented Rainbow Band Separation (RBS) attacks on Rainbow. Later, Thomae [50] applied the attacks to other MQ-schemes using the concept of good keys which is a generalization of the RBS attacks. In this subsection, we analyze security of ELSA against the key recovery attacks (KRAs) using equivalent keys and good keys.

Let \(F^{(i)}\) \((1 \le i \le m)\) be symmetric matrices associated to the homogeneous quadratic part of the i-th component of the central map \(\mathcal F\). The matrices \(F^{(i)}\) are depicted in Fig. 1, where white parts denote zero entries and gray parts denote arbitrary entries. The matrices are the same as those of Rainbow [44]. After mounting the replacement attack described in Sect. 3.2, we get symmetric matrices \(\overline{F}^{(i)}\) \((1 \le i \le m)\) representing the quadratic part of the i-th component of \(\overline{\mathcal{F}}^{(i)}\) which is depicted in Fig. 2.

Fig. 1.
figure 1

Symmetric matrices for quadratic parts of \(\mathcal F\).

Full size image
Fig. 2.
figure 2

Symmetric matrices for quadratic parts of \(\overline{\mathcal{F}}\).

Full size image

Analogously, we denote \(P^{(i)}\) \((1 \le i \le m)\) be symmetric matrices representing the quadratic part of the i-th component of the public key \(\mathcal P\). Due to the structure of \(\mathcal{F}\), we know that certain coefficients in \(\mathcal {F}^{(i)}\) are systematically zero. Since \(\mathcal{P}= S \circ \mathcal{F} \circ T\), we obtain \(\mathcal{F}={\widetilde{S}} \circ \mathcal{P} \circ {\widetilde{T}}\), where \({\widetilde{S}}=S^{-1}\) and \({\widetilde{T}}=T^{-1}\). From this, we get the following equality:

$$\begin{aligned} \mathcal {F}^{(i)}={\widetilde{T}}^\mathsf{T}\left( \displaystyle \sum _{j=1}^{m} {\widetilde{s}_{ij} P^{(j)}}\right) {\widetilde{T}},\ \forall 1\le i \le m. \end{aligned}$$

The corresponding system of equations is:

$$\begin{aligned} f_{\beta \gamma }^{(i)}=\displaystyle \sum _{x=1}^{m} \displaystyle \sum _{y=1}^{n} \displaystyle \sum _{z=1}^{n} c_{yz}^{(x)} {\widetilde{s}_{ix}} {\widetilde{t}_{y\beta }} {\widetilde{t}_{z\gamma }} \end{aligned}$$
(1)

for some coefficient \(c_{yz}^{(x)}\), as we have already known that \(f_{\beta \gamma }^{(i)}=0\) for some \(i,\beta ,\gamma \) by the construction of \(\mathcal{F}\). Since the number equations obtained by (1) equals the number of zeros in all \(\mathcal{F}^{(k)}\), we get \( \displaystyle \frac{kr(r+1)+mu(u+1)}{2}+ku(n-u)\) cubic equations. The number of variables in \({\widetilde{S}}\) and \({\widetilde{T}}\) is \(n^2 +m^2\). The number of equations for \(\overline{\mathcal{F}}\) is

$$\begin{aligned} \displaystyle \frac{k(n-l)(n+l+1)+u(n-r)(n+r+1)}{2}-r[(l+k)k+(n-r)u]-u(l+k). \end{aligned}$$

The complexity of solving such systems using HF5 is very large. To improve this complexity, we use the concept of equivalent keys [50, 51]. Let \({\mathbb {GL}}_n(\mathbb F_q)\) be a general linear group of degree n over \(\mathbb F_q\), for an integer n.

Definition 3.1

[Equivalent Key]. Let \(S, S'\in {\mathbb {GL}}_m(\mathbb F_q)\) and \(T, T'\in {\mathbb {GL}}_n (\mathbb F_q)\) and \(\mathcal{F}, \mathcal{F}'\in \mathbb F_q[x_1, ... , x_n]^m\). We say that \((\mathcal{F}, S, T)\) is equivalent to \((\mathcal{F}', S', T')\) if and only if \(S\circ \mathcal{F}\circ T= S'\circ \mathcal{F}'\circ T'\) and \(\mathcal{F}|_I=\mathcal{F}'|_I\), that is, \(\mathcal{F}\) and \(\mathcal{F}'\) share the same structure when restricted to a fixed index set \(I=\{I^{(1)} , \cdots I^{(m)}\}\).

If \(S\circ \mathcal{F}\circ T=\mathcal{P}= S'\circ \mathcal{F}'\circ T'\), where \(\mathcal F'\) preserves all systematic zero coefficients of \(\mathcal F\) then we call \(S'\) and \(T'\) equivalent keys. Thus, an attacker who has any of equivalent keys can forge signatures on any messages. If we can find simpler equivalent keys, we can reduce the number of variables in S and T. If there are two invertible linear maps \(\varSigma \in \mathbb { GL}_m(\mathbb F_q)\) and \(\varOmega \in \mathbb {GL}_n(\mathbb F_q)\) such that

$$\begin{aligned} \mathcal{P}=S\circ \varSigma ^{-1}\circ (\varSigma \circ \mathcal{F} \circ \varOmega ) \circ \varOmega ^{-1} \circ T, \end{aligned}$$

and \(\mathcal{F'}(=\varSigma \circ \mathcal{F} \circ \varOmega )\) and \(\mathcal{F}\) have the same structure then \((\mathcal{F}', S', T')\) is an equivalent key.

Fig. 3.
figure 3

Equivalent keys of ELSA w.r.t. \(\mathcal{F}\).

Full size image
Fig. 4.
figure 4

Equivalent keys of ELSA w.r.t. \(\overline{\mathcal{F}}\).

Full size image

For the original central map \(\mathcal{F}\), its equivalent keys are the same as those of Rainbow since the matrices \((F^{(1)}, \cdots , F^{(m)})\) are the same as those of Rainbow [50]. Thus, the equivalent keys for \(\mathcal F\) are of the form given in Fig. 3, in this case, \(\mathcal {F'}^{(i)}\) also have same form as \(\mathcal {F'}^{(i)}\) given in Fig. 1.

Next, we find equivalent keys for the central map \(\overline{\mathcal{F}}\). To preserve the structure in second layer, we can find \(\varOmega \) and \(\varSigma \) of the form given in Fig. 4, so we get equivalent keys of the form given in Fig. 4. However, we can find simpler equivalent keys than ones given in Fig. 4 to improve the complexity significantly by changing the preservation set, i.e., the set of indices for the quadratic terms with zero coefficients. For it, we consider the generalized version of \(\overline{\mathcal{F}}\) denoted by \(\widehat{\mathcal{F}}\) which is depicted in Fig. 5. So, we need to find equivalent keys \((\widehat{\mathcal {F}}', S', T')\) such that \(\widehat{\mathcal {F}'}^{(i)}\) preserves the generalized version \(\widehat{\mathcal{F}}^{(i)}\).

Fig. 5.
figure 5

\(\widehat{\mathcal{F}}\): Generalized version of \(\overline{\mathcal{F}}\).

Full size image

Lemma 3.1

For the generalized central map \(\widehat{\mathcal{F}}\) given in Fig. 5, we can find equivalent keys \(S'\) and \(T'\) of the form given in Fig. 6 with high probability, where gray parts denote arbitrary entries and white parts denote zero entries and there are ones at the diagonal.

Fig. 6.
figure 6

Equivalent keys of ELSA w.r.t. \(\widehat{\mathcal{F}}\).

Full size image

Proof

As in [50], we can find \(\varSigma \) and \(\varOmega \) given in Fig. 6. With high probability, there exist equivalent keys \((S', T')\) of the form given in Fig. 6.    \(\square \)

After applying the transformations \(\varSigma \) and \(\varOmega \) in Lemma 3.1., we also get the central map \(\widehat{\mathcal {F}}'=\varSigma \circ \widehat{\mathcal {F}} \circ \varOmega \) as in Fig. 5. From the equivalent key given in Fig. 6, we get a system of \(\displaystyle \frac{k(n-l)(n+l+1)}{2}-kr(l+k)\) cubic equations and \(\displaystyle \frac{u^2(2l+2k+u+1)}{2}\) quadratic equations with \(n(n-u)+k(u-k-r)-l^2-r^2\) variables. However, the complexity of solving such a system is still large: for ELSA with \((\mathbb F_q, l,k,r,u)=(\mathbb F_{2^8}, 6, 28,30,15)\), lower bound on the complexity of solving the system by HF5 is \(2^{1696}\). To further decrease this complexity, we use the notion of good keys which is a generalization of equivalent keys. Good keys don’t preserve all the zero coefficients of \(\mathcal{F}\), but just some of them. Hence, we can choose \(\varSigma \) and \(\varOmega \) more widely and further reduce the number of variables.

Definition 3.2

[Good Key]. Let \(S, S''\in \mathbb {GL}_n(\mathbb F_q)\) and \(T, T''\in \mathbb {GL}_m(\mathbb F_q)\) and \(\mathcal{F}, \mathcal{F}''\in \mathbb F_q[x_1, ... , x_n]^m\), and \(J=\{J^{(1)}, \cdots , J^{(m)} \}\subset I=\{I^{(1)}, \cdots , I^{(m)} \}\) for all k with at least one \(J^{(k)}\ne \phi \). We say that \((\mathcal{F}'', S'', T'')\) is a good key for \((\mathcal F\), \(S,\,T)\) if and only if \(S\circ \mathcal{F}\circ T= S''\circ \mathcal{F}''\circ T''\) and \(\mathcal{F}|_J=\mathcal{F}''|_J\).

To find good keys, let \((\mathcal {F'}, S', T')\) be an equivalent key for ELSA. If

$$\begin{aligned} \mathcal{P}=S'\circ \mathcal {F}'\circ T'=(S'\circ \varSigma '^{-1}) \circ (\varSigma ' \circ \mathcal{F}' \circ \varOmega ') \circ (\varOmega '^{-1} \circ T') \end{aligned}$$

for some two linear maps \(\varSigma ' \in \mathbb {GL}_m(\mathbb F_q)\) and \(\varOmega ' \in \mathbb {GL}_n(\mathbb F_q)\), and \(\mathcal {F}''=\varSigma ' \circ \mathcal {F}'\circ \varOmega '\) satisfies the condition in above definition, then

$$\begin{aligned} (\mathcal {F}'', \ S'', \ T'')=(\varSigma ' \circ \mathcal {F}'\circ \varOmega ', \ S'\circ \varSigma '^{-1},\ \varOmega '^{-1} \circ T'), \end{aligned}$$

\(S''\) and \(T''\) are good keys. The following proposition shows the existence of good keys for ELSA.

Lemma 3.2

Let \((S', \widehat{\mathcal {F}}', T')\) be an equivalent key for ELSA given in Fig. 6. Then there are good keys \((S'', \widehat{\mathcal{F}}'', T'')\) of the form given in Fig. 7. Only the last column of \(\widetilde{T''}\) contains arbitrary values in the first \(l+k+r\) rows, which are equal to the corresponding values in \(\widetilde{T'}\). Respectively, only u values of the k-th row of \(\widetilde{S''}\) contain arbitrary values, which are equal to the corresponding values in \(\widetilde{S'}\).

Proof

Using linear algebra, we can obtain unique \(\varSigma '\) and \(\varOmega '\) given in Fig. 7. It shows the existence of a good key \((S'', T'')\) of the form given in Fig. 7.   \(\square \)

Fig. 7.
figure 7

Good keys of ELSA.

Full size image
Fig. 8.
figure 8

Central map \(\widehat{\mathcal {F}}''\) after applying \(\varSigma '\) and \(\varOmega '\) in Lemma 3.2.

Full size image

Finally, after applying the transformations \(\varSigma '\) and \(\varOmega '\), we get the central map \(\widehat{\mathcal {F}}''=\varSigma ' \circ \widehat{\mathcal{F}}' \circ \varOmega '\) as given in Fig. 8. Finally, we obtain the following Theorem.

Theorem 3.1

The main complexity of the key recovery attack using good keys on ELSA is determined by solving \(n-1\) bihomogeneous equations and m quadratic equations with n variables.

After obtaining one column of \(T'\) and one row of \(S'\), all the other parts of \(T'\) and \(S'\) are revealed by linear equations as in [50]. Consequently, we recover the equivalent keys \(T'\) and \(S'\).

We find different equivalent keys for three types of central maps \(\mathcal F\), \(\overline{\mathcal{F}}\) and \(\widehat{\mathcal{F}}\), where \(\mathcal F\), \(\overline{\mathcal{F}}\) and \(\widehat{\mathcal{F}}\) are the original central map, the resulting central map after the replacement attack and the general version of \(\overline{\mathcal{F}}\), respectively. The KRAs using equivalent keys for \(\widehat{\mathcal{F}}\) are more effective than those for \(\mathcal F\) and \(\overline{\mathcal{F}}\). However, \(\mathcal F\), \(\overline{\mathcal{F}}\) and \(\widehat{\mathcal{F}}\) have the same forms of good keys resulting in the same complexities given in Theorem 3.1. Table 2 shows improvements of lower bound (\(\alpha =2\)) and upper bound (\(\alpha =2.8\)) on the complexities of solving such a system by HF5 achieved by the KRAs using equivalent keys and good keys for ELSA with \((\mathbb F_q, l,k,r,u)=(\mathbb F_{2^8},6,28,30,15)\).

Table 2. Lower-bounds/upper-bounds on the complexities of the KRAs using equivalent keys and good keys for ELSA under different forms of central maps, \(\mathcal F\), \(\overline{\mathcal{F}}\) and \(\widehat{\mathcal{F}}\) with \((F_{2^8}, 6,28,30,15)\)
Full size table

Key Recovery Attacks using Linear Part of the Central Map. It is also known that some coefficients of linear terms in the central map are zero. This does not significantly affect the KRAs since the number of quadratic terms with zero coefficients is much larger than that of linear terms with zero coefficients. When we reduce the number of variables in good key recovery, we use \(\varOmega '\) where each coordinate function has at least \(n-1\) linear terms (See Lemma 3.2). Even if \(\mathcal {F'}^{(k)}\) has only one linear term for each k, \(\mathcal {F'}^{(k)}\circ \varOmega '\) has at least \(n-1\) linear terms. Nevertheless, if there is no linear term in \(\mathcal {F}\), we can get nm linear terms with zero coefficients of \(\mathcal {F'}\circ \varOmega '\) and n variables in the constant part of \(\widetilde{T''}\) by choosing \(\varOmega \) and \(\varOmega '\) carefully satisfying Lemmas 3.1 and 3.2. Then we can set \(\varSigma '=\left( \widetilde{S'}\right) ^{-1}=S'\) so that the variables in \(\widetilde{S''}\) are removed. Finally, we get a system of \(m(n+1)\) quadratic equations with \(2n-u\) variables. In this case, for ELSA with \((F_{2^8},6,28,30,15)\), the complexity of solving this system by HF5 is \(2^{71}\).

3.4 Rank-Based Attacks

\(\bullet \) MinRank attack. In MinRank attacks, one tries to find linear combinations \(M=\sum _{i=1}^m \mu _i P^{(i)}\) of the matrices \(P^{(i)}\), where M has a minimal rank. Underlying idea of an algorithm to solve this MinRank problem [48] is to search for a vector lying in the kernel of the desired linear combination M. Complexity of the MinRank attack is determined by that of finding the linear combination. Since the forms of symmetric matrices of ELSA w.r.t. \(\mathcal{F}\) are the same as those of Rainbow, we can get that its complexity against the attack is \(q^{l+k+1}\) from [9, 44]. Next, by using similar technique, we investigate the complexity of ELSA w.r.t. \(\widehat{\mathcal{F}}\) against the attack in Proposition 3.1.

Proposition 3.1

The complexity of ELSA w.r.t. \(\widehat{\mathcal{F}}\) against the MinRank attack is \(min\{q^{l+2r-k+1}, q^{l+2r+1}, q^{2l+k+1}\}\).

Proof. In MinRank attacks, we must find a vector \(v \in \mathbb F_q^n\) such that \(v\in \ker P\), where P is a matrix with the minimal rank in Span\(\{P^{(i)}\}\). The probability for finding such a vector is the same as that of finding \(v' \in \mathbb F_q^n\) such that \(v' \in \ker Q\), where Q is a matrix with the minimal rank in Span\(\{\widehat{F}^{(i)}\}\) and \(\widehat{F}^{(i)}\) is the matrix of the quadratic part of \(\widehat{\mathcal{F}}\). More precisely, \(\widehat{F}^{(i)}\) has of the form \(\left( \begin{array}{ccc} * &{} 0 &{} * \\ 0 &{} 0 &{} * \\ * &{} * &{} 0 \\ \end{array} \right) \) in the first layer as given in Fig. 2. Then \(\widehat{F}^{(i)} \cdot (0,*,0)^T=(0,0,*)^T\). Let \(w_i=\widehat{F}^{(i)} \cdot (0, *,0)^T=(0,0,*)^T\). Then the probability that \(w_i\) is linearly dependent is

$$\begin{aligned} 1-\prod _{i=0}^{k-1}(1-\frac{q^i}{q^{r}}) > 1/q^{r-k+1}. \end{aligned}$$

Note that \(\sum _{i=1}^{k} \lambda _i\widehat{F}^{(i)}\) has a minimal rank. Hence, the probability of \(v' \in \ker (\sum _{i=1}^{k} \lambda _i\widehat{F}^{(i)})\) for a random vector \(v'\) and non-trivial \(\lambda _i\) is \(1/q^{l+r} \cdot 1/q^{r-k+1}=1/q^{l+2r-k+1}\), where the provability that the vector \(v'\) has of the form \((0,*,0)\) is \(1/q^{l+r}\). Similarly, the probabilities for \(\widehat{F}^{(i)} \cdot (*,0,0)\) and \(\widehat{F}^{(i)} \cdot (0,0,*)\) are \(1/q^{l+2r+1}\) and \(1/q^{2l+k+1}\), respectively.    \(\square \)

Finally, the complexity of ELSA against the MinRank attack is \(min\{q^{l+k+1}, q^{l+2r-k+1},\) \(q^{l+2r+1}, \ q^{2l+k+1}\}\).

  • HighRank Attack. In HighRank attacks, one tries to identify the variables appearing the lowest number of times in the central polynomials. The variables \(x_{l+k+r+1}, \cdots , x_n\) appear only in the quadratic terms of the central polynomials \((\mathcal{F}^{(k+1)}, \cdots , \mathcal{F}^{(k+u)})\) of the second layer of ELSA. Thus, it is similar to that of Rainbow. As in [44], we get its complexity against the HighRank attacks is \(q^{u} \cdot \frac{n^3}{6}\).

  • Kipnis-Shamir Attack (UOV Attack). Kipnis-Shamir attack [34] was originally used to break the balanced Oil and Vinegar signature scheme [41]. We consider the generalization to the unbalanced case. We have already known that the complexity of ELSA w.r.t. \(\mathcal{F}\) against the Kipnis-Shamir attack is \(q^{n-2u-1} \cdot u^4\) as in [44] since the forms of symmetric matrices of ELSA w.r.t. \(\mathcal{F}\) are the same as those of Rainbow.

Now, we give security analysis of ELSA with the central map \(\widehat{\mathcal{F}}\) against the Kipnis-Shamir attacks. We first define the following four index sets as

$$\begin{aligned}&\qquad \qquad D_1=\{i| 1 \le i \le l\}, \ D_2=\{i| l+1 \le i \le l+k\}, \\&D_3=\{i| l+k+1 \le i \le l+k+r\}, \ D_4=\{i| l+k+r+1 \le i \le n\}. \end{aligned}$$

We define five meaningful subspaces of \(\mathbb F_q^n\) for the attacks on ELSA as

$$\begin{aligned}&V_{1000}=\{(x_1, \cdots , x_n)| x_i=0, i \notin D_1\}, V_{0100}=\{(x_1, \cdots , x_n)| x_i=0, i \notin D_2\}, \\&V_{0010}=\{(x_1, \cdots , x_n)| x_i=0, i \notin D_3\}, V_{0001}=\{(x_1, \cdots , x_n)| x_i=0, i \notin D_4\}, \\&\qquad \qquad \qquad \qquad V_{1110}=\{(x_1, \cdots , x_n)| x_i=0, i \in D_4\}. \end{aligned}$$

The goal of the attacks is to find the preimage of the above subspaces under an equivalent key \(T'\). We use the following property: any linear combinations of the matrices \(\widehat{F}^{(1)}, \cdots , \widehat{F}^{(m)}\) is of the form \(\left( \begin{array}{cccc} * &{} * &{} * &{} 0 \\ * &{} * &{} * &{} 0 \\ * &{} * &{} * &{} * \\ 0 &{} 0 &{} * &{} 0 \\ \end{array} \right) \cdots (*)\) from Fig. 2. The following Theorems show why invariant subspaces exist with a certain probability.

Lemma 3.3

Let \(\phi : \mathbb F_q^n \rightarrow \mathbb F_q^n\) be a linear transformation of the form \((*)\). Then we get that \(\phi (V_{0001})\), \(\phi (V_{1000})\), and \(\phi (V_{0100})\) are subspaces of \(V_{0010}\), \(V_{1110}\) and \(V_{1110}\), respectively.

Note that the image of other subspaces except the three subspaces in Lemma 3.3 under the map \(\phi \) is the full space \(\mathbb F_q^n\).

Let \(H=\sum _{i=1}^m \lambda _i \widehat{F}^{(i)}\) be a linear combination of the matrices \(\widehat{F}^{(i)}\). Note that H has the form of \((*)\). Then we get the following Theorem as in [34].

Theorem 3.2

Assume that, for some k (\( 1 \le k \le m)\), the matrix \(\widehat{F}^{(k)}\) is invertible. Then, the map \((\widehat{F}^{(k)})^{-1} \cdot H\) has nontrivial invariant subspace \(\phi (V_{0001})\), \(\phi (V_{1000})\) and \(\phi (V_{0100})\) with probability not less than \(q^{-r+u}\), \(q^{-k-r}\) and \(q^{-l-r}\), respectively.

Proof. They are obtained from the following fact: \([(\widehat{F}^{(k)})^{-1} \cdot \widehat{F}^{(i)}](V_{0001}) \subset (\widehat{F}^{(k)})^{-1} (V_{0010})\) and \(V_{0001} \subset (\widehat{F}^{(k)})^{-1} (V_{0010})\), let \(\varPhi =(\widehat{F}^{(k)})^{-1} \cdot \widehat{F}^{(i)}\), then as in [33], we have

$$\begin{aligned} Pr[\varPhi (V_{0001}) \subset V_{0010}] \ge q^{-r+u}, \end{aligned}$$

where \(u=dim(V_{0001})\) and \(r=dim(V_{0010})\). Thus, we get a nontrivial invariant subspace \(V_{0001}\) with probability not less than \(q^{-r+u}\).    \(\square \)

Theorem 3.3

Let \(W=\sum _{i=1}^m \lambda _i P^{(i)}\) be a linear combination of the matrices \(P^{(i)}\) and let \(P^{(k)}\) (for some k, \(1 \le k \le m)\) be invertible. Then the map \((P^{(k)})^{-1} \cdot W\) has nontrivial invariant subspaces \(V_{0010}\), \(V_{1110}\) and \(V_{1110}\) which are subspaces of \(T^{-1}(V_{0010})\), \(T^{-1}(V_{1000})\) and \(T^{-1}(V_{0100})\) with probability not less than \(q^{-r+u}\), \(q^{-k-r}\) and \(q^{-l-r}\), respectively.

Proof. They are obtained from the Theorem 3.2 and the following:

$$\begin{aligned}&(P^{(k)})^{-1} \cdot W=(P^{(k)})^{-1} \cdot \sum _{i=1}^m \lambda _i P^{(i)}=(T^T \cdot F^{(k)} \cdot T)^{-1} \cdot \sum _{i=1}^m \lambda _i \cdot (T^T \cdot \widehat{F}^{(i)} \cdot T) \\&\qquad \qquad \qquad \quad =T^{-1} \cdot ( \sum _{i=1}^m \lambda _i (\widehat{F}^{(k)})^{-1} \cdot \widehat{F}^{(i)}) \cdot T. \end{aligned}$$
$$\begin{aligned}&(P^{(k)})^{-1} \cdot W(T^{-1}(V_{0001}))=(T^{-1} \cdot ( \sum _{i=1}^m \lambda _i (\widehat{F}^{(k)})^{-1} \cdot \widehat{F}^{(i)}) \cdot T)(T^{-1}(V_{0001})) \\&\qquad \qquad =T^{-1} \cdot ( \sum _{i=1}^m \lambda _i (F^{(k)})^{-1} \cdot F^{(i)})(V_{0001}) \subset T^{-1}(V_{0010}). \end{aligned}$$

Thus, we get a nontrivial invariant subspace \(V_{0001}\) with probability not less than \(q^{-r+u}\).    \(\square \)

Consequently, the complexity of ELSA against the Kipnis-Shamir attack is \(min\{q^{r-u}, q^{k+r}, q^{l+r},\ q^{n-2u-1} \cdot u^4 \}\).

Based on these security analysis, we can select secure parameter sets \((\mathbb F_q, l, k, r, u)\) that achieve given security levels.

4 Existential Unforgeability of ELSA

Here, we prove existential unforgeability of ELSA against an adaptive chosen-message attack under the hardness of the MQ-problem induced by a public key of ELSA.

4.1 Formal Security Model and Complexity Assumption

In this section, we describe formal security models of signature schemes. The most general security notion of signature schemes is existential unforgeability against an adaptive chosen-message attack. Its formal security model is defined as follows:

Existential Unforgeability against Adaptive Chosen-Message Attacks (EUF-acma). An adversary \(\mathcal A\)’s advantage \(Adv_{\mathcal{PKS}, \mathcal{A}}\) is defined as its probability of success in the following game between a challenger \(\mathcal C\) and \(\mathcal A\):

  • Setup. The challenger runs Setup algorithm and its resulting system parameters are given to \(\mathcal A\).

  • Sign Queries. \(\mathcal A\) issues the following queries: adaptively, \(\mathcal A\) requests a signature on a message \(\mathtt{m}_i\), \(\mathcal C\) returns a signature \(\sigma _i\).

  • Output. Eventually, \(\mathcal A\) outputs \(\sigma ^*\) on a message \(\mathtt{m}^*\) and wins the game if

    1. (i)

      Verify \((\mathtt{m}^*, \sigma ^*)=1\),

    2. (ii)

      \(\mathtt{m}^*\) has never requested to the Sign oracle.

Definition 4.1

A forger \(\mathcal{A} (t, g_H, q_S, \epsilon )\)-breaks a signature scheme if \(\mathcal A\) runs in time at most t, \(\mathcal A\) makes at most \(q_H\) queries to the hash oracle, \(q_S\) queries to the signing oracle and \(Adv_{\mathcal{PKS}, \mathcal{A}}\) is at least \(\epsilon \). A signature scheme is \((t, q_E, q_S, \epsilon )\)-EUF-acma if no forger \((t, q_H, q_S, \epsilon )\)-breaks it in the above game.

Next, we need to define the following sets as:

  • \(\mathcal{MQ}_{ELSA}(\mathbb F_q, m, n)\): a set of all quadratic equations defined over \(\mathbb F_q\) with m equations and n variables induced by all public keys of ELSA\((\mathbb F_q, l, k, r, u)\), where \(m=k+u\) and \(n=l+r+m\).

  • \(\mathcal{MQ}_{R}(\mathbb F_q, m, n)\): a set of all random quadratic equations defined over \(\mathbb F_q\) of m equations and n variables.

Definition 4.2

We say that the MQ-problem in \(\mathcal{MQ}_{X}(\mathbb F_q, m, n)\) is \((t, \epsilon )\)-hard if no t-time algorithm has advantage at least \(\epsilon \) in solving the MQ-problem in \(\mathcal{MQ}_{X}(\mathbb F_q, m, n)\).

To prove existential unforgeability of ELSA against an adaptive chosen-message attack, we want to find a reduction to the hardness of MQ-problem in \(\mathcal{MQ}_{ELSA}(\mathbb F_q, m, n)\). The hardness of the MQ-problem for a system of m quadratic equations with n variables mainly depends on the selection of \(\mathbb F_q\), m and n. However, the security of ELSA against the attacks presented in §3 depends on the selection of the specific parameter set \((\mathbb F_q, l, k, r, u)\) such that \(m=k+u\) and \(n=l+r+m\). If the parameter set \((\mathbb F_q, l, k, r, u)\) is chosen be secure against the MinRank attack, HighRank attack and Kipnis-Shamir attack, then it remains only two attacks to consider: the direct attack and KRAs with good keys. In Theorem 3.1, we have shown that the security of KRAs with good keys for ELSA is still reduced to the intractability of the MQ-problem, i.e., the complexity of the KRAs using good keys on ELSA is determined by solving \(n-1\) bihomogeneous equations and m quadratic equations with n variables.

4.2 Existential Unforgeability

Now, we prove existential unforgeability of ELSA against an adaptive chosen-message attack under the hardness of the MQ-problem induced by a public key of ELSA in the random oracle model.

Theorem 4.1

If the MQ-problem in \(\mathcal{MQ}_{ELSA}(\mathbb F_q, m, n)\) is \((t', \varepsilon ')\)-hard, ELSA\((\mathbb F_q, l, k, r, u)\) is \((t, q_{H}, q_S, \varepsilon )\)-EUF-acma, for any t and \(\varepsilon \) satisfying

$$\begin{aligned} \varepsilon \ge \texttt {e} \cdot (q_S+1) \cdot \varepsilon ', \ t' \ge t+q_H \cdot c_V+q_S \cdot c_S, \end{aligned}$$

where \(\texttt {e}\) is the base of the natural logarithm, and \(c_S\) and \(c_V\) are time for a signature generation and a signature verification, respectively, where \(m=k+u,\) and \(n=l+r+m\) if the parameter set \((\mathbb F_q, l, k, r, u)\) is chosen to be secure against the MinRank attack, HighRank attack, Kipnis-Shamir attack and KRAs using good keys.

Proof. An instance \((\mathcal{P}, \eta )\) of the MQ-problem in \(\mathcal{MQ}_{ELSA}(\mathbb F_q, m, n)\) is given, where \(\mathcal P\) is a quadratic system of m equations and n variables. Suppose that \(\mathcal A\) is a forger who breaks ELSA\((\mathbb F_q, l, k, r, u)\) with the target public key \(\mathcal P\). We will construct an algorithm \(\mathcal B\) which outputs a solution \(\mathbf{x} \in \mathbb F_q^n\) such that \(\mathcal{P}(\mathbf{x})=\eta \) by using \(\mathcal A\). Algorithm \(\mathcal B\) performs the following simulation by interacting with \(\mathcal A\).

Setup. Algorithm \(\mathcal B\) sets \(PK=\mathcal P\), which is a public key of ELSA\((\mathbb F_q, l, k, r, u)\).

At any time, \(\mathcal A\) can query a random oracle H and Sign oracle. To answer these queries, \(\mathcal B\) does the following:

For H-queries, \(\mathcal B\) maintains a list of tuples \((\mathtt{m}_i, c_i, \tau _i)\) as explained below. We call this list \(H\texttt {-list}\). When \(\mathcal A\) queries H at \(\mathtt{m}_i \in \{0, 1\}^*\),

  1. 1.

    If the query already appears on \(H\texttt {-list}\) in a tuple \((\mathtt{m}_i, c_i, \tau _i, \mathcal{P}(\tau _i))\) then \(\mathcal B\) returns \(H(\mathtt{m}_i)=\mathcal{P}(\tau _i)\).

  2. 2.

    Otherwise, \(\mathcal B\) picks a random coin \(c_i \in \{0, 1\}\) with \(Pr[c_i=0]=\frac{1}{q_S+1}\).

    • If \(c_i=1\) then \(\mathcal B\) chooses a random \(\tau _i \in \mathbb F_q^n\), adds a tuple \((\mathtt{m}_i, c_i, \tau _i, \mathcal{P}(\tau _i))\) to \(H\texttt {-list}\) and returns \(H(\mathtt{m}_i)=\mathcal{P}(\tau _i)\).

    • If \(c_i=0\) then \(\mathcal B\) adds \((\mathtt{m}_i, c_i, *, \eta )\) to \(H\texttt {-list}\) from the instance and returns \(H(\mathtt{m}_i)=\eta \).

Sign Queries. When \(\mathcal A\) makes a Sign-query on \(\mathtt{m}_i\), \(\mathcal B\) finds the corresponding tuple \((\mathtt{m}_i, c_i, \tau _i, \mathcal{P}(\tau _i))\) from \(H\texttt {-list}\).

  • If \(c_i=1\) then \(\mathcal B\) responds with \(\tau _i\).

  • If \(c_i=0\) then \(\mathcal B\) reports failure and terminates.

All responses to Sign queries not aborted are valid. If \(\mathcal B\) doesn’t abort as a result of \(\mathcal A\)’s Sign query then \(\mathcal A\)’s view in the simulation is identical to its view in the real attack.

Output. Finally, \(\mathcal A\) produces a signature \(\mathbf{\tau }^*\) on a message \(\mathtt{m}^*\). If it is not valid then \(\mathcal B\) reports failure and terminates. Otherwise, a query on \(m^*\) already appears on \(H\texttt {-list}\) in a tuple \((\mathtt{m}^*, c^*, \tau ^*, \mathcal{P}(\tau ^*))\): if \(c_*=1\) then reports failure and terminates. Otherwise, \(c^*=0\), i.e., (\(c^*, \mathtt{m}^*, *, \eta )\), then \(\mathcal{P}(\mathbf{\tau }^*)=\eta \). Finally, \(\mathcal B\) outputs \(\mathbf{\tau }^*\) is a solution of \(\mathcal P\).

To show that \(\mathcal B\) solves the given instance with probability at least \(\varepsilon '\), we analyze three events needed for \(\mathcal B\) to succeed:

  • \(E_1\): \(\mathcal B\) doesn’t abort as a result of \(\mathcal A\)’s Sign query.

  • \(E_2\): \(\mathcal A\) generates a valid and nontrivial signature forgery \(\tau _i\) on \(\mathtt{m}_i\).

  • \(E_3\): Event \(E_2\) occurs, \(c_i=0\) for the tuple containing \(\mathtt{m}_i\) in \(H\texttt {-list}\).

Algorithm \(\mathcal B\) succeeds if all of these events happen. The probability \(Pr[E_1 \wedge E_3]\) is decomposed as

$$\begin{aligned} Pr[E_1 \wedge E_3]=Pr[E_1] \cdot Pr[E_2 \wedge E_1] \cdot Pr[E_3|E_1 \wedge E_2] \ \cdots \ (**). \end{aligned}$$

The probability that \(\mathcal B\) doesn’t abort as a result of \(\mathcal A\)’s Sign query is at least \((1-\frac{1}{q_S+1})^{q_S}\) since \(\mathcal A\) makes at most \(q_S\) queries to the Sign oracle. Thus, \(Pr[E_1] \ge (1-\frac{1}{q_S+1})^{q_S}\). If \(\mathcal B\) doesn’t abort as a result of \(\mathcal A\)’s Sign query then \(\mathcal A\)’s view is identical to its view in the real attack. Hence, \(Pr[E_1 \wedge E_2] \ge \varepsilon \). Given that events \(E_1\), \(E_2\) and \(E_3\) happened, \(\mathcal B\) will abort if \(\mathcal A\) generates a forgery with \(c_i=1\). Thus, all the remaining \(c_i\) are independent of \(\mathcal A\)’s view. Since \(\mathcal A\) could not have issued a signature query for the output we know that c is independent of \(\mathcal A\)’s current view and therefore \(Pr[c=0|E_1 \wedge E_2] =\frac{1}{q_S+1}\). Then we get \(Pr[E_3|E_1 \wedge E_2] \ge \frac{1}{q_S+1}\). From \((**)\), \(\mathcal B\) produces the correct answer with probability at least

$$\begin{aligned} (1-\frac{1}{q_S+1})^{q_S} \cdot \varepsilon \cdot \frac{1}{q_S+1} \ \ge \ \frac{1}{\texttt {e}} \cdot \frac{\varepsilon }{(q_S+1)} \ \ge \ \varepsilon '. \end{aligned}$$

Algorithm \(\mathcal B\)’s running time is the same as \(\mathcal A\)’s running time plus the time that takes to respond to \(q_H\) H-queries, and \(q_S\) Sign-queries. The H- and Sign-queries require a signature verification and a signature generation, respectively. We assume that a signature generation and a signature verification take time \(c_S\) and \(c_V\), respectively. Thus, the total running time is at most \(t' \ge t+q_H \cdot c_V+q_S \cdot c_S\).    \(\square \)

Table 3. Complexities of ELSA\((\mathbb F_{2^8}, 6, 28, 30, 15)\) against all the attacks.
Full size table
Table 4. Performance, key sizes and signature sizes of ours, classical-ones and post-quantum ones.
Full size table

5 Selection of Parameter and Implementation

Here, we evaluate practical feasibility of ELSA targeting a recent Intel processor. We choose a secure and optimal parameter for ELSA and provide comparisons between ours, classical ones and Post-Quantum ones in terms of performance, key sizes and signature sizes.

5.1 Selection of Secure and Optimal Parameter

We want to select secure parameter set \((\mathbb F_q, l, k, r, u)\) for ELSA with the optimal secret key size at a 128-bit security level where \(m=k+u\) and \(n=l+r+m\). Based on our security analysis in Sect. 3, we choose \((\mathbb F_{2^8}, 6, 28, 30, 15)\) at the 128-bit security level. We summarize complexities of our parameter against the known attacks in Table 3. For computing of complexities against direct attacks and KRAs using good keys, we use HF5 with \(\omega =2\).

5.2 Result and Comparison

We implement ELSA\((\mathbb F_{2^8}, 6, 28, 30, 15)\) on an Intel Core i5-6600 3.3 GHz whose result is an average of 1,000 measurements for each function using the C++ programming language with g++ compiler. We follow the standard practice of disabling Turbo Boost and hyperthreading. For comparison, we also implement Rainbow\((\mathbb F_{2^8},36,21,22)\) on the same platform based on open source codes given by the eBACS project [6] since there is no record for Rainbow at the 128-bit security level. Table 4 gives benchmarking results of ELSA and compares the benchmarks to state-of-the-art results from the literatures or given by the eBACS project [6].

Our scheme is the fastest signature scheme in both signing and verification among classical ones and Post-Quantum ones. Compared to Rainbow, the secret key size of ELSA is reduced by a factor of 88% maintaining the same public key size. Compared to enTTS, the public key size of ELSA have reduced by a factor of 40%. Signing of ELSA is about 3.2 times faster than that of Rainbow. Signing and verification of ELSA is hundreds of times faster than those of MQDSS, respectively. Signing and verification of ELSA is about 17.2 times and 2.3 times faster than those of BLISS-BI, respectively. It takes 6 \(\upmu \)s and 13.3 \(\upmu \)s for signing and verification, respectively.

6 Conclusion

We have proposed a new MQ-signature scheme, ELSA, based on a hidden layer of quadratic equations. Our scheme is the fastest signature scheme in both signing and verification among classical ones as well as Post-Quantum ones. Compared to Rainbow, the secret key size in ELSA is reduced by a factor of 88% maintaining the same public key size. Signing of ELSA is about 3.2 times than that of Rainbow on Intel Core i5-6600. It takes 6.3 \(\upmu \)s and 13.39 \(\upmu \)s for signing and verification, respectively. There is still room for improvements in terms of performance. We believe that our scheme is a leading candidate for low-cost constrained devices. We have also shown that ELSA\((\mathbb F_q, l, k, r, u)\) is existential unforgeable against an adaptive chosen-message attack under the hardness of the MQ-problem in \(\mathcal{MQ}_{ELSA}(\mathbb F_q, m, n)\) in the random oracle model. However, this reduction doesn’t mean the reduction to the MQ-problem in \(\mathcal{MQ}_{R}(\mathbb F_q, m, n)\) although it haven’t been proved that the public key of the MQ-schemes could be distinguished from random one. It still remains an open problem to construct a high-speed MQ-signature schemes with a security reduction to the hardness of the MQ-problem in \(\mathcal{MQ}_R(\mathbb F_q, m, n)\).