Abstract
We construct the most efficient known pairing-based NIZK shuffle argument. It consists of three subarguments that were carefully chosen to obtain optimal efficiency of the shuffle argument:
-
1.
A same-message argument based on the linear subspace QANIZK argument of Kiltz and Wee,
-
2.
A (simplified) permutation matrix argument of Fauzi, Lipmaa, and Zając,
-
3.
A (simplified) consistency argument of Groth and Lu.
We prove the knowledge-soundness of the first two subarguments in the generic bilinear group model, and the culpable soundness of the third subargument under a KerMDH assumption. This proves the soundness of the shuffle argument. We also discuss our partially optimized implementation that allows one to prove a shuffle of \(100\,000\) ciphertexts in less than a minute and verify it in less than 1.5 min.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Consider the case of using mix-networks [9] in e-voting, where n voters individually encrypt their vote using a blindable public-key cryptosystem and send the encrypted votes to a bulletin board. After the vote casting period ends, the first mix-server gets all encrypted votes from the bulletin board. The mix-servers are ordered sequentially, creating a mix-network, and it is assumed that some of them are honest. The kth mix-server obtains input ciphertexts \((\mathfrak {M}_i)_{i \,=\, 1}^n\), shuffles them, and sends the resulting ciphertext tuple \((\mathfrak {M}'_i)_{i \,=\, 1}^n\) to the next mix-server. Shuffling means that the mix-server generates a random permutation \(\sigma \leftarrow _r S_n\) and a vector \(\varvec{t}\) of randomizers, and sets \(\mathfrak {M}'_i = \mathfrak {M}_{\sigma (i)} + \mathsf {Enc}_{\mathsf {pk}} (\mathfrak {0}; t_i)\).Footnote 1
If at least one of the mix-servers behaves honestly, the link between a voter and his votes is completely hidden. However, in the malicious model, a corrupt mix-server can do an incorrect shuffle, resulting in a set of decrypted votes that do not reflect the original voters’ votes. Hence there needs to be some additional steps to achieve security against corruption.
The cryptographically prudent way to proceed is to get each mix-server to prove in zero-knowledge [18] that her shuffle was done correctly. The resulting proof is known as a (zero-knowledge) shuffle argument. Based on earlier work [25, 34], in CT-RSA 2016, Fauzi and Lipmaa (FL, [14]) proposed the then most efficient shuffle argument in the common reference string (CRS, [8]) model in terms of prover’s computation.Footnote 2 Importantly, the FL shuffle argument is based on the standard Elgamal cryptosystem. The culpable soundness [25, 26] of the FL shuffle argument is proven under a knowledge assumption [10] and three computational assumptions. Intuitively, culpable soundness means that if a cheating adversary produces an invalid shuffle (yet accepted by the verifier) together with the secret key, then one can break one of the underlying knowledge or computational assumptions.
While the FL shuffle argument is quite efficient for the prover, it is quite inefficient for the verifier. More precisely, while the prover’s online cost is only dominated by 4n exponentiations in \(\mathbb {G}_1\), the verifier’s online cost is dominated by 8n pairings. (See Table 1.) Depending on the concrete implementation, a pairing can be up to 8 times slower than a \(\mathbb {G}_1\) exponentiation. Such a large gap is non-satisfactory since verification time is more important in practice.
In ACNS 2016, González and Ràfols [20] proposed a new shuffle argument that importantly relies only on standard (falsifiable) assumptions. However, they achieve this (and efficient computation) by allowing the CRS to be quadratically long in n. Since in e-voting applications one could presumably have \(n > 2^{20}\), quadratic CRS length will not be acceptable in such applications.
In Asiacrypt 2016, Fauzi, Lipmaa and Zając (FLZ, [15]) improved on the efficiency of the FL shuffle argument by proving knowledge-soundness (not culpable soundness) in the generic bilinear group model (GBGM, [35, 39]). By additionally using batching techniques, they sped up the verification time of the FL shuffle argument approximately 3.5 times and the online verification time approximately twice. Here, the precise constants depend on how efficient operations such pairings and exponentiations in different groups are relative to each other; they do not provide an implementation of their shuffle.
However, due to the construction of the FLZ argument, they need each message to be encrypted twice, in \(\mathbb {G}_1\) and \(\mathbb {G}_2\). Since Elgamal cannot guarantee security in such a case, they use the non-standard ILin cryptosystem of Escala et al. [13]. This means that each ciphertext in this case will consist of 6 group elements, which makes storing and transmitting them more burdensome.
This results in several concrete drawbacks. First, since the prover’s online complexity includes shuffling the ciphertexts and uses a non-standard cryptosystem (amongst other things), the prover’s online complexity in the FLZ shuffle argument is more than 4 times worse (using the comparison given in [15]) than in the FL shuffle argument. Second, since plaintexts in this shuffle argument are elements of \(\mathbb {Z}_q\), decryption requires computing a discrete logarithm, which means that plaintexts must be small elements of \(\mathbb {Z}_q\) (e.g. only 40 bits long). This rules out voting mechanisms with sufficiently complex ballots, such as the single transferable vote. Third, the GBGM knowledge-soundness proof of this shuffle argument means that there must exist a generic adversary that knows the discrete logarithm of each ballot submitted by each individual voter. Such a version of soundness (named white-box soundness in [14]) seems to be more dubious than culpable soundness achieved by the Groth-Lu [25] and FL shuffle arguments. (See [14] for more thorough comparison of these two soundness definitions.) Fourth, the CRS of this shuffle argument has public keys in both \(\mathbb {G}_1\) and \(\mathbb {G}_2\), which makes it more difficult to design an efficient shuffle or to prove its soundness in the GBGM. Indeed, [15] used a computer algebra system to derive knowledge-soundness of their shuffle argument.
This brings us to the main question of this paper:
Is it possible to construct a NIZK shuffle argument that shares the best features of the FL and the FLZ shuffle arguments? That is, it would use standard Elgamal (and in only one group), be (non-whitebox) sound, have linear-length CRS, have prover as efficient or better than in the FL shuffle argument, and have verifier as efficient or better than in the FLZ shuffle argument. Moreover, can one simplify (significantly?) the soundness proof of the FLZ shuffle argument while not losing in efficiency?
Our Constructions. We answer the main question positively, constructing a new pairing-based NIZK shuffle argument that is more efficient than prior work in essentially all parameters. As in [14], we use the Elgamal cryptosystem (with plaintexts in \(\mathbb {G}_2\)), which means that unlike [15], compatible voting mechanisms are not restricted by the size of the plaintext space. We construct more efficient subarguments, which sometimes leads to a significant efficiency gain. Since the CRS has very few elements from \(\mathbb {G}_2\), the new shuffle has much simpler soundness proofs than in the case of the FLZ shuffle argument. Moreover, as in [14, 25] (but not in [15, 34]), we do not give the generic adversary in our soundness proof access to the discrete logarithms of encrypted messages. Our high-level approach in the shuffle argument is as follows; it is similar to the approach in the FL shuffle argument except that we use (significantly) more efficient subarguments.
We first let the prover choose a permutation matrix and commit separately to its every row. The prover then proves that the committed matrix is a permutation matrix, by proving that each row is a unit vector, including the last row which is computed explicitly, see Sect. 4.2. We construct a new unit vector argument based on the square span programs of Danezis et al. [11]; it is similar to but somewhat simpler than the 1-sparsity argument of [15]. Basically, to show that a vector \(\varvec{a}\) is unit vector, we choose polynomials \((P_i (X))_{i \in [0 \, .. \, n]}\) that interpolate a certain matrix (and a certain vector) connected to the definition of “unit vectorness”, and then commit to \(\varvec{a}\) by using a version of the extended Pedersen commitment scheme, \(\mathfrak {c} = \sum _{i\,=\,1}^n a_i [P_i ({\chi })]_{1} + r [\varrho ]_{1}\) for trapdoor values \((\chi , \varrho )\) and randomizer r. (This commitment scheme, though for different polynomials \(P_i (X)\), was implicitly used first by Groth [24] in EUROCRYPT 2016, and then used in the FLZ shuffle argument; similar commitment schemes have been used before [19, 23, 32].) The new unit vector argument differs from the corresponding (1-sparsity) argument in [15] by a small optimization that makes it possible to decrease the number of trapdoor elements by one. If the unit vector argument for each row is accepting, it follows that the committed matrix is a permutation matrix [14]. The knowledge-soundness proof of the new unit vector argument is almost trivial, in contrast to the very complex machine-assisted knowledge-soundness proof in [15].
We then use the same high-level idea as previous NIZK shuffle arguments [14, 15, 25, 34] to obtain a shuffle argument from a permutation matrix argument. Namely, we construct a verification equation that holds tautologically under a corresponding KerMDH [36] assumption. That is, if the permutation matrix argument is knowledge-sound, the mentioned verification equation holds, and the KerMDH assumption holds, then the prover has used his committed permutation matrix to also shuffle the ciphertexts.
However, as in [14, 15, 25, 34], the resulting KerMDH assumption itself will not be secure if we use here the same commitment scheme as before. Intuitively, this is since the polynomials \(P_i (X)\) were carefully chosen to make the permutation matrix argument as efficient as possible. Therefore, we define an alternative version of the extended Pedersen commitment scheme with the commitment computed as \(\mathfrak {\hat{c}} = \sum a_i [\hat{P}_i ({\chi })]_{1} + r [\hat{\varrho }]_{1}\) for trapdoor values \((\chi , \hat{\varrho })\) and randomizer r. Here, \(\hat{P}_i (X)\) are well-chosen polynomials that satisfy a small number of requirements, including that \(\{P_i (X) \hat{P}_j (X)\}_{1 \le i, j \le n}\) is linearly independent.
Before going on, we obviously need an efficient argument (that we call, following [14], a same-message argument) to show that \(\mathfrak {c}\) and \(\mathfrak {\hat{c}}\) commit to the same vector \(\varvec{a}\) (and use the same randomness r) while using different shrinking commitment schemes. We first write down the objective of this argument as the requirement that  belongs to a subspace generated by a certain matrix \(\varvec{M}\). After doing that, we use the quasi-adaptive NIZK (QANIZK, [28, 29]) argument of Kiltz and Wee (EUROCRYPT 2015, [30]) for linear subspaces to construct an efficient same-message argument. Since we additionally need it to be knowledge-sound, we give a proof in GBGM.
belongs to a subspace generated by a certain matrix \(\varvec{M}\). After doing that, we use the quasi-adaptive NIZK (QANIZK, [28, 29]) argument of Kiltz and Wee (EUROCRYPT 2015, [30]) for linear subspaces to construct an efficient same-message argument. Since we additionally need it to be knowledge-sound, we give a proof in GBGM.
The new consistency argument is similar to but again more efficient than the consistency arguments of previous pairing-based shuffles. Here, we crucially use the fact that neither the permutation matrix argument nor the same-message argument add “too many” \(\mathbb {G}_2\) elements to the CRS. Hence, while the Groth-Lu and FL shuffle arguments require two consistency verification equations, for us it suffices to only have one. (The Lipmaa-Zhang [34] and FLZ shuffle arguments have only one consistency verification equation, but this was compensated by using a non-standard cryptosystem with ciphertexts of length 6.)
In fact, we generalize the consistency argument to prove that given a committed matrix \(\varvec{E}\) and two tuples of ciphertexts \(\varvec{\mathfrak {M}}'\) and \(\varvec{\mathfrak {M}}\), it holds that \(\mathsf {Dec}_{\mathsf {sk}} (\varvec{\mathfrak {M}}') = \varvec{E} \cdot \mathsf {Dec}_{\mathsf {sk}} (\varvec{\mathfrak {M}})\). Moreover, we prove that the consistency argument is culpably sound [25, 26] under a suitable KerMDH [36] assumption, and we prove that the concrete KerMDH assumption holds in the GBGM.
Finally, we will give a standard (i.e., non-culpable) soundness proof for the full shuffle argument, assuming that the used commitment scheme is computationally binding, the same-message argument and the permutation matrix argument are knowledge-sound, and the consistency argument is culpably sound. Additionally, as in the FLZ shuffle argument, we use batching techniques [4] to speed up verification time. However, we use batching in a more aggressive manner than in the FLZ shuffle argument.
Efficiency Comparison. We provide the first implementation of a pairing-based shuffle argument. Our implementation is built on top of the freely available libsnark library, [6]. In fact, we implement two versions of the new shuffle argument, where in the second version we switch the roles of the groups \(\mathbb {G}_1\) and \(\mathbb {G}_2\). In the first case we get better overall prover’s computation, while in the second case we get the most efficient online computation for both prover and verifier, and overall the most efficient verifier.
Table 1 shows a comparison between both versions of the new shuffle argument and prior state of the art CRS-based shuffle arguments with either the best prover’s computational complexity or best verifier’s computational complexity. Hence, we for instance do not include in this comparison table prior work by Groth and Lu [25] or Lipmaa and Zhang [34], since their shuffle arguments are slower than [14, 15] in both prover’s and verifier’s computation. We also do not include the shuffle argument of González and Ràfols [20] since it has quadratic CRS length. In each row, the argument with best efficiency or best security property is highlighted.
Units (the main parameter) are defined in Table 3 in Sect. 7. One should compare the number of units, which is a weighted sum of different exponentiations and pairings, and hence takes into account the fact that (say) computations in \(\mathbb {G}_1\) and \(\mathbb {G}_2\) take different time. Moreover, this table counts separately the number of general exponentiations, multi-exponentiations, and fixed-base exponentiations, since the last two can be much more efficient than general exponentiations. We take this into account by using different unit values for these three types of exponentiations, see Table 3 for the number of units required for each type of operation. Note that we use our implementation of each operation in libsnark to compute the number of units.
Table 2 gives the running time of the new shuffle argument (without and with switching the groups) on our test machine. As seen from this table, our preliminary implementation enables one to prove a shuffle argument in less than 1 min and verify it in less than 1.5 min for \(n = 100\,000\). After switching the groups, the prover’s online computation takes less than 15 s and online verification takes less than 3 min for \(n = 300\,000\). This means that the new shuffle argument is actually ready to be used in practice. Section 7 provides more information about implementation, including the definition of units and data about the test machine.
2 Preliminaries
Let \(S_n\) be the symmetric group on n elements, i.e., all elements of the group are permutations on n elements. All vectors will be by default column vectors. By \(\varvec{a} = (a_i)_{i\,=\,1}^n\) we denote column vectors and by \(\varvec{a} = (a_1, \dots , a_n)\) we denote row vectors. For a matrix \(\varvec{A}\), \(\varvec{A}_i\) is its ith row vector and \(\varvec{A}^{(i)}\) is its ith column vector. A Boolean \(n \times n\) matrix \(\varvec{A}\) is a permutation matrix representing \(\sigma \in S_n\), when \(A_{i j} = 1\) iff \(\sigma (i) = j\). Clearly, in this case \(\varvec{A} \varvec{x} = (x_{\sigma (i)})_{i\,=\,1}^n\) for any vector \(\varvec{x}\).
For a field \(\mathbb {F}\), let \(\mathbb {F}[\varvec{X}]\) be the ring of multivariate polynomials over \(\mathbb {F}\), and let \(\mathbb {F}[\varvec{X}^{\pm 1}]\) be the ring of multivariate Laurent polynomials over \(\mathbb {F}\). For any (Laurent) polynomials \(f_i (X)\), \(i \in [1 \, .. \, n]\), we denote \(\varvec{f} (X) = (f_i (X))_{i\,=\,1}^n\).
Let \((\omega _i)_{i\,=\,1}^{n\,+\,1}\) be \(n + 1\) different values in \(\mathbb {Z}_q\). For example, one can define \(\omega _i = i\). Define the following polynomials:
-
\(Z (X) = \prod _{i\,=\,1}^{n\,+\,1} (X - \omega _i)\): the unique degree \(n + 1\) monic polynomial such that \(Z (\omega _i) = 0\) for all \(i \in [1 \, .. \, n]\).
-
\(\ell _i (X) = \prod _{\begin{array}{c} j\,=\,1, j \ne i \end{array}}^{n\,+\,1} \frac{X - \omega _j}{\omega _i - \omega _j}\): the ith Lagrange basis polynomial, i.e., the unique degree n polynomial such that \(\ell _i (\omega _i) = 1\) and \(\ell _i (\omega _j) = 0\) for \(j \ne i\).
Cryptography. Let \(\kappa \) be the security parameter; intuitively it should be difficult to break a hardness assumption or a protocol in time \(O (2^\kappa )\). If \(f (\kappa )\) is a negligible function then we write \(f (\kappa ) \approx _\kappa 0\). We use type-III, asymmetric, pairings [17]. Assume we use a secure bilinear group generator \(\mathsf {BG}\) that on input \((1^\kappa )\) returns \((q, \mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, \mathfrak {g}_1, \mathfrak {g}_2, \bullet )\), where \(\mathbb {G}_1\), \(\mathbb {G}_2\), and \(\mathbb {G}_T\) are three groups of prime order q, \(\bullet : \mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T\), \(\mathfrak {g}_1\) generates \(\mathbb {G}_1\), \(\mathfrak {g}_2\) generates \(\mathbb {G}_2\), and \(\mathfrak {g}_T = \mathfrak {g}_1 \bullet \mathfrak {g}_2\) generates \(\mathbb {G}_T\). It is required that \(\bullet \) is efficiently computable, bilinear, and non-degenerate.
To implement pairing-based cryptography, we use the libsnark library [6] which currently provides (asymmetric) Ate pairings [27] over Barreto-Naehrig curves [2, 37] with 256 bit primes. Due to recent advances in computing discrete logarithms [31] this curve does not guarantee 128 bits of security, but still roughly achieves 100 bits of security [1].
Within this paper, we use additive notation combined with the bracket notation [13] and denote the elements of \(\mathbb {G}_z\), \(z \in \{1, 2, T\}\), as in \([a]_{z}\) (even if a is unknown). Alternatively, we denote group elements by using the Fraktur font as in \(\mathfrak {b}\). We assume that \(\cdot \) has higher precedence than \(\bullet \); for example, \(b \mathfrak {a} \bullet \mathfrak {c} = (b \mathfrak {a}) \bullet \mathfrak {c}\); while this is not important mathematically, it makes a difference in implementation since exponentiation in \(\mathbb {G}_1\) is cheaper than in \(\mathbb {G}_T\). In this notation, we write the generator of \(\mathbb {G}_z\) as \(\mathfrak {g}_z = [1]_{z}\) for \(z \in \{1, 2, T\}\). Hence, \([a]_{z} = a \mathfrak {g}_z\), so the bilinear property can be written as \( [a]_{1} \bullet [b]_{2} = (a b) [1]_{T}= [a b]_{T}\).
We freely combine additive notation with vector notation, by defining say \([a_1, \dots , a_s]_{z} = ([a_1]_{z}, \dots , [a_s]_{z})\), and \([\varvec{A}]_{1} \bullet [\varvec{B}]_{2} = [\varvec{A B}]_{T}\) for matrices \(\varvec{A}\) and \(\varvec{B}\) of compatible size. We sometimes misuse the notation and, say, write \([\varvec{A}]_{2} \varvec{B}\) instead of the more cumbersome \((\varvec{B}^\top [\varvec{A}]_{2}^\top )^\top \). Hence, if \(\varvec{A}\), \(\varvec{B}\) and \(\varvec{C}\) have compatible dimensions, then \((\varvec{B}^\top [\varvec{A}]_{1}^\top )^\top \bullet [\varvec{C}]_{2} = [\varvec{A}]_{1} \varvec{B} \bullet [\varvec{C}]_{2} = [\varvec{A}]_{1} \bullet \varvec{B} [\varvec{C}]_{2}\).
Recall that a distribution \(\mathcal {D}_{par}\) that outputs matrices of group elements \([\varvec{M}]_{1} \in \mathbb {G}_1^{n \times t}\) is witness-sampleable [28], if there exists a distribution \(\mathcal {D}'_{par}\) that outputs matrices of integers \(\varvec{M}' \in \mathbb {Z}_q^{n \times t}\), such that \([\varvec{M}]_{1}\) and \([\varvec{M}']_{1}\) have the same distribution.
We use the Elgamal cryptosystem [12] \((\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})\) in group \(\mathbb {G}_2\). In Elgamal, the key generator \(\mathsf {Gen}(1^\kappa )\) chooses a secret key \(\mathsf {sk}\leftarrow _r \mathbb {Z}_q\) and a public key \(\mathsf {pk}\leftarrow [1, \mathsf {sk}]_{2}\) for a generator \([1]_{2}\) of \(\mathbb {G}_2\) fixed by \(\mathsf {BG}\). The encryption algorithm sets \(\mathsf {Enc}_{\mathsf {pk}} (\mathfrak {m}; r) = ([0]_{2}, \mathfrak {m}) + r \cdot \mathsf {pk}\) for \(\mathfrak {m}\in \mathbb {G}_2\) and \(r \leftarrow _r \mathbb {Z}_q\). The decryption algorithm sets \(\mathsf {Dec}_{\mathsf {sk}} (\mathfrak {M}_1, \mathfrak {M}_2) = \mathfrak {M}_2 - \mathsf {sk}\cdot \mathfrak {M}_1\). Note that \(\mathsf {Enc}_{\mathsf {pk}} (\mathfrak {0}; r) = r \cdot \mathsf {pk}\). The Elgamal cryptosystem is blindable, with \(\mathsf {Enc}_{\mathsf {pk}} (\mathfrak {m}; r_1) + \mathsf {Enc}_{\mathsf {pk}} (\mathfrak {0}; r_2) = \mathsf {Enc}_{\mathsf {pk}} (\mathfrak {m}; r_1 + r_2)\). Clearly, if \(r_2\) is uniformly random, then \(r_1 + r_2\) is also uniformly random.
Finally, for \([a]_{1} \in \mathbb {G}_1\), and \([\varvec{b}]_{2} \in \mathbb {G}_2^{1 \times 2}\), let \([a]_{1} \circ [\varvec{b}]_{2} := [a \cdot \varvec{b}]_{T} = [a \cdot b_1, a \cdot b_2]_{T} \in \mathbb {G}_T^{1 \times 2}\). Analogously, for \([\varvec{a}]_{1} \in \mathbb {G}_1^n\), and \([\varvec{B}]_{2} \in \mathbb {G}_2^{n \times 2}\), let \([\varvec{a}]_{1}^\top \circ [\varvec{B}]_{2} := \sum _{i = 1}^n [a_i]_{1} \circ [\varvec{B}_i]_{2} \in \mathbb {G}_T^2\). Intuitively, here \([\varvec{b}]_{2}\) is an Elgamal ciphertext and \([\varvec{B}]_{2}\) is a vector of Elgamal ciphertexts.
Kernel Matrix Assumptions [36]. Let \(k \in \mathbb {N}\). We call \(\mathcal {D}_{k + d, k}\) a matrix distribution [13] if it outputs matrices in \(\mathbb {Z}_q^{(k\,+\,d) \times k}\) of full rank k in polynomial time. W.l.o.g., we assume that the first k rows of \(\varvec{A} \leftarrow \mathcal {D}_{k + d, k}\) form an invertible matrix. We denote \(\mathcal {D}_{k + 1, k}\) as \(\mathcal {D}_k\).
Let \(\mathcal {D}_{k + d, k}\) be a matrix distribution and \(z \in \{1, 2\}\). The \(\mathcal {D}_{k + d, k}\) -KerMDH assumption [36] holds in \(\mathbb {G}_z\) relative to algorithm \(\mathsf {BG}\), if for all probabilistic polynomial-time \(\mathcal {A}\),
By varying the distribution \(\mathcal {D}_{k\,+\,d, k}\), one can obtain various assumptions (such as the SP assumption of Groth and Lu [25] or the PSP assumption of Fauzi and Lipmaa [14]) needed by some previous shuffle arguments.
Since we use KerMDH to prove soundness of subarguments of the shuffle argument, we define a version of this assumption with an auxiliary input that corresponds to the CRS of the shuffle argument. We formalize it by defining a valid CRS distribution \(\mathcal {D}_{n\,+\,d, \,d}\) to be a joint distribution of an \((n + d) \times d\) matrix distribution and a distribution of auxiliary inputs \(\mathsf {aux}\), such that
-
1.
\(\mathsf {aux}\) contains only elements of the groups \(\mathbb {G}_1\), \(\mathbb {G}_2\), and \(\mathbb {G}_T\),
-
2.
\(\mathcal {D}_{n + d, d}\) outputs as a trapdoor \(\mathsf {td}\) all the used random coins from \(\mathbb {Z}_q\).
We denote this as \((\varvec{M}, \mathsf {aux}; \mathsf {td}) \leftarrow _r \mathcal {D}_{n\,+\,d, d}\). We prove the culpable soundness of the consistency argument under a variant of the KerMDH assumption that allows for an auxiliary input.
Definition 1
(KerMDH with an auxiliary input). Let \(\mathcal {D}_{n + d, d}\) be a valid CRS distribution. The \(\mathcal {D}_{n + d, d}\)-KerMDH assumption with an auxiliary input holds in \(\mathbb {G}_z\), \(z \in \{1, 2\}\), relative to algorithm \(\mathsf {BG}\), if for all probabilistic polynomial-time \(\mathcal {A}\),
Commitment Schemes. A (pairing-based) trapdoor commitment scheme is a pair of efficient algorithms \((\mathsf {K}, \mathsf {com})\), where \(\mathsf {K}(\mathsf {gk})\) (for \(\mathsf {gk}\leftarrow \mathsf {BG}(1^\kappa )\)) outputs a commitment key \(\mathsf {ck}\) and a trapdoor \(\mathsf {td}\), and the commitment algorithm outputs \(\mathfrak {a}\leftarrow \mathsf {com}(\mathsf {gk}, \mathsf {ck}, \varvec{a}; r)\). A commitment scheme is computationally binding if for any \(\mathsf {ck}\) output by \(\mathsf {K}\), it is computationally infeasible to find \((\varvec{a}, r) \ne (\varvec{a}', r)\), such that \(\mathsf {com}(\mathsf {gk}, \mathsf {ck}, \varvec{a}; r) = \mathsf {com}(\mathsf {gk}, \mathsf {ck}, \varvec{a}'; r')\). A commitment scheme is perfectly hiding if for any \(\mathsf {ck}\) output by \(\mathsf {K}\), the distribution of the output of \(\mathsf {com}(\mathsf {gk}, \mathsf {ck}, \varvec{a}; r)\) does not depend on \(\varvec{a}\), assuming that r is uniformly random. A commitment scheme is trapdoor, if given access to \(\mathsf {td}\) it is trivial to open the commitment to any value.
Throughout this paper, we use the following trapdoor commitment scheme, first implicitly used by Groth [24]. Fix some linearly independent polynomials \(P_i (X)\). Let \(\mathsf {gk}\leftarrow \mathsf {BG}(1^\kappa )\), and \(\mathsf {td}= (\chi , \varrho ) \leftarrow _r \mathbb {Z}_q^2\). Denote \(\varvec{P} = (P_i (\chi ))_{i\,=\,1}^n\). Let  , and
, and  . We will call it the \(((P_i (X))_{i\,=\,1}^n, X_\varrho )\) -commitment scheme.
. We will call it the \(((P_i (X))_{i\,=\,1}^n, X_\varrho )\) -commitment scheme.
Several variants of this commitment scheme are known to be perfectly hiding and computational binding under a suitable computational assumption [19, 23, 32]. Since this commitment scheme is a variant of the extended Pedersen commitment scheme, it can be proven to be computationally binding under a suitable KerMDH assumption [36].
Theorem 1
Let  be the distribution of \(\mathsf {ck}\) in this commitment scheme. The \(((P_i (X))_{i\,=\,1}^n, X_\varrho )\)-commitment scheme is perfectly hiding, and computationally binding under the \(\mathcal {D}^{((P_i (X))_{i\,=\,1}^n, X_\varrho )}_n\)-KerMDH assumption. It is trapdoor with \(\mathsf {td}= (\chi , \varrho )\).
be the distribution of \(\mathsf {ck}\) in this commitment scheme. The \(((P_i (X))_{i\,=\,1}^n, X_\varrho )\)-commitment scheme is perfectly hiding, and computationally binding under the \(\mathcal {D}^{((P_i (X))_{i\,=\,1}^n, X_\varrho )}_n\)-KerMDH assumption. It is trapdoor with \(\mathsf {td}= (\chi , \varrho )\).
Proof
(Sketch). Given two different openings \((\varvec{a}, r)\) and \((\varvec{a}', r')\) to a commitment, \((\varvec{a} - \varvec{a}', r - r')\) is a solution to the KerMDH problem. Perfect hiding is obvious, since \(\varrho \) is not 0, and hence \(r [\varrho ]_{1}\) is uniformly random. Given \((\varvec{a}, r)\), one can open \(\mathsf {com}(\mathsf {gk}, \mathsf {ck}, \varvec{a}; r)\) to \((\varvec{a}', r')\) by taking \(r' = r + (\sum _{i\,=\,1}^n (a_i - a'_i) P_i (\chi )) / \varrho \). \(\square \)
Generic Bilinear Group Model. A generic algorithm uses only generic group operations to create and manipulate group elements. Shoup [39] formalized it by giving algorithms access to random injective encodings \(\langle \langle \mathfrak {a} \rangle \rangle \) instead of real group elements \(\mathfrak {a}\). Maurer [35] considered a different formalization, where the group elements are given in memory cells, and the adversary is given access to the address (but not the contents) of the cells. For simplicity, let’s consider Maurer’s formalization. The memory cells initially have some input (in our case, the random values generated by the CRS generator together with other group elements in the CRS). The generic group operations are handled through an oracle that on input \((op, i_1, \dots , i_n)\), where op is a generic group operation and \(i_j\) are addresses, first checks that memory cells in \(i_j\) have compatible type \(z \in \{1, 2, T\}\) (e.g., if \(op = +\), then \(i_1\) and \(i_2\) must belong to the same group \(\mathbb {G}_z\)), performs op on inputs \((i_1, \dots , i_n)\), stores the output in a new memory cell, and then returns the address of this cell. In the generic bilinear group model (GBGM), the oracle can also compute the pairing \(\bullet \). In addition, the oracle can answer equality queries.
We will use the following, slightly less formal way of thinking about the GBGM. Each memory cell has an implicit polynomial attached to it. A random value generated by the CRS generator is assigned a new indeterminate. If an \((+, i_1, i_2)\) (resp., \((\bullet , i_1, i_2)\)) input is given to the oracle that successfully returns address \(i_3\), then the implicit polynomial attached to \(i_3\) will be the sum (resp., product) of implicit polynomials attached to \(i_1\) and \(i_2\). Importantly, since one can only add together elements from the same group (or, from the memory cells with the same type), this means that any attached polynomials with type 1 or 2 can only depend on the elements of the CRS that belong to the same group.
A generic algorithm does not know the values of the indeterminates (for her they really are indeterminates), but she will know all attached polynomials. At any moment, one can ask the oracle for an equality test between two memory cells \(i_1\) and \(i_2\). A generic algorithm is considered to be successful if she makes — in polynomial time — an equality test query \((=, i_1, i_2)\) that returns success (the entries are equal) but \(i_1\) and \(i_2\) have different polynomials \(F_1 (\varvec{X})\) and \(F_2 (\varvec{X})\) attached to them. This is motivated by the Schwartz-Zippel lemma [38, 40] that states that if \(F_1 (\varvec{X}) \ne F_2 (\varvec{X})\) as a polynomial, then there is negligible probability that \(F_1 (\varvec{\chi }) = F_2 (\varvec{\chi })\) for uniformly random \(\varvec{\chi }\).
Zero Knowledge. Let \(\mathcal {R}= \{(u, w)\}\) be an efficiently computable binary relation with \(|w| = \textsf {poly}(|u|)\). Here, u is a statement, and w is a witness. Let \(\mathcal {L}= \{u: \exists w, (u, w) \in \mathcal {R}\}\) be an \(\mathbf {NP}\)-language. Let \(n = |u|\) be the input length. For fixed n, we have a relation \(\mathcal {R}_n\) and a language \(\mathcal {L}_n\). Since we argue about group elements, both \(\mathcal {L}_n\) and \(\mathcal {R}_n\) are group-dependent and thus we add \(\mathsf {gk}\) (output by \(\mathsf {BG}\)) as an input to \(\mathcal {L}_n\) and \(\mathcal {R}_n\). Let \(\mathcal {R}_n (\mathsf {gk}) := \{(u, w): (\mathsf {gk}, u, w) \in \mathcal {R}_n\}\).
A non-interactive argument for a group-dependent relation family \(\mathcal {R}\) consists of four probabilistic polynomial-time algorithms: a setup algorithm \(\mathsf {BG}\), a common reference string (CRS) generator \(\mathsf {K}\), a prover \(\mathsf {P}\), and a verifier \(\mathsf {V}\). Within this paper, \(\mathsf {BG}\) is always the bilinear group generator that outputs \(\mathsf {gk}\leftarrow (q, \mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, \mathfrak {g}_1, \mathfrak {g}_2, \bullet )\). For \(\mathsf {gk}\leftarrow \mathsf {BG}(1^\kappa )\) and \((\mathsf {crs}, \mathsf {td}) \leftarrow \mathsf {K}(\mathsf {gk}, n)\) (where n is input length), \(\mathsf {P}(\mathsf {gk}, \mathsf {crs}, u, w)\) produces an argument \(\pi \), and \(\mathsf {V}(\mathsf {gk}, \mathsf {crs}, u, \pi )\) outputs either 1 (accept) or 0 (reject). The verifier may be probabilistic, to speed up verification time by the use of batching techniques [4].
A non-interactive argument \(\varPsi \) is perfectly complete, if for all \(n = \textsf {poly}(\kappa )\),
\(\varPsi \) is adaptively computationally sound for \(\mathcal {L}\), if for all \(n = \textsf {poly}(\kappa )\) and all non-uniform probabilistic polynomial-time adversaries \(\mathcal {A}\),
We recall that in situations where the inputs have been committed to using a computationally binding trapdoor commitment scheme, the notion of computational soundness does not make sense (since the commitments could be to any input messages). Instead, one should either prove culpable soundness or knowledge-soundness.
\(\varPsi \) is adaptively computationally culpably sound [25, 26] for \(\mathcal {L}\) using a polynomial-time decidable binary relation \(\mathcal {R}^{\mathsf {glt}} = \{\mathcal {R}^{\mathsf {glt}}_n\}\) consisting of elements from \(\bar{\mathcal {L}}\) and witnesses \(w^{\mathsf {glt}}\), if for all \(n = \textsf {poly}(\kappa )\) and all non-uniform probabilistic polynomial-time adversaries \(\mathcal {A}\),
For algorithms \(\mathcal {A}\) and \(\mathsf {Ext}_\mathcal {A}\), we write \((y; y') \leftarrow (\mathcal {A}|| \mathsf {Ext}_{\mathcal {A}}) (\chi )\) if \(\mathcal {A}\) on input \(\chi \) outputs y, and \(\mathsf {Ext}_{\mathcal {A}}\) on the same input (including the random tape of \(\mathcal {A}\)) outputs \(y'\). \(\varPsi \) is knowledge-sound, if for all \(n = \textsf {poly}(\kappa )\) and all non-uniform probabilistic polynomial-time adversaries \(\mathcal {A}\), there exists a non-uniform probabilistic polynomial-time extractor \(\mathsf {Ext}_{\mathcal {A}}\), such that for every auxiliary input \(\mathsf {aux}\in \{0, 1\}^{\textsf {poly}(\kappa )}\),
Here, \(\mathsf {aux}\) can be seen as the common auxiliary input to \(\mathcal {A}\) and \(\mathsf {Ext}_{\mathcal {A}}\) that is generated by using benign auxiliary input generation [7].
\(\varPsi \) is perfectly (composable) zero-knowledge [21], if there exists a probabilistic polynomial-time simulator \(\mathsf {S}\), such that for all stateful non-uniform probabilistic adversaries \(\mathcal {A}\) and \(n = \textsf {poly}(\kappa )\), \(\varepsilon _0 = \varepsilon _1\), where
Shuffle Argument. In a (pairing-based) shuffle argument [25], the prover aims to convince the verifier that, given system parameters \(\mathsf {gk}\) output by \(\mathsf {BG}\), a public key \(\mathsf {pk}\), and two tuples of ciphertexts \( \varvec{\mathfrak {M}}\) and \(\varvec{\mathfrak {M}}'\), the second tuple is a permutation of rerandomized versions of the first. More precisely, we will construct a shuffle argument that is sound with respect to the following relation:
A number of pairing-based shuffle arguments have been proposed in the literature, [14, 15, 20, 25, 34].
3 New Shuffle Argument
Intuitively, in the new shuffle argument the prover first commits to the permutation \(\sigma \) (or more precisely, to the corresponding permutation matrix), then executes three subarguments (the same-message, the permutation matrix, and the consistency arguments). Each of the subarguments corresponds to one check performed by the verifier (see Protocol 2). However, since all subarguments use the same CRS, they are not independent. For example, the permutation matrix argument uses the \(((P_i (X))_{i\,=\,1}^n, X_\varrho )\)-commitment scheme and the consistency argument uses the \(((\hat{P}_i (X))_{i\,=\,1}^n, X_{\hat{\varrho }})\)-commitment scheme for different polynomials \((\hat{P}_i (X))_{i = 1}^n\). (See Eqs. (3) and (5) for the actual definition of \(P_i (X)\) and \(\hat{P}_i (X)\)). Both commitment schemes share a part of their trapdoor (\(\chi \)), while the second part of the trapdoor is different (either \(\varrho \) or \(\hat{\varrho }\)). Moreover, the knowledge-soundness of the same-message argument is a prerequisite for the knowledge-soundness of the permutation matrix argument. The verifier recovers explicitly the commitment to the last row of the permutation matrix (this guarantees that the committed matrix is left stochastic), then verifies the three subarguments.
The full description of the new shuffle argument is given in Protocol 1 (the CRS generation and the prover) and in Protocol 2 (the verifier). The CRS has entries that allow to efficiently evaluate all subarguments, and hence also both commitment schemes. The CRS in Protocol 1 includes three substrings, \(\mathsf {crs}_{sm}\), \(\mathsf {crs}_{pm}\), and \(\mathsf {crs}_{con}\), that are used in the three subarguments. To prove and verify (say) the first subargument (the same-message argument), one needs access to \(\mathsf {crs}_{sm}\). However, the adversary of the same-message argument will get access to the full CRS. For the sake of exposition, the verifier’s description in Protocol 2 does not include batching. In Sect. 6, we will explain how to speed up the verifier considerably by using batching techniques.
We will next briefly describe the subarguments. In Sect. 4, we will give more detailed descriptions of each subargument, and in Sect. 5, we will prove the security of the shuffle argument.
Same-Message Argument. Consider the subargument of the new shuffle argument where the verifier only computes \(\mathfrak {a}_{n}\) and then performs the check on Step 4 of Protocol 2 for one concrete i. We will call it the same-message argument [14]. In Sect. 4.1 we motivate this name, by showing that if the same-message argument accepts, then the prover knows a message \(\varvec{a}\) and a randomizer r, such that \(\mathfrak {a}_i = [\sum a_i P_i (\chi ) + r \varrho ]_{1}\) and \(\hat{\mathfrak {a}}_i = [\sum a_i \hat{P}_i (\chi ) + r \hat{\varrho }]_{1}\) both commit to \(\varvec{a}\) with randomizer r, by using respectively the \(((P_i (X))_{i\,=\, 1}^n, X_\varrho )\)-commitment scheme and the \(((\hat{P}_i (X))_{i\,=\,1}^n, X_{\hat{\varrho }})\)-commitment scheme.
For the same-message argument to be knowledge-sound, we will require that \(\{P_i (X)\}_{i\,=\,1}^n\) and \(\{\hat{P}_i (X)\}_{i\,=\,1}^n\) are both linearly independent sets.


Permutation Matrix Argument. Consider the subargument of Protocols 1 and 2, where (i) the prover computes \(\varvec{\mathfrak {a}}\) and \(\pi _{pm}\), and (ii) the verifier computes \(\mathfrak {a}_{n}\) and then checks the verification equation on Step 5 of Protocol 2. We will call it the permutation matrix argument. In Sect. 4.2 we motivate this name, by proving in the GBGM that if the verifier accepts the permutation matrix argument, then either the prover knows how to open \((\mathfrak {a}_1, \dots , \mathfrak {a}_n)\) as a \(((P_i (X))_{i\,=\,1}^n, X_\varrho )\)-commitment to a permutation matrix or we can break the same-message argument. For this, we first prove the security of a subargument of the permutation matrix argument — the unit vector argument [14] — where the verifier performs the verification Step 5 for exactly one i.
For the unit vector argument to be efficient, we need to make a specific choice of the polynomials \(P_i (X)\) (see Eq. (3)). For the knowledge-soundness of the unit vector argument, we additionally need that \(\{P_i (X)\}_{i = 0}^n\) and \(\{P_i (X)\}_{i\,=\,1}^n \cup \{1\}\) are linearly independent.
In [15], the verifier adds \([\alpha ]_{1} + [P_0]_{1}\) from the CRS to \(\mathfrak {a}_i\) (and adds \([\alpha ]_{2} - [P_0]_{2}\) from the CRS to \(\mathfrak {b}_i\)), while in our case, the verifier samples \(\alpha \) itself during verification. Due to this small change, we can make the CRS independent of \(\alpha \). (In fact, it suffices if the verifier chooses \(\alpha \) once and then uses it at each verification.) This makes the CRS shorter, and also simplifies the latter soundness proof. For this optimization to be possible, one has to rely on the same-message argument (see Sect. 5).
Consistency Argument. Consider the subargument of the new shuffle argument where the prover only computes \(\pi _{con}\) and the verifier performs the check on Step 6 of Protocol 2. We will call it the consistency argument. In Sect. 4.3 we motivate this name, by showing that if \(\varvec{\hat{\mathfrak {a}}}\) \((\{\hat{P}_i (X)\}, X_{\hat{\varrho }})\)-commits to a permutation, then \(\mathsf {Dec}(\mathfrak {M}'_i) = \mathsf {Dec}(\mathfrak {M}_{\sigma (i)})\) for the same permutation \(\sigma \) that the prover committed to earlier. We show that the new consistency argument is culpably sound under a (novel) variant of the KerMDH computational assumption [36] that we describe in Sect. 4.3. In particular, the KerMDH assumption has to hold even when the adversary is given access to the full CRS of the shuffle argument.
For the consistency argument to be sound (and in particular, for the KerMDH variant to be secure in the GBGM), we will require that \(\{\hat{P}_i (X)\}_{i\,=\,1}^n\) and \(\{P_i (X) \hat{P}_j (X)\}_{1 \le i, j \le n}\) are both linearly independent sets.
4 Subarguments
Several of the following knowledge-soundness proofs use the GBGM and therefore we will first give common background for those proofs. In the GBGM, the generic adversary in each proof has only access to generic group operations, pairings, and equality tests. However, she will have access to the full CRS of the new shuffle argument.
Let \(\varvec{\chi } = (\chi , \alpha , \beta , \hat{\beta }, \varrho , \hat{\varrho }, \mathsf {sk})\) be the tuple of all random values generated by either \(\mathsf {K}\) or \(\mathsf {V}\). Note that since \(\alpha \) is sampled by the verifier each time, for an adversary it is essentially an indeterminate. Thus, for the generic adversary each element of \(\varvec{\chi }\) will be an indeterminate. Let us denote the tuple of corresponding indeterminates by \(\varvec{X} = (X, X_\alpha , X_{\beta }, X_{\hat{\beta }}, X_\varrho , X_{\hat{\varrho }}, X_S)\).
The adversary is given oracle access to the full CRS. This means that for each element of the CRS, she knows the attached (Laurent) polynomial in \(\varvec{X}\). E.g., for the CRS element \([\beta \varrho + \hat{\beta } \hat{\varrho }]_{1}\), she knows that the attached polynomial is \(X_\beta X_\varrho + X_{\hat{\beta }} X_{\hat{\varrho }}\). Each element output by the adversary can hence be seen as a polynomial in \(\varvec{X}\). Moreover, if this element belongs to \(\mathbb {G}_z\) for \(z \in \{1, 2\}\), then this polynomial has to belong to the span of attached polynomials corresponding to the elements of CRS from the same group. Observing the definition of \(\mathsf {crs}\) in Protocol 1, we see that this means that each \(\mathbb {G}_z\) element output by the adversary must have an attached polynomial of the form \(\mathsf {crs}_z (\varvec{X}, T, t)\) for symbolic values T and t:
where \(T^\dagger (X)\) is in the span of \(\{((P_i (X) + P_0 (X))^2 - 1) / Z (X)\}_{i\,=\,1}^n\) (it will be a polynomial due to the definition of \(P_i (X)\) and \(P_0 (X)\)), \(T^* (X)\) is in the span of \(\{\hat{P}_i (X)\}_{i\,=\,1}^n\), and t(X) is in the span of \(\{P_i (X)\}_{i\,=\,1}^n\). (Here we use Lemma 1, given below, that states that \(\{P_i (X)\}_{i\,=\,1}^n \cup \{1\}\) and \(\{P_i (X)\}_{i\,=\,0}^n\) are two bases of degree-\(\le n\) polynomials.) We will follow the same notation in the rest of the paper. E.g., polynomials with a star (like \(b^* (X)\)) are in the span of \(\{\hat{P}_i (X)\}_{i\,=\,1}^n\).
4.1 Same-Message Argument
For the sake of this argument, let \(\varvec{P} (X) = (P_i (X))_{i\,=\,1}^n\) and \(\varvec{\hat{P}} (X) = (\hat{P}_i (X))_{i\,=\,1}^n\) be two families of linearly independent polynomials. We do not specify the parameters X, \(X_\varrho \) and \(X_{\hat{\varrho }}\) in the case when they take their canonical values \(\chi \), \(\varrho \), and \(\hat{\varrho }\).
In the same-message argument, the prover aims to prove that given \(\mathfrak {a}, \hat{\mathfrak {a}} \in \mathbb {G}_1\), she knows \(\varvec{a}\) and r, such that  for
for

and  and
and  . That is, \(\mathfrak {a}\) and \(\hat{\mathfrak {a}}\) are commitments to the same vector \(\varvec{a}\) with the same randomness r, but using the \(((P_i (X))_{i\,=\,1}^n, X_\varrho )\)-commitment scheme and the \(((\hat{P}_i (X))_{i\,=\,1}^n, X_{\hat{\varrho }})\)-commitment scheme correspondingly.
. That is, \(\mathfrak {a}\) and \(\hat{\mathfrak {a}}\) are commitments to the same vector \(\varvec{a}\) with the same randomness r, but using the \(((P_i (X))_{i\,=\,1}^n, X_\varrho )\)-commitment scheme and the \(((\hat{P}_i (X))_{i\,=\,1}^n, X_{\hat{\varrho }})\)-commitment scheme correspondingly.
We construct the same-message argument by essentially using the (second) QANIZK argument of Kiltz and Wee [30] for the linear subspace

However, as we will see in the proof of the permutation matrix argument, we need knowledge-soundness of the same-message argument. Therefore, while we use exactly the QANIZK argument of Kiltz and Wee, we prove its knowledge-soundness in the GBGM: we show that if the verifier accepts then the prover knows a witness \(\varvec{w}\) such that \((\mathfrak {a}, \hat{\mathfrak {a}}) = \varvec{w}^\top \cdot [\varvec{M}]_{1}\). Moreover, we need it to stay knowledge-sound even when the adversary has access to an auxiliary input.
More precisely, denote by \(\mathcal {D}^{sm}_{n, 2}\) the distribution of matrices \(\varvec{M}\) in Eq. (1) given that \((\chi , \varrho , \hat{\varrho }) \leftarrow _r \mathbb {Z}_q \times (\mathbb {Z}_q^*)^2\). For \(k \ge 1\), let \(\mathcal {D}_k\) be a distribution such that the \(\mathcal {D}_k\)-KerMDH assumption holds. Clearly, \(\mathcal {D}^{sm}_{n, 2}\) is witness-sampleable.
For a matrix \(\varvec{A} \in \mathbb {Z}_q^{(k\,+\,1) \times k}\), let \(\varvec{\bar{A}} \in \mathbb {Z}_q^{k \times k}\) denote the upper square matrix of \(\varvec{A}\). The same-message argument (i.e., the Kiltz-Wee QANIZK argument that  ) for witness-sampleable distributions is depicted as follows:
) for witness-sampleable distributions is depicted as follows:

Clearly, the verification accepts since  .
.
For the sake of efficiency, we will assume \(k = 1\) and  . Then, \(\varvec{\bar{A}} = 1\), \(\varvec{K} = (\beta , \hat{\beta })^\top \), \(\varvec{Q} = ( \beta P_1 + \hat{\beta } \hat{P}_1, \dots , \beta P_n + \hat{\beta } \hat{P}_n, \beta \varrho + \hat{\beta } \hat{\varrho } )^\top \), and \(\varvec{C} = \varvec{K}\). Thus, \(\mathsf {crs}_{sm}\) and \(\mathsf {td}_{sm}\) are as in Protocol 1. In the case of a shuffle,
. Then, \(\varvec{\bar{A}} = 1\), \(\varvec{K} = (\beta , \hat{\beta })^\top \), \(\varvec{Q} = ( \beta P_1 + \hat{\beta } \hat{P}_1, \dots , \beta P_n + \hat{\beta } \hat{P}_n, \beta \varrho + \hat{\beta } \hat{\varrho } )^\top \), and \(\varvec{C} = \varvec{K}\). Thus, \(\mathsf {crs}_{sm}\) and \(\mathsf {td}_{sm}\) are as in Protocol 1. In the case of a shuffle,  , and thus \(\pi _{sm} \leftarrow [\beta P_{\sigma ^{-1} (i)} + \hat{\beta } \hat{P}_{\sigma ^{-1} (i)}]_{1} + r [\beta \varrho +\hat{\beta } \hat{\varrho }]_{1}\) as in Protocol 1. The verifier has to check that \(\pi _{sm} \bullet [1]_{2} = \mathfrak {a}\bullet [\beta ]_{2} + \hat{\mathfrak {a}} \bullet [\hat{\beta }]_{2}\), as in Protocol 2. The simulator, given the trapdoor \(\mathsf {td}_{sm} = (\beta , \hat{\beta })^\top \), sets \(\pi _{sm} \leftarrow \beta \mathfrak {a}+ \hat{\beta } \hat{\mathfrak {a}}\).
, and thus \(\pi _{sm} \leftarrow [\beta P_{\sigma ^{-1} (i)} + \hat{\beta } \hat{P}_{\sigma ^{-1} (i)}]_{1} + r [\beta \varrho +\hat{\beta } \hat{\varrho }]_{1}\) as in Protocol 1. The verifier has to check that \(\pi _{sm} \bullet [1]_{2} = \mathfrak {a}\bullet [\beta ]_{2} + \hat{\mathfrak {a}} \bullet [\hat{\beta }]_{2}\), as in Protocol 2. The simulator, given the trapdoor \(\mathsf {td}_{sm} = (\beta , \hat{\beta })^\top \), sets \(\pi _{sm} \leftarrow \beta \mathfrak {a}+ \hat{\beta } \hat{\mathfrak {a}}\).
Theorem 2
Assume \(\mathsf {crs}= (\mathsf {crs}_{sm}, \mathsf {aux})\) where \(\mathsf {aux}\) does not depend on \(\beta \) or \(\hat{\beta }\). The same-message argument has perfect zero knowledge for \(\mathcal {L}_{\varvec{M}}\). It has adaptive knowledge-soundness in the GBGM.
Proof
Zero Knowledge: follows from \(\pi _{sm} = [\varvec{Q}^\top \varvec{\chi }]_{1} =[\varvec{K}^\top \varvec{M}^\top \varvec{\chi }]_{1} = [\varvec{K}^\top \varvec{y}]_{1}\).
Knowledge-soundness: In the generic group model, the adversary knows polynomials \(A (\varvec{X}) = crs_1 (\varvec{X}, A, a)\), \(\hat{A} (\varvec{X}) = crs_1 (\varvec{X}, \hat{A}, \hat{a})\), and \(\pi (\varvec{X}) = crs_1 (\varvec{X}, \Pi , \pi )\), such that \(\mathfrak {a}= [A (\varvec{\chi })]_{1}\), \(\hat{\mathfrak {a}} = [\hat{A} (\varvec{\chi })]_{1}\), \(\pi _{sm} = [\pi (\varvec{\chi })]_{1}\).
Because the verification accepts, by the Schwartz–Zippel lemma, from this it follows (with all but negligible probability) that \(\pi (\varvec{X}) = X_{\beta } A (\varvec{X}) +X_{\hat{\beta }} \hat{A} (\varvec{X})\) as a polynomial. Now, the only elements in \(\mathsf {crs}\) in group \(\mathbb {G}_1\) that depend on \(X_{\beta }\) and \(X_{\hat{\beta }}\) are the elements from \(\mathsf {crs}_{sm}\): (a) \(X_{\beta } P_i (X) + X_{\hat{\beta }} \hat{P}_i (X)\) for each i, and (b) \(X_{\beta } X_\varrho + X_{\hat{\beta }} X_{\hat{\varrho }}\). Thus, we must have that for some \(\varvec{a}\) and r,
Hence, \(A (\varvec{X}) = \sum _{i\,=\,1}^n a_i P_i (X) + r X_\varrho \) and \(\hat{A} (\varvec{X}) = \sum _{i\,=\,1}^n a_i \hat{P}_i (X) + r X_{\hat{\varrho }}\). Thus, \(\mathfrak {a}\) and \(\hat{\mathfrak {a}}\) commit to the same vector \(\varvec{a}\) using the same randomness r. \(\square \)
Remark 1
Here, the only thing we require from the distribution \(\mathcal {D}^{sm}_{n, 2}\) is witness-sampleability and therefore exactly the same zero-knowledge argument can be used with any two shrinking commitment schemes. \(\square \)
4.2 Permutation Matrix Argument
In this section, we show that a subargument of the new shuffle argument (see Protocols 1 and 2), where the verifier only computes \(\mathfrak {a}_{n}\) as in prover Step 2 and then checks verification Step 5, gives us a permutation matrix argument. However, we first define the unit vector argument, prove its knowledge-soundness, and then use this to prove knowledge-soundness of the permutation matrix argument. The resulting permutation matrix argument is significantly simpler than in the FLZ shuffle argument [15].
Unit Vector Argument. In a unit vector argument [14], the prover aims to convince the verifier that he knows how to open a commitment \(\mathfrak {a}\) to \((\varvec{a}, r)\), such that exactly one coefficient \(a_I\), \(I \in [1 \, .. \, n]\), is equal to 1, while other coefficients of \(\varvec{a}\) are equal to 0. Recall [14, 15] that if we define  and
and  , then \(\varvec{a}\) is a unit vector iff
, then \(\varvec{a}\) is a unit vector iff
where \(\circ \) denotes the Hadamard (entry-wise) product of two vectors. Really, this equation states that \(a_i \in \{0, 1\}\) for each \(i \in [1 \, .. \, n]\), and that \(\sum a_i = 1\).
Similar to the 1-sparsity argument in [15], we construct the unit vector argument by using a variant of square span programs (SSP-s, [11]). To proceed, we need to define the following polynomials. For \(i \in [1 \, .. \, n]\), set \(P_i (X)\) to be the degree n polynomial that interpolates the ith column of the matrix \(\varvec{V}\), i.e.,
Set
i.e., \(P_0 (X)\) is the polynomial that interpolates \(\varvec{b} - \varvec{1}_{n\,+\,1}\). Define \(Q (X) = (\sum _{i\,=\,1}^n a_i P_i (X) + P_0 (X))^2 - 1\). Due to the choice of the polynomials, Eq. (2) holds iff \(Q (\omega _i) = 0\) for all \(i \in [1 \, .. \, n\,+\,1]\), which holds iff \(Z (X) \mid Q (X) \), [15].
Lemma 1
([14, 15]). The sets \(\{P_i (X)\}_{i\,=\,1}^{n} \cup \{P_0 (X)\}\) and \(\{P_i (X)\}_{i\,=\,1}^{n} \cup \{1\}\) are both linearly independent.
Clearly, both \(\{P_i (X)\}_{i\,=\,1}^{n} \cup \{P_0 (X)\}\) and \(\{P_i (X)\}_{i\,=\,1}^{n} \cup \{1\}\) are a basis of all polynomials of degree \(\le n\).
Let
As explained before, \(\{\hat{P}_i (X)\}_{i\,=\,1}^{n}\) are needed in the same-message argument and in the consistency argument. Due to that, the CRS has entries allowing to efficiently compute \([\hat{P}_i (\chi )]_{1}\), which means that a generic adversary of the unit vector argument of the current section has access to those polynomials.
Let \(\mathcal {U}_n\) be the set of all unit vectors of length n. The unit vector argument is the following subargument of the new shuffle argument:

This argument is similar to the 1-sparsity argument presented in [15], but with a different CRS, meaning we cannot directly use their knowledge-soundness proof. Moreover, here the verifier generates \(\alpha \) randomly, while in the argument of [15], \(\alpha \) is generated by \(\mathsf {K}\). Fortunately, the CRS of the new shuffle argument is in a form that facilitates writing down a human readable and verifiable knowledge-soundness proof while [15] used a computer algebra system to solve a complicated system of polynomial equations.
The only problem of this argument is that it guarantees that the committed vector is a unit vector only under the condition that \(A_0 = 0\) (see the statement of the following theorem). However, this will be fine since in the soundness proof of the shuffle argument, we can use the same-message argument to guarantee that \(A_0 = 0\).
Theorem 3
The described unit vector argument is perfectly complete and perfectly witness-indistinguishable. Assume that \(\{P_i (X)\}_{i\,=\,1}^n \cup \{1\}\), and \(\{P_i (X)\}_{i\,=\,1}^n \cup \{P_0 (X)\}\) are two linearly independent sets. Assume that the same-message argument accepts. The unit vector argument is knowledge-sound in the GBGM in the following sense: there exists an extractor \(\mathsf {Ext}\) such that if the verifier accepts Eq. 6 for \(j = i\), then \(\mathsf {Ext}\) returns \((r_j, I_j \in [1 \, .. \, n])\), such that
We note that the two requirements for linear independence follow from Lemma 1.
Proof
Completeness: For an honest prover, and \(I = \sigma ^{-1} (j)\), \(\mathfrak {a}_j = [P_I (\chi ) + r_j \varrho ]_{1}\), \(\mathfrak {b}_j = [P_I (\chi ) + r_j \varrho ]_{2}\), and \(\mathfrak {c}_j = [r_j ( 2 (P_I (\chi ) + r_j \varrho + P_0 (\chi )) - r_j \varrho ) + h(\chi ) Z (\chi ) / \varrho ]_{1}\) for \(r_j \in \mathbb {Z}_q\). Hence, the verification equation assesses that \((P_I (\chi ) + r_j \varrho + \alpha + P_0 (\chi )) \cdot (P_I (\chi ) + r_j \varrho - \alpha + P_0 (\chi )) - \left( r_j ( 2 (P_I (\chi ) + r_j \varrho + P_0 (\chi )) - r_j \varrho ) + h(\chi ) Z (\chi ) / \varrho \right) \cdot \varrho - (1 - \alpha ^2) = 0\). This simplifies to the claim that \((P_{I} (\chi ) + P_0 (\chi ))^2 - 1 - h(\chi ) Z (\chi ) = 0\), or \(h(\chi ) = ((P_I (\chi ) + P_0 (\chi ))^2 - 1) / Z (\chi )\) which holds since the prover is honest.
Knowledge-Soundness: Assume a generic adversary has returned \(\mathfrak {a}= [A (\varvec{\chi })]_{1}, \mathfrak {b}= [B (\varvec{\chi })]_{2}, \mathfrak {c}= [C (\varvec{\chi })]_{2}\), for attached polynomials \(A (\varvec{X}) = crs_1 (\varvec{X}, A, a)\), \(B (\varvec{X}) = crs_2 (\varvec{X}, B, b)\), and \(C (\varvec{X}) = crs_1 (\varvec{X}, C, c)\), such that verification in Step 5 of Protocol 2 accepts. Observing this verification equation, it is easy to see that for the polynomial \(V_{uv} (\varvec{X}) := (A (\varvec{X}) + X_\alpha + P_0 (X))\cdot (B (\varvec{X}) - X_\alpha + P_0 (X)) - C (\varvec{X}) \cdot X_\varrho - (1 - X_\alpha ^2)\), the verification equation assesses that \(V_{uv} (\varvec{\chi }) = 0\). Since we are in the GBGM, the adversary knows all coefficients of \(A (\varvec{X})\), \(B (\varvec{X})\), \(C (\varvec{X})\), and \(V_{uv} (\varvec{X})\).
Moreover, due to the knowledge-soundness of the same-message argument, we know that \(A (\varvec{X}) = a (X) + A_\varrho X_\varrho \) for \(a (X) \in \textsf {span}\{P_i (X)\}_{i = 1}^n\). This simplifies correspondingly the polynomial \(V_{uv} (\varvec{X})\).
Now, let \(V_{uv} (\varvec{X} \setminus X)\) be equal to \(V_{uv} (\varvec{X})\) but without X being considered as an indeterminate; in particular, this means that the coefficients of \(V_{uv} (\varvec{X} \setminus X)\) can depend on X. Since the verifier accepts, \(V_{uv} (\varvec{\chi }) = 0\), so by the Schwartz–Zippel lemma, with all but negligible probability \(V_{uv} (\varvec{X})\cdot X_\varrho = 0\) and hence also \(V_{uv} (\varvec{X} \setminus X)\cdot X_\varrho = 0\) as a polynomial. The latter holds iff all coefficients of \(V_{uv} (\varvec{X} \setminus X) \cdot X_\varrho \) are equal to 0. We will now consider the corollaries from the fact that coefficients \(C_M\) of the following monomials M of \(V_{uv} (\varvec{X} \setminus X) \cdot X_\varrho \) are equal to 0, and use them to prove the theorem:
-
 : \(C_M = b (X) - a (X) + B_0 P_0 (X) = 0\). Since \(\{P_i (X)\}_{i = 0}^n\) is linearly independent, we get that \(B_0 = 0\), \(b (X) = a (X)\).
: \(C_M = b (X) - a (X) + B_0 P_0 (X) = 0\). Since \(\{P_i (X)\}_{i = 0}^n\) is linearly independent, we get that \(B_0 = 0\), \(b (X) = a (X)\). -
 : \(C_M = - Z (X) c^\dagger (X) - 1 + (a(X) + P_0 (X))(b(X) + (B_0 + 1) P_0(X)) = 0\): since \(B_0 = 0\) and \(b (X) = a (X)\), we get that \(C_M = -Z (X) c^\dagger (X) - 1 + (a (X) + P_0 (X))^2 = 0\), or alternatively $$\begin{aligned} C^\dagger (X) = \frac{(a (X) + P_0 (X))^2 - 1}{Z(X)} \end{aligned}$$
: \(C_M = - Z (X) c^\dagger (X) - 1 + (a(X) + P_0 (X))(b(X) + (B_0 + 1) P_0(X)) = 0\): since \(B_0 = 0\) and \(b (X) = a (X)\), we get that \(C_M = -Z (X) c^\dagger (X) - 1 + (a (X) + P_0 (X))^2 = 0\), or alternatively $$\begin{aligned} C^\dagger (X) = \frac{(a (X) + P_0 (X))^2 - 1}{Z(X)} \end{aligned}$$and hence, \(Z (X) \mid ((a(X) + P_0 (X))^2 - 1)\).
Therefore, due to the definition of \(P_i (X)\) and the properties of square span programs, \(a (X) = P_{I_j} (X)\) for some \(I_j \in [1 \, .. \, n]\), and Eq. (6) holds. Denote \(r_j := A_\varrho \). The theorem follows from the fact that we have a generic adversary who knows all the coefficients, and thus we can build an extractor that just outputs two of them, \((r_j, I_j)\).
Witness-indistinguishability: Consider a witness \((\varvec{a}, r_j)\). If \(\varvec{a}\) is fixed and the prover picks \(r_j \leftarrow _r \mathbb {Z}_q\) (as in the honest case), then an accepting argument \((\mathfrak {a}_j, \mathfrak {b}_j)\) has distribution \(\{([a']_{1},[a']_{2}): a' \leftarrow _r \mathbb {Z}_q\}\) and \(\mathfrak {c}_j\) is uniquely fixed by \((\mathfrak {a}_j, \mathfrak {b}_j)\) and the verification equation. Hence an accepting argument \((\mathfrak {a}_j, \mathfrak {b}_j, \mathfrak {c}_j)\) has equal probability of being constructed from any valid \(\varvec{a} \in \mathcal {U}_n\). \(\square \)
Remark 2
While a slight variant of this subargument was proposed in [15], they did not consider its privacy separately. It is easy to see that neither the new argument nor the 1-sparsity argument [15] is zero-knowledge in the case of type-III pairings. Knowing the witness, the prover can produce \(\mathfrak {b}_j\) such that \(\mathfrak {a}_j \bullet [1]_{2} = [1]_{1} \bullet \mathfrak {b}_j\). On the other hand, given an arbitrary input \(\mathfrak {a}\in \mathbb {G}_1\) as input, the simulator cannot construct such \(\mathfrak {b}\) since there is no efficient isomorphism from \(\mathbb {G}_1\) to \(\mathbb {G}_2\). Witness-indistinguishability suffices in our application. \(\square \)
Permutation Matrix Argument. A left stochastic matrix (i.e., its row vectors add up to \(\varvec{1}^\top \)) where every row is 1-sparse is a permutation matrix, [34]. To guarantee that the matrix is left stochastic, it suffices to compute \(\mathfrak {a}_n\) explicitly, i.e., \(\mathfrak {a}_n = [\sum _{j\,=\,1}^n P_j (\chi )]_{1} - \sum _{j = 1}^{n - 1} \mathfrak {a}_{j}\). After that, we need to perform the unit vector argument on every \(\mathfrak {a}_{j}\); this guarantees that Eq. (6) holds for each row. Since a unit vector is also a 1-sparse vector, we get the following result.
Theorem 4
The permutation matrix argument of this section is perfectly complete and perfectly witness-indistinguishable. Assume that \(\{P_i (X)\}_{i\,=\,1}^n \cup \{1\}\) is a linearly independent set. The permutation matrix argument is knowledge-sound in the GBGM in the following sense: there exists an extractor \(\mathsf {Ext}\) such that if the verifier accepts the verification equation on Step 5 of Protocol 2 for all \(j \in [1 \, .. \, n]\), and \(\mathfrak {a}_n\) is explicitly computed as in Protocol 2, then \(\mathsf {Ext}\) outputs \((\sigma \in S_n, \varvec{r})\), such that for all \(j \in [1 \, .. \, n]\), \(\mathfrak {a}_j = [P_{\sigma ^{-1} (j)} (\chi ) + r_j \varrho ]_{1}\).
Proof
Knowledge-soundness follows from the explicit construction of \(\mathfrak {a}_n\), and from the fact that we have a generic adversary that knows all the coefficients, and thus also knows \((\sigma , \varvec{r})\). More precisely, from the knowledge-soundness of the unit vector argument, for each \(j \in [1 \, .. \, n]\) there exists an extractor that outputs \((\varvec{a}_j, r_j)\) such that \(\varvec{a}_j\) is a unit vector with a 1 at some position \(I_j \in [1 \, .. \, n]\) and \(\mathfrak {a}_j = [P_{I_j} (\chi ) + r_j \varrho ]_{1}\). Since \([\sum _{j\,=\,1}^{n} P_{I_j} (\chi )]_{1} = \sum _{j\,=\,1}^{n} \mathfrak {a}_{j} = [\sum _{j\,=\,1}^{n} P_j (\chi )]_{1}\), by the Schwartz-Zippel lemma we have that with overwhelming probability \(\sum _{j\,=\,1}^{n} P_{I_j} (X) = \sum _{j\,=\,1}^{n} P_j (X)\) as a polynomial. Since due to Lemma 1 \(\{P_i (X)\}_{i\,=\,1}^n\) is linearly independent, this means that \((I_1, \dots , I_n)\) is a permutation of \([1 \, .. \, n]\), so \((\varvec{a}_j)_{j\,=\,1}^n\) is a permutation matrix.
Witness-indistinguishability follows from the witness-indistinguishability of the unit vector argument. \(\square \)
4.3 Consistency Argument
The last subargument of the shuffle argument is the consistency argument. In this argument the prover aims to show that, given \(\varvec{\hat{\mathfrak {a}}}\) that commits to a matrix \(\varvec{E} \in \mathbb {Z}_q^{n \times n}\) and two tuples (\(\varvec{\mathfrak {M}}\) and \(\varvec{\mathfrak {M}}'\)) of Elgamal ciphertexts, it holds that \(\mathsf {Dec}_{\mathsf {sk}} (\varvec{\mathfrak {M}}') = \varvec{E} \cdot \mathsf {Dec}_{\mathsf {sk}} (\varvec{\mathfrak {M}})\). Since we use a shrinking commitment scheme, each \(\varvec{\hat{\mathfrak {a}}}\) can commit to any matrix \(\varvec{E}\). Because of that, we use the fact that the permutation matrix argument is knowledge-sound in the GBGM, and thus there exists an extractor (this is formally provern in Sect. 3) that, after the same-message and the permutation matrix argument, extracts \(\varvec{E}\) and randomizer vectors \(\varvec{r}\) and \(\varvec{t}\), such that  . Hence, the guilt relation is
. Hence, the guilt relation is

We note that in the case of a shuffle argument, \(\varvec{E}\) is a permutation matrix. However, we will prove the soundness of the consistency argument for the general case of arbitrary matrices.
The new (general) consistency argument for a valid CRS distribution \(\mathcal {D}_{n\,+\,1, 1}\), such that \(\mathsf {td}_{con} = (\chi , \hat{\varrho })\), works as follows. Note that the prover should be able to work without knowing the Elgamal secret key, and that \([\varvec{M}]_{1} = \mathsf {ck}\).

Next, we prove that the consistency argument is culpably sound under a suitable KerMDH assumption (with an auxiliary input). After that, we prove that this variant of the KerMDH assumption holds in the GBGM, given that the auxiliary input satisfies some easily verifiable conditions.
Theorem 5
Assume that \(\mathcal {D}^{con}_{n}\) is a valid CRS distribution, where the matrix distribution outputs  for
for  . The consistency argument is perfectly complete and perfectly zero knowledge. Assume that the \(\mathcal {D}^{con}_{n}\)-KerMDH assumption with an auxiliary input holds in \(\mathbb {G}_1\). Then the consistency argument is culpably sound using \(\mathcal {R}^{\mathsf {glt}}_{con}\) with the CRS \(\mathsf {crs}= ([\varvec{M}]_{1}, \mathsf {aux})\).
. The consistency argument is perfectly complete and perfectly zero knowledge. Assume that the \(\mathcal {D}^{con}_{n}\)-KerMDH assumption with an auxiliary input holds in \(\mathbb {G}_1\). Then the consistency argument is culpably sound using \(\mathcal {R}^{\mathsf {glt}}_{con}\) with the CRS \(\mathsf {crs}= ([\varvec{M}]_{1}, \mathsf {aux})\).
Proof
Perfect completeness: In the case of the honest prover,  .
.
Culpable soundness: Assume that \(\mathcal {A}_{con}\) is an adversary that, given input \((\mathsf {gk}, \mathsf {crs}_{con})\) for \(\mathsf {crs}_{con} = (\varvec{M}, \mathsf {aux}) \leftarrow _r \mathcal {D}^{con}_{n}\), returns \(u = (\varvec{\mathfrak {M}}, \varvec{\mathfrak {M}}')\), \(\pi _{con} = (\varvec{\hat{\mathfrak {a}}}, \mathfrak {t}, \varvec{\mathfrak {N}})\) and \(w^{\mathsf {glt}} = (\varvec{E}, \varvec{r})\). \(\mathcal {A}_{con}\) succeeds iff (i) the verifier of the consistency argument accepts, (ii)  , and (iii) \(\mathsf {Dec}_{\mathsf {sk}} (\varvec{\mathfrak {M}}') = \varvec{E} \cdot \mathsf {Dec}_{\mathsf {sk}} (\varvec{\mathfrak {M}})\). Assume \(\mathcal {A}_{con}\) succeeds with probability \(\varepsilon \).
, and (iii) \(\mathsf {Dec}_{\mathsf {sk}} (\varvec{\mathfrak {M}}') = \varvec{E} \cdot \mathsf {Dec}_{\mathsf {sk}} (\varvec{\mathfrak {M}})\). Assume \(\mathcal {A}_{con}\) succeeds with probability \(\varepsilon \).
We construct the following adversary \(\mathcal {A}_{ker}\) that breaks the \(\mathcal {D}^{con}_{n}\)-KerMDH assumption with auxiliary input. \(\mathcal {A}_{ker}\) gets an input \((\mathsf {gk}, [\varvec{M}]_{1}, \mathsf {aux}) \) where \(\mathsf {gk}\leftarrow \mathsf {BG}(1^\kappa )\) and \(\mathsf {crs}_{ker} = ([\varvec{M}]_{1}, \mathsf {aux}) \leftarrow _r \mathcal {D}^{con}_{n}\), and is supposed to output \([\varvec{c}]_{2}\), such that \(\varvec{\varvec{M}}^\top \varvec{c} = \varvec{0}\) but \(\varvec{c} \ne \varvec{0}\).
On such an input, \(\mathcal {A}_{ker}\) first parses the auxiliary input as \(\mathsf {aux}= (\mathsf {aux}', \mathsf {pk})\), then picks \(\mathsf {sk}' \leftarrow _r \mathbb {Z}_q\) and creates \(\mathsf {crs}_{con} = ([\varvec{M}]_{1}, (\mathsf {aux}', \mathsf {pk}'))\), where \(\mathsf {pk}' = ([1]_{2}, [\mathsf {sk}']_{2})\). Note that \(\mathsf {crs}_{ker}\) and \(\mathsf {crs}_{con}\) have the same distribution. \(\mathcal {A}_{ker}\) makes a query to \(\mathcal {A}_{con}\) with input \((\mathsf {gk}, \mathsf {crs}_{con})\).
After obtaining the answer \(u = (\varvec{\mathfrak {M}}, \varvec{\mathfrak {M}}')\), \(\pi _{con} = (\varvec{\hat{\mathfrak {a}}}, \mathfrak {t}, \varvec{\mathfrak {N}})\) and \(w^{\mathsf {glt}} = (\varvec{E}, \varvec{r})\) from \(\mathcal {A}_{con}\), he does the following:
-
1.
If \([\varvec{\hat{P}}]_{1}^\top \circ \varvec{\mathfrak {M}}' - \varvec{\hat{\mathfrak {a}}}^\top \circ \varvec{\mathfrak {M}} \ne \mathfrak {t}\circ \mathsf {pk}' - [\hat{\varrho }]_{1} \circ \varvec{\mathfrak {N}}\) then abort.
-
2.
Use \(\mathsf {sk}'\) to decrypt: \(\varvec{\mathfrak {m}} \leftarrow \mathsf {Dec}_{\mathsf {sk}'} (\varvec{\mathfrak {M}})\), \(\varvec{\mathfrak {m}}' \leftarrow \mathsf {Dec}_{\mathsf {sk}'} (\varvec{\mathfrak {M}}')\), \(\mathfrak {n}\leftarrow \mathsf {Dec}_{\mathsf {sk}'} (\varvec{\mathfrak {N}})\).
-
3.
Return
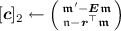 .
.
Let us now analyze \(\mathcal {A}_{ker}\)’s success probability. With probability \(1 - \varepsilon \), \(\mathcal {A}_{ker}\) fails, in which case \(\mathcal {A}_{ker}\) will abort. Otherwise, the verification equation holds. Decrypting the right-hand sides of each \(\circ \) in the verification equation in Step 6, we get that  .
.
Since \(\mathcal {A}_{con}\) is successful, then  , hence we get
, hence we get

Since \(\mathcal {A}_{con}\) is successful, then \(\varvec{\mathfrak {m}}' \ne \varvec{E} \varvec{\mathfrak {m}}\), which means that \(\varvec{c} \ne \varvec{0}\) but \(\varvec{M}^\top \varvec{c} = \varvec{0}\). Thus, \(\mathcal {A}_{ker}\) solves the \(\mathcal {D}^{con}_{n}\)-KerMDH problem with probability \(\varepsilon \).
Perfect Zero-Knowledge: The simulator \(\mathsf {S}_{con} (\mathsf {gk}, \mathsf {crs}, (\varvec{\mathfrak {M}}, \varvec{\mathfrak {M}}'), \mathsf {td}_{con} = (\chi , \hat{\varrho }))\) proceeds like the prover in the case \(\varvec{E} = \varvec{I}\) (the identity matrix) and \(\varvec{t} = \varvec{0}\), and then computes an \(\varvec{\mathfrak {N}}\) that makes the verifier accept. More precisely, the simulator sets \(\varvec{r} \leftarrow _r \mathbb {Z}_q\), \(\varvec{\hat{\mathfrak {a}}} \leftarrow [\varvec{\hat{P}}]_{1} + \varvec{r} [\hat{\varrho }]_{1}\), \(r_t \leftarrow _r \mathbb {Z}_q\), \(\mathfrak {t}\leftarrow r_t [\hat{\varrho }]_{1}\), and \(\varvec{\mathfrak {N}}\leftarrow (\varvec{\hat{P}} / \hat{\varrho } + \varvec{r})^\top \varvec{\mathfrak {M}} - (\varvec{\hat{P}} / \hat{\varrho })^\top \varvec{\mathfrak {M}}' + r_t \cdot \mathsf {pk}\). \(\mathsf {S}_{con}\) then outputs \(\pi _{con} \leftarrow (\varvec{\hat{\mathfrak {a}}}, \mathfrak {t}, \varvec{\mathfrak {N}})\).
Due to the perfect hiding property of the commitment scheme, \((\varvec{\hat{\mathfrak {a}}}, \mathfrak {t})\) has the same distribution as in the real protocol. Moreover,
and thus this choice of \(\varvec{\mathfrak {N}}\) makes the verifier accept. Since \(\mathfrak {t}\) is uniformly random and \(\varvec{\mathfrak {N}}\) is uniquely defined by \((\varvec{\hat{\mathfrak {a}}}, \mathfrak {t})\) and the verification equation, we have a perfect simulation. \(\square \)
Example 1
In the case of the shuffle argument, \(\varvec{E}\) is a permutation matrix with \(E_{i j} = 1\) iff \(j = \sigma (i)\). Thus,  , and \(\varvec{E} \varvec{\mathfrak {m}} = (\mathfrak {m}_{\sigma (i)})_{i\,=\,1}^n\). Hence in the shuffle argument, assuming that it has been already established that \(\varvec{E}\) is a permutation matrix, then after the verification in Step 6 one is assured that \(\varvec{\mathfrak {m}'} = (\mathfrak {m}_{\sigma (i)})_{i\,=\,1}^n\). \(\square \)
, and \(\varvec{E} \varvec{\mathfrak {m}} = (\mathfrak {m}_{\sigma (i)})_{i\,=\,1}^n\). Hence in the shuffle argument, assuming that it has been already established that \(\varvec{E}\) is a permutation matrix, then after the verification in Step 6 one is assured that \(\varvec{\mathfrak {m}'} = (\mathfrak {m}_{\sigma (i)})_{i\,=\,1}^n\). \(\square \)
We will now prove that the used variant of KerMDH with auxiliary input is secure in the GBGM. Before going on, we will establish the following linear independence result.
Lemma 2
The set \(\varPsi _\times := \{P_i (X) \hat{P}_j (X)\}_{1 \le i , j \le n} \cup \{\hat{P}_i (X)\}_{i\,=\,1}^n\) is linearly independent.
Proof
By Lemma 1, for each \(j \in [1 \, .. \, n]\) we have that \(\{P_i (X) \hat{P}_j (X)\}_{1 \le i \le n} \cup \{\hat{P}_j (X)\}\) is linearly independent. Hence to show that \(\varPsi _\times \) is linearly independent, it suffices to show that for all \(1 \le j < k \le n\), the span of sets \(\{P_i (X) \hat{P}_j (X)\}_{1 \le i \le n} \cup \{\hat{P}_j (X)\}\) and \(\{P_i (X) \hat{P}_k (X)\}_{1 \le i \le n} \cup \{\hat{P}_k (X)\}\) only intersect at 0. This holds since for non-zero vectors \((\varvec{a}, \varvec{b})\) and integers (A, B), \(\sum _{i = 1}^n a_i P_i (X) \hat{P}_j (X) + A \hat{P}_j (X) = (\sum _{i = 1}^n a_i P_i (X) + A) X^{(j + 1) (n + 1)}\) has degree at most \(n + (j + 1)(n + 1) < (k + 1)(n + 1)\), while \(\sum _{i = 1}^n b_i P_i (X) \hat{P}_k (X) + B \hat{P}_k (X) = (\sum _{i = 1}^n b_i P_i (X) + B) X^{(k + 1) (n + 1)}\) has degree at least \((k + 1)(n + 1)\). \(\square \)
Theorem 6
Assume that \((\hat{P}_i (X))_{i = 1}^n\) satisfy the following properties:
-
\(\{\hat{P}_i (X)\}_{i = 1}^n\) is linearly independent,
-
\(\{P_i (X) \hat{P}_j (X)\}_{1 \le i, j \le n}\) is linearly independent,
Assume also that the second input \(\mathsf {aux}\) output by \(\mathcal {D}^{con}_{n}\) satisfies the following property. The subset \(\mathsf {aux}_2\) of \(\mathbb {G}_2\)-elements in \(\mathsf {aux}\) must satisfy that
-
\(\mathsf {aux}_2\) does not depend on \(\hat{\varrho }\),
-
the only element in \(\mathsf {aux}_2\) that depends on \(\varrho \) is \([\varrho ]_{2}\),
-
the only elements in \(\mathsf {aux}_2\) that depend on \(\chi \) are \([P_i (\chi )]_{2}\) for \(i \in [0 \, .. \, n]\).
Then in the GBGM, the \(\mathcal {D}^{con}_{n}\)-KerMDH assumption with an auxiliary input holds in \(\mathbb {G}_1\).
Clearly, \((P_i (X))_{i = 1}^n\), \((\hat{P}_i (X))_{i = 1}^n\), and \(\mathsf {crs}\) in Protocol 1 (if used as \(\mathsf {aux}\)) satisfy the required properties.
Proof
Consider a generic group adversary \(\mathcal {A}_{ker}\) who, given  as an input, outputs a non-zero solution
as an input, outputs a non-zero solution  to the KerMDH problem, i.e.,
to the KerMDH problem, i.e.,  . In the generic model, each element in \(\mathsf {aux}_2\) has some polynomial attached to it. Since \(\mathcal {A}_{ker}\) is a generic adversary, he knows polynomials \(M_i (\varvec{X})\) (for each i) and \(N(\varvec{X})\), such that \(\mathfrak {m}_i = [M_i (\varvec{\chi })]_{2}\) and \(\mathfrak {n}= [N(\varvec{\chi })]_{2}\). Those polynomials are linear combinations of the polynomials involved in \(\mathsf {aux}_2\).
. In the generic model, each element in \(\mathsf {aux}_2\) has some polynomial attached to it. Since \(\mathcal {A}_{ker}\) is a generic adversary, he knows polynomials \(M_i (\varvec{X})\) (for each i) and \(N(\varvec{X})\), such that \(\mathfrak {m}_i = [M_i (\varvec{\chi })]_{2}\) and \(\mathfrak {n}= [N(\varvec{\chi })]_{2}\). Those polynomials are linear combinations of the polynomials involved in \(\mathsf {aux}_2\).
Hence, if  is a solution to the KerMDH problem, then
is a solution to the KerMDH problem, then  or equivalently, \(\hat{V}_{ker} (\varvec{\chi })= 0\), where
or equivalently, \(\hat{V}_{ker} (\varvec{\chi })= 0\), where
for coefficients known to the generic adversary. By the Schwartz–Zippel lemma, from this it follows (with all but negligible probability) that \(\hat{V}_{ker} (\varvec{X}) = 0\) as a polynomial.
Due to the assumptions on \(\mathsf {aux}_2\), and since \(\{P_i (X)\}_{i = 0}^n \cup \{1\}\) and \(\{P_i (X)\}_{i = 0}^n \cup \{P_0 (X)\}\) are interchangeable bases of degree-\((\le n)\) polynomials, we can write
where \(m_i (\varvec{X})\) does not depend on X, \(X_\varrho \) or \(X_{\hat{\varrho }}\).
Since \(\sum \hat{P}_i (X) M_i (\varvec{X})\) does not depend on \(X_{\hat{\varrho }}\), we get from \(\hat{V}_{ker} (\varvec{X}) = 0\) that \(\sum _{i = 1}^n \hat{P}_i (X) M_i (\varvec{X}) = N(\varvec{X}) = 0\).
Next, we can rewrite \(\sum _{i = 1}^n \hat{P}_i (X) M_i (\varvec{X}) = 0\) as
Due to assumptions on \(\mathsf {aux}_2\), this means that
-
\(\sum _{i = 1}^n \sum _{j = 1}^n M_{i j} \hat{P}_i (X) P_j (X) = 0\). Since \(\{\hat{P}_i (X) P_j (X)\}_{i, j \in [1 \, .. \, n]}\) is linearly independent, \(M_{i j} = 0\) for all \(i, j \in [1 \, .. \, n]\),
-
\(\sum _{i = 1}^n M'_i \hat{P}_i (X) = 0\). Since \(\{\hat{P}_i (X)\}_{i \in [1 \, .. \, n]}\) is linearly independent, \(M'_i = 0\) for all \(i \in [1 \, .. \, n]\).
-
\(\sum _{i = 1}^n m_i (\varvec{X}) \hat{P}_i (X) = 0\). Since \(m_i (\varvec{X})\) does not depend on X and \(\{\hat{P}_i (X)\}_{i \in [1 \, .. \, n]}\) is linearly independent, we get \(m_i (\varvec{X}) = 0\) for all \(i \in [1 \, .. \, n]\).
Hence, \(M_i (\varvec{X}) = 0\) for each \(i \in [1 \, .. \, n]\). Thus, with all but negligible probability, we have that \(N(\varvec{X}) = M_i (\varvec{X}) = 0\), which means  . \(\square \)
. \(\square \)
5 Security Proof of Shuffle
Theorem 7
The new shuffle argument is perfectly complete.
Proof
We showed the completeness of the same-message argument (i.e., that the verification equation on Step 4 holds) in Sect. 4.1, the completeness of the unit vector argument (i.e., that the verification equation on Step 5 holds) in Theorem 3, and the completeness of the consistency argument (i.e., that the verification equation on Step 6 holds) in Sect. 4.3. \(\square \)
Theorem 8
(Soundness of Shuffle Argument). Assume that the following sets are linearly independent:
-
\(\{P_i (X)\}_{i = 0}^n\),
-
\(\{P_i (X)\}_{i = 1}^n \cup \{1\}\),
-
\(\{P_i (X) \hat{P}_j (X)\}_{1 \le i, j \le n}\).
Let \(\mathcal {D}^{con}_{n}\) be as before with \(([\varvec{M}]_{1}, \mathsf {aux})\), such that \(\mathsf {aux}\) is equal to the CRS in Protocol 1 minus the elements already in \([\varvec{M}]_{1}\). If the \(\mathcal {D}_1\)-KerMDH assumption holds in \(\mathbb {G}_2\), the \(\mathcal {D}^{((P_i (X))_{i\,=\,1}^n, X_\varrho )}_n\)-KerMDH and \(\mathcal {D}^{((\hat{P}_i (X))_{i = 1}^n, X_{\hat{\varrho }})}_n\)-KerMDH assumptions hold and the \(\mathcal {D}^{con}_{n}\)-KerMDH assumption with auxiliary input holds in \(\mathbb {G}_1\), then the new shuffle argument is sound in the GBGM.
Proof
First, from the linear independence of \(\{P_i (X) \hat{P}_j (X)\}_{1 \le i, j \le n}\), we get straightforwardly that \(\{\hat{P}_j (X)\}_{j = 1}^n\) is also linearly independent. We construct the following simple sequence of games.
-
 This is the original soundness game. Let \(\mathcal {A}_{sh}\) be an adversary that breaks the soundness of the new shuffle argument. That is, given \((\mathsf {gk}, \mathsf {crs})\), \(\mathcal {A}_{sh}\) outputs \(u = (\varvec{\mathfrak {M}}, \varvec{\mathfrak {M}}')\) and an accepting proof \(\pi \), such that for all permutations \(\sigma \), there exists \(i \in [1 \, .. \, n]\), such that \(\mathsf {Dec}_{\mathsf {sk}} (\mathfrak {M}'_i) \ne \mathsf {Dec}_{\mathsf {sk}} (\mathfrak {M}_{\sigma (i)})\).
This is the original soundness game. Let \(\mathcal {A}_{sh}\) be an adversary that breaks the soundness of the new shuffle argument. That is, given \((\mathsf {gk}, \mathsf {crs})\), \(\mathcal {A}_{sh}\) outputs \(u = (\varvec{\mathfrak {M}}, \varvec{\mathfrak {M}}')\) and an accepting proof \(\pi \), such that for all permutations \(\sigma \), there exists \(i \in [1 \, .. \, n]\), such that \(\mathsf {Dec}_{\mathsf {sk}} (\mathfrak {M}'_i) \ne \mathsf {Dec}_{\mathsf {sk}} (\mathfrak {M}_{\sigma (i)})\). -
 Here, we let \(\mathcal {A}_{con}\) herself generate a new secret key \(\mathsf {sk}\leftarrow _r \mathbb {Z}_q\) and set \(\mathsf {pk}\leftarrow [1, \mathsf {sk}]_{2}\). Since the distribution of \(\mathsf {pk}\) is witness-sampleable, then for any (even omnipotent) adversary \(\mathcal {B}\), \(|\Pr [\mathsf {GAME}_1 (\mathcal {B}) = 1] - \Pr [\mathsf {GAME}_0 (\mathcal {B}) = 1]| = 0\) (i.e., \(\mathsf {GAME}_1\) and \(\mathsf {GAME}_0\) are indistinguishable).
Here, we let \(\mathcal {A}_{con}\) herself generate a new secret key \(\mathsf {sk}\leftarrow _r \mathbb {Z}_q\) and set \(\mathsf {pk}\leftarrow [1, \mathsf {sk}]_{2}\). Since the distribution of \(\mathsf {pk}\) is witness-sampleable, then for any (even omnipotent) adversary \(\mathcal {B}\), \(|\Pr [\mathsf {GAME}_1 (\mathcal {B}) = 1] - \Pr [\mathsf {GAME}_0 (\mathcal {B}) = 1]| = 0\) (i.e., \(\mathsf {GAME}_1\) and \(\mathsf {GAME}_0\) are indistinguishable).
Now, consider \(\mathsf {GAME}_1\) in more detail. Clearly, under given assumptions and due to the construction of \(\mathsf {crs}\) in Protocol 1 the same-message and permutation matrix arguments are knowledge-sound. Hence there exist extractors \(\mathsf {Ext}_{sm:i}^{\mathcal {A}}\) and \(\mathsf {Ext}_{pm}^{\mathcal {A}}\) such that the following holds:
-
If the same-message argument verifier accepts \((\mathfrak {a}_i, \hat{\mathfrak {a}}_i, \pi _{sm:i}) \leftarrow \mathcal {A}_{sm} (\mathsf {gk}, \mathsf {crs}_{sh}; r')\), then \(\mathsf {Ext}_{sm:i}^{\mathcal {A}} (\mathsf {gk}, \mathsf {crs}_{sh}; r')\) outputs the common opening \((\varvec{E}'_i, r_i)\) of \(\mathfrak {a}_i\) and \(\hat{\mathfrak {a}}_i\).
-
If the permutation matrix argument verifier accepts \(((\mathfrak {a}_i)_{i = 1}^{n - 1}, \pi _{pm}) \leftarrow \mathcal {A}_{pm}(\mathsf {gk}, \mathsf {crs}_{sh}; r')\), then \(\mathsf {Ext}_{pm}^{\mathcal {A}} (\mathsf {gk}, \mathsf {crs}_{sh}; r')\) outputs a permutation matrix \(\varvec{E}\) and vector \(\varvec{r}\) such that \(\varvec{\mathfrak {a}} = [\varvec{E}^\top \varvec{P} + \varvec{r} \varrho ]_{1}\) (here, \(\mathfrak {a}_n\) is computed as in Protocol 1).
We construct the following adversary \(\mathcal {A}_{con}\), see Protocol 3, that breaks the culpable soundness of the consistency argument using \(\mathcal {R}_{con}^{\mathsf {glt}}\) with auxiliary input. \(\mathcal {A}_{con}\) gets an input \((\mathsf {gk}, \mathsf {crs}_{con})\) where \(\mathsf {gk}\leftarrow \mathsf {BG}(1^\kappa )\), and \(\mathsf {crs}_{con} \leftarrow ([\varvec{M}]_{1}, \mathsf {aux}) \leftarrow _r \mathcal {D}^{con}_{n}\). \(\mathcal {A}_{con}\) is supposed to output \((u, \pi _{con}, w^{\mathsf {glt}})\) where \(u = (\varvec{\mathfrak {M}}, \varvec{\mathfrak {M}}')\), \(\pi _{con} = (\varvec{\hat{\mathfrak {a}}}, \mathfrak {t}, \varvec{\mathfrak {N}})\), and \(w^{\mathsf {glt}} = (\varvec{E}, \varvec{r})\) such that \(\varvec{\hat{\mathfrak {a}}} = [\varvec{E}^\top \varvec{\hat{P}} + \varvec{r} \hat{\varrho }]_{1}\), \(\pi _{con}\) is accepting, and \(\mathsf {Dec}_{\mathsf {sk}} (\varvec{\mathfrak {M}}') \ne \varvec{E} \cdot \mathsf {Dec}_{\mathsf {sk}} (\varvec{\mathfrak {M}})\).

It is clear that if \(\mathcal {A}_{con}\) does not abort, then he breaks the culpable soundness of the consistency argument. Let us now analyze the probability that \(\mathcal {A}_{con}\) does abort in any step.
-
1.
\(\mathcal {A}_{con}\) aborts in Step 3 if \(\mathcal {A}_{sh}\) fails, i.e., with probability \(1 - \varepsilon _{sh}\).
-
2.
\(\mathcal {A}_{con}\) will never abort in Step 4b since by our definition of knowledge-soundness, \(\mathsf {Ext}_{sm:i}^{\mathcal {A}}\) always outputs a valid opening as part of the witness.
-
3.
\(\mathcal {A}_{con}\) aborts in Step 6 only when he has found two different openings of \(\mathfrak {a}_i\) for some \(i \in [1 \, .. \, n]\). Hence, the probability of abort is upper bounded by \(n \varepsilon _{binding}\), where \(\varepsilon _{binding}\) is the probability of breaking the binding property of the \(((P_i (X))_{i = 1}^n, \varrho )\)-commitment scheme.
Thus, \(\mathcal {A}_{con}\) aborts with probability \(\le 1 - \varepsilon _{sh} + n \varepsilon _{binding}\), or succeeds with probability \(\varepsilon _{con} \ge \varepsilon _{sh} - n \varepsilon _{binding}\). Hence \(\varepsilon _{sh} \le \varepsilon _{con} + n \varepsilon _{binding}\). Since under the assumptions of this theorem, both \(\varepsilon _{con}\) and \(\varepsilon _{binding}\) are negligible, we have that \(\varepsilon _{sh}\) is also negligible. \(\square \)
Theorem 9
The new shuffle argument is perfectly zero-knowledge.
Proof
We proved that the permutation matrix argument is witness-indistinguishable (Theorem 4), and that the same-message argument is zero-knowledge (Theorem 2) and hence also witness-indistinguishable.
We will construct a simulator \(\mathsf {S}_{sh}\), that given a CRS \(\mathsf {crs}\) and trapdoor \(\mathsf {td}= (\chi , \hat{\varrho })\) simulates the prover in Protocol 1. \(\mathsf {S}_{sh}\) takes any pair \((\varvec{\mathfrak {M}}, \varvec{\mathfrak {M}}')\) as input and performs the steps in Protocol 4. Clearly, the simulator computes \(((\mathfrak {a}_i)_{i = 1}^{n - 1}, (\hat{\mathfrak {a}}_i)_{i = 1}^{n - 1}, \pi _{uv}, \pi _{sm})\) exactly as an honest prover with permutation \(\sigma = \mathrm {Id}\) would, which ensures correct distribution of these values. Moreover, since the commitment scheme is perfectly hiding and the permutation matrix and same-message arguments are witness-indistinguishable, the distribution of these values is identical to that of an honest prover that uses a (possibly different) permutation \(\sigma '\) and randomness values to compute \(\varvec{\mathfrak {M}}'\) from \(\varvec{\mathfrak {M}}\).
On the other hand, on the last step, \(\mathsf {S}_{sh}\) uses the simulator \(\mathsf {S}_{con}\) of the consistency argument from Theorem 5. Since \(\pi _{con}\) output by \(\mathsf {S}_{sh}\) has been computed exactly as by \(\mathsf {S}_{con}\) in Theorem 5, the verification equation in Step 6 of Protocol 2 accepts. Moreover, as in Theorem 5, \((\varvec{\hat{\mathfrak {a}}}, \mathfrak {t})\) has the same distribution as in the real protocol due to the perfect hiding of the commitment scheme, and \(\varvec{\mathfrak {N}}\) is uniquely fixed by \((\varvec{\hat{\mathfrak {a}}}, \mathfrak {t})\) and the verification equation. Hence the simulation is perfect. \(\square \)

6 Batching
The following lemma, slightly modified from [15, 33] (and relying on the batching concept introduced in [4]), shows that one can often use a batched version of the verification equations.
Lemma 3
Assume \(1< t < q\). Assume \(\varvec{y}\) is a vector chosen uniformly random from \([1 \, .. \, t]^{k\,-\,1} \times \{1\}\), \(\varvec{\chi }\) is a vector of integers in \(\mathbb {Z}_q\), and \((f_i)_{i \in [1 \, .. \, k]}\) are some polynomials of arbitrary degree. If there exists \(i \in [1 \, .. \, k]\) such that \(f_i (\varvec{\chi }) ([1]_{1} \bullet [1]_{2}) \ne [0]_{T}\) then \(\sum _{i = 1}^k f_i (\varvec{\chi }) y_i \cdot ([1]_{1} \bullet [1]_{2}) = [0]_{T}\) with probability \(\le \frac{1}{t}\).
Proof
Let us define a multivariate polynomial \(V(Y_1, \dots , Y_{k - 1}) =\sum _{i = 1}^{k - 1} f_i (\varvec{\chi }) Y_i + f_k (\varvec{\chi }) \ne 0\). By the Schwartz–Zippel lemma \(V(y_1, \dots , y_{k - 1}) = 0\) with probability \(\le \frac{1}{t}\). Since \([1]_{1} \bullet [1]_{2} \ne [0]_{T}\), we get that \(\sum _{i = 1}^k f_i (\varvec{\chi }) y_i \cdot ([1]_{1} \bullet [1]_{2}) = [0]_{T}\) with probability \(\le \frac{1}{t}\). \(\square \)

For the sake of concreteness, the full batched version of the verifier of the new shuffle argument is described in Protocol 5. The following corollary follows immediately from Lemma 3. It implies that if the non-batched verifier in Protocol 2 does not accept then the batched verifier in Protocol 5 only accepts with probability \(\le \frac{3}{t}\). This means that with all but negligible probability, the non-batched verifier accepts iff the batched verifier accepts. In practice a verifier could even set (say) \(t = 3 \cdot 2^{40}\).
Corollary 1
Let \(1< t < q\). Assume \(\varvec{\chi } = (\chi , \alpha , \beta , \hat{\beta }, \varrho , \hat{\varrho }, \mathsf {sk}) \in \mathbb {Z}_q^4 \times (\mathbb {Z}_q^*)^2 \times \mathbb {Z}_q\). Assume \((y_{1 j})_{j \in [1 \, .. \, n - 1]}\), and \(y_{2 1}\) are values chosen uniformly random from \([1 \, .. \, t]\), and set \(y_{1 n} = y_{2 2} = 1\).
-
If there exists \(i \in [1 \, .. \, n]\) such that the ith verification equation on Step 5 of Protocol 2 does not hold, then the verification equation on Step 6 of Protocol 5 holds with probability \(\le \frac{1}{t}\).
-
If there exists \(i \in [1 \, .. \, n]\) such that the ith verification equation on Step 4 of Protocol 2 does not hold, then the verification equation on Step 7 of Protocol 5 holds with probability \(\le \frac{1}{t}\).
-
If the verification equation on Step 6 of Protocol 2 does not hold, then the verification equation on Step 9 of Protocol 5 holds with probability \(\le \frac{1}{t}\).
7 Implementation
We implement the new shuffle argument in C++ using the libsnark library [6]. This library provides an efficient implementation of pairings over several different elliptic curves. We run our measurements on a machine with the following specifications: (i) Intel Core i5-4200U CPU with 1.60 GHz and 4 threads; (ii) 8 GB RAM; (iii) 64bit Linux Ubuntu 16.10; (iv)Compiler GCC version 6.2.0.
In addition, libsnark provides algorithms for multi-exponentiation and fixed-base exponentiation. Here, an n-wide multi-exponentiation means evaluating an expression of the form \(\sum _{i = 1}^n L_i \mathfrak {a}_i\), and n fixed-base exponentiations means evaluating an expression of the form \((L_1 \mathfrak {b}, \dots , L_n \mathfrak {b})\), where \(L_i \in \mathbb {Z}_q\) and \(\mathfrak {b}, \mathfrak {a}_i \in \mathbb {G}_k\). Both can be computed significantly faster than n individual scalar multiplications. (See Table 3.) Importantly, most of the scalar multiplications in the new shuffle argument can be computed by using either a multi-exponentiation or a fixed-base exponentiation.
We also optimize a sum of n pairings by noting that the final exponentiation of a pairing can be done only once instead of n times. All but a constant number of pairings in our protocol can use this optimization. We use parallelization to further optimize computation of pairings and exponentiations.
To generate the CRS, we have to evaluate Lagrange basis polynomials \((\ell _i (X))_{i \in [1 \, .. \, n + 1]}\) at \(X = \chi \). In our implementation, we pick \(\omega _j = j\) and make two optimizations. First, we precompute \(Z (\chi ) = \prod _{j\,=\,1}^{n + 1} (\chi - j)\). This allows us to write \(\ell _i (\chi ) = Z(\chi ) / ((\chi - i) \prod _{\begin{array}{c} j = 1, j \ne i \end{array}}^{n + 1} (i - j))\). Second, denote \(F_i = \prod _{\begin{array}{c} j = 1 \\ j \ne i \end{array}}^{n + 1} (i - j)\). Then for \(i \in [1 \, .. \, n]\), we have \(F_{i + 1} = (i F_i) / (i - n - 1)\). This allows us to compute all \(F_i\) with 2n multiplications and n divisions. Computing all \(\ell _i(\chi ) = \frac{Z(\chi )}{(\chi - i) F_i}\) takes \(4 n + 2\) multiplications and \(2 n+ 1\) divisions.
Notes
- 1.
Throughout this paper, we use additive notation combined with the bracket notation of [13]. We also denote group elements by using the Fraktur script as in \(\mathfrak {\mathfrak {M}}_i\) or \(\mathfrak {0}\). Thus, adding \(\mathsf {Enc}_{\mathsf {pk}} (\mathfrak {0}; t_i)\) results in a blinded version of \(\mathfrak {M}_{\sigma (i)}\).
- 2.
References
Barbulescu, R., Duquesne, S.: Updating Key Size Estimations for Pairings. Technical Report 2017/334, IACR (2017). http://eprint.iacr.org/2017/334. Revision from 26 April 2017
Barreto, P.S.L.M., Naehrig, M.: Pairing-friendly elliptic curves of prime order. In: Preneel, B., Tavares, S. (eds.) SAC 2005. LNCS, vol. 3897, pp. 319–331. Springer, Heidelberg (2006). https://doi.org/10.1007/11693383_22
Bayer, S., Groth, J.: Efficient zero-knowledge argument for correctness of a shuffle. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 263–280. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_17
Bellare, M., Garay, J.A., Rabin, T.: Batch verification with applications to cryptography and checking. In: Lucchesi, C.L., Moura, A.V. (eds.) LATIN 1998. LNCS, vol. 1380, pp. 170–191. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0054320
Ben-Sasson, E., Chiesa, A., Green, M., Tromer, E., Virza, M.: Secure sampling of public parameters for succinct zero knowledge proofs. In: IEEE SP 2015, pp. 287–304 (2015)
Ben-Sasson, E., Chiesa, A., Tromer, E., Virza, M.: Succinct non-interactive zero knowledge for a von Neumann architecture. In: USENIX 2014, pp. 781–796 (2014)
Bitansky, N., Canetti, R., Paneth, O., Rosen, A.: On the existence of extractable one-way functions. In: STOC 2014, pp. 505–514 (2014)
Blum, M., Feldman, P., Micali, S.: Non-interactive zero-knowledge and its applications. In: STOC 1988, pp. 103–112 (1988)
Chaum, D.: Untraceable electronic mail, return addresses, and digital pseudonyms. Commun. ACM 24(2), 84–88 (1981)
Damgård, I.: Towards practical public key systems secure against chosen ciphertext attacks. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 445–456. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_36
Danezis, G., Fournet, C., Groth, J., Kohlweiss, M.: Square span programs with applications to succinct NIZK arguments. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 532–550. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45611-8_28
Elgamal, T.: A public key cryptosystem and a signature scheme based on discretelogarithms. IEEE Trans. Inf. Theor. 31(4), 469–472 (1985)
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.L.: An algebraic framework for Diffie-Hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_8
Fauzi, P., Lipmaa, H.: Efficient culpably sound NIZK shuffle argument without random oracles. In: Sako, K. (ed.) CT-RSA 2016. LNCS, vol. 9610, pp. 200–216. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-29485-8_12
Fauzi, P., Lipmaa, H., Zając, M.: A shuffle argument secure in the generic model. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 841–872. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_28
Furukawa, J., Sako, K.: An efficient scheme for proving a shuffle. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 368–387. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_22
Galbraith, S.D., Paterson, K.G., Smart, N.P.: Pairings for cryptographers. Discrete Appl. Math. 156(16), 3113–3121 (2008)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof-systems. In: STOC 1985, pp. 291–304 (1985)
Golle, P., Jarecki, S., Mironov, I.: Cryptographic primitives enforcing communication and storage complexity. In: Blaze, M. (ed.) FC 2002. LNCS, vol. 2357, pp. 120–135. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36504-4_9
González, A., Ráfols, C.: New techniques for non-interactive shuffle and range arguments. In: Manulis, M., Sadeghi, A.-R., Schneider, S. (eds.) ACNS 2016. LNCS, vol. 9696, pp. 427–444. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-39555-5_23
Groth, J.: Simulation-sound NIZK proofs for a practical language and constant size group signatures. In: Lai, X., Chen, K. (eds.) ASIACRYPT 2006. LNCS, vol. 4284, pp. 444–459. Springer, Heidelberg (2006). https://doi.org/10.1007/11935230_29
Groth, J.: A verifiable secret shuffle of homomorphic encryptions. J. Cryptol. 23(4), 546–579 (2010)
Groth, J.: Short pairing-based non-interactive zero-knowledge arguments. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 321–340. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_19
Groth, J.: On the size of pairing-based non-interactive arguments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 305–326. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_11
Groth, J., Lu, S.: A non-interactive shuffle with pairing based verifiability. In: Kurosawa, K. (ed.) ASIACRYPT 2007. LNCS, vol. 4833, pp. 51–67. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-76900-2_4
Groth, J., Ostrovsky, R., Sahai, A.: New techniques for noninteractive zero-knowledge. J. ACM 59(3), 11 (2012)
Hess, F., Smart, N.P., Vercauteren, F.: The Eta pairing revisited. IEEE Trans. Inf. Theor. 52(10), 4595–4602 (2006)
Jutla, C.S., Roy, A.: Shorter quasi-adaptive NIZK proofs for linear subspaces. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8269, pp. 1–20. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42033-7_1
Jutla, C.S., Roy, A.: Switching lemma for bilinear tests and constant-size NIZK proofs for linear subspaces. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 295–312. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44381-1_17
Kiltz, E., Wee, H.: Quasi-adaptive NIZK for linear subspaces revisited. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 101–128. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_4
Kim, T., Barbulescu, R.: Extended tower number field sieve: a new complexity for the medium prime case. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 543–571. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_20
Lipmaa, H.: Progression-free sets and sublinear pairing-based non-interactive zero-knowledge arguments. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 169–189. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_10
Lipmaa, H.: Prover-efficient commit-and-prove zero-knowledge SNARKs. In: Pointcheval, D., Nitaj, A., Rachidi, T. (eds.) AFRICACRYPT 2016. LNCS, vol. 9646, pp. 185–206. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-31517-1_10
Lipmaa, H., Zhang, B.: A more efficient computationally sound non-interactive zero-knowledge shuffle argument. In: Visconti, I., De Prisco, R. (eds.) SCN 2012. LNCS, vol. 7485, pp. 477–502. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32928-9_27
Maurer, U.M.: Abstract models of computation in cryptography. In: Smart, N.P. (ed.) Cryptography and Coding 2005. LNCS, vol. 3796, pp. 1–12. Springer, Heidelberg (2005). https://doi.org/10.1007/11586821_1
Morillo, P., Ràfols, C., Villar, J.L.: The kernel matrix Diffie-Hellman assumption. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10031, pp. 729–758. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53887-6_27
Pereira, G.C.C.F., Simplício Jr., M.A., Naehrig, M., Barreto, P.S.L.M.: A family of implementation-friendly BN elliptic curves. J. Syst. Softw. 84(8), 1319–1326 (2011)
Schwartz, J.T.: Fast probabilistic algorithms for verification of polynomial identities. J. ACM 27(4), 701–717 (1980)
Shoup, V.: Lower bounds for discrete logarithms and related problems. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 256–266. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_18
Zippel, R.: Probabilistic algorithms for sparse polynomials. In: Ng, E.W. (ed.) Symbolic and Algebraic Computation. LNCS, vol. 72, pp. 216–226. Springer, Heidelberg (1979). https://doi.org/10.1007/3-540-09519-5_73
Acknowledgment
The majority of this work was done while the first author was working at the University of Tartu, Estonia. This work was supported by the European Union’s Horizon 2020 research and innovation programme under grant agreement No 653497 (project PANORAMIX) and grant agreement No 731583 (project SODA), by institutional research funding IUT2-1 of the Estonian Ministry of Education and Research, and by the Danish Independent Research Council, Grant-ID DFF-6108-00169.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Fauzi, P., Lipmaa, H., Siim, J., Zając, M. (2017). An Efficient Pairing-Based Shuffle Argument. In: Takagi, T., Peyrin, T. (eds) Advances in Cryptology – ASIACRYPT 2017. ASIACRYPT 2017. Lecture Notes in Computer Science(), vol 10625. Springer, Cham. https://doi.org/10.1007/978-3-319-70697-9_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-70697-9_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-70696-2
Online ISBN: 978-3-319-70697-9
eBook Packages: Computer ScienceComputer Science (R0)





 :
:  :
: 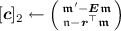 .
. This is the original soundness game. Let
This is the original soundness game. Let  Here, we let
Here, we let 