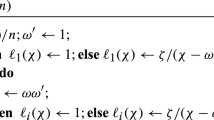A Subversion-Resistant SNARK

Abstract

While zk-SNARKs are widely studied, the question of what happens when the CRS has been subverted has received little attention. In ASIACRYPT 2016, Bellare, Fuchsbauer and Scafuro showed the first negative and positive results in this direction, proving also that it is impossible to achieve subversion soundness and (even non-subversion) zero knowledge at the same time. On the positive side, they constructed an involved sound and Sub-ZK argument system for NP. We make Groth’s zk-SNARK for Circuit-SAT from EUROCRYPT 2016 computationally knowledge-sound and perfectly composable Sub-ZK with minimal changes. We just require the CRS trapdoor to be extractable and the CRS to be publicly verifiable. To achieve the latter, we add some new elements to the CRS and construct an efficient CRS verification algorithm. We also provide a definitional framework for sound and Sub-ZK SNARKs and describe implementation results of the new Sub-ZK SNARK.

1 Introduction

Combined effort of a large number of recent research papers (to only mention a few, [17, 22, 26, 27, 30, 31, 35]) has made it possible to construct very efficient succinct non-interactive zero-knowledge arguments of knowledge (zk-SNARKs) for both the Boolean and the Arithmetic Circuit-SAT and thus for NP. The most efficient known approach for constructing zk-SNARKs for the Arithmetic Circuit-SAT is based on Quadratic Arithmetic Programs (QAP, [22]).

In a QAP, the prover builds a set of polynomial equations that are then checked by the verifier by using a small number of pairings. QAP-based zk-SNARKs have additional nice properties that make them applicable in verifiable computation [21, 22, 35] where the client outsources some computation to the server, who returns the computation result together with a succinct efficiently-verifiable correctness argument. Especially due to this application, zk-SNARKs have several heavily optimized implementations [7, 8, 15, 35]. Other applications of zk-SNARK include cryptocurrencies [4]. See, e.g., [27] for more references.

One drawback of zk-SNARKs is that they are all based on non-falsifiable assumptions (like the knowledge assumptions [16], or the generic bilinear group model, GBGM [12, 33, 34, 36]). In fact, Gentry and Wichs [23] showed that non-falsifiable assumptions are needed to construct zk-SNARKs for non-trivial languages. The currently most efficient zk-SNARK for Arithmetic Circuit-SAT was proposed by Groth (EUROCRYPT 2016, [27]) who proved it to be knowledge-sound in the GBGM. In Groth’s zk-SNARK, the argument consists of only 3 bilinear group elements and the verifier has to check a single pairing equation, dominated by the computation of only 3 bilinear (type III [20]) pairings and $m_0$ exponentiations, where $m_0$ is the statement size.

After the Snowden revelations, there has been a recent surge of interest in constructing cryptographic primitives and protocols secure against active subversion. In the context of zk-SNARKs, while the common reference string (CRS) model [11] is widely accepted to be the proper model, one has to be very careful to guarantee that the CRS has been created correctly. In [2], Bellare, Fuchsbauer and Scafuro tackled this problem by studying how much security one can still achieve when the CRS generator cannot be trusted. They proved several negative and positive results. In particular, they showed that it is impossible to achieve subversion soundness and (even non-subversion) zero knowledge simultaneously, the essential reason being that the zero knowledge simulator can be used to break subversion soundness.

In one of their positive solutions, Bellare et al. show that it is possible to get (non-subversion) soundness and computational subversion zero knowledge (Sub-ZK, ZK even if the the CRS is not trusted). Their main new idea is to use a knowledge assumption in the Sub-ZK proof, so that the simulator can extract a “trapdoor” from the untrusted CRS and then use this trapdoor to simulate the argument. While neat, the resulting argument system is quite complicated. Moreover, the non-interactive Sub-ZK argument system of [2] has linear communication; in the case of zk-SNARKs one presumably has to employ different techniques. We also need to take care to define and implement statistical Sub-ZK.

Our Contributions. We will take Groth‘s zk-SNARK from EUROCRYPT 2016 [27] as a starting point since, as mentioned before, it is currently the most efficient and thus the most attractive zk-SNARK.¹ We propose a minimal modification to Groth‘s zk-SNARK that makes it computationally knowledge-sound in what we call the “subversion generic bilinear group model” (Sub-GBGM) and perfect composable Sub-ZK. In fact, we consider two different versions of perfect Sub-ZK: (i) the version with an efficient subverter, where we assume the existence of an efficient extractor and prove Sub-ZK under a knowledge assumption, and (ii) the version with a computationally unbounded subverter, where we assume the existence of a computationally unbounded extractor and prove Sub-ZK unconditionally.

We change Groth’s zk-SNARK by adding extra elements to the CRS so that the CRS will become publicly verifiable; this minimal step (clearly, some public verifiability of the CRS is needed in the case the CRS generator cannot be trusted) will be sufficient to obtain Sub-ZK. However, choosing which elements to add to the CRS is not straightforward since the zk-SNARK must remain knowledge-sound even given enlarged CRS; adding too many or just “wrong” elements to the CRS can break the knowledge-soundness. (We will give a simple example about that in Sect. 6). On the other hand, importantly, the prover and the verifier of the new zk-SNARK are unchanged compared to Groth’s SNARK [27]. In the rest of the introduction, we will only outline the novel properties of the new SNARK as compared to [27].

We start by defining perfect subversion-complete (this includes the requirement that an honestly generated CRS is accepted by the CRS verification), computationally adaptively knowledge-sound, and statistically unbounded (or composable) Sub-ZK SNARKs. These definitions are similar to but subtly different from the non-subversion security definitions as given in, say, [25]. First, since one cannot check whether the subverter uses perfectly uniform coins (or, the CRS trapdoor) to generate the CRS, we divide the CRS generation into three different algorithms:

• generation of the CRS trapdoor $\mathsf {tc}$ (a probabilistic algorithm $\mathsf {K}_{\mathsf {tc}}$),

• creation of the CRS from $\mathsf {tc}$ (a deterministic algorithm $\mathsf {K}_{\mathsf {crs}}$), and

• creation of the simulation trapdoor from $\mathsf {tc}$ (a deterministic algorithm $\mathsf {K}_{\mathsf {ts}}$).

While we cannot check that $\mathsf {K}_{\mathsf {tc}}$ works correctly, we will guarantee that given a fixed $\mathsf {tc}$, $\mathsf {K}_{\mathsf {crs}}$ has been executed on this $\mathsf {tc}$. More precisely, we require that a Sub-ZK SNARK satisfies a CRS trapdoor extractability property that allows one to extract $\mathsf {tc}$ used by the subverter, s.t. if the subverted CRS $\mathsf {crs}$ is accepted by the CRS verification algorithm (see below) then $\mathsf {K}_{\mathsf {tc}}$ maps $\mathsf {tc}$ to $\mathsf {crs}$. The extractability requirement forces our ZK proof to use either a computationally unbounded extractor or a knowledge assumption. While we use the Sub-ZK definition with an efficient subverter and extractor throughout this introduction and the paper (mainly, since it is actually more difficult to achieve²), we will discuss the case of computationally unbounded subverter and extractor in Sect. 9.

In the proof of knowledge-soundness, we use (a version of) the GBGM. Using GBGM seems to be the best we can do since Groth’s non-Sub zk-SNARK is proven knowledge-sound in GBGM and as mentioned above, the use of a knowledge assumption or the generic model in the knowledge-soundness proof is necessary due to the impossibility result of Gentry and Wichs [23]. However, following Bellare et al. [2], we weaken the usual definition of GBGM by allowing the generic adversary to create (under realistic restrictions) random elements in the source groups without knowing their discrete logarithms. We call the resulting somewhat weaker model the subversion generic bilinear group model (Sub-GBGM). Following Groth [27] (the main difference being that modeling a more powerful generic adversary and taking into account new CRS elements will complicate the proof somewhat), we prove that the new SNARK is (adaptively) knowledge-sound in the Sub-GBGM even in the case of type-I pairings. (We emphasize once more that Groth’s zk-SNARK is proven knowledge-sound in the GBGM, and that Sub-GBGM is actually a weaker model than the GBGM.) This provides a hedge against possible future cryptanalysis that finds an efficient isomorphism between the two source groups.

Consider the case of efficient subverter. In the proof of perfect composable Sub-ZK, we use a well-known knowledge assumption (see, e.g., [17]) that we call BDH-KE. We argue that BDH-KE makes sense in the Sub-GBGM. The Sub-ZK proof of the only previously known non-interactive Sub-ZK argument system by Bellare et al. [2] also relies on knowledge assumptions. We follow the main idea of [2] by first using BDH-KE to extract the CRS trapdoor $\mathsf {tc}$ from the CRS and then construct a non-subversion simulator (that gets a part of the $\mathsf {tc}$ as an input) to simulate the argument. However, since we construct a zk-SNARK, our concrete approach is different from [2].

Also here, we rely on the existence of the efficient CRS verification algorithm $\mathsf {CV}$. We show that if $\mathsf {CV}$ accepts a $\mathsf {crs}$, then $\mathsf {crs}$ has been computed correctly by $\mathsf {K}_{\mathsf {crs}}$ from a $\mathsf {tc}$ bijectively fixed by $\mathsf {crs}$. From this, it follows under the BDH-KE assumption that for any subverter that produces a $\mathsf {crs}$ accepted by $\mathsf {CV}$, there exists an extractor that produces $\mathsf {tc}$ such that $\mathsf {K}_{\mathsf {crs}}$ given $\mathsf {tc}$ outputs $\mathsf {crs}$.

We emphasize that our security proofs of knowledge-soundness and of Sub-ZK are in incomparable models. The knowledge-soundness proof uses the full power of Sub-GBGM in the case of any pairings (including type-I). The Sub-ZK proof, on the other hand, uses a concrete standard-looking knowledge assumption BDH-KE that holds in the the GBGM but does not hold in the Sub-GBGM in the case of type-I pairings. (In the case of computationally unbounded subverter, we even do not need BDH-KE.) This enables us to construct an efficient Sub-ZK SNARK that uses type-III pairings, while guaranteeing its knowledge-soundness even in the case of type-I pairings.

General Design Recommendations. We do not expect that constructing Sub-ZK SNARKs can be done automatically, in particular since our framework points to the necessity of making CRS publicly verifiable which potentially means adding new elements to the CRS. Since knowledge-soundness proofs of many SNARKs are very subtle, it seems to be difficult to give a general “theorem” about which SNARKs can be modified to be Sub-ZK or even whether their CRS can be made verifiable without a major reconstruction. Whether a SNARK remains sound after that must be proven separately in each case.

However, we can still give a few recommendations for designing a Sub-ZK SNARK from a non subversion-secure SNARK (or from scratch) when using the same approach as the current paper:

• 1. Division of duties: make sure that $\mathsf {K}$ can be divided into randomized $\mathsf {K}_{\mathsf {tc}}$, deterministic $\mathsf {K}_{\mathsf {ts}}$, and deterministic $\mathsf {K}_{\mathsf {crs}}$.

• 2. CRS trapdoor extractability: for each element of $\mathsf {tc}$, make sure that it can be extracted from the CRS. For this, one can use a generic proof of knowledge, a specific knowledge-assumption, or a computationally unbounded extractor. A few additional properties described in Sect. 7 can also help.

• 3. CRS verifiability: the CRS must be publicly verifiable.

• 4. Sound approach: make sure that the previous steps do not hurt the knowledge-soundness. To achieve it, one should aim at designing a SNARK with a very simple CRS or where CRS verifiability comes naturally. Depending on the SNARK in question, this step may be the most difficult one.

On Efficiency. Since the new zk-SNARK is closely based on the most efficient known non-subversion zk-SNARK of Groth [27], it has comparable efficiency. Importantly, the new CRS verification algorithm $\mathsf {CV}$ has to be executed only by the prover (this is since we achieve Sub-ZK and non-subversion knowledge-soundness). This means that it suffices for $\mathsf {CV}$ to have the same computational complexity as the prover’s algorithm. The initial $\mathsf {CV}$ we describe in Fig. 1 is quite inefficient. However, as we show in Sect. 8 (see the full version [1] for more information), by using batching techniques the $\mathsf {CV}$ algorithm can be sped up to be faster than the prover’s algorithm (at the information-theoretical security level $2^{-80}$) and even faster at the information-theoretical security level $2^{-40}$. We implemented the new SNARK by using the libsnark [8] library and in the full version [1], we back up the last claim by concrete numbers.

An interesting open question is to minimize the computational complexity of the CRS verification. In particular, in most of the known zero-knowledge argument systems, either the argument length is at least linear and hence the verification algorithm takes at least linear time (e.g., the Groth-Sahai proofs [28]) or the CRS length is at least linear and hence the CRS verification algorithm takes at least linear time. A SNARK where both CRS and the argument are succinct is called fully succinct. See [7, 9, 15, 26, 30] for work on zk-SNARKs with sublinear CRS. However, existing fully succinct zk-SNARK are not really practical, see [7] for discussions. Moreover, it is not clear a priori how to make it Sub-ZK. An important open research topic hence is to construct an efficient fully succinct non-interactive Sub-ZK argument system.

Due to the lack of space, comparison to the MPC approach and implementation results are only given in the full version [1].

2 Preliminaries

For a matrix $M \in \mathbb {Z}_p^{n \times m}$, we denote by $\varvec{M}_i$ the ith row of M and by $\varvec{M}^{(j)}$ the jth column of M. PPT stands for probabilistic polynomial-time, and NUPPT stands for non-uniform PPT. We write $f (\kappa ) \approx _\kappa g (\kappa )$, if $f (\kappa ) - g (\kappa )$ is negligible as a function of $\kappa$. For an algorithm $\mathsf {A}$, let $\mathrm {range}(\mathsf {A})$ be the range of $\mathsf {A}$, i.e., the set of of valid outputs of $\mathsf {A}$. For an algorithm $\mathsf {A}$, let $\mathsf {RND}(\mathsf {A})$ denote the random tape of $\mathsf {A}$, and let $r \leftarrow _r \mathsf {RND}(\mathsf {A})$ denote the random choice of the randomizer r from $\mathsf {RND}(\mathsf {A})$. By $y \leftarrow \mathsf {A}(\mathsf {x}; r)$ we denote the fact that $\mathsf {A}$, given an input $\mathsf {x}$ and a randomizer r, outputs y. When we use this notation then r represents the full random tape of $\mathsf {A}$. For algorithms $\mathsf {A}$ and $\mathsf {X}_\mathsf {A}$, we write $(y \,\Vert \,y') \leftarrow (\mathsf {A}\,\Vert \,\mathsf {X}_\mathsf {A}) (\chi ; r)$ as a shorthand for $y \leftarrow \mathsf {A}(\chi ; r)$, $y' \leftarrow \mathsf {X}_\mathsf {A}(\chi ; r)$. In both cases, $\mathsf {X}_\mathsf {A}$ and $\mathsf {A}$ use internally the same randomness r.

In the new argument system, we will use a small number of indeterminates, and we assume that each indeterminate has a canonical concrete value (a uniformly random element of $\mathbb {Z}_p$ or $\mathbb {Z}_p^*$). The canonical value of $X, X_\alpha , X_\beta , X_\gamma , X_\delta$ (resp., $Y_i$) will be $\chi , \alpha , \beta , \gamma , \delta$ (resp., $\upsilon _i$, for $i \in \{1, 2, 3\}$). The canonical value of the vector $\varvec{X}= (X, X_\alpha , X_\beta , X_\gamma , X_\delta )$ (resp., $\varvec{Y}= (Y_1, Y_2, Y_3)$) will be $\varvec{x}= (\chi , \alpha , \beta , \gamma , \delta )$ (resp., $\varvec{y}= (\upsilon _1, \upsilon _2, \upsilon _3)$).

Interpolation. Assume n is a power of two, and let $\omega$ be the n-th primitive root of unity modulo p. Such $\omega$ exists, given that $n \mid (p - 1)$. Then,

• $\ell (X) := \prod _{i = 1}^n (X- \omega ^{i - 1}) = X^n - 1$ is the unique degree n monic polynomial such that $\ell (\omega ^{i - 1}) = 0$ for all $i \in [1 \, .. \, n]$.

• For $i \in [1 \, .. \, n]$, let $\ell _i (X)$ be the ith Lagrange basis polynomial, i.e., the unique degree $n - 1$ polynomial s.t. $\ell _i (\omega ^{i - 1}) = 1$ and $\ell _i (\omega ^{j - 1}) = 0$ for $i \ne j$. Clearly,

  $$\begin{aligned} \ell _i (X) := \frac{\ell (X)}{\ell ' (\omega ^{i - 1}) (X- \omega ^{i - 1})} = \frac{(X^n - 1) \omega ^{i - 1}}{n (X- \omega ^{i - 1})}. \end{aligned}$$

  (1)

Thus, $\ell _i (\omega ^{i - 1}) = 1$ while $\ell _i (\chi ) = (\chi ^n - 1) \omega ^{i - 1} / (n (\chi - \omega ^{i - 1}))$ for $\chi \ne \omega ^{i - 1}$. Given any $\chi \in \mathbb {Z}_p$, Algorithm 1 (see, e.g., [5]) computes $\ell _i (\chi )$ for $i \in [1 \, .. \, n]$. It can be implemented by using $4 n - 2$ multiplications and divisions in $\mathbb {Z}_p$.

Clearly, $L_{\varvec{a}} (X) := \sum _{i = 1}^n a_i \ell _i (X)$ is the interpolating polynomial of $\varvec{a}$ at points $\omega ^{i - 1}$, with $L_{\varvec{a}} (\omega ^{i - 1}) = a_i$, and its coefficients can thus be computed by executing an inverse Fast Fourier Transform in time $\varTheta (n \log n)$. Moreover, $(\ell _j (\omega ^{i - 1}))_{i = 1}^n = \varvec{e}_j$ (the jth unit vector) and $(\ell (\omega ^{i - 1}))_{i = 1}^n = \varvec{0}_n$.

Elliptic Curves and Bilinear Maps. On input $1^\kappa$, a bilinear map generator $\mathsf {genbp}$ returns ${\textsf {gk}}= (p, \mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, \hat{e}, \mathfrak {g}_1, \mathfrak {g}_2)$, where $\mathbb {G}_1$, $\mathbb {G}_2$ and $\mathbb {G}_T$ are three additive cyclic groups of prime order p (with $\log p = \varOmega (\kappa )$) and $\mathfrak {g}_z$ is a random generator of $\mathbb {G}_z$ for $z \in \{1, 2, T\}$. We denote the elements of $\mathbb {G}_1$, $\mathbb {G}_2$, and $\mathbb {G}_T$ by using Fraktur as in $\mathfrak {g}_1$. Additionally, $\hat{e}$ is an efficient bilinear map $\hat{e}:\mathbb {G}_1 \times \mathbb {G}_2 \rightarrow \mathbb {G}_T$ that satisfies in particular the following two properties: (i) $\hat{e}(\mathfrak {g}_1, \mathfrak {g}_2) \ne 1$, and (ii) $\hat{e}(a \mathfrak {g}_1, b \mathfrak {g}_2) = (a b) \hat{e}(\mathfrak {g}_1, \mathfrak {g}_2)$.

We give $\mathsf {genbp}$ another input, n (intuitively, the input length), and allow p to depend on n. We assume that all algorithms that handle group elements verify by default that their inputs belong to corresponding groups and reject if not. Usually, arithmetic in (say) $\mathbb {G}_1$ is considerably cheaper than in $\mathbb {G}_2$; hence, we count separately exponentiations in both groups.

We use the bracket notation. That is, for an integer x, we denote $\left[ x\right] _{z} := x \mathfrak {g}_z$ even when x is unknown. We denote $\left[ x\right] _{1} \bullet \left[ y\right] _{2} := \hat{e}(\left[ x\right] _{1}, \left[ y\right] _{2})$, hence $\left[ x y\right] _{T} = \left[ x\right] _{1} \bullet \left[ y\right] _{2}$. We denote $\left[ a_1, \dots , a_s\right] _{z} = (\left[ a_1\right] _{z}, \dots , \left[ a_s\right] _{z})$.

To speed up interpolation and other related computation, we will need the existence of the n-th, where n is a power of 2, primitive root of unity modulo p. For this, it suffices that $(n + 1) \mid (p - 1)$ (recall that p is the elliptic curve group order). Fortunately, given $\kappa$ and a practically relevant value of n, one can easily find a Barreto-Naehrig curve such that $(n + 1) \mid (p - 1)$ holds [8].

Quadratic Arithmetic Programs. Quadratic Arithmetic Program (QAP) was introduced by Gennaro et al. [22] as a language where for an input $\mathsf {x}$ and witness $\mathsf {w}$, $(\mathsf {x}, \mathsf {w}) \in {\mathbf {R}}$ can be verified by using a parallel quadratic check, and that has an efficient reduction from the well-known language (either Boolean or Arithmetic) Circuit-SAT. Hence, an efficient zk-SNARK for QAP results in an efficient zk-SNARK for Circuit-SAT.

For an m-dimensional vector $\varvec{A}$, let For an n-dimensional vector $\varvec{M}^{(0)}$ and an $n \times m$ matrix M over finite field $\mathbb {F}$, let $\mathsf {aug} (M) := (\varvec{M}^{(0)}, M)$. Let $m_0< m$ be a non-negative integer. An instance $\mathcal {Q}$ of the QAP language is specified by $(\mathbb {F}, m_0, \mathsf {aug} (U), \mathsf {aug} (V), \mathsf {aug} (W))$ where $U, V, W \in \mathbb {F}^{n \times m}$.

In the case of Arithmetic Circuit-SAT, n is the number of multiplication gates and m to the number of wires in the circuit. Here, we consider arithmetic circuits that consist only of fan-in-2 multiplication gates, but either input of each multiplication gate can be a weighted sum of some wire values, [22].

For a fixed instance $\mathcal {Q}$ of QAP, define the relation ${\mathbf {R}}$ as follows:

$$ {\mathbf {R}}_{\mathcal {Q}} = \left\{ \begin{aligned}&(\mathsf {x}, \mathsf {w}) :\mathsf {x}= (A_1, \dots , A_{m_0})^\top \wedge \mathsf {w}= (A_{m_0+ 1}, \dots , A_m)^\top \wedge \\&(\mathsf {aug} (U) \cdot \mathsf {aug} (\varvec{A})) \circ (\mathsf {aug} (V) \cdot \mathsf {aug} (\varvec{A})) = \mathsf {aug} (W) \cdot \mathsf {aug} (\varvec{A}) \end{aligned} \right\} $$

where $\varvec{a} \circ \varvec{b} = (a_i b_i)_{i = 1}^n$ denotes the entrywise product of vectors $\varvec{a}$ and $\varvec{b}$.

In a cryptographic setting, it is more convenient to work with the following alternative definition of QAP and of the relation ${\mathbf {R}}_{\mathcal {Q}}$. (This corresponds to the original definition of QAP in [22]). Let $\mathbb {F} = \mathbb {Z}_p$, such that $\omega$ is the n-th primitive root of unity modulo p. (This requirement is needed for the sake of efficiency, and we will make it implicitly throughout the current paper.) Let $\mathcal {Q} = (\mathbb {Z}_p, m_0, \mathsf {aug} (U), \mathsf {aug} (V), \mathsf {aug} (W))$ be a QAP instance. For $j \in [0 \, .. \, m]$, define $u_j (X) := L_{\varvec{U}^{(j)}} (X)$, $v_j (X) := L_{\varvec{V}^{(j)}} (X)$, and $w_j (X) := L_{\varvec{W}^{(j)}} (X)$. Thus, $u_j, v_j, w_j \in \mathbb {Z}_p^{(\le n - 1)} [X]$.

An QAP instance $\mathcal {Q}_p$ is specified by the so defined $(\mathbb {Z}_p, m_0, \{u_j, v_j, w_j\}_{j = 0}^m)$. This instance defines the following relation, where we assume that $A_0 = 1$:

$$ {\mathbf {R}}_{\mathcal {Q}_p} = \left\{ \begin{aligned}&(\mathsf {x}, \mathsf {w}) :\mathsf {x}= (A_1, \dots , A_{m_0})^\top \wedge \mathsf {w}= (A_{m_0+ 1}, \dots , A_m)^\top \wedge \\&\textstyle \left( \sum _{j = 0}^m A_j u_j (X)\right) \left( \sum _{j = 0}^m A_j v_j (X)\right) \equiv \sum _{j = 0}^m A_j w_j (X) \pmod {\ell (X)} \end{aligned} \right\} $$

Alternatively, $(\mathsf {x}, \mathsf {w}) \in {\mathbf {R}}$ if there exists a (degree $\le n - 2$) polynomial $h(X)$, s.t.

$$ \textstyle \left( \sum _{j = 0}^m A_j u_j (X)\right) \left( \sum _{j = 0}^m A_j v_j (X)\right) - \sum _{j = 0}^m A_j w_j (X) = h(X) \ell (X) . $$

Clearly, ${\mathbf {R}}_{\mathcal {Q}} = {\mathbf {R}}_{\mathcal {Q}_p}$, given that $\mathcal {Q}_p$ is constructed from $\mathcal {Q}$ as above.

3 Definitions: SNARKs and Subversion Zero Knowledge

Next, we define subversion zk-SNARKs and all their properties. To achieve subversion zero knowledge (Sub-ZK), we augment a zk-SNARK by requiring the existence of an efficient CRS verification algorithm. As outlined in Sect. 1, we also subdivide the CRS generation algorithm into three efficient algorithms.

Our definition of (statistical unbounded) Sub-ZK for SNARKs is motivated by the definition of [2]. We also define statistical composable Sub-ZK. As in [25], the definition of unbounded zero knowledge guarantees security for any (polynomial) number of queries to the prover or simulator, while the definition of composable zero knowledge guarantees security only in the case of a single query. Following [25] we prove that a statistical composable Sub-ZK argument system is also statistical unbounded Sub-ZK.

3.1 Syntax

Let $\mathcal {R}$ be a relation generator, such that $\mathcal {R}(1^\kappa )$ returns a polynomial-time decidable binary relation ${\mathbf {R}}= \{(\mathsf {x}, \mathsf {w})\}$. Here, $\mathsf {x}$ is the statement and $\mathsf {w}$ is the witness. We assume that $\kappa$ is explicitly deductible from the description of ${\mathbf {R}}$. The relation generator also outputs auxiliary information $\mathsf {z}_{{\mathbf {R}}}$ that will be given to the honest parties and the adversary. As in [27, Sect. 2.3], $\mathsf {z}_{{\mathbf {R}}}$ will be equal to ${\textsf {gk}}\leftarrow \mathsf {genbp}(1^\kappa , n)$ for a well-defined n. Because of this, we will also give $\mathsf {z}_{{\mathbf {R}}}$ as an input to the honest parties; if needed, one can include an additional auxiliary input as an input to the adversary. We recall that the choice of p and thus of the groups $\mathbb {G}_z$ depends on n. Let $\mathcal {L}_{{\mathbf {R}}} = \{\mathsf {x}: \exists \mathsf {w}, (\mathsf {x}, \mathsf {w}) \in {\mathbf {R}}\}$ be an $\mathbf {NP}$-language.

A (subversion-resistant) non-interactive zero-knowledge argument system $\varPsi$ for $\mathcal {R}$ consists of seven PPT algorithms:

 

CRS trapdoor generator::

$\mathsf {K}_{\mathsf {tc}}$ is a probabilistic algorithm that, given $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$, outputs a CRS trapdoor $\mathsf {tc}$. Otherwise, it outputs a special symbol $\bot$.

Simulation trapdoor generator::

$\mathsf {K}_{\mathsf {ts}}$ is a deterministic algorithm that, given $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {tc})$ where $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$ and $\mathsf {tc}\in \mathrm {range}(\mathsf {K}_{\mathsf {tc}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}})) \setminus \{\bot \}$, outputs the simulation trapdoor $\mathsf {ts}$. Otherwise, it outputs $\bot$.

CRS generator::

$\mathsf {K}_{\mathsf {crs}}$ is a deterministic algorithm that, given $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {tc})$, where $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$ and $\mathsf {tc}\in \mathrm {range}(\mathsf {K}_{\mathsf {tc}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}})) \setminus \{\bot \}$, outputs $\mathsf {crs}$. Otherwise, it outputs $\bot$. For the sake of efficiency and readability, we divide $\mathsf {crs}$ into $\mathsf {crs}_{\mathsf {P}}$ (the part needed by the prover), $\mathsf {crs}_{\mathsf {V}}$ (the part needed by the verifier), and $\mathsf {crs}_{\mathsf {CV}}$ (the part needed only by $\mathsf {CV}$ and not by $\mathsf {P}$ or $\mathsf {V}$).

CRS verifier::

$\mathsf {CV}$ is a probabilistic algorithm that, given $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs})$, returns either 0 (the CRS is incorrectly formed) or 1 (the CRS is correctly formed),

Prover::

$\mathsf {P}$ is a probabilistic algorithm that, given $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}_{\mathsf {P}}, \mathsf {x}, \mathsf {w})$ for $\mathsf {CV}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}) = 1$ and $(\mathsf {x}, \mathsf {w}) \in {\mathbf {R}}$, outputs an argument $\pi$. Otherwise, it outputs $\bot$.

Verifier::

$\mathsf {V}$ is a probabilistic algorithm that, given $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}_{\mathsf {V}}, \mathsf {x}, \pi )$, returns either 0 (reject) or 1 (accept).

Simulator::

$\mathsf {S}$ is a probabilistic algorithm that, given $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}, \mathsf {ts}, \mathsf {x})$ where $\mathsf {CV}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}) = 1$, outputs an argument $\pi$.

We also define the (non-subverted) CRS generation algorithm $\mathsf {K}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}})$ that first sets $\mathsf {tc}\leftarrow \mathsf {K}_{\mathsf {tc}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}})$ and then outputs $(\mathsf {crs}\,\Vert \,\mathsf {ts}) \leftarrow (\mathsf {K}_{\mathsf {crs}}\,\Vert \,\mathsf {K}_{\mathsf {ts}}) ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {tc})$.

One can remove $\mathsf {S}$ from the definition of $\varPsi$, and instead require that for each PPT verifier $\mathsf {V}^*$ there exists a corresponding PPT simulator $\mathsf {S}$. We follow [27] and other SNARK literature by letting $\varPsi$ to fix $\mathsf {S}$; this guarantees that there exists a single simulator that simulates the CRS for all subverters. In the case of non subversion-resistant QANIZKs, existence of a single simulator is required [29]. See Definition 5 and Remark 1 for a longer discussion.

SNARKs. A non-interactive argument system is succinct if the proof size is polynomial in $\kappa$ and the verifier runs in time polynomial in $\kappa$ + $|\mathsf {x}|$. A succinct non-interactive argument of knowledge is usually called SNARK. A zero knowledge SNARK is abbreviated to zk-SNARK.

Discussions. A (non subversion-resistant) non-interactive zero-knowledge argument system is defined as a tuple $(\mathsf {K}, \mathsf {P}, \mathsf {V}, \mathsf {S})$, see, e.g., [27]. We will now briefly motivate the differences compared to the established syntax of non-interactive zero-knowledge argument systems. Section 3.2 will give formal security definitions where the above syntactic definition will become an important part.

The division of $\mathsf {K}$ into 3 subalgorithms $\mathsf {K}_{\mathsf {tc}}$, $\mathsf {K}_{\mathsf {ts}}$, and $\mathsf {K}_{\mathsf {crs}}$ is usually not needed, but the $\mathsf {K}$ algorithm of many known non-interactive zero-knowledge argument systems (and all SNARKs that we know) satisfies such a division. $\mathsf {K}_{\mathsf {tc}}$ just generates all randomness ($\mathsf {tc}$), needed to compute $\mathsf {crs}$ and $\mathsf {ts}$, and then $\mathsf {K}_{\mathsf {crs}}$ and $\mathsf {K}_{\mathsf {ts}}$ compute from $\mathsf {tc}$ deterministically $\mathsf {crs}$ and $\mathsf {ts}$. We note that such division can be formalized by requiring the $\mathsf {crs}$ to be witness-sampleable [29] that also seems to be a reasonable requirement in the case one is interested in subversion-resistance. Really, an important subgoal of Sub-ZK is to guarantee that the subverted CRS is consistent with at least some choice of $\mathsf {tc}$. This means that for each $\mathsf {tc}$ there must exist corresponding $\mathsf {crs}$ (accepted by $\mathsf {CV}$) and $\mathsf {ts}$ (that can be used by the simulator to simulate subverted $\mathsf {crs}$ corresponding to $\mathsf {tc}$).

The existence of efficient $\mathsf {CV}$ will be crucial to obtain Sub-ZK. To guarantee Sub-ZK, it is intuitively clear that the honest prover should at least check the correctness of the CRS. Efficiency-wise, since the prover in known SNARK constructions (including say [22, 27] and the current paper) takes superlinear time, this is fine unless the CRS verification will be even slower. For the sake of clarity, however, we do not assume that $\mathsf {CV}$ is a part of the $\mathsf {P}$ algorithm; instead we assume that an honest prover first runs $\mathsf {CV}$ and given that it accepts, runs $\mathsf {P}$. This is since, in practice one could execute many zero-knowledge arguments by using the same CRS; it is natural to require that the prover executes $\mathsf {CV}$ only once. On the other hand, since we are not aiming to get subversion (knowledge-)soundness, the honest verifier does not have to execute CRS verification.

Finally, $\mathsf {crs}_{\mathsf {P}}$ (resp., $\mathsf {crs}_{\mathsf {V}}$) is the part of the CRS given to an honest prover (resp., an honest verifier), and $\mathsf {crs}_{\mathsf {CV}}$ is the part of CRS not needed by the prover or the verifier except to run $\mathsf {CV}$. The distinction between $\mathsf {crs}_{\mathsf {P}}$, $\mathsf {crs}_{\mathsf {V}}$, and $\mathsf {crs}_{\mathsf {CV}}$ is not important from the security point of view, but in many cases $\mathsf {crs}_{\mathsf {V}}$ is significantly shorter than $\mathsf {crs}_{\mathsf {P}}$. Keeping $\mathsf {crs}_{\mathsf {CV}}$ separate helps one to evaluate better the additional efficiency penalty introduced by subversion security.

3.2 Security Definitions

A Sub-ZK SNARK has to satisfy various security definitions. The most important ones are subversion-completeness (an honest prover convinces an honest verifier, and an honestly generated CRS passes the CRS verification test), computational knowledge-soundness (if a prover convinces an honest verifier, then he knows the corresponding witness), and statistical Sub-ZK (given a possibly subverted CRS, an argument created by the honest prover reveals no side information). In the case of Sub-ZK, we will consider the case of an efficient subverter and a computationally unbounded distinguisher; in Sect. 9 we will discuss the case when also the subverter is unbounded. Next, we will give definitions of those properties that guarantee both composability and subversion resistance.

To keep the new security definitions as close to the accepted security definitions of zk-SNARKs as possible, we will start with non subversion-resistant security definitions from [27] (that will be stated below for the sake of completeness), albeit by using our notation, and modify them by adding elements of subversion as in Bellare et al. [2]. To ease the reading, we will the differences between non-subversion and subversion definitions. We use the division of CRS generation into three different algorithms also in the non subversion-resistant case. As motivated in Sect. 3.1, we also give $\mathsf {z}_{{\mathbf {R}}}$ as an input to all honest parties. Finally, the notions of unbounded (ZK is guaranteed against an adversary who can arbitrarily query an oracle that outputs either proofs or simulations) and composable (ZK is guaranteed against an adversary who has to distinguish a single argument from a simulation) zero knowledge follow the definitions given in [25] and are in fact equal in our case.

As [27], we define all security notions against a non-uniform adversary. However, since our security reductions are uniform, it is a simple matter to consider only uniform adversaries, as it was done by Bellare et al. [2] (see also [24]).

Definition 1

(Perfect Completeness [27]). A non-interactive argument $\varPsi$ is perfectly complete for $\mathcal {R}$, if for all $\kappa$, all $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$, $\mathsf {tc}\in \mathrm {range}(\mathsf {K}_{\mathsf {tc}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}})) \setminus \{\bot \}$, and $(\mathsf {x}, \mathsf {w}) \in {\mathbf {R}}$,

$$ \Pr \left[ \mathsf {crs}\leftarrow \mathsf {K}_{\mathsf {crs}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {tc}): \mathsf {V}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}_{\mathsf {V}}, \mathsf {x}, \mathsf {P}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}_{\mathsf {P}}, \mathsf {x}, \mathsf {w})) = 1 \right] = 1. $$

Definition 2

(Perfect Subversion-Completeness). A non-interactive argument $\varPsi$ is perfectly subversion-complete for $\mathcal {R}$, if for all $\kappa$, all $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$, $\mathsf {tc}\in \mathrm {range}(\mathsf {K}_{\mathsf {tc}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}})) \setminus \{\bot \}$, and $(\mathsf {x}, \mathsf {w}) \in {\mathbf {R}}$,

Definition 3

(Computational Knowledge-Soundness [27]). $\varPsi$ is computationally (adaptively) knowledge-sound for $\mathcal {R}$, if for every NUPPT $\mathsf {A}$, there exists a NUPPT extractor $\mathsf {X}_\mathsf {A}$, s.t. for all $\kappa$,

$$ \Pr \left[ \begin{aligned}&({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \leftarrow \mathcal {R}(1^\kappa ), (\mathsf {crs}\,\Vert \,\mathsf {ts}) \leftarrow \mathsf {K}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}), \\&r \leftarrow _r \mathsf {RND}(\mathsf {A}), ((\mathsf {x}, \pi ) \,\Vert \,\mathsf {w}) \leftarrow (\mathsf {A}\,\Vert \,\mathsf {X}_\mathsf {A}) ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}; r):\\&(\mathsf {x}, \mathsf {w}) \not \in {\mathbf {R}}\wedge \mathsf {V}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}_{\mathsf {V}}, \mathsf {x}, \pi ) = 1 \end{aligned} \right] \approx _\kappa 0. $$

Here, $\mathsf {z}_{{\mathbf {R}}}$ can be seen as a common auxiliary input to $\mathsf {A}$ and $\mathsf {X}_\mathsf {A}$ that is generated by using a benign [10] relation generator; we recall that we just think of $\mathsf {z}_{{\mathbf {R}}}$ as being the description of a secure bilinear group. A knowledge-sound argument system is called an argument of knowledge.

Next, we define statistically unbounded ZK. Unbounded (non-Sub) ZK was not defined in [27], presumably because it is a corollary of composable non-Sub ZK as shown in [25]. Hence, we will first give a modified version of the definition of non-Sub ZK from [25]; in [25], $\mathsf {K}$ will only output a $\mathsf {crs}$ and a CRS simulator $\mathsf {S}_{\mathsf {crs}}$ will return $(\mathsf {crs}\,\Vert \,\mathsf {ts})$. As in [27], we find it more convenient to let $\mathsf {S}_{\mathsf {crs}}$ (whom we call $\mathsf {K}$) to generate also the honest $\mathsf {crs}$.

Definition 4

(Statistically Unbounded ZK [25]). $\varPsi$ is statistically unbounded Sub-ZK for $\mathcal {R}$, if for all $\kappa$, all $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$, and all computationally unbounded $\mathsf {A}$, $\varepsilon ^{unb}_0 \approx _\kappa \varepsilon ^{unb}_1$, where

$$ \varepsilon ^{unb}_b = \Pr [(\mathsf {crs}\,\Vert \,\mathsf {ts}) \leftarrow \mathsf {K}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}): \mathsf {A}^{\mathsf {O}_b (\cdot , \cdot )} ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}) = 1] . $$

Here, the oracle $\mathsf {O}_0 (\mathsf {x}, \mathsf {w})$ returns $\bot$ (reject) if $(\mathsf {x}, \mathsf {w}) \not \in {\mathbf {R}}$, and otherwise it returns $\mathsf {P}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}_{\mathsf {P}}, \mathsf {x}, \mathsf {w})$. Similarly, $\mathsf {O}_1 (\mathsf {x}, \mathsf {w})$ returns $\bot$ (reject) if $(\mathsf {x}, \mathsf {w}) \not \in {\mathbf {R}}$, and otherwise it returns $\mathsf {S}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}, \mathsf {ts}, \mathsf {x})$. $\varPsi$ is perfectly unbounded Sub-ZK for $\mathcal {R}$ if one requires that $\varepsilon ^{unb}_0 = \varepsilon ^{unb}_1$.

The following definition of unbounded Sub-ZK differs from this as follows. Since we allow the CRS to be subverted, the CRS is generated by a subverter who also returns $\mathsf {z}_{\mathsf {\Sigma }}$. The adversary’s access to $\mathsf {z}_{\mathsf {\Sigma }}$ models the possibility that the subverter and the adversary collaborate. The extractor $\mathsf {X}_{\mathsf {\Sigma }}$ extracts $\mathsf {tc}$ from $\mathsf {\Sigma }$, and then $\mathsf {tc}$ is used to generate the simulation trapdoor $\mathsf {ts}$ that is then given as an auxiliary input to the adversary and to the oracle $\mathsf {O}_1$. In [25], $\mathsf {tc}$ was not given to the adversary because $\mathsf {K}$ was not required to return $\mathsf {tc}$ and thus was not guaranteed to exist; adding this input to the adversary only increases the power of the adversary. In our construction, it does not matter since a computationally unbounded $\mathsf {A}$ could compute $\mathsf {ts}$ herself (see Algorithm 5 in Fig. 3). If we allow both the subverter and the extractor to be computationally unbounded, we would not need to rely on a knowledge assumption; the Sub-ZK proof in Sect. 7 would also simplify.

A weaker version of Sub-ZK definition would require that the extractor only outputs $\mathsf {ts}$ that is used then for simulation. We prefer the current definition since it is stronger and allows us to prove CRS trapdoor extractability (see Definition 8). Since we consider statistical ZK, achieving our stronger definition will concur almost no extra cost if we also allow $\mathsf {X}_{\mathsf {\Sigma }}$ to be computationally unbounded.

Definition 5

(Statistically Unbounded Sub-ZK). $\varPsi$ is statistically unbounded Sub-ZK for $\mathcal {R}$, if for any NUPPT subverter $\mathsf {\Sigma }$ there exists a NUPPT $\mathsf {X}_{\mathsf {\Sigma }}$, such that for all $\kappa$, all $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$, and all computationally unbounded $\mathsf {A}$, $\varepsilon ^{unb}_0 \approx _\kappa \varepsilon ^{unb}_1$, where $\varepsilon ^{unb}_b$ is defined as

Here, the oracle $\mathsf {O}_0 (\mathsf {x}, \mathsf {w})$ returns $\bot$ (reject) if $(\mathsf {x}, \mathsf {w}) \not \in {\mathbf {R}}$, and otherwise it returns $\mathsf {P}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}_{\mathsf {P}}, \mathsf {x}, \mathsf {w})$. Similarly, $\mathsf {O}_1 (\mathsf {x}, \mathsf {w})$ returns $\bot$ (reject) if $(\mathsf {x}, \mathsf {w}) \not \in {\mathbf {R}}$, and otherwise it returns $\mathsf {S}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}, \mathsf {ts}, \mathsf {x})$. $\varPsi$ is perfectly unbounded Sub-ZK for $\mathcal {R}$ if one requires that $\varepsilon ^{unb}_0 = \varepsilon ^{unb}_1$.

Remark 1

(Comparison to Sub-ZK Definition of [2]). Let $\mathsf {O}_b$ be defined as before. In [2], it is required that for any (non-uniform) PPT subverter $\mathsf {\Sigma }$ there exists a (non-uniform) PPT simulator $(\mathsf {X}_{\mathsf {\Sigma }}, \mathsf {S})$, such that for all $\kappa$, $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$, all $(\mathsf {x}, \mathsf {w}) \in {\mathbf {R}}$, and all (non-uniform) PPT $\mathsf {A}$, $\varepsilon _0^{bfs} \approx _\kappa \varepsilon _1^{bfs}$, where

$$ \varepsilon _b^{bfs} = \Pr \left[ \begin{aligned}&\text{ if } b = 0 \text{ then } r \leftarrow _r \mathsf {RND}(\mathsf {\Sigma }), \mathsf {crs}\leftarrow \mathsf {\Sigma }({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}; r)\\&\text{ else } (\mathsf {crs}, r) \leftarrow \mathsf {X}_{\mathsf {\Sigma }} ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \text{ fi }: \mathsf {A}^{\mathsf {O}_b (\cdot , \cdot )} ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}, r) \end{aligned} \right] . $$

First, [2] defines computational Sub-ZK while we define statistical Sub-ZK. This by itself changes several aspects of the definition. E.g., we could just let $\mathsf {A}$ to compute $\mathsf {ts}$ and $\mathsf {z}_{\mathsf {\Sigma }}$ from $\mathsf {crs}$ instead of giving them as extra inputs to $\mathsf {A}$.

Second, compared to [2], we give to $\mathsf {A}$ extra information, $\mathsf {ts}$ and $\mathsf {z}_{\mathsf {\Sigma }}$. Having access to $\mathsf {ts}$ means that one can implement SNARKs for different relations using the same CRS [25]. Really, given $\mathsf {ts}$, $\mathsf {A}$ will be able to both form and simulate arguments for any of the considered relations. Having access to $\mathsf {z}_{\mathsf {\Sigma }}$ models, as already mentioned, the possibility that $\mathsf {\Sigma }$ and $\mathsf {A}$ are collaborating. (Bellare et al. only allow the subverter to communicate r, the secret coins.) In this sense, our definition is stronger compared to [2].

Third, Bellare et al. required that for each $\mathsf {\Sigma }$ there exists a simulator $(\mathsf {X}_{\mathsf {\Sigma }}, \mathsf {S})$. We consider it to be more natural to think of $\mathsf {X}_{\mathsf {\Sigma }}$ as an extractor and allow only $\mathsf {X}_{\mathsf {\Sigma }}$ to depend on $\mathsf {\Sigma }$. In the SNARK literature, extractors usually depend on the adversary (here, $\mathsf {\Sigma }$) while there is a single simulator that works for all adversaries. In particular, this is a formal requirement in the case of QANIZKs, [29]. Also Bellare et al. used $\mathsf {X}_{\mathsf {\Sigma }}$ as an extractor in their construction. In this sense, our definition is stronger compared to [2].

Fourth, we give to $\mathsf {X}_{\mathsf {\Sigma }}$ the same coins r as to $\mathsf {\Sigma }$, while Bellare et al. allow $\mathsf {X}_{\mathsf {\Sigma }}$ to generate its own coins, only requiring that the distribution of $(\mathsf {crs}, r)$ is computationally indistinguishable from the output of $\mathsf {\Sigma }$. Also in this sense, our definition seems to be stronger.

Finally, we use explicitly the syntax of subversion-resistant SNARKs from Sect. 3.1, assuming the existence of algorithms $\mathsf {K}_{\mathsf {ts}}$ and $\mathsf {CV}$. While it might seem to be restrictive, as argued in Sect. 3.1, existence of both $\mathsf {K}_{\mathsf {ts}}$ and $\mathsf {CV}$ seems to be necessary for subversion-resistance.   $\square$

In the case of composable ZK, the adversary can only see one purported (i.e., real or simulated) argument $\pi$, instead of being able to make many queries to a purported prover oracle as in the case of unbounded ZK. If composable ZK is defined carefully, it will be at least as strong as unbounded ZK while potentially allowing for simpler ZK proofs, [25]. We will show that the same holds in the case of Sub-ZK.

Definition 6

(Statistically Composable ZK [27]). $\varPsi$ is statistically composable Sub-ZK for $\mathcal {R}$, if for any NUPPT subverter $\mathsf {\Sigma }$ there exists a NUPPT $\mathsf {X}_{\mathsf {\Sigma }}$, such that for all $\kappa$, $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$, all $(\mathsf {x}, \mathsf {w}) \in {\mathbf {R}}$, and all computationally unbounded $\mathsf {A}$, $\varepsilon ^{comp}_0 \approx _\kappa \varepsilon ^{comp}_1$, where

$$ \varepsilon ^{comp}_b = \Pr \left[ \begin{aligned}&(\mathsf {crs}\,\Vert \,\mathsf {ts}) \leftarrow \mathsf {K}( {\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}),\\&\text{ if } b = 0 \text{ then } \pi \leftarrow \mathsf {P}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}_{\mathsf {P}}, \mathsf {x}, \mathsf {w})\\&\text{ else } \pi \leftarrow \mathsf {S}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}, \mathsf {ts}, \mathsf {x}) \text{ fi }: \mathsf {A}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}, \mathsf {ts}, \pi ) = 1 \end{aligned} \right] . $$

$\varPsi$ is perfectly composable Sub-ZK for $\mathcal {R}$ if one requires that $\varepsilon _0^{comp} = \varepsilon _1^{comp}$.

Next, we define statistical composable subversion zero knowledge (Sub-ZK). This definition is related to but crucially different from the definition of (computational) composable ZK from [25]. Most importantly, [25] defines two properties, the first being reference string indistinguishability, meaning that the CRS generated by honest $\mathsf {K}$ and the CRS simulated by a simulator $\mathsf {S}_{\mathsf {crs}}$ should be indistinguishable. We will use the CRS generated by the subverter in both the real and the simulated case. The second property in [25] is simulation indistinguishability. Our definition of composable Sub-ZK is similar to the definition of simulation indistinguishability in [25]. However, instead of simulating the CRS, we use $\mathsf {crs}$ generated by the subverter, assume that an extractor extracts $\mathsf {tc}$ from $\mathsf {crs}$, compute $\mathsf {ts}$ from $\mathsf {tc}$ by using $\mathsf {K}_{\mathsf {ts}}$, and finally verify that $\mathsf {CV}$ accepts $\mathsf {crs}$. We also quantify over all valid $(\mathsf {x}, \mathsf {w}) \in {\mathbf {R}}$ instead of letting the adversary to choose it; since we deal with statistical Sub-ZK this results in an equivalent definition.

Moreover, we differ from the definition of composable non-Sub ZK in [27] as follows. The CRS is generated by $\mathsf {\Sigma }$ who also returns $\mathsf {z}_{\mathsf {\Sigma }}$. $\mathsf {A}$’s access to $\mathsf {z}_{\mathsf {\Sigma }}$ models the possibility that $\mathsf {\Sigma }$ and $\mathsf {A}$ collaborate; although of course $\mathsf {A}$ could just recompute it. $\mathsf {X}_{\mathsf {\Sigma }}$ extracts $\mathsf {tc}$ from $\mathsf {\Sigma }$, and then $\mathsf {tc}$ is used to generate the simulation trapdoor $\mathsf {ts}$ that is then given as an auxiliary input to $\mathsf {A}$.

Definition 7

(Statistically Composable Sub-ZK). $\varPsi$ is statistically composable Sub-ZK for $\mathcal {R}$, if for any NUPPT subverter $\mathsf {\Sigma }$ there exists a NUPPT $\mathsf {X}_{\mathsf {\Sigma }}$, such that for all $\kappa$, all $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$, all $(\mathsf {x}, \mathsf {w}) \in {\mathbf {R}}$, and all computationally unbounded $\mathsf {A}$, $\varepsilon ^{comp}_0 \approx _\kappa \varepsilon ^{comp}_1$, where $\varepsilon ^{comp}_b$ is defined as

$\varPsi$ is perfectly composable Sub-ZK for $\mathcal {R}$ if one requires that $\varepsilon _0^{comp} = \varepsilon _1^{comp}$.

Now, we will prove the following result that makes it possible to operate in the rest of the paper with the simpler composable Sub-ZK definition. It is motivated by a similar result of Groth (ASIACRYPT 2006, [25]) that considers computational non subversion-resistant zero knowledge. As seen from below, we can establish the same result for statistical zero knowledge, but then we have to restrict the number of oracle calls to a polynomial number.

Theorem 1

(i) Statistical composable Sub-ZK implies statistical unbounded Sub-ZK, assuming that $\mathsf {A}$ is given access to polynomially many oracle calls. (ii) Perfect composable Sub-ZK implies perfect unbounded Sub-ZK, even if given access to an unbounded number of oracle calls.

Proof

(i) Statistical Sub-ZK. Assume that the adversary can make up to $q (\kappa )$ oracle queries for some fixed polynomial q. We define a sequence of $q (\kappa ) + 1$ oracles $\mathsf {O}'_0 (\mathsf {x}, \mathsf {w}), \ldots ,$ $\mathsf {O}'_{q (\kappa )} (\mathsf {x}, \mathsf {w})$. Given the jth adversarial query $(\mathsf {x}_j, \mathsf {w}_j)$, the oracle $\mathsf {O}'_k (\cdot , \cdot )$ responds with $\mathsf {O}_1 (\mathsf {x}_j, \mathsf {w}_j)$ for $j \in [1 \, .. \, k]$ and $\mathsf {O}_0 (\mathsf {x}_j, \mathsf {w}_j)$ for $j \in [k + 1 \, .. \, q (\kappa )]$. Hence, $\mathsf {O}'_0 = \mathsf {O}_0$ and $\mathsf {O}'_{q (\kappa )} = \mathsf {O}_1$.

Due to the statistical composable Sub-ZK property, we get that for $i \in [0 \, .. \, q (\kappa ) - 1]$, $\varepsilon _i \approx _\kappa \varepsilon _{i + 1}$, where $\varepsilon _i$ is defined as

$$ \Pr \left[ \begin{aligned}&r \leftarrow _r \mathsf {RND}(\mathsf {\Sigma }), (\mathsf {crs}, \mathsf {z}_{\mathsf {\Sigma }}\,\Vert \,\mathsf {tc}) \leftarrow (\mathsf {\Sigma }\,\Vert \,\mathsf {X}_{\mathsf {\Sigma }}) ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}; r),\\&\mathsf {ts}\leftarrow \mathsf {K}_{\mathsf {ts}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {tc}): \mathsf {CV}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}) = 1 \wedge \mathsf {A}^{\mathsf {O}'_i (\cdot , \cdot )} ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}, \mathsf {ts}, \mathsf {z}_{\mathsf {\Sigma }}) = 1 \end{aligned} \right] ,$$

since the oracles can be efficiently implemented given $\mathsf {crs}$ and $\mathsf {ts}$, and inserting $\pi$ as the answer to the ith query. Since $\varepsilon _0 = \varepsilon ^{unb}_0$, q is a polynomial, and $\varepsilon ^{unb}_0 = \varepsilon _0 \approx _\kappa \dots \approx _\kappa \varepsilon _{q (\kappa )} = \varepsilon ^{unb}_1$, we get that $\varepsilon ^{unb}_0 \approx _\kappa \varepsilon ^{unb}_1$ and hence the claim holds.

(ii) Perfect Sub-ZK. As above, but assume q is the actual (possibly unbounded) number of queries. We get $\varepsilon ^{unb}_0 = \varepsilon _0 = \dots = \varepsilon _{q (\kappa )} = \varepsilon ^{unb}_1$, and hence $\varepsilon ^{unb}_0 = \varepsilon ^{unb}_1$, and the claim holds.   $\square$

In [25], composable ZK was a stronger requirement than unbounded ZK since in the case of composable ZK, (i) the simulated CRS was required to be indistinguishable from the real CRS, and (ii) the adversary got access to $\mathsf {ts}$. In the case of our Sub-ZK definitions, there is no such difference and it is easy to see that composable Sub-ZK and unbounded Sub-ZK are in fact equal notions.

In the proof that the new SNARK is Sub-ZK (see Theorem 5), we require that if $\mathsf {\Sigma }$ generates a $\mathsf {crs}$ accepted by $\mathsf {CV}$ then there exists a NUPPT extractor $\mathsf {X}_{\mathsf {\Sigma }}$ that generates a CRS trapdoor $\mathsf {tc}$ that corresponds to $\mathsf {crs}$; that is, $\mathsf {K}_{\mathsf {crs}}$ on input $\mathsf {tc}$ outputs $\mathsf {crs}$. We formalize this property—that intuitively gives us a stronger version of witness-sampleability—as follows.

Definition 8

(Statistical CRS Trapdoor Extractability). $\varPsi$ has statistical CRS trapdoor extractability for $\mathcal {R}$, if for any NUPPT subverter $\mathsf {\Sigma }$ there exists a NUPPT $\mathsf {X}_{\mathsf {\Sigma }}$, s.t. for all $\kappa$ and all $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$,

$$ \Pr \left[ \begin{aligned}&r \leftarrow _r \mathsf {RND}(\mathsf {\Sigma }), (\mathsf {crs}, \mathsf {z}_{\mathsf {\Sigma }}\,\Vert \,\mathsf {tc}) \leftarrow (\mathsf {\Sigma }\,\Vert \,\mathsf {X}_{\mathsf {\Sigma }}) ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}; r):\\&\mathsf {CV}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}) = 1 \wedge \mathsf {K}_{\mathsf {crs}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {tc}) \ne \mathsf {crs}\end{aligned} \right] \approx _\kappa 0 . $$

$\varPsi$ has perfect CRS trapdoor extractability for $\mathcal {R}$ if the same property holds but with $\approx _\kappa$ changed to $=$.

4 GBGM and Sub-GBGM

Preliminaries: Generic Bilinear Group Model. In Sect. 6, we will prove that the new zk-SNARK is knowledge-sound in the subversion generic bilinear group model (Sub-GBGM). In the current subsection, we will introduce the GBGM [12, 33, 34, 36], by following the exposition in [33]. After that, we will introduce the Sub-GBGM.

We start by picking a random asymmetric bilinear group ${\textsf {gk}}:= (p, \mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T, \hat{e}) \leftarrow \mathsf {genbp}(1^\kappa , n)$. Consider a black box $\mathbf {B}$ that can store values from additive groups $\mathbb {G}_1, \mathbb {G}_2, \mathbb {G}_T$ in internal state variables $\mathsf {cell}_1, \mathsf {cell}_2, \dots$, where for simplicity we allow the storage space to be infinite (this only increases the power of a generic adversary). The initial state consists of some values $(\mathsf {cell}_1, \mathsf {cell}_2, \dots , \mathsf {cell}_{|inp|})$, which are set according to some probability distribution. Each state variable $\mathsf {cell}_i$ has an accompanying type $\mathsf {type}_i \in \{1, 2, T, \bot \}$. We assume initially $\mathsf {type}_i = \bot$ for $i > |inp|$. The black box allows computation operations on internal state variables and queries about the internal state. No other interaction with $\mathbf {B}$ is possible.

Let $\varPi$ be an allowed set of computation operations. A computation operation consists of selecting a (say, t-ary) operation $f \in \varPi$ together with $t + 1$ indices $i_1, i_2, \dots , i_{t + 1}$. Assuming inputs have the correct type, $\mathbf {B}$ computes $f (\mathsf {cell}_{i_1}, \dots , \mathsf {cell}_{i_t})$ and stores the result in $\mathsf {cell}_{i_{t + 1}}$. For a set $\varSigma$ of relations, a query consists of selecting a (say, t-ary) relation $\varrho \in \varSigma$ together with t indices $i_1, i_2, \dots , i_t$. Assuming inputs have the correct type, $\mathbf {B}$ replies to the query with $\varrho (\mathsf {cell}_{i_1}, \dots , \mathsf {cell}_{i_t})$. In the GBGM, we define $\varPi = \{+, \hat{e}\}$ and $\varSigma = \{=\}$, where

• 1. On input $(+, i_1, i_2, i_3)$: if $\mathsf {type}_{i_1} = \mathsf {type}_{i_2} \ne \bot$ then set $\mathsf {cell}_{i_3} \leftarrow \mathsf {cell}_{i_1} + \mathsf {cell}_{i_2}$ and $\mathsf {type}_{i_3} \leftarrow \mathsf {type}_{i_1}$.

• 2. On input $(\hat{e}, i_1, i_2, i_3)$: if $\mathsf {type}_{i_1} = 1$ and $\mathsf {type}_{i_2} = 2$ then set $\mathsf {cell}_{i_3} \leftarrow \hat{e}(\mathsf {cell}_{i_1}, \mathsf {cell}_{i_2})$ and $\mathsf {type}_{i_3} \leftarrow T$.

• 3. On input $(=, i_1, i_2)$: if $\mathsf {type}_{i_1} = \mathsf {type}_{i_2} \ne \bot$ and $\mathsf {cell}_{i_1} = \mathsf {cell}_{i_2}$ then return 1. Otherwise return 0.

Since we are proving lower bounds, we will give a generic adversary $\mathsf {A}$ additional power. We assume that all relation queries are for free. We also assume that $\mathsf {A}$ is successful if after $\tau$ operation queries, he makes an equality query $(=, i_1, i_2)$, $i_1 \ne i_2$, that returns 1; at this point $\mathsf {A}$ quits. Thus, if $\mathsf {type}_i \ne \bot$, then $\mathsf {cell}_i = F_i (\mathsf {cell}_1, \dots , \mathsf {cell}_{|inp|})$ for a polynomial $F_i$ known to $\mathsf {A}$.

Sub-GBGM. By following Bellare et al. [2], we enhance the power of generic bilinear group model [12, 33, 34, 36]. Since the power of the generic adversary will increase, security proofs in the resulting Sub-GBGM will be somewhat more realistic than in the GBGM model.

As noted by Bellare et al. [2], it is known how to hash into elliptic curves and thus create group elements without knowing their discrete logarithms. However, it is not known how to create four elements $\left[ 1\right] _{z}$, $\left[ a\right] _{z}$, $\left[ b\right] _{z}$, and $\left[ a b\right] _{z}$ without knowing either a or b. The corresponding assumption—that may also be true in the case of symmetric pairings—was named DH-KE(A) in [2].

However, asymmetric pairings are much more efficient than symmetric pairings. If we work in the type III pairing setting where there is no efficient isomorphism either from $\mathbb {G}_1$ to $\mathbb {G}_2$ or from $\mathbb {G}_2$ to $\mathbb {G}_1$, then clearly an adversary cannot, given $\left[ a\right] _{z}$ for $z \in \{1, 2\}$ and an unknown a, compute $\left[ a\right] _{3 - z}$. In the same vein, it seems reasonable to make a stronger assumption (that we call BDH-KE, a simplification of the asymmetric PKE assumption of [17]) that if an adversary creates $\left[ a\right] _{1}$ and $\left[ a\right] _{2}$ then she knows a. Really, since there is no polynomial-time isomorphism from $\mathbb {G}_1$ to $\mathbb {G}_2$ (or back), it seems to be natural to assume that one does not have to worry about an adversary knowing some trapdoor that would break the BDH-KE assumption. Since BDH-KE is not a falsifiable assumption, this does not obviously mean that it must hold for each type III pairing. Instead, the BDH-KE assumption can be interpreted as a stronger definition of the type III pairing setting. We formalize the added adversarial power as follows.

We give the generic model adversary an additional power to effectively create new indeterminates $Y_i$ in groups $\mathbb {G}_1$ and $\mathbb {G}_2$ (e.g., by hashing into elliptic curves), without knowing their values. We note since $\left[ Y\right] _{1} \bullet \left[ 1\right] _{2} = \left[ Y\right] _{T}$ and $\left[ 1\right] _{1} \bullet \left[ Y\right] _{2} = \left[ Y\right] _{T}$, the adversary that has generated an indeterminate Y in $\mathbb {G}_z$ can also operate with Y in $\mathbb {G}_T$. Formally, this means that $\varPi$ will contain one more operation $\mathsf {create}$, with the following semantics:

• 4. On input $(\mathsf {create}, i, t)$: if $\mathsf {type}_i = \bot$ and $t \in \{1, 2, T\}$ then set $\mathsf {cell}_i \leftarrow \mathbb {Z}_p$ and $\mathsf {type}_i \leftarrow t$.

The semantics of $\mathsf {create}$ dictates that the actual value of the indeterminate $Y_i$ is uniformly random in $\mathbb {Z}_p$, that is, the adversary cannot create indeterminates for which she does not know the discrete logarithm and that yet are not random. This assumption is needed for the lower bound on the generic adversary’s time to be provable in Theorem 3.

In the type III setting, this semantics does not allow the adversary to create the same indeterminate $Y_i$ in both groups $\mathbb {G}_1$ and $\mathbb {G}_2$; she can only create a representation of a known to her integer in both groups. We formalize this by making the following Bilinear Diffie-Hellman Knowledge of Exponents (BDH-KE) assumption: if the adversary, given random generators $\mathfrak {g}_1 = \left[ 1\right] _{1} \in \mathbb {G}_1$ and $\mathfrak {g}_2 = \left[ 1\right] _{2} \in \mathbb {G}_2$, can generate elements $\left[ \alpha _1\right] _{1} \in \mathbb {G}_1$ and $\left[ \alpha _2\right] _{2} \in \mathbb {G}_2$, such that $\left[ 1\right] _{1} \bullet \left[ \alpha _2\right] _{2} = \left[ \alpha _1\right] _{1} \bullet \left[ 1\right] _{2}$, then the adversary knows the value $\alpha _1 = \alpha _2$. To simplify the further use of the BDH-KE assumption in security reductions, we give the adversary access to $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$. As before, $\mathsf {z}_{{\mathbf {R}}}$ just contains ${\textsf {gk}}$, that is, the description of the bilinear group together with $\left[ 1\right] _{1}$ and $\left[ 1\right] _{2}$.

Definition 9

(BDH-KE). We say that $\mathsf {genbp}$ is BDH-KE secure for $\mathcal {R}$ if for any $\kappa$, $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$, and NUPPT adversary $\mathsf {A}$ there exists a NUPPT extractor $\mathsf {X}_\mathsf {A}$, such that

$$ \Pr \left[ \begin{aligned}&r \leftarrow _r \mathsf {RND}(\mathsf {A}), (\left[ \alpha _1\right] _{1}, \left[ \alpha _2\right] _{2} \,\Vert \,a) \leftarrow (\mathsf {A}\,\Vert \,\mathsf {X}_\mathsf {A}) ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}; r):\\ {}&\left[ \alpha _1\right] _{1} \bullet \left[ 1\right] _{2} = \left[ 1\right] _{1} \bullet \left[ \alpha _2\right] _{2} \wedge a \ne \alpha _1 \end{aligned} \right] \approx _\kappa 0. $$

The BDH-KE assumption is a simple special case of the PKE assumption as used in the case of asymmetric pairings say in [17]. In the PKE assumption of [17], adversary is given as an input the tuple $\{(\left[ \chi ^i\right] _{1}, \left[ \chi ^i\right] _{2})\}_{i = 0}^n$ for some $n \ge 0$, and it is assumed that if an adversary outputs $(\left[ \alpha \right] _{1}, \left[ \alpha \right] _{2})$ then she knows $(a_0, a_1, \dots , a_n)$, such that $\alpha = \sum _{i = 0}^{n} a_i \chi ^i$. In our case, $n = 0$. BDH-KE can also be seen as an asymmetric-pairing version of the original KE assumption [16].

We think that for the following reasons, the BDH-KE assumption is more natural than the DH-KE assumption by Bellare et al. [2] which states that if the adversary can create elements $\left[ \alpha _1\right] _{z}$, $\left[ \alpha _2\right] _{z}$ and $\left[ \alpha _1 \alpha _2\right] _{z}$ of the group $\mathbb {G}_z$ then she knows either $\alpha _1$ or $\alpha _2$.

First, the BDH-KE assumption is well suited to type-III pairings that are by far the most efficient pairings. The DH-KE assumption is tailored to type-I pairings. In the case of type-III pairings, DH-KE assumption can still be used, but it results in inefficient protocols. For example in [2], in security proofs the authors employs an adversary that extracts either $\alpha _1$ or $\alpha _2$. Since it is not known a priori which value will be extracted, several elements in the argument system have to be doubled, for the case $\alpha _1$ is extracted and for the case $\alpha _2$ is extracted.

Second, most of the efficient SNARKs are constructed to be sound and zero-knowledge in the (most efficient) type-III setting. While the SNARK of Groth [27] is known to be sound in the case of both symmetric and asymmetric pairings, in the case of symmetric pairings it will be much less efficient. To take the advantage of already known efficient SNARKs, it is only natural to keep the type-III setting. In the current paper, we are able to have the best of both worlds. As in the case of [27], we construct a SNARK that uses type-III pairings. On the one hand, we prove it to be Sub-ZK solely under the BDH-KE assumption. On the other hand, we prove that it is (adaptively) knowledge-sound in the Sub-GBGM, independently of whether one uses type-I, type-II, or type-III pairings. This provides a partial hedge against cryptanalysis: even if one were to later find an efficient isomorphism between $\mathbb {G}_1$ and $\mathbb {G}_2$, this would only break the Sub-ZK of the new SNARK but leave the soundness property intact.

5 New Sub-ZK Secure SNARK

Consider a QAP instance $\mathcal {Q}_p = (\mathbb {Z}_p, m_0, \{u_j, v_j, w_j\}_{j = 0}^m)$. The goal of the prover of a QAP argument of knowledge [22, 27] is to show that for public $(A_1, \dots , A_{m_0})$ and $A_0 = 1$, the prover knows $(A_{m_0+ 1}, \dots , A_m)$ and a degree $\le n - 2$ polynomial $h(X)$, such that

$$\begin{aligned} h(X) = \frac{a (X) b (X) - c (X)}{\ell (X)}, \end{aligned}$$

(2)

where $a (X) = \sum _{j = 0}^m A_j u_j (X)$, $b (X) = \sum _{j = 0}^m A_j v_j (X)$, $c (X) = \sum _{j = 0}^m A_j w_j (X)$.

5.1 Construction

Next, we describe a Sub-ZK SNARK for $\mathcal {R}$ that is closely based on the (non subversion-resistant) SNARK by Groth from EUROCRYPT 2016 [27]. See Figs. 1 and 2. As always, we assume implicitly that each algorithm checks that their inputs belong to correct groups and that $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$.

This SNARK uses crucially several random variables, $\chi , \alpha , \beta , \gamma , \delta$. As in [27], $\alpha$ and $\beta$ (and the inclusion of $\alpha \beta$ in the verification equation) will guarantee that $\mathfrak {a}$, $\mathfrak {b}$, and $\mathfrak {c}$ are computed by using the same coefficients $A_i$. The role of $\gamma$ and $\delta$ is to make the three products in the verification equation “independent” of each other. Due to the lack of space, we omit a more precise intuition behind Groth’s SNARK and refer an interested reader to [27].

As emphasized before, the new Sub-ZK SNARK is closely based on Groth’s zk-SNARK. In fact, the differences between the construction of the two SNARKs can be summarized very briefly:

• (i) We add to the CRS $2 n + 3$ new elements (see the variable $\mathsf {crs}_{\mathsf {CV}}$ in Fig. 1) that are needed for $\mathsf {CV}$ to work efficiently.

• (ii) We divide the CRS generation algorithm into three algorithms, $\mathsf {K}_{\mathsf {tc}}$, $\mathsf {K}_{\mathsf {ts}}$, and $\mathsf {K}_{\mathsf {crs}}$. Groth’s CRS generation algorithm returns $\mathsf {K}_{\mathsf {crs}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {K}_{\mathsf {tc}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}))$ (minus the mentioned $\mathsf {crs}_{\mathsf {CV}}$ part) as the CRS and $\mathsf {K}_{\mathsf {ts}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {K}_{\mathsf {tc}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}))$ as the simulation trapdoor.

• (iii) We describe an efficient CRS verification algorithm $\mathsf {CV}$ (see Fig. 1).

Fig. 1.

The CRS generation and verification of the Sub-ZK SNARK for $\mathcal {R}$

Fig. 2.

The prover and the verifier of the Sub-ZK SNARK for $\mathcal {R}$ (unchanged from Groth’s zk-SNARK)

It is straightforward to see that Groth’s original zk-SNARK does not achieve Sub-ZK. Really, since neither $\left[ \ell _i (\chi )\right] _{1}$ nor $\left[ \chi ^i\right] _{1}$ are given to the prover, he cannot check the correctness of $\left[ u_j (\chi )\right] _{1}$ and $\left[ v_j (\chi )\right] _{1}$. This means that a subverter can change those values to some bogus values and due to that, the proof computed by an honest prover and a simulated proof (that relies on the knowledge of trapdoor elements $\alpha$ and $\beta$ and does not use the CRS elements $\left[ u_j (\chi )\right] _{1}$ and $\left[ v_j (\chi )\right] _{1}$; see Fig. 3) will have different distributions.

We prove the completeness of the new SNARK in the rest of this section. We postpone the full proof of knowledge-soundness to Sect. 6 and of zero knowledge to Sect. 7. We analyze the efficiency of this SNARK in Sect. 8.

5.2 Subversion Completeness

In the proof of subversion-completeness, we need the following result that hopefully is of independent interest.

Lemma 1

Given $(\left[ \chi ^{n - 1}, (\ell _i (\chi ))_{i = 1}^{n}\right] _{1}, \left[ 1, \chi \right] _{2}, \left[ 1\right] _{T})$ as an input, Algorithm 2 checks that $\left[ \ell _i (\chi )\right] _{1}$ has been correctly computed for all $i \in [1 \, .. \, n]$. It can be implemented by using $n + 1$ pairings, $n - 1$ exponentiations in $\mathbb {G}_2$, and $n - 1$ exponentiations in $\mathbb {G}_T$.

Proof

Recalling that $\ell _i (X) = (X^n - 1) \omega ^{i - 1} / (n (X- \omega ^{i - 1}))$ are as given by Eq. (1), the proof is straightforward. Really, by induction on i, at any concrete value of i, $\zeta = (\chi ^n - 1) \omega ^{i - 1} / n$ and $\omega ' = \omega ^{i - 1}$. Thus $\left[ \ell _i (\chi )\right] _{1} \bullet (\left[ \chi \right] _{2} - \left[ \omega '\right] _{2}) = \left[ (\chi - \omega ^{i - 1}) \cdot \ell _i (\chi )\right] _{T} = \left[ \zeta \right] _{T}$ iff $\left[ \ell _i (\chi )\right] _{1}$ was correctly computed if $\chi \ne \omega ^{i - 1}$. If $\chi = \omega ^{i - 1}$, then $(\chi - \omega ^{i - 1}) \cdot \ell _i (\chi ) = (\chi ^n - 1) \omega ^{i - 1} / n = 0$, since $\omega$ is the n-th primitive root of unity.   $\square$

For $z \in \{1, 2\}$, let $\mathsf {crs}_z$ be the subset of the (honest or subverted) $\mathsf {crs}$ that consists of all elements of $\mathbb {G}_z$.

Theorem 2

The new SNARK of Sect. 5.1 is perfectly subversion-complete.

Proof

$\mathsf {CV}$ accepts an honestly generated CRS: this can be established by a simple but tedious calculation. Basically, $\mathsf {CV}$ accepts due to the properties of the bilinear map, and due to the definitions of $\ell (X)$ and $\ell _i (X)$. We only prove the correctness of two of the least obvious steps.

Step 6 of $\mathsf {CV}$ holds since $\left[ (u_j (\chi ) \beta + v_j (\chi ) \alpha + w_j (\chi )) / \delta \right] _{1} \bullet \left[ \delta \right] _{2} = \left[ u_j (\chi )\right] _{1} \bullet \left[ \beta \right] _{2} + \left[ v_j (\chi )\right] _{1} \bullet \left[ \alpha \right] _{2} + \left[ w_j (\chi )\right] _{1} \bullet \left[ 1\right] _{2}$ iff $\left[ (u_j (\chi ) \beta + v_j (\chi ) \alpha + w_j (\chi )) / \delta \cdot \delta \right] _{T} = \left[ u_j (\chi ) \beta + v_j (\chi ) \alpha + w_j (\chi )\right] _{T}$ which is a tautology.

Similarly, Lemma 1 has established that Algorithm 2 works correctly. Thus, Step 8 of $\mathsf {CV}$ holds since $\left[ \chi ^i \ell (\chi ) / \delta \right] _{1} \bullet \left[ \delta \right] _{2} = \left[ \chi ^{i + 1}\right] _{1} \bullet \left[ \chi ^{n - 1}\right] _{2} - \left[ \chi ^i\right] _{1} \bullet \left[ 1\right] _{2}$ iff $\left[ \chi ^i \ell (\chi ) / \delta \cdot \delta \right] _{T} = \left[ \chi ^{i + 1} \cdot \chi ^{n - 1} - \chi ^i\right] _{T}$ iff $\left[ \chi ^i \ell (\chi )\right] _{T} = \left[ \chi ^i (\chi ^n - 1)\right] _{T}$, which is a tautology since $\ell (\chi ) = \chi ^n - 1$.

$\mathsf {V}$ accepts an honestly generated argument: In the honest case, see Fig. 2, $\mathfrak {a}= \left[ A (\varvec{x})\right] _{1}$, $\mathfrak {b}= \left[ B (\varvec{x})\right] _{2}$, and $\mathfrak {c}= \left[ C (\varvec{x})\right] _{1}$, where $A (\varvec{x}) = \sum _{j = 0}^m A_j u_j (\chi ) + \alpha + r_a \delta$, $B (\varvec{x}) = \sum _{j = 0}^m A_j v_j (\chi ) + \beta + r_b \delta$, and $C (\varvec{x}) = r_b A (\varvec{x}) + r_a (B (\varvec{x}) - r_b \delta ) + \sum _{j = m_0+ 1}^m (u_j (\chi ) \beta + v_j (\chi ) \alpha + w_j (\chi )) / \delta + h(\chi ) \ell (\chi ) / \delta$. Clearly,

$$\begin{aligned} A (\varvec{x}) B (\varvec{x}) -&r_b A (\varvec{x}) \delta - r_a (B (\varvec{x}) - r_b \delta ) \delta \\ =&\textstyle (\sum _{j = 0}^m A_j u_j (\chi ) + \alpha ) \cdot (\sum _{j = 0}^m A_j v_j (\chi ) + \beta ) \\ =&\textstyle (\sum _{j = 0}^m A_j u_j (\chi )) \cdot (\sum _{j = 0}^m A_j v_j (\chi )) + \alpha \sum _{j = 0}^m A_j v_j (\chi ) + \\&\textstyle \beta \sum _{j = 0}^m A_j u_j (\chi ) + \alpha \beta . \end{aligned}$$

Let $V(\varvec{x}) = A (\varvec{x}) B (\varvec{x}) - C (\varvec{x}) \delta - \sum _{j = 0}^{m_0} A_j (u_j (\chi ) \beta + v_j (\chi ) \alpha + w_j (\chi )) - \alpha \beta$. Hence, $V(\varvec{x}) = a^\dagger (\chi ) b^\dagger (\chi ) - c^\dagger (\chi ) - h(\chi ) \ell (\chi )$. Due to the definition of $h(\varvec{X})$, $V(\varvec{x}) = 0$. Thus, $\left[ V(\varvec{x})\right] _{T} = \left[ 0\right] _{T}$, which is what the verification equation ascertains.   $\square$

6 Proof of Knowledge-Soundness

Since we are proving knowledge-soundness (and not subversion knowledge-soundness), the following security proof is similar to the corresponding proof in [27]. The main difference is in the need to take into account added elements to the CRS and to incorporate new indeterminates $Y_i$ created by the adversary. This means that the proof will be slightly (but not much) more complicated than the proof in [27].

Remark 2

It is easy to see that the knowledge-soundness of the new SNARK (and hence also Groth’s SNARK) can be trivially broken by adding a single well-chosen element to the CRS. Namely, after adding $\left[ \alpha \beta / \delta \right] _{1}$ to the CRS in Fig. 1, a malicious prover $\mathsf {P}^*$ can set $\mathfrak {a} \leftarrow (\sum _{j = 0}^{m_0} A_j \left[ (u_j (\chi ) \beta + v_j (\chi ) \alpha + w_j (\chi )) / \gamma \right] _{1})$, $\mathfrak {b} \leftarrow \left[ \gamma \right] _{2}$, and $\mathfrak {c} \leftarrow \left[ -\alpha \beta / \delta \right] _{1}$. Clearly, $\mathsf {V}$ accepts this argument.   $\square$

Next, we will prove adaptive knowledge-soundness even in the case when one uses symmetric pairings, as it was done in [27]. The use of symmetric pairings means that the generic adversary gets additional power compared to Sub-GBGM: in particular, we do not assume that BDH-KE holds, and moreover, in the asymmetric variant of the following theorem, the generic adversary will be allowed to create new indeterminates $Y_i$ in both $\mathbb {G}_1$ and $\mathbb {G}_2$, without knowing their discrete logarithms. Since this only increases the power of the generic adversary, it provides some hedge against future cryptanalytic attacks that say make it possible to compute an efficient isomorphism between $\mathbb {G}_1$ and $\mathbb {G}_2$, or at least show that BDH-KE does not hold in the concrete groups.

Theorem 3

(Knowledge-soundness). Consider the new argument system of Sect. 5.1. It is adaptively knowledge-sound in the Sub-GBGM even in the case of symmetric pairings. More precisely, any generic adversary attacking the knowledge-soundness of the new argument system in the symmetric setting requires $\varOmega (\sqrt{p / n})$ computation.

Proof

Assume the symmetric setting, $\mathbb {G}_1 = \mathbb {G}_2$. Let $\varvec{X}$ be the vector of indeterminates created by $\mathsf {K}_{\mathsf {tc}}$ and $\varvec{Y} = (Y_1, \dots , Y_q)^\top$ (for a non-negative integer q) be the vector of indeterminates created by the generic adversary.

The three elements output by a generic adversary are equal to $\mathfrak {a}= \left[ A (\varvec{x}, \varvec{y})\right] _{1}$, $\mathfrak {b}= \left[ B (\varvec{x}, \varvec{y})\right] _{1}$, and $\mathfrak {c}= \left[ C (\varvec{x}, \varvec{y})\right] _{1}$, where, for $T \in \{A, B, C\}$,

$$ \begin{aligned} T (\varvec{X}, \varvec{Y}) =&T_\alpha X_\alpha + T_\beta X_\beta + T_\gamma X_\gamma + T_\delta X_\delta + T_c (X) + \\&\textstyle \sum _{j = 0}^{m_0} T_j \cdot \frac{u_j (X) X_\beta + v_j (X) X_\alpha + w_j (X)}{X_\gamma } + \\&\textstyle \sum _{j = m_0+ 1}^m T_j \cdot \frac{u_j (X) X_\beta + v_j (X) X_\alpha + w_j (X)}{X_\delta } + \frac{T_h (X) \ell (X)}{X_\delta } + \sum _{i = 1}^{q} T_{yi} Y_i . \end{aligned} $$

Here, $T_c (X)$ is a degree $\le n - 1$ and $T_h (X)$ is a degree $\le n -2$ polynomial. Thus, $T (\varvec{X}, \varvec{Y}) \cdot X_\gamma X_\delta$ is a degree $(n - 2) + n - 1 + 2 = 2 n - 1$ polynomial.

Since the only difference compared to the knowledge-soundness proof in [27] is in the addition of the terms $\sum _{i = 1}^q T_{y i} Y_i$ to those three polynomials, it suffices that we show that $T_{y i} = 0$ for $T \in \{A, B, C\}$ and $i \in [1 \, .. \, q]$. After that, the knowledge-soundness of the new SNARK follows from the knowledge-soundness of Groth’s SNARK.

Motivated by the verification equation in Fig. 2, define

$$ \begin{aligned} V(\varvec{X}, \varvec{Y}) :=&A (\varvec{X}, \varvec{Y}) B (\varvec{X}, \varvec{Y}) - C (\varvec{X}, \varvec{Y}) X_\delta -\\&\textstyle \sum _{j = 0}^{m_0} A_j \left( u_j (X) X_\beta + v_j (X) X_\alpha +w_j (X)\right) - X_\alpha X_\beta \end{aligned} , $$

where the Laurent polynomials $A (\varvec{X}, \varvec{Y})$, $B (\varvec{X}, \varvec{Y})$, and $C (\varvec{X}, \varvec{Y})$ are as given before. The verification equation states that $\left[ V(\varvec{x}, \varvec{y})\right] _{T} = \left[ 0\right] _{T}$ and hence in the case of a generic adversary, $V(\varvec{X}, \varvec{Y}) \cdot X_\gamma ^2 X_\delta ^2 = 0$ as a polynomial or equivalently, each of the coefficients of $V(\varvec{X}, \varvec{Y})$ is 0.

First, the coefficient of $X_\alpha ^2$ in $V(\varvec{X}, \varvec{Y})$ is $A_\alpha B_\alpha$. Thus, from $V(\varvec{X}, \varvec{Y}) = 0$ it follows that $A_\alpha B_\alpha = 0$. Since $A (\varvec{X}, \varvec{Y})$ and $B (\varvec{X}, \varvec{Y})$ play dual roles in the symmetric case, we can assume, w.l.o.g., that $B_\alpha = 0$ (the same assumption was made in [27]).

Because $B_\alpha = 0$, the following claims hold:

• from the coefficient of $X_\alpha X_\beta$, $A_\alpha B_\beta + A_\beta B_\alpha - 1 = 0$. Thus, $A_\alpha B_\beta = 1$ (and in particularly, neither of them is equal to 0).

• from the coefficient of $X_\alpha Y_j$, $j \in [1 \, .. \, q]$, $A_\alpha B_{y j} + A_{y j} B_\alpha = 0$. Thus, $B_{y j} = 0$,

• from the coefficient of $X_\beta Y_j$, $j \in [1 \, .. \, q]$, $A_\beta B_{y j} + A_{y j} B_\beta = 0$. Thus, $A_{y j} = 0$,

• from the coefficient of $X_\delta Y_j$, $j \in [1 \, .. \, q]$, $C_{y j} = B_{y j} r_a + A_{y j} r_b$. Thus, $C_{y j} = 0$,

Since the coefficients $A_{y j}$, $B_{y j}$, and $C_{y j}$ were the only coefficients that are new compared to the knowledge-soundness proof of [27], the rest of the current proof follows from the knowledge-soundness proof of [27].

Let us now compute a lower bound to the efficiency of a generic adversary (this was not done in [27], our bound clearly also holds in the case of Groth’s SNARK). Assume that after some $\tau$ steps, the adversary has made a successful equality query $(=, i_1, i_2)$, i.e., $\mathsf {cell}_{i_1} = \mathsf {cell}_{i_2}$ for $i_1 \ne i_2$. Hence, she has found a collision $D_1 (\varvec{x}, \varvec{y}) = D_2 (\varvec{x}, \varvec{y})$ such that $D_1 (\varvec{X}, \varvec{Y}) \ne D_2 (\varvec{X}, \varvec{Y})$. Redefine $D_j (\varvec{X}, \varvec{Y}) := D_j (\varvec{X}, \varvec{Y}) \cdot X_\gamma X_\delta$ (if $\mathsf {type}_{i_1} \in \{1, 2\}$) and $D_j (\varvec{X}, \varvec{Y}) := D_j (\varvec{X}, \varvec{Y}) \cdot X_\gamma ^2 X_\delta ^2$ (if $\mathsf {type}_{i_1} = T$) for $j \in \{1, 2\}$, this guarantees that $D_j (\varvec{X}, \varvec{Y})$ is a polynomial. Thus,

$$\begin{aligned} D_1 (\varvec{x}, \varvec{y}) - D_2 (\varvec{x}, \varvec{y}) \equiv 0 \pmod {p}. \end{aligned}$$

(3)

Note that

• If $\mathsf {type}_{i_1} = 1$, then $\deg D_j (\varvec{X}, \varvec{Y}) \le 2 n - 1 =: d_1$,

• If $\mathsf {type}_{i_1} = 2$, then $\deg D_j (\varvec{X}, \varvec{Y}) \le 2 n - 1 =: d_2$, and thus

• If $\mathsf {type}_{i_1} = T$, then $\deg D_j (\varvec{X}, \varvec{Y}) \le 2 \cdot (2 n - 1) = 4 n - 2 =: d_T$.

Clearly, $\varvec{x}= (\chi , \alpha , \beta , \gamma , \delta )$ is chosen uniformly random from $\mathbb {Z}_p^3 \times (\mathbb {Z}_p^*)^2$. Due to the assumption that the canonical values of $Y_i$ are uniformly random in $\mathbb {Z}_p$, $\varvec{y}= (\upsilon _1, \upsilon _2, \upsilon _3)$ is a uniformly random value in $\mathbb {Z}_p^3$. Hence, due to the Schwartz-Zippel lemma and since $D_1 (\varvec{X}, \varvec{Y}) \ne D_2 (\varvec{X}, \varvec{Y})$ as a polynomial, Eq. (3) holds with probability at most $\deg D_j (\varvec{X}, \varvec{Y}) / (p - 1) \le d_{\mathsf {type}_{i_1}} / (p - 1)$. Clearly, an adversary working in time $\tau$ can generate up to $\tau$ new group elements. Then the probability that there exists a collision between any two of those group elements is upper bounded by $\left( {\begin{array}{c}\tau \\ 2\end{array}}\right) \cdot \deg D_j (\varvec{X}, \varvec{Y}) / (p - 1) \le \left( {\begin{array}{c}\tau \\ 2\end{array}}\right) \cdot d_{\mathsf {type}_{i_1}}/ (p - 1) \le \tau ^2 / 2 \cdot d_{\mathsf {type}_{i_1}} / (p - 1)$. Thus, a successful adversary on average requires time at least $\tau$, where $\tau ^2 \ge 2 (p - 1) / d_{\mathsf {type}_{i_1}} \ge 2 (p - 1) / d_T = 2 (p - 1) / (4 n - 2)$, to produce a collision. Simplifying, we get $\tau = \varOmega (\sqrt{p / n})$.   $\square$

7 Proof of Perfect Composable Subversion ZK

Before proving Theorem 4, we first prove the following helpful lemma that has a simple but tedious proof.

Lemma 2

Let $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$, and let $\mathsf {crs}$ be any CRS such that $\mathsf {CV}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}) = 1$. Then, with probability 1, $\mathsf {crs}= \mathsf {K}_{\mathsf {crs}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {tc})$ for a $\mathsf {tc}$ bijectively corresponding to $\left[ \chi , \alpha , \beta , \gamma , \delta \right] _{1}$.

Proof

In what follows, we will consider each line in the construction of $\mathsf {CV}$ in Fig. 1 separately, and write down the corollary from that line. We note that the CRS verification equations in Fig. 1 were written down as if the CRS were already correctly formed; e.g., there we have a check that $\left[ \beta \right] _{1} \bullet \left[ 1\right] _{2} = \left[ 1\right] _{1} \bullet \left[ \beta \right] _{2}$ which may fail (and then obviously there exists no such $\beta$). However, before these equations are checked, it is of course not known that $\beta$ in the left hand side (LHS) and in the right hand side (RHS) are equal. Therefore, in this proof only, in each step below, we use $D_1$ as the temporary name of the yet-unestablished LHS variable and $D_2$ as the temporary name of the yet-unestablished RHS variable.

Fig. 3.

Algorithms used in extraction and simulation, where $\iota \in \{\chi , \alpha , \beta , \gamma , \delta \}$

We assume that $\iota$ in $\left[ \iota \right] _{1}$ is already established for $\iota \in \{\chi , \alpha , \beta , \gamma , \delta \}$. (In particular, $\chi$ is established on Step 3 when $i = 1$.) We can do it since $\left[ \iota \right] _{1}$ information-theoretically fixes $\iota$.

• 1. For $\iota \in \{\gamma , \delta \}$: after that we know that $\iota \ne 0$, and hence there is a bijection between a valid $\mathsf {tc}\in \mathbb {Z}_p^3 \times (\mathbb {Z}_p^*)^2$ and the value hidden in $\left[ \chi , \alpha , \beta , \gamma , \delta \right] _{1}$.

• 2. For $\iota \in \{\alpha , \beta , \gamma , \delta \}$: from $\left[ \iota \right] _{1} \bullet \left[ 1\right] _{2} = \left[ 1\right] _{1} \bullet \left[ D_2\right] _{2}$ we get $\left[ \iota \right] _{T} = \left[ D_2\right] _{T}$. This implies $\left[ \iota - D_2\right] _{T} = \left[ 0\right] _{T}$. Since $\left[ 1\right] _{T}$ is not the unity element, $\left[ D_2\right] _{2} = \left[ \iota \right] _{2}$.

• 3. For $i = 1$ to $n - 1$:k we can assume by induction that we have already established $\left[ \chi ^{i - 1}\right] _{1}$. Since $\left[ D_1\right] _{T} = \left[ \chi ^{i - 1}\right] _{1} \bullet \left[ \chi \right] _{2}$, we get $\left[ D_1\right] _{T} = \left[ \chi ^i\right] _{T}$.

• 4. For $i = 1$ to n: $\omega ' = \omega ^{i - 1}$ and $\zeta = (\chi ^n - 1) \omega ^{i - 1} / n$ in the algorithm Algorithm 2 are computed by the CRS verifier. For $\chi \ne \omega ^{i - 1}$, the equation $\left[ D_1\right] _{1} \bullet (\left[ \chi \right] _{2} - \left[ \omega '\right] _{2}) = \left[ \zeta \right] _{T}$ implies $\left[ D_1\right] _{1} = \left[ \zeta / (\chi - \omega ')\right] _{1} = \left[ (\chi ^n - 1) \omega ^{i - 1} / (n (\chi - \omega ^{i - 1}))\right] _{1} = \left[ \ell _i (\chi )\right] _{1}$. For $\chi = \omega ^{i - 1}$, we get $D_1 \cdot (\chi - \omega ^{i - 1}) = \zeta$, since $\omega ^{i - 1}$ is a root of unity and $\zeta = (\chi ^n - 1) \omega ^{i - 1} / n$, thus both sides of the equation are 0.

• 5. For $j = 0$ to m:

  • (a) $\left[ D_1\right] _{1} = \sum _{i = 1}^{n} U_{i j} \left[ \ell _i (\chi )\right] _{1}$ implies $\left[ D_1\right] _{1} = \left[ \sum _{i = 1}^{n} U_{i j} \ell _i (\chi )\right] _{1} = \left[ u_j (\chi )\right] _{1}$.

  • (b) $\left[ D_1\right] _{1} = \sum _{i = 1}^{n} V_{i j} \left[ \ell _i (\chi )\right] _{1}$ implies $\left[ D_1\right] _{1} = \left[ \sum _{i = 1}^{n} V_{i j} \ell _i (\chi )\right] _{1} = \left[ v_j (\chi )\right] _{1}$.

  • (c) Clearly, $\left[ w_k (\chi )\right] _{1}$ is computed correctly.

  • (d) $\left[ v_j (\chi )\right] _{1} \bullet \left[ 1\right] _{2} = \left[ 1\right] _{1} \bullet \left[ D_2\right] _{2}$ implies $\left[ D_2\right] _{2} = \left[ v_j (\chi )\right] _{2}$.

• 6. For $j = m_0+ 1$ to m: $\left[ D_1\right] _{1} \bullet \left[ \delta \right] _{2} = \left[ u_j (\chi )\right] _{1} \bullet \left[ \beta \right] _{2} + \left[ v_j (\chi )\right] _{1} \bullet \left[ \alpha \right] _{2} + \left[ w_j (\chi )\right] _{1} \bullet \left[ 1\right] _{2}$ implies $\left[ D_1\right] _{1} = \left[ (u_j (\chi ) \beta + v_j (\chi ) \alpha + w_j (\chi )) / \delta \right] _{1}$.

• 7. $\left[ \chi ^{n - 1}\right] _{1} \bullet \left[ 1\right] _{2} = \left[ 1\right] _{1} \bullet \left[ D_2\right] _{2}$ implies $\left[ D_2\right] _{2} = \left[ \chi ^{n - 1}\right] _{2}$,

• 8. For $i = 0$ to $n - 2$: $\left[ D_1\right] _{1} \bullet \left[ \delta \right] _{2} = \left[ \chi ^{i + 1}\right] _{1} \bullet \left[ \chi ^{n - 1}\right] _{2} - \left[ \chi ^i\right] _{1} \bullet \left[ 1\right] _{2}$ implies $\left[ D_1\right] _{1} = \left[ \chi ^i \ell (\chi ) / \delta \right] _{1}$.

• 9. $\left[ \alpha \right] _{1} \bullet \left[ \beta \right] _{2} = \left[ D_2\right] _{T}$ implies $\left[ D_2\right] _{T} = \left[ \alpha \beta \right] _{T}$.

By direct observation, it is clear that we have now established all elements of the $\mathsf {crs}_{\mathsf {P}}$ in Fig. 1. Hence, $\mathsf {crs}= \mathsf {K}_{\mathsf {crs}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {tc})$.   $\square$

Theorem 4

The SNARK from Sect. 5.1 has perfect CRS trapdoor extractability under the BDH-KE assumption.

Proof

Let $\mathsf {\Sigma }$ be a subverter, and let $r \leftarrow _r \mathsf {RND}(\mathsf {\Sigma })$. Let $\iota \in \{\chi , \alpha , \beta , \gamma , \delta \}$. Let $\mathsf {\Sigma }^\iota ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}; r)$ be as in Algorithm 3 in Fig. 3. Since $\mathsf {CV}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs})$ accepts, $\mathsf {crs}$ must contain $(\left[ \iota \right] _{1}, \left[ \iota \right] _{2})$. Hence, by the BDH-KE assumption, there exists a NUPPT extractor $\mathsf {X}^\iota _{\mathsf {\Sigma }}$, such that if $\mathsf {CV}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}) = 1$ then $\iota \leftarrow \mathsf {X}^\iota _{\mathsf {\Sigma }} ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}; r)$.

Finally, we construct the (NUPPT) extractor $\mathsf {X}_{\mathsf {\Sigma }} ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}; r)$ in Algorithm 4 in Fig. 3. By the BDH-KE assumption, if $\mathsf {CV}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}) = 1$ then $\mathsf {tc}\leftarrow \mathsf {X}_{\mathsf {\Sigma }} ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}; r)$ satisfies $\mathsf {tc}\in \mathrm {range}(\mathsf {K}_{\mathsf {tc}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}))$.

To prove CRS trapdoor extractability, assume that $\mathsf {crs}$ is returned by $\mathsf {\Sigma }$ and $\mathsf {tc}$ is returned by $\mathsf {X}_{\mathsf {\Sigma }}$. In addition, assume that $\mathsf {CV}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}) = 1$. By $\mathsf {CV}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}) = 1$ and Lemma 2, $\mathsf {K}_{\mathsf {crs}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {tc}) = \mathsf {crs}$. The claim follows.   $\square$

In Theorem 5, we also need the next simple lemma.

Lemma 3

Let $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$, and let $\mathsf {crs}$ be any CRS such that $\mathsf {CV}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}) = 1$. Consider any values of $\mathfrak {a}$, $\mathfrak {b}$, and $(A_j)_{j = 0}^{m_0}$. Then there exists at most one value $\mathfrak {c}$, such that $\mathsf {V}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}_{\mathsf {V}}, \mathsf {x}, (\mathfrak {a}, \mathfrak {b}, \mathfrak {c})) = 1$.

Proof

Assume that $\mathfrak {c}_0$ and $\mathfrak {c}_1$ are both accepted by the verifier. That means (see Fig. 2) that $\mathfrak {c}_k \bullet \left[ \delta \right] _{2} = \left[ s\right] _{T}$ for $k \in \{0, 1\}$, where s is some k-independent value. By bilinearity, $(\mathfrak {c}_1 - \mathfrak {c}_0) \bullet \left[ \delta \right] _{2} = \left[ 0\right] _{T}$. Since $\delta \ne 0$ (this is guaranteed by $\mathsf {CV}$ accepting $\mathsf {crs}$) and the pairing is non-degenerate, we have $\mathfrak {c}_0 = \mathfrak {c}_1$.   $\square$

Theorem 5

The SNARK from Sect. 5.1 is perfectly composable Sub-ZK under the BDH-KE assumption.

Proof

We use the same simulator $\mathsf {S}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}, \mathsf {ts}, \mathsf {x})$ as defined in [27], see Algorithm 5 in Fig. 3. Fix a subverter $\mathsf {\Sigma }$, and let $\mathsf {X}_{\mathsf {\Sigma }}$ be as defined in Theorem 4, see Algorithm 4 in Fig. 3. Fix $\kappa$, $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \leftarrow \mathcal {R}(1^\kappa )$, $(\mathsf {x}, \mathsf {w}) \in {\mathbf {R}}$, and an adversary $\mathsf {A}$. As in Definition 7, assume $r \leftarrow _r \mathsf {RND}(\mathsf {\Sigma })$, $(\mathsf {crs}, \mathsf {z}_{\mathsf {\Sigma }}) \leftarrow \mathsf {\Sigma }({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}; r)$ such that $\mathsf {CV}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}) = 1$, $\mathsf {tc}\leftarrow \mathsf {X}_{\mathsf {\Sigma }} ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}; r)$, $\mathsf {ts}\leftarrow \mathsf {K}_{\mathsf {ts}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {tc})$. Assume that $\pi _0 \leftarrow \mathsf {P}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}_{\mathsf {P}}, \mathsf {x}, \mathsf {w})$ ($b = 0$) and $\pi _1 \leftarrow \mathsf {S}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}, \mathsf {ts}, \mathsf {x})$ ($b = 1$). It is sufficient to show that $\pi _0$ and $\pi _1$ have the same distribution.

Case $b = 0$. The honest prover creates $\mathfrak {a}\leftarrow \ldots + r_a \left[ \delta \right] _{1}$ and $\mathfrak {b}\leftarrow \ldots + r_b \left[ \delta \right] _{2}$ for uniformly random $r_a$ and $r_b$. Since $\delta \ne 0$ (this is guaranteed by $\mathsf {CV}$ accepting $\mathsf {crs}$) and the pairing is non-degenerate, $\mathfrak {a}$ and $\mathfrak {b}$ are uniformly random. We know by the perfect CRS trapdoor extractability (Theorem 4) that $\mathsf {K}_{\mathsf {crs}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {tc}) = \mathsf {crs}$. Thus, $(\mathsf {crs}, \mathsf {ts})$ are created as in the first step of the definition of perfect subversion-completeness (Definition 2). Since the new SNARK satisfies perfect subversion-completeness (Theorem 2), $\mathsf {V}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}_{\mathsf {V}}, \mathsf {x}, \pi _0) = 1$. By Lemma 3, the verification equation, $\mathsf {crs}$, $\mathfrak {a}$, and $\mathfrak {b}$ uniquely determine the acceptable $\mathfrak {c}$.

Case $b = 1$. Here, by the definition of the simulator, $\mathfrak {a}$ and $\mathfrak {b}$ are uniformly random. Moreover, $\pi _1$ is explicitly created so that $\mathsf {V}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}_{\mathsf {V}}, \mathsf {x}, \pi _1) = 1$. Since $\mathsf {CV}$ accepts then by Lemma 3, the verification equation, $\mathsf {crs}$, $\mathfrak {a}$, and $\mathfrak {b}$ uniquely determine the acceptable $\mathfrak {c}$.

Since $\mathsf {CV}$ accepts $\mathsf {crs}$, in both cases $\mathfrak {a}$ and $\mathfrak {b}$ are uniformly random and $\mathfrak {c}$ is uniquely determined by them, $\mathsf {crs}$, and the verification equation, the real and the simulated arguments have identical distributions.   $\square$

The following result follows directly from Theorems 1 and 5.

Theorem 6

The SNARK from Sect. 5.1 is perfectly unbounded Sub-ZK under the BDH-KE assumption.

8 Efficiency

CRS Length.The CRS contains ${\textsf {gk}}$ (that includes $(\left[ 1\right] _{1}, \left[ 1\right] _{2})$) and a number of additional elements. Not counting ${\textsf {gk}}$, the number of CRS elements in different groups is given by the following table. Hence, the total size of the CRS is $4 m + 3 n + 13$ group elements.

	$\mathbb {G}_1$	$\mathbb {G}_2$	$\mathbb {G}_T$	Total
$\mathsf {crs}_{\mathsf {P}}$	3$m + n -m_0+ 4$	$m + 3$	0	$4m + n - m_0+ 7$
$\mathsf {crs}_{\mathsf {V}}$	$m_0$ + 1	2	1	$m_0+ 4$
$\mathsf {crs}_{\mathsf {CV}}$	2n	3	0	$2n + 3$
Total	3$m + 3n + 5$	$m + 7$	1	4$m + 3n + 13$

One element (namely, $\left[ \delta \right] _{2})$ belongs both to $\mathsf {crs}_{\mathsf {P}}$ and $\mathsf {crs}_{\mathsf {V}}$ and thus the numbers in the “total” row are not equal to the sum of the numbers in previous rows.

In Groth’s zk-SNARK [27] the CRS consists of $m + 2 n$ elements of $\mathbb {G}_1$ and n elements of $\mathbb {G}_2$. On top of it, we added $2 n + 3$ group elements to make the CRS verification possible and also some elements to speed up the prover’s computation and the verifier’s computation; the latter elements can alternatively be computed from the rest of the CRS.

CRS Generation: Computational Complexity. Assume that ${\textsf {gk}}$ has already been computed. One can compute $\mathsf {crs}$ by first computing all CRS elements within brackets, and then compute their bracketed versions. One can evaluate $u_j (\chi )$, $v_j (\chi )$, and $w_j (\chi )$ for each $j \in [0 \, .. \, m]$ in time $\varTheta (n)$ by using precomputed values $\ell _i (\chi )$ for $i \in [1 \, .. \, n]$ and the fact that the matrices U, V, W contain $\varTheta (n)$ non-zero elements. The rest of the CRS can be computed efficiently by using straightforward algorithms.

By using Algorithm 1, the whole CRS generation dominated by $3 m + 3 n + 5$ exponentiations in $\mathbb {G}_1$, $m + 7$ exponentiations in $\mathbb {G}_2$, and 1 exponentiation in $\mathbb {G}_T$ (one per CRS element) and $\varTheta (n)$ multiplications/divisions in $\mathbb {Z}_p$.

$\mathsf {CV}$’s Computational Complexity. We assume that it is difficult to subvert ${\textsf {gk}}$; this makes sense assuming that the SNARK uses well-known bilinear groups (say, the Barreto-Naehrig curves). Consider the CRS verification algorithm in Fig. 1. It is clear that all other steps but Step 4 are efficient (computable in $\varTheta (n)$ cryptographic operations); this follows from the fact that U, V, and W are sparse. Computation in those steps is dominated by $6 m + 5 n -4m_0+ 8$ pairings. On top of it, one has to execute $s (U) + s (V) + s (W)$ exponentiations in $\mathbb {G}_1$, where s(M) is the number of “large” (i.e., large enough so that exponentiating with them is expensive) entries in the matrix M. Often, s(M) are very small.

By using Algorithm 2, one can check that $\left[ \ell _i (\chi )\right] _{1}$ has been correctly computed for all $i \in [1 \, .. \, n]$ in $n + 1$ pairings, $n - 1$ exponentiations in $\mathbb {G}_2$ and n exponentiations in $\mathbb {G}_T$. Hence, the whole CRS verification algorithm is dominated by $6 m + 6 n -4m_0+9$ pairings, $s (U) + s (V) + s (W)$ exponentiations in $\mathbb {G}_1$, $n - 1$ exponentiations in $\mathbb {G}_2$, and n exponentiations in $\mathbb {G}_T$.

In addition, one can speed up $\mathsf {CV}$ by using batching [3]. Namely, clearly if $\sum _{i = 1}^s t_i (\left[ a_i\right] _{1} \bullet \left[ b_i\right] _{2}) = \left[ c\right] _{T}$ for uniformly random $t_i$, then w.h.p., $\left[ a_i\right] _{1} \bullet \left[ b_i\right] _{2} = \left[ c\right] _{T}$ for each individual $i \in [1 \, .. \, s]$. The speed up follows from the use of bilinear properties and from the fact that exponentiation is faster than pairing. Moreover, one can further slightly optimize this by assuming $t_s = 1$ [18, 32].

Full batched version of $\mathsf {CV}$ is described in the full version [1]. As we show there, a batched $\mathsf {CV}$ will be dominated by $5 (m + n) -4m_0+ s (U) + s (V)$ (mostly, short-exponent) exponentiations in $\mathbb {G}_1$ and $m + s (W)$ (mostly, short-exponent) exponentiations in $\mathbb {G}_2$. Since an exponentiation with short exponent is significantly less costly than a pairing, this will decrease the execution time of $\mathsf {CV}$ significantly. (See the full version [1] for concrete numbers).

We note that after taking batching into account, $\mathsf {CV}$ will become a probabilistic algorithm, and will accept incorrect CRSs with negligible probability. This means that one has to modify some of the previous security results. For example, Theorems 4 and 5 will be modified as follows.

Theorem 7

After batching $\mathsf {CV}$, the SNARK from Sect. 5.1 has statistical CRS trapdoor extractability under the BDH-KE assumption.

Theorem 8

After batching $\mathsf {CV}$, the SNARK from Sect. 5.1 is statistically composable Sub-ZK under the BDH-KE assumption.

As in [27], the prover’s computational complexity is dominated by the need to compute $h(X)$ (3 interpolations, 1 polynomial multiplication, and 1 polynomial division; in total $\varTheta (n \log n)$ non-cryptographic operations in $\mathbb {Z}_p$), followed by ${(n - 1) + (s (A) + 1) + 1 + (s (A) + 1) + s (A_1, \dots , A_{m_0}) \le n + 3 s (A) + 2}$ exponentiations in $\mathbb {G}_1$ and $s (A) + 1$ exponentiations in $\mathbb {G}_2$, where s(A) is the number of large elements in A (i.e., large enough so that exponentiating with them would be expensive). This means that the prover’s computation is dominated by $\varTheta (n \log n)$ non-cryptographic operations and $\varTheta (n)$ cryptographic operations.

The verifier executes a single pairing equation that is dominated by 3 pairings and $m_0$ exponentiations in $\mathbb {G}_1$. The exponentiations can be done offline since they do not depend on the argument $\pi$ but only on the common input $(A_1, \dots , A_{m_0})$. Hence, the verifier’s computation is dominated by $\varTheta (m_0)$ cryptographic operations but her online computation is only dominated by 3 pairings.

The argument consists of 2 elements from $\mathbb {G}_1$ and 1 element from $\mathbb {G}_2$.

9 The Case of Unbounded Subverter

Since we consider statistical Sub-ZK, it is natural to ask what will happen if also the subverter is computationally unbounded. It comes out that in this case, several definitions and proofs would actually simplify. For this reason, we decided to first present the case of efficient subverter.

Assume now that the subverter $\mathsf {\Sigma }$ is computationally unbounded. Then we need a computationally unbounded extractor $\mathsf {X}_{\mathsf {\Sigma }}$ (otherwise, it will not be able to even execute $\mathsf {\Sigma }$). corresponding version of Definition 5 with changes being .

Definition 10

(Statistically Unbounded ). $\varPsi$ is statistically unbounded Sub-ZK for $\mathcal {R}$, if for any subverter $\mathsf {\Sigma }$ there exists a $\mathsf {X}_{\mathsf {\Sigma }}$, such that for all $\kappa$, all $({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}) \in \mathrm {range}(\mathcal {R}(1^\kappa ))$, and all computationally unbounded $\mathsf {A}$, $\varepsilon ^{unb}_0 \approx _\kappa \varepsilon ^{unb}_1$, where $\varepsilon ^{unb}_b$ is defined as

$$ \Pr \left[ \begin{aligned}&r \leftarrow _r \mathsf {RND}(\mathsf {\Sigma }), (\mathsf {crs}, \mathsf {z}_{\mathsf {\Sigma }}\,\Vert \,\mathsf {tc}) \leftarrow (\mathsf {\Sigma }\,\Vert \,\mathsf {X}_{\mathsf {\Sigma }}) ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}; r), \\&\mathsf {ts}\leftarrow \mathsf {K}_{\mathsf {ts}}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {tc}): \mathsf {CV}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}) = 1 \wedge \mathsf {A}^{\mathsf {O}_b (\cdot , \cdot )} ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}, \mathsf {ts}, \mathsf {z}_{\mathsf {\Sigma }}) = 1 \end{aligned} \right] . $$

Here, the oracle $\mathsf {O}_0 (\mathsf {x}, \mathsf {w})$ returns $\bot$ (reject) if $(\mathsf {x}, \mathsf {w}) \not \in {\mathbf {R}}$, and otherwise it returns $\mathsf {P}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}_{\mathsf {P}}, \mathsf {x}, \mathsf {w})$. Similarly, $\mathsf {O}_1 (\mathsf {x}, \mathsf {w})$ returns $\bot$ (reject) if $(\mathsf {x}, \mathsf {w}) \not \in {\mathbf {R}}$, and otherwise it returns $\mathsf {S}({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}, \mathsf {crs}, \mathsf {ts}, \mathsf {x})$. $\varPsi$ is perfectly unbounded for $\mathcal {R}$ if one requires that $\varepsilon ^{unb}_0 = \varepsilon ^{unb}_1$.

An unbounded $\mathsf {\Sigma }$ can obviously break the BDH-KE assumption by creating elements of $\mathbb {G}_1$ and $\mathbb {G}_2$ as he wants; however, because she is unbounded, we can of course still argue that $\mathsf {\Sigma }$ will know their discrete logarithms, or more formally, that $\mathsf {X}_{\mathsf {\Sigma }}$ will be able to extract them. Since the extraction is now unconditional (i.e., it does not depend on any assumptions), it means that $\mathsf {X}_{\mathsf {\Sigma }}$ can extract the discrete logarithm of any element of $\mathbb {G}_z$.

In particular, there is no need anymore to include $\left[ \gamma \right] _{1}$ to the CRS (this makes the CRS shorter by 1 element), or handle it in $\mathsf {CV}$ (that is, one could remove the check that $\left[ \gamma \right] _{1} \bullet \left[ 1\right] _{2} = \left[ 1\right] _{1} \bullet \left[ \gamma \right] _{2}$) or in security proofs (e.g., in Lemma 2, one would not have to use the equation $\left[ \iota \right] _{1} \bullet \left[ 1\right] _{2} = \left[ 1\right] _{1} \bullet \left[ \iota \right] _{2}$ to establish $\left[ \gamma \right] _{1}$, or define $\mathsf {\Sigma }^\gamma ({\mathbf {R}}, \mathsf {z}_{{\mathbf {R}}}; r)$ inside Theorem 4).

Moreover, if the CRS has the (easily satisfied) bijectivity property required in Sect. 7 (see Lemma 2), it means that the requirement that $\mathsf {X}_{\mathsf {\Sigma }}$ returns $\mathsf {tc}$ (instead of just returning $\mathsf {ts}$) is not restrictive anymore.

10 Related Work

Bellare et al. [2] also showed that one can achieve simultaneously subversion soundness and non-interactive witness-indistinguishability (NIWI) by using a (CRS-less) NIWI argument system. However, the known (CRS-less) NIWI argument systems are not succinct. Construction of more efficient NIWI argument systems is a very interesting open question.

Ben-Sasson et al. [6] proposed an efficient MPC approach to achieve security in the case one can trust at least one CRS creator. We emphasize that [2] and the current paper study the scenario where you can trust none. In such a case, the approach of [6] still works but it is not efficient. For example, the computational cost of $\mathsf {CV}$ (see Sect. 8) in the new SNARK is very small compared to the cost of the joint CRS creation and verification protocol in [6]. Nevertheless, while the starting point of their approach is different, it actually resulted in a somewhat similar solution. See [1] for a longer comparison.

Independently, Fuchsbauer [19] also constructed subversion-resistant SNARKs. The importance of subversion-resistant SNARKs was also recognized in [13, 14] although no construction was given. In particular, [14] described a practical attack against SNARKs as used in known contingent payment protocols and proposed to use a Sub-ZK SNARK.