An Algorithm for Tight Frame Grouplet to Compute Association Fields

Abstract

Tight frame grouplet transform is a kind of weighted multiscale Haar transform with a causality imposed on the association field. Defined with a causality property, multiscale association fields become more flexible to construct grouplets which can adapt the different geometry structure in different scales. Grouplet transform uses the block matching algorithm to compute association field coefficients, which needs more operations than the computation of grouplet coefficients. An algorithm named LD-PO based on line detection and partial ordering is proposed to make grouplet transform become more efficient. It takes the place of block matching algorithm to compute association field coefficients. The LD-PO algorithm uses line detection masks and the feature of partial ordering to compute geometric flow in an image. Experimental results show that tight frame grouplet using LD-PO algorithm can also reconstruct an image with no loss. Compared with the block matching algorithm, it’s complexity to compute association field coefficients is fewer and the loss of grouplet coefficients’ sparsity can be ignored.

1 Introduction

Images often contain regions composed of locally oriented structures. These geometric structures provide fundamental features for many problems in computer vision and image processing [1]. It is required to improve state of image processing algorithms to efficiently represent these complex structures.

Wavelet bases are the optimal bases that represent point singularity. They can adapt the processing resolution to the local image regularity [2]. However, the discontinuity of natural images is usually represented by smooth curves because natural objects’ edges and borders are smooth. Wavelet bases are suboptimal to represent images that contain complex geometrical structures because their square support is not adapted to represent linear singularity. To take advantage of geometrical image regularities in space or time, Mallat proposed grouplet orthogonal bases and tight frames [3]. In spirit of the “Gestalt” psychophysics school [4,5,6], the geometry is constructed with grouping processes which define multiscale association fields [7]. Many researchers have applied grouplet model to practice. A reduced reference perceptual image quality measure based on the grouplet transform is proposed in [8]. In order to get better fusion effect, grouplet transform is applied and coefficients are fused by PCNN [9]. An advanced grouplet transform is proposed that make use of the advantage of Greedy algorithm and Dynamic Programming algorithm in association fields pruning [10]. A grouplet framework is presented to be applied to inpainting and synthesis [11].

This paper introduces algorithm based on line detection and partial ordering to compute association fields which is along the orientation of geometric flow [12,13,14]. Section 2 describes the coefficient layer computation of tight frame grouplet. Section 3 introduces algorithm based on line detection and partial ordering in the association field layer computation. Experimental results are described in Sect. 4 to show advantages of the presented algorithm LD-PO.

2 Tight Frame Grouplet Coefficients Layer Computation

2.1 Forward Decomposition

Different from orthogonal grouplet, tight frame grouplet is redundant and can be constructed without an embedded subgrid structure. It ascribes to the use of partial ordering. To an image $F$ including $N$ samples, a grouplet frame transforms it into multiscale difference coefficients and coarse scale average coefficients. We can get these coefficients from successive grouping and computation according to multiscale association fields.

Initialize $a = F$. A new array $s[n]$ which ensures energy conservation is created to store the support size of the averaging coefficients of $F$. At the initialization, for $j = 0$, since $a = F$, it results that $s[m] = 1$ for any integer $1 \le m \le N$. For $j$ going from 1 to $J$, the averaging size is update by

$$ \hat{s} = s[m] + s[\tilde{m}], $$

(1)

difference coefficient is computed by

$$ d_{j} [\tilde{m}] = (a[\tilde{m}] - a[m])\sqrt {\frac{{{\text{s[m]}}s[\tilde{m}]}}{{{\hat{\text{s}}}}}} , $$

(2)

average coefficient is computed by

$$ \hat{a} = \frac{{{\text{s[m]}}a[m] + s[\tilde{m}]a[\tilde{m}]}}{{\hat{s}}}. $$

(3)

These values are stored “in place”: $a[m] = \hat{a}$ and $s[m] = \hat{s}$. At the coarsest scale $2^{J}$, for all m, the average coefficients are normalized:

$$ a_{J} [m] = a[m]\sqrt {s[m]} . $$

(4)

A forward decomposition transforms an image $F$ of size $N$ into a family of $J + 1$ grouplet coefficient arrays $\left\{ {d_{j} [m],a_{J} [m]} \right\}_{1 \le j \le J}$. For a signal of $N$, Eqs. (1), (2) and (3) compute the $(J + 1)N$ grouplet coefficients with $O(JN)$ operations.

2.2 Backward Decomposition

A backward decomposition can restore an image $F$ from its grouplet coefficients $\left\{ {d_{j} [m],a_{J} [m]} \right\}_{1 \le j \le J}$. Tight frame grouplet has an infinite number of left inverses because of the redundant representation. The best inverse for noise removal by thresholding is the pseudo-inverse [3].

The average coefficient normalization (4) is then inverted

$$ \forall m,a[m] = \frac{{a_{J} [m]}}{{\sqrt {s[m]} }}. $$

(5)

Each grouping operator is then inverted in the reverse order it was calculated. For $j$ decreasing from $J$ to 1, the scale support is updates by

$$ \tilde{s} = s[m] - s[\tilde{m}]. $$

(6)

By inverting the grouplet transform (2) and (3), the finer scale average coefficients are computed:

$$ \tilde{a}_{ - } = a[m] + d_{j} [\tilde{m}]\frac{{\sqrt {\tilde{s}} }}{{\sqrt {s[\tilde{m}]s[m]} }} $$

(7)

and

$$ \tilde{a}_{ + } = a[m] - d_{j} [\tilde{m}]\frac{{\sqrt {s[\tilde{m}]} }}{{\sqrt {\tilde{s}s[m]} }}. $$

(8)

[3] also proves that the pseudo-inverse is implemented with equal averaging weights on causal and anti-causal reconstructions:

$$ \tilde{a} = \frac{{\tilde{a}_{ - } + a[\tilde{m}]}}{2}{\text{ and }}a[\tilde{m}] = \tilde{a}. $$

(9)

The averaging size is then updated $s[m] = \tilde{s}.$

At the end of the loop over all $j$ and $n$, this left inverse reconstructs the image $F = a$. If $F$ has $N$ samples, this reconstruction is performed with $O(JN)$ operations.

3 Tight Frame Grouplet Association Field Layer Computation

3.1 The Complexity of Block Matching Algorithm

For a giving image $F \in {\mathbb{R}}^{2}$ that has $N = n \times n$ pixels, we need to estimate the local texture orientation and the association fields $\left\{ {A_{j} [m]} \right\}$ store the difference of positions among different points. Block matching algorithm [15] is used to compute association fields in [3], it finds the $p = m$ which minimizes this distance:

$$ {\text{m}} = \mathop {\arg \hbox{min} }\limits_{\begin{subarray}{l} p \in N(\hat{m}) \\ p\,\text{ }{before}\text{ }\,\tilde{m} \end{subarray} } \sum\limits_{n \in B(p)} {\left| {a[n] - a[n + m - p]} \right|^{k} with\text{ }\,\,k = 1\text{ }\,\,or\text{ }\,\,{\text{k}} = 2} . $$

(10)

In Eq. (10), the size of the neighborhoods $N(\hat{m})$ is $K \cdot B(p)$ is a block of $P$ points. The block matching computes the $JN$ values of the $J$ association fields $A_{j}$ with $O(JNKP)$ operations. If we compute all association fields from the finest scale association field $A_{1}$, the computational complexity becomes $O(NKP + JN)$. It’s important to point out that the value of $J$ is usually far less than the value of $KP$ when it comes to the practical application. It means that the complexity of a whole tight frame grouplet is up to the complexity of association field layer computation. Proposed algorithm in this paper is aimed to reduce the complexity and it just need $O(JN)$ operations, which will be proved in Sect. 3.2.

3.2 Proposed Algorithm Based on Line Detection and Partial Ordering

It is well known that discrete wavelet transform has an orientation selectivity. For example, for a scale $2^{j}$ that increases from $2^{1}$ to $2^{J}$, and for all $0 \le n < 2^{ - j} N$, the Haar transform groups consecutive average coefficients $a[2n]$ and $a[2n + 1]$, and it computes a next scale average

$$ a[n] = \frac{a[2n] + a[2n + 1]}{2}, $$

(11)

together with a normalized difference:

$$ d_{j} [n] = (a[2n + 1] - a[2n])\sqrt {2^{(j - 1)} } . $$

(12)

In scale $2^{j}$, we first compute coefficients along the horizontal direction and then along the vertical direction according to Eqs. (11) and (12). The image is then divided into four parts: average coefficients $LL$, difference coefficients along the horizontal direction $HL$, difference coefficients along the vertical direction $LH$ and difference coefficients along the diagonal direction $HH.$

It is obviously not enough to express images with complex shapes and textures in three orientations. In contrast to determining the direction from the coarse scale in discrete wavelet transform, a new geometric flow computation algorithm named LD-PO based on line detection and partial ordering is proposed. For spatial geometric grouping, a grouplet partial ordering can be defined with respect to a preferential direction of angle $\theta$. A point $x = (x_{1} ,x_{2} ) \in {\mathbb{R}}^{2}$ is said to be before $\tilde{x} = (\tilde{x}_{1} ,\tilde{x}_{2} ) \in {\mathbb{R}}^{2}$ with respect to a partial ordering of angle $\theta$ if

$$ x_{1} \cos \theta + x_{2} \sin \theta < \tilde{x}_{1} \cos \theta + \tilde{x}_{2} \sin \theta . $$

(13)

Proposed algorithm LD-PO aims to compute geometric flow from pixel level. It is normally hard to complete the computation, but the use of partial ordering dramatically simplifies the computation. Figure 1(a) shows a binary image. The red line is discretized and represented by black pixels. If partial ordering of angle $\theta = 0$ in Eq. (13) is used, which means that coefficients are ordered by columns by columns, the red line then can be regard as a geometric flow of this binary image and the flow’s orientation is from right to left. A point $\tilde{m}$ is grouped with $m$ which is before $\tilde{m}$, if point $\tilde{m}$ and $m$ are along the same geometric flow. The angle range from $m$ to $\tilde{m}$ is $( - 90^\circ , + 90^\circ )$. The difference of positions is stored in an association field array: $A_{j} [\tilde{m}] = m - \tilde{m}$.

Fig. 1.

Binary image. (Color figure online)

In this paper, geometric flow is regarded as the composition of numerous polygonal lines in pixel-level. Proposed algorithm LD-PO looks for polygonal lines by running a $3 \times 3$ mask through the image. The response of the mask at any point is acquired by computing the sum of products of the coefficients with the gray levels contained in the region encompassed by the mask:

$$ R = \sum\limits_{i = 1}^{9} {w_{i} z_{i} } . $$

(14)

In Eq. (14), $z_{i}$ is the gray level of the pixel associated with mask coefficient $w_{i}$ Particularly, $z_{i}$ takes value in set $\{ 0,1\}$ in binary image. As usual, the response of the mask is defined with respect to its center location. Figure 2 (b), (c) and (d) are line detection masks which will respond strongly to lines oriented at $0^\circ$, lines oriented at $+ 45^\circ$ and lines oriented at $- 45^\circ$ respectively.

Fig. 2.

$3 \times 3$ mask. (a) General mask; (b), (c), (d) mask of detecting direction of 0°, +45° and −45° separately.

When association field array $A_{j} [\tilde{m}]$ is computed by $3 \times 3$ mask, the angle from $m$ to $\tilde{m}$ takes value in set $\{ - 45^\circ ,0^\circ , + 45^\circ \}$. Proposed algorithm LD-PO uses line detection masks $LD_{i}$ in Fig. 2 to find the $m$ which maximizes:

$$ m = \arg \hbox{max} \text{ }|\sum\limits_{j = 1}^{9} {BP_{{\tilde{m}}} [j] \times LD_{i} [j]} |. $$

(15)

$BP_{{\tilde{m}}}$ is a $3 \times 3$ image matrix, in which center location point $\tilde{m}$ is. It’s then transformed into a binary matrix by:

$$ BP_{{\tilde{m}}} [i] = \left\{ {\begin{array}{*{20}l} 0 \hfill & {if\,\,\,BP_{{\tilde{m}}} [i] < Av} \hfill \\ 1 \hfill & {others} \hfill \\ \end{array} } \right. , {\text{for integer}}\text{ }i \in [1,9]. $$

(16)

Thresholding criteria $Av$ is the average gray value of image matrix $BP_{{\tilde{m}}}$ in Eq. (16). Notation $i$ in Eq. (15) represents the direction that mask $LD$ detects. The LD-PO algorithm computes absolute value of the sum of products to void discussing opposite situation in Fig. 1(b), in which situation the best response is a negative value.

After finding the best point $m$, we associate point $\tilde{m}$ to m and update association field array: $A_{j} [\tilde{m}] = m - \tilde{m}$ in scale $2^{j}$. The size of binary matrix $BP$ and line detection mask $LD$ is a fixed value 9 and it needs to compute just 3 times to find the best orientation. To an image $F$ with $N$ samples, proposed algorithm LD-PO computes the $JN$ values of the $J$ association fields $A_{j}$ with $O(27JN) = O(JN)$ operations, which has the same complexity as forward decomposition.

4 Experimental Results and Conclusions

We perform experiments to validate the efficiency of the proposed LD-PO algorithm and compare it with block matching algorithm used by Mallat in [3]. Standard test images in Fig. 3 are selected whose gray level is 256, including Lena of size $512 \times 512$ and Babar of size $128 \times 128$. Each image is transformed by tight frame grouplet respectively using LD-PO algorithm and block matching to compute association fields.

Fig. 3.

Test image. (a) Lena, size of $512 \times 512$. (b) Babar, size of $128 \times 128$.

Figure 4 shows experimental results on image Lena by tight frame grouplet using block matching and results of proposed LD-PO algorithm are showed in Fig. 5. According to the comparison of (a) and (b) in Figs. 4 and 5, LD-PO algorithm can also describe detail information. Figure 5(d) is the result of inverse grouplet transform, which shows LD-PO algorithm’s same ability to reconstruct image perfectly like block matching algorithm.

Fig. 4.

Results of block matching. (a) Detail of scale $2^{1} .$ (b) Detail of scale $2^{2} .$ (c) The approximation. (d) Reconstructed image.

Fig. 5.

Results of LD-PO algorithm. (a) Detail of scale $2^{1} .$ (b) Detail of scale $2^{2} .$ (c) The approximation. (d) Reconstructed image.

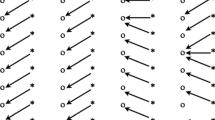
Figure 6 describes image Babar’s geometric flow in scale $2^{1}$, in which scale the flow is the finest. Geometric flow computed by block matching is showed in Fig. 6(a) and (c). Flow computed by LD-PO algorithm is showed in Fig. 6(b) and (d). According to the comparison of (a) and (b), although some of the arrows are a bit messy, geometric flow represents the texture orientation successfully in Fig. 6(b). The reason resulting messy arrows is that line detection masks respond strongly to lines on one pixel thick. These messy arrows well represent the edge of geometric flow.

Fig. 6.

Association field of image Babar in scale $2^{1} .$ (a) Association field computed by block matching. (b) Association field computed by LD-PO algorithm. (c), (d) is the area that shown in red rectangle of (a), (b) separately (Color figure online)

From Tables 1 and 2, we can see that the proposed LO-PO algorithm need less time than block matching to compute association field coefficients with little loss of sparsity. Errors of reconstruction can also be ignored.

Table 1. Block matching for tight frame grouplet transform.

Table 2. LD-PO algorithm for tight frame grouplet transform.

Conclusion.

In this paper, the computation of association field is improved by LD-PO algorithm. Compared with block matching, the experimental results show that the new method reflects a high efficiency in tight frame grouplet to compute association field coefficients. The tight frame grouplet using proposed algorithm will be applied widely in the future, such as image zooming based on geometric flow, SAR image road detecting, image compression based on texture and so on. How to use it to image processing application widely will be the emphasis of our research in the future.