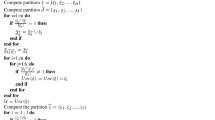Keywords

1 Introduction

The CART [3, 10, 17] is a sophisticated Decision Tree [11, 12] algorithm. It is direct viewing, can extract knowledge rules preferably and suitable to deal with classification problems [21]. It outperforms several other popular decision tree algorithms with respect to simplicity, comprehensibility, classification accuracy and being able to handle mixed-type data. Moreover CART efficiently deals with missing values, uses cost-complexity pruning strategy and can handle outliers. But, when the data has large number of attributes and involves impurity, the decision tree constitutive property is poor and difficult to find some information that could have been found and be useful. Another problem with the CART cross validation method is that it can be computationally too expensive, because it requires the growing and pruning of auxiliary trees as well. In order to overcome these drawbacks, rough set based attribute reduction has been introduced. Ever since the introduction of rough set theory by Pawlak [9] in 1982, many extensions have been made [16, 19, 20, 22]. The MPBRS [7, 9] is an excellent rough set based tool for attribute reduction. The indiscernibility relation and set approximation remains unaltered before and after reduction. The positive region computed, involves maximum number of objects. As a result the reduced attribute set involves all the significant attributes eliminating all insignificant attributes. This paper also studies CART based on Pawlak rough set [9] and BDTRS [1, 2, 8] for attribute reduction. In this research work we have used R [4, 6, 13], version 3.2.2, for experimentation and implementation of MPBRS. Data sets have been taken from UCI Machine learning repository.

In Sect. 2, Pawlak rough set, BDTRS, MPBRS and CART are introduced. Section 3, discusses about processing steps, algorithm and execution process in R environment. Experimental results and concluding remarks are presented in Sects. 4 and 5 respectively.

2 Theoretical Background

2.1 Pawlak’s Rough Set Model [9, 13]

An information system is defined as: \( S = (U, At,\left\{ { V_{a } | a \in At} \right\}, \,\left\{ {I_{a} | a \in At} \right\}), \) where, \( U_{ } \) is a finite nonempty set of objects, \( At \) is a finite nonempty set of attributes, \( V_{a} \) is a nonempty set values of \( a \in At \) and \( I_{a} :U \to V_{a} \) is an information function that maps an object in \( U \) to exactly one value in \( V_{a} \). The approximations of \( X \subseteq U \) with respect of equivalence relation \( R \) can be defined according to its upper and lower approximations.

Positive region:

$$ POS_{R} \left( X \right) = {\underline{R}} X = \mathop \cup \nolimits \left\{ {\left[ x \right]_{R} |P\left( {X/[x]_{R} } \right) = 1,\left[ x \right]_{R} \in \pi_{R} } \right\}. $$

Negative region:

$$ NEG_{R} \left( X \right) = U - \bar{R}X = \mathop \cup \nolimits \left\{ {\left[ x \right]_{R} |P\left( {X/[x]_{R} } \right) = 0,\left[ x \right]_{R} \in \pi_{R} } \right\}. $$

Boundary region:

figure a

2.2 Bayesian Decision Theoretic Rough Set [1, 2, 8, 15]

Let, \( D_{POS } \) denotes the positive region in BDTRS model. For an equivalence class, \( \left[ x \right]_{c} \in \pi_{A} \),

$$ D_{POS} \left( {\left[ x \right]_{c} } \right) = \left\{ {D_{i} \in \pi_{D} :P\left( {D_{i} /\left[ x \right]_{c} } \right) > P\left( {D_{i} } \right)} \right\}. $$

For equivalence classes \( \left[ x \right]_{c} \) and \( \left[ y \right]_{c} \) the elements of a positive decision-based discernibility matrix, \( M_{{D_{pos} }} \) is defined as follows.

$$ M_{{D_{POS} }} \left( {\left[ x \right]_{c} ,\left[ y \right]_{c} } \right) = \left\{ {a \in C : I_{a} \left( x \right) \ne I_{a} \left( y \right) {\bigwedge } D_{POS} \left( {\left[ x \right]_{c} } \right) \ne D_{POS} \left( {\left[ y \right]_{c} } \right)} \right\}. $$

A positive decision reduct is a prime implicant of the reduced disjunctive form of the discernibility function.

$$ f\left( {M_{{D_{POS} }} } \right) = {\bigwedge } \left\{ {{\bigvee }\left( {M_{{D_{POS} }} \left( {\left[ x \right]_{c} ,\left[ y \right]_{c} } \right)} \right) : \forall x,y \in U\left( {M_{{D_{POS} }} \left( {\left[ x \right]_{c} ,\left[ y \right]_{c} } \right) \ne \emptyset } \right)} \right\}. $$

In order to derive the reduced disjunctive form, the discernibility function \( f\left( {M_{{D_{POS} }} } \right) \) is transformed by using the absorption and distributive laws. Accordingly, finding the set of reducts can be modeled based on the manipulation of a Boolean function.

2.3 Maximum Probabilistic Based Rough Set [7, 9, 18]

Maximum probabilistic based rough set is a stronger form of other rough set models.

The precision of an equivalence class \( \left[ x \right]_{c} \in \pi_{c} \) for predicting a decision class \( D_{i} \in \pi_{D} \) can be defined. We denote it by \( P_{max} (D_{i} ,\left[ x \right]_{c} ) \) and are defined as follows:

$$ P_{max} \left( {D_{i} ,\left[ x \right]_{c} } \right) = \frac{{\left| {\left[ x \right]_{c} \mathop \cap \nolimits D_{i} } \right|}}{{\begin{array}{*{20}c} {max} \\ j \\ \end{array} \left| {\left[ x \right]_{c} \mathop \cap \nolimits D_{i} } \right|}}. $$

For a decision class, \( D_{i} \in \pi_{D} , \) the Maximum probabilistic based rough set lower and upper approximations with respect to a partition \( \pi_{c} \) can be defined as:

$$ {\underline{apr}}_{{{ \hbox{max} }\left( {\pi_{C} } \right)}} \left( {D_{i} } \right) = \left\{ {x \in U:P_{max} \left( {D_{i} ,\left[ x \right]_{c} } \right) = \frac{{\left| {\left[ x \right]_{c} \mathop \cap \nolimits D_{i} } \right|}}{{\begin{array}{*{20}c} {max} \\ j \\ \end{array} \left| {\left[ x \right]_{c} \mathop \cap \nolimits D_{i} } \right|}} = 1} \right\}, $$
$$ \overline{apr}_{{{ \hbox{max} }\left( {\pi_{C} } \right)}} \left( {D_{i} } \right) = \left\{ {x \in U:P_{max} \left( {D_{i} ,\left[ x \right]_{c} } \right) = \frac{{\left| {\left[ x \right]_{c} \mathop \cap \nolimits D_{i} } \right|}}{{\begin{array}{*{20}c} {max} \\ j \\ \end{array} \left| {\left[ x \right]_{c} \mathop \cap \nolimits D_{i} } \right|}} > 0} \right\}. $$

The positive, boundary and negative regions of \( D_{i} \in \pi_{D} \) with respect to \( \pi_{C} \) are defined by:

$$ \begin{aligned} POS_{{max\left( {\pi_{c} } \right)}} \left( {D_{i} } \right) & = POS_{max} \left( {D_{i} ,\pi_{c} } \right) = \left\{ {x \in U:P_{max} \left( {D_{i} ,\left[ x \right]_{c} } \right) = \frac{{\left| {\left[ x \right]_{c} \mathop \cap \nolimits D_{i} } \right|}}{{\begin{array}{*{20}c} {max} \\ j \\ \end{array} \left| {\left[ x \right]_{c} \mathop \cap \nolimits D_{i} } \right|}} = 1} \right\} \\ BND_{{max\left( {\pi_{c} } \right)}} \left( {D_{i} } \right) & = BND_{max} \left( {D_{i} ,\pi_{c} } \right) \\ & = \left\{ {x \in U:0 < P_{max} \left( {D_{i} ,\left[ x \right]_{c} } \right) = \frac{{\left| {\left[ x \right]_{c} \mathop \cap \nolimits D_{i} } \right|}}{{\begin{array}{*{20}c} {max} \\ j \\ \end{array} \left| {\left[ x \right]_{c} \mathop \cap \nolimits D_{i} } \right|}} < 1} \right\} \\ NEG_{{max\left( {\pi_{c} } \right)}} \left( {D_{i} } \right) & = NEG_{max} \left( {D_{i} ,\pi_{c} } \right) = \left\{ {x \in U:P_{max} \left( {D_{i} ,\left[ x \right]_{c} } \right) = \frac{{\left| {\left[ x \right]_{c} \mathop \cap \nolimits D_{i} } \right|}}{{\begin{array}{*{20}c} {max} \\ j \\ \end{array} \left| {\left[ x \right]_{c} \mathop \cap \nolimits D_{i} } \right|}} = 0} \right\}. \\ \end{aligned} $$

Attribute Significance [9].

The consistency factor is defined as \( \gamma \left( {C,D} \right) = \left| {POS_{C} \left( D \right)} \right|/\left| U \right| \). The decision table is consistent if \( \gamma \left( {C,D} \right) = 1 \). The significance, \( \sigma \left( a \right), \) of any attributes \( a, \) can be defined as:

$$ \sigma \left( {C,D} \right)\left( a \right) = \left( {\gamma \left( {C,D} \right) - \gamma \left( {C - \left\{ a \right\},D} \right)} \right)/\gamma \left( {C,D} \right) = 1 - \left( {\gamma \left( {C - \left\{ a \right\},D} \right)/\gamma \left( {C,D} \right)} \right). $$

Where, \( 0 \le \sigma \left( a \right) \le 1 \).

2.4 Decision Tree: CART [3, 10, 11, 17]

The CART algorithm starts with the initial decision table (data set) \( D, \) attribute set \( At \) and gini-index, as attribute selection method. Initially, it creates a node, \( N, \) which incorporates \( D. \) If all the objects of \( D \) belong to same class, node \( N \) is returned as leaf node. Otherwise, select a condition attribute (that maximizes the reduction in impurity of \( D \)) that divides \( D, \) in a manner such that height of the tree is as small as possible. The node \( N \) is labeled with the selected attribute. After that, branches are grown from \( N \) for each of the outcomes of the splitting attributes. The algorithm works recursively on each subset of \( D. \) Recursion may stop in one of these cases:

  • All the objects of a node belong to a particular class (same class).

  • There are no attributes left on which the objects may be further be separated.

  • There are no objects for a particular branch and a partition is empty.

Gini Index.

CART uses Gini-index for choosing the best attribute in the process of data partition. The Gini-index for a data set \( D, \) having \( m \) decision classes is calculated as:

$$ Gini\left( D \right) \, = 1- \sum\nolimits_{i = 1}^{m} {p_{i}^{2} .} $$
(1)

Where p i is the probability that an object in \( D \), belongs to class \( C \). If a binary partition on condition attribute \( A, \) partitions \( D \) into subsets \( D_{1} \) and \( D_{2} \), the Gini-index, given that partitioning is:

$$ Gini_{\text{A}} \left( D \right) \, = \frac{{\left| {D_{1} } \right|}}{D}Gini\left( {D_{1} } \right) \, + \frac{{\left| {D_{2} } \right|}}{D}Gini\left( {D_{{\mathbf{2}}} } \right). $$
(2)

For every attribute, all of the possible splits are calculated. For a particular attribute, the point producing the lowest Gini index is chosen as the split point. Reduction in impurity on a condition attribute \( A, \) is:

$$ \Delta Gini\left( A \right) \, = Gini\left( D \right) \, - Gini_{A} \left( D \right). $$
(3)

The condition attribute that results in maximum reduction of impurity is chosen as the splitting attribute.

3 Implementation of MPBRS-Based CART

3.1 Processing Steps

This section shows the implementation and execution procedure for MPBRS-based CART. Implementation of BDTRS is done in [8]. MPBRS-based decision tree induction is performed in two basic steps. First, attribute reduction and second, decision tree induction using the reduced information. Procedure for attribute reduction is shown in Algorithm-1(AttReduction ()). Case: 1, Case: 2 and Case: 3 represent MPBRS, BDTRS and Pawlak rough set respectively for attribute reduction. Based on rough set theory equivalent classes [9] are computed. Procedure for computation of positive region, discernibility matrix [15], discernibility function [19] and reduced attribute set are shown in Algorithm-1. The discernibility function is a conjunction over the disjunction of the matrix elements. The function can be transformed in to a reduced attribute set using absorption and distributive laws of Boolean algebra. The classical CART is implemented in package ‘rpart’ of R. Induction of decision tree using R commands has been shown in Sect. 3.3.

3.2 Algorithm

figure b

3.3 Execution of CART and MPBRS-Based CART in R Environment

Decision Tree Induction Using CART.

This section explains decision tree induction by taking housing [5] as example data set. Installation procedure of R and relevant packages (“RoughSets” [14], “rpart” etc.) are available in Comprehensive R Archive Network (CRAN). In order to perform attribute reduction, raw data (in .txt, .csv, .xlsx etc. format) is first converted into data frame object which is then converted into DecisionTable format. For this, functions like read.table(), SF.asDecisionTable() [14] may be used. The package “rpart” is installed using the R command: > library(rpart). Similarly other packages like “rattle”, “caret”, “RoughSets” etc. are also installed. The Decision Tree, T1 obtained from the following commands is shown in Fig. 1.

Fig. 1.
figure 1

Decision Tree T1 using CART method (Left hand side), before attribute reduction and Decision Tree T2 using MPBRS-CART() method (Right hand side) after attribute reduction.

Full size image
figure c

Decision Tree Induction Using MPBRS-Based CART.

MPBRS-based CART is inducted in two steps. Step 1: Performs data reduction by MPBRS. Step2: Decision Tree induction based on the output of Step 1. Following R commands are executed on housing data set (housing.csv format). Reduced attribute set is shown in Table 1.

Table 1. Attribute reduction using MPBRS model on housing dataset.
Full size table
figure d

The procedure for decision tree induction is same as CART and hence not repeated. The decision tree (T2) thus obtained is shown in Fig. 1.

4 Experimental Results and Discussion

The data sets used for experimentation are: Cervical Cancer (858 objects with 36 attributes) [23], Spambase (4601 objects with 57 attributes) [24] and housing (506 objects with 14 attributes). The housing data set is already introduced in the previous section. Each of these data sets has been studied by MPBRS, BDTRS and Pawlak rough set. For housing data, at first, we pre-processed the sample data (D) and filled in missing values using built in functions available in R. Next, we run the original algorithm CART, on D, to construct a Decision Tree T1 as shown in Fig. 1.

After that, we run Case: 1 of Algorithm-1 (attribute reduction by MPBRS) to reduce the insignificant attributes of D. We reduced the number of attributes down to 9, saved the new sample data set as D red . The deleted attributes are: ‘ZN’, ‘NOX’, ‘PTRATIO’ and ‘INDUS’. We computed attribute significance of all the attributes to show that deleted attributes have little effect on decision making. This is shown in Table 1. We further computed consistency factor (C.F) (shown in Table 2) which remains same (one) before and after attribute reduction. This ensures that the integrity of the data set remains unchanged after attribute reduction. Finally, we run CART on the reduced data set D red , to construct a simplified decision tree, T2 (Fig. 1). The above mentioned experimental procedure is repeated using the functions AttReduction() (Algorithm-1) and CART method for Cervical Cancer and Spambase data sets. The results obtained from the computations are shown in Table 2.

Table 2. Comparison of CART, MPBRS-CART, BDTRS-CART and Pawlak-CART using Cervical Cancer, Spambase and housing data sets.
Full size table

For housing data, tree T1, shows that the classification tree has 15 nodes (7 internal and 8 leaf nodes). On the other hand, Tree T2, of Fig. 1 shows that the classification tree has 11 nodes (5 internal and 6 leaf nodes). The domain of decision column (Minimum: 5 and Maximum: 50) is divided in to six equivalent classes: C1, C2, C3, C4, C5 and C6. There are eight (8) classification rules corresponding to the leaf nodes of T1 and six (6) rules corresponds to T2. For example, the classification rule: “If (RAD <= 3) and (B <= 300) and (LSTAT > 11.5) and (INDUS <= 9.7) then MEDV = C5”, corresponds to leaf node C5 of tree T1. Similar results obtained from the other two data sets and the comparison of CART, MPBRS-CART, BDTRS-CART and Pawlak-CART methods are shown in the Table 2. It can be observed from Table 2 that CART model deals with the original unreduced data set, whereas, other three approaches work on the reduced data set. The MPBRS method gives the best attribute reduction. As a result, number of nodes, number of leaf nodes, depth and average length of the classification rules has been decreased for all the three approaches except classical CART Model. This ultimately improves the classification accuracy of the decision trees as shown in Fig. 2.

Fig. 2.
figure 2

Classification accuracy of CART, MPBRS-CART, BDTRS-CART and Pawlak based CART on Cervical Cancer, Spambase and housing data sets.

Full size image

On the other hand, the rough set based decision tree approach suffers in terms of total execution time as it involves the attribute reduction phase also. The minimal increase of execution time is acceptable, keeping the classification accuracy and reduction of tree complexity (shown in Fig. 3) in mind. Tree complexity mainly depends on the average length of the decision rules which is lowest in case of MPBRS-based CART method for all data sets.

Fig. 3.
figure 3

Complexity representation of CART, MPBRS-CART, BDTRS-CART and Pawlak based CART on Cervical Cancer, Spambase and housing data sets.

Full size image

5 Conclusion

Efficiency of CART-based decision tree becomes an issue of concern to deal with high-dimensional large data sets. This study focuses on reducing number of insignificant attributes from the original data set before induction of CART-based decision tree. The reduced attribute set preserves the indiscernibility relation and set approximation. This is ensured by computing attribute significance and consistency factor. In this research work we have also implemented the MPBRS using R language in order to study the classical CART. The experimental results show that the decision tree induced by MPBRS-based CART is the simplest and most efficient in terms of depth, number of nodes, average rule length and classification accuracy compared to the other methods mentioned in this work.