Abstract
SPARX is a family of ARX-based block ciphers proposed at ASIACRYPT 2016. This family was designed with the aim of providing provable security against single-characteristic linear and differential cryptanalysis. SPARX-128/128 and SPARX-128/256 are two members of this family which operate on data blocks of length 128 bits and keys of length 128 and 256 bits, respectively. In this work, we propose a zero-correlation distinguisher that covers 5 steps (20 rounds) for both variants of SPARX-128. Then, using specific linear masks at its output and utilizing some properties of the employed linear layer and S-box, we extend this distinguisher to 5.25 steps (21 rounds).
By exploiting some properties of the key schedule, we extend the 20-round distinguisher by 4 rounds to present a 24-round multidimensional zero-correlation attack against SPARX-128/256, i.e., 6 steps out of 10 steps. The 24-round attack is then extended to a 25-round (6.25 out of 10 steps) zero-correlation attack against SPARX-128/256 with the full codebook by using the developed 21-round distinguisher. In addition, we extend the 21-round distinguisher by one round to launch a 22-round multidimensional zero-correlation attack against SPARX-128/128, i.e., 5.5 steps out of 8 steps.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
With the aim of developing block ciphers with provable security against single-characteristic linear and differential cryptanalysis, Dinu et al. [7] proposed a new ARX-based family of block ciphers at ASIACRYPT 2016. They achieved this goal by proposing a new strategy, namely, the long trail strategy, which is different from the well-studied wide trail strategy [6] that is used by many S-box based block ciphers. The long trail strategy encourages the use of a rather weak but large S-boxes such as ARX-based S-boxes along with a very light linear transformation layer. Adopting this strategy in the SPARX family allowed the designers to prove the security of the cipher against single-characteristic linear and differential cryptanalysis by bounding the maximum linear and differential probabilities for any number of rounds.
SPARX-128/128 and SPARX-128/256 are two members of the SPARX family which employ a data block of length 128 bits using 128 and 256 key bits, respectively. The only known attacks against these two variants were developed by the designers. These attacks were found using integral cryptanalysis based on Todo’s division property [11] and cover 22 and 24 rounds of SPARX-128/128 and SPARX-128/256, respectively, in the chosen plaintext attack model.
Zero-correlation [4] is one of the relatively new techniques that is used to analyze symmetric-key primitives, where the attacker utilizes a linear approximation of probability exactly 1/2 over \(r_m\) rounds to act as a distinguisher. Then, this distinguisher can be utilized in a key recovery attack such that the keys which lead to this distinguisher are excluded. This technique proves its success against many of the recently proposed block ciphers as exemplified by the work done in [4, 10, 12,13,14].
In this paper, we evaluate the security of SPARX-128 in the known plaintext attack model using the zero-correlation cryptanalysis. First, we present a 20-round zero-correlation distinguisher. Then, we use a specific linear mask at the output of this 20-round distinguisher and exploit some properties of the employed linear layer and S-box to add one more round and create a 21-round zero-correlation distinguisher. To turn these distinguishers into key recovery attacks, we take advantage of the property of the S-box that permits the existence of a two-round linear approximation that holds with probability 1. Then, by exploiting the key schedule relations, we place this deterministic two-round linear approximation in a position that enables us to extend the 20-round distinguisher by 4 complete rounds, i.e., including the linear layer, to launch a 24-round key recovery attack against SPARX-128/256 using multidimensional zero-correlation attack. This 24-round attack is, then, extended by one more round using the 21-round distinguisher to launch a 25-round zero-correlation attack against SPARX-128/256 using the full codebook. In addition, we extend the 21-round distinguisher to launch a 22-round attack against SPARX-128/128.
The remainder of the paper is organized as follows. In Sect. 2, the notations used throughout the paper and the specifications of SPARX-128/128 and SPARX-128/256 are presented. Section 3 presents a brief introduction about zero-correlation and multidimensional zero-correlation attacks. In Sect. 4, we present our distinguisher for SPARX-128/128 and SPARX-128/256. Afterwards, in Sect. 5, we provide a detailed description of our multidimensional zero-correlation attacks against SPARX-128/128 and SPARX-128/256, and finally we conclude the paper in Sect. 6.
2 Description of SPARX-128/128 and SPARX-128/256
The following notations are used throughout the paper:
-
K: The master key.
-
\(k_i\): The \(i^{th}\) 16-bit of the key state, where \(0 \le i \le 7\) for SPARX-128/128, and \(0 \le i \le 15\) for SPARX-128/256.
-
\(k_i^j\): The \(i^{th}\) 16-bit of the key state after applying the key schedule permutation j times, where \(0 \le i \le 7\), \(0 \le j \le 32\) for SPARX-128/128, and \(0 \le i \le 15\), \(0 \le j \le 20\) for SPARX-128/256.
-
\(K_i\): The \(i^{th}\) 32-bit of the key state, where \(0 \le i \le 3\) for SPARX-128/128, and \(0 \le i \le 7\) for SPARX-128/256.
-
\(K_i^j\): The \(i^{th}\) 32-bit of the key state after applying the key schedule permutation j times, where \(0 \le i \le 3\), \(0 \le j \le 32\) for SPARX-128/128, and \(0 \le i \le 7\), \(0 \le j \le 20\) for SPARX-128/256.
-
\(RK_{(a,i)}\): The 32-bit round key used at branch a of round i where \(0 \le i \le 32\) (resp. \(0 \le i \le 40\)) for SPARX-128/128 (resp. SPARX-128/256), and \(0\le a \le 3\), with \(a=0\) corresponding to the left branch.
-
\(X_{(a,i)}\) (\(Y_{(a,i)}\)): The left (right) 16-bit input at branch a of round i where \(0 \le i \le 32\) (resp. \(0 \le i \le 40\)) for SPARX-128/128 (resp. SPARX-128/256), \(0\le a \le 3\), with \(a=0\) corresponding to the left branch, and the LSBs of both \(X_{(a,i)}\) and \(Y_{(a,i)}\) start from the right.
-
\(X_{(a,i)}[i,j,\cdots ,k]\): The \(i,j,\cdots ,k\) bits of \(X_{(a,i)}\).
-
\(X_{(a,i)}[i:j]\): The bits from i to j of \(X_{(a,i)}\), where \(i\le j\).
-
w: The number of 32-bit words, i.e., \(w = 4\) for a 128-bit block and \(w = 8\) for a 256-bit master key.
-
\(R^4\): The iteration of 4 rounds of SPECKEY [2, 3] with their corresponding key additions.
-
\(L_w\): Linear mixing layer used in SPARX with w-word block size. Thus, \(L_4\) represents the linear mixing layer used in SPARX-128/128 and SPARX-128/256.
-
\(\boxplus \): Addition mod \(2^{16}\).
-
\(\oplus \): Bitwise XOR.
-
\(\lll q\) (\(\ggg q\)): Rotation of a word by q bits to the left (right).
-
\(\Vert \): Concatenation of bits.
2.1 Specifications of SPARX-128/128 and SPARX-128/256
SPARX [7, 8] is a family of ARX-based Substitution-Permutation Network (SPN) block ciphers. It follows the SPN design construction while using ARX-based S-boxes instead of S-boxes based on look-up tables. The ARX-based S-boxes form a specific category of S-boxes that rely solely on addition, rotation and XOR operations to provide both non-linearity and diffusion. The SPARX family adopts the 32-bit SPECKEY ARX-based S-box (S), shown in Fig. 1, which resembles one round of SPECK-32 [2, 3] with only one difference, that is, the key is added to the whole 32-bit state instead of just half the state as in SPECK-32.
For a given member of the SPARX family whose block size is n bits, the plaintext is divided into \(w = n/32\) words of 32 bits each. Then, the SPECKEY S-box (S), is applied to w words in parallel, and iterated r times interleaved by the addition of independent subkeys. Then, a linear mixing layer (\(L_w\)) is applied to ensure diffusion between the words. As depicted in Fig. 1, the structure made of a key addition followed by S is called a round while the structure made of r rounds followed by \(L_w\) is called a step. Thus, the ciphertext corresponding to a given plaintext is generated by iterating such steps. The number of steps and the number of rounds in each step depend on both the block size and the key length of the cipher.
SPARX-128/128 and SPARX-128/256 are two members of the SPARX family which operate on 128-bit blocks using 128-bit and 256-bit keys, respectively. Both variants use 4 rounds in each step and iterate over 8 and 10 steps, i.e., the total number of rounds is 32 and 40, respectively. More precisely, in SPARX-128/128 and SPARX-128/256, 4 SPECKEY S-boxes (S) are iterated simultaneously for 4 times, while being interleaved by the addition of the round keys and then a linear mixing layer (\(L_4\)) is applied, as shown in Fig. 2 which also depicts the structure of \(L_4\).
SPARX-128/128 key schedule. The 128-bit master key instantiates the key state, denoted by \(k_0^0\Vert k_1^0\Vert k_2^0\Vert k_3^0\Vert k_4^0\Vert k_5^0\Vert k_6^0\Vert k_7^0\). Then, the \(4 \times 32\)-bit round keys used in branch number 0 of the first step are extracted. Afterwards, the permutation illustrated in Fig. 3 is applied and then the \(4 \times 32\)-bit round keys used in branch number 1 of the first step are extracted. The application of the permutation and the extraction of the keys are interleaved until all the round keys encompassing the post-whitening ones are generated. This means that the round keys of a given branch in step j are generated first and then the key state is updated.
SPARX-128/256 key schedule. The 256-bit master key instantiates the key state, denoted by \(k_0^0\Vert k_1^0\Vert k_2^0\Vert k_3^0\Vert k_4^0\Vert k_5^0\Vert k_6^0\Vert k_7^0\Vert k_8^0\Vert k_9^0\) \(\Vert k_{10}^0\Vert k_{11}^0\Vert k_{12}^0\Vert k_{13}^0\Vert k_{14}^0\Vert k_{15}^0\). First, the \(4 \times 32\)-bit round keys used in branch number 0 of the first step are extracted. Then, the \(4 \times 32\)-bit round keys used in branch number 1 of the first step are extracted. Afterwards, the permutation illustrated in Fig. 4 is applied and then the \(4 \times 32\)-bit round keys used in branch number 2 and 3 of the first step are extracted. The application of the permutation and the extraction of the keys are interleaved until all the round keys encompassing the post-whitening ones are generated.
3 Multidimensional Zero-Correlation Linear Cryptanalysis
In the traditional linear cryptanalysis [9], the attacker tries to find a linear relation between an input x and an output y of an n-bit block cipher function f that has the following form:
where \(\circ \) is a bitwise dot product operation and \(\varGamma _{x}\) (\(\varGamma _{y}\)) is the input (output) linear mask. This linear relation has a probability p, and in this type of attack it should be far from 1/2 or equivalently its correlation \(C = 2 \times p - 1\) is not zero. The following lemmas are used to specify the propagation of linear masks through the different operations (XOR, branch, and S-box) that are used in the round function.
Lemma 1
(XOR operation [4, 12]): Either the three linear masks at an XOR \(\oplus \) are equal or the correlation over \(\oplus \) is exactly zero.
Lemma 2
(Branching operation [4, 12]): Either the three linear masks at a branching point \(\bullet \) sum up to 0 or the correlation over \(\bullet \) is exactly zero.
Lemma 3
(S-box permutation [4, 12]): Over an S-box S, if the input and output masks are neither both zero nor both nonzero, the correlation over S is exactly zero.
Later on, Bogdanov and Rijmen [4] proposed a new technique called zero-correlation cryptanalysis which, in contrast to the linear cryptanalysis, exploits linear relations with correlation exactly zero to exclude wrong keys which lead to this linear approximation. To remove the burden of the high data complexity of the zero-correlation attack and the statistical independence for multiple zero-correlation linear approximations, Bogdanov et al. [5] proposed the multidimensional zero-correlation attack. In this technique, we have m different linear approximations with zero-correlation, where all the \(l=2^m-1\) non-zero linear approximations involved in the spanned linear space of these m linear approximations should have zero-correlation. The zero-correlation linear approximation over \(r_m\) rounds can act as a distinguisher, then the attacker can prepend/append additional rounds called analysis rounds. The attack proceeds by gathering N plaintext/ciphertext pairs and creating an array of counters V[z], where \(|z|=m\) bits, and initializing it to zero. Then, for each plaintext/ciphertext pair and key guess, the attacker computes the corresponding bits needed to apply the m linear approximations to compute z and increments the corresponding counter by one. Afterwards, the attacker computes the statistic T [5]:

The right key has T that follows \(\chi ^2\)-distribution with mean \(\mu _0=l\frac{2^n-N}{2^n-1}\), and variance \(\sigma _0^2=2l(\frac{2^n-N}{2^n-1})^2\), while the statistic for the wrong key guess follows \(\chi ^2\)-distribution with mean \(\mu _1=l\) and variance \(\sigma _1^2=2l\) [5]. The number of known plaintexts required by the attack can be estimated as follows [5]:
where \(\gamma \) (resp. \(\zeta \)) denotes the probability to incorrectly discard the right key (resp. the probability to incorrectly accept a random key as the right key) and \(Z_p=\phi ^{-1}(p)\) (\(0< p < 1\)), \(\phi \) is the cumulative function of the standard normal distribution. According to the required \(\gamma \) and \(\zeta \) probabilities, the decision threshold is set to \(\tau = \mu _0+\sigma _0Z_{1-\gamma }=\mu _1-\sigma _1Z_{1-\zeta }\).
4 Zero-Correlation Distinguisher of SPARX-128/128 and SPARX-128/256
In this section, we present a 20-round zero-correlation distinguisher for SPARX-128/128 and SPARX-128/256, which will be exploited later in our attacks against 22 rounds (5.5 steps out of 8) of SPARX-128/128 and 24, 25 rounds (6, 6.25 steps out of 10) of SPARX-128/256. As depicted in Fig. 5, this distinguisher begins with only branch 0 containing a linear mask \(\alpha _0\) at round i. Then, by propagating this linear mask 2 steps forward, and by utilizing Lemmas 1 and 2, we have linear masks 0 and \(\alpha _4\) applied on \(X_{(1,i+8)}Y_{(1,i+8)}\) and \(X_{(3,i+8)}Y_{(3,i+8)}\), respectively. From the other side, at round \(i+20\), branch 0 has a linear mask \(\beta _0\), branch 1 has no linear mask, and branch 2 and 3 have linear masks \(\beta _1\) and \(\beta _2\), respectively. The linear masks \(\beta _1\) and \(\beta _2\) are chosen such that \(L_4(\beta _1,\beta _2)=(\beta _0,0)\). This choice enables us to pass one step backward with only one word having a linear mask \(\beta _3\) at branch 2. Then, following Lemmas 1 and 2, we can propagate the linear masks backward for one additional step and a linear layer to end with branch 1 and 3 having a non-zero linear mask \(\beta _6\) and a zero linear mask before applying the inverse of \(R^4\) to obtain \(X_{(1,i+8)}Y_{(1,i+8)}\) and \(X_{(3,i+8)}Y_{(3,i+8)}\), respectively. Here, \(R^4\) can be considered as a one big S-box, and hence, from Lemma 3, this linear approximation has a zero-correlation.
5 Multidimensional Zero-Correlation Cryptanalysis of SPARX-128/128 and SPARX-128/256
The following observations, which stem from the structure of SPARX-128/128 and SPARX-128/256, are exploited in our attacks.
Observation 1
As depicted in Fig. 6a, there is a 2-round linear approximation that holds with probability 1 (\(0x0080\;0x4001\rightarrow 0x0004\; 0x0004\)).
Observation 2
As illustrated in Fig. 6b, the linear mask \(0\beta \beta 0\), where 0 and \(\beta \) denote 0x0000 and 16-bit non-zero linear mask, respectively, propagates through the linear layer \(L_4\) as \(\beta \beta 00\), i.e., \(L_4(0\beta \beta 0)=\beta \beta 00\).
Observation 3
From Observation 2 and the specification of the S-box, the 20-round distinguisher can be extended to 21-round distinguisher, as shown in Fig. 6c.
5.1 24-Round Multidimensional Zero-Correlation Attack on SPARX-128/256
In this attack, and in order to maximize the number of attacked rounds, we have chosen to place the 20-round distinguisher at the bottom, and add 4 analysis rounds at the top to launch a 24-round attack against SPARX-128/256. Taking into account the key schedule relations, the top 4 analysis rounds involve all the master key bits, and in order to be able to extend 4 rounds above the distinguisher, we utilize Observation 1. In particular, we choose a specific linear mask at branch 0 at the beginning of our 20-round zero-correlation distinguisher. This specific linear mask, after propagating it backward through the linear layer \(L_4\), enables us to bypass 2 rounds of branch 0 with probability 1 by exploiting Observation 1 and thus have an extended distinguisher (the dotted one in Fig. 7).
Key Recovery. Here, we chose \(\beta =0x0abc\), where a, b, c are 4-bit non-zero linear masks. Then, the attack proceeds by gathering enough plaintext/ciphertext pairs. Afterwards, we guess the round keys involved in the analysis rounds to estimate the statistic T. However, the complexity of the attack following this strategy exceeds the complexity of exhaustive search. Therefore, we use the partial compression technique in order to reduce the time complexity of the attack as follows:
Step 1. Allocate an array of counters \(N_1[X_1]\) and initialize it to zeros, where \(X_1=X_{(0,0)}Y_{(0,0)}||X_{(1,0)}Y_{(1,0)}\) \(||X_{(2,0)}Y_{(2,0)}||(X_{(0,24)}[0:11]\oplus Y_{(0,24)}[0:11]\oplus Y_{(2,24)}[0:11]\oplus X_{(3,24)}[0:11])\), i.e., \(|X_{1}|=108\) bits. Then, from the gathered plaintext/ciphertext pairs compute \(X_1\) and increment the corresponding counter. Since all the non-zero 16-bit linear masks in the ciphertext equal \(\beta =0x0abc\), then, we can store only \((X_{(0,24)}[0:11]\oplus Y_{(0,24)}[0:11]\oplus Y_{(2,24)}[0:11]\oplus X_{(3,24)}[0:11])\) instead of storing each one separately to apply the linear mask \(\beta \).
Step 2. Allocate an array of counters \(N_2[X_2]\) and initialize it to zeros, where \(X_2=X_{(0,0)}Y_{(0,0)}||X_{(1,3)}[0,1,7:15]Y_{(1,3)}[0:10]\) \(||X_{(2,0)}Y_{(2,0)}||(X_{(0,24)}[0:11]\oplus Y_{(0,24)}[0:11]\oplus Y_{(2,24)}[0:11]\oplus X_{(3,24)}[0:11])\), i.e., \(|X_{2}|=98\) bits. Then, guess \(K_4,K_5,K_6\) and partially encrypt \(X_1\) to compute \(X_2\) and add the corresponding counter \(N_1[X_1]\) to \(N_2[X_2]\).
Step 3. Allocate an array of counters \(N_3[X_3]\) and initialize it to zeros, where \(X_3=X_{(0,0)}Y_{(0,0)}||X'_{(1,3)}[2,10]Y'_{(1,3)}[2]\) \(||X_{(2,0)}Y_{(2,0)}||(X_{(0,24)}[0:11]\oplus Y_{(0,24)}[0:11]\oplus Y_{(2,24)}[0:11]\oplus X_{(3,24)}[0:11])\), i.e., \(|X_{3}|=79\) bits. Then, guess 22 bits of \(K_7\) (\(K_7[0:10,16,17,23:31]\equiv \) \(k_{14}[0,1,7:15],k_{15}[0:10]\)) and partially encrypt \(X_2\) to compute \(X_3\) and add the corresponding counter \(N_2[X_2]\) to \(N_3[X_3]\). Since the linear mask on \(X'_{(1,3)}Y'_{(1,3)}\) is \(0x0404\;0x0004\), i.e., we need to compute only 3 bits of \(X'_{(1,3)}Y'_{(1,3)}\), and we need only to know 22 bits of \(X_{(1,3)}[0,1,7:15]Y_{(1,3)}[0:10]\) and 22 bits of \(K_7\) to compute this linear mask.
Step 4. Allocate an array of counters \(N_4[X_4]\) and initialize it to zeros, where \(X_4=X_{(0,0)}Y_{(0,0)}||X'_{(1,3)}[2,10]Y'_{(1,3)}[2]\) \(||X_{(2,3)}[0,1,7:15]Y_{(2,3)}[0:10]||(X_{(0,24)}[0:11]\oplus Y_{(0,24)}[0:11]\oplus Y_{(2,24)}[0:11]\oplus X_{(3,24)}[0:11])\), i.e., \(|X_{4}|=69\) bits. Then, guess the remaining 10 bits of \(K_7\) and partially encrypt \(X_3\) to compute \(X_4\) and add the corresponding counter \(N_3[X_3]\) to \(N_4[X_4]\).
Step 5. Allocate an array of counters \(N_5[X_5]\) and initialize it to zeros, where \(X_5=X_{(0,0)}Y_{(0,0)}||X'_{(1,3)}[2,10]Y'_{(1,3)}[2]\) \(||X'_{(2,3)}[10]||(X_{(0,24)}[0:11]\oplus Y_{(0,24)}[0:11]\oplus Y_{(2,24)}[0:11]\oplus X_{(3,24)}[0:11])\), i.e., \(|X_{5}|=48\) bits. Then, guess 22 bits of \(R(K_0)\) (\(R(K_0)[0:10,16,17,23:31]\)) and partially encrypt \(X_4\) to compute \(X_5\) and add the corresponding counter \(N_4[X_4]\) to \(N_5[X_5]\).
Step 6. Allocate an array of counters \(N_6[X_6]\) and initialize it to zeros, where \(X_6=X_{(0,1)}[0:5,7:15]Y_{(0,1)}[0:14]||X'_{(1,3)}[2,10]Y'_{(1,3)}[2]\) \(||X'_{(2,3)}[10]||(X_{(0,24)}[0:11]\oplus Y_{(0,24)}[0:11]\oplus Y_{(2,24)}[0:11]\oplus X_{(3,24)}[0:11])\), i.e., \(|X_{6}|=46\) bits. Then, guess the remaining 10 bits of \(R(K_0)\) and partially encrypt \(X_5\) to compute \(X_6\) and add the corresponding counter \(N_5[X_5]\) to \(N_6[X_6]\).
Step 7. Allocate an array of counters \(N_7[X_7]\) and initialize it to zeros, where \(X_7=X_{(0,2)}[7]Y_{(0,2)}[0,14]||X'_{(1,3)}[2,10]Y'_{(1,3)}[2]\) \(||X'_{(2,3)}[10]||(X_{(0,24)}[0:11]\oplus Y_{(0,24)}\) \([0:11]\oplus Y_{(2,24)}[0:11]\oplus X_{(3,24)}[0:11])\), i.e., \(|X_{7}|=19\) bits. Then, guess 30 bits of \(K_1\) (\(k_2[0:5,7:15],k_3[0:14]\)) and partially encrypt \(X_6\) to compute \(X_7\) and add the corresponding counter \(N_6[X_6]\) to \(N_7[X_7]\).
The steps of the key recovery phase are summarized in Table 1, where the second column gives the keys to be guessed in each step. The third column presents the saved state in each step after the partial encryption, the fourth column is the counter size for each obtained state in the corresponding step, and the fifth column quantifies the time complexity of each step measured in 24-round encryption by considering the number of S-box accesses.
After Step 7, we have guessed 190 key bits (gK) from the master key and evaluated \(X_7\), that contains all the 19 bits involved in computing the zero-correlation masks. Therefore, to recover the master key, the following steps are performed:
-
1.
Allocate an array of counters V[z], where \(|z|=\) 12 bits.
-
2.
For \(2^{19}\) values of \(X_7\)
-
(a)
Evaluate all 12 basis zero-correlation masks on \(X_7\) and calculate z.
-
(b)
Update the counter V[z] by \(V[z] = V[z] + N_7[X_7]\).
-
(a)
-
3.
For each guessed key gK, compute
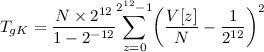 .
. -
4.
If \(T_k < \tau \), then the guessed values of gK are key candidates.
-
5.
Exhaustively search all the remaining key candidates with \(2^{66}\) values for the 66 bits of the key that are not retrieved by the above steps of the attack using 2 plaintext/ciphertext pairs.
Attack complexity. Since the beginning of the distinguisher has a specific linear mask and the end of the distinguisher has a variable 12-bit linear mask \(\beta \), then \(m=12\), and hence \(l=2^{12}-1\). Here, we set \(\gamma =2^{-2.7}\) and \(\zeta =2^{-30}\) and hence we have \(z_{1-\gamma } \approx 1\) and \(z_{1-\zeta } \approx 6\). According to Eq. (2), the data complexity is about \(2^{125.5}\) known plaintexts. The total time complexity of the attack encompasses the time complexity of two phases. The first is the time required to reduce the key search space which can be computed from Table 1. The second is the time required to retrieve the whole master key by exhaustively searching the remaining \(2^{190}\times 2^{-30}=2^{160}\) key candidates with the \(2^{66}\) key bits not involved in the attack using 2 plaintext/ciphertext pairs. Therefore, the total time complexity of the attack is \(2^{229.4}+2\times 2^{160}\times 2^{66}\approx 2^{229.65}\) 24-round encryptions.
25-round Zero-Correlation Attack on SPARX-128/256. The above attack can be extended one more round to launch a key recovery attack against 25-round of SPARX-128/256 with the full codebook. This extra round can be obtained by selecting the linear masks at the end of the distinguisher as in Observation 3 to convert the 20-round distinguisher to 21-round distinguisher. However, at this time we will use only one zero-correlation linear approximation. Therefore, we require the full codebook. The time complexity of the attack is dominated by Step 7, and it will be \(2^{227.4}\) instead of \(2^{229.4}\) because we store only 10 bits instead of 12 bits at the end of the distinguisher.
5.2 22-Round Multidimensional Zero-Correlation Attack on SPARX-128/128
As depicted in Fig. 8, in this attack we use the 21-round zero-correlation distinguisher obtained by utilizing Observation 3. Then, we append an additional round at the bottom of the distinguisher. In the previous attack, the analysis rounds were placed above the distinguisher, therefore, the relation of the round keys to the master key was straightforward and we use the master key relations in the attack from the beginning. However, in this attack, we place the analysis round at the bottom of the distinguisher, and hence the relation of the round keys to the master key is not trivial. Therefore, we will perform the attack on the round keys. Then, we will explain how to recover the master key from the recovered round keys. In order to balance the time complexity and the data complexity, we choose \(\alpha _0\) having linear masks in the first 30-bit only.
Key Recovery. Similar to the previous attack, we first gather N plaintext/ciphertext pairs, and then proceed as follows:
Step 1. Allocate an array of counters \(N_1[X_1]\) and initialize it to zeros, where \(X_1=X_{(0,0)}[0:13]Y_{(0,0)}[0:15]||X_{(0,22)}[0:13]Y_{(0,22)}[2:13]\) \(||X_{(2,22)}[0:4,11]\) \(Y_{(2,22)}[2:4,11]||X_{(3,22)}[0:13] Y_{(3,22)}[2:13]\), i.e., \(|X_{1}|=92\) bits. Then, from the N plaintext/ciphertext pairs compute \(X_1\) and increment the corresponding counter.
Step 2. Allocate an array of counters \(N_2[X_2]\) and initialize it to zeros, where \(X_2=X_{(0,0)}[0:13]Y_{(0,0)}[0:15]||X_{(0,22)}[0:13]Y_{(0,22)}[2:13]\) \(||X_{(2,21)}[9]Y_{(2,21)}[9]\)
\(||X_{(3,22)}[0:13] Y_{(3,22)}[2:13]\), i.e., \(|X_{2}|=84\) bits. Then, guess \(RK_{(2,22)}[2:4,11,16:20,27]\) and partially decrypt \(X_1\) to compute \(X_2\) and add the corresponding counter \(N_1[X_1]\) to \(N_2[X_2]\).
Step 3. Allocate an array of counters \(N_3[X_3]\) and initialize it to zeros, where \(X_3=X_{(0,0)}[0:13]Y_{(0,0)}[0:15]||X_{(0,22)}[0:13]Y_{(0,22)}[2:13]\) \(||X_{(2,21)}[9]Y_{(2,21)}[9]\)
\(||X_{(3,21)}[0,2] Y_{(3,21)}[2]\), i.e., \(|X_{3}|=61\) bits. Then, guess \(RK_{(3,22)}[2:13,16:29]\) and partially decrypt \(X_2\) to compute \(X_3\) and add the corresponding counter \(N_2[X_2]\) to \(N_3[X_3]\).
Step 4. Allocate an array of counters \(N_4[X_4]\) and initialize it to zeros, where \(X_4=X_{(0,0)}[0:13]Y_{(0,0)}[0:15]||X_{(0,21)}[0,2,9]Y_{(0,21)}[2,9]\) \(||X_{(2,21)}[9]Y_{(2,21)}[9]\)
\(||X_{(3,21)}[0,2] Y_{(3,21)}[2]\), i.e., \(|X_{4}|=40\) bits. Then, guess \(RK_{(0,22)}[2:13,16:29]\) and partially decrypt \(X_3\) to compute \(X_4\) and add the corresponding counter \(N_3[X_3]\) to \(N_4[X_4]\).
To determine the surviving round key candidates, we proceed as in the previous attack in Sect. 5.1 with \(m=30\), and hence \(|z|=\) 30 bits. Moreover, instead of using \(X_7\), we use \(X_4\). The number of surviving round key candidates is \(2^{62}\times 2^{-\zeta }\). To retrieve the master key, we will, first, retrieve the 128-bit key after applying the key permutation 20 times, i.e., \(K_0^{20}||K_1^{20}||K_2^{20}||K_3^{20}\) and, afterwards, we just revert the key schedule permutation 20 times to retrieve the master key. We have retrieved \(RK_{(0,22)}[2:13,16:29]\) which allows us to deduce \(K_2^{20}[2:13,16:29]\), see Fig. 9. Retrieving the remaining 102 bits of \(K_0^{20}||K_1^{20}||K_2^{20}||K_3^{20}\) can be done as follows:
-
1.
We guess \(K_0^{20},K_3^{20}\) and the remaining 6 bits of \(K_2^{20}\) to compute \(RK_{(1,21)},\) \(RK_{(1,23)},\) \( RK_{(2,21)}, RK_{(2,22)}\). Hence in total we have \(2^{62-\zeta +32+32+6-10=122-\zeta }\) remaining key candidates for \(K_0^{20},K_2^{20},K_3^{20},RK_{(3,22)}[2:13,16:29]\) \(,RK_{(1,21)},\) \(RK_{(1,23)},\) \( RK_{(2,21)}\), because we have 10-bit filter on \(RK_{(2,22)}[2:4,11,16:20,27]\).
-
2.
We guess the remaining 6 bits of \(RK_{(3,22)}\) to compute \(RK_{(2,20)},RK_{(1,22)},K_1^{20}\). Therefore, in total we have \(2^{122-\zeta +6}\) key candidates for \(K_0^{20},K_1^{20},K_2^{20},K_3^{20}\).
-
3.
We apply the inverse of the key permutation 20 times to retrieve \(2^{122-\zeta +6}\) key candidates for K, i.e., the master key.
-
4.
We test the remaining key candidates using one plaintext/ciphertext pairs to identify the correct key.
Attack complexity. Here, we set \(m=30\) (and hence \(l=2^{30}-1\)), \(\gamma =2^{-2.7}\), and \(\zeta =2^{-26}\). Thus \(z_{1-\gamma } \approx 1\) and \(z_{1-\zeta } \approx 5.54\). The data complexity is \(2^{116.2}\) known plaintexts, which can be computed from Eq. (2). In this case, the total time complexity of the attack is determined by the time complexity of three stages. The first is the time required to reduce the key search space which is dominated by Step 4 and equals \(2^{61}\times 2^{10+26+26}\times \frac{1}{22\times 4}\approx 2^{116.54}\). The second is the time required to retrieve the whole master key and equals \(2^{62-26+32+32+6} \times \frac{3}{22\times 4}+ 2^{122-26+6}\times \frac{2}{22\times 4}+2^{122-26+6}\times \frac{20\times 2}{22\times 4}+ 2^{102}\approx 2^{103}\). The third is the time required by the data collection phase which is equal to \(2^{116.2}\). Therefore, the time complexity of the attack is \(2^{116.54}+ 2^{103}+2^{116.2}\approx 2^{117.38}\) 22-round encryptions.
Remark: It is worth noting that the above zero-correlation attacks are also applicable to 15 rounds of SPARX-64/128 using the zero-correlation distinguisher shown in Fig. 10 (see also [1]). The details of this attack are omitted from this version of the paper due to space limitations.
6 Conclusion
In this paper, we presented 20 and 21-round zero-correlation distinguishers that are used to launch key recovery attacks against 24, 25 rounds (6, 6.25 out of 10 steps) of SPARX-128/256 and 22 rounds (5.5 out of 8 steps) of SPARX-128/128. To the best of our knowledge these are the first third party attacks against SPARX-128/128 and SPARX-128/256.
References
Abdelkhalek, A., Tolba, M., Youssef, A.M.: Impossible differential attack on reduced round SPARX-64/128. In: Joye, M., Nitaj, A. (eds.) AFRICACRYPT 2017. LNCS, vol. 10239, pp. 135–146. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-57339-7_8
Beaulieu, R., Shors, D., Smith, J., Treatman-Clark, S., Weeks, B., Wingers, L.: The SIMON and SPECK families of lightweight block ciphers. Cryptology ePrint Archive, Report 2013/404 (2013). http://eprint.iacr.org/2013/404
Beaulieu, R., Shors, D., Smith, J., Treatman-Clark, S., Weeks, B., Wingers, L.: SIMON and SPECK: block ciphers for the internet of things. Cryptology ePrint Archive, Report 2015/585 (2015). http://eprint.iacr.org/2015/585
Bogdanov, A., Geng, H., Wang, M., Wen, L., Collard, B.: Zero-correlation linear cryptanalysis with FFT and improved attacks on ISO standards camellia and CLEFIA. In: Lange, T., Lauter, K., Lisoněk, P. (eds.) SAC 2013. LNCS, vol. 8282, pp. 306–323. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-43414-7_16
Bogdanov, A., Leander, G., Nyberg, K., Wang, M.: Integral and multidimensional linear distinguishers with correlation zero. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 244–261. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_16
Daemen, J., Rijmen, V.: The wide trail design strategy. In: Honary, B. (ed.) Cryptography and Coding 2001. LNCS, vol. 2260, pp. 222–238. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45325-3_20
Dinu, D., Perrin, L., Udovenko, A., Velichkov, V., Großschädl, J., Biryukov, A.: Design strategies for ARX with provable bounds: Sparx and LAX. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10031, pp. 484–513. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53887-6_18
Dinu, D., Perrin, L., Udovenko, A., Velichkov, V., Groschdl, J., Biryukov, A.: Design strategies for ARX with provable bounds: SPARX and LAX (Full Version). Cryptology ePrint Archive, Report 2016/984 (2016). http://eprint.iacr.org/2016/984
Matsui, M., Yamagishi, A.: A new method for known plaintext attack of FEAL cipher. In: Rueppel, R.A. (ed.) EUROCRYPT 1992. LNCS, vol. 658, pp. 81–91. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-47555-9_7
Sun, L., Fu, K., Wang, M.: Improved zero-correlation cryptanalysis on SIMON. In: Lin, D., Wang, X.F., Yung, M. (eds.) Inscrypt 2015. LNCS, vol. 9589, pp. 125–143. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-38898-4_8
Todo, Y.: Structural evaluation by generalized integral property. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 287–314. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_12
Wang, Y., Wu, W.: Improved multidimensional zero-correlation linear cryptanalysis and applications to LBlock and TWINE. In: Susilo, W., Mu, Y. (eds.) ACISP 2014. LNCS, vol. 8544, pp. 1–16. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08344-5_1
Wen, L., Wang, M., Bogdanov, A., Chen, H.: Multidimensional zero-correlation attacks on lightweight block cipher HIGHT: improved cryptanalysis of an ISO standard. Inf. Proces. Lett. 114(6), 322–330 (2014)
Xu, H., Jia, P., Huang, G., Lai, X.: Multidimensional zero-correlation linear cryptanalysis on 23-round LBlock-s. In: Qing, S., Okamoto, E., Kim, K., Liu, D. (eds.) ICICS 2015. LNCS, vol. 9543, pp. 97–108. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-29814-6_9
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Key Schedule Relations for SPARX-128/128
B Zero-Correlation Distinguisher for SPARX-64/128
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG
About this paper
Cite this paper
Tolba, M., Abdelkhalek, A., Youssef, A.M. (2018). Multidimensional Zero-Correlation Linear Cryptanalysis of Reduced Round SPARX-128. In: Adams, C., Camenisch, J. (eds) Selected Areas in Cryptography – SAC 2017. SAC 2017. Lecture Notes in Computer Science(), vol 10719. Springer, Cham. https://doi.org/10.1007/978-3-319-72565-9_22
Download citation
DOI: https://doi.org/10.1007/978-3-319-72565-9_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-72564-2
Online ISBN: 978-3-319-72565-9
eBook Packages: Computer ScienceComputer Science (R0)









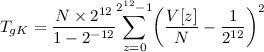 .
.

