Abstract
Allocating the right amount of resources to each service in any of the data centers in a cloud environment is a very difficult task. This task becomes much harder due to the dynamic nature of the workload and the fact that while long term statistics about the demand may be known, it is impossible to predict the exact demand in each point in time. As a result, service providers either over allocate resources and hurt the service cost efficiency, or run into situation where the allocated local resources are insufficient to support the current demand. In these cases, the service providers deploy overflow mechanisms such as redirecting traffic to a remote data center or temporarily leasing additional resources (at a higher price) from the cloud infrastructure owner. The additional cost is in many cases proportional to the amount of overflow demand.
In this paper we propose a stochastic based placement algorithm to find a solution that minimizes the expected total cost of ownership in case of two data centers. Stochastic combinatorial optimization was studied in several different scenarios. In this paper we extend and generalize two seemingly different lines of work and arrive at a general approximation algorithm for stochastic service placement that works well for a very large family of overflow cost functions. In addition to the theoretical study and the rigorous correctness proof, we also show using simulation based on real data that the approximation algorithm performs very well on realistic service workloads.
This paper was supported in part by the Neptune Consortium, Israel and by the Israeli Ministry of Science, Technology and Space.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
In this case, the goal is to find an integral solution, in which services cannot be split between bins. Later on, we also consider fractional solutions, which allow splitting a service between several bins.
- 2.
While we present the results only for SP-MED, we try to keep the discussion in this section as general as possible, so that it is clear what properties are required from a cost function to fall into our framework.
- 3.
For example, for SP-MED, \(\epsilon (S)=C_1 \sum _{j=1}^k \sigma _j \psi _0^j(S_j) (\frac{\pi }{2} - \arctan (\varDelta _j))\).
- 4.
A similar (simpler and easier to state) result also holds for the other two cost functions we have examined. See Appendix D.
- 5.
At first, we also wanted to compare our algorithm with variants of the algorithms considered in [3, 4] for the SBP problem. In both papers, the authors consider the algorithms First Fit and First Fit Decreasing [12] with item size equal to the effective size, which is the mean value of the item plus an extra value that guarantees an overflow probability is at most some given value p. Their algorithm chooses an existing bin when possible, and otherwise opens a new bin. However, when the number of bins is fixed in advance, taking effective size rather than size does not change much. For a new item (regardless of its size or effective size) we keep choosing the bin that is less occupied, but this time we measure occupancy with respect to effective size rather than size. Thus, if elements come in a random order, the net outcome of this is that the two bins are almost balanced and a new item is placed in each bin with almost equal probability.
References
Kleinberg, J., Rabani, Y., Tardos, É.: Allocating bandwidth for bursty connections. SIAM J. Comput. 30(1), 191–217 (2000)
Goel, A., Indyk, P.: Stochastic load balancing and related problems. In: IEEE FOCS 1999, pp. 579–586 (1999)
Wang, M., Meng, X., Zhang, L.: Consolidating virtual machines with dynamic bandwidth demand in data centers. In: IEEE INFOCOM 2011, pp. 71–75 (2011)
Breitgand, D., Epstein, A.: Improving consolidation of virtual machines with risk-aware bandwidth oversubscription in compute clouds. In: IEEE INFOCOM 2012, pp. 2861–2865 (2012)
Nikolova, E., Kelner, J.A., Brand, M., Mitzenmacher, M.: Stochastic shortest paths via Quasi-convex maximization. In: Azar, Y., Erlebach, T. (eds.) ESA 2006. LNCS, vol. 4168, pp. 552–563. Springer, Heidelberg (2006). https://doi.org/10.1007/11841036_50
Nikolova, E.: Approximation algorithms for offline risk-averse combinatorial optimization. Approximation, Randomization, and Combinatorial Optimization, pp. 338–351. Algorithms and Techniques (2010)
Shabtai, G., Raz, D., Shavitt, Y.: Risk aware stochastic placement of cloud services: the multiple data center case. In: ALGOCLOUD 2017 (2017)
Esseen, C.G.: A moment inequality with an application to the central limit theorem. Scand. Actuarial J. 1956(2), 160–170 (1956)
Shevtsova, I.: An improvement of convergence rate estimates in the Lyapunov theorem. Dokl. Math. 82, 862–864 (2010)
Ibragimov, I.A., Linnik, Y.V.: Independent and Stationary Sequences of Random Variables. Wolters-Noordhoff, Groningen (1971)
O’Donnell, R.: Analysis of Boolean Functions. Cambridge University Press, Cambridge (2014)
Michael, R.G., David, S.J.: Computers and Intractability: A Guide to the Theory of NP-Completeness. W.H. Freeman, New York (1979)
Acknowledgments
We want to thank Liran Rotem for helping us with the proof of Proposition 1 and useful discussion of the Berry-Esseen Theorem and Fubini’s Theorem. We also want to thank Boaz Klartag, Ryan O’Donnell and Terry Tao for answering our questions in email, and Ryan for referring us to relevant references.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Proving SP-MED Falls into Our Framework
By definition the expected deviation of a single bin is \(Dev_{S_j}= \frac{1}{\sigma _j \sqrt{2 \pi }} \int _{c_j}^{\infty } (x - c_j) e^{-\frac{(x-\mu _j)^2}{2\sigma _j^2}} dx\). Doing the variable change \(t = \frac{x - \mu _j}{\sigma _j}\) and then the variable change \(y = \frac{-t^2}{2}\) we get:
where \(\phi \) is the probability density function (pdf) of the standard normal distribution and \(\varPhi \) is its cumulative distribution function (CDF). Denoting \(g(\varDelta ) = \phi (\varDelta ) - \varDelta (1-\varPhi (\varDelta ) )\) we see that \(Dev_{S_j}=\sigma _j~ g(\varDelta _j)\). With two bins Dev is a function from \([0, 1]^2\) to \({\mathbf {R}}\) and \(Dev(a,b)=\sigma _1 g(\varDelta _1)+ \sigma _2 g(\varDelta _2)\) where the first bin has mean \(a\mu \) and variance bV, the second bin has mean \((1-a)\mu \) and variance \((1-b)V\) and \(\sigma _j,\varDelta _j\) are defined as above.
Lemma 3
Dev respects the symmetry, uni-modality and central saddle point properties.
Proof
-
Symmetry: Let us define \(\sigma _1(b)=\sqrt{b}~\sigma \), \(\sigma _2(b)=\sqrt{1-b}~\sigma \), \(\varDelta _1(a,b)=\frac{c_1-a\mu }{\sigma _1(b)}\) and \(\varDelta _2(a,b)=\frac{c_2-(1-a)\mu }{\sigma _2(b)}\). We know that \(Dev(a,b)=\sigma _1(b) g(\varDelta _1(a,b))+\sigma _2(b) g(\varDelta _2(a,b))\). To prove the symmetry \(Dev(a,b)=Dev(1-a-\frac{c_2-c_1}{\mu }, 1-b)\), it is enough to show that the following four equations hold: \(\sigma _1(b)=\sigma _2(1-b)\), \(\sigma _2(b)=\sigma _1(1-b)\), \(\varDelta _1(a,b)=\varDelta _2(1-a+\frac{c_1-c_2}{\mu }, 1-b)\) and \(\varDelta _2(a,b)=\varDelta _1(1-a+\frac{c_1-c_2}{\mu }, 1-b)\).
Indeed, \(\sigma _1(1-b) = \sqrt{1-b} ~\sigma = \sigma _2(b)\) and similarly \(\sigma _2(1-b) = \sigma _1(b)\). Also, \(\varDelta _2(1-a-\frac{c_2-c_1}{\mu }, 1-b) = \frac{c_2-(1-(1-a+\frac{c_1-c_2}{\mu }))\mu }{\sigma _2(1-b)}\). A similar check shows that \(\varDelta _1(1-a-\frac{c_2-c_1}{\mu }, 1-b) = \varDelta _2(a,b)\). This proves the symmetry. We remark that for \(c_1=c_2\) this simply says we can switch the names of the first and second bin.
-
 : Calculations show that \(\frac{\partial ^2 Dev}{\partial a^2} = \mu ^2 [\frac{\phi (\varDelta _2)}{\sigma _2} + \frac{\phi (\varDelta _1)}{\sigma _1}] \ge 0\). It follows that for any \(0< b < 1\), Dev(a) is convex and has a unique minimum. The unique point (m(b), b) on the valley is the one where \(\varDelta _1 = \varDelta _2\).
: Calculations show that \(\frac{\partial ^2 Dev}{\partial a^2} = \mu ^2 [\frac{\phi (\varDelta _2)}{\sigma _2} + \frac{\phi (\varDelta _1)}{\sigma _1}] \ge 0\). It follows that for any \(0< b < 1\), Dev(a) is convex and has a unique minimum. The unique point (m(b), b) on the valley is the one where \(\varDelta _1 = \varDelta _2\). -
Central saddle point: We first explicitly determine what Dev restricted to the valley is as a function \(D(b)=Dev(m(b),b)\) of b. As \(Dev(a,b)=\sigma _1 g(\varDelta _1)+\sigma _2 g(\varDelta _2)\) and on the valley \(\varDelta _1=\varDelta _2\) we see that on the valley \(Dev(a,b)=(\sigma _1+\sigma _2) g(\varDelta _1)\). However, \(\sigma _1 + \sigma _2\) also simplifies to \(\frac{c_1-a\mu }{\varDelta _1}+\frac{c_2-(1-a)\mu }{\varDelta _2}=\frac{c-\mu }{\varDelta _1}\). Altogether, we conclude that on the valley \(Dev(a,b)=(c-\mu ) \frac{g(\varDelta _1)}{\varDelta _1}\) is a function of \(\varDelta _1\) alone.
It is a straight forward calculation that \(\frac{\partial Dev(\varDelta _1)}{\partial \varDelta _1} = - (c-\mu )~ \frac{\phi (\varDelta _1)}{\varDelta _1^2} < 0\). We will also show that \(\frac{\partial \varDelta _1}{\partial b}\) is negative when \(b \le \frac{1}{2}\) and positive when \(b \ge \frac{1}{2}\). As \(\frac{\partial D}{\partial b}=\frac{\partial Dev}{\partial \varDelta _1} \cdot \frac{\partial \varDelta _1}{\partial b}\), we see that D(b) is increasing for \(b \le \frac{1}{2}\) and decreasing for \(b \ge \frac{1}{2}\) as claimed.
To analyze \(\frac{\partial \varDelta _1}{\partial b}\) we write \(\varDelta _1=\frac{e_1}{\sigma _1}\) and \(\varDelta _2=\frac{e_2}{\sigma _2}\) where \(e_1=c_1-a\mu \) is the spare capacity in bin 1 and \(e_2=c_2-(1-a)\mu \) is the spare capacity in bin 2. We notice that \(e=e_1+e_2=c-\mu \) the total spare capacity in the system. Now \(\varDelta _1=\varDelta _2\) implies \(e_1\sigma _2=e_2 \sigma _1=(e-e_1)\sigma _1\). Therefore, \(e_1(\sigma _1+\sigma _2)=e \sigma _1\) and \(\varDelta _1=\frac{e}{\sigma _1+\sigma _2}=\frac{c-\mu }{\sigma }(\frac{1}{\sqrt{b}+\sqrt{1-b}})\) and notice that \(\varDelta =\frac{c-\mu }{\sigma }\) is independent of b. All that remains is to differentiate the function \(\frac{1}{\sqrt{b}+\sqrt{1-b}}\).
We remark that we could simplify the proof by using Lagrange multipliers. However, since here it is easy to explicitly find Dev restricted to the valley we prefer the explicit solution. Later, we will not be able to explicitly find the restriction to the valley and we use instead Lagrange multipliers that solves the problem with an implicit description of the valley.
B Proving SP-MWOP Falls into Our Framework
Recall that
With two bins WOFP is a function from \([0, 1]^2\) to \({\mathbf {R}}\) and \(WOFP(a,b)=\max {\left\{ 1-\varPhi (\varDelta _1),1-\varPhi (\varDelta _2)\right\} }\) where the first bin has mean \(a\mu \) and variance bV, the second bin has mean \((1-a)\mu \) and variance \((1-b)V\). \(\sigma _j,\varDelta _j\) were previously defined.
Lemma 4
WOFP respects the symmetry, uni-modality and central saddle point properties.
Proof
-
Symmetry: The same proof as in Appendix A shows \(WOFP(a,b)=WOFP(1-a-\frac{c_2-c_1}{\mu }, 1-b)\).
-
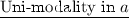 : Fix b. Denote \(OFP_{1}(a,b)=OFP_1(a\mu ,bV)=1-\varPhi (\varDelta _1)\). It is a simple calculation that \(\frac{\partial OFP_{1}}{\partial a}(a,b)=\frac{\mu }{\sqrt{b}\sigma } \cdot \phi (\varDelta _1) > 0\). Similarly, if \(OFP_{2}(a,b)\) denotes the overflow probability in the second bin when the first bin has total mean \(a\mu \) and total variance bV, then \(\frac{\partial OFP_{2}}{\partial a}=\frac{-\mu }{\sqrt{1-b}\sigma } \cdot \phi (\varDelta _2) < 0\). Thus, \(OFP_{1}\) is monotonically increasing in a and \(OFP_{2}\) is monotonically decreasing in a, and therefore there is a unique minimum for OFP(a, b) (when b is fixed and a is free) that is obtained when \(OFP_{1}(a,b)=OFP_{2}(a,b)\), i.e., when \(\varDelta _1=\varDelta _2\).
: Fix b. Denote \(OFP_{1}(a,b)=OFP_1(a\mu ,bV)=1-\varPhi (\varDelta _1)\). It is a simple calculation that \(\frac{\partial OFP_{1}}{\partial a}(a,b)=\frac{\mu }{\sqrt{b}\sigma } \cdot \phi (\varDelta _1) > 0\). Similarly, if \(OFP_{2}(a,b)\) denotes the overflow probability in the second bin when the first bin has total mean \(a\mu \) and total variance bV, then \(\frac{\partial OFP_{2}}{\partial a}=\frac{-\mu }{\sqrt{1-b}\sigma } \cdot \phi (\varDelta _2) < 0\). Thus, \(OFP_{1}\) is monotonically increasing in a and \(OFP_{2}\) is monotonically decreasing in a, and therefore there is a unique minimum for OFP(a, b) (when b is fixed and a is free) that is obtained when \(OFP_{1}(a,b)=OFP_{2}(a,b)\), i.e., when \(\varDelta _1=\varDelta _2\). -
Central saddle point: We first explicitly determine what WOFP restricted to the valley is as a function \(D(b)=WOFP(m(b),b)\) of b. From before we know that on the valley \(\varDelta _1=\varDelta _2\). Therefore, following the same reasoning as in the SP-MED case,
$$\begin{aligned} \varDelta _1(b)= & {} \frac{c-\mu }{\sigma }\frac{1}{\sqrt{b}+\sqrt{1-b}}. \end{aligned}$$It follows that D(b) is monotonically decreasing in b for \(b \le \frac{1}{2}\) and increasing otherwise. The maximal point is obtained in the saddle point that is the center of the symmetry.
By Theorem 2 we know that the optimal fractional solution is obtained on the bottom sorted path. In fact, for SP-MWOP we can say a bit more:
Lemma 5
The optimal fractional solution for SP-MWOP is the unique point that is the intersection of the valley and the bottom sorted path, and in this point \(\varDelta _1=\varDelta _2\).
Proof
Let us assume by contradiction that the optimal point \(P^*=(a^*, b^*)\) is not the point I which is the intersection point of the valley and the bottom sorted path. By Theorem 2, \(P^*\) is on the bottom sorted path. W.l.o.g. let us assume that \(P^*\) is left to the valley (the other case is similar). Since the valley is the curve defined by \(\varDelta _1 = \varDelta _2\), it is easy to see that \(\varDelta _1(a^*, b^*) > \varDelta _2(a^*, b^*)\) and therefore \(WOFP(a^*, b^*) = 1-\varPhi (\varDelta _2(a^*, b^*))\). Now, let us look at the point \(P'=\frac{I+P^*}{2}=(a', b')\). \(P'\) is within the polygon confined by the bottom and upper sorted paths (by convexity) and is also left to the valley. Also, \(a' > a^*\) and \(b' \ge b^*\) and as before, \(\varDelta _1(a', b') > \varDelta _2(a', b')\) and \(WOFP(a', b') = 1-\varPhi (\varDelta _2(a', b'))\). Moreover, \(\varDelta _2\) is monotonically increasing in a and in b (i.e., \(\frac{\partial \varDelta _2}{\partial a}(a,b) > 0\) and \(\frac{\partial \varDelta _2}{\partial b}(a,b) > 0\)), so \(\varDelta _2(a', b') > \varDelta _2(a^*, b^*)\), and therefore \(WOFP(a', b') < WOFP(a^*, b^*)\), in contradiction to the optimality assumption of the point \(P^*\). Therefore, we must conclude that \(P^*=I\).
C Proving SP-MOP Falls into Our Framework
Recall that \(OFP=1-\prod _{j=1}^k (1-OFP_j)\) where \(OFP_j=1-\varPhi (\varDelta _j)\). With two bins OFP is a function from \([0, 1]^2\) to \({\mathbf {R}}\) and \(OFP(a,b)=1-\varPhi (\varDelta _1)\varPhi (\varDelta _2)\) where the first bin has mean \(a\mu \) and variance bV, the second bin has mean \((1-a)\mu \) and variance \((1-b)V\) and \(\sigma _j,\varDelta _j\) were previously defined.
Lemma 6
OFP respects the symmetry and uni-modality properties.
Proof
-
Symmetry: The same proof as in Appendix A shows \(OFP(a,b)=OFP(1-a-\frac{c_2-c_1}{\mu }, 1-b)\).
-
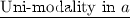 : Fix b. \(\frac{\partial ^2 OFP}{\partial ^2 a} = \mu ^2 [ \frac{\varDelta _1}{\sigma _1^2} \phi (\varDelta _1) \varPhi (\varDelta _2) + \frac{\varDelta _2}{\sigma _2^2} \phi (\varDelta _2) \varPhi (\varDelta _1) + \frac{2}{\sigma _1 \sigma _2} \phi (\varDelta _1)\phi (\varDelta _2)]\). In particular \(\frac{\partial ^2 OFP}{\partial ^2 a} >0\) and for every fixed b, OFP(a, b) is convex over \(a \in [0..1]\) and has a unique minimum \(a=m(b)\).
: Fix b. \(\frac{\partial ^2 OFP}{\partial ^2 a} = \mu ^2 [ \frac{\varDelta _1}{\sigma _1^2} \phi (\varDelta _1) \varPhi (\varDelta _2) + \frac{\varDelta _2}{\sigma _2^2} \phi (\varDelta _2) \varPhi (\varDelta _1) + \frac{2}{\sigma _1 \sigma _2} \phi (\varDelta _1)\phi (\varDelta _2)]\). In particular \(\frac{\partial ^2 OFP}{\partial ^2 a} >0\) and for every fixed b, OFP(a, b) is convex over \(a \in [0..1]\) and has a unique minimum \(a=m(b)\).
Proving there exists a unique maximum over the valley is more challenging. We wish to find all extremum points of the cost function D (OFP in our case) over the valley \({\left\{ (m(b),b)\right\} }\). Define \(V(a,b)=a-m(b)\). Then we wish to maximize D(a, b) subject to \(V(a,b)=0\). Before, we computed the restriction D(b) of the cost function over the valley and found its extremum points. However, here we do not know how to explicitly find D(b). Instead, we use Lagrange multipliers that allow working with the implicit form \(V(a,b)=0\) without explicitly finding D(b). We prove a general result:
Lemma 7
If a cost function D is differentiable twice over \([0, 1] \times [0, 1]\), then any extremum point Q of D over the valley must have zero gradient at Q, i.e., \(\nabla (D)(Q)=0\).
Proof
Using Lagrange multipliers we find that at any extremum point Q of D over the valley,
For some real value \(\lambda \). However,
because Q is on the valley and \(\frac{\partial D}{\partial a}(Q)=0\). As \(V(a,b)=a-m(b)\), \(\frac{\partial V}{\partial a}(Q)=1\). We conclude that \(\lambda =0\). This implies that \(\frac{\partial D}{\partial b}(Q)=0\). Hence, \(\nabla (D)(Q)=0\).
Lemma 8
OFP respects the central saddle point property.
Proof
Let \(Q=(a,b)\) be an extremum point of OFP over the valley. We look at the range \(b \in [0..\frac{1}{2})\), \(b \ge \frac{1}{2}\) is obtained by the symmetry. Then, by Lemma 7:
Dividing the two equations we get
Plugging the partial derivatives of \(\varDelta _i\) by a and b, we get the equation
As \(b \le \frac{1}{2}\), \(b < 1-b\) and we conclude that at Q \(\varDelta _1 < \varDelta _2\). However, using the log-concavity of the normal c.d.f function \(\varPhi \) we prove that:
Lemma 9
\(\frac{\partial OFP}{\partial a}=0\) at a point \(Q=(a,b)\) with \(b \le \frac{1}{2}\) implies \(\varDelta _1 \ge \varDelta _2\).
Proof
The condition \(\frac{\partial OFP}{\partial a}=0\) is equivalent to
As \(b < \frac{1}{2}\), \(b < 1-b\) and \(\sigma _1 < \sigma _2\). Hence,
Denote \(h(\varDelta )=\frac{\phi (\varDelta )}{\varPhi (\varDelta )}\). We will prove that h is monotone decreasing, and this implies that \(\varDelta _1 > \varDelta _2\).
To see that h is monotone decreasing define \(H(\varDelta )=\ln (\varPhi (\varDelta ))\). Then \(h=H'\). Therefore, \(h'=H''\). However, \(\varPhi \) is log-concave, hence \(H'' <0\). We conclude that \(h' < 0\) and h is monotone decreasing.
Together, this implies that the only extremum point of OFP over the valley is at \(b=\frac{1}{2}\). However, at \(b=0\), the best is to fill the largest bin to full capacity with variance 0, and thus, \(OFP(m(0),0)=1-\varPhi (\varDelta )\) where \(\varDelta =\frac{c-\mu }{\sigma }\). On the other hand, at \(b=\frac{1}{2}\), \(OFP(a=m(\frac{1}{2}),\frac{1}{2})= 1-\varPhi (\frac{c_1-a \mu }{\sqrt{\frac{1}{2}}\sigma })\varPhi (\frac{c_2-(1-a)\mu }{\sqrt{\frac{1}{2}}\sigma })\). As \((c_1-a \mu )+(c_2-(1-a) \mu )=c-\mu \), either \(c_1-a \mu \) or \(c_2-(1-a) \mu \) is at most \(\frac{c-\mu }{2}\) and therefore \(\varPhi (\sqrt{2} \frac{c_1-a \mu }{\sigma })\varPhi (\sqrt{2}\frac{c_2-(1-a)\mu }{\sigma }) \le \varPhi (\sqrt{2} \frac{c-\mu }{2\sigma })=\varPhi (\frac{c-\mu }{\sqrt{2} \sigma }) \le \varPhi (\frac{c-\mu }{\sigma })\). We conclude that \(OFP(a,\frac{1}{2}) \ge OFP(m(0),0)\) and there is a unique maximum point on the valley and it is obtained at \(b=\frac{1}{2}\).
D Error Induced by the Reduction to the Normal Distribution
The error in our algorithm stems from two different parts:
-
The error induced by the reduction to the normal case, and
-
The error the algorithm has on the normal distribution, mainly induced because the algorithm outputs an integral solution rather than the optimal fractional solution.
We analyze separately each kind of error and in this section we analyze the error induced by the reduction to the normal case. For SP-MED we gave a complete analysis of the error in Proposition 1. The analogous (and simpler) Proposition for SP-MWOP is:
Proposition 3
(SP-MWOP) . Given n independent random variables \(X=(X^{(1)},\ldots ,X^{(n)})\) with mean \(\mu ^{(i)}\), variance \(V^{(i)}={\mathbb {E}}(|X^{(i)}-\mu ^{(i)}|^2)\) and \(\rho ^{(i)}={\mathbb {E}}(|X^{(i)}-\mu ^{(i)}|^3)\) and a partition \(S={\left\{ S_1,\ldots ,S_k\right\} }\),
where \(C_0\) is the constant defined in Theorem 5,
and \(\psi _0^{max}(S) = \max _{j=1}^k \psi _0^j(S_j)\).
Proof
Let \(X_j = \sum _{i \in S_j} X^{(i)}\), \(N_j = N(\sum _{i \in S_j} \mu ^{(i)}, \sum _{i \in S_j} V^{(i)})\) and \(F_{X_j},F_{N_j}\) be their cumulative distribution functions. Then, for every j,
where the inequality is by Theorem 5. Let \(j'\) be the bin with maximum overflow probability under X, and \(j''\) be the bin with maximum overflow probability under N. Clearly,
Therefore,
and hence,
A similar argument works for SP-MOP using
and,
E Error Induced by Outputting an Integral Solution
Here we need to show that rounding the fractional solution to integral in the Normal case does not induce much error. For that we need to assume that the system has some spare capacity and that no input service is too dominant. We define two parameters:
-
Spare capacity: We define a new system constant, relative spare capacity, denoted by \(\alpha \) where
$$\begin{aligned} \alpha= & {} \frac{c -\mu }{\mu }, \end{aligned}$$i.e., it expresses the spare capacity as a fraction of the total mean. We assume that the system has some constant (possibly small) relative spare capacity.
-
No dominant service: As before, we represent service i with the point \(P^{(i)}=(a^{(i)},b^{(i)})\) and \(P^{(1)}+P^{(2)}+\ldots +P^{(n)}=(1,1)\). Thus, \(\sum _i |P^{(i)}| \ge |(1,1)| = \sqrt{2}\) (by the triangle inequality) and \(\sum _i |P^{(i)}| \le 2\) (because the length of the longest increasing path from (0, 0) to (1, 1), is obtained by the path going from (0, 0) to (1, 0) and then to (1, 1)). Hence, the average length of an input point \(P^{(i)}\) is somewhere between \(\frac{\sqrt{2}}{n}\) and \(\frac{2}{n}\). Our assumption states that no element takes more than L times its “fair” share, i.e., that for every i, \(|P^{(i)}| \le \frac{L}{n}\).
Also, we only consider solutions where each bin is allocated services with total mean not exceeding its capacity. Equivalently, we only consider solutions where \(\varDelta _j \ge 0\) for every \(1 \le j \le k\). We will later see that under these conditions the sorting algorithm solves all three cost functions with a small error going fast to zero with n. We prove:
Theorem 6
Let \(OPT_f\) be the fractional optimal solution. If D is differentiable, the difference between the cost on the integral point found by the sorting algorithm and the cost on the optimal integral (or fractional) point is at most \(\min {\left\{ |\nabla D(\xi _1)| , |\nabla D(\xi _2)|\right\} } \frac{L}{n}\), where \(\xi _1 \in [O_1,OPT_f]\), \(\xi _2 \in [OPT_f,O_2]\) and \(O_1\) and \(O_2\) are the two points on the bottom sorted path between which \(OPT_f\) lies.
Proof
Suppose we run the sorting algorithm on some input. Let \(OPT_{int}\) be the integral optimal solution, \(OPT_f\) the fractional optimal solution and \(OPT_{sort}\) the integral point the sorting algorithm finds on the bottom sorted path. We wish to bound \(D(OPT_{sort})-D(OPT_{int})\) and clearly it is at most \(D(OPT_{sort})-D(OPT_f)\). We now look at the two points \(O_1\) and \(O_2\) on the bottom sorted path between which \(OPT_f\) lies (and notice that as far as we know it is possible that \(OPT_{sort}\) is none of these points). Since \(D(OPT_f) \le D(OPT_{sort}) \le D(O_1)\) and \(D(OPT_f) \le D(OPT_{sort}) \le D(O_2)\) the error the sorting algorithm makes is at most
We now apply the mean value theorem and use our assumption that for every i, \(|P^{(i)}| \le \frac{L}{n}\).
We remark that in fact the proof shows something stronger: the cost of any (not necessarily optimal) fractional solution on the bottom sorted path, is close to the cost of the integral point to the left or to the right of it on the bottom sorted path. We now specialize Theorem 6 for SP-MED and SP-MWOP.
1.1 E.1 SP-MED
Lemma 10
The difference between the expected deviation in the integral point found by the sorting algorithm and the optimal integral (or fractional) point for SP-MED is at most \(\frac{1}{\sqrt{2 \pi e}} \cdot \frac{1}{\alpha } \cdot \frac{L}{n} \cdot \mu \). In particular, when \(L={\tiny {_o}}(n)\) and \(\alpha \) is a constant, the error is \({\tiny {_o}}(\mu )\).
Proof
We know from Theorem 6 that the difference is at most
where \(\xi _1 \in [O_1,OPT_f]\), \(\xi _2 \in [OPT_f,O_2]\) and \(O_1\) and \(O_2\) are the two points on the bottom sorted path between which \(OPT_f\) lies. Plugging the partial derivatives, we see that
Moreover, \(\frac{\sigma }{2 \sqrt{1-b}}~ \phi (\varDelta _2)=\frac{\sigma }{2 \sqrt{1-b}}~ \frac{1}{\varDelta _2}~ \varDelta _2 \phi (\varDelta _2)\) and a simple calculation shows that the function \(\varDelta \phi (\varDelta )\) maximizes at \(\varDelta =1\) with value at most \(\frac{1}{\sqrt{2 \pi e}}\). By our assumption that \(\varDelta _j \ge 0\) for every j, we get that
Applying the same argument on \(O_2\) shows the error can also be bounded by \(\frac{V}{2\sqrt{2 \pi e}} ~ \frac{1}{c_1 - a\mu }\).
However, \((c_1 - a\mu ) + (c_2 - (1-a)\mu ) = c - \mu \) which is the total spare capacity, and at least one of the bins takes spare capacity that is at least half of that, namely \(\frac{c-\mu }{2}\). Since the error is bounded by either term, we can choose the one where the spare capacity is at least \(\frac{c-\mu }{2}\) and we therefore see that the error is at most \(\frac{V}{2\sqrt{2 \pi e}} ~ \frac{2}{c-\mu }\). Since we assume \(c-\mu \ge \alpha \mu \) for some constant \(\alpha >0\), the error is at most \(\frac{V}{\sqrt{2 \pi e}} ~ \frac{1}{\alpha \mu }\). As we assume \(V \le \mu ^2\), \(\frac{V}{\mu } \le \mu \) which completes the proof.
This shows the approximation factor goes to 1 and linearly (in the number of services) fast. Thus, from a practical point of view the theorem is very satisfying.
1.2 E.2 SP-MWOP
Lemma 11
The difference between minimal worst overflow probability in the integral point found by the sorting algorithm and the optimal integral (or fractional) point for SP-MWOP is at most \(O(\frac{L}{\alpha n})\). In particular, when \(L={\tiny {_o}}(n)\) and \(\alpha \) is a constant, the difference is \({\tiny {_o}}(1)\).
Proof
We know from Theorem 6 that the difference is at most
where \(\xi _1=(a_1,b_1) \in [O_1,OPT_f]\), \(\xi _2=(a_2,b_2) \in [OPT_f,O_2]\) and \(O_1\) and \(O_2\) are the two points on the bottom sorted path between which \(OPT_f\) lies, and notice that even though WOFP is not differentiable when \(\varDelta _1=\varDelta _2\), it is differentiable everywhere else. We plug the partial derivatives and also replace \(\frac{\phi (\varDelta _2)}{\sigma _2}\) with \(\frac{\varDelta _2 \phi (\varDelta _2)}{c_2-(1-a)\mu }\) and similarly for the other term. We get:
The term \(\varDelta \phi (\varDelta )\) maximizes at \(\varDelta =1\) with value at most \(\frac{1}{\sqrt{2 \pi e}}\). Also, \((c_1 - a_2\mu ) + (c_2 - (1-a_1)\mu ) = c - \mu -(a_2-a_1)\mu \ge c-\mu \frac{L}{n} \ge \frac{\alpha }{2}\mu \), where \(\alpha \) is the total space capacity, and a constant by our assumption. Hence, at least one of the terms \(\frac{\mu }{c_2-(1-a_1)\mu }\),\(\frac{\mu }{c_1-a_2\mu }\) is at most \(\frac{4}{\alpha }\). Also, for that term, the spare capacity is maximal, and therefore it takes at least half of the variance. Altogether, the difference is at most \(O(\frac{L}{\alpha n})\) which completes the proof.
F Unbalancing Bin Capacities Is Always Better
Suppose we are given a capacity budget c and we have the freedom to choose capacities \(c_1,c_2\) that sum up to c for two bins. Which choice is the best? Offhand, it is possible that for each input there is a different choice of \(c_1\) and \(c_2\) that minimizes the cost. In contrast, we show that for the three cost functions we consider in this paper, the minimum cost always decreases as the difference \(c_2 - c_1\) increases.
Lemma 12
Given a capacity budget c and either SP-MED, SP-MWOP or SP-MOP cost function, the minimum cost decreases as \(c_2 - c_1\) increases. In particular the best choice is having a single bin with capacity c and the worst choice is splitting the capacities evenly between the two bins.
Proof
Recall that \(\varDelta _1(a,b) = \frac{c_1 - a\mu }{\sigma \sqrt{b}}\) and \(\varDelta _2(a,b) = \frac{c_2 - (1-a)\mu }{\sigma \sqrt{1-b}}\). Therefore, if we reduce \(c_1\) by \(\tilde{c}\) and increase \(c_2\) by \(\tilde{c}\), we get
Similarly, \(\tilde{\varDelta }_2(a,b) = \varDelta _2(a+\frac{\tilde{c}}{\mu },b)\).
Let \(Dev_{c_1,c_2}(a,b)\) denote the expected deviation with bin capacities \(c_1,c_2\), \(WOFP_{c_1,c_2}(a,b)\) denote the worst overflow probability with bin capacities \(c_1,c_2\) and \(OFP_{c_1,c_2}(a,b)\) denote the overflow probability with bin capacities \(c_1,c_2\). As
i.e., each cost graph is shifted left by \(\frac{\tilde{c}}{\mu }\).
Notice that the bottom sorted path does not depend on the bin capacities and is the same for every value of \(c_1\) and \(c_2\) we choose. Let (a, b) be the optimal fractional solution for bin capacities \(c_1,c_2\). We know that (a, b) is on the bottom sorted path. Let \(\tilde{a}=a-\frac{\tilde{c}}{\mu }\). We saw that the cost function \(D \in {\left\{ Dev, WOFP, OFP\right\} }\) satisfies \(D_{c_1-\tilde{c}, c_2+\tilde{c}}(\tilde{a},b)=D_{c_1,c_2}(a,b)\). The point \((\tilde{a},b)\) lies to the left of the bottom sorted path and therefore above it. As the optimal solution for bin capacities \(c_1-\tilde{c}, c_2+\tilde{c}\) is also on the bottom sorted path and is strictly better than any internal point, we conclude that the expected deviation for bin capacities \(c_1-\tilde{c}, c_2+\tilde{c}\) is strictly smaller than the expected deviation for bin capacities \(c_1,c_2\).
An immediate corollary is the trivial fact that putting all the capacity budget in one bin is best. Obviously, this is not always possible nor desirable, but if there is tolerance in each bin capacity, we recommend minimizing the number of bins.
Our simulation results, both on synthetic normally distributed data and on real independent data, also clearly show this phenomenon. Figure 9 shows the cost of the sorting algorithm for the three cost functions as a function of \(\frac{c}{\mu }\), for \(\frac{c_1}{c} \in {\left\{ 0.1, 0.2, 0.3, 0.4, 0.5\right\} }\) and synthetic normally distributed data. We can clearly see that the cost decreases as \(\frac{c_1}{c}\) decreases in both data sets. The results for real independent data are very similar and we omit them due to lack of space.
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG
About this paper
Cite this paper
Shabtai, G., Raz, D., Shavitt, Y. (2018). Risk Aware Stochastic Placement of Cloud Services: The Case of Two Data Centers. In: Alistarh, D., Delis, A., Pallis, G. (eds) Algorithmic Aspects of Cloud Computing. ALGOCLOUD 2017. Lecture Notes in Computer Science(), vol 10739. Springer, Cham. https://doi.org/10.1007/978-3-319-74875-7_5
Download citation
DOI: https://doi.org/10.1007/978-3-319-74875-7_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-74874-0
Online ISBN: 978-3-319-74875-7
eBook Packages: Computer ScienceComputer Science (R0)


 : Calculations show that
: Calculations show that 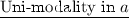 : Fix b. Denote
: Fix b. Denote 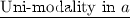 : Fix b.
: Fix b. 