Path-Gradient – A Theory of Computing Full Intensity-Transition Between Two Points

Abstract

A major challenge for path-based segmentation methods is to select the optimum scale capturing the total intensity variation across object interfaces without losing small-scale structures. Minimum barrier distance (MBD) attempts to alleviate this issue using a unique path-cost function that computes the maximum intensity variation on the path. Two major concerns of MBD are related to high computational complexity and convoluted trajectory of the optimum path between two points on either side of an object interface limiting benefits of MBD. Here, we introduce the notion of path-gradient (PG) that exhibits similar behavior as MBD for object segmentation with significantly reduced computation. The formulation of PG allows the addition of a regularization term in path cost, which improves segmentation still at considerably reduced computation cost than regular MBD. Efficient algorithms for computing PG and regularized PG are presented and their segmentation performances are compared with that of MBD.

1 Introduction

Large data volumes acquired daily in many imaging application areas including medical imaging, remote sensing, industrial applications, character recognition, etc. have created the need for automated and quantitative assessment of targeted knowledge. It is imperative to define target objects in an image before extracting quantitative or descriptive information. This process of locating and delineating a target object in an image is referred to as segmentation, which has a rich history, and is a fundamental task in many computerized imaging applications [1]. There are three major segmentation paradigms based on: shape [2], boundary [3], and region-continuity [4]. Shape-based approaches [2] take advantage of the inherent correlation among structures in a shape to formulate an analytic model representing the mean and variance of shape instances in a family. Boundary-based segmentation methods locate and delineate an object boundary under a pre-defined optimization criterion. Region-based approaches attempt to grow object regions in an image from a set of seeds under a pre-defined criterion of region continuity [5, 6].

Continuity of an object in a region-based segmentation method is imposed using prior definitions of path-strength or path-cost [7]. Path-strength and path-cost are formulated using pre-defined local affinity or step-cost functions, respectively. Intensity gradient makes major contributions in the computation of such local functions. A major challenge in formulating such functions is the dichotomy between capturing the total intensity variation across object interfaces and the preservation of small-scale structures. It defines a tradeoff for selection of the optimum scale satisfying the fine balance between the object scale and the gradient (transition) width, and a fixed choice of scale is bound to fail due to variability among images and even at different locations within an image. Recently, there have been attempts, e.g., the minimum barrier distance (MBD) [8, 9], to define the path-cost in a manner that computes the maximum intensity variation along the entire path without depending upon accurate gradient computation within the local function. Two major concerns with MBD are related to high computational complexity and convoluted trajectory of the optimum path between two points on either side of an object interface limiting benefits of MBD.

In this paper, we introduce a new formulation of path-cost that captures the entire geodesic gradient over the path instead of total intensity variation used in MBD and demonstrate its applications in image segmentation. Specifically, we introduce the formulation of path-gradient (PG) based region growing and present its theoretical properties and an efficient algorithm for its computation. The cost-function of PG is modified to add regularization term that stops convoluted trajectories of an optimum path while allowing an optimum path to follow the continuity within an object structure. An efficient algorithm for computation of regularized path-gradient (RPG) is presented. Finally, the computational complexity and segmentation results of MBD, PG, and RPG are presented and discussed.

2 Theory and Algorithms

2.1 Definition of Path-Gradient and Regularized Path-Gradient

In this section, we introduce the notion of “path-gradient”. An $n$-dimensional rectilinear grid is represented by ${\mathbb{Z}}_{ + }^{n}$, where ${\mathbb{Z}}_{ + }$ is the set of positive integers. An element of ${\mathbb{Z}}_{ + }^{n}$ will be abbreviated as a spatial element or spel, e.g., a pixel for $n\, = \,2$ and a voxel for $n = 3$. In a digital space, adjacencies are used to define path-continuity. In two-dimension (2-D), standard 4- and 8-adjacencies are used, while 6-, 18-, or 26-adjacencies are used in 3-D [7]. We will use $\alpha$ to denote an adjacency relation. The pair $\left( {{\mathbb{Z}}_{ + }^{n} ,\;\alpha } \right)$ denotes a digital space. A digital image on $\left( {{\mathbb{Z}}_{ + }^{n} ,\;\alpha } \right)$ is defined by a triple $\left( {{\mathbb{Z}}_{ + }^{n} ,\;\alpha ,\;f} \right)$, where $f:{\mathbb{Z}}_{ + }^{n} \to {\mathbb{Z}}$| ${\mathbb{Z}}$ is the set of all integers, is the image intensity function; note that some imaging techniques, e.g., CT imaging, generate digital images with negative intensity values. A digital path, or simply a path $\pi_{p,q}$ is a sequence of spels $\left\langle {p_{0} \, = \,p, p_{1} , \cdots ,p_{l - 1} \, = \,q} \right\rangle$, where every two successive spels are $\alpha$-adjacent. The gradient-strength of a path $\pi_{p,q}$ is defined as follows:

$$ \begin{array}{*{20}c} {\tau \left( {\pi_{p,q} } \right)\, = \,\mathop {\hbox{max} }\nolimits_{{r \in \pi_{p,q} }} \left| {f\left( p \right)\, - \,f\left( r \right)} \right|.} \\ \end{array} $$

(1)

Using the above formulation of gradient-strength of a path, the path-gradient or PG in a digital setup from $p$ to $q$, where $p,\;q \in {\mathbb{Z}}_{ + }^{n}$, is defined as follows:

$$ \begin{array}{*{20}c} {\Delta \left( {p,q} \right)\, = \,\mathop {\hbox{min} }\nolimits_{{\pi_{p,q} \, \in \,\Pi _{p,q} }} \tau \left( {\pi_{p,q} } \right). } \\ \end{array} $$

(2)

It is obvious from the above formulation that the PG function $\Delta$ fails to satisfy the symmetry property, i.e., $\Delta \left( {p,\;q} \right)\, \ne \,\Delta \left( {q,\;p} \right)$. On the other hand, it satisfies the triangular rule, i.e., $\forall p,\;q,\;r\, \in \,{\mathbb{Z}}_{ + }^{n}$,

$$ \begin{array}{*{20}c} {\Delta \left( {p,\;q} \right)\, \le \,\Delta \left( {p,\;r} \right)\, + \,\Delta \left( {r,\;q} \right). } \\ \end{array} $$

(3)

Here, it may be worthy to examine its relation to MBD [8, 9]. Both PG and MBD are formulated using intensity differences along paths. The major difference in their formulation is that, in MBD, the difference is computed between any two variable points on a path, while, for PG, the difference is computed from the starting point on a path, which is fixed and may be interpreted as the “seed” in imaging applications. This subtle change in the formulation of gradient-strength of a path significantly simplifies its computational algorithm allowing for the addition of a regularization term, which enhances its performance in image segmentation. The gradient-strength of a path for regularized path-gradient or RPG is defined as follows:

$$ \begin{array}{*{20}c} {\ddot{\tau }\left( {\pi_{p,q} } \right)\, = \,\left( {1 - K} \right)\mathop {\hbox{max} }\limits_{{r \in \pi_{p,q} }} \left| {f\left( p \right)\, - \,f\left( r \right)} \right|\, + \,KL\left( {\pi_{p,q} } \right), } \\ \end{array} $$

(4)

where, $K$ is the regularization constant, and $L$ is the path-length, i.e., the number of spels on the path $\pi_{p,q}$. Finally, the RPG is computed as follows:

$$ \begin{array}{*{20}c} {\ddot{\Delta }\left( {p,q} \right)\, = \,\mathop {\hbox{min} }\nolimits_{{\pi_{p,q} \in \varPi_{p,q} }} \ddot{\tau }\left( {\pi_{p,q} } \right). } \\ \end{array} $$

(5)

Like PG, RPG is not symmetric but satisfies the triangular rule.

2.2 Algorithms

In this section, we present efficient algorithms for computing PG and RPG using wave propagation with dynamic programming. It can be shown that an efficient wave propagation algorithm for accurate computation of a path-cost function requires the existence of a geodesic from any spel to another spel under the specific cost function. A path $\pi_{p,q}$ between two spels $p,q$ is a geodesic if for any $r$ on $\pi_{p,q}$, the sub-paths $\pi_{p,r}$ and $\pi_{r,q}$ on $\pi_{p,q}$ are minimum cost paths between $p,r$ and $r,q$, respectively. The existence of geodesic ensures that, during wave propagation, the function value at a spel can be determined from the function-value and additional information (if needed) at the specific neighbor preceding on the geodesic. It is interesting to note that the triangular property does not guarantee the validity of geodesic from one spel to another. For example, the minimum barrier distance (MBD) satisfies the triangular property, while it fails to guarantee the existence of a geodesic between every two spels. It can be shown that PG guarantees the existence of a geodesic from a spel to another. Note that, due to non-symmetry of the PG function, the geodesic from $p$ to $q$ may be different from that from $q$ to $p$. In the following, a wave-propagation algorithm is presented to compute PG from a seed spel $s$ to any spel in the image domain. Theorems 1 and 2 state that the algorithm terminates in a finite number of steps, and it accurately computes PG from $s$ at termination. In this paper, proofs of the theorems are omitted due to the space limitation.

Theorem 1.

For any digital image $\left( {{\mathbb{Z}}_{ + }^{n} ,\alpha ,f} \right)$ with a bounded image domain, for any seed spel $s$, Algorithm 1 for computing PG terminates in a finite number of iterations.

Theorem 2.

For any digital image $\left( {{\mathbb{Z}}_{ + }^{n} ,\alpha ,f} \right)$ with a bounded image domain, for any seed spel $s$, at the termination of Algorithm 1, the output function $f_{\text{PG}}$ accurately computes the PG value $\Delta (s, \cdot )$ at individual spels following Eq. (2).

The algorithm for RPG is relatively more complex than Algorithm 1 for computation of PG. The fundamental difficulty in computing RPG is that the existence of a geodesic from one spel to another is not guaranteed for RPG. To overcome this challenge, we develop a dynamic programming algorithm for RPG computation where the queue of spels is maintained in the ascending order of path length from the seed spel. It can be shown that the algorithm terminates in a finite number of steps, and the above subtle change allows accurate computation of RPG.

Theorem 3.

For any digital image $\left( {{\mathbb{Z}}_{ + }^{n} ,\alpha ,f} \right)$ with a bounded image domain, for any seed spel $s$, and the regularization constant $K \in \left[ {0,1} \right]$, Algorithm 2 for computing RPG terminates in a finite number of iteration.

Theorem 4.

For any digital image $\left( {{\mathbb{Z}}_{ + }^{n} ,\alpha ,f} \right)$ with a bounded image domain, for any seed spel $s$, at the termination of Algorithm 2, the output function $f_{\text{RPG}}$ accurately computes the RPG value $\ddot{\Delta }(s, \cdot )$ at individual spels following Eq. (5).

3 Experimental Results

We present preliminary experimental results to—(1) demonstrate fundamental differences and similarities between three path-cost based segmentation region-growing segmentation methods, namely MBD, PG, and RPG and (2) examine the effectiveness of RPG in segmenting tree-like objects and compare it with MBD and PG.

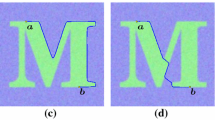
For the first experiment, an image (size: 640 × 360), shown in Fig. 1, was generated and downgraded with blur (7 × 7 window averaging), white Gaussian noise (contrast-to-noise ratio: 8), and background intensity inhomogeneity (100% of the object-background contrast uniformly distributed across image-width). Optimum paths using the three methods MBD, PG and RPG between several pairs of pixels were examined. Two sets of pixel-pairs were used to examine the optimum paths between two points across object-background interface and those connecting two distant pixels within the same objects. In the top row of Fig. 1, pixels pairs were selected across the object-background interface. Different pixel pairs were selected at regions with different inhomogeneity to examine their behavior under the combined field of a slow varying inhomogeneity and rapid intensity variation across object-background interface. In the bottom row of the figure, both pixels in a pair was chosen inside the object region, while separated by a long geodesic distance to examine whether the regularization terms influence the optimum path to move out and in of the object region. In the top row, MBD and PG generated convoluted trajectories of optimum paths for two pixels across the object-background interface artificially lowering the minimum barrier distance or path-gradient value between them. A small regularization term in RPG reduces the convolutedness of the optimum path while ensuring that the path remains confined inside the object for a pair of distant pixels within the same object.

Fig. 1.

Comparison of optimum cost-paths computed using different methods. Top row from left to right: optimum cost-paths using MBD, PG, and RPG generated between four different pairs of nearby pixel pairs one inside the object, while the other in the background (inter-object pixel pairs). See text for details.

To examine the effectiveness of RPG in segmenting tree-like objects, a silhouette image of a tree (size: 1770 × 2400) was downloaded from an internet site,¹ which was downgraded with blur (17 × 17 window averaging), white Gaussian noise (contrast-to-noise ratio: 8), and background intensity inhomogeneity (75% of the object-background contrast uniformly distributed across image-height). Individual methods were applied to the degraded test image using a single seed point and resultant distance transform maps were thresholded [10] to get binary segmentation results. The degraded test image and segmentation results using a single seed are presented in the top row of Fig. 2. It is noticeable from these segmentation results that MBD and PG produce similar segmentation results while RPG performs better than both methods in terms of the extents of tree branches. Segmentation results using the three methods on the same image with two seeds are presented in the bottom row of the figure. As observed from the segmentation results of the bottom row, the segmentation performances of MBD and PG are similar, while RPG significantly improves the segmentation. More interestingly, the improvement in the segmentation result using the second seed is greater for RPG as compared to that of MBD or PG. These experimental results confirm the advantages of the regularization term in the path cost function.

Fig. 2.

Comparison of segmentation results using different methods. Top row from left to right: An image of tree with the seed marked in magenta; segmentation results using MBD, PG, and RPG. Bottom row: Same as top row but using two seeds. Segmentation results using MBD and PG are visually similar, while the improvements using RPG are apparent.

To assess the computational performance of the three methods, the 2-D image of Fig. 2 was used, while a 3-D image (size: 256 × 256 × 256) was generated from the CT-based segmentation of pulmonary airway mask after degrading with blur (3 × 3 × 3 window averaging), white Gaussian noise (contrast-to-noise ratio: 8), and background intensity inhomogeneity (75% of the object-background contrast uniformly distributed in the axial direction). For the 2-D image, a single seed pixel was placed at the middle of the main tree-trunk, while a seed voxel was selected inside the trachea for the 3-D airway phantom image. Execution time was calculated as the mean over 100 executions of each method on a given image. The execution times for MBD, PG and RPG were 18.89 s, 1.03 s, and 3.54 s, respectively for the 2-D image and 43.15 s, 3.87 s, and 17.7 s, respectively for the 3-D image.

4 Conclusions

In this paper, we have introduced a new notion of PG as means to capture the full intensity transition between two points, which overcomes the fundamental challenge related to scale in region growing methods using conventional gradient computation. The theoretical properties of PG are discussed, and it is further extended to RPG by adding a regularization term in the path-cost function to stop convoluted trajectories of the optimum path between two points across object-interface, while allowing an optimum path to follow a curved path satisfying the continuity of an object region. Efficient algorithms for computation of both PG and RPG have been presented. Experimental results have demonstrated similarity in performance in MBD and PG in terms of consistency of behavior of optimum paths as well as segmentation of a tree-like object in the presence of image degradation, while PG is computed significantly more efficiently than MBD. Improvements in the consistency of optimum paths as well as segmentation results using RPG have been experimentally demonstrated. More elaborately, the regularization term in RPG added the ability to enforce a straightness on the convoluted trajectories of an optimum path while maintaining continuity within an object structure. Finally, it has been shown that, both in 2-D and 3-D, RPG requires more computation time than PG, while less than MBD.