Abstract
Subversion zero knowledge for non-interactive proof systems demands that zero knowledge (ZK) be maintained even when the common reference string (CRS) is chosen maliciously. SNARKs are proof systems with succinct proofs, which are at the core of the cryptocurrency Zcash, whose anonymity relies on ZK-SNARKs; they are also used for ZK contingent payments in Bitcoin.
We show that under a plausible hardness assumption, the most efficient SNARK schemes proposed in the literature, including the one underlying Zcash and contingent payments, satisfy subversion ZK or can be made to at very little cost. In particular, we prove subversion ZK of the original SNARKs by Gennaro et al. and the almost optimal construction by Groth; for the Pinocchio scheme implemented in libsnark we show that it suffices to add 4 group elements to the CRS. We also argue informally that Zcash is anonymous even if its parameters were set up maliciously.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
One of the primary motivations for succinct non-interactive arguments (SNARG) was verifiable computation. Consider a client that outsources resource-intensive computation to a powerful server, which attaches a proof to the result, so the client is convinced that it was computed correctly. For this to be meaningful, verification of such a proof must be considerably more efficient than performing the computation in the first place. SNARG systems provide such proofs and an impressive line of research has led to more and more efficient systems with proofs of size less than a kilobyte that can be verified in milliseconds. The reason why SNARGs are not used in outsourcing of computation is that computing a proof for complex computations is still not practical. (For example, a proof in Zcash, which is for a very simple statement, takes minutes to compute on a PC.)
Zero-knowledge (ZK) SNARGs are used when some inputs to the computation come from the prover (the server in our example), who wants to keep its inputs private. ZK systems guarantee that a proof does not reveal more about private inputs than what can be inferred from the result of the computation. If the proofs prove knowledge of the private inputs, they are called SNARKs. ZK-SNARKs are already deployed, for example in Zcash [Zca], which is a cryptocurrency like Bitcoin [Nak09], based on the Zerocash protocol [BCG+14a]. As opposed to Bitcoin, where all transactions are public, Zcash payments are fully anonymous and protect the users’ privacy. Zcash achieves this by using SNARK proofs that are zero-knowledge.
Zero-knowledge contingent payments use SNARKs for fair exchange of information against payments over the Bitcoin network, assuming that the information can be verified (in the sense that it can be formalized as the witness of an NP statement), e.g. solutions to a Sudoku puzzle. Bitcoin’s scripting language defines Pay-to-PubkeyHash transactions, which are bound to a hash value y and can be redeemed by exhibiting a preimage, i.e., some x s.t. \(H(x)=y\). In a contingent payment Alice, the seller, chooses a key k, encrypts the information she is offering as c under k and sends c together with \(y:=H(k)\) to Bob, the buyer. Bob makes a transaction to y. To redeem it, Alice must publish the preimage k, which then allows Bob to decrypt c and obtain the purchased information. To prevent Alice from cheating, she must prove that c encrypts the desired information under a preimage of y, for which she can use SNARKs. Zero-knowledge guarantees that no information is leaked before being paid.
The main drawback of SNARKs is that they require system parameters that must be generated in a trusted way. In particular, whoever knows the randomness used when setting them up can convince verifiers of false statements (violating soundness of the system), which for Zerocash translates to counterfeiting money. The authors of Zerocash write: “[D]ue to the zk-SNARK, our construction requires a one-time trusted setup of public parameters. The trust affects soundness of the proofs, though anonymity continues to hold even if the setup is corrupted by a malicious party.” [BCG+14a]. The last statement is then not elaborated any further.
For ZK contingent payments (ZKCP) the parameters are generated by the buyer, which prevents the seller from cheating. However, Campanelli et al. [CGGN17] recently showed that the buyer can cheat in the reference implementation of ZKCP, which allows for selling the solution to a Sudoku puzzle. By maliciously setting up the parameters, the buyer can learn information about the solution from the SNARK proof sent by the seller before paying. This shows that not only soundness but also zero knowledge of SNARKs breaks down in the face of parameter subversion.
In this work we look at whether zero knowledge can be salvaged when the parameters are set up in a malicious way and analyze the most efficient SNARK constructions in the literature, including the one [BCTV14] that underlies Zcash and ZKCP. We base our analyses on the theoretical framework introduced by Bellare et al. [BFS16], who formalized the notion of subversion zero knowledge.
 A zero-knowledge proof [GMR89] is a protocol between a prover and a verifier that allows the former to convince the latter of the validity of a statement without revealing anything else. The three main properties of a ZK proof system are that an honestly computed proof for a valid statement should convince a verifier (completeness); but there is no way that a malicious prover can convince a verifier of false statements (soundness); and nothing but the truth of the statement is revealed (zero knowledge).
A zero-knowledge proof [GMR89] is a protocol between a prover and a verifier that allows the former to convince the latter of the validity of a statement without revealing anything else. The three main properties of a ZK proof system are that an honestly computed proof for a valid statement should convince a verifier (completeness); but there is no way that a malicious prover can convince a verifier of false statements (soundness); and nothing but the truth of the statement is revealed (zero knowledge).
In non-interactive ZK proofs [BFM88], the prover only sends one message (the proof) to the verifier. NIZK systems rely on a common reference string (CRS) to which both prover and verifier have access and which must be set up in a trusted way (for SNARKs the CRS is often called parameters). Without such a CRS, NIZK systems are not possible [GO94].
NIZK proof systems exist for every \(\text {NP}\) language [BFM88, BDMP91]. A language L is an \(\text {NP}\) language if it can be defined via a polynomial-time computable relation \({R}\): a statement x is in L iff there exists a witness w of length polynomial in the length of x such that \({R}(x,w)=\mathsf {true}\). In verifiable computation a server’s private input would be a witness. For ZK contingent payments, the ciphertext c, the hash value y and the Sudoku challenge are the statement. The witness is the plaintext of c (the Sudoku solution) and the encryption key k.
Zero knowledge is formalized via a simulator that generates a CRS in which it can embed a trapdoor. The trapdoor must allow the simulator to produce proofs without a witness for the proven statement. ZK requires that there exists a simulator whose simulated CRSs and proofs are computationally indistinguishable from real ones. If both types are distributed equivalently then we have perfect ZK. Groth et al. [GOS06b, GOS06a, Gro06, GS08] constructed NIZK proof systems based on groups equipped with a pairing, i.e., an efficiently computable bilinear map. They gave the first perfect ZK system for all \(\text {NP}\) languages and very efficient schemes for specific languages based on standard cryptographic hardness assumptions.
 Another line of work considered the size of proofs from a theoretical point of view, leading to schemes with a proof size that is sublinear in the length of the proved statement [Mic00]. SNARGs are succinct non-interactive arguments, where succinct means that the proof length only depends (polynomially) on the security parameter. They are arguments (as opposed to proofs) because soundness only holds against efficient provers. This is the best achievable notion, since SNARGs are perfect-ZK, which implies that every CRS has a trapdoor. SNARKs are succinct non-interactive arguments of knowledge, for which a valid proofs implies that the prover knows the witness.
Another line of work considered the size of proofs from a theoretical point of view, leading to schemes with a proof size that is sublinear in the length of the proved statement [Mic00]. SNARGs are succinct non-interactive arguments, where succinct means that the proof length only depends (polynomially) on the security parameter. They are arguments (as opposed to proofs) because soundness only holds against efficient provers. This is the best achievable notion, since SNARGs are perfect-ZK, which implies that every CRS has a trapdoor. SNARKs are succinct non-interactive arguments of knowledge, for which a valid proofs implies that the prover knows the witness.
The first NIZK system with proofs whose size is independent of the proven statement (and its witness) was given by Groth [Gro10] using bilinear groups; it was later improved by Lipmaa [Lip12]. Gennaro et al. [GGPR13] introduced the notion of a quadratic span program (QSP), showed how to efficiently convert any boolean circuit into a QSP and then constructed a SNARK system for QSPs whose proofs consist of 8 elements of a bilinear group. They gave another construction based on quadratic arithmetic programs (QAP), which represent arithmetic circuits, whose inputs are elements from a finite field \({{\mathbb F}}\) and whose gates add or multiply \({{\mathbb F}}\) elements. QAPs are preferred in practice due to their greater efficiency. As circuit satisfiability is NP-complete, SNARKs exist for all NP languages.
Parno et al. [PHGR13] improved on [GGPR13], making the conversion from circuits to QAPs more efficient and reducing the proof size. They implemented their scheme and named it “Pinocchio”. Ben-Sasson et al. [BCG+13, BCTV14] improve the conversion of actual program code to QAPs, reduce the size of SNARK parameters and implement their results as libsnark [BCG+14b]. The size of SNARK proofs for boolean circuits was then further reduced by Danezis et al. [DFGK14], who modified QSP to square span programs and built a system for them whose proofs consist of only 4 group elements.
Recently, Groth [Gro16] presented the most efficient SNARK construction to date, which is for arithmetic circuits and whose proofs consist of only 3 group elements (and require 3 pairings to verify). All previous bilinear-group-based SNARKs are proven under strong cryptographic assumptions (knowledge assumptions), for which there is evidence that they might be unavoidable [GW11, BCCT12]. Starting from Bitansky et al.’s [BCI+13] linear interactive proof framework, Groth [Gro16] achieves his result by proving security directly in the generic-group model [Sho97] (which implies all previously considered assumptions). He also shows that SNARKs over asymmetric bilinear groups must contain elements from both source groups, meaning that the proof size of his construction is only one element short of the optimal size. Recently, Fuchsbauer et al. [FKL17] proved Groth’s scheme secure under a “q-type” variant of the discrete log assumption in the algebraic group model, in which adversaries are restricted adversaries can only output group elements if they were obtained by applying the group operation to previously received group elements.
 The Snowden revelations documented the NSA’s efforts to subvert standards, for which an illustrative example is the NSA-designed and ISO-standardized Dual EC random number generator. Its parameters include two elliptic-curve points, whose respective discrete logarithms can act as a backdoor that can be exploited to break TLS [CNE+14]. NIZK systems are particularly prone to parameter subversion, since their CRS must be subvertible by design: zero knowledge requires that an honest CRS is indistinguishable from a backdoored CRS, where the backdoor is the trapdoor used to simulate proofs. For SNARKs the parameters always contain a backdoor and anyone knowing it can simulate proofs for false statements, which means breaking soundness.
The Snowden revelations documented the NSA’s efforts to subvert standards, for which an illustrative example is the NSA-designed and ISO-standardized Dual EC random number generator. Its parameters include two elliptic-curve points, whose respective discrete logarithms can act as a backdoor that can be exploited to break TLS [CNE+14]. NIZK systems are particularly prone to parameter subversion, since their CRS must be subvertible by design: zero knowledge requires that an honest CRS is indistinguishable from a backdoored CRS, where the backdoor is the trapdoor used to simulate proofs. For SNARKs the parameters always contain a backdoor and anyone knowing it can simulate proofs for false statements, which means breaking soundness.
Motivated by this, Bellare et al. [BFS16] ask what security can be maintained for NIZKs when its trusted parameters are subverted. They formalize different notions of resistance to CRS subversion and investigate their achievability. They define subversion soundness (S-SND), meaning that no adversary can generate a (malicious) CRS together with a valid proof \(\pi \) for a false statement x.
They also give a subversion-resistant analogue for zero knowledge. Recall that ZK assumes that there exists a CRS simulator  , which returns a simulated CRS
, which returns a simulated CRS  and an associated simulation trapdoor
and an associated simulation trapdoor  , and a proof simulator \(\mathsf {Sim}.\mathsf {pf}\) that outputs proofs on input a valid instance x and
, and a proof simulator \(\mathsf {Sim}.\mathsf {pf}\) that outputs proofs on input a valid instance x and  , such that no efficient adversary can distinguish the following: either being given
, such that no efficient adversary can distinguish the following: either being given  and an oracle implementing \(\mathsf {Sim}.\mathsf {pf}\), or an honest
and an oracle implementing \(\mathsf {Sim}.\mathsf {pf}\), or an honest  and an oracle returning honestly computed proofs. Subversion ZK (S-ZK) requires that for any adversary \(\mathsf {X}\) creating a malicious CRS
and an oracle returning honestly computed proofs. Subversion ZK (S-ZK) requires that for any adversary \(\mathsf {X}\) creating a malicious CRS  in any way it likes using randomness (coins) r, there exists a simulator \(\mathsf{Sim}_\mathsf{X}.\mathsf{crs}\) returning a simulated CRS
in any way it likes using randomness (coins) r, there exists a simulator \(\mathsf{Sim}_\mathsf{X}.\mathsf{crs}\) returning a simulated CRS  with trapdoor
with trapdoor  together with simulated coins \(r'\), as well as a proof simulator \(\mathsf{Sim}_\mathsf{X}.\mathsf{pf}\), such that no adversary can distinguish the following: being given
together with simulated coins \(r'\), as well as a proof simulator \(\mathsf{Sim}_\mathsf{X}.\mathsf{pf}\), such that no adversary can distinguish the following: being given  and \(r'\) and a \(\mathsf{Sim}_\mathsf{X}.\mathsf {pf}\) oracle, or a
and \(r'\) and a \(\mathsf{Sim}_\mathsf{X}.\mathsf {pf}\) oracle, or a  output by \(\mathsf {X}\), together with the used coins r and an honest proof oracle. The authors also define a subversion-resistant notion (S-WI) of witness-indistinguishability [FLS90] (see Sects. 2.3 and 2.4).
output by \(\mathsf {X}\), together with the used coins r and an honest proof oracle. The authors also define a subversion-resistant notion (S-WI) of witness-indistinguishability [FLS90] (see Sects. 2.3 and 2.4).
Following [GO94], Bellare et al. [BFS16] first show that S-SND cannot be achieved together with (standard) ZK for non-trivial languages (for trivial ones the verifier needs no proof to check validity of statements). This is because ZK allows breaking soundness by subverting the CRS. They then show that S-SND can be achieved together with S-WI. Their main result is a construction that achieves both S-ZK (and thus S-WI) and SND.
 To achieve S-ZK, a simulator must be able to simulate proofs under a CRS output by a subvertor, so it cannot simply embed a trapdoor as in standard ZK. Bellare et al. [BFS16] base S-ZK on a knowledge assumption, which is the type of assumption on which security (in particular, knowledge soundness) of SNARKs relies. It states that an algorithm can only produce an output of a certain form if it knows some underlying information. This is formalized by requiring the existence of an extractor that extracts this information from the algorithm. In their scheme this information acts as the simulation trapdoor, which under their knowledge assumption can be obtained from a subvertor outputting a CRS.
To achieve S-ZK, a simulator must be able to simulate proofs under a CRS output by a subvertor, so it cannot simply embed a trapdoor as in standard ZK. Bellare et al. [BFS16] base S-ZK on a knowledge assumption, which is the type of assumption on which security (in particular, knowledge soundness) of SNARKs relies. It states that an algorithm can only produce an output of a certain form if it knows some underlying information. This is formalized by requiring the existence of an extractor that extracts this information from the algorithm. In their scheme this information acts as the simulation trapdoor, which under their knowledge assumption can be obtained from a subvertor outputting a CRS.
Concretely, they assume that for a bilinear group \((\mathbb {G},+)\) with a generator \(P\) any algorithm that outputs a Diffie-Hellman tuple \((P,s_1P,s_2P,s_1s_2P)\) for some \(s_1,s_2\), must know either \(s_1\) or \(s_2\). They call their assumption Diffie-Hellman knowledge-of-exponent assumption (DH-KEA) and note that a tuple \((P,S_1,S_2,S_3)\) of this form can be verified via a (symmetric) bilinear map  by checking
by checking  . A question that arises is: who chooses the group \(\mathbb {G}\) in their scheme? Bellare et al. address this by making the group \(\mathbb {G}\) part of the scheme specification. This begs the question whether the subversion risk has not simply been shifted from the CRS to the choice of the group. They argue that the group generation algorithm is deterministic and public, so users can create the group themselves, and it is thus reproducible, whereas the CRS is inherently not.
. A question that arises is: who chooses the group \(\mathbb {G}\) in their scheme? Bellare et al. address this by making the group \(\mathbb {G}\) part of the scheme specification. This begs the question whether the subversion risk has not simply been shifted from the CRS to the choice of the group. They argue that the group generation algorithm is deterministic and public, so users can create the group themselves, and it is thus reproducible, whereas the CRS is inherently not.
 A way to avoid the problem of generating a trusted CRS for NIZK systems is by proving its security in the random-oracle model (ROM) [BR93]. Instead of a CRS, all parties are assumed to have access to a truly random function (which is modeled as an oracle returning random values). In practice the random oracle is replaced by a cryptographic hash function and a proof in the ROM can be viewed as a security heuristic for the resulting scheme.
A way to avoid the problem of generating a trusted CRS for NIZK systems is by proving its security in the random-oracle model (ROM) [BR93]. Instead of a CRS, all parties are assumed to have access to a truly random function (which is modeled as an oracle returning random values). In practice the random oracle is replaced by a cryptographic hash function and a proof in the ROM can be viewed as a security heuristic for the resulting scheme.
For NIZK systems whose CRS is a uniform random string, e.g. PCP-based constructions like [BSBC+17] recently, one can in practice set the CRS to a common random-looking public value such as the digits of \(\mathrm{\pi }\) or the output of a standardized hash function on a fixed input. This intuitively guarantees that no one has embedded a trapdoor. For the Groth-Sahai proof system [GS08] the CRS consists of random elements of an elliptic-curve group; they can be set up by hashing a common random string directly into the elliptic curve [BF01, BCI+10].
For practical SNARKs the situation is different: there are no CRS-less constructions in the random-oracle model and the CRS is highly structured. The parameters typically contain elements of the form \((P,\tau P,\tau ^2P)\), where \(P\) is a generator of a group \(\mathbb {G}\) and \(\tau \) is a random value. Soundness completely breaks down if the value \(\tau \) is known to anyone. Unfortunately, there is no known way of creating such a triple obliviously, that is, without knowing the value \(\tau \).
 In order to show subversion zero knowledge of SNARK schemes, we assume that computing elements \((P,\tau P,\tau ^2P)\) cannot be done without knowing \(\tau \). (Looking ahead, we actually make a weaker assumption in asymmetric bilinear groups by requiring the adversary to return \((P_{1},\tau P_{1},\tau ^2P_{1})\in \mathbb {G}_{1}^3\) as well as \((P_{2},\tau P_{2})\in \mathbb {G}_{2}^2\), which makes the structure of the triple verifiable using the bilinear map.) Under this assumption, which we call square knowledge of exponent (SKE) assumption (Definition 14), we then prove subversion ZK of five relevant SNARK constructions from the literature or slight variants of them.
In order to show subversion zero knowledge of SNARK schemes, we assume that computing elements \((P,\tau P,\tau ^2P)\) cannot be done without knowing \(\tau \). (Looking ahead, we actually make a weaker assumption in asymmetric bilinear groups by requiring the adversary to return \((P_{1},\tau P_{1},\tau ^2P_{1})\in \mathbb {G}_{1}^3\) as well as \((P_{2},\tau P_{2})\in \mathbb {G}_{2}^2\), which makes the structure of the triple verifiable using the bilinear map.) Under this assumption, which we call square knowledge of exponent (SKE) assumption (Definition 14), we then prove subversion ZK of five relevant SNARK constructions from the literature or slight variants of them.
As an additional sanity check, we prove that SKE holds in the generic group model (Theorem 16). Following Groth [Gro16], we assume that the bilinear group description is part of the specification of the language for which the proof system is defined (and not part of the CRS as in [BFS16]). Following his previous work [DFGK14], we let the CRS generation algorithm sample random group generators (in contrast to [BFS16], which assumes a fixed group generator). This intuitively leads to weaker assumptions required to prove soundness.
To show subversion zero knowledge of existing SNARK schemes, we proceed as follows. Standard zero knowledge holds because the randomness used to compute the CRS allows the simulator to produce proofs that are distributed equivalently to honestly generated proofs under the (honestly computed) CRS. However, for S-ZK this must hold even for a CRS that was computed in any arbitrary way. While we cannot guarantee that the CRS subvertor used random values when computing the CRS, we first show how to verify that the structure of the CRS is as prescribed. (For the asymmetric Pinocchio scheme [BCTV14] this requires us to extend the CRS slightly.)
Another difference between standard and subversion ZK is that in the former the simulator creates the CRS and thus knows the simulation trapdoor, whereas for S-ZK the CRS is produced by the subvertor, so it might not be clear how proofs can be simulated at all. Now if the CRS contains elements \((P,\tau P,\tau ^2P)\), whose correct structure can be verified via the pairing, then under our SKE assumption we can extract the value \(\tau \). SKE thus allows the simulator to obtain parts of the randomness even from a maliciously generated CRS. Unfortunately, the simulation trapdoor typically contains other values that the S-ZK simulator cannot extract.
Our next step is then to demonstrate that proofs can be simulated using \(\tau \) only, or to show how under our assumption more values can be extracted that then enable simulation. Our final step is to show that if a CRS passes the verification procedure we define, then proofs that were simulated using the partial trapdoor are distributed like real proofs. This shows that the analyzed scheme is S-ZK under our SKE assumption. While knowledge assumptions are strong assumptions, they seem unavoidable since S-ZK implies 2-move interactive ZK by letting the verifier create the CRS. And such schemes require extractability assumptions [BCPR14].
Since simulated proofs are by definition independent of a witness, our results imply that under a verified, but possibly malicious, CRS, proofs for different witnesses are equally distributed. As a corollary we thereby obtain that all SNARKs we consider satisfy subversion witness indistinguishability unconditionally (i.e., no assumptions required).
We note that Ben-Sasson et al. [BCG+15] also consider making a CRS verifiable. Their goal is to protect soundness against subversion by sampling the secret values underlying a CRS in a distributed way. Only if all participants in the CRS-creation protocol collude can they break soundness. To guarantee a correctly distributed CRS, the participant(s) must prove adherence to the protocol via NIZK proofs [Sch91, FS87] secure in the random-oracle model. The protocol thus returns verifiable SNARK parameters. The parameters used for Zcash were set up using this multiparty protocol, which was recently detailed by Bowe et al. [BGG17].
Our Results
As already discussed, SNARKs are not subversion-sound because their CRS contains the simulation trapdoor. In this work we look at subversion resistance of their zero-knowledge property and investigate several SNARK constructions from the literature that are based on bilinear groups. In particular,
-
1.
the first QSP-based and 2. QAP-based constructions [GGPR13];
-
3.
optimized Pinocchio [BCTV14] as implemented in libsnark [BCG+14b]; and
-
4.
and 5. the two most efficient constructions by Groth et al. [DFGK14, Gro16].
We make the (reasonable) assumption that a privacy-conscious prover (whose protection is the goal of zero knowledge) first checks whether the CRS looks plausible (to whatever extent this is possible) before publishing a proof with respect to it. All of our results implicitly make this assumption.
We start with the first SNARK construction for QAPs by Gennaro et al. [GGPR13] and show how to verify that the CRS is correctly formed. We then show that under the square knowledge of exponent (SKE) assumption their construction satisfies subversion zero knowledge as defined in [BFS16]. The same holds for their QSP-based SNARK. (Due to space constraints, and since these results follow in much the same way as the next one, we defer our results on GGPR to the full version [Fuc17].)
We next turn to the optimized version of Pinocchio over asymmetric bilinear groups due to Ben-Sasson et al. [BCTV14]. For this construction we show that adding 4 group elements to the CRS makes it efficiently checkable. We then prove that the scheme with this slightly extended CRS satisfies subversion zero knowledge under SKE, whereas the original scheme, which is implemented in libsnark [BCG+14b], succumbs to a parameter-subversion attack [CGGN17]. For the SNARK by Danezis, Fournet, Groth and Kohlweiss [DFGK14], we show that CRS well-formedness can be efficiently verified without modifying the CRS and that S-ZK holds analogously to Pinocchio.
Finally, we consider the most efficient SNARK scheme by Groth [Gro16] and again show that the scheme is already subversion-zero-knowledge under SKE. Proving this is more involved than for the previous schemes, since the value \(\tau \), for which \(P,\tau P,\tau ^2P,\ldots \) are contained in the CRS does not suffice to simulate proofs, as for the previous schemes. We show that, using SKE twice, another value can be extracted, which together with \(\tau \) then enables proof simulation. As corollaries, we get that S-WI holds unconditionally for all considered schemes.
 Campanelli et al. [CGGN17] show that Pinocchio as implemented in libsnark [BCG+14b] is not subversion-zero-knowledge by exhibiting an attack. As countermeasures they propose to instead use one of the older SNARKs by Gennaro et al. [GGPR13], as they allow verification of CRS well-formedness, which yields witness indistinguishability. They admit that for applications for which there is only one witness, like selling a Sudoku solution, WI is vacuous (as any protocol satisfies WI).
Campanelli et al. [CGGN17] show that Pinocchio as implemented in libsnark [BCG+14b] is not subversion-zero-knowledge by exhibiting an attack. As countermeasures they propose to instead use one of the older SNARKs by Gennaro et al. [GGPR13], as they allow verification of CRS well-formedness, which yields witness indistinguishability. They admit that for applications for which there is only one witness, like selling a Sudoku solution, WI is vacuous (as any protocol satisfies WI).
They refer to Bellare et al.’s [BFS16] S-ZK system and conjecture that “the techniques extend to the original QSP/QAP protocol in [GGPR13]” (which we proved rigorously). Moreover, “[i]t is however not clear if those techniques extend to Pinocchio” and “it would require major changes in the current implementation of ZKCP protocols”. (We show that it suffices to add 4 group elements to the CRS and perform the checks of well-formedness.) They recommend following the Zcash approach [BCG+15, BGG17] and using an interactive protocol that lets the prover and verifier compute the CRS together.
In other concurrent work Abdolmaleki et al. [ABLZ17] present a S-ZK variant of Groth’s SNARK [Gro16]. They need to modify the scheme, thereby reducing efficiency, and they prove their result under a stronger assumption. In particular, they extend the CRS by 2d group elements (where d is the number of multiplication gates in the circuit representing the relation). Their assumption states that any adversary that for generators \(P_{1}\in \mathbb {G}_{1}^*\) and \(P_{2}\in \mathbb {G}_{2}^*\) outputs a pair of the form \((sP_{1},sP_{2})\) must know s. As they note, their assumption is false in groups with a symmetric (“Type-1”) bilinear map as well as in asymmetric groups of Type 2, whereas our SKE assumption holds generically in all bilinear group settings. They claim security of their scheme under their own definition of S-ZK, which is a statistical notion, in contrast to original computational S-ZK notion [BFS16], which we considerFootnote 1.
 We show that for all analyzed schemes except asymmetric Pinocchio, it suffices to verify the parameters once in order to guarantee subversion zero knowledge. Any already deployed parameters can thus be continued to be used after verification. Subversion-ZK of Pinocchio can be obtained by adding 4 group elements to the CRS.
We show that for all analyzed schemes except asymmetric Pinocchio, it suffices to verify the parameters once in order to guarantee subversion zero knowledge. Any already deployed parameters can thus be continued to be used after verification. Subversion-ZK of Pinocchio can be obtained by adding 4 group elements to the CRS.
For Pinocchio-based ZK contingent payments this means that the scheme can be made secure by slightly augmenting the size of the parameters and having the seller verify them. No additional interaction between seller and buyer (as recommended by Campanelli et al. [CGGN17]) is thus required. Of course, admitting additional interaction could lead to more efficient schemes than using the (costly) CRS verification.
The SNARK parameters used in Zcash have been computed by running the multi-party protocol from [BCG+15, BGG17] and verifiability of this process is achieved via random-oracle NIZK proofs. Let us define a CRS subvertor that runs this protocol, playing the roles of all parties, and outputs the resulting CRS, including the ROM proofs. Since the latter guarantee CRS well-formedness, under SKE there exists an efficient extractor that can extract the simulation trapdoor from the subvertor. Using the trapdoor, proofs can be simulated (as specified in Sect. 4). We thus conclude that, assuming that users verify the CRS and that the SKE assumption holds in the used bilinear group, Zcash provides a subversion-resistant form of anonymity in the random oracle model. Thus, even if all parties involved in creating the parameters were malicious, Zcash is still anonymous.
We content ourselves with the above argument, as a formal proof would be beyond the scope of this paper. Bowe et al. [BGG17] subsequently proved that their protocol is S-ZK with a polynomially small (not negligible) simulation error in the random-oracle model without making knowledge assumptions.
2 Definitions
2.1 Notation
If x is a (binary) string then |x| is its length. If S is a finite set then |S| denotes its size and  denotes picking an element uniformly from S and assigning it to s. We denote by \(\lambda \in {{\mathbb N}}\) the security parameter and by \(1^{\lambda }\) its unary representation.
denotes picking an element uniformly from S and assigning it to s. We denote by \(\lambda \in {{\mathbb N}}\) the security parameter and by \(1^{\lambda }\) its unary representation.
Algorithms are randomized unless otherwise indicated. “PT” stands for “polynomial time”, whether for randomized or deterministic algorithms. By \(y \leftarrow A(x_1,\ldots ; r)\) we denote the operation of running algorithm A on inputs \(x_1,\ldots \) and coins r and letting y denote the output. By  , we denote letting \(y \leftarrow A(x_1,\ldots ; r)\) for random r. We denote by \([A(x_1,\ldots )]\) the set of points that have positive probability of being output by A on inputs \(x_1, \ldots \).
, we denote letting \(y \leftarrow A(x_1,\ldots ; r)\) for random r. We denote by \([A(x_1,\ldots )]\) the set of points that have positive probability of being output by A on inputs \(x_1, \ldots \).
For our security definitions we use the code-based game framework [BR06]. A game \(\mathrm{G}\) (e.g. Fig. 1) usually depends on a scheme and executes one or more adversaries. It defines oracles for the adversaries as procedures. The game eventually returns a boolean. We let \(\Pr [\mathrm{G}]\) denote the probability that \(\mathrm{G}\) returns \(\mathsf {true}\).
We recall the standard notions of soundness, knowledge-soundness, witness-indistinguishability and zero knowledge for NIZKs, which assume the CRS is trusted and then give their subversion-resistant counterparts that were introduced in [BFS16]. We mainly follow their exposition and start with the syntax.
2.2 NP Relations and NI Systems
 Consider
Consider  . For \(x\in \{0,1\}^*\) we let
. For \(x\in \{0,1\}^*\) we let  be the witness set of x. \({R}\) is an \(\mathbf {NP}\) relation if it is PT and there is a polynomial \(P_{R}\) such that every w in \({R}(x)\) has length at most \(P_{R}(|x|)\) for all x. We let
be the witness set of x. \({R}\) is an \(\mathbf {NP}\) relation if it is PT and there is a polynomial \(P_{R}\) such that every w in \({R}(x)\) has length at most \(P_{R}(|x|)\) for all x. We let  be the language associated to \({R}\). We will consider relations output by a PT relation generator
be the language associated to \({R}\). We will consider relations output by a PT relation generator  (which may also output some auxiliary information z that is given to the adversary). We assume \(\lambda \) can be deduced from
(which may also output some auxiliary information z that is given to the adversary). We assume \(\lambda \) can be deduced from  and note that definitions from [BFS16], which are for one fixed relation \({R}\), are easily recovered by defining
and note that definitions from [BFS16], which are for one fixed relation \({R}\), are easily recovered by defining  .
.
 A non-interactive (NI) system \(\mathsf {\Pi }\) for relation generator
A non-interactive (NI) system \(\mathsf {\Pi }\) for relation generator  specifies the following PT algorithms. Via
specifies the following PT algorithms. Via  one generates a common reference string
one generates a common reference string  . Via
. Via  the honest prover, given x and \(w\in {R}(x)\), generates a proof \({\pi }\) that \(x\in L({R})\). Via
the honest prover, given x and \(w\in {R}(x)\), generates a proof \({\pi }\) that \(x\in L({R})\). Via  a verifier can produce a decision \(d\in \{\mathsf {true},\mathsf {false}\}\) indicating whether \({\pi }\) is a valid proof that \(x\in L({R})\). We require (perfect) completeness, that is, for all \(\lambda \in {{\mathbb N}}\), all
a verifier can produce a decision \(d\in \{\mathsf {true},\mathsf {false}\}\) indicating whether \({\pi }\) is a valid proof that \(x\in L({R})\). We require (perfect) completeness, that is, for all \(\lambda \in {{\mathbb N}}\), all  , all
, all  , all \(x\in L({R})\), all \(w\in {R}(x)\) and all
, all \(x\in L({R})\), all \(w\in {R}(x)\) and all  we have
we have  . We also assume that \(\mathsf {\Pi .V}\) returns \(\mathsf {false}\) if any of its arguments is \(\bot \).
. We also assume that \(\mathsf {\Pi .V}\) returns \(\mathsf {false}\) if any of its arguments is \(\bot \).
2.3 Standard Notions: SND, KSND, WI and ZK
 Soundness means that it is hard to create a valid proof for any \(x\not \in L({R})\). We consider computational soundness as opposed to a statistical one, which is the notion achieved by SNARGs.
Soundness means that it is hard to create a valid proof for any \(x\not \in L({R})\). We consider computational soundness as opposed to a statistical one, which is the notion achieved by SNARGs.
Definition 1
(SND). An NI system \(\mathsf {\Pi }\) for relation generator  is sound if
is sound if  is negligible for all PT adversaries \(\mathsf {A}\), where
is negligible for all PT adversaries \(\mathsf {A}\), where  and game \(\mathrm{SND}\) is specified in Fig. 1.
and game \(\mathrm{SND}\) is specified in Fig. 1.
 This strengthening of soundness [BG93] means that a prover that outputs a valid proof must know the witness. Formally, there exists an extractor that can extract the witness from the prover. The notion implies soundness, since for a proof of a wrong statement there exists no witness.
This strengthening of soundness [BG93] means that a prover that outputs a valid proof must know the witness. Formally, there exists an extractor that can extract the witness from the prover. The notion implies soundness, since for a proof of a wrong statement there exists no witness.
Definition 2
(KSND). An NI system \(\mathsf {\Pi }\) for relation generator  is knowledge-sound if for all PT adversaries \(\mathsf {A}\) there exists a PT extractor \(\mathsf {E}\) such that
is knowledge-sound if for all PT adversaries \(\mathsf {A}\) there exists a PT extractor \(\mathsf {E}\) such that  is negligible, where
is negligible, where  and game \(\mathrm{KSND}\) is specified in Fig. 1.
and game \(\mathrm{KSND}\) is specified in Fig. 1.
Note that (as for the following two notions) the output of game \(\mathrm{KSND}\) is efficiently computable, which is not the case for \(\mathrm{SND}\), since membership in \(L({R})\) may not be efficiently decidable. This can be an issue when proving security of more complex systems that use a system \(\mathsf {\Pi }\) as a building block.
 Witness-indistinguishability [FLS90] requires that proofs for the same statement using different witnesses are indistinguishable. The adversary can adaptively request multiple proofs for statements x under one of two witnesses \(w_0,w_1\); it receives proofs under \(w_b\) for a challenge bit b which it must guess.
Witness-indistinguishability [FLS90] requires that proofs for the same statement using different witnesses are indistinguishable. The adversary can adaptively request multiple proofs for statements x under one of two witnesses \(w_0,w_1\); it receives proofs under \(w_b\) for a challenge bit b which it must guess.
Definition 3
(WI). An NI system \(\mathsf {\Pi }\) for relation generator  is witness-indistinguishable if
is witness-indistinguishable if  is negligible for all PT adversaries \(\mathsf {A}\), where
is negligible for all PT adversaries \(\mathsf {A}\), where  and game \(\mathrm{WI}\) is specified in Fig. 1.
and game \(\mathrm{WI}\) is specified in Fig. 1.
 Zero knowledge [GMR89] means that no information apart from the fact that \(x\in L({R})\) is leaked by the proof. It is formalized by requiring that a simulator, who can create the CRS, can compute proofs without being given a witness, so that CRS and proofs are indistinguishable from real ones. In particular, the distinguisher \(\mathsf {A}\) can adaptively request proofs by supplying an instance and a valid witness for it. The proof is produced either by the honest prover using the witness, or by the simulator. The adversary outputs a guess \(b'\).
Zero knowledge [GMR89] means that no information apart from the fact that \(x\in L({R})\) is leaked by the proof. It is formalized by requiring that a simulator, who can create the CRS, can compute proofs without being given a witness, so that CRS and proofs are indistinguishable from real ones. In particular, the distinguisher \(\mathsf {A}\) can adaptively request proofs by supplying an instance and a valid witness for it. The proof is produced either by the honest prover using the witness, or by the simulator. The adversary outputs a guess \(b'\).
Definition 4
(ZK). An NI system \(\mathsf {\Pi }\) for  is zero-knowledge if \(\mathsf {\Pi }\) specifies additional PT algorithms \(\mathsf {\Pi .Sim}.\mathsf {crs}\) and \(\mathsf {\Pi .Sim}.\mathsf {pf}\) such that
is zero-knowledge if \(\mathsf {\Pi }\) specifies additional PT algorithms \(\mathsf {\Pi .Sim}.\mathsf {crs}\) and \(\mathsf {\Pi .Sim}.\mathsf {pf}\) such that  is negligible for all PT adversaries \(\mathsf {A}\), where
is negligible for all PT adversaries \(\mathsf {A}\), where  and game \(\mathrm{ZK}\) is specified in Fig. 1.
and game \(\mathrm{ZK}\) is specified in Fig. 1.
An NI system \(\mathsf {\Pi }\) is statistical zero-knowledge if the above holds for all (not necessarily PT) adversaries \(\mathsf {A}\). It is perfect zero-knowledge if  .
.
2.4 Notions for Subverted CRS: S-SND, S-KSND, S-WI and S-ZK
For all notions considered in the previous section the CRS is assumed to be honestly generated. Bellare et al. [BFS16] ask what happens when the CRS is maliciously generated and define subversion-resistant analogues S-SND, S-WI and S-ZK, in which the adversary chooses the CRS. The following three definitions are from [BFS16].
 This asks that if the adversary creates a CRS in any way it likes, it is still unable to prove false statements under it. We accordingly modify the soundness game \(\mathrm{SND}\) by letting the adversary choose
This asks that if the adversary creates a CRS in any way it likes, it is still unable to prove false statements under it. We accordingly modify the soundness game \(\mathrm{SND}\) by letting the adversary choose  in addition to x and \({\pi }\).
in addition to x and \({\pi }\).
Definition 5
(S-SND). An NI system \(\mathsf {\Pi }\) for generator  is subversion-sound if
is subversion-sound if  is negligible for all PT adversaries \(\mathsf {A}\), where
is negligible for all PT adversaries \(\mathsf {A}\), where  and game \(\mathrm{S-SND}\) is specified in Fig. 1.
and game \(\mathrm{S-SND}\) is specified in Fig. 1.
 This notion demands that even when the subvertor creates a CRS in any way it likes, it can still not decide which of two witnesses of its choice were used to create a proof. The adversary is modeled as a two-stage algorithm: it first outputs a CRS
This notion demands that even when the subvertor creates a CRS in any way it likes, it can still not decide which of two witnesses of its choice were used to create a proof. The adversary is modeled as a two-stage algorithm: it first outputs a CRS  along with state information (which could e.g. contain a trapdoor associated to
along with state information (which could e.g. contain a trapdoor associated to  ) passed to the second stage. The second stage is then defined like for the honest-CRS game \(\mathrm{WI}\), where via its \(\textsc {Prove}\) oracle, the adversary can adaptively query proofs for instances under one of two witnesses.
) passed to the second stage. The second stage is then defined like for the honest-CRS game \(\mathrm{WI}\), where via its \(\textsc {Prove}\) oracle, the adversary can adaptively query proofs for instances under one of two witnesses.
Definition 6
(S-WI). An NI system \(\mathsf {\Pi }\) for generator  is subversion-witness-indistinguishable if
is subversion-witness-indistinguishable if  is negligible for all PT adversaries \(\mathsf {A}\), where
is negligible for all PT adversaries \(\mathsf {A}\), where  and game \(\mathrm{S-WI}\) is specified in Fig. 1. An NI system \(\mathsf {\Pi }\) is perfect S-WI if
and game \(\mathrm{S-WI}\) is specified in Fig. 1. An NI system \(\mathsf {\Pi }\) is perfect S-WI if  .
.
 This notion considers a CRS subvertor \(\mathsf {X}\) that returns an arbitrarily formed CRS. Subversion ZK now asks that for any such \(\mathsf {X}\) there exists a simulator that is able to simulate (1) the full view of the CRS subvertor, including its coins, and (2) proofs for adaptively chosen instances without knowing the witnesses. The simulator consists of \(\mathsf {S}.\mathsf {crs}\), which returns a CRS, coins for \(\mathsf {X}\) and a trapdoor which is then used by its second stage \(\mathsf {S}.\mathsf {pf}\) to simulate proofs. The adversary’s task is to decide whether it is given a real CRS and the coins used to produce it, and real proofs (case \(b=1\)); or whether it is given a simulated CRS and coins, and simulated proofs (case \(b=0\)).
This notion considers a CRS subvertor \(\mathsf {X}\) that returns an arbitrarily formed CRS. Subversion ZK now asks that for any such \(\mathsf {X}\) there exists a simulator that is able to simulate (1) the full view of the CRS subvertor, including its coins, and (2) proofs for adaptively chosen instances without knowing the witnesses. The simulator consists of \(\mathsf {S}.\mathsf {crs}\), which returns a CRS, coins for \(\mathsf {X}\) and a trapdoor which is then used by its second stage \(\mathsf {S}.\mathsf {pf}\) to simulate proofs. The adversary’s task is to decide whether it is given a real CRS and the coins used to produce it, and real proofs (case \(b=1\)); or whether it is given a simulated CRS and coins, and simulated proofs (case \(b=0\)).
Definition 7
(S-ZK). An NI system \(\mathsf {\Pi }\) for  is subversion-zero-knowledge if for all PT CRS subvertors \(\mathsf {X}\) there exists a PT simulator \(\mathsf {S}=(\mathsf {S}.\mathsf {crs},\mathsf {S}.\mathsf {pf})\) such that for all PT adversaries \(\mathsf {A}\) the function
is subversion-zero-knowledge if for all PT CRS subvertors \(\mathsf {X}\) there exists a PT simulator \(\mathsf {S}=(\mathsf {S}.\mathsf {crs},\mathsf {S}.\mathsf {pf})\) such that for all PT adversaries \(\mathsf {A}\) the function  is negligible, where
is negligible, where  and game \(\mathrm{S-ZK}\) is specified in Fig. 1.
and game \(\mathrm{S-ZK}\) is specified in Fig. 1.
The definition is akin to ZK for interactive proof systems [GMR89], when interpreting the CRS as the verifier’s first message. The simulator must produce a full view of the verifier (including coins and a transcript of its interaction with the \(\textsc {Prove}\) oracle). On the other hand, to imply ZK of NI systems, the simulator needs to produce the CRS before learning the statements for which it must simulate proofs. Moreover, the simulator can depend on \(\mathsf {X}\) but not on \(\mathsf {A}\).
 For completeness we give a subversion-resistant analogue for knowledge soundness (not considered in [BFS16]), as this is the relevant notion for SNARKs. We modify game \(\mathrm{KSND}\) and let the adversary choose
For completeness we give a subversion-resistant analogue for knowledge soundness (not considered in [BFS16]), as this is the relevant notion for SNARKs. We modify game \(\mathrm{KSND}\) and let the adversary choose  in addition to x and \(\pi \). We are not aware of any construction that achieves S-KSND and some form of WI.
in addition to x and \(\pi \). We are not aware of any construction that achieves S-KSND and some form of WI.
Definition 8
(S-KSND). An NI system \(\mathsf {\Pi }\) for generator  is subversion-knowledge-sound if for all PT adversaries \(\mathsf {A}\) there exists a PT extractor \(\mathsf {E}\) such that
is subversion-knowledge-sound if for all PT adversaries \(\mathsf {A}\) there exists a PT extractor \(\mathsf {E}\) such that  is negligible, where
is negligible, where  and game \(\mathrm{S-KSND}\) is specified in Fig. 1.
and game \(\mathrm{S-KSND}\) is specified in Fig. 1.
2.5 Bilinear Groups and Assumptions
 The SNARK constructions we consider are based on bilinear groups, for which we introduce a new type of knowledge-of-exponent assumption. We distinguish between asymmetric and symmetric groups.
The SNARK constructions we consider are based on bilinear groups, for which we introduce a new type of knowledge-of-exponent assumption. We distinguish between asymmetric and symmetric groups.
Definition 9
An asymmetric-bilinear-group generator  is a PT algorithm that takes input a security parameter \(1^\lambda \) and outputs a description of a bilinear group
is a PT algorithm that takes input a security parameter \(1^\lambda \) and outputs a description of a bilinear group  with the following properties:
with the following properties:
-
p is a prime of length \(\lambda \);
-
\((\mathbb {G}_{1},+)\), \((\mathbb {G}_{2},+)\) and \((\mathbb {G}_T,\cdot )\) are groups of order p;
-
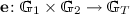 is a bilinear map, that is, for all \(a,b\in {{\mathbb Z}}_p\) and \(S\in \mathbb {G}_{1}\), \(T\in \mathbb {G}_{2}\) we have:
is a bilinear map, that is, for all \(a,b\in {{\mathbb Z}}_p\) and \(S\in \mathbb {G}_{1}\), \(T\in \mathbb {G}_{2}\) we have:  ;
; -
 is non-degenerate, that is, for \(P_{1}\in \mathbb {G}_{1}^*\) and \(P_{2}\in \mathbb {G}_{2}^*\) (i.e., \(P_{1}\) and \(P_{2}\) are generators)
is non-degenerate, that is, for \(P_{1}\in \mathbb {G}_{1}^*\) and \(P_{2}\in \mathbb {G}_{2}^*\) (i.e., \(P_{1}\) and \(P_{2}\) are generators)  generates \(\mathbb {G}_T\).
generates \(\mathbb {G}_T\).
Moreover, we assume that group operations and the bilinear map can be computed efficiently, membership of the groups and equality of group elements can be decided efficiently, and group generators can be sampled efficiently.
A symmetric-bilinear-group generator  returns a bilinear group with \(\mathbb {G}_{1}=\mathbb {G}_{2}\), which we denote by \(\mathbb {G}\), and with a symmetric non-degenerate bilinear map
returns a bilinear group with \(\mathbb {G}_{1}=\mathbb {G}_{2}\), which we denote by \(\mathbb {G}\), and with a symmetric non-degenerate bilinear map  .
.
 We recall the assumptions under which SNARKs in the literature were proven sound. The following assumptions are from [DFGK14], who adapted PDH from [Gro10] to asymmetric groups, and TSDH from [BB04, Gen04].
We recall the assumptions under which SNARKs in the literature were proven sound. The following assumptions are from [DFGK14], who adapted PDH from [Gro10] to asymmetric groups, and TSDH from [BB04, Gen04].
Definition 10
(
q
-PDH). The \(q(\lambda )\)
-power Diffie-Hellman assumption holds for an asymmetric group generator  if
if  is negligible for all PT \(\mathsf {A}\), where
is negligible for all PT \(\mathsf {A}\), where  and \(\mathrm{PDH}\) is defined in Fig. 2.
and \(\mathrm{PDH}\) is defined in Fig. 2.
The q-PDH assumption for symmetric group generators  is defined analogously by letting \(\mathbb {G}_{1}=\mathbb {G}_{2}\) and \(P_{1}=P_{2}\) (\(\mathsf {A}\) thus only receives 2q group elements).
is defined analogously by letting \(\mathbb {G}_{1}=\mathbb {G}_{2}\) and \(P_{1}=P_{2}\) (\(\mathsf {A}\) thus only receives 2q group elements).
Definition 11
(
q
-TSDH). The \(q(\lambda )\)
-target-group strong Diffie-Hellman assumption holds for an asymmetric group generator  if
if  is negligible for all PT adversaries \(\mathsf {A}\), where
is negligible for all PT adversaries \(\mathsf {A}\), where  and \(\mathrm{TSDH}\) is defined in Fig. 2.
and \(\mathrm{TSDH}\) is defined in Fig. 2.
The q-TSDH assumption for symmetric group generators  is defined analogously by letting \(\mathbb {G}_{1}=\mathbb {G}_{2}\) and \(P_{1}=P_{2}\) (\(\mathsf {A}\) thus only receives \(q+1\) group elements).
is defined analogously by letting \(\mathbb {G}_{1}=\mathbb {G}_{2}\) and \(P_{1}=P_{2}\) (\(\mathsf {A}\) thus only receives \(q+1\) group elements).
 The knowledge-of-exponent assumption [Dam92, HT98, BP04] in a group \(\mathbb {G}\) states that an algorithm \(\mathsf {A}\) that is given two random generators \(P,Q\in \mathbb {G}^*\) and outputs (cP, cQ) must know c. This is formalized by requiring that there exists an extractor for \(\mathsf {A}\) which given \(\mathsf {A}\)’s coins outputs c. This has been considered in the bilinear-group setting [AF07] where \(\mathsf {A}\)’s output (cP, cQ) can be verified by using the bilinear map. Generalizations of KEA were made by Groth [Gro10], who assumes that for every \(\mathsf {A}\) that on input \((P,Q,sP,sQ,s^2P,s^2Q,\ldots ,s^qP,s^qQ)\) returns (cP, cQ) an extractor can extract \((a_0,\ldots ,a_q)\) such that \(c = \sum _{i=0}^q a_is^i\). Danezis et al. [DFGK14] port Groth’s assumption to asymmetric groups as follows.
The knowledge-of-exponent assumption [Dam92, HT98, BP04] in a group \(\mathbb {G}\) states that an algorithm \(\mathsf {A}\) that is given two random generators \(P,Q\in \mathbb {G}^*\) and outputs (cP, cQ) must know c. This is formalized by requiring that there exists an extractor for \(\mathsf {A}\) which given \(\mathsf {A}\)’s coins outputs c. This has been considered in the bilinear-group setting [AF07] where \(\mathsf {A}\)’s output (cP, cQ) can be verified by using the bilinear map. Generalizations of KEA were made by Groth [Gro10], who assumes that for every \(\mathsf {A}\) that on input \((P,Q,sP,sQ,s^2P,s^2Q,\ldots ,s^qP,s^qQ)\) returns (cP, cQ) an extractor can extract \((a_0,\ldots ,a_q)\) such that \(c = \sum _{i=0}^q a_is^i\). Danezis et al. [DFGK14] port Groth’s assumption to asymmetric groups as follows.
Definition 12
(
q
-PKE). The \(q(\lambda )\)
-power knowledge of exponent assumption holds for  w.r.t. the class
w.r.t. the class  of auxiliary input generators if for every PT
of auxiliary input generators if for every PT  and PT adversary \(\mathsf {A}\) there exists a PT extractor \(\mathsf {E}\) s.t.
and PT adversary \(\mathsf {A}\) there exists a PT extractor \(\mathsf {E}\) s.t.  is negligible, where
is negligible, where  and \(\mathrm{PKE}\) is defined in Fig. 2.
and \(\mathrm{PKE}\) is defined in Fig. 2.
The q-PKE assumption for symmetric generators  is defined by letting \(\mathbb {G}_{1}=\mathbb {G}_{2}\) but again choosing
is defined by letting \(\mathbb {G}_{1}=\mathbb {G}_{2}\) but again choosing  thus again receives \(2q+2\) group elements).
thus again receives \(2q+2\) group elements).
Bellare et al. [BFS16] consider deterministically generated groups (whereas for SNARK systems the group will be part of the relation \({R}\) output by a relation generator  ). They therefore need to define all other assumptions, such as DLin [BBS04], with respect to this fixed group. BFS introduce a new type of KEA, called DH-KEA, which assumes that if \(\mathsf {A}\) outputs a Diffie-Hellman (DH) tuple \((sP,tP,stP)\) w.r.t. the fixed \(P\), then \(\mathsf {A}\) must know either s or t. The auxiliary input given to \(\mathsf {A}\) are two additional random generators \(H_0,H_1\). The intuition is that while an adversary may produce one group element without knowing its discrete logarithm by hashing into the elliptic curve [BF01, SvdW06, BCI+10], it seems hard to produce a DH tuple without knowing at least one of the logarithms.
). They therefore need to define all other assumptions, such as DLin [BBS04], with respect to this fixed group. BFS introduce a new type of KEA, called DH-KEA, which assumes that if \(\mathsf {A}\) outputs a Diffie-Hellman (DH) tuple \((sP,tP,stP)\) w.r.t. the fixed \(P\), then \(\mathsf {A}\) must know either s or t. The auxiliary input given to \(\mathsf {A}\) are two additional random generators \(H_0,H_1\). The intuition is that while an adversary may produce one group element without knowing its discrete logarithm by hashing into the elliptic curve [BF01, SvdW06, BCI+10], it seems hard to produce a DH tuple without knowing at least one of the logarithms.
Definition 13
(DH-KEA). Let  be a deterministic group generator; let
be a deterministic group generator; let  , with game \(\mathrm{DHKE}\) defined in Fig. 3. The Diffie-Hellman knowledge of exponent assumption holds for
, with game \(\mathrm{DHKE}\) defined in Fig. 3. The Diffie-Hellman knowledge of exponent assumption holds for  if for every PT \(\mathsf {A}\) there exists a PT \(\mathsf {E}\) s.t.
if for every PT \(\mathsf {A}\) there exists a PT \(\mathsf {E}\) s.t.  is negligible.
is negligible.
 We now consider a weakening of DH-KEA where we prescribe \(s=t\); that is, if \(\mathsf {A}\) on input \(P\) outputs a pair \((sP,s^2P)\) then \(\mathsf {E}\) extracts s. This assumption is weaker than (i.e., implied by) DH-KEA. As we consider groups with randomly sampled generators, we let \(\mathsf {A}\) choose the generator \(P\) itself and assume that there exists an extractor that extracts s when \(\mathsf {A}\) outputs a tuple \((P,sP,s^2P)\). This allows us to choose a random generator when setting up parameters of a scheme. The security of such schemes then follows from assumptions such as PDH, as defined above, where the generators are chosen randomly.
We now consider a weakening of DH-KEA where we prescribe \(s=t\); that is, if \(\mathsf {A}\) on input \(P\) outputs a pair \((sP,s^2P)\) then \(\mathsf {E}\) extracts s. This assumption is weaker than (i.e., implied by) DH-KEA. As we consider groups with randomly sampled generators, we let \(\mathsf {A}\) choose the generator \(P\) itself and assume that there exists an extractor that extracts s when \(\mathsf {A}\) outputs a tuple \((P,sP,s^2P)\). This allows us to choose a random generator when setting up parameters of a scheme. The security of such schemes then follows from assumptions such as PDH, as defined above, where the generators are chosen randomly.
Definition 14
(SKE). Let  be a symmetric-group generator and define
be a symmetric-group generator and define  , where game \(\mathrm{SKE}\) is defined in Fig. 3. The square knowledge of exponent assumption holds for
, where game \(\mathrm{SKE}\) is defined in Fig. 3. The square knowledge of exponent assumption holds for  if for every PT \(\mathsf {A}\) there exists a PT \(\mathsf {E}\) s.t.
if for every PT \(\mathsf {A}\) there exists a PT \(\mathsf {E}\) s.t.  is negligible.
is negligible.
 For asymmetric bilinear-group generators, we make assumption SKE in the first source group \(\mathbb {G}_{1}\). Unlike for symmetric groups, a tuple \((S_0,sS_0,s^2S_0)\in \mathbb {G}_{1}^3\) is not verifiable via an asymmetric pairing. To make it verifiable, we weaken the assumption and require \(\mathsf {A}\) to additionally output a \(\mathbb {G}_{2}\)-element \(T_0\) as well as \(T_1=sT_0\), which enables verification (as done in game
For asymmetric bilinear-group generators, we make assumption SKE in the first source group \(\mathbb {G}_{1}\). Unlike for symmetric groups, a tuple \((S_0,sS_0,s^2S_0)\in \mathbb {G}_{1}^3\) is not verifiable via an asymmetric pairing. To make it verifiable, we weaken the assumption and require \(\mathsf {A}\) to additionally output a \(\mathbb {G}_{2}\)-element \(T_0\) as well as \(T_1=sT_0\), which enables verification (as done in game  ).
).
Definition 15
(SKE). Let  be an asymmetric-group generator and define
be an asymmetric-group generator and define  , where game \(\mathrm{SKE}\) is defined in Fig. 3. The SKE assumption holds for
, where game \(\mathrm{SKE}\) is defined in Fig. 3. The SKE assumption holds for  in the first source group if for every PT \(\mathsf {A}\) there exists a PT \(\mathsf {E}\) s.t.
in the first source group if for every PT \(\mathsf {A}\) there exists a PT \(\mathsf {E}\) s.t.  is negligible.
is negligible.
We note that in addition to verifiability these additional elements \(T_0\) and \(T_1\) actually add to the plausibility of the assumption for asymmetric groups. Even if outputting \(S_2\) was not required, one could argue that the following stronger assumption holds in Type-3 bilinear groups, in which DDH holds in \(\mathbb {G}_{1}\) and in \(\mathbb {G}_{2}\): it is hard to compute \((S_0,S_1,T_0,T_1)\in \mathbb {G}_{1}^2\times \mathbb {G}_{2}^2\) with  without knowing the logarithms of \(S_1\) to base \(S_0\) (or equivalently \(T_1\) to base \(T_0\)):Footnote 2 an adversary might choose \(S_0\) and \(S_1\) obliviously by hashing into the group; but if it was able to compute from them the respective \(T_0\) and \(T_1\) then this would break DDH in \(\mathbb {G}_{1}\). (Given a DDH challenge \((S_0,S_1={s_1}S_0,S_2={s_2}S_0,R)\), compute \(T_0\) and \(T_1\) as above; then we have \(R=s_1s_2S_0\) iff
without knowing the logarithms of \(S_1\) to base \(S_0\) (or equivalently \(T_1\) to base \(T_0\)):Footnote 2 an adversary might choose \(S_0\) and \(S_1\) obliviously by hashing into the group; but if it was able to compute from them the respective \(T_0\) and \(T_1\) then this would break DDH in \(\mathbb {G}_{1}\). (Given a DDH challenge \((S_0,S_1={s_1}S_0,S_2={s_2}S_0,R)\), compute \(T_0\) and \(T_1\) as above; then we have \(R=s_1s_2S_0\) iff  .) Of course, this argument breaks down if there is an efficiently computable homomorphism from \(\mathbb {G}_{1}\) to \(\mathbb {G}_{2}\) or vice versa.
.) Of course, this argument breaks down if there is an efficiently computable homomorphism from \(\mathbb {G}_{1}\) to \(\mathbb {G}_{2}\) or vice versa.
Finally, we note that q-PKE with \(q=0\) does not imply SKE, since a PKE adversary must return (V, W) which is a multiple of the received \((P_{1},P_{2})\), while an SKE adversary can choose the “basis” \((S_0,T_0)\) itself. The converse does not hold either (SKE\(\not \Rightarrow \)PKE), since an SKE adversary must return \(S_2=s^2S_0\).
2.6 SKE in the Generic-Group Model
We show that SKE holds in the generic-group model. We show it for symmetric generic groups, which implies the result for asymmetric groups (where the adversary has less power). As [BFS16] did for DH-KEA, we reflect hashing into elliptic curves by providing the adversary with an additional generic operation: it can create new group elements without knowing their discrete logarithms (which are not known to the extractor either).
Theorem 16
SKE, as defined in Definition 14, holds in the generic-group model with hashing into the group.
In the proof we will use the following lemma, which we prove first.
Lemma 17
Let \({{\mathbb F}}\) be a field and let \(A,B,C\in {{\mathbb F}}[X_1,\ldots ,X_k]\), with degree of A, B and C at most 1. If \(A\cdot C = B^2\) then for some \(s\in {{\mathbb F}}\): \(B=s\cdot A\).
Proof
Let \(\alpha _i,\beta _i,\gamma _i\), for \(0\le i\le k\), denote the coefficients of \(X_i\) (where \(X_0:=1\)) in A, B, C, respectively. If \(A=0\) then \(B=0\) and the theorem follows. Assume thus \(A\ne 0\); Define \(j:=\min \{i\in [0,k]:\alpha _j\ne 0\}\) and \(s:=\beta _j\cdot \alpha _j^{-1}\).
To prove the lemma, we will now show that for all \(i\in [0,k]\):
From \(A\cdot C=B^2\) we have
From \(L(0,\ldots ,0)=0\), we get: (I) \(\beta _0^2 = \alpha _0\gamma _0\), which implies that Eq. (1) holds for \(i=0\): either \(\alpha _0=0\), then from (I): \(\beta _0=0\); or \(\alpha _0\ne 0\), then \(j=0\) and Eq. (1) holds as well.
Let now \(i\in [1,k]\) be arbitrarily fixed and let \(e_i\) denote the vector \((0,\ldots ,0,1, 0,\ldots ,0)\) with 1 at position i. Consider \(L(e_i)=0\), which together with (I) yields
Similarly, from \(L(2e_i)=0\), we have \( 4\beta _0\beta _i+4\beta _i^2 - 2\alpha _0\gamma _i - 2\alpha _i\gamma _0 - 4\alpha _i\gamma _i = 0, \) which after subtracting Eq. (3) twice yields: (II) \(\beta _i^2 = \alpha _i\gamma _i\). If \(\alpha _i=0\) then \(\beta _i=0\), which shows Eq. (1). For the remainder let us assume \(\alpha _i\ne 0\).
Plugging (II) into Eq. (3) yields: (III) \( 2\beta _0\beta _i = \alpha _0\gamma _i - \alpha _i\gamma _0 \).
If \(\alpha _0\ne 0\) then \(j=0\) and plugging (I) and (II) into (III) yields
Solving for \(\beta _i\) yields the unique solution \(\beta _i=\beta _0\alpha _0^{-1}\alpha _i\), which shows Eq. (1) for the case \(\alpha _0\ne 0\).
Let us now assume \(\alpha _0=0\). By (I) we have \(\beta _0=0\). If \(i=j\) then Eq. (1) holds by definition of s. Assume \(i\ne j\). From \(L(e_i+e_j)\) we have (since \(\alpha _0=\beta _0=0\)):
where we used (II) and \(\alpha _i\gamma _0=\alpha _j\gamma _0=0\) (which follows from (III) and \(\alpha _0=\beta _0=0\)). Together with (II) the latter yields
Solving for \(\beta _i\) yields the unique solution \(\beta _i=\beta _j\alpha _j^{-1}\alpha _i\), which concludes the proof. \(\square \)
Proof
(of Theorem 16 ). In the “traditional” generic-group model, group elements are represented by random strings and an adversary \(\mathsf {A}\) only has access to operations on them (addition of elements in \(\mathbb {G}\), multiplication of elements in \(\mathbb {G}_T\) and pairing of elements in \(\mathbb {G}\)) via oracles. In particular, \(\mathsf {A}\) can only produce new \(\mathbb {G}\) elements by adding received elements.
We also need to reflect the fact that by “hashing into the group”, \(\mathsf {A}\) can create a new group element without knowing its discrete logarithm w.r.t. one of the received elements. We extend the generic-group model and provide the adversary with an additional operation, namely to request a new group element “independently of the received ones”. (And neither the adversary nor the extractor we construct knows its discrete logarithm.)
For SKE the adversary \(\mathsf {A}\) receives the group element \(P\) and needs to output \((S_0,S_1,S_2)\) where for some s, t: \(S_0=tP\), \(S_1=sS_0=stP\) and \(S_2=s^2 S_0=s^2tP\). The adversary can produce these group elements by combining the received generator \(P\) with newly generated (“hashed”) group elements that it has requested. We represent the latter as \(x_iP\), for \(i=1,\ldots k\), for some k. The extractor keeps track of the group operations performed by \(\mathsf {A}\) and thus knows
such that \(\mathsf {A}\)’s output \((S_0,S_1,S_2)\) is of the form
Note that the extractor does however not know \(x:=(x_1,\ldots ,x_k)\).
Assume the adversary wins and  . Taking the logarithms of the latter yields
. Taking the logarithms of the latter yields
Since the adversary has no information about \(x_1,\ldots ,x_k\) (except for a negligible information leak by comparing group elements, which we ignore), the values in Eq. (4) are generated independently of \(x_1,\ldots ,x_k\). By the Schwartz-Zippel lemma the probability that Eq. (5) holds when \(x_1,\ldots ,x_k\) are randomly chosen is negligible, except if the left-hand side corresponds to the zero polynomial. With overwhelming probability we thus have
By Lemma 17 we have that \(B=s\,A\) for some \(s\in {{\mathbb F}}\). The extractor computes and returns s, which is correct since \(S_1=B(\vec x)P= sA(\vec x)P= s\,S_0\). \(\square \)
3 SNARKs
We start with a formal definition of SNARGs and SNARKs.
Definition 18
(SNARG). An NI system \(\mathsf {\Pi }=(\mathsf {\Pi .Pg},\mathsf {\Pi .P},\mathsf {\Pi .V})\) is a succinct non-interactive argument for relation generator  if it is complete and sound, as in Definition 1, and moreover succinct, meaning that for all \(\lambda \in {{\mathbb N}}\), all
if it is complete and sound, as in Definition 1, and moreover succinct, meaning that for all \(\lambda \in {{\mathbb N}}\), all  , all
, all  , all \(x\in L({R})\), all \(w\in {R}(x)\) and all
, all \(x\in L({R})\), all \(w\in {R}(x)\) and all  we have \(|\pi | = \text {poly}(\lambda )\) and
we have \(|\pi | = \text {poly}(\lambda )\) and  runs in time \(\text {poly}(\lambda +|x|)\).
runs in time \(\text {poly}(\lambda +|x|)\).
Definition 19
(SNARK). A SNARG \(\mathsf {\Pi }\) is a succinct non-interactive argument of knowledge if it satisfies knowledge soundness, as in Definition 2.
Gennaro et al. [GGPR13] base their SNARK constructions on quadratic programs. In particular, they show how to convert any boolean circuit into a quadratic span program and any arithmetic circuit into a quadratic arithmetic program (QAP).
Definition 20
(QAP). A quadratic arithmetic program over a field \({{\mathbb F}}\) is a tuple
where \(A_i(X),B_i(X),C_i(X),Z(X)\in {{\mathbb F}}[X]\), which define a language of statements \((s_1,\ldots ,s_n)\in {{\mathbb F}}^n\) and witnesses \((s_{n+1},\ldots ,s_m)\in {{\mathbb F}}^{m-n}\) such that

for some degree-\((d-2)\) quotient polynomial H(X), where d is the degree of Z(X) (we assume the degrees of all \(A_i(X),B_i(X),C_i(X)\) are at most \(d-1\)).
All of the discussed SNARK constructions are for QAPs defined over a bilinear group. We will thus consider relation generators  of the following form:
of the following form:
Definition 21
(QAP relation). A QAP relation generator  is a PT algorithm that on input \(1^{\lambda }\) returns a relation description of the following form:
is a PT algorithm that on input \(1^{\lambda }\) returns a relation description of the following form:

For \(x\in {{\mathbb F}}^{n}\) and \(w\in {{\mathbb F}}^{m-n}\) we define \({R}(x,w)=\mathsf {true}\) iff there exists \(H(X)\in {{\mathbb F}}[X]\) so that Eq. (6) holds for \(s:= x\,\Vert \,w\) (where “\(\,\Vert \)” denotes concatenation).
4 Asymmetric Pinocchio
The CRS of SNARKs systems is usually split into a (long) part  , used to compute proofs, and a (short) part
, used to compute proofs, and a (short) part  , used to verify them. Pinocchio [PHGR13] is one of the central SNARK systems. Ben-Sasson et al. [BCTV14] proposed a variant in asymmetric groups for which they also shorten the verification key. Their system is implemented in libsnark [BCG+14b] and underlies Zcash.
, used to verify them. Pinocchio [PHGR13] is one of the central SNARK systems. Ben-Sasson et al. [BCTV14] proposed a variant in asymmetric groups for which they also shorten the verification key. Their system is implemented in libsnark [BCG+14b] and underlies Zcash.
Campanelli et al. [CGGN17] show that the protocol is not subversion-zero-knowledge and expect major changes to make it secure. In the following we show that by adding merely 4 group elements to the CRS (which we denote by  for “checking key”), we can enable verification of well-formedness of
for “checking key”), we can enable verification of well-formedness of  by using the pairing available in the bilinear group. We then show that under SKE (Definition 15), our modification of the scheme from [BCTV14] achieves subversion zero knowledge. The protocol is given in Fig. 4, where we underlined our modifications. Below we define procedure CRS verification, which a prover runs on a CRS before using it the first time.
by using the pairing available in the bilinear group. We then show that under SKE (Definition 15), our modification of the scheme from [BCTV14] achieves subversion zero knowledge. The protocol is given in Fig. 4, where we underlined our modifications. Below we define procedure CRS verification, which a prover runs on a CRS before using it the first time.
Theorem 22
([PHGR13, BCTV14]). Let  be a relation generator that on input \(1^{\lambda }\) returns a QAP of degree at most \(d(\lambda )\) over \(\textit{Gr}\). Define
be a relation generator that on input \(1^{\lambda }\) returns a QAP of degree at most \(d(\lambda )\) over \(\textit{Gr}\). Define  that returns the first output \(\textit{Gr}\) of
that returns the first output \(\textit{Gr}\) of  and let \(q:=4d+4\). If the q-PDH, the q-PKE and the 2q-SDH assumptions hold for
and let \(q:=4d+4\). If the q-PDH, the q-PKE and the 2q-SDH assumptions hold for  then the scheme in Fig. 4 without including
then the scheme in Fig. 4 without including  in the CRS is knowledge-sound. Moreover, it is statistical zero-knowledge.
in the CRS is knowledge-sound. Moreover, it is statistical zero-knowledge.
Inspecting the proof of the theorem in [PHGR13], it is easily seen that the additional elements contained in  can be produced by the reduction. Moreover, knowledge soundness is independent of the prove algorithm \(\mathsf {\Pi .P}\), and a correctly generated CRS passes CRS verification. This yields the following.
can be produced by the reduction. Moreover, knowledge soundness is independent of the prove algorithm \(\mathsf {\Pi .P}\), and a correctly generated CRS passes CRS verification. This yields the following.
Corollary 23
(to Theorem 22
). Let  and
and  be as in Theorem 22. If the q-PDH, the q-PKE and the 2q-SDH assumptions hold for
be as in Theorem 22. If the q-PDH, the q-PKE and the 2q-SDH assumptions hold for  for \(q:=4d+4\) then the scheme in Fig. 4 is knowledge-sound statistical zero-knowledge.
for \(q:=4d+4\) then the scheme in Fig. 4 is knowledge-sound statistical zero-knowledge.

adapted from [BCTV14].
S-ZK Asymmetric Pinocchio,
 On input
On input  , let \(\{a_{i,j}\}\), \(\{b_{i,j}\}\), \(\{c_{i,j}\}\), \(\{z_k\}\) denote the coefficients of polynomials \(A_i(X)\), \(B_i(X)\), \(C_i(X)\) and Z(X), respectively, for \(0\le i\le m\) and \(0\le j\le d-1\) and \(0\le k\le d\).
, let \(\{a_{i,j}\}\), \(\{b_{i,j}\}\), \(\{c_{i,j}\}\), \(\{z_k\}\) denote the coefficients of polynomials \(A_i(X)\), \(B_i(X)\), \(C_i(X)\) and Z(X), respectively, for \(0\le i\le m\) and \(0\le j\le d-1\) and \(0\le k\le d\).
-
1.
Check \(P_{1}\ne 0_{\mathbb {G}_{1}}\) and \(P_{2}\ne 0_{\mathbb {G}_{2}}\).
-
2.
Check correct choice of secret values:
 ,
,  and
and 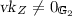 .
. -
3.
Check consistency of
 : Check
: Check  ; and for \(i=1,\ldots ,d\):
; and for \(i=1,\ldots ,d\): 
-
4.
Check consistency of
 : for \(i=0,\ldots ,m+3\):
: for \(i=0,\ldots ,m+3\): 
-
5.
Check consistency of
 :
:  (Note that for an honest CRS we have
(Note that for an honest CRS we have  .)
.) -
6.
Check consistency of
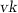 : for \(i=0,\ldots ,n\):
: for \(i=0,\ldots ,n\):  and
and 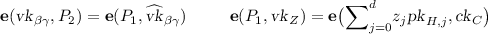
-
7.
Check consistency of
 : for \(i=0,\ldots ,m+3\):
: for \(i=0,\ldots ,m+3\): 
-
8.
If all checks in 1.–7. succeeded then return \(\mathsf {true}\) and otherwise \(\mathsf {false}\).
Remark 24
The condition that in Key generation \(\rho _A,\rho _B,\beta ,\gamma \) and \(Z(\tau )\) must be non-zero is not made explicit in [BCTV14]. However if \(\gamma =0\) then any \(\pi _K\) satisfies the verification equation in 3; and if \(\beta =0\) and \(\gamma \ne 0\) then no \(\pi _K\) satisfies it. If \(Z(\tau )=0\) or \(\rho _A=0\) or \(\rho _B=0\) then  and setting \(\pi _B\) and \(\pi _C\) to zero always satisfies the equation in 4 in verification.
and setting \(\pi _B\) and \(\pi _C\) to zero always satisfies the equation in 4 in verification.
CRS Verifiability. We show that a CRS  that passes verification is constructed as in Key generation; in particular, there exist \(\tau ,\alpha _A,\alpha _B,\alpha _C\in {{\mathbb F}}\) and \(\rho _A,\rho _B,\beta ,\gamma ,\in {{\mathbb F}}^*\) such that
that passes verification is constructed as in Key generation; in particular, there exist \(\tau ,\alpha _A,\alpha _B,\alpha _C\in {{\mathbb F}}\) and \(\rho _A,\rho _B,\beta ,\gamma ,\in {{\mathbb F}}^*\) such that  is computed as in Key generation. Let \(\tau ,\alpha _A,\alpha _B,\alpha _C,\rho _A,\rho _B,\gamma ,\xi \in {{\mathbb F}}\) be the values defined by the logarithms of the elements
is computed as in Key generation. Let \(\tau ,\alpha _A,\alpha _B,\alpha _C,\rho _A,\rho _B,\gamma ,\xi \in {{\mathbb F}}\) be the values defined by the logarithms of the elements  ,
,  ,
,  and
and  , respectively. Check 2. ensures that \(\rho _{A}\), \(\rho _{B}\), \(\gamma \), \(\xi \) and \(Z(\tau )\) are all non-zero. Set \(\beta :=\xi \gamma ^{-1}\ne 0\).
, respectively. Check 2. ensures that \(\rho _{A}\), \(\rho _{B}\), \(\gamma \), \(\xi \) and \(Z(\tau )\) are all non-zero. Set \(\beta :=\xi \gamma ^{-1}\ne 0\).
Check 3. ensures that  is correctly computed w.r.t. \(\tau \). Check 4. ensures that
is correctly computed w.r.t. \(\tau \). Check 4. ensures that  and
and  are correctly computed w.r.t. \(\tau \), \(\rho _A\), \(\rho _B\), \(\alpha _A\) and \(\alpha _B\). Check 5. ensures that
are correctly computed w.r.t. \(\tau \), \(\rho _A\), \(\rho _B\), \(\alpha _A\) and \(\alpha _B\). Check 5. ensures that  is correctly computed: since by 4.,
is correctly computed: since by 4.,  and \(Z(\tau )\ne 0\), we have
and \(Z(\tau )\ne 0\), we have  . Check 6. ensures that
. Check 6. ensures that  and
and  are correctly computed and Check 7. does the same for
are correctly computed and Check 7. does the same for  and
and  .
.
This shows that with respect to  and
and  (which implicitly define the randomness used in a CRS), all remaining elements
(which implicitly define the randomness used in a CRS), all remaining elements  , as well as
, as well as  and
and  are defined as prescribed by Key generation.
are defined as prescribed by Key generation.
Trapdoor Extraction. In order to prove subversion zero knowledge, we now show how to construct a simulator \((\mathsf {\Pi .Sim}.\mathsf {crs},\mathsf {\Pi .Sim}.\mathsf {pf})\) for a CRS subvertor \(\mathsf {X}\). Let \(\mathsf {X}\) be a CRS subvertor that outputs  . Define \(\mathsf {X}'(1^{\lambda };r)\) that runs
. Define \(\mathsf {X}'(1^{\lambda };r)\) that runs  , parses the output as above and returns
, parses the output as above and returns  . By SKE for
. By SKE for  (Definition 15) there exists a PT algorithm \(\mathsf {E}_{\mathsf {X}'}\) such that if for some \(\tau \in {{\mathbb F}}\):
(Definition 15) there exists a PT algorithm \(\mathsf {E}_{\mathsf {X}'}\) such that if for some \(\tau \in {{\mathbb F}}\):  and
and  then with overwhelming probability \(\mathsf {E}_{\mathsf {X}'}\) extracts \(\tau \). Using \(\mathsf {E}_{\mathsf {X}'}\) we define the CRS simulator \(\mathsf {S}.\mathsf {crs}\) which computes
then with overwhelming probability \(\mathsf {E}_{\mathsf {X}'}\) extracts \(\tau \). Using \(\mathsf {E}_{\mathsf {X}'}\) we define the CRS simulator \(\mathsf {S}.\mathsf {crs}\) which computes  as follows: On input \(1^\lambda \):
as follows: On input \(1^\lambda \):
-
1.
Sample randomness for \(\mathsf {X}\):
 .
. -
2.
Run
 .
. -
3.
If
 passes CRS verification then
passes CRS verification then 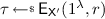 ; else \(\tau \leftarrow \bot \).
; else \(\tau \leftarrow \bot \). -
4.
Return
 .
.
Proof Simulation. Given  , trapdoor \(\tau \) and a statement \(x\in {{\mathbb F}}^n\), the proof simulator \(\mathsf {S}.\mathsf {pf}\) is defined as follows:
, trapdoor \(\tau \) and a statement \(x\in {{\mathbb F}}^n\), the proof simulator \(\mathsf {S}.\mathsf {pf}\) is defined as follows:
-
1.
If \(\tau =\bot \) then return \(\bot \).
-
2.
Use \(\tau \) to compute \(Z(\tau )\) (which in a verified CRS is non-zero). Compute the following “simulation keys”:

-
3.
Compute
 and
and 
-
4.
Choose
 and define \(\pi := (\pi _A,\pi '_A,\pi _B,\pi '_B,\pi _C,\pi '_C,\pi _K,\pi _H)\) with:
and define \(\pi := (\pi _A,\pi '_A,\pi _B,\pi '_B,\pi _C,\pi '_C,\pi _K,\pi _H)\) with: 
Theorem 25
Let  be a QAP generator defining a bilinear-group generator
be a QAP generator defining a bilinear-group generator  for which SKE holds. Then the scheme in Fig. 4 for
for which SKE holds. Then the scheme in Fig. 4 for  satisfies subversion zero knowledge.
satisfies subversion zero knowledge.
Proof
Consider  and let E denote the event that
and let E denote the event that  passes CRS verification but \(\mathsf {E}_{\mathsf {X}'}\) fails to extract \(\tau \). From Check 3 in CRS verification, we have
passes CRS verification but \(\mathsf {E}_{\mathsf {X}'}\) fails to extract \(\tau \). From Check 3 in CRS verification, we have  and
and  ; thus
; thus  is a valid SKE tuple. By the SKE assumption the probability of E is thus negligible. It now suffices to show that, conditioned on E not happening, the probability that \(\mathsf {A}\) outputs 1 in game S-ZK when \(b=0\) is the same as when \(b=1\).
is a valid SKE tuple. By the SKE assumption the probability of E is thus negligible. It now suffices to show that, conditioned on E not happening, the probability that \(\mathsf {A}\) outputs 1 in game S-ZK when \(b=0\) is the same as when \(b=1\).
If  fails CRS verification then \(\tau =\bot \) and both prover and proof simulator return \(\bot \). If
fails CRS verification then \(\tau =\bot \) and both prover and proof simulator return \(\bot \). If  verifies then (because of \(\lnot E\)) \(\mathsf {E}_{\mathsf {X}'}\) extracts \(\tau \).
verifies then (because of \(\lnot E\)) \(\mathsf {E}_{\mathsf {X}'}\) extracts \(\tau \).
We show that the outputs of the prover and the proof simulator are distributed equivalently. Above we showed that for a valid CRS there exist \(\tau ,\rho _A,\rho _B,\beta ,\gamma ,\alpha _A,\alpha _B,\alpha _C\in {{\mathbb F}}\) with \(\rho _{A}\ne 0\), \(\rho _{B}\ne 0\), \(\beta \ne 0\), \(\gamma \ne 0\) and \(Z(\tau )\ne 0\) such that  and
and  are defined as in Items 4. and 5. in Key generation.
are defined as in Items 4. and 5. in Key generation.
Because of this, \(\delta _A Z(\tau )\rho _{A}P_{1}\), the \((m+2)\)-th summand in \(\pi _A\) is uniformly random. And so are the \((m+3)\)-th summand \(\delta _B Z(\tau )\rho _{B}P_{1}\) of \(\pi _B\) and the \((m+4)\)-th summand \(\delta _C Z(\tau )\rho _{A}\rho _{B}P_{1}\) in \(\pi _C\). But this means that \(\pi _A\), \(\pi _B\) and \(\pi _C\) are uniformly random group elements. For fixed  , \(\pi _A\), \(\pi _B\) and \(\pi _C\) the Eq. (2). of Verify uniquely determine \(\pi '_A\), \(\pi '_B\) and \(\pi '_C\), while the Eqs. 3. and 4. uniquely determine \(\pi _K\) and \(\pi _H\) (since
, \(\pi _A\), \(\pi _B\) and \(\pi _C\) the Eq. (2). of Verify uniquely determine \(\pi '_A\), \(\pi '_B\) and \(\pi '_C\), while the Eqs. 3. and 4. uniquely determine \(\pi _K\) and \(\pi _H\) (since  and
and  ).
).
Since for a valid CRS the values \(\rho _{A}\) and \(\rho _{B}\) are non-zero, the simulated proof elements \(\pi _A\), \(\pi _B\) and \(\pi _C\) are also uniformly random. Thus, it suffices to show that the remaining proof elements satisfy the verification equations:

This concludes the proof. \(\square \)
Corollary 26
The scheme in Fig. 4 for a QAP generator  satisfies perfect subversion witness indistinguishability.
satisfies perfect subversion witness indistinguishability.
Proof
In Theorem 25 we showed that proofs under a (possibly maliciously generated but) valid CRS are uniform group elements subject to satisfying the verification equation. Proofs using different witnesses are thus equally distributed. \(\square \)
 Danezis et al. [DFGK14] define square span programs, which are described by only one set \(\{A_i(X)\}_i\) of polynomials (cf. Definition 20). They show how to convert any boolean circuit into an SSP. They construct a zk-SNARK for SSPs with proofs only consisting of 4 elements of an asymmetric bilinear group.
Danezis et al. [DFGK14] define square span programs, which are described by only one set \(\{A_i(X)\}_i\) of polynomials (cf. Definition 20). They show how to convert any boolean circuit into an SSP. They construct a zk-SNARK for SSPs with proofs only consisting of 4 elements of an asymmetric bilinear group.
Analogously to the SNARK from [BCTV14], their scheme is shown to satisfy subversion ZK by observing that (1) the structure of a CRS can be verified via the bilinear map; (2) the trapdoor \(\tau \) (s in their notation) can be extracted analogously to the SNARK analyzed above; and (3) proofs can be simulated using s by simply following the simulation procedure described in [DFGK14]. (When s is known, the element \(G^\beta \) (in their multiplicative notation) can be obtained from the CRS element \(G^{\beta t(s)}\) since \(t(s)\ne 0\).)
5 Groth’s Near-Optimal SNARK
Groth [Gro16] proposed the most efficient zk-SNARK system to date. He drastically reduced the proof size for QAP-based SNARKs to 3 group elements and verification to one equation using 3 pairings. He achieves this by proving soundness directly in the generic-group model. His system is given in Fig. 5, to which we added a procedure CRS verification defined below.
Theorem 27
([Gro16]). The scheme in Fig. 5 is knowledge-sound against adversaries that only use a polynomial number of generic bilinear group operations. Moreover, it has perfect zero knowledge.
Groth’s SNARK [Gro16] with CRS verification (in bold)
 On input
On input  , let \(\{a_{i,j}\}\), \(\{b_{i,j}\}\), \(\{c_{i,j}\}\), \(\{z_k\}\) denote the coefficients of \(A_i(X)\), \(B_i(X)\), \(C_i(X)\) and Z(X), respectively.
, let \(\{a_{i,j}\}\), \(\{b_{i,j}\}\), \(\{c_{i,j}\}\), \(\{z_k\}\) denote the coefficients of \(A_i(X)\), \(B_i(X)\), \(C_i(X)\) and Z(X), respectively.
-
1.
Check \(P_{1}\ne 0_{\mathbb {G}_{1}}\) and \(P_{2}\ne 0_{\mathbb {G}_{2}}\).
-
2.
Check \(\alpha ,\beta ,\gamma ,\delta \) and \(Z(\tau )\) are non-zero:
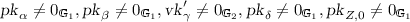
-
3.
Check consistency of
 and
and  : check
: check 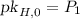 and
and  .
.For \(i=1,\ldots ,d\):

-
4.
Check consistency of the remaining
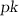 elements:
elements: 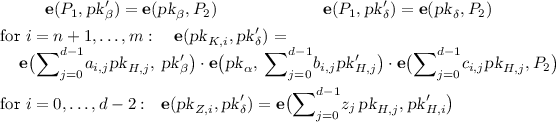
-
5.
Check consistency of the remaining
 elements: check
elements: check  and
and  . For \(i = 0,\ldots ,n\):
. For \(i = 0,\ldots ,n\): 
-
6.
If all checks in 1.–5. succeeded then return \(\mathsf {true}\) and otherwise \(\mathsf {false}\).
CRS Verifiability. Let \(\tau ,\alpha ,\beta ,\gamma ,\delta \) denote the logarithms of  . By Check 2. in CRS verification, \(\alpha ,\beta ,\gamma ,\delta ,Z(\tau )\) are non-zero. It follows by inspection that if all checks in 3.–5. pass then the remaining elements of
. By Check 2. in CRS verification, \(\alpha ,\beta ,\gamma ,\delta ,Z(\tau )\) are non-zero. It follows by inspection that if all checks in 3.–5. pass then the remaining elements of  and
and  are correctly computed.
are correctly computed.
Trapdoor Extraction. Let \(\mathsf {X}\) be a CRS subvertor that outputs  . Define \(\mathsf {X}'(1^{\lambda };r)\) that runs
. Define \(\mathsf {X}'(1^{\lambda };r)\) that runs  , parses the output as above and returns
, parses the output as above and returns  . For a valid CRS this corresponds to \((P_{1},\tau P_{1},\tau ^2P_{1},P_{2},\tau P_{2})\) for some \(P_{1}\in \mathbb {G}_{1}\), \(P_{2}\in \mathbb {G}_{2}\) and \(\tau \in {{\mathbb F}}\). By SKE there exists a PT algorithm \(\mathsf {E}_{\mathsf {X}'}\) which from a valid tuple extracts \(\tau \) with overwhelming probability.
. For a valid CRS this corresponds to \((P_{1},\tau P_{1},\tau ^2P_{1},P_{2},\tau P_{2})\) for some \(P_{1}\in \mathbb {G}_{1}\), \(P_{2}\in \mathbb {G}_{2}\) and \(\tau \in {{\mathbb F}}\). By SKE there exists a PT algorithm \(\mathsf {E}_{\mathsf {X}'}\) which from a valid tuple extracts \(\tau \) with overwhelming probability.
Define another algorithm \(\mathsf {X}''(1^{\lambda };(r,r'))\) that runs  and extracts \(\tau \leftarrow \mathsf {E}_{\mathsf {X}'}(1^{\lambda },r;r')\), computes \(Z(\tau )\) (which is non-zero in a valid CRS) and sets
and extracts \(\tau \leftarrow \mathsf {E}_{\mathsf {X}'}(1^{\lambda },r;r')\), computes \(Z(\tau )\) (which is non-zero in a valid CRS) and sets  (which for a valid CRS yields \(P'_1=\delta ^{-1}P_{1}\)). Finally, \(\mathsf {X}''\) returns
(which for a valid CRS yields \(P'_1=\delta ^{-1}P_{1}\)). Finally, \(\mathsf {X}''\) returns  . For a valid CRS this corresponds to \(\big (P'_1,\delta P'_1, {\delta ^2}P'_1,P_2,{\delta }P_2\big )\). By SKE there exist a PT algorithm \(\mathsf {E}_{\mathsf {X}''}\) that on input \(r''=(r,r')\) returns \(\delta \) with overwhelming probability.
. For a valid CRS this corresponds to \(\big (P'_1,\delta P'_1, {\delta ^2}P'_1,P_2,{\delta }P_2\big )\). By SKE there exist a PT algorithm \(\mathsf {E}_{\mathsf {X}''}\) that on input \(r''=(r,r')\) returns \(\delta \) with overwhelming probability.
Using \(\mathsf {E}_{\mathsf {X}'}\) and \(\mathsf {E}_{\mathsf {X}''}\), we define the CRS simulator \(\mathsf {S}.\mathsf {crs}\) as follows: On input \(1^\lambda \) do the following:
-
Sample randomness for \(\mathsf {X}\) and \(\mathsf {E}_{\mathsf {X}'}\):
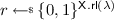 ;
; 
-
Run

-
If
 verifies then \(\tau \leftarrow \mathsf {E}_{\mathsf {X}'}(1^{\lambda },r;r')\) and
verifies then \(\tau \leftarrow \mathsf {E}_{\mathsf {X}'}(1^{\lambda },r;r')\) and  , else \((\tau ,\delta )\leftarrow (\bot ,\bot )\)
, else \((\tau ,\delta )\leftarrow (\bot ,\bot )\)
-
Return
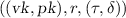
Remark 28
Proof simulation is defined in [Gro16] using the full randomness of the CRS and does not work with the trapdoor \((\tau ,\delta )\), as the simulator requires \(\alpha \) and \(\beta \), which SKE does not allow to extract. Note that it is impossible to extract \(\alpha \), since a valid CRS can be computed without knowing \(\alpha \): obliviously sample a random generator  and then compute
and then compute  and, for all i,
and, for all i,  and \(pk_{K,i}\) from
and \(pk_{K,i}\) from  . In the following we show how to simulate a proof without knowledge of \(\alpha \) and \(\beta \).
. In the following we show how to simulate a proof without knowledge of \(\alpha \) and \(\beta \).
Proof Simulation. Given  , trapdoor \((\tau ,\delta )\) and a statement \(x\in {{\mathbb F}}^n\), the proof simulator \(\mathsf {S}.\mathsf {pf}\) does the following:
, trapdoor \((\tau ,\delta )\) and a statement \(x\in {{\mathbb F}}^n\), the proof simulator \(\mathsf {S}.\mathsf {pf}\) does the following:
-
1.
If \((\tau ,\delta )=(\bot ,\bot )\) then return \(\bot \).
-
2.
Choose
 and define the proof \(\pi := (\pi _A,\pi '_B,\pi _C)\) as follows
and define the proof \(\pi := (\pi _A,\pi '_B,\pi _C)\) as follows 
Theorem 29
Let  be a QAP generator defining a bilinear-group generator
be a QAP generator defining a bilinear-group generator  for which SKE holds. Then Groth’s SNARK [Gro16] with CRS verification (Fig. 5) for
for which SKE holds. Then Groth’s SNARK [Gro16] with CRS verification (Fig. 5) for  satisfies subversion zero knowledge.
satisfies subversion zero knowledge.
Proof
Let E denote the event that  passes CRS verification but either \(\mathsf {E}_{\mathsf {X}'}\) or \(\mathsf {E}_{\mathsf {X}''}\) fails to extract \(\tau \) and \(\delta \). Since a correct
passes CRS verification but either \(\mathsf {E}_{\mathsf {X}'}\) or \(\mathsf {E}_{\mathsf {X}''}\) fails to extract \(\tau \) and \(\delta \). Since a correct  satisfies
satisfies  as well as
as well as  , by SKE (Definition 15), the probability that \(\mathsf {E}_{\mathsf {X}'}\) fails when \(\mathsf {X}'\) outputs
, by SKE (Definition 15), the probability that \(\mathsf {E}_{\mathsf {X}'}\) fails when \(\mathsf {X}'\) outputs  is negligible. A correct CRS also satisfies both
is negligible. A correct CRS also satisfies both  and
and  , thus again by SKE, the probability that \(\mathsf {E}_{\mathsf {X}''}\) fails when
, thus again by SKE, the probability that \(\mathsf {E}_{\mathsf {X}''}\) fails when  is also negligible. By a union bound, the probability of E is thus negligible.
is also negligible. By a union bound, the probability of E is thus negligible.
It now suffices to show that, conditioned on E not happening, game S-ZK when \(b=0\) is distributed as game S-ZK when \(b=1\). If  fails verification then \((\tau ,\delta )=(\bot ,\bot )\) and both the prover and the proof simulator return \(\bot \).
fails verification then \((\tau ,\delta )=(\bot ,\bot )\) and both the prover and the proof simulator return \(\bot \).
If  verifies then we show that the outputs of the prover and the proof simulator are distributed equivalently. Above we argued that for some non-zero \(\alpha ,\beta ,\gamma ,\delta \) and \(\tau \) with \(Z(\tau )\ne 0\) we have that
verifies then we show that the outputs of the prover and the proof simulator are distributed equivalently. Above we argued that for some non-zero \(\alpha ,\beta ,\gamma ,\delta \) and \(\tau \) with \(Z(\tau )\ne 0\) we have that  and
and  are defined as in 3. and 4. in Key generation.
are defined as in 3. and 4. in Key generation.
Since for a valid CRS both  and
and  are non-zero, for honestly generated proofs the elements
are non-zero, for honestly generated proofs the elements  in \(\pi _A\), and
in \(\pi _A\), and  in \(\pi '_B\), make \(\pi _A\) and \(\pi '_B\) uniformly random. For fixed
in \(\pi '_B\), make \(\pi _A\) and \(\pi '_B\) uniformly random. For fixed  , \(\pi _A\) and \(\pi '_B\), the verification equation uniquely determines \(\pi _C\), since
, \(\pi _A\) and \(\pi '_B\), the verification equation uniquely determines \(\pi _C\), since  .
.
In a simulated proof \(\pi _A\) and \(\pi '_B\) are also uniformly random, so it suffices to show that the simulated \(\pi _C\) satisfies the verification equation:

This concludes the proof. \(\square \)
Corollary 30
Groth’s SNARK [Gro16] with CRS verification for a QAP generator  (Fig. 5) satisfies perfect subversion witness indistinguishability.
(Fig. 5) satisfies perfect subversion witness indistinguishability.
Proof
The corollary follows analogously to Corollary 26. \(\square \)
Notes
- 1.
It is not clear how their scheme can achieve statistical S-ZK, considering that the success of the simulator relies on a computational assumption. They also claim that their notion is stronger because they let the subvertor \(\mathsf {X}\) pass “extra information” to the adversary \(\mathsf {A}\), whereas \(\mathsf {A}\) “only” receives \(\mathsf {X}\)’s coins r in [BFS16]. But \(\mathsf {A}\) can itself compute any such information from r.
- 2.
When fixing the generators \(S_0\) and \(T_0\), this corresponds to the assumption made by Abdolmaleki et al. [ABLZ17] to show S-ZK of their SNARK.
References
Abdolmaleki, B., Baghery, K., Lipmaa, H., Zając, M.: A subversion-resistant SNARK. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10626, pp. 3–33. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_1
Abe, M., Fehr, S.: Perfect NIZK with adaptive soundness. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 118–136. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_7
Boneh, D., Boyen, X.: Short signatures without random oracles. In: Cachin, C., Camenisch, J.L. (eds.) EUROCRYPT 2004. LNCS, vol. 3027, pp. 56–73. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24676-3_4
Boneh, D., Boyen, X., Shacham, H.: Short group signatures. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 41–55. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_3
Bitansky, N., Canetti, R., Chiesa, A., Tromer, E.: From extractable collision resistance to succinct non-interactive arguments of knowledge, and back again. In: Goldwasser, S. (ed.) ITCS 2012, pp. 326–349. ACM, January 2012
Ben-Sasson, E., Chiesa, A., Genkin, D., Tromer, E., Virza, M.: SNARKs for C: verifying program executions succinctly and in zero knowledge. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 90–108. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_6
Ben-Sasson, E., Chiesa, A., Garman, C., Green, M., Miers, I., Tromer, E., Virza, M.: Zerocash: decentralized anonymous payments from bitcoin. In: 2014 IEEE Symposium on Security and Privacy, pp. 459–474. IEEE Computer Society Press, May 2014
Ben-Sasson, E., Chiesa, A., Genkin, D., Tromer, E., Virza, M.: libsnark (2014). https://github.com/scipr-lab/libsnark
Ben-Sasson, E., Chiesa, A., Green, M., Tromer, E., Virza, M.: Secure sampling of public parameters for succinct zero knowledge proofs. In: 2015 IEEE Symposium on Security and Privacy, pp. 287–304. IEEE Computer Society Press, May 2015
Brier, E., Coron, J.-S., Icart, T., Madore, D., Randriam, H., Tibouchi, M.: Efficient indifferentiable hashing into ordinary elliptic curves. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 237–254. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_13
Bitansky, N., Chiesa, A., Ishai, Y., Paneth, O., Ostrovsky, R.: Succinct non-interactive arguments via linear interactive proofs. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 315–333. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_18
Bitansky, N., Canetti, R., Paneth, O., Rosen, A.: On the existence of extractable one-way functions. In: Shmoys, D.B. (ed.) 46th ACM STOC, pp. 505–514. ACM Press, May/June 2014
Ben-Sasson, E., Chiesa, A., Tromer, E., Virza, M.: Succinct non-interactive zero knowledge for a von Neumann architecture. In: Fu, K., Jung, J. (eds.) USENIX Security Symposium, pp. 781–796. USENIX Association (2014)
Blum, M., De Santis, A., Micali, S., Persiano, G.: Noninteractive zero-knowledge. SIAM J. Comput. 20(6), 1084–1118 (1991)
Boneh, D., Franklin, M.: Identity-based encryption from the Weil pairing. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 213–229. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_13
Blum, M., Feldman, P., Micali, S.: Non-interactive zero-knowledge and its applications (extended abstract). In: 20th ACM STOC, pp. 103–112. ACM Press, May 1988
Bellare, M., Fuchsbauer, G., Scafuro, A.: NIZKs with an untrusted CRS: security in the face of parameter subversion. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 777–804. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_26
Bellare, M., Goldreich, O.: On defining proofs of knowledge. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 390–420. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_28
Bowe, S., Gabizon, A., Green, M.D.: A multi-party protocol for constructing the public parameters of the pinocchio zk-SNARK. Cryptology ePrint Archive, Report 2017/602 (2017). http://eprint.iacr.org/2017/602
Bellare, M., Palacio, A.: The knowledge-of-exponent assumptions and 3-round zero-knowledge protocols. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 273–289. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_17
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: Ashby, V. (ed.) ACM CCS 93, pp. 62–73. ACM Press, November 1993
Bellare, M., Rogaway, P.: The security of triple encryption and a framework for code-based game-playing proofs. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 409–426. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_25
Ben-Sasson, E., et al.: Computational integrity with a public random string from quasi-linear PCPs. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10212, pp. 551–579. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_19
Campanelli, M., Gennaro, R., Goldfeder, S., Nizzardo, L.: Zero-knowledge contingent payments revisited: attacks and payments for services. In: Thuraisingham, B.M., Evans, D., Malkin, T., Xu, D. (eds.) ACM CCS 17, pp. 229–243. ACM Press, October/November 2017
Checkoway, S., Niederhagen, R., Everspaugh, A., Green, M., Lange, T., Ristenpart, T., Bernstein, D.J., Maskiewicz, J., Shacham, H., Fredrikson, M.: On the practical exploitability of Dual EC in TLS implementations. In: Fu, K., Jung, J. (ed.) USENIX Security Symposium, pp. 319–335. USENIX Association (2014)
Damgård, I.: Towards practical public key systems secure against chosen ciphertext attacks. In: Feigenbaum, J. (ed.) CRYPTO 1991. LNCS, vol. 576, pp. 445–456. Springer, Heidelberg (1992). https://doi.org/10.1007/3-540-46766-1_36
Danezis, G., Fournet, C., Groth, J., Kohlweiss, M.: Square span programs with applications to succinct NIZK arguments. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 532–550. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-45611-8_28
Fuchsbauer, G., Kiltz, E., Loss, J.: The algebraic group model and its applications. Cryptology ePrint Archive, Report 2017/620 (2017). http://eprint.iacr.org/2017/620
Feige, U., Lapidot, D., Shamir, A.: Multiple non-interactive zero knowledge proofs based on a single random string (extended abstract). In: 31st FOCS, pp. 308–317. IEEE Computer Society Press, October 1990
Fiat, A., Shamir, A.: How To prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Fuchsbauer, G.: Subversion-zero-knowledge SNARKs. Cryptology ePrint Archive, Report 2017/587 (2017). http://eprint.iacr.org/2017/587
Gennaro, R.: Multi-trapdoor commitments and their applications to proofs of knowledge secure under concurrent man-in-the-middle attacks. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 220–236. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_14
Gennaro, R., Gentry, C., Parno, B., Raykova, M.: Quadratic span programs and succinct NIZKs without PCPs. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 626–645. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_37
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Goldreich, O., Oren, Y.: Definitions and properties of zero-knowledge proof systems. J. Cryptol. 7(1), 1–32 (1994)
Groth, J., Ostrovsky, R., Sahai, A.: Non-interactive zaps and new techniques for NIZK. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 97–111. Springer, Heidelberg (2006). https://doi.org/10.1007/11818175_6
Groth, J., Ostrovsky, R., Sahai, A.: Perfect non-interactive zero knowledge for NP. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 339–358. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_21
Groth, J.: Simulation-sound NIZK proofs for a practical language and constant size group signatures. In: Lai, X., Chen, K. (eds.) ASIACRYPT 2006. LNCS, vol. 4284, pp. 444–459. Springer, Heidelberg (2006). https://doi.org/10.1007/11935230_29
Groth, J.: Short pairing-based non-interactive zero-knowledge arguments. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 321–340. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_19
Groth, J.: On the size of pairing-based non-interactive arguments. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 305–326. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_11
Groth, J., Sahai, A.: Efficient non-interactive proof systems for bilinear groups. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 415–432. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78967-3_24
Gentry, C., Wichs, D.: Separating succinct non-interactive arguments from all falsifiable assumptions. In: Fortnow, L., Vadhan, S.P. (eds.) 43rd ACM STOC, pp. 99–108. ACM Press, June 2011
Hada, S., Tanaka, T.: On the existence of 3-round zero-knowledge protocols. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 408–423. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055744
Lipmaa, H.: Progression-free sets and sublinear pairing-based non-interactive zero-knowledge arguments. In: Cramer, R. (ed.) TCC 2012. LNCS, vol. 7194, pp. 169–189. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28914-9_10
Micali, S.: Computationally sound proofs. SIAM J. Comput. 30(4), 1253–1298 (2000)
Nakamoto, S.: Bitcoin: a peer-to-peer electronic cash system (2009). http://bitcoin.org/bitcoin.pdf
Parno, B., Howell, J., Gentry, C., Raykova, M.: Pinocchio: nearly practical verifiable computation. In: 2013 IEEE Symposium on Security and Privacy, pp. 238–252. IEEE Computer Society Press, May 2013
Schnorr, C.-P.: Efficient signature generation by smart cards. J. Cryptol. 4(3), 161–174 (1991)
Shoup, V.: Lower bounds for discrete logarithms and related problems. In: Fumy, W. (ed.) EUROCRYPT 1997. LNCS, vol. 1233, pp. 256–266. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-69053-0_18
Shallue, A., van de Woestijne, C.E.: Construction of rational points on elliptic curves over finite fields. In: Hess, F., Pauli, S., Pohst, M. (eds.) ANTS 2006. LNCS, vol. 4076, pp. 510–524. Springer, Heidelberg (2006). https://doi.org/10.1007/11792086_36
Zcash. http://z.cash
Acknowledgments
The author would like to thank Mihir Bellare and Rosario Gennaro for helpful discussions and the anonymous reviewers for PKC’18 for their valuable comments. The author is supported by the French ANR EfTrEC project (ANR-16-CE39-0002).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Fuchsbauer, G. (2018). Subversion-Zero-Knowledge SNARKs. In: Abdalla, M., Dahab, R. (eds) Public-Key Cryptography – PKC 2018. PKC 2018. Lecture Notes in Computer Science(), vol 10769. Springer, Cham. https://doi.org/10.1007/978-3-319-76578-5_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-76578-5_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-76577-8
Online ISBN: 978-3-319-76578-5
eBook Packages: Computer ScienceComputer Science (R0)



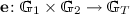 is a bilinear map, that is, for all
is a bilinear map, that is, for all  ;
; is non-degenerate, that is, for
is non-degenerate, that is, for  generates
generates 

 ,
,  and
and  .
. : Check
: Check  ; and for
; and for 
 : for
: for 
 :
:  (Note that for an honest CRS we have
(Note that for an honest CRS we have  .)
.) : for
: for  and
and 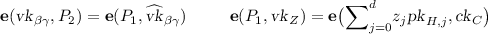
 : for
: for 
 .
. .
. passes
passes  ; else
; else  .
.
 and
and 
 and define
and define 

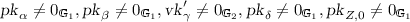
 and
and  : check
: check 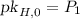 and
and  .
.
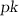 elements:
elements: 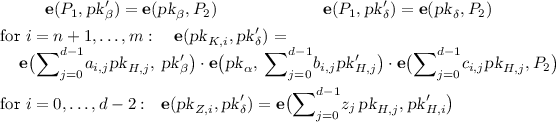
 elements: check
elements: check  and
and 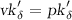 . For
. For 
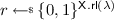 ;
; 

 verifies then
verifies then  , else
, else 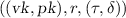
 and define the proof
and define the proof 
