Abstract
We consider a setting where users store their encrypted documents on a remote server and can selectively share documents with each other. A user should be able to perform keyword searches over all the documents she has access to, including the ones that others shared with her. The contents of the documents, and the search queries, should remain private from the server.
This setting was considered by Popa et al. (NSDI ’14) who developed a new cryptographic primitive called Multi-Key Searchable Encryption (MKSE), together with an instantiation and an implementation within a system called Mylar, to address this goal. Unfortunately, Grubbs et al. (CCS ’16) showed that the proposed MKSE definition fails to provide basic security guarantees, and that the Mylar system is susceptible to simple attacks. Most notably, if a malicious Alice colludes with the server and shares a document with an honest Bob then the privacy of all of Bob’s search queries is lost.
In this work we revisit the notion of MKSE and propose a new strengthened definition that rules out the above attacks. We then construct MKSE schemes meeting our definition. We first give a simple and efficient construction using only pseudorandom functions. This construction achieves our strong security definition at the cost of increasing the server storage overhead relative to Mylar, essentially replicating the document each time it is shared. We also show that high server storage overhead is not inherent, by giving an alternate (albeit impractical) construction that manages to avoid it using obfuscation.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Searchable (symmetric) encryption (SSE) [6, 9, 14, 33] allows a user to outsource her encrypted documents to a remote server. Later, she (or someone she authorizes) can send the server encrypted keyword search queries and receive the set of (encrypted) documents matching her keyword. Ideally, even a compromised server would not learn anything about the user’s data or her queries. This functionality can in theory be achieved using techniques such as Oblivious RAM and Fully Homomorphic Encryption, but the efficiency overhead makes the resultant schemes largely impractical.
To allow for more practical schemes, SSE relaxes the ideal security requirement and allows the server to learn some leakage—namely the access pattern of which documents are returned by each query. The initial SSE definitions failed to capture natural attacks, and were revised by several follow-up works culminating in the work of Curtmula et al. [9], who gave meaningful definitions that captured the intuitive security goal. There are now constructions of SSE schemes that meet this definition and are simple, practically efficient, and updatable [5, 21, 34]. We also note that there have been several works [22, 28, 36] showing that the leakage provided by SSE can already be too damaging to give meaningful security guarantees in some contexts. Despite such attacks, it seems that in many cases SSE can provide meaningful security for certain data sets, even if it is imperfect.
One benefit of outsourcing data to the cloud is that it allows users to easily share data with each other. Therefore, it is natural to consider a setting where a large group of users store their individual documents, encrypted under their own keys, on a remote cloud server, where each document can be shared with an arbitrary subset of other users. As with SSE, a user should be able to perform keyword search queries over all of the documents she has access to, including both her own documents and the ones shared with her. A trivial solution is to have each user generate a new SSE key for each set of documents she wishes to share, and provide this key to the authorized group of users. However, this solution has two main drawbacks: the user must maintain many keys (one for each set of documents shared with her), and the query size scales with the number of documents that have been shared with the user. These limitations are undesirable in many realistic scenarios, since a user may have tens of thousands of document sets shared with her.
To avoid these drawbacks, Popa et al. [29, 30] introduced the notion of Multi-Key Searchable Encryption (MKSE) to specifically address the query size problem. They provided a formal definition of MKSE along with a construction using bilinear maps, and an implementation of their scheme within a framework called Mylar for building secure web-applications over encrypted data. As part of the framework, they provide a number of prototype applications, including a chat room and a medical application.
The MKSE definition of [29, 30] aimed at capturing the following intuitive security guarantee: the scheme hides the content of both queries and stored documents, and the only information leaked is whether a given query matched any of the keywords in a given document. This should hold even when a subset of corrupted users colludes with the server. However, Grubbs et al. [17] showed that Mylar does not achieve this goal, and suffers from several serious security deficiencies, far beyond the limited leakage inherent in SSE. While some of these issues only apply to the particular design choices of Mylar and its applications, others are more general problems with the proposed MKSE definition. Recently, Van Rompay et al. [32] designed a different attack that pointed to another problem with the proposed MKSE definition. All these deficiencies remain present in follow up works that build on top of the MKSE definition of [29, 30], such as the work of Kiayias et al. [23]. We outline the three main issues below.
Separating Data and Query Privacy. The first issue with the MKSE definition is that it separately defines data privacy and query privacy, although it is intuitively clear that data and query privacy are inherently intertwined. Indeed, the server learns which documents are returned in response to a query, so knowing the contents of these documents leaks information about the contents of the query, and vice versa. Therefore, the two properties cannot be meaningfully defined in isolation. This observation has already been made in the context of single-key SSE by Curtmula et al. [9], who showed that earlier definitions that separated data and query privacy did not meaningfully rule out trivially insecure schemes. The work of [17] gives analogous examples in the context of MKSE, showing that there are trivially insecure schemes which satisfy the proposed definition.
Malicious Users Sharing Data. The second issue with the MKSE definition is more subtle. If an honest user Alice shares her document with a malicious user Mallory, then clearly privacy of her document is inherently lost. This limitation is intuitive, and users know they should not share their data with people they do not trust. But if Mallory shares her document with an honest Bob, one does not (and should not) expect Bob’s security to be compromised. Unfortunately, [17] show that the proposed MKSE notion of [29, 30] does not guarantee any privacy for Bob’s search queries in this scenario. In particular, the security game designed to capture query privacy in this setting [30, Definition 5.6] explicitly prevents the adversary from sharing documents with the honest user (whose queries the adversary is trying to learn). Not only is this issue overlooked in the definition, but it is actually inherent to the proposed MKSE syntax, so every construction which realizes this syntax (e.g., the follow-up works of [23, 35]) necessarily inherits this flaw. According to the original MKSE definition, when Mallory shares a document with Bob, a share key \(\varDelta \) is generated. The share key \(\varDelta \) does not depend on Mallory’s set, and allows any query under Bob’s key to be transformed into a query under Mallory’s key. Therefore, a malicious server, colluding with Mallory, can use \(\varDelta \) to transform every query Bob makes into a query under Mallory’s key, and the transformed query can then be executed offline against a set of single-word documents containing the full dictionary. Thus, if Mallory shares a document with Bob, the server can (through this offline dictionary attack) recover all keywords Bob searched for.
Searching by Comparing Queries and Encrypted Keywords. The third issue is that the MKSE definition implicitly restricts the algorithmic structure of the scheme to encrypt each keyword in the document separately, and search in a document by comparing the given query to each of the encrypted keywords. Thus, a “hit” reveals not only that the query appears in the document, but also which (encrypted) keyword it matched. Van Rompay et al. [32] show that this allows the server to compare queries issued by different users (even if both users are honest), and encrypted keywords from different documents (when they match the same keyword token).
1.1 Our Contribution
In this work, we propose a new MKSE definition that does not suffer from the above issues. In particular, our definition simultaneously addresses data and query privacy in a holistic manner, explicitly considers malicious data owners that may share data with honest users, and prevents the adversary from comparing queries issued by different users and keywords from different documents. We then propose a simple construction which provably satisfies our definition using only Pseudo-Random Functions (PRFs). Queries in this scheme consist of a single PRF image, and searching in a document is constant-time, but the server storage overhead is high. In particular, each time a document is shared with a user, it is essentially replicated, causing the per-document server storage overhead to be linear in the number of users the document is shared with.
We initially conjectured that such overhead is inherent to achieving our stronger MKSE definition. However, we show that proving such a conjecture will be quite challenging, since it will require ruling out the existence of certain program obfuscators. Concretely, in Sect. 5, we construct an MKSE scheme that uses obfuscation (specifically, public-coin differing-input obfuscation [20]) and requires per-document server storage that is roughly the document size plus the number of users it is shared with. (The construction has constant query size and polynomial time search.) We view our construction as providing evidence that a more efficient construction may possibly achieve the stronger MKSE notion with optimal server storage overhead.
Overview of Our MKSE Definition. We consider users that can take on two types of roles: data owners and queriers. Data owners have a document they wish to share with some subset of the users. Each document has its own associated data key \(K^d\), where the data owner “encrypts” the document using this key, and uploads the encrypted document to the server. Each user has a query key \(K^u\) that it uses to issue search queries. When a data owner shares a document d with a user u they create a share key \(\varDelta _{u,d}\) which depends on the keys \(K^u,K^d\), as well as the encrypted document, and store \(\varDelta _{u,d}\) on the server. When a querier wants to search for some keyword, he “encrypts” the keyword using his query key \(K^u\), and sends the resulting encrypted query to the server. For each document d that was shared with the user u, the server uses the share key \(\varDelta _{u,d}\) to execute the encrypted query over the encrypted document, and learns if the keyword is contained in that document. This allows the server to return all relevant documents the querier has access to and which contain the keyword.
The main syntactic difference between our notion, and the MKSE notion used in Mylar, is in how the share key \(\varDelta _{u,d}\) is generated. As noted above, the share key in Mylar depends only on the keys \(K^u,K^d\), whereas in our notion it also depends on the encrypted document. By tying the share key to the document, we can ensure that each query can only be executed on the specific documents that were shared with the querier, rather than on arbitrary documents, even if the server has the key \(K^d\).
To define security, we consider a share graph between data owners (documents) and queriers, representing who shares data with whom, where some subset of data owners are malicious and collude with the server. The desired security guarantee is that the server learns nothing about the contents of the documents belonging to the honest data owners, or the keywords being queried, beyond the access pattern of which documents are returned by each query (i.e., out of the documents shared with the querier, which ones contain the queried keyword). We provide an indistinguishability-based definition where the adversary chooses the documents and data keys belonging to the malicious data owners, and two potential values (a “left” and a “right” value) for each query and each document belonging to an honest data owner. The left and right values must lead to the same access pattern, and the queries of each querier must be distinct. The adversary then gets all encrypted documents, share keys, and encrypted queries, and should not be able to distinguish whether these were created using the left or right values.
Since the adversary only learns the access pattern of which documents are returned by each query, the above definition captures the minimal leakage for schemes that reveal the access pattern, which seems to be the case in all practical schemes. This is a significant qualitative improvement over the leakage allowed by the previous definition of [30] and the corresponding schemes. Most importantly, when a malicious user Mallory is colluding with the sever and shares some data with Bob, the previous schemes completely leaked the contents of Bob’s query wheres our definition still only reveals the access pattern. We note that similar to single-key SSE, leaking the access pattern does reveal some potentially sensitive information and in some scenarios (e.g., when combined with auxiliary information about the documents) this may allow a sufficiently powerful attacker to completely recover the query, as shown in the single-key SSE setting by the recent works [4, 18, 22, 28, 31, 36]. In the multi-key setting this might be amplified since, whenever malicious data owners share documents with honest querier, the adversary already knows (and even chooses) the contents of these documents and hence can learn more information by seeing which of these documents match the query. For example, if the shared documents correspond to every individual word in a dictionary, then by seeing which document matches a given query the contents of the query are completely revealed. However, this is not a very natural scenario, and in many settings it is reasonable to believe that leaking the access pattern alone may not reveal significant information about the query. Furthermore, users can perform sanity checks on the documents shared with them to test how much leakage the server will get on their queries, and refuse to accept shared documents if they lead to too much leakage. Understanding when access pattern leakage is acceptable and when it is not is a fascinating and important direction for future study.
One implementation concern in the above notion of MKSE comes from how the share key \(\varDelta _{u,d}\) is generated, since it relies on knowledge of both the data-owner’s key \(K^d\) for the document being shared, the user’s querier key \(K^u\), and the encrypted document itself. We envision that the data owner simply sends the data key \(K^d\) to the querier via a secure channel. The querier then downloads the encrypted document from the server, generates \(\varDelta _{u,d}\), and uploads it to the server. Note that the querier can also check at this point that the document was encrypted correctly, and therefore in the security definition we always assume that documents are encrypted honestly.
Finally, our default definition is selective, meaning the adversary specifies the entire share graph, the data, and the queries ahead of time. We can also consider adaptive security for SSE (a notion introduced by [9] in the single-user setting) in which the adversary generates queries on the fly during the course of the attack. Furthermore, our definition is indistinguishability based, where one could also consider a simulation-based version (as introduced in the single-user setting by [9]) in which the simulator, given the share graph, document sizes, and access patters, produces the encrypted documents and queries. We discuss these alternate variants in Sect. 6, and note that our PRF-based construction described below satisfies the strongest security notion (adaptive, simulation-based) when the PRF is instantiated in the random-oracle model.
Overview of the PRF-Based Construction. We provide a simple and efficient MKSE scheme based only on the existence of one-way functions. As noted above, each share key \(\varDelta _{u,d}\) contains a copy of the document, which allows Search to use only this value (and not the encrypted document).
If \(\varDelta _{u,d}\) is “allowed” to encode the entire document, a natural approach is to assign to each querier a PRF key \(K^u\) for a PRF F, and store in \(\varDelta _{u,d}\) the images of \(F\left( K^u,\cdot \right) \) on all keywords in the document. However, this construction is fundamentally insecure, since the share keys themselves leak information, even if the querier never makes any queries, and even if all data owners are honest. More specifically, consider the case of two honest data owners that share their documents with an honest querier. Then the two share keys reveal the number of keywords that appear in both documents. This is because the token associated with each keyword depends only on the keyword and the querier key, and not on the document.
To solve this issue we use another layer of PRF images, where the first layer generates PRF keys for a second layer that will be applied to a document-specific random identifier. Concretely, when generating \(\varDelta _{u,d}\), we assign a random value r to the document. For every keyword w in the document, we generate a (second layer) PRF key \(k^w=F\left( K^u,w\right) \), and compute a token \(t^w\) for w as \(t^w=F\left( k^w,r\right) \). Using perfect hashing [11], these tokens are inserted into a hash table to accelerate searching. The share key \(\varDelta _{u,d}\) consists of r and the hash table containing the tokens. (Notice that if r is chosen from a sufficiently large domain, then with overwhelming probability each document is assigned a unique identifier, and so the share keys associated with two documents reveal no information about their intersection.)
To search for keyword w in her documents, the querier sends the query \(k^w=F\left( K^u,w\right) \) to the server. Searching for \(k^w\) in a document with \(\varDelta _{u,d}=\left( r,D'\right) \) (where \(D'\) is a hash table of tokens) is performed by searching the hash table \(D'\) on the key \(F\left( k^w,r\right) \). This query reveals no information about w. Notice that the scheme uses the encrypted document only to generate \(\varDelta _{u,d}\), so the document can simply be encrypted with its own unique symmetric encryption key.
1.2 Related Work
Single User Schemes. First introduced by Song et al. [33], the notion of (single user) Searchable Encryption has been extensively studied in the last decade (see [3, 12] for a survey of many of these works). The first works (e.g., [6, 14, 33]) constructed schemes under several (simulation-based or indistinguishability-based) security definitions. These definitions separated the properties of query and data privacy, and were shown by [9] to be insecure (by a fairly simple attack). Curtmola et al. [9] also presented a unified definition that combined both properties.
Multi-User Schemes. In this model multiple users can issue queries to a single dataset which is encrypted under a single key that is known to all users. Consequently, most works in this setting focus on access control, and efficient revocation of querying privileges. Following the work of [9], who provided the first definitions and constructions, there have been three main approaches to enforcing access control across the documents: traditional access control mechanisms [10, 25, 37], broadcast encryption [9, 26], and attribute-based encryption [7, 24].
We emphasize that in the multi-user setting, there is a single dataset owned by a single data owner, so using such schemes in settings with multiple data owners would require instantiating the scheme separately for each dataset, and thus the query size would be linear in the number of datasets shared with the querier. This should be contrasted with the multi-key setting which is the focus of this work, in which users can search over multiple datasets by issuing a single query whose size is independent of the number of datasets being searched.
Multi-key Schemes. In this setting multiple users share data encrypted under their own keys, and search across the data shared with them by issuing a single query whose size is independent of the number of shared datasets. First introduced by Popa et al. [29], follow-up works that build on [29] focused on optimizing server storage, and eliminating the trusted party needed to distribute data and querier keys [23]; mitigating attacks in which a malicious data owner shares a dictionary dataset with the querier, by having the querier explicitly determine which data owners are allowed to share data with her [35]Footnote 1; and constructing schemes that are secure in restricted security models when honest data owners only share their documents with honest queriers, or when a single data owner has not shared his dataset with anyone else [35] (in both models, the server might be corrupted). We note that since these works use the syntax of [29] (in particular, share keys are generated independently of the shared set), the aforementioned attacks of [17] apply to these works as well.
Other Related Models. The notion of Key Aggregate Searchable Encryption (KASE), introduced by [8], considers a data owner who has several documents, each encrypted under a unique key. This allows data owners to share different subsets of their documents with different users. The goal is to grant search access to a subset of documents by providing one aggregate key whose length is independent of the number of documents (whereas in a naive solution, the key size would scale with the number of documents), and the querier issues one query for every subset of documents shared under the aggregate key (whereas in the MKSE setting, the user issues a single query, regardless of the number of documents shared with her). Thus, this model is fundamentally different from MKSE (as pointed out in [8]). We note that the construction of [8] is vulnerable to dictionary attacks (as shown by [23]).
2 Preliminaries
In the following, \(\lambda \) denotes a security parameter, and \(\mathsf{{negl}}\left( \lambda \right) \) denotes a function that is negligible in \(\lambda \). We use \(\approx \) to denote computational indistinguishability, and \(S \setminus T\) to denote the difference between sets S, T. We use \(\Pr \left[ E\ :\ E_1,\cdots ,E_n\right] \) to denote the probability of event E given events \(E_1,\cdots ,E_n\). For strings \(x=x_1\cdots x_n,y=y_1\cdots y_m\), \(x\circ y\) denotes their concatenation, i.e., \(x\circ y=x_1\cdots x_ny_1\cdots y_m\). We use standard cryptographic definitions of one-way functions (OWFs), one-way permutations (OWPs), collision resistant hash functions (CRHFs), pseudorandom functions (PRFs), and existentially-unforgeable signature schemes (see, e.g., [15, 16]).
3 Defining Multi-Key Searchable Encryption
In this section we define the notion of Multi-Key Searchable Encryption (MKSE) schemes. Intuitively, an MKSE scheme allows data owners to share their documents with queriers who can later query these documents under their own keying material, while preserving both data and query privacy. In the definition, documents are represented as sets of keywords, so searching in a document translates to checking set membership; see the discussion following the definition.
Definition 1
(Multi-Key Searchable Encryption). We say that a tuple \(\left( \textsf {DataKeyGen},\textsf {QueryKeyGen},\textsf {ProcessSet},\textsf {Share},\textsf {Query},\textsf {Search}\right) \) of PPT algorithms is a Multi-Key Searchable Encryption (MKSE) scheme for a universe \(\mathcal{{U}}\), if the following holds.
-
Syntax:
-
\(\textsf {DataKeyGen}\) takes as input the security parameter \(1^{\lambda }\), and outputs a data key K.
-
\(\textsf {QueryKeyGen}\) takes as input the security parameter \(1^{\lambda }\), and outputs a query key \(K^u\).
-
\(\textsf {ProcessSet}\) takes as input a data key K and a set S, and outputs a processed set T.
-
\(\textsf {Share}\) takes as input a data key K, a query key \(K^u\), and a processed set T, and generates a user-specific share key \(\varDelta \).
-
\(\textsf {Query}\) takes as input an element \(w \in \mathcal{{U}}\) and a query key \(K^u\), and outputs a query q.
-
\(\textsf {Search}\) takes as input a user-specific share key \(\varDelta \), a query q, and a processed set T, and outputs \(b \in \{0,1\}\).
-
-
Correctness: For every security parameter \(\lambda \in \mathbb {N}\), data set \(S \subseteq \mathcal{{U}}\), and element \(w \in \mathcal{{U}}\):
$$\begin{aligned} \Pr \left[ \textsf {Search}\left( \varDelta , q, T\right) = b\ :\ \begin{array}{rl} K &{}\leftarrow \textsf {DataKeyGen}\left( 1^{\lambda }\right) \\ K^u &{}\leftarrow \textsf {QueryKeyGen}\left( 1^{\lambda }\right) \\ T &{}\leftarrow \textsf {ProcessSet}\left( K,S\right) \\ \varDelta &{}\leftarrow \textsf {Share}\left( K, K^u,T\right) \\ q &{}\leftarrow \textsf {Query}\left( K^u,w\right) \end{array}\right] \ge 1 - \mathsf{{negl}}\left( \lambda \right) \end{aligned}$$where \(b = 0\) if \(w \notin S\), otherwise \(b = 1\).
-
Security: Every PPT adversary \(\mathcal {A}\) has only a \(\mathsf{{negl}}\left( \lambda \right) \) advantage in the following security game with a challenger \(\mathcal {C}\):
-
1.
\(\mathcal {A}\) sends to \(\mathcal {C}\):
-
A set \(\mathcal {Q}= \{1, \dots , m\}\) of queriers, a set \(\mathcal {D}= \{1, \dots , n\}\) of data owners, and a subset \(\mathcal {D}_c\subseteq \mathcal {D}\) of corrupted data owners.
-
For every \(i \in \mathcal {D}_c\), a data key \(K_i\).
-
For every \(i\in \mathcal {D}\), two sets \(S_i^0,S_i^1\subseteq \mathcal{{U}}\), where \(\left| S_i^0\right| = \left| S_i^1\right| \) for \(i \notin \mathcal {D}_c\), and \(S_i^0 = S_i^1\) for \(i \in \mathcal {D}_c\).
-
A bipartite share graph \(G = \left( \mathcal {Q}, \mathcal {D}, E\right) \).
-
For every \(j\in \mathcal {Q}\), two sequences of distinct keywords \(\left( w_{j,1}^0, \dots , w_{j,k_j}^0\right) \) and \(\left( w_{j,1}^1, \dots , w_{j,k_j}^1\right) \) (for some \(k_j\in \mathbb {N}\)), such that for every \(i\in \mathcal {D}\), if \(\left( j, i\right) \in E\) then for every \(1\le l\le k_j\), \(w_{j,l}^0 \in S_i^0\) if and only if \(w_{j,l}^1 \in S_i^1\).
-
-
2.
\(\mathcal {C}\) performs the following:
-
Chooses a random bit \(b \leftarrow \{0,1\}\).
-
For each querier \(j \in \mathcal {Q}\), generates \(K^u_j \leftarrow \textsf {QueryKeyGen}\left( 1^{\lambda }\right) \).
-
For each data owner \(i \in \mathcal {D}\setminus \mathcal {D}_c\), generates \(K_i \leftarrow \textsf {DataKeyGen}\left( 1^{\lambda }\right) \).
-
For each set \(S_i^b,i\in \mathcal {D}\), generates \(T_i \leftarrow \textsf {ProcessSet}\left( K_i,S_i^b\right) \).
-
For each edge \(\left( j, i\right) \in E\), generates \(\varDelta _{j,i} \leftarrow \textsf {Share}\left( K_i, K^u_j,T_i\right) \).
-
For each querier j and keyword \(w_{j,l}^b, 1\le l\le k_j\), generates a query \(q_{j,l} \leftarrow \textsf {Query}\left( K^u_j,w_{j,l}^b\right) \).
-
Sends \(\left\{ T_{i}\right\} _{i\in \mathcal {D}}\), \(\left\{ \varDelta _{j,i}\right\} _{\left( j,i\right) \in E}\), and \(\left( q_{j,1},\cdots ,q_{j,k_j}\right) _{j\in \mathcal {Q}}\) to \(\mathcal {A}\).
-
-
3.
A outputs a guess \(b'\), and its advantage is \(\mathsf{{Adv}}_{\mathcal {A}}\left( 1^{\lambda }\right) =\frac{1}{2}-\Pr \left[ b=b'\right] \).
-
1.
Discussion. In Definition 1, sets of keywords are shared with queriers, and share keys are generated by an honest party. Such schemes can be easily adapted to the setting in which documents are shared between users: each document d is associated with the set S of keywords it contains; and an encryption of d is stored alongside the processed set \(T_S\). Searching for keywords in d is performed by searching for the keyword in S, where if the search outputs 1 then the encryption of d is returned to the querier. Moreover, a trusted party is not needed to generate the share keys: we envision that each user will generate her own share keys whenever a document is shared with her. More specifically, when a data owner i shares a document \(d_i\) with a querier j, the data owner will send his data key \(K_i\) to the querier via a secure channel. The querier will then download the processed set \(T_i\) and the encryption of \(d_i\) from the server, and generate \(\varDelta _{j,i}\) herself. This use case also clarifies our assumption that sets are honestly processed: j can verify that \(T_i\) was honestly generated by processing \(S_i\) (which can be extracted from \(d_i\)) using \(K_i\), and comparing to \(T_i\). (Without loss of generality, \(\textsf {ProcessSet}\) is deterministic since any randomness can be provided in \(K_i\).)
Notice that in our definition, the share key is (syntactically) “tied” to the set for which it was generated (\(\textsf {Share}\) depends not only on the data and query keys, but also on the processed set). This should be contrasted with the syntax used in [29, 30] in which the algorithm generating the share keys depends only on the data and query keys. Consequently, resultant schemes inherently guarantee no query privacy when malicious data owners share their sets with honest queriers (as discussed in the introduction). Indeed, when \(\varDelta \) is independent of the set then a malicious server colluding with the data owner can use the data key K to encrypt any set S of his choosing (in particular, a dictionary), then use \(\varDelta \) to search for the query in S. Since K was generated independently of the set, the correctness of the scheme guarantees that the output of search will be correct, and so the server can recover the queried keyword.
Similar to previous works in the field, our definition allows for some information leakage. Specifically, since the adversary is restricted to choosing sets and queries for which \(w_{j,l}^0 \in S_i^0\Leftrightarrow w_{j,l}^1 \in S_i^1\) for every \(\left( j, i\right) \in E\) (see the last bullet in Step 1 of the security game), the scheme leaks the access pattern of which subset of documents is returned in response to each query. Additionally, since we require that each querier makes distinct queries, if a querier makes repeated queries then this might be leaked to the server. Finally, we note that our definition is selective: the adversary is required to specify in advance the sets, queries, and share graph. Possible extensions and generalizations include adaptive security, where the adversary can adaptively choose sets and queries, add edges to the share graph, and corrupt data owners; and simulation-based security, which guarantees that the view of every PPT adversary can be simulated given only the aforementioned leakage (namely, the access patterns and the sizes of the sets). We elaborate on these alternative definitions in Sect. 6.
4 MKSE with Fast Search
In this section we describe our MKSE scheme based on PRFs. Concretely, we will prove the following theorem.
Theorem 1
(MKSE (Sublinear Search)). Assume that OWFs exist. Then there exists a secure MKSE scheme in which searching for keywords in a set S takes \(\mathsf{{poly}}\left( \lambda \right) \) time, where \(\lambda \) is the security parameter.
Moreover, data and query keys, as well as queries, have length \(\mathsf{{poly}}\left( \lambda \right) \), and for a set S, its processed version and share keys have size \(\left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \).
We first describe our construction, then analyze its properties.
Construction 1
(MKSE (Sublinear Search)). The construction uses a PRF F, and a symmetric-key encryption scheme \(\left( \textsf {KeyGen}, \mathsf{{Enc}}, \mathsf{{Dec}}\right) \), as building blocks.
-
 outputs a symmetric key \(K_{\mathsf{{SE}}} \leftarrow \textsf {KeyGen}\left( 1^{\lambda }\right) \).
outputs a symmetric key \(K_{\mathsf{{SE}}} \leftarrow \textsf {KeyGen}\left( 1^{\lambda }\right) \). -
 outputs a uniformly random PRF key \(K_{\mathsf{{PRF}}} \leftarrow \{0,1\}^{\lambda }\).
outputs a uniformly random PRF key \(K_{\mathsf{{PRF}}} \leftarrow \{0,1\}^{\lambda }\). -
 outputs \(\mathsf{{Enc}}_{K_{\mathsf{{SE}}}}\left( S\right) \).
outputs \(\mathsf{{Enc}}_{K_{\mathsf{{SE}}}}\left( S\right) \). -
 operates as follows:
operates as follows:-
Generates a uniformly random string \(r \leftarrow \{0,1\}^{\lambda }\).
-
Decrypts \(S \leftarrow \mathsf{{Dec}}_{K_{\mathsf{{SE}}}}\left( T\right) \).
-
Initializes \(D=\emptyset \). For each keyword \(w_i \in S\), computes \(k_i' = F_{K_{\mathsf{{PRF}}}}\left( w_i\right) \) and \(d_i = F_{k_i'}\left( r\right) \), and adds \(d_i\) to D.
-
Inserts D into a perfect hash table [11] to obtain \(D'\).
-
Outputs \(\varDelta = \left( r,D'\right) \).
-
-
 outputs \(F_{K_{\mathsf{{PRF}}}}\left( w\right) \).
outputs \(F_{K_{\mathsf{{PRF}}}}\left( w\right) \). -
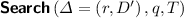 operates as follows:
operates as follows:-
Computes \(d' = F_q\left( r\right) \).
-
Performs a hash table query on \(D'\) for \(d'\), and outputs 1 if and only if \(d'\) was found.
-
The next claim states that Construction 1 is secure, and summarizes its parameters.
Claim 1
Assume that Construction 1 is instantiated with a PRF F, and a secure symmetric encryption scheme, then it is a secure MKSE scheme.
Moreover, data and query keys have length \(\mathsf{{poly}}\left( \lambda \right) \), and for a set S the processed set has size \(\left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \). Furthermore, searching in a set S takes time \(\mathsf{{poly}}(\lambda )\) and queries have size \(\mathsf{{poly}}(\lambda )\).
Proof
The correctness of the scheme follows directly from the correctness of the underling primitives, and its complexity follows directly from the construction and from the following theorem due to Fredman et al. [11].
Theorem 2
(Perfect hashing [11]). Given a set D of n keys from a universe \(\mathcal {U}\), there exists a method that runs in expected \(O\left( n\right) \) time and constructs a lookup table \(D'\) of size \(O\left( n\right) \) such that membership queries (i.e., given \(x\in \mathcal {U}\), determine if \(x\in S\)) can be answered in constant time.
We now argue that the scheme is secure.
For every \(i\in \mathcal {D}\), let \(S_i^0,S_i^1\) be the sets \(\mathcal {A}\) chose for data owner i, and let \(\mathcal{{W}}_j^0,\mathcal{{W}}_j^1\) be the sets of queries \(\mathcal {A}\) chose for querier \(j\in \mathcal {Q}\). Let \(F^1\) denote the PRF called in \(\textsf {Query}\) and to compute \(k_i'\) in \(\textsf {Share}\), and let \(F^2\) be the PRF invoked to compute \(d_i\) in \(\textsf {Share}\). Let \(\mathsf{{view}}_0,\mathsf{{view}}_1\) denote the view of \(\mathcal {A}\) in the security game when \(b=0,1\) (respectively). We show that \(\mathsf{{view}}_0\approx \mathsf{{view}}_1\) using a sequence of hybrid distributions, and conclude that \(\mathcal {A}\) has only a \(\mathsf{{negl}}\left( \lambda \right) \) advantage in the security game. As the data keys, and encrypted sets, of corrupted data owners are identically distributed in both views (because \(S_i^0=S_i^1\) for every \(i\in \mathcal {D}_c\)), we can fix these values into \(\mathsf{{view}}_0,\mathsf{{view}}_1\), and all hybrid distributions, without decreasing the computational distance. Moreover, if F is sufficiently expanding then with overwhelming probability, all images of the form \(F^1_K\left( w\right) \), and \(F^2_{k_i'}\left( r\right) \) (for query keys K, keywords w, set identifiers r, and \(k_i'\)) are distinct, so it suffices to bound the computational distance conditioned on this event. We now define the hybrids.
For \(b \in \{0,1\}\), let \(\mathcal {H}_0^b\) be the distribution obtained from \(\mathsf{{view}}_b\) by replacing \(F^1\) with a random function \(\mathcal {R}\). (We think of \(\mathcal {R}\) as taking two inputs, the first being a querier index. Thus, \(\mathcal {R}\) defines a family \(\left\{ \mathcal {R}_j\right\} _j\) of functions, as does \(F^1\).) That is, for all queriers j, and \(w_l \in \mathcal{{W}}_j^b\), we have \(q'_{j,l} = \mathcal {R}\left( w_i \right) \) (the tag is used to denote queries in \(\mathcal {H}_0^b\); queries in \(\mathsf{{view}}_b\) are untagged). Then \(\mathsf{{view}}_b \approx \mathcal {H}_0^b\) follows from the pseudorandomness of F by a standard hybrid arguments in which we replace the invocations of \(F^1\) (used to generate the queries and share keys) of one querier at a time.
We now define \(\mathcal {H}_1^b\) to be identical to \(\mathcal {H}_0^b\), except that \(F^2\) is replaced with the random function \(\mathcal {R}\) (notice that here, the first input of \(\mathcal {R}\) corresponds to a query \(q'\)), and the keyword tokens in every share key \(\varDelta _{j,i}\) are generated as follows. For every \(w_l \in S_i^b \cap \mathcal{{W}}_j^b\), the corresponding token \(d_{i,j,l}\) is computed as \(F^2_{q'_{j,l}}\left( r\right) \) (i.e., identically to how it is generated in \(\mathcal {H}_0^b\); this is needed since \(q'_{j,l}\) appears in \(\mathcal {H}_1^b\) and so consistency of these tokens with \(F^2\) can be efficiently checked). For every \(w_l \in S_i^b \setminus \mathcal{{W}}_j^b\), \(d_{i,j,l}'\) is chosen randomly subject to the constraint that \(d'_{i,j,l} \notin \left\{ F^2_{q'_{j,l'}}(r)~:~w_{l'} \in \mathcal{{W}}_j^b \right\} \). (This can be efficiently achieved by re-sampling, assuming F is sufficiently stretching.) All values in \(\varDelta _{j,i}\) are then hashed.
To show that \(\mathcal {H}_0^b \approx \mathcal {H}_1^b\), we first define an intermediate hybrid \(\mathcal {H}^{b,\star }\) in which for every querier j, every data owner i, and every keyword \(w_l\in S_i^b\setminus \mathcal{{W}}_j^b\), the token \(d_{i,j,l}'\) in \(\varDelta _{j,i}\) is replaced with a random value, subject to the constraint that it is not in \(\left\{ F^2_{q'_{j,l'}}(r)~:~w_{l'} \in \mathcal{{W}}_j^b \right\} \), where r is the random identifier associated with \(\varDelta _{j,i}\). Then \(\mathcal {H}_0^b\approx \mathcal {H}^{b,\star }\) follows from the pseudorandomness of F by a standard hybrid argument in which we replace the tokens one at a time (and use the assumption that all images of F are unique).
To show that \(\mathcal {H}_1^b\approx \mathcal {H}^{b,\star }\), we define a series of sub-hybrids, replacing \(F^2\) with a random function for a single query of a single querier at a time. (Notice that each query of each querier represents a unique key for \(F^2\) in all share keys associated with that querier.) Concretely, denote \(m = \left| \mathcal {Q}\right| \), and for every \(j\in \mathcal {Q}\), let \(l_j:=\left| \mathcal{{W}}_j^b\right| \). For every \(1\le j\le m\) and \(0\le l\le l_j\), define \(\mathcal {H}^{b,j,l}\) to be the distribution obtained from \(\mathcal {H}^{b,\star }\) by generating the queries of the first \(j-1\) queriers, and the first l queries of querier j, with \(\mathcal {R}\) (instead of \(F^2\)), and generating the keyword tokens in share keys accordingly. Then \(\mathcal {H}^{b,1,0}=\mathcal {H}^{b,\star }\), and \(\mathcal {H}^{b,m,l_m}=\mathcal {H}_1^b\). For every \(1\le j \le m\) and \(1\le l\le l_j\), \(\mathcal {H}^{b,j,l}\approx \mathcal {H}^{b,j,l-1}\) by the pseudorandomness of \(F^2\). Moreover, \(\mathcal {H}^{b,j,0}=\mathcal {H}^{b,j-1,l_{j-1}}\) for every \(1< j \le m\), so \(\mathcal {H}^{b,1,0}\approx \mathcal {H}^{b,m,l_m}\) (since \(m=\mathsf{{poly}}\left( \lambda \right) \), and \(l_j=\mathsf{{poly}}\left( \lambda \right) \) for every \(j\in \mathcal {Q}\)).
Finally, let \(\mathcal {H}^b_2\) be identical to \(\mathcal {H}^b_1\) except that the encrypted sets of all honest data owners \(i \notin \mathcal {D}_c\) encrypt \(\mathbf {0}\) (instead of \(S_i^b\)). Then \(\mathcal {H}^b_1 \approx \mathcal {H}^b_2\) follows from the security of the encryption scheme by a standard hybrid argument in which the encrypted sets are replaced one at a time. Notice that \(\mathcal {H}^0_2 = \mathcal {H}^1_2\) and so \(\mathsf{{view}}_0\approx \mathsf{{view}}_1\). \(\square \)
Remark 1
Notice that \(\mathcal {H}^b_2\) depends only on the share graph, the sets of corrupted data owners, the sizes of sets of honest data owners, and the access patterns; and can be efficiently generated given these values. This implies that the view of every PPT adversary can be efficiently simulated given only these values, namely, Construction 1 is simulation-secure (as defined in Sect. 6).
The proof of Theorem 1 now follows as a corollary from Claim 1.
Proof of Theorem
1. We instantiate Construction 1 with any sufficiently stretching PRF (e.g., \(F:\{0,1\}^{\lambda }\times \{0,1\}^{n}\rightarrow \{0,1\}^{2\left( \lambda +n\right) }\), whose existence follows from the existence of OWFs), and a secure symmetric encryption scheme (which can be constructed from F). Then the security of the scheme, as well as the length of data keys, query keys, and processed sets, follow directly from Claim 1. As for search time, since keywords have length \(O\left( \lambda \right) \) then evaluating F takes \(\mathsf{{poly}}\left( \lambda \right) \) time, and the outputs have length \(\mathsf{{poly}}(\lambda )\). Searching in a set S takes 1 hash query and thus the overall time is \( \mathsf{{poly}}\left( \lambda \right) \) time, and queries have length \(\mathsf{{poly}}\left( \lambda \right) \). \(\square \)
5 MKSE with Short Share Keys
In this section we describe an MKSE scheme with short share keys which employs a program obfuscator as a building block. We first show (Sect. 5.1) a scheme based on differing-inputs obfuscation (diO), then show (Sect. 5.2) that a slightly modified construction can be based on public-coin differing-inputs obfuscation (pc-diO). We note that though there is evidence that diO for general circuits might not exist [2, 13], no such implausibility results are known for pc-diO.
5.1 MKSE from Differing-Inputs Obfuscation
We construct a secure MKSE scheme using a diO obfuscator for Turing Machines (TMs). Concretely, we prove the following for a universe \(\mathcal {U}\) of size \(\left| \mathcal {U}\right| \le \mathsf{{poly}}\left( 2^{\lambda }\right) \):
Theorem 3
(MKSE (Short Share Keys)). Assume that CRHFs, and diO for TMs with polynomial blowup, exist. Then there exists a secure MKSE in which share keys have size \(\mathsf{{poly}}\left( \lambda \right) \), for a security parameter \(\lambda \). Moreover, data and query keys, as well as queries, have length \(\mathsf{{poly}}\left( \lambda \right) \), and given a set S, its processed version has size \(\left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \), and searching in it takes \(\mathsf{{poly}}\left( \lambda ,\left| S\right| \right) \) time.
The high-level idea of the constructions is to encrypt sets under their data key, and queries under the query key of the querier, using a standard (symmetric) encryption scheme. The share key will be an obfuscation of a program that has both keys hard-wired into it, and thus allows for searching (even though queries and sets are encrypted under different keys) by decrypting the ciphertexts and comparing the underlying keywords. However, to make this rough intuition work, we need to handle a few subtleties.
First, to obtain security, the program should take the entire set as input. Otherwise (i.e., if it operates on a single set element at a time), its output would reveal not only whether the queried keyword appears in the set, but also where it appears. To see why this violates security, consider the case in which the same set \(S_i\) is shared with two different queriers j and \(j'\): the additional information of where in the set a query appears allows the server to check whether j and \(j'\) queried the same keyword (even when \(j,j'\) and data owner i are all honest). Notice that since the program takes the entire set as input, it cannot be represented as a circuit (since then share keys will not have sublinear size). Therefore, we implement the program as a TM, and use an obfuscator for TMs.
Second, as noted in the introduction, share keys should only allow searching for keywords in the sets for which they were generated. That is, a share key \(\varDelta _{j,i}\) between querier j and data owner i should be “tied” to the set \(S_i\) of i. We achieve this by hard-wiring a hash \(h\left( S_i\right) \) of \(S_i\) into the program \(P_{j,i}\) obfuscated in \(\varDelta _{j,i}\), where \(P_{j,i}\) checks that its input set is consistent with the hash. Notice that the hard-wired hash prevents us from using an indistinguishability obfuscator [1]. Indeed, if i is honest then in the security game (Definition 1), the adversary chooses a pair \(S_i^0,S_i^1\) of (possibly different) sets for i, and \(\varDelta _{j,i}\) has either \(h\left( S_i^0\right) \) (in the game with \(b=0\)) or \(h\left( S_i^1\right) \) (in the game with \(b=1\)) hard-wired into it. In particular, the underlying programs are not functionally equivalent, so we cannot rely on indistinguishability obfuscation, and need to use a stronger primitive. Concretely, our constructions rely on the existence of a diO, or a pc-diO, obfusctor. We proceed to describe the diO-based construction (the pc-diO-based construction is described in Sect. 5.2).
The last ingredient we need is a signature scheme, which will be used to sign queries. Specifically, a query for keyword w will consist of an encryption c of w, and a signature on c; and share keys will have the corresponding verification key hard-wired into them. Intuitively, signatures are used to guarantee the server can only search for queries the querier actually issued, similar to the way the hashed set prevents the server from searching in sets that were not shared with the querier. Concretely, the signatures guarantee that the share keys in the security game for \(b=0\) and \(b=1\) are differing-inputs even given the entire view of the adversary, and allows us to rely on diO security. (Roughly, a pair of programs are differing-inputs if it is infeasible for a PPT algorithm to find an input on which their outputs differ.)
Remark 2
We note that if one is willing to change the MKSE syntax, allowing the server to return encrypted answers which the querier then decrypts, then a scheme with similar complexity could be constructed from Fully Homomorphic Encryption (using Oblivious RAM or Private Information Retrieval). However, following previous works in the field [17, 23, 29] we focus on the setting in which the server gets the answers in the clear (and queriers do not need to decrypt). This may be crucial in some situations, e.g., when huge documents are associated with small keyword sets. In a solution based on Fully Homomorphic Encryption, the computation of a search is proportional to the total size of all the huge documents, while in our obfuscation-based MKSE scheme the work is proportional to the total number of keywords, and the size of the returned documents.
We now describe our MKSE scheme. As will become evident from the security proof, due to the technicalities of using diO security we will need a special type of encryption (which, nonetheless, can be constructed from any standard encryption scheme) that we call double encryption. It is similar to the encryption scheme used in the “2-key trick” of Naor and Yung [27] (to convert a CPA-secure encryption scheme into a CCA-secure one), except it does not use non-interactive zero-knowledge proofs to prove that ciphertexts encrypt the same value.
Definition 2
(Double encryption). Let \(\lambda \in \mathbb {N}\) be a security parameter. Given a symmetric encryption scheme \(\left( \textsf {KeyGen},\mathsf{{Enc}},\mathsf{{Dec}}\right) \), we define a double symmetric encryption scheme \(\mathsf{{E}}^2=\left( \textsf {KeyGen}^2,\mathsf{{Enc}}^2,\mathsf{{Dec}}^2\right) \) as follows:
-
\(\textsf {KeyGen}^2\), on input \(1^{\lambda }\), generates \(\textsf {K}_L\leftarrow \textsf {KeyGen}\left( 1^{\lambda }\right) \) and \(\textsf {K}_R\leftarrow \textsf {KeyGen}\left( 1^{\lambda }\right) \), and outputs \(\textsf {K}=\left( \textsf {K}_L,\textsf {K}_R\right) \).
-
\(\mathsf{{Enc}}^2\), on input a key \(\textsf {K}=\left( \textsf {K}_L,\textsf {K}_R\right) \) and a message m, computes \(c_L\leftarrow \mathsf{{Enc}}\left( \textsf {K}_L,m\right) \) and \(c_R\leftarrow \mathsf{{Enc}}\left( \textsf {K}_R,m\right) \), and outputs \(c=\left( c_L,c_R\right) \).
-
\(\mathsf{{Dec}}^2\), on input a key \(\textsf {K}=\left( \textsf {K}_L,\textsf {K}_R\right) \) and a ciphertext \(c=\left( c_L,c_R\right) \), outputs \(\mathsf{{Dec}}\left( \textsf {K}_L,c_L\right) \). (Notice that decryption disregards the “right” component of c.)
We are now ready to describe our MKSE scheme.
Construction 2
(MKSE (Short Share Keys)). The MKSE uses the following building blocks:
-
an obfuscator \(\mathcal {O}\),
-
a hash function h,
-
a double symmetric encryption scheme \(\left( \textsf {KeyGen},\mathsf{{Enc}},\mathsf{{Dec}}\right) \), and
-
a signature scheme \(\left( \textsf {KeyGen}_{s},\textsf {Sign},\textsf {Ver}\right) \),
and is defined as follows:
-
 generates a random encryption key \(\textsf {K}\leftarrow \textsf {KeyGen}\left( 1^{\lambda }\right) \) and outputs \(\textsf {K}\).
generates a random encryption key \(\textsf {K}\leftarrow \textsf {KeyGen}\left( 1^{\lambda }\right) \) and outputs \(\textsf {K}\). -
 generates a random encryption key \(\textsf {K}^u\leftarrow \textsf {KeyGen}\left( 1^{\lambda }\right) \), and a random signing and verification key pair \(\left( \textsf {sk}^u,\textsf {vk}^u\right) \leftarrow \textsf {KeyGen}_s\left( 1^{\lambda }\right) \), and outputs \(K^u=\left( \textsf {K}^u,\textsf {sk}^u,\textsf {vk}^u\right) \).
generates a random encryption key \(\textsf {K}^u\leftarrow \textsf {KeyGen}\left( 1^{\lambda }\right) \), and a random signing and verification key pair \(\left( \textsf {sk}^u,\textsf {vk}^u\right) \leftarrow \textsf {KeyGen}_s\left( 1^{\lambda }\right) \), and outputs \(K^u=\left( \textsf {K}^u,\textsf {sk}^u,\textsf {vk}^u\right) \). -
 encrypts each element \(s\in \mathcal{{S}}\) as \(c\left( s\right) \leftarrow \mathsf{{Enc}}\left( \textsf {K},s\right) \), and outputs \(\left\{ c\left( s\right) \ :\ s\in \mathcal{{S}}\right\} \).
encrypts each element \(s\in \mathcal{{S}}\) as \(c\left( s\right) \leftarrow \mathsf{{Enc}}\left( \textsf {K},s\right) \), and outputs \(\left\{ c\left( s\right) \ :\ s\in \mathcal{{S}}\right\} \). -
 generates \(\widetilde{P}\leftarrow \mathcal {O}\left( P_{\textsf {K},\left( \textsf {K}^u,\textsf {vk}^u\right) ,h\left( T_S\right) }\right) \) where \(P_{\textsf {K},\left( \textsf {K}^u,\textsf {vk}^u\right) ,h\left( T_S\right) }\) is the TM defined in Fig. 1, and outputs \(\varDelta =\widetilde{P}\).
generates \(\widetilde{P}\leftarrow \mathcal {O}\left( P_{\textsf {K},\left( \textsf {K}^u,\textsf {vk}^u\right) ,h\left( T_S\right) }\right) \) where \(P_{\textsf {K},\left( \textsf {K}^u,\textsf {vk}^u\right) ,h\left( T_S\right) }\) is the TM defined in Fig. 1, and outputs \(\varDelta =\widetilde{P}\). -
 generates \(c\leftarrow \mathsf{{Enc}}\left( \textsf {K}^u,w\right) \) and \(\sigma \leftarrow \textsf {Sign}\left( \textsf {sk}^u,c\right) \), and outputs \(\left( c,\sigma \right) \).
generates \(c\leftarrow \mathsf{{Enc}}\left( \textsf {K}^u,w\right) \) and \(\sigma \leftarrow \textsf {Sign}\left( \textsf {sk}^u,c\right) \), and outputs \(\left( c,\sigma \right) \). -
 outputs \(\varDelta \left( T_S,q\right) \).
outputs \(\varDelta \left( T_S,q\right) \).
Program \(P_{\textsf {K},\left( \textsf {K}^u,\textsf {vk}^u\right) ,h\left( T_S\right) }\) used to generate share keys in Construction 2
The following claim states that if the obfuscator \(\mathcal {O}\) used in Construction 2 is a secure diO obfuscator, and all building blocks are secure, then Construction 2 is an MKSE scheme (as in Definition 1).
Claim 2
(MKSE (Short Share Keys)). If Construction 2 is instantiated with a secure diO obfuscator for TMs, and assuming the security of all building blocks, then Construction 2 is a secure MKSE.
Moreover, if the encryption and signature schemes have \(\mathsf{{poly}}\left( \lambda \right) \)-length keys, and incur a \(\mathsf{{poly}}\left( \lambda \right) \) overhead, then data and query keys, as well as queries, have length \(\mathsf{{poly}}\left( \lambda \right) \), and for a set S, its corresponding processed set has size \(\left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \). Furthermore, if: (1) evaluating h on length-n inputs takes \(H_T\left( n\right) \) time, and outputs a hash of length \(H_{\ell }\left( n\right) \); and (2) there exist functions \(\textsf {s},T_{\mathcal {O}}:\mathbb {N}\rightarrow \mathbb {N}\) such that for every TM M, \(\left| \mathcal {O}\left( M\right) \right| \le \textsf {s}\left( \left| M\right| \right) \), and running \(\mathcal {O}\left( M\right) \) on inputs of length n takes \(T_{\mathcal {O}}\left( \textsf {TIME}\left( M,n\right) \right) \) time, where \(\textsf {TIME}\left( M,n\right) \) is the running time of M on length-n inputs; then running \(\textsf {Search}\) on a set S takes \(T_{\mathcal {O}}\left( H_T\left( \left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \right) +\left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \right) \) time, and share keys have size \(\textsf {s}\left( H_{\ell }\left( \left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \right) \cdot \mathsf{{poly}}\left( \lambda \right) \right) \).
Remark 3
We note that the security of Construction 2 does not require the diO obfuscator to be secure with relation to arbitrary auxiliary inputs, but rather it is only required to guarantee security against a specific class of auxiliary inputs, as specified in the proof of Claim 2.
Proof of Claim
2. The correctness of the scheme follows directly from the correctness of the underlying primitives. We now argue that the scheme is secure.
Let \(\mathcal {A}\) be a PPT adversary in the security game of Definition 1, let \(\textsf {K}_i\) be the data key \(\mathcal {A}\) chose for data owner i, and let \(\mathcal{{W}}^0,\mathcal{{W}}^1\) be the sets of queries \(\mathcal {A}\) chose (for all other values chosen by \(\mathcal {A}\), we use the notation of Definition 1). We proceed through a sequence of hybrids. Recall that the view of \(\mathcal {A}\) in the security game consists of the encrypted sets \(T_{S_i^b}\) for every \(i\in \mathcal {D}\), queries q for every \(w\in \mathcal{{W}}^b\), and for every edge \(\left( j,i\right) \in E\), the obfuscated program \(\varDelta _{j,i}\). In particular, since the keys, and encrypted sets, of corrupted data owners are identically distributed when \(b=0,1\) (because \(S_i^0=S_i^1\) for every \(i\in \mathcal {D}_c\), and they are encrypted using the same keys), we can fix these values into all hybrid distributions, without decreasing the computational distance. Moreover, we assume without loss of generality that all data keys \(\textsf {K}_i\) chosen by \(\mathcal {A}\) are valid. We now define the hybrids.
-
\(\mathbf {\mathsf{{view}}_0}\): \(\mathsf{{view}}_0\) is the view of \(\mathcal {A}\) in the security game with \(b=0\).
-
\(\mathbf {\mathcal {H}_0}\): In hybrid \(\mathcal {H}_0\), the keys \(\textsf {K}=\left( \textsf {K}_L,\textsf {K}_R\right) ,\textsf {K}^u=\left( \textsf {K}_L^u,\textsf {K}_R^u\right) \) in every obfuscated program \(P_{\textsf {K},\left( \textsf {K}^u,\textsf {vk}^u\right) ,h\left( T_{S^0}\right) }\) are replaced with the keys \(\textsf {K}'=\left( \textsf {K}_L,\mathbf {0}\right) ,\textsf {K}^{u\prime }=\left( \textsf {K}_L^u,\mathbf {0}\right) \).
\(\mathcal {H}_0\approx \mathsf{{view}}_0\) by the diO security of \(\mathcal {O}\) (and a standard hybrid argument over all obfuscated programs in \(\mathsf{{view}}_0,\mathcal {H}_0\)), because the TMs in each of the share keys \(\varDelta _{j,i}\) in \(\mathsf{{view}}_0,\mathcal {H}_0\) are differing-inputs. Indeed, they are actually functionally equivalent (given any auxiliary input), since \(\mathsf{{Dec}}^2\) completely disregards the right ciphertext, and so replacing the right secret key with the all-0 string does not affect functionality.
-
\(\mathbf {\mathcal {H}_1}\): In hybrid \(\mathcal {H}_1\), the encrypted set \(T_i\) of every honest data owner \(i\notin \mathcal {D}_c\) is generated as the encryption of \(\left( S_i^0,S_i^1\right) \) with \(\mathsf{{Enc}}^L\) (see Definition 3 below) instead of \(\mathsf{{Enc}}^2\). (Notice that this also affects the share keys.)
To prove that \(\mathcal {H}_0\approx \mathcal {H}_1\), we will use the following lemma.
Lemma 1
Let \(\star \in \left\{ L,R\right\} \). For every pair \(\left( m_L,m_R\right) \) of messages, the following distributions are computationally indistinguishable, when \(\mathsf{{E}}^2,\mathsf{{E}}^{\star }\) use the same underlying encryption scheme \(\mathsf{{E}}=\left( \textsf {KeyGen},\mathsf{{Enc}},\mathsf{{Dec}}\right) \).
-
\(\mathcal {D}_1\): generate \(\textsf {K}=\left( \textsf {K}_L,\textsf {K}_R\right) \leftarrow \textsf {KeyGen}^2\left( 1^{\lambda }\right) \) and \(c\leftarrow \mathsf{{Enc}}^2\left( \textsf {K},m_{\star }\right) \), and output \(\left( \textsf {K}_{\star },c\right) \).
-
\(\mathcal {D}_2\): generate \(\textsf {K}=\left( \textsf {K}_L,\textsf {K}_R\right) \leftarrow \textsf {KeyGen}^{\star }\left( 1^{\lambda }\right) \) and \(c\leftarrow \mathsf{{Enc}}^{\star }\left( \textsf {K},\left( m_L,m_R\right) \right) \), and output \(\left( \textsf {K}_{\star },c\right) \).
Proof
We prove the lemma for the case \(\star =L\) (the case \(\star =R\) is similar) by showing that indistinguishability follows from the security of the underlying scheme \(\mathsf{{E}}\). Given a distinguisher \(\mathsf{{D}}\) between \(\mathcal {D}_1,\mathcal {D}_2\), we construct a distinguisher \(\mathsf{{D}}'\) (that has \(m_L\) hard-wired into it) between encryptions according to \(\mathsf{{E}}\) of \(m_L,m_R\). Given a ciphertext c, \(\mathsf{{D}}'\) operates as follows: generates \(\textsf {K}'\leftarrow \textsf {KeyGen}\left( 1^{\lambda }\right) \), computes \(c'\leftarrow \mathsf{{Enc}}\left( \textsf {K}',m_L\right) \), and outputs \(\mathsf{{D}}\left( \textsf {K}',\left( c',c\right) \right) \). Notice that if c encrypts \(m_L\) then the input to \(\mathsf{{D}}\) is distributed according to \(\mathcal {D}_1\), otherwise it is distributed according to \(\mathcal {D}_2\), so the distinguishing advantage of \(\mathsf{{D}}'\) is equal to that of \(\mathsf{{D}}\) which (by the security of \(\mathsf{{E}}\)) is negligible. \(\square \)
By a standard hybrid argument, Lemma 1 implies that polynomially many ciphertexts (generated by \(\mathsf{{E}}^2\) or by \(\mathsf{{E}}^L\), with the same or different keys), together with the keys of the “left” component, are computationally indistinguishable.
We prove \(\mathcal {H}_0\approx \mathcal {H}_1\) by reducing any distinguisher \(\mathsf{{D}}\) between \(\mathcal {H}_0,\mathcal {H}_1\) to a distinguisher \(\mathsf{{D}}'\) between encryptions generated according to \(\mathsf{{E}}^L\) or \(\mathsf{{E}}^2\). We hard-wire into \(\mathsf{{D}}'\) the querier keys and their queries, as well as the keys and encrypted sets of corrupted data owners, and the share keys associated with them. (This is possible because the encryption and signing keys of queriers, and their queries, are identically distributed in \(\mathcal {H}_0,\mathcal {H}_1\), and independent of the encrypted sets; and since the share keys \(\varDelta _{j,i}\) for \(i\in \mathcal {D}_c\) depend only on the keys of data owner i, querier j, and the encrypted set \(T_i\), which are identically distributed in both hybrids.) \(\mathsf{{D}}'\) operates as follows: given a sequence of ciphertexts (the encrypted sets of honest data owners), and the keys corresponding to the ciphertexts in the left components, \(\mathsf{{D}}'\) honestly generates the hashes of encrypted sets of honest data owners, and uses the hard-wired querier keys, together with the keys for the left component in the ciphertexts of honest data owners, to generate the share keys between queriers and honest data owners. (Notice that since we have removed the key of the right component in ciphertexts of honest data owners, these are not needed to generate the share keys.) The values obtained in this way are distributed identically to \(\mathcal {H}_0\) (if the input ciphertexts were generated with \(\mathsf{{E}}^2\)) or \(\mathcal {H}_1\) (if they were generated with \(\mathsf{{E}}^L\)), so \(\mathsf{{D}}'\) has the same distinguishing advantage as \(\mathsf{{D}}\).
We now define the next hybrids.
-
\(\mathbf {\mathcal {H}_2:}\) In hybrid \(\mathcal {H}_2\) the queries \(\left( w_{j,1}^0,\cdots ,w_{j,k_j}^0\right) \) of every querier \(j\in \mathcal {Q}\) are generated using \(\mathsf{{Enc}}^L\) with message \(\left( w_{j,l}^0,w_{j,l}^1\right) ,1\le l\le k_j\), instead of \(\mathsf{{Enc}}^2\).
\(\mathcal {H}_1\approx \mathcal {H}_2\) by a similar argument to the one used to show \(\mathcal {H}_0\approx \mathcal {H}_1\).
-
\(\mathbf {\mathcal {H}_3:}\) In hybrid \(\mathcal {H}_3\), the generation of share keys \(\varDelta _{j,i}\) is modified as follows: (1) the hard-wired keys are \(\left( \mathbf {0},\textsf {K}_{R,i}\right) ,\left( \mathbf {0},\textsf {K}_{R,j}^u\right) \), where \(\left( \textsf {K}_{L,i},\textsf {K}_{R,i}\right) ,\left( \textsf {K}_{L,i}^u,\textsf {K}_{R,j}^u\right) \) are the encryption keys of data owner i and querier j, respectively; and (2) the program P uses \(\mathsf{{Dec}}^R\) (instead of \(\mathsf{{Dec}}^2\)) to decrypt c and \(T_S'\).
\(\mathcal {H}_3\approx \mathcal {H}_2\) by the diO security of \(\mathcal {O}\), as we now show. Let d denote the number of share keys available to the adversary (i.e., \(d=\left| E\right| \)), and order them in some arbitrary way: \(\varDelta ^1,\cdots ,\varDelta ^d\). We define a sequence of hybrids \(\mathcal {H}^0,\cdots ,\mathcal {H}^d\), where in \(\mathcal {H}^l\), the first l share keys are generated as in \(\mathcal {H}_3\) (we denote these keys by \(\varDelta _{k}'\)), and all other share keys are generated as in \(\mathcal {H}_2\). We show that \(\mathcal {H}^l\approx \mathcal {H}^{l-1}\) for every \(1\le l\le d\), and conclude that \(\mathcal {H}_2=\mathcal {H}^0\approx \mathcal {H}^d=\mathcal {H}_3\).
Fix some \(1\le l^*\le d\), and let \(\left( j,i\right) \) be the edge for which \(\varDelta ^{l^*}\) was generated. We fix all the keywords \(\mathcal{{W}}^0,\mathcal{{W}}^1\), and the sets \(S_{i'}^0,S_{i'}^1\) for \(i'\in \mathcal {D}\), into \(\mathcal {H}^{l^*},\mathcal {H}^{l^*-1}\) (this is possible because these values are identical in both hybrids). We additionally fix the keys of every querier \({j'},j'\ne j\) and data owner \({i'},i'\ne i\), the queries that querier \(j'\) makes, the processed sets \(T_{i'},i'\ne i\), and share keys \(\varDelta _{j',i'},\varDelta _{j',i'}'\) (this is possible because these values are identically distributed in both hybrids). We now argue that \(\varDelta _{j,i}',\varDelta _{j,i}\) sampled in \(\mathcal {H}^{l^*},\mathcal {H}^{l^*-1}\) (respectively) form a differing-sinputs family of TMs with respect to the auxiliary information \(\textsf {aux}\) available to \(\mathcal {A}\) (and so \(\mathcal {H}^{l^*}\approx \mathcal {H}^{l^*-1}\) by the diO security of \(\mathcal {O}\)). This auxiliary information consists of the values we have fixed into \(\mathcal {H}^{l^*},\mathcal {H}^{l^*-1}\), the public verification key \(\textsf {vk}_{j}^u\) for signatures of querier j, all queries querier j makes, the encrypted set \(T_i\) of data owner i, and all \(\varDelta _{j,i'},\varDelta _{j',i}\) for \(i'\ne i,j'\ne j\) such that \(\left( j,{i'}\right) ,\left( {j'},{i}\right) \in E\). Let \(\mathcal {P},\mathcal {P}'\) denote the distributions over programs obfuscated in \(\varDelta _{j,i},\varDelta _{j,i}'\), and let \(\mathsf{{D}}\) be a PPT algorithm that obtains \(\left( P,P'\right) \leftarrow \mathcal {P}\times \mathcal {P}'\) and \(\textsf {aux}\). In particular, notice that \(\mathsf{{D}}\) knows the hash \(h\left( T_i\right) \), and the encryption keys \(\textsf {K}_i,\textsf {K}_j^u\) (but not the secret signing key \(\textsf {sk}_{j}^u\)), since these appear in either P or \(P'\). We show that \(\mathsf{{D}}\) succeeds in finding a differing input only with negligible probability.
Consider first the inputs (for \(P,P'\)) available to \(\mathsf{{D}}\) in \(\textsf {aux}\), i.e., the encrypted set \(T_i\) (which encrypts the elements of \({S_i^0}\) in the left components, and the elements of \(S_i^1\) in the right components; this holds even if \(i\in \mathcal {D}_c\) since in that case \(S_i^0=S_i^1\)), and the queries of querier j. For every such query q there exists a pair \(\left( w_L,w_R\right) \) of keywords such that q is of the form \(q=\left( c=\left( c_L,c_R\right) ,\sigma \right) \) where \(c_{\star }\leftarrow \mathsf{{Enc}}\left( \textsf {K}_{\star ,j}^u,m_{\star }\right) ,\star \in \left\{ L,R\right\} \), \(\sigma \leftarrow \textsf {Sign}\left( \textsf {sk}_{j}^u,c\right) \), and \(w_L\in S_i^0\Leftrightarrow w_R\in S_i^1\). (Here, \(\left( \textsf {KeyGen},\mathsf{{Enc}},\mathsf{{Dec}}\right) \) is the encryption scheme used as a building block in the double encryption scheme.) In particular, \(P\left( q,T_i\right) =P'\left( q,T_i\right) \) since the checks in Steps (1)–(2) succeed in both cases, and Steps (4)–(5) return the same outcome (P searches for \(w_L\) in \(S_i^0\), since it decrypts using \(\mathsf{{Dec}}^2\), whereas \(P'\) searches for \(w_R\) in \(S_i^1\), since it decrypts with \(\mathsf{{Dec}}^R\) and the right component of \(T_i\) encrypts \(S_i^1\); and \(w_L\in S_i^0\Leftrightarrow w_R\in S_i^1\)). In particular, both programs have the same running time in this case.
Next, we claim that for every other possible input \(\left( T',c',\sigma '\right) \) that \(\mathsf{{D}}\) chooses (and does not appear in \(\textsf {aux}\)), \(P\left( T',c',\sigma '\right) =P'\left( T',c',\sigma '\right) =0\) except with negligible probability. Indeed, if \(\left( c',\sigma '\right) \ne q\) (where q is some query of querier j) then by the existential unforgeability of the signature scheme, with overwhelming probability \(\sigma '\) is not a valid signature for \(c'\), so the check in Step (1) fails in both \(P,P'\) (in particular, both programs have the same running time in this case). Moreover, if \(T'\ne T_i\) then by the collision resistance of h, with overwhelming probability \(h\left( T'\right) \ne h\left( T_i\right) \), so the check in Step (2) fails (and again, \(P,P'\) have the same running time). Therefore, \(P,P'\) are differing inputs with relation to the auxiliary information \(\textsf {aux}\).
We now define the final set of hybrids.
-
\(\mathbf {\mathcal {H}_4:}\) In hybrid \(\mathcal {H}_4\), the queries \(\left( w_{j,1}^1,\cdots ,w_{j,k_j}^1\right) \) of every querier \(j\in \mathcal {Q}\) are generated using \(\mathsf{{Enc}}^2\) with message \(\left( w_{j,l}^1,w_{j,l}^1\right) ,1\le l\le k_j\), instead of \(\mathsf{{Enc}}^L\) with message \(\left( w_{j,l}^0,w_{j,l}^1\right) ,1\le l\le k_j\).
\(\mathcal {H}_3\approx \mathcal {H}_4\) by a similar argument to the one used to prove \(\mathcal {H}_1\approx \mathcal {H}_2\).
-
\(\mathbf {\mathcal {H}_5:}\) In hybrid \(\mathcal {H}_5\), the encrypted set \(T_i\) of every honest data owner \(i\notin \mathcal {D}_c\) is generated as the encryption of \(\left( S_i^1,S_i^1\right) \) with \(\mathsf{{Enc}}^2\) instead of with \(\mathsf{{Enc}}^L\).
\(\mathcal {H}_4\approx \mathcal {H}_5\) by a similar argument to the one used to prove \(\mathcal {H}_0\approx \mathcal {H}_1\).
-
\(\mathbf {\mathcal {H}_6:}\) In hybrid \(\mathcal {H}_6\), the obfuscated program for every edge \(\left( j,i\right) \in E\) is generated as follows: (1) the hard-wired keys are \(\textsf {K}=\left( \textsf {K}_{L,i},\textsf {K}_{R,i}\right) ,\textsf {K}=\left( \textsf {K}_{L,j}^u,\textsf {K}_{R,j}^u\right) \), instead of \(\textsf {K}'=\left( \mathbf {0},\textsf {K}_{R,i}\right) ,\textsf {K}^{u\prime }=\left( \mathbf {0},\textsf {K}_{R,j}^u\right) \); and (2) \(\mathsf{{Dec}}^2\) is used for decryption (instead of \(\mathsf{{Dec}}^R\)).
\(\mathcal {H}_6\approx \mathcal {H}_5\) by the diO security of \(\mathcal {O}\), using a standard hybrid argument in which the obfuscated programs are replaced one at a time. When replacing the program for edge \(\left( j,i\right) \) from \(P'\) (in \(\mathcal {H}_5\)) to P (in \(\mathcal {H}_6\)), the PPT \(\mathsf{{D}}\) (which should find a differing input) is given (as part of the auxiliary information \(\textsf {aux}\)) the sets \(S_{i'}^1,i'\in \mathcal {D}\); the keywords in \(\mathcal{{W}}^1\) and the corresponding queries; the encryption keys of all data owners \({i'},i'\ne i\) and querier \({j'},j'\ne j\); the signing and verification keys of all queriers \({j'},j'\ne j\); and all encrypted sets \(T_{i'},i'\in \mathcal {D}\). Also, from \(P,P'\) the distinguisher learns the encryption keys \(\textsf {K}_i,\textsf {K}_j^u\), and the verification key \(\textsf {vk}_{j}^u\). We show that except with negligible probability, \(\mathsf{{D}}\) fails to find a differing input (the argument is similar to that used to prove \(\mathcal {H}_3\approx \mathcal {H}_2\)).
The inputs (for \(P,P'\)) available to \(\mathsf{{D}}\) in \(\textsf {aux}\), i.e., the encrypted set \(T_{i}\), and queries \(q=\left( c,\sigma \right) \) of querier j (where \(c\leftarrow \mathsf{{Enc}}^2\left( \textsf {K}_j^u,m\right) \) for some m, and \(\sigma \leftarrow \textsf {Sign}\left( \textsf {sk}_{j}^u,c\right) \)), are not differing-inputs (even though \(P'\) decrypts the right component of c, whereas P decrypts the left component) because both components of c encrypt m according to \(\mathsf{{Enc}}\) (so both \(P,P'\) search for m in \(S_i^1\)). For every other possible input \(\left( T',c',\sigma '\right) \) that \(\mathsf{{D}}\) chooses, \(P\left( T',c',\sigma '\right) =P'\left( T',c',\sigma '\right) =0\) except with negligible probability: if \(\left( c',\sigma '\right) \ne q\) (where q is some query of querier j) then with overwhelming probability \(\sigma '\) is not a valid signature on \(c'\) (by the existential unforgeability of the signature scheme); whereas if \(T'\ne T_i\) then with overwhelming probability \(h\left( T'\right) \ne h\left( T_i\right) \) (by the collision resistance of h). Consequently, \(\mathcal {H}_5\approx \mathcal {H}_6\). Since \(\mathcal {H}_6\) is the view of \(\mathcal {A}\) in the security game with \(b=1\), we conclude that \(\mathcal {A}\) has only negligible advantage in the security game.
Finally, we analyze the complexity of the scheme. Data and query keys, which are simply encryption and signing keys, have size \(\mathsf{{poly}}\left( \lambda \right) \). Queries are ciphertext for length-\(O\left( \lambda \right) \) keywords (since the universe is at most of size \(2^{\lambda }\)), together with signatures on these ciphertexts. Similarly, a processed set consists of encryptions of each of its keywords, so its size is \(\left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \). Regarding share keys, the TM has size \(H_{\ell }\left( \left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \right) \cdot \mathsf{{poly}}\left( \lambda \right) \) (since \(\left| h\left( T_S\right) \right| \le H_{\ell }\left( \left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \right) \)), and so by the assumption on the blowup caused by obfuscation, share keys have size \(\textsf {s}\left( H_{\ell }\left( \left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \right) \cdot \mathsf{{poly}}\left( \lambda \right) \right) \). Finally, \(\textsf {Search}\) consists of running the obfuscated TM, which requires computing the hash (\(H_T\left( \left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \right) \) time), and performing \(O\left( \left| S\right| \right) \) operations, each taking \(\mathsf{{poly}}\left( \lambda \right) \) time, so \(\textsf {TIME}\left( M,\left| S\right| \right) = H_T\left( \left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \right) +\left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \), and consequently the running time is \(T_{\mathcal {O}}\left( H_T\left( \left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \right) +\left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \right) \). \(\square \)
The following encryption scheme was used to prove Claim 2:
Definition 3
Given a symmetric encryption scheme \(\left( \textsf {KeyGen},\mathsf{{Enc}},\mathsf{{Dec}}\right) \), and \(\star \in \left\{ L,R\right\} \), define an encryption scheme \(\mathsf{{E}}^{\star }=\left( \textsf {KeyGen}^{\star },\mathsf{{Enc}}^{\star },\mathsf{{Dec}}^{\star }\right) \) as follows:
-
\(\textsf {KeyGen}^{\star }\) operates as \(\textsf {KeyGen}^2\) from Definition 2. Namely, on input \(1^{\lambda }\) it generates \(\textsf {K}_L\leftarrow \textsf {KeyGen}\left( 1^{\lambda }\right) \), \(\textsf {K}_R\leftarrow \textsf {KeyGen}\left( 1^{\lambda }\right) \), and outputs \(\textsf {K}=\left( \textsf {K}_L,\textsf {K}_R\right) \).
-
\(\mathsf{{Enc}}^{\star }\), on input a key \(\textsf {K}=\left( \textsf {K}_L,\textsf {K}_R\right) \) and a message \(m=\left( m_L,m_R\right) \), computes \(c_L\leftarrow \mathsf{{Enc}}\left( \textsf {K}_L,m_L\right) \) and \(c_R\leftarrow \mathsf{{Enc}}\left( \textsf {K}_R,m_R\right) \), and outputs \(c=\left( c_L,c_R\right) \).
-
\(\mathsf{{Dec}}^{\star }\), on input a key \(\textsf {K}=\left( \textsf {K}_L,\textsf {K}_R\right) \) and a ciphertext \(c=\left( c_L,c_R\right) \), outputs \(\mathsf{{Dec}}\left( \textsf {K}_{\star },c_{\star }\right) \).
The proof of Theorem 3 now follows as a corollary from Claim 2.
Proof of Theorem
3. We instantiate Construction 2 with the double encryption scheme of Definition 2, based on the encryption scheme whose existence follows from the existence of a CRHF; the hash function with a Merkle Hash Tree (MHT) hash based on the CRHF; and instantiate \(\mathcal {O}\) with the diO obfuscator. Then the security of the scheme, as well as the length of data and query keys, queries, and processed sets, follow directly from Claim 2. Regarding share keys, the MHT has \(\mathsf{{poly}}\left( \lambda \right) \)-length outputs, and \(\mathcal {O}\) causes only a polynomial blowup, so by Claim 2, share keys have length \(\mathsf{{poly}}\left( \lambda \right) \). Finally, generating the MHT for a set of size s takes time \(s\cdot \mathsf{{poly}}\left( \lambda \right) \), and so the runtime of \(\textsf {Search}\) is \(\mathsf{{poly}}\left( \lambda ,\left| S\right| \right) \). \(\square \)
5.2 MKSE from Public-Coin Differing-Inputs Obfuscation
In this section we show that a slight modification of Construction 2 is secure assuming the underlying obfuscator is a pc-diO obfuscator for TMs. More specifically, we only need to use a signature scheme with some “special” properties. Concretely, we prove the following for a universe \(\mathcal {U}\) of size \(\left| \mathcal {U}\right| \le \mathsf{{poly}}\left( 2^{\lambda }\right) \):
Theorem 4
(MKSE from pc-diO (short share keys)). Assume that OWPs, CRHFs, and pc-diO for TMs with polynomial blowup, exist. Then there exists a secure MKSE in which share keys have size \(\mathsf{{poly}}\left( \lambda \right) \), where \(\lambda \) is a security parameter. Moreover, data and query keys, as well as queries, have length \(\mathsf{{poly}}\left( \lambda \right) \), and given a set S, its processed version has size \(\left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \), and searching in it takes \(\mathsf{{poly}}\left( \lambda ,\left| S\right| \right) \) time.
The reason we need to change the MKSE scheme outlined in Sect. 5.1 is that it cannot use a pc-diO obfuscator. (Roughly speaking, pc-diO guarantees indistinguishability of the obfuscated programs only as long as it is infeasible for a PPT adversary to find an input on which they differ, even given the randomness used to sample the programs.) Indeed, for every querier j and data owner i, the randomness used to sample the program \(P_{j,i}\) (i.e., the program obfuscated in the share key \(\varDelta _{j,i}\)) includes the signing key of querier j. This allows one to sign arbitrary messages, meaning the obfuscated programs in the security game when \(b=0\) and \(b=1\) are not differing-inputs. (The program \(P_{j,i}\) for querier j and data owner i contains \(h\left( S_i^0\right) \) when \(b=0\), and \(h\left( S_i^1\right) \) when \(b=1\), so a differing input would be a query on any keyword contained in one and not the other. The query can be efficiently generated since the encryption and signing keys appear in the randomness used to sample \(P_{j,i}\).)
To overcome this issue, we introduce a new signature primitive which we call dual-mode signatures. Roughly, a dual-mode signature scheme is an existentially-unforgeable signature scheme associated with an additional \(\textsf {SpecialGen}\) algorithm that given a list of messages, generates “fake” signatures on these messages, and a “fake” verification key under which they can be verified. These “fake” signatures and key are computationally indistinguishable from honestly generated signatures and verification key, and the “fake” verification key cannot be used to successfully sign other messages, even given the randomness used to generate the “special mode” verification key and signatures. (This rules out the trivial construction in which \(\textsf {SpecialGen}\) simply runs the key generation and signing algorithms.) Due to space limitations, we defer the formal definition to the full version [19].
One can think of the \(\textsf {SpecialGen}\) algorithm as a way of “puncturing” the signing key from the procedure that generates the verification key and signatures. We use this viewpoint to prove security based on pc-diO security and dual-mode signatures: we first replace the actual verification key used in \(P_{j,i}\), and the signatures in the queries of j, with ones generated by \(\textsf {SpecialGen}\); and then use pc-diO security to replace the obfuscated program from one containing \(h\left( S_i^0\right) \) to one containing \(h\left( S_i^1\right) \). (Notice that now the randomness used to sample \(P_{j,i}\) does not contain the signing key, so one cannot sign queries that j did not issue.)
In the full version [19], we construct dual-mode signatures from OWPs and CRHFs:
Theorem 5
Assume that OWPs and CRHFs exist. Then there exists a dual-mode signature scheme. Moreover, there exists a polynomial \(p\left( \lambda \right) \) such that signatures on length-n messages have length \(5p\left( \lambda \right) \cdot \left( n+1\right) \), signing keys have length \(2p\left( \lambda \right) +\lambda \), and verification keys have length \(2p\left( \lambda \right) \).
We instantiate Construction 2 with a pc-diO obfuscator and the dual-mode signatures of Theorem 5. The properties of the resultant scheme are summarized in the following claim (whose proof is similar to that of Claim 2).
Claim 3
(MKSE (Short Share Keys) from pc-diO). If Construction 2 is instantiated with a secure pc-diO obfuscator for TMs and a secure dual-mode signature scheme, and assuming the security of all building blocks, then Construction 2 is a secure MKSE.
Moreover, if on messages of length n the dual-mode signature scheme outputs signing and verification keys of length \(\mathsf{{poly}}\left( \lambda \right) \), and signatures of length \(n\cdot \mathsf{{poly}}\left( \lambda \right) \), then the following holds for the MKSE scheme for universe \(\mathcal{{U}}\). Data and query keys have length \(\mathsf{{poly}}\left( \lambda \right) \), queries have length \(\log \left| \mathcal {U}\right| \cdot \mathsf{{poly}}\left( \lambda \right) \), and for a set S, its corresponding processed set has size \(\left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \). Furthermore, if: (1) evaluating h on length-n inputs takes \(H_T\left( n\right) \) time, and outputs a hash of length \(H_{\ell }\left( n\right) \); and (2) there exist functions \(\textsf {s},T_{\mathcal {O}}:\mathbb {N}\rightarrow \mathbb {N}\) such that for every TM M, \(\left| \mathcal {O}\left( M\right) \right| \le \textsf {s}\left( \left| M\right| \right) \), and running \(\mathcal {O}\left( M\right) \) on inputs of length n takes \(T_{\mathcal {O}}\left( \textsf {TIME}\left( M,n\right) \right) \) time, where \(\textsf {TIME}\left( M,n\right) \) is the running time of M on length-n inputs; then: running \(\textsf {Search}\) on a set S takes \(T_{\mathcal {O}}\left( H_T\left( \left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \right) + \left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) + \mathsf{{poly}}\left( \lambda ,\log \left| \mathcal {U}\right| \right) \right) \) time, and share keys have size \(\textsf {s}\left( H_{\ell }\left( \left| S\right| \cdot \mathsf{{poly}}\left( \lambda \right) \right) \cdot \mathsf{{poly}}\left( \lambda \right) \right) \).
Proof
The correctness and complexity of the scheme is proven similarly to Claim 2. (The only difference is in the length of queries, which contain a signature on a keyword \(w\in \mathcal {U}\), and the running time of \(\textsf {Search}\), which needs to verify the signature. In both cases, the increase in complexity is caused because signatures on \(w\in \mathcal {U}\) have length \(\log \left| \mathcal {U}\right| \cdot \mathsf{{poly}}\left( \lambda \right) \).)
The security proof proceeds in a sequence of hybrids similar to the proof of Claim 2, but introduces additional complications due to using a weaker obfuscator primitive. More specifically, let \(\mathcal {A}\) be a PPT adversary in the security game of Definition 1, and let \(\mathsf{{view}}_b,b\in \{0,1\}\) denote its view in the security game with bit b. We define hybrids \(\mathcal {H}_0,\mathcal {H}_1\), and \(\mathcal {H}_2\) as in the proof of Claim 2, and \(\mathsf{{view}}_0\approx \mathcal {H}_0\) by the same arguments. Indeed, as discussed there, the obfuscated programs in \(\mathsf{{view}}_0,\mathcal {H}_0\) are differing inputs in relation to every auxiliary input, and in particular when this auxiliary input is the randomness used by the sampler to sample the programs. \(\mathcal {H}_0\approx \mathcal {H}_2\) because the indistinguiushability argument did not use diO security.
Next, we define a new hybrid \(\mathcal {H}_2'\) in which the signatures on the queries \(\mathcal{{W}}_j^0\) of every querier j, and his verification key \(\textsf {vk}_j\), are generated using the \(\textsf {SpecialGen}\) algorithm (instead of the \(\textsf {KeyGen}\) and \(\textsf {Sign}\) algorithms). We show that \(\mathcal {H}_2'\approx \mathcal {H}_2\) by the indistinguishability of standard and special modes of the dual-mode signature scheme. We condition both hybrids on the values of the sets \(S_i^0,S_i^1\) of data owners, their data keys, the processed sets, the encryption keys of the queriers, the keywords they search for, and their encryptions. (This is possible by an averaging argument, since these values are identically distributed in both hybrids.) Let m denote the number of queriers, then we define a sequence of hybrids \(\mathcal {H}^0,\cdots ,\mathcal {H}^m\), where in \(\mathcal {H}^j\), the signatures and verification key of the first j queriers are generated using \(\textsf {SpecialGen}\), and the signatures and verification keys of all other queriers are honestly generated (using \(\textsf {KeyGen}\) and \(\textsf {Sign}\)). We prove that \(\mathcal {H}^j\approx \mathcal {H}^{j-1}\) for every \(1\le j\le m\), and conclude that \(\mathcal {H}_2=\mathcal {H}^0\approx \mathcal {H}^m=\mathcal {H}_2'\).
Fix some j. Given a distinguisher \(\mathsf{{D}}\) between \(\mathcal {H}^j,\mathcal {H}^{j-1}\), we construct a distinguisher \(\mathsf{{D}}'\) (with the same distinguishing advantage) between the real and special-mode verification key and signatures on the ciphertexts encrypting the keywords in \(\mathcal{{W}}_j^0\), and conclude that \(\mathcal {H}^j\approx \mathcal {H}^{j-1}\) by the indistinguishability of standard and special modes property. We hard-wire into \(\mathsf{{D}}'\) the signing, verification keys, and queries of every \(j'\ne j\), as well as all share keys \(\varDelta _{j',i}\) for \(i\in \mathcal {D}\) (this is possible because these values are identically distributed in \(\mathcal {H}^j,\mathcal {H}^{j-1}\) and so we can fix them into both hybrids). Given a verification key \(\textsf {vk}\), and a list L of signatures on the ciphertexts of querier j, \(D'\) generates for every edge \(\left( j,i\right) \in E\) the program \(P_{\textsf {K},\left( \textsf {K}^u,\textsf {vk}\right) ,h\left( T\right) }\) (where \(\textsf {K},\textsf {K}^u\), and \(h\left( T\right) \) are taken from the hard-wired values), and uses \(\mathcal {O}\) to generate the obfuscated program \(\varDelta _{j,i}\). Then, \(\mathsf{{D}}'\) generates the queries of querier j by concatenating the corresponding signature to each ciphertext of j. Together with the hard-wired values, this gives the entire hybrid, and \(\mathsf{{D}}'\) runs \(\mathsf{{D}}\) on the hybrid, and outputs whatever \(\mathsf{{D}}\) outputs. Notice that if \(\textsf {vk}\) and the signatures were honestly generated, then the input to \(\mathsf{{D}}\) is distributed according to \(\mathcal{{H}}^{j-1}\), otherwise it is distributed according to \(\mathcal{{H}}^j\), so \(\mathsf{{D}}'\) and \(\mathsf{{D}}\) have the same distinguishing advantage.
Next, we define \(\mathcal {H}_3\) as in the proof of Claim 2 (but notice that the verification keys in every \(\varDelta _{j,i}\) were generated using \(\textsf {SpecialGen}\)), and claim that \(\mathcal {H}_2'\approx \mathcal {H}_3\) by the pc-diO security of \(\mathcal {O}\). We define the hybrids \(\mathcal {H}^0,\cdots ,\mathcal {H}^d\) as in the argument that \(\mathcal {H}_2\approx \mathcal {H}_3\) in the proof of Claim 2 (except that we use \(\mathcal {H}_2'\) instead of \(\mathcal {H}_2\)), and show that \(\mathcal {H}^l\approx \mathcal {H}^{l-1}\) for every \(1\le l\le d\).
Fix some \(1\le l^*\le d\), and let \(\left( j,i\right) \) be the edge for which \(\varDelta ^{l^*}\) was generated. We hard-wire the sets \(S_{i'}^0,S_{i'}^1,i'\in \mathcal {D}\), and all the keywords that queriers ask about (in both the 0-experiment and the 1-experiment), into \(\mathcal {H}^{l^*},\mathcal {H}^{l^*-1}\) (this is possible because these values are identical in both hybrids). We additionally hard-wire the keys of every querier \({j'},j'\ne j\) and data owner \({i'},i'\ne i\), the encrypted sets \(T_{i'},i'\ne i\), the queries of querier \(j'\), and the share keys \(\varDelta _{j',i'},\varDelta _{j',i'}'\) (\(\varDelta _{j',i'}\) denotes a key in \(\mathcal {H}_2'\), \(\varDelta _{j',i'}'\) denotes a key in \(\mathcal {H}_3\)). (This is possible because these values are identically distributed in both hybrids.) We show that \(\varDelta _{j,i},\varDelta _{j,i}'\) sampled in \(\mathcal {H}^{l^*-1},\mathcal {H}^{l^*}\) (respectively) form a public-coin differing-inputs family of TMs (and conclude that \(\mathcal {H}^{l^*-1}\approx \mathcal {H}^{l^*}\) by the pc-diO security of \(\mathcal {O}\)).
Let \(\mathcal {P},\mathcal {P}'\) denote the distributions over programs obfuscated in \(\varDelta _{j,i},\varDelta _{j,i}'\), and let \(\mathsf{{D}}\) be a PPT algorithm that obtains \(\left( P,P'\right) \leftarrow \mathcal {P}\times \mathcal {P}'\) and r, where r is the randomness used to sample \(P,P'\). We assume the “worst-case” scenario in which all the values we have fixed into \(\mathcal {H}^{l^*},\mathcal {H}^{l^*-1}\) are known to \(\mathsf{{D}}\). Notice that from the randomness r of the sampler, \(\mathsf{{D}}\) learns the encryption keys \(\textsf {K}_i,\textsf {K}_j^u\) (the left component of these keys is needed to generate P, whereas the right component is needed to generate \(P'\)), as well as the encrypted set \(T_i\), the verification key \(\textsf {vk}_{j}^u\) for signatures of querier j, and the queries of j (which consist of encryptions of keywords, and signatures on these encryptions; the signatures were generated together with the verification key by \(\textsf {SpecialGen}\)). (We note that from these values \(\mathsf{{D}}\) can compute on its own the share keys \(\varDelta _{j',i},\varDelta _{j',i}'\) for \(\left( {j'},i\right) \in E\), and \(\varDelta _{j,i'},\varDelta _{j,i'}'\) for \(\left( {j},{i'}\right) \in E\).) We show that \(\mathsf{{D}}\) succeeds in finding a differing input only with negligible probability.
Consider first the inputs (for \(P,P'\)) which \(\mathsf{{D}}\) knows (from the hard-wired values, or what it can deduce from r), i.e., the encrypted set \(T_i\) (which encrypts the elements of \({S_i^0}\) in the left components, and the elements of \(S_i^1\) in the right components; for \(i\in \mathcal {D}_c\) this holds since \(S_i^0=S_i^1\)), and the queries of querier j. For every such query q there exists a pair \(\left( w_L,w_R\right) \) of keywords such that q is of the form \(q=\left( c=\left( c_L,c_R\right) ,\sigma \right) \) where \(c_{\star }\leftarrow \mathsf{{Enc}}\left( \textsf {K}_{\star ,j}^u,m_{\star }\right) ,\star \in \left\{ L,R\right\} \), \(\sigma \) is a valid signature on c (generated by \(\textsf {SpecialGen}\)), and \(w_L\in S_i^0\Leftrightarrow w_R\in S_i^1\). In particular, \(P\left( q,T_i\right) =P'\left( q,T_i\right) \) except with negligible probability since except with negligible probability, the checks in Steps (1)–(2) succeed in both cases (by indistinguishability of the standard and special modes of the signature scheme, \(\sigma \) is indistinguishable from a valid signature on c, which by the correctness of the signature scheme, would pass verification), and Steps (4)–(5) return the same outcome (P searches for \(w_L\) in \(S_i^0\), since it decrypts using \(\mathsf{{Dec}}^2\), whereas \(P'\) searches for \(w_R\) in \(S_i^1\), since it decrypts with \(\mathsf{{Dec}}^R\) and the right component of \(T_i\) encrypts \(S_i^1\); and \(w_L\in S_i^0\Leftrightarrow w_R\in S_i^1\)).
Next, we claim that for every other possible input \(\left( T',c',\sigma '\right) \) that \(\mathsf{{D}}\) chooses, \(P\left( T',c',\sigma '\right) =P'\left( T',c',\sigma '\right) =0\) except with negligible probability. Indeed, if \(\left( c',\sigma '\right) \ne q\) (where q is some query of querier j) then by the property that special-mode keys cannot sign additional messages, with overwhelming probability \(\sigma '\) is not a valid signature for \(c'\), so the check in Step (1) fails in both \(P,P'\). Moreover, if \(T'\ne T_i\) then by the collision resistance of h, with overwhelming probability \(h\left( T'\right) \ne h\left( T_i\right) \), so the check in Step (2) fails. Therefore, \(P,P'\) are public-coin differing-inputs.
We now define the last set of hybrids. (These hybrids differ from the corresponding hybrids in the proof of Claim 2 only in that the verification keys and signatures are generated in the special mode.)
-
\(\mathbf {\mathcal {H}_4:}\) In hybrid \(\mathcal {H}_4\), the queries \(\left( w_{j,1}^1,\cdots ,w_{j,k_j}^1\right) \) of every querier \(j\in \mathcal {Q}\) are generated using \(\mathsf{{Enc}}^2\) with message \(\left( w_{j,l}^1,w_{j,l}^1\right) ,1\le l\le k_j\), instead of \(\mathsf{{Enc}}^L\) with message \(\left( w_{j,l}^0,w_{j,l}^1\right) ,1\le l\le k_j\).
\(\mathcal {H}_3\approx \mathcal {H}_4\) by a similar argument to the one used to prove \(\mathcal {H}_1\approx \mathcal {H}_2\).
-
\(\mathbf {\mathcal {H}_5:}\) In hybrid \(\mathcal {H}_5\), the encrypted set \(T_i\) of every honest data owner \(i\notin \mathcal {D}_c\) is generated as the encryption of \(\left( S_i^1,S_i^1\right) \) with \(\mathsf{{Enc}}^2\) instead of with \(\mathsf{{Enc}}^L\).
\(\mathcal {H}_4\approx \mathcal {H}_5\) by a similar argument to the one used to prove \(\mathcal {H}_0\approx \mathcal {H}_1\).
-
\(\mathbf {\mathcal {H}_6:}\) In hybrid \(\mathcal {H}_6\), the obfuscated program for every edge \(\left( j,i\right) \in E\) is generated as follows: (1) the hard-wired keys are \(\textsf {K}=\left( \textsf {K}_{L,i},\textsf {K}_{R,i}\right) ,\textsf {K}=\left( \textsf {K}_{L,j}^u,\textsf {K}_{R,j}^u\right) \), instead of \(\textsf {K}'=\left( \mathbf {0},\textsf {K}_{R,i}\right) ,\textsf {K}^{u\prime }=\left( \mathbf {0},\textsf {K}_{R,j}^u\right) \); and (2) \(\mathsf{{Dec}}^2\) is used for decryption (instead of \(\mathsf{{Dec}}^R\)).
We show that \(\mathcal {H}_6\approx \mathcal {H}_5\) follows from the pc-diO security of \(\mathcal {O}\) by a standard hybrid argument in which the obfuscated programs are replaced one at a time. When replacing the program for edge \(\left( j,i\right) \) from \(P'\) (in \(\mathcal {H}_5\)) to P (in \(\mathcal {H}_6\)), we hard-wire into the PPT \(\mathsf{{D}}\) (which should find a differing input) the sets \(S_{i'}^1\) for every \({i'}\in \mathcal {D}\), the keywords searched for (in the 1-experiment) by all queriers, the encryption keys of all data owners \({i'},i'\ne i\) and queriers \({j'},j'\ne j\), the signing, verification keys, and queries of all queriers \({j'},j'\ne j\), and all encrypted sets \(T_{i'},i'\ne i\). Also, from the randomness r of the sampler (of \(P,P'\)), \(\mathsf{{D}}\) learns the encryption keys \(\textsf {K}_i,\textsf {K}_j^u\), the (special-mode) verification key \(\textsf {vk}_{s,j}^u\), the encryptions of the keywords which querier j searches for, together with the signatures on these ciphertexts, and the encrypted set \(T_i\).
We claim that \(\mathsf{{D}}\) finds a differing input only with negligible probability. The argument is similar to that used to prove \(\mathcal {H}_3\approx \mathcal {H}_2'\). The inputs (for \(P,P'\)) available to \(\mathsf{{D}}\) (from the hard-wired values, and the randomness of the sampler), i.e., the encrypted set \(T_i\), and queries \(q=\left( c,\sigma \right) \) of querier j, where \(c\leftarrow \mathsf{{Enc}}^2\left( \textsf {K}_j^u,m\right) \) for some m, and \(\sigma \) is a signature for c (generated using \(\textsf {SpecialGen}\)), are not differing-inputs (even though \(P'\) decrypts the right component of c, whereas P decrypts the left component) because both components of c encrypt m according to \(\mathsf{{Enc}}\) (so both \(P,P'\) search for m in \(S_i^1\)), where \(\mathsf{{Enc}}\) is the encryption scheme underlying \(\mathsf{{Enc}}^2,\mathsf{{Enc}}^L,\mathsf{{Enc}}^R\). For every other possible input \(\left( T',c',\sigma '\right) \) that \(\mathsf{{D}}\) chooses, \(P\left( T',c',\sigma '\right) =P'\left( T',c',\sigma '\right) =0\) except with negligible probability: if \(\left( c',\sigma '\right) \ne q\) (where q is some query of querier j) then with overwhelming probability \(\sigma '\) is not a valid signature on \(c'\) (by the property that special-mode signatures cannot sign additional messages); whereas if \(T'\ne T_i\) then with overwhelming probability \(h\left( T'\right) \ne h\left( T_i\right) \) (by the collision resistance of h).
In our final new hybrid \(\mathcal {H}_6'\), the signatures on the queries \(\mathcal{{W}}_j^0\) of every querier j, and his verification key \(\textsf {vk}_j\), are honestly generated (using the \(\textsf {KeyGen}\) and \(\textsf {Sign}\) algorithms). Then \(\mathsf{{view}}_1=\mathcal {H}_6'\approx \mathcal {H}_6\) by the same arguments used to show \(\mathcal {H}_2'\approx \mathcal {H}_2\). \(\square \)
Theorem 4 now follows as a corollary from Claim 3 and Theorem 5, and since the existence of symmetric encryption follows from the existence of CRHFs.
6 Extensions and Open Problems
In this section we discuss possible extensions of our MKSE definition and constructions, and point out a few open problems in the field.
We have focused on a selective, indistinguishability-based MKSE notion (Definition 1). One could also consider several other formulations, as we now discuss.
Simulation-based security. First, one can consider a selective simulation-based notion, in which the real-world view of any PPT adversary can be efficiently simulated given only “minimal” information. More specifically, at the onset of the execution the adversary chooses (as in Definition 1) sets of queriers, data owners, and corrupted data owners; a share graph; keyword sets for all data owners; data keys for corrupted data owners; and a (possibly empty) set of distinct keyword queries for each querier. The simulator is then given the sets and data keys of corrupted data owners; the sizes of the sets of honest data owners; the share graph; and for each keyword query w of querier j, and every edge \(\left( j,i\right) \) in the graph, whether \(w\in S_i\) or not (where \(S_i\) is the set of data owner i). The simulator then generates a complete simulated adversarial view, namely processed sets for all data owners, share keys for all edges in the share graph, and queries for every keyword query. Intuitively, we say that an MKSE is simulation-secure if for every PPT adversary there exists a PPT simulator as above, such that the real and simulated views are computationally indistinguishable. The PRF-based MKSE (Construction 1) is simulation-secure (see Remark 1), and we leave it as an open problem to determine whether the MKSE with short share keys (Construction 2, based on diO or pc-diO) is simulation-secure.
A natural question that arises in this context is whether indistinguishability-based security (as in Definition 1) implies simulation-based security (as outlined above). One approach towards tackling this question is to describe an algorithm that, given the input of the simulator (as specified above), generates an assignment for the sets of the honest data owners, and for all keyword queries, in a way that is consistent with the outcome of searching for these keywords. Concretely, this approach reduces the task of constructing a simulator to the following graph problem: given a bipartite graph \(G=\left( L,R,E\right) \); a set \(\left\{ n_v\ :\ v\in R\right\} \) of natural numbers; and for every \(u \in L\), a set of coloring of the edges touching u in two colors (blue and red), assign a set \(S_v\subseteq \mathcal {U}\) to every \(v\in R\) (recall that \(\mathcal {U}\) is a universe of possible keywords), and a value \(w_u^c\in \mathcal {U}\) to every \(u\in L\) and every coloring c of the edges that touch u, such that the following holds:
-
1.
For every \(v\in R\), \(\left| S_v\right| =n_v\).
-
2.
For every \(u\in L\), and two colorings \(c_1,c_2\) of the edges touching u, \(w_u^{c_1}\ne w_u^{c_2}\).
-
3.
For every \(u\in L\), every coloring c of the edges that touch u, and every edge \(\left( u,v\right) \in E\), \(c\left( u,v\right) =\text {blue}\) if and only if \(w_u^c \in S_v\), where \(c\left( u,v\right) \) is the color of the edge \(\left( u,v\right) \) in the coloring c.
(We note that Item 1 guarantees that sets have the “right” size; Item 2 guarantees that the queries made by each querier are distinct; and Item 3 guarantees that the assignments to the sets and keywords searched for are consistent.) At a high level, the main challenge is in finding an assignment for the set that would be consistent over the queries of multiple queriers, while simultaneously satisfying the restriction on the size of the set. Intuitively, this issue does not arise in the PRF-based construction since each share key \(\varDelta _{j,i}\) encodes the entire set, and the \(\textsf {Search}\) algorithm does not use the processed set at all (so issues of consistency across different queriers do not arise).
Adaptive security. Another possible dimension of generalizing Definition 1 is to consider an (either indistinguishability-based or simulation-based) adaptive definition. At a high level, in this setting the adversary may adaptively generate queriers, data owners (with their sets and data keys), edges in the share graph, and keyword queries, and immediately receives the resultant values. (For example, when an adversary specifies a new data owner and his data key and set, he receives the corresponding processed set; when he adds an edge to the share graph, he receives the corresponding share key, etc.) The security requirement should hold as long as at the end of the execution, the data sets, share graph, and queries satisfy the restrictions imposed by the (selective) security definition (in a simulation-based definition, the only restriction is that the queries of each querier are distinct; in an indistinguishability-based definition there are further restrictions as specified in Definition 1).
Natural approaches towards proving adaptive security, even for the PRF-based construction (Construction 1), seem to run into “selective opening type” issues: in the security proof, we would naturally want to replace the pseudorandom images of the PRF F in share keys with random values, however we do not a-priori know which values the adversary will ask to be “opened” (by making a keyword query for a keyword in the set corresponding to the share key; recall that these queries constitute a key for F). Consequently, we cannot a-priori determine which values should remain pseudorandom (so that they can later be opened). However, we can show that Construction 1 is adaptively simulation-secure in the Random Oracle model, namely when all evaluations of F are replaced with calls to the random oracle (replacing \(F_K\left( x\right) \) with a call to \(\textsf {RO}\left( K,x\right) \)). The random oracle circumvents such “selective opening type” issues since any (randomly assigned) output of the random oracle can later be “explained” by consistently assigning the random oracle outputs at other (related) points.
Efficiency and security tradeoffs. Finally, an interesting avenue for future research is exploring the tradeoffs between efficiency of the MKSE scheme, and the underlying assumptions. Our MKSE with short share keys (Construction 2) indicates the hardness of proving an unconditional lower bound on the size of share keys, since it would require ruling out the existence of diO for a specific class of samplers. However, it does not rule out the possibility of constructing an MKSE scheme with short share keys based on weaker assumptions (such as the existence of iO for TMs, or ideally, on the existence of OWFs). More generally, one could ask how the search time, and size of share keys, relate to each other; and if there is a lower bound on “search time plus share key size”.
Notes
- 1.
This functionality was also discussed in [29], but was not defined as part of the MKSE syntax.
References
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S., Yang, K.: On the (im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_1
Bellare, M., Stepanovs, I., Waters, B.: New negative results on differing-inputs obfuscation. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 792–821. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_28
Bösch, C., Hartel, P., Jonker, W., Peter, A.: A survey of provably secure searchable encryption. ACM Comput. Surv. 47(2), 18:1–18:51 (2014)
Cash, D., Grubbs, P., Perry, J., Ristenpart, T.: Leakage-abuse attacks against searchable encryption. In: Ray, I., Li, N., Kruegel, C. (eds.) ACM CCS 2015, pp. 668–679. ACM Press, October 2015
Cash, D., Jaeger, J., Jarecki, S., Jutla, C.S., Krawczyk, H., Rosu, M.-C., Steiner, M.: Dynamic searchable encryption in very-large databases: data structures and implementation. In: NDSS 2014. The Internet Society, February 2014
Chang, Y.-C., Mitzenmacher, M.: Privacy preserving keyword searches on remote encrypted data. In: Ioannidis, J., Keromytis, A., Yung, M. (eds.) ACNS 2005. LNCS, vol. 3531, pp. 442–455. Springer, Heidelberg (2005). https://doi.org/10.1007/11496137_30
Chen, X., Li, J., Huang, X., Li, J., Xiang, Y., Wong, D.S.: Secure outsourced attribute-based signatures. IEEE Trans. Parallel Distrib. Syst. 25(12), 3285–3294 (2014)
Cui, B., Liu, Z., Wang, L.: Key-aggregate searchable encryption (KASE) for group data sharing via cloud storage. IEEE Trans. Comput. 65(8), 2374–2385 (2016)
Curtmola, R., Garay, J.A., Kamara, S., Ostrovsky, R.: Searchable symmetric encryption: improved definitions and efficient constructions. In: Juels, A., Wright, R.N., di Vimercati, S.D.C. (eds.) ACM CCS 2006, pp. 79–88. ACM Press, October/November 2006
Dong, C., Russello, G., Dulay, N.: Shared and searchable encrypted data for untrusted servers. J. Comput. Secur. 19(3), 367–397 (2011)
Fredman, M.L., Komlós, J., Szemerédi, E.: Storing a sparse table with O(1) worst case access time. In: FOCS 1982, pp. 165–169 (1982)
Fuller, B., Varia, M., Yerukhimovich, A., Shen, E., Hamlin, A., Gadepally, V., Shay, R., Mitchell, J.D., Cunningham, R.K.: SoK: cryptographically protected database search. In: 2017 IEEE Symposium on Security and Privacy, SP 2017, 22–26 May 2017, San Jose, CA, USA, pp. 172–191 (2017)
Garg, S., Gentry, C., Halevi, S., Wichs, D.: On the implausibility of differing-inputs obfuscation and extractable witness encryption with auxiliary input. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 518–535. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_29
Goh, E.-J.: Secure indexes. Cryptology ePrint Archive, Report 2003/216 (2003)
Goldreich, O.: The Foundations of Cryptography - Basic Techniques, vol. 1. Cambridge University Press, Cambridge (2001)
Goldreich, O.: The Foundations of Cryptography - Basic Applications, vol. 2. Cambridge University Press, Cambridge (2004)
Grubbs, P., McPherson, R., Naveed, M., Ristenpart, T., Shmatikov, V.: Breaking web applications built on top of encrypted data. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S. (eds.) ACM CCS 2016, pp. 1353–1364. ACM Press, October 2016
Grubbs, P., Sekniqi, K., Bindschaedler, V., Naveed, M., Ristenpart, T.: Leakage-abuse attacks against order-revealing encryption. In: 2017 IEEE Symposium on Security and Privacy, pp. 655–672. IEEE Computer Society Press, May 2017
Hamlin, A., Shelat, A., Weiss, M., Wichs, D.: Multi-key searchable encryption, revisited. Cryptology ePrint Archive, Report 2018/018 (2018)
Ishai, Y., Pandey, O., Sahai, A.: Public-coin differing-inputs obfuscation and its applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 668–697. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_26
Kamara, S., Papamanthou, C., Roeder, T.: Dynamic searchable symmetric encryption. In: Yu, T., Danezis, G., Gligor, V.D. (eds.) ACM CCS 2012, pp. 965–976. ACM Press, October 2012
Kellaris, G., Kollios, G., Nissim, K., O’Neill, A.: Generic attacks on secure outsourced databases. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S. (eds.) ACM CCS 2016, pp. 1329–1340. ACM Press, October 2016
Kiayias, A., Oksuz, O., Russell, A., Tang, Q., Wang, B.: Efficient encrypted keyword search for multi-user data sharing. In: Askoxylakis, I., Ioannidis, S., Katsikas, S., Meadows, C. (eds.) ESORICS 2016. LNCS, vol. 9878, pp. 173–195. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45744-4_9
Li, J., Chen, X., Li, M., Li, J., Lee, P.P.C., Lou, W.: Secure deduplication with efficient and reliable convergent key management. IEEE Trans. Parallel Distrib. Syst. 25(6), 1615–1625 (2014)
Li, J., Li, J., Chen, X., Jia, C., Liu, Z.: Efficient keyword search over encrypted data with fine-grained access control in hybrid cloud. In: Xu, L., Bertino, E., Mu, Y. (eds.) NSS 2012. LNCS, vol. 7645, pp. 490–502. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34601-9_37
Liu, Z., Wang, Z., Cheng, X., Jia, C., Yuan, K.: Multi-user searchable encryption with coarser-grained access control in hybrid cloud. In: 2013 4th International Conference on Emerging Intelligent Data and Web Technologies, pp. 249–255 (2013)
Naor, M., Yung, M.: Public-key cryptosystems provably secure against chosen ciphertext attacks. In: STOC 1990, pp. 427–437 (1990)
Naveed, M., Kamara, S., Wright, C.V.: Inference attacks on property-preserving encrypted databases. In: Ray, I., Li, N., Kruegel, C. (eds.) ACM CCS 2015, pp. 644–655. ACM Press, October 2015
Popa, R.A., Stark, E., Valdez, S., Helfer, J., Zeldovich, N., Balakrishnan, H.: Building web applications on top of encrypted data using Mylar. In: Proceedings of 11th USENIX Symposium on Networked Systems Design and Implementation, NSDI 2014, pp. 157–172 (2014)
Popa, R.A., Zeldovich, N.: Multi-key searchable encryption. Cryptology ePrint Archive, Report 2013/508 (2013)
Pouliot, D., Wright, C.V.: The shadow nemesis: inference attacks on efficiently deployable, efficiently searchable encryption. In: Weippl, E.R., Katzenbeisser, S., Kruegel, C., Myers, A.C., Halevi, S. (eds.) ACM CCS 2016, pp. 1341–1352. ACM Press, October 2016
Van Rompay, C., Molva, R., Önen, M.: A leakage-abuse attack against multi-user searchable encryption. In: PoPETs 2017, no. 3, p. 168 (2017)
Song, D.X., Wagner, D., Perrig, A.: Practical techniques for searches on encrypted data. In: 2000 IEEE Symposium on Security and Privacy, pp. 44–55. IEEE Computer Society Press, May 2000
Stefanov, E., Papamanthou, C., Shi, E.: Practical dynamic searchable encryption with small leakage. In: NDSS 2014. The Internet Society, February 2014
Tang, Q.: Nothing is for free: security in searching shared and encrypted data. IEEE Trans. Inf. Forensics Secur. 9(11), 1943–1952 (2014)
Zhang, Y., Katz, J., Papamanthou, C.: All your queries are belong to us: the power of file-injection attacks on searchable encryption. In: 25th USENIX Security Symposium, USENIX Security 2016, pp. 707–720 (2016)
Zhao, F., Nishide, T., Sakurai, K.: Multi-user keyword search scheme for secure data sharing with fine-grained access control. In: Kim, H. (ed.) ICISC 2011. LNCS, vol. 7259, pp. 406–418. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31912-9_27
Acknowledgments
We thank the anonymous PKC reviewers for suggesting to use hashing to reduce search time to O(1) in Construction 1. This work was supported by NSF grants CNS-1314722, CNS-1413964, TWC-1664445 and TWC-1646671. The third author was supported in part by The Eric and Wendy Schmidt Postdoctoral Grant for Women in Mathematical and Computing Sciences.
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Hamlin, A., Shelat, A., Weiss, M., Wichs, D. (2018). Multi-Key Searchable Encryption, Revisited. In: Abdalla, M., Dahab, R. (eds) Public-Key Cryptography – PKC 2018. PKC 2018. Lecture Notes in Computer Science(), vol 10769. Springer, Cham. https://doi.org/10.1007/978-3-319-76578-5_4
Download citation
DOI: https://doi.org/10.1007/978-3-319-76578-5_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-76577-8
Online ISBN: 978-3-319-76578-5
eBook Packages: Computer ScienceComputer Science (R0)


 outputs a symmetric key
outputs a symmetric key  outputs a uniformly random PRF key
outputs a uniformly random PRF key  outputs
outputs  operates as follows:
operates as follows: outputs
outputs 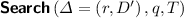 operates as follows:
operates as follows: generates a random encryption key
generates a random encryption key  generates a random encryption key
generates a random encryption key  encrypts each element
encrypts each element  generates
generates  generates
generates  outputs
outputs 
