Abstract
Constrained pseudorandom functions allow for delegating “constrained” secret keys that let one compute the function at certain authorized inputs—as specified by a constraining predicate—while keeping the function value at unauthorized inputs pseudorandom. In the constraint-hiding variant, the constrained key hides the predicate. On top of this, programmable variants allow the delegator to explicitly set the output values yielded by the delegated key for a particular set of unauthorized inputs.
Recent years have seen rapid progress on applications and constructions of these objects for progressively richer constraint classes, resulting most recently in constraint-hiding constrained PRFs for arbitrary polynomial-time constraints from Learning With Errors (LWE) [Brakerski, Tsabary, Vaikuntanathan, and Wee, TCC’17], and privately programmable PRFs from indistinguishability obfuscation (iO) [Boneh, Lewi, and Wu, PKC’17].
In this work we give a unified approach for constructing both of the above kinds of PRFs from LWE with subexponential \(\exp (n^{\varepsilon })\) approximation factors. Our constructions follow straightforwardly from a new notion we call a shift-hiding shiftable function, which allows for deriving a key for the sum of the original function and any desired hidden shift function. In particular, we obtain the first privately programmable PRFs from non-iO assumptions.
C. Peikert—This material is based upon work supported by the National Science Foundation under CAREER Award CCF-1054495 and CNS-1606362. The views expressed are those of the authors and do not necessarily reflect the off or position of the National Science Foundation or the Sloan Foundation.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Since the introduction of pseudorandom functions (PRFs) more than thirty years ago by Goldreich et al. [19], many variants of this fundamental primitive have been proposed. For example, constrained PRFs (also known as delegatable or functional PRFs) [9, 11, 22] allow issuing “constrained” keys which can be used to evaluate the PRF on an “authorized” subset of the domain, while preserving the pseudorandomness of the PRF values on the remaining unauthorized inputs.
Assuming the existence of one-way functions, constrained PRFs were first constructed for the class of prefix-fixing constraints, i.e., the constrained key allows evaluating the PRF on inputs which start with a specified bit string [9, 11, 22]. Subsequently, by building on a sequence of works [2, 3, 7] that gave PRFs from the Learning With Errors (LWE) problem [28], Brakerski and Vaikuntanathan [14] constructed constrained PRFs where the set of authorized inputs can be specified by an arbitrary polynomial-time predicate, although for a weaker security notion that allows the attacker to obtain only a single constrained key and function value.
In the original notion of constrained PRF, the constrained key may reveal the constraint itself. Boneh et al. [8] proposed a stronger variant in which the constraint is hidden, calling them privately constrained PRFs—also known as constraint-hiding constrained PRFs (CHC-PRFs)—and gave several compelling applications, like searchable symmetric encryption, watermarking PRFs, and function secret sharing [10]. They also constructed CHC-PRFs for arbitrary polynomial-time constraining functions under the strong assumption that indistinguishability obfuscation (iO) exists [4, 17]. Soon after, CHC-PRFs for various constraint classes were constructed from more standard LWE assumptions:
-
Boneh et al. [6] constructed them for the class of point-function constraints (i.e., all but one input is authorized).
-
Thorough a different approach, Canetti and Chen [15] constructed them for constraints in NC\(^{1}\), i.e., polynomial-size formulas.
-
Most recently, Brakerski et al. [13] improved on the construction from [6] to support arbitrary polynomial-size constraints.
All these constructions have a somewhat weaker security guarantee compared to the iO-based construction of [8], namely, the adversary gets just one constrained key (but an unbounded number of function values), whereas in [8] it can get unboundedly many constrained keys. Indeed, this restriction reflects a fundamental barrier: CHC-PRFs that are secure for even two constrained keys (for arbitrary constraining functions) imply iO [15].
Boneh et al. [8] also defined and constructed what they call privately programmable PRFs (PP-PRFs), which are CHC-PRFs for the class of point functions along with an additional programmability property: when deriving a constrained key, one can specify the outputs the key yields at the unauthorized points. They showed how to use PP-PRFs to build watermarking PRFs, a notion defined in [16]. While the PP-PRF and resulting watermarking PRF from [8] were based on indistinguishability obfuscation, Kim and Wu [23] later constructed watermarking PRFs from LWE, but via a different route that does not require PP-PRFs. To date, it has remained an open question whether PP-PRFs exist based on more standard (non-iO) assumptions.
1.1 Our Results
Our main contribution is a unified approach for constructing both constraint-hiding constrained PRFs for arbitrary polynomial-time constraints, and privately programmable PRFs, from LWE with subexponential \(\exp (n^{\varepsilon })\) approximation factors (i.e., inverse error rates), for any constant \(\varepsilon > 0\). Both objects follow straightforwardly from a single LWE-based construction that we call a shift-hiding shiftable function (SHSF). Essentially, an SHSF allows for deriving a “shifted” key for a desired shift function, which remains hidden. The shifted key allows one to evaluate the sum of the original function and the shift function. We construct CHC-PRFs and PP-PRFs very simply by using an appropriate shift function, which is zero at authorized inputs, and either pseudorandom or programmed at unauthorized inputs.
CHC-PRFs. In comparison with [13], while we achieve the same ultimate result of CHC-PRFs for arbitrary constraints (with essentially the same efficiency metrics), our construction is more modular and arguably a good deal simpler.Footnote 1 Specifically, our SHSF construction uses just a few well-worn techniques from the literature on LWE-based fully homomorphic and attribute-based cryptography [5, 18, 20, 21], and we get a CHC-PRF by invoking our SHSF with an arbitrary PRF as the shift function. By contrast, the construction from [13] melds the FHE/ABE techniques with a specific LWE-based PRF [2], and involves a handful of ad-hoc techniques to deal with various technical complications that arise.
PP-PRFs. Our approach also yields the first privately programmable PRFs from LWE, or indeed, any non-iO assumption. In fact, our PP-PRF allows for programming any polynomial number of inputs. Previously, the only potential approach for constructing PP-PRFs without iO [23] was from CHC-PRFs having certain extra properties (which constructions prior to our work did not possess), and was limited to programming only a logarithmic number of inputs.
1.2 Techniques
As mentioned above, the main ingredient in our constructions is what we call a shift-hiding shiftable function (SHSF). We briefly describe its properties. We have a keyed function \(\mathsf {Eval} : \mathcal {K} \times \mathcal {X} \rightarrow \mathcal {Y}\), where \(\mathcal {Y}\) is some finite additive group, and an algorithm \(\mathsf {Shift} (\cdot ,\cdot )\) to derive shifted keys. Given a secret key \(msk\in \mathcal {K}\) and a function \(H: \mathcal {X} \rightarrow \mathcal {Y}\), we can derive a shifted key \(sk_{H} \leftarrow \mathsf {Shift} (msk,H)\). This key has the following two main properties:
-
\(sk_H\) hides the shifting function H, and
-
given \(sk_H\) we can compute an approximation of \(\mathsf {Eval} (msk,\cdot ) + H(\cdot )\) at any input, i.e., there exists a “shifted evaluation” algorithm \(\mathsf {SEval} \) such that for every \(x \in \mathcal {X}\),
$$\begin{aligned} \mathsf {SEval} (sk_H,x) \approx \mathsf {Eval} (msk,x) + H(x). \end{aligned}$$(1)
We emphasize that the SHSF itself does not have any pseudorandomness property; this will come from “rounding” the function in our PRF constructions, described next.
CHC-PRFs and PP-PRFs. We first briefly outline how we use SHSFs to construct CHC-PRFs and PP-PRFs. To construct a CHC-PRF we instantiate the SHSF with range \(\mathcal {Y} = \mathbb {Z}_q^m\) for an appropriately chosen q. The CHC-PRF key is just a SHSF master key \(msk\).
-
To evaluate on an input \(x \in \mathcal {X}\) using \(msk\) we output
 , where
, where  denotes (coordinate-wise) “rounding” from \(\mathbb {Z}_q\) to \(\mathbb {Z}_p\) for some appropriate \(p \ll q\).
denotes (coordinate-wise) “rounding” from \(\mathbb {Z}_q\) to \(\mathbb {Z}_p\) for some appropriate \(p \ll q\). -
To generate a constrained key for a constraint circuit
 , we sample a key k for an ordinary PRF F, define the shift function \(H_{C,k}(x) := C(x) \cdot F_{k}(x)\), and output the shifted key $$\begin{aligned} sk_C \leftarrow \mathsf {Shift} (msk,H_{C,k}). \end{aligned}$$
, we sample a key k for an ordinary PRF F, define the shift function \(H_{C,k}(x) := C(x) \cdot F_{k}(x)\), and output the shifted key $$\begin{aligned} sk_C \leftarrow \mathsf {Shift} (msk,H_{C,k}). \end{aligned}$$Since \(\mathsf {Shift} \) hides the circuit \(H_{C,k}\), it follows that \(sk_C\) hides C.
-
To evaluate on an input x using the constrained key \(sk_{C}\), we output
 .
.
Observe that for authorized inputs x (where \(C(x)=0\)), we have \(H_{C,k}(x) = 0\), so \(\mathsf {SEval} (sk_{C},x) \approx \mathsf {Eval} (msk,x)\) and therefore their rounded counterparts are equal with high probability. (This relies on the additional property that \(\mathsf {Eval} (msk,x)\) is not to close to a “rounding border.”) For unauthorized points x (where \(C(x)=1\)), to see that the CHC-PRF output is pseudorandom given \(sk_C\), notice that by Eq. (1), the output is (with high probability)

Because F is a pseudorandom function, \(H(x) = F_{k}(x)\) completely “randomizes” the right-hand side above.
Turning now to PP-PRFs, for simplicity consider the case where we want to program the constrained key at a single input \(x^{*}\) (generalizing to polynomially many inputs is straightforward). A first idea is to use the same algorithms as in the above CHC-PRF, except that to program a key to output y at input \(x^*\) we define the shift function
where \(y' \in \mathbb {Z}_q^m\) is chosen uniformly conditioned on  . As before, the programmed key is just the shifted key \(sk_{x^*,y} \leftarrow \mathsf {Shift} (msk,H_{x^*,y})\). By Eq. (1), evaluating on the unauthorized input \(x^*\) using \(sk_{x^{*},y}\) indeed yields
. As before, the programmed key is just the shifted key \(sk_{x^*,y} \leftarrow \mathsf {Shift} (msk,H_{x^*,y})\). By Eq. (1), evaluating on the unauthorized input \(x^*\) using \(sk_{x^{*},y}\) indeed yields  . However, it is unclear whether the true (non-programmed) value of the function at the unauthorized input \(x = x^{*}\) is pseudorandom given \(sk_{x^{*},y}\): in particular, because y is chosen by the adversary, \(y' \in \mathbb {Z}_q^{m}\) may not be uniformly random.
. However, it is unclear whether the true (non-programmed) value of the function at the unauthorized input \(x = x^{*}\) is pseudorandom given \(sk_{x^{*},y}\): in particular, because y is chosen by the adversary, \(y' \in \mathbb {Z}_q^{m}\) may not be uniformly random.
To address this issue, we observe that the above construction satisfies a weaker pseudorandomness guarantee: if the adversary does not specify y but instead y is uniformly random, then by Eq. (2) the PP-PRF is pseudorandom at \(x^{*}\). This observation leads us to our actual PP-PRF construction: we instantiate two of the above “weak” PP-PRFs with keys \(msk_1\) and \(msk_2\). To generate a programmed key for input \(x^*\) and output y, we first generate random additive shares \(y_1, y_2\) such that \(y = y_1 + y_2\), and output the programmed key \(sk_{x^*,y} := (sk_{x^*,y_1}, sk_{x^*,y_2})\) where \(sk_{x^*,y_i} \leftarrow \mathsf {Shift} (msk_{i}, H_{x^{*}, y_{i}})\) for \(i=1,2\). Each evaluation algorithm (ordinary and programmed) is then defined simply as the sum of the corresponding evaluation algorithm from the “weak” construction using the two component keys. Because both programmed keys are generated for random target outputs \(y_{i}\), we can prove pseudorandomness of the real function value.
Constructing SHSFs. We now give an overview of our construction of shift-hiding shifted functions. For simplicity, suppose the range of the functions is \(\mathcal {Y} = \mathbb {Z}_q\); extending this to \(\mathbb {Z}_q^{m}\) (as in our actual constructions) is straightforward. As in [6, 23] our main tools are the “gadget-matrix homomorphisms” developed in the literature on fully homomorphic and attribute-based cryptography [5, 18, 20, 21].
At a high level, our SHSF works as follows. The master secret key is just an LWE secret \(\mathbf {s}\) whose first coordinate is 1. A shifted key for a shift function \(H :\mathcal {X} \rightarrow \mathbb {Z}_q\) consists of LWE vectors (using secret \(\mathbf {s}\)) relative to some public matrices that have been “shifted” by multiples of the gadget matrix \(\mathbf {G}\) [24]; more specifically, the multiples are the bits of FHE ciphertexts encrypting H, and the \(\mathbb {Z}_q\)-entries of the FHE secret key \(sk\). To compute the shifted function on an input x, we do the following:
-
1.
Using the gadget homomorphisms for boolean gates [5, 18] on the LWE vectors corresponding to the FHE encryption of H, we compute LWE vectors relative to some publicly computable matrices, shifted by multiples of \(\mathbf {G}\) corresponding to the bits of an FHE ciphertext encrypting H(x).
-
2.
Then, using the gadget homomorphisms for hidden linear functions [20] with the LWE vectors corresponding to the FHE secret key, we compute LWE vectors relative to some publicly computable matrix \(\mathbf {B}_{x}\), but shifted by \((H(x)+e) \mathbf {G}\) where \(H(x)+e \approx H(x) \in \mathbb {Z}_q\) is the “noisy plaintext” arising as the inner product of the FHE ciphertext and secret key. Taking just the first column, we therefore have an LWE sample relative to some vector \(\mathbf {b}_{x} + (H(x) + e) \mathbf {u}_{1}\), where \(\mathbf {u}_{1}\) is the first standard basis (column) vector.
-
3.
Finally, because the first coordinate of the LWE secret \(\mathbf {s}\) is 1, the above LWE sample is simply
 .
.
With the above in mind, we then define the (unshifted) function itself on an input x to simply compute \(\mathbf {b}_{x}\) from the public parameters as above, and output  . This yields Eq. (1).
. This yields Eq. (1).
2 Preliminaries
We denote row vectors by lower-case bold letters, e.g., \(\mathbf {a}\). We denote matrices by upper-case bold letters, e.g., \(\mathbf {A}\). The Kronecker product \(\mathbf {A}\otimes \mathbf {B}\) of two matrices (or vectors) \(\mathbf {A}\) and \(\mathbf {B}\) is obtained by replacing each entry \(a_{i,j}\) of \(\mathbf {A}\) with the block \(a_{i,j} \mathbf {B}\). The Kronecker product obeys the mixed-product property: \((\mathbf {A}\otimes \mathbf {B})(\mathbf {C}\otimes \mathbf {D}) = (\mathbf {A}\mathbf {C}) \otimes (\mathbf {B}\mathbf {D})\) for any matrices \(\mathbf {A}, \mathbf {B}, \mathbf {C}, \mathbf {D}\) with compatible dimensions.
2.1 Gadgets and Homomorphisms
Here we recall “gadgets” [24] over \(\mathbb {Z}_q\) and several of their homomorphic properties, some of which were implicit in [18], and which were developed and exploited further in [5, 20, 21].
For an integer modulus q, the gadget (or powers-of-two) vector over \(\mathbb {Z}_q\) is defined as

For every \(u \in \mathbb {Z}_q\), there is an (efficiently computable) binary vector  such that
such that  . Phrased differently,
. Phrased differently,
for a certain binary  , namely, the one that selects all the products of the corresponding entries of \(\mathbf {x}\) and \(\mathbf {g}\).
, namely, the one that selects all the products of the corresponding entries of \(\mathbf {x}\) and \(\mathbf {g}\).
The gadget matrix is defined as
where  . We often drop the subscript n when it is clear from context. We use algorithms \(\mathsf {BoolEval}\) and \(\mathsf {LinEval}\), which have the following properties.
. We often drop the subscript n when it is clear from context. We use algorithms \(\mathsf {BoolEval}\) and \(\mathsf {LinEval}\), which have the following properties.
-
\(\mathsf {BoolEval} (C, x, \mathbf {A})\), given a boolean circuit
 of depth d, an
of depth d, an 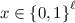 , and some \(\mathbf {A}\in \mathbb {Z}_q^{n \times (\ell +1)m}\), outputs an integral matrix \(\mathbf {R}_{C,x} \in \mathbb {Z}^{(\ell +1)m \times k m}\) with \(m^{O(d)}\)-bounded entries for which $$\begin{aligned} (\mathbf {A}+ (1,x) \otimes \mathbf {G}) \cdot \mathbf {R}_{C,x} = \mathbf {A}_{C} + C(x) \otimes \mathbf {G}, \end{aligned}$$(6)
, and some \(\mathbf {A}\in \mathbb {Z}_q^{n \times (\ell +1)m}\), outputs an integral matrix \(\mathbf {R}_{C,x} \in \mathbb {Z}^{(\ell +1)m \times k m}\) with \(m^{O(d)}\)-bounded entries for which $$\begin{aligned} (\mathbf {A}+ (1,x) \otimes \mathbf {G}) \cdot \mathbf {R}_{C,x} = \mathbf {A}_{C} + C(x) \otimes \mathbf {G}, \end{aligned}$$(6)where \(\mathbf {A}_{C} \in \mathbb {Z}_q^{n \times m}\) depends only on \(\mathbf {A}\) and C (and not on x).Footnote 2
-
\(\mathsf {LinEval} (\mathbf {x}, \mathbf {C})\), given an
 and a matrix \(\mathbf {C}\in \mathbb {Z}_q^{n \times \ell m}\), outputs an integral matrix \(\mathbf {R}_{\mathbf {x}} \in \mathbb {Z}^{2 \ell m \times m}\) with \({{\mathrm{poly}}}(m,\ell )\)-bounded entries such that, for all \(\mathbf {A}, \mathbf {C}\in \mathbb {Z}_q^{n \times \ell m}\) and \(\mathbf {k}\in \mathbb {Z}_q^{\ell }\),
and a matrix \(\mathbf {C}\in \mathbb {Z}_q^{n \times \ell m}\), outputs an integral matrix \(\mathbf {R}_{\mathbf {x}} \in \mathbb {Z}^{2 \ell m \times m}\) with \({{\mathrm{poly}}}(m,\ell )\)-bounded entries such that, for all \(\mathbf {A}, \mathbf {C}\in \mathbb {Z}_q^{n \times \ell m}\) and \(\mathbf {k}\in \mathbb {Z}_q^{\ell }\), 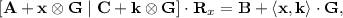 (7)
(7)where \(\mathbf {B}\in \mathbb {Z}_q^{n \times m}\) depends only on \(\mathbf {A}\) and \(\mathbf {C}\) (and not on \(\mathbf {x}\) or \(\mathbf {k}\)).Footnote 3 More generally, for
 by applying the above to the \(\ell \)-bit chunks of \(\mathbf {x}\), in Eq. (7) we replace
by applying the above to the \(\ell \)-bit chunks of \(\mathbf {x}\), in Eq. (7) we replace  with \((\mathbf {x}\cdot (\mathbf {I}_{k} \otimes \mathbf {k}^{t})) \otimes \mathbf {G}\), and now \(\mathbf {R}_{\mathbf {x}} \in \mathbb {Z}^{(k+1) \ell m \times k m}\), \(\mathbf {A}\in \mathbb {Z}_q^{n \times k \ell m}\), and \(\mathbf {B}\in \mathbb {Z}_q^{n \times k m}\).
with \((\mathbf {x}\cdot (\mathbf {I}_{k} \otimes \mathbf {k}^{t})) \otimes \mathbf {G}\), and now \(\mathbf {R}_{\mathbf {x}} \in \mathbb {Z}^{(k+1) \ell m \times k m}\), \(\mathbf {A}\in \mathbb {Z}_q^{n \times k \ell m}\), and \(\mathbf {B}\in \mathbb {Z}_q^{n \times k m}\).
2.2 Fully Homomorphic Encryption
We use the GSW (leveled) fully homomorphic encryption scheme [18] \((\mathsf {KG},\mathsf {Enc}, \mathsf {Eval})\), whose relevant properties for our needs are summarized as follows (we use only a symmetric-key version, which is sufficient for our purposes):
-
\(\mathsf {KG} (1^\lambda , q)\), given a security parameter \(\lambda \) and a requested modulus q, outputs a secret key \(\mathbf {k}\in \mathbb {Z}_q^{\tau }\) (for some \(\tau = {{\mathrm{poly}}}(\lambda ,\log q)\)).
-
\(\mathsf {Enc} (\mathbf {k},m)\), given a secret key \(\mathbf {k}\) and a message
 , outputs a ciphertext ct, which is a binary string.
, outputs a ciphertext ct, which is a binary string. -
\(\mathsf {Eval} (C, ct_1, \ldots , ct_{\ell })\), given a boolean circuit
 and ciphertexts \(ct_1, ct_2, \ldots , ct_{\ell }\), outputs a ciphertext
and ciphertexts \(ct_1, ct_2, \ldots , ct_{\ell }\), outputs a ciphertext 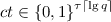 .
.
Notice that in the above definition there is no explicit decryption algorithm. Instead we express the essential “noisy” linear relation between the result of homomorphic evaluation and the secret key: for any \(\mathbf {k}\leftarrow \mathsf {KG} (1^{\lambda }, q)\), any boolean circuit  of depth at most d, any messages
of depth at most d, any messages  and ciphertexts \(ct_{j} \leftarrow \mathsf {Enc} (\mathbf {k},m_{j})\) for \(j=1,\ldots ,\ell \), we have
and ciphertexts \(ct_{j} \leftarrow \mathsf {Enc} (\mathbf {k},m_{j})\) for \(j=1,\ldots ,\ell \), we have
for some integral error vector  , where \(B = \lambda ^{O(d)}\). In other words, multiplying (the \(\tau \)-bit chunks of) the result of homomorphic evaluation with the secret key yields a “noisy” version of a robust encoding of the result (where the encoding is via the powers of two). While the robust encoding allows the noise to be removed, we will not need to do so explicitly.
, where \(B = \lambda ^{O(d)}\). In other words, multiplying (the \(\tau \)-bit chunks of) the result of homomorphic evaluation with the secret key yields a “noisy” version of a robust encoding of the result (where the encoding is via the powers of two). While the robust encoding allows the noise to be removed, we will not need to do so explicitly.
More generally, if the circuit C has k-bit output, then \(\mathsf {Eval} \) outputs a ciphertext in  and Eq. (8) holds with
and Eq. (8) holds with  replaced by
replaced by  .
.
2.3 Learning with Errors
For a positive integer dimension n and modulus q, and an error distribution \(\chi \) over \(\mathbb {Z}\), the LWE distribution and decision problem are defined as follows. For an \(\mathbf {s}\in \mathbb {Z}^{n}\), the LWE distribution \(A_{\mathbf {s},\chi }\) is sampled by choosing a uniformly random \(\mathbf {a}\leftarrow \mathbb {Z}_q^{n}\) and an error term \(e \leftarrow \chi \), and outputting  .
.
Definition 1
The decision-LWE\(_{n,q,\chi }\) problem is to distinguish, with non-negligible advantage, between any desired (but polynomially bounded) number of independent samples drawn from \(A_{\mathbf {s},\chi }\) for a single \(\mathbf {s}\leftarrow \mathbb {Z}_q^{n}\), and the same number of uniformly random and independent samples over \(\mathbb {Z}_q^{n+1}\).
In this work we use a form of LWE where the first coordinate of the secret vector \(\mathbf {s}\) is 1, i.e. \(\mathbf {s}= (1,\bar{\mathbf {s}})\) where \(\bar{\mathbf {s}} \leftarrow \mathbb {Z}_q^{n-1}\). It is easy to see that this is equivalent to LWE with an \((n-1)\)-dimensional secret: the transformation mapping \((\mathbf {a}, b) \in \mathbb {Z}_q^{n-1} \times \mathbb {Z}_q\) to \(((r,\mathbf {a}) , b + r)\) for a uniformly random \(r \in \mathbb {Z}_q\) (chosen freshly for each sample) maps samples from \(A_{\bar{\mathbf {s}},\chi }\) to samples from \(A_{\mathbf {s},\chi }\), and maps uniform samples to uniform samples.
A standard instantiation of LWE is to let \(\chi \) be a discrete Gaussian distribution (over \(\mathbb {Z}\)) with parameter \(r = 2\sqrt{n}\). A sample drawn from this distribution has magnitude bounded by, say, \(r\sqrt{n} = \varTheta (n)\) except with probability at most \(2^{-n}\). For this parameterization, it is known that LWE is at least as hard as quantumly approximating certain “short vector” problems on n-dimensional lattices, in the worst case, to within \(\tilde{O}(q\sqrt{n})\) factors [27, 28]. Classical reductions are also known for different parameterizations [12, 26].
2.4 One Dimensional Rounded Short Integer Solution
As in [6, 14, 23] we make use of a special “one-dimensional, rounded” variant of the short integer solution problem (SIS). For the parameters we will use, this problem is actually no easier to solve than LWE is, but it is convenient to define it separately.
Definition 2
(1D-R-SIS [6, 14]). Let \(p \in \mathbb {N}\) and let \(p_1< p_2< \cdots < p_k\) be pairwise coprime and coprime with p. Let \(q = p \cdot \prod _{i=1}^k p_i\). Then for positive numbers \(m \in \mathbb {N}\) and B, the 1D-R-SIS\(_{m,p,q,B}\) problem is as follows: given a uniformly random vector \(\mathbf {v}\leftarrow \mathbb {Z}_q^m\), find \(\mathbf {z}\in \mathbb {Z}^m\) such that  and
and
For sufficiently large \(p_{1} \ge B \cdot {{\mathrm{poly}}}(k, \log q)\), solving 1D-R-SIS is at least as hard as approximating certain “short vector” problems on k-dimensional lattices, in the worst case, to within certain \(B \cdot {{\mathrm{poly}}}(k)\) factors [1, 6, 14, 25].
3 Shift-Hiding Shiftable Functions
Here we present our construction of what we call shift-hiding shiftable functions (SHSFs), which we use in our subsequent constructions of CHC-PRFs and PP-PRFs. Because there are several parameters and we need some specific algebraic properties, we do not give an abstract definition of SHSF, but instead just give a construction (Sect. 3.2) and show the requisite properties (Sect. 3.3).
3.1 Notation
Let \(\mathsf {GSW} = (\mathsf {KG},\mathsf {Enc},\mathsf {Eval})\) denote the GSW fully homomorphic encryption scheme (Sect. 2.2), where the secret key is in \(\mathbb {Z}_q^{\tau }\) for some \(\tau = \tau (\lambda )\). Recall that homomorphic evaluation of a function with k output bits produces a  -bit ciphertext.
-bit ciphertext.
Our construction represents shift functions  by (bounded-size) boolean circuits. Specifically, we let
by (bounded-size) boolean circuits. Specifically, we let  for
for  be a boolean circuit where \(H'(x)\) is the binary decomposition of H(x), so that, following Eq. (5),
be a boolean circuit where \(H'(x)\) is the binary decomposition of H(x), so that, following Eq. (5),
Let \(U(H',x) = H'(x)\) denote a universal circuit for boolean circuits  of size \(\sigma \), and let \(U_{x}(\cdot ) = U(\cdot ,x)\). Its homomorphic analogue is as follows: letting \(\overline{z}\) be the total length of fresh GSW ciphertexts encrypting a circuit of size \(\sigma \), for any \(x \in \{0,1\}^{\ell }\) define
of size \(\sigma \), and let \(U_{x}(\cdot ) = U(\cdot ,x)\). Its homomorphic analogue is as follows: letting \(\overline{z}\) be the total length of fresh GSW ciphertexts encrypting a circuit of size \(\sigma \), for any \(x \in \{0,1\}^{\ell }\) define
Observe that \(\overline{U}_{x}\) can be implemented as a boolean circuit of size (and hence depth) \({{\mathrm{poly}}}(\lambda , \sigma )\).
3.2 Construction
Here we give the tuple of algorithms \((\mathsf {Setup},\mathsf {KeyGen},\mathsf {Eval}, \mathsf {Shift}, \mathsf {SEval},\mathcal {S})\) that make up our SHSF. For security parameter \(\lambda \) and constraint circuit size \(\sigma \) the algorithms are parameterized by some \(n = {{\mathrm{poly}}}(\lambda , \sigma )\) and \(q = 2^{{{\mathrm{poly}}}(\lambda , \sigma )}\), with  ; we instantiate these more precisely in Sect. 3.4 below.
; we instantiate these more precisely in Sect. 3.4 below.
Construction 1
Let  and \(\mathcal {Y} = \mathbb {Z}_q^m\). Define:
and \(\mathcal {Y} = \mathbb {Z}_q^m\). Define:
-
\(\mathsf {Setup} (1^\lambda , 1^{\sigma })\): Sample uniformly random and independent matrices \(\mathbf {A}\in \mathbb {Z}_q^{n \times (\overline{z}+1) m}\) and \(\mathbf {C}\in \mathbb {Z}_q^{n \times \tau m}\), and output \(pp= (\mathbf {A}, \mathbf {C})\).
(The n-by-m chunks of \(\mathbf {A}\) will correspond to the \(\overline{z}\) bits of a GSW encryption of the shift function; similarly, the chunks of \(\mathbf {C}\) will correspond to the GSW secret key in \(\mathbb {Z}_q^{\tau }\).)
-
\(\mathsf {KeyGen} (pp)\): Sample \(\mathbf {s}' \leftarrow \mathbb {Z}_q^{n-1}\) and set \(\mathbf {s}=(1,\mathbf {s}')\). Output the master secret key \(msk= \mathbf {s}\).
-
 : compute
: compute  (13)
(13)and let
 (14)
(14)(Observe that by Eq. (6), \(\mathbf {A}_{x}=\mathbf {A}_{C}\) for the circuit \(C=\overline{U}_{x}\), and does not depend on the “dummy” ciphertext \(0^{\overline{z}}\), which stands in for a GSW encryption of a shift function.)
Next, compute
 (15)
(15)and let
 (16)
(16)(Observe that this corresponds to taking \(\mathbf {k}= \mathbf {0}\) in Eq. (7), so \(\mathbf {B}_{x}\) does not depend on the “dummy” ciphertext \(0^{\overline{z}}\); it depends only on \(\mathbf {A}_{x}\), hence \(\mathbf {A}\) and x, and \(\mathbf {C}\).)
Finally, output
$$\begin{aligned} \mathbf {s}\cdot \mathbf {B}_{x} \cdot (\mathbf {I}_{m} \otimes \mathbf {r}^{t} \otimes \mathbf {u}_{1}^{t}) \in \mathbb {Z}_q^{m}, \end{aligned}$$(17)where
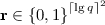 is as in Eq. (10) and \(\mathbf {u}_{1} \in \mathbb {Z}^{m}\) is the first standard basis vector.
is as in Eq. (10) and \(\mathbf {u}_{1} \in \mathbb {Z}^{m}\) is the first standard basis vector. -
\(\mathsf {Shift} (pp,msk,H)\): for a shift function
 whose binary decomposition
whose binary decomposition  can be implemented by a circuit of size \(\sigma \), sample a GSW encryption key \(\mathbf {k}\leftarrow \mathsf {GSW.KG} (1^{\lambda }, q)\), then encrypt \(H'\) bit-by-bit under this key to obtain a ciphertext \(ct \leftarrow \mathsf {GSW.Enc} _{\mathbf {k}}(H')\). Next, let $$\begin{aligned} \mathbf {a}&= \mathbf {s}(\mathbf {A}+ (1,ct) \otimes \mathbf {G}) + \mathbf {e}\end{aligned}$$(18)$$\begin{aligned} \mathbf {c}&= \mathbf {s}(\mathbf {C}+ \mathbf {k}\otimes \mathbf {G}) + \mathbf {e}' \end{aligned}$$(19)
can be implemented by a circuit of size \(\sigma \), sample a GSW encryption key \(\mathbf {k}\leftarrow \mathsf {GSW.KG} (1^{\lambda }, q)\), then encrypt \(H'\) bit-by-bit under this key to obtain a ciphertext \(ct \leftarrow \mathsf {GSW.Enc} _{\mathbf {k}}(H')\). Next, let $$\begin{aligned} \mathbf {a}&= \mathbf {s}(\mathbf {A}+ (1,ct) \otimes \mathbf {G}) + \mathbf {e}\end{aligned}$$(18)$$\begin{aligned} \mathbf {c}&= \mathbf {s}(\mathbf {C}+ \mathbf {k}\otimes \mathbf {G}) + \mathbf {e}' \end{aligned}$$(19)where \(\mathbf {e}\) and \(\mathbf {e}'\) are error vectors whose entries are sampled independently from \(\chi \). Output
$$\begin{aligned} sk_H = (ct, \mathbf {a}, \mathbf {c}). \end{aligned}$$(20)(Recall that \(\mathbf {A}' = \mathbf {A}+ (1,ct) \otimes \mathbf {G}\) and \(\mathbf {C}' = \mathbf {C}+ \mathbf {k}\otimes \mathbf {G}\) support homomorphic operations on ct and \(\mathbf {k}\) via right-multiplication by short matrices, using the gadget homomorphisms. Shifted evaluation, defined next, performs such right-multiplications on \(\mathbf {a}\approx \mathbf {s}\mathbf {A}', \mathbf {c}\approx \mathbf {s}\mathbf {C}'\).)
-
\(\mathsf {SEval} (pp,sk_H,x)\): On input \(sk_H = (ct, \mathbf {a}, \mathbf {c})\) and
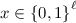 , compute $$\begin{aligned} \mathbf {R}_{ct}&= \mathsf {BoolEval} (\overline{U}_{x}, ct, \mathbf {A}) \end{aligned}$$(21)$$\begin{aligned} \mathbf {a}_{x}&= \mathbf {a}\cdot \mathbf {R}_{ct}. \end{aligned}$$(22)
, compute $$\begin{aligned} \mathbf {R}_{ct}&= \mathsf {BoolEval} (\overline{U}_{x}, ct, \mathbf {A}) \end{aligned}$$(21)$$\begin{aligned} \mathbf {a}_{x}&= \mathbf {a}\cdot \mathbf {R}_{ct}. \end{aligned}$$(22)(By Eq. (6), we have \(\mathbf {a}_{x} \approx \mathbf {s}(\mathbf {A}_{x} + \overline{U}_{x}(ct) \otimes \mathbf {G})\), where recall that \(\overline{U}_{x}(ct)\) is a GSW encryption of \(H'(x)\), computed homomorphically.)
Next, compute
$$\begin{aligned} \mathbf {R}'_{ct}&= \mathsf {LinEval} (\overline{U}_{x}(ct), \mathbf {C}) \end{aligned}$$(23)$$\begin{aligned} \mathbf {b}_{x}&= [\mathbf {a}_{x} \mid \mathbf {c}] \cdot \mathbf {R}'_{ct}. \end{aligned}$$(24)(By Eqs. (7) for \(\mathsf {LinEval} \) and (8) for GSW decryption, we have \(\mathbf {b}_{x} \approx \mathbf {s}(\mathbf {B}_{x} + \mathbf {h}' \otimes \mathbf {G})\), where \(\mathbf {h}'\) is a noisy version of the robust encoding \(H'(x) \otimes \mathbf {g}\).)
Finally, output
$$\begin{aligned} \mathbf {b}_{x} \cdot (\mathbf {I}_{m} \otimes \mathbf {r}^{t} \otimes \mathbf {u}_{1}^{t}) \in \mathbb {Z}_q^{m}, \end{aligned}$$(25)where \(\mathbf {r}, \mathbf {u}_{1}\) are as in \(\mathsf {Eval} \) above.
(Here the \(\mathbf {I}_{m} \otimes \mathbf {r}^{t}\) term reconstructs a noisy version of \(H(x) \in \mathbb {Z}_q^{m}\) from \(\mathbf {h}'\) as in Eq. (10), and the \(\mathbf {u}_{1}^{t} \in \mathbb {Z}^{m}\) term selects the first column of \(\mathbf {G}\), whose inner product with \(\mathbf {s}\) is 1.)
-
\(\mathcal {S}(1^{\lambda }, 1^{\sigma })\): Sample a GSW secret key \(\mathbf {k}\leftarrow \mathsf {GSW.KG} (1^\lambda , q)\) and compute (by encrypting bit-by-bit) \(ct \leftarrow \mathsf {GSW.Enc} _{\mathbf {k}}(C)\), where C is some arbitrary size-\(\sigma \) boolean circuit. Sample uniformly random and independent \(\mathbf {A}\leftarrow \mathbb {Z}_q^{n \times (\overline{z}+1)m}, \mathbf {a}\leftarrow \mathbb {Z}_q^{(\overline{z}+1)m}\), \(\mathbf {C}\leftarrow \mathbb {Z}_q^{n \times \tau m}, \mathbf {c}\leftarrow \mathbb {Z}_q^{\tau m}\). Output \(pp=(\mathbf {A}, \mathbf {C})\) and \(sk = (ct, \mathbf {a}, \mathbf {c})\).
3.3 Properties
Here we prove the three main properties of our SHSF that we will use in subsequent sections.
Lemma 1
(Shift Hiding). Assuming the hardness of LWE\(_{n-1,q,\chi }\) and CPA security of the GSW encryption scheme, for any PPT \(\mathcal {A}\) and any \(\sigma = \sigma (\lambda ) = {{\mathrm{poly}}}(\lambda )\),

where \(\mathsf {RealKey}\) and \(\mathsf {IdealKey}\) are the respective views of \(\mathcal {A}\) in the experiments defined in Fig. 1.
Proof
Let \(\mathcal {A}\) be any polynomial-time adversary. To show that Eq. (26) holds we define a sequence of hybrid experiments and show that they are indistinguishable.
- Hybrid \(H_0\)::
-
This is the experiment \(\mathsf {RealKey} \).
- Hybrid \(H_1\)::
-
This is the same as \(H_{0}\), except that we modify how the \(\mathbf {A}\) and \(\mathbf {C}\) are constructed as follows: after we generate ct and \(\mathbf {k}\) we choose uniformly random \(\mathbf {A}'\) and \(\mathbf {C}'\) and set
$$\begin{aligned} \mathbf {A}&= \mathbf {A}' - (1,ct) \otimes \mathbf {G}\end{aligned}$$(27)$$\begin{aligned} \mathbf {C}&= \mathbf {C}' - \mathbf {k}\otimes \mathbf {G}. \end{aligned}$$(28) - Hybrid \(H_2\)::
-
This is the same as \(H_{1}\), except that we sample the \(\mathbf {a}_i\) and \(\mathbf {c}_j\) uniformly at random from \(\mathbb {Z}_q^m\).
- Hybrid \(H_{3}\)::
-
This is the same as \(H_{2}\), except that we again directly choose \(\mathbf {A}, \mathbf {C}\) uniformly at random (without choosing \(\mathbf {A}', \mathbf {C}'\)).
- Hybrid \(H_4\)::
-
This is the same as \(H_{2}\), except that ct encrypts the (arbitrary) size-\(\sigma \) circuit C (as in \(\mathcal {S}\)) instead of \(H'\), i.e., we set \(ct \leftarrow \mathsf {GSW.Enc} _{\mathbf {k}'}(C)\). Observe that this is exactly the experiment \(\mathsf {IdealKey} \).
Claim 1
\(H_0\) and \(H_1\) are identical.
Proof
This is because \(\mathbf {A}'\) and \(\mathbf {C}'\) are uniformly random and independent of ct and \(\mathbf {k}\).
Claim 2
Assuming the hardness of \(\mathsf {LWE} _{n-1,q,\chi }\), we have \(H_1 {\mathop {\approx }\limits ^{c}}H_2\).
Proof
We use any adversary \(\mathcal {A}\) that attempts to distinguish \(H_1\) from \(H_2\) to build an adversary \(\mathcal {A}'\) that solves \(\mathsf {LWE} _{n-1,q,\chi }\) with the same advantage. First, \(\mathcal {A}'\) receives samples \((\mathbf {A}',\mathbf {a}) \in \mathbb {Z}_q^{n \times (\overline{z}+1)m} \times \mathbb {Z}_q^{(\overline{z}+1)m}\) and \((\mathbf {C}',\mathbf {c}) \in \mathbb {Z}_q^{n \times \tau m} \times \mathbb {Z}_q^{\tau m}\), then proceeds exactly as in \(H_1\) to interact with \(\mathcal {A}\), and outputs what \(\mathcal {A}\) outputs. If the samples are LWE samples from \(A_{\mathbf {s},\chi }\) where \(\mathbf {s}= (1,\mathbf {s}')\) for \(\mathbf {s}' \leftarrow \mathbb {Z}_q^{n-1}\), then
for error vectors \(\mathbf {e}, \mathbf {e}'\) whose entries are drawn from \(\chi \), therefore \(\mathcal {A}\)’s view is identical to its view in \(H_1\). If the samples are uniformly random, then \(\mathcal {A}\)’s view is identical to its view in \(H_2\). This proves the claim.
Claim 3
\(H_{2}\) and \(H_{3}\) are identical.
Proof
This is because \(\mathbf {A}', \mathbf {C}'\) are uniformly random and independent of ct and \(\mathbf {k}\).
Claim 4
If \(\mathsf {GSW} \) is CPA-secure then \(H_3 {\mathop {\approx }\limits ^{c}}H_4\).
Proof
This follows immediately from the fact that the GSW secret key \(\mathbf {k}\leftarrow \mathsf {GSW}.\mathsf {KG} (1^{\lambda }, q)\) is used only to encrypt H (yielding ct) or the arbitrary circuit C, respectively, in \(H_{3}\) and \(H_{4}\).
This completes the proof of Lemma 1.
Lemma 2
(Border Avoiding). For any PPT \(\mathcal {A}\), \(i \in [m]\), \(\lambda \in \mathbb {N}\) and \(\sigma = {{\mathrm{poly}}}(\lambda )\), assuming the hardness of 1D-R-SIS\(_{(\overline{z} + \tau + 1)m,p,q,B}\) for some large enough \(B = m^{{{\mathrm{poly}}}(\lambda ,\sigma )} = \lambda ^{{{\mathrm{poly}}}(\lambda )}\), we have

Proof
We show how to use an adversary which finds an \(x \in \mathcal {X}\) such that
for some \(i \in [m]\) to solve 1D-R-SIS.
Given a (uniformly random) 1D-R-SIS\(_{(\overline{z}+ \tau + 1) m,p,q,B}\) challenge \(\mathbf {v}= (\mathbf {a}, \mathbf {c}) \in \mathbb {Z}_q^{(\overline{z}+1)m} \times \mathbb {Z}_q^{\tau m}\), we put \(\mathbf {a}, \mathbf {c}\) in the \(sk\) given to \(\mathcal {A}\), and generate \(pp\) in the same way as in the \(\mathcal {S}\) algorithm. Let x be a query output by \(\mathcal {A}\), and consider the response
where \(\mathbf {R}_{ct}, \mathbf {R}'_{ct}\) are \(m^{{{\mathrm{poly}}}(\lambda ,\sigma )}\)-bounded matrices as computed by \(\mathsf {SEval} \), and \(\mathbf {U}\) is a binary matrix. Now if Eq. (30) holds for some \(i \in [m]\), then \((\mathbf {y}_x)_i \in \tfrac{q}{p} (\mathbb {Z}+ \tfrac{1}{2}) + [-B,B]\), which means that the ith column of \(\mathbf {T}\) is a valid 1D-R-SIS\(_{(\overline{z}+\tau +1)m,p,q,B}\) solution to the challenge \(\mathbf {v}= (\mathbf {a},\mathbf {c})\), as desired.
Lemma 3
(Approximate Shift Correctness). For any shift function  whose binary decomposition
whose binary decomposition  can be represented by a boolean circuit of size \(\sigma \), and any
can be represented by a boolean circuit of size \(\sigma \), and any  ,
,  , \(msk\leftarrow \mathsf {KeyGen} (pp)\) and \(sk_H \leftarrow \mathsf {Shift} (pp,msk,H)\), we have
, \(msk\leftarrow \mathsf {KeyGen} (pp)\) and \(sk_H \leftarrow \mathsf {Shift} (pp,msk,H)\), we have
where the approximation hides some \(\lambda ^{{{\mathrm{poly}}}(\lambda )}\)-bounded error vector.
Proof
Let \(\mathbf {a}, \mathbf {a}_x, \mathbf {b}_x, \mathbf {c}, \mathbf {A}_x\) and \(\mathbf {B}_x\) be as defined in algorithms \(\mathsf {SEval}\), \(\mathsf {Eval}\) and \(\mathsf {Shift}\). First, observe that by definition of \(\mathbf {a}\approx \mathbf {s}(\mathbf {A}+ (1,ct) \otimes \mathbf {G})\), \(\mathbf {a}_{x} = \mathbf {a}\cdot \mathbf {R}_{ct}\), and Eq. (6), we have
where the approximation hides an error vector with entries bounded by \(m^{{{\mathrm{poly}}}(\lambda ,\sigma )} = \lambda ^{{{\mathrm{poly}}}(\lambda )}\). Similarly, by definition of \(\mathbf {b}_{x}\), the generalized Eq. (7), and the generalized Eq. (8) we have
where the approximation hides some \(\lambda ^{{{\mathrm{poly}}}(\lambda )}\)-bounded error, and \(\mathbf {e}_x\) is also \(\lambda ^{{{\mathrm{poly}}}(\lambda )}\)-bounded. Therefore, by Eq. (10), the mixed-product property, and because \(\mathbf {G}\cdot \mathbf {u}_{1}^{t} = \mathbf {u}_{1}^{t} \in \mathbb {Z}_q^{n}\), and the first coordinate of \(\mathbf {s}\) is 1, the output of \(\mathsf {SEval} (pp, sk_{H},x)\) is
where again the approximations hide \(\lambda ^{{{\mathrm{poly}}}(\lambda )}\)-bounded error vectors, as claimed.
The following is an immediate consequence of Lemma 3.
Corollary 1
Fix the same notation as in Lemma 3. If for all \(i \in [m]\) we have
then
3.4 Parameter Instantiation
We now instantiate the LWE parameters n, q and the 1D-R-SIS parameter k to correspond with subexponential \(\exp (n^{\varepsilon })\) and \(\exp (k^{\varepsilon })\) approximation factors for the underlying worst-case lattice problems, for an arbitrary desired constant \(\varepsilon > 0\). Let \(B=\lambda ^{{{\mathrm{poly}}}(\lambda )}\) be the bound from Corollary 1. For 1D-R-SIS we need to choose k sufficiently large primes \(p_{i} = B \cdot {{\mathrm{poly}}}(\lambda ) = \lambda ^{{{\mathrm{poly}}}(\lambda )}\) to get an approximation factor of
for k-dimensional lattices. Therefore, we can choose a sufficiently large \(k={{\mathrm{poly}}}(\lambda )\) to make this factor \(\exp (k^{\varepsilon })\). We then set
which corresponds to some \(\lambda ^{{{\mathrm{poly}}}(\lambda )}\) approximation factor for n-dimensional lattices. Again, we can choose a sufficiently large \(n={{\mathrm{poly}}}(\lambda )\) to make this factor \(\exp (n^{\varepsilon })\).
4 Constraint-Hiding Constrained PRF
In this section we formally define constraint-hiding constrained PRFs (CHC-PRFs) and give a construction based on our shiftable PRF from Sect. 3.
4.1 Definition
Here we give the definition of CHC-PRFs, specializing the simulation-based definition of [15] to the case of a single constrained-key query.
Definition 3
A constrained function is a tuple of efficient algorithms \((\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Eval}, \mathsf {Constrain}, \mathsf {CEval})\) having the following interfaces (where the domain \(\mathcal {X}\) and range \(\mathcal {Y}\) may depend on the security parameter):
-
\(\mathsf {Setup} (1^{\lambda }, 1^{\sigma })\), given the security parameter \(\lambda \) and an upper bound \(\sigma \) on the size of the constraining circuit, outputs public parameters \(pp\).
-
\(\mathsf {KeyGen} (pp)\), given the public parameters \(pp\), outputs a master secret key \(msk\).
-
\(\mathsf {Eval} (pp,msk,x)\), given the master secret key and an input \(x \in \mathcal {X}\), outputs some \(y \in \mathcal {Y}\).
-
\(\mathsf {Constrain} (pp,msk,C)\), given the master secret key and a circuit C of size at most \(\sigma \), outputs a constrained key \(sk_C\).
-
\(\mathsf {CEval} (pp,sk_C,x)\), given a constrained key \(sk_C\) and an input \(x \in \mathcal {X}\), outputs some \(y \in \mathcal {Y}\).
Definition 4
A constrained function is a constraint-hiding constrained PRF (CHC-PRF) if there is a PPT simulator \(\mathcal {S}\) such that, for any PPT adversary \(\mathcal {A}\) (that without loss of generality never repeats a query) and any \(\sigma = \sigma (\lambda ) = {{\mathrm{poly}}}(\lambda )\),

where \(\mathsf {Real}\) and \(\mathsf {Ideal}\) are the respective views of \(\mathcal {A}\) in the experiments defined in Fig. 2.
The above simulation-based definition simultaneously captures privacy of the constraining function, pseudorandomness on unauthorized inputs, and correctness of constrained evaluation on authorized inputs. The first two properties (privacy and pseudorandomness) follow because in the ideal experiment, the simulator must generate a constrained key without knowing the constraining function, and the adversary gets oracle access to a function that is uniformly random on unauthorized inputs.
For correctness, we claim that the real experiment is computationally indistinguishable from a modified one where each query x is answered as \(\mathsf {CEval} (pp, sk_{C}, x)\) if x is authorized (i.e., \(C(x)=0\)), and as \(\mathsf {Eval} (pp, msk, x)\) otherwise. In particular, this implies that \(\mathsf {Eval} (pp, msk, x) = \mathsf {CEval} (pp, sk_{C}, x)\) with all but negligible probability for all the adversary’s authorized queries x. Indistinguishability of the real and modified experiments follows by a routine hybrid argument, with the ideal experiment as the intermediate one. In particular, the reduction that links the ideal and modified real experiments itself answers authorized queries x using \(\mathsf {CEval} \), and handles unauthorized queries by passing them to its oracle.
4.2 Construction
We now describe our construction of a CHC-PRF for domain  and range \(\mathcal {Y} = \mathbb {Z}_p^{m}\), which handles constraining circuits of size \(\sigma \). It uses the following components:
and range \(\mathcal {Y} = \mathbb {Z}_p^{m}\), which handles constraining circuits of size \(\sigma \). It uses the following components:
-
A pseudorandom function \(\mathsf {PRF} =(\mathsf {PRF.KG}, \mathsf {PRF.Eval})\) having domain
 and range \(\mathbb {Z}_q^{m}\), with key space
and range \(\mathbb {Z}_q^{m}\), with key space  .
. -
The shift hiding shiftable function \(\mathsf {SHSF} = (\mathsf {Setup},\mathsf {KeyGen},\mathsf {Eval}, \mathsf {Shift}, \mathsf {SEval},\mathsf {Sim})\) from Sect. 3, which has parameters q, B that appear in the analysis below.
For a boolean circuit C of size at most \(\sigma \) and some  define the function
define the function  as
as
Notice that the size of (the binary decomposition of) \(H_{C,k}\) is upper bounded by
where s is the circuit size of (the binary decomposition of) \(\mathsf {PRF}.\mathsf {Eval} (k,\cdot )\).
Construction 2
Our CHC-PRF with domain  and range \(\mathcal {Y} = \mathbb {Z}_p^m\) is defined as follows:
and range \(\mathcal {Y} = \mathbb {Z}_p^m\) is defined as follows:
-
\(\mathsf {Setup} (1^\lambda , 1^{\sigma })\): output \(pp\leftarrow \mathsf {SHSF}.\mathsf {Setup} (1^\lambda , 1^{\sigma '})\) where \(\sigma '\) is defined as in Eq. (49).
-
\(\mathsf {KeyGen} (pp)\): output \(msk\leftarrow \mathsf {SHSF}.\mathsf {KeyGen} (pp)\).
-
 : compute \(\mathbf {y}_x = \mathsf {SHSF}.\mathsf {Eval} (pp,msk,x)\) and output
: compute \(\mathbf {y}_x = \mathsf {SHSF}.\mathsf {Eval} (pp,msk,x)\) and output  .
. -
\(\mathsf {Constrain} (pp,msk,C)\): on input a circuit C of size at most \(\sigma \), sample a PRF key \(k \leftarrow \mathsf {PRF.KG} (1^{\lambda })\) and output \(sk_C \leftarrow \mathsf {SHSF}.\mathsf {Shift} (pp,msk,H_{C,k})\).
-
\(\mathsf {CEval} (pp,sk_C,x)\): on input a constrained key \(sk_C\) and
 , output
, output  .
.
4.3 Security Proof
Theorem 1
Construction 2 is a constraint-hiding constrained PRF assuming the hardness of \(\mathsf {LWE} _{n-1,q,\chi }\) and 1D-R-SIS\(_{(z \sigma ' + \tau + 1)m, p, q, B}\) (where \(z, \tau \) are respectively the lengths of fresh GSW ciphertexts and secret keys as used in \(\mathsf {SHSF} \)), the CPA security of the GSW encryption scheme, and that \(\mathsf {PRF} \) is a pseudorandom function.
Proof
Our simulator \(\mathcal {S}(1^{\lambda }, 1^{\sigma })\) for Construction 2 simply outputs \(\mathsf {SHSF}.\mathsf {\mathcal {S}} (1^{\lambda }, 1^{\sigma '})\). Now let \(\mathcal {A}\) be any polynomial-time adversary. To show that \(\mathcal {S}\) satisfies Definition 4 we define a sequence of hybrid experiments and show that they are indistinguishable. Before defining the experiments in detail, we first define a particular “bad” event in all but one of them.
Definition 5
In each of the following hybrid experiments except \(H_{0}\), each query x is answered as  for some \(\mathbf {y}_{x}\) that is computed in a certain way. Define \(\mathsf {Borderline} \) to be the event that at least one such \(\mathbf {y}_x\) has some coordinate in \(\tfrac{q}{p} (\mathbb {Z}+ \tfrac{1}{2}) + [-B,B]\).
for some \(\mathbf {y}_{x}\) that is computed in a certain way. Define \(\mathsf {Borderline} \) to be the event that at least one such \(\mathbf {y}_x\) has some coordinate in \(\tfrac{q}{p} (\mathbb {Z}+ \tfrac{1}{2}) + [-B,B]\).
- Hybrid \(H_0\)::
-
This is the ideal experiment \(\mathsf {Ideal} _{\mathcal {A}, \mathcal {S}}\).
- Hybrid \(H_{1}\)::
-
This is the same as \(H_{0}\), except that on every unauthorized query x (i.e., where \(C(x)=1\)), instead of returning a uniformly random value from \(\mathbb {Z}_p^{m}\), we choose \(\mathbf {y}_{x} \leftarrow \mathbb {Z}_q^{m}\) and output
 .
. - Hybrid \(H_2\)::
-
This is the same as \(H_{1}\), except that we abort the experiment if \(\mathsf {Borderline} \) happens.
- Hybrid \(H_3\)::
-
This is the same as \(H_{2}\), except that we initially choose a PRF key \(k \leftarrow \mathsf {PRF.KG} (1^{\lambda })\) and change how unauthorized queries x (i.e., where \(C(x) = 1\)) are handled, answering all queries according to a slightly modified \(\mathsf {CEval} \). Specifically, for any query x we answer
 where $$\begin{aligned} \mathbf {y}_{x} = \mathsf {SHSF}.\mathsf {SEval} (pp,sk,x) - C(x) \cdot \mathsf {PRF.Eval} (k,x). \end{aligned}$$(50)
where $$\begin{aligned} \mathbf {y}_{x} = \mathsf {SHSF}.\mathsf {SEval} (pp,sk,x) - C(x) \cdot \mathsf {PRF.Eval} (k,x). \end{aligned}$$(50) - Hybrid \(H_4\)::
-
This is the same as \(H_{3}\), except that \((pp,sk)\) are generated as in the real experiment. More formally we instantiate \(pp\leftarrow \mathsf {SHSF}.\mathsf {Setup} (1^\lambda ,1^{\sigma '})\), \(msk\leftarrow \mathsf {SHSF}.\mathsf {KeyGen} (pp)\) and compute \(sk\leftarrow \mathsf {SHSF}.\mathsf {Shift} (pp,msk,H_{C,k})\).
- Hybrid \(H_5\)::
-
This is the same as \(H_{4}\), except that we answer all evaluation queries as in the \(\mathsf {Eval} \) algorithm, i.e., we output
 where $$\begin{aligned} \mathbf {y}_{x} = \mathsf {SHSF}.\mathsf {Eval} (pp,msk,x). \end{aligned}$$(51)
where $$\begin{aligned} \mathbf {y}_{x} = \mathsf {SHSF}.\mathsf {Eval} (pp,msk,x). \end{aligned}$$(51) - Hybrid \(H_6\)::
-
This is the same as \(H_{5}\), except that we no longer abort when \(\mathsf {Borderline} \) happens. Observe that this is exactly the real experiment \(\mathsf {Real} _{\mathcal {A}}\).
We now prove that adjacent pairs of hybrid experiments are indistinguishable.
Claim 5
Experiments \(H_{0}\) and \(H_{1}\) are identical.
Proof
This follows directly from the fact that p divides q.
Claim 6
Assuming that 1D-R-SIS\(_{(z \sigma ' + \tau + 1)m,p,q,B}\) is hard, we have \(H_1 {\mathop {\approx }\limits ^{c}}H_2\). In particular, in \(H_1\) the event \(\mathsf {Borderline} \) happens with negligible probability.
Proof
Let \(\mathcal {A}\) be an adversary attempting to distinguish \(H_1\) and \(H_2\). We want to show that in \(H_1\) event \(\mathsf {Borderline} \) happens with negligible probability. Let x be a query made by \(\mathcal {A}\). If \(C(x)=1\) then \(\mathbf {y}_x\) is uniformly random in \(\mathbb {Z}_q^{m}\), so for any \(i \in [m]\) we have
If \(C(x)=0\), the claim follows immediately by the border-avoiding property of \(\mathsf {SHSF}\) (Lemma 2).
Claim 7
If \(\mathsf {PRF} \) is a pseudorandom function then \(H_2 {\mathop {\approx }\limits ^{c}}H_3\).
Proof
We use any adversary \(\mathcal {A}\) that attempts to distinguish \(H_2\) from \(H_3\) to build an adversary \(\mathcal {A}'\) having the same advantage against the pseudorandomness of \(\mathsf {PRF} \). Here \(\mathcal {A}'\) is given access to an oracle \(\mathcal {O}\) which is either \(\mathsf {PRF.Eval} (k,\cdot )\) for \(k \leftarrow \mathsf {PRF.KG} (1^\lambda )\), or a uniformly random function  . We define \(\mathcal {A}'\) to proceed as in \(H_{2}\) to simulate the view of \(\mathcal {A}\), except that on each query x it sets
. We define \(\mathcal {A}'\) to proceed as in \(H_{2}\) to simulate the view of \(\mathcal {A}\), except that on each query x it sets
and answers  . Finally, \(\mathcal {A}'\) outputs whatever \(\mathcal {A}\) outputs. Clearly, if \(\mathcal {O}\) is \(\mathsf {PRF.Eval} (k,\cdot )\) then the view of \(\mathcal {A}\) is identical to \(H_3\), whereas if the oracle is \(f(\cdot )\) then the view of \(\mathcal {A}\) is identical to its view in \(H_2\). This proves the claim.
. Finally, \(\mathcal {A}'\) outputs whatever \(\mathcal {A}\) outputs. Clearly, if \(\mathcal {O}\) is \(\mathsf {PRF.Eval} (k,\cdot )\) then the view of \(\mathcal {A}\) is identical to \(H_3\), whereas if the oracle is \(f(\cdot )\) then the view of \(\mathcal {A}\) is identical to its view in \(H_2\). This proves the claim.
Claim 8
Assuming the hardness of \(\mathsf {LWE} _{n-1,q,\chi }\) and CPA-security of \(\mathsf {GSW} \), \(H_3 {\mathop {\approx }\limits ^{c}}H_4\).
Proof
This follows immediately from the shift hiding property of \(\mathsf {SHSF}\), i.e., Lemma 1.
Claim 9
\(H_4\) and \(H_5\) are identical.
Proof
This follows by Corollary 1 and noticing that both experiments abort if \(\mathsf {Borderline}\) happens.
Claim 10
Under the hypotheses of Theorem 1, we have \(H_5 {\mathop {\approx }\limits ^{c}}H_6\).
Proof
This follows by combining all the previous claims and recalling that we have proved that \(\mathsf {Borderline} \) happens with negligible probability in \(H_1\).
This completes the proof of Theorem 1.
5 Privately Programmable PRF
In this section we formally define privately programmable PRFs (PP-PRFs) and give a construction based on our shiftable PRF from Sect. 3.
5.1 Definitions
We start by giving a variety of definitions related to “programmable functions” and privately programmable PRFs. In particular, we give a simulation-based definition that is adapted from [8].
Definition 6
A programmable function is a tuple \((\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Eval},\) \( \mathsf {Program}, \mathsf {PEval})\) of efficient algorithms having the following interfaces (where the domain \(\mathcal {X}\) and range \(\mathcal {Y}\) may depend on the security parameter):
-
\(\mathsf {Setup} (1^{\lambda },1^k)\), given the security parameter \(\lambda \) and a number k of programmable inputs, outputs public parameters \(pp\).
-
\(\mathsf {KeyGen} (pp)\), given the public parameters \(pp\), outputs a master secret key \(msk\).
-
\(\mathsf {Eval} (pp,msk,x)\), given the master secret key and an input \(x \in \mathcal {X}\), outputs some \(y \in \mathcal {Y}\).
-
 , given the master secret key \(msk\) and k pairs \((x_i, y_i) \in \mathcal {X} \times \mathcal {Y}\) for distinct \(x_{i}\), outputs a programmed key \(sk_{\mathcal {P}}\).
, given the master secret key \(msk\) and k pairs \((x_i, y_i) \in \mathcal {X} \times \mathcal {Y}\) for distinct \(x_{i}\), outputs a programmed key \(sk_{\mathcal {P}}\). -
\(\mathsf {PEval} (pp,sk_{\mathcal {P}},x)\), given a programmed key \(sk_{\mathcal {P}}\) and an input \(x \in \mathcal {X}\), outputs some \(y \in \mathcal {Y}\).
We now give several definitions that capture various functionality and security properties for programmable functions. We start with the following correctness property for programmed inputs.
Definition 7
A programmable function is statistically programmable if for all \(\lambda ,k={{\mathrm{poly}}}(\lambda ) \in \mathbb {N}\), all sets of k pairs \(\mathcal {P} = \{(x_i,y_i)\} \subseteq \mathcal {X} \times \mathcal {Y}\) (with distinct \(x_{i}\)), and all \(i \in [k]\) we have
We now define a notion of weak simulation security, in which the adversary names the inputs at which the function is programmed, but the outputs are chosen at random (and not revealed to the adversary). As before, we always assume without loss of generality that the adversary never queries the same input x more than once in the various experiments we define.
Definition 8
A programmable function is weakly simulation secure if there is a PPT simulator \(\mathcal {S}\) such that for any PPT adversary \(\mathcal {A}\) and any polynomial \(k = k(\lambda )\),

where \(\mathsf {RealWeakPPRF}\) and \(\mathsf {IdealWeakPPRF}\) are the respective views of \(\mathcal {A}\) in the procedures defined in Fig. 3.
Similarly to Definition 4, the above definition simultaneously captures privacy of the programmed inputs given the programmed key, pseudorandomness on those inputs, and correctness of \(\mathsf {PEval} \) on non-programmed inputs.
Definition 9
A programmable function is a weak privately programmable PRF if it is statistically programmable (Definition 7) and weakly simulation secure (Definition 8).
We now define a notion of (non-weak) simulation security for programmable functions. This differs from the weak notion in that the adversary specifies the programmed inputs and corresponding outputs, and the simulator in the ideal game is also given these input-output pairs. The simulator needs this information because otherwise the adversary could trivially distinguish the real and ideal experiments by checking whether \(\mathsf {PEval} (pp, sk_{\mathcal {P}}, x_{i}) = y_{i}\) for one of the programmed input-output pairs \((x_{i}, y_{i})\). Simulation security itself therefore does not guarantee any privacy of the programmed inputs; below we give a separate simulation-based definition which does.
Definition 10
A programmable function is simulation secure if there is a PPT simulator \(\mathcal {S}\) such that for any PPT adversary \(\mathcal {A}\) and any polynomial \(k = k(\lambda )\),

where \(\mathsf {Real}\) and \(\mathsf {Ideal}\) are the respective views of \(\mathcal {A}\) in the procedures defined in Fig. 4.
We mention that a straightforward hybrid argument similar to one from [6] shows that simulation security implies that \((\mathsf {KeyGen},\mathsf {Eval})\) is a pseudorandom function.
Finally, we define a notion of privacy for the programmed inputs. This says that a key programmed on adversarially chosen inputs and random corresponding outputs (that are not revealed to the adversary) does not reveal anything about the programmed inputs.
Definition 11
A programmable function is privately programmable if there is a PPT simulator \(\mathcal {S}\) such that for any PPT adversary \(\mathcal {A}\) and any polynomial \(k = k(\lambda )\),

where \(\mathsf {RealPPRFPrivacy} \) and \(\mathsf {IdealPPRFPrivacy} \) are the respective views of \(\mathcal {A}\) in the procedures defined in Fig. 5.
We now give our main security definition for PP-PRFs.
Definition 12
A programmable function is a privately programmable PRF if it is statistically programmable, simulation secure, and privately programmable.
5.2 From Weak PP-PRFs to PP-PRFs
In this section we describe a general construction of a privately programmable PRF from any weak privately programmable PRF. Let \(\varPi ' = (\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Eval}, \mathsf {Program}, \mathsf {PEval})\) be a programmable function with domain \(\mathcal {X}\) and range \(\mathcal {Y}\), where we assume that \(\mathcal {Y}\) is a finite additive group. The basic idea behind the construction is simple: define the function as the sum of two parallel copies of \(\varPi '\), and program it by programming the copies according to additive secret-sharings of the desired outputs. Each component is therefore programmed to uniformly random outputs, as required by weak simulation security.
Construction 3
We construct a programmable function \(\varPi \) as follows:
-
\(\varPi .\mathsf {Setup} (1^{\lambda },1^k)\): generate \(pp_i \leftarrow \varPi '.\mathsf {Setup} (1^{\lambda },1^k)\) for \(i=1,2\) and output \(pp= (pp_1,pp_2)\).
-
\(\varPi .\mathsf {KeyGen} (pp)\): on input \(pp= (pp_1,pp_2)\) generate \(msk_i \leftarrow \varPi '.\mathsf {KeyGen} (pp_i)\) for \(i=1,2\), and output \(msk=(msk_1,msk_2)\).
-
\(\varPi .\mathsf {Eval} (pp,msk,x)\): on input \(pp= (pp_1,pp_2)\), \(msk=(msk_1,msk_2)\), and \(x \in \mathcal {X}\) output
$$ \varPi '.\mathsf {Eval} (pp_1,msk_1,x) + \varPi '.\mathsf {Eval} (pp_2,msk_2,x). $$ -
\(\varPi .\mathsf {Program} (pp,msk,\mathcal {P})\): on input \(pp= (pp_1,pp_2)\), \(msk=(msk_1,msk_2)\), k pairs \((x_i,y_i) \subset \mathcal {X} \times \mathcal {Y}\), first sample uniformly random \(r_{i} \leftarrow \mathcal {Y}\) for \(i \in [k]\), then output \(sk_{\mathcal {P}}=(sk_{1}, sk_{2})\) where
$$\begin{aligned} sk_1&\leftarrow \varPi '.{\textsf {Program}}(pp_1,msk_1,\mathcal {P}_1 = \{(x_i, r_{i})\})\end{aligned}$$(58)$$\begin{aligned} sk_2&\leftarrow \varPi '.{\textsf {Program}}(pp_2,msk_2,\mathcal {P}_2 = \{(x_i,y_{i}-r_{i})\}). \end{aligned}$$(59) -
\(\varPi .\mathsf {PEval} (pp,sk_{\mathcal {P}},x)\): on input \(pp= (pp_1,pp_2)\), \(sk_{\mathcal {P}} = (sk_1,sk_2)\), and \(x \in \mathcal {X}\) output
$$ \varPi '.\mathsf {PEval} (pp_1,sk_1,x) + \varPi '.\mathsf {PEval} (pp_2,sk_2,x). $$
Theorem 2
If \(\varPi '\) is a weak privately programmable PRF then Construction 3 is a privately programmable PRF.
Proof
This follows directly from Theorems 3 and 4, which respectively prove the simulation security and private programmability of Construction 3, and from the statistical programmability of \(\varPi '\), which obviously implies the statistical programmability of Construction 3.
Theorem 3
If \(\varPi '\) is a weak privately programmable PRF then \(\varPi \) is simulation secure.
Due to space constraints, the (straightforward) proof of Theorem 3 is deferred to the full version.
Theorem 4
If \(\varPi '\) is weakly simulation secure then \(\varPi \) is privately programmable.
Proof
Let \(\mathcal {S}'\) be the simulator algorithm for the weak simulation security of \(\varPi '\). Our simulator \(\mathcal {S}(1^\lambda ,1^k)\) for the private programmability of \(\varPi \) simply generates \((pp_i,sk_i) \leftarrow \mathcal {S}'(1^\lambda ,1^k)\) for \(i=1,2\) and outputs \((pp= (pp_1,pp_2), sk= (sk_1,sk_2))\). To show that \(\mathcal {S}\) satisfies Definition 12 we define the following hybrids and show that they are indistinguishable.
- Hybrid \(H_0\)::
-
This is the experiment \(\mathsf {RealPPRFPrivacy} _{\mathcal {A}}\) from Fig. 5.
- Hybrid \(H_1\)::
-
This experiment is the same as the previous one, except that we generate \((pp_1,sk_1) \leftarrow \mathcal {S}'(1^{\lambda }, 1^{k})\).
- Hybrid \(H_2\)::
-
This experiment is the same as the previous one, except that we generate \((pp_{2}, sk_{2}) \leftarrow \mathcal {S}'(1^\lambda ,1^k)\). Observe that this experiment is identical to the experiment \(\mathsf {IdealPPRFPrivacy} _{\mathcal {A},\mathcal {S}}\) from Fig. 5.
Claim 11
We have \(H_0 {\mathop {\approx }\limits ^{c}}H_1\).
Proof
Let \(\mathcal {A}\) be an adversary attempting to distinguish \(H_0\) and \(H_1\). We build an adversary \(\mathcal {A}'\) against the weak simulation security of \(\varPi '\), which runs \(\mathcal {A}\) internally. When \(\mathcal {A}\) outputs  , \(\mathcal {A}'\) also outputs
, \(\mathcal {A}'\) also outputs  , receiving \((pp_1, sk_1)\) in response. Then \(\mathcal {A}'\) generates \(pp_2 \leftarrow \varPi '.\mathsf {Setup} (1^\lambda ,1^k)\) and \(msk_2 \leftarrow \varPi '.\mathsf {KeyGen} (pp_2)\), and chooses uniformly random \(r_i \leftarrow \mathcal {Y}\) for \(i \in [k]\). It then generates
, receiving \((pp_1, sk_1)\) in response. Then \(\mathcal {A}'\) generates \(pp_2 \leftarrow \varPi '.\mathsf {Setup} (1^\lambda ,1^k)\) and \(msk_2 \leftarrow \varPi '.\mathsf {KeyGen} (pp_2)\), and chooses uniformly random \(r_i \leftarrow \mathcal {Y}\) for \(i \in [k]\). It then generates  . Finally it gives \((pp=(pp_1,pp_2),sk=(sk_1,sk_2))\) to \(\mathcal {A}\). It is straightforward to see that if \(\mathcal {A}'\) is in \(\mathsf {RealWeakPPRF} \) (respectively, \(\mathsf {IdealWeakPPRF} \)) then the view of \(\mathcal {A}\) is identical to its view \(H_0\) (resp., \(H_{1}\)). So by weak simulation security of \(\varPi '\), we have \(H_{0} {\mathop {\approx }\limits ^{c}}H_{1}\).
. Finally it gives \((pp=(pp_1,pp_2),sk=(sk_1,sk_2))\) to \(\mathcal {A}\). It is straightforward to see that if \(\mathcal {A}'\) is in \(\mathsf {RealWeakPPRF} \) (respectively, \(\mathsf {IdealWeakPPRF} \)) then the view of \(\mathcal {A}\) is identical to its view \(H_0\) (resp., \(H_{1}\)). So by weak simulation security of \(\varPi '\), we have \(H_{0} {\mathop {\approx }\limits ^{c}}H_{1}\).
Claim 12
We have \(H_1 {\mathop {\approx }\limits ^{c}}H_2\).
Proof
This is entirely symmetrical to the proof of Claim 11, so we omit it.
This completes the proof of Theorem 4.
5.3 Construction of Weak Privately Programmable PRFs
In this section we construct a weak privately programmable PRF from our shiftable function of Sect. 3. We first define the auxiliary function that the construction will use. For  where the \(x_{i}\) are distinct, define the function
where the \(x_{i}\) are distinct, define the function  as
as
Notice that the circuit size of  is upper bounded by some \(\sigma ' = {{\mathrm{poly}}}(n,k,\log q)\).
is upper bounded by some \(\sigma ' = {{\mathrm{poly}}}(n,k,\log q)\).
Construction 4
Our weak privately programmable PRF with input space  and output space \(\mathcal {Y} = \mathbb {Z}_p^m\) uses the SHSF from Sect. 3 with parameters q, B chosen as in Sect. 3.4, and is defined as follows:
and output space \(\mathcal {Y} = \mathbb {Z}_p^m\) uses the SHSF from Sect. 3 with parameters q, B chosen as in Sect. 3.4, and is defined as follows:
-
\(\mathsf {Setup} (1^\lambda , 1^k)\): Output \(pp\leftarrow \mathsf {SHSF}.\mathsf {Setup} (1^\lambda , 1^{\sigma '})\).
-
\(\mathsf {KeyGen} (pp)\): Output \(msk\leftarrow \mathsf {SHSF}.\mathsf {KeyGen} (pp)\).
-
 : Compute \(\mathbf {y}_x = \mathsf {SHSF}.\mathsf {Eval} (pp,msk,x)\) and output
: Compute \(\mathbf {y}_x = \mathsf {SHSF}.\mathsf {Eval} (pp,msk,x)\) and output 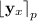 .
. -
\(\mathsf {Program} (pp,msk,\mathcal {P})\): Given k pairs
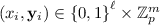 where the \(x_{i}\) are distinct, for each \(i \in [k]\) compute \(\mathbf {w}_i\) as follows: choose \(\mathbf {y}'_i \leftarrow \mathbb {Z}_q^m\) uniformly at random conditioned on
where the \(x_{i}\) are distinct, for each \(i \in [k]\) compute \(\mathbf {w}_i\) as follows: choose \(\mathbf {y}'_i \leftarrow \mathbb {Z}_q^m\) uniformly at random conditioned on  , and set $$\begin{aligned} \mathbf {w}_i = \mathbf {y}'_i - \mathsf {SHSF}.\mathsf {Eval} (pp,msk,x_i). \end{aligned}$$(61)
, and set $$\begin{aligned} \mathbf {w}_i = \mathbf {y}'_i - \mathsf {SHSF}.\mathsf {Eval} (pp,msk,x_i). \end{aligned}$$(61)Output \(sk_{\mathcal {P}} \leftarrow \mathsf {SHSF}.\mathsf {Shift} (pp,msk,H_{\{(x_i,\mathbf {w}_i)\}})\).
-
\(\mathsf {PEval} (pp,sk_{\mathcal {P}},x)\): output
 .
.
5.4 Security Proof
Theorem 5
Construction 4 is a weak privately programmable PRF (Definition 9) assuming the hardness of \(\mathsf {LWE} _{n-1,q,\chi }\) and 1D-R-SIS\(_{(z \sigma ' + \tau + 1)m, p, q, B}\) (where \(z, \tau \) are respectively the lengths of fresh GSW ciphertexts and secret keys as used in \(\mathsf {SHSF} \)) and the CPA security of the GSW encryption scheme.
Proof
The proof follows immediately by Theorems 6 and 7 below.
Theorem 6
Assuming the hardness of \(\mathsf {LWE} _{n-1,q,\chi }\) and 1D-R-SIS\(_{(z \sigma ' + \tau + 1)m, p, q, B}\) and the CPA security of the GSW encryption scheme, Construction 4 is weakly simulation secure.
Proof
Our simulator \(\mathcal {S}(1^{\lambda },1^{k})\) for Construction 4 simply outputs \((pp, sk) \leftarrow \mathsf {SHSF}.\mathsf {\mathcal {S}} (1^\lambda ,1^{\sigma '})\). Let \(\mathcal {A}\) be any polynomial-time adversary. To show that \(\mathcal {S}\) satisfies Definition 10 we define a sequence of hybrid experiments and show that they are indistinguishable.
- Hybrid \(H_0\)::
-
This is the simulated experiment \(\mathsf {IdealWeakPPRF} _{\mathcal {A}, \mathcal {S}}\) (Fig. 3).
- Hybrid \(H_{1}\)::
-
This is the same as the previous experiment, except that on query
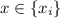 , instead of returning a uniformly random value from \(\mathbb {Z}_p^{m}\), we choose \(\mathbf {y}_{x} \leftarrow \mathbb {Z}_q^{m}\) and output
, instead of returning a uniformly random value from \(\mathbb {Z}_p^{m}\), we choose \(\mathbf {y}_{x} \leftarrow \mathbb {Z}_q^{m}\) and output  .
. - Hybrid \(H_2\)::
-
This is the same as the previous experiment, except that we abort if the event \(\mathsf {Borderline} \) happens, where \(\mathsf {Borderline} \) is as in Definition 5.
- Hybrid \(H_3\)::
-
This is the same as the previous experiment, except that we initially choose uniformly random \(\mathbf {w}'_i \leftarrow \mathbb {Z}_q^m\) for \(i \in [k]\) and change how queries for
 are answered (the “else” clause in \(\mathsf {IdealWeakPPRF} _{\mathcal {A},\mathcal {S}}\)): for \(x=x_{j}\), we answer as
are answered (the “else” clause in \(\mathsf {IdealWeakPPRF} _{\mathcal {A},\mathcal {S}}\)): for \(x=x_{j}\), we answer as  , where $$\begin{aligned} \mathbf {y}_{x} = \mathsf {SHSF}.\mathsf {SEval} (pp,sk,x) -\mathbf {w}'_j. \end{aligned}$$(62)
, where $$\begin{aligned} \mathbf {y}_{x} = \mathsf {SHSF}.\mathsf {SEval} (pp,sk,x) -\mathbf {w}'_j. \end{aligned}$$(62) - Hybrid \(H_4\)::
-
This is the same as the previous experiment, except that we generate \(pp\) and \(sk\) as follows: we generate \(pp\leftarrow \mathsf {Setup} (1^\lambda ,1^k)\), \(msk\leftarrow \mathsf {KeyGen} (pp)\) and \(sk\leftarrow \mathsf {SHSF}.\mathsf {Shift} (pp,msk,H_{\{(x_i,\mathbf {w}'_i)\}})\).
- Hybrid \(H_5\)::
-
This is the same as the previous experiment, except that we answer all queries as in the \(\mathsf {Eval} \) algorithm, i.e., we output
$$\begin{aligned} \lfloor {\textsf {SHSF}.\textsf {Eval}(pp, msk,x)}\rceil _{p}. \end{aligned}$$(63) - Hybrid \(H_6\)::
-
This is the same as the previous experiment, except that here we generate \(sk\) as in the real game. Specifically, for each \(i \in [k]\) we choose a uniformly random vector \(\mathbf {y}_i \leftarrow \mathbb {Z}_p^{m}\) and uniformly random \(\mathbf {y}'_i \leftarrow \mathbb {Z}_q^{m}\) conditioned on
 , and then set $$\begin{aligned} \mathbf {w}_i = \mathbf {y}'_i - \mathsf {SHSF}.\mathsf {Eval} (pp,msk,x). \end{aligned}$$(64)
, and then set $$\begin{aligned} \mathbf {w}_i = \mathbf {y}'_i - \mathsf {SHSF}.\mathsf {Eval} (pp,msk,x). \end{aligned}$$(64)We then set \(sk\leftarrow \mathsf {SHSF}.\mathsf {Shift} (pp,msk,H_{\{(x_i,\mathbf {w}_i)\}})\).
- Hybrid \(H_7\)::
-
This is the same as the previous experiment, except that we no longer abort when \(\mathsf {Borderline} \) happens. Observe that this is the real experiment \(\mathsf {IdealRealPPRF} _{\mathcal {A}}\) (Fig. 3).
The proofs of indistinguishability (either computational or statistical) for adjacent hybrids are straightforward, and are deferred to the full version for lack of space.
Theorem 7
Construction 4 is statistically programmable.
Proof
Fix any  . We need to show that for any \(i \in [k]\),
. We need to show that for any \(i \in [k]\),

By Lemma 3 we have
where the approximation hides some B-bounded error and the last equality holds because \(\mathbf {w}_i = \mathbf {y}'_i - \mathsf {SHSF}.\mathsf {Eval} (pp,msk,x_i)\). Because \(\mathbf {y}'_{i}\) is chosen uniformly at random such that  , the probability that some coordinate of \(\mathsf {SHSF}.\mathsf {SEval} (pp, sk_{\mathcal {P}}, x_{i})\) is in \(\tfrac{q}{p} (\mathbb {Z}+ \tfrac{1}{2}) + [-B,B]\) is at most \(2m B p/q = {{\mathrm{negl}}}(\lambda )\), which establishes Eq. (65).
, the probability that some coordinate of \(\mathsf {SHSF}.\mathsf {SEval} (pp, sk_{\mathcal {P}}, x_{i})\) is in \(\tfrac{q}{p} (\mathbb {Z}+ \tfrac{1}{2}) + [-B,B]\) is at most \(2m B p/q = {{\mathrm{negl}}}(\lambda )\), which establishes Eq. (65).
Notes
- 1.
Our construction was actually developed independently of [13], though not concurrently; we were unaware of its earlier non-public versions.
- 2.
This property is obtained by composing homomorphic addition and multiplication of \(\mathbf {G}\)-multiples; the extra 1 attached to x is needed to support NOT gates.
- 3.
We stress that \(\mathsf {LinEval} \) does not need to know \(\mathbf {k}\), which we view as representing a secret linear function that is hidden by \(\mathbf {C}\).
References
Ajtai, M.: Generating hard instances of lattice problems. Quaderni di Matematica 13, 1–32 (2004). Preliminary version in STOC 1996
Banerjee, A., Peikert, C.: New and improved key-homomorphic pseudorandom functions. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8616, pp. 353–370. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_20
Banerjee, A., Peikert, C., Rosen, A.: Pseudorandom functions and lattices. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 719–737. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_42
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S.P., Yang, K.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 6:1–6:48 (2012). Preliminary version in CRYPTO 2001
Boneh, D., Gentry, C., Gorbunov, S., Halevi, S., Nikolaenko, V., Segev, G., Vaikuntanathan, V., Vinayagamurthy, D.: Fully key-homomorphic encryption, arithmetic circuit ABE and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_30
Boneh, D., Kim, S., Montgomery, H.: Private puncturable PRFs from standard lattice assumptions. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 415–445. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_15
Boneh, D., Lewi, K., Montgomery, H., Raghunathan, A.: Key homomorphic PRFs and their applications. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 410–428. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_23
Boneh, D., Lewi, K., Wu, D.J.: Constraining pseudorandom functions privately. In: Fehr, S. (ed.) PKC 2017. LNCS, vol. 10175, pp. 494–524. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54388-7_17
Boneh, D., Waters, B.: Constrained pseudorandom functions and their applications. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 280–300. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-42045-0_15
Boyle, E., Gilboa, N., Ishai, Y.: Function secret sharing. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 337–367. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46803-6_12
Boyle, E., Goldwasser, S., Ivan, I.: Functional signatures and pseudorandom functions. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 501–519. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54631-0_29
Brakerski, Z., Langlois, A., Peikert, C., Regev, O., Stehlé, D.: Classical hardness of learning with errors. In: STOC, pp. 575–584 (2013)
Brakerski, Z., Tsabary, R., Vaikuntanathan, V., Wee, H.: Private Constrained PRFs (and More) from LWE. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017. LNCS, vol. 10677, pp. 264–302. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_10
Brakerski, Z., Vaikuntanathan, V.: Constrained key-homomorphic PRFs from standard lattice assumptions. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 1–30. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_1
Canetti, R., Chen, Y.: Constraint-hiding constrained PRFs for NC\(^1\) from LWE. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017. LNCS, vol. 10210, pp. 446–476. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_16
Cohen, A., Holmgren, J., Nishimaki, R., Vaikuntanathan, V., Wichs, D.: Watermarking cryptographic capabilities. In: STOC, pp. 1115–1127 (2016)
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS, pp. 40–49 (2013)
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_5
Goldreich, O., Goldwasser, S., Micali, S.: How to construct random functions. J. ACM 33(4), 792–807 (1986). Preliminary version in FOCS 1984
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Predicate encryption for circuits from LWE. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 503–523. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48000-7_25
Gorbunov, S., Vaikuntanathan, V., Wichs, D.: Leveled fully homomorphic signatures from standard lattices. In: STOC, pp. 469–477 (2015)
Kiayias, A., Papadopoulos, S., Triandopoulos, N., Zacharias, T.: Delegatable pseudorandom functions and applications. In: CCS, pp. 669–684 (2013)
Kim, S., Wu, D.J.: Watermarking cryptographic functionalities from standard lattice assumptions. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10401, pp. 503–536. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_17
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_41
Regev, D.M.O.: Worst-case to average-case reductions based on Gaussian measures. SIAM J. Comput. 37(1), 267–302 (2007). Preliminary version in FOCS 2004
Peikert, C.: Public-key cryptosystems from the worst-case shortest vector problem. In: STOC, pp. 333–342 (2009)
Peikert, C., Regev, O., Stephens-Davidowitz, N.: Pseudorandomness of Ring-LWE for any ring and modulus. In: STOC, pp. 461–473 (2017)
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. J. ACM 56(6), 1–40 (2009). Preliminary version in STOC 2005
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Peikert, C., Shiehian, S. (2018). Privately Constraining and Programming PRFs, the LWE Way. In: Abdalla, M., Dahab, R. (eds) Public-Key Cryptography – PKC 2018. PKC 2018. Lecture Notes in Computer Science(), vol 10770. Springer, Cham. https://doi.org/10.1007/978-3-319-76581-5_23
Download citation
DOI: https://doi.org/10.1007/978-3-319-76581-5_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-76580-8
Online ISBN: 978-3-319-76581-5
eBook Packages: Computer ScienceComputer Science (R0)


 , where
, where  denotes (coordinate-wise) “rounding” from
denotes (coordinate-wise) “rounding” from  , we sample a key k for an ordinary PRF F, define the shift function
, we sample a key k for an ordinary PRF F, define the shift function  .
. .
. of depth d, an
of depth d, an 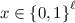 , and some
, and some  and a matrix
and a matrix 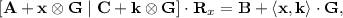
 by applying the above to the
by applying the above to the  with
with  , outputs a ciphertext ct, which is a binary string.
, outputs a ciphertext ct, which is a binary string. and ciphertexts
and ciphertexts 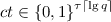 .
. : compute
: compute 



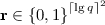 is as in Eq. (
is as in Eq. ( whose binary decomposition
whose binary decomposition  can be implemented by a circuit of size
can be implemented by a circuit of size 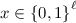 , compute
, compute 

 and range
and range  .
. : compute
: compute  .
. , output
, output  .
. .
. where
where  where
where  , given the master secret key
, given the master secret key 


 : Compute
: Compute 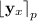 .
.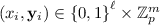 where the
where the  , and set
, and set  .
.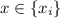 , instead of returning a uniformly random value from
, instead of returning a uniformly random value from  .
. are answered (the “else” clause in
are answered (the “else” clause in  , where
, where  , and then set
, and then set 