Abstract
The random-oracle model by Bellare and Rogaway (CCS’93) is an indispensable tool for the security analysis of practical cryptographic protocols. However, the traditional random-oracle model fails to guarantee security when a protocol is composed with arbitrary protocols that use the same random oracle. Canetti, Jain, and Scafuro (CCS’14) put forth a global but non-programmable random oracle in the Generalized UC framework and showed that some basic cryptographic primitives with composable security can be efficiently realized in their model. Because their random-oracle functionality is non-programmable, there are many practical protocols that have no hope of being proved secure using it. In this paper, we study alternative definitions of a global random oracle and, perhaps surprisingly, show that these allow one to prove GUC-secure existing, very practical realizations of a number of essential cryptographic primitives including public-key encryption, non-committing encryption, commitments, Schnorr signatures, and hash-and-invert signatures. Some of our results hold generically for any suitable scheme proven secure in the traditional ROM, some hold for specific constructions only. Our results include many highly practical protocols, for example, the folklore commitment scheme \(\mathcal {H}(m\Vert r)\) (where m is a message and r is the random opening information) which is far more efficient than the construction of Canetti et al.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
The random-oracle model (ROM) [3] is an overwhelmingly popular tool in cryptographic protocol design and analysis. Part of its success is due to its intuitive idealization of cryptographic hash functions, which it models through calls to an external oracle that implements a random function. Another important factor is its capability to provide security proofs for highly practical constructions of important cryptographic building blocks such as digital signatures, public-key encryption, and key exchange. In spite of its known inability to provide provable guarantees when instantiated with a real-world hash function [14], the ROM is still widely seen as convincing evidence that a protocol will resist attacks in practice.
Most proofs in the ROM, however, are for property-based security notions, where the adversary is challenged in a game where he faces a single, isolated instance of the protocol. Security can therefore no longer be guaranteed when a protocol is composed. Addressing this requires composable security notions such as Canetti’s Universal Composability (UC) framework [10], which have the advantage of guaranteeing security even if protocols are arbitrarily composed.
UC modeling. In the UC framework, a random oracle is usually modeled as an ideal functionality that a protocol uses as a subroutine in a so-called hybrid model, similarly to other setup constructs such as a common reference string (CRS). For example, the random-oracle functionality \(\mathcal {F} _\mathrm {RO}\) [21] simply assigns a random output value h to each input m and returns h. In the security proof, the simulator executes the code of the subfunctionality, which enables it to observe the queries of all involved parties and to program any random-looking values as outputs. Setup assumptions play an important role for protocols in the UC model, as many important cryptographic primitives such as commitments simply cannot be achieved [13]; other tasks can, but have more efficient instantiations with a trusted setup.
An important caveat is that this way of modeling assumes that each instance of each protocol uses its own separate and independent instance of the subfunctionality. For a CRS this is somewhat awkward, because it raises the question of how the parties should agree on a common CRS, but it is even more problematic for random oracles if all, supposedly independent, instances of \(\mathcal {F} _\mathrm {RO}\) are replaced in practice with the same hash function. This can be addressed using the Generalized UC (GUC) framework [12] that allows one to model different protocol instances sharing access to global functionalities. Thus one can make the setup functionality globally available to all parties, meaning, including those outside of the protocol execution as well as the external environment.
Global UC random oracle. Canetti et al. [15] indeed applied the GUC framework to model globally accessible random oracles. In doing so, they discard the globally accessible variant of \(\mathcal {F} _\mathrm {RO}\) described above as of little help for proving security of protocols because it is too “strict”, allowing the simulator neither to observe the environment’s random-oracle queries, nor to program its answers. They argue that any shared functionality that provides only public information is useless as it does not give the simulator any advantage over the real adversary. Instead, they formulate a global random-oracle functionality that grants the ideal-world simulator access to the list of queries that the environment makes outside of the session. They then show that this shared functionality can be used to design a reasonably efficient GUC-secure commitment scheme, as well as zero-knowledge proofs and two-party computation. However, their global random-oracle functionality rules out security proofs for a number of practical protocols, especially those that require one to program the random oracle.
Our Contributions. In this paper, we investigate different alternative formulations of globally accessible random-oracle functionalities and protocols that can be proven secure with respect to these functionalities. For instance, we show that the simple variant discarded by Canetti et al. surprisingly suffices to prove the GUC-security of a number of truly practical constructions for useful cryptographic primitives such as digital signatures and public-key encryption. We achieve these results by carefully analyzing the minimal capabilities that the simulator needs in order to simulate the real-world (hybrid) protocol, while fully exploiting the additional capabilities that one has in proving the indistinguishability between the real and the ideal worlds. In the following, we briefly describe the different random-oracle functionalities we consider and which we prove GUC-secure using them.
Strict global random oracle. First, we revisit the strict global random-oracle functionality \(\mathcal {G} _{\mathsf {sRO}} \) described above and show that, in spite of the arguments of Canetti et al. [15], it actually suffices to prove the GUC-security of many practical constructions. In particular, we show that any digital signature scheme that is existentially unforgeable under chosen-message attack in the traditional ROM also GUC-realizes the signature functionality with \(\mathcal {G} _{\mathsf {sRO}} \), and that any public-key encryption (PKE) scheme that is indistinguishable under adaptive chosen-ciphertext attack in the traditional ROM GUC-realizes the PKE functionality under \(\mathcal {G} _{\mathsf {sRO}} \) with static corruptions.
This result may be somewhat surprising as it includes many schemes that, in their property-based security proofs, rely on invasive proof techniques such as rewinding, observing, and programming the random oracle, all of which are tools that the GUC simulator is not allowed to use. We demonstrate, however, that none of these techniques are needed during the simulation of the protocol, but rather only show up when proving indistinguishability of the real and the ideal worlds, where they are allowed. A similar technique was used It also does not contradict the impossibility proof of commitments based on global setup functionalities that simply provide public information [12, 13] because, in the GUC framework, signatures and PKE do not imply commitments.
Programmable global random oracles. Next, we present a global random-oracle functionality \(\mathcal {G} _\mathsf {pRO} \) that allows the simulator as well as the real-world adversary to program arbitrary points in the random oracle, as long as they are not yet defined. We show that it suffices to prove the GUC-security of Camenisch et al.’s non-committing encryption scheme [8], i.e., PKE scheme secure against adaptive corruptions. Here, the GUC simulator needs to produce dummy ciphertexts that can later be made to decrypt to a particular message when the sender or the receiver of the ciphertext is corrupted. The crucial observation is that, to embed a message in a dummy ciphertext, the simulator only needs to program the random oracle at random inputs, which have negligible chance of being already queried or programmed. Again, this result is somewhat surprising as \(\mathcal {G} _\mathsf {pRO} \) does not give the simulator any advantage over the real adversary either.
We also define a restricted variant \(\mathcal {G} _\mathsf {rpRO} \) that, analogously to the observable random oracle of Canetti et al. [15], offers programming subject to some restrictions, namely that protocol parties can check whether the random oracle was programmed on a particular point. If the adversary tries to cheat by programming the random oracle, then honest parties have a means of detecting this misbehavior. However, we will see that the simulator can hide its programming from the adversary, giving it a clear advantage over the real-world adversary. We use it to GUC-realize the commitment functionality through a new construction that, with only two exponentiations per party and two rounds of communication, is considerably more efficient than the one of Canetti et al. [15], which required five exponentiations and five rounds of communication.
Programmable and observable global random oracle. Finally, we describe a global random-oracle functionality \(\mathcal {G} _\mathsf {rpoRO} \) that combines the restricted forms of programmability and observability. We then show that this functionality allows us to prove that commitments can be GUC-realized by the most natural and efficient random-oracle based scheme where a commitment \(c = \mathcal {H} (m\Vert r)\) is the hash of the random opening information r and the message m.
Transformations between different oracles. While our different types of oracles allow us to securely realize different protocols, the variety in oracles partially defies the original goal of modeling the situation where all protocols use the same hash function. We therefore explore some relations among the different types by presenting efficient protocol transformations that turn any protocol that securely realizes a functionality with one type of random oracle into a protocol that securely realizes the same functionality with a different type.
Other Related Work. Dodis et al. [17] already realized that rewinding can be used in the indistinguishability proof in the GUC model, as long as it’s not used in the simulation itself. In a broader sense, our work complements existing studies on the impact of programmability and observability of random oracles in security reductions. Fischlin et al. [18] and Bhattacharyya and Mukherjee [6] have proposed formalizations of non-programmable and weakly-programmable random oracles, e.g., only allowing non-adaptive programmability. Both works give a number of possibility and impossibility results, in particular that full-domain hash (FDH) signatures can only be proven secure (via black-box reductions) if the random oracle is fully programmable [18]. Non-observable random oracles and their power are studied by Ananth and Bhaskarin [1], showing that Schnorr and probabilistic RSA-FDH signatures can be proven secure. All these works focus on the use of random oracles in individual reductions, whereas our work proposes globally re-usable random-oracle functionalities within the UC framework. The strict random oracle functionality \(\mathcal {G} _{\mathsf {sRO}} \) that we analyze is comparable to a non-programmable and non-observable random oracle, so our result that any unforgeable signature scheme is also GUC-secure w.r.t. \(\mathcal {G} _{\mathsf {sRO}} \) may seem to contradict the above results. However, the \(\mathcal {G} _{\mathsf {sRO}} \) functionality imposes these restrictions only for the GUC simulator, whereas the reduction can fully program the random oracle.
Summary. Our results clearly paint a much more positive picture for global random oracles than was given in the literature so far. We present several formulations of globally accessible random-oracle functionalities that allow to prove the composable security of some of the most efficient signature, PKE, and commitment schemes that are currently known. We even show that the most natural formulation, the strict global random oracle \(\mathcal {G} _{\mathsf {sRO}} \) that was previously considered useless, suffices to prove GUC-secure a large class of efficient signature and encryption schemes. By doing so, our work brings the (composable) ROM back closer to its original intention: to provide an intuitive idealization of hash functions that enables to prove the security of highly efficient protocols. We expect that our results will give rise to many more practical cryptographic protocols that can be proven GUC-secure, among them known protocols that have been proven secure in the traditional ROM model.
2 Preliminaries
In the rest of this work, we use “iff” for “if and only if”, “w.l.o.g.” for “without loss of generality”, and \(n \in \mathbb {N}\) to denote the security parameter. A function \(\varepsilon (n)\) is negligible if it is asymptotically smaller than \(1/p(n)\) for every polynomial function p. We denote by  that x is a sample from the uniform distribution over the set X. When \(\mathsf {A}\) is a probabilistic algorithm, then \(y := \mathsf {A}(x;r)\) means that y is assigned the outcome of a run of \(\mathsf {A}\) on input x with coins r. Two distributions X and Y over a domain \(\varSigma (n)\) are said to be computationally indistinguishable, written \(X \approx Y\), if for any PPT algorithm \(\mathcal {A}\), \(|\mathcal {A} (X(s)) - \mathcal {A} (Y(s))|\) is negligible for all \(s \in \varSigma (n)\).
that x is a sample from the uniform distribution over the set X. When \(\mathsf {A}\) is a probabilistic algorithm, then \(y := \mathsf {A}(x;r)\) means that y is assigned the outcome of a run of \(\mathsf {A}\) on input x with coins r. Two distributions X and Y over a domain \(\varSigma (n)\) are said to be computationally indistinguishable, written \(X \approx Y\), if for any PPT algorithm \(\mathcal {A}\), \(|\mathcal {A} (X(s)) - \mathcal {A} (Y(s))|\) is negligible for all \(s \in \varSigma (n)\).
2.1 The Basic and Generalized UC Frameworks
Basic UC. The universal composability (UC) framework [9, 10] is a framework to define and prove the security of protocols. It follows the simulation-based security paradigm, meaning that security of a protocol is defined as the simulatability of the protocol based on an ideal functionality \(\mathcal {F}\). In an imaginary ideal world, parties hand their protocol inputs to a trusted party running \(\mathcal {F} \), where \(\mathcal {F} \) by construction executes the task at hand in a secure manner. A protocol \(\pi \) is considered a secure realization of \(\mathcal {F}\) if the real world, in which parties execute the real protocol, is indistinguishable from the ideal world. Namely, for every real-world adversary \(\mathcal {A}\) attacking the protocol, we can design an ideal-world attacker (simulator) \({\mathcal {S}} \) that performs an equivalent attack in the ideal world. As the ideal world is secure by construction, this means that there are no meaningful attacks on the real-world protocol either.
One of the goals of UC is to simplify the security analysis of protocols, by guaranteeing secure composition of protocols and, consequently, allowing for modular security proofs. One can design a protocol \(\pi \) assuming the availability of an ideal functionality \(\mathcal {F} '\), i.e., \(\pi \) is a \(\mathcal {F} '\)-hybrid protocol. If \(\pi \) securely realizes \(\mathcal {F} \), and another protocol \(\pi '\) securely realizes \(\mathcal {F} '\), then the composition theorem guarantees that \(\pi \) composed with \(\pi '\) (i.e., replacing \(\pi '\) with \(\mathcal {F} '\)) is a secure realization of \(\mathcal {F}\).
Security is defined through an interactive Turing machine (ITM) \(\mathcal {Z} \) that models the environment of the protocol and chooses protocol inputs to all participants. Let \(\textsc {EXEC}_{\pi , \mathcal {A}, \mathcal {Z} }\) denote the output of \(\mathcal {Z} \) in the real world, running with protocol \(\pi \) and adversary \(\mathcal {A} \), and let \(\textsc {IDEAL}_{\mathcal {F}, {\mathcal {S}}, \mathcal {Z} }\) denote its output in the ideal world, running with functionality \(\mathcal {F} \) and simulator \({\mathcal {S}} \). Protocol \(\pi \) securely realizes \(\mathcal {F} \) if for every polynomial-time adversary \(\mathcal {A}\), there exists a simulator \({\mathcal {S}} \) such that for every environment \(\mathcal {Z} \), \(\textsc {EXEC}_{\pi , \mathcal {A}, \mathcal {Z} }\approx \textsc {IDEAL}_{\mathcal {F}, {\mathcal {S}}, \mathcal {Z} }\).
Generalized UC. A Basic UC protocol using random oracles is modeled as a \(\mathcal {F} _\mathsf {RO} \)-hybrid protocol. Since an instance of a Basic UC functionality can only be used by a single protocol instance, this means that every protocol instance uses its own random oracle that is completely independent of other protocol instances’ random oracles. As the random-oracle model is supposed to be an idealization of real-world hash functions, this is not a very realistic model: Given that we only have a handful of standardized hash functions, it’s hard to argue their independence across many protocol instances.
To address these limitations of Basic UC, Canetti et al. [12] introduced the Generalized UC (GUC) framework, which allows for shared “global” ideal functionalities (denoted by \(\mathcal {G} \)) that can be used by all protocol instances. Additionally, GUC gives the environment more powers in the UC experiment. Let \(\textsc {GEXEC}_{\pi , \mathcal {A}, \mathcal {Z} }\) be defined as \(\textsc {EXEC}_{\pi , \mathcal {A}, \mathcal {Z} }\), except that the environment \(\mathcal {Z} \) is no longer constrained, meaning that it is allowed to start arbitrary protocols in addition to the challenge protocol \(\pi \). Similarly, \(\textsc {GIDEAL}_{\mathcal {F}, {\mathcal {S}}, \mathcal {Z} }\) is equivalent to \(\textsc {IDEAL}_{\mathcal {F}, {\mathcal {S}}, \mathcal {Z} }\) but \(\mathcal {Z} \) is now unconstrained. If \(\pi \) is a \(\mathcal {G} \)-hybrid protocol, where \(\mathcal {G} \) is some shared functionality, then \(\mathcal {Z} \) can start additional \(\mathcal {G} \)-hybrid protocols, possibly learning information about or influencing the state of \(\mathcal {G} \).
Definition 1
Protocol \(\pi \) GUC-emulates protocol \(\varphi \) if for every adversary \(\mathcal {A} \) there exists an adversary \({\mathcal {S}} \) such that for all unconstrained environments \(\mathcal {Z} \), \(\textsc {GEXEC}_{\pi , \mathcal {A}, \mathcal {Z} }\approx \textsc {GEXEC}_{\varphi , {\mathcal {S}}, \mathcal {Z} }\).
Definition 2
Protocol \(\pi \) GUC-realizes ideal functionality \(\mathcal {F} \) if for every adversary \(\mathcal {A} \) there exists a simulator \({\mathcal {S}} \) such that for all unconstrained environments \(\mathcal {Z} \), \(\textsc {GEXEC}_{\pi , \mathcal {A}, \mathcal {Z} }\approx \textsc {GIDEAL}_{\mathcal {F}, {\mathcal {S}}, \mathcal {Z} }\).
GUC gives very strong security guarantees, as the unconstrained environment can run arbitrary protocols in parallel with the challenge protocol, where the different protocol instances might share access to global functionalities. However, exactly this flexibility makes it hard to reason about the GUC experiment. To address this, Canetti et al. also introduced Externalized UC (EUC). Typically, a protocol \(\pi \) uses many local hybrid functionalities \(\mathcal {F} \) but only uses a single shared functionality \(\mathcal {G} \). Such protocols are called \(\mathcal {G} \)-subroutine respecting, and EUC allows for simpler security proofs for such protocols. Rather than considering unconstrained environments, EUC considers \(\mathcal {G} \)-externally constrained environments. Such environments can invoke only a single instance of the challenge protocol, but can additionally query the shared functionality \(\mathcal {G} \) through dummy parties that are not part of the challenge protocol. The EUC experiment is equivalent to the Basic UC experiment, except that it considers \(\mathcal {G} \)-externally constrained environments: A \(\mathcal {G} \)-subroutine respecting protocol \(\pi \) EUC-emulates a protocol \(\varphi \) if for every polynomial-time adversary \(\mathcal {A}\) there is an adversary \(\mathcal {S}\) such that for every \(\mathcal {G} \)-externally constrained environment \(\textsc {EXEC}^{\mathcal {G}}_{\pi , \mathcal {A}, \mathcal {Z} }\approx \textsc {EXEC}^{\mathcal {G}}_{\varphi , {\mathcal {S}}, \mathcal {Z} }\). Figure 2(b) depicts EUC-emulation and shows that this setting is much simpler to reason about than GUC-emulation: We can reason about this static setup, rather than having to imagine arbitrary protocols running alongside the challenge protocol. Canetti et al. prove that showing EUC-emulation is useful to obtain GUC-emulation.
Theorem 1
Let \(\pi \) be a \(\mathcal {G} \)-subroutine respecting protocol, then protocol \(\pi \) GUC-emulates protocol \(\varphi \) if and only if \(\pi \) \(\mathcal {G}\)-EUC-emulates \(\varphi \).
Conventions. When specifying ideal functionalities, we will use some conventions for ease of notation. For a non-shared functionality with session id \(\mathsf {sid} \), we write “On input x from party \(\mathcal {P} \)”, where it is understood the input comes from machine \((\mathcal {P} , \mathsf {sid})\). For shared functionalities, machines from any session may provide input, so we always specify both the party identity and the session identity of machines. In some cases an ideal functionality requires immediate input from the adversary. In such cases we write “wait for input x from the adversary”, which is formally defined by Camenisch et al. [7].
2.2 Basic Building Blocks
One-Way Trapdoor Permutations. A (family of) one-way trapdoor permutations is a tuple \(\mathsf {OWTP}:= (\mathsf {OWTP}.\mathsf {Gen},\mathsf {OWTP}.\mathsf {Sample},\mathsf {OWTP}.\mathsf {Eval},\mathsf {OWTP}.\mathsf {Invert})\) of PPT algorithms. On input n; \(\mathsf {OWTP}.\mathsf {Gen}\) outputs: a permutation domain \(\varSigma \) (e.g., \(\mathbb {Z}_N\) for an RSA modulus N), and efficient representations of, respectively, a permutation \(\varphi \) in the family (e.g., an RSA public exponent e), and of its inverse \(\varphi ^{-1}\) (e.g., an RSA secret exponent d). Security requires that no PPT adversary can invert a point \(y=\varphi (x)\) for a random challenge template \((\varSigma ,\varphi ,y)\) with non-negligible probability. We will often use OWTPs to generate public and secret keys for, e.g., signature schemes or encryption schemes by, e.g., setting \(\mathsf {pk} = (\varSigma ,\varphi )\) and \(\mathsf {sk} = \varphi ^{-1}\). W.l.o.g. in the following we assume that the representation of \(\varSigma \) also includes the related security parameter \(n \), and secret keys also include the public part. Notice that, in general, \(\mathsf {OWTP}.\mathsf {Invert}\) also takes \(\varphi \) as input, although in practice this might be unnecessary, depending on the particular OWTP in exam.
Signature Schemes. A (stateless) signature scheme is a tuple \(\mathsf {SIG} = (\mathsf {KGen}, \mathsf {Sign}, \mathsf {Verify})\) of polynomial time algorithms, where \(\mathsf {KGen} \) and \(\mathsf {Sign} \) can be probabilistic and \(\mathsf {Verify} \) is deterministic. On input the security parameter, \(\mathsf {KGen} \) outputs a public/secret key pair \((\mathsf {pk},\mathsf {sk})\). \(\mathsf {Sign} \) takes as input \(\mathsf {sk}\) (and we write this as a shorthand notation \(\mathsf {Sign} _\mathsf {sk} \)) and a message m, and outputs a signature \(\sigma \). \(\mathsf {Verify} \) takes as input a public key \(\mathsf {pk}\) (and we write this as a shorthand notation \(\mathsf {Verify} _\mathsf {pk} \)), a message m and a signature \(\sigma \), and outputs a single bit denoting acceptance or rejection of the signature. The standard security notion we assume for signature schemes is existential unforgeability under chosen message attacks (EUF-CMA) [20], which we recall here briefly. In such game-based security notion, an adversary is allowed to perform a number of signature queries, adaptively, on messages of his choice for a secret key generated by a challenger. Then, he wins the game if he manages to output a valid signature for a fresh message for that key. We say that a signature scheme is EUF-CMA secure if no PPT adversary can win this game with more than negligible probability.
Public-Key Encryption Schemes. A public-key encryption scheme is a tuple of PPT algorithms \(\varPi = (\mathsf {KGen},\mathsf {Enc},\mathsf {Dec})\). On input \(n \), \(\mathsf {KGen} \) outputs a public/private key pair \((\mathsf {pk},\mathsf {sk})\). \(\mathsf {Enc} \) takes as input a public key \(\mathsf {pk}\) (and we write this as a shorthand notation \(\mathsf {Enc} _\mathsf {pk} \)) and a plaintext m, and outputs a ciphertext c. \(\mathsf {Dec} \) takes as input a secret key \(\mathsf {sk}\) (and we write this as a shorthand notation \(\mathsf {Dec} _\mathsf {sk} \)) and a ciphertext c, and outputs either \(\bot _m\) or a message m. The standard security notion we assume for public-key encryption schemes is indistinguishability under adaptive chosen message attacks (IND-CCA2) [2], which we recall here briefly. In such game-based security notion, an adversary sends a challenge plaintext of his choice to an external challenger, who generates a key pair and either responds to the adversary with an encryption of the challenge plaintext, or with the encryption of a random plaintext (having the same leakage as the original plaintext, in case we are considering corruption models), the goal of the adversary being to distinguish which is the case. We say that a PKE scheme is IND-CCA2 secure if no PPT adversary can win this game with more than negligible advantage over guessing, even if allowed to query adaptively a decryption oracle on any ciphertext of his choice – except the challenge ciphertext.
The strict global random oracle functionality \(\mathcal {G} _{\mathsf {sRO}} \) that does not give any extra power to anyone (mentioned but not defined by Canetti et al. [15]).
3 Strict Random Oracle
This section focuses on the so-called strict global random oracle \(\mathcal {G} _{\mathsf {sRO}} \) depicted in Fig. 1, which is the most natural definition of a global random oracle: on a fresh input m, a random value h is chosen, while on repeating inputs, a consistent answer is given back. This natural definition was discussed by Canetti et al. [15] but discarded as it does not suffice to realize \(\mathcal {F} _\mathsf {COM} \). While this is true, we will argue that \(\mathcal {G} _{\mathsf {sRO}} \) is still useful to realize other functionalities.
The code of \(\mathcal {G} _{\mathsf {sRO}}\) is identical to that of a local random oracle \(\mathcal {F} _\mathrm {RO}\) in UC. In Basic UC, this is a very strong definition, as it gives the simulator a lot of power: In the ideal world, it can simulate the random oracle \(\mathcal {F} _\mathrm {RO}\), which gives it the ability to observe all queries and program the random oracle on the fly (cf. Fig. 2(a)). In GUC, the global random oracle \(\mathcal {G} _{\mathsf {sRO}} \) is present in both worlds and the environment can access it (cf. Fig. 2(b)). In particular, the simulator is not given control of \(\mathcal {G} _{\mathsf {sRO}} \) and hence cannot simulate it. Therefore, the simulator has no more power over the random oracle than explicitly offered through the interfaces of the global functionality. In the case of \(\mathcal {G} _{\mathsf {sRO}}\), the simulator can neither program the random oracle, nor observe the queries made.
As the simulator obtains no relevant advantage over the real-world adversary when interacting with \(\mathcal {G} _{\mathsf {sRO}} \), one might wonder how it could help in security proofs. The main observation is that the situation is different when one proves that the real and ideal world are indistinguishable. Here one needs to show that no environment can distinguish between the real and ideal world and thus, when doing so, one has full control over the global functionality. This is for instance the case when using the (distinguishing) environment in a cryptographic reduction: as depicted in Fig. 3, the reduction algorithm \(\mathcal {B} \) simulates the complete view of the environment \(\mathcal {Z} \), including the global \(\mathcal {G} _{\mathsf {sRO}} \), allowing \(\mathcal {B} \) to freely observe and program \(\mathcal {G} _{\mathsf {sRO}} \). As a matter of facts, \(\mathcal {B} \) can also rewind the environment here – another power that the simulator \({\mathcal {S}} \) does not have but is useful in the security analysis of many schemes. It turns out that for some primitives, the EUC simulator does not need to program or observe the random oracle, but only needs to do so when proving that no environment can distinguish between the real and the ideal world.
This allows us to prove a surprisingly wide range of practical protocols secure with respect to \(\mathcal {G} _{\mathsf {sRO}} \). First, we prove that any signature scheme proven to be EUF-CMA in the local random-oracle model yields UC secure signatures with respect the global \(\mathcal {G} _{\mathsf {sRO}} \). Second, we show that any public-key encryption scheme proven to be IND-CCA2 secure with local random oracles yields UC secure public-key encryption (with respect to static corruptions), again with the global \(\mathcal {G} _{\mathsf {sRO}}\). These results show that highly practical schemes such as Schnorr signatures [23], RSA full-domain hash signatures [3, 16], RSA-PSS signatures [5], RSA-OAEP encryption [4], and the Fujisaki-Okamoto transform [19] all remain secure when all schemes share a single hash function that is modeled as a strict global random oracle. This is remarkable, as their security proofs in the local random-oracle model involve techniques that are not available to an EUC simulator: signature schemes typically require programming of random-oracle outputs to simulate signatures, PKE schemes typically require observing the adversary’s queries to simulate decryption queries, and Schnorr signatures need to rewind the adversary in a forking argument [22] to extract a witness. However, it turns out, this rewinding is only necessary in the reduction \(\mathcal {B} \) showing that no distinguishing environment \(\mathcal {Z} \) can exist and we can show that all these schemes can safely be used in composition with arbitrary protocols and with a natural, globally accessible random-oracle functionality \(\mathcal {G} _{\mathsf {sRO}} \).
The signature functionality \(\mathcal {F} _{\mathsf {SIG}} \) due to Canetti [11]
3.1 Composable Signatures Using \(\mathcal {G} _{\mathsf {sRO}} \)
Let \(\mathsf {SIG} = (\mathsf {KGen}, \mathsf {Sign}, \mathsf {Verify})\) be an EUF-CMA secure signature scheme in the ROM. We show that this directly yields a secure realization of UC signatures \(\mathcal {F} _{\mathsf {SIG}} \) with respect to a strict global random oracle \(\mathcal {G} _{\mathsf {sRO}} \). We assume that \(\mathsf {SIG} \) uses a single random oracle that maps to \(\left\{ {0,1} \right\} ^{\ell (n)}\). Protocols requiring multiple random oracles or mapping into different ranges can be constructed using standard domain separation and length extension techniques.
We define \(\pi _\mathsf {SIG} \) to be \(\mathsf {SIG} \) phrased as a GUC protocol. Whenever an algorithm of \(\mathsf {SIG} \) makes a call to a random oracle, \(\pi _\mathsf {SIG} \) makes a call to \(\mathcal {G} _{\mathsf {sRO}} \).
-
1.
On input \((\mathsf {KeyGen}, \mathsf {sid})\), signer \(\mathcal {P} \) proceeds as follows.
-
Check that \(\mathsf {sid} = (\mathcal {P} , \mathsf {sid} ')\) for some \(\mathsf {sid} '\), and no record \((\mathsf {sid}, \mathsf {sk})\) exists.
-
Run \((\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {SIG}.\mathsf {KGen} (n)\) and store \((\mathsf {sid}, \mathsf {sk})\).
-
Output \((\mathsf {KeyConf}, \mathsf {sid}, \mathsf {pk})\).
-
-
2.
On input \((\mathsf {Sign}, \mathsf {sid}, m)\), signer \(\mathcal {P} \) proceeds as follows.
-
Retrieve record \((\mathsf {sid}, \mathsf {sk})\), abort if no record exists.
-
Output \((\mathsf {Signature}, \mathsf {sid}, \sigma )\) with \(\sigma \leftarrow \mathsf {SIG}.\mathsf {Sign} (\mathsf {sk}, m)\).
-
-
3.
On input \((\mathsf {Verify}, \mathsf {sid}, m, \sigma , \mathsf {pk} ')\) a verifier \(\mathcal {V} \) proceeds as follows.
-
Output \((\mathsf {Verified}, \mathsf {sid}, f)\) with \(f \leftarrow \mathsf {SIG}.\mathsf {Verify} (\mathsf {pk} ', \sigma , m)\).
-
We will prove that \(\pi _\mathsf {SIG} \) will realize UC signatures. There are two main approaches to defining a signature functionality: using adversarially provided algorithms to generate and verify signature objects (e.g., the 2005 version of [9]), or by asking the adversary to create and verify signature objects (e.g., [11]). For a version using algorithms, the functionality will locally create and verify signature objects using the algorithm, without activating the adversary. This means that the algorithms cannot interact with external parties, and in particular communication with external functionalities such as a global random oracle is not permitted. We could modify an algorithm-based \(\mathcal {F} _{\mathsf {SIG}} \) to allow the sign and verify algorithms to communicate only with a global random oracle, but we choose to use an \(\mathcal {F} _{\mathsf {SIG}} \) that interacts with the adversary as this does not require special modifications for signatures with global random oracles.
Theorem 2
If \(\mathsf {SIG} \) is EUF-CMA in the random-oracle model, then \(\pi _\mathsf {SIG} \) GUC-realizes \(\mathcal {F} _{\mathsf {SIG}} \) (as defined in Fig. 4) in the \(\mathcal {G} _{\mathsf {sRO}} \)-hybrid model.
Proof
By the fact that \(\pi _\mathsf {SIG} \) is \(\mathcal {G} _{\mathsf {sRO}} \)-subroutine respecting and by Theorem 1, it is sufficient to show that \(\pi _\mathsf {SIG} \) \(\mathcal {G} _{\mathsf {sRO}} \)-EUC-realizes \(\mathcal {F} _{\mathsf {SIG}} \). We define the UC simulator \(\mathcal {S}\) as follows.
-
1.
Key Generation. On input \((\mathsf {KeyGen}, \mathsf {sid})\) from \(\mathcal {F} _{\mathsf {SIG}} \), where \(\mathsf {sid} = (\mathcal {P} , \mathsf {sid} ')\) and \(\mathcal {P} \) is honest.
-
Simulate honest signer “\(\mathcal {P} \)”, and give it input \((\mathsf {KeyGen}, \mathsf {sid})\).
-
When “\(\mathcal {P} \)” outputs \((\mathsf {KeyConf}, \mathsf {sid}, \mathsf {pk})\) (where \(\mathsf {pk}\) is generated according to \(\pi _\mathsf {SIG} \)), send \((\mathsf {KeyConf}, \mathsf {sid}, \mathsf {pk})\) to \(\mathcal {F} _{\mathsf {SIG}} \).
-
-
2.
Signature Generation. On input \((\mathsf {Sign}, \mathsf {sid},m)\) from \(\mathcal {F} _{\mathsf {SIG}} \), where \(\mathsf {sid} = (\mathcal {P} , \mathsf {sid} ')\) and \(\mathcal {P} \) is honest.
-
Run simulated honest signer “\(\mathcal {P} \)” with input \((\mathsf {Sign}, \mathsf {sid},m)\).
-
When “\(\mathcal {P} \)” outputs \((\mathsf {Signature}, \mathsf {sid}, \sigma )\) (where \(\sigma \) is generated according to \(\pi _\mathsf {SIG} \)), send \((\mathsf {Signature}, \mathsf {sid}, \sigma )\) to \(\mathcal {F} _{\mathsf {SIG}} \).
-
-
3.
Signature Verification. On input \((\mathsf {Verify}, \mathsf {sid},m,\sigma ,\mathsf {pk} ')\) from \(\mathcal {F} _{\mathsf {SIG}} \), where \(\mathsf {sid} = (\mathcal {P} , \mathsf {sid} ')\).
-
Run
 , and send \((\mathsf {Verified}, \mathsf {sid}, f)\) to \(\mathcal {F} _{\mathsf {SIG}} \).
, and send \((\mathsf {Verified}, \mathsf {sid}, f)\) to \(\mathcal {F} _{\mathsf {SIG}} \).
-
We must show that \(\pi _\mathsf {SIG} \) realizes \(\mathcal {F} _{\mathsf {SIG}} \) in the Basic UC sense, but with respect to \(\mathcal {G} _{\mathsf {sRO}} \)-externally constrained environments, i.e., the environment is now allowed to access \(\mathcal {G} _{\mathsf {sRO}} \) via dummy parties in sessions unequal to the challenge session. Without loss of generality, we prove this with respect to the dummy adversary.
During key generation, \(\mathcal {S}\) invokes the simulated honest signer \(\mathcal {P} \), so the resulting keys are exactly like in the real world. The only difference is that in the ideal world \(\mathcal {F} _{\mathsf {SIG}}\) can abort key generation in case the provided public key \(\mathsf {pk}\) already appears in a previous \(\mathsf {sigrec}\) record. But if this happens it means that \(\mathcal {A} \) has successfully found a collision in the public key space, which must be exponentially large as the signature scheme is EUF-CMA by assumption. This means that such event can only happen with negligible probability.
For a corrupt signer, the rest of the simulation is trivially correct: the adversary generates keys and signatures locally, and if an honest party verifies a signature, the simulator simply executes the verification algorithm as a real world party would do, and \(\mathcal {F} _{\mathsf {SIG}}\) does not make further checks (the unforgeability check is only made when the signer is honest). When an honest signer signs, the simulator creates a signature using the real world signing algorithm, and when \(\mathcal {F} _{\mathsf {SIG}}\) asks the simulator to verify a signature, \(\mathcal {S}\) runs the real world verification algorithm, and \(\mathcal {F} _{\mathsf {SIG}}\) keeps records of the past verification queries to ensure consistency. As the real world verification algorithm is deterministic, storing verification queries does not cause a difference. Finally, when \(\mathcal {S}\) provides \(\mathcal {F} _{\mathsf {SIG}}\) with a signature, \(\mathcal {F} _{\mathsf {SIG}}\) checks that there is no stored verification query exists that states the provided signature is invalid. By completeness of the signature scheme, this check will never trigger.
The only remaining difference is that \(\mathcal {F} _{\mathsf {SIG}} \) prevents forgeries: if a verifier uses the correct public key, the signer is honest, and we verify a signature on a message that was never signed, \(\mathcal {F} _{\mathsf {SIG}}\) rejects. This would change the verification outcome of a signature that would be accepted by the real-world verification algorithm. As this event is the only difference between the real and ideal world, what remains to show is that this check changes the verification outcome only with negligible probability. We prove that if there is an environment that causes this event with non-negligible probability, then we can use it to construct a forger \(\mathcal {B} \) that breaks the EUF-CMA unforgeability of \(\mathsf {SIG} \).
Our forger \(\mathcal {B} \) plays the role of \(\mathcal {F} _{\mathsf {SIG}} \), \({\mathcal {S}} \), and even the random oracle \(\mathcal {G} _{\mathsf {sRO}} \), and has black-box access to the environment \(\mathcal {Z} \). Then \(\mathcal {B} \) receives a challenge public key \(\mathsf {pk} \) and is given access to a signing oracle \(\mathcal {O}^\mathtt{{\mathsf {Sign} (\mathsf {sk}, \cdot )}} \) and to a random oracle \(\mathsf {RO} \). It responds \(\mathcal {Z} \)’s \(\mathcal {G} _{\mathsf {sRO}} \) queries by relaying queries and responses to and from \(\mathsf {RO} \). It runs the code of \(\mathcal {F} _{\mathsf {SIG}} \) and \({\mathcal {S}} \), but uses \(\mathcal {O}^\mathtt{{\mathsf {Sign} (\mathsf {sk}, m)}} \) instead of \(\mathcal {F} _{\mathsf {SIG}} \)’s signature generation interface to generate signatures. If the unforgeability check of \(\mathcal {F} _{\mathsf {SIG}} \) triggers for a cryptographically valid signature \(\sigma \) on message m, then we know that \(\mathcal {B} \) made no query \(\mathcal {O}^\mathtt{{\mathsf {Sign} (\mathsf {sk}, m)}} \), meaning that \(\mathcal {B} \) can submit \((\sigma , m)\) to win the EUF-CMA game. \(\square \)
3.2 Composable Public-Key Encryption Using \(\mathcal {G} _{\mathsf {sRO}} \)
Let \(\mathsf {PKE} = (\mathsf {KGen}, \mathsf {Enc}, \mathsf {Dec})\) be a CCA2 secure public-key encryption scheme in the ROM. We show that this directly yields a secure realization of GUC public-key encryption \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \), as recently defined by Camenisch et al. [8] and depicted in Fig. 5, with respect to a strict global random oracle \(\mathcal {G} _{\mathsf {sRO}} \) and static corruptions. As with our result for signature schemes, we require that \(\mathsf {PKE} \) uses a single random oracle that maps to \(\left\{ {0,1} \right\} ^{\ell (n)}\).
We define \(\pi _\mathsf {PKE} \) to be \(\mathsf {PKE} \) phrased as a GUC protocol.
-
1.
On input \((\mathsf {KeyGen},\mathsf {sid},n)\), party \(\mathcal {P} \) proceeds as follows.
-
Check that \(\mathsf {sid} = (\mathcal {P} , \mathsf {sid} ')\) for some \(\mathsf {sid} '\), and no record \((\mathsf {sid}, \mathsf {sk})\) exists.
-
Run \((\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {PKE}.\mathsf {KGen} (n)\) and store \((\mathsf {sid}, \mathsf {sk})\).
-
Output \((\mathsf {KeyConf}, \mathsf {sid}, \mathsf {pk})\).
-
-
2.
On input \((\mathsf {Encrypt},\mathsf {sid},\mathsf {pk} ',m)\), party \(\mathcal {Q} \) proceeds as follows.
-
Set \(c \leftarrow \mathsf {PKE}.\mathsf {Enc} (\mathsf {pk} ', m)\) and output \((\mathsf {Ciphertext}, \mathsf {sid}, c)\).
-
-
3.
On input \((\mathsf {Decrypt},\mathsf {sid},c)\), party \(\mathcal {P} \) proceeds as follows.
-
Retrieve \((\mathsf {sid}, \mathsf {sk})\), abort if no such record exist.
-
Set \(m \leftarrow \mathsf {PKE}.\mathsf {Dec} (\mathsf {sk}, c)\) and output \((\mathsf {Plaintext}, \mathsf {sid}, m)\).
-
Theorem 3
Protocol \(\pi _\mathsf {PKE} \) GUC-realizes \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) with static corruptions with leakage function \(\mathcal {L} \) in the \(\mathcal {G} _{\mathsf {sRO}} \)-hybrid model if \(\mathsf {PKE} \) is CCA2 secure with leakage \(\mathcal {L} \) in the ROM.
Proof
By the fact that \(\pi _\mathsf {PKE} \) is \(\mathcal {G} _{\mathsf {sRO}} \)-subroutine respecting and by Theorem 1, it is sufficient to show that \(\pi _\mathsf {PKE} \) \(\mathcal {G} _{\mathsf {sRO}} \)-EUC-realizes \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \).
We define simulator \({\mathcal {S}} \) as follows.
-
1.
On input \((\mathsf {KEYGEN}, \mathsf {sid})\).
-
Parse \(\mathsf {sid} \) as \((\mathcal {P} , \mathsf {sid} ')\). Note that \(\mathcal {P} \) is honest, as \(\mathcal {S}\) does not make \(\mathsf {KeyGen} \) queries on behalf of corrupt parties.
-
Invoke the simulated receiver “\(\mathcal {P} \)” on input \((\mathsf {KeyGen},\mathsf {sid})\) and wait for output \((\mathsf {KeyConf}, \mathsf {sid}, \mathsf {pk})\) from “\(\mathcal {P} \)”.
-
Send \((\mathsf {KeyConf}, \mathsf {sid}, \mathsf {pk})\) to \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \).
-
-
2.
On input
 with \(m \in \mathcal {M} \).
with \(m \in \mathcal {M} \).-
\({\mathcal {S}} \) picks some honest party “\(\mathcal {Q} \)” and gives it input \((\mathsf {Encrypt},\mathsf {sid},\mathsf {pk} ',m)\). Wait for output \((\mathsf {Ciphertext}, \mathsf {sid}, c)\) from “\(\mathcal {Q} \)”.
-
Send \((\mathsf {Ciphertext}, \mathsf {sid}, c)\) to \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \).
-
-
3.
On input
 .
.-
\(\mathcal {S}\) does not know which message is being encrypted, so it chooses a dummy plaintext \(m' \in \mathcal {M} \) with \(\mathcal {L} (m')=l\).
-
Pick some honest party “\(\mathcal {Q} \)” and give it input \((\mathsf {Encrypt},\mathsf {sid},\mathsf {pk},m')\), Wait for output \((\mathsf {Ciphertext}, \mathsf {sid}, c)\) from “\(\mathcal {Q} \)”.
-
Send \((\mathsf {Ciphertext}, \mathsf {sid}, c)\) to \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \).
-
-
4.
On input \((\mathsf {Decrypt}, \mathsf {sid}, c)\).
-
Note that \(\mathcal {S}\) only receives such input when \(\mathcal {P} \) is honest, and therefore \(\mathcal {S}\) simulates “\(\mathcal {P} \)” and knows its secret key \(\mathsf {sk} \).
-
Give “\(\mathcal {P} \)” input \((\mathsf {Decrypt},\mathsf {sid},c)\) and wait for output \((\mathsf {Plaintext}, \mathsf {sid}, m)\) from “\(\mathcal {P} \)”.
-
Send \((\mathsf {Plaintext}, \mathsf {sid}, m)\) to \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \).
-
What remains to show is that \(\mathcal {S}\) is a satisfying simulator, i.e., no \(\mathcal {G} _{\mathsf {sRO}} \)-externally constrained environment can distinguish the real protocol \(\pi _\mathsf {PKE} \) from \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) with \(\mathcal {S}\). If the receiver \(\mathcal {P} \) (i.e., such that \(\mathsf {sid} = (\mathcal {P} , \mathsf {sid} ')\)) is corrupt, the simulation is trivially correct: \(\mathcal {S}\) only creates ciphertexts when it knows the plaintext, so it can simply follow the real protocol. If \(\mathcal {P} \) is honest, \(\mathcal {S}\) does not know the message for which it is computing ciphertexts, so a dummy plaintext is encrypted. When the environment submits that ciphertext for decryption by \(\mathcal {P} \), the functionality \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) will still return the correct message. Using a sequence of games, we show that if an environment exists that can notice this difference, it can break the CCA2 security of \(\mathsf {PKE} \).
Let \(\mathsf {Game}\) 0 be the game where \({\mathcal {S}} \) and \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) act as in the ideal world, except that \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) passes the full message m in  inputs to \({\mathcal {S}} \), and \({\mathcal {S}} \) returns a real encryption of m as the ciphertext. It is clear that \(\mathsf {Game}\) 0 is identical to the real world \(\textsc {EXEC}^{\mathcal {G}}_{\pi , \mathcal {A}, \mathcal {Z} }\). Let \(\mathsf {Game}\) i for \(i=1,\ldots ,q_\mathrm {E}\), where \(q_\mathrm {E}\) is the number of \(\mathsf {Encrypt}\) queries made by \(\mathcal {Z} \), be defined as the game where for \(\mathcal {Z} \)’s first i \(\mathsf {Encrypt}\) queries, \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) passes only \(\mathcal {L} (m)\) to \({\mathcal {S}} \) and \({\mathcal {S}} \) returns the encryption of a dummy message \(m'\) so that \(\mathcal {L} (m') = \mathcal {L} (m)\), while for the \(i+1\)-st to \(q_\mathrm {E}\)-th queries, \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) passes m to \({\mathcal {S}} \) and \({\mathcal {S}} \) returns an encryption of m. It is clear that \(\mathsf {Game}\) \(q_\mathrm {E}\) is identical to the ideal world \(\textsc {IDEAL}^{\mathcal {G}}_{\mathcal {F}, {\mathcal {S}}, \mathcal {Z} }\).
inputs to \({\mathcal {S}} \), and \({\mathcal {S}} \) returns a real encryption of m as the ciphertext. It is clear that \(\mathsf {Game}\) 0 is identical to the real world \(\textsc {EXEC}^{\mathcal {G}}_{\pi , \mathcal {A}, \mathcal {Z} }\). Let \(\mathsf {Game}\) i for \(i=1,\ldots ,q_\mathrm {E}\), where \(q_\mathrm {E}\) is the number of \(\mathsf {Encrypt}\) queries made by \(\mathcal {Z} \), be defined as the game where for \(\mathcal {Z} \)’s first i \(\mathsf {Encrypt}\) queries, \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) passes only \(\mathcal {L} (m)\) to \({\mathcal {S}} \) and \({\mathcal {S}} \) returns the encryption of a dummy message \(m'\) so that \(\mathcal {L} (m') = \mathcal {L} (m)\), while for the \(i+1\)-st to \(q_\mathrm {E}\)-th queries, \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) passes m to \({\mathcal {S}} \) and \({\mathcal {S}} \) returns an encryption of m. It is clear that \(\mathsf {Game}\) \(q_\mathrm {E}\) is identical to the ideal world \(\textsc {IDEAL}^{\mathcal {G}}_{\mathcal {F}, {\mathcal {S}}, \mathcal {Z} }\).
By a hybrid argument, for \(\mathcal {Z} \) to have non-negligible probability to distinguish between \(\textsc {EXEC}^{\mathcal {G}}_{\pi , \mathcal {A}, \mathcal {Z} }\) and \(\textsc {IDEAL}^{\mathcal {G}}_{\mathcal {F}, {\mathcal {S}}, \mathcal {Z} }\), there must exist an i such that \(\mathcal {Z} \) distinguishes with non-negligible probability between \(\mathsf {Game}\) \((i-1)\) and \(\mathsf {Game}\) i. Such an environment gives rise to the following CCA2 attacker \(\mathcal {B} \) against \(\mathsf {PKE} \).
Algorithm \(\mathcal {B} \) receives a challenge public key \(\mathsf {pk} \) as input and is given access to decryption oracle \(\mathcal {O}^\mathtt{{\mathsf {Dec} (\mathsf {sk}, \cdot )}} \) and random oracle \(\mathsf {RO} \). It answers \(\mathcal {Z} \)’s queries \(\mathcal {G} _{\mathsf {sRO}} (m)\) by relaying responses from its own oracle \(\mathsf {RO} (m)\) and lets \(\mathcal {S}\) use \(\mathsf {pk} \) as the public key of \(\mathcal {P} \). It largely runs the code of \(\mathsf {Game}\) \((i-1)\) for \({\mathcal {S}} \) and \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \), but lets \({\mathcal {S}} \) respond to inputs \((\mathsf {Dec}, \mathsf {sid}, c)\) from \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) by calling its decryption oracle \(m = \mathcal {O}^\mathtt{{\mathsf {Decrypt} (\mathsf {sk},c)}} \). Note that \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) only hands such inputs to \({\mathcal {S}} \) for ciphertexts c that were not produced via the \(\mathsf {Encrypt}\) interface of \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \), as all other ciphertexts are handled by \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) itself.
Let \(m_0\) denote the message that Functionality \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) hands to \(\mathcal {S}\) as part of the i-th  input. Algorithm \(\mathcal {B} \) now sets \(m_1\) to be a dummy message \(m'\) such that \(\mathcal {L} (m') = \mathcal {L} (m_0)\) and hands \((m_0,m_1)\) to the challenger to obtain the challenge ciphertext \(c^*\) that is an encryption of \(m_b\). It is clear that if \(b=0\), then the view of \(\mathcal {Z} \) is identical to that in \(\mathsf {Game}\) \((i-1)\), while if \(b=1\), it is identical to that in \(\mathsf {Game}\) i. Moreover, \(\mathcal {B} \) will never have to query its decryption oracle on the challenge ciphertext \(c^*\), because any decryption queries for \(c^*\) are handled by \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) directly. By outputting 0 if \(\mathcal {Z} \) decides it runs in \(\mathsf {Game}\) \((i-1)\) and outputting 1 if \(\mathcal {Z} \) decides it runs in \(\mathsf {Game}\) i, \(\mathcal {B} \) wins the CCA2 game with non-negligible probability. \(\square \)
input. Algorithm \(\mathcal {B} \) now sets \(m_1\) to be a dummy message \(m'\) such that \(\mathcal {L} (m') = \mathcal {L} (m_0)\) and hands \((m_0,m_1)\) to the challenger to obtain the challenge ciphertext \(c^*\) that is an encryption of \(m_b\). It is clear that if \(b=0\), then the view of \(\mathcal {Z} \) is identical to that in \(\mathsf {Game}\) \((i-1)\), while if \(b=1\), it is identical to that in \(\mathsf {Game}\) i. Moreover, \(\mathcal {B} \) will never have to query its decryption oracle on the challenge ciphertext \(c^*\), because any decryption queries for \(c^*\) are handled by \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) directly. By outputting 0 if \(\mathcal {Z} \) decides it runs in \(\mathsf {Game}\) \((i-1)\) and outputting 1 if \(\mathcal {Z} \) decides it runs in \(\mathsf {Game}\) i, \(\mathcal {B} \) wins the CCA2 game with non-negligible probability. \(\square \)
4 Programmable Global Random Oracle
We now turn our attention to a new functionality that we call the programmable global random oracle, denoted by \(\mathcal {G} _\mathsf {pRO}\). The functionality simply extends the strict random oracle \(\mathcal {G} _{\mathsf {sRO}}\) by giving the adversary (real-world adversary \(\mathcal {A} \) and ideal-world adversary \({\mathcal {S}} \)) the power to program input-output pairs. Because we are in GUC or EUC, that also means that the environment gets this power. Thus, as in the case of \(\mathcal {G} _{\mathsf {sRO}}\), the simulator is thus not given any extra power compared to the environment (through the adversary), and one might well think that this model would not lead to the realization of any useful cryptographic primitives either. To the contrary, one would expect that the environment being able to program outputs would interfere with security proofs, as it destroys many properties of the random oracle such as collision or preimage resistance.
As it turns out, we can actually realize public-key encryption secure against adaptive corruptions (also known as non-committing encryption) in this model: we prove that the PKE scheme of Camenisch et al. [8] GUC-realizes \(\mathcal {F}_{\mathsf {PKE}} \) against adaptive corruptions in the \(\mathcal {G} _\mathsf {pRO} \)-hybrid model. The security proof works out because the simulator equivocates dummy ciphertexts by programming the random oracle on random points, which are unlikely to have been queried by the environment before.
4.1 The Programmable Global Random Oracle \(\mathcal {G} _\mathsf {pRO}\)
The functionality \(\mathcal {G} _\mathsf {pRO}\) (cf. Fig. 6) is simply obtained from \(\mathcal {G} _{\mathsf {sRO}}\) by adding an interface for the adversary to program the oracle on a single point at a time. To this end, the functionality \(\mathcal {G} _\mathsf {pRO}\) keeps an internal list of preimage-value assignments and, if programming fails (because it would overwrite a previously taken value), the functionality \(\mathsf {abort}\)s, i.e., it replies with an error message \(\bot \).
Notice that our \(\mathcal {G} _\mathsf {pRO} \) functionality does not guarantee common random-oracle properties such as collision resistance: an adversary can simply program collisions into \(\mathcal {G} _\mathsf {pRO} \). However, this choice is by design, because we are interested in achieving security with the weakest form of a programmable global random oracle to see what can be achieved against the strongest adversary possible.
4.2 Public-Key Encryption with Adaptive Corruptions from \(\mathcal {G} _\mathsf {pRO} \)
We show that GUC-secure non-interactive PKE with adaptive corruptions (often referred to as non-committing encryption) is achievable in the hybrid \(\mathcal {G} _\mathsf {pRO}\) model by proving the PKE scheme by Camenisch et al. [8] secure in this model. We recall the scheme in Fig. 7 based on the following building blocks:
-
a family of one-way trapdoor permutations \(\mathsf {OWTP} = (\mathsf {OWTP}.\mathsf {Gen}, \mathsf {OWTP}.\mathsf {Sample}, \mathsf {OWTP}.\mathsf {Eval}, \mathsf {OWTP}.\mathsf {Invert})\), where domains \(\varSigma \) generated by \(\mathsf {OWTP}.\mathsf {Gen} (1^n)\) have cardinality at least \(2^{n}\);
-
a block encoding scheme \((\mathsf {EC},\mathsf {DC})\), where \(\mathsf {EC}:\left\{ {0,1} \right\} ^* \rightarrow (\left\{ {0,1} \right\} ^{\ell {(n)}})^*\) is an encoding function such that the number of blocks that it outputs for a given message m depends only on the leakage \(\mathcal {L} (m)\), and \(\mathsf {DC}\) its deterministic inverse (possibly rejecting with \(\bot \) if no preimage exists).
Public-key encryption scheme secure against adaptive attacks [8] based on one-way permutation \(\mathsf {OWTP}\) and encoding function \((\mathsf {EC},\mathsf {DC})\).
Theorem 4
Protocol \(\pi _\mathsf {PKE} \) in Fig. 7 GUC-realizes \(\mathcal {F}_{\mathsf {PKE}}\) with adaptive corruptions and leakage function \(\mathcal {L} \) in the \(\mathcal {G} _\mathsf {pRO}\)-hybrid model.
Proof
We need to show that \(\pi _\mathsf {PKE} \) GUC-realizes \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \), i.e., that, given any environment \(\mathcal {Z} \) and any real-world adversary \(\mathcal {A} \), there exists a simulator \(\mathcal {S}\) such that the output distribution of \(\mathcal {Z} \) interacting with \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \), \(\mathcal {G} _\mathsf {pRO}\), and \(\mathcal {S}\) is indistinguishable from its output distribution when interacting with \(\pi _\mathsf {PKE} \), \(\mathcal {G} _\mathsf {pRO}\), and \(\mathcal {A} \). Because \(\pi _\mathsf {PKE} \) is \(\mathcal {G} _{\mathsf {sRO}} \)-subroutine respecting, by Theorem 1 it suffices to show that \(\pi _\mathsf {PKE} \) \(\mathcal {G} _\mathsf {pRO} \)-EUC-realizes \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \).
The simulator \(\mathcal {S}\) is depicted in Fig. 8. Basically, it generates an honest key pair for the receiver and responds to  and \(\mathsf {Decrypt}\) inputs by using the honest encryption and decryption algorithms, respectively. On
and \(\mathsf {Decrypt}\) inputs by using the honest encryption and decryption algorithms, respectively. On  inputs, however, it creates a dummy ciphertext c composed of \(c_1 = \varphi (x)\) for a freshly sampled x (but rejecting values of x that were used before) and randomly chosen \(c_{2,1},\ldots ,c_{2,k}\) and \(c_3\) for the correct number of blocks k. Only when either the secret key or the randomness used for this ciphertext must be revealed to the adversary, i.e., only when either the receiver or the party \(\mathcal {Q} \) who created the ciphertext is corrupted, does the simulator program the random oracle so that the dummy ciphertext decrypts to the correct message m. If the receiver is corrupted, the simulator obtains m by having it decrypted by \(\mathcal {F}_{\mathsf {PKE}} \); if the encrypting party \(\mathcal {Q} \) is corrupted, then m is included in the history of inputs and outputs that is handed to \({\mathcal {S}} \) upon corruption. The programming is done through the \(\texttt {Program}\) subroutine, but the simulation aborts in case programming fails, i.e., when a point needs to be programmed that is already assigned. We will prove in the reduction that any environment causing this to happen can be used to break the one-wayness of the trapdoor permutation.
inputs, however, it creates a dummy ciphertext c composed of \(c_1 = \varphi (x)\) for a freshly sampled x (but rejecting values of x that were used before) and randomly chosen \(c_{2,1},\ldots ,c_{2,k}\) and \(c_3\) for the correct number of blocks k. Only when either the secret key or the randomness used for this ciphertext must be revealed to the adversary, i.e., only when either the receiver or the party \(\mathcal {Q} \) who created the ciphertext is corrupted, does the simulator program the random oracle so that the dummy ciphertext decrypts to the correct message m. If the receiver is corrupted, the simulator obtains m by having it decrypted by \(\mathcal {F}_{\mathsf {PKE}} \); if the encrypting party \(\mathcal {Q} \) is corrupted, then m is included in the history of inputs and outputs that is handed to \({\mathcal {S}} \) upon corruption. The programming is done through the \(\texttt {Program}\) subroutine, but the simulation aborts in case programming fails, i.e., when a point needs to be programmed that is already assigned. We will prove in the reduction that any environment causing this to happen can be used to break the one-wayness of the trapdoor permutation.
We now have to show that \(\mathcal {S}\) successfully simulates a real execution of the protocol \(\pi _\mathsf {PKE} \) to a real-world adversary \(\mathcal {A} \) and environment \(\mathcal {Z} \). To see this, consider the following sequence of games played with \(\mathcal {A} \) and \(\mathcal {Z} \) that gradually evolve from a real execution of \(\pi _\mathsf {PKE} \) to the simulation by \(\mathcal {S}\).
Let \(\mathsf {Game}\) 0 be a game that is generated by letting an ideal functionality \(\mathcal {F} _0\) and a simulator \({\mathcal {S}} _0\) collaborate, where \(\mathcal {F} _0\) is identical to \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \), except that it passes the full message m along with  inputs to \({\mathcal {S}} _0\). The simulator \({\mathcal {S}} _0\) simply performs all key generation, encryption, and decryption using the real algorithms, without any programming of the random oracle. The only difference between \(\mathsf {Game}\) 0 and the real world is that the ideal functionality \(\mathcal {F} _0\) aborts when the same ciphertext c is generated twice during an encryption query for the honest public key. Because \({\mathcal {S}} _0\) generates honest ciphertexts, the probability that the same ciphertext is generated twice can be bounded by the probability that two honest ciphertexts share the same first component \(c_1\). Given that \(c_1\) is computed as \(\varphi (x)\) for a freshly sampled x from \(\varSigma \), and given that x is uniformly distributed over \(\varSigma \) which has size at least \(2^n \), the probability of a collision occurring over \(q_\mathrm {E}\) encryption queries is at most \(q_\mathrm {E}^2/2^n \).
inputs to \({\mathcal {S}} _0\). The simulator \({\mathcal {S}} _0\) simply performs all key generation, encryption, and decryption using the real algorithms, without any programming of the random oracle. The only difference between \(\mathsf {Game}\) 0 and the real world is that the ideal functionality \(\mathcal {F} _0\) aborts when the same ciphertext c is generated twice during an encryption query for the honest public key. Because \({\mathcal {S}} _0\) generates honest ciphertexts, the probability that the same ciphertext is generated twice can be bounded by the probability that two honest ciphertexts share the same first component \(c_1\). Given that \(c_1\) is computed as \(\varphi (x)\) for a freshly sampled x from \(\varSigma \), and given that x is uniformly distributed over \(\varSigma \) which has size at least \(2^n \), the probability of a collision occurring over \(q_\mathrm {E}\) encryption queries is at most \(q_\mathrm {E}^2/2^n \).
Let \(\mathsf {Game}\) 1 to \(\mathsf {Game}\) \(q_\mathrm {E}\) be games for a hybrid argument where gradually all ciphertexts by honest users are replaced with dummy ciphertexts. Let \(\mathsf {Game}\) i be the game with a functionality \(\mathcal {F} _i\) and simulator \({\mathcal {S}} _i\) where the first \(i-1\)  inputs of \(\mathcal {F} _i\) to \({\mathcal {S}} _i\) include only the leakage \(\mathcal {L} (m)\), and the remaining such inputs include the full message. For the first \(i-1\) encryptions, \({\mathcal {S}} _i\) creates a dummy ciphertext and programs the random oracle upon corruption of the party or the receiver as done by \({\mathcal {S}} \) in Fig. 8, aborting in case programming fails. For the remaining
inputs of \(\mathcal {F} _i\) to \({\mathcal {S}} _i\) include only the leakage \(\mathcal {L} (m)\), and the remaining such inputs include the full message. For the first \(i-1\) encryptions, \({\mathcal {S}} _i\) creates a dummy ciphertext and programs the random oracle upon corruption of the party or the receiver as done by \({\mathcal {S}} \) in Fig. 8, aborting in case programming fails. For the remaining  inputs, \({\mathcal {S}} _i\) generates honest encryptions of the real message.
inputs, \({\mathcal {S}} _i\) generates honest encryptions of the real message.
One can see that \(\mathsf {Game}\) \(q_\mathrm {E}\) is identical to the ideal world with \(\mathcal {F} _\mathsf {PKE}^\mathcal {L} \) and \({\mathcal {S}} \). To have a non-negligible advantage distinguishing the real from the ideal world, there must exist an \(i \in \{1,\ldots ,q_\mathrm {E}\}\) such that \(\mathcal {Z} \) and \(\mathcal {A} \) can distinguish between \(\mathsf {Game}\) \((i-1)\) and \(\mathsf {Game}\) i. These games are actually identical, except in the case that \(\mathsf {abort} \) happens during the programming of the random oracle \(\mathcal {G} _\mathsf {pRO}\) for the i-th ciphertext, which is a real ciphertext in \(\mathsf {Game}\) \((i-1)\) and a dummy ciphertext in \(\mathsf {Game}\) i. We call this the \(\mathsf {ROABORT}\) event. We show that if there exists an environment \(\mathcal {Z} \) and real-world adversary \(\mathcal {A} \) that make \(\mathsf {ROABORT}\) happen with non-negligible probability \(\nu \), then we can construct an efficient algorithm \(\mathcal {B} \) (the “reduction”) with black-box access to \(\mathcal {Z} \) and \(\mathcal {A} \) that is able to invert \(\mathsf {OWTP}\).
Our reduction \(\mathcal {B} \) must only simulate honest parties, and in particular must provide to \(\mathcal {A} \) a consistent view of their secrets (randomness used for encryption, secret keys, and decrypted plaintexts, just like \(\mathcal {S}\) does) when they become corrupted. Moreover, since we are not in the idealized scenario, there is no external global random oracle functionality \(\mathcal {G} _\mathsf {pRO}\): instead, \(\mathcal {B} \) simulates \(\mathcal {G} _\mathsf {pRO} \) for all the parties involved, and answers all their oracle calls.
Upon input the \(\mathsf {OWTP} \) challenge \((\varSigma ,\varphi ,y)\), \(\mathcal {B} \) runs the code of \(\mathsf {Game}\) \((i-1)\), but sets the public key of the receiver to \(\mathsf {pk} = (\varSigma ,\varphi )\). Algorithm \(\mathcal {B} \) answers the first \(i-1\) encryption requests with dummy ciphertexts and the \((i+1)\)-st to \(q_\mathrm {E}\)-th queries with honestly generated ciphertexts. For the i-th encryption request, however, it returns a special dummy ciphertext with \(c_1 = y\).
To simulate \(\mathcal {G} _\mathsf {pRO} \), \(\mathcal {B} \) maintains an initially empty list \(\mathsf {List}_\mathcal {H} \) to which pairs (m, h) are either added by lazy sampling for \(\mathsf {HashQuery} \) queries, or by programming for \(\mathsf {ProgramRO} \) queries. (Remember that the environment \(\mathcal {Z} \) can program entries in \(\mathcal {G} _\mathsf {pRO} \) as well.) For requests from \(\mathcal {Z} \), \(\mathcal {B} \) actually performs some additional steps that we describe further below.
It answers \(\mathsf {Decrypt}\) requests for a ciphertext \(c = (c_1,c_{2,1}, \ldots , c_{2,k}, c_3)\) by searching for a pair of the form \((x\Vert k\Vert m,c_3) \in \mathsf {List}_\mathcal {H} \) such that \(\varphi (x)=c_1\) and \(m = \mathsf {DC} (c_{2,1}\oplus h_1,\ldots , c_{2,k}\oplus h_k)\), where \(h_j = \mathcal {H} (x\Vert j)\), meaning that \(h_j\) is assigned the value of a simulated request \((\mathsf {HashQuery},x\Vert j)\) to \(\mathcal {G} _\mathsf {pRO} \). Note that at most one such pair exists for a given ciphertext c, because if a second \((x'\Vert k\Vert m',c_3) \in \mathsf {List}_\mathcal {H} \) would exist, then it must hold that \(\varphi (x')=c_1\). Because \(\varphi \) is a permutation, this means that \(x=x'\). Since for each \(j=1,\ldots ,k\), only one pair \((x\Vert j,h_j) \in \mathsf {List}_\mathcal {H} \) can be registered, this means that \(m' = \mathsf {DC} (c_{2,1}\oplus h_1,\ldots ,c_{2,k}\oplus h_k) = m\) because \(\mathsf {DC} \) is deterministic. If such a pair \((x\Vert k\Vert m,c_3)\) exists, it returns m, otherwise it rejects by returning \(\bot _m\).
One problem with the decryption simulation above is that it does not necessarily create the same entries into \(\mathsf {List}_\mathcal {H} \) as an honest decryption would have, and \(\mathcal {Z} \) could detect this by checking whether programming for these entries succeeds. In particular, \(\mathcal {Z} \) could first ask to decrypt a ciphertext \(c = (\varphi (x), c_{2,1},\ldots ,c_{2,k},c_3)\) for random \(x,c_{2,1},\ldots ,c_{2,k},c_3\) and then try to program the random oracle on any of the points \(x\Vert j\) for \(j=1,\ldots ,k\) or on \(x\Vert k\Vert m\). In \(\mathsf {Game}\) \((i-1)\) and \(\mathsf {Game}\) i, such programming would fail because the entries were created during the decryption of c. In the simulation by \(\mathcal {B} \), however, programming would succeed, because no valid pair \((x\Vert k\Vert m,c_3) \in \mathsf {List}_\mathcal {H} \) was found to perform decryption.
To preempt the above problem, \(\mathcal {B} \) checks all incoming requests \(\mathsf {HashQuery} \) and \(\mathsf {ProgramRO} \) by \(\mathcal {Z} \) for points of the form \(x\Vert j\) or \(x\Vert k\Vert m\) against all previous decryption queries \(c = (c_1,c_{2,1},\ldots ,c_{2,k},c_3)\). If \(\varphi (x) = c_1\), then \(\mathcal {B} \) immediately triggers (by mean of appropriate \(\mathsf {HashQuery}\) calls) the creation of all random-oracle entries that would have been generated by a decryption of c by computing \(m' = \mathsf {DC} (c_{2,1}\oplus \mathcal {H} (x\Vert 1),\ldots ,c_{2,k}\oplus \mathcal {H} (x\Vert k))\) and \(c'_3 = \mathcal {H} (x\Vert k\Vert m')\). Only then does \(\mathcal {B} \) handle \(\mathcal {Z} \)’s original \(\mathsf {HashQuery} \) or \(\mathsf {ProgramRO} \) request.
The only remaining problem is if during this procedure \(c'_3 = c_3\), meaning that c was previously rejected during by \(\mathcal {B} \), but it becomes a valid ciphertext by the new assignment of \(\mathcal {H} (x\Vert k\Vert m) = c'_3 = c_3\). This happens with negligible probability, though: a random value \(c'_3\) will only hit a fixed \(c_3\) with probability \(1/|\varSigma | \le 1/2^n \). Since up to \(q_\mathrm {D}\) ciphertexts may have been submitted with the same first component \(c_1 = \varphi (x)\) and with different values for \(c_3\), the probability that it hits any of them is at most \(q_\mathrm {D}/2^n \). The probability that this happens for at least one of \(\mathcal {Z} \)’s \(q_\mathrm {H}\) \(\mathsf {HashQuery} \) queries or one of its \(q_\mathrm {P}\) \(\mathsf {ProgramRO} \) queries during the entire execution is at most \((q_\mathrm {H}+q_\mathrm {P})q_\mathrm {D}/2^n \).
When \(\mathcal {A} \) corrupts a party, \(\mathcal {B} \) provides the encryption randomness that it used for all ciphertexts that such party generated. If \(\mathcal {A} \) corrupts the receiver or the party that generated the i-th ciphertext, then \(\mathcal {B} \) cannot provide that randomness. Remember, however, that \(\mathcal {B} \) is running \(\mathcal {Z} \) and \(\mathcal {A} \) in the hope for the \(\mathsf {ROABORT} \) event to occur, meaning that the programming of values for the i-th ciphertext fails because the relevant points in \(\mathcal {G} _\mathsf {pRO} \) have been assigned already. Event \(\mathsf {ROABORT} \) can only occur at the corruption of either the receiver or of the party that generated the i-th ciphertext, whichever comes first. Algorithm \(\mathcal {B} \) therefore checks \(\mathsf {List}_\mathcal {H} \) for points of the form \(x\Vert j\) or \(x\Vert k\Vert m\) such that \(\varphi (x)=y\). If \(\mathsf {ROABORT} \) occurred, then \(\mathcal {B} \) will find such a point and output x as its preimage for y. If it did not occur, then \(\mathcal {B} \) gives up. Overall, \(\mathcal {B} \) will succeed whenever \(\mathsf {ROABORT} \) occurs. Given that \(\mathsf {Game}\) \((i-1)\) and \(\mathsf {Game}\) i are different only when \(\mathsf {ROABORT} \) occurs, and given that \(\mathcal {Z} \) and \(\mathcal {A} \) have non-negligible probability of distinguishing between \(\mathsf {Game}\) \((i-1)\) and \(\mathsf {Game}\) i, we conclude that \(\mathcal {B} \) succeeds with non-negligible probability. \(\square \)
5 Restricted Programmable Global Random Oracles
The strict and the programmable global random oracles, \(\mathcal {G} _{\mathsf {sRO}} \) and \(\mathcal {G} _\mathsf {pRO} \), respectively, do not give the simulator any extra power compared to the real world adversary/environment. Canetti and Fischlin [13] proved that it is impossible to realize UC commitments without a setup assumption that gives the simulator an advantage over the environment. This means that, while \(\mathcal {G} _{\mathsf {sRO}} \) and \(\mathcal {G} _\mathsf {pRO} \) allowed for security proofs of many practical schemes, we cannot hope to realize even the seemingly simple task of UC commitments with this setup. In this section, we turn our attention to programmable global random oracles that do grant an advantage to the simulator.
5.1 Restricting Programmability to the Simulator
Canetti et al. [15] defined a global random oracle that restricts observability only adversarial queries, (hence, we call it the restricted observable global random oracle \(\mathcal {G} _{\mathsf {roRO}} \)), and show that this is sufficient to construct UC commitments. More precisely, if \(\mathsf {sid} \) is the identifier of the challenge session, a list of so-called illegitimate queries for \(\mathsf {sid} \) can be obtained by the adversary, which are queries made on inputs of the form \((\mathsf {sid}, \ldots )\) by machines that are not part of session \(\mathsf {sid} \). If honest parties only make legitimate queries, then clearly this restricted observability will not give the adversary any new information, as it contains only queries made by the adversary. In the ideal world, however, the simulator \(\mathcal {S}\) can observe all queries made through corrupt machines within the challenge session \(\mathsf {sid} \) as it is the ideal-world attacker, which means it will see all legitimate queries in \(\mathsf {sid} \). With the observability of illegitimate queries, that means \(\mathcal {S}\) can observe all hash queries of the form \((\mathsf {sid}, \ldots )\), regardless of whether they are made by honest or corrupt parties, whereas the real-world attacker does not learn anything form the observe interface.
The global random-oracle functionalities \(\mathcal {G} _{\mathsf {roRO}} \), \(\mathcal {G} _\mathsf {rpRO} \), and \(\mathcal {G} _\mathsf {rpoRO} \) with restricted observability, restricted programming, and combined restricted observability and programming, respectively. Functionality \(\mathcal {G} _{\mathsf {roRO}} \) contains only the \(\texttt {Query}\) and \(\texttt {Observe}\) interfaces, \(\mathcal {G} _\mathsf {rpRO} \) contains only the \(\texttt {Query}\), \(\texttt {Program}\), and \(\texttt {IsProgrammed}\) interfaces, and \(\mathcal {G} _\mathsf {rpoRO} \) contains all interfaces.
We recall the restricted observable global random oracle \(\mathcal {G} _{\mathsf {roRO}} \) due to Canetti et al. [15] in a slightly modified form in Fig. 10. In their definition, it allows ideal functionalities to obtain the illegitimate queries corresponding to their own session. These functionalities then allow the adversary to obtain the illegitimate queries by forwarding the request to the global random oracle. Since the adversary can spawn any new machine, and in particular an ideal functionality, the adversary can create such an ideal functionality and use it to obtain the illegitimate queries. We chose to explicitly model this adversarial power by allowing the adversary to query for the illegitimate queries directly.
Also in Fig. 10, we define a restricted programmable global random oracle \(\mathcal {G} _\mathsf {rpRO} \) by using a similar approach to restrict programming access from the real-world adversary. The adversary can program points, but parties in session \(\mathsf {sid} \) can check whether the random oracle was programmed on a particular point \((\mathsf {sid}, \ldots )\). In the real world, the adversary is allowed to program, but honest parties can check whether points were programmed and can, for example, reject signatures based on a programmed hash. In the ideal world, the simulator controls the corrupt parties in \(\mathsf {sid} \) and is therefore the only entity that can check whether points are programmed. Note that while it typically internally simulates the real-world adversary that may want to check whether points of the form \((\mathsf {sid}, \ldots )\) are programmed, the simulator can simply “lie” and pretend that no points are programmed. Therefore, the extra power that the simulator has over the real-world adversary is programming points without being detected.
It may seem strange to offer a new interface allowing all parties to check whether certain points are programmed, even though a real-world hash function does not have such an interface. However, we argue that if one accepts a programmable random oracle as a proper idealization of a clearly non-programmable real-world hash function, then it should be a small step to accept the instantiation of the \(\texttt {IsProgrammed}\) interface that always returns “false” to the question whether any particular entry was programmed into the hash function.
5.2 UC-Commitments from \(\mathcal {G} _\mathsf {rpRO} \)
We now show that we can create a UC-secure commitment protocol from \(\mathcal {G} _\mathsf {rpRO} \). A UC-secure commitment scheme must allow the simulator to extract the message from adversarially created commitments, and to equivocate dummy commitments created for honest committers, i.e., first create a commitment that it can open to any message after committing. Intuitively, achieving the equivocability with a programmable random oracle is simple: we can define a commitment that uses the random-oracle output, and the adversary can later change the committed message by programming the random oracle. Achieving extractability, however, seems difficult, as we cannot extract by observing the random-oracle queries. We overcome this issue with the following approach. The receiver of a commitment chooses a nonce on which we query random oracle, interpreting the random oracle output as a public key \(\mathsf {pk} \). Next, the committer encrypts the message to \(\mathsf {pk} \) and sends the ciphertext to the receiver, which forms the commitment. To open, the committer reveals the message and the randomness used to encrypt it.
This solution is extractable as the simulator that plays the role of receiver can program the random oracle such that it knows the secret key corresponding to \(\mathsf {pk} \), and simply decrypt the commitment to find the message. However, we must take care to still achieve equivocability. If we use standard encryption, the simulator cannot open a ciphertext to any value it learns later. The solution is to use non-committing encryption, which, as shown in Sect. 4, can be achieved using a programmable random oracle. We use a slightly different encryption scheme, as the security requirements here are slightly less stringent than full non-committing encryption, and care must be taken that we can interpret the result of the random oracle as a public key, which is difficult for constructions based on trapdoor one-way permutations such as RSA. This approach results in a very efficient commitment scheme: with two exponentiations per party (as opposed to five) and two rounds of communication (as opposed to five), it is considerably more efficient than the one of [15].
Let \(\mathsf {COM}_{\mathcal {G} _\mathsf {rpRO}}\) be the following commitment protocol, parametrized by a group \(\mathbb {G}= \langle g \rangle \) of prime order q. We require an algorithm \(\mathsf {Embed} \) that maps elements of \(\left\{ {0,1} \right\} ^{\ell (n)}\) into \(\mathbb {G}\), such that for  , \(\mathsf {Embed} (h)\) is statistically close to uniform in \(\mathbb {G}\). Furthermore, we require an efficiently computable probabilistic algorithm \(\mathsf {Embed} ^{-1}\), such that for all \(x \in \mathbb {G}\), \(\mathsf {Embed} (\mathsf {Embed} ^{-1}(x)) = x\) and for
, \(\mathsf {Embed} (h)\) is statistically close to uniform in \(\mathbb {G}\). Furthermore, we require an efficiently computable probabilistic algorithm \(\mathsf {Embed} ^{-1}\), such that for all \(x \in \mathbb {G}\), \(\mathsf {Embed} (\mathsf {Embed} ^{-1}(x)) = x\) and for  , \(\mathsf {Embed} ^{-1}(x)\) is statistically close to uniform in \(\left\{ {0,1} \right\} ^{\ell (n)}\). \(\mathsf {COM}_{\mathcal {G} _\mathsf {rpRO}}\) assumes authenticated channels \(\mathcal {F} _\mathsf {auth} \) as defined by Canetti [9].
, \(\mathsf {Embed} ^{-1}(x)\) is statistically close to uniform in \(\left\{ {0,1} \right\} ^{\ell (n)}\). \(\mathsf {COM}_{\mathcal {G} _\mathsf {rpRO}}\) assumes authenticated channels \(\mathcal {F} _\mathsf {auth} \) as defined by Canetti [9].
-
1.
On input \((\mathsf {Commit}, \mathsf {sid}, x)\), party \(\mathcal {C} \) proceeds as follows.
-
Check that \(\mathsf {sid} = (\mathcal {C}, \mathcal {R}, \mathsf {sid} ')\) for some \(\mathcal {C} \), \(\mathsf {sid} '\). Send \(\mathsf {Commit}\) to \(\mathcal {R} \) over \(\mathcal {F} _\mathsf {auth} \) by giving \(\mathcal {F} _\mathsf {auth} \) input \((\mathsf {Send}, (\mathcal {C}, \mathcal {R}, \mathsf {sid}, 0), ``\mathsf {Commit}{\text {''}})\).
-
\(\mathcal {R} \), upon receiving \((\mathsf {Sent}, (\mathcal {C}, \mathcal {R}, \mathsf {sid}, 0), ``\mathsf {Commit}{\text {''}})\) from \(\mathcal {F} _\mathsf {auth} \), takes a nonce
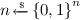 and sends the nonce back to \(\mathcal {C} \) by giving \(\mathcal {F} _\mathsf {auth} \) input \((\mathsf {Send}, (\mathcal {R}, \mathcal {C}, \mathsf {sid}, 0), n)\).
and sends the nonce back to \(\mathcal {C} \) by giving \(\mathcal {F} _\mathsf {auth} \) input \((\mathsf {Send}, (\mathcal {R}, \mathcal {C}, \mathsf {sid}, 0), n)\). -
\(\mathcal {C} \), upon receiving \((\mathsf {Sent}, (\mathcal {R}, \mathcal {C}, \mathsf {sid}, 0), n)\), queries \(\mathcal {G} _\mathsf {rpRO} \) on \((\mathsf {sid}, n)\) to obtain \(h_n\). It checks whether this point was programmed by giving \(\mathcal {G} _{\mathsf {roRO}} \) input \((\mathsf {IsProgrammed}, (\mathsf {sid}, n))\) and aborts if \(\mathcal {G} _{\mathsf {roRO}} \) returns \((\mathsf {IsProgrammed}, 1)\).
-
Set \(\mathsf {pk} \leftarrow \mathsf {Embed} (h_n)\).
-
Pick a random
 and \(\rho \in \mathbb {Z}_q\). Set \(c_1 \leftarrow g^r\), query \(\mathcal {G} _\mathsf {rpRO} \) on \((\mathsf {sid}, \mathsf {pk} ^r)\) to obtain \(h_r\) and let \(c_2 \leftarrow h_r \oplus x\).
and \(\rho \in \mathbb {Z}_q\). Set \(c_1 \leftarrow g^r\), query \(\mathcal {G} _\mathsf {rpRO} \) on \((\mathsf {sid}, \mathsf {pk} ^r)\) to obtain \(h_r\) and let \(c_2 \leftarrow h_r \oplus x\). -
Store (r, x) and send the commitment to \(\mathcal {R} \) by giving \(\mathcal {F} _\mathsf {auth} \) input \((\mathsf {Send}, (\mathcal {C}, \mathcal {R}, \mathsf {sid}, 1), (c_1, c_2))\).
-
\(\mathcal {R} \), upon receiving \((\mathsf {Sent}, (\mathcal {C}, \mathcal {R}, \mathsf {sid}, 1), (c_1, c_2))\) from \(\mathcal {F} _\mathsf {auth}\) outputs \((\mathsf {Receipt}, \mathsf {sid})\).
-
-
2.
On input \((\mathsf {Open}, \mathsf {sid})\), \(\mathcal {C} \) proceeds as follows.
-
It sends (r, x) to \(\mathcal {R} \) by giving \(\mathcal {F} _\mathsf {auth} \) input \((\mathsf {Send}, (\mathcal {C}, \mathcal {R}, \mathsf {sid}, 2), (r, x))\).
-
\(\mathcal {R} \), upon receiving \((\mathsf {Sent}, (\mathcal {C}, \mathcal {R}, \mathsf {sid}, 1), (r, x))\):
-
Query \(\mathcal {G} _\mathsf {rpRO} \) on \((\mathsf {sid}, n)\) to obtain \(h_n\) and let \(\mathsf {pk} \leftarrow \mathsf {Embed} (h_n)\).
-
Check that \(c_1 = g^r\).
-
Query \(\mathcal {G} _\mathsf {rpRO} \) on \((\mathsf {sid}, \mathsf {pk} ^r)\) to obtain \(h_r\) and check that \(c_2 = h_r \oplus x\).
-
Check that none of the points was programmed by giving \(\mathcal {G} _{\mathsf {roRO}} \) inputs \((\mathsf {IsProgrammed}, (\mathsf {sid}, n))\) and \((\mathsf {IsProgrammed}, \mathsf {pk} ^r)\) and asserting that it returns \((\mathsf {IsProgrammed}, 0)\) for both queries.
-
Output \((\mathsf {Open}, \mathsf {sid}, x)\).
-
-
The commitment functionality \(\mathcal {F} _\mathsf {COM} \) by Canetti [9].
\(\mathsf {COM}_{\mathcal {G} _\mathsf {rpRO}}\) is a secure commitment scheme under the computational Diffie-Hellman assumption, which given a group \(\mathbb {G}\) generated by g of prime order q, challenges the adversary to compute \(g^{\alpha \beta }\) on input \((g^\alpha , g^\beta )\), with  .
.
Theorem 5
\(\mathsf {COM}_{\mathcal {G} _\mathsf {rpRO}}\) GUC-realizes \(\mathcal {F} _\mathsf {COM} \) (as defined in Fig. 11) in the \(\mathcal {G} _{\mathsf {roRO}} \) and \(\mathcal {F} _\mathsf {auth} \) hybrid model under the CDH assumption in \(\mathbb {G}\).
Proof
By the fact that \(\mathsf {COM}_{\mathcal {G} _\mathsf {rpRO}}\) is \(\mathcal {G} _\mathsf {rpRO} \)-subroutine respecting and by Theorem 1, it is sufficient to show that \(\mathsf {COM}_{\mathcal {G} _\mathsf {rpRO}}\) \(\mathcal {G} _\mathsf {rpRO} \)-EUC-realizes \(\mathcal {F} _\mathsf {COM} \).
We describe a simulator \(\mathcal {S}\) by defining its behavior in the different corruption scenarios. In all scenarios, whenever the simulated real-world adversary makes an \(\mathsf {IsProgrammed} \) query or instructs a corrupt party to make such a query on a point that \({\mathcal {S}} \) has programmed, the simulator intercepts this query and simply replies \((\mathsf {IsProgrammed}, 0)\), lying that the point was not programmed.
When both the sender and the receiver are honest, \(\mathcal {S}\) works as follows.
-
1.
When \(\mathcal {F} _\mathsf {COM}\) asks \(\mathcal {S}\) for permission to output \((\mathsf {Receipt}, \mathsf {sid})\):
-
Parse \(\mathsf {sid} \) as \((\mathcal {C}, \mathcal {R}, \mathsf {sid} ')\) and let “\(\mathcal {C} \)” create a dummy commitment by choosing
 , letting \(c_1 = g^r\), choosing
, letting \(c_1 = g^r\), choosing  .
. -
When “\(\mathcal {R} \)” outputs \((\mathsf {Receipt}, \mathsf {sid})\), allow \(\mathcal {F} _\mathsf {COM}\) to proceed.
-
-
2.
When \(\mathcal {F} _\mathsf {COM}\) asks \(\mathcal {S}\) for permission to output \((\mathsf {Open}, \mathsf {sid}, x)\):
-
Program \(\mathcal {G} _\mathsf {rpRO}\) by giving \(\mathcal {G} _{\mathsf {roRO}} \) input \((\mathsf {ProgramRO}, (\mathsf {sid}, \mathsf {pk} ^r), c_2 \oplus x)\), such that the commitment \((c_1, c_2)\) commits to x.
-
Give “\(\mathcal {C} \)” input \((\mathsf {Open}, \mathsf {sid})\) instructing it to open its commitment to x.
-
When “\(\mathcal {R} \)” outputs \((\mathsf {Open}, \mathsf {sid}, x)\), allow \(\mathcal {F} _\mathsf {COM}\) to proceed.
-
If the committer is corrupt but the receiver is honest, \(\mathcal {S}\) works as follows.
-
1.
When the simulated receiver “\(\mathcal {R} \)” notices the commitment protocol starting (i.e., receives \((\mathsf {Sent}, (\mathcal {C}, \mathcal {R}, \mathsf {sid}, 0), ``\mathsf {Commit}\)”) from “\(\mathcal {F} _\mathsf {auth} \)”):
-
Choose nonce n as in the protocol.
-
Before sending n, choose
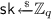 and set \(\mathsf {pk} \leftarrow g^\mathsf {sk} \).
and set \(\mathsf {pk} \leftarrow g^\mathsf {sk} \). -
Program \(\mathcal {G} _\mathsf {rpRO}\) by giving \(\mathcal {G} _\mathsf {rpRO}\) input \((\mathsf {ProgramRO}, (\mathsf {sid}, n), \mathsf {Embed} ^{-1}(\mathsf {pk}))\). Note that this simulation will succeed with overwhelming probability as n is freshly chosen, and note that as \(\mathsf {pk} \) is uniform in \(\mathbb {G}\), by definition of \(\mathsf {Embed} ^{-1}\) the programmed value \(\mathsf {Embed} ^{-1}(\mathsf {pk})\) is uniform in \(\left\{ {0,1} \right\} ^{\ell (n)}\).
-
\(\mathcal {S}\) now lets “\(\mathcal {R} \)” execute the remainder the protocol honestly.
-
When “\(\mathcal {R} \)” outputs \((\mathsf {Receipt}, \mathsf {sid})\), \(\mathcal {S}\) extracts the committed value from \((c_1, c_2)\). Query \(\mathcal {G} _\mathsf {rpRO} \) on \((\mathsf {sid}, c_1^\mathsf {sk})\) to obtain \(h_r\) and set \(x \leftarrow c_2 \oplus h_r\).
-
Make a query with \(\mathcal {F} _\mathsf {COM} \) on \(\mathcal {C} \)’s behalf by sending \((\mathsf {Commit}, \mathsf {sid}, x)\) on \(\mathcal {C} \)’s behalf to \(\mathcal {F} _\mathsf {COM} \).
-
When \(\mathcal {F} _\mathsf {COM}\) asks permission to output \((\mathsf {Receipt}, \mathsf {sid})\), allow.
-
-
2.
When “\(\mathcal {R} \)” outputs \((\mathsf {Open}, \mathsf {sid}, x)\):
-
Send \((\mathsf {Open}, \mathsf {sid})\) on \(\mathcal {C} \)’s behalf to \(\mathcal {F} _\mathsf {COM} \).
-
When \(\mathcal {F} _\mathsf {COM}\) asks permission to output \((\mathsf {Open}, \mathsf {sid}, x)\), allow.
-
If the receiver is corrupt but the committer is honest, \(\mathcal {S}\) works as follows.
-
1.
When \(\mathcal {F} _\mathsf {COM}\) asks permission to output \((\mathsf {Receipt}, \mathsf {sid})\):
-
Parse \(\mathsf {sid} \) as \((\mathcal {C}, \mathcal {R}, \mathsf {sid} ')\).
-
Allow \(\mathcal {F} _\mathsf {COM}\) to proceed.
-
When \(\mathcal {F} _\mathsf {COM}\) receives \((\mathsf {Receipt}, \mathsf {sid})\) from \(\mathcal {F} _\mathsf {COM} \) as \(\mathcal {R} \) is corrupt, it simulates “\(\mathcal {C} \)” by choosing
 , computing \(c_1 = g^r\), and choosing
, computing \(c_1 = g^r\), and choosing  .
.
-
-
2.
When \(\mathcal {F} _\mathsf {COM}\) asks permission to output \((\mathsf {Open}, \mathsf {sid}, x)\):
-
Allow \(\mathcal {F} _\mathsf {COM}\) to proceed.
-
When \(\mathcal {S}\) receives \((\mathsf {Open}, \mathsf {sid}, x)\) from \(\mathcal {F} _\mathsf {COM}\) as \(\mathcal {R} \) is corrupt, \(\mathcal {S}\) programs \(\mathcal {G} _\mathsf {rpRO}\) by giving \(\mathcal {G} _\mathsf {rpRO} \) input \((\mathsf {ProgramRO}, (\mathsf {sid}, \mathsf {pk} ^r), c_2 \oplus x)\), such that the commitment \((c_1, c_2)\) commits to x.
-
\(\mathcal {S}\) inputs \((\mathsf {Open}, \mathsf {sid})\) to “\(\mathcal {C} \)”, instructing it to open its commitment to x.
-
What remains to show is that \(\mathcal {S}\) is a satisfying simulator, i.e., no \(\mathcal {G} _\mathsf {rpRO} \)-externally constrained environment can distinguish \(\mathcal {F} _\mathsf {COM}\) and \(\mathcal {S}\) from \(\mathsf {COM}_{\mathcal {G} _\mathsf {rpRO}}\) and \(\mathcal {A}\). When simulating an honest receiver, \(\mathcal {S}\) extracts the committed message correctly: Given \(\mathsf {pk} \) and \(c_1 = g^r\) for some r, there is a unique value \(\mathsf {pk} ^r\), and the message x is uniquely determined by \(c_2\) and \(\mathsf {pk} ^r\). Simulator \(\mathcal {S}\) also simulates an honest committer correctly. When committing, it does not know the message, but can still produce a commitment that is identically distributed as long as the environment does not query the random oracle on \((\mathsf {sid}, \mathsf {pk} ^r)\). When \(\mathcal {S}\) later learns the message x, it must equivocate the commitment to open to x, by programming \(\mathcal {G} _\mathsf {rpRO} \) on \((\mathsf {sid}, \mathsf {pk} ^r)\), which again succeeds unless the environment makes a random oracle query on \((\mathsf {sid}, \mathsf {pk} ^r)\). If there is an environment that triggers such a \(\mathcal {G} _\mathsf {rpRO} \) with non-negligible probability, we can construct an attacker \(\mathcal {B}\) that breaks the CDH problem in \(\mathbb {G}\).
Our attacker \(\mathcal {B} \) plays the role of \(\mathcal {F} _\mathsf {COM} \), \({\mathcal {S}} \), and \(\mathcal {G} _\mathsf {rpRO} \), and has black-box access to the environment. \(\mathcal {B} \) receives CDH problem \(g^\alpha , g^\beta \) and is challenged to compute \(g^{\alpha \beta }\). It simulates \(\mathcal {G} _\mathsf {rpRO} \) to return \(h_n \leftarrow \mathsf {Embed} ^{-1}(g^\alpha )\) on random query \((\mathsf {sid}, n)\). When simulating an honest committer committing with respect to this \(\mathsf {pk} \), set \(c_1 \leftarrow g^\beta \) and  . Note that \(\mathcal {S}\) cannot successfully open this commitment, but remember that we consider an environment that with non-negligible probability makes a \(\mathcal {G} _\mathsf {rpRO} \) query on \(\mathsf {pk} ^r (= g^{\alpha \beta })\) before the commitment is being opened. Next, \(\mathcal {B} \) will choose a random \(\mathcal {G} _\mathsf {rpRO} \) query on \((\mathsf {sid}, m)\). With nonnegligible probability, we have \(m = g^{\alpha \beta }\), and \(\mathcal {B} \) found the solution to the CDH challenge. \(\square \)
. Note that \(\mathcal {S}\) cannot successfully open this commitment, but remember that we consider an environment that with non-negligible probability makes a \(\mathcal {G} _\mathsf {rpRO} \) query on \(\mathsf {pk} ^r (= g^{\alpha \beta })\) before the commitment is being opened. Next, \(\mathcal {B} \) will choose a random \(\mathcal {G} _\mathsf {rpRO} \) query on \((\mathsf {sid}, m)\). With nonnegligible probability, we have \(m = g^{\alpha \beta }\), and \(\mathcal {B} \) found the solution to the CDH challenge. \(\square \)
5.3 Adding Observability for Efficient Commitments
While the commitment scheme \(\mathsf {COM}_{\mathcal {G} _\mathsf {rpRO}}\) from the restricted programmable global random oracle is efficient for a composable commitment scheme, there is still a large efficiency gap between composable commitments from global random oracles and standalone commitments or commitments from local random oracles. Indeed, \(\mathsf {COM}_{\mathcal {G} _\mathsf {rpRO}}\) still requires multiple exponentiations and rounds of interaction, whereas the folklore commitment scheme \(c = \mathcal {H} (m\Vert r)\) for message m and random opening information r consists of computing a single hash function.
We extend \(\mathcal {G} _\mathsf {rpRO} \) to, on top of programmability, offer the restricted observability interface of the global random oracle due to Canetti et al. [15]. With this restricted programmable and observable global random oracle \(\mathcal {G} _\mathsf {rpoRO} \) (as shown in Fig. 10), we can close this efficiency gap and prove that the folklore commitment scheme above is a secure composable commitment scheme with a global random oracle.
Let \(\mathsf {COM}_{\mathcal {G} _\mathsf {rpoRO}}\) be the commitment scheme that simply hashes the message and opening, phrased as a GUC protocol using \(\mathcal {G} _\mathsf {rpoRO} \) and using authenticated channels, which is formally defined as follows.
-
1.
On input \((\mathsf {Commit}, \mathsf {sid}, x)\), party C proceeds as follows.
-
Check that \(\mathsf {sid} = (C, R, \mathsf {sid} ')\) for some C, \(\mathsf {sid} '\).
-
Pick
 and query \(\mathcal {G} _\mathsf {rpoRO} \) on \((\mathsf {sid}, r, x)\) to obtain c.
and query \(\mathcal {G} _\mathsf {rpoRO} \) on \((\mathsf {sid}, r, x)\) to obtain c. -
Send c to R over \(\mathcal {F} _\mathsf {auth} \) by giving \(\mathcal {F} _\mathsf {auth} \) input \((\mathsf {Send}, (C, R, \mathsf {sid}, 0), c)\).
-
R, upon receiving \((\mathsf {Sent}, (C, R, \mathsf {sid}, 0), c)\) from \(\mathcal {F} _\mathsf {auth} \), outputs \((\mathsf {Receipt}, \mathsf {sid})\).
-
-
2.
On input \((\mathsf {Open}, \mathsf {sid})\), C proceeds as follows.
-
It sends (r, x) to R by giving \(\mathcal {F} _\mathsf {auth} \) input \((\mathsf {Send}, (C, R, \mathsf {sid}, 2), (r, x))\).
-
R, upon receiving \((\mathsf {Sent}, (C, R, \mathsf {sid}, 1), (r, x))\) from \(\mathcal {F} _\mathsf {auth}\), queries \(\mathcal {G} _\mathsf {rpoRO} \) on \((\mathsf {sid}, r, x)\) and checks that the result is equal to c, and checks that \((\mathsf {sid}, r, x)\) is not programmed by giving \(\mathcal {G} _\mathsf {rpoRO} \) input \((\mathsf {IsProgrammed}, (\mathsf {sid}, r, x))\) and aborting if the result is not \((\mathsf {IsProgrammed}, 0)\). Output \((\mathsf {Open}, \mathsf {sid}, x)\).
-
Theorem 6
\(\mathsf {COM}_{\mathcal {G} _\mathsf {rpoRO}}\) GUC-realizes \(\mathcal {F} _\mathsf {COM} \) (as defined in Fig. 11), in the \(\mathcal {G} _\mathsf {rpoRO} \) and \(\mathcal {F} _\mathsf {auth} \) hybrid model.
Proof
By the fact that \(\mathsf {COM}_{\mathcal {G} _\mathsf {rpoRO}} \) is \(\mathcal {G} _\mathsf {rpoRO} \)-subroutine respecting and by Theorem 1, it is sufficient to show that \(\mathsf {COM}_{\mathcal {G} _\mathsf {rpoRO}} \) \(\mathcal {G} _\mathsf {rpoRO} \)-EUC-realizes \(\mathcal {F} _\mathsf {rpo\text {-}COM} \).
We define a simulator \(\mathcal {S}\) by describing its behavior in the different corruption scenarios. For all scenarios, \(\mathcal {S}\) will internally simulate \(\mathcal {A} \) and forward any messages between \(\mathcal {A}\) and the environment, the corrupt parties, and \(\mathcal {G} _\mathsf {rpoRO} \). It stores all \(\mathcal {G} _\mathsf {rpoRO} \) queries that it makes for \(\mathcal {A}\) and for corrupt parties. Only when \(\mathcal {A} \) directly or through a corrupt party makes an \(\texttt {IsProgrammed} \) query on a point that \({\mathcal {S}} \) programmed, \({\mathcal {S}} \) will not forward this query to \(\mathcal {G} _\mathsf {rpoRO} \) but instead return \((\mathsf {IsProgrammed}, 0)\). When we say that \(\mathcal {S}\) queries \(\mathcal {G} _\mathsf {rpoRO} \) on a point (s, m) where s is the challenge \(\mathsf {sid} \), for example when simulating an honest party, it does so through a corrupt dummy party that it spawns, such that the query is not marked as illegitimate.
When both the sender and the receiver are honest, \(\mathcal {S}\) works as follows.
-
1.
When \(\mathcal {F} _\mathsf {rpo\text {-}COM}\) asks \(\mathcal {S}\) for permission to output \((\mathsf {Receipt}, \mathsf {sid})\):
-
Parse \(\mathsf {sid} \) as \((C, R, \mathsf {sid} ')\) and let “C” commit to a dummy value by giving it input \((\mathsf {Commit}, \mathsf {sid}, \bot )\), except that it takes
 instead of following the protocol.
instead of following the protocol. -
When “R” outputs \((\mathsf {Receipt}, \mathsf {sid})\), allow \(\mathcal {F} _\mathsf {rpo\text {-}COM}\) to proceed.
-
-
2.
When \(\mathcal {F} _\mathsf {rpo\text {-}COM}\) asks \(\mathcal {S}\) for permission to output \((\mathsf {Open}, \mathsf {sid}, x)\):
-
Choose a random
 and program \(\mathcal {G} _\mathsf {rpoRO}\) by giving it input \((\mathsf {ProgramRO}, (\mathsf {sid}, r, x), c)\), such that the commitment c commits to x. Note that since r is freshly chosen at random, the probability that \(\mathcal {G} _\mathsf {rpoRO} \) is already defined on \((\mathsf {sid}, r, x)\) is negligible, so the programming will succeed with overwhelming probability.
and program \(\mathcal {G} _\mathsf {rpoRO}\) by giving it input \((\mathsf {ProgramRO}, (\mathsf {sid}, r, x), c)\), such that the commitment c commits to x. Note that since r is freshly chosen at random, the probability that \(\mathcal {G} _\mathsf {rpoRO} \) is already defined on \((\mathsf {sid}, r, x)\) is negligible, so the programming will succeed with overwhelming probability. -
Give “C” input \((\mathsf {Open}, \mathsf {sid})\) instructing it to open its commitment to x.
-
When “R” outputs \((\mathsf {Open}, \mathsf {sid}, x)\), allow \(\mathcal {F} _\mathsf {rpo\text {-}COM}\) to proceed.
-
If the committer is corrupt but the receiver is honest, \(\mathcal {S}\) works as follows.
-
1.
When simulated receiver “R” outputs \((\mathsf {Receipt}, \mathsf {sid})\):
-
Obtain the list \(\mathcal {Q} _{\mathsf {sid}}\) of all random oracle queries of form \((\mathsf {sid}, \ldots )\), by combining the queries that \(\mathcal {S}\) made on behalf of the corrupt parties and the simulated honest parties, and by obtaining the illegitimate queries made outside of \(\mathcal {S}\) by giving \(\mathcal {G} _\mathsf {rpoRO} \) input \((\mathsf {Observe}, \mathsf {sid})\).
-
Find a non-programmed record \(((\mathsf {sid}, r, x), c) \in \mathcal {Q} _\mathsf {sid} \). If no such record is found, set x to a dummy value.
-
Make a query with \(\mathcal {F} _\mathsf {rpo\text {-}COM} \) on C’s behalf by sending \((\mathsf {Commit}, \mathsf {sid}, x)\) on C’s behalf to \(\mathcal {F} _\mathsf {rpo\text {-}COM} \).
-
When \(\mathcal {F} _\mathsf {rpo\text {-}COM}\) asks permission to output \((\mathsf {Receipt}, \mathsf {sid})\), allow.
-
-
2.
When “R” outputs \((\mathsf {Open}, \mathsf {sid}, x)\):
-
Send \((\mathsf {Open}, \mathsf {sid})\) on C’s behalf to \(\mathcal {F} _\mathsf {rpo\text {-}COM} \).
-
When \(\mathcal {F} _\mathsf {rpo\text {-}COM}\) asks permission to output \((\mathsf {Open}, \mathsf {sid}, x)\), allow.
-
If the receiver is corrupt but the committer is honest, \(\mathcal {S}\) works as follows.
-
1.
When \(\mathcal {F} _\mathsf {rpo\text {-}COM}\) asks permission to output \((\mathsf {Receipt}, \mathsf {sid})\):
-
Parse \(\mathsf {sid} \) as \((C, R, \mathsf {sid} ')\).
-
Allow \(\mathcal {F} _\mathsf {rpo\text {-}COM}\) to proceed.
-
When \(\mathcal {S}\) receives \((\mathsf {Receipt}, \mathsf {sid})\) from \(\mathcal {F} _\mathsf {rpo\text {-}COM} \) as R is corrupt, it simulates “C” by choosing
 instead of following the protocol.
instead of following the protocol.
-
-
2.
When \(\mathcal {F} _\mathsf {rpo\text {-}COM}\) asks permission to output \((\mathsf {Open}, \mathsf {sid}, x)\):
-
Allow \(\mathcal {F} _\mathsf {rpo\text {-}COM}\) to proceed.
-
When \(\mathcal {S}\) receives \((\mathsf {Open}, \mathsf {sid}, x)\) from \(\mathcal {F} _\mathsf {rpo\text {-}COM}\) as R is corrupt, choose
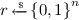 and program \(\mathcal {G} _\mathsf {rpoRO}\) by giving \(\mathcal {F} _\mathsf {rpo\text {-}COM} \) input \((\mathsf {ProgramRO}, (\mathsf {sid}, r, x), c)\), such that the commitment c commits to x. Note that since r is freshly chosen at random, the probability that \(\mathcal {G} _\mathsf {rpoRO} \) is already defined on \((\mathsf {sid}, r, x)\) is negligible, so the programming will succeed with overwhelming probability.
and program \(\mathcal {G} _\mathsf {rpoRO}\) by giving \(\mathcal {F} _\mathsf {rpo\text {-}COM} \) input \((\mathsf {ProgramRO}, (\mathsf {sid}, r, x), c)\), such that the commitment c commits to x. Note that since r is freshly chosen at random, the probability that \(\mathcal {G} _\mathsf {rpoRO} \) is already defined on \((\mathsf {sid}, r, x)\) is negligible, so the programming will succeed with overwhelming probability. -
\(\mathcal {S}\) inputs \((\mathsf {Open}, \mathsf {sid})\) to “C”, instructing it to open its commitment to x.
-
We must show that \(\mathcal {S}\) extracts the correct value from a corrupt commitment. It obtains a list of all \(\mathcal {G} _\mathsf {rpoRO} \) queries of the form \((\mathsf {sid}, \ldots )\) and looks for a non-programmed entry \((\mathsf {sid}, r, x)\) that resulted in output c. If this does not exist, then the environment can only open its commitment successfully by later finding a preimage of c, as the honest receiver will check that the point was not programmed. Finding such a preimage happens with negligible probability, so committing to a dummy value is sufficient. The probability that there are multiple satisfying entries is also negligible, as this means the environment found collisions on the random oracle.
Next, we argue that the simulated commitments are indistinguishable from honest commitments. Observe that the commitment c is distributed equally to real commitments, namely uniform in \(\left\{ {0,1} \right\} ^{\ell (n)}\). The simulator can open this value to the desired x if programming the random oracle succeeds. As it first takes a fresh nonce  and programs \((\mathsf {sid}, r, x)\), the probability that \(\mathcal {G} _\mathsf {rpoRO} \) is already defined on this input is negligible. \(\square \)
and programs \((\mathsf {sid}, r, x)\), the probability that \(\mathcal {G} _\mathsf {rpoRO} \) is already defined on this input is negligible. \(\square \)
6 Unifying the Different Global Random Oracles
At this point, we have considered several notions of global random oracles that differ in whether they offer programmability or observability, and in whether this power is restricted to machines within the local session, or also available to other machines. Having several coexisting variants of global random oracles, each with their own set of schemes that they can prove secure, is somewhat unsatisfying. Indeed, if different schemes require different random oracles that in practice end up being replaced with the same hash function, then we’re back to the problem that motivated the concept of global random oracles.
We were able to distill a number of relations and transformations among the different notions, allowing a protocol that realizes a functionality with access to one type of global random oracle to be efficiently transformed into a protocol that realizes the same functionality with respect to a different type of global random oracle. A graphical representation of our transformation is given in Fig. 12.
Relations between different notions of global random oracles. An arrow from \(\mathcal {G} \) to \(\mathcal {G} '\) indicates the existence of simple transformation such that any protocol that \(\mathcal {G} \)-EUC-realizes a functionality \(\mathcal {F} \), the transformed protocol \(\mathcal {G} '\)-EUC-realizes the transformed functionality \(\mathcal {F} \) (cf. Theorem 7).
The transformations are very simple and hardly affect efficiency of the protocol. The \(\mathsf {s2ro}\) transformation takes as input a \(\mathcal {G} _{\mathsf {sRO}} \)-subroutine-respecting protocol \(\pi \) and transforms it into a \(\mathcal {G} _{\mathsf {roRO}} \)-subroutine respecting protocol \(\pi ' = \mathsf {s2ro}(\pi )\) by replacing each query \((\mathsf {HashQuery}, m)\) to \(\mathcal {G} _{\mathsf {sRO}} \) with a query \((\mathsf {HashQuery}, (\mathsf {sid}, m))\) to \(\mathcal {G} _{\mathsf {roRO}} \), where \(\mathsf {sid} \) is the session identifier of the calling machine. Likewise, the \(\mathsf {p2rp}\) transformation takes as input a \(\mathcal {G} _\mathsf {pRO} \)-subroutine-respecting protocol \(\pi \) and transforms it into a \(\mathcal {G} _\mathsf {rpRO} \)-subroutine respecting protocol \(\pi ' = \mathsf {p2rp}(\pi )\) by replacing each query \((\mathsf {HashQuery}, m)\) to \(\mathcal {G} _\mathsf {pRO} \) with a query \((\mathsf {HashQuery}, (\mathsf {sid}, m))\) to \(\mathcal {G} _\mathsf {rpRO} \) and replacing each query \((\mathsf {ProgramRO}, m,h)\) to \(\mathcal {G} _\mathsf {pRO} \) with a query \((\mathsf {ProgramRO}, (\mathsf {sid}, m), h)\) to \(\mathcal {G} _\mathsf {rpRO} \), where \(\mathsf {sid} \) is the session identifier of the calling machine. The other transformation \(\mathsf {rp2rpo}\) simply replaces \(\mathsf {HashQuery} \), \(\mathsf {ProgramRO} \), and \(\mathsf {IsProgrammed} \) queries to \(\mathcal {G} _\mathsf {rpRO} \) with identical queries to \(\mathcal {G} _\mathsf {rpoRO} \).
Theorem 7
Let \(\pi \) be a \(\mathcal {G} _{\mathsf {x}\mathrm {RO}} \)-subroutine-respecting protocol and let \(\mathcal {G} _{\mathsf {y}\mathrm {RO}} \) be such that there is an edge from \(\mathcal {G} _{\mathsf {x}\mathrm {RO}} \) to \(\mathcal {G} _{\mathsf {y}\mathrm {RO}} \) in Fig. 12, where \(\mathsf {x},\mathsf {y}\in \{\mathsf {s}, \mathsf {ro}, \mathsf {p}, \mathsf {rp}, \mathsf {rpo}\}\). Then if \(\pi \) \(\mathcal {G} _{\mathsf {x}\mathrm {RO}} \)-EUC-realizes a functionality \(\mathcal {F} \), where \(\mathcal {F} \) is an ideal functionality that does not communicate with \(\mathcal {G} _{\mathsf {x}\mathrm {RO}} \), then \(\pi ' = \mathsf {x2y}(\pi )\) is a \(\mathcal {G} _{\mathsf {y}\mathrm {RO}} \)-subroutine-respecting protocol that \(\mathcal {G} _{\mathsf {y}\mathrm {RO}} \)-EUC-realizes \(\mathcal {F} \).
Proof
(sketch). We first provide some detail for the \(\mathsf {s2ro}\) transformation. The other transformations can be proved in a similar fashion, so we only provide an intuition here.
As protocol \(\pi \) \(\mathcal {G} _{\mathsf {sRO}} \)-EUC-realizes \(\mathcal {F} \), there exists a simulator \({\mathcal {S}} _\mathsf {s}\) that correctly simulates the protocol with respect to the dummy adversary. Observe that \(\mathcal {G} _{\mathsf {roRO}} \) offers the same \(\mathsf {HashQuery} \) interface to the adversary as \(\mathcal {G} _{\mathsf {sRO}} \), and that the \(\mathcal {G} _{\mathsf {roRO}} \) only gives the simulator extra powers. Therefore, given the dummy-adversary simulator \({\mathcal {S}} _\mathsf {s}\) for \(\pi \), one can build a dummy-adversary simulator \({\mathcal {S}} _\mathsf {ro}\) for \(\mathsf {s2ro}(\pi )\) as follows. If the environment makes a query \((\mathsf {HashQuery}, x)\), either directly through the dummy adversary, or indirectly by instructing a corrupt party to make that query, \({\mathcal {S}} _\mathsf {ro}\) checks whether x can be parsed as \((\mathsf {sid},x')\) where \(\mathsf {sid} \) is the challenge session. If so, then it passes a direct or indirect query \((\mathsf {HashQuery}, x')\) to \({\mathcal {S}} _\mathsf {s}\), depending whether the environment’s original query was direct or indirect. If x cannot be parsed as \((\mathsf {sid},x')\), then it simply relays the query to \(\mathcal {G} _{\mathsf {roRO}} \). Simulator \({\mathcal {S}} _\mathsf {ro}\) relays \({\mathcal {S}} _\mathsf {s}\)’s inputs to and outputs from \(\mathcal {F} \). When \({\mathcal {S}} _\mathsf {s}\) makes a \((\mathsf {HashQuery},x')\) query to \(\mathcal {G} _{\mathsf {sRO}} \), \({\mathcal {S}} _\mathsf {ro}\) makes a query \((\mathsf {HashQuery},(\mathsf {sid},x'))\) to \(\mathcal {G} _{\mathsf {roRO}} \) and relays the response back to \({\mathcal {S}} _\mathsf {s}\). Finally, \({\mathcal {S}} _\mathsf {ro}\) simply relays any \(\mathsf {Observe} \) queries by the environment to \(\mathcal {G} _{\mathsf {roRO}} \). Note, however, that these queries do not help the environment in observing the honest parties, as they only make legitimate queries.
To see that \({\mathcal {S}} _\mathsf {ro}\) is a good simulator for \(\mathsf {s2ro}(\pi )\), we show that if there exists a distinguishing dummy-adversary environment \(\mathcal {Z} _\mathsf {ro}\) for \(\mathsf {s2ro}(\pi )\) and \({\mathcal {S}} _\mathsf {ro}\), then there also exists a distinguishing environment \(\mathcal {Z} _\mathsf {s}\) for \(\pi \) and \({\mathcal {S}} _\mathsf {s}\), which would contradict the security of \(\pi \). The environment \(\mathcal {Z} _\mathsf {s}\) runs \(\mathcal {Z} _\mathsf {ro}\) by internally executing the code of \(\mathcal {G} _{\mathsf {roRO}} \) to respond to \(\mathcal {Z} _\mathsf {ro}\)’s \(\mathcal {G} _{\mathsf {roRO}} \) queries, except for queries \((\mathsf {HashQuery},x)\) where x can be parsed as \((\mathsf {sid},x')\), for which \(\mathcal {Z} _\mathsf {s}\) reaches out to its own \(\mathcal {G} _{\mathsf {sRO}} \) functionality with a query \((\mathsf {HashQuery},x')\).
The \(\mathsf {p2rp}\) transformation is very similar to \(\mathsf {s2ro}\) and prepends \(\mathsf {sid} \) to random oracle queries. Moving to the restricted programmable RO only reduces the power of the adversary by making programming detectable to honest users through the \(\mathsf {IsProgrammed} \) interface. The simulator, however, maintains its power to program without being detected, because it can intercept the environment’s \(\mathsf {IsProgrammed} \) queries for the challenge \(\mathsf {sid} \) and pretend that they were not programmed. The environment cannot circumvent the simulator and query \(\mathcal {G} _\mathsf {rpRO} \) directly, because \(\mathsf {IsProgrammed} \) queries for \(\mathsf {sid} \) must be performed from a machine within \(\mathsf {sid} \).
Finally, the \(\mathsf {rp2rpo}\) transformation increases the power of both the simulator and the adversary by adding a \(\mathsf {Observe} \) interface. Similarly to the \(\mathsf {s2ro}\) simulator, however, the interface cannot be used by the adversary to observe queries made by honest parties, as these queries are all legitimate. \(\square \)
Unfortunately, we were unable to come up with security-preserving transformations from non-programmable to programmable random oracles that apply to any protocol. One would expect that the capability to program random-oracle entries destroys the security of many protocols that are secure for non-programmable random oracles. Often this effect can be mitigated by letting the protocol, after performing a random-oracle query, additionally check whether the entry was programmed through the \(\mathsf {IsProgrammed} \) interface, and rejecting or aborting if it was. While this seems to work for signature or commitment schemes where rejection is a valid output, it may not always work for arbitrary protocols with interfaces that may not be able to indicate rejection. We leave the study of more generic relations and transformations between programmable and non-programmable random oracles as interesting future work.
References
Ananth, P., Bhaskar, R.: Non observability in the random oracle model. In: Susilo, W., Reyhanitabar, R. (eds.) ProvSec 2013. LNCS, vol. 8209, pp. 86–103. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-41227-1_5
Bellare, M., Desai, A., Pointcheval, D., Rogaway, P.: Relations among notions of security for public-key encryption schemes. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 26–45. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055718
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: ACM CCS 93
Bellare, M., Rogaway, P.: Optimal asymmetric encryption. In: De Santis, A. (ed.) EUROCRYPT 1994. LNCS, vol. 950, pp. 92–111. Springer, Heidelberg (1995). https://doi.org/10.1007/BFb0053428
Bellare, M., Rogaway, P.: The exact security of digital signatures-how to sign with RSA and Rabin. In: Maurer, U. (ed.) EUROCRYPT 1996. LNCS, vol. 1070, pp. 399–416. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68339-9_34
Bhattacharyya, R., Mukherjee, P.: Non-adaptive programmability of random oracle. Theor. Comput. Sci. 592, 97–114 (2015)
Camenisch, J., Enderlein, R.R., Krenn, S., Küsters, R., Rausch, D.: Universal composition with responsive environments. In: Cheon, J.H., Takagi, T. (eds.) ASIACRYPT 2016. LNCS, vol. 10032, pp. 807–840. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53890-6_27
Camenisch, J., Lehmann, A., Neven, G., Samelin, K.: UC-secure non-interactive public-key encryption. In: IEEE CSF 2017 (2017)
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. Cryptology ePrint Archive, Report 2000/067 (2000)
Canetti, R.: Universally composable security: a new paradigm for cryptographic protocols. In: FOCS 2001 (2001)
Canetti, R.: Universally composable signature, certification, and authentication. In: CSFW 2004 (2004)
Canetti, R., Dodis, Y., Pass, R., Walfish, S.: Universally composable security with global setup. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 61–85. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-70936-7_4
Canetti, R., Fischlin, M.: Universally composable commitments. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 19–40. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_2
Canetti, R., Goldreich, O., Halevi, S.: The random oracle methodology, revisited (preliminary version). In: ACM STOC 1998 (1998)
Canetti, R., Jain, A., Scafuro, A.: Practical UC security with a global random oracle. In: ACM CCS 2014 (2014)
Coron, J.-S.: On the exact security of full domain hash. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 229–235. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44598-6_14
Dodis, Y., Shoup, V., Walfish, S.: Efficient constructions of composable commitments and zero-knowledge proofs. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 515–535. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_29
Fischlin, M., Lehmann, A., Ristenpart, T., Shrimpton, T., Stam, M., Tessaro, S.: Random oracles with(out) programmability. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 303–320. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_18
Fujisaki, E., Okamoto, T.: Secure integration of asymmetric and symmetric encryption schemes. J. Cryptol. 26(1), 80–101 (2013)
Goldwasser, S., Micali, S., Rivest, R.L.: A digital signature scheme secure against adaptive chosen-message attacks. SIAM J. Comput. 17(2), 281–308 (1988)
Nielsen, J.B.: Separating random oracle proofs from complexity theoretic proofs: the non-committing encryption case. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 111–126. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45708-9_8
Pointcheval, D., Stern, J.: Security arguments for digital signatures and blind signatures. J. Cryptol. 13(3), 361–396 (2000)
Schnorr, C.P.: Efficient signature generation by smart cards. J. Cryptol. 4(3), 161–174 (1991)
Acknowledgements
We thank Ran Canetti, Alessandra Scafuro, and the anonymous reviewers for their valuable comments. This work was supported by the ERC under grant PERCY (#321310) and by the EU under CHIST-ERA project USE-IT.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Camenisch, J., Drijvers, M., Gagliardoni, T., Lehmann, A., Neven, G. (2018). The Wonderful World of Global Random Oracles. In: Nielsen, J., Rijmen, V. (eds) Advances in Cryptology – EUROCRYPT 2018. EUROCRYPT 2018. Lecture Notes in Computer Science(), vol 10820. Springer, Cham. https://doi.org/10.1007/978-3-319-78381-9_11
Download citation
DOI: https://doi.org/10.1007/978-3-319-78381-9_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-78380-2
Online ISBN: 978-3-319-78381-9
eBook Packages: Computer ScienceComputer Science (R0)






 , and send
, and send 
 with
with  .
.




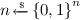 and sends the nonce back to
and sends the nonce back to  and
and 
 , letting
, letting  .
.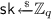 and set
and set  , computing
, computing  .
. and query
and query  instead of following the protocol.
instead of following the protocol. and program
and program  instead of following the protocol.
instead of following the protocol.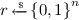 and program
and program 
