Fiat-Shamir and Correlation Intractability from Strong KDM-Secure Encryption

Abstract

A hash function family is called correlation intractable if for all sparse relations, it is hard to find, given a random function from the family, an input-output pair that satisfies the relation (Canetti et al., STOC 1998). Correlation intractability (CI) captures a strong Random-Oracle-like property of hash functions. In particular, when security holds for all sparse relations, CI suffices for guaranteeing the soundness of the Fiat-Shamir transformation from any constant round, statistically sound interactive proof to a non-interactive argument. However, to date, the only CI hash function for all sparse relations (Kalai et al., Crypto 2017) is based on general program obfuscation with exponential hardness properties.

We construct a simple CI hash function for arbitrary sparse relations, from any symmetric encryption scheme that satisfies some natural structural properties, and in addition guarantees that key recovery attacks mounted by polynomial-time adversaries have only exponentially small success probability - even in the context of key-dependent messages (KDM). We then provide parameter settings where ElGamal encryption and Regev encryption plausibly satisfy the needed properties. Our techniques are based on those of Kalai et al., with the main contribution being substituting a statistical argument for the use of obfuscation, therefore greatly simplifying the construction and basing security on better-understood intractability assumptions.

In addition, we extend the definition of correlation intractability to handle moderately sparse relations so as to capture the properties required in proof-of-work applications (e.g. Bitcoin). We also discuss the applicability of our constructions and analyses in that regime.

The full version [25] is available at https://eprint.iacr.org/2018/131.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The random oracle methodology [12, 39] models cryptographic hash functions as completely random functions. The model yields simple constructions of cryptographic primitives both in theory and practice, but is known to be inherently unsound in principle [26, 32, 44, 51, 68]. A natural alternative is to formalize concrete “random-oracle-like” properties of hash functions, and then (a) construct hash functions that provably demonstrate these properties based on established hardness assumptions, and (b) show how security of applications follow from these properties. Indeed, a number of such notions have been proposed and used in the literature, with multiple applications e.g. [10, 11, 18, 23, 26, 29, 47, 52, 57].

Correlation intractability. We focus on one of such notion called correlation intractability, defined by Canetti et al. [26]. Correlation intractability attempts to capture the following property of random functions. Consider a random function O from $\{0,1\}^n$ to $\{0,1\}^m$, along with some fixed binary relation $R:\{0,1\}^n\times \{0,1\}^m\rightarrow \{0,1\}$ such that for any $x\in \{0,1\}^n$, the fraction of $y\in \{0,1\}^m$ such that R(x, y) holds is at most $\mu$. Then, the best possible way to find x such that R(x, O(x)) holds is to randomly try different x’s. The probability of success after t attempts is at most $t\mu$. A function family is correlation intractable (CI) if it behaves similarly against polytime algorithms. Specifically, a function family H is correlation intractable if, for any relation R with negligible density $\mu$, no polytime adversary can, given the description of a function $h:\{0,1\}^n\rightarrow \{0,1\}^m$ chosen randomly from H, find x such that R(x, h(x)) holds, except with negligible probability. Note that there are no secrets here: The adversary sees the entire description of h, which succinctly encodes the values h(x) for all possible values of x.

Correlation intractability captures a large class of natural properties of random functions. For example, the infeasibility of finding preimages of any fixed value c in the range can be formalized as correlation intractability w.r.t. any constant relations $R_c = \{ (x, c)~|~\forall x \text { in the domain} \}$. The “fixed output value” in the example can be extended to “a sufficiently long fixed prefix”, e.g. sufficiently many leading 0s. Indeed, correlation intractability (in its quantitative form) is the natural formalization of the requirements expected from the hash function used for mining chaining values in the Bitcoin protocol [66] and other applications relied on proof-of-work [35]. We further discuss these application later on.

Another natural and prominent application of correlation intractable hash functions is their use for sound realization of the Fiat-Shamir (FS) heuristic [39]. Recall that, originally, the idea of Fiat and Shamir was to transform a three-message, public coin identification scheme to a signature scheme by having the signer first generate the first prover message $\alpha$ of the identification scheme (incorporating the message-to-be-signed in the identity), then computing the verifier message as $\beta =h(\alpha )$ for some public hash function h, and then having the signature consist of $(\alpha ,\gamma )$, where $\gamma$ is the corresponding third message of the identification scheme. Verification first reconstructs $\beta =h(\alpha )$ and then verifies the identification. It can be seen that if h is modeled as a random function, then the resulting signature scheme is unforgeable [1]. In fact, the same transform can be used to build a non-interactive argument from any public-coin interactive proof (even multi-round ones), as long as the initial proof is resettably sound (see e.g. [13]).¹ Furthermore, if the original proof is honest-verifier zero-knowledge, then the resulting non-interactive protocol (in the random oracle model) is a non-interactive zero-knowledge argument [12, 39].

It has been demonstrated that CI families that withstand arbitrary binary relations suffice for realizing the Fiat-Shamir heuristic in the case of constant-round proofs. That is, if the initial interactive proof is constant-round and is statistically sound, then computational soundness of the resulting non-interactive protocol holds even when the random oracle is replaced by a CI hash function family that withstands arbitrary binary relations (the only difference from the original Fiat-Shamir heuristic is that now the resulting protocol has an initial verifier message that determines the actual function h in the CI family.) Indeed, CI families that withstand arbitrary binary relations are entropy preserving [24], and entropy preserving families suffice for the soundness of the Fiat-Shamir heuristic for constant-round proofs [10]. A direct proof is also implicit in [59, Sect. 4]. (We note that soundness for the case of three-message proofs was observed already in [36, 49].)

Constructing correlation intractable hash functions. Canetti et al. [26] show that there do not exist CI function families where the key is shorter than the input, but leave open the possibility of CI functions with longer keys. Still no construction of CI functions, even for restricted cases, was known until very recently. Furthermore, over the years evidence accumulated that coming up with CI functions, and in particular a sound instantiation of the FS paradigm, would not be easy. Goldwasser and Kalai [44] construct a public coin interactive argument (i.e. a protocol that is only computationally sound) that becomes unsound if it is turned into an non-interactive argument by applying the Fiat-Shamir transformation with any function. Bitansky et al. show that it is impossible to prove soundness of the FS paradigm using a black-box reduction to falsifiable assumptions [14].

Recently, two papers independently suggested using an obfuscated puncturable pseudorandom function family as a CI family. Canetti et al. [24] show that this construction is CI for relations that are computable by circuits of a priori bounded polynomial size, assuming sub-exponentially secure puncturable pseudorandom functions and indistinguishability obfuscation, and in addition, input hiding obfuscation for evasive functions. Kalai et al. [59] show that the same construction is CI for arbitrary relations, assuming sub-exponentially secure puncturable pseudorandom functions and indistinguishability obfuscation, plus exponentially secure point obfuscation. In particular, the latter result implies that this function family suffices for sound realization of the Fiat-Shamir heuristic (when applied to constant-round interactive proofs).

1.1 Our Results

We provide new constructions of CI function families for arbitrary binary relations. Compared to [24, 59], our constructions are dramatically more efficient, and are based on better-understood assumptions. Furthermore, while sampling a hash function from the family of obfuscated puncturable PRFs involves secret randomness, we present candidates where the sampling can be done with only public randomness.

The main tool (or, abstraction) we use is symmetric encryption with the following two properties: First, the scheme should guarantee that polynomial time key-recovery attacks have only exponentially small success probability even after seeing encryptions of key-dependent messages (KDM). That is, for any super-polynomial function s, for an arbitrary key-dependency function f (not necessarily computable in polynomial time), any polynomial time adversary that obtains $c=\mathsf {Enc}(k,f(k))$ outputs k with probability no more than $\frac{s(\lambda )}{ 2^{\lambda }}$, where $\lambda$ is the key length.

The second property, which we refer to as universal ciphertexts, is statistical. Loosely speaking, it requires that any ciphertext is “decryptable” under any key. More precisely, the requirement is that (a) for every key, random ciphertexts decrypt to random messages; (b) for every key k and message m, the encryption algorithm generates ciphertexts that are uniformly sampled from the space of ciphertexts that are decrypted to m with key k. (The actual definition includes also public parameters, which are omitted here for simplicity.) Given an encryption scheme that satisfies the above requirements, we obtain the following result:

Theorem 1

(Informally stated). Assuming the existence of encryption schemes that have universal ciphertexts and that are exponentially KDM-secure against polytime key-recovery attacks, there exist:

• Correlation intractable hash functions for arbitrary binary sparse relations.

• Hash functions that guarantee soundness of the Fiat-Shamir transformation, when applied to interactive proof-systems.

• Non-interactive, publicly verifiable arguments for all languages computable in polynomial-time and bounded polynomial space (in particular, the class $\mathsf {SC}$).

The last bullet follows by applying the Fiat-Shamir transformation to the recent public-coin, constant-round interactive proof-system of Reingold et al. [74].

Our second main contribution is in providing concrete instantiations of Theorem 1. Specifically, we show that variants of El-Gamal encryption [37] and Regev encryption [72] satisfy the universal ciphertext property and plausibly satisfy the foregoing exponential security against KDM key recovery.

Non-interactive zero-knowledge. As an additional result, we show that if the Fiat-Shamir transformation is applied to a three-round honest-verifier zero-knowledge proof, and the CI function family in use is programmable, then the resulting protocol is a Non-Interactive Zero-Knowledge ($\textsf {NIZK}$) argument, with the description of the hash function serving as a common reference string. (Here programmability means that, given random values a, b from the family’s domain and range, respectively, it is possible to efficiently sample a random function h from the family such that $h(a)=b$.) We also observe that the CI functions we construct are programmable. Furthermore, if the initial three-round protocol is delayed-input (as in, e.g., [38]), then the resulting NIZK argument is both adaptive ZK and adaptively sound. We thus have:

Theorem 2

(Informally stated). Assuming the existence of encryption schemes that have universal ciphertexts and that are exponentially KDM-secure against polytime key-recovery attacks, there exist $\textsf {NIZK}$ arguments for all of $\mathsf {NP}$. Furthermore, these $\textsf {NIZK}$s have adaptive soundness and zero-knowledge.

We note that, prior to this work, $\textsf {NIZK}$ arguments for $\mathsf {NP}$ were not known based on any variant of the Diffie-Hellman assumption in groups that do not admit bilinear pairings, nor any variant of the $\mathsf {LWE}$ assumption—even exponentially strong ones. Also, for the $\textsf {NIZK}$ application we only need the CI family to withstand relations that are exponentially sparse, which somewhat relaxes the assumption. For example, if the soundness of the interactive proof system is $2^{-\lambda ^\epsilon }$, then we can tolerate encryption schemes where the success probability of polytime key-recovery attack is $\frac{\text {superpoly}(\lambda )}{ 2^{\lambda - \lambda ^\epsilon }}$.

Quantitative correlation intractability and its connection to the Bitcoin protocol. A central component in the Bitcoin protocol [66] is a probabilistic mechanism for guaranteeing that the amount of influence participants have on the process of producing the public ledger is proportional to their computing power. The idea here is that since each individual entity has only a fraction of the overall computing power, the influence of each entity is limited. Indeed, the core validity of the currency (i.e., the mechanism for preventing double spending) hinges upon that guarantee.

The Bitcoin mechanism for limiting influence was sketched earlier in the introduction: In order to incorporate a block of new transactions in the public registry, the individual (“miner”) is asked to present a value x such that the pair (x, h(x)) satisfies some known relation $R_w$, where h is a hash function defined by the protocol, and w is determined by the current state of the system, the new block, and the miner’s identity. $R_w$ is set so that it is “moderately sparse”. That is, for any x, w the fraction of values y such that $R_w(x,y)$ holds is small, but not too small.

Clearly, if h were a random function then this mechanism would work well: Given w, the best way to find x such that $R_w(x,h(x))$ holds is to keep guessing random x’s until one is found. This means that the probability of success is proportional to the number of guesses, which is correlated to the computational power of the miner. However, when h is an explicit function with a succinct description, it is not clear how to provide rigorous guarantees regarding the amount of time needed to find a “wining x” given w. Indeed, “shortcut attacks” on the Bitcoin mechanism have been reported, e.g. [53].

We argue that correlation intractability, or more precisely a quantitative variant of the notion, captures the properties needed from the underlying hash function so as to guarantee the soundness of the Bitcoin mechanism for limiting influence. Specifically, say that a binary relation $R:\{0,1\}^n\times \{0,1\}^m\rightarrow \{0,1\}$ is $\mu$-sparse if for any $x\in \{0,1\}^n$, the fraction of $y\in \{0,1\}^m$ such that R(x, y) holds is at most $\mu$. A family H of functions $h:\{0,1\}^n\rightarrow \{0,1\}^m$ is f -correlation intractable if for any binary $\mu$-sparse relation R and for any adversary Adv that runs in time t, the probability that Adv, given a random function h in H, outputs x such that R(x, h(x)) holds is at most $f(t,\mu )$. The smaller f grows the better the guarantee. Clearly we must have $f(t,\mu )\ge t\mu$. A good “fudge function” f will not grow much faster than that.

It should also be stressed that the quantitative correlation intractability, as presented here, only bounds the success probability in solving a single challenge. Asserting the overall stability of the protocol would require bounding the aggregate success probability over multiple related challenges. Formalizing a set of properties for concrete, non-idealized hash functions, that would suffice for the security of Bitcoin-like applications, as well as proposing constructions with rigorous analyses is a fascinating research direction.

1.2 Our Techniques

The construction of our CI hash function is simple. Let $(\mathsf {Enc}, \mathsf {Dec})$ be an encryption scheme with key space K, message space M and ciphertext space C. The constructed hash function family $H=\{h_c\}_{c\in C}$, where $h_c:K\rightarrow M$, is defined by $h_c(k)=\mathsf {Dec}_k(c)$. That is, a function $h_c$ in the family is defined via a ciphertext $c\in C$. Given an input k, the function $h_c$ decrypts c using key k and returns the decrypted plaintext.

In general, key generation (i.e., choosing a random $c\in C$) is done by encrypting a random message with a random key. We note however that for both of our specific candidates, choosing a random ciphertext can be done obliviously and publicly without any secret randomness.

A high level rationale for the construction may be the following: Consider a ciphertext $c=\mathsf {Enc}(k,m)$ where both k and m are random. If the encryption scheme is good, then it should be guaranteed that, when trying to decrypt c with any key $k'\ne k$, then the result should be completely “random looking”. Intuitively, this means that finding a key $k'$ such that $\mathsf {Dec}(k',c)=m'$ for some target $m'$ should be hard. The universal ciphertexts property guarantees that a random ciphertext looks like the result of encrypting a random message with a random key. KDM security guarantees that the above intuition applies even when considering relations that look at both the key and the corresponding message together (as is indeed the case for correlation intractability).

Indeed, the crux of the proof is in translating correlation intractability, which is a requirement on the (in)ability of polynomial time adversaries to find structure in a succinctly represented public function (namely the decryption algorithm along with a random ciphertext), to a secrecy requirement on the corresponding encryption process.

The actual proof is strongly inspired by that of [59]. In fact, we follow essentially the same sequence of logical steps. However, the argumentation used to move from one step to the next is different in some key places. Specifically, our goal is to turn an adversary A that breaks correlation intractability of the hash function into an adversary that breaks KDM security of the underlying encryption scheme. Following [59], we start by considering a conditional experiment where we fix some random value $k^*$, and consider only the probability that A, given the hash key c, outputs a key k such that the correlation $R(k, \mathsf {Dec}(k,c))$ holds, and in addition $k=k^*$. While this probability is very small, it allows us to move (with some loss) to a different experiment where the value c that A sees is the result of encrypting $f(k^*)$ with key $k^*$, where f is a function related to R. We now observe that recovering the right $k^*$ corresponds to breaking the KDM security of the scheme.

As in [59], the price of this analytical approach is an exponential loss in security against guessing attacks. On the other hand, in the case of the [59] scheme and analysis, the critical switch from one conditional experiment to another relies on sub-exponentially secure indistinguishability obfuscation. Here, in contrast, the move is purely statistical.

1.3 A Closer Look at the Hardness Assumptions

We sketch the assumptions we use and briefly discuss their plausibility.

The scheme based on ElGamal encryption. We first consider the ElGamal based scheme. For simplicity, we discuss a restricted case where both the key and the message are represented by group elements. (See Sect. 6 for a more general construction and the associated assumption.) Assuming there exists a family of groups $\mathbb {G}(\lambda )$ of sizes $N(\lambda )\approx 2^\lambda$, with a generator g and efficient group operations, such that for any super-polynomial function s, any (not necessarily efficiently computable) function $f: [N]\rightarrow [N]$, and any polynomial time adversary A:

$$ \mathop {\Pr }\limits _{k,a\leftarrow [N]} \left[ A \left( g^{a},g^{ak+f(k)} \right) =k \right] \le \frac{s(\lambda )}{2^\lambda } $$

We discuss the plausibility of this assumption. For the discrete-log problem over $\mathbb {F}^*_q$, there are well-known sub-exponential time algorithms with constant success probability [2, 30]. However, a $2^t$-time algorithm with constant success probability does not necessary imply a polynomial time algorithms with success probability $2^{-t}$. For example, Pollard’s rho algorithm [70] runs in time $O(2^{\lambda /2})$ and achieves constant success probability. But its polynomial time version only gives polynomial advantage over simply guessing. In fact, Shoup [77] shows that any generic algorithm (like Pollard’s rho algorithm) cannot achieve success probability better than $O(T^2/2^{\lambda })$ if it only makes T oracle queries.

However, the index-calculus algorithm does achieve a $2^{-\lambda /c}$ success probability if it is allowed to have a super-polynomial preprocessing phase, keep advices of polynomial size, and run a polynomial time online phase. We leave the algorithm and analysis in Appendix A. Although it is not a complete polynomial time algorithm (i.e. without a super-polynomial preprocessing phase) with non-trivial success probability, it suggests that the extra structure of the group $\mathbb {F}_q^*$ can be utilized even if the algorithm is restricted in polynomial time in a meaningful model.

Still, the above assumption is plausible for the discrete-log problem over elliptic curve groups (ECDLP), especially for those defined over prime fields. Over decades, ECDLP algorithms only out-perform generic algorithms for specific families of curves (e.g. [42, 63]). Useful factor bases for index calculus algorithms were not known for the elliptic curve groups, until the work of Semaev [76] which proposes the use of summation polynomials, later developed by Gaudry [41] and Diem [31]. But so far they are only known to out-perform Pollard’s rho algorithm for elliptic curve groups defined over $\mathbb {F}_{q^n}$ when certain relations of q and n hold. For elliptic curve groups defined over prime fields, the recent attempts by [69] and others provide plausible factor bases. Still, no algorithms are known to achieve non-negligible success probability with less than $O(2^{\lambda /2})$ running time. See [40] for a survey of the recent progress on ECDLP.

To conclude, based on the current understanding ECDLP for curves defined over prime fields, polytime algorithms that perform super-polynomially better than guessing appear to be out of reach. In particular, any such algorithm must exploit more structures in the elliptic curve groups than in generic groups [77].

The scheme based on Regev encryption. Consider the Regev scheme [73] with an even polynomial modulus $q(\lambda )\in \mathsf {poly}(\lambda )$, and key space $\{ 0, ..., B-1 \} ^{\ell }$ where $B^{\ell } \in [2^{\lambda -\log (\lambda )}, 2^{\lambda +\log (\lambda )}]$ and $B\le q$. The message space is $\{0,1\}^w$ where $w(\lambda )\in \mathsf {poly}(\lambda )$. For the security of this scheme we make the following assumption: for any (not necessarily efficiently computable) function $f: \{ 0, ..., B-1 \} ^{\ell }\rightarrow \{0,1\}^w$, any super-polynomial function s, and any polynomial time adversary A:

where $f_j( \mathbf {k} )$ denotes the $j^{th}$ bit of $f( \mathbf {k} )$.

Note that super-polynomial algorithms that break LWE with constant success probability are known (e.g. [8, 16, 60, 61, 75], see the analyses and surveys of [4, 55, 62, 65, 67]). Still, within this setting of parameters, especially given a polynomial size modulus q and high noise magnitude q / 2, we are not aware of any polynomial time algorithms that succeed in guessing the key super-polynomially better than a random guess.

Possible relaxations on the assumptions of success probability. The restriction on the success probability (smaller than $\frac{s(\lambda )}{2^\lambda }$ for any super-polynomial s) mentioned in the foregoing paragraphs suffices for implying correlation intractability for all negligible sparse relations under any given input and output length parameters. We note that even if there are polynomial time algorithms that achieve better success probability for these problems, our result may still apply to correlation intractability for certain classes of relations. For example, if a polynomial time algorithm were found for LWE that succeeds with probability $2^{-\lambda /3}$, then the Regev-based hash function may still be secure for Fiat-Shamir transformation applied on a 3-round proof system where the length of the first message is $\lambda$, the length of the second message is $2\lambda /3$, and the soundness of the protocol is $2^{-2\lambda /3}$.

On the quantitative hardness of our assumptions. One may wonder if the ElGamal or Regev-like hash functions were used for proof-of-work, what are the precise bounds of the “fudge function” f we can guarantee. For the ElGamal-based function, as we mentioned before, the Pollard’s rho algorithm achieves success probability $O(T^2/2^{\lambda })$ in T steps for any group of size $\approx 2^{\lambda }$. So the smallest possible f is $O(T^2 \cdot \mu )$, which is far from the dream bound $T\cdot \mu$. For LWE, when T is relatively small (say a small polynomial), the success probabilities of LWE solvers are typically tiny and less studied, so the precise bound is unclear to us. We leave to future work any additional quantitative analysis of the possible values for f for the concrete functions.

1.4 Additional Related Works

Notions related to Fiat-Shamir paradigm. Hada, Tanaka [49] and Dwork et al. [36] show that the existence of correlation intractable functions implies the soundness of Fiat-Shamir paradigm for proofs, which in turn rules out the possibility of constant-round public-coin zero-knowledge proofs for languages beyond $\mathsf {BPP}$. This means that, assuming KDM-secure encryption as defined above, there do not exist constant-round public-coin zero-knowledge protocols with negligible soundness error for languages beyond $\mathsf {BPP}$.

Among the attempts to better capture the property of a hash function suitable for the Fiat-Shamir paradigm, Barak et al. define entropy-preserving hashing and show it is sufficient for Fiat-Shamir [10]. Dodis et al. then provide a property of condensers that is necessary for entropy-preserving hashing [33]. It is shown by Canetti et al. that entropy-preservation is implied by correlation intractability w.r.t. sparse relations whose memberships are not efficiently checkable [24].

A different way of reducing rounds in interactive proofs was shown by Kalai and Raz [58]. However, in contrast to the Fiat-Shamir paradigm, the Kalai-Raz transform inherently yields a private-coin argument-system (and in particular does not yield $\textsf {NIZK}$ proof-systems).

Background on KDM. The potential security risk of encrypting one’s own key was noted already in the seminal work of Goldwasser and Micali [45]. Potential applications and suitable formalizations were provided by Camenisch and Lysyanskaya [22] and Black, Rogaway and Shrimpton [15]. More recently, Gentry’s breakthrough construction of fully homomorphic encryption also utilizes KDM security in a fundamental way for the “bootstrapping” process (transforming somewhat homomorphic schemes to fully homomorphic ones) [43].

Encryption schemes that are KDM secure² with respect to the class of affine functions were constructed by Boneh et al. [19], Applebaum et al. [6] and Brakerski and Goldwasser [20]. Using techniques developed in [5, 9, 21] the foregoing schemes can be amplified to provide security for the class of KDM functions computable by polynomial-size circuits. Canetti et al. [28] construct strong KDM-secure encryption from multi-bit point obfuscation. However, their construction inherently does not have the universal ciphertexts property. We also note that fully-homomorphic encryption schemes that are KDM secure w.r.t. the identity function are automatically KDM secure for arbitrary polynomial functions [9]. However achieving KDM secure FHE w.r.t. the identity function from standard assumptions is an open problem.

Haitner and Holenstein [50] showed limitations to the possibility of constructing KDM secure encryption schemes via blackbox techniques. They first show that there is no fully blackbox reduction from the KDM security of an encryption scheme (with respect to a certain class of functions) to the existence of one-way permutations. More relevant for us is their second result, which shows that there is no reduction from the KDM security of an encryption scheme to “essentially any cryptographic assumption” if the adversary can obtain an encryption of an arbitrary function g of the key, and the reduction treats both the adversary and the function g as black boxes. A significant difference from our notion of KDM security with respect to all functions is that [50] assume that the adversary also obtains oracle access to the function g, which is not the case in our setting. Namely, we only provide the adversary with an encryption of g(k), where k is the key, but no additional access to g. Indeed, the oracle constructed by Haitner and Holenstein becomes useless in this setting.

The works of Halevi, Krawczyk [51] and Hofheinz, Unruh [56] construct several variants of KDM symmetric encryption assuming only pseudorandom functions. However these schemes don’t achieve the level of security we require (exponentially small probability of key-recovery) and we were unable to extend them to schemes that do.

Relation to Extremely Lossy Functions (ELFs). Our work bears a high-level similarity to the work of Zhandry [79] in terms of the motivation, constructions and assumptions. However, the actual contributions are very different.

In terms of the motivation, both papers attempt to capture the properties of random oracles. Our paper focuses on correlation intractability and its implication to Fiat-Shamir, whereas [79] defines the notion of k-ary output-intractability, where the relation checks k output values and an additional auxiliary input w. Indeed, as was mentioned in [79], k-ary output-intractability roughly corresponds to a special case of k-ary correlation intractability (namely, correlation intractability where the relation R takes k pairs of values (x, y).) However, k-ary output-intractability is interesting only for $k>1$. For $k=1$, output intractability is trivially satisfiable. In contrast, in this work we concentrate on correlation intractability with $k=1$.

In terms of constructions and assumptions, both papers make exponential hardness assumptions on discrete-log or DDH type problems. However the precise ways of making the assumptions are different. [79] assumes that for DDH over group size $B(\lambda )\approx 2^{\lambda }$, the best attack takes time $B(\lambda )^c$ for some constant c. Whereas we assume (modulo KDM) that all the polynomial time algorithm solves discrete-log problem with success probability less than $\frac{\text {superpoly}(\lambda )}{ B(\lambda ) }$.

1.5 Organization

In Sect. 2 we provide standard notations and definitions that will be used throughout this work. In Sect. 3 we give an overview of our construction, focusing on the discrete-log based construction as a warm-up. In Sect. 4 we formally define our notion of “universal ciphertexts” and strong KDM security. In Sect. 5 we show how to use encryption schemes satisfying the foregoing properties to construct correlation intractable functions. In Sect. 6 we describe parameter settings where the variants of ElGamal and Regev encryption schemes plausibly satisfy these properties. Finally, in Sect. 7 we show how to construct $\textsf {NIZK}$s for NP from our correlation intractable functions.

2 Preliminaries

Notations and terminology. Denote $\mathbb {R}$, $\mathbb {Z}$, $\mathbb {N}$ as the set of reals, integers and natural numbers. Let $\mathbb {Z}_q$ denote $\mathbb {Z}/(q\mathbb {Z})$. For $n\in \mathbb {N}$, let [n] denote $\{ 1, 2, ..., n \}$. The rounding operation $\left\lfloor a \right\rceil :\mathbb {Z}_q \rightarrow \mathbb {Z}_p$ is defined as multiplying a by p / q and rounding the result to the nearest integer.

In cryptography, the security parameter (denoted as $\lambda$) is a variable that is used to parameterize the computational complexity of the cryptographic algorithm or protocol, and the adversary’s probability of breaking security. An algorithm is “efficient” if it runs in (probabilistic) polynomial time over $\lambda$.

For any definition based on computational hardness, we refer the relevant security level to the success probability of any efficient adversary. For example, a security notion is subexponential if for every efficient adversary there exists $\epsilon >0$ such that the adversary’s advantage is less or equal to $2^{-\lambda ^\epsilon }$.

Many experiments and probability statements in this paper contain randomized algorithms. When a variable v is drawn uniformly random from the set S we denote as $v{\in _R}S$ or $v\leftarrow U(S)$, sometimes abbreviated as v when the context is clear. Distributions written in multiple lines under $\Pr$ means they are sampled in sequence.

A function ensemble $\mathcal {F}$ has a key generation function $g: \mathcal {S} \rightarrow \mathcal {K}$; on a seed $s\in \mathcal {S}(\lambda )$, g produces a key $k\in \mathcal {K}(\lambda )$ for a function with domain $\mathcal {D}(\lambda )$ and range $\mathcal {C}(\lambda )$:

$$ \mathcal {F} = \{ f_k: \mathcal {D}(\lambda ) \rightarrow \mathcal {C}(\lambda ), k = g(s), s\in \mathcal {S}(\lambda ) \}_{\lambda \in \mathbb {N}} $$

The bit-lengths of the seed, key, input and output are denoted as $\sigma$, $\kappa$, $\ell$ and w, unless specified otherwise.

The main object studied in this article is families of public key hash functions. We assume the key k is public. For certain key generation algorithm g, publishing k implies publishing s (e.g. when g is the identity function). We call such functions public-coin. By default we treat the bit-length of its input as being equal to the security parameter, i.e. $|\mathcal {D}(\lambda )| = 2^\lambda$.

2.1 Correlation Intractability

We recall the definition of correlation intractability [27].

Definition 1

(Density of a binary relations). A binary relation $R = R(\lambda ) \subseteq \{ ~(x, y) ~|~ x \in \mathcal {D}(\lambda ), y\in \mathcal {C}(\lambda ) ~ \}$ has density $\mu = \mu (\lambda )$ if for every $x \in \mathcal {D}(\lambda )$ it holds that $\Pr _{y\in \mathcal {C}(\lambda )}[~ (x,y)\in R(\lambda ) ~] < \mu (\lambda )$. A relation R is sparse if it has negligible density.

Definition 2

(Correlation intractability w.r.t. binary sparse relations [27]). A family of functions $\mathcal {H}= \{ H_k: \mathcal {D}(\lambda ) \rightarrow \mathcal {C}(\lambda ) \}_{\lambda \in \mathbb {N}}$ is correlation intractable w.r.t. binary sparse relations if for every polynomial-size adversary A and every sparse relation R, there is a negligible function $\mathsf {negl}(\cdot )$ such that:

We introduce a quantitative generalization of correlation intractability.

Definition 3

(f-correlation intractability). A family of functions $\mathcal {H}= \{ H_k: \mathcal {D}(\lambda ) \rightarrow \mathcal {C}(\lambda ) \}_{\lambda \in \mathbb {N}}$ is f-correlation intractable w.r.t. a function $f: \mathbb {N}\times [0,1] \rightarrow [0,1]$ if for all time function $T(\cdot )$, for all density function $\mu (\cdot )$, for every adversary A of running time $T(\lambda )$, and every relation R with density $\mu (\lambda )$, it holds that

For example, random oracles satisfy f-correlation intractability for $f(T, \mu ) = T \cdot \mu$. Definition 2 can be viewed as f-correlation intractability w.r.t. $f(T, \mu ) = T \cdot \mu$, for all polynomial $T(\cdot )$, and all negligible $\mu (\cdot )$. In the rest of the paper, “correlation intractability” refers to Definition 2 unless explicitly stated otherwise.

Survey of impossible parameters for correlation intractability. For some parameters relevant to the length of seed, key, input and output of the function, correlation intractability w.r.t. binary sparse relations is impossible to achieve. We survey some of the results.

[27] shows that a function family cannot be correlation intractable when the bit-length of the key $\kappa (\lambda )$ of the function is short compared to the bit-length of the input $\ell (\lambda )$:

Claim 1

([27]). $\mathcal {H}_\lambda$ is not correlation intractable w.r.t. efficiently checkable relations when $\kappa (\lambda )\le \ell (\lambda )$.

Proof

Consider the diagonalization relation $R_{\mathsf {diag}} = \{(k, h_k(k))| k\in \mathcal {K}(\lambda ) \}$. The attacker outputs k.   $\square$

The impossibility result generalizes to keys that are slightly larger than the bit-length of the input, but still smaller than the sum of the bit-length of input plus output $\ell (\lambda )+w(\lambda )$. The idea is to consider an extension of the diagonalization relation s.t. the relation checks a prefix of k—as long as the key is not too long, the relation is still sparse, albeit not necessarily efficient checkable.

Claim 2

([27]). $\mathcal {H}_\lambda$ is not correlation intractable w.r.t. possibly inefficiently checkable relations when $\kappa (\lambda )\le \ell (\lambda )+w(\lambda ) - \omega (\log (\lambda ))$.

We also observe when the “family size” of the function is relatively small, precisely, when the seed length is small w.r.t. the output length, then the function family is not correlation intractable w.r.t. possibly inefficiently checkable relations. This case is not ruled out by Claim 2 when the key is potentially long but derived from a short seed (e.g. from applying a PRG on a short seed).

Claim 3

$\mathcal {H}_\lambda$ is not correlation intractable when the seed space $\mathcal {S}(\lambda )$ and the range $\mathcal {C}(\lambda )$ satisfies $|\mathcal {S}(\lambda )|\le \mathsf {negl}(\lambda )\cdot |\mathcal {C}(\lambda )|$.

Proof

Fix the hash function family $\mathcal {H}_\lambda$, consider the relation $R_{\mathcal {H}}$ that collects every functions in the function family $R_\mathcal {H}= \{(x, h_k(x))~|~ s\in \mathcal {S}, ~ k=g(s), ~ x\in \mathcal {D}(\lambda ) \}$. The density of the relation less or equal to $|\mathcal {S}(\lambda ) |/ |\mathcal {C}(\lambda )|\le \mathsf {negl}(\lambda )$. The attacker simply outputs any input.   $\square$

For the discussions of the other impossibility results, we refer the readers to [27] for the details.

2.2 Fiat-Shamir Heuristics

Definition 4

(Interactive proof-systems [46]). An interactive proof-system for a language L is a protocol between a prover P and a verifier V. The prover’s runtime is unbounded. The verifier runs in probabilistic polynomial time. The protocol satisfies

• $\mathbf {Completeness}$: For every $x\in L$, the verifier V accepts with probability 1 after interacting with P on common input x.

• $\mathbf {Soundness}$: For every $x\notin L$ and every cheating prover $P^*$, the verifier accepts with negligible probability after interacting with $P^*$ on common input x.

An interactive protocol is called an argument-system if it satisfies Definition 4 except that the prover is restricted to run in (non-uniform) polynomial time. An interactive proof or argument is called public-coin if the verifier’s messages are random coins.

Correlation intractability and public-coin interactive proofs. Consider a language L and a 3-round public-coin interactive proof $\varPi$ for L. Let $\alpha ,\beta ,\gamma$ be the 3 messages in the protocol ($\alpha$ and $\gamma$ are sent by the prover P, $\beta$ is sent by the verifier V). The relation $R_{\notin L, \varPi }$ is defined by

$$\begin{aligned} R_{\notin L, \varPi } = \left\{ \big ( (x,\alpha ), \beta ) \;:\; x \notin L \text { and } \exists \gamma \text { s.t. } V(x, \alpha ,\beta ,\gamma ) = \mathsf {Accept} \right\} . \end{aligned}$$

(1)

Observe that the relation $R_{\notin L, \varPi }$ is sparse due to the statistical soundness of the underlying proof, i.e. the density of $R_{\notin L, \varPi }$ is equal to the soundness error of $\varPi$.

Interestingly, correlation intractability can also capture a stronger notion of soundness called adaptive soundness. We say that a 3 message interactive proof-system as above has adaptive soundness, if the message $\alpha$ sent by the honest prover does not depend on x, and soundness is guaranteed even if the adversary may choose the input $x \not \in L$ on which to cheat after seeing $\beta$. For such protocols we define the relation $R_{\notin L, \varPi }$ as

$$\begin{aligned} R_{\notin L, \varPi } = \left\{ \big ( \alpha , \beta \big ) \;:\; \exists x,\gamma \text { s.t. } x \notin L \wedge V(x, \alpha ,\beta ,\gamma ) = \mathsf {Accept} \right\} \end{aligned}$$

(2)

Again, the relation $R_{\notin L, \varPi }$ is sparse due to the adaptive soundness of $\varPi$.

Correlation intractability also implies the soundness of Fiat-Shamir for general constant-round public-coin interactive proof-systems. Without loss of generality assuming the number of rounds in the starting proof-system is 2c for a constant c. In the resulting 2-message argument, the verifier samples c independent correlation intractable hash functions. For $i\in \{ 1, 2, ..., c \}$, the prover applies the $i^{th}$ hash function on $(\alpha _1||\beta _1||...||\alpha _{i-1}||\beta _{i-1}||\alpha _i)$ to generate $\beta _i$, where $\alpha _i$ is the $i^{th}$ message from the prover in the starting proof-system. The message from the prover in the resulting 2-message argument is then $(\alpha _1||\beta _1||...||\alpha _{c}||\beta _{c})$.

It is shown that the transformation above yields a sound 2-message argument if the hash functions are entropy preserving [10]. Given that CI families that withstand arbitrary binary relations are entropy preserving [24], we have

Lemma 1

([10, 24, 36, 49]). Assuming correlation intractable function family w.r.t. all binary sparse relations exists, then the Fiat-Shamir transformation is sound when applied on any constant-round public-coin interactive proof-systems.

3 A Warm-Up Construction from Discrete Logarithm

We present a simple construction based on the discrete-log program as a warm-up to the general scheme. Along the way we will give the rationale of the proof strategy adapted from the work of Kalai et al. [59], and explain the level of KDM security we need for the underlying discrete-log problem.

Let $\mathbb {G}$ be a cyclic group where the discrete-log problem is hard. Assume the size of $\mathbb {G}$ is roughly $2^\lambda$ where $\lambda$ is the security parameter. Let g be a generator of $\mathbb {G}$, $A = g^a, B = g^b$ be two random elements in $\mathbb {G}$. Consider the following length preserving function $H: \{ 1, ..., |\mathbb {G}| \} \rightarrow \mathbb {G}$

$$\begin{aligned} H_{A, B}(x):= A^x \cdot B = g^{ax+b} \in \mathbb {G}. \end{aligned}$$

(3)

Theorem 4

Given $\mathbb {G}(\lambda )$ of sizes $N(\lambda )\approx 2^\lambda$, with a generator g and efficient group operations, such that for any super-polynomial function s, any (not necessarily efficiently computable) function $f: [N]\rightarrow [N]$, and any polynomial time adversary A:

$$ \mathop {\Pr }\limits _{k,a\leftarrow [N]} \left[ A \left( g^{a},g^{ak+f(k)} \right) =k \right] \le \frac{s(\lambda )}{2^\lambda }. $$

Then $H_{A, B}$ is correlation intractable w.r.t. all sparse relations.

Towards a contradiction, let R be any sparse relation with negligible density $\mu (\lambda )$. Suppose there exists an efficient adversary $\mathsf {Adv}$ that breaks correlation intractability w.r.t. R with non-negligible probability $\nu$:

$$\begin{aligned} \mathop {\Pr }\limits _{A, B} \Big [ \Big ( \mathsf {Adv}(H_{A, B}) \rightarrow x \Big ) \wedge \Big ( \big ( x, H_{A, B}(x) \big )\in R \Big ) \Big ]\ge \nu , \end{aligned}$$

(4)

where the notation $\mathsf {Adv}(H_{A, B}) \rightarrow x$ simply means that we use x to refer to the string that $\mathsf {Adv}(H_{A, B})$ outputs.

In the first step, we translate the probability of outputting some x to the probability of outputting a particular $x^*$. For a random $x^*$ from the domain, the probability that the adversary outputs $x^*$ as the answer is greater or equal to $\nu$ divided by the domain size

(5)

Focusing on a single $x^*$ costs a huge loss in the success probability. The readers may wonder what is the motivation of doing so. The purpose of fixing an input $x^*$ is to prepare for replacing the winning condition $\big ( x^*, H_{A, B}(x^*) \big )\in R$ by another condition that is “key independent”. Towards this goal, consider the following sampling procedure: first sample a random $y^*$ from the range, then sample the key $(A', B')$ randomly under the condition $H_{A',B'}(x^*) = y^*$. Now we use the fact that H is a “one-universal” function, which means that for a fixed input, a uniformly random key projects the input to a uniformly random output. In turn, a uniformly random output corresponds to a uniformly random key. Therefore the key $(A', B')$ obtained from reverse sampling distributes the same as before. Hence we have

(6)

Given that $y^* = H_{A', B'}(x^*)$, we can change the winning condition in Eq. (6) into one which is independent from the function $H_{A', B'}$:

(7)

Separating the winning condition $(x^*, y^*)\in R$ from the hash key paves the way for connecting correlation intractability to a property that is only about hiding one specific point in the key (instead of hiding a bunch of potential input-output pairs in the relation). In the next statement, the first equality follows by the definition of conditional probability. The inequality follows from Eq. (7) together with the fact that R is $\mu$ sparse:

(8)

The LHS of Eq. (8) spells out as an efficient adversary’s success probability of finding the input $x^*$ embedded in $A', B'$, where the key $A', B'$ is sampled conditioned on mapping some input-output pair in the relation $(x^*, y^*)\in R$. Let’s examine $A', B'$, and for simplicity consider only the constant relations $R_c = \{ (x, c)~|~\forall x\in \{0,1\}^\lambda \}$. Fix a $c^*\in \mathbb {G}$, a random input-output pair from $R_{c^*}$ distributes as $(x^*, c^*)$, where $x^*$ is uniformly random from $\{0,1\}^\lambda$. For $A' = g^{a'}$, $B = g^{b'}$ sampled randomly from the set $\{ g^{a'}, g^{b'} ~|~ g^{z^*} := c^* = g^{a' x^* +b'} \}$, where $z^*$ is explicitly defined as the discrete-log of $c^*$ over base g for the convenience of explanation. Observe that the marginal distribution of $a'$ is uniform, and $b'$ equals to $z^* - a' x^*$. In other words, the adversary is asked to find $x^*$ given $A' = g^{a'}$, $B' = g^{z^* - a' x^*}$ where $z^*$ is fixed. The hardness of this problem follows directly from the hardness of the discrete-log problem.

What is the hardness required for the underlying discrete-log problem in order to form a contradiction? For the probability in the hypothesis $\frac{\nu (\lambda )}{2^\lambda \cdot \mu (\lambda )}$, where $\nu$ is a non-negligible function; $\mu$, the density of a sparse relation, is an arbitrary negligible function. We can form a contradiction by assuming that every polynomial time algorithm for the discrete-log problem over $\mathbb {G}$ succeeds with probability less than $s(\lambda )/2^\lambda$ for any super-polynomial function s.

What happens when we consider all sparse relations instead of only the constant relations? For a general sparse relation, sampling a random pair $(x^*, y^*)$ from the relation may result into an output $y^*$ that is correlated to the input $x^*$. Take the “fixed point” relation $R_{x=y}:= \{ (x,y)~|~ x=y \}$ as an example. A random input-output pair from $R_{x=y}$ distributes as $(x^*, x^*)$, where $x^*$ is uniformly random. For $A' = g^{a'}$, $B = g^{b'}$ sampled randomly from the set $\{ g^{a'}, g^{b'} ~|~ g^{z^*(x^*)} := x^* = g^{a' x^* +b'} \}$, where $z^*(x^*)$ is the discrete-log of $x^*$ over base g (unlike in the previous example, now $z^*$ depends on the input $x^*$). The marginal distribution of $a'$ is still uniform, and $b'$ equals to $z^*(x^*) - a' x^*$. In other words, the adversary is asked to find $x^*$ given $A' = g^{a'}$, $B' = g^{z^*(x^*) - a' x^*}$ where $z^*(\cdot )$ is a function on $x^*$, $a'$ is independent from $x^*$ and uniform. The latter corresponds to the hardness of finding the decryption key $x^*$ given a ciphertext of ElGamal encryption with uniform randomness $a'$, and key-dependent message $z^*(x^*)$.

To summarize, the proof strategy translates the hardness of finding any solution in a sparse relation to the hardness of finding the key from the encryption of possibly key-dependent messages. The translation is purely statistical, but it results into a significant cost in the final computational assumption—the success probability for any polytime attacker has to be extremely small. To capture arbitrary relations, arbitrary key dependency functions are considered.

4 Encryption Scheme with Universal Ciphertext and KDM Security

Let $\mathcal {M} = \{ \mathcal {M}_\lambda \}_{\lambda \in \mathbb {N}}$ be an ensemble of message spaces (i.e., $\mathcal {M}_\lambda$ is the message space with respect to security parameter $\lambda \in \mathbb {N}$). An encryption scheme, with respect to the message space $\mathcal {M}$, consists of three probabilistic polynomial-time algorithm $\mathsf {PP\text {-}Gen}$, $\mathsf {Enc}$ and $\mathsf {Dec}$. The public-parameter generation algorithm $\mathsf {PP\text {-}Gen}$ gets as input $1^\lambda$ and outputs some public-parameters pp (without loss of generality we assume that pp contains $\lambda$). Given the public-parameters pp, a key $k \in \{0,1\}^\lambda$ and a message $m \in \mathcal {M}_\lambda$ the encryption algorithm $\mathsf {Enc}$ outputs a ciphertext c. The decryption algorithm $\mathsf {Dec}$ gets as input the public-parameters pp, a key k as well as a ciphertext c and outputs a message in $\mathcal {M}_\lambda$. We require that (with probability 1), for every setting of the public-parameters pp, message $m \in \mathcal {M}_\lambda$ and key $k \in \{0,1\}^\lambda$ it holds that $\mathsf {Dec}(pp,k,\mathsf {Enc}(pp,k,m))=m$.

In many encryption schemes each ciphertext is associated with some particular key. We will be interested in schemes where this is not the case. Namely, ciphertexts are not associated with a specific key, but rather “make sense” under any possible key. We denote by $\mathcal {C}_{pp}$ the distribution obtained by encrypting a random message using a random key. Namely, the distribution $\mathsf {Enc}(pp,k,m)$ where $k \in _R \{0,1\}^\lambda$ and $m \in _R \mathcal {M}_\lambda$.

Definition 5

(Universal Ciphertexts). We say that an encryption scheme $(\mathsf {PP\text {-}Gen},\mathsf {Enc},\mathsf {Dec})$ with respect to message space $\mathcal {M}=\{\mathcal {M}_\lambda \}_{\lambda \in \mathbb {N}}$ has universal ciphertexts if the following two conditions hold for all constant $\eta >0$, for all (sufficiently large) $\lambda \in \mathbb {N}$ and public parameters $pp \in \mathsf {PP\text {-}Gen}(1^\lambda )$:

• 1. For every fixed key $k^*\in \{0,1\}^\lambda$, a random ciphertext decrypts to a random message. Namely, the distribution $m \leftarrow \mathsf {Dec}(pp,k^*,c)$, where $c \leftarrow \mathcal {C}_{pp}$, is $2^{-(1+\eta )\lambda }$-statistically close to uniform.

• 2. For all $k^*\in \{0,1\}^\lambda$ and $m^* \in \mathcal {M}_\lambda$, the following distributions are $2^{-(1+\eta )\lambda }$-statistically close

  • $c \leftarrow \mathcal {C}_{pp}$ conditioned on $\mathsf {Dec}(pp,k^*,c) = m^*$.

  • c is sampled from $c \leftarrow \mathsf {Enc}(pp,k^*,m^*)$ (i.e., a fresh encryption of $m^*$ under public parameters pp and key $k^*$).

Definition 6

($\epsilon$-KDM Security). Let $\epsilon = \epsilon (\lambda ) \in [0,1]$. We say that an encryption scheme $(\mathsf {PP\text {-}Gen},\mathsf {Enc},\mathsf {Dec})$ is $\epsilon$-KDM secure, if for every polynomial-time adversary $\mathcal {A}$, for all sufficiently large values of $\lambda$ and any (possibly inefficient) function $f: \{0,1\}^\lambda \rightarrow \mathcal {M}_{\lambda }$ it holds that:

5 Correlation Intractability from Universal-Ciphertexts KDM Encryption

Let $\mathsf {PP\text {-}Gen}$, $\mathsf {Enc}$, $\mathsf {Dec}$ be an encryption scheme with respect to an ensemble of message spaces $\mathcal {M} = \{\mathcal {M}_\lambda \}_{\lambda \in \mathbb {N}}$, as defined in Sect. 4. For public parameters pp recall that we denote by $\mathcal {C}_{pp}$ the distribution obtained by encrypting a random message using a random key (with respect to public parameters pp).

Construction 5

We construct a hash function family $\mathcal {H} = \{\mathcal {H}_\lambda : \{0,1\}^\lambda \rightarrow \mathcal {M}_\lambda \}_{\lambda \in \mathbb {N}}$ as follows.

The key generation algorithm of the hash function takes input $1^\lambda$, samples public parameters pp of the encryption scheme and a random ciphertext $c \leftarrow \mathcal {C}_{pp}$. The hash key is $hk = (pp,c)$. On input the key (pp, c) and a message to be hashed $\alpha \in \{0,1\}^{\lambda }$, the hashing algorithm views $\alpha$ as a key of the encryption scheme and outputs $\mathsf {Dec}(pp,\alpha ,c)$.

The main result that we prove in this section is if the encryption scheme has universal ciphertexts (as per Definition 5) and is $\varepsilon$-KDM secure (as per Definition 6), for sufficiently small $\varepsilon =\varepsilon (\lambda )>0$, then Construction 5 forms a correlation intractable hash function family.

Theorem 6

If there exists an encryption scheme with universal ciphertexts that is $\varepsilon$-KDM secure for $\varepsilon \le \left( \mathsf {poly}(\lambda )\cdot 2^\lambda \cdot \mu (\lambda )\right) ^{-1}$, then Construction 5 is correlation intractable for all sparse relations with negligible density $\mu (\lambda )$.

5.1 Proof of Theorem 6

Let R be any sparse relation with negligible density $\mu =\mu (\lambda )$. Suppose toward a contradiction that there exists a probabilistic polynomial-time adversary $\mathsf {Adv}$ that breaks the correlation intractability of Construction 5 with non-negligible probability $\nu =\nu (\lambda )$. Namely,

$$\begin{aligned} \mathop {\Pr }\limits _{hk} \Big [ \mathsf {Adv}(H_{hk}) \text { outputs some }\alpha \wedge \big ( \alpha , H_{hk}(\alpha ) \big )\in R \Big ]\ge \nu (\lambda ). \end{aligned}$$

Thus, by construction of our hash function it holds that:

(9)

where here and below we use pp to denote public parameters sampled from $\mathsf {PP\text {-}Gen}(1^\lambda )$.

For the analysis, we consider a relaxed relation $R'$ where $(\alpha , \beta )\in R'$ if $(\alpha , \beta )\in R$ or if the first $\left\lfloor \log (\nu /2\mu ) \right\rceil$ bits of $\beta$ are all 0. The density of $R'$ is bounded by $\mu '\le 4\mu /\nu$, which is negligible when $\mu$ is negligible. Looking ahead, the purpose of “padding” R is so that the marginal distribution of $\alpha ^*$, obtained from jointly sampling a pair $(\alpha ^*, \beta ^*)$ randomly from $R'$, is close to uniform. More specifically, following [59, Proposition 3.4] we can bound the point-wise multiplicative difference (or ratio) between these distributions:

Fact 7

For all $\alpha '\in \{0,1\}^\lambda$, $\beta '\in \mathcal {M}_\lambda$,

(10)

Since $R \subseteq R'$, Eq. (9) implies that:

(11)

We will use Eq. (11) to show that $\mathsf {Adv}$ breaks the KDM security of our encryption scheme, with respect to the randomized KDM function f that given a key $\alpha ^*$, outputs a random $\beta ^*$ such that $(\alpha ^*,\beta ^*) \in R'$.

We now fix some setting of the public parameters pp. Using the structure of $R'$, and the fact that our encryption scheme has universal ciphertexts (property 2 of Definition 5), it holds that:

(12)

where the first inequality is due to Fact 7; the second is due to the universal ciphertexts property.

Our key step is captured by the following proposition, which relates the adversary’s advantage of recovering the specific key $\alpha ^*$ in a ciphertext encrypting possibly key-dependent messages, to the advantage of outputting any $\alpha$ that breaks correlation intractability. While the winning probability in the key-recovery game is exponentially small, it is lower bounded by a function of the success probability of breaking correlation intractability.

Proposition 1

For every setting of the public-parameters pp it holds that:

Proof

Fix the public parameters pp. By the fact that the random variables $(\alpha ^*,\beta ^*)$ and c are independent, it holds that:

(13)

By definition of conditional probability, it holds that:

(14)

where the inequality follows from the density of $R'$.

Claim 8

The following two distributions are $2^{-(1+\eta )\lambda }$-close:

• 1. $(\alpha ^*,c)$: such that $\alpha ^* \in _R \{0,1\}^\lambda$, $\beta ^* \in _R \mathcal {M}_\lambda$ and $c \leftarrow \mathcal {C}_{pp}$ conditioned on $\mathsf {Dec}(pp,\alpha ^*,c)=\beta ^*$.

• 2. $(\alpha ^*,c')$: such that $\alpha ^* \in _R \{0,1\}^\lambda$ and $c' \leftarrow \mathcal {C}_{pp}$.

Proof

A different way to sample the exact same distribution as in item (2) is to first sample $\alpha ^* \in _R \{0,1\}^\lambda$, then $c'' \leftarrow \mathcal {C}_{pp}$ and finally $c' \leftarrow \mathcal {C}_{pp}$ conditioned on $\mathsf {Dec}(pp,\alpha ^*,c') = \mathsf {Dec}(pp,\alpha ^*,c'')$.

By the universal ciphertext property 5(1) of the encryption scheme, the distribution $\mathsf {Dec}(pp,\alpha ^*,c'')$ is $2^{-(1+\eta )\lambda }$ close to the uniform distribution over $\mathcal {M}_\lambda$. The claim follows.   $\square$

Combining Claim 8 together with Eqs. (13) and (14) yields that:

(15)

This concludes the proof of Proposition 1.    $\square$

Using Proposition 1 and Eq. (12) we obtain that:

Thus, $\mathsf {Adv}$ breaks KDM security with probability $\varepsilon \ge (1/\mathsf {negl}) \cdot 2^{-\lambda }$, in contradiction to our assumption.

6 Candidate KDM Encryption with Universal Ciphertexts

We present two encryption schemes that satisfy the ciphertext universality (Definition 5), and plausibly satisfy $\epsilon$-KDM security (Definition 6) for exponentially small $\epsilon$.

6.1 Discrete-Log Based

We first present the encryption scheme based on a generic multiplicative group, and then specify its instantiation over the elliptic curve groups. The scheme can be viewed as a bit-encryption variant of ElGamal.

Construction 9

Fix a small constant $\eta >0$ (e.g. $\eta = 0.01$). Let the message space be $\mathcal {M} = \{ \mathcal {M}_\lambda \}_{\lambda \in \mathbb {N}}$, where $\mathcal {M}_\lambda = \{0,1\}^{w(\lambda )}$ and $w=w(\lambda )\in \mathbb {N}$. We construct an encryption scheme as follows.

• Public parameters Generation $\mathsf {PP\text {-}Gen}(1^\lambda )$: the key-generation algorithm selects a prime $N=N(\lambda )\ge 2^{(1+2\eta )\lambda }$, a group $\mathbb {G}= \mathbb {G}(\lambda )$ of size N, and a generator g (the exact algorithm for determining these depends on the specific group family we use - see instantiations below).

  Let $\mathsf {ext}: \mathbb {G}\rightarrow \{0,1\}$ be a deterministic efficiently computable function that outputs 0 on $\lceil N/2 \rceil$ of the group elements, and 1 on the remaining $\lfloor N/2 \rfloor$ elements.

  The public-parameters pp include a concise³ description of the group G, generator g, and function $\mathsf {ext}$.

• Encrypt $\mathsf {Enc}(pp,k,y)$: We view k as an integer in $[2^\lambda ]$. Let $y_1\dots y_w \in \{0,1\}$ be the bit decomposition of y.

  For each $j\in [w]$, sample $a_j {\in _R} \{ 0,1,...,N-1 \}$ and let $A_j:=g^{a_j}$. Sample $C_j$ uniformly from $\mathsf {ext}^{-1}(y_j)$ and let $B_j = C_j \cdot A_j^{ k}$. Output $c = ( A_j, B_j )_{j\in [w]}$ as the ciphertext.

• Decrypt $\mathsf {Dec}(pp,k,c)$: Decompose the ciphertext c as $( A_j, B_j )_{j\in [w]}$. For $j\in [w]$, let $C_j = B_j/A_j^{ k}$ and let the $j^{th}$ output bit be $\mathsf {ext}(C_j)$.

Remark 1

To ensure the KDM problem is as hard as possible, the group order is set to be a prime so that not only the discrete-log problem but also the decisional Diffie-Hellman problem is plausibly hard.

Since the group order is a prime, a deterministic function that extracts a bit from the group cannot be perfectly balanced. So we set the group order to be slightly larger than $2^{(1+\eta )\lambda }$ in order to allow $2^{-(1+\eta )\lambda }$-statistical distance for the statistical properties.

We first show that the scheme satisfies the universal ciphertext requirement (see Definition 5).

Proposition 2

The encryption scheme of Construction 9 has universal ciphertexts.

Proof

The first condition in Definition 5 follows from the fact that for a fixed encryption key k, and random ciphertext $(A_j,B_j)_{j \in [w]}$, it holds that each $C_j = B_j/A_j^k$ is uniformly distributed and so we only need to account for the deviation from $\mathsf {ext}$. Overall we get that the output is at most $2^{-(1+\eta ) \lambda }$-close to uniform.

The second condition in Definition 5 can be verified as follows. For every $j \in [w]$ and every possible value of $A_j$, there are exactly $|\mathsf {ext}^{-1}(y_j)|$ possible values $B_j$ that $\mathsf {Enc}$ can output, and each of them is equally likely. Therefore, each pair $(A_j, B_j)$ subject to the condition $\mathsf {ext}(B_j \cdot A_j^{k}) = w_j$ is equally likely to be output by $\mathsf {Enc}$, and thus the distribution output by $\mathsf {Enc}$ is identical to a random ciphertext for the given plaintext.   $\square$

As noted above, we need to assume that Construction 9 is exponentially KDM secure.

Assumption 10

(KDM security for the discrete-log based encryption). Let $\lambda \in \mathbb {N}$, $w(\lambda )\in \mathsf {poly}(\lambda )$. There exists a family of groups $\mathbb {G}(\lambda )$ (of efficiently computable sizes $N(\lambda )$, with efficiently computable generators, efficient group operations, and efficient $\mathsf {ext}: \mathbb {G}\rightarrow \{0,1\}$) such that for all function $f: \{ 1, \dots , 2^\lambda \} \rightarrow \{0,1\}^w$ (including those that are not efficiently computable), the following holds. For any polynomial-time adversary $\mathsf {Adv}$, for a uniformly random $k \in \{ 1, \dots , 2^\lambda \}$; for each $j\in [w]$, sample $a_j{\in _R} \{ 0, 1, ..., N \}$, $C_j {\in _R}\mathsf {ext}^{-1}(f(k)_j)$. The probability that adversary outputs k on input $(A_j = g^{a_j}, B_j=g^{a_j k }\cdot C_j)_{j\in [w]}$ is smaller than $\frac{1}{2^\lambda \cdot \mathsf {negl}(\lambda )}$, i.e.

Thus, using Theorem 6, we obtain the following corollary.

Corollary 1

Suppose that Assumption 10 holds. Then, there exists correlation intractable function for all sparse relations.

Remark 2

In Assumption 10, if the function f is a constant (i.e. is independent of the key), the problem can be reduced from the discrete-log problem over $\mathbb {G}$ with the key restricted to $\{ 1, \dots , 2^\lambda \}$, i.e. computing $k\in \{ 1, \dots , 2^\lambda \}$ given g, $g^k\in \mathbb {G}$. In the reduction, the discrete-log attacker, given g, $g^k$, and f, can sample $(A_j, B_j)_{j\in [w]}$ from the correct distribution, send over to the adversary in Assumption 10.

Remark 3

We chose bit encryption for simplicity of notation. Instead of representing messages as bits, we can represent them in any base b, as long as there is an efficient and nearly-regular map $\mathsf {ext}$ from $\mathbb {G}$ to $\{ 0, \dots , b-1 \}$. The regularity requirement, however, is quite strong: because of the first requirement in Definition 5, the preimage size of every digit under $\mathsf {ext}$ must be very close to the average, so that the statistical distance between $\mathsf {ext}(\mathbb {G})$ and uniform is $2^{-(1+2\eta )\lambda }$.

We can use seeded extractors and put the seed in the public parameters. Specifically, if we choose N to be at least $2^{2(1+2\eta )\lambda } \cdot b$ and $\mathsf {ext}: \mathbb {G}\rightarrow [b]$ to be a pairwise independent hash function, then for the average seed, by the leftover hash lemma [54, Lemma 4.8], the output will be $\sqrt{|\mathbb {G}|/b} = 2^{-(1+2\eta )\lambda }$-close to uniform. This ensures that a good seed exists (nonconstructively). If want to make sure the average seed is good with all but exponential probability, we can choose N to be at least $2^{4(1+2\eta )\lambda } \cdot b$ instead. Then for the average seed, the output will be $\sqrt{|\mathbb {G}|/b} = 2^{-2(1+2\eta )\lambda }$-close to uniform, and therefore for all but a $1-2^{-(1+2\eta )\lambda }$ fraction of the seeds, it will be at least $2^{-(1+2\eta )\lambda }$-close to uniform, as required.

An instantiation over elliptic curves groups. The group $\mathbb {G}$ and the extraction function $\mathsf {ext}$ are chosen such that they avoid the known weakness instances of the underlying ECDLP, and at the same time enjoy the statistical properties.

An elliptic curve group $E(\mathbb {F}_q)$ is represent by the curve E (in the short Weierstrass form) over finite field $\mathbb {F}_q$: $E(\mathbb {F}_q) = \{ ~(x,y) ~|~ y^2 = x^3 +ax+b \bmod q~ \} \cup \mathcal {O}$. Choose the curve (namely, choose a, b and q) so that q is an odd prime, the order of the group $\# E(\mathbb {F}_q)$ is a prime $N>2^{(1+2\eta )\lambda }$.

In the short Weierstrass form, if $(x, y)\in E(\mathbb {F}_q)$, then $(x, -y)\in E(\mathbb {F}_q)$. Any point P whose y-coordinate is zero does not exist in a prime order group, since $P = (x,0)$ implies the order of P is 2. So one option of the extraction function $\mathsf {ext}: E(\mathbb {F}_q)\rightarrow \{0,1\}$ is to take the sign of the y-coordinate of a point $P = (x,y)\in E(\mathbb {F}_q)$. To be precise, if $y\in \{ 1,...,(q-1)/2 \}$, output 1; if $y\in \{ (q+1)/2, ..., q-1 \}$, output 0. As an exception, if $P = \mathcal {O}$, output 0.

6.2 LWE Based

The LWE based encryption scheme is a variant of Regev’s scheme [73]. We remark that the hash function obtained by applying Construction 5 on Construction 11 yields a variant of Ajtai’s hash function [3], in the sense that we apply rounding on the output vector.

Construction 11

The message space is $\mathcal {M} = \{ \mathcal {M}_\lambda \}_{\lambda \in \mathbb {N}}$, where $\mathcal {M}_\lambda = \{0,1\}^{w(\lambda )}$ and $w=w(\lambda )\in \mathbb {N}$. We construct an encryption scheme as follows.

• Public parameters generation $\mathsf {PP\text {-}Gen}(1^\lambda )$ : Fix an even number $q(\lambda )$ as the modulus. Select $B(\lambda ), \ell (\lambda ) \in \mathbb {N}$ such that $B^{\ell } \in [2^{\lambda -\log (\lambda )}, 2^{\lambda +\log (\lambda )}]$ and $B\le q$. The public-parameters pp are $(B,q,\ell )$.

• Representation of the secret key: we view the secret key $k \in \{0,1\}^\lambda$ as a vector $\mathbf {k} \in \{ 0, ..., B(\lambda )-1 \} ^{\ell (\lambda )}$, written as a column vector.

• Encryption $\mathsf {Enc}(pp, \mathbf {k} ,y)$ : Given a message $y\in \{0,1\}^w$. For $j\in [w]$, sample $\mathbf {a} _j{\in _R}\mathbb {Z}_q^{1\times \ell }$. compute $b_j = y_j\cdot \frac{q}{2} + e_j - \mathbf {a} _j\cdot \mathbf {k} \pmod q$, where $e_j\leftarrow U( [0,q/2)\cap \mathbb {Z})$. Output $c = ( \mathbf {a} _j, b_j )_{j\in [w]}$ as the ciphertext.

• Decryption $\mathsf {Dec}(pp, \mathbf {k} ,c)$ : View c as $( \mathbf {a} _j, b_j )_{j\in [w]}$. For $j\in [w]$, let the $j^{th}$ output bit be $\left\lfloor b_j + \mathbf {a} _j\cdot \mathbf {k} \bmod q \right\rceil _2$, where $\left\lfloor \cdot \right\rceil _2: \mathbb {Z}_q\rightarrow \{0,1\}$ outputs 0 if the input is from [0, q / 2), 1 if the input is from $[q/2, q-1]$.

The parameters are set according to the following constraints to minimize the adversary’s advantage on the KDM problem, and to guarantee the statistical properties. The choices of parameters are guided by the reductions from the worst case problems, as well as the known attacks (e.g. [7, 8, 16, 60, 61, 75]), even though some of the attacks were designed to achieve non-trivial (sub)exponential running time and do not clearly achieving non-trivial success probability when running in polynomial time.

• 1. q is even so that we can get perfect ciphertext-universality.

• 2. The error term e is sampled uniformly from $[0,q/2)\cap \mathbb {Z}$, differing from the typical setting of discrete Gaussian distribution. Noise sampled uniformly from a sufficiently large range is as good as Gaussian for some parameter settings [34, 64]. In particular, q / 2 is sufficiently large, even larger than the typical settings of the norm of the noise.

• 3. B, $\ell$, q are selected so that each coordinate of the secret vector has enough entropy (i.e. $B>\sqrt{n}$), the vector dimension $\ell$ is sufficiently close to $\lambda$, B / q is not too small (i.e. $q/B\in \mathsf {poly}(\lambda )$). One way of setting the parameter is to let $q = O(\lambda ^3)$, $B(\lambda ) = 2^{\left\lfloor \log \lambda \right\rceil }$, $\ell (\lambda ) = \left\lfloor \frac{\lambda }{\left\lfloor \log \lambda \right\rceil } \right\rceil$.

We first show that the scheme satisfies the universal ciphertext requirement (see Definition 5).

Proposition 3

The encryption scheme of Construction 11 has universal ciphertexts.

Proof

The first property (as per Definition 5(1)) follows immediately from the perfect 1-universality of the decryption function.

The second property (as per Definition 5(2)) can be verified as follows. For $j\in [w]$, the randomness in the encryption includes $\mathbf {a} _j \in \mathbb {Z}_q^{1\times \ell }$ and the error term $e_j\in \mathbb {Z}_q$. For all $y_j^{*}\in \{0,1\}$ and $\mathbf {k} ^*\in \{ 0, ..., B-1 \} ^{\ell }$, $(b_j, \mathbf {a} _j)\in \mathbb {Z}_q \times \mathbb {Z}_q^n$ is sampled uniformly random conditioned on $b_j + \mathbf {a} _j \cdot \mathbf {k} ^* \bmod q\in y^*_j\cdot \frac{q}{2}+[0,q/2)\cap \mathbb {Z}$. Viewing the equality as a 1-universal function $\mathbf {a} _j \cdot \mathbf {k} ^* \bmod q \in y^*_j\cdot \frac{q}{2}+[0,q/2)\cap \mathbb {Z}- b_j$ with key $\mathbf {a} _j$, the marginal distribution of $\mathbf {a} _j$ is uniform over $\mathbb {Z}_q^{1\times \ell }$. Then, $e_j = b_j - y^*_j\cdot \frac{q}{2} + \mathbf {a} _j\cdot \mathbf {k} ^*$ is distributed uniformly over $[0,q/2)\cap \mathbb {Z}$.    $\square$

Assumption 12

(KDM security for LWE-based encryption). Let $\lambda \in \mathbb {N}$, $w(\lambda )\in \mathsf {poly}(\lambda )$. For all functions $f: \{ 0, ..., B-1 \} ^{\ell }\rightarrow \{0,1\}^w$ (including those who are not efficiently computable). The probably that any polynomial time adversary $\mathsf {Adv}$, given $\{ \mathbf {a} _j, \mathbf {a} _j\cdot \mathbf {k} + e_j + f_j( \mathbf {k} )\cdot q/2 \} _{j\in [w]}$ where $\mathbf {k} {\in _R} \{ 0, ..., B-1 \} ^{\ell }$, $\mathbf {a} _j{\in _R}\mathbb {Z}_q^{1\times \ell }$, $e_j{\in _R}[0,q/2)\cap \mathbb {Z}$, outputs $\mathbf {k}$ is smaller than $\frac{1}{2^\lambda \cdot \mathsf {negl}(\lambda )}$, i.e.

Thus, using Theorem 6, we obtain the following corollary.

Corollary 2

Suppose that Assumption 12 holds. Then, there exists correlation intractable function for all sparse relations.

Remark 4

In Assumption 12, if the function f is a constant (i.e. is independent of the key), then the problem is equivalent to search-LWE (for the same distributions of secret, noise, and public matrices, and the same requirement on the success probability as described in Assumption 12).

7 $\textsf {NIZK}$ from Fiat-Shamir

In this section we show how to use our hash functions to construct non-interactive zero-knowledge ($\textsf {NIZK}$) arguments for $\mathsf {NP}$. We follow the folklore approach of applying the Fiat-Shamir transformation to a constant-round public-coin honest-verifier zero-knowledge proof-system. The point however is that we can establish soundness based on a concrete assumption (with a meaningful security reduction) rather than just heuristically assuming that the Fiat-Shamir transformation preserves soundness. Further, we show that if we start from an interactive proof with adaptive soundness (where the instance x can be chosen adaptively in the last message), as in [38]; then in the resulting $\textsf {NIZK}$, the soundness and zero-knowledge properties hold even if the instance is chosen adaptively given the CRS.

We remark that for this result to go through we require an additional property from the hash function family that we use, beyond correlation intractability. Namely, that it is possible to efficiently sample a uniformly random hash function h from the family, conditioned on $h(a)=b$, for some arbitrary fixed values a and b. We refer to this property as “programmability”.

Definition 7

(Programmability of hash function). A hash function ensemble $\mathcal {H} = \{ h_k: \mathcal {D}(\lambda ) \rightarrow \mathcal {C}(\lambda ) \}_{\lambda \in \mathbb {N}}$ is called programmable if there exists an efficient algorithm M that given $x\in \mathcal {D}(\lambda )$ and $y\in \mathcal {C}(\lambda )$, outputs a uniformly random hash function $h_k$ from the family such that $h_k(x)=y$.

Translating the requirement to the hash function instantiated using our KDM-secure encryption scheme, it means the encryption algorithm given a key a and message b outputs the ciphertext efficiently.

We recall the definition of $\textsf {NIZK}$ with adaptive soundness and zero-knowledge.

Definition 8

($\textsf {NIZK}$ with adaptive soundness and ZK [17, 38]). Let $\lambda \in \mathbb {N}$ be the security parameter. A non-interactive (computational) zero-knowledge argument system ($\textsf {NIZK}$) for an $\mathsf {NP}$ language $\mathcal {L}\in \mathsf {NP}$, with witness relation $R_\mathcal {L}$, is a pair of probabilistic polynomial-time algorithms (P, V) such that:

• ${\mathbf {Completeness}}$: For every $x\in \mathcal {L}$ and witness w for x (i.e., $(x,w \in R_\mathcal {L})$), for all $\sigma \in \{0,1\}^{\mathsf {poly}(\lambda )}$,

  $$\begin{aligned} V \big ( \sigma , x, P(x, \sigma , w) \big ) = 1 . \end{aligned}$$

• ${\mathbf {Adaptive\ Soundness}}$: For every polynomial-size cheating prover $P^*$, we have

  

• Adaptive Zero-Knowledge: There exists a probabilistic polynomial-time simulator $S = (S_1, S_2)$ such that for every polynomial time adversary $A = (A_1, A_2)$,

  

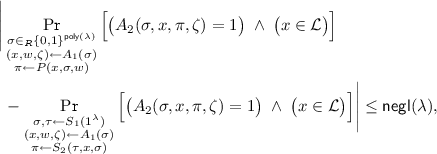
  where $\zeta$ (resp., $\tau$) denote an internal state of the adversary (resp., simulator).

The random string $\sigma$ received by both P and V is referred to as the common random string or CRS.

We establish the following result.

Theorem 13

Assume there exists one-way functions and a programmable correlation intractable function ensemble for all sparse relations. Then, any language in $\mathsf {NP}$ has a non-interactive zero-knowledge argument-system with adaptive soundness and adaptive zero-knowledge.

As a corollary of Theorem 13 and the results obtained in the previous sections, we obtain that:

Corollary 3

If either Assumption 10 or Assumption 12 holds, then any language in $\mathsf {NP}$ has a non-interactive zero-knowledge argument-system with adaptive soundness and adaptive zero-knowledge.

The readers are referred to the full version [25] for the Proof of Theorem 13.

Appendices

Appendices

A Success Probability of Polynomial Time Algorithms on Discrete-Log Problem

The discrete-log problem over $\mathbb {F}_q^*$ can be solved by the index calculus algorithms in heuristic subexponential time $\exp (C(\log q)^{1/3}(\log \log q)^{2/3})$.

We consider a (commonly used) variant of the index calculus algorithm with an online phase and an offline phase. The offline (preprocessing) phase only gets the modulus q and the generator g, the online phase gets the challenge $h\equiv g^x \bmod q$, computes x. The offline part calculates the discrete log of $\log _g (2)$, $\log _g (3)$, ..., $\log _g (B)$. The online phase picks a random r, try to factorize $g^r\cdot h \equiv g^{r+x} \bmod q$ in $\mathbb {Z}$, see if all the factors are smaller or equal to a prescribed prime bound B. If $g^r\cdot h = 2^{x_2} \cdot 3^{x_3} \cdot ... \cdot B^{x_B}$, then $r+x \equiv \log _g (2)\cdot x_2+\log _g (3)\cdot x_3 + ... + \log _g(B) \cdot x_B \bmod \phi (q)$.

The algorithm achieves $O(2^{-\frac{\lambda }{c}})$ success probability even if the online phase is only allowed to run in polynomial time, and the preprocessing phase is allowed to spend super-polynomial running time, but restricted to leave polynomially many bits as the advice for the online phase. The analysis of the success probability relies on the estimation of the number of smooth integers $\varPsi (q,B)$, which stands for the number of integers in the range [1, q] whose factors are all under B. Since the online phase is forced to receive only polynomial size advice and run in polynomial time, B will be chosen as a polynomial, whereas $q \approx 2^\lambda$.

The smooth integer bound can be derived from Rankin [71] (see the survey of [48]) that for any $A>1$, $\varPsi (q, \log (q)^A) = q^{1- 1/A +O\left( \frac{1}{\log \log q} \right) }$. This means the probability of a number within $[1, 2^\lambda ]$ to be $O(\lambda ^c)$ smooth is $2^{-\frac{\lambda }{c} + O(\frac{\lambda }{\log \lambda })}$.