Abstract
Ciphertext-policy attribute-based encryption (CP-ABE) is a promising primitive for enforcing access control policies defined by data owner on outsourced data. We propose a novel primitive called server-aided directly revocable CP-ABE with verifiable delegation, denoted by sarCP-ABE. In sarCP-ABE, the workloads about revocation are delegated to an aide-server, and the data owner only needs to generate a normal ciphertext as in a pure CP-ABE system. A user can be directly revoked by updating a public revocation list. To prevent a revoked user from decrypting, the aide server can update the aide-ciphertext with current revocation list, and an auditor can publicly check the correctness of the updated aide-ciphertext. At last, the proposed scheme can be proved selectively secure against chosen-plaintext attack on both original and updated ciphertext.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Cloud Computing is a promising primitive which enables large amounts of resources to be easily accessible to cloud users. Although data storage on public cloud provides an ease of accessibility, it also raises concerns on data confidentiality. Due to poor scalability and complex key management, the traditional encryption schemes, such as identity based encryption, can’t satisfy the requirements of various commercial applications that have a large amount of users.
Sahai and Waters [1] introduced the concept of attribute-based encryption (ABE). ABE can be divided into two kinds [2]: key-policy ABE (KP-ABE) and ciphertext-policy ABE (CP-ABE). In CP-ABE, without prior knowledge of who will decrypt the data, data owner encrypts data with an access policy, and a user can decrypt the ciphertext if and only if his/her attributes satisfy the access policy specified by the ciphertext. Pure CP-ABE is not sufficient for an access control system since users are not static, and users’ access privileges should be revoked when they withdraw from the system.
Although, many revocable ABE schemes have been proposed to solve the revocation problem, the requirement of interaction between authority and non-revoked users in indirect revocation method [3,4,5,6,7,8], and the troublesome workloads related to a large revocation list for data owner in direct revocation method [9,10,11,12,13], limit the commercial applications of CP-ABE to a large extent.
In 2015, Shi et al. [14] gave a directly revocable KP-ABE scheme while the data owner still need to generate a ciphertext that is linear to the size of the revocation cover. In 2016, Cui et al. [15] proposed a server-aided indirect revocable ABE which delegates the overheads of data users resulted in key updates to a aide-server. In 2007, Yamada et al. [16] gave two generic constructions of recoverable ABE from ABE.
Inspired by the direct revocation method in [14], and aiming at alleviating the workloads of revocation for data owner, we propose a server-aided directly revocable CP-ABE with verifiable revocation delegation.
2 Preliminaries
Multilinear Maps. Let \(\mathbb G_0,\mathbb G_1,...,\mathbb G_{d+3}\) be cyclic groups of prime order p. Multilinear maps consist of \(d+3\) mappings \(\{ {e_i}:{\mathbb G_0} \times {\mathbb G_i} \rightarrow {\mathbb G_{i + 1}}|i=0,...,d+2\}\), for \(i=0,...,d+2\), (i) if \(g_0\) is a generator of \(\mathbb G_0\), \({g_{i + 1}} = {e_i}({g_0},{g_i})\) is a generator of \(\mathbb G_{i+1}\); (ii) \(\forall a,b \in \mathbb Z_p\), \({e_i}(g_0^a,g_i^b) = {e_i}{({g_0},{g_i})^{ab}}\); (iii) \(e_i\) can be efficiently computed.
\(d+4\) Multilinear Decisional Diffie-Hellman Assumption (\(d+4\)-MDDH). Let \(\mathcal{G}(\lambda )\rightarrow (p,{\mathbb G_0},{\mathbb G_1}, ... ,{\mathbb G_{d + 3}},{e_0},{e_1}, \ldots ,{e_{d + 2}})\) be a generator of multilinear groups. Given  , where \({z_0}, ... ,{z_{d }},{d_1},{d_2},{d_3},c{ \in _R}\mathbb Z_p^*\) are unknown, there is no polynomial algorithm \(\mathcal A\) that can distinguish \(g_{d + 3}^{c{z_0} \cdots {z_{d}}{d_1}{d_2}{d_3}}\) from a random element \(Z{ \in _R}{\mathbb G_{d + 3}}\) with a non-negligible advantage.
, where \({z_0}, ... ,{z_{d }},{d_1},{d_2},{d_3},c{ \in _R}\mathbb Z_p^*\) are unknown, there is no polynomial algorithm \(\mathcal A\) that can distinguish \(g_{d + 3}^{c{z_0} \cdots {z_{d}}{d_1}{d_2}{d_3}}\) from a random element \(Z{ \in _R}{\mathbb G_{d + 3}}\) with a non-negligible advantage.
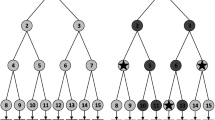
Subset Cover. Let \(\mathcal{T}_{id}\) be a full binary tree, depth(x) denote the depth of node x such that \(depth(root)=0\), \(path(x)=\{ {x_{{i_0}}}, \ldots ,{x_{{i_{depth(x)}}}}\} \) denote the path from the root to node x. A list of revoked users R corresponds to a set of leaf nodes in \(\mathcal{T}_{id}\). \(\forall x \in R\), mark all nodes of path(x), and subset cover cover(R) is the set of unmarked nodes that are the direct children of marked nodes in \(\mathcal{T}_{id}\), more details refer to [17].
3 Definition and Security Model
3.1 Definition
The sarCP-ABE scheme consists of eight algorithms.
\(\mathbf{Setup (}\lambda \mathrm{{)}} \rightarrow (PP,MSK)\), takes a security parameter \(\lambda \) as input, and outputs the public parameters PP and master secret key MSK.
\(\mathbf{Server KeyGen (}PP\mathrm{{)}} \rightarrow (SPK,SSK)\), takes PP as input, and outputs server’s public key SPK and secret key SSK.
\(\mathbf{User KeyGen (}PP,SPK,id\mathrm{{,}}S,MSK\mathrm{{)}} \rightarrow S{K_{id,S}}\), takes as input PP, server’s public key SPK, identity id, attributes S, master secret key MSK, and outputs secret key \(S{K_{id,S}}\).
\(\mathbf{Encrypt (}PP,M,(\mathbb W,\rho )\mathrm{{)}} \rightarrow CT\), takes as input PP, message M, access structure \((\mathbb W,\rho )\), and outputs a ciphertext CT.
\(\mathbf{Aide - Enc (}PP,CT\mathrm{{,}}R,SSK\mathrm{{)}} \rightarrow CT'\), takes as input PP, CT, SSK, revocation list R, and outputs an aide-ciphertext \(CT'\).
\(\mathbf{Decrypt (}PP,CT,CT',S{K_{id,S}}\mathrm{{,}}R\mathrm{{)}} \rightarrow M\) , takes as input PP, CT, \(CT'\), R, secret key \(S{K_{id,S}}\) of identity id, and outputs a plaintext M if \(id\notin R\) and S satisfies the access policy; else, outputs a reject symbol \(\bot \).
\(\mathbf{Update (}PP,CT'\mathrm{{,}}R,R'\mathrm{{)}} \rightarrow C\hat{T}\), takes as input PP, \(CT'\), R, new revocation list \(R'\) such that \(R\subset R'\), and outputs an updated aide-ciphertext \(C\hat{T}\).
\(\mathbf{Verify (}PP\mathrm{{,SPK,}}CT',C\hat{T},R,R'\mathrm{{)}} \rightarrow 1\), takes as input PP, SPK, \(CT',R\), \(C\hat{T},R'\), and outputs 1 if \(C\hat{T}\) is correct; otherwise, outputs 0.
3.2 Security Model
Selective security for original ciphertext. The selective security against chosen-plaintext attack on original ciphertext, IND-s-CPA-OC in brief, is defined by following game between a challenger \(\mathcal C\) and an adversary \(\mathcal A\).
Init: \(\mathcal {A}\) outputs a target access structure \((\mathbb W^*,\rho ^*)\) that will be used to generate a challenge ciphertext.
Setup. \(\mathcal C\) runs the \(\mathrm{{{ Setup}(}}\lambda \mathrm{{)}}\) algorithm and gives the system public parameters PP to \(\mathcal A\). \(\mathcal A\) is allowed to generate the secret key of aide server, but it is asked to send the public key SPK to \(\mathcal C\).
Phase 1. \(\mathcal A\) makes \(\mathrm{{KeyGen(}}i{d_i}\mathrm{{,}}{S_i}\mathrm{{)}}\) queries for \(\mathrm{{(}}i{d_1}\mathrm{{,}}{S_1}\mathrm{{),}}\; ... ,\mathrm{{(}}i{d_{q_1}}\mathrm{{,}}{S_{q_1}}\mathrm{{)}}\), \(\mathcal C\) returns \(S{K_{i{d_i},{S_i}}}\) to \(\mathcal A\).
Challenge. \(\mathcal A\) submits two messages \(M_0,M_1\) of equal length, an access structure \((\mathbb W^*,\rho ^*)\), a revocation list R to \(\mathcal C\). None of the sets \({S_1},\; ... ,{S_{{q_1}}}\) from Phase 1 satisfies \((\mathbb W^*,\rho ^*)\). \(\mathcal C\) flips a random coin \(\beta { \in _R}\{ 0,1\} \) and generates the challenge ciphertext \(CT^*\) with \(M_\beta \) and aide-ciphertext \(CT'^*\) under revocation list R. At last, \(\mathcal C\) returns \(C{T^*},C{T'^{*}}\) to \(\mathcal A\).
Phase 2. \(\mathcal A\) makes \(\mathrm{{KeyGen(}}i{d_i}\mathrm{{,}}{S_i}\mathrm{{)}}\) queries for \(\mathrm{{(}}i{d_{q_1+1}}\mathrm{{,}}{S_{q_1+1}}\mathrm{{),}}\; ... ,\mathrm{{(}}i{d_{q}}\mathrm{{,}}{S_{q}}\mathrm{{)}}\) as in Query Phase 1 with the restriction that \({S_{{q_1} + 1}}\mathrm{{,}}\;...,{S_q}\) should not satisfy the challenge access structure \((\mathbb W^*,\rho ^*)\).
Guess. \(\mathcal A\) outputs a guess bit \(\beta '{ \in _R}\{ 0,1\} \) and wins the game if \(\beta '=\beta \). The advantage of \(\mathcal A\) is defined to be \(Adv(\mathcal{A}) = \left| {\Pr [\beta ' = \beta ] - {1/2}} \right| \).
Selective security for updated ciphertext. The selective security against chosen-plaintext attack on updated ciphertext, IND-s-CPA-UC in brief, is same as IND-s-CPA-OC except the challenge phase.
Challenge. \(\mathcal A\) submits two messages \(M_0,M_1\) of equal length, an access structure \((\mathbb W^*,\rho ^*)\), a prior revocation list R, a new revocation list \(R'\) where \(R \subset R'\) to \(\mathcal C\). None of the sets \({S_1},\; ... ,{S_{{q_1}}}\) from Phase 1 satisfies \((\mathbb W^*,\rho ^*)\). \(\mathcal C\) flips a random coin \(\beta { \in _R}\{ 0,1\} \) and generates the challenge ciphertext \(CT^*\) with \(M_\beta \) and aide-ciphertext \(CT'^*\) under revocation list R, and then generates update aide-ciphertext \(C{\hat{T}^*}\) under revocation list \(R'\). At last, \(\mathcal C\) returns \(C{T^*},C{\hat{T}^*}\) to \(\mathcal A\).
Verifiability of revocation delegation. The verifiability of aide-ciphertext is defined by following game between a challenger \(\mathcal C\) and an adversary \(\mathcal A\).
Init, Setup and Query Phase are same as IND-s-CPA-OC.
Challenge. \(\mathcal A\) submits a message M of equal length, an access structure \((\mathbb W^*,\rho ^*)\), a prior revocation list R to \(\mathcal C\). None of the sets \({S_1},\; ... ,{S_{{q_1}}}\) from Phase 1 satisfies \((\mathbb W^*,\rho ^*)\). \(\mathcal C\) generates ciphertext \(CT^*\) with M and aide-ciphertext \(CT'^*\) under revocation list R. At last, \(\mathcal C\) returns \(C{T^*},CT'^*\) to \(\mathcal A\).
Guess. \(\mathcal A\) generates update aide-ciphertext \(C{\hat{T}^*}\) under revocation list \(R'\), where \(R \subset R'\). \(\mathcal A\) wins the game if \(\mathrm{{Verify(}}PP\mathrm{{,}}CT'^*,C{\hat{T}}^*,R,R'\mathrm{{)}} \rightarrow 1\) and the distributions of \(C{\hat{T}}^*\) and \(C\tilde{T}\) are distinguishable, where \(\mathrm{{Update(}}PP,CT'^*\mathrm{{,}}R,R'\mathrm{{)}} \rightarrow C\tilde{T}\) are normally produced by \(\mathcal C\).
4 Our Construction
Let \(\mathbb U = \{ a{t_1},...,a{t_{|\mathbb U|}}\} \) be the attribute universe and \(\mathbb {ID} = \{ i{d_1},...,i{d_{|\mathbb {ID}|}}\} \) be the user universe in the system. Let d, such that \(2^d=|\mathbb {ID}|\), be the depth for all leaves in the full binary tree of identities.
\(\mathbf{{Setup}( }\lambda \mathrm{{)}} \rightarrow (PP,MSK)\): Given the security parameter \(\lambda \), it generates \(d+3\) multilinear maps: \(\{ {e_i}:{\mathbb G_0} \times {\mathbb G_i} \rightarrow {\mathbb G_{i + 1}}|i=0,...,d+2\}\), where \(\mathbb G_0,\mathbb G_1,...,\mathbb G_{d+3}\) are cyclic group of prime order p. Let \(g_0\) be a random generator of \(\mathbb G_0\), and then \({g_{i + 1}} = {e_i}({g_0},{g_i})\) is a generator of \(\mathbb G_{i+1}\) for \(i=0,1,...,d+2\). The authority chooses \(\alpha ,b{ \in _R}\mathbb Z_p^*\) randomly and computes \(g_{d + 2}^\alpha ,g_{d+2}^b\). For each attribute \(at_i\in \mathbb U\), it selects \(t_i{ \in _R}\mathbb Z_p^*\) randomly and sets \({T_i} = g_{0}^{{t_i}}\). The authority chooses an efficient map \(H:{\{ 0,1\} ^*} \rightarrow {\mathbb G_0}\). Let \({\mathcal{T}_{id}}\) denote a binary tree according to the revocation list R. At last, the authority sets master secret key as \(MSK = \alpha ,\{ {t_i},i = 1,...,|\mathbb U|\} \) and publishes public parameters \(PP = \{p,{\mathbb {G}_0},{\mathbb {G}_1}, ... ,{\mathbb {G}_{d + 3}},{e_0},...,{e_{d + 2}},{T_1},...,{T_{|\mathbb {U}|}},g_0,g_{d + 2}^b,{e_{d + 2}}{(g_0,g_{d + 2})^\alpha },\mathbb {U},\mathbb {ID},H,d,{\mathcal{T}_{id}}\}\).
\(\mathrm{\mathbf{Server KeyGen\mathrm (}}PP) \rightarrow (SPK,SSK)\): The aide server randomly chooses \(c{ \in _R}\mathbb Z_p^*\), keeps secret key \(SSK = c\) secretly and publishes public key \(SPK = g_0^c\).
\(\mathrm{\mathbf{User KeyGen\mathrm (}}PP,SPK,id\mathrm{{,}}S,MSK\mathrm{{)}} \rightarrow S{K_{id,S}}\): The authority can generate the secret key \(S{K_{id,S}} = (K,L,\{ {K_x}:\forall x \in S)\) as follows.
-
Let \({{path(}}id{{) = \{ }}{x_{{i_0}}}\mathrm{{,}}...\mathrm{{,}}{x_{{i_d}}}\mathrm{{\} }}\) and \({P_{{x_{{i_{_0}}}}}} = {e_0}(g_0^b,H({x_{{i_0}}}))\).
-
For \(k=1\) to d , compute \({P_{{x_{{i_k}}}}} = {e_k}({P_{{x_{{i_{k - 1}}}}}},H({x_{{i_k}}}))\), let \(P_{id}^{} = {e_{d + 1}}({P_{{x_{{i_d}}}}},g_0^c)\).
-
Choose \(a,r{ \in _R}\mathbb Z_p^*\), compute \(K = g_{d + 2}^{\alpha - ar}P_{id}^r,L = g_0^r,{K_i} = g_{d+2}^{a{r}t_i^{ - 1}},\forall a{t_i} \in S\).
\(\mathrm{\mathbf{Encrypt\mathrm (}}PP,M,(\mathbb W,\rho )\mathrm{{)}} \rightarrow CT\): Given a message M, access structure \((\mathbb W,\rho )\), where \(\mathbb W\) is a \(l\times k\) matrix and \(\rho \) is a map from each row \(\mathbb W_i\) of \(\mathbb W\) to an attribute \(a{t_{\rho (i)}}\), the data owner generates ciphertext \(CT = ({C}, {C'},{\{{C_{i}}\} _{i \in [l]}})\) can be generated as follows.
-
Choose \(s,{v_2},...,{v_{k}}{ \in _R}\ \mathbb Z_p^*\) randomly, and construct vector
 .
. -
Compute \(C = M \cdot {e_{d + 2}}{({g_0},{g_{d + 2}})^{\alpha s}},C' = g_0^s\).
-
For \(i=1,...,l\), compute \({C_i} = T_i^{{\lambda _i}}\), where
 .
.
\(\mathrm{\mathbf{Aided-Enc\mathrm (}}PP,CT,R,SSK\mathrm{{)}} \rightarrow CT'\): Given CT, and a revocation list R, the aide-server generates aide-ciphertext \(CT' = \{ {D_x}:\forall x \in {{cover}}(R)\}\) as follows.
-
Let \({{path(}}x\mathrm{{) = \{ }}{x_{{i_0}}}\mathrm{{,}}...\mathrm{{,}}{x_{{i_{depth(x)}}}}\mathrm{{\} }}\) and \({P_{{x_{{i_{_0}}}}}} = {e_0}(g_0^b,H({x_{{i_0}}}))\).
-
For \(k=1\) to depth(x), compute \({P_{{x_{{i_k}}}}} = {e_k}({P_{{x_{{i_{k - 1}}}}}},H({x_{{i_k}}}))\), let \(P_x^{} = {P_{{x_{{i_{depth(x)}}}}}}\).
-
Compute \({D_x} = {e_{depth(x) + 1}}{({P_x},C')^c}\).
\(\mathrm{\mathbf{Decrypt\mathrm (}}PP,CT,CT',SK_{id,S},R\mathrm{{ )}} \rightarrow M\): If \(id \notin R\) and S satisfies access structure \((\mathbb W,\rho )\), the message can be recovered as follows.
-
Since \(id \notin R\), there always exists \(x \in ({{path(}}id\mathrm{{)}} \cap {{cover}}(R)\mathrm{{)}}\). Let \(path(id)=\mathrm{{\{ }}{x_{{i_0}}}\mathrm{{,}}... \mathrm{{,}}{x_{{i_{depth(x)}}}}\mathrm{{,}}...\mathrm{{,}}{x_{{i_d}}}\mathrm{{\} }}\), where \({x_{{i_{depth(x)}}}} = x,{x_{{i_d}}} = id\). Let \(Q_{{x_{{i_{depth(x)}}}}}^{'} = D_x\), and for \(k = depth(x) + 1\) to d compute \(Q_{{x_{{i_{_k}}}}}^{'} = {e_{k + 1}}(Q_{{x_{{i_{_{k - 1}}}}}}^{'},H({x_{{i_k}}}))\). Then, \(Q_{id} = Q_{{x_{{i_{_d}}}}}^{'} = P_{id}^s\). Since S satisfies \((\mathbb W,\rho )\), there exists \(\{ {\omega _i}:i \in I\} \) such that\(\sum \limits _{i \in I} {{\omega _i}{\mathbb W_i}} = (1,0,...,0)\), where \(I = \{ i:a{t_{\rho (i)}} \in {S}\} \).
-
Computes \(M = \frac{{C \cdot {e_{d + 2}}(L,{Q_{id}})}}{{{e_{d + 2}}(C',K)\prod \limits _{i \in I} {{e_{d + 2}}{{({K_i},{C_i})}^{{\omega _i}}}} }}\).
\(\mathrm{\mathbf{Update\mathrm (}}PP,CT'\mathrm{{,}}R,R'\mathrm{{)}} \rightarrow C\hat{T}\): Given an aide-ciphertext \(CT'\) under revocation list R and a new revocation list \(R'\) where \(R \subset R'\), the updated aide-ciphertext \(C\hat{T}' = \{ {\hat{D}_x}:\forall x \in {{cover}}(R')\} \) can be generated as follows.
-
For each \(x' \in {{cover}}(R')\), if there exists \(x \in {{cover}}(R)\) such that \(x=x'\), let \(\hat{D}_{x'} = {D_x}\);
-
Else, there exists \(x \in {{cover}}(R)\) that x is an ancestor of \(x'\). Let \({{path}}(x') = {{path}}(x) \cup \{ {x_{{i_{depth(x) + 1}}}}, ...,{x_{{i_{depth(x')}}}}\} \) such that \({x_{{i_{depth(x)}}}} = x,{x_{{i_{depth(x')}}}} = x'\). Let \(P_{{x_{{i_{depth(x)}}}}}^{'} = {D_x}\), compute \(P_{{x_{{i_k}}}}^{'} = {e_{k + 1}}(P_{{x_{{i_{k - 1}}}}}^{'},H({x_{{i_k}}}))\) for \(k = depth(x)\,+\,1,...,depth(x')\), and let \({\hat{D}_{x'}} = P_{{x_{{i_{depth(x')}}}}}^{'}\).
\(\mathrm{\mathbf{Verify\mathrm (}}PP\mathrm{{,}}SPK,CT',C\hat{T}',R,R'\mathrm{{)}} \rightarrow 1\): The correctness of \(C\hat{T}'\) can be publicly verified by an auditor as follows.
-
For each \(x \in {{cover}}(R)\), \({{path(}}x\mathrm{{) = \{ }}{x_{{i_0}}},...,{x_{{i_{depth(x)}}}}\mathrm{{\} }}\), let \({P_{{x_{{i_{_0}}}}}} = {e_0}(g_0^b,H({x_{{i_0}}}))\); compute \({P_{{x_{{i_k}}}}} = {e_k}({P_{{x_{{i_{k - 1}}}}}},H({x_{{i_k}}}))\) for \(k=1\) to depth(x); let \(P_x = {P_{{x_{{i_{depth(x)}}}}}}\), compute \(P_x^{'} = {e_{depth(x) + 1}}({P_x},C')\), and verify whether \({e_{depth(x) + 2}}({D_x},{g_0}) = {e_{depth(x) + 2}}(P_x^{'},g_0^c)\) holds or not. If not, output 0.
-
Otherwise, for each \(x \in {{cover}}(R) \cap {{cover}}(R')\), verify whether \(\hat{D}_x = {D_x}\) holds or not. If not, output 0.
-
Otherwise, for each \(i\in [0,d]\), find out all the nodes \({x_1}, ... ,{x_k}\) such that \({x_t} \in {{cover}}(R') - {{cover}}(R)\) where \(depth({x_t}) = i,t \in [0,k]\); choose \({a_1}, ... ,{a_k}{ \in _R}\mathbb Z_p\) at random, compute \(P_{{x_t}}^{'} = {e_{depth({x_t}) + 1}}({P_{{x_t}}},C')\) and verify
$$\begin{aligned} \prod \limits _{t = 1}^k {{e_{depth({x_t}) + 2}}({{(P_{{x_t}}^{'})}^{{a_t}}},g_0^c)} = {e_{depth({x_t}) + 2}}({g_0},\prod \limits _{t = 1}^k {{{(\hat{D}_{{x_t}}^{})}^{{a_t}}}} ) \end{aligned}$$(1) -
If there exists \(i\in [0,d]\) such that Eq. (1) does not hold, then output 0; otherwise, return 1.
5 Security Results
Due to space limitation, we only give the security results. The complete proof and efficiency analysis will be given in the full paper.
Theorem 1
If the d + 4-MDDH assumption holds and the challenge matrix \(\mathbb W^*\) is of size \({l^*} \times {k^*}\) such that \({l^*},{k^*} \le q\), there is no polynomial time adversary that can win the IND-s-CPA-OC game with non-negligible advantage \(\varepsilon \).
Theorem 2
If d + 4-MDDH assumption holds, there is no polynomial adversary that can win the IND-s-CPA-UC game with non-negligible advantage \(\varepsilon \).
Theorem 3
The proposed sarCP-ABE scheme can achieve verifiability of revocation delegation.
6 Conclusion
In this paper, we introduce a new primitive, called server-aided directly revocable CP-ABE with verifiable revocation delegation to achieve efficient user revocation. We give the formal security model, propose a concrete sarCP-ABE scheme, and then prove that the proposed sarCP-ABE scheme is selectively secure under the security. The proposed sarCP-ABE scheme can support verifiable (complete) revocation delegation. Comparing with previous directly revocable ABE schemes, the workloads about revocation are delegated to the aide-server.
References
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_27
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine grained access control of encrypted data. In: Proceedings of the 13th ACM Conference on Computer and Communications Security, pp. 89–98. ACM (2006)
Pirretti, M., Traynor, P., McDaniel, P., Waters, B.: Secure attribute-based systems. In: Proceedings of the 13th ACM conference on Computer and communications security, pp. 99–112. ACM (2006)
Liang, X., Lu, R., Lin, X., Shen, X.: Ciphertext policy attribute based encryption with efficient revocation. Technical report, University of Waterloo (2010)
Ostrovsky R., Sahai A., Waters, B.: Attribute-based encryption with non-monotonic access structures. In: Proceedings of ACM Conference on Computer and Communication Security, pp. 195–203. ACM (2007)
Hur, J., Noh, D.: Attribute-based access control with efficient revocation in data outsourcing systems. IEEE Trans. Parallel Distrib. Syst. 22(7), 1214–1221 (2011)
Sahai, A., Seyalioglu, H., Waters, B.: Dynamic credentials and ciphertext delegation for attribute-based encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 199–217. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_13
Xie, X., Ma, H., Li, J., Chen, X.: New ciphertext-policy attribute-based access control with efficient revocation. In: Mustofa, K., Neuhold, E.J., Tjoa, A.M., Weippl, E., You, I. (eds.) ICT-EurAsia 2013. LNCS, vol. 7804, pp. 373–382. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36818-9_41
Attrapadung, N., Imai, H.: Conjunctive broadcast and attribute-based encryption. In: Shacham, H., Waters, B. (eds.) Pairing 2009. LNCS, vol. 5671, pp. 248–265. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03298-1_16
Yu, S., Wang, C., Ren, K., Lou, W.: Attribute based data sharing with attribute revocation. In: Proceedings of the 5th ACM Symposium on Information, Computer and Communications Security, pp. 261–270. ACM (2010)
Jahid, S., Mittal, P., Borisov, N.: EASiER: Encryption-based access control in social networks with efficient revocation. In: Proceedings of the 6th ACM Symposium on Information, Computer and Communications Security, pp. 411–415. ACM (2011)
Zhang, Y., Chen, X., Li, J., Li, H., Li, F.: FDR-ABE: attribute-based encryption with flexible and direct revocation. In: 5th International Conference on Intelligent Networking and Collaborative Systems-2013, pp. 38–45. IEEE (2013)
Naruse, T., Mohri, M., Shiraishi, Y.: Attribute-based encryption with attribute revocation and grant function using proxy re-encryption and attribute key for updating. In: Park, J., Stojmenovic, I., Choi, M., Xhafa, F. (eds.) Future Information Technology 2014. LNEE, vol. 276, pp. 119–125. Springer, Berlin, Heidelberg (2014). https://doi.org/10.1007/978-3-642-40861-8_18
Shi, Y., Zheng, Q., Liu, J., Han, Z.: Directly revocable key-policy attribute-based encryption with verifiable ciphertext delegation. Inf. Sci. 295, 221–231 (2015)
Cui, H., Deng, R.H., Li, Y., Qin, B.: Server-aided revocable attribute-based encryption. In: Askoxylakis, I., Ioannidis, S., Katsikas, S., Meadows, C. (eds.) ESORICS 2016. LNCS, vol. 9879, pp. 570–587. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45741-3_29
Yamada, K., Attrapadung, N., Emura, K., Hanaoka, G., Tanaka, K.: Generic constructions for fully secure revocable attribute-based encryption. In: Foley, S.N., Gollmann, D., Snekkenes, E. (eds.) ESORICS 2017. LNCS, vol. 10493, pp. 532–551. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66399-9_29
Boldyreva, A., Goyal, V., Kumar, V. : Identity-based encryption with efficient revocation. In: Proceedings of the 15th ACM Conference on Computer and Communications Security, pp. 417–426. ACM (2008)
Acknowledgment
This work was supported in part by the National Natural Science Foundation of China (Nos. 61602512, 61632012, 61373154, 61371083, 61672239), in part by China Postdoctoral Science Foundation of China (No. 2016M591629), in part by National Key Research and Development Program (Nos. 2016YFB0800101 and 2016YFB0800100), Innovative Research Groups of the National Natural Science Foundation of China (No. 61521003).
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Yu, G., Ma, X., Cao, Z., Zhu, W., Zeng, G. (2018). Server-Aided Directly Revocable Ciphertext-Policy Attribute-Based Encryption with Verifiable Delegation. In: Qing, S., Mitchell, C., Chen, L., Liu, D. (eds) Information and Communications Security. ICICS 2017. Lecture Notes in Computer Science(), vol 10631. Springer, Cham. https://doi.org/10.1007/978-3-319-89500-0_15
Download citation
DOI: https://doi.org/10.1007/978-3-319-89500-0_15
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89499-7
Online ISBN: 978-3-319-89500-0
eBook Packages: Computer ScienceComputer Science (R0)



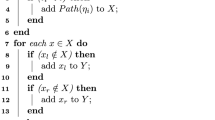
 .
. .
.