Abstract
Since the inception of pairing-based constructions in cryptography, the authentication in group key agreement (GKA) protocol has been usually achieved by pairings. But due to high computation cost of pairing such constructions are inefficient for practical implementation, specially for low power devices. Also, in almost all such constructions leakage of both the keys- the long-term secret key and the ephemeral key has not been considered for security guarantee. In this view, construction of an efficient and secure GKA protocol is desired. In this paper, we propose an authenticated GKA protocol without pairing. We have achieved security of the proposed scheme following the most standard and recent security notion namely the EGBG model. In particular, we have proved the authenticated key exchange (AKE) security and the mutual authentication (MA) security with full forward secrecy, considering leakage of both the keys long-term and ephemeral, adopting a comparatively efficient technique, the game hopping technique. Our proposed scheme is more efficient in the view of computation and operation time with compare to the existing similar schemes, hence it is more acceptable for the tiny processors. To the best of our knowledge ours is the first pairing free balanced AGKA protocol secure in the EGBG model.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Group key agreement
- Authentication
- Insider security
- Forward security
- Mutual authentication
- Batch verification
1 Introduction
A group key agreement (GKA) protocol ensures establishment of a common session key among the group members that remains unknown to outsiders. The GKA protocol is applicable in various real world communication networks such as ad-hoc networks, wireless sensor networks and body area networks, where devices are involved in sharing common secret data over an open channel. There are numerous other real life examples of GKA including distributed computations, video conferencing, multi-user games, etc. The key establishment protocols can be categorized into two sets: key transport protocols and key agreement protocols. In the former, the session key is derived by one of the powerful nodes and then the key is transferred securely to all the members of the group. In the latter, a common session key is derived by all the members by interactive participation in an agreement protocol. Moreover, group key agreement protocols can be further categorized into balanced and imbalanced protocols. All the participants in balanced GKA share same computing burden whereas in imbalanced protocols a powerful node verifies all the received signatures. As established by Bellare and Rogaway (CRYPTO 1993) [2], authentication is an essential security requirement for key exchange protocols, otherwise the man in the middle (MITM) attack yields the protocol vulnerable to impersonation attacks. Precisely, we provide here a construction of an authenticated group key agreement (AGKA) protocol. We rely on the application of PKI based signature for the purpose. Motivated by Shamir’s idea of identity-based (ID) cryptosystem [20], we deploy our scheme on the ID-based setting to avoid overhead of certificate management due to classical PKI setup.
After the seminal work of Diffie and Hellman [10], there has been extensive efforts to convert their two-party key exchange protocol to multi-party key exchange protocol [6, 14, 21]. Among the most notable works, Joux’s one round three-party key agreement protocol [15] is considered as a significant contribution for practical GKA protocol due to the functionality of pairing. Based on Joux’s work [15], Barua et al. [1] have presented protocols of multi-party key agreement in two flavors unauthenticated- based on ternary trees and authenticated- from bilinear maps. Unfortunately, their protocols are secure against only passive adversaries. The first provable security model for authenticated key exchange (AKE) security was introduced by Bresson et al. [3,4,5] but their protocol accounts O(n) rounds, which is very expensive. Further, Katz and Yung improved the model in [17] and proposed a scalable compiler which transforms any unauthenticated GKA into an authenticated one. Later, Katz and Shin [16] modeled the insider security in GKA protocols. In 2009, Gorantla et al. [11] proposed a security model, we call it the GBG model, which addresses the forward secrecy and key compromise impersonation resilience (KCIR) for GKA protocols to take into account authenticated key exchange (AKE) security and mutual authentication (MA) security. Their model was revisited and enhanced by Zhao et al. [29] in 2011. They improved the GBG model to stronger extended GBG model, we call it the EGBG model, where they addressed both, the leakage of secret key as well as the leakage of ephemeral key independently.
The authenticated ID-based GKA protocol was first formalized by Choi et al. [7] in 2004, but their scheme was found vulnerable to insider colluding attack [28]. In 2007, Kyung-Ah [18] claimed that scheme in [7] is vulnerable to another insider colluding attack and improved the protocol. Unfortunately, none of these AGKA protocols could achieve the perfect forward secrecy. Perfect forward secrecy allows the compromise of long term secret keys of all participants maintaining all earlier shared secrets unrevealed. In 2011, Wu et al. [27] presented a provably secure ID-AGKE protocol from pairings, providing forward secrecy and security against the insider attacks. Later, Wu et al. [26] presented their first revocable ID-based AGKE (RID-AGKE) protocol, which is provably secure and can resist malicious participants as well. The major limitation of existing literature is, not to consider the ephemeral key leakage [29]. In 2015, Teng et al. [22] presented first ID-based AGKA protocol secure in EGBG model. Their protocol claims MA security with KCIR, achieving full forward secrecy. This protocol includes extensive number of pairing operations (\(2n^2-2n\)) which is inefficient for practical implementations specially for low power devices. The session key in their construction is concatenation of \(k_i\) where \(k_i\)s are randomly chosen strings of length k. Therefore, the leakage of randomness will reveal the session key and hence, to the best of our knowledge, there is no existing protocol secure in EGBG model. Our AGKA protocol does not use any pairing operation and hence turns to be very much suitable for the computational performance, especially during the implementation with limited resource. We have proved the security following the EGBG model. Moreover, our efficiency analysis asserts that our scheme is more efficient in the view of computation and operation time with compare to the existing similar schemes.
Rest of the paper is organized as follows: in Sect. 2, we introduce necessary definitions, corresponding hardness assumption, the AGKA protocol and security model for AGKA. The proposed AGKA scheme is described in Sect. 3. The security analysis and efficiency comparison have been presented in Sects. 4 and 5 respectively, followed by the conclusion in Sect. 6.
2 AGKA Protocol and Its Security
In this section, we introduce mathematical definitions, hardness assumptions, the notion of AGKA protocol and security model for it. If X is a set, then  denotes the operation of choosing an element y of X according to the uniform random distribution on X.
denotes the operation of choosing an element y of X according to the uniform random distribution on X.
2.1 Definitions and Assumptions
Definition 1
(Computational Diffie-Hellman Problem (CDHP)). Let G be an additive cyclic group (precisely an elliptic curve group) of order q with generator P. Let \(CDH: G \times G \rightarrow G\) be a map defined by
The computational Diffie-Hellman problem (CDHP) is to evaluate CDH(X, Y) given  without the knowledge of \(a,b \in \mathbb {Z}_{q}^{*}\). (Note that obtaining \(a\in \mathbb {Z}_{q}^{*}\), given \(P,X\in G\) is solving the elliptic curve discrete logarithm problem (ECDLP)).
without the knowledge of \(a,b \in \mathbb {Z}_{q}^{*}\). (Note that obtaining \(a\in \mathbb {Z}_{q}^{*}\), given \(P,X\in G\) is solving the elliptic curve discrete logarithm problem (ECDLP)).
Definition 2
(Computational Diffie-Hellman Assumption). Given a security parameter \(\lambda \), let  . The computational Diffie-Hellman assumption (CDHA) states that for any PPT algorithm \(\mathcal {A}\) which attempts to solve CDHP, its advantage
. The computational Diffie-Hellman assumption (CDHA) states that for any PPT algorithm \(\mathcal {A}\) which attempts to solve CDHP, its advantage
is negligible in \(\lambda \). We say that the \((t, \epsilon )\)-CDH assumption holds in group G if there is no algorithm which takes at most t running time and can solve CDHP with at least a non-negligible advantage \(\epsilon \).
2.2 AGKA Protocol
Suppose there are total n participants \(U_1, U_2,\ldots ,U_n\) and any subset with \((n \ge 2)\) can run the protocol \((\pi )\). Each participant is provided with a (public, private) key pair. In our protocol, we refer by session a running instance. Each participant is allowed to run multiple sessions concurrently. An \(i^{th}\) instance of the protocol is represented as \(\varPi ^i_U\) where U is the corresponding user or participant. We define two identities, the session identity \(sid^i_{U}\) which is the session dependent information computed by user U at its \(i^{th}\) instance using the shared information in that session, and the partner identity \(pid^i_{U}\) which is a set of identities of the participants who are involved in generation of the session key with \(\varPi ^i_U\). We say an instance \(\varPi ^i_U\) accepts when it computes a valid session key sk. We say instances \(\varPi ^i_U\) and \(\varPi ^j_{U'}\)(for \(\varPi ^i_U\ne \varPi ^j_{U'}\)) are partnered iff (i) they have both accepted (ii) \(sid^i_{U} = sid^j_{U'}\) (iii) \(pid^i_{U} = pid^j_{U'}\). We further define the term freshness.
Definition 3
(Freshness). An instance \(\varPi ^i_U\) is referred to be fresh if it satisfies the following conditions:
-
1.
If the instance \(\varPi ^i_U\) is accepted, neither \(U_i\) nor any of its partnered instances can query Reveal key oracle.
-
2.
No participant is allowed to query Corrupt and Reveal Ephemeral Key simultaneously.
-
3.
In a partnered instance between \(U_i\) and \(U_j\), if an adversary \(\mathcal A\) corrupts \(U_j\), any message sent from \(U_j\) to \(U_i\) must actually come from \(U_j\).
We precisely present here two round interactive authenticated key agreement protocol divided into Setup, KeyGen, Key Agreement and Key Computation phases. We assume existence of a private key generator (PKG) who generates long-term private keys for the users. The users interact among them using their private keys to share session dependent information sid, which leads to compute the session key.
2.3 Security Model for AGKA Protocol
We analyze the security of proposed protocol within the standard security frame of indistinguishability. For the purpose we define the following experiment between the challenger \(\mathcal {C}\) and the adversary \(\mathcal {A}\):
-
Setup: On input a security parameter \(1^{\lambda }\), the challenger \(\mathcal {C}\) runs \(\mathbf KeyGen (1^{\lambda })\) to generate the public parameter \(Params \) and the system key pair \((pk, msk)\) and gives the adversary \(\mathcal {A}\) the public key \(pk\). msk is the master secret of the system.
-
Queries: \(\mathcal {A}\) can adaptively make the following queries:
– Execute(\(\varPi ^i_U\)): Any time the adversary \(\mathcal {A}\) can query for the complete transcripts of an honest execution among the users selected by himself.
– Send(\(\varPi ^i_U, m\)): During the normal execution of the protocol, this query returns the reply generated by instance \(\varPi ^i_U\).
– Reveal Key (\(\varPi ^i_U\)): When the oracle is accepted, this query outputs the group session key.
– Corrupt(\(U_i\)): This query models the reveal of long-term secret key. The participant is honest iff adversary \(\mathcal {A}\) has not made any Corrupt query.
– Ephemeral Key Reveal(\(\varPi ^i_U\)): This query models the reveal of ephemeral key of participant \(U_i\) for instance \(\varPi ^i_U\).
– Test(\(\varPi ^i_U\)): This query can be made only once during the execution of protocol \(\pi \). The challenger responds with a session key.
-
Challenge: During the Test query, the challenger randomly selects a bit
 and returns the real session key if \(b=0\) or a random value if \(b=1\).
and returns the real session key if \(b=0\) or a random value if \(b=1\). -
Guess: \(\mathcal {A}\) outputs its guess \(b'\) for b.
The adversary succeeds in breaking the security if \(b' = b\). We denote this event by \(Succ_\mathcal {A}\) and define \(\mathcal {A}\)’s advantage as \(Adv_\mathcal {A}(1^k) \overset{\text {def}}{=}| 2Pr[Succ_\mathcal {A}] - 1|\).
Definition 4
(AKE-Security). Let \(\mathcal { A}_{ake}\) be an adversary against AKE-security. It is allowed to make queries to the Execute, Send, RevealKey, Corrupt and Ephemeral Key Reveal oracles. It is allowed to make a single Test query to the instance \(\varPi _{U}^{i}\) at the end of the phase and given the challenge session key \(sk_{ch,b}\) (depending on bit b). Finally, \(\mathcal { A}_{ake}\) outputs a bit \(b'\) and wins the game if (1) \(b=b'\) and (2) the instance \(\varPi _{U}^{i}\) is fresh till the end of the game. The advantage of \(\mathcal { A}_{ake}\) is \(Adv_{\mathcal { A}_{ake}}=|2Pr[Succ_{\mathcal { A}_{ake}}]-1|\). The protocol is called AKE-secure if the adversary’s advantage \(Adv_{\mathcal { A}_{ake}}\) is negligible.
Definition 5
(MA-Security with Outsider KCIR). Let \(\mathcal { A}_{ma,out}\) be an outsider adversary against MA-security. Let \(pid_{U}^{i}\) be a set of identities of participant in the group with whom \(\varPi _{U}^{i}\) wishes to establish a session key and \(sid_{U}^{i}\) denotes a session id of an instance \(\varPi _{U}^{i}\). \(\mathcal { A}_{ma,out}\) is allowed to make queries to the Execute, Send, RevealKey, Corrupt and EphemeralKey Reveal oracles. \(\mathcal { A}_{ma,out}\) breaks the MA-security with outsider KCIR notion if at some point there is an uncorrupted instance \(\varPi _{U}^{i}\) with the key \(sk_{U}^{i}\) and another party \(U'\) which is uncorrupted when \(\varPi _{U}^{i}\) accepts such that there are no other insiders in \(pid_{U}^{i}\) and the following conditions hold:
-
there is no instance \(\varPi _{U'}^{i'}\) with \((pid_{U'}^{i'},sid_{U'}^{i'})=(pid_{U}^{i},sid_{U}^{i})\) or,
-
there is an instance \(\varPi _{U'}^{i'}\) with \((pid_{U'}^{i'},sid_{U'}^{i'})=(pid_{U}^{i},sid_{U}^{i})\) which has accepted with \(sk_{U'}^{i'}\ne sk_{U}^{i}\).
Definition 6
(MA-security with insider KCIR). Let \(\mathcal { A}_{ma,in}\) be an insider adversary against MA-security. It is allowed to query Execute, Send, RevealKey, Corrupt and EmphemeralKey Reveal oracles. It breaks the MA-security with insider KCIR if at some point there is an uncorrupted instance \(\varPi _{U}^{i}\) which has accepted with the secret key \(sk_{U}^{i}\) and another party \(U'\) which is uncorrupted when \(\varPi _{U}^{i}\) accepts and
-
there is no instance \(\varPi _{U'}^{i'}\) with \((pid_{U'}^{i'},sid_{U'}^{i'})=(pid_{U}^{i},sid_{U}^{i})\) or,
-
there is an instance \(\varPi _{U'}^{i'}\) with \((pid_{U'}^{i'},sid_{U'}^{i'})=(pid_{U}^{i},sid_{U}^{i})\) which has accepted with \(sk_{U'}^{i'}\ne sk_{U}^{i}\).
3 Authenticated Group Key Agreement Protocol
Our AGKA protocol consists of following algorithms:
- Setup(\(1^{\lambda }\))::
-
On input security parameter \(1^{\lambda }\), the PKG generates the system parameters \(Params \) in the following steps:
– Chooses an elliptic curve group G of prime order q . Let P be a generator of group G
– Computes system’s public key as \(P_{pub}=sP\) by choosing a master secret
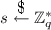
– Chooses cryptographic hash functions \(H_1:\{0,1\}^*\times G \rightarrow \mathbb {Z}_{q}^{*}\), \(H_2:\{0,1\}^*\times G\times G \rightarrow \mathbb {Z}_{q}^{*}\), \(H_3:\{0,1\}^* \rightarrow \mathbb {Z}_{q}^{*}\) and \(H:\{0,1\}^* \rightarrow \{0,1\}^k\)
– Finally, publishes the system parameters
\(Params =\{G, q, H_1, H_2, H_3,H, P_{pub} \}\) and keeps the master key secret.
- KeyGen(s)::
-
The PKG performs the following for all the group members:
– Chooses
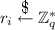 and computes \(R_i=r_i P\)
and computes \(R_i=r_i P\)– Computes the private key for the user \(U_i\) as \(x_i=r_i+sH_1(ID_i,R_i)\)
– The user \(U_i\) can verify the private key as \(x_iP=R_i+H_1(ID_i,R_i)P_{pub}\)
- Key Agreement(\(x_i,pid\))::
-
This protocol runs in the following two rounds:
– Round 1:
Each user \(U_i (1\le i\le n)\) does the following
\(\bullet \) Chooses
 and computes \(l_i=H_3(eph_i,x_i)\) and \(L_i=l_iP\)
and computes \(l_i=H_3(eph_i,x_i)\) and \(L_i=l_iP\)\(\bullet \) Chooses a random string \(k_i \in \{0,1\}^k\) of length k. Each user, except \(U_n\) computes \(H(k_i)\). The user \(U_n\) masks the randomness as \(\tilde{k}_n=H(k_n,x_n)\) where \(x_n\) is long-term secret of \(U_n\). Now, he computes \(H(\tilde{k}_n)\).
\(\bullet \) Broadcasts the tuple \({<}L_i, H(k_i),H(\tilde{k}_n), R_i{>}\) to all \(n-1\) members.
– Round 2:
On receiving the message \({<}L_j, H(k_j),H(\tilde{k}_n),R_j{>}\), each user \(U_i\) performs the following:
\(\bullet \) Computes \(U_{ij}=l_iL_j\) and \(L=L_1 \parallel L_2 \parallel \ldots \parallel L_n \)
\(\bullet \) Each user, except \(U_n\) computes \(K_{ij}=H(U_{ij})\oplus k_i\). The user \(U_n\) computes \(mask=H(U_{ij})\oplus \tilde{k}_n\)
\(\bullet \) Chooses another random number \(t_i \in \mathbb {Z}_{q}^{*}\) and compute \(T_i=t_il_iP\). Also, computes the signature on \({<}L, T_i{>}\) as
\(\sigma _i=t_il_i+x_iH_2(ID_i, L, T_i, pid)\)
\(\bullet \) Broadcasts \({<}K_{ij}(1\le j \le n, j \ne i), mask, \sigma _i, T_i{>}\) to all \(n-1\) members
- Key Computation (\(K_{ji},sid,pid\))::
-
Upon receiving \({<}K_{ji}, mask, \sigma _i, T_i{>}\), each user verifies the received signature as:
$$ \sigma _i P=T_i+(R_i+H_1(ID_i, R_i)P_{pub})H_2(ID_i,L,T_i,pid) $$Each user \(U_i\) then computes \(\tilde{k}_j=H(U_{ji}) \oplus K_{ji}\). Similarly, \(\tilde{k}_n\) can be computed using mask. Note that, \(U_{ij}=l_iL_j=l_il_jP=l_jl_iP=l_jL_i=U_{ji}\). Each user \(U_i\) checks the correctness of \(k_i\) as \(H(k_j)=H(\tilde{k}_j)\) for \((1\le j \le n, j \ne i)\) and computes the session identity \(sid=H(k_1)\parallel H(k_2) \parallel \ldots \parallel H(\tilde{k}_n)\). Finally, the session key is computed as \(sk=H(k_1 \parallel k_2 \parallel \ldots \parallel \tilde{k}_n \parallel sid \parallel pid)\).
Batch Verification: A signature scheme, independently EUF-ACMA secure does not guarantee its security in batch signature. Recall that, the signature algorithms proposed by Schnorr [19], Hess [12] are not secure when used as batch signature. Recently, in a noted contribution by Horng [13], an efficient method was introduced to derive batch signature. Adopting the concept of small exponent test in [13], each member will choose a random vector \(v=(v_1,v_2,\ldots ,v_n)\), where \(v_i\) ranges between 1 and \(2^t\), each \(v_i\) is random, to make sure the property of non-repudiation. To avoid any computational overhead, t is a very small value with error probability at most \(2^{-t}\). Any forged signature can be easily detected with a glitch of probability \(2^{-t}\). Below we present the correctness of our batch verification.
where \(h_{i1}=H_1(ID_i,R_i)\) and \(h_{i2}=H_2(ID_i, L,T_i, pid)\).
4 Security Analysis
In our security proof, we cover the most recent security concept which achieves the AKE and MA security, where the latter covers the impersonation attacks. Particularly, we consider key compromise impersonation (KCI) resilience against insider and outsider adversaries as discussed in [11]. An outsider adversary may compromise the long-term private key of all parties except one. An outsider adversary is successful in KCI attack if it can impersonate an uncorrupted instance (in our case the ephemeral key) of an uncorrupted party to an uncorrupted instance of any of the corrupted parties. The adversary’s goal is to break the confidentiality of the session private key and to break the MA-security. An adversary is called insider adversary if it succeeds in corrupting a party and participating in a protocol session representing the corrupted party. An insider adversary is successful in breaking KCI security if it succeeds to impersonate an uncorrupted instance of an uncorrupted party A to another uncorrupted instance of another party B. The only goal of an insider adversary is to break the MA-security.
Theorem 1
We first show that our protocol is AKE-secure under the hardness of CDH problem and under the condition that the underlying signature scheme is UF-CMA secure and \(H_1,H_2,H_3,H\) are random oracles. The advantage of \(\mathcal { A}_{ake}\) is upper bounded by the following term
where n is the number of participants.
Proof
We prove the theorem via game hopping technique. Let \(E_i\) be an event that \(\mathcal { A}_{ake}\) wins the i-th AKE-security game. Furthermore, let \(\rho _i\) be the advantage of \(\mathcal { A}_{ake}\) in game i. We set \(\rho _i=|2Pr[S_i]-1|\). Our idea of game hopping technique is motivated by [9]. If an event \(E'\) occurs during \(\mathcal { A}_{ake}'\)s execution and it is detectable by simulator, then \(E'\) is independent of \(E_i\). We say that two games \(Game_i, Game_{i+1}\) are identical unless an event \(E'\) occurs such that \(Pr[E_{i+1}|E']=1/2\).
-
Game0: This game is the same as original AKE-security game. The advantage is given by \(Adv_{\mathcal { A}_{ake}}=|2Pr[E_0]-1|=\rho _0\).
-
Game1: This is a game as Game0 except that the simulation of an event fails if an event ‘Forge’ occurs, which means that \(\mathcal { A}_{ake}\) issues a Send query with \((m_i,\sigma _i)\), where user \(U_i\) is not corrupted and \(m_i\) was not output in the previous instance of \(U_i\). According to the AKE-security for KCI attacks definition, \(\mathcal { A}_{ake}\) can corrupt up to \(n-1\) parties, but it cannot modify messages at the instances of corrupted users. If Forge occurs, it can be used to fake signatures given a public key as follows: the public key is assigned to one person where the other \(n-1\) parties are assumed to be normal according to the protocol. Since \(n-1\) parties are corrupt, the secret keys of those \(n-1\) parties are known. The only secret key which corresponds to the public key of the Unf-CMA game can be queried to the signing oracle. The signing oracle is available from the underlying signature scheme. It is obvious that the probability that \(\mathcal { A}_{cma}\) does not corrupt a party is 1/n, such that holds \(Adv_{\mathcal { A}}\ge \frac{1}{n}Pr[Forge]\Leftrightarrow Pr[Forge]\le n Adv_{\mathcal { A}_{cma}}\).
-
Game2: This game is the same as the previous but the simulation fails if an event ‘Collision’ appears. This is the case when one of the random oracles produces a collision. This happens when \(H_{1}(ID_i,R_i)=H_1(ID_i',R_i)\), with |I| possible values for \(ID_{i}'\), where I is the identity space, or \(H_{1}(ID_i,R_i)=H_1(ID_i,R_i')\), with q possible values for \(R_i'\), or \(H_{1}(ID_i,R_i)=H_1(ID_i',R_i')\) with q|I| possible variations for \((ID_i',R_i')\). Since the input of the second hash function consists of 3 entries, there are 6+1 options for a possible collision with in total \(q^2|ID|\) possible value for all options of collisions. Analogously there are 3 options for the collision of \(H_3\) with total \(\lambda !|q-1|\) possible values and 1 collision option for the H function with \(\lambda !\) possible values in total. Each of the Execute and Send queries requires a query to one of the random oracles, such that the number of random oracle queries is bounded by \((q_s+q_e+q_{H_1}+q_{H_2}+q_{H_3}+q_H)^2\). The probability of Collision is:
$$\begin{aligned} Pr[Collision]\le \frac{(q_s+q_e+q_{H_1}+q_{H_2}+q_{H_3}+q_H)^2}{2^{\lambda }} \end{aligned}$$ -
Game3: The game is the same as the previous one, except that the simulation fails when a ‘Repeat’ event occurs. A ‘Repeat’ event happens when an instance of user \(U_i\) chooses a nonce \(\kappa _i\) that was also used by another instance of the user \(U_i\). The maximum of instances which can choose a nonce is \(q_e+q_s\), therefore
$$\begin{aligned} Pr[Repeat]\le \frac{(q_s+q_e)^2}{2^{\lambda }} \end{aligned}$$ -
Game4: This game differs from the previous game by \(\mathcal { A}_{ake}\)’ randomly chosen value \(\nu \) from the set of values which is bounded by Execute and Send queries, i.e. \(x_i\in \{1,\ldots ,q_s+q_e\}\). This value states for the guess of the session in which the adversary will be tested. If \(\mathcal { A}_{ake}\) chooses a different session where he issues Test queries, then the simulation aborts. Otherwise, the event that the adversary picks the right session for being tested, happens with the probability of \(1/(q_e+q_s)\). The probability that the simulation aborts is correspondingly given by \(1-\frac{1}{(q_e+q_s)}\). Therefore we can say that the probability of event \(E_4\) (correct guess) is the reduced probability of the previous event from Game3 plus the abort probability, i.e.
$$\begin{aligned} Pr[E_4]= Pr[E_3]\frac{1}{(q_s+q_e)}+\frac{1}{2}\left( 1-\frac{1}{q_s+q_e}\right) \end{aligned}$$ -
Game5: This game differs from previous game by the differences in answers to the Send queries during the Test session. We assume that in round 1 the values \(l_{i}\) are randomly chosen from \(\{0,1\}^{\lambda }\). All other calculations are the same as in the previous game. Since in the previous game, the values \(l_i\) are results of a hash function, i.e. \(l_i=H_3(\cdot )\), where \(H_3\) is represented as a random oracle, then an adversary \(\mathcal { A}_{ake}\) can distinguish between Game4 and Game5 only if the inputs \(x_i,x_i'\) are distinct. Let \(\tilde{E}\) be an event where the adversary succeeds to distinguish the values of a hash function. Then the probability is \(|Pr[E_4]-Pr[E_5]|\le Pr[\tilde{E}]\). When \(\mathcal { A}_{ake}\) can distinguish between the random and real value, then we can also solve the CDH problem as follows. Let \(U_i\) be a random party involved in the test session, then we set \(R_i=aP\) and \(L_i=bP\). Let C be a randomly chosen value from \(\{0,1\}^{\lambda }\). If \(\tilde{E}\) occurs, then the probability that C chosen from the random oracle table is also the solution of CDH problem, is at least \(1/(q_{H_3})\). It follows, that \(Adv_{CDH}\ge \frac{1}{nq_{H_3}}Pr[\tilde{E}]\).
-
Game6: The difference of this game to the previous one is that the test session aborts if \(\mathcal { A}_{ake}\) issues a query \((k_1||\ldots ||k_n||sid_i||pid_i)\). Since the adversary does not get any information about \(k_n\), he can only guess the value with a probability of \(1/2^{\lambda }\). \(\mathcal { A}_{ake}\) issues at most \(q_{H}\) Test queries. Thus follows:
$$\begin{aligned} |Pr[E_6]- Pr[E_5]|\le \frac{q_{H}}{2^{\lambda }} \end{aligned}$$The advantage of \(\mathcal { A}_{ake}\) in this game satisfies the following equation: \(\rho _5=2\frac{q_{H}}{2^{\lambda }}+\rho _6\). The advantage \(\rho _6\) is 0, if \(\mathcal { A}_{ake}\) does not issue a querry to the H oracle on the correct value \((k_1||\ldots ||k_n||sid_i||pid_i)\).
Combining all the probabilities from the presented games, the advantage of \(\mathcal { A}_{ake}\) is negligible. \(\square \)
In the following theorem, we formulate the MA-security for our protocol.
Theorem 2
We first show that our protocol is MA-secure under the hardness of CDH problem and under the condition that the underlying signature scheme is UF-CMA secure and \(H_1,H_2,H_3,H\) are random oracles. The advantage of \(\mathcal { A}_{ma}\) is upper bounded by the following term
where n is the number of participants.
Proof
The proof follows using the game hopping technique as in the proof of previous theorem. Since the descriptions of the games is very similar to the already presented proof of AKE-security, we sketch it here and show only the final result. The game sequence ends after the third game, where the Forge, Collision and Repeat events could be resolved during the three games. If the game does not abort, it follows that all honest parties from \(pid_i\) compute the same secret key, such that \(Pr[E_3]=0\).
5 Efficiency Analysis
In this section, we compare the efficiency of our proposed AGKA protocol with some recent ID-based GKA protocols [22, 24,25,26,27] (Table 1).
Remark 1
Here, \(\dag \) represents the computation cost of scalar multiplication by a small random integer. Note that the execution time of a scalar multiplication \(v_iP\) (where \(v_i \in [1;2^t]\)) is far less than the usual scalar multiplication in elliptic curve and hence we ignore this for our computation. Here, we consider \(n=5\), for operation time computation. For the operation timings, we refer to [8].
From the above table, it is clear that our proposed AGKA do not require any expensive operation like pairing and hence very efficient with compare to the existing schemes. To the best of our knowledge, ours is the first pairing free balanced AGKA protocol secure in the strong security model, the EGBG model.
6 Conclusion
This paper presents an authenticated group key agreement protocol secure in extended GBG (EGBG) model. The computation cost makes the results interesting especially for low power devices. In the security analysis we allow both the leakage of long term secret key and ephemeral key (of course for different users), as privileged in EGBG model. In particular, we have proved the authenticated key exchange (AKE) security and the mutual authentication (MA) security with full forward secrecy. Moreover, we have done an efficiency analysis and have shown that our scheme is more efficient in the view of computation and operation time with compare to the existing similar schemes which are more acceptable for the tiny processors. To the best of our knowledge, ours is the first pairing free balanced AGKA protocol secure in the EGBG model.
References
Barua, R., Dutta, R., Sarkar, P.: Extending Joux’s protocol to multi party key agreement. In: Johansson, T., Maitra, S. (eds.) INDOCRYPT 2003. LNCS, vol. 2904, pp. 205–217. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-24582-7_15
Bellare, M., Rogaway, P.: Entity authentication and key distribution. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 232–249. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_21
Bresson, E., Chevassut, O., Pointcheval, D.: Provably authenticated group Diffie-Hellman key exchange — the dynamic case. In: Boyd, C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 290–309. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45682-1_18
Bresson, E., Chevassut, O., Pointcheval, D.: Dynamic group Diffie-Hellman key exchange under standard assumptions. In: Knudsen, L.R. (ed.) EUROCRYPT 2002. LNCS, vol. 2332, pp. 321–336. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-46035-7_21
Bresson, E., Chevassut, O., Pointcheval, D., Quisquater, J.-J.: Provably authenticated group Diffie-Hellman key exchange. In: Proceedings of the 8th ACM Conference on Computer and Communications Security, pp. 255–264. ACM (2001)
Burmester, M., Desmedt, Y.: A secure and efficient conference key distribution system. In: De Santis, A. (ed.) EUROCRYPT 1994. LNCS, vol. 950, pp. 275–286. Springer, Heidelberg (1995). https://doi.org/10.1007/BFb0053443
Choi, K.Y., Hwang, J.Y., Lee, D.H.: Efficient ID-based group key agreement with bilinear maps. In: Bao, F., Deng, R., Zhou, J. (eds.) PKC 2004. LNCS, vol. 2947, pp. 130–144. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24632-9_10
Debiao, H., Jianhua, C., Jin, H.: An ID-based proxy signature schemes without bilinear pairings. Ann. Telecommun.-annales des télécommunications 66(11–12), 657–662 (2011)
Dent, A.W.: A note on game-hopping proofs. IACR Cryptology ePrint Archive 2006:260 (2006)
Diffie, W., Hellman, M.: New directions in cryptography. IEEE Trans. Inf. Theory 22(6), 644–654 (1976)
Gorantla, M.C., Boyd, C., González Nieto, J.M.: Modeling key compromise impersonation attacks on group key exchange protocols. In: Jarecki, S., Tsudik, G. (eds.) PKC 2009. LNCS, vol. 5443, pp. 105–123. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00468-1_7
Hess, F.: Efficient identity based signature schemes based on pairings. In: Nyberg, K., Heys, H. (eds.) SAC 2002. LNCS, vol. 2595, pp. 310–324. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36492-7_20
Horng, S.-J., Tzeng, S.-F., Pan, Y., Fan, P., Wang, X., Li, T., Khan, M.K.: b-SPECS+: batch verification for secure pseudonymous authentication in vanet. IEEE Trans. Inf. Forensics Secur. 8(11), 1860–1875 (2013)
Ingemarsson, I., Tang, D., Wong, C.: A conference key distribution system. IEEE Trans. Inf. Theory 28(5), 714–720 (1982)
Joux, A.: A one round protocol for tripartite Diffie–Hellman. In: Bosma, W. (ed.) ANTS 2000. LNCS, vol. 1838, pp. 385–393. Springer, Heidelberg (2000). https://doi.org/10.1007/10722028_23
Katz, J., Shin, J.S.: Modeling insider attacks on group key-exchange protocols. In: Proceedings of the 12th ACM Conference on Computer and Communications Security, pp. 180–189. ACM (2005)
Katz, J., Yung, M.: Scalable protocols for authenticated group key exchange. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 110–125. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-540-45146-4_7
Kyung-Ah, S.: Further analysis of ID-based authenticated group key agreement protocol from bilinear maps. IEICE Trans. Fundam. Electron. Commun. Comput. Sci. 90(1), 295–298 (2007)
Schnorr, C.P.: Efficient identification and signatures for smart cards. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 239–252. Springer, New York (1990). https://doi.org/10.1007/0-387-34805-0_22
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_5
Steiner, M., Tsudik, G., Waidner, M.: Key agreement in dynamic peer groups. IEEE Trans. Parallel Distrib. Syst. 11(8), 769–780 (2000)
Teng, J., Wu, C., Tang, C., Tian, Y.: A strongly secure identity-based authenticated group key exchange protocol. Sci. China Inf. Sci. 58(9), 1–12 (2015)
Wei, F., Wei, Y., Ma, C.: Attack on an ID-based authenticated group key exchange protocol with identifying malicious participants. IJ Netw. Secur. 18(2), 393–396 (2016)
Wu, T.-Y., Tsai, T.-T., Tseng, Y.-M.: A provably secure revocable ID-based authenticated group key exchange protocol with identifying malicious participants. Sci. World J. 2014 (2014)
Wu, T.-Y., Tseng, Y.-M.: Towards ID-based authenticated group key exchange protocol with identifying malicious participants. Informatica 23(2), 315–334 (2012)
Wu, T.-Y., Tseng, Y.-M., Tsai, T.-T.: A revocable ID-based authenticated group key exchange protocol with resistant to malicious participants. Comput. Netw. 56(12), 2994–3006 (2012)
Wu, T.-Y., Tseng, Y.-M., Yu, C.-W.: A secure ID-based authenticated group key exchange protocol resistant to insider attacks. J. Inf. Sci. Eng. 27(3), 915–932 (2011)
Zhang, F., Chen, X.: Attack on an ID-based authenticated group key agreement scheme from PKC 2004. Inf. Process. Lett. 91(4), 191–193 (2004)
Zhao, J., Gu, D., Gorantla, M.C.: Stronger security model of group key agreement. In: Proceedings of the 6th ACM Symposium on Information, Computer and Communications Security, pp. 435–440. ACM (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Sharma, G., Sahu, R.A., Kuchta, V., Markowitch, O., Bala, S. (2018). Authenticated Group Key Agreement Protocol Without Pairing. In: Qing, S., Mitchell, C., Chen, L., Liu, D. (eds) Information and Communications Security. ICICS 2017. Lecture Notes in Computer Science(), vol 10631. Springer, Cham. https://doi.org/10.1007/978-3-319-89500-0_52
Download citation
DOI: https://doi.org/10.1007/978-3-319-89500-0_52
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-89499-7
Online ISBN: 978-3-319-89500-0
eBook Packages: Computer ScienceComputer Science (R0)





 and returns the real session key if
and returns the real session key if 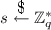
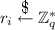 and computes
and computes  and computes
and computes