A Hybrid Heuristic for the Probabilistic Capacitated Vehicle Routing Problem with Two-Dimensional Loading Constraints

Abstract

The Probabilistic Capacitated Vehicle Routing Problem (PCVRP) is a generalization of the classical Capacitated Vehicle Routing Problem (CVRP). The main difference is the stochastic presence of the customers, that is, the number of them to be visited each time is a random variable, where each customer associates with a given probability of presence.

We consider a special case of the PCVRP, in which a fleet of identical vehicles must serve customers, each with a given demand consisting in a set of rectangular items. The vehicles have a two-dimensional loading surface and a maximum capacity.

The resolution of problem consists in finding an a priori route visiting all customers which minimizes the expected length over all possibilities. We propose a hybrid heuristic, based on a branch-and-bound algorithm, for the resolution of the problem. The effectiveness of the approach is shown by means of computational results.

1 Introduction

In the last decades, several variants of Vehicle Routing Problem (VRP) have been studied since the initial work of Dantzig and Ramser [9]. In its classical form, the VRP consists in building routes starting and ending at a depot, to satisfy the demand of a given set of customers, with a fleet of identical vehicles.

In particular, the capacitated Vehicle Routing Problem (CVRP) is a well known variation of the VRP [25], defined as follows: we are given a complete undirected graph $G=(V,E)$ in which V is the set of $n+1$ vertexes corresponding to the depot and the n customers. For each vertex $v_{i}$ is associated a demand $d_{i}$. The demand of each customer is generally expressed by a positive integer that represents the weight of the demand. A set of K identical vehicles is available at the depot. Each vehicle has a capacity Q. The CVRP calls for the determination of vehicles routes with minimal total cost.

Recently, mixed vehicle routing and packing problems have been studied [8, 15, 16]. This problem is called CVRP with two-dimensional loading constraints (2L-CVRP). In 2L-CVRP, two-dimensional packing problems are considered where all vehicles have a single rectangular loading surface whose width and height are equal to W and H, respectively. Each customer is associated with a set of rectangular items whose total weight is equal to $d_{i}$. Solving 2L-CVRP consists in determining the optimal set of vehicles routes of minimal cost to satisfy the demand of the set of customers and without overlapping the loading surface. It is clear that 2L-CVRP is strongly NP-Hard since it generalizes the CVRP (Fig. 1).

Fig. 1.

Example of solution of 2L-CVRP

The 2L-CVRP has an important applications in the fields of logistics or goods distribution. However, in almost all-real world applications, randomness is an inherent characteristic of the problems. For example, in practice whenever a company, in a given day, is faced with only deliveries to a random subset of its usual set of customers, it will not be able to redesign the routes every day since it is not sufficiently important to justify the required effort and cost. Besides, the system’s operator may not have the resources for doing so. Even more importantly the operator may have other priorities.

In both cases, the problem of designing routes can very well modeled by introducing a new variant of 2L-CVRP with the above described constraints, denoted as 2L-PCVRP. Among several motivations, 2L-PCVRP is introduced to formulate and analyze models which are more appropriate for real world problems. 2L-PCVRP is characterized by the stochastic presence of the customers. It means that the number of customers to be visited each time is a random variable, where the probability that a certain customer requires a visit is given. This class of problems differs from the Stochastic Vehicle Routing Problem (SVRP) in the sense that here we are concerned only with routing costs without the introduction of additional parameters [3, 5, 22, 23].

2L-PCVRP has not been previously studied in the literature. The only closely related work we are aware of is the deterministic version 2L-CVRP [16] and Probabilistic Vehicle Routing Problem (PVRP) [4].

In fact, compared with the number of studies available on classical CVRP, relatively few papers have been published on optimizing both routing of vehicles and loading constraints. For deterministic 2L-CVRP, Iori et al. [16] presented an exact algorithm for the solution of the problem. The algorithm is making use of both classical valid inequalities from CVRP literature and specific inequalities associated with infeasible loading constraints. The algorithm was evaluated on benchmark instances from the CVRP literature, showing a satisfactory behavior for small-size instances. In order to deal with more larger sized instances, heuristic algorithms have been proposed. Gendereau et al. [13] developed a Tabu search for the 2L-CVRP. The resolution of the routing aspect is handled through the use of Taburoute, a Tabu search heuristic developed by Gendreau et al. [12] for the CVRP. Some improvements were proposed to the above Tabu search, Fuellerer et al. [10] have proposed an Ant Colony Optimization algorithm, as a generalization of savings algorithm by Clarke and Wright [7] through the addition of loading constraints.

Our aim is to develop a hybrid heuristic for the 2L-PCVRP, to solve the perturbation of the initial problem 2L-CVRP, through a combination of sweep heuristic [14] and a branch and bound algorithm [1].

This paper is organized as follows: Sect. 2 exhibits a detailed description of the problem. Section 3 presents the proposed algorithm for the solution of the 2L-PCVRP. In Sect. 4, computational results are discussed and Sect. 5 draws some conclusions.

2 Problem Description

2L-PCVRP is a NP-Hard since it generalizes two NP-Hard problems that have been treated separately 2L-CVRP and PVRP [4]. In fact, 2L-PCVRP belongs to the class of Probabilistic Combinatorial Optimization Problems (PCOP) which was introduced by Jaillet [17] and studied in [1, 4, 6].

So, 2L-PCVRP is formulated as follows. We consider a complete undirected graph $G=(V,E)$, in which V defines the set of $n+1$ vertex corresponding to the depot $v_{0}$ and the n customers $(v_{1},..., v_{n})$. Each customer $v_{i}$ is associated with a set of $m_{i}$ rectangular items, whose total weight is equal to his demand $d_{i}$, and each having specific width and height equal to $w_{il}$ and $h_{il}$, $(l=1, .., m_{i})$. A fleet of identical vehicles is available. Each vehicle has a capacity Q and a rectangular loading surface S, for loading operations, whose width and height are respectively equal to W and H.

Let P be the probability distribution defined on the subset of V: $\mathbb {P}(V)$, $\tau$ be a given an a priori route through V. Let $L_{\tau }$ be a real random variable defined on, $\mathbb {P}(V)$, which in an a priori route $\tau$ and for each S of $\mathbb {P}(V)$, associates the length of the route through S. For each subset $S \subseteq V$, we consider $\mathcal {U}$ a modification method, it consists in erasing from $\tau$ the absent vertices by remaining in the same order. The solution of the problem consists on finding an a priori route visiting all points that minimizes the expected length $\mathbb {E}$ of a route $\tau$ [4, 17] (Fig. 2).

$$\begin{aligned} \mathbb {E}(L_{\tau ,\mathcal {U}})=\sum _{S\subseteq V}p(S)L_{\tau ,\mathcal {U}}(S) \end{aligned}$$

(1)

Fig. 2.

Example of a priori route for PVRP

In our approach, the priori route is built satisfying the next conditions:

• 1. Each route starts and ends at the depot.

• 2. The total customers demands on one route does not exceed vehicle routing capacity Q.

• 3. All the items of a given customer must be loaded on the same vehicle (each customer is visited once).

• 4. Items don’t have a fixed orientation (a rotation of $90^{\circ }$ is allowed).

• 5. The items delivered on each route must fit within the loading surface S of the vehicle, their total weight should not exceed capacity Q.

• 6. The loading and unloading surface side of the vehicle is placed at height H.

An alternative approach to define 2L-PCVRP is as a combination of the probabilistic travelling salesman problem (PTSP), with a loading constraints which are closely related to the classical and extensively studied 2BPP [20, 21]. The PTSP is the probabilistic version of the well-known problem Travelling salesman problem (TSP), which was introduced by Jaillet [6, 17, 18]. PTSP calls for the determination of priori route of minimal expected total length and 2BPP occurs in determination of packing the given set of rectangular items into the loading surface of the vehicle.

3 Hybrid Heuristic for 2L-PCVRP

Few papers have proposed methods of resolution for PCOPs [1, 4, 24], in this section we present a hybrid heuristic for the solution of 2L-PCVRP based on a branch and bound algorithm for PTSP which proved to be a successful technique. The hybrid heuristic proceed in two stages:

• 1. Sweep Algorithm [14]: we determine clusters (groups of customers) satisfying the six conditions cited above.

• 2. Each obtained cluster is considered an instance of PTSP, we solve it with the branch and bound algorithm [1].

3.1 Sweep Algorithm

The customers are swept in a clockwise direction around a center gravity which is the depot and assigned to groups. Specifically, the sweep algorithm is the following:

Step 1: Calculate for each customer, his polar coordinate $\theta _{i}$ in relation to the depot. Renumber the customers according to polar coordinates so that:

$$\begin{aligned} \theta _{i} < \theta _{i+1}\text {, } 1\le i\le n \end{aligned}$$

(2)

Step 2: Start from the non clustered customer j with smallest angle $\theta _{j}$ construct a new cluster by sweeping consecutive customers $j + 1$, $j + 2\dots$ until the capacity and the bounding of loading surface constraints will not allow the next customer to be added. This means that each cluster must lead to a feasible packing (items of cluster customers are packed without overlapping the loading surface).

It is clear that it is complex to take into account the 2BPP with the loading of the items into the vehicles, with the additional side constraint that all the items of any given customer must be loaded into the same bin. Concerning the complexity, note that the 2BPP is an NP-hard combinatorial optimization problem (see [11]). To this end, simple packing heuristic Bottom-Left [2] is used to solve 2BPP instances. Bottom-Left consists in packing the current item in the lowest possible position, left justified of open bin; if no bin can allocate it, a new one is initialized. The algorithm has $\mathcal {O}(n^{2})$ time complexity.

Step 3: Continue Step 2 until all customers are included in a cluster.

Step 4: Solving each cluster, is tantamount solving an instance of PTSP, where each customer has a probability of presence $p_{i}$. The solution consists in finding a priori route visiting the cluster customers which minimizes the expected total length of the route $\tau$.

3.2 Probabilistic Branch and Bound Algorithm

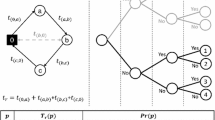
The overall aim is to perform a depth-first traversal of a binary tree by assigning to each branch a probabilistic evaluation. We consider M the distance matrix between the customers. This exact algorithm for solution of the PTSP, is based on the expected length of a route introduced by Jaillet [17]. Let d(i, j) be a distance between the customers $i=$ ABCD$\dots =v_{1}v_{2}v_{3}\dots$, $j = \text {ABCD}\dots =v_{1}v_{2}v_{3}\dots$, and $p=P(k)$ $\forall k\in \tau$, $q=1-p$ where p is the probability of presence, the expected length of a route $\tau$ is shown by (3) (Table 1).

Table 1. Matrix example

$$\begin{aligned} E(L_{\tau })=p^{2}\sum _{r=0}^{n-2}q^{r}\sum _{i=1}^{n}d(i,T^{r}(i)) \end{aligned}$$

(3)

Where $T^{r}(i)$ is the successor number r of i in the route $\tau$.

This design takes the form of “Branch and Bound of Little et al. [19]” but in the probabilistic framework, by deriving the equations of the evaluations, in order to direct the search space towards the promising sub-spaces (i.e., the possibility of finding the optimal solution is very likely).

In the same manner of Littel’s algorithm for the TSP, we reduce the matrix. The lower bound for the TSP equals $Ev_{TSP}$, which will help us to calculate the initial evaluation for the PTSP.

$$\begin{aligned} Ev_{TSP}(n)= \sum _{i=1}^{n} \min R_{i} + \sum _{j=1}^{n} \min C_{j} \end{aligned}$$

(4)

where $R_{i}$ is the $i^{th}$ row and $C_{i}$ is the $j^{th}$ column.

Let $G=(V,E,M)$ be a graph such as $|V|= n$, V is the set of vertices, E the set of edges and M is distance matrix. The probabilistic evaluation $P.E_{PTSP}$: which is defined as follows is considered as a lower evaluation for the PTSP.

$$\begin{aligned} P.E_{\varOmega }=P.Ev_{PTSP}(n)=Ev_{TSP}(n)(p^{2}\sum _{r=0}^{n-2}q^{r})=Ev_{TSP}(n)p(1-q^{n-1}) \end{aligned}$$

(5)

This first evaluation associated with the root $\varOmega$ of the tree shown in Fig. 3. Then, for the next two nodes of the tree, the next two transitional probabilistic evaluations are given due to choice of an arc, according to its effect on the construction of the optimal route. For the arc AB (the same for other arcs):

• 1. Choose AB: increase the expected length of the route at least by

  $$\begin{aligned} P.Ev_{AB}= & {} P.Ev_{\varOmega }+ p^{2} \sum _{r=1}^{n-2} q^{r} [{\min }_{X \ne A}^{(r)}d(A,X)] + p^{2}Ev_{TSP_{Next}} \end{aligned}$$

  (6)

  Where $Ev_{TSP_{Next}}$ is the evaluation of resulting matrix for the TSP where row A and column B are removed.

• 2. Not choose AB: increase the expected length of the route at least by

  $$\begin{aligned} P.Ev_ {\overline{AB}} =&P.Ev_{\varOmega }+ p^{2}[{\min }_{K\ne B}^{(1)} d(A,K)+ {\min }_{K \ne A}^{(1)}(d(K,B))] \\&+\, p^{2} \mathop {\sum }\limits _{r=2}^{n-2}q^{r}[{\min }_{X \ne K}^{(r)}d(A,X)+ {\min }_{X \ne B}^{(r)} d(K,X)] \nonumber \end{aligned}$$

  (7)

  $P.Ev_{\overline{AB}}$ represents the probabilistic penalty cost for the arc $\overline{AB}$, $min^{(i)}d(A,X)$ is the $i^{th}$ minimum of row A, n is the size of the initial matrix. These formulas are valid for all iterations.

The construction starts from the root of the tree, which equals $P.E_{\varOmega }$. The problem is divided into two sub-problems with the approach (depth-first, breadth-first) according to the probabilistic penalties cost. After the penalty calculation, it is easily to get the biggest probabilistic penalty cost. So, we separate according to this arc. First remove the row, column and replace the chosen arc by $\infty$ to prohibiting the parasitic circuits (Table 2).

Table 2. Probabilistic penalties

According to this probabilistic penalty calculation, we construct the first branching of the tree, which is shown in Fig. 3.

Fig. 3.

Branching of the tree for the PTSP

The search continues until all branches that have been visited are either eliminated or the end of the process is reached. That is, the present evaluation is less than the all evaluations, which are defined by the expected length of each final branch by profiting that the expected length can be calculated in $O(n^{2})$ time Jaillet [17].

4 Computational Results

In this section, we first compare our method over the benchmark proposed by Iori et al. [16] for the deterministic 2L-CVRP (we suppose that all customers are present). Next, we exhibit the new instances for 2L-PCVRP, before analyzing the performance of the proposed heuristic on those instances. The final results are reported at the end. The algorithm was coded in Java and all tests were performed on a typical PC with i5-5200U CPU (2.2 GHz) under Windows 8 system.

4.1 Comparison on the 2L-CVRP

By assuming that all customers have a probability of occurrence ($p=1$), deterministic instances of 2L-CVRP are obtained. In this case, our algorithm is only compared to the approach proposed by Iori et al. [16]. The algorithm of Iori was coded in C and was run on a PC with CPU 3 GHz. Because Gendreau et al. [13] and Fuellerer et al. [10] do not solve the problem under the same constraints as we do, direct comparisons with their algorithms can not be made.

To test their algorithm, Iori et al. proposed a benchmark of five classes, for a total of 180 instances. The benchmark presents the coordinates $(x_{i},y_{i})$, the demand $d_{i}$ and the items $m_{i}$ of each customer.

Five classes are considered, which differ in number of customers, number of items, generated items and vehicle capacity. In the first class of instances, each customer has only one item of width and height equal to 1. However, we observed that packing was not constraining so the instances are reduced to the classical CVRP. For the other classes, each customer has 1 to r items in type r $(1\le r \le 5)$. The number of items and items dimensions were randomly generated. For all five classes the loading surface of vehicles was fixed to $W=20$ and $H=40$. The largest instance have up to 255 customers, 786 items and a fleet of 51 vehicles. Table 3 summarizes the different benchmark classes.

Table 3. Classes used for the generation of items

Table 4 presents the comparison of the two approaches. Since the unloading constrains are not considered in our approach, we only compared the total time spent by routing procedures. In each case, we indicate the number of solved instances by both algorithms as well as the average of routing CPU time in seconds for solving those instances.

Table 4. Comparison of two algorithms for deterministic 2L-CVRP

Table 5. Summary of final results

Overall, our algorithm was able to solve instances with up to 255 customers and 786 items while the algorithm of Iori et al. was limited to maximum of 35 customers and 114 items. For the 53 instances solved by both algorithms, our hybrid heuristic took only few seconds compared to hundreds and thousands for the algorithm of Iori et al. This is a very considerable gain, if we take also into account the different performances of the machines used to run the two algorithms.

4.2 Probabilistic Instances

We exploited the 2L-CVRP benchmark described in the previous section to generate our probabilistic instances. Since packing problems do not occur for the class of type 1, when solving all its instances, so we omit it from tests. For each of the 4 classes, we performed tests on 14 instances that differ in numbers of customers varying in $\{15,20,25,30,35,45,50,75,100,120,134,150,200,255\}$ (255 the largest number of customers in the benchmark). For the $14*4=56$ instances, we generated 5 different probabilistic instances, for a total of 280, by varying the probability of presence $p \in \{0.1\text {, } 0.3\text {, } 0.5\text {, }0.7\text {, } 0.9\}$.

The computational results are summarized in Table 5. Each instance is represented by a four digits number : the first two digits corresponds to the instance number, while the last two digits identify the instance class. The column denoted “n" represents the number of customers. The table shows $T_{clust}$ representing the CPU time used by the sweep algorithm. $T_{rout}$ gives the CPU time for generating routes to all clusters using the branch and bound algorithm. $T_{tot}$ reports the total CPU time used by the overall heuristic ($T_{tot}=T_{clust}+T_{rout}$). All times are expressed in seconds.

By observing Table 5, we may see that the proposed heuristic was able to solve all instances with up to 255 customers within moderate computing time. We observed that the heuristic is sensitive to the type of items. In fact, $T_{clust}$ arise increasingly from class 2 to class 5 and this is explained by the fact that class 5 is characterized by a large number of items compared to the rest of classes, if we consider the same instance. This is a typical feature of 2BPP.

As matter of fact, $T_{clust}$, including the CPU time for packing customers items, absorbs a very large part of $T_{tot}$.

When addressing larger instances of 2L-PCVRP, the complexity of the problem increases consistently. This is, however, not surprising because it is well known that the two problems PTSP and 2BPP are NP-hard. We can observe, for the same probability of presence, an increase of $T_{tot}$ going to a factor of 4 (from 1 s to 4 s).

Table 5 shows that a higher percentage of stochastic customers (low values of probability of presence p) increases the complexity of the problem, as indicated by $T_{tot}$. For example, when the probability of presence equals 0.1, $T_{tot}$ increases from 166 ms to 1.55 s through all tested instances.

5 Conclusion and Future Work

This paper has introduced a probabilistic variant of 2L-CVRP, where each customer has a probability of presence. 2L-PCVRP combines the well known probabilistic travelling salesman problem and the two-dimensional bin packing problem.

A hybrid heuristic was presented to deal with the new variant, 2L-PCVRP. The heuristic, is consisted of two phases, where in the first phase, the sweep algorithm was used to generate clusters of customers. Each cluster is solved using a branch and bound algorithm.

The proposed heuristic solved successfully all instances derived for 2L-PCVRP, involving up to 255 customers and 786 items. On the deterministic 2L-CVRP, the heuristic outperformed another state-of-the-art of an exact algorithm.

Future work will consider different variants where, for example, stochastic customers and items are considered.