Leveraging Uncertainty Analysis of Data to Evaluate User Influence Algorithms of Social Networks

Abstract

Identifying of highly influential users in social networks is critical in various practices, such as advertisement, information recommendation, and surveillance of public opinion. According to recent studies, different existing user influence algorithms generally produce different results. There are no effective metrics to evaluate the representation abilities and the performance of these algorithms for the same dataset. Therefore, the results of these algorithms cannot be accurately evaluated and their limits cannot be effectively observered. In this paper, we propose an uncertainty-based Kalman filter method for predicting user influence optimal results. Simultaneously, we develop a novel evaluation metric for improving maximum correntropy and normalized discounted cumulative gain (NDCG) criterion to measure the effectiveness of user influence and the level of uncertainty fluctuation intervals of these algorithms. Experimental results validate the effectiveness of the proposed algorithm and evaluation metrics for different datasets.

1 Introduction

Recent advancements in measuring user influence have resulted in a proliferation of methods which learn various features of datasets. Even when discussing the same topic, different algorithms usually produce different results [2], because of differences in user roles and evaluation metrics, as well as because of improper application scenarios, etc.

Existing research on user influence algorithms can be divided into four categories focusing on four primary areas: (1) message content, (2) network structure, (3) both network structure and message content, and (4) user behaviors. However, these studies and evaluation criteria have not been used to assess the reliability of the algorithms or the error intervals of such reliability.

Algorithms based on message content consider only the influence of ordered pairs, as well as pairs in the incorrect order. These algorithms have not investigate how other social behaviors influence people and information. Network structure approaches often assume that the perception of distance between users has a positive proportional relationship with the degree of influence between users, such as PageRank, Degree Centrality, IARank, KHYRank, K-truss, etc. However, not considering user interest and time for evaluation of user influence. Some studies (including TunkRank, TwitterRank [9], and LDA and its series of topic models) have considered message content and network structure. The majority of algorithms have adopted the Kendall correlation coefficient and friend recommendation scenarios. In addition to considering user behavior, Bizid et al. [1] applied supervised learning algorithms to identify prominent influencers and evaluate the effectiveness of the algorithm. However, when recall is used to evaluate the effectiveness of algorithms for a specific event, differences are not reflected with respect to the relative order of influence among individuals.

To address the above issues, this paper proposes an uncertainty-based Kalman filtering method for predicting optimal user influence result. Additionally, we propose a novel evaluation metric for improving the maximum correntropy and NDCG criterion [4] for measuring user influence effectiveness and the margin of error values for the uncertainty fluctuations of different algorithms.

To summarize, our contributions are as follows:

• (1) An uncertainty-based Kalman filter method is proposed for predicting optimal user influence results. The method uses a measurement matrix, state-transition matrix, and has minimum measurement errors, allowing the method to produce the optimal approximation of (1) the true user-influence value sequence and (2) the periodic measurements of changes in user influence.

• (2) We propose a metric for evaluating user influence algorithms. The metric uses impact-factors and margins of error to evaluate user influence algorithms. This is achieved by improving the maximum correntropy and NDCG criterion for measuring the effectiveness of user influence.

• (3) We propose a method for comparing different influence algorithms and obtaining the error ratios for different algorithms.

2 Problem Formulation

Suppose that there are two algorithms (1 and 2) used to calculate user influence. A common method for performing such calculations is to first apply a mathematical expression for user influence. If the true value of user influence is fixed, then the true value set can be defined as $T=\{Y_{n}\}$, where $Y_{n}$ is the true value of the measurements. The eigen function of this set can be expressed as follows:

$$\begin{aligned} G_{T}(y) = \left\{ \begin{aligned} 1&y_{i}\in T \\ 0&y_{i}\notin T \end{aligned} \right. \end{aligned}$$

(1)

In addition, the measurements have a certain fluctuation range. Therefore, we treated the measurements as a fuzzy set of the true values, and defined it as follows:

$$\begin{aligned} \widehat{T} = \left\{ y,u_{\widehat{T}}(y)|y\in [0,1]\right\} \end{aligned}$$

(2)

where $\widehat{T}$ is the fuzzy set of the true values and $u_{\widehat{T}}(y)$ is a membership function, indicating the probability that y belongs to the true value set.

Fig. 1.

Architecture of IKFE algorithm.

3 Proposed Model

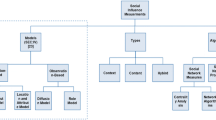
This section focuses on our proposed model (improved Kalman filter estimation, IKFE); the associated framework is shown in Fig. 1. Section 3.1 describes our representation of the user influence function, among the true values ($x_k$), optimal estimate values ($\hat{x}_k$), predictive values ($\hat{x}_{k|k-1}$), and measurement values ($z_k$) for user influence produced different algorithms. Section 3.2 illustrates the optimal estimates and parameter learning for user influence.

3.1 Function of User Influence

The initial value of a user’s influence, such as $a_k^1$, $a_k^2$, and $a_k^3$, was the result of one of the different influence algorithms at time k in Fig. 1. This value was regarded as a state variable to be estimated; the measurements of its calculated values were regarded as the measurements of its state.

• (1) True Value of User Influence: The true value of user influence at time k can be expressed by the optimal estimated user influence value and the optimal estimation error that occurs in the computing process:

  $$\begin{aligned} x_k = \widehat{x}_k + r_k \end{aligned}$$

  (3)

  where $x_k$ is the true value vector at time k; $\widehat{x}_k$ is the optimal estimated value vector at time k; and $r_k$ is the estimated error vector at time k.

• (2) User Influence Prediction and Value: We used a state-transition matrix to model changes in user influence. We could consider the process error to be the uncertainty. The true value of user influence at time k is generated from the state transition of users’ influence at time $k-1$, which is expressed as

  $$\begin{aligned} x_k = F_{k-1}x_{k-1} + w_{k-1} \end{aligned}$$

  (4)

  where $F_{k-1}$ denotes the state-transition matrix at time $k-1$ and $w_{k-1}$ denotes the process error at time $k-1$.

  The predicted value of user influence at time k, which is generated based on the users’ states at time $k-1$, can be expressed as the product of the state transition matrix, as well as the optimal estimate at time $k-1$.

  $$\begin{aligned} \widehat{x}_{k|k-1} = F_{k-1}\widehat{x}_{k-1} \end{aligned}$$

  (5)

• (3) User Influence Measurements and Values: The following equation can be computed the relationship between the measured value and the true values of user influence, which can be expressed as follows:

  $$\begin{aligned} z_{k} = H_{k}x_{k} + v_{k} \end{aligned}$$

  (6)

  where $z_{k}$ denotes the measured value of user influence at time k, $H_{k}$ denotes the measurement matrix, $v_{k}$ denotes the measurement error, and $x_{k}$ is the true value of user influence at time k.

3.2 Optimal Estimate of User Influence

Based on Eq. (3) and the goal of achieving the minimum error for optimal estimates can be expressed as follows:

$$\begin{aligned} minJ_{k} = E[r_{k}^{T}r_{k}] \end{aligned}$$

(7)

The best estimate of user influence at time k can be expressed as follows:

$$\begin{aligned} \widehat{x}_{k} = \widehat{x}_{k|k-1} + G_{k}(z_{k}-H_{k}\widehat{x}_{k|k-1}) \end{aligned}$$

(8)

where $G_k$ is the Kalman filter’s gain [5].

4 Evaluation of User Influence Algorithms

In this section, we discuss our proposed metrics for evaluating user influence (improving the maximum correntropy criterion, IMCC) and the error intervals between different user influence algorithms. Section 4.1 presents our proposed criterion for evaluating user influence. In Sect. 4.2, metrics are applied to measure the margin of error of user influence algorithms.

4.1 Proposed Criterion

It can be seen from Eq. (6) that the measurement of user influence is to restore the true value of user influence through the measurement matrix ($H_{k}$). Specifically, the correntropy of the measurement sequence generated from the state-of-the-art algorithm and true value sequence is maximized (improving maximum correntropy criterion), which can be expressed as follows:

$$\begin{aligned} Sim(X,Y) = E[\ell (X,Y)]=\int \ell (X,Y)\, dP_{X,Y}(x,y) \end{aligned}$$

(9)

where X is the measurement sequence, Y is the true value sequence, $P_{X,Y}(x,y)$ expresses an unknown joint probability distribution, and $\ell (X,Y)$ is a shift-invariant Mercer kernel function. $\ell (X,Y)$ can be expressed as follows:

$$\begin{aligned} \ell (X,Y) = exp\left( -\frac{e^2}{2\sigma ^2}\right) \end{aligned}$$

(10)

where $e=X-Y$, $\sigma$ indicates the window size of the kernel function, and $\sigma >0$. The derivation is presented in [3]. Thus, we can obtain the following optimal target:

$$\begin{aligned} argmax\frac{1}{N}\sum _{i=1}^{N}G\left( e_i\right) \end{aligned}$$

(11)

where N is the number of users in the sample. The function $G\left( e_i\right)$ can be expressed as follows:

$$\begin{aligned} \sum _{i=1}^{T}\frac{\left( 2^{R_i}-1\right) + f_i}{\log _{2}\left( i+1\right) + \varDelta l_i} \end{aligned}$$

(12)

where $R_i$ indicates the standard influence score of user i, and T is the truncation level at which $G\left( e_i\right)$ is computed. Here, $\varDelta l_i$ denotes the error intervals of i in the results. $f_i$ represents the adjustment factor of i’s influence, which can be expressed as follows:

$$\begin{aligned} f_{i} = \sum _{z=1}^{n}w_{iz} \frac{k_{iz}}{\varDelta t_{iz} + 1} \end{aligned}$$

(13)

where $w_{iz}$ indicates the weighted value of user i being the maker of topic z, $k_{iz}$ is the number of messages sent by user i regarding topic z, and $\varDelta t_{iz}$ denotes the length of time that user i participated in the discussion of topic z.

4.2 Evaluation of User Influence Algorithms

Substituting the measurement of user influence calculated by corresponding algorithms and the results of manual scoring in Eq. (6) yields the following proportional relationship between the measurement error of Algorithms 1 and 2. This can be expressed as follows:

$$\begin{aligned} I = \frac{\left( H_{k}^{'} - H_{k(2)}\right) ^{-1}v_{k(2)}}{\left( H_{k}^{'} - H_{k(1)}\right) ^{-1}v_{k(1)}} \Longrightarrow \frac{v_{k(2)}}{v_{k(1)}} = \left( \frac{I - H_{k(2)}}{I - H_{k(1)}}\right) \end{aligned}$$

(14)

Equation (14) shows that the measurement errors of Algorithm 1 and 2 depend on the measurement matrix, and they are inversely proportional to the shift-invariant Mercer kernel function and proportional to the maximum correntropy. The detailed derivation process is not shown here due to lack of space.

5 Experiment

Experimental data were obtained from two data sets: RepLab-2014¹, and the Twitter dataset obtained from our own network spider, as listed in Table 1. The results for the top 10, top 20, top 40 user sequences computed by our proposed algorithm were compared with the results from state-of-the-art algorithms with single-feature algorithms for identifying user influence (using NDCG, the Kendall correlation coefficient, and the IMCC metric).

Table 1. Experimental datasets

Table 2. Evaluation of NDCG and IMCC based on Paired Tests Bootstrap Tests and estimated difference required for satisfying achieved significance level (ASL), $ASL < \alpha$ $(\alpha$ = 0.05; Twitter dataset).

5.1 Evaluation Criteria

To evaluate the validity of the IKFE algorithm and IMCC metric, the IKFE algorithm was compared with TwitterRank (TR) [9], Topic-Behavior Influence Tree (TBIT) [10], ProfileRank (ProR) [7] and single-feature-based algorithms for measuring user influence in the two datasets.

5.2 Performance Analysis

Analysis of $\sigma$ Parameter and IKFE Algorithm. Figure 2 show that the parameter $\sigma$ takes different window sizes, such as 10, 20, and 40, thus impacting the performance of the algorithm. Especially, a window size of 10 results in a significantly different performance of the algorithm compared to window sizes of 20 and 40. As the window size increases, the performance of various algorithms’ capacity approximates the same. For the IKFE algorithm, user influence shows a slow decrease from time k to $k+1$. Figure 3 shows that the values of single-feature algorithms show a greater change than those of other algorithms. In other words, IKFE algorithm is better able to synthesize features. Simultaneously, the fluctuation range of the IKFE algorithm is limited.

Fig. 2.

Trend of algorithms for different $\sigma$ based on the Kendall coefficient for the RepLab-2014 dataset.

Fig. 3.

Correlation of IKFE algorithm and other algorithms by the Kendall on different topics at k + 1 time.

Comparison Metrics. As in previous work [6], we set $B = 1,000$ (B is the number of bootstrap samples). In Table 2, the p-value denoted by “Sig. (2-tailed)” is two-sided. Our results show different p-values for different window sizes. The results for the IMCC metric are not significant at the 0.05 level, whereas those for the NDCG are significant when experimenting with user sequences on $c^3$ (cross-topics) or different window sizes. It can be observed that the IMCC is more sensitive [6] than the NDCG. The IMCC is better that the NDCG in terms of estimated differences as the discriminative power described by [8].

6 Conclusions

We used IKFE, an uncertainty-based improved Kalman filter method, to predict the optimal user influence results. Additionally, we proposed IMCC, a metric for evaluating influence algorithms by improving the maximum correntropy and NDCG criterion. Next, we will study how to evaluate user influence algorithms of communities in social networks.