Keywords

1 Introduction

After financial crisis, credit risk has been considered more serious, especially in over-the-counter market, which lacks margin and collateral. So many credit derivatives, such as credit default swap (CDS), collateralized debt obligation, have been created and used in financial activities to manager such risks. To manage the credit risk of interest rate swap (IRS), credit contingent interest rate swap (CCIRS) is designed and traded in the market [16].

CCIRS is a contract which provides protection to the fixed rate payer for avoiding the default risk of the floating rate payer in an IRS contract. The fixed rate payer purchases a CCIRS contract from the credit protection seller at the initial time and the protection seller will compensate the credit loss of the protection buyer in the IRS contract if the default incident happen during the life of the deal. This credit derivative offers a new way to deal with the counterparty risk of IRS. It is similar to CDS, though the value of the its underling IRS can be positive or negative.

The inventions of those credit instruments provide an effective method to separate and transfer the credit risk. However, to buy them, a lot of money should be paid to the protection seller which will occupy the funds of companies and cause a corresponding increasing in liquidity strain. No doubt that this financial problem will pose a new challenge to the operation of companies.

To solve CCIRS initial cost problem, using the fact of the value of IRS might positive or negative, we design a new CCIRS with a special item, which is a later clause to reduce the initial cost of purchasing this credit derivative. Then we establish a pricing model to valuation this new product, we can even find that an appropriate item will make a zero cost of this credit instrument in the purchasing time.

To pricing a credit derivative, there are usually two frameworks: Structure and Reduced form ones. In our pricing model, the reduced form framework is used. That is, the default is assumed to be governed by a default hazard rate with parameters inferred from market data and macroeconomic variables. In the literatures, Duffie [6], Lando [8] and Jarrow [11] gave examples of research following this approach. The structure and pricing model for ordinary IRS has been presented in [2]. Duffie and Huang [7] discussed the default risk of IRS under the framework of reduced form. Li [10] studied the valuation of IRS with default risk under the contingent claim analysis framework. Brigo et al. [3] considered the Credit Valuation Adjustment of IRS with considering the wrong way risk. The pricing of single-name CCIRS was given in [12] by Liang et al., where a Partial Differential Equation (PDE) model is established with some numerical results. Using multi-factors Affine Jump Diffusion model, Liang and Xu [13] obtain a semi-closed solution of the price of single-name CCIRS.

Due to the IRS being the underlying asset, the value of the protection contract is closely connected with the stochastic interest rate. In this paper, we use a single factor model where the main factor of the default intensity is the stochastic interest rate. The model can be changed to a PDE problem. Using the PDE methods, a semi-closed form solution of the pricing model is obtained. In short words, in this paper, 1. we design a CCIRS with a new payment way; 2. under reduced framework, the new product has been valued; 3. a semi-closed form of the solution is obtained; 4. numerical examples are presented, with different parameters. The comparison of the origin and new designs are also shown.

This article is organized as follows. In Sect. 2, we give model assumptions, establish and solve the pricing model of CCIRS with the special item under the reduced form framework. In Sect. 3, numerical results are provided. The conclusion of the paper is given in Sect. 4.

2 Model Formulation

In this section, we develop a continuous time valuation framework for pricing CCIRS with the special item. First of all, let us explain the contract. Consider an IRS contract between two parties, the fixed rate payer Party A and the floating rate payer Party B. At the view point of Party A, we assume that Party A is a default-free institution and Party B has a positive probability of default before the final maturity. To avoid the counterparty risk, Party A buys a special protection contract with Party C. At the initial time, A pays a premium to C. Before the expiry time of IRS, if B defaults, A will receive compensation from C if A has any loss. The contract is ended after A receiving the compensation. On the contrary, if B doesn’t default during the life of the contract, at the termination time, the protection buyer A needs pay another later premium to protection seller C. We call this particular clause a later cash flow item. The later premium is the one predetermined in the contract, which will affect the initial premium, and is interesting to study. Figure 1 is a conventional diagram of the process of this product.

Fig. 1.
figure 1

Structure of CCIRS with the special item

Full size image

2.1 Model Assumptions

Using the probability space \((\varOmega , \mathcal {G}, \mathcal {G}_t, Q)\) to model the uncertain market, where Q is the risk-neutral measure, and \(\mathcal {G}_t\) represents all market information up to time t. As usual, we can write \(\mathcal {G}_t=\mathcal {F}_t\vee \mathcal {H}_t\), where \(\mathcal {F}_t\) is the filtration contains all the market information except defaults. \(\mathcal {H}_t=\sigma \{{1_{\{\tau <s\}}\mid s\le t}\}\) represents the default information of Party B. Let \(\tau \) be the default time of floating rate payer in the swap contract, assume it a \(\mathcal {G}_t\) stopping time, i.e. \(\{\tau \le t\}\in \mathcal {G}_t\). The default time \(\tau \) can be defined as

$$\begin{aligned} \tau =\inf \big \{t; \int _0^t\lambda _sds\ge \eta \big \}, \end{aligned}$$

where \(\eta \) is the unit mean exponential random variable and \(\lambda \) is the default intensity. So the distributions of conditional default probability of Party B can be given by

$$\begin{aligned} Prob\big [\tau \le t | \mathcal {F}_t\big ]=1-\exp \big (-\int _0^t\lambda _sds\big ). \end{aligned}$$

We assume the risk free interest rate \(r_t\), which is \(\mathcal {F}_t\) adapted, follows the stochastic CIR process:

$$\begin{aligned} dr_t=\kappa (\theta -r_t)dt+\sigma \sqrt{r_t}dW_t, \end{aligned}$$

where \(\kappa \), \(\theta \) and \(\sigma \) are positive constants, which represent the speed of adjustment, the mean and the volatility of \(r_t\) respectively. The condition \(\kappa \theta >{\sigma ^2}/{2}\) is required to insure \(r_t\) to be a positive process. \(W_t\) is a standard Brown motion.

Let \(\tilde{P}\) be the notional principal of the IRS and \(r^*\) be the predetermined swap rate the fixed rate payer A promises to pay. The value of the IRS for Party A without considering the counterparty risk at time t before maturity T is denoted by f(t, r). We approximate the discrete payments with a continuous stream of cash flows, i.e., in this IRS contract, Party A needs pay \(\tilde{P}(r_t-r^*)dt\) to Party B continuously. Thus, under the risk-neutral measure Q, f(t, r) can be represented as

$$\begin{aligned} f(t,r)=E^Q[\int _t^T\tilde{P}(r_s-r^*)e^{-\int _t^sr_\theta d\theta }ds|\mathcal {F}_t], \end{aligned}$$

Due to the fact that the value of a default-free floating rate loan equals its principal (see [4]), we obtain

$$\begin{aligned} 1=E^Q[\int _t^Tr_se^{-\int _t^sr_\theta d\theta }ds+e^{-\int _t^Tr_\theta d\theta }|\mathcal {F}_t]. \end{aligned}$$

So we can derive the following equality

$$\begin{aligned} f(t,r)= & {} \tilde{P}-\tilde{P}E^Q[e^{-\int _t^Tr_\theta d\theta }|\mathcal {F}_t]-\tilde{P}r^*E^Q[\int _t^Te^{-\int _t^sr_\theta d\theta }ds|\mathcal {F}_t],\\= & {} \tilde{P}-\tilde{P}B(t,T)-\tilde{P}r^*\int _t^TB(t,s)ds. \end{aligned}$$

Here, B(t, s) is the price of a s-maturity zero-coupon bond at time t, which has closed form expression within the CIR framework (see [5]).

2.2 Price of the Contract

An analysis of the cash flows of the protection contract is as follows:

  • At the initial time, Party A pays an initial premium to protection seller Party C.

  • Suppose at \(\tau \le T\), the Party B cannot fulfill its obligations. There are two cases: 1. the valuation of the residual payoff of the IRS contract with respect to Party A is positive, the Party C compensates the loss \((1-R)f^+(\tau ,r_\tau )\) to Party A, where \(f^+(\tau ,r_\tau )=\max \{f(\tau ,r_\tau ),0\}\) and R is the recovery rate; 2. the valuation of IRS is non-positive, the contract CCIRS stops without any cash flow between Party A and Party C.

  • If \(\tau >T\), there is no default by Party B during the life of the IRS contract and the Party A has no loss. The Party A pays the later floating premium \(\alpha \tilde{P}Tr_T\) to C. Here \(\alpha \) is the adjustable factor and we call \(\alpha \) later premium rate.

There are several reasons for setting the later premium as \(\alpha \tilde{P}Tr_T\). First, we expect to reduce the initial premium for buying the protection contract through adjusting the later premium rate, which significantly makes the contract flexible. Thus, the company can choose the appropriate contract to free up money for investment in the production of other items. Secondly, the setting makes the later premium linearly change with the life of the contract. Finally, a floating premium setting makes the later premium decreasing with the floating interest rate. Through the above analysis, under the risk-neutral measure Q, the price of the protection contract can be described as

$$\begin{aligned} E^Q[1_{\{t<\tau <T\}}f^+(\tau ,r_\tau )(1-R)e^{-\int _t^{\tau }r_\theta d\theta }-1_{\{\tau >T\}}\alpha \tilde{P} Tr_T e^{-\int _t^Tr_\theta d\theta }|\mathcal {G}_t]. \end{aligned}$$
(1)

Using the results in [8], (1) can be rewritten as

$$\begin{aligned} 1_{\{t<\tau \}}E^Q[\int _t^T\lambda _u f^+(u,r_u)(1-R)e^{-\int _t^{u}(r_\theta +\lambda _\theta ) d\theta }du-\alpha \tilde{P}T r_T e^{-\int _t^T(r_\theta +\lambda _\theta ) d\theta }|\mathcal {F}_t]. \end{aligned}$$

Let \((\mathcal {F}_t)_{t\ge 0}\) be the filtration generated by the process \(r_t\) and the intensity process \(\lambda \) is smooth function of \(r_t\). By the strong Markov property of \(r_t\), we obtain the following representation of the pre-default value V of the protection contract

$$\begin{aligned} V(t,r,\alpha )=E^Q[\int _t^T\lambda _u f^+(u,r_u)(1-R)e^{-\int _t^{u}(r_\theta +\lambda _\theta ) d\theta }du-\alpha \tilde{P}T r_T e^{-\int _t^T(r_\theta +\lambda _\theta ) d\theta }|r_t=r]. \nonumber \\ \end{aligned}$$
(2)

If the protection contract signed at time t, the buyer A needs to pay the initial premium \(V(t,r_t,\alpha )\) to the protection seller. By Fubini theorem, we can obtain

$$\begin{aligned} V(t,r,\alpha )= & {} \int _t^T E^Q[\lambda _u f^+(u,r_u)(1-R)e^{-\int _t^{u}(r_\theta +\lambda _\theta ) d\theta }|r_t=r]du\\&-\,\alpha \tilde{P}TE^Q[r_Te^{-\int _t^T(r_\theta +\lambda _\theta ) d\theta }|r_t=r]. \end{aligned}$$

Denote

$$\begin{aligned} \varphi _1(t,r;u)= & {} E^Q[\lambda f^+(u,r_u)(1-R)e^{-\int _t^{u}(r_\theta +\lambda _\theta ) d\theta }|r_t=r],\quad 0\le t\le u,\end{aligned}$$
(3)
$$\begin{aligned} \varphi _2(t,r;T)= & {} E^Q[r_Te^{-\int _t^T(r_\theta +\lambda _\theta ) d\theta }|r_t=r],\quad 0\le t\le T. \end{aligned}$$
(4)

Below we will use the PDE methods to solve (3) and (4). To describe the joint behavior of interest rate \(r_t\) and the default intensity of Party B, we assume they are correlated through affine dependence, i.e.

$$\begin{aligned} \lambda _t=ar_t+b, \end{aligned}$$
(5)

where a, b are positive constants. In this situation, the default intensity \(\lambda _t\) is a monotone increasing function with respect to the interest rate \(r_t\). So the floating rate payer will present a higher default risk as the interest rate rising up.

Suppose that \(\varphi _1, \varphi _2\) satisfy suitable regularity conditions. Using the Feynman-Kac formula, the expectation in (3) is also a solution to the equation

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial \varphi _1}{\partial t}+\kappa (\theta -r)\frac{\partial \varphi _1}{\partial r}+\frac{1}{2}r\sigma ^2\frac{\partial ^2\varphi _1}{\partial r^2}-(ar+r+b)\varphi _1=0, &{} 0<r<\infty , 0\le t\le u, \\ \varphi _1(u,r)=(ar+b)f^+(u,r)(1-R), &{} 0<r<\infty , \end{array} \right. \nonumber \\ \end{aligned}$$
(6)

where u is any time between 0 and T.

Referencing [14, 15], (6) has a explicit solution

$$\begin{aligned} \varphi _1(t,r;u)=e^{-(p\kappa \theta +\kappa q+\sigma ^2pq+b)(u-t)-pr}r^qw(t,r;u), \end{aligned}$$
(7)

where

$$\begin{aligned}&w(t,r;u)=\int _0^\infty f^+(u,\xi )(1-R)(a\xi +b)e^{p\xi }\xi ^{-q}G(t,r;u,\xi )d\xi ,\nonumber \\&p=\frac{-\kappa -\sqrt{\kappa ^2+2(a+1)\sigma ^2}}{\sigma ^2}, \qquad q=1-\frac{2\kappa \theta }{\sigma ^2},\nonumber \\&G(t,r;u,\xi )=\varepsilon e^{-\phi -\varphi }(\frac{\psi }{\phi })^{\frac{\nu }{2}}I_\nu (2(\phi \psi )^\frac{1}{2}),\\&\varepsilon =\frac{2(\kappa +\sigma ^2p)}{\sigma ^2(1-e^{-(\kappa +\sigma ^2p)(u-t)})},\quad \phi =\varepsilon re^{-(\kappa +\sigma ^2p)(u-t)},\nonumber \\&\psi =\varepsilon \xi ,\quad \nu =\frac{2(\kappa \theta +\sigma ^2q)-\sigma ^2}{\sigma ^2},\nonumber \end{aligned}$$
(8)

and \(I_\nu (\cdot )\) is the modified Bessel function of the first kind of order \(\nu \), i.e.,

$$I_\nu (2(\phi \psi )^\frac{1}{2})=(\phi \psi )^{\frac{\nu }{2}}\sum ^\infty _{k=0}\frac{(\phi \psi )^k}{k!\varGamma (\nu +k+1)}.$$

We can also see that \(\varphi _2\) is the solution of the equation

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{\partial \varphi _2}{\partial t}+\kappa (\theta -r)\frac{\partial \varphi _2}{\partial r}+\frac{1}{2}r\sigma ^2\frac{\partial ^2\varphi _2}{\partial r^2}-(ar+r+b)\varphi _2=0, &{} 0<r<\infty , 0\le t\le T, \\ \varphi _2(T,r)=r, &{} 0<r<\infty . \end{array} \right. \nonumber \\ \end{aligned}$$
(9)

Using the methods in [15], we can obtain

$$\begin{aligned} \varphi _2(t,r;T)=\frac{\varepsilon ^{\nu +1}e^{-\phi }\varGamma (2-q+\nu )}{(\varepsilon -p)^{2-q+\nu }\varGamma (\nu +1)}M(2-q+\nu ,\nu +1,\frac{\varepsilon \phi }{\varepsilon -p}), \end{aligned}$$
(10)

where \(M(x,y,z)=\sum _{k=0}^{\infty }((x)_k/(k!(y)_k)z^k)\) is the confluent hypergeometric function and \((x)_k\) is defined by \((x)_k=x(x+1)\cdots (x+k-1)\) for \(k>0\), \((x)_0=1\).

Then we can state the main result from the above analysis.

Theorem 1

The pre-default value of CCIRS with the later premium item is given by

$$\begin{aligned} V(t,r,\alpha )=\int _t^T\varphi _1(t,r;u)du-\alpha \tilde{P}T\varphi _2(t,r;T). \end{aligned}$$
(11)

where \(\varphi _1\) and \(\varphi _2\) are given by (7) and (10) respectively.

From (4), it can be shown that \(\varphi _2>0\). Therefore the price of the protection contract is linearly decreasing with the later premium rate \(\alpha \) going up. If a company wants to buy a protection contract with a lower price, it can sign the contract with a higher \(\alpha \). Thus, this special item makes this CCIRS contract more flexible and more attractive because it has its own advantage for reducing the funding cost, that is to say, supplying liquidity at initial time.

Remark 1

  1. (i)

    The intensity model (5) assumes \(\lambda _t\) is positive affine dependence with \(r_t\). We can use the inverse CIR model [9] to describe the negative correlation between \(\lambda _t\) and \(r_t\), i.e.

    $$\lambda _t=\frac{a}{r_t}+b.$$

    Using the similar methods above, we can also obtain the solutions

    $$\begin{aligned} \varphi _1= & {} e^{-(p\kappa \theta +\kappa q+\sigma ^2pq+b)(u-t)-pr}r^q\int _0^\infty f^+(u,\xi )(1-R)(\frac{a}{\xi }+b)e^{p\xi }\xi ^{-q}G(t,r;u,\xi )d\xi ,\nonumber \\ \end{aligned}$$
    (12)
    $$\begin{aligned} \varphi _2= & {} \frac{\varepsilon ^{\nu +1}e^{-\phi }\varGamma (2-q+\nu )}{(\varepsilon -p)^{2-q+\nu }\varGamma (\nu +1)}M(2-q+\nu ,\nu +1,\frac{\varepsilon \phi }{\varepsilon -p}), \end{aligned}$$
    (13)

    where \(G(t,r;u,\xi )\) is the fundamental solution of CIR process shown in (8). p, q are the solution of the following equations

    $$\begin{aligned} q\kappa \theta +\frac{1}{2}\sigma ^2q(q-1)-a=0,\quad p\kappa +\frac{1}{2}\sigma ^2p^2-1=0. \end{aligned}$$
  2. (ii)

    In the above model, we assume floating rate payer has a default risk. Similarly, we can price the protection contract if the protection buyer is the floating rate payer. i.e., the fixed rate payer is the one who has the default risk. The price of the protection contract can be written as

    $$\begin{aligned} E^Q[1_{\{t<\tau <T\}}f^-(\tau ,r_\tau )(1-R)e^{-\int _t^{\tau }r_\theta d\theta }-1_{\{\tau >T\}}\alpha \tilde{P} T r_T e^{-\int _t^Tr_\theta d\theta }|\mathcal {G}_t], \end{aligned}$$
    (14)

    where \(f^-(\tau ,r_\tau )=\max (-f(\tau ,r_\tau ),0)\) is the valuation of the residual payoff of the IRS contract with respect to the floating rate payer at time \(\tau \). R is the recovery rate of IRS contract when default occurs.

  3. (iii)

    The main content of our model design is to add a later payment clause in the contract to reduce the initial premium. This idea can also be used in CDS contract, whose reference assets are the corporation bonds.    \(\mathrm{None}\)

3 Numerical Results

In this section, we provide a numerical example to illustrate how market parameters affect the value of the protection contract. Throughout the numerical analysis, unless otherwise stated, the basic parameters are given as follows:

$$\kappa =0.3, \theta =0.02, \sigma =0.02, \tilde{P}=1, T=1, a=9, b=0.2, R=0.4, r^*=0.04.$$
Fig. 2.
figure 2

V and r, t

Full size image
Fig. 3.
figure 3

V and \(\alpha \)

Full size image

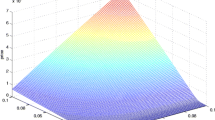
The Fig. 2 shows the relationship between the price of the contract, interest rate r and life time T of the contract. The later premium rate \(\alpha =0.05\).

Firstly, the curve shows that the value of the protection contract is decreasing with respect to t. Under the same conditions, with t approximates to T, the value of residual payoff of the IRS contract is smaller, so the protection contract will have a lower price.

Secondly, Fig. 2 shows that the value of the protection contract is increasing with r at the initial time. Actually, according to the intensity model (5), higher r will generate a higher default intensity. In addition, with a higher initial interest rate, when default event happens, the probability of positive value of IRS is bigger. That is, the protection seller is more likely to compensate the loss.

Let \(r_0=0.05\), we plot the price curve with different later premium rate \(\alpha \) in Fig. 3. The value of the contract is linearly decreasing with respect to \(\alpha \). It is consistent with the Eq. (11). In fact, the later premium will increase with bigger \(\alpha \). So at the initial time, the contract will have a lower price. Especially, when \(\alpha \) is appropriate, the price of CCIRS will be zero at initial time. That means the protection buyer should not pay anything at the signing date of the contract. Thus, it will reduce the funding costs when the company signs the CCIRS. If the fixed rate payer wants a protection for the IRS and has insufficient capital at the initial time, it could purchase a CCIRS with a proper later premium rate \(\alpha \).

Fig. 4.
figure 4

V and a

Full size image
Fig. 5.
figure 5

V and b

Full size image

Figures 4 and 5 show the sensitivity of the price of the contract to the intensity parameters a, b respectively. Larger a, b mean a bigger default probability. It causes the increase of the price of the protection contract.

Fig. 6.
figure 6

Comparison of the values of old and new designs

Full size image

Figure 6 shows the value of the CCIRS with new and old designs at the initial time, the below one is \(\alpha =0.05\), and the up one is \(\alpha =0\). i.e. the up and below are the values of the old and new designs respectively. r indicates the interest rate at initial time. It is clear that as the late payment condition, at initial time, the new design contract is cheaper than the traditional one for the buyer.

4 Conclusions

In this paper, we design a new credit contingent interest rate swap with a later payment item and provide its pricing model for valuation. Using the CIR model to describe the floating interest rate, under the reduced form framework, we calculate the price this derivative with a default intensity relevant to interest rate. The semi-closed form solutions of the pricing model are presented. We find that the later cash flow item will reduce the initial premium efficiently. At last, the numerical results show that the price of the contract is increasing with the short interest rate. A appropriate later premium rate, as in Fig. 3, will make the price of the contract be zero at the signing date. We hope that our work would be helpful for industries when they want to increase the cash liquidity in financial activities.