Effective Semi-supervised Learning Based on Local Correlation

Abstract

Traditionally, the manipulation of unlabeled instances is solely based on prediction of the existing model, which is vulnerable to ill-posed training set, especially when the labeled instances are limited or imbalanced. To address this issue, this paper investigate the local correlation based on the entire data distribution, which is leveraged as informative guidance to ameliorate the negative influence of biased model. To formulate the self-expressive property between instances within a limited vicinity, we develop the sparse self-expressive representation learning method based on column-wise sparse matrix optimization. Optimization algorithm is presented via alternating iteration. Then we further propose a novel framework, named semi-supervised learning based on local correlation, to effectively integrate the explicit prior knowledge and the implicit data distribution. In this way, the individual prediction from the learning model is refined by collective representation, and the pseudo-labeled instances are selected more effectively to augment the semi-supervised learning performance. Experimental results on multiple classification tasks indicate the effectiveness of the proposed algorithm.

1 Introduction

Machine learning has manifested its superiority in providing effective and efficient solutions for various applications [1,2,3,4,5]. In order to learn a robust model, the labeled instances are indispensable in that they convey precious prior knowledge and offer informative instruction. Unfortunately, manually labeling is labor-intensive and time-consuming. The cost associated with the labeling process often renders a fully labeled training set infeasible. In contrast, the acquisition of unlabeled instances is relatively inexpensive. One can easily have access to abundant unlabeled instances. As a result, when dealing with machine learning problems, we typically have to start with very limited labeled instances and plenty of unlabeled ones [6,7,8].

Recent researches indicate that the unlabeled instances, when used in conjunction with the labeled instances, can produce considerable improvement in learning performance. Semi-supervised learning [9, 10], as a machine learning mechanism that jointly explores both labeled and unlabeled instances, has aroused widespread research attention. In semi-supervised learning, the exploration into unlabeled instances is largely dependent on the model trained with the labeled instances. On one hand, the insufficient or imbalanced labeled instances are inclined to lead to ill-posed learning model, which will consequently jeopardize the learning performance of semi-supervised learning. On the other hand, pair-wise feature similarity is widely used when estimating the data distribution, which is not necessarily plausible for semantic-level recommendation of class labels.

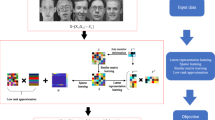
To address the aforementioned issues, this paper proposes a novel, named semi-supervised learning based on local correlation. Robust local correlation between the instances is estimated via sparse self-expressive representation learning, which formulates the self-expressive property between instances within a limited vicinity into a column-wise sparse matrix optimization problem. Based on the local correlation, an augmented semi-supervised learning framework is implemented, which takes into account both the explicit prior knowledge and the implicit data distribution. The learning sub-stages, including individual prediction, collective refinement, and dynamic model update with pseudo-labeling, are iterated until convergence. Finally, an effective learning model is obtained with encouraging experimental results on multiple classification applications.

2 Notation

In the text that follows, we let matrix $\varvec{X} = \left[ {\varvec{x}_{1} , \ldots ,\varvec{x}_{n} } \right] = \varvec{X}_{L} \mathop {\bigcup }\nolimits \varvec{X}_{U} \in {\mathbb{R}}^{m \times n}$ denote the entire dataset, where m is the dimension of features, and n is the total number of instances. In $\varvec{X}$, each column $\varvec{x}_{i}$ represents a m-dimensional instance. $\varvec{X}_{L} \in {\mathbb{R}}^{{m \times n_{L} }}$ and $\varvec{X}_{U} \in {\mathbb{R}}^{{m \times n_{U} }}$ are the labeled and unlabeled dataset, respectively, where n _L and n _U are the numbers of labeled and unlabeled instances, respectively. The corresponding class labels of the instances are denoted as matrix $\varvec{Y} = \varvec{Y}_{L} \mathop {\bigcup }\nolimits \varvec{Y}_{U} \in {\mathbb{R}}^{c \times n}$, where c is the number of classes, and $\varvec{Y}_{L} \in {\mathbb{R}}^{{c \times n_{L} }}$ and $\varvec{Y}_{U} \in {\mathbb{R}}^{{c \times n_{U} }}$ are the label matrices corresponding to the labeled and unlabeled dataset, respectively. For the labeled instance $\varvec{x} \in \varvec{X}_{L}$, its label $\varvec{y} \in \varvec{Y}_{L}$ is already known and denoted as a c-dimensional binary vector $\varvec{y} = \left[ {y_{1} , \ldots ,y_{c} } \right]^{T} \in \left\{ {0,1} \right\}^{c}$, whose ith element y _i (1 ≤ i ≤ c) is a class indicator, i.e. y _i  = 1 if instance $\varvec{x}$ falls into class i, and y _i  = 0 otherwise. For the unlabeled instance $\varvec{x} \in \varvec{X}_{U}$, its label $\varvec{y} \in \varvec{Y}_{U}$ is unrevealed and initially evaluated as $\varvec{y} = 0$.

3 Robust Local Correlation Estimation

The locally linear property is widely applicable for smooth manifolds. In this scenario, an instance can be concisely represented by its close neighbors. As a result, the underlying local correlation is an effective reflection of the data distribution, and can be subsequently leveraged as instructive guidance to improve the performance of model learning. Given the instance matrix $\varvec{X}$, we develop a robust local correlation estimation method in a unsupervised fashion, which aims to infer a correlation matrix $\varvec{W} \in {\mathbb{R}}^{n \times n}$ based on the instances themselves regardless of their labels. The formulation is based on two major considerations. On one hand, an instance can be represented as a linear combination of the closely related neighbors. On the other hand, only a small number of neighbors are involved for the representation of an instance. In light of that, we estimate the robust local correlation between the instances via a novel Sparse Self-Expressive Representation Learning (SSERL), which is formulated as the follows.

$$ \begin{array}{*{20}l} {\min_{\varvec{W}} \left\| {\varvec{W}^{T} } \right\|_{2,1} } \hfill \\ {{\text{s}}.{\text{t}}.\,\varvec{X}\, = \,\varvec{XW},\,{\text{diag}}\left( \varvec{W} \right)\, = \,0,\,\varvec{W}\, \ge \,0} \hfill \\ \end{array} $$

(1)

where the minimization of ℓ_2,1-norm $\left\| {\varvec{W}^{T} } \right\|_{2,1}$ ensures column sparsity of $\varvec{W}$.

To make the problem more flexible, the equality constraint $\varvec{X} = \varvec{XW}$ is relaxed to allow expressive errors [11], and the corresponding objective is modified as follows.

$$ \begin{array}{*{20}l} {\min_{\varvec{W}} {\mathcal{L}}\left( \varvec{W} \right) = \left\| {\varvec{X} - \varvec{XW}} \right\|_{F}^{2} + \lambda \left\| {\varvec{W}^{T} } \right\|_{2,1} } \hfill \\ {{\text{s}}.{\text{t}}.\,{\text{diag}}\left( \varvec{W} \right)\, = \,0,\,\varvec{W}\, \ge \,0} \hfill \\ \end{array} $$

(2)

In ${\mathcal{L}}\left( \varvec{W} \right)$, the first term stands for the self-expressive loss and the second term is the column sparsity regularization. λ quantifies the tradeoff between the two terms.

The optimization problem (2) is not directly solvable. According to the general half-quadratic framework for regularized robust learning [12], we introduce an augmented cost function ${\mathcal{A}}\left( {\varvec{W},\varvec{p}} \right)$ as follows.

$$ {\mathcal{A}}\left( {\varvec{W},\varvec{p}} \right) = \left\| {\varvec{X} - \varvec{XW}} \right\|_{F}^{2} + \lambda {\text{Tr}}\left( {\varvec{WPW}^{T} } \right) $$

(3)

where $\varvec{p}$ is an auxiliary vector, and $\varvec{P}$ is a diagonal matrix defined as $\varvec{P} = {\text{diag}}\left( \varvec{p} \right)$. The operator ${\text{diag}}\left( \cdot \right)$ places a vector on the main diagonal of a square matrix.

With $\varvec{W}$ given, the i-th entry of $\varvec{p}$ is calculated as follows.

$$ p_{i} = \frac{1}{{2\left\| {\varvec{w}_{i} } \right\|_{2} }} $$

(4)

With $\varvec{p}$ fixed, $\varvec{W}$ can be optimized in a column-by-column manner as follows.

$$ \varvec{w}_{i} = \left( {\varvec{X}^{T} \varvec{X} + \lambda p_{i} \varvec{I}} \right)^{ - 1} \varvec{X}^{T} \varvec{x}_{i} $$

(5)

Based on (4) and (5), the auxiliary vector $\varvec{p}$ and the correction matrix $\varvec{W}$ are jointly optimized in an alternating iterative way. At the end of each iteration, the following post-processing is further implemented according to the constraints.

$$ \left\{ {\begin{array}{*{20}l} {\varvec{W}_{\Omega } = 0,\Omega = \left\{ {\left( {i,j} \right) |1 \le i = j \le n} \right\}} \hfill \\ {\varvec{W} = \hbox{max} \left( {\varvec{W},0} \right)} \hfill \\ \end{array} } \right. $$

(6)

After convergence, the optimal correlation matrix $\varvec{W}$ is obtained, which can serve as an informative clue for the revelation of the underlying data distribution and the construction of the subsequent model learning.

4 Semi-supervised Learning Based on Local Correlation

Different from the traditional semi-supervised learning mechanism that solely depends on the classification model when exploring the unlabeled instances, the proposed SSL-LC takes into account both model prediction and local correlation. By iteration of the following three steps, SSL-LC is implemented in an effective way and the optimal learning model is obtained after convergence of the algorithm.

Step 1: Individual Label Prediction by Supervised Learning

As we know, for the labeled dataset $\varvec{X}_{L} \in {\mathbb{R}}^{{m \times n_{L} }}$, the corresponding label set $\varvec{Y}_{L} \in {\mathbb{R}}^{{c \times n_{L} }}$ is known beforehand. Using $\left( {\varvec{X}_{L} ,\varvec{Y}_{L} } \right)$ as training dataset, the classification model ${\mathcal{H}}_{\theta } :{\mathbb{R}}^{m} \to {\mathbb{R}}^{c}$ can be obtained with off-the-shelf optimization methods. Specifically, probabilistic model can be applied based on the posterior distribution $P(\varvec{y}|\varvec{x};\theta )$ of label $\varvec{y}$ conditioned on the input $\varvec{x}$, where θ is the optimal parameter for ${\mathcal{H}}_{\theta }$ given $\left( {\varvec{X}_{L} ,\varvec{Y}_{L} } \right)$. For the unlabeled instance $\varvec{x} \in \varvec{X}_{U}$, its label $\varvec{y}$ is unknown and need to be predicted by the trained classification model ${\mathcal{H}}_{\theta }$. The prediction is given in the form of a c-dimensional vector $\tilde{\varvec{y}} = \left[ {P\left( {y_{1} = 1\left| {\varvec{x};\theta } \right.} \right), \ldots ,P\left( {y_{c} = 1\left| {\varvec{x};\theta } \right.} \right)} \right]^{T} \in \left[ {0,1} \right]^{c}$. For the i-th entry $P\left( {y_{i} = 1\left| {\varvec{x};\theta } \right.} \right)$, larger value indicates higher probability that $\varvec{x}$ falls into the i-th class with respect to ${\mathcal{H}}_{\theta }$, and vice versa. Based on the learning model ${\mathcal{H}}_{\theta }$, prediction can be made on each unlabeled instance individually. The predicted label set is collectively denoted as $\tilde{\varvec{Y}}_{U}$, which represents the classification estimation from the model point of view. With the dynamic update of model ${\mathcal{H}}_{\theta }$, the predicted label $\tilde{\varvec{Y}}_{U}$ is also dynamically renewed.

Step 2: Collective Label Refinement by Self-expressing

In addition to the posterior probability estimated by model ${\mathcal{H}}_{\theta }$, the label of an unlabeled instance $\varvec{x} \in \varvec{X}_{U}$ can further be concisely represented by its closely related neighbors. The local correlation $\varvec{W}$ calculated via SSERL reflects the underlying relevance between instances within the vicinity, and thus can serve as an informative guidance for self-expressive representation of labels. In this way, robust label refinement is achieved against potential classification errors. To be specific, the entire label matrix can be denoted as $\varvec{Y}_{p} = \left[ {\varvec{Y}_{L} ,\tilde{\varvec{Y}}_{U} } \right]$ after inference via classification. For further refinement, the local correlation matrix $\varvec{W}$ is leveraged to obtain the self-expressive representation of labels in the form of $\varvec{Y}_{s} = \varvec{Y}_{p} \varvec{W}$. By this means, the self-expressive property with respect to the instances is transferred to the labels, and the column-wise sparsity of $\varvec{W}$ guarantees the concision of representation within a constrained vicinity. Then $\varvec{Y}_{s}$ is normalized to obtain a legitimate probability estimation $\varvec{Y}_{n}$, whose j-th column is calculated as:

$$ \left[ {\varvec{Y}_{n} } \right]_{j} = \frac{{\left[ {\varvec{Y}_{s} } \right]_{j} }}{{\max_{i} \left[ {\varvec{Y}_{s} } \right]_{ij} }} $$

(7)

Finally, since $\varvec{Y}_{L}$ is already known and does not need to be estimated, the refined label matrix is calculated as:

$$ \varvec{Y}_{r} = \left[ {\varvec{Y}_{L} ,0^{{c \times n_{U} }} } \right] + \varvec{Y}_{n} \odot \left[ {0^{{c \times n_{L} }} ,1^{{c \times n_{U} }} } \right] $$

(8)

where $\odot$ is the element-wise product of two matrices.

Step 3: Semi-supervised Model Update by Pseudo-labeling

As discussed above, the effectiveness of semi-supervised learning stems from the comprehensive exploration on both labeled and unlabeled instances, in which the unlabeled instances with high predictive confidence are assigned with pseudo-labels and recommended to the learner as additional training data. The predictive confidence is the key measurement for selection of unlabeled instances. For the j-th instance, its predictive confidence is conveniently calculated as:

$$ c_{j} = \max_{i} \left[ {\varvec{Y}_{n} \odot \left[ {0^{{c \times n_{L} }} ,1^{{c \times n_{U} }} } \right]} \right]_{ij} $$

(9)

which naturally filters out the labeled instances. Since $\varvec{Y}_{n}$ is dependent on $\varvec{Y}_{p}$ and $\varvec{W}$, both individual classification prediction and collective local correlation are effectively integrated in the semi-supervised learning strategy. Based on the predictive confidence defined in (9), reliable and informative unlabeled instances can be selected and recommended for model update. The pseudo-label $\hat{\varvec{y}}_{j}$ associated with the j-th instance is defined as:

$$ \left( {\hat{\varvec{y}}_{j} } \right)^{i} = \left\{ {\begin{array}{*{20}c} {1,} & {i = \arg \max_{i} \left[ {\varvec{Y}_{n} \odot \left[ {0^{{c \times n_{L} }} ,1^{{c \times n_{U} }} } \right]} \right]_{ij} } \\ {0,} & {i \ne \arg \max_{i} \left[ {\varvec{Y}_{n} \odot \left[ {0^{{c \times n_{L} }} ,1^{{c \times n_{U} }} } \right]} \right]_{ij} } \\ \end{array} } \right. $$

(10)

Using the pseudo-labeled instances as additional training data, the learning model ${\mathcal{H}}_{\theta }$ is re-trained, which brings about updated $\varvec{Y}_{p}$ and $\varvec{Y}_{r}$.

5 Experiments

To validate the effectiveness of SSL-LC, we apply it to classification tasks on malware [7] and patent [6] dataset respectively, in comparison with the following methods:

• Supervised learning (SL), which trains classifier based on the labeled dataset $\varvec{T} = \left( {\varvec{X}_{L} ,\varvec{Y}_{L} } \right)$, and arrives at individual prediction $\varvec{Y}_{p}$ accordingly.

• Supervised learning with local correlation (SL-LC), which further refines the prediction with $\varvec{W}$ and obtains $\varvec{Y}_{r}$.

• Semi-supervised learning (SSL), which selects pseudo-labeled instances $\varvec{R}$ based on unrefined prediction $\varvec{Y}_{p}$, and updates classifier based on $\varvec{T}\mathop {\bigcup }\nolimits \varvec{R}$.

Experiment 1: Comparison of Different Number of Labeled Instances.

Firstly, we compare the classification performance with different number of labeled instances, i.e. $\left| \varvec{T} \right|$. The classification performance is illustrated in Fig. 1(1).

Fig. 1.

The classification performance with different number of (1) labeled instances and (2) recommended instances.

Detailed analysis of experimental results are as follows, where “>” stands for “outperform(s)”.

• SL-LC > SL, SSL-LC > SSL. Under the instructive guidance of local correlation, the individual prediction on a single instance can be further refined via collective representation. Therefore, the classification results are more coherent to the intrinsic data distribution and less vulnerable to overfitting with local correlation refinement.

• SSL > SL, SSL-LC > SL-LC. Compared with supervised learning, semi-supervised learning further leverages the unlabeled instances to extend the training dataset, and thus receives higher classification performance.

• When the number of labeled instances is large enough, the difference between the four methods is negligible. It is indicated that the proposed SSL-LC is especially helpful for classification problems with insufficient labeled instances.

Experiment 2: Comparison of Different Number of Recommended Instances.

We further compare the classification performance with different number of recommended instances, i.e. K, where SL and SL-LC are treated as special cases of SSL and SSL-LC with K = 0. The classification performance is illustrated in Fig. 1(2).

As we can see, at first, the classification accuracy improves with the increase of K, because the model can learn from more and more instances. However, when K is large enough, further increase will lead to deterioration of classification performance. This results from the incorporation of the less confident pseudo-labeled instances, which inevitably brings about unreliable model.

6 Conclusion

In this paper, we have proposed an effective semi-supervised learning framework based on local correlation. Compared with traditional semi-supervised learning methods, the contributions of the work are as follows. Firstly, both the explicit prior knowledge and the implicit data distribution are integrated into a unified learning procedure, where the individual prediction from the dynamically updated learning model is refined by collective representation. Secondly, robust local correlation, rather than pair-wise similarity, is leveraged for model augment, which is formulated as a column-wise sparse matrix optimization problem. Last but not least, effective optimization is designed, in which the optimal solution is progressively reached in an iterative fashion. Experiments on multiple classification tasks indicate the effectiveness of the proposed algorithm.