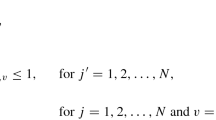Abstract
The interval scheduling problem is one variant of the scheduling problem. In this paper, we propose a novel variant of the interval scheduling problem, whose definition is as follows: given jobs are specified by their release times, deadlines and profits. An algorithm must start a job at its release time on one of m identical machines, and continue processing until its deadline on the machine to complete the job. All the jobs must be completed and the algorithm can obtain the profit of a completed job as a user’s satisfaction. It is possible to process more than one job at a time on one machine. The profit of a job is distributed uniformly between its release time and deadline, that is its interval, and the profit gained from a subinterval of a job decreases in reverse proportion to the number of jobs whose intervals intersect with the subinterval on the same machine. The objective of our variant is to maximize the total profit of completed jobs.
This formulation is naturally motivated by best-effort requests and responses to them, which appear in many situations. In best-effort requests and responses, the total amount of available resources for users is always invariant and the resources are equally shared with every user. We study online algorithms for this problem. Specifically, we show that for the case where the profits of jobs are arbitrary, there does not exist an algorithm whose competitive ratio is bounded. Then, we consider the case in which the profit of each job is equal to its length, that is, the time interval between its release time and deadline. For this case, we prove that for \(m = 2\) and \(m \ge 3\), the competitive ratios of a greedy algorithm are at most 4 / 3 and at most 3, respectively. Also, for each \(m \ge 2\), we show a lower bound on the competitive ratio of any deterministic algorithm.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Arkin, E.M., Silverberg, E.B.: Scheduling jobs with fixed start and end times. Discrete Appl. Math. 18(1), 1–8 (1987)
Baruah, S.K., Haritsa, J.R.: Scheduling for overload in real-time systems. IEEE Trans. Comput. 46(9), 1034–1039 (1997)
Borodin, A., El-Yaniv, R.: Online Computation and Competitive Analysis. Cambridge University Press, Cambridge (1998)
Bouzina, K.I., Emmons, H.: Interval scheduling on identical machines. J. Global Optim. 9(3–4), 379–393 (1996)
Canetti, R., Irani, S.: Bounding the power of preemption in randomized scheduling. SIAM J. Comput. 27(4), 993–1015 (1998)
Carlisle, M.C., Lloyd, E.L.: On the k-coloring of intervals. Discrete Appl. Math. 59(3), 225–235 (1995)
DasGupta, B., Palis, M.A.: Online real-time preemptive scheduling of jobs with deadlines on multiple machines. J. Sched. 4(6), 297–312 (2001)
Epstein, L., Levin, A.: Improved randomized results for the interval selection problem. Theoret. Comput. Sci. 411(34–36), 3129–3135 (2010)
Faigle, U., Nawijn, W.M.: Note on scheduling intervals on-line. Discrete Appl. Math. 58(1), 13–17 (1995)
Fung, S.P.Y., Poon, C.K., Zheng, F.: Online interval scheduling: randomized and multiprocessor cases. J. Comb. Optim. 16(3), 248–262 (2008)
Fung, S.P.Y., Poon, C.K., Yung, D.K.W.: On-line scheduling of equal-length intervals on parallel machines. Inf. Process. Lett. 112(10), 376–379 (2012)
Fung, S.P.Y., Poon, C.K., Zheng, F.: Improved randomized online scheduling of intervals and jobs. Theor. Comput. Syst. 55(1), 202–228 (2014)
Kolen, A.W.J., Lenstra, J.K., Papadimitriou, C.H., Spieksma, F.C.R.: Interval scheduling: a survey. Naval Res. Logist. 54(5), 530–543 (2007)
Kovalyov, M.Y., Ng, C.T., Cheng, T.C.E.: Fixed interval scheduling: models, applications, computational complexity and algorithms. Eur. J. Oper. Res. 178(2), 331–342 (2007)
Lipton, R.J., Tomkins, A.: Online interval scheduling. In: Proceedings of the Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, pp. 302–311 (1994)
Miyazawa, H., Erlebach, T.: An improved randomized on-line algorithm for a weighted interval selection problem. J. Sched. 7(4), 293–311 (2004)
Sankowski, P., Zaroliagis, C.: The power of migration for online slack scheduling. In: Proceedings of the 24th Annual European Symposium on Algorithms, pp. 75:1–75:17 (2016)
Seiden, S.S.: Randomized online interval scheduling. Oper. Res. Lett. 22(4–5), 171–177 (1998)
Sleator, D.D., Tarjan, R.E.: Amortized efficiency of list update and paging rules. Commun. ACM 28(2), 202–208 (1985)
Woeginger, G.J.: On-line scheduling of jobs with fixed start and end times. Theoret. Comput. Sci. 130(1), 5–16 (1994)
Acknowledgments
This work was supported by JSPS KAKENHI Grant Number 26730008.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer International Publishing AG, part of Springer Nature
About this paper
Cite this paper
Kobayashi, K.M. (2018). Online Interval Scheduling to Maximize Total Satisfaction. In: Wang, L., Zhu, D. (eds) Computing and Combinatorics. COCOON 2018. Lecture Notes in Computer Science(), vol 10976. Springer, Cham. https://doi.org/10.1007/978-3-319-94776-1_10
Download citation
DOI: https://doi.org/10.1007/978-3-319-94776-1_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-94775-4
Online ISBN: 978-3-319-94776-1
eBook Packages: Computer ScienceComputer Science (R0)