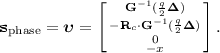Quantum FHE (Almost) As Secure As Classical

Abstract

Fully homomorphic encryption schemes (FHE) allow to apply arbitrary efficient computation to encrypted data without decrypting it first. In Quantum FHE (QFHE) we may want to apply an arbitrary quantumly efficient computation to (classical or quantum) encrypted data.

We present a QFHE scheme with classical key generation (and classical encryption and decryption if the encrypted message is itself classical) with comparable properties to classical FHE. Security relies on the hardness of the learning with errors (LWE) problem with polynomial modulus, which translates to the worst case hardness of approximating short vector problems in lattices to within a polynomial factor. Up to polynomial factors, this matches the best known assumption for classical FHE. Similarly to the classical setting, relying on LWE alone only implies leveled QFHE (where the public key length depends linearly on the maximal allowed evaluation depth). An additional circular security assumption is required to support completely unbounded depth. Interestingly, our circular security assumption is the same assumption that is made to achieve unbounded depth multi-key classical FHE.

Technically, we rely on the outline of Mahadev (arXiv 2017) which achieves this functionality by relying on super-polynomial LWE modulus and on a new circular security assumption. We observe a connection between the functionality of evaluating quantum gates and the circuit privacy property of classical homomorphic encryption. While this connection is not sufficient to imply QFHE by itself, it leads us to a path that ultimately allows using classical FHE schemes with polynomial modulus towards constructing QFHE with the same modulus.

The full version of this work is available at https://eprint.iacr.org/2018/338.

Supported by the Israel Science Foundation (Grant No. 468/14), Binational Science Foundation (Grants No. 2016726, 2014276), and by the European Union Horizon 2020 Research and Innovation Program via ERC Project REACT (Grant 756482) and via Project PROMETHEUS (Grant 780701).

1 Introduction

A fully homomorphic encryption (FHE) scheme [17, 32] is one where the transformation $\mathsf {Enc}(x) \rightarrow \mathsf {Enc}(f(x))$ can be performed efficiently for any efficiently computable f, without violating the security of the scheme. This primitive is very useful for cryptographic applications, and in particular it allows private outsourcing of computation. That is, using the resources of a powerful third party to perform a computation without giving up privacy. In recent years it was shown how to construct FHE based on standard cryptographic assumptions (mostly lattice related), including ones that are assumed to be secure against quantum adversaries. In particular, it was shown [1, 5, 6, 9, 10, 20] that FHE can be based on the hardness of the learning with errors (LWE) problem introduced by Regev [29]. LWE was proven to be as hard to solve as the hardness of finding approximate shortest vectors in arbitrary worst-case lattices, a task for which no significant quantum speedup is known. The approximation factor directly relates to a parameter of the LWE problem known as the noise ratio, expressed as a function of the dimension of the problem.¹ Initial schemes [9] relied on LWE with sub-exponential noise ratio, and thus the hardness of sub-exponential approximation for lattice problems. Extensive research effort improved the schemes all the way down to only requiring a polynomial noise ratio [10], which is the gold standard for LWE-based security.

Understanding the capabilities and boundaries of FHE in various computational models is a fundamental question in cryptographic study. In this work, we focus on extending the set of supported functions f to the set of functions computable in quantum polynomial time, at the necessary cost of the evaluation process itself becoming quantum as well. This extension is called Quantum FHE (QFHE).

With developments in quantum computing occurring at an increasing rate, one could anticipate outsourcing of quantum computation becoming a quite common. Specifically it is quite likely that the first scalable quantum computers will be very expensive and require specialized maintenance and thus will not be directly available to the public. Rather, users will need to send their inputs to be processed by third party providers. If privacy is desired in this scenario, then QFHE could become a useful tool. While current research on QFHE, including this work, is well within the theoretical regime, developing theoretical tools and techniques could serve as basis for the development of concrete systems in due time.

Previous Works. Broadbent and Jeffery [11] showed that any classical FHE scheme can be translated into a quantum one that supports a limited set of gates (specifically, the evaluation of Clifford gates). Their idea is quite natural and elegant, and while not explicitly stated in this way, is related to the well established cryptographic notion of key encapsulation mechanisms (KEM). They rely on the notion of quantum one time pad (QOTP) that allows to information theoretically encrypt a quantum state using a single-use classical random pad. They propose to encrypt a quantum state using a QOTP, and then encrypt the pad itself using a classical homomorphic encryption scheme. They then show that Clifford operations in the quantum regime translate into applying a public operation on the quantum part of the QOTP ciphertext, and applying public classical operations on the classical secret bits of the pad. The latter can be applied homomorphically since the secret bits of the pad are encrypted using a classical FHE scheme. They also show that evaluating an a-priori bounded number of non-Clifford gates is possible at the cost of the ciphertext size blowing up polynomially with the number of supported non-Clifford gates.

Dulek, Schaffner and Speelman [14] showed how to transfer the dependence on the number of non-Clifford gates from the ciphertext to the key. Specifically, their key generation involves generating a quantum gadget for every non-Clifford gate to be evaluated throughout the lifetime of the scheme, and transferring these gadgets to the homomorphic evaluator. The gadgets are consumed after a single use and their quantum nature prevents them from being duplicated or shared. This allowed for the first time to outsource quantum computation privately and compactly, but at the cost of quantum preprocessing. The [14] solution used the KEM approach as well, but required the decryption complexity of the classical FHE scheme to be bounded (roughly logarithmic space). They instantiate their scheme with the [9] FHE scheme, thus inheriting its unfavorable properties, but we believe it can also be instantiated using newer schemes such as [5, 6, 20], but it is not clear whether it applies to schemes based on the hardness of polynomial lattice approximation due to the sequentialization technique of [10] used in these schemes.

Mahadev [21] very recently presented a scheme whose key generation process is completely classical. This immediately implies that the keys can be duplicated and there is no longer a global bound on the total homomorphic capacity of the system. This scheme also uses key encapsulation, and requires specific properties of the underlying classical homomorphic encryption. An important property of the [21] scheme is that the homomorphic evaluation of each quantum gate is not necessarily perfectly correct, but rather it is only guaranteed to be within small trace distance of the correct state. These errors accumulate so in the worst case they are multiplied by the total circuit size. Thus, in order to achieve correctness up to a negligible trace distance, the per-gate error needs to be negligible as well. In the [21] solution, the per-gate error is (inversely) related to the noise rate of the underlying LWE assumption, so in order to achieve correctness for all polynomial size circuits, it is required to rely on the hardness of super-polynomial approximation to lattice problems (or even larger, depending on the type of computation and the user’s desired level of confidence).

Another unusual requirement of [21] from the underlying classical FHE scheme is randomness recoverability. Namely, that using the secret key it is possible to recover the randomness of a ciphertext. This is achieved using the dual scheme to the [1, 10, 20] scheme, but requires changing the secret key from being a single vector to a trapdoor to the lattice corresponding to the public key. This would all be in the realm of low order technicalities, except for the issue of circular security, which we explain next. Even in the classical setting, relying on LWE alone only allows to construct leveled FHE, where an a-priori bound on the depth (but not on the size) of evaluated circuits needs to be known. Overcoming this issue to obtain a scheme that is secure for any depth requires encrypting the scheme’s own secret key, and explicitly assuming that this does not adversely impact the security of the scheme. Making this assumption for standard LWE-based encryption is by now the norm, but one might be less confident about making this assumption for new distributions of secret keys.

To conclude this overview, we note that there is a distinction in the literature between QFHE for classical vs. for quantum inputs. The former requires that the encryption and key generation process are completely classical, so that quantum computation on classical inputs can be outsourced by a classical entity. This distinction could suggest that the two notions are incomparable, however we believe that it is instructive to aspire to achieve a notion that generalizes both. Specifically, we propose to aspire for QFHE with classical keys, that can encrypt classical messages using a classical encryption process, and can encrypt quantum messages using a quantum process, and likewise if the output of homomorphic evaluation is classical then it should be decryptable by a classical decryption process. This stronger notion is in fact achieved by [21], although this property is not highlighted.

Our Results and Approach. We present a QFHE scheme using the high level outline of [21], but with per-gate error that decays exponentially with the noise rate of the underlying LWE assumption. Thus, using polynomial noise rate we are able to achieve exponentially small per-gate error, which means that we can securely evaluate any polynomial (or even super-polynomial) quantum circuit while incurring only an exponentially small skew between the output of homomorphic evaluation and the desired result. We do this by (again) relying on key encapsulation, this time using the (primal) [1, 10, 20] scheme as the KEM component. As for the distribution of secret keys, we do not require to use a lattice trapdoor as secret key, but our scheme requires publishing an encryption of the secret key of a [20]-style scheme, and keeping the randomness used to generate this encryption as a part of its own secret key.

Therefore, if we wish to create a scheme that works for a-priori unbounded depth, we need to assume circular security respective to a key containing a standard LWE key as well as randomness that was used to generate encryptions of this key. Interestingly, this exact assumption is required in order to construct unbounded depth classical multi-key FHE from [20]-style encryption [8, 12, 25, 28].²

In terms of our approach, we observe that the [21] method is implicitly intimately connected to the circuit privacy property of the underlying classical homomorphic scheme. Circuit privacy is the property that after homomorphically evaluating a function f, the resulting ciphertext $\mathsf {Enc}(f(x))$ does not contain any information about f except the value f(x) (even statistically). While circuit privacy is not a sufficient condition, it appears to be necessary for ensuring functionality in the [21] method.

Circuit private homomorphic encryption schemes are useful for various applications and this property has been extensively studied in the FHE literature, e.g. in [4, 13, 16, 18]. However, this property is usually considered to be a security feature, and we find it quite curious that in the quantum setting it turns out to be related to the correctness of homomorphic evaluation.

Through the circuit privacy lens, the [21] scheme can be viewed as applying the most rudimentary method for achieving function privacy, known as noise flooding [16]. This method guarantees privacy that is roughly relative to the noise rate of the underlying LWE assumption, hence super-polynomial rate is required to achieve privacy with all but negligible probability. It is not immediately clear how to apply more modern circuit privacy approaches in the QFHE setting (due to the additional properties required for quantum homomorphic evaluation), and the bulk of our technical work goes towards developing techniques to allow this application. We elaborate more on our techniques below.

1.1 Technical Overview

Our basic approach, traced back to [11], is to rely on key encapsulation. The ciphertext is encrypted using a quantum one time pad (QOPT), and the (classical) secret pad is encrypted using a classical FHE. QOTP encryption of a qubit can be expressed as applying a random Pauli operation, namely a random bit flip and a random phase flip. This allows to easily evaluate Clifford gates. As observed in previous works [14, 21], a missing piece that would imply QFHE is being able to homomorphically evaluate the CNOT operation on a given quantum state, but given a classical control bit in encrypted form. To be more explicit, given a 2-qubit superposition $\sum _{a,b} \alpha _{a,b} |{a,b}\rangle$ and an encrypted control bit x, output an encapsulated encryption of $\sum _{a,b} \alpha _{a,b} |{a,b\oplus ax}\rangle$, i.e. a two-qubit register and a classically encrypted pad that would decrypt the quantum register to the aforementioned superposition. The encapsulated version we produce will be a superposition of the form $\sum _{a,b} (-1)^{a \gamma _{\mathrm {phase}}} \alpha _{a,b} |{a,b\oplus ax \oplus \gamma _{\mathrm {flip}}}\rangle$ for some bits $\gamma _{\mathrm {flip}}, \gamma _{\mathrm {phase}}$, together with encryptions of the bits $\gamma _{\mathrm {flip}}, \gamma _{\mathrm {phase}}$. One can verify that indeed $\sum _{a,b} (-1)^{a \gamma _{\mathrm {phase}}} \alpha _{a,b} |{a,b\oplus ax \oplus \gamma _{\mathrm {flip}}}\rangle$ can be corrected to the prescribed output using a proper bit flip and phase flip. We start by describing at a high level the [21] approach and its relation to circuit privacy.

The [21] Approach and Circuit Privacy. Given $\sum _{a,b} \alpha _{a,b} |{a,b}\rangle$ and $\mathsf {Enc}(x)$, the idea is to apply classical homomorphic evaluation to generate a superposition of the form

$$ \sum _{a,b,\mu } \alpha _{a,b} |{a,b\oplus \mu }\rangle |{\mathsf {Enc}(ax\oplus \mu )}\rangle |{\mu }\rangle $$

(we ignore normalization factors). This can be done using the properties of the classical FHE by applying to $\mathsf {Enc}(x)$ the function $f_{a,\mu }(x)=ax\oplus \mu$. Now, measure the register containing $|{\mathsf {Enc}(ax\oplus \mu )}\rangle$ to obtain some ciphertext $c'$, let $\gamma _{\mathrm {flip}}$ denote the bit that it encrypts and note that $\mu = ax \oplus \gamma _{\mathrm {flip}}$. Then the remainder superposition is: $\sum _{a,b} \alpha _{a,b} |{a,b\oplus ax \oplus \gamma _{\mathrm {flip}}}\rangle |{ax\oplus \gamma _{\mathrm {flip}}}\rangle$. So far we used the homomorphic ciphertext to introduce an added ax term into the $|{b}\rangle$ register. Finally, to remove the last register $|{ax\oplus \gamma _{\mathrm {flip}}}\rangle$, measure it in the Hadamard basis, or alternatively, apply Fourier Transform and measure the result. We get a measured bit w and the state $\sum _{a,b} (-1)^{(wx)a} \alpha _{a,b} |{a,b\oplus ax \oplus \gamma _{\mathrm {flip}}}\rangle$ (with a global factor $(-1)^{w \gamma _{\mathrm {flip}}}$ that can be ignored). Therefore, setting $\gamma _{\mathrm {phase}}=wx$ should complete the proof.

Unfortunately, this outline is too simplistic. We ignored the fact that there are many possible ciphertexts of the form $\mathsf {Enc}(ax\oplus \mu )$, and the specific ciphertext output by homomorphically evaluating $f_{a,\mu }$ might depend on $a, \mu$, which means that measuring it might collapse the superposition completely. This is why circuit privacy seems useful, since it will ensure that regardless of $a,\mu$ the distribution of $\mathsf {Enc}(ax\oplus \mu )$ depends only on the bit it encrypts. However, making a ciphertext private necessarily requires randomness, and we cannot use classical randomness since it will cause the superposition to collapse just as before. Therefore, the randomness is taken in superposition, and after measuring $c'$ we are left with an additional register containing the randomness conditioned on $c'$. In a sense the privacy transformation transferred the information about the applied circuit from the ciphertext to the randomness register. We are thus left with $\sum _{a,b} (-1)^{a \gamma _{\mathrm {phase}}} \alpha _{a,b} |{a,b\oplus ax \oplus \gamma _{\mathrm {flip}}}\rangle |{r_{a}}\rangle$ and we need to find a way to get rid of this additional randomness register.

In [21] it is shown that using their specific scheme, it is possible to express $r_a$ as $r_0\oplus (a r_1)$ where $r_0, r_1$ are binary vectors, and thus again measuring this register in the Hadamard basis will be effective. This crucially relies on having a one-to-one mapping between the randomness in the privacy transformation and the ciphertext $c'$. This property indeed holds for noise flooding, but not for later privacy techniques.

To complete this description, we note that after the Hadamard measurement, the value of $r_1$ now contributes to $\gamma _{\mathrm {phase}}$, and an additional process involving the lattice trapdoor is introduced in order to show that a classical encryption of the new $\gamma _{\mathrm {phase}}$ can be recovered.

Our Solution. We are inspired by the circuit privacy argument of Bourse et al. [4] which is applicable to encryption schemes of the type introduced in [20] (henceforth referred to as GSW) and shows how to achieve circuit privacy with polynomial noise rate. In GSW an encryption of a bit x is represented by a matrix over ${\mathbb Z}_q$ for some modulus q of the form $\mathbf {{C}}=\mathbf {{A}}\mathbf {{R}}_c+x\mathbf {{G}}$, where $\mathbf {{A}}$ is the public key of the scheme, $\mathbf {{R}}_c$ is a matrix of low norm (say all entries are $\ll q$) and $\mathbf {{G}}$ is a special “gadget” matrix. For our purposes it will be useful to choose the modulus q to be even (this does not have an effect on the resulting hardness assumption). The circuit privacy argument of [4] implies that if we sample a integer vector $\mathbf {r}$ from a discrete Gaussian distribution over the set $\{ \mathbf {r} : \mathbf {{G}}\mathbf {r}= a \tfrac{q}{2} \mathbf {\Delta }\pmod {q} \}$ (for some vector $\mathbf {\Delta }$), and compute the vector $\mathbf {c}'=\mathbf {{C}}\mathbf {r}+(\tfrac{q}{2} \mu +y)\mathbf {\Delta }$, where y is a discrete Gaussian over ${\mathbb Z}$, then $\mathbf {c}'$ is a circuit private representation of $ax\oplus \mu$, i.e. $\mathbf {c}'$ does not reveal information about $a,\mu$ beyond the value $ax\oplus \mu$.³

Let us now see how this method fits into the [21] outline. Specifically, every $\mathbf {c}'$ in this setting will have multiple randomness values associated with it, so there is no longer a single $r_a$ associated with each $\mathbf {c}'$. We will therefore try to find an alternative structural property of the randomness register that will allow us to remove it without collapsing the superposition. Looking closely, we see that the randomness consistent with $\mathbf {c}'$ is a discrete Gaussian over variables $\mathbf {r},y,\mu$ s.t. $\{ \mathbf {r} : \mathbf {{G}}\mathbf {r}= a \tfrac{q}{2} \mathbf {\Delta }\pmod {q} \}$ and $\mathbf {c}'=\mathbf {{C}}\mathbf {r}+(\tfrac{q}{2} \mu +y)\mathbf {\Delta }= \mathbf {{A}}\mathbf {{R}}_c\mathbf {r}+(\tfrac{q}{2} (ax\oplus \mu ) +y)\mathbf {\Delta }$. Indeed we observe that this is a Gaussian superposition over the solutions of a set of linear equations modulo q. In other words over a coset of a q-ary lattice, where the coset is determined by $\mathbf {c}'$ and by $a \tfrac{q}{2} \mathbf {\Delta }$. This suggests a way out, if we are willing to replace the binary Fourier Transform with q-ary Fourier Transform $\big (\mathrm {FT}_q: |{\mathbf {x}}\rangle \rightarrow \sum |{\mathbf {w}}\rangle e^{-\frac{2\pi i}{q}\langle \mathbf {w}, \mathbf {x}\rangle }\big )$. As a rule of thumb, applying $\mathrm {FT}_q$ on different cosets of the same lattice, results in the same output, up to a phase that depends on the difference between the cosets. In our case, the difference is a multiple of a, just like we wanted.

Unfortunately, things are not so simple. First of all, indeed the phase is a multiple of a, but since we applied $\mathrm {FT}_q$, this phase might be relative to a q-ary root of unity, and not to $(-1)$ as we require for our key encapsulation.⁴ Luckily, in our case the difference between the cosets is a multiple of $\tfrac{q}{2}$, which translates to a phase relative to $(-1)$. A greater difficulty comes from the fact that we are not actually uniform over a the coset, but rather Gaussian, which makes the transference between the pre-$\mathrm {FT}_q$ and post-$\mathrm {FT}_q$ regimes more messy. In particular, instead of all points having the same phase shift, each measured value receives phase contributions from many sources which can interfere with each other. It is known that if the Gaussian parameter is large enough (larger than the so called “smoothing parameter” of the lattice), then the interference is negligible. Unfortunately this is not the case here, and we need to explicitly analyze the post-$\mathrm {FT}_q$ superposition in order to show that the effect of the interference only amounts to exponentially small trace distance.

Finally, we note that in order to make the analysis go through, we add an additional component to the privacy transformation and actually set $\mathbf {c}'=\mathbf {{C}}\mathbf {r}+\mathbf {{A}}\hat{\mathbf {r}}+(\tfrac{q}{2} \mu +y)\mathbf {\Delta }$, with $\hat{\mathbf {r}}$ being an additional Gaussian parameter. This allows us to prove useful properties for the resulting lattice, as well as provides us with a way to recover the new $\gamma _{\mathrm {phase}}$ without requiring lattice trapdoors, but rather using only an encrypted form of $\mathbf {{R}}_c$ and the LWE secret key.

1.2 Paper Organization

The main technical contribution of this paper is the homomorphic evaluation of classically controlled CNOT, which is outlined above in Sect. 1.1 and formally analyzed in Sect. 5.

General preliminaries appear in Sect. 2, preliminaries related to the definition of homomorphic encryption and results from previous works that we use appear in Sect. 3. In Sect. 4 we describe how to put together the components from previous works together with our classically controlled CNOT to create the QFHE scheme.

2 Preliminaries

We denote the unit ball by $\mathcal{B}_m = \{\mathbf {x} \in {\mathbb R}^m : \left\| {\mathbf {x}} \right\| _2 \le 1\}$, we omit the subscript when m is clear from the context. Similarly we denote the unit cube by $\mathcal{H}_m = \{\mathbf {x} \in {\mathbb R}^m : \forall i. \; \mathbf {x}[i] \in (-1, 1]\}$. We will sometimes use the shorthand $\mathcal{B}_m^t$, $\mathcal{H}_m^t$ to denote $t\cdot \mathcal{B}_m$, $t \cdot \mathcal{H}_m$ respectively.

Let $F: X \rightarrow {\mathbb C}$, and let $W \subseteq X$, then we denote $F(W)=\sum _{x\in W}F(x)$. For all $q \in {\mathbb N}$ we let ${\mathbb Z}_q$ denote the ring of integers modulo q. We represent elements in ${\mathbb Z}_q$ using numbers in the range $(-\tfrac{q}{2}, \tfrac{q}{2}] \cap {\mathbb Z}$. We denote by $\left[ {x} \right] _q$ the value y s.t. $y = x \pmod {q}$ and $y \in (-\tfrac{q}{2}, \tfrac{q}{2}]$. We let $\left[ {{\mathbb Z}} \right] _q$ denote the set ${\mathbb Z}\cap (-\tfrac{q}{2}, \tfrac{q}{2}]$.

We say that we $\delta$-compute a quantum state if we compute a superposition that is within trace distance $O(\delta )$ of that state.

Quantum Rejection Sampling. We recall that quantum rejection sampling allows to take a superposition $\sum _{x\in X} \alpha _x |{x}\rangle$ and any sequence $\{\alpha '_x\}_x$ s.t. $\left| {\alpha '_x} \right| \le 1$ for all x, and produce a superposition $\tfrac{1}{A}\sum _{x\in X} \alpha _x \alpha '_x |{x}\rangle$, where $A = \sum _{x\in X} \left| {\alpha _x \alpha '_x} \right| ^2$. The success probability of this procedure (i.e. the probability of not rejecting) is A. If it is efficient to generate the original superposition then the process can be repeated until successful, 1/A times in expectation.

Log-Infinity Uniformity. It will be convenient for us to consider a measure we call log-infinity variance.⁵

Definition 2.1

The log-infinity variance of a vector $\mathbf {v} \in ({\mathbb R}^{+})^m$ is defined as

$$\begin{aligned} {\mathsf {loginf}}(\mathbf {v}) = \ln \left( \frac{\max _i \mathbf {v}[i]}{\min _i \mathbf {v}[i]}\right) . \end{aligned}$$

(1)

If ${\mathsf {loginf}}(\mathbf {v}) \le \epsilon$, we say that $\mathbf {v}$ is $\epsilon$-$\mathsf {loginf}$ uniform.

We will often use $\mathsf {loginf}$-uniformity for general indexed sets $V = \{v_z \in {\mathbb R}^{+}\}_{z \in M}$, where M is some set of indices.

The following properties are easy to verify by definition.

Lemma 2.2

Let $V = \{v_z\}_{z \in M}$ be $\epsilon$-$\mathsf {loginf}$ uniform. Then the following hold:

• 1. Conditioning. $\forall M' \subseteq M$ the sequence $V' = \{v_z\}_{z \in M'}$ is $\epsilon$-$\mathsf {loginf}$ uniform.

• 2. Aggregation. $\forall a_1, \ldots , a_k \in {\mathbb R}^{+}$ the sequence $\{a_1 v_{z_1} + \cdots + a_k v_{z_k} \}_{z_1, \ldots , z_k \in M}$ is $\epsilon$-$\mathsf {loginf}$ uniform.

• 3. $\ell ^p_p$-Uniformity. Let $p \in {\mathbb R}^{+}$. The distribution defined on M by assigning probabilities $\Pr [z] \propto v^p_z$ is within statistical distance $O(p \epsilon )$ of uniform.

2.1 Quantum One Time Pad

The quantum one time pad (QOTP) allows to encrypt a qubit in an information theoretically secure manner using two random classical bits as symmetric key. Encrypting a multi-qubit state can be done in a bit by bit manner (using an independently sampled symmetric key for each qubit in the state).

• $\mathsf {QOTP}.\mathsf {Keygen}()$. Sample two classical bits $x,z{\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}\{0,1\}$ and outputs (x, z).

• $\mathsf {QOTP}.\mathsf {Enc}((x,z), \phi )$. Given a qubit $\phi$ apply the Pauli transformation $X^xZ^z$ to $\phi$ and output the resulting $\hat{\phi }$. More explicitly, the applied transformation is: $(\alpha _0|{0}\rangle +\alpha _1|{1}\rangle ) \rightarrow (\alpha _0|{x}\rangle +(-1)^z\alpha _1|{\bar{x}}\rangle )$.

• $\mathsf {QOTP}.\mathsf {Dec}((x,z), \hat{\phi })$. Apply the reverse transformation $Z^zX^x$ to $\hat{\phi }$.

We note that if the message to be encrypted $\phi$ is classical, then it is possible to generate a syntactically correct and unconditionally secure QOTP of $\phi$ using a classical algorithm by simply applying a classical one time pad using randomness x, and setting $z=0$. Furthermore, given any QOTP encryption of a classical value, it is possible to measure $\hat{\phi }$ and the resulting classical value can be correctly decrypted using the key (x, z) (or even (x, 0)) by the standard classical one time pad decryption.

2.2 Discrete and Periodic Gaussians

For $s >0$ we define the Gaussian density function $\rho _s(\mathbf {x}) :=e^{-\pi (\Vert {\mathbf {x}} \Vert /s)^2}$, where $\mathbf {x}\in {\mathbb R}^n$. For a set of points $X \subseteq {\mathbb R}^n$ we denote $\rho _s(X) = \sum _{\mathbf {x}\in X} \rho _s(\mathbf {x})$. The discrete Gaussian distribution $D_{{{\mathbb Z}^n},{s}}$ is one that is supported only over $\mathbf {x}\in {\mathbb Z}^n$ and such that $\Pr [D_{{{\mathbb Z}^n},{s}}=\mathbf {x}] \propto \rho _s(\mathbf {x})$.

Definition 2.3

(Periodic Gaussian). The q-periodic Gaussian function $\rho _{s,q}$ is the periodic continuation of $\rho _s$. Namely $\rho _{s,q}(\mathbf {x}) = \rho _s(\mathbf {x}+q{\mathbb Z}^m)$.

We show next that when s is sufficiently smaller than q, $\rho _{s,q}(\mathbf {x})$ is close to the non-periodic (but truncated) Gaussian.

Lemma 2.4

  Let $s>0$, $q \in {\mathbb N}$, $\mathbf {x}\in {\mathbb Z}^m$ be such that $\Vert {\left[ {\mathbf {x}} \right] _q}\Vert < q/4$. Then

$$\begin{aligned} 1 \le \frac{\rho _{s,q}(\mathbf {x})}{\rho _{s}(\left[ {\mathbf {x}} \right] _q)} < 1+2^{- ( \frac{1}{2}(q/s)^2 - m)} \end{aligned}$$

(2)

Proof

The lower bound holds by definition. For the upper bound,

$$\begin{aligned} \frac{\rho _{s,q}(\mathbf {x})}{\rho _{s}(\left[ {\mathbf {x}} \right] _q)}&= \frac{\sum _{\mathbf {v} \in {\mathbb Z}^m}(\rho _{s}(\left[ {\mathbf {x}} \right] _q+q\mathbf {v})}{\rho _{s}(\left[ {\mathbf {x}} \right] _q)}\end{aligned}$$

(3)

$$\begin{aligned}&= \sum _{\mathbf {v} \in {\mathbb Z}^m} \exp \left( -\pi \left( \Vert {\left[ {\mathbf {x}} \right] _q+q\mathbf {v}} \Vert ^2 - \Vert {\left[ {\mathbf {x}} \right] _q} \Vert ^2 \right) / s^2 \right) \end{aligned}$$

(4)

$$\begin{aligned}&= 1 + \underbrace{\sum _{\mathbf {v} \in {\mathbb Z}^m\setminus \{\mathbf {0}\}} \exp \left( -\pi \left( \Vert {\left[ {\mathbf {x}} \right] _q+q\mathbf {v}} \Vert ^2 - \Vert {\left[ {\mathbf {x}} \right] _q} \Vert ^2 \right) / s^2 \right) }_{\text {denote by}\,\,{\delta }} \end{aligned}$$

(5)

However, since $\Vert {\left[ {\mathbf {x}} \right] _q} \Vert < q/4$, it holds that for all $\mathbf {v} \in {\mathbb Z}^m\setminus \{\mathbf {0}\}$

$$\begin{aligned} \Vert {\left[ {\mathbf {x}} \right] _q+q\mathbf {v}} \Vert ^2 - \Vert {\left[ {\mathbf {x}} \right] _q} \Vert ^2&\ge \Vert {q\mathbf {v}} \Vert \cdot (\Vert {q\mathbf {v}} \Vert - 2 \Vert {\left[ {\mathbf {x}} \right] _q} \Vert )\end{aligned}$$

(6)

$$\begin{aligned}&> \Vert {q\mathbf {v}} \Vert \cdot (\Vert {q\mathbf {v}} \Vert - q/2)\end{aligned}$$

(7)

$$\begin{aligned}&\ge \Vert {q\mathbf {v}} \Vert \cdot (\Vert {q\mathbf {v}} \Vert /2)\end{aligned}$$

(8)

$$\begin{aligned}&= \Vert {{q\mathbf {v}}} \Vert ^2/2 \end{aligned}$$

(9)

Therefore

$$\begin{aligned} \delta&\le \rho \left( \left( \frac{q}{s\sqrt{2}}{\mathbb Z}^m\right) \setminus \{\mathbf {0}\}\right) \end{aligned}$$

(10)

$$\begin{aligned}&\le 2^{m - \frac{1}{2}(q/s)^2}, \end{aligned}$$

(11)

where the last inequality follows by Lemma 2.10, with $t=\frac{q}{s\sqrt{2}}$.    $\square$

For one dimensional Gaussians, another bound can be achieved.

Lemma 2.5

Let $q \in {\mathbb N}$, $s>0$ and $x \in \left[ {{\mathbb Z}} \right] _q$. Then

$$\begin{aligned} \rho _{s,q}(x) \le 2\rho _s(x)/(1-\rho _s(q)) \end{aligned}$$

(12)

Proof

We expand the expression:

$$\begin{aligned} \rho _{s,q}(x)&= \sum _{j \in {\mathbb Z}} e^{-\pi \left( \frac{{x+j q}}{s}\right) ^2}\end{aligned}$$

(13)

$$\begin{aligned}&= \sum _{j \in {\mathbb N}} e^{-\pi \left( \frac{{\left| {x} \right| +j q}}{s}\right) ^2} + \sum _{j \in {\mathbb N}} e^{-\pi \left( \frac{{(q-\left| {x} \right| )+j q}}{s}\right) ^2}\end{aligned}$$

(14)

$$\begin{aligned}&\le \sum _{j \in {\mathbb N}} e^{-\pi \left( \frac{{x}}{s}\right) ^2}\cdot e^{-\pi j \left( \frac{{q}}{s}\right) ^2} + \sum _{j \in {\mathbb N}} e^{-\pi \left( \frac{{(q-\left| {x} \right| )}}{s}\right) ^2}\cdot e^{-\pi j \left( \frac{{q}}{s}\right) ^2}. \end{aligned}$$

(15)

Since $e^{-\pi \left( \frac{{(q-\left| {x} \right| )}}{s}\right) ^2} \le e^{-\pi \left( \frac{{{x}}}{s}\right) ^2}$, and $\sum _{j \in {\mathbb N}} e^{-\pi j \left( \frac{{q}}{s}\right) ^2} = 1/(1-e^{-\pi \left( \frac{{q}}{s}\right) ^2})$, the lemma follows.    $\square$

Corollary 2.6

Let $s>0$, $q \in {\mathbb N}$, $\mathbf {x}\in {\mathbb Z}^m$ be such that $\Vert {\left[ {\mathbf {x}} \right] _q}\Vert \ge t$. Then

$$\begin{aligned} \rho _{s,q}(\mathbf {x}) \le \frac{2^m \rho _s(t)}{1- m \rho _s(q)}, \end{aligned}$$

(16)

Proof

We will use Lemma 2.5 as follows:

$$\begin{aligned} \rho _{s,q}(\mathbf {x})&\le \prod _{i=1}^m \rho _{s,q}(x_i) \le \prod _{i=1}^m \frac{2\rho _s(x)}{1-\rho _s(q)} \le \frac{2^m}{1-m \rho _s(q)}\cdot \rho _s(\mathbf {x}) \le \frac{2^m \rho _s(t)}{1-m \rho _s(q)}. \end{aligned}$$

2.3 Lattices

A lattice, formally, is a discrete subgroup of ${\mathbb R}^m$. In this work we focus on integer lattices, which are subgroups of ${\mathbb Z}^m$. Any lattice can be represented as the ${\mathbb Z}$-span of a set of basis vectors. The basis is usually represented as a matrix $\mathbf {{B}}$ whose columns are the elements of the basis. The lattice spanned by the basis $\mathbf {{B}} \in {\mathbb Z}^{m \times k}$ is denoted $\mathcal{L}(\mathbf {{B}}) = \{\mathbf {{B}}\mathbf {t} : \mathbf {t}\in {\mathbb Z}^k \}$. We will usually consider full rank lattices where $\mathbf {{B}}$ is a square matrix. A coset of a lattice is defined by a vector $\mathbf {c} \in {\mathbb R}^m$ and denoted as $\mathbf {c}+\varLambda = \{\mathbf {x}: \mathbf {x}-\mathbf {v} \in \varLambda \}$ (note that many different $\mathbf {c}$ vectors can define the same coset). The dual of $\varLambda$ is the set $\varLambda ^* = \{\mathbf {y} : \forall \mathbf {x} \in \varLambda .\;\; \langle \mathbf {y}, \mathbf {x} \rangle \in {\mathbb Z}\}$.

The following is an immediate corollary from Banaszczyk’s transference theorems [2].

Corollary 2.7

Let $\varLambda$ be a rank n lattice, and assume that $\varLambda$ contains k linearly independent vectors of length $\le \ell$. Then any set of $(n-k+1)$ linearly independent vectors in $\varLambda ^*$ contains a vector of length $\ge 1/\ell$.

Specifically, if $\varLambda$ contains $(n-1)$ linearly independent vectors of length $\le \ell$, then all vectors in $\varLambda ^*$ of length $< 1/\ell$ are on the same line.

Given a lattice $\varLambda \subseteq {\mathbb R}^m$, we say that $\mathbf {{T}} \in {\mathbb Z}^{m \times m'}$ is a $\sigma$-trapdoor for $\varLambda$ if it has the same rank as $\varLambda$ and its orthogonalized norm $\left\| {\widetilde{\mathbf {{T}}}} \right\|$ is at most $\sigma$. The orthogonalized norm is the maximal norm of the columns of $\widetilde{\mathbf {{T}}}$, which is in turn the Gram-Schmidt orthogonalization of the columns of ${\mathbf {{T}}}$. An upper bound on the norm of the columns of ${\mathbf {{T}}}$ itself is also an upper bound for its trapdoor quality.

The $\epsilon$-smoothing parameter of the lattice $\varLambda$, denoted $\eta _\epsilon (\varLambda )$ is defined as the maximal Gaussian measure over $\varLambda$ whose Fourier Transform is concentrated around $\mathbf {0}$. For our purposes we will only require the following two properties proven in [19, 23, 29].

Lemma 2.8

If $\varLambda$ is of rank m and has a $\sigma$-trapdoor then for all $\epsilon < 1/2$ it holds that $\eta _\epsilon (\varLambda ) \le \sigma \cdot \sqrt{\tfrac{1}{\pi }\log (4m/\epsilon )}$.

Lemma 2.9

If $\eta _\epsilon (\varLambda ) \le s$ then the sequence $\{\rho _s(\varLambda +\mathbf {d})\}_{\mathbf {d} \in {\mathbb R}^m}$ is $O(\epsilon )$-$\mathsf {loginf}$ uniform.

We also use the following lemma, a parameterized version of [31, Lemma 7], which is in turn a simplified version of [2], and follows by an identical proof.

Lemma 2.10

For any m dimensional lattice $\varLambda$, for all $\mathbf {d} \in {\mathbb R}^m$ and for all s, t it holds that

$$\begin{aligned} \rho _s((\varLambda +\mathbf {d}) \setminus \mathcal{B}_m^t) \le 2^{m-(t/s)^2} \rho _s(\varLambda ). \end{aligned}$$

(17)

2.4 The Class of q-Ary Lattices

This class of lattices that is very useful in cryptography, and plays a prominent role in this work as well. A lattice is q-ary, for a modulus $q\in {\mathbb N}$, if it contains all of the vectors in $q\mathbf {{I}}$ (where $\mathbf {{I}}$ is the identity matrix). All such lattices have full rank.

Every matrix of the form $\mathbf {{L}} \in {\mathbb Z}_q^{n \times m}$ defines two useful q-ary lattices. The “perp lattice” $\varLambda ^{\perp }_q(\mathbf {{L}}) = \{\mathbf {x}: \mathbf {{L}}\mathbf {x}=0 \pmod {q} \}$, and the row span ${\mathrm {Span}_q}(\mathbf {{L}}) = \{\mathbf {y} \in {\mathbb Z}^m : \exists \mathbf {s} \in {\mathbb Z}_q^n.\;\; \mathbf {y} = \mathbf {s}\mathbf {{L}} \pmod {q} \}$, which contrary to our usual convention will be considered as a lattice of row vectors. The dual of ${\mathrm {Span}_q}(\mathbf {{L}})$ is $\tfrac{1}{q}\varLambda ^{\perp }_q(\mathbf {{L}})$. For all $\mathbf {v} \in {\mathbb Z}_q^n$ define $\varLambda ^{\perp }_q(\mathbf {{L}}, \mathbf {v}) = \{\mathbf {x}: \mathbf {{L}}\mathbf {x}=\mathbf {v} \pmod {q} \}$ and note that these are cosets of $\varLambda ^{\perp }_q(\mathbf {{L}})$.

Translating Corollary 2.7, we get the following.

Corollary 2.11

If $\varLambda ^{\perp }_q(\mathbf {{L}})$ contains $(n-1)$ linearly independent vectors of length $\le \ell$, then all vectors in ${\mathrm {Span}_q}(\mathbf {{L}})$ of length $< q/\ell$ are on the same line.

For all n, we define the gadget matrix $\mathbf {{G}}\in {\mathbb Z}_q^{n \times n \left\lceil \log q \right\rceil }$ as the block matrix $\mathbf {{G}}= [\mathbf {{I}} \Vert 2 \mathbf {{I}} \Vert \cdots \Vert 2^{\left\lceil \log q \right\rceil -1} \mathbf {{I}}]$ (where $\mathbf {{I}}$ is the $n \times n$ identity matrix). For all $\mathbf {{V}}\in \{0,1\}^{n \times k}$ we define $\mathbf {{G}}^{-1}(\mathbf {{V}}) \in \{0,1\}^{n \left\lceil \log q \right\rceil \times k}$ to be the binary matrix s.t. $\mathbf {{G}}\mathbf {{G}}^{-1}(\mathbf {{V}})=\mathbf {{V}}\pmod {q}$. The matrix $\mathbf {{G}}$ has a $\sqrt{5}$-trapdoor (for any values of n, q).

By the leftover hash lemma, for all $m > (n \log q+2)$, all but $2^{-n}$ fraction of the matrices $\mathbf {{L}} \in {\mathbb Z}_q^{n \times m}$ have a $\sqrt{m}$-trapdoor. The matrix $\mathbf {{G}}$ also has a $\sqrt{m}$-trapdoor (which is efficiently computable, but we will not require it for the purpose of this work).

Lastly, the following is a direct corollary of the fact that $\tfrac{1}{q}{\mathrm {Span}_q}(\mathbf {{D}})$ is the dual of $\varLambda ^{\perp }_q(\mathbf {{D}})$, the Poisson summation formula and basic properties of the Fourier Transform (see, e.g., [30]).

Corollary 2.12

For any full rank $\mathbf {{D}} \in {\mathbb Z}_q^{n \times m}$, for all $\mathbf {v}\in {\mathbb Z}_q^n$, $\mathbf {w} \in {\mathbb Z}_q^m$ and any $\sigma \in {\mathbb R}^{+}$ it holds that

$$\begin{aligned} \sum _{\mathbf {x}\in \varLambda ^{\perp }_q(\mathbf {{D}}, \mathbf {v})} \rho _{\sigma }(\mathbf {x}) e^{-\frac{2\pi i}{q} \langle \mathbf {w}, \mathbf {x}\rangle }&= \tfrac{\sigma ^{m}}{q^{n}} \cdot \sum _{\mathbf {t} \in {\mathbb Z}^{n}} \rho _{q/\sigma }(\mathbf {w}+\mathbf {t}\mathbf {{D}}) \cdot e^{\frac{2\pi i}{q} \langle \mathbf {t}, \mathbf {v}\rangle } \end{aligned}$$

(18)

$$\begin{aligned}&= \tfrac{\sigma ^{m}}{q^{n}} \cdot \sum _{\mathbf {t} \in {\mathbb Z}_q^{n}} \rho _{q/\sigma ,q}(\mathbf {w}+\mathbf {t}\mathbf {{D}}) \cdot e^{\frac{2\pi i}{q} \langle \mathbf {t}, \mathbf {v}\rangle }. \end{aligned}$$

(19)

2.5 Learning with Errors

The learning with errors (LWE) problem was defined by Regev [29]. In this work we exclusively use the decisional version. The $\mathrm {LWE}_{n,m,q,\chi }$ problem, for $n,m,q\in {\mathbb N}$ and for a distribution $\chi$ supported over ${\mathbb Z}$ is to distinguish between the distributions $(\mathbf {{A}}, \mathbf {s}\mathbf {{A}}+\mathbf {e} \pmod {q})$ and $(\mathbf {{A}}, \mathbf {u})$, where $\mathbf {{A}}$ is uniform in ${\mathbb Z}_q^{n \times m}$, $\mathbf {s}$ is a uniform row vector in ${\mathbb Z}_q^n$, $\mathbf {e}$ is a uniform row vector drawn from $\chi ^m$, and $\mathbf {u}$ is a uniform vector in ${\mathbb Z}_q^m$. Often we consider the hardness of solving $\mathrm {LWE}$ for any $m=\mathrm{poly}(n \log q)$. This problem is denoted $\mathrm {LWE}_{n,q,\chi }$.

As shown in [27, 29], the $\mathrm {LWE}_{n,q,\chi }$ problem with $\chi$ being the discrete Gaussian distribution with parameter $\sigma = \alpha q \ge 2 \sqrt{n}$ (i.e. the distribution over ${\mathbb Z}$ where the probability of x is proportional to $e^{-\pi (\left| {x} \right| /\sigma )^2}$, see more details below), is at least as hard as approximating the shortest independent vector problem ($\mathsf {SIVP}$) to within a factor of $\gamma = {\widetilde{O}}({n}/\alpha )$ in worst case dimension n lattices. This is proven using a quantum reduction. Classical reductions (to a slightly different problem) exist as well [7, 26] but with somewhat worse parameters. The best known (classical or quantum) algorithm for these problems run in time $2^{{\widetilde{O}}(n/\log \gamma )}$, and in particular are conjectured to be intractable for $\gamma = \mathrm{poly}(n)$.

2.6 The q-Ary Fourier Transform

We will use the following flavor of Fourier Transform over the ring ${\mathbb Z}_q$ for $q\in {\mathbb N}$ (this is sometimes called discrete Fourier Transform) which maps functions $f: {\mathbb Z}^n \rightarrow {\mathbb C}$ to ${\hat{f}}: {\mathbb Z}^n_q \rightarrow {\mathbb C}$ as

$$\begin{aligned} {\hat{f}}_q(\mathbf {w}) = \sum _{\mathbf {x} \in {\mathbb Z}^n} f(\mathbf {x}) \cdot e^{-\frac{2 \pi i}{q}\langle \mathbf {w}, \mathbf {x} \rangle }. \end{aligned}$$

(20)

We note that if f is only supported over the cube modulo q, i.e. over $\mathcal{H}_n^{q/2} \cap {\mathbb Z}_q^n$, then the q-ary Fourier Transform operator is unitary (up to a global normalization factor).

2.7 Generating Gaussian Superpositions over Lattices

It has been shown in previous works [7, 19] how to sample from a Gaussian superposition over a lattice, or a coset of a lattice, given a good enough basis. We observe that these methods can be extended to generating a Gaussian superposition by carefully repeating the argument from [7, Sect. 5], replacing rejection sampling with quantum rejection sampling, and neglecting the far tail of the Gaussian distribution. We state the result only for integer lattices to avoid handling matters of precision.

Lemma 2.13

(Lattice Superposition Generation). Let $\varLambda = \mathcal{L}(\mathbf {{B}}) \subseteq {\mathbb Z}^m$ be an m-dimensional lattice, let $\mathbf {c} \in {\mathbb Z}^m$ and let $r \ge \sqrt{\ln (2m+4)/\pi } \cdot \Vert {\widetilde{\mathbf {{B}}}} \Vert$. Let $\delta \in (0,1)$. Then there exists a quantum expected polynomial time algorithm $\mathsf {GenGauss}$ s.t. $\mathsf {GenGauss}(\mathbf {{B}}, \mathbf {c}, r, 1/\delta )$ outputs a quantum state which is within $O(\delta )$ trace distance of

$$\begin{aligned} \frac{1}{\sqrt{\rho _r(\varLambda +\mathbf {c})}}\sum _{\mathbf {x} \in \varLambda +\mathbf {c}}\rho _{\sqrt{2}r}(\mathbf {x})|{\mathbf {x}}\rangle . \end{aligned}$$

(21)

Furthermore if $r \ge \sqrt{\log (4m/\delta )/\pi } \cdot \Vert {\widetilde{\mathbf {{B}}}} \Vert$ then the resulting quantum state is supported only over ${\mathbb Z}^m \cap \mathcal{B}_m^{r \sqrt{m + \log (1/\delta )}}$.

A proof is provided in the full version for the sake of completeness.

3 Homomorphic Encryption Tools and Techniques

3.1 Classical Homomorphic Encryption and Bootstrapping

We now define fully homomorphic encryption in the classical and quantum setting, and introduce Gentry’s bootstrapping theorem.

A homomorphic (public-key) encryption scheme $\mathsf {HE}=(\mathsf {HE.Keygen}, \mathsf {HE.Enc}, \mathsf {HE.Dec}, \mathsf {HE.Eval})$ is a tuple of $\text{ ppt }$ algorithms as follows ($\lambda$ is the security parameter):

• Key generation $( \mathsf {pk}, \mathsf {sk}) {\leftarrow }\mathsf {HE.Keygen}(1^\lambda )$: Outputs a public encryption key $\mathsf {pk}$ and a secret decryption key $\mathsf {sk}$.

• Encryption $c {\leftarrow }\mathsf {HE.Enc}( \mathsf {pk},x)$: Using the public key $\mathsf {pk}$, encrypts a single bit message $x\in \{0,1\}$ into a ciphertext c.

• Decryption $x{\leftarrow }\mathsf {HE.Dec}( \mathsf {sk},c)$: Using the secret key $\mathsf {sk}$, decrypts a ciphertext c to recover the message $x\in \{0,1\}$.

• Homomorphic evaluation $\widehat{c} {\leftarrow }\mathsf {HE.Eval}(\mathcal{C}, (c_1, \ldots , c_\ell ), \mathsf {pk})$: Using the public key $\mathsf {pk}$, applies a circuit $\mathcal{C}:\{0,1\}^\ell \rightarrow \{0,1\}^{\ell '}$ to $c_1, \ldots , c_\ell$, and outputs ciphertexts $\widehat{c}_1, \ldots , \widehat{c}_{\ell '}$.

We overload the functionality of the encryption and decryption procedures by allowing the encryption to take multi-bit messages as input, and produce a sequence of ciphertexts corresponding to a bit-by-bit encryption. Similarly we allow the decryption to take as input a sequence of ciphertexts, decrypt them one after the other and output the result. We note that when we refer to the “decryption complexity” of the scheme, we refer to the single ciphertext procedure (although we will mostly be concerned with computation depth which remains the same in the overloaded version).

A homomorphic encryption scheme is said to be secure if it is semantically secure.

Full homomorphism and leveled full homomorphism is defined next.⁶

Definition 3.1

(compactness and full homomorphism). A scheme $\mathsf {HE}$ is fully homomorphic, if for any efficiently computable circuit $\mathcal{C}$ and any set of inputs $x_1, \ldots , x_{\ell }$, letting $( \mathsf {pk}, \mathsf {sk}){\leftarrow }\mathsf {HE.Keygen}(1^\lambda )$ and $c_i {\leftarrow }\mathsf {HE.Enc}( \mathsf {pk},x_i)$, it holds that

$$ \Pr \left[ \mathsf {HE.Dec}( \mathsf {sk},\mathsf {HE.Eval}(\mathcal{C}, (c_1, \ldots , c_\ell ), \mathsf {pk})) \ne \mathcal{C}(x_1, \ldots , x_\ell ) \right] = \mathrm{negl}(\lambda ). $$

A fully homomorphic encryption scheme is compact if its decryption circuit is independent of the evaluated function. The scheme is leveled fully homomorphic if it takes $1^L$ as additional input in key generation, and can only evaluate depth L Boolean circuits.

Gentry’s bootstrapping theorem shows how to go from limited amount of homomorphism to full homomorphism. This method has to do with the augmented decryption circuit and, in the case of pure fully homomorphism, relies on the weak circular security property of the scheme.

Definition 3.2

(Bootstrappable Homomorphic Encryption). Consider a homomorphic encryption scheme $\mathsf {HE}$. Let $( \mathsf {sk}, \mathsf {pk})$ be properly generated keys and let $\mathcal{C}$ be the set of properly decryptable ciphertexts. Then the set of augmented decryption functions, $\{f_{c_1, c_2}\}_{c_1, c_2 \in \mathcal{C}}$ is defined by

$$ f_{c_1, c_2}(x) = \overline{\mathsf {HE.Dec}_{x}(c_1) \wedge \mathsf {HE.Dec}_x(c_2)}. $$

Namely, the function that uses its input as secret key, decrypts $c_1, c_2$ and returns the $\mathrm {NAND}$ of the results.

The scheme $\mathsf {HE}$ is bootstrappable if it can homomorphically evaluate its family of augmented decryption circuits.

Definition 3.3

A public key encryption scheme $\mathsf {PKE}$ is said to be weakly circular secure if it is secure even against an adversary who gets encryptions of the bits of the secret key.

The bootstrapping theorem is thus as follows.

Theorem 3.4

(bootstrapping [16, 17]). A bootstrappable homomorphic encryption scheme can be transformed into a leveled fully homomorphic encryption scheme with the same decryption circuit, ciphertext space and public key.

Furthermore, if the aforementioned scheme is also weakly circular secure, then it can be made into a (non-leveled) fully homomorphic encryption scheme.

3.2 Quantum Fully Homomorphic Encryption

A quantum fully homomorphic encryption (QFHE) is one that can encrypt qubit registers and apply quantum circuits to encrypted data. For the purpose of this paper we will only consider QFHE schemes with classical keys.

We start by considering quantum homomorphic encryption. This is a scheme with similar syntax to the classical setting described above, and is likewise defined as a sequence of algorithms $(\mathsf {HE.Keygen}, \mathsf {QHE.Enc}, \mathsf {QHE.Dec}, \mathsf {QHE.Eval})$. The syntactic differences are as follows.

• 1. $\mathsf {HE.Keygen}$ remains a classical probabilistic algorithm.

• 2. $\mathsf {QHE.Enc}$ takes as input a qubit x rather than a bit, and outputs a ciphertext represented in qubits.

• 3. $\mathsf {QHE.Dec}$ takes as input a ciphertext represented as a quantum register and outputs the plaintext as a qubit.

• 4. $\mathsf {QHE.Eval}$ takes as input a classical description of a quantum circuit with $\ell$ input qubits and $\ell '$ output qubits, and a sequence of $\ell$ quantum ciphertexts. Its output is a sequence of $\ell '$ quantum ciphertexts.

A quantum homomorphic encryption scheme is secure if it is semantically secure. For the definition of quantum semantic security see [11].

Definition 3.5

(compactness and full homomorphism). A scheme $\mathsf {QHE}$ is fully homomorphic, if for any BQP circuit $\mathcal{C}$ and any $\ell$-qubit state $x_1, \ldots , x_{\ell }$, the states $\rho _1, \rho _2$ defined henceforth are within negligible trace distance.

We define $\rho _1$ to be the $\ell '$-qubit state of the output of $\mathcal{C}(x_1, \ldots , x_{\ell })$. We define $\rho _2$ to be the $\ell '$-qubit state produced as follows. Generate $( \mathsf {pk}, \mathsf {sk}){\leftarrow }\mathsf {HE.Keygen}(1^\lambda )$ and $c_i {\leftarrow }\mathsf {HE.Enc}( \mathsf {pk},x_i)$, and output $\mathsf {QHE.Dec}( \mathsf {sk},\mathsf {QHE.Eval}(\mathcal{C}, (c_1, \ldots , c_\ell ), \mathsf {pk}))$. As in the classical case, a fully homomorphic encryption scheme is compact if its decryption circuit is independent of the evaluated function. The scheme is leveled fully homomorphic if it takes $1^L$ as additional input in key generation, and can only evaluate depth L Boolean circuits.

3.3 GSW-Style Classical FHE with Polynomial Modulus

We consider the LWE based fully homomorphic encryption scheme of Gentry, Sahai and Waters [20]. Specifically we use a result due to Brakerski and Vaikuntanathan [10] showing that it is possible to achieve secure FHE using polynomial modulus.

Theorem 3.6

([10]). There exist polynomials $q_0(n),B_{\mathrm {r}}(n),B_{\mathrm {e}}(n)$, and a (classical) bootstrappable fully homomorphic encryption scheme parameterized by any function q(n) s.t. $\forall n. \; q(n) \in [ q_0(n), 2^n ]$, with the following properties.

• 1. The scheme is secure based on the $\mathrm {LWE}_{n,q,\chi }$ assumption, with $\chi = D_{{\mathbb Z}, 2 \sqrt{n}}$, and thus on the hardness of $\mathsf {SIVP}_\gamma$ for $\gamma = {\widetilde{O}}(\sqrt{n} \cdot q)$. Specifically if q is polynomial then so is $\gamma$.

• 2. The public key of the scheme is a matrix $\mathbf {{A}} \in {\mathbb Z}_q^{n \times m}$ for some $m = O(n \log q)$, for $m > n (\log q+2)$, of the form , where $\mathbf {{B}} \in {\mathbb Z}_q^{(n-1)\times m}$ is a random matrix, $\mathbf {s}{\mathop {\leftarrow }\limits ^{\scriptscriptstyle {\$}}}{\mathbb Z}_q^{n-1}$, and $\left\| {\mathbf {e}} \right\| \le B_{\mathrm {e}}(n)$. The secret key is the vector $\mathbf {s}$.

• 3. When the output of a homomorphic evaluation is a ciphertext encrypting a bit $x\in \{0,1\}$, this ciphertext is a matrix $\mathbf {{C}}\in {\mathbb Z}_q^{n \times n \left\lceil \log q \right\rceil }$ of the form $\mathbf {{C}}=\mathbf {{A}}\mathbf {{R}}_c+x\mathbf {{G}}\pmod {q}$ where $\mathbf {{R}}_c\in {\mathbb Z}^{m \times n \left\lceil \log q \right\rceil }$. Furthermore, the maximum Euclidean norm of any column in $\mathbf {{R}}_c$ is at most $B_{\mathrm {r}}(n)$ (note that this bound is independent on q, so long as q is in the aforementioned regime).

• 4. There exists a deterministic polynomial time computable function

  $$ \mathsf {TrackRand}((\mathcal{C}, (c_1, \ldots , c_\ell ), \mathsf {pk}), (r_1, \ldots , r_\ell ), (x_1, \ldots , x_\ell )) $$

  whose input consists of $(\mathcal{C}, (c_1, \ldots , c_\ell ), \mathsf {pk})$ which is an input to the homomorphic evaluation function, as well as the random tapes and messages $r_i, x_i$ used to generate each of the ciphertexts $c_i$. Its output is the matrix $\mathbf {{R}}_c$ (where $\mathbf {{C}}= \mathbf {{A}}\mathbf {{R}}_c+x\mathbf {{G}}$ is the output of the original homomorphic evaluation). Furthermore, the depth of $\mathsf {TrackRand}$ is only dependent on the depth of $\mathcal{C}$.

We note that property 4 was not proven directly in [10] but follows from analysis of the GSW method in followups [1, 3].

3.4 A Randomness Propagating Classical FHE Scheme

We show that using the scheme from Theorem 3.6 it is possible to generate a cryptosystem with the same properties, but that in addition produces, as the output of $\mathsf {Eval}$ an encryption of the randomness $\mathbf {{R}}_c$ of the output ciphertext. We call such a scheme randomness propagating.

Corollary 3.7

(Randomness Propagating Classical FHE). There exists a (parameterized) scheme with the exact same properties as that of the scheme from Theorem 3.6, but with an additional property

• 5. The output of homomorphic evaluation is a ciphertext $\mathbf {{C}}$ as above, in addition to an encryption of $\mathbf {{R}}_c$ (in bit representation).

The idea for constructing the scheme relies on bootstrapping and is similar to the construction of fully-dynamic multi-key FHE by [8] via bootstrapping the schemes of [12, 25].

Proof

Since the scheme from Theorem 3.6 is bootstrappable, it can be extended to one that supports homomorphic evaluation of depth L circuits, for any a-priori polynomial L. In the new scheme, we change the encryption procedure to first encrypt the message and then encrypt the randomness that was used to generate that first ciphertext. Then, to perform the new homomorphic evaluation, first produce $\mathbf {{C}}$ using the homomorphic evaluation of the original scheme, and then homomorphically evaluate $\mathsf {TrackRand}$ on the encryption of the randomness in order to produce the encryption of $\mathbf {{R}}_c$. Since the decryption function did not change, it is possible to choose L large enough so that the scheme remains bootstrappable.    $\square$

4 Our Quantum FHE Scheme

Our scheme follows an outline going back to Broadbent and Jeffery [11] and used also in [14, 21]. The idea is to encrypt messages using a quantum one-time pad (QOTP), and then encrypt the secret pad using a classical FHE scheme (this is often called key encapsulation or hybrid encryption in cryptographic literature). It is shown in [11] that applying Clifford gates on the encrypted message can be carried out by applying it to the QOTP encrypted state, and applying an appropriate classical operation on the encapsulated key. Since the encapsulated key is encrypted using a classical FHE, this classical operation can be carried out thus completing the homomorphic evaluation.

However, to allow evaluating general BQP functionality, it is required to evaluate gates beyond the Clifford family, in particular it is sufficient to evaluate the Toffoli gate. It has been shown (see, e.g., [21, Appendix A.3]) that in order to carry out this operation, it is sufficient to be able to evaluate a CNOT operation on a quantum input with an encrypted classical control bit. Specifically, it is sufficient to support the operation that takes as input a register encoding a general 2-qubit superposition $\sum _{a,b} \alpha _{a,b} |{a,b}\rangle$ and an encrypted control bit x, and output an encapsulated encryption of $\sum _{a,b} \alpha _{a,b} |{a,b\oplus ax}\rangle$. Namely a QOTP encrypted state together with a classical encryption of the QOTP key.

Our encryption scheme will be based on the key encapsulation methodology, using the randomness propagating scheme from Corollary 3.7 as the key encapsulation scheme (this is sometimes called a “key encapsulation mechanism”, or KEM). To show that this scheme can indeed evaluate a CNOT with a classical control bit we prove the following theorem which constitutes the main technical contribution of this work. We present the theorem here and explain how to use it to construct our quantum FHE scheme. The theorem is then proven in Sect. 5 below.

Theorem 4.1

For all $\delta$ and an appropriately set value of $q=\mathrm{poly}(n, \log (1/\delta ))$, let and $\mathbf {{C}} = \mathbf {{A}} \mathbf {{R}}_c+ x \mathbf {{G}}\pmod {q}$ be such that there exist global $\mathrm{poly}(n\log q)$ bounds on the norms of $\mathbf {e}, \mathbf {{R}}_c$ and such that $\mathbf {{B}}$ has a $\sqrt{m}$-trapdoor (which does not need to be known to any entity).

There exists a quantum polynomial time algorithm taking as input $\mathbf {{A}}, \mathbf {{C}}$ and a general superposition over two qubits $\sum _{a,b} \alpha _{a,b} |{a,b}\rangle$. Its output, with probability $1-O(\delta )$, is a superposition over two qubits of the form

$$\begin{aligned} \sum _{a,b} (-1)^{a \cdot \gamma _{\mathrm {phase}}} \alpha _{a,b} |{a,b\oplus ax \oplus \gamma _{\mathrm {flip}}}\rangle , \end{aligned}$$

(22)

as well as two vectors $\mathbf {c}_{\mathrm {flip}}, \mathbf {c}_{\mathrm {phase}}$ and two implicit vectors $\mathbf {s}_{\mathrm {flip}}, \mathbf {s}_{\mathrm {phase}}$, defined as a function of $\mathbf {s}, \mathbf {e}, \mathbf {{R}}_c,x$, s.t.

$$\begin{aligned} |\left[ {\langle \mathbf {c}_{\mathrm {flip}}, \mathbf {s}_{\mathrm {flip}}\rangle - \tfrac{q}{2} \gamma _{\mathrm {flip}}} \right] _q| \le q/10, \end{aligned}$$

(23)

and likewise for $\langle \mathbf {c}_{\mathrm {phase}}, \mathbf {s}_{\mathrm {phase}}\rangle$.

We note that we purposely provide a theorem with parameterized dependence on $\delta$, even though it would have been sufficient to just show that there exists a negligible $\delta$ for which the theorem holds. We do this to emphasize the robustness of our techniques that allow taking the error to be even exponentially small in the security parameter while still keeping q polynomial.

Putting the Components Together. We follow a similar outline to [21], with the required changes from our different method of evaluating classically controlled CNOT. Security follows immediately from the KEM mechanism by combining the security of the quantum one time pad and the security of the classical homomorphic encryption. This argument is identical to previous works.

Let $\delta > 2^{-\mathrm{poly}(n)}$ be some negligible function. We start with instantiating the randomness propagating scheme from Corollary 3.7. We let q be the (polynomial in n) value implied by Theorem 4.1, when instantiated with the bounds $B_{\mathrm {e}}(n),B_{\mathrm {r}}(n)$ from Corollary 3.7 (note that these bounds are independent of q so there is no circularity here), and instantiate the randomness propagating scheme accordingly. We furthermore notice that since the matrix $\mathbf {{B}}$ in the public key is uniformly sampled, it has a $\sqrt{m}$-trapdoor with all but negligible probability. Since the scheme is bootstrappable, it can be extended to support depth L computation for any predefined polynomial L. We will set a proper value for L later.

As explained, we use this scheme as KEM (key encapsulator) for a QOTP. As in previous works, homomorphically evaluating a BQP circuit is done gate by gate (or rather layer by layer). Clifford gates are evaluated as in [11]. To evaluate CNOT with classical control, we recall that by Corollary 3.7, and our definition of q, the structure of the matrices $\mathbf {{A}}, \mathbf {{C}}$ allows to apply Theorem 4.1 to obtain an output 2-bit register, along with the values $\mathbf {c}_{\mathrm {flip}}, \mathbf {c}_{\mathrm {phase}}$.

From this point and on, our outline is again similar to [21]. We note that the values $\gamma _{\mathrm {flip}}, \gamma _{\mathrm {phase}}$ can be recovered via a (classical) polynomial time process out of $\mathbf {c}_{\mathrm {flip}}, \mathbf {c}_{\mathrm {phase}}$ using $(\mathbf {s}, \mathbf {e}, \mathbf {{R}}_c,x)$ by computing the vectors $\mathbf {s}_{\mathrm {flip}},\mathbf {s}_{\mathrm {phase}}$, evaluating the respective inner product and rounding to the nearest multiple of q/2. Since we have encryptions of these values, we can set L to be large enough to allow us to apply this process homomorphically, followed by bootstrapping the resulting value, thus getting a bootstrapped KEM encryption of $\gamma _{\mathrm {flip}},\gamma _{\mathrm {phase}}$. In other words, we set L to be large enough so that the resulting scheme is bootstrappable even after evaluating the quantum circuit.

This completes the proof. We can use Theorem 3.4 to bootstrap the resulting scheme to a leveled FHE of any desired depth, while still relying on the same $\mathrm {LWE}$ assumption as the original scheme. Recalling Theorem 3.6, the $\mathrm {LWE}$ parameters used imply hardness under the hardness of approximating $\mathsf {SIVP}$ to within a factor of ${\widetilde{O}}(\sqrt{n} q) = \mathrm{poly}(n)$. Alternatively, if we assume circular security, we get a (non-leveled) FHE scheme. We will need to assume the circular security of the randomness propagating scheme, i.e. of a scheme that also encrypts the randomness used to generate ciphertexts. Interestingly, as we mention above, this assumption was already proposed in the literature for bootstrapping LWE-based multi-key FHE schemes [8, 12, 25].

5 Evaluating a Classically Controlled CNOT

In this section we prove Theorem 4.1 by providing a BQP algorithm, setting parameters and a value for q and proving that the requirements of the theorem are met.

5.1 The Algorithm

We define $m'=m+n\left\lceil \log q \right\rceil +2$. The choice of parameters for the values $\sigma , q$ is described in Sect. 5.2 below. We recall that we use the term “$\delta$-computing a quantum state” to refer to computing a state that is within $O(\delta )$ trace distance of the prescribed state.

• 1. We start with a superposition $\sum _{a,b} \alpha _{a,b} |{a,b}\rangle$ stored in a register we denote by $\mathrm {INP}$.

• 2. Use the algorithm from Sect. 2.7 to $\delta$-compute the superposition

  $$\begin{aligned} |{{\psi }}\rangle = \frac{1}{\sqrt{\rho _{\frac{\sigma }{\sqrt{2}}}({\mathbb Z}^{m+2})}} \sum _{\begin{array}{c} \hat{\mathbf {r}}\in {\mathbb Z}^m \\ y, \mu \in {\mathbb Z} \end{array}} \rho _{\sigma }(\hat{\mathbf {r}}, y, \mu ) |{\hat{\mathbf {r}}, y, \mu }\rangle . \end{aligned}$$

  (24)

  Specifically, our choice of parameters will ensure that we generate a quantum state which is supported only over ${\mathbb Z}^{m+2} \cap \mathcal{H}_{m+2}^{q/2}$ but is within trace distance $O(\delta )$ from the above.

• 3. We note that it is possible to $\delta$-compute, for any vector $\mathbf {v} \in {\mathbb Z}_q^n$, the superposition

  $$\begin{aligned} |{\psi _{\mathbf {v}}}\rangle = \frac{1}{\sqrt{\rho _{\frac{\sigma }{\sqrt{2}}}(\varLambda ^{\perp }_q(\mathbf {{G}}, \mathbf {v}))}} \sum _{\mathbf {r} \in \varLambda ^{\perp }_q(\mathbf {{G}}, \mathbf {v})} \rho _{\sigma }(\mathbf {r}) |{\mathbf {r}}\rangle , \end{aligned}$$

  (25)

  again we will show that we generate a superposition supported only over ${\mathbb Z}^{n \left\lceil \log q \right\rceil } \cap \mathcal{H}_{n \left\lceil \log q \right\rceil }^{q/2}$ which is within trace distance $O(\delta )$ from the above. For all $a\in \{0,1\}$ we define , and using the above we $\delta$-compute the superposition

  $$\begin{aligned} \sum _{a,b} \alpha _{a,b} |{a,b}\rangle \underbrace{|{\psi _{\mathbf {v}_a}}\rangle |{{\psi }}\rangle }_{\text {register}\,\, {\varPsi }}. \end{aligned}$$

  (26)

• 4. Let $\mu _0$ denote the least significant bit of $\mu$ (the last coordinate in the $\varPsi$ register), we apply the transformation $|{a,b}\rangle \rightarrow |{a,b\oplus \mu _0}\rangle$ to the $\mathrm {INP}$ register.

• 5. Consider the (classical, deterministic) ciphertext randomization function $\mathsf {RandCT}_{\mathbf {{A}},\mathbf {{C}}}(\tilde{\mathbf {r}}) : {\mathbb Z}^{m'} \rightarrow {\mathbb Z}_q^{n \left\lceil \log q \right\rceil }$ which is defined as follows. Parse $\tilde{\mathbf {r}}$ as a concatenation of $\mathbf {r} \in {\mathbb Z}^{n\left\lceil \log q \right\rceil }$, $\hat{\mathbf {r}}\in {\mathbb Z}^{m}$, $y, \mu \in {\mathbb Z}$ and compute

  

  (27)

  Apply $\mathsf {RandCT}$ to the register $\varPsi$, and add the output to a new $|{0}\rangle$ register. Measure the new register to obtain a value $\mathbf {c}'$.

• 6. Apply q-ary Fourier Transform (see Sect. 2.6) over ${\mathbb Z}_q$ to the register $\varPsi$, and measure the result to obtain a value $\mathbf {w}$. We note that since $\varPsi$ contains a superposition which is supported over ${\mathbb Z}^{m'} \cap \mathcal{H}_{m'}^{q/2}$, the q-ary Fourier Transform is indeed a unitary transformation.

• 7. Output the register $\mathrm {INP}$, and the vectors $\mathbf {c}_{\mathrm {flip}}= \mathbf {c}'$ and $\mathbf {c}_{\mathrm {phase}}= \mathbf {w}$, relative to $\mathbf {s}_{\mathrm {flip}}= [-\mathbf {s}, 1]$ and

  

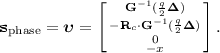
5.2 Parameters and Definitions

The following matrix $\mathbf {{D}}\in {\mathbb Z}_q^{2n \times m'}$, where $m'=m+n\left\lceil \log q \right\rceil +2$, and the lattices induced by it will play a central role in our analysis. This matrix is defined as follows.

(28)

The $m'-1$ columns of the following matrix are all in the lattice $\varLambda ^{\perp }_q(\mathbf {{D}})$:

$$\begin{aligned} {\mathbf {{T}}'}= \left[ \begin{array}{c|c|c} \mathbf {{T}}_{\mathbf {{G}}} &{} \mathbf {{0}} &{} \mathbf {0} \\ -\mathbf {{R}}_c\mathbf {{T}}_{\mathbf {{G}}} &{} \mathbf {{T}}_{\mathbf {{B}}} &{} \mathbf {0}\\ \mathbf {0} &{} - \mathbf {e} \mathbf {{T}}_{\mathbf {{B}}} &{} 0\\ \mathbf {0} &{} \mathbf {0} &{} 2\\ \end{array} \right] \in {\mathbb Z}^{m' \times (m'-1)}, \end{aligned}$$

(29)

where $\mathbf {{T}}_{\mathbf {{G}}} \in {\mathbb Z}^{n \left\lceil \log q \right\rceil \times n \left\lceil \log q \right\rceil }$ is a $\sqrt{n \left\lceil \log q \right\rceil }$-trapdoor for $\mathbf {{G}}$ and $\mathbf {{T}}_{\mathbf {{B}}} \in {\mathbb Z}^{m \times m}$ is a $\sqrt{m}$-trapdoor for $\mathbf {{B}}$. Note that we will never need to explicitly compute ${\mathbf {{T}}'}$. We furthermore notice that the columns of ${\mathbf {{T}}'}$ are vectors in $\varLambda ^{\perp }_q(\mathbf {{D}})$ since

$$\begin{aligned} \mathbf {{D}}{\mathbf {{T}}'}= \mathbf {{0}} \pmod {q}. \end{aligned}$$

(30)

An additional important vector is the offset vector:

(31)

where (i.e. all zeros except the last coordinate). We note that

(32)

Finally we consider the row vector ${\mathbf {d}^*}= [2\mathbf {e}\mathbf {{R}}_c\Vert 2\mathbf {e} \Vert 2 \Vert 0]$ (which we prove below is the shortest vector in ${\mathrm {Span}_q}(\mathbf {{D}})$).

Setting the Parameters. We let $p= \mathrm{poly}(n\log q)$ denote a polynomial upper bound on $\max \left\{ \Vert {{\mathbf {{T}}'}} \Vert , 10 \cdot \Vert {\varvec{{\upsilon }}} \Vert , \Vert {{\mathbf {d}^*}} \Vert \right\}$ (where $\Vert {{\mathbf {{T}}'}} \Vert$ refers to the maximal column norm), and set

$$\begin{aligned} \sigma = {p\cdot \sqrt{2n\log q +m'(\log q +1) + {2}\log (4m'/\delta ) + 1}}, \end{aligned}$$

(33)

finally we set $q = 2 \cdot \left\lceil 10 \cdot p \cdot \sigma \cdot \sqrt{m' + \log (1/\delta )} \right\rceil$, it will be useful for us that q is even.

One might be worried about circularity of this definition, since $p, \sigma$ are used to determine the value of q but depend themselves on $\log q$. Indeed this situation frequently occurs when choosing parameters for LWE-based constructions, but it is easily resolved since the dependence of $p,\sigma$ on q is logarithmic. Specifically, upper bound $\log q$ in the expressions for $p, \sigma$ by, e.g., $\log ^2 n$, and compute the value of q that is implied by these values of $p, \sigma$. The result will be $q = \mathrm{poly}(n)$ which indeed justifies the bound $\log q < \log ^2 n$.

Properties of Lattices Induced by $\mathbf {{D}}$. We prove a few properties that will be useful down the line.

We let $p$ denote an upper bound on the $\ell _2$ norm of the columns of ${\mathbf {{T}}'}$, note that $p=\mathrm{poly}(n \log q)$ for a suitable polynomial. We now invoke Corollary 2.11 to conclude that ${\mathrm {Span}_q}(\mathbf {{D}})$ has at most a single nonzero vector of norm $< q/p$ (up to multiplication by scalar). The next claim identifies the shortest vector in ${\mathrm {Span}_q}(\mathbf {{D}})$.

Claim 5.1

The shortest vector in ${\mathrm {Span}_q}(\mathbf {{D}})$ is the vector ${\mathbf {d}^*}= [2\mathbf {e}\mathbf {{R}}_c\Vert 2\mathbf {e} \Vert 2 \Vert 0]$ (where ${\mathbf {d}^*}= {\mathbf {t}^*}\mathbf {{D}}\pmod {q}$ for ${\mathbf {t}^*}= 2 \cdot [ -x (\mathbf {s}, -1) \Vert (\mathbf {s}, -1) ]$). All vectors in ${\mathrm {Span}_q}(\mathbf {{D}})$ that are not integer multiples of ${\mathbf {d}^*}$ are of length at least q/p.

Proof

Since ${\mathbf {{T}}'}$ contains $(m'-1)$ vectors in $\varLambda ^{\perp }_q(\mathbf {{D}})$ of length at most p, Corollary 2.11 guarantees that ${\mathrm {Span}_q}(\mathbf {{D}})$ has at most a single nonzero vector of norm $< q/p$ (up to integer multiplications). We next verify that the shortest of these vectors is ${\mathbf {d}^*}$.

We can verify that indeed ${\mathbf {d}^*}\in {\mathrm {Span}_q}(\mathbf {{D}})$ since ${\mathbf {d}^*}= {\mathbf {t}^*}\mathbf {{D}} \pmod {q}$. Furthermore, $\left\| {{\mathbf {d}^*}} \right\| \le p < q/p$, and therefore either ${\mathbf {d}^*}$ is the shortest vector, or is an integer multiple of a shorter vector. However, ${\mathbf {d}^*}$ is only divisible by 2 (recall that ${\mathrm {Span}_q}(\mathbf {{D}})$ is an integer lattice), and the vector ${\mathbf {d}^*}/2 = [\mathbf {e}\mathbf {{R}}_c\Vert \mathbf {e} \Vert 1 \Vert 0]$ is not in ${\mathrm {Span}_q}(\mathbf {{D}})$ since q|2.    $\blacksquare$

For the next claim we recall the definition of $\mathsf {loginf}$-uniformity in Definition 2.1 and its properties from Lemma 2.2.

Claim 5.2

The sequence $\big \{\rho _{{\tilde{\sigma }}}(\varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}}))\big \}_{\hat{\mathbf {v}}\in {\mathbb Z}_q^{2n}}$ is $O(\delta )$-$\mathsf {loginf}$ uniform for any ${\tilde{\sigma }}\ge p\cdot \sqrt{\tfrac{1}{\pi }\log (4m'/\delta )}$.

Proof

Denote $\mathbf {h} = [\mathbf {e} \mathbf {{R}}_c\Vert \mathbf {e} \Vert 1 \Vert 0]$ and notice that $\mathbf {h}$ is orthogonal to all columns of ${\mathbf {{T}}'}$. By definition it holds that $\rho _{{\tilde{\sigma }}}(\varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}})) = \sum _{\tilde{\mathbf {r}}\in \varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}})} \rho _{{\tilde{\sigma }}}(\tilde{\mathbf {r}})$, and we can decompose each element in this sum to a component parallel to $\mathbf {h}$ and one orthogonal to $\mathbf {h}$:

$$\begin{aligned} \rho _{{\tilde{\sigma }}}(\varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}}))&= \sum _{\tilde{\mathbf {r}}\in \varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}})} \rho _{{\tilde{\sigma }}}(\tilde{\mathbf {r}})\\&= \sum _{k \in {\mathbb Z}} \rho _{{\tilde{\sigma }}}(k/\left\| {\mathbf {h}} \right\| ) \sum _{\begin{array}{c} \tilde{\mathbf {r}}\in \varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}}) \\ \mathbf {h}\tilde{\mathbf {r}}=k \end{array}} \rho _{{\tilde{\sigma }}}(\tilde{\mathbf {r}}- k \mathbf {h} / \left\| {\mathbf {h}} \right\| ^2). \end{aligned}$$

Fix a value of $k \in {\mathbb Z}$ and consider the sum $\sum \rho _{{\tilde{\sigma }}}(\tilde{\mathbf {r}}- k \mathbf {h} / \left\| {\mathbf {h}} \right\| ^2)$ ranging over all $\tilde{\mathbf {r}}\in \varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}})$ for which $\mathbf {h}\tilde{\mathbf {r}}=k$. Consider the lattice $\widehat{\varLambda }_{\mathbf {{D}}}$ containing all vectors in $\varLambda ^{\perp }_q(\mathbf {{D}})$ which are orthogonal to $\mathbf {h}$. Then the set of vectors $S = \{(\tilde{\mathbf {r}}- k \mathbf {h} / \left\| {\mathbf {h}} \right\| ^2): \tilde{\mathbf {r}}\in \varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}}), \mathbf {h}\tilde{\mathbf {r}}=k\}$ is exactly a coset of $\widehat{\varLambda }_{\mathbf {{D}}}$, and furthermore is supported only over the hyperplane that is orthogonal to $\mathbf {h}$.

Since ${\mathbf {{T}}'}$ is an $p$-trapdoor for $\widehat{\varLambda }_{\mathbf {{D}}}$ (for $p$ defined above), then $\eta _{\delta }(\widehat{\varLambda }_{\mathbf {{D}}}) \le p\cdot \sqrt{\tfrac{1}{\pi }\log (4(m'-1)/\delta )} \le {\tilde{\sigma }}$. Lemma 2.9 implies therefore that the sequence $\{\rho _{\tilde{\sigma }}(\widehat{\varLambda }_{\mathbf {{D}}}+\mathbf {d})\}_{\mathbf {d} \perp \mathbf {h}}$ is $O(\delta )$-$\mathsf {loginf}$ uniform. Since the decomposition above shows that $\rho _{{\tilde{\sigma }}}(\varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}}))$ is a linear combination of elements from the above sequence, applying Lemma 2.2 concludes the proof.   $\blacksquare$

5.3 Analysis

We now prove that the algorithm described above indeed has the properties required in the theorem statement.

Before Ciphertext Randomization. Recall that in the end of Step 3 of the algorithm, we $\delta$-compute the superposition

$$\begin{aligned} \sum _{a,b} \alpha _{a,b} |{a,b}\rangle |{\psi _{\mathbf {v}_a}}\rangle |{{\psi }}\rangle , \end{aligned}$$

(34)

which can also be written as

$$\begin{aligned} \sum _{a,b} \alpha _{a,b} |{a,b}\rangle \tfrac{1}{\sqrt{\rho _{\frac{\sigma }{\sqrt{2}}}({\mathbb Z}_q^{m+2}) \rho _{\frac{\sigma }{\sqrt{2}}}(\varLambda ^{\perp }_q(\mathbf {{G}}, \mathbf {v}_a))}} \sum _{\mathbf {r}, \hat{\mathbf {r}}, y, \mu } \rho _\sigma (\mathbf {r}, \hat{\mathbf {r}}, y, \mu ) |{\mathbf {r}, \hat{\mathbf {r}}, y, \mu }\rangle , \end{aligned}$$

(35)

where the sum is over all $\mathbf {r} \in \varLambda ^{\perp }_q(\mathbf {{G}}, \mathbf {v}_a)$, $\hat{\mathbf {r}}\in {\mathbb Z}^m$, $y, \mu \in {\mathbb Z}$.

Recall that by Lemma 2.8, since $\mathbf {{G}}$ has a O(1)-trapdoor then $\eta _{\delta }(\varLambda ^{\perp }_q(\mathbf {{G}})) \le O(\log (n \log q / \delta ))$. It follows by Lemma 2.9 that the set $\big \{\rho _{\tfrac{\sigma }{\sqrt{2}}}(\varLambda ^{\perp }_q(\mathbf {{G}}, \mathbf {v}))\big \}_{\mathbf {v} \in {\mathbb Z}_q^n}$ is $\delta$-$\mathsf {loginf}$ uniform. Therefore, the above is within $O(\delta )$ trace distance of the superposition

$$\begin{aligned} \tfrac{1}{\sqrt{ \rho _{\frac{\sigma }{\sqrt{2}}}(\varLambda ^{\perp }_q(\mathbf {{G}})\times {\mathbb Z}^{m+2})}} \sum _{a,b} \alpha _{a,b} |{a,b}\rangle \sum _{\mathbf {r}, \hat{\mathbf {r}}, y, \mu } \rho _\sigma (\mathbf {r}, \hat{\mathbf {r}}, y, \mu ) |{\mathbf {r}, \hat{\mathbf {r}}, y, \mu }\rangle , \end{aligned}$$

(36)

with $\mathbf {r}, \hat{\mathbf {r}}, y, \mu$ as before.

After applying Step 4, the resulting superposition is thus (ignoring global normalization)

$$\begin{aligned} \sum _{a,b} \alpha _{a,b} \sum _{\mathbf {r}, \hat{\mathbf {r}}, y, \mu } \rho _\sigma (\mathbf {r}, \hat{\mathbf {r}}, y, \mu ) |{a,b\oplus \mu _0}\rangle |{\mathbf {r}, \hat{\mathbf {r}}, y, \mu }\rangle . \end{aligned}$$

(37)

Ciphertext Randomization. In Step 5 we compute

$$\begin{aligned} \sum _{a,b} \alpha _{a,b} \sum _{\mathbf {r}, \hat{\mathbf {r}}, y, \mu } \rho _\sigma (\mathbf {r}, \hat{\mathbf {r}}, y, \mu ) |{a,b\oplus \mu _0}\rangle |{\mathbf {r}, \hat{\mathbf {r}}, y, \mu }\rangle \underbrace{|{\mathsf {RandCT}_{\mathbf {{A}},\mathbf {{C}}}(\mathbf {r}, \hat{\mathbf {r}}, y, \mu )}\rangle }_{\mathbf {c}'}, \end{aligned}$$

(38)

and measure $\mathbf {c}'$. We prove next that with all but $O(\delta )$ probability, $\mathbf {c}'$ is a ciphertext that decrypts to the value $\mu ' = \mu _0 \oplus a x$.

Claim 5.3

It holds that

$$\begin{aligned} |\left[ {(-\mathbf {s} , 1) \cdot \mathbf {c}' -\tfrac{q}{2} \mu '} \right] _q|<q/10 \end{aligned}$$

(39)

with probability $1-O(\delta )$.

Proof

Consider the register holding $\mathbf {c}'$ before it is measured, we have (recalling that $\mathbf {r}$ is only supported over values where $\mathbf {{G}}\mathbf {r}=\mathbf {v}_a \pmod {q}$ and that q is even)

Recalling that $(-\mathbf {s}, 1) \mathbf {{A}}= \mathbf {e}$, we get that for $\mathbf {c}'$ as above

$$\begin{aligned} (-\mathbf {s}, 1) \mathbf {c}'&= (\mathbf {e} \mathbf {{R}}_c\mathbf {r}+ \mathbf {e}\hat{\mathbf {r}}+ y) + \tfrac{q}{2} \mu ' \pmod {q}\\&= \mathbf {h} \tilde{\mathbf {r}}+ \tfrac{q}{2} \mu ' \pmod {q}, \end{aligned}$$

where the vector $\mathbf {h} = [\mathbf {e} \mathbf {{R}}_c\Vert \mathbf {e} \Vert 1 \Vert 0]$ (which also equals ${\mathbf {d}^*}/2$) is as defined in Claim 5.2. By definition of p we have that $\Vert {\mathbf {h}} \Vert \le p/2$.

Therefore, it holds that in order for $\mathbf {c}'$ to not comply with Eq. (39), it must be the case that $\left| {\mathbf {h} \tilde{\mathbf {r}}} \right| > q/10$. Due to the bound on the norm of $\mathbf {h}$, this means that it must be the case that $\left\| {\tilde{\mathbf {r}}} \right\| > q/(5p) \ge \sigma \sqrt{m'+\log (1/\delta )}$. The probability that this happens, by Lemma 2.10, is at most

$$\begin{aligned} \frac{\rho _{\frac{\sigma }{\sqrt{2}}}\big (\varLambda ^{\perp }_q(\mathbf {{G}})\times {\mathbb Z}^{m+2} \setminus \mathcal{B}^{q/(5p)}_{m'}\big )}{\rho _{\frac{\sigma }{\sqrt{2}}}(\varLambda ^{\perp }_q(\mathbf {{G}})\times {\mathbb Z}^{m+2})} \le \delta , \end{aligned}$$

(40)

and the claim follows.    $\blacksquare$

We note that by definition after measuring $\mathbf {c}'$, it holds that $\mathbf {r}, \hat{\mathbf {r}}, y, \mu$ are only supported over values for which

(41)

where $\mathbf {{D}}$ is as defined in Eq. (28).

Namely, up to this point, we $\delta$-computed the superposition

$$\begin{aligned} \sum _{a,b} \frac{\alpha _{a,b}}{\sqrt{\rho _{\frac{\sigma }{\sqrt{2}}}(\varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}}_a))} } |{a,b \oplus ax\oplus \mu '}\rangle \sum _{\tilde{\mathbf {r}}\in \varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}}_a)} \rho _\sigma (\tilde{\mathbf {r}}) |{\tilde{\mathbf {r}}}\rangle , \end{aligned}$$

(42)

where we note that since we defined $\mu '=ax\oplus \mu _0$ then it holds that $b\oplus \mu _0=b\oplus ax \oplus \mu '$.

Fourier Transform and Measurement. From Claim 5.2 we deduce that we can remove the $\hat{\mathbf {v}}_a$-dependent normalization factor from Eq. (42) at the cost of $O(\delta )$ trace distance, so we conclude that at this point, before Step 6 of the algorithm, we $\delta$-computed

$$\begin{aligned} \sum _{a,b} \alpha _{a,b} |{a,b \oplus ax\oplus \mu '}\rangle \underbrace{\sum _{\tilde{\mathbf {r}}\in \varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}}_a)} \rho _\sigma (\tilde{\mathbf {r}}) |{\tilde{\mathbf {r}}}\rangle }_{\text {denote}\,\, |{\phi _a}\rangle }. \end{aligned}$$

(43)

In Step 6, we apply a q-ary Fourier transform on the register holding $|{\tilde{\mathbf {r}}}\rangle$. We recall that this register is actually supported only over ${\mathbb Z}^{m'} \cap \mathcal{H}^{q/2}_{m'}$, and therefore we can perform q-ary Fourier Transform as a unitary operation. Since the state of the register is $O(\delta )$-close in trace distance to the superposition in Eq. (43), the output of this operation will be $O(\delta )$ close in trace distance to the q-ary Fourier transform of Eq. (43). Formally, the q-ary Fourier transform of $|{\phi _a}\rangle$ is

$$\begin{aligned} |{\hat{\phi }_a}\rangle&= \sum _{\mathbf {w} \in {\mathbb Z}_q^{m'}} |{\mathbf {w}}\rangle \sum _{\tilde{\mathbf {r}}\in \varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}}_a) } \rho _{\sigma }(\tilde{\mathbf {r}}) e^{-\frac{2\pi i}{q} \langle \mathbf {w}, \tilde{\mathbf {r}}\rangle }. \end{aligned}$$

(44)

By Corollary 2.12 it holds that

$$\begin{aligned} \sum _{\tilde{\mathbf {r}}\in \,\,\varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}}_a) } \rho _{\sigma }(\tilde{\mathbf {r}}) e^{-\frac{2\pi i}{q} \langle \mathbf {w}, \tilde{\mathbf {r}}\rangle } = \tfrac{\sigma ^{m'}}{q^{2n}} \cdot \sum _{\mathbf {t} \in {\mathbb Z}_q^{2n}} \rho _{q/\sigma ,q}(\mathbf {w}+\mathbf {t}\mathbf {{D}}) \cdot e^{\frac{2\pi i}{q} \langle \mathbf {t}, \hat{\mathbf {v}}_a \rangle }, \end{aligned}$$

(45)

where we recall the definition of periodic Gaussian from Sect. 2.2: $\rho _{\sigma ',q}(x)=\rho _{\sigma '}(x+q{\mathbb Z})$. Therefore it holds that

$$\begin{aligned} |{\hat{\phi }_a}\rangle&=\tfrac{\sigma ^{m'}}{q^{2n}} \cdot \sum _{\mathbf {w} \in {\mathbb Z}_q^{m'}} |{\mathbf {w}}\rangle \sum _{\mathbf {t} \in {\mathbb Z}_q^{2n}} \rho _{q/\sigma ,q}(\mathbf {w}+\mathbf {t}\mathbf {{D}}) \cdot e^{\frac{2\pi i}{q} \langle \mathbf {t}, \hat{\mathbf {v}}_a \rangle }\end{aligned}$$

(46)

$$\begin{aligned}&=\tfrac{\sigma ^{m'}}{q^{2n}} \cdot \sum _{\mathbf {w} \in {\mathbb Z}_q^{m'}} |{\mathbf {w}}\rangle \sum _{\mathbf {t} \in {\mathbb Z}_q^{2n}} \rho _{q/\sigma ,q}((\mathbf {w}-\mathbf {d}_w)+\mathbf {t}\mathbf {{D}}) \cdot e^{\frac{2\pi i}{q} \langle \mathbf {t}-\mathbf {t}_w, \hat{\mathbf {v}}_a \rangle }. \end{aligned}$$

(47)

For all $\mathbf {w}$, let $\mathbf {d}_w$ denote the vector in ${\mathrm {Span}_q}(\mathbf {{D}})$ that is closest to $\mathbf {w}$ and let $\mathbf {t}_w\in {\mathbb Z}_q^{2n}$ be s.t. $\mathbf {t}_w\mathbf {{D}}=\mathbf {d}_w\pmod {q}$. We let W denote the set of vectors that are close to ${\mathrm {Span}_q}(\mathbf {{D}})$

$$\begin{aligned} W=\{\mathbf {w} \in {\mathbb Z}_q^{m'} : \left\| {\mathbf {w}-\mathbf {d}_w} \right\| \le q/p\}. \end{aligned}$$

(48)

We define

$$\begin{aligned} |{\hat{\phi }'_a}\rangle&= \tfrac{\sigma ^{m'}}{q^{2n}} \sum _{\mathbf {w} \in W} |{\mathbf {w}}\rangle \sum _{k \in {\mathbb Z}_q} \rho _{q/\sigma ,q}((\mathbf {w}-\mathbf {d}_w)+k{\mathbf {d}^*}) \cdot e^{\frac{2\pi i}{q} \langle k {\mathbf {t}^*}-\mathbf {t}_w, \hat{\mathbf {v}}_a \rangle }. \end{aligned}$$

(49)

Claim 5.4

The trace distance between (the normalized versions of) the superpositions $|{\hat{\phi }_a}\rangle$ and $|{\hat{\phi }'_a}\rangle$ is $O(\delta )$.

Proof

We start by bounding the norm of the difference $\Vert {\hat{\phi }_a - \hat{\phi }'_a} \Vert ^2$. We first consider $\mathbf {w} \in {\mathbb Z}_q^{m'} \setminus W$. Then in particular it holds that $\left\| {\left[ {\mathbf {w}+\mathbf {d}} \right] _q} \right\| \ge q/p$ for all $\mathbf {d} \in {\mathrm {Span}_q}(\mathbf {{D}})$ and therefore

$$\begin{aligned} \left| {\sum _{\mathbf {t} \in {\mathbb Z}_q^{2n}} \rho _{q/\sigma ,q}(\mathbf {w}+\mathbf {t}\mathbf {{D}}) \cdot e^{\frac{2\pi i}{q} \langle \mathbf {t}, \hat{\mathbf {v}}_a \rangle }} \right|&\le \frac{q^{2n} \cdot 2^{m'} \cdot \rho _{q/\sigma }(q/p) }{ (1-m' \rho _{q/\sigma }(q))}\end{aligned}$$

(50)

$$\begin{aligned}&= 2^{2n \log q + m'} \cdot \frac{e^{-\pi (\sigma /p)^2}}{1-m' e^{-\pi \sigma ^2}}. \end{aligned}$$

(51)

Since we chose $\sigma = {p\cdot \sqrt{2n\log q +m'(\log q +1) + 2\log (4m'/\delta ) + 1}}$ then in particular $m' e^{-\pi \sigma ^2} < 1/2$ and $2^{2n \log q + m'} \cdot e^{-\pi (\sigma /p)^2} < \delta \cdot q^{-m'} / 2$ which implies that the above is bounded by $\delta \cdot q^{-m'}$.

Now let us consider $w \in W$, the absolute value of the difference between $\hat{\phi }_a$, $\hat{\phi }'_a$ at $\mathbf {w}$ is at most

$$\begin{aligned} \sum _{\begin{array}{c} \{\mathbf {t} \in {\mathbb Z}_q^{2n}: \\ \mathbf {t} \ne k {\mathbf {t}^*}\bmod {q} \} \end{array}} \rho _{q/\sigma ,q}((\mathbf {w}-\mathbf {d}_w)+\mathbf {t}\mathbf {{D}}). \end{aligned}$$

(52)

If $\mathbf {t} \ne k {\mathbf {t}^*}\pmod {q}$ then $\left[ {\mathbf {t}\mathbf {{D}}} \right] _q \ge q/p$. This is since ${\mathbf {d}^*}= \left[ {{\mathbf {t}^*}\mathbf {{D}}} \right] _q$ is the only vector in ${\mathrm {Span}_q}(\mathbf {{D}})$ of length $< q/p$, up to integer multiples. Since $\Vert {\left[ {\mathbf {x}} \right] _q} \Vert \le \Vert {\mathbf {x}} \Vert$ it follows that for all $\mathbf {x}$, if $\Vert {\left[ {\mathbf {x}} \right] _q} \Vert < q/p$ then $\left[ {\mathbf {x}} \right] _q=\left[ {k{\mathbf {d}^*}} \right] _q$ for some $k \in {\mathbb Z}_q$.

By definition of W we have $\left\| {\mathbf {w}-\mathbf {d}_w} \right\| \le q/p$ and therefore by triangle inequality $\Vert {\left[ {(\mathbf {w}-\mathbf {d}_w)+\mathbf {t}\mathbf {{D}}} \right] _q} \Vert \le 2q/p$. Using a similar argument to above we get

$$\begin{aligned} \sum _{\begin{array}{c} \{\mathbf {t} \in {\mathbb Z}_q^{2n}: \\ \mathbf {t} \ne k {\mathbf {t}^*}\bmod {q} \} \end{array}} \rho _{q/\sigma ,q}((\mathbf {w}-\mathbf {d}_w)+\mathbf {t}\mathbf {{D}}) \le \frac{q^{2n} \cdot 2^{m'} \cdot \rho _{q/\sigma }(2q/p) }{ (1-m' \rho _{q/\sigma }(q))} < \delta \cdot q^{-m'}. \end{aligned}$$

(53)

It follows that:

$$\begin{aligned} \Vert {\hat{\phi }_a - \hat{\phi }'_a} \Vert ^2 \le \left( \tfrac{\sigma ^{m'}}{q^{2n}}\right) ^2 q^{m'} \cdot (\delta \cdot q^{-m'})^2 < \left( \tfrac{\sigma ^{m'}}{q^{2n}}\right) ^2 \cdot \delta . \end{aligned}$$

(54)

We now lower bound $\Vert {\hat{\phi }_a} \Vert$ by simply looking at $\mathbf {w}=\mathbf {0}$:

$$\begin{aligned} \Vert {\hat{\phi }_a} \Vert \ge \sum _{\tilde{\mathbf {r}}\in \varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}}_a) \cap \mathcal{H}^{q/2}_{m'}} \rho _{\sigma ,q}(\tilde{\mathbf {r}}) = \sum _{\tilde{\mathbf {r}}\in \varLambda ^{\perp }_q(\mathbf {{D}}, \hat{\mathbf {v}}_a)} \rho _{\sigma }(\tilde{\mathbf {r}}), \end{aligned}$$

(55)

however by Claim 5.2, this is lower bounded by

$$\begin{aligned} (1-O(\delta ))\rho _{\sigma }(\varLambda ^{\perp }_q(\mathbf {{D}})) = (1-O(\delta )) \tfrac{\sigma ^{m'}}{q^{2n}} \rho _{q/\sigma }({\mathrm {Span}_q}(\mathbf {{D}})) \ge (1-O(\delta )) \tfrac{\sigma ^{m'}}{q^{2n}}. \end{aligned}$$

Where the first equality follows from Corollary 2.12. The claim thus follows.    $\blacksquare$

We conclude that up to this point we $\delta$-computed the superposition

$$\begin{aligned} \sum _{a,b} \alpha _{a,b} |{a,b \oplus ax\oplus \mu '}\rangle \sum _{\mathbf {w} \in W} |{\mathbf {w}}\rangle \sum _{k \in {\mathbb Z}_q} \rho _{q/\sigma ,q}((\mathbf {w}-\mathbf {d}_w)+k{\mathbf {d}^*}) \cdot e^{\frac{2\pi i}{q} \langle k {\mathbf {t}^*}-\mathbf {t}_w, \hat{\mathbf {v}}_a \rangle }. \end{aligned}$$

(56)

The next step is to measure the register $|{\mathbf {w}}\rangle$. Since $\mathbf {w} \in W$ it holds that $\left\| {\mathbf {w}-\mathbf {d}_w} \right\| < q/p$. We are left with the superposition

$$\begin{aligned} \sum _{a,b} \alpha _{a,b} |{a,b \oplus ax\oplus \mu '}\rangle \sum _{k \in {\mathbb Z}_q} \rho _{q/\sigma ,q}((\mathbf {w}-\mathbf {d}_w)+k{\mathbf {d}^*}) \cdot e^{\frac{2\pi i}{q} \langle k {\mathbf {t}^*}-\mathbf {t}_w, \hat{\mathbf {v}}_a \rangle }. \end{aligned}$$

(57)

We recall that $\hat{\mathbf {v}}_a$ can be written as for . Let us now analyze the term $\langle k {\mathbf {t}^*}-\mathbf {t}_w, \hat{\mathbf {v}}_a \rangle \pmod {q}$ that is the exponent of the above expression (the $\bmod q$ comes from this term bing in the exponent of the q-th root of unity). We recall that ${\mathbf {t}^*}= 2 \cdot [ -x (\mathbf {s}, -1) \Vert (\mathbf {s}, -1) ]$ is a multiple of 2, and therefore $\frac{q}{2} {\mathbf {t}^*}= \mathbf {0} \pmod {q}$. Let us also denote $\mathbf {t}_w= [\mathbf {t}_1 \Vert \mathbf {t}_2]$, where $\mathbf {t}_1, \mathbf {t}_2 \in {\mathbb Z}_q^n$. We get that

(58)

(59)

and plugging into the superposition above we have

$$\begin{aligned} \sum _{a,b} \alpha _{a,b} |{a,b \oplus ax\oplus \mu '}\rangle \sum _{k \in {\mathbb Z}_q} \rho _{q/\sigma ,q}((\mathbf {w}-\mathbf {d}_w)+k{\mathbf {d}^*}) \cdot e^{\frac{2\pi i}{q} \langle k {\mathbf {t}^*}-\mathbf {t}_w, \hat{\mathbf {v}}_0 \rangle } \cdot (-1)^{ a \cdot \langle \mathbf {t}_1 , \mathbf {\Delta } \rangle }. \end{aligned}$$

Rearranging, we get that the above is equal to

$$\begin{aligned} \sum _{a,b} \alpha _{a,b} (-1)^{ a \cdot \langle \mathbf {t}_1 , \mathbf {\Delta } \rangle } |{a,b \oplus ax\oplus \mu '}\rangle \cdot \underbrace{\left( \sum _{k \in {\mathbb Z}_q} \rho _{q/\sigma ,q}((\mathbf {w}-\mathbf {d}_w)+k{\mathbf {d}^*}) \cdot e^{\frac{2\pi i}{q} \langle k {\mathbf {t}^*}-\mathbf {t}_w, \hat{\mathbf {v}}_0 \rangle } \right) }_{\text {Constant scaling factor, independent of a, b.}}. \end{aligned}$$

We can thus remove the constant scaling factor and remain with

$$\begin{aligned} \sum _{a,b} \alpha _{a,b} (-1)^{ a \cdot \langle \mathbf {t}_1 , \mathbf {\Delta } \rangle } |{a,b \oplus ax\oplus \mu '}\rangle . \end{aligned}$$

(60)

It is left to be shown that $\langle \mathbf {t}_1, \mathbf {\Delta } \rangle \pmod {2}$ is efficiently recoverable given $\mathbf {{R}}_c, x$. We recall that we can write $\mathbf {w} = \mathbf {t}_w\mathbf {{D}}+\mathbf {e}_w\pmod {q}$ with $\Vert {{\mathbf {e}_w}} \Vert \le q/p$. Next, we consider the vector

(61)

and note that

(62)

which implies that

$$\begin{aligned} \mathbf {w}\cdot \varvec{{\upsilon }}= (\mathbf {t}_w\mathbf {{D}}+\mathbf {e}_w)\cdot \varvec{{\upsilon }}= \mathbf {t}_w\mathbf {{D}}\varvec{{\upsilon }}+\mathbf {e}_w\varvec{{\upsilon }}= \tfrac{q}{2} \langle \mathbf {t}_1, \mathbf {\Delta } \rangle +\mathbf {e}_w\varvec{{\upsilon }}\pmod {q}, \end{aligned}$$

(63)

and since $\left| {{\mathbf {e}_w\varvec{{\upsilon }}}} \right| \le \left\| {\mathbf {e}_w} \right\| \cdot \left\| {\varvec{{\upsilon }}} \right\| \le q/p \cdot (p/10) \le q/10$, the theorem follows.