Abstract
In Eurocrypt 2018, Luykx and Preneel described hash-key-recovery and forgery attacks against polynomial hash based Wegman-Carter-Shoup (WCS) authenticators. Their attacks require \(2^{n/2}\) message-tag pairs and recover hash-key with probability about \(1.34\, \times \, 2^{-n}\) where n is the bit-size of the hash-key. Bernstein in Eurocrypt 2005 had provided an upper bound (known as Bernstein bound) of the maximum forgery advantages. The bound says that all adversaries making \(O(2^{n/2})\) queries of WCS can have maximum forgery advantage \(O(2^{-n})\). So, Luykx and Preneel essentially analyze WCS in a range of query complexities where WCS is known to be perfectly secure. Here we revisit the bound and found that WCS remains secure against all adversaries making \(q \ll \sqrt{n} \times 2^{n/2}\) queries. So it would be meaningful to analyze adversaries with beyond birthday bound complexities.
In this paper, we show that the Bernstein bound is tight by describing two attacks (one in the “chosen-plaintext model” and other in the “known-plaintext model”) which recover the hash-key (hence forges) with probability at least  based on \(\sqrt{n} \times 2^{n/2}\) message-tag pairs. We also extend the forgery adversary to the Galois Counter Mode (or GCM). More precisely, we recover the hash-key of GCM with probability at least \(\frac{1}{2}\) based on only \(\sqrt{\frac{n}{\ell }} \times 2^{n/2}\) encryption queries, where \(\ell \) is the number of blocks present in encryption queries.
based on \(\sqrt{n} \times 2^{n/2}\) message-tag pairs. We also extend the forgery adversary to the Galois Counter Mode (or GCM). More precisely, we recover the hash-key of GCM with probability at least \(\frac{1}{2}\) based on only \(\sqrt{\frac{n}{\ell }} \times 2^{n/2}\) encryption queries, where \(\ell \) is the number of blocks present in encryption queries.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Wegman-Carter Authentication. In 1974 [GMS74], Gilbert, MacWilliams and Sloane considered a coding problem which is essentially an one-time authentication protocol (a fresh key is required for every authentication). Their solutions required a key which is as large as the message to be authenticated. Later in 1981, Wegman and Carter [WC81] proposed a simple authentication protocol based on an almost strongly universal\(_2\) hash function which was described in their early work in [CW79]. The hash-key size is the order of logarithm of message length (which is further reduced by some constant factor due to Stinson [Sti94]). The hash-key can be the same for every authentication, but it needs a fresh constant sized random key (used to mask the hash-output). More precisely, let \(\kappa \) be a hash-key of an n-bit hash function \(\rho _{\kappa }\) and \(R_1, R_2, \ldots \) be a stream of secret n-bit keys. Given a message m and its unique message number \(\mathscr {n}\) (also known as a nonce), the Wegman-Carter (WC) authenticator computes \(R_{\mathscr {n}} \oplus \rho _{\kappa }(m)\) as a tag.
Almost Xor-Universal or AXU Hash. In [Kra94] Krawczyk had shown that almost strong universal\(_2\) property can be relaxed to a weaker hash (named as AXU or almost-xor universal hash by Rogaway in [Rog95]). The polynomial hashing [dB93, BJKS94, Tay94], division hashing [KR87, Rab81] are such examples of AXU hash functions which were first introduced in a slightly different context. Afterwards, many AXU hash functions have been proposed for instantiating Wegman-Carter authentication [Sho96, HK97, Ber05a, BHK+99, MV04]. A comprehensive survey of universal hash functions can be found in [Ber07, Nan14]. Among all known examples, the polynomial hashing is very popular as it requires hash-key of constant size and, both key generation and hash computation are very fast.
Wegman-Carter-Shoup or WCS Authenticator. To get rid of onetime masking in Wegman-Carter authenticator, Brassard (in [Bra83]) proposed to use a pseudorandom number generator which generates the keys \(R_1, R_2, \ldots , \) from a short master key K. However, in some application, message number can come in arbitrary order and so a direct efficient computation of \(R_{\mathscr {n}}\) is much desired (it is alternatively known as pseudorandom function or PRF). Brassard pointed out that the Blum-Blum-Shub pseudorandom number generator [BBS86] outputs can be computed directly. As blockciphers are more efficient, Shoup ([Sho96]) considered the following variant of WC authentication:
where \(e_K\) is a keyed blockcipher modeled as a pseudorandom permutation (PRP). This was named as WCS authenticator by Bernstein in [Ber05b].
The use of PRPs enables practical and fast instantiations of WCS authenticators. The WCS authentication mechanism implicitly or explicitly has been used in different algorithms, such as Poly1305-AES [Ber05a] and Galois Counter Mode or GCM [MV04, AY12]. GCM was adopted in practice, e.g. [MV06, JTC11, SCM08]. GCM and its randomized variants, called RGCM [BT16], are used in TLS 1.2 and TLS 1.3.
1.1 Known Security Analysis of WCS prior to Luykx-Preneel Eurocrypt 2018
Hash-Key Recovery Attacks of WCS. Forgery and key-recovery are the two meaningful security notions for an authenticator. Whenever we recover hash-key, the security is completely lost as any message can be forged. Security of WCS relies on the nonce which should not repeat over different executions [Jou, HP08]. Most of the previously published nonce respecting attacks aim to recover the polynomial key [ABBT15, PC15, Saa12, ZTG13] based on multiple verification attempts. The total number of message blocks in all verification attempts should be about \(2^n\) to achieve some significant advantage.
Provable Security Analysis of WCS. The WC authenticator based on polynomial hashing has maximum forgery or authenticity advantage \(\frac{v \ell }{2^n}\) against all adversaries who make at most q authentication queries and v verification queries consisting of at most \(\ell \) blocks. By applying the standard PRP-PRF switching lemma, WCS (which is based on a random permutation \(\pi \)) has an authenticity advantage at most \(\frac{v \ell }{2^n} + \frac{(v+q)^2}{2^n}\). So the bound becomes useless as q approaches \(2^{n/2}\) (birthday complexity). Shoup proved that the advantage is at most \(\frac{v \ell }{2^n}\) for all \(q < 2^{\frac{n- \log \ell }{2}}\) [Sho96]. So, when \(\ell = 2^{10}\), \(n = 128\), the above bound says that the authenticity advantage is at most \(v\ell /2^{128}\), whenever \(q \le 2^{59}\). This is clearly better than the classical bound. However, the application of Shoup’s bound would be limited if we allow large \(\ell \).
Bernstein Bound. Finally, Bernstein [Ber05b] provided an improved bound for WCS which is valid for wider range of q. The maximum authenticity advantage is shown to be bounded above by
for all q, where \(\rho _{\kappa }\) is an \(\epsilon \)-AXU hash function. Thus, when \(q= O(2^{n/2})\), the maximum success probability is \(O(v \cdot \epsilon )\) which is clearly negligible for all reasonable choices of v and \(\epsilon \). For example, the forgery advantage against 128-bit WCS based on polynomial hashing is at most (1) \(1.7v\ell \times 2^{-128}\) when \(q \le 2^{64}\), and (2) \(3000v\ell \times 2^{-128}\) when \(q = 2^{66}\) (so WCS remains secure even if we go beyond birthday bound query complexity).
1.2 Understanding the Result Due to Luykx and Preneel in [LP18]
False-key or True-key set. All known key-recovery attacks focus on reducing the set of candidate keys, denoted \(\mathscr {T}\!\), which contains the actual key. But the set of candidate keys, also called true-key set, is constructed from verification attempts. Recently, a true-key set (equivalently false-key set which is simply the complement of the true-key set) is constructed from authentication queries only. After observing some authentication outputs of a WCS based on a blockcipher \(e_K\), some choices for the key can be eliminated using the fact that outputs of the blockcipher are distinct. More precisely, we can construct the following false-key set \(\mathscr {F}\!\) based on a transcript \(\tau := ((\mathscr {n}_1, m_1, t_1), \ldots , (\mathscr {n}_q, m_q, t_q))\) where \(t_i = e_K(\mathscr {n}_i)\oplus \rho _{\kappa }(m_i)\):
It is easy to see that the hash-key \(\kappa \not \in \mathscr {F}\!\), since otherwise, there would exist \(i \ne j\), \(e_K(\mathscr {n}_i) = e_K(\mathscr {n}_j)\), which is a contradiction. So, a random guess of a key from outside the false-key set would be a correct guess with probability at least \(\frac{1}{2^n - \mathbb {E}(|\mathscr {F}\!|)}\). This simple but useful observation was made in [LP18]. We also use this idea in our analysis.
– Lower bound on the expected size of false-key set.
Based on the above discussion, one natural approach would be to maximize the false-key set to obtain higher key-recovery advantage. This has been considered in [LP18]. Proposition 3.1 of [LP18] states that
\(\mathbb {E}(|\mathscr {F}\!|) \ge \frac{q(q-1)}{4}\), for all \(q < \sqrt{2^n -3}\).
In other words, expected size of the false-key set grows quadratically. They have stated the following in Sect. 3 of [LP18].
“We describe chosen-plaintext attacks which perfectly match the bounds for both polynomial-based WCS MACs and GCM.”
Issue 1: The Luykx-Preneel attack is no better than random guessing. Their attack can eliminate about one fourth keys. In other words, there are still three-fourth candidate keys are left. So, the key-recovery advantage \(\mathsf {KR}(q)\) is about \(\frac{1.34}{2^n}\) (1.34 times more than a random guess attack without making any query). Naturally, as the key-recovery advantage is extremely negligible, claiming such an algorithm as an attack is definitely under question.
– Upper bound on the expected size of false-key set.
Now we discuss the other claim of [LP18]. They claimed that (Theorem 5.1 of [LP18]) the size of the false-key set cannot be more than \(q(q+1)/2\) after observing q responses of polynomial-based WCS. In other words, irrespective of the length of queries \(\ell \), the upper bound of the size of the false-key set is independent of \(\ell \). At a first glance this seem to be counter-intuitive as the number of roots of a polynomial corresponding to a pair of query-responses can be as large as \(\ell \). So, at best one may expect the size of the false-key set can be \({q \atopwithdelims ()2}\ell \). But, on the other extreme there may not be a single root for may pairs of queries. On the average, the number of roots for every pair of messages turns out to be in the order of \(q^2\), independent of \(\ell \). We investigate the proof of Theorem 5.1 of [LP18] and in the very first line they have mentioned that
“Using Thm. 4.1, Cor. 5.1, and Prop. 5.3, we have...”
However, the Cor 5.1 is stated for all \(q \le M_{\gamma }\) (a parameter defined in Eq. 41 of [LP18]). They have not studied how big \(M_{\gamma }\) can be. We provide an estimation which allows us to choose \(M_{\gamma }\) such that \(\ell {M_{\gamma } \atopwithdelims ()2} = 2^n - \ell \). With this bound, the Theorem 5.1 can be restated as
By combining Proposition 3.1 and a corrected version of Theorem 5.1 as just mentioned, we can conclude that
In other words, authors have found a tight estimate of expected size of the false-key set in a certain range of q.
Issue 2: Usefulness of an upper bound of the false-key set: The lower bound of the expected false-key set immediately leads to a lower bound of key-recovery advantage. However, an upper bound of the expected false-key set does not lead to an upper bound of key-recovery advantage. This is mainly due to the fact, the key-recovery advantage based on q authentication responses can be shown as
The inequality follows from the Jensen inequality. So an upper bound of \(\mathbb {E}(|\mathscr {F}\!|)\) does not give any implication on \(\mathsf {KR}(q)\). Moreover, dealing the expression \(\mathbb {E}(1/(2^n -|\mathscr {F}\!|))\) directly is much harder. So the usefulness of an upper bound of the expected size of false-key set is not clear to us (other than understanding tightness of size of the false-key set which could be of an independent interest).
1.3 Our Contributions
In this paper, we resolve the optimality issue of the Bernstein bound. We first provide a tight alternative expression of the Berstein bound. In particular, we observe that \(\textsf {B}(q, v) = \varTheta (v \cdot \epsilon \cdot e^{\frac{q^2}{2^{n+1}}})\). So WCS is secure against all adversaries with \(q \ll \sqrt{n} \times 2^{n/2}\) queries. An adversary must make about \(\sqrt{n} \times 2^{n/2}\) queries to obtain some significant advantage. In this paper we describe three attacks to recover the hash key and analyze their success probabilities.
-
1.
The first two attacks (in the known-plaintext and the chosen-plaintext models) are against WCS based on a polynomial hash; they also work for other hashes satisfying certain regular property. Our attacks are also based a false-key (equivalently a true-key set) as described in the Luykx-Preneel attack. Unlike the Luykx-Preneel attack, we however choose message randomly in case of chosen-plaintext model. The query complexity of our attacks is also beyond the birthday complexity. In particular, these attacks require \(\sqrt{n 2^{n}}\) authentication queries. So the bound due to Bernstein is tight (even in the known-plaintext model) when \(q \approx \sqrt{n 2^{n}}\).
-
2.
We also extend these attacks to the authentication algorithm of GCM which utilizes the ciphertext of GCM encryption to reduce the complexity of encryption queries. In particular, if each encryption query contains \(\ell \) blocks, then this attack requires \(\sqrt{\frac{n}{\ell }\times 2^{n}}\) encryption queries to recover the hash key used in GCM authentication. We have proved that our forgery is optimum by proving a tight upper bound on the maximum forgery advantage.
-
3.
We also provide a simple proof on the tightness of the false-key set which works for all q. In particular, we show that the expected size of the false-key set is at most \(q(q-1)/2^n\).
2 Preliminaries
Notations. We write  to denote that the random variable \(\mathsf {X}\) is sampled uniformly (and independently from all other random variables defined so far) from the set \(\mathscr {X}\). Let \((a)_b := a(a-1) \cdots (a-b+1)\) for two positive integers \(b \le a\). A tuple \((x_1, \ldots , x_q)\) is simply denoted as \(x^q\). We call \(x^q\) coordinate-wise distinct if \(x_i\)’s are distinct. We write the set \(\{1, 2, \ldots , m\}\) as [m] for a positive integer m. We use standard asymptotic notations such as \(o(\cdot )\), \(O(\cdot )\), \(\varTheta (\cdot )\) and \(\varOmega (\cdot )\) notations. For real functions f(x), g(x), we write \(f = O(g)\) (equivalently \(g = \varOmega (f)\)) if there is some positive constant C such that \(f(x) \le C g(x)\) for all x. If both \(f = O(g)\) and \(g = O(f)\) hold then we write \(f = \varTheta (g)\). We write \(f(x) = o(g(x))\) if \(\displaystyle \lim _{x \rightarrow \infty }\) \(\frac{f(x)}{g(x)} = 0\).
to denote that the random variable \(\mathsf {X}\) is sampled uniformly (and independently from all other random variables defined so far) from the set \(\mathscr {X}\). Let \((a)_b := a(a-1) \cdots (a-b+1)\) for two positive integers \(b \le a\). A tuple \((x_1, \ldots , x_q)\) is simply denoted as \(x^q\). We call \(x^q\) coordinate-wise distinct if \(x_i\)’s are distinct. We write the set \(\{1, 2, \ldots , m\}\) as [m] for a positive integer m. We use standard asymptotic notations such as \(o(\cdot )\), \(O(\cdot )\), \(\varTheta (\cdot )\) and \(\varOmega (\cdot )\) notations. For real functions f(x), g(x), we write \(f = O(g)\) (equivalently \(g = \varOmega (f)\)) if there is some positive constant C such that \(f(x) \le C g(x)\) for all x. If both \(f = O(g)\) and \(g = O(f)\) hold then we write \(f = \varTheta (g)\). We write \(f(x) = o(g(x))\) if \(\displaystyle \lim _{x \rightarrow \infty }\) \(\frac{f(x)}{g(x)} = 0\).
Jensen Inequality. We write \(\mathbb {E}(\mathsf {X})\) to denote the expectation of a real valued random variable \(\mathsf {X}\). A twice differentiable function f is called convex if for all x (from the domain of f), \(f''(x) > 0\). For example, (1)  is a convex function over the set of all positive real numbers and (2) \(\frac{1}{N -x}\) is convex over the set of all positive real number less than N. For every convex function f and a real valued random variable \(\mathsf {X}\), \(\mathbb {E}(f(\mathsf {X})) \ge f(\mathbb {E}(\mathsf {X}))\) (Jensen Inequality). In particular, for all positive random variable \(\mathsf {X}\),
is a convex function over the set of all positive real numbers and (2) \(\frac{1}{N -x}\) is convex over the set of all positive real number less than N. For every convex function f and a real valued random variable \(\mathsf {X}\), \(\mathbb {E}(f(\mathsf {X})) \ge f(\mathbb {E}(\mathsf {X}))\) (Jensen Inequality). In particular, for all positive random variable \(\mathsf {X}\),
and for all positive random variable \(\mathsf {Y}< N\),
Lemma 1
Let \(0 < \epsilon \le \sqrt{2} - 1\). Then, for all positive real \(x \le \epsilon \),
Proof
It is well known (from calculus) that \( e^{-x} \le 1 - x + \frac{x^2}{2}\) for all real x. Let \(\eta = 1 + \epsilon < \sqrt{2}\). So
\(\square \)
We also know that \(1 - x \le e^{-x}\). So, the above result informally says that \(1- x\) and \(e^{-x}\) are “almost” the same whenever x is a small positive real number.
2.1 Security Definitions
Pseudorandom Permutation Advantage. Let \(\mathsf {Perm}_{\mathfrak {B}}\) be the set of all permutations over \(\mathfrak {B}\). A blockcipher over a block set \(\mathfrak {B}\) is a function \(e : \mathscr {K}\times \mathfrak {B}\rightarrow \mathfrak {B}\) such that for all key \(k \in \mathscr {K}\), \(e(k, \cdot ) \in \mathsf {Perm}_{\mathfrak {B}}\). So, a blockcipher is a keyed family of permutations. A uniform random permutation or URP is denoted as \(\pi \), where  . The pseudorandom permutation advantage of a distinguisher \(\mathscr {A}\) against a blockcipher e is defined as
. The pseudorandom permutation advantage of a distinguisher \(\mathscr {A}\) against a blockcipher e is defined as

Let \(\mathbb {A}(q, t)\) denote the set of all adversaries which runs in time at most t and make at most q queries to either a blockcipher or a random permutation. We write \(\mathsf {Adv}^{\mathrm {prp}}(q, t) = \displaystyle \max _{\mathscr {A}\in \mathbb {A}(q, t)} \mathsf {Adv}^{\mathrm {prp}}_{e}(\mathscr {A})\).
Authenticator. A nonce based authenticator with nonce space \(\mathscr {N}\), key space \(\mathscr {K}\), message space \(\mathscr {M}\) and tag space \(\mathfrak {B}\) is a function \(\gamma : \mathscr {K}\times \mathscr {N}\times \mathscr {M}\rightarrow \mathfrak {B}\). We also write \(\gamma (k, \cdot , \cdot )\) as \(\gamma _k(\cdot , \cdot )\) and hence a nonce based authenticator can be viewed as a keyed family of functions. We say that (n, m, t) is valid for \(\gamma _k\) (or for a key k when \(\gamma \) is understood) if \(\gamma _k(n,m) = t\). We define a verifier \(\mathsf {Ver}_{ \gamma _k} : \mathscr {N}\times \mathscr {M}\times \mathfrak {B}\rightarrow \{0,1\}\) as
We also simply write \(\mathsf {Ver}_{ k}\) instead of \(\mathsf {Ver}_{ \gamma _k}\).
An adversary \(\mathscr {A}\) against a nonce based authenticator makes authentication queries to \(\gamma _K\) and verification queries to \(\mathsf {Ver}_{ K}\) for a secretly sampled  . An adversary is called
. An adversary is called
-
nonce-respecting if nonces in all authentication queries are distinct,
-
single-forgery (or multiple-forgery) if it submits only one (or more than one) verification query,
-
key-recovery if it finally returns an element from key space.
In this paper we only consider nonce-respecting algorithm. We also assume that \(\mathscr {A}\) does not submit a verification query (n, m, t) to \(\mathsf {Ver}_{ \gamma _K}\) for which (n, m) has already been previously queried to the authentication oracle. Let \(\mathbb {A}(q, v, t)\) denote the set of all such nonce-respecting algorithms which runs in time t and make at most q queries to an authenticator and at most v queries to its corresponding verifier. In this paper our main focus on analyzing the information-theoretic adversaries (which can run in unbounded time). So we write \(\mathbb {A}(q, v) = \cup _{t < \infty }~ \mathbb {A}(q, v, t)\).
View of an Adversary. An adversary \(\mathscr {A}\in \mathbb {A}(q, v)\) makes queries \((n_1, m_1)\), \(\ldots \), \((n_q, m_q)\) to an authenticator \(\gamma _K\) adaptively and obtain responses \(t_1, \ldots , t_q\) respectively. It also makes \((n'_1, m'_1, t'_1), \ldots , (n'_v, m'_v, t'_v)\) to verifier \(\mathsf {Ver}_{ K}\) and obtain responses \(b_1, \ldots , b_v \in \{0,1\}\) respectively. The authentication and verification queries can be interleaved and adaptive. Note that all \(n_i\)’s are distinct as we consider only nonce-respecting adversary, however, \(n'_i\)’s are not necessarily distinct and can match with \(n_j\) values. We also assume that both q and v are fixed and hence non-random. We call the tuple
view and denote it as \(\mathsf {view}(\mathscr {A}^{\gamma _K, \mathsf {Ver}_{ K}})\) (which is a random variable induced by the randomness of \(\mathscr {A}\) and the key of \(\gamma \)). Let
be the set of all possible views. We say that a view \(\tau \in \mathscr {V}\) is realizable if
Authenticity Advantage. Following the notation of the view of an adversary as denoted above, we define the authenticity advantage of \(\mathscr {A}\) as
In words, it is the probability that \(\mathscr {A}\) submits a valid verification query which has not been obtained through a previous authentication query. In this paper, we are interested in the following maximum advantages for some families of adversaries:
So \(\mathsf {Auth}_{\gamma }(q, v)\) is the maximum advantage for all information theoretic adversaries with the limitation that it can make at most q authentication queries and v verification queries. It is shown in [BGM04, Ber05a] that
Key-recovery Advantage. A full-key-recovery algorithm \(\mathscr {A}\) is an adversary interacting with \(\gamma _K\) and \(\mathsf {Ver}_{ K}\) and finally it aims to recover the key K. Once the key K is recovered, the full system is broken and so one can forge as many times as it wishes. For some authenticators, we can do the forgeries when a partial key is recovered. Let \(\mathscr {K}= \mathscr {K}' \times \mathscr {H}\!\) for some sets \(\mathscr {K}'\) and \(\mathscr {H}\!\). We call \(\mathscr {H}\!\) hash-key space. Let  .
.
Definition 1
(key-recovery advantage). A hash-key recovery algorithm (or we simply say that a key-recovery algorithm) \(\mathscr {A}\) is an adversary interacting with \(\gamma _K\) and \(\mathsf {Ver}_{ K}\) and finally it returns \(\mathbf {h}\), an element from \(\mathscr {H}\!\). We define key-recovery advantage of \(\mathscr {A}\) against \(\gamma \) as
The above probability is computed under randomness of \(\mathscr {A}\) and \(K = (K', H)\).
Similar to the maximum authenticity advantages, we define
When \(v = 0\), we simply write \(\mathsf {KR}_{\gamma }(q, t)\) and \(\mathsf {KR}_{\gamma }(q)\). A relationship between key-recovery advantage and authenticity advantage is the following which can be proved easily \(\mathsf {KR}_{\gamma }(q) \le \mathsf {Auth}_{\gamma }(q, 1)\).
Authenticated Encryption. In addition to nonce and message, an authenticated encryption \(\gamma '\) takes associated data and returns a ciphertext-tag pair. A verification algorithm \(\mathsf {Ver}_{ \gamma '}\) takes a tuple of nonce, associated data, ciphertext and tag, and determines whether it is valid (i.e. there is a message corresponding to this ciphertext and tag) or not. A forgery adversary \(\mathscr {A}\) submits a fresh tuple (not obtained through encryption queries) of nonce, associated data, ciphertext and tag. Similar to authenticity advantage of an authenticator, authenticity of an adversary \(\mathscr {A}\), denoted \(\mathsf {Auth}_{\gamma '}(\mathscr {A})\) is the probability that it submits a fresh valid tuple.
Almost XOR Universal and \(\varDelta \) -Universal Hash Function. Let \(\rho : \mathscr {H}\!\times \mathscr {M}\rightarrow \mathscr {B}\), for some additive commutative group \(\mathscr {B}\). We denote the subtraction operation in the group as “−”. We call \(\rho \) \(\epsilon \)-\(\varDelta \)U (\(\epsilon \)-\(\varDelta \)-universal) if for all \(x \ne x' \in \mathscr {M}\) and \(\delta \in \mathfrak {B}\),
Here, the probability is taken under the uniform distribution  . Note that \(\epsilon \ge 1/N\) (since, for any fixed \(x, x'\), \(\sum _\delta \Pr (\rho _{\kappa }(x) - \rho _{\kappa }(x') = \delta ) = 1\)). When \(\mathscr {B}= \{0,1\}^b\) for some positive integer b and the addition is “\(\oplus \)” (bit-wise XOR operation), we call \(\rho \) \(\epsilon \)-almost-xor-universal or \(\epsilon \)-AXU hash function.
. Note that \(\epsilon \ge 1/N\) (since, for any fixed \(x, x'\), \(\sum _\delta \Pr (\rho _{\kappa }(x) - \rho _{\kappa }(x') = \delta ) = 1\)). When \(\mathscr {B}= \{0,1\}^b\) for some positive integer b and the addition is “\(\oplus \)” (bit-wise XOR operation), we call \(\rho \) \(\epsilon \)-almost-xor-universal or \(\epsilon \)-AXU hash function.
3 Known Analysis of WCS
We describe a real and an idealized version of WCS.
Definition 2
(WCS authenticator). Let \(e_K\) be a blockcipher over a commutative group \(\mathfrak {B}\) of size N with a key space \(\mathscr {K}'\) and \(\rho _{\kappa }: \mathscr {M}\rightarrow \mathfrak {B}\) is a keyed hash function with a key space \(\mathscr {K}\). On an input \((\mathscr {n}, M) \in \mathfrak {B}\times \mathscr {M}\), we define the output of WCS as
Here, the pair \((K, \kappa )\), called secret key, is sampled uniformly from \(\mathscr {K}' \times \mathscr {K}\).
An idealized version of WCS is based on a uniform random permutation  (replacing the blockcipher e) and it is defined as
(replacing the blockcipher e) and it is defined as
where the hash key  (and independent of the random permutation).
(and independent of the random permutation).
WCS is a nonce based authenticator in which \(\mathscr {n}\) is the nonce and M is a message. The most popular choice of \(\mathfrak {B}\) is \(\{0,1\}^n\) for some positive integer n and the blockcipher is AES [DR05, Pub01] (in which \(n = 128\)). The WCS and the ideal-WCS authenticators are computationally indistinguishable provided the underlying blockcipher e is a pseudorandom permutation. More formally, one can easily verify the following relations by using standard hybrid reduction;
where \(t'\) is the time to compute \(q + v\) executions of hash functions \(\rho _{\kappa }\).
Polynomial Hash. Polynomial hash is a popular candidate for the keyed hash function in WCS (also used in the tag computation of GCM [MV04]). Here we assume that \(\mathfrak {B}\) is a finite field of size N. Given any message \(M := (m_1, \ldots , m_{d}) \in \mathfrak {B}^{d}\) and a hash key \(\kappa \in \mathscr {K}= \mathfrak {B}\), we define the polynomial hash output as
There are many variations of the above definition. Note that it is not an AXU hash function over variable-length messages (as appending zero blocks will not change the hash value). To incorporate variable length message, we sometimes preprocess the message before we run the polynomial hash. One such example is to pad a block which encodes the length of the message. One can simply prepend the constant block 1 to the message. These can be easily shown to be \(\frac{\ell }{N}\)-AXU over the padded message space \(\mathscr {M}= \cup _{i=1}^{\le \ell }\mathfrak {B}^{i}\). In this paper we ignore the padding details and for simplicity, we work only on the padded messages. Whenever we use the polynomial hash in the WCS authenticator, we call its hash-key \(\kappa \) the polynomial-key.
Nonce Misuse. The input \(\mathscr {n}\) is called nonce which should not repeat over different executions. Joux [Jou] and Handschuh and Preneel [HP08] exhibit attacks which recover the polynomial key the moment a nonce is repeated. For any two messages \(M \ne M' \in \mathfrak {B}^{d}\),
which is a nonzero polynomial in \(\kappa \) of degree at most d. By solving roots of the polynomial (which can be done efficiently by Berlekamp’s algorithm [Ber70] or the Cantor-Zassenhaus algorithm [CZ81]), we can recover the polynomial key. So it is an essential for a WCS authenticator to keep the nonce unique.
3.1 Shoup and Bernstein Bound on WCS
Let \(\mathsf {iWCS}\) (we simply call it ideal-WCS) be based on a URP and an \(\epsilon \)-AXU hash function \(\rho \). When we replace the outputs of URP by uniform random values, Wegman and Carter had shown that (in [WC81]) the forgery advantage os less than \(v \epsilon \) (independent of the number of authentication queries). So by applying the classical PRP-PRF switching lemma, we obtain
So the classical bound is useless as q approaches \(\sqrt{N}\) or as v approaches to \(\epsilon ^{-1}\). In [Sho96] Shoup provided an alternative bound (which is improved and valid in a certain range of q). In particular, he proved
The above bound is a form of multiplicative (instead of additive form of the classical bounds). Thus, the above bound is simplified as
So the ideal-WCS is secure up to \(q \le \sqrt{\epsilon ^{-1}}\) queries. When \(\epsilon = 1/N\), it says that authentication advantage is less \(2v \cdot \epsilon \) for all \(q \le \sqrt{N}\). In other words, ideal-WCS is secure against birthday complexity adversaries. However, when the hash function is polynomial hash, Shoup’s bound says that the ideal-WCS is secure up to \(q \le \sqrt{N/\ell }\). For example, when we authenticate messages of sizes about \(2^{24}\) bytes (i.e. \(\ell = 2^{20}\)) using AES-based ideal-WCS, we can ensure security up to \(q = 2^{54}\) queries. Like the classical bound, it also does not provide guarantees for long-term keys. Bernstein proved the following stronger bound for WCS.
Theorem 1
(Bernstein Bound([Ber05b])). For all q and v
As a simple corollary (recovering the hash-key implies forgery), for all \(v \ge 1\) we have
The key-recovery bound was not presented in [Ber05b], but it is a simple straightforward corollary from the fact that recovering hash-key implies forgery.
3.2 Interpretation of the Bernstein Bound
We now provide the interpretation of the bound which is crucial for understanding the optimality of ideal-WCS. As \(1 - x \le e^{-x}\), we have
Obviously, the Bernstein bound becomes more than one when \(q(q+1)/2 \ge N \ln N\) (note that \(\epsilon \ge N^{-1}\)). So we assume that \(q(q+1)/2\le N \ln N\). We denote \(n = \log _2 N\). By Lemma 1, we have

where  . Thus, \(\textsf {B}(q, v) = \varTheta (v \cdot \epsilon \cdot e^{\frac{q(q+1)}{2N}}).\) Let us introduce another parameter \(\delta \), called the tolerance level. We would now solve for q and v satisfying \(\textsf {B}(q, v) = \delta \) (or the inequality \(\textsf {B}(q, v) \ge \delta \)) for any fixed constant \(\delta \). In other words, we want to get a lower bound of q and v to achieve at least \(\delta \) authenticity advantage.
. Thus, \(\textsf {B}(q, v) = \varTheta (v \cdot \epsilon \cdot e^{\frac{q(q+1)}{2N}}).\) Let us introduce another parameter \(\delta \), called the tolerance level. We would now solve for q and v satisfying \(\textsf {B}(q, v) = \delta \) (or the inequality \(\textsf {B}(q, v) \ge \delta \)) for any fixed constant \(\delta \). In other words, we want to get a lower bound of q and v to achieve at least \(\delta \) authenticity advantage.
-
1.
Case 1. When \(v \cdot \epsilon = \delta \) and \(q \ge 1\) we have \(\textsf {B}(q, \ell ) \ge \delta \). In other words, one needs to have sufficient verification attempts (and only one authentication query suffices) to have some significant advantage. We would like to note that even when \(q = O(\sqrt{N})\), \(\textsf {B}(q, v) = \varTheta (v \cdot \epsilon )\). So the advantages remain same up to some constant factor for all values of \(q = O(\sqrt{N})\). In other words, we can not exploit the number of authentication queries within the birthday-bound complexity.
-
2.
Case 2. \(v \cdot \epsilon < \delta \). Let us assume that \(v \epsilon /\delta = N^{\beta }\) for some positive real \(\beta \). In this case one can easily verify that \(q = \varOmega (\sqrt{\delta N \log N})\) to achieve at least \(\delta \) advantage. In other words, if \(q = o(\sqrt{N \log N})\) and \(v = o(\epsilon ^{-1})\) then \(\textsf {B}(q, v) = o(1)\).
Tightness of the bound for the Case 1. We have seen that when \(q = O(\sqrt{N})\), we have \( \mathsf {Auth}_{\gamma }(q, v) = O (v \cdot \epsilon )\). In fact, it can be easily seen to be tight (explained below) when the hash function is the polynomial hash function \(\textsf {Poly}_M(\kappa )\).
Key Guess Forgery/Key-Recovery. Suppose WCS is based on the polynomial hash. Given a tag t of a known nonce-message pair (n, M) with \(M \in \mathfrak {B}^{\ell }\), a simple guess attack works as follows. It selects a subset \(\mathfrak {B}_1 \subseteq \mathfrak {B}\) of size \(\ell \) and defines a message \(M' \in \mathscr {M}\) and \(t'\) such that the following identity as a polynomial in x holds:
If \(\kappa \in \mathfrak {B}_1\) then it is easy to verify that \(t'\) is the tag for the nonce-message pair \((n, M')\). The success probability of the forging attack is exactly \(\ell /N\). If the forgery is allowed to make v forging attempts, it first chooses v disjoint subsets \(\mathfrak {B}_1, \ldots , \mathfrak {B}_v \subseteq \mathfrak {B}\), each of size \(\ell \). It then performs the above attack for each set \(\mathfrak {B}_i\). The success probability of this forgery is exactly \(v \ell /N\). The same attack was used to eliminate false keys systematically narrowing the set of potential polynomial keys and searching for “weak” keys.
Remark 1
The tightness of multiple-forgery advantage for WCS based on the polynomial hash can be extended similarly to all those hash functions \(\rho \) for which there exist \(v+1\) distinct messages \(M_1, \ldots , M_v, M\) and \(c_1, \ldots , c_v \in \mathfrak {B}\) such that
Why the Bernstein bound is better than the classical birthday bound? One may think the Bernstein bound is very close to the classical birthday bound of the form \(q^2/2^n\) and they differ by simply logarithmic factor. However, these two bound are quite different in terms of the data or query limit in the usage of algorithms. We illustrate the difference through an example. Let \(n = 128\), and the maximum advantage we can allow is \(2^{-32}\). Suppose a construction C has maximum forgery advantage \(\frac{q^2}{n2^n}\) (a beyond birthday bound with logarithmic factor). Then we must have the constraint \(q \le 2^{51.5}\). Whereas, WCS can be used for at most \(2^{64}\) queries. In other words, Bernstein bound actually provide much better life time of key than the classical birthday bound.
4 False-Key/True-Key Set: A Tool for Key-Recovery and Forgery
Our main goal of the paper is to obtain hash-key-recovery attacks against WCS and GCM. Note that we do not recover the blockcipher key. So key-recovery advantage of whats follows would mean the probability to recover the hash-key only.
Query System and Transcript. A key-recovery (with no verification attempt) or a single forgery adversary has two components. The first component \(\mathbf {Q}\), called query system, is same for both key-recovery and forgery. It makes queries to \(\mathsf {WCS}_{K, \kappa }\) adaptively and obtains responses. Let \((\mathscr {n}_1, M_1)\), \(\ldots \), \((\mathscr {n}_q, M_q)\) be authentication queries with distinct \(\mathscr {n}_i\) (i.e., the query system is nonce-respecting) and let \(t_i\) denote the response of ith query. Let \(\tau := \tau (\mathbf {Q}) = ((\mathscr {n}_1, M_1, t_1), \ldots , (\mathscr {n}_q, M_q, t_q))\) denote the transcript.
Based on the transcript, a second component of forgery returns a fresh \((\mathscr {n}, M, t)\) (not in the transcript). If \(\mathscr {n}\ne \mathscr {n}_i\) for all i then the forgery of WCS is essentially reduced to a forgery of the URP (in particular, forging the value of \(\pi (\mathscr {n})\)). Hence, the forgery advantage in that case is at most \(1/(N-q)\). The most interesting case arises when \(\mathscr {n}= \mathscr {n}_i\) for some i. Similarly, the second component of a key-recovery adversary returns an element \(k \in \mathscr {K}\) (key space of the random function) based on the transcript \(\tau \) obtained by the query system.
Definition 3
(False-key set [LP18]). With each \(\tau = ((\mathscr {n}_1, M_1, t_1)\), \(\ldots \), \((\mathscr {n}_q, M_q, t_q))\), we associate a set
and we call it the false-key set.
Note that \(\Pr (\kappa \in \mathscr {F}\!_{\tau }) = 0\) and so the term false-key set is justified. In other words, the true key \(\kappa \) can be any one of the elements from \(\mathscr {T}\!:= \mathscr {K}\setminus \mathscr {F}\!_{\tau }\), called the true-key set. Given a query system \(\mathbf {Q}\), let us consider the key-recovery adversary which simply returns a random key \(\mathbf {k}\) from the true-key set. Let us denote the key-recovery adversary as \(\mathbf {Q}_{TK}\). The following useful bound is established in [LP18].
Lemma 2
([LP18]). Following the notation as described above we have
Proof
Given a transcript \(\tau \), the probability that \(\mathbf {k}= \kappa \) is exactly \(\frac{1}{N - |\mathscr {F}\!_{\tau }|}\). Then,
Here the expectation is taken under the randomness of the transcript. A transcript depends on the randomness of \(\pi \), \(\kappa \) and the random coins of the query system. Note that the function \(f(x) = \frac{1}{N-x}\) is convex in the interval (0, N) and so by using Jensen inequality, we have \(\textsf {KR}_{\mathsf {WCS}}(\mathbf {Q}_{TK}) \ge ~ \frac{1}{N - \mathbb {E}(|\mathscr {F}\!_{\tau (\mathbf {Q})}|)}.\) \(\square \)
In [LP18], it was also shown that \(\mathbb {E}(|\mathscr {F}\!_{\tau (\mathbf {Q})}| \le q(q+1)/2\) for all \(q < M_{\gamma }\) where
where \(\tau \) denotes the transcript \(((m_1, t_1), \ldots , (m_q, t_q))\) (ignoring nonce values as these are redundant). A straight forward estimation of \(M_{\gamma }\) is \(2^{n/2}/\sqrt{\ell }\). Here we give a very simple proof of the above bound for all q.
Lemma 3
For all q, \(\mathbb {E}(|\mathscr {F}\!_{\tau (\mathbf {Q})}| \le q(q+1)/2\).
Proof
We define an indicator random variable \(\mathsf {I}_x\) which takes value 1 if and only if there exists \(i \ne j\) such that \(\rho _{x}(M_i) - \rho _{x}(M_j) + t_j - t_i = 0\). We observe that \(|\mathscr {F}\!_{\tau }| = \sum _{x \in \mathscr {K}} \mathsf {I}_x\).
Let us denote \(\pi (n_i)\) as \(\mathsf {V}_i\). Note that for all i, \(t_i = \mathsf {V}_i + \rho _{\kappa }(M_i)\). Now, \(\mathbb {E}(|\mathscr {F}\!_{\tau }|) = \sum _{x \in \mathscr {K}} \mathbb {E}( \mathsf {I}_x)\). We write \(p_x = \mathbb {E}( \mathsf {I}_x)\) which is nothing but the probability that there exists \(i \ne j\) such that \(\mathsf {V}_i - \mathsf {V}_j = \rho _{x}(M_i) - \rho _{\kappa }(M_i) +\rho _{x}(M_i) + \rho _{\kappa }(M_i)\). By using the union bound we have \(p_x \le {q \atopwithdelims ()2}/(N-1)\). So
We can clearly assume that \(q < N\) and so by using simple inequality the lemma follows. \(\square \)
True-key Set. Instead of the false-key set we focus on the true key set. The set \(\mathscr {T}\!_{\tau } := \mathscr {K}\setminus \mathscr {F}\!_{\tau }\) is called the true-key set. In terms of the true-key set, we can write \(\textsf {KR}_{\mathsf {WCS}}(\mathbf {Q}_{TK}) = \mathbb {E}(\frac{1}{|\mathscr {T}\!_{\tau (\mathbf {Q})}|})\). Let \(\pi (\mathscr {n}_i) = \mathsf {V}_i\) and \(a_{i,x} := a_{i,x}(\kappa ) := \rho _{\kappa }(M_i) - \rho _x(M_i)\). We can equivalently define the true-key set as
Now we define an indicator random variable \(\mathsf {I}_{x}\) as follows:
Let \(p_x\) denote the probability that \(\mathsf {V}_1 + a_{1,x}, \ldots , \mathsf {V}_q + a_{q,x}\) are distinct. So,
When we want to minimize the expected value of the size of the true-key set, we need to upper bound the probability \(p_x\) for all x. We use this idea while we analyze our key-recovery attacks.
5 Key-Recovery Security Attacks of WCS
5.1 A Chosen-Plaintext Key-Recovery Attack
In this section we provide a chosen-plaintext attack against any WCS based on any blockcipher and a keyed hash function which satisfies a reasonable assumption, called differential regular. This property is satisfied by the polynomial hash. A function \(f: \mathscr {M}\rightarrow \mathfrak {B}\) is called regular if  . Now we define a special type of keyed hash functions.
. Now we define a special type of keyed hash functions.
Definition 4
A keyed hash function \(\rho _{\kappa }: \mathscr {K}\rightarrow \mathfrak {B}\) is called differential regular if for all distinct \(x, k \in \mathscr {K}\), the function mapping \(M \in \mathscr {M}\) to \(\rho _{k}(M) - \rho _x(M)\) is regular.
The polynomial hash is clearly differential regular. For example, when the message space is \(\mathfrak {B}\) and \(\kappa \ne x\), the function mapping \(m \in \mathfrak {B}\) to \(\rho _{\kappa }(m) - \rho _x(m) = m(\kappa - x)\) is regular.
Theorem 2
Suppose \(\mathsf {WCS}\) is based on a blockcipher and a keyed differential regular hash function \(\rho \). Then,
where \(N' = |\mathscr {K}|\) (size of the hash-key space). In particular, when \(q(q-1) = 2N \log N'\) we have \(\textsf {KR}_{\mathsf {WCS}}(q, \ell ) \ge 1/2\).
Interpretation of the result. When \(N' = N\) (key size is same as the block size), we can achieve 0.5 key-recovery advantage after making roughly \(\sqrt{2N \log N}\) authentication queries . If \(N' = N^c\) for some \(c > 1\) (the hash-key size is larger than the block size) we need roughly \(\sqrt{2cN \log N}\) (which is a constant multiple of the number queries required for hash-key space of size N) authentication queries.
Proof
Suppose \(\mathsf {WCS}:= \mathsf {WCS}_{K, \kappa }\) is the WCS authenticator based on a blockcipher \(e_K\) and a keyed differential regular hash function \(\rho _{\kappa }\). We describe our key-recovery attackFootnote 1 \(\mathscr {A}\) as follows:
-
1.
Choose q messages
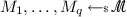 and make authentication queries \((\mathscr {n}_i, M_i)\), \(i \in [q]\) for distinct nonces \(\mathscr {n}_i\)’s.
and make authentication queries \((\mathscr {n}_i, M_i)\), \(i \in [q]\) for distinct nonces \(\mathscr {n}_i\)’s. -
2.
Let \(t_1, \ldots , t_q\) be the corresponding responses.
-
3.
Construct the true-key set
$$ \mathscr {T}\!_{\tau } = \{k \mid (t_i-\rho _{k}(M_i))'s \,\,\mathrm{are \,\,distinct}\}. $$ -
4.
Return a key
 .
.
Here, \(\tau = ((\mathscr {n}_1, M_1, t_1), \ldots , (\mathscr {n}_q, M_q, t_q))\) is the transcript of the adversary \(\mathscr {A}\). We also note that \(\Pr (\kappa \in \mathscr {T}\!_{\tau }) = 1\) and so we have seen that \(\textsf {KR}_{\mathsf {WCS}}(\mathscr {A}) = \mathbb {E}(\frac{1}{|\mathscr {T}\!_{\tau }|})\). Here the expectation is taken under randomness of transcript. The randomness of a transcript depends on the randomness of K, \(\kappa \) and the messages \(M_i\). By using Jensen inequality, we have
We will now provide an upper bound of \(\mathbb {E}(|\mathscr {T}\!_{\tau }|)\). In fact, we will provide an upper bound on the conditional expectation after conditioning the blockcipher key K and hash-key \(\kappa \). Note that \(t_i = e_K(\mathscr {n}_i) + \rho _{\kappa }(M_i)\) and hence the true-key set is the set of all x for which \(R_{i,x} := e_K(\mathscr {n}_i) + \rho _{\kappa }(M_i) - \rho _{x}(M_i)\) are distinct for all \(i \in [q]\).
Claim
Given K and \(\kappa \), the conditional distributions of \(R_{i,x}\)’s are uniform and independent over \(\mathfrak {B}\), whenever \(x \ne \kappa \).
Proof of the Claim. Once we fix K and \(\kappa \), for every \(x \ne \kappa \), \(\rho _{\kappa }(M_i) - \rho _{x}(M_i)\) is uniformly distributed (as \(\rho \) is differentially regular). So \(e_K(\mathscr {n}_i) + \rho _{\kappa }(M_i) - \rho _{x}(M_i)\)’s are also uniformly and independently distributed since \(e_K(\mathscr {n}_i)\)’s are some constants nd \(M_i\)’s are independently sampled.
Now we write \(|\mathscr {T}\!_{\tau }| = \sum _{x} \mathsf {I}_x\) where \(\mathsf {I}_x\) is the indicator random variable which takes values 1 if and only if \(R_{i,x}\) are distinct for all i. Note that \(R_{i,x}\) are distinct for all i has probability exactly \(\prod _{i=1}^{q-1}(1 -\frac{i}{N})\) (same as the birthday paradox bound). As \(1 - x \le e^{-x}\) for all x, we have \(\mathbb {E}(\mathsf {I}_x) = \Pr (\mathsf {I}_{x} =1) \le e^{-\frac{q(q-1)}{N}}\). So,
This bound is true for all K and \(\kappa \) and hence \(\mathbb {E}(|\mathscr {T}\!|) \le 1 + (N'-1)e^{-\frac{q(q-1)}{2N}}\). This completes the proof. \(\square \)
5.2 Known-Plaintext Attack
Now we show a known-plaintext attack for polynomial-based hash in which we do not assume any randomness of messages. So our previous analysis does not work in this case. We first describe a combinatorial result which would be used in our known plaintext key-recovery advantage analysis.
Lemma 4
Let \(\mathsf {V}_1, \ldots ,\mathsf {V}_q\) be a uniform without replacement sample from \(\mathfrak {B}\) and \(a_1, \ldots ,a_q \in \mathfrak {B}\) be some distinct elements, for some \(q \le N/6\). Then,
Proof
For \(1 \le \alpha \le q\), let \(h_{\alpha }\) denote the number of tuples \(v^{\alpha } = (v_1, \ldots ,v_{\alpha })\) such that \(v_1 + a_1, \ldots ,v_{\alpha } + a_{\alpha }\) are distinct. Clearly, \(h_1 = N\). Now we establish some recurrence relation between \(h_{\alpha + 1}\) and \(h_{\alpha }\). We also abuse the term \(h_{\alpha }\) to represent the set of solutions \(v^{\alpha } = (v_1, \ldots ,v_{\alpha })\) such that \(v_1 + a_1, \ldots ,v_{\alpha } + a_{\alpha }\) are distinct.
Given any solution \(v^{\alpha }\) (among the \(h_{\alpha }\) solutions), we want to estimate the number of ways we can choose \(v_{\alpha +1}\). Note that
Let \(S_{\alpha } := \{v_1 +a_1 - a_{\alpha +1}, \ldots , v_{\alpha } +a_{\alpha } - a_{\alpha +1}\}\). As \(v^{\alpha }\) is one solution from \(h_{\alpha }\), the size of the set \(S_{\alpha }\) is exactly \(\alpha \). Note that if \(v_i = v_j + a_j - a_{\alpha }\) then j must be different from i as \(a_i\)’s are distinct. For any \(i \ne j \le \alpha \), we denote \(h'_{\alpha }(i,j)\) be the number of \(v^{\alpha }\) such that \(v_1 + a_1, \ldots , v_{\alpha } + a_{\alpha }\) are distinct and \(v_i + a_i = v_j + a_j\) (once again we abuse this term to represent the set of solutions). So by the principle of inclusion and exclusion, we write
Claim
For all \(i \ne j \le \alpha \), \(h'_{\alpha }(i,j) \le \frac{h_{\alpha }}{N - 2\alpha }\).
Proof of claim. Let us assume \(i = \alpha \) and \(j = \alpha -1\). The proof for the other cases will be similar. Any solution for \(h'_{\alpha }(\alpha , \alpha -1)\) is a solution for \(h_{\alpha -1}\) and \(v_{\alpha } = v_{\alpha -1} + a_{\alpha -1} - a_{\alpha }\). However, all solutions corresponding to \(h_{\alpha }\) satisfy the solution corresponding to \(h_{\alpha -1}\) and \(v_{\alpha }\) is not a member of a set of size at most \(2\alpha \). So the claim follows.
Now, we have
In other words,
Now we simplify the upper bound as follows.
provided \(\alpha (N+1) - 3\alpha ^2 \ge \alpha N/2\), equivalently \((N +2) \ge 6 \alpha \). So for all \(\alpha \le q \le N/6\) we have
By multiplying the ratio for all \(1 \le \alpha \le q-1\) and the fact that \(h_1 = N\), we have \(h_q \le (N)_q e^{-q^2/4N}\). The lemma follows from the definition that \(p_x = \frac{h_q}{(N)_q}\). \(\square \)
Now we consider the key-recovery adversary considered in [LP18]. However, they considered transcripts with \(\sqrt{N}\) queries and were able to show a key-recovery advantage about  . However, we analyze it for all queries q and the key-recovery advantage can reach to
. However, we analyze it for all queries q and the key-recovery advantage can reach to  for \(q = O(\sqrt{N \log N})\).
for \(q = O(\sqrt{N \log N})\).
Theorem 3
Suppose \(m_1, \ldots , m_q \in \mathfrak {B}\) be distinct messages and \(\mathscr {n}_1, \ldots , \mathscr {n}_q\) be distinct nonces. Let \(t_i = \mathsf {WCS}_{\pi , \kappa }(\mathscr {n}_i, m_i)\) where \(\rho _{\kappa }\) is the polynomial hash. Then, there is an algorithm \(\mathscr {A}\) which recovers the hash-key \(\kappa \) with probability at least
So when \(q = \sqrt{4N \log N}\), the key-recovery advantage is at least \(\frac{1}{2}\).
Proof
We denote \(\pi (\mathscr {n}_i) = \mathsf {V}_i\). So \(\mathsf {V}_1, \ldots ,\mathsf {V}_q\) forms a without replacement random sample from \(\mathfrak {B}\). We write \(t_i = \mathsf {V}_i + \rho _{\kappa }(m_i) = \mathsf {V}_i + \kappa \cdot m_i\). As before we define the true-key set as
Clearly \(\kappa \in \mathscr {T}\!\). Let us fix \( x \ne \kappa \) and denote \(a_i = (\kappa - x) \cdot m_i\). Note that \(a_i\)’s are distinct. So given a hash-key \(\kappa \), we write the size of true-key set \(|\mathscr {T}\!|\) as the sum of the indicator random variables as follows: \(|\mathscr {T}\!| = 1 + \sum _{x \ne \kappa } \mathsf {I}_x\) where \(\mathsf {I}_x\) takes value 1 if and only if \(\mathsf {V}_1 + a_1, \ldots ,\mathsf {V}_q + a_q\) are distinct. So,
where
By Lemma 4, we know that \(p_x \le e^{-\frac{q^2}{4N}}\) and hence \(\mathbb {E}(|\mathscr {T}\!|~|~ \kappa ) \le 1 + (N-1)e^{-\frac{q^2}{4N}}\). This is true for all hash-keys \(\kappa \) and hence we have \(\mathbb {E}(|\mathscr {T}\!|) \le 1 + (N-1)e^{-\frac{q^2}{4N}}\). This completes the proof. \(\square \)
6 Key-Recovery Security Analysis of GCM
Definition of GCM. We briefly describe how GCM works. We refer the reader to see [MV04] for details. Here \(\mathfrak {B}= \{0,1\}^n\) (with \(n = 128\)) Let \(e_{K}\) be a blockcipher as before. We derive hash-key as \(\kappa = e_K(0^n)\). Given a message \((m_1, \ldots , m_{\ell }) \in \mathfrak {B}^{\ell }\) and a nonce \(\mathscr {n}\in \{0,1\}^{b - s}\) for some s, we define the ciphertext as
where \(\langle i \rangle \) represents s-bit encoding of the integer i. Finally, the tag is computed as xor of \(\mathsf {V}:= e_K(\mathscr {n}\Vert \langle 1 \rangle )\) and the output of the polynomial hash of the associated data and the ciphertext with length encoding. So, \(t = \mathsf {V}\oplus c_0 \kappa \oplus c_1 \kappa ^2 \oplus \cdots \) where \(c_0\) is the block which encodes the length of message (same as the ciphertext) and the associated data.
In other words, the tag is computed as a WCS authentication over the ciphertext with the hash-key derived from the blockcipher. So, one can have a similar key-recovery attack as stated in Theorem 2 which requires roughly \(\sqrt{n} \times 2^{n/2}\) authentication queries. More precisely, after making \(2^{68}\) authentication queries with the first message block random we can recover \(e_K(0)\) with probability at least 1 / 2. Note that the ciphertext blocks are uniformly distributed as it is an XOR of message blocks and some blockcipher outputs independent of the message blocks. Now we show a more efficient algorithm \(\mathscr {B}\) which utilize the length of messages as described below.
-
1.
Choose q messages
 and fix some associated data \(A_i = A\). Make authentication queries \((\mathscr {n}_i, M_i, A)\), \(i \in [q]\) for distinct nonces \(\mathscr {n}_i\)’s.
and fix some associated data \(A_i = A\). Make authentication queries \((\mathscr {n}_i, M_i, A)\), \(i \in [q]\) for distinct nonces \(\mathscr {n}_i\)’s. -
2.
Let \((C_1, t_1), \ldots , (C_q, t_q)\) be the corresponding responses.
-
3.
Let \(M_{i} = m_{i,1} \Vert \cdots m_{i, \ell }\) and \(C_{i} = c_{i,1} \Vert \cdots c_{i, \ell }\) where \(\mathscr {n}_{i,j}, c_{i,j} \in \mathfrak {B}\). Construct a set
$$ \mathscr {V}' = \{\mathsf {V}'_{i,j} := m_{i,j} \oplus c_{i,j} \mid i \in [q], j \in [\ell ]\} $$ -
4.
Construct the true-key set
$$ \mathscr {T}\!= \{k \in \mathfrak {B}\mid t_i \oplus \rho _{k}(A, C_i) \not \in \mathscr {V}' ~\forall i \in [q]\}. $$ -
5.
Return a key
 .
.
Remark 2
One may incorporate the relation that \(t_i \oplus \rho _{k}(A, C_i)\)’s are distinct while defining the true-key set. We can gain some complexity up to some small constant factor. For the sake of simplicity of the analysis and the attack, we keep the basic simple attack algorithm as described above.
Theorem 4
Let \(N = 2^n\) where n is the block size of the blockcipher used in GCM.
In particular, when \(\ell q^2 = N \log N\) we have \(\textsf {KR}_{\mathsf {GCM}}(q, \ell ) \ge 1/2\).
For example, when \(n = 128, \ell = 2^{15}\) we now need \(q = 2^{60}\) encryption queries to recover \(\kappa = e_K(0)\). Once we recover \(\kappa \), we can forge as many times as required. Moreover, one can define a universal forgery (for any chosen message and associated data but not the nonce).
Proof
From the permutation nature of the blockcipher, it is easy to see that \(e_K(0) \in \mathscr {T}\!\) as defined in the algorithm. So, as before
We will now provide an upper bound of \(\mathbb {E}(|\mathscr {T}\!_{\tau }|)\). In fact, we will provide an upper bound of the conditional expectation after conditioning the blockcipher key K (so that all blockcipher outputs are fixed). Since message blocks are uniformly distributed, the ciphertext blocks are also uniformly distributed (due to one-time padding). This proves that after conditioning the blockcipher key K,

Now, we define an indicator random variable \(\mathsf {I}_{x}\) to be one if \(R_{i,x} \not \in \mathscr {V}'\) for all \(i \in [q]\) and 0 otherwise. So, from the definition of \(\mathscr {T}\!\), it is easy to see that
Condition a blockcipher key K (and hence the hash-key \(\kappa = e_K(0^n)\) is fixed), and fix some \(x \ne \kappa \). Now,
When \(x = \kappa \), clearly, \(\mathsf {I}_x =1\). So,
This bound is true for all blockcipher keys K and hence \(\mathbb {E}(|\mathscr {T}\!|) \le 1 + Ne^{-\frac{\ell q^2}{N}}\). This completes the proof. \(\square \)
We show that when \(\ell q^2 = \sqrt{2N log N}\), we achieve some significant forgery advantage. Bernstein proved an upper bound of the forgery advantage for WCS. A similar proof is also applicable for GCM. In particular, we show that forgery advantage of GCM for single forging attempt is at most \(\frac{\ell }{N}\cdot O(e^{\frac{4 \ell q^2}{N}})\). So when we consider v forging attempts, the maximum forging advantage is at most \(v \cdot \frac{\ell }{N} \cdot O(e^{\frac{4 \sigma q}{N}})\). So our forgery algorithm (which is induced from the key-recovery algorithm) is also optimum for GCM. We denote the maximum forging advantage as \(\mathsf {Auth}_{\mathsf {GCM}}(q, v, \sigma , \ell )\) where \(\sigma \) denotes the total number of blocks present in message and associated data in all q encryption queries, and \(\ell \) denotes the number of blocks present in associated data and message or ciphertext for the largest query among all encryption and verification attempts. A similar result has been stated in Appendix C of [IOM12a] (full version of [IOM12b]).
Theorem 5
Let \(\mathsf {GCM}\) be based on the ideal n-bit random permutation \(\pi \). Then, for all q, v and \(\ell \),
Proof
We use \(x^q\) to denote a q tuple \((x_1, \ldots , x_q)\). For positive integers \(r \le m\), we write \((m)_r := m(m-1) \cdots (m-r+1)\). Bernstein proved an upper bound of the interpolation probability of a random permutation \(\pi \) as described below. Let \(\delta _N(q) = (1- (q-1)/N)^{-q/2}.\)
Theorem 4.2 in [Ber05b] showed that for all \(0 < r \le N\),
Note that for any r distinct inputs \(x_1, \ldots , x_r\) and outputs \(y_1, \ldots , y_r\) the probability that \(\pi (x_1) = y_1, \ldots , \pi (x_r) = y_r\) is exactly \(\frac{1}{(N)_r}\). We use this result to prove our result.
Without loss of generality we assume that \(\mathscr {A}\) is deterministic and the nonce in the forging attempt is one of the nonce in the encryption queries (since otherwise the bound can be shown to be smaller that what we claimed). We also assume that adversary makes single forging attempt (i.e. \(v =1\)). Let \(\mathscr {A}\) make queries \((n_i, m_i, a_i)\) and obtain response \((c_i, t_i)\) where \(m_i = (m_i[1], \ldots , m_i[\ell _i])\), \(a_i = (a_i[1] , \ldots , a_i[\ell _i'])\) and \(c_i = (c_i[1], \ldots , c_i[\ell _i])\) and let \(\sigma = \sum _{i=1}^{q} (\ell _i + \ell '_i)\) (total number of blocks in all queries). We call \((n^q, m^q, a^q, c^q, t^q)\) transcript (for encryption queries).
Let \((n^*, a^*, c^*, t^*)\) denote the forging attempt where \(c^*\) contains \(\ell ^*\) blocks. According to our simplification, let \(n^* = n_i\) for some i. So \(c^q, t^q\) determine the whole transcript including the forging attempt. Let us write \(z_i = m_i \oplus c_i\). It is also easy to see that \(t^q, z^q\) also determine the transcript.
Let F denote the forgery event, \(n^* = n_i\) and \(d = t^* \oplus t_i\). Moreover, for every k (a candidate of hash key), we set \(y_i(k) = t_i \oplus \rho _k(a_i \Vert c_i)\). Now, \(\Pr (F) = \Pr (\rho _{\kappa }(a_i \Vert c_i) \oplus \rho _{\kappa }(a^* \Vert m^*) = d)\). This can be written as the following sum
where the sum is taken over all \(t^q\) and all those \(z^q\) for which all blocks of \(z_i\)’s are distinct. The event \(E(\kappa )\) denotes that \(\pi (n_1 \Vert \langle 1 \rangle )= y_1(\kappa ), \ldots , \pi (n_q \Vert \langle 1 \rangle ) = y_q(\kappa )\) and \(\pi (n_i \Vert \langle j \rangle ) = z_i[j]\) for all \(1 \le i \le q\), \(1 \le j \le \ell _i\).
Now conditioning on any \(\pi (0) := \kappa = k\) such that \(\rho _{\kappa }(a_i \Vert c_i) \oplus \rho _{\kappa }(a^* \Vert c^*) = d\) (there are at most \(\max \{\ell _i + \ell '_i, \ell ^* + \ell ^{'*}\}+1 \le \ell \) choices of k), the conditional probability is reduced to \(\Pr (E(k))\) which should be \(\frac{1}{(N-1)_{q + \sigma }}\) (note that \(\pi (0)\) is conditioned and the event E(k) defines \(q + \sigma \) many inputs-outputs of \(\pi \)). So,
Note that in the above sum, we vary all distinct values of z blocks and so there are \((N)_{\sigma }\) such choices of z. Now it remains to simplify the bound.
The inequality (a) follows from Eq. 23 with N as \(N-\sigma \). This provides the forgery bound for GCM (without using the privacy bound for GCM). For the values of q, \(\ell \) and \(\sigma \) of our interest, we can assume that \(\sigma \le N/2\) and \(1 - x = \varTheta (e^{-x})\) (Lemma 1). So we can rewrite the upper bound of the forgery advantage of GCM as
The proof for v forging attempts simply follows by multiplying above bound by v. \(\square \)
Remark 3
The above bound says that, as long as \(q\sigma = o(N \log N)\), the forgery advantage is negligible and hence we need \(q \sigma \) to be in the order of \(N \log N\) to get non-negligible advantage. Along with our forgery adversary on GCM, we have shown the above forgery bound of GCM is indeed tight.
7 Conclusion
In this paper we describe key-recover attacks on WCS and GCM. The query complexity of the attack match with the Bernstein bound and hence we prove the tightness of Bernstein bound. Although the query complexity of our attacks are optimal, a straightforward implementation would require O(N) memory and time complexity. Very recently Leurent and Sibleyras [LS18] demonstrated attacks for WCS. They have described a method to recover hash key of WCS (and counter mode encryption) with \(O(2^{2n/3})\) query and time complexity. However, the success probability analysis of their attack is heuristic. It would be an interesting problem to see whether our concrete analysis can be adapted to their attacks.
Notes
- 1.
We note that the similar attack is considered in [LP18] where the messages are fixed and distinct. However in their attacks the analysis is done for \(q \le 2^{n/2}\) whereas, we analyze for all q.
References
Abdelraheem, M.A., Beelen, P., Bogdanov, A., Tischhauser, E.: Twisted polynomials and forgery attacks on GCM. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 762–786. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_29
Aoki, K., Yasuda, K.: The security and performance of “GCM” when short multiplications are used instead. In: Kutyłowski, M., Yung, M. (eds.) Inscrypt 2012. LNCS, vol. 7763, pp. 225–245. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38519-3_15
Blum, L., Blum, M., Shub, M.: A simple unpredictable pseudo-random number generator. SIAM J. Comput. 15(2), 364–383 (1986)
Berlekamp, E.R.: Factoring polynomials over large finite fields. Math. Comput. 24(111), 713–735 (1970)
Bernstein, D.J.: The Poly1305-AES message-authentication code. In: Gilbert, H., Handschuh, H. (eds.) FSE 2005. LNCS, vol. 3557, pp. 32–49. Springer, Heidelberg (2005). https://doi.org/10.1007/11502760_3
Bernstein, D.J.: Stronger security bounds for Wegman-Carter-Shoup authenticators. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 164–180. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_10
Bernstein, D.J.: Polynomial evaluation and message authentication. http://cr.yp.to/papers.html#pema. ID b1ef3f2d385a926123e1517392e20f8c. Citations in this document, 2 (2007)
Bellare, M., Goldreich, O., Mityagin, A.: The power of verification queries in message authentication and authenticated encryption. IACR Cryptology ePrint Archive, 2004:309 (2004)
Black, J., Halevi, S., Krawczyk, H., Krovetz, T., Rogaway, P.: UMAC: fast and secure message authentication. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 216–233. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_14
Bierbrauer, J., Johansson, T., Kabatianskii, G., Smeets, B.: On families of hash functions via geometric codes and concatenation. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 331–342. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_28. http://cr.yp.to/bib/entries.html#1994/bierbrauer
Brassard, G.: On computationally secure authentication tags requiring short secret shared keys. In: Chaum, D., Rivest, R.L., Sherman, A.T. (eds.) Advances in Cryptology, pp. 79–86. Springer, Boston, MA (1983). https://doi.org/10.1007/978-1-4757-0602-4_7
Bellare, M., Tackmann, B.: The multi-user security of authenticated encryption: AES-GCM in TLS 1.3. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 247–276. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53018-4_10
Carter, L., Wegman, M.N.: Universal classes of hash functions. J. Comput. Syst. Sci. 18(2), 143–154 (1979)
Cantor, D.G., Zassenhaus, H.: A new algorithm for factoring polynomials over finite fields. Math. Comput. 36(154), 587–592 (1981)
den Boer, B.: A simple and key-economical unconditional authentication scheme. J. Comput. Secur. 2, 65–71 (1993). http://cr.yp.to/bib/entries.html#1993/denboer
Daemen, J., Rijmen, V.: Rijndael/AES. In: van Tilborg, H.C.A. (ed.) Encyclopedia of Cryptography and Security, pp. 520–524. Springer, Boston (2005). https://doi.org/10.1007/0-387-23483-7
Gilbert, E.N., MacWilliams, F.J., Sloane, N.J.A.: Codes which detect deception. Bell Labs Tech. J. 53(3), 405–424 (1974)
Halevi, S., Krawczyk, H.: MMH: software message authentication in the Gbit/second rates. In: Biham, E. (ed.) FSE 1997. LNCS, vol. 1267, pp. 172–189. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052345
Handschuh, H., Preneel, B.: Key-recovery attacks on universal hash function based MAC algorithms. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 144–161. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_9
Iwata, T., Ohashi, K., Minematsu, K.: Breaking and repairing GCM security proofs (2012)
Iwata, T., Ohashi, K., Minematsu, K.: Breaking and repairing GCM security proofs. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 31–49. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32009-5_3
Joux, A.: Comments on the draft GCM specification-authentication failures in NIST version of GCM
JTC1: ISO/IEC 9797–1:2011 information technology - security techniques - message authentication codes (MACs) - part 1: Mechanisms using a block cipher (2011)
Karp, R.M., Rabin, M.O.: Efficient randomized pattern-matching algorithms. IBM J. Res. Dev. 31, 249–260 (1987). http://cr.yp.to/bib/entries.html#1987/karp
Krawczyk, H.: LFSR-based hashing and authentication. In: Desmedt, Y.G. (ed.) CRYPTO 1994. LNCS, vol. 839, pp. 129–139. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48658-5_15
Luykx, A., Preneel, B.: Optimal forgeries against polynomial-based MACs and GCM. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10820, pp. 445–467. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_17
Leurent, G., Sibleyras, F.: The missing difference problem, and its applications to counter mode encryption. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018. LNCS, vol. 10821, pp. 745–770. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_24
McGrew, D.A., Viega, J.: The security and performance of the Galois/Counter Mode (GCM) of operation. In: Canteaut, A., Viswanathan, K. (eds.) INDOCRYPT 2004. LNCS, vol. 3348, pp. 343–355. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30556-9_27
McGrew, D., Viega, J.: The use of Galois Message Authentication Code (GMAC) in IPsec ESP and AH. Technical report, May 2006
Nandi, M.: On the minimum number of multiplications necessary for universal hash functions. In: Cid, C., Rechberger, C. (eds.) FSE 2014. LNCS, vol. 8540, pp. 489–508. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46706-0_25
Procter, G., Cid, C.: On weak keys and forgery attacks against polynomial-based MAC schemes. J. Cryptol. 28(4), 769–795 (2015)
NIST FIPS Pub. 197: Advanced encryption standard (AES). Federal information processing standards publication, 197(441):0311 (2001)
Rabin, M.O.: Fingerprinting by random polynomials (1981). http://cr.yp.to/bib/entries.html#1981/rabin. Note: Harvard Aiken Computational Laboratory TR-15-81
Rogaway, P.: Bucket hashing and its application to fast message authentication. In: Coppersmith, D. (ed.) CRYPTO 1995. LNCS, vol. 963, pp. 29–42. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-44750-4_3
Saarinen, M.-J.O.: Cycling attacks on GCM, GHASH and other polynomial MACs and hashes. In: Canteaut, A. (ed.) FSE 2012. LNCS, vol. 7549, pp. 216–225. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34047-5_13
Salowey, J., Choudhury, A., McGrew, D.: AES Galois Counter Mode (GCM) cipher suites for TLS. Technical report, August 2008
Shoup, V.: On fast and provably secure message authentication based on universal hashing. In: Koblitz, N. (ed.) CRYPTO 1996. LNCS, vol. 1109, pp. 313–328. Springer, Heidelberg (1996). https://doi.org/10.1007/3-540-68697-5_24
Stinson, D.R.: Universal hashing and authentication codes. Des. Codes Cryptogr. 4(3), 369–380 (1994)
Taylor, R.: An integrity check value algorithm for stream ciphers. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 40–48. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_4
Wegman, M.N., Carter, L.: New hash functions and their use in authentication and set equality. J. Comput. Syst. Sci. 22(3), 265–279 (1981)
Zhu, B., Tan, Y., Gong, G.: Revisiting MAC forgeries, weak keys and provable security of Galois/Counter Mode of operation. In: Abdalla, M., Nita-Rotaru, C., Dahab, R. (eds.) CANS 2013. LNCS, vol. 8257, pp. 20–38. Springer, Cham (2013). https://doi.org/10.1007/978-3-319-02937-5_2
Acknowledgments
The author would like to thank Anirban Ghatak, Eik List, Subhamoy Maitra, Bart Mennink and anonymous reviewers for their useful comments. The author would also like to thank Atul Luykx for the initial discussion of the paper. This work is supported by R. C. Bose Center for Cryptology and Security.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Nandi, M. (2018). Bernstein Bound on WCS is Tight. In: Shacham, H., Boldyreva, A. (eds) Advances in Cryptology – CRYPTO 2018. CRYPTO 2018. Lecture Notes in Computer Science(), vol 10992. Springer, Cham. https://doi.org/10.1007/978-3-319-96881-0_8
Download citation
DOI: https://doi.org/10.1007/978-3-319-96881-0_8
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-96880-3
Online ISBN: 978-3-319-96881-0
eBook Packages: Computer ScienceComputer Science (R0)





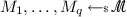 and make authentication queries
and make authentication queries  .
. and fix some associated data
and fix some associated data  .
.