Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Fuzzy Cognitive Maps (FCMs) constitute neuro-fuzzy systems, which are able to model complex systems [5, 6]. Recently, Fuzzy Grey Cognitive Maps (FGCM) has been proposed as a FCM extension [15]. It is an innovative and flexible model based on Grey Systems Theory and Fuzzy Cognitive Maps. FGCM is based on GST, that it has become a very worthy theory for solving problems within domains with high uncertainty, under discrete small and incomplete data sets [16, 18, 19].

FGCMs offer several advantages in comparison with others similar techniques. First, the FGCM model is designed specifically for multiple meanings (grey) environments. Second, FGCM allows the defining of relationships between concepts. Through this characteristic, more reliable decisional models for interrelated environments are defined. Third, the FGCM technique is able to quantify the grey influence of the relationships between concepts. Through this attribute, a better support in grey environments can be reached. Finally, with this FGCM model it is possible to develop a what-if analysis with the purpose of describing possible grey scenarios. IT projects risks are modelled to illustrate the proposed technique.

Furthermore, FGCMs provide an intuitive, yet precise way of expressing concepts and reasoning about them at their natural level of abstraction [18, 19]. By transforming decision modelling into causal graphs, decision makers with no technical background can understand all of the components in a given situation. In addition, with a FGCM, it is possible to identify and consider the most relevant factor that seems to affect the expected target variable.

In this work, it is investigated the application of the mathematical formulation of FGCMs and the efficient NHL algorithm for FGCMs in simulating process control problems in industry. More specifically, the FGCM modeling procedure and its new unsupervised learning algorithm of NHL are applied to model and analyze a benchmark two-tank process control problem in industry [20, 21].

The unsupervised Hebbian learning rule improves the FGCM structure, eliminates the deficiencies in the usage of FGCM and enhances the flexibility and dynamical behavior of the FGCM model. The FGCM model and its updated FGCM structure after learning, guarantee the successful implementation of the proposed modeling procedure for real case problems.

The outline of this chapter is as follows. Section 2 presents briefly the Grey System Theory. Section 3 describes the Fuzzy Grey Cognitive Maps technique. Section 4 introduces the experiments. In Sect. 5, the discussion of the results and Sect. 6 concludes the chapter.

2 Grey Systems Theory

Grey Systems Theory (GST) has become a worthy set of techniques within environments with high uncertainty, under discrete small and incomplete data sets [3]. GST is designed to study small data samples with poor information. It has been successfully applied in engineering, energy, agriculture, geology, meteorology, medicine, industry, military science, transportation, business, and so on.

According to the degree of known information, if the system information is fully known (whole understanding), the system is called a white system, while the system information is completely unknown is called a black system. A system with partial information known and partial information unknown is grey system.

GST considers the information fuzziness, because it can flexibly deal with it [7, 8, 23]. Moreover, fuzzy mathematics holds some previous information (usually based on experience); while grey systems deal with objective data, they do not require any more information other than the data sets that need to be disposed [22]. Moreover, GST fits better with multiple meanings environments than fuzzy logic.

Let \(U\) be the universal set. Then a grey set \(\mathbf {G} \in U\) is defined by its both mappings. Note that

$$\begin{aligned} \mathbf {G} = \left\{ \begin{array}{ll} \overline{\mu }_{G}\left( g\right) : g &{} \rightarrow \left[ 0,1 \right] \\ \underline{\mu }_{G}\left( g\right) : g &{} \rightarrow \left[ 0,1 \right] \end{array}\right. \end{aligned}$$
(1)

where \(\underline{\mu }_{G}\left( x\right) \) is the lower membership function, \(\overline{\mu }_{G}\left( x\right) \) is the upper one and \(\underline{\mu }_{G}\left( x\right) \le \overline{\mu }_{G}\left( x\right) \). Also, GST extends fuzzy logic, since the grey set \(\mathbf {G}\) becomes a fuzzy set when \(\underline{\mu }_{G}\left( x\right) = \overline{\mu }_{G}\left( x\right) \).

The crisp value of a grey number is unknown, but we know the range within the value is included.

A grey number with both a lower limit (\(\underline{g}\)) and an upper limit (\(\overline{g}\)) is called an interval grey number [8], and it is denoted as \(\otimes g \in \left[ \underline{g},\overline{g} \right] | \underline{g} \le \overline{g}\). If a grey number \(\otimes g\) has just lower limit is denoted as \(\otimes g \in \left[ \underline{g},+\infty \right) \), and if it has only upper limit is \(\otimes g \in \left( -\infty , \overline{g} \right] \). A black number would be \(\otimes g \in \left( - \infty ,+\infty \right) \), and a white number is \(\otimes g \in \left[ \underline{g},\overline{g} \right] ,\underline{g} = \overline{g}\). There is not any information available about black numbers and the whole information is known about white numbers.

The conversion of grey numbers in white ones is called whitenization [8], and the whitenization value is computed as follows

$$\begin{aligned} \hat{g} = \alpha \cdot \underline{g} + \left( 1 - \alpha \right) \cdot \overline{g} \;|\; \alpha \in \left[ 0,1 \right] \end{aligned}$$
(2)

when \(\alpha = 0.5\) is called equal mean whitenization.

The length of a grey number is computed as \(\ell \left( \otimes g\right) =\mid \underline{g}-\overline{g}\mid \). In that sense, if the length of the grey number is zero (\(\ell \left( \otimes g\right) =0\)), it is a white number. In other sense, if \(\ell \left( \otimes g\right) =\infty \), the grey number is not necessarily a black number, because the length of a grey number with only one limit (lower or upper), \(\otimes g\in \left[ \underline{g},+\infty \right) \) or \(\otimes g\in \left( -\infty ,\overline{g}\right] \), is infinite but it is not a black number.

A more detailed explanation of grey numbers operations and FGCMs can be found at [15].

3 Fuzzy Grey Cognitive Maps

3.1 Theoretical Background

Fuzzy Grey Cognitive Map is an innovative soft computing technique. FGCMs are dynamical systems involving feedback, where the effect of change in a node may affect other nodes, which in turn can affect the node initiating the change [15]. A FGCM models unstructured knowledge through causalities through imprecise concepts and grey relationships between them based on FCM [5, 6].

The FGCM nodes are variables, representing concepts. The relationships between nodes are represented by directed edges. An edge linking two nodes models the grey causal influence of the causal variable on the effect variable.

Since FGCMs are hybrid methods mixing grey systems and neural networks, each cause is measured by its grey intensity as

$$\begin{aligned} \otimes w_{ij} \in \left[ \underline{w}_{ij}, \overline{w}_{ij} \right] | \underline{w}_{ij} \le \overline{w}_{ij}, \{ \underline{w}_{ij},\overline{w}_{ij} \} \in \left[ -1,+1 \right] \end{aligned}$$
(3)

where \(i\) is the pre-synaptic (cause) node and \(j\) the post-synaptic (effect) one.

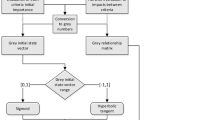
FGCM dynamics begins with the design of the initial grey vector state \(\otimes \varvec{C}^{0}\), which represents a proposed initial grey stimuli. We denote the initial grey vector state with \(n\) nodes as

$$\begin{aligned} \begin{array}{ll} \otimes \varvec{C}^{(0)} &{} = \left( \otimes {c}_{1}^{(0)} \quad \otimes {c}_{2}^{(0)} \quad \ldots \quad \otimes {c}_{n}^{(0)} \right) \\ &{} = \Bigg ( \left[ \underline{c}_{1}^{(0)}, \overline{c}_{1}^{(0)} \right] \quad \left[ \underline{c}_{2}^{(0)}, \overline{c}_{2}^{(0)} \right] \quad \ldots \quad \left[ \underline{c}_{n}^{(0)}, \overline{c}_{n}^{(0)} \right] \Bigg ) \end{array} \end{aligned}$$
(4)

The updated nodes’ states [15] are computed in an iterative inference process with an activation function, which mapping monotonically the grey node value into its normalized range \(\left[ 0,+1 \right] \) or \(\left[ -1,+1 \right] \). The unipolar sigmoid function is the most used one  [2] in FCM and FGCM when the concept value maps in the range \(\left[ 0,1 \right] \). If \(f\left( \cdot \right) \) is a sigmoid, then the \(i\) component of the grey vector state \(\otimes \varvec{C}^{(t+1)}\) after the inference would be update with the Eq. 5.

$$\begin{aligned} \otimes {c}^{(t+1)}_{j}&= f \left( \otimes {c}^{(t)}_{j} + \sum _{i=1}^{n} \otimes w_{ij}\cdot \otimes {c}^{(t)}_{i} \right) \nonumber \\&= f \left( \otimes {c}^{(t+)}_j \right) \nonumber \\&= f \left( \left[ {\underline{c}}^{(t+)}_j, {\overline{c}}^{(t+)}_j \right] \right) \nonumber \\&= \left[ f \left( {\underline{c}}^{(t+)}_j\right) , f \left( {\overline{c}}^{(t+)}_j\right) \right] \\&= \left[ \left( 1+e^{-\lambda \cdot {\underline{c}}^{(t+)}_j}\right) ^{-1}, \left( 1+e^{-\lambda \cdot {\overline{c}}^{(t+)}_j}\right) ^{-1} \right] \nonumber \\&= \left[ {\underline{c}}^{(t+1)}_j, {\overline{c}}^{(t+1)}_j \right] \nonumber \end{aligned}$$
(5)

On the other hand, when the concepts’ states map in the range \(\left[ -1,+1\right] \) the function used would be the hyperbolic tangent.

The nodes’ states evolve along the FGCM dynamics. The FGCM inference process finish when the stability is reached. The steady grey vector state represents the effect of the initial grey vector state on the state of each FGCM node.

After its inference process, the FGCM reaches one stable state following a number of iterations. It settles down to a fixed pattern of node states, the so-called grey hidden pattern or grey fixed-point attractor. Furthermore, the state could to keep cycling between several fixed states, known as a limit grey cycle. Using a continuous activation function, a third state would be a grey chaotic attractor. It happens when, instead of stabilizing, the FGCM continues to produce different grey vector states for each iteration  [1].

3.2 FGCM Construction

FGCMs, as FCMs [4, 9–11], can be built by experts or with raw data. We focus on a deductive approach based on experts’ knowledge about the system’s domain. The experts’ team establish the number and categories of nodes (or concepts) relevant for the FGCM model. Furthermore, experts know which nodes influence others; for the corresponding nodes they determine the intensity of the influence and its sign (negative or positive). Each expert, indeed, determines the influence of one node on another as negative or positive and then evaluates the degree of influence using a linguistic variable, such as strong influence, medium influence, weak influence, etc. This is a procedure commonly used for FCM  [13].

For FGCMs a grey causal weight should be determined. It is a little bit complex because it is not a fuzzy number, but a grey one. In this sense, we will use a class of grey numbers that vibrate around a base value, denoted as \(\otimes w_{ij}^a \in \left[ w_{ij}^{a}-{\varvec{\theta }}, w_{ij}^{a}+{\varvec{\theta }} \right] \).

Moreover, the vibration value \({\varvec{\theta }}\) would be determined according with the uncertainty about the base value. If the base value has not uncertainty associated, then \({\varvec{\theta }}=0\). This is the case for a white number. If the base value is completely unknown, then \({\varvec{\theta }}=\infty \) for the general case and \({\varvec{\theta }}\le \{1|2\}\) in FGCM models. The base value \(w_{ij}^{a}\) is calculated as weights in FCM  [13].

The Eq. 6 shows the computation of the \(\otimes w_{ij}^{a}\) upper and lower limits.

$$\begin{aligned} \otimes w_{ij}^a \in \left\{ \begin{array}{llrcl} \left[ -1, +1 \right] &{} if &{} \left( a + {\varvec{\theta }} > +1\right) &{} \wedge &{} \left( a - {\varvec{\theta }} < -1 \right) \\ \left[ a - {\varvec{\theta }}, +1 \right] &{} if &{} \left( -1 \le a - {\varvec{\theta }} \le +1 \right) &{}\wedge &{} \left( a + {\varvec{\theta }} > +1\right) \\ \left[ -1, a + {\varvec{\theta }} \right] &{} if &{} \left( -1 \le a + {\varvec{\theta }} \le +1\right) &{}\wedge &{} \left( a - {\varvec{\theta }} < -1\right) \\ \left[ a - {\varvec{\theta }}, a + {\varvec{\theta }} \right] &{} if &{} \left( -1 \le a - {\varvec{\theta }} \le +1 \right) &{}\wedge &{} \left( -1 \le a + {\varvec{\theta }} \le +1 \right) \end{array} \right. \end{aligned}$$
(6)

3.3 FGCM’s Benefits Over FCM

FGCMs have several benefits over conventional FCM  [14]. A FGCM compute the desired steady states of the models by handling uncertainty and hesitancy present in the experts judgements for causal relations among concepts as well as within the initial concepts states.

FCM would need measures of the associated uncertainty in weights and concepts. The FGCM concepts have a greyness value to represent the degree of uncertainty associated to each node and each edge. Note that, even if the FCM dynamics would get the same steady state than FGCM after the whitenization process, the FGCM proposal handles the inner fuzziness and grey uncertainty.

Furthermore, it is possible to compute different whitenization state values. This paper uses the equal mean whitenization with \(\alpha = 0.5\), but it is possible to calculate an optimistic or pessimistic whitenization. The whitenization value vibrates between the grey number limits. The final whitenization value depends of the parameter \(\alpha \). Lower \(\alpha \) values generate higher whitenization values closer to the upper limit.

Furthermore, FGCM includes greyness as an uncertainty measurement. Higher values of greyness mean that the results have a higher uncertainty degree. It is computed as follows

$$\begin{aligned} {\varvec{\phi }} (\otimes C_{i}) = \frac{\vert \ell (\otimes C_{i})\vert }{\ell (\otimes {\varvec{\psi }})} \end{aligned}$$
(7)

where \(\vert \ell (\otimes C_{i})\vert \) is the absolute value of the length of grey node \(\otimes C_{i}\) state value, and \(\ell (\otimes {\varvec{\psi }})\) is the absolute value of the range in the information space, denoted by \(\otimes {\varvec{\psi }}\). FGCM maps the nodes’ states within an interval \([0, 1]\) or \([-1, +1]\) if negative values are allowed. In this sense,

$$\begin{aligned} \ell (\otimes {\varvec{\psi }}) = \left\{ \begin{array}{lll} 1 &{} if &{} \{\otimes C_{i},\otimes w_{i}\} \subseteq \left[ 0,1 \right] \\ 2 &{} if &{} \{\otimes C_{i},\otimes w_{i}\} \subseteq \left[ -1,+1 \right] \end{array}\right. \end{aligned}$$
(8)

As an overview, FGCM model shows several advantages over the FCM one [17], as the following:

  • The reasoning process’ output would incorporate the greyness expressed in grey values.

  • It is a generalization and can be applied to closer approximate decision making in humans.

  • It enables modelling of the uncertainty and experts hesitancy associated to the description of the causal relations between the concepts and to the concept states.

  • FGCMs are able to model more kinds of relationships than FCM do. For instance, it is possible to run models with relations where the intensity is not known at all (\(\otimes w_i \in [-1, +1]\)) or just partially known.

3.4 Learning FGCMs with Nonlinear Hebbian Rules

Recently, Nonlinear Hebbian (NHL) based algorithm has been applied to FGCM Learning [14]. The learning algorithm extracts hidden and worthy knowledge from experts. It can increase the FGCMs effectiveness and their implementation in real-world problems.

The NHL algorithm is based on that all FGCM nodes are triggering at each iteration and updating their states grey values. During the FGCM dynamics the edges’ grey weights are updated and the new weight \(\otimes w_{ji}^{(t)}\) is derived for iteration step \(t\).

The NHL rule for updating FGCM grey weights is computed as follows

$$\begin{aligned} \varDelta \otimes w_{ji}^{(t)} = {\varvec{\eta }}_k \cdot \otimes c_j^{(t-1)} \cdot (\otimes c_i^{(t-1)} - \otimes c_j^{(t-1)} \cdot \otimes w_{ji}^{(t-1)}) \end{aligned}$$
(9)

Also, this proposal introduces three criteria for the NHL-FGCM algorithm. The first criterion is the maximization of the objective function \(J\), which has been defined by Hebbs rule

$$\begin{aligned} \begin{array}{rl} \mathrm{maximize } &{} J = E\{z^2\}\\ \mathrm{subject to: } &{} \mid \mid \mathbf {w} \mid \mid \ = 1 \end{array} \end{aligned}$$
(10)

where \(J = \sum _{k=1}^{m} (O_k)^2\), \(O\) are the output values, \(m\) the number of output nodes, \(z = f(\cdot )\), and \(f\) is the activation function.

The second one is the minimization of the difference between two subsequent value of the outputs values.

$$\begin{aligned} \mid O_k^{(t+1)} - O_k^{(t)} \mid < \varepsilon \end{aligned}$$
(11)

where \(\varepsilon \) is the tolerance value (usually \(0.001\)). Finally, the third criterion is the stability of the grey vector state.

4 Experiments

In order to investigate and demonstrate the performance of the proposed FGCM model, in comparison with conventional FCM, an industrial application, concerning a chemical process control problem, has been considered. FCMs were successfully applied to model control process [21] and in this study, our purpose is to show the functionality of FGCMs to effectively model and analyze known chemical process control problems in industry.

4.1 Process Control Problem Description

We consider the reference chemical process control system described in [20]. It consists of two tanks, three valves, one heating element and two thermometers for each tank, as depicted in Fig. 1.

Each tank has an inlet valve and an outlet valve. The outlet valve of the first tank is the inlet valve of the second tank. The objective of the control system is firstly to keep the height of liquid, in both tanks, between some limits, an upper limit \(H_{max}\) and a low limit \(H_{min}\), and secondly the temperature of the liquid in both tanks must be kept between a maximum value \(T_{max}\) and a minimum value \(T_{min}\).

Fig. 1
figure 1

An illustration of the chemical process example [12, 21]

Full size image

The temperature of the liquid in tank 1 is regulated through a heating element. The temperature of the liquid in tank 2 is measured through a sensor thermometer; when the temperature of the liquid two decreases, valve 2 needs opening, so hot liquid comes into tank 2 from tank 1. The control objective is to keep values of these variables in the following range of values:

$$\begin{aligned} \begin{array}{l} H1_{min} \le H1 \le H1_{max} \\ H2_{min} \le H2 \le H2_{max} \\ T1_{min} \le T1 \le T1_{max} \\ T2_{min} \le T2 \le T2_{max} \end{array} \end{aligned}$$
(12)

where, according to the experts, \(H1_{min} = 0.55\), \(H1_{max} = 0.75\), \(H2_{min} = 0.75\), \(H2_{max} = 0.80\), \(T1_{min} = 0.75\), \(T1_{max} = 0.82\), \(T2_{min} = 0.65\), and \(T2_{max} = 0.75\).

Three experts constructed the FCM and jointly determined the concepts of the FCM [13, 20]. Variables and states of the system, such as the height of the liquid in each tank or the temperature, are the concepts of the FCM model, which describes the system. The values of the concepts correspond to the real measurements of the physical magnitude. Each concept of the FCM takes a value, which ranges in the interval \([0, 1]\) and it is obtained after threshold the real measurement of the variable or state, which each concept represent.

4.2 FGCM Model

Based on the conventional FCM proposed in [20] for the considered problem we constructed a FGCM model sharing a similar structure. It consists of eight concepts, as illustrated in Fig. 2.

Fig. 2
figure 2

FGCM control model

Full size image

For the purposes of our study, the three experts that participated in [20, 21] assigned new if-then rules that describe the influences from concepts \(c_i\) to concepts \(c_j, i=1\ldots 5,j=1\ldots 5\). The inferences of the rules are linguistic weights described by grey weights as Eq. 3.

For the construction process of FGCMs, the three experts were also assigned the vibration values of each one fuzzy relationship. Thus, grey weights with their vibration values as obtained from the experts for the construction of the FGCM model are apposed in Table 1. The greyness of each one weight is calculated following the mathematical formulation suggested by Salmeron [15] and described in Sect. 2.

The final grey weights with their greyness, apposed in Table 2, are used for the simulation analysis of FGCM dynamics.

4.3 FGCM Dynamics

We have performed two experiments. The first one aims to demonstrate the performance of FGCM instead of the conventional FCM, on a real case scenario, whereas the second one is more general and aims to demonstrate its performance on initial grey values of concepts.

Table 1 FGCM nodes and their descriptions
Full size table
Table 2 FGCM edges and grey weights
Full size table

  • First case study of FGCM control problem. A set of real measurements were provided as input to FGCM as in the case of conventional FCM model in [21]. For the first case study, the initial grey vector is formed as follows

    $$\begin{aligned} \begin{array}{rl} \otimes c_1 = &{} \Big ([0.48,0.48], [0.57,0.57], [0.58,0.58], [0.68,0.68],\Big . \\ &{} \Big .\; \;[0.58,0.58], [0.59,0.59], [0.52,0.52], [0.58,0.58]\Big ) \end{array} \end{aligned}$$
    (13)

    The results of the reasoning process obtained with FGCM without learning (Eq. 5) and FGCM with NHL learning (Eq. 9), at each iteration \(t\), till convergence at a steady state are apposed in Tables  3 and 5.

    The results in both cases show that the four decision output nodes take values within the decision ranges. Especially in the case of FGCMs with NHL learning the values of concepts converge at a steady state which is the upper limit of the decision range with zero greyness. The zero greyness in decision concepts show that the system performs with an efficient way to the acceptable steady state. The updated adjacency matrix for case study 1 is shown at Eq. 16.

  • Second case study of FGCM control problem. In this case, a more general scenario considering grey values (not white ones as the previous case study) of concepts as initial ones, in a measurement range was considered. For the second case study, the initial grey vector is formed as follows

    $$\begin{aligned} \begin{array}{rl} \otimes c_2 = &{} \Big ([0.55,0.75], [0.7,0.8], [0.4,0.7], [0.5,0.8],\Big . \\ &{} \Big .\; \;[0.4,0.7], [0.7,0.85], [0.65,0.8], [0.3,0.7]\Big ) \end{array} \end{aligned}$$
    (14)

    The results of the reasoning process obtained with FGCM without learning (Eq. 5) and FGCM with NHL learning (Eq. 9), at each iteration \(t\), till convergence at a steady state are apposed in Tables 4 and 6.

    Table 3 First case study-results without learning
    Full size table
    Table 4 Second case study-results without learning
    Full size table
    Table 5 First case study-results with NHL learning
    Full size table
    Table 6 Second case study-results with NHL learning
    Full size table

    The results in both cases also show that the four decision output nodes take values within the decision ranges. Especially in the case of NHL algorithm, the results show that the output values of four decision concepts reach the upper limit of the Eq. 12 with a zero greyness value. The zero greyness means that there is no uncertainty in the decision concepts at the steady state. This is a meaningful result which shows that the decision concepts can be calculated with a zero uncertainty degree. The updated adjacency matrix for case study 2 is shown at Eq. 17.

  • Third case study of FGCM control problem. In this scenario, random grey values of concepts were used as initial ones. Following the reasoning process of FGCM without learning (Eq. 5) and FGCM with NHL learning (Eq. 9), the results apposed in Table 5 were produced. For the third case study, the initial grey vector is formed as follows

    $$\begin{aligned} \begin{array}{rl} \otimes c_3^{rand} = &{} \Big ([0.34,0.54], [0.25,0.46], [0.19,0.53], [0.37,0.82],\Big . \\ &{} \Big .\; \;[0.93,0.94], [0.29,0.83], [0.42,0.84], [0.88,0.98]\Big ) \end{array} \end{aligned}$$
    (15)

    The results in both cases also show that the four decision output nodes take values within the decision ranges. The updated adjacency matrix for case study 2 is shown at Eq. 18.

It is obvious, that in all the examined cases, the output concepts take values with the accepted limits and with very small or zero greyness.

5 Discussion of Results

The most significant weaknesses of the FCMs, namely their dependence on the experts beliefs, and the potential convergence to undesired steady states, can be overcome by learning procedures. However, in this work, we succeeded to produce desired equilibrium regions for the four decision-outputs of the process control problem without using learning algorithms in FGCMs.

The results produced by the FGCM model without learning are acceptable and control the system without any learning process. Furthermore, if the NHL learning process is used in the case of FGCMs, the outputs continue to be within the desired limits having the advantage of zero greyness. The whitenization values reach the upper limit of the desired ranges (Eqs. 3, 4, 5 above).

Also, it is proved that using the NHL algorithm in FGCMs we improve the conventional FCM model trained with NHL algorithm [12], which exhibit equilibrium behavior within the desired regions. With the proposed procedure the experts suggest the initial grey weights of the FGCM, and then using the NHL algorithm a new weight matrix is derived that can be used for any set of initial values of concepts.

It is concluded that, the FGCM and the FGCM with NHL learning affect the dynamical behavior of the system and the equilibrium values for decision concepts are within desired regions defined at Eq. 12.

The NHL algorithm is problem-dependent, starts using the initial weight matrix but all the process is independent from the initial values for grey concepts and the system succeed to converge in desired equilibrium regions for appropriate learning parameters.

The results of the FGCM dynamics show that the capability of FGCM to produce a length and greyness estimation at the outputs offers an advantage over FCM; the output greyness can be considered as an additional indicator of the quality of a decision, with respect to the information incompleteness at the input of the cognitive map. This is an important cue regarding the quality of the decisions obtained from FGCM in the presence of uncertainty.

The new FGCM model that copes with the inability of the current models to co-evaluate the greyness introduced into a complex system due to uncertainty and imperfect facts is explored in this work. The mathematical formalization of the grey systems theory has been considered instead of the conventional fuzzy sets theory, which is the basis of the current FCM models. The applicability of the proposed FGCM model extends to a variety of domains. In this paper, we demonstrated its effectiveness with numeric, reproducible examples, on chemical process control for decision making.

6 Conclusions

In this work, the FGCM model and the proposed NHL learning algorithm were applied for processing an industrial process control problem. The proposed mathematical formulation of FGCMs and the implementation of the NHL algorithm have been effectively applied. Experimental results based on simulations of a process control system, verify the effectiveness, validity and especially the advantageous behavior of the proposed grey-based methodology of constructing and learning FCMs.

The benefits of FGCMs over conventional FCMs make evident the significance of developing a greyness-based cognitive model such as FGCM. The case studies presented in this paper are representative and facilitate both demonstration and benchmarking purposes. The development of more complex models are enabled by the proposed mathematical framework, involving more interacting factors, by following the same methodological approach.

The proposed NHL algorithm sustains a formal methodology for FGCMs training, improving the functional FCM reliability and providing the FCM developers with learning parameters to adjust the influence of concepts. This type of learning rule accompanied with the good knowledge of the given system, guarantee the successful implementation of the proposed process in industrial process control problems.

Future research objectives include the exploration of even more challenging applications and improvements of the presented model towards further approximation of human cognition and intuition.