Identity-Based Cryptosystems and Quadratic Residuosity

Abstract

Three approaches are currently used for devising identity-based encryption schemes. They respectively build on pairings, quadratic residues ($\mathsf {QR}$), and lattices. Among them, the $\mathsf {QR}$-based scheme proposed by Cocks in 2001 is notable in that it works in standard RSA groups: its security relies on the standard quadratic residuosity assumption. But it has also a number of deficiencies, some of them have been subsequently addressed in follow-up works. Currently, one of the main limitations of Cocks’ scheme resides in its apparent lack of structure. This considerably restricts the range of possible applications. For example, given two Cocks ciphertexts, it is unknown how to evaluate of a function thereof.

Cocks’ scheme is believed to be non-homomorphic. This paper disproves this conjecture and proposes a constructive method for computing over Cocks ciphertexts. The discovery of the hidden algebraic structure behind Cocks encryption is at the core of the method. It offers a better understanding of Cocks’ scheme. As a further illustration of the importance of the knowledge of the underlying structure, this paper shows how to anonymize Cocks ciphertexts without increasing their size or sacrificing the security.

Finally and of independent interest, this paper presents a simplified version of the abstract identity-based cryptosystem with short ciphertexts of Boneh, Gentry, and Hamburg.

1 Introduction

Identity-based cryptography is an extension of the public-key paradigm which was first put forward by Shamir [25]. As discussed in [20, Chapter 1], a major issue with public-key cryptography is the management of trust. Another issue to be dealt with is to recover the public key and accompanying certificate, verify it, and then only encrypt and send messages. Identity-based cryptography aims at solving these practical issues by simplifying the key management.

While identity-based signature schemes were quickly proposed (already in his 1984 paper, Shamir presented such a scheme), identity-based encryption (IBE) schemes seem harder to develop and only came later. The first implementation of an IBE scheme was proposed by Desmedt and Quisquater [13] in 1986. It is however non-standard in the sense that it requires tamper-proof hardware for its security. The realization of a truly practical IBE scheme remained elusive until a breakthrough paper by Boneh and Franklin [7] in 2001, and concurrently by Sakai et al. [24]. The Boneh-Franklin IBE scheme makes use of bilinear maps. Its publication was quickly followed up by a large number of works. More recently, lattices were considered as a building block for constructing IBE schemes [16]. Again this gave rise to a number of follow-up works.

A totally different approach was described back in 2001 by Cocks in a short 4-page paper [12]. Cocks’ IBE scheme only requires elementary mathematics. Encryption merely involves a couple of operations modulo an RSA modulus and the evaluation of Jacobi symbols. Its security rests on the standard quadratic residuosity assumption in the random oracle model. Despite its simplicity, Cocks’ scheme received less attention from the research community, compared to the pairing-based or lattice-based constructions. We believe that this is mainly due to the apparent lack of structure behind Cocks’ scheme. In this paper, we identify Cocks ciphertexts as elements of a certain algebraic group. This makes Cocks’ scheme amenable to applications that were previously not possible. In particular, it can now be used in applications where computing over ciphertexts is required. Typical applications include electronic voting, auction systems, private information retrieval, or cloud computing.

Related Work. Since it appeared in 2001, a handful of variants of Cocks’ IBE scheme have been proposed in the literature, aiming at enhancing certain features of the original scheme or offering extra properties.

Cocks’ scheme is known not to be anonymous. The ciphertexts leak information about their recipient’s identity. The anonymity aspect in Cocks-like cryptosystems was first considered by Di Crescenzo and Saraswat in [14] (and incidentally in [8]). Subsequently, Ateniese and Gasti [2] and, more recently, Clear et al. [11] proposed concurrent anonymous cryptosystems derived from Cocks’ scheme. Table 1 in [11] gives a comparison of these two latter schemes. The scheme by Clear et al. features the best encryption and decryption times (i.e., 79 ms and 27 ms for a 128-bit message with a key-size of 1024 bits in their setting). The Ateniese-Gasti scheme is slower but has a smaller ciphertext expansion.

Cocks’ scheme is mostly attractive when used with the hybrid encryption paradigm encrypting a short session key. Indeed messages are encrypted in a bit-by-bit fashion with Cocks’ IBE scheme. It therefore looses its practicability when long messages need to be encrypted. The ciphertext expansion issue was addressed by Boneh, Gentry, and Hamburg [8]. They propose a space-efficient, anonymous IBE scheme based on the quadratic residuosity. However, the encryption in their scheme is time-consuming. Encryption time is quartic in the security parameter per message bit. Several possible trade-offs are discussed in [8, Sect. 5.3] and [19].

The work closest to ours is a recent paper by Clear, Hughes, and Tewari [10]. They develop a xor-homomorphic variant of Cocks’ scheme. This is elegantly achieved by seeing ciphertexts as elements (of the multiplicative group) in a certain quotient ring. The homomorphism property then naturally pops up as an application of the corresponding multiplication operation. A similar scheme was independently found —and generalized to higher power residue symbols— by Boneh, LaVigne, and Sabin [9]. As explained in [9], these schemes are however less efficient, bandwidth-wise, than the original Cocks’ scheme.

Our Contributions. Motivated by the work of [10], we were interested in finding the exact algebraic structure behind Cocks’ scheme. We quote from [23]:

“We believe that studying and understanding the mathematics that underlies the associated cryptosystems is a useful aid to better understand their properties and their security.”

Interestingly, the results of Rubin and Silverberg [23] (appearing earlier in [22]) were instrumental in our work. In a nutshell, we consider the torus viewed as a ‘degenerate’ representation of the torus where ${\mathbb {F}}_{p^2}$ is replaced with ${\mathbb {F}}_p(\delta )$ where $\delta \in {\mathbb {F}}_p^\times$. We then extend the setting modulo an RSA composite through Chinese remaindering. We show that the Cocks ciphertexts are squares in the so-obtained algebraic structure and form a quasi-group. The underlying group law yields the sought-after homomorphism. Compared to the approach in [10] there is no ciphertext expansion —the ciphertexts in [10] are twice longer. More importantly, it directly applies to Cocks’ scheme. This is somewhat surprising. It points out that the original Cocks’ IBE scheme is inherently homomorphic. In this regard, it shares similarities with the Goldwasser-Micali [public-key] encryption scheme [17]. We note that both schemes are semantically secure under the quadratic residuosity assumption and have comparable performance.

Another contribution is an anonymous variant of Cocks’s scheme. Anonymous identity-based schemes are important cryptographic tools as they constitute the central building block for public-key encryption with keyword search (PEKS). The companion PEKS scheme derived from our anonymous IBE scheme is detailed in Appendix D. Compared to the earlier $\mathsf {QR}$-based¹ scheme by Di Crescenzo and Saraswat [14], it reduces the size of the searchable ciphertexts by a typical factor of 2 without sacrificing the security.

Of independent interest, we present in Appendix E a simplified version of the abstract IBE system with short ciphertexts of Boneh, Gentry, and Hamburg [8].

2 Definitions and Notation

In this section, we review the classical notions of semantic security and of anonymity for identity-based encryption. We also formally present the quadratic residuosity assumption and a variant thereof.

2.1 Identity-Based Encryption

An identity-based encryption scheme [7] (or IBE in short) is defined as a tuple of four polynomial-time algorithms $(\mathtt {SETUP}, \mathtt {EXTRACT},\mathtt {ENCRYPT}, \mathtt {DECRYPT})$:

• Setup. The setup algorithm $\mathtt {SETUP}$ is a randomized algorithm that, taking a security parameter $1^\kappa$ as input, outputs the system parameters $\mathsf {mpk}$ together with the master secret key $\mathsf {msk}$: $(\mathsf {mpk},\mathsf {msk}) \mathop {\leftarrow }\limits ^{R}\mathtt {SETUP}(1^\kappa )$. The message space is denoted by $\mathcal {M}$.

• Key derivation. The key derivation algorithm $\mathtt {EXTRACT}$ takes as input an identity $\mathsf {id}$ and, using the master secret key $\mathsf {msk}$, returns a secret key for the user with identity $\mathsf {id}$: $\mathsf {usk}\leftarrow \mathtt {EXTRACT}_\mathsf {msk}(\mathsf {id})$.

• Encryption. The encryption algorithm $\mathtt {ENCRYPT}$ is a randomized algorithm that takes as input an identity $\mathsf {id}$ and a plaintext $m \in \mathcal {M}$, and returns a ciphertext C. We write $C \leftarrow \mathtt {ENCRYPT}_\mathsf {mpk}(\mathsf {id},m)$.

• Decryption. The decryption algorithm $\mathtt {DECRYPT}$ takes as input secret key $\mathsf {usk}$ (corresponding to identity $\mathsf {id}$) and a ciphertext C and returns the corresponding plaintext m or a special symbol $\bot$ indicating that the ciphertext is invalid. We write $m \leftarrow \mathtt {DECRYPT}_\mathsf {usk}(C)$ if C is a valid ciphertext and $\bot \leftarrow \mathtt {DECRYPT}_\mathsf {usk}(C)$ if it is not.

It is required that $\mathtt {DECRYPT}_\mathsf {usk}(\mathtt {ENCRYPT}_\mathsf {mpk}(\mathsf {id},m)) = m$ for any identity $\mathsf {id}$ and all messages $m \in \mathcal {M}$, where $(\mathsf {mpk},\mathsf {msk}) \mathop {\leftarrow }\limits ^{R}\mathtt {SETUP}(1^\kappa )$ and $\mathsf {usk}\leftarrow \mathtt {EXTRACT}_\mathsf {msk}(\mathsf {id})$.

2.2 Security Notions

Semantic Security. The notion of indistinguishability of encryptions [17] captures a strong notion of data-privacy: The adversary should not learn anything about a plaintext given its encryption, beyond the length of the plaintext. The definitions for the public-key setting naturally extend to the identity-based paradigm. The standard definition is strengthened by allowing the adversary to issue chosen private-key extraction queries [7].

We view an adversary $\mathcal {A}$ as a pair $(\mathcal {A}_1, \mathcal {A}_2)$ of probabilistic algorithms. This corresponds to adversary $\mathcal {A}$ running in two stages. Upon receiving the system parameters $\mathsf {mpk}$, in the “find” stage, algorithm $\mathcal {A}_1$ issues private-key extraction queries $\mathsf {id}_1,\cdots ,\mathsf {id}_{n_1}$ and receives back the private key $\mathsf {usk}_i$ corresponding to identity $\mathsf {id}_i$: $\mathsf {usk}_i \leftarrow \mathtt {EXTRACT}_\mathsf {msk}(\mathsf {id}_i)$. The queries may be asked adaptively. Once the adversary decides not to make further oracle queries, it outputs a challenge identity $\mathsf {id}^*$ (with $\mathsf {id}^* \ne \mathsf {id}_i$, $1\le i\le n_1$), two (different) equal-size messages $m_0$ and $m_1 \in \mathcal {M}$ (where $\mathcal {M}$ denotes the message space), and some state information s. In the “guess” stage, algorithm $\mathcal {A}_2$ receives a challenge ciphertext C which is the encryption of $m_b$ for identity $\mathsf {id}^*$ where b is chosen uniformly at random in $\{0,1\}$. Algorithm $\mathcal {A}_2$ can issue more private-key extraction queries $\mathsf {id}_{n_1+1},\cdots ,\mathsf {id}_{n_2}$; the only restriction is that $\mathsf {id}_i \ne \mathsf {id}^*$, $n_1 < i \le n_2$. The goal of $\mathcal {A}_2$ is to guess the value of b from s and C. Formally, a public-key encryption scheme is said indistinguishable (or semantically secure) if

$$\begin{aligned} \hbox {Pr}\left[ \begin{array}{@{}l@{}} (\mathsf {mpk},\mathsf {msk}) \mathop {\leftarrow }\limits ^{R}\mathtt {SETUP}(1^\kappa ),\\ (\mathsf {id}^*,m_0,m_1,s) \leftarrow \mathcal {A}_1^{\mathtt {EXTRACT}_\mathsf {msk}(\cdot )}(\mathsf {mpk}),\\ b \mathop {\leftarrow }\limits ^{R}\{0,1\}, C \leftarrow \mathtt {ENCRYPT}_\mathsf {mpk}(\mathsf {id}^*,m_b) \end{array}\,: \mathcal {A}_2^{\mathtt {EXTRACT}_\mathsf {msk}(\cdot )}(s,C) = b\right] - \frac{1}{2} \end{aligned}$$

is negligible in the security parameter for any polynomial-time adversary $\mathcal {A}$; the probability is taken over the random coins of the experiment according to the distribution induced by $\mathtt {SETUP}$ and over the random coins of the adversary.

Adversary $\mathcal {A}= (\mathcal {A}_1,\mathcal {A}_2)$ can encrypt any message of its choice, for any identity of its choice. In other words, the adversary can mount chosen-identity, chosen-plaintext attacks ($\mathsf {ID}$-$\mathsf {CPA}$). Hence, we write $\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$the security notion achieved by a semantically secure identity-based encryption scheme.

Remark 1

When the message space is $\mathcal {M}= \{0,1\}$, the previous probability simplifies to

$$\begin{aligned} \hbox {Pr}\left[ \begin{array}{@{}l@{}} (\mathsf {mpk},\mathsf {msk}) \mathop {\leftarrow }\limits ^{R}\mathtt {SETUP}(1^\kappa ),\\ (\mathsf {id}^*,s) \leftarrow \mathcal {A}_1^{\mathtt {EXTRACT}_\mathsf {msk}(\cdot )}(\mathsf {mpk}),\\ b \mathop {\leftarrow }\limits ^{R}\{0,1\}, C \leftarrow \mathtt {ENCRYPT}_\mathsf {mpk}(\mathsf {id}^*,b) \end{array}\,: \mathcal {A}_2^{\mathtt {EXTRACT}_\mathsf {msk}(\cdot )}(s,C) = b\right] - \frac{1}{2}. \end{aligned}$$

Anonymity. Analogously, the notion of anonymity captures a strong requirement about privacy: a ciphertext should not reveal the identity of the recipient. More formally, it is defined as a straightforward adaptation of key privacy [4] to the identity-based paradigm [1].

As before, we view an adversary $\mathcal {A}$ as a pair $(\mathcal {A}_1, \mathcal {A}_2)$ of probabilistic algorithms. In the “find” stage, algorithm $\mathcal {A}_1$ issues private-key extraction queries $\mathsf {id}_1,\cdots ,\mathsf {id}_{n_1}$ and receives back the private key $\mathsf {usk}_i$ corresponding to identity $\mathsf {id}_i$: $\mathsf {usk}_i \leftarrow \mathtt {EXTRACT}_\mathsf {msk}(\mathsf {id}_i)$. The queries may be asked adaptively. Once the adversary decides not to make further oracle queries, it outputs two (different) challenge identities $\mathsf {id}^*_0$ and $\mathsf {id}^*_1$ (with $\mathsf {id}^*_0,\mathsf {id}^*_1 \ne \mathsf {id}_i$, $1\le i\le n_1$), a message $m \in \mathcal {M}$, and some state information s. In the “guess” stage, algorithm $\mathcal {A}_2$ receives a challenge ciphertext C which is the encryption of m for identity $\mathsf {id}_b^*$ where b is chosen uniformly at random in $\{0,1\}$. Algorithm $\mathcal {A}_2$ can issue more private-key extraction queries $\mathsf {id}_{n_1+1},\cdots ,\mathsf {id}_{n_2}$; the only restriction is that $\mathsf {id}_i \ne \mathsf {id}^*_0,\mathsf {id}^*_1$, $n_1 < i \le n_2$. The goal of $\mathcal {A}_2$ is to recover the value of b from s and C.

An IBE scheme is said to be anonymous if

$$\begin{aligned} \hbox {Pr}\left[ \begin{array}{@{}l@{}} (\mathsf {mpk},\mathsf {msk}) \mathop {\leftarrow }\limits ^{R}\mathtt {SETUP}(1^\kappa ),\\ (\mathsf {id}^*_0,\mathsf {id}^*_1,m,s) \leftarrow \mathcal {A}_1^{\mathtt {EXTRACT}_\mathsf {msk}(\cdot )}(\mathsf {mpk}),\\ b \mathop {\leftarrow }\limits ^{R}\{0,1\}, C \leftarrow \mathtt {ENCRYPT}_\mathsf {mpk}(\mathsf {id}^*_b,m) \end{array}\,: \mathcal {A}_2^{\mathtt {EXTRACT}_\mathsf {msk}(\cdot )}(s,C) = b\right] - \frac{1}{2} \end{aligned}$$

is negligible in the security parameter for any polynomial-time adversary $\mathcal {A}$; the probability is taken over the random coins of the experiment according to the distribution induced by $\mathtt {SETUP}$ and over the random coins of the adversary. We write $\mathsf {ANO}$-$\mathsf {ID}$-$\mathsf {CPA}$ the corresponding security notion achieved by an anonymous IBE scheme.

Semantic Security and Anonymity. Of course, the goals of indistinguishability and anonymity can be combined to give rise to the $\mathsf {ANO}$-$\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$ security notion. Halevi’s sufficient condition [18] was extended to IBE schemes in [1]. Namely, an IBE scheme is $\mathsf {ANO}$-$\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$ if it is $\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$ and if

$$\begin{aligned} \hbox {Pr}\left[ \begin{array}{@{}l@{}} (\mathsf {mpk},\mathsf {msk}) \mathop {\leftarrow }\limits ^{R}\mathtt {SETUP}(1^\kappa ),\\ (\mathsf {id}^*_0,\mathsf {id}^*_1,m,s) \leftarrow \mathcal {A}_1^{\mathtt {EXTRACT}_\mathsf {msk}(\cdot )}(\mathsf {mpk}),\\ b \mathop {\leftarrow }\limits ^{R}\{0,1\}, r \mathop {\leftarrow }\limits ^{R}\mathcal {M}\text { and } |r|_2 = |m|_2,\\ C \leftarrow \mathtt {ENCRYPT}_\mathsf {mpk}(\mathsf {id}^*_b,r) \end{array}\,: \mathcal {A}_2^{\mathtt {EXTRACT}_\mathsf {msk}(\cdot )}(s,C) = b\right] - \frac{1}{2} \end{aligned}$$

is negligible in the security parameter for any polynomial-time adversary $\mathcal {A}$; the probability is taken over the random coins of the experiment according to the distribution induced by $\mathtt {SETUP}$ and over the random coins of the adversary. The difference is that a random message r is encrypted as opposed to the message m chosen by $\mathcal {A}$; the only restriction being that r and m must be of equal length.

2.3 Complexity Assumptions

It is useful to introduce some notation. Let $N = pq$ be the product of two primes p and q. The set of integers whose Jacobi symbol is 1 is denoted by $\mathbb {J}_N$, $\mathbb {J}_N = \bigl \{ a \in \mathbb {Z}_N^* \mid \textstyle \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{a}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{a}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{a}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{a}}{{N}} \right) \mathclose {}} = 1 \bigr \}$; the set of quadratic residues is denoted by $\mathbb {QR}_N$, $\mathbb {QR}_N = \bigl \{ a \in \mathbb {Z}_N^* \mid \textstyle \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{a}}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{a}}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{a}}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{a}}{{p}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{a}}{{q}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{a}}{{q}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{a}}{{q}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{a}}{{q}} \right) \mathclose {}} = 1 \bigr \}$. Notice that $\mathbb {QR}_N$ is a subset of $\mathbb {J}_N$.

This leads to the following computational assumption [17]. Basically, it says that quadratic residues cannot be distinguished from quadratic non-residues modulo an RSA composite $N=pq$.

Definition 1

(Quadratic Residuosity Assumption). Let $\mathop {\mathsf {RSAgen}}$ be a probabilistic algorithm which, given a security parameter $\kappa$, outputs primes p and q and their product $N = pq$. The Quadratic Residuosity ( $\mathsf {QR}$ ) assumption relative to $\mathop {\mathsf {RSAgen}}$ asserts that the success probability defined as the distance

$$\begin{aligned} \left| \hbox {Pr}[\mathcal {D}(x,N)=1 \mid x \mathop {\leftarrow }\limits ^{R}\mathbb {QR}_N] - \hbox {Pr}[\mathcal {D}(x,N)=1 \mid x \mathop {\leftarrow }\limits ^{R}\mathbb {J}_N \setminus \mathbb {QR}_N] \right| \end{aligned}$$

is negligible for any probabilistic polynomial-time distinguisher $\mathcal {D}$; the probabilities are taken over the experiment of running $(N,p,q) \leftarrow \mathop {\mathsf {RSAgen}}(1^\kappa )$ and choosing at random $x \in \mathbb {QR}_N$ and $x \in \mathbb {J}_N \setminus \mathbb {QR}_N$.

A stronger assumption is introduced in [8]. It says that the $\mathsf {QR}$ assumption holds in the presence of a hash square-root oracle. More formally, the assumption is defined as follows.

Definition 2

(Interactive Quadratic Residuosity Assumption). Again let $\mathop {\mathsf {RSAgen}}$ be a probabilistic algorithm which, given a security parameter $\kappa$, outputs primes p and q and their product $N = pq$. Let also $\mathcal {H}$ be a hash function that on input an arbitrary bit-string returns an element in $\mathbb {J}_N$ and let $\mathcal {O}$ be a hash square-root oracle that maps an input pair (N, s) to one of $\mathcal {H}(s)^{1/2} \,\mathrm {mod}$ N or ($u\mathcal {H}(x))^{1/2}\,\mathrm {mod}$ N, for some quadratic non-residue $u \in \mathbb {J}_N$. The Interactive Quadratic Residuosity ( $\mathsf {IQR}$ ) assumption asserts that the success probability defined as the distance

$$\begin{aligned} \left| \hbox {Pr}[\mathcal {D}^\mathcal {O}(x,N)=1 \mid x \mathop {\leftarrow }\limits ^{R}\mathbb {QR}_N] - \hbox {Pr}[\mathcal {D}^\mathcal {O}(x,N)=1 \mid x \mathop {\leftarrow }\limits ^{R}\mathbb {J}_N \setminus \mathbb {QR}_N] \right| \end{aligned}$$

is negligible for any probabilistic polynomial-time distinguisher $\mathcal {D}$; the probabilities are taken over the experiment of running $(N,p,q) \leftarrow \mathop {\mathsf {RSAgen}}(1^\kappa )$, choosing at random oracle $\mathcal {O}$, and choosing at random $x \in \mathbb {QR}_N$ and $x \in \mathbb {J}_N \setminus \mathbb {QR}_N$.

Remark 2

As noted in [8] the $\mathsf {IQR}$ assumption is equivalent to the $\mathsf {QR}$ assumption in the random oracle model [5].

3 Review of Cocks’ Scheme

In 2001, Cocks published an identity-based encryption scheme that does not rely on pairings over elliptic curves [12]. Cocks’ scheme works in standard RSA groups and its security relies on the quadratic residuosity assumption (in the random oracle model). The encryption processes one bit at a time. To simplify the presentation, we assume that messages being encrypted are in the set $\{-1,1\}$. For example, the map $\mu : \{0,1\} \rightarrow \{-1,1\},\ b \mapsto m = (-1)^b$ maps a bit b to a message $m \in \mathcal {M}= \{\pm 1\}$. The inverse map is given by $\mu ^{-1}(m) = (1-m)/2$.

3.1 Description

Cocks’ scheme proceeds as follows.

• $\mathtt {SETUP}(1^\kappa )$ . Given a security parameter $\kappa$, $\mathtt {SETUP}$ generates an RSA modulus $N = pq$ where p and q are prime. It also selects an element $u \in \mathbb {J}_N\setminus \mathbb {QR}_N$. The system parameters are $\mathsf {mpk}=\{N, u, \mathcal {H}\}$ where $\mathcal {H}$ is a cryptographic hash function mapping bit-strings to $\mathbb {J}_N$. The master secret key is $\mathsf {msk}= \{p,q\}$.

• $\mathtt {EXTRACT}_\mathsf {msk}(\mathsf {id})$ . Using hash function $\mathcal {H}$, $\mathtt {EXTRACT}$ sets $R_\mathsf {id}= \mathcal {H}(\mathsf {id})$. If $R_\mathsf {id}\in \mathbb {QR}_N$ it computes $r_\mathsf {id}= {R_\mathsf {id}}^{1/2}\,\mathrm {mod}$ N; otherwise it computes $r_\mathsf {id}= (uR_\mathsf {id})^{1/2} \,$ N. $\mathtt {EXTRACT}$ returns user’s private key $\mathsf {usk}= \{r_\mathsf {id}\}$.

• $\mathtt {ENCRYPT}(\mathsf {id}, m)$ To encrypt a message $m \in \{\pm 1\}$ for user with identity $\mathsf {id}$, $\mathtt {ENCRYPT}$ chooses at random $t, \bar{t} \in \mathbb {Z}/N\mathbb {Z}$ such that $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{t}}}{{N}} \right) \mathclose {}} = m$. It then computes

  $$\begin{aligned} c = t + \frac{R_\mathsf {id}}{t}\,\,\mathrm{{mod}}\,\,N \quad \text {and}\quad \bar{c} = \bar{t} + \frac{u R_\mathsf {id}}{\bar{t}} \,\,\mathrm {mod}\,\,N \end{aligned}$$

  where $R_\mathsf {id}= \mathcal {H}(\mathsf {id})$. The returned ciphertext is $C = (c, \bar{c})$.

• $\mathtt {DECRYPT}_\mathsf {usk}(C)$ . From $\mathsf {usk}= \{r_\mathsf {id}\}$ and $C = (c,\bar{c})$, if ${r_\mathsf {id}}^2 \equiv \mathcal {H}(\mathsf {id}) (\hbox {mod}\,{N}), \mathtt {DECRYPT}$ sets $\gamma = c$; otherwise it sets $\gamma = \bar{c}$. Plaintext m is then recovered as

  $$\begin{aligned} m = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\gamma + 2 r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\gamma + 2 r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\gamma + 2 r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\gamma + 2 r_\mathsf {id}}}{{N}} \right) \mathclose {}}. \end{aligned}$$

Remark 3

The above description is a generalization of the original scheme. In [12], Cocks considers Blum integers; namely, RSA moduli $N = pq$ with $p, q \equiv 3 \,\,(\text {mod}\,\,{4})$. Doing so, it follows that $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{-1}}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{-1}}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{-1}}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{-1}}{{p}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{-1}}{{q}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{-1}}{{q}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{-1}}{{q}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{-1}}{{q}} \right) \mathclose {}} = -1$ and therefore $-1 \in \mathbb {J}_N\setminus \mathbb {QR}_N$. The original scheme corresponds to the choice $u = -1$. The above description also slightly generalizes the one offered in [8, Appendix A] in that parameter u is not necessarily chosen as a random quadratic non-residue in $\mathbb {J}_N$.

Remark 4

Alternatively, the decryption algorithm can recover plaintext m as $m = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\gamma -2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\gamma -2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\gamma -2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\gamma -2r_\mathsf {id}}}{{N}} \right) \mathclose {}}$. The correctness of the decryption follows by remarking that when ${r_\mathsf {id}}^2 \equiv \mathcal {H}(\mathsf {id})\,\, (\hbox {mod}\,{N})$, $\gamma \pm 2r_\mathsf {id}\equiv t (1 \pm \frac{r_\mathsf {id}}{t})^2\,\, (\hbox {mod}\,{N})$ yielding $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\gamma \pm 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\gamma \pm 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\gamma \pm 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\gamma \pm 2r_\mathsf {id}}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t}}{{N}} \right) \mathclose {}} = m$. Likewise, when ${r_\mathsf {id}}^2 \equiv u\mathcal {H}(\mathsf {id})\,\, (\hbox {mod}\,{N})$, $\gamma \pm 2r_\mathsf {id}\equiv \bar{t}(1 \pm \frac{r_\mathsf {id}}{\bar{t}})^2 \,\,(\hbox {mod}\,{N})$ and thus $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\gamma \pm 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\gamma \pm 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\gamma \pm 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\gamma \pm 2r_\mathsf {id}}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{t}}}{{N}} \right) \mathclose {}} = m$.

3.2 Security Analysis

The next proposition shows that the generalized Cocks’ scheme is semantically secure under the $\mathsf {QR}$ assumption in the random oracle model. Equivalently, as mentioned in Remark 2, the scheme is semantically secure under the $\mathsf {IQR}$ assumption in the standard model.

Proposition 1

The scheme of Sect. 3.1 is $\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$ under the quadratic residuosity assumption in the random oracle model.

Proof

The proof can be found in Appendix A.   $\square$

4 A Useful Representation

Let ${\mathbb {F}}_q$ denote the finite field with q elements, where $q=p^r$ is a prime power. The order of the multiplicative group ${\mathbb {F}}_{p^r}^\times = {\mathbb {F}}_{p^r} \setminus \{0\}$ is $p^r - 1$. Note that $p^r - 1 = \prod _{d\mid r} \varPhi _d(p)$ where $\varPhi _d(x)$ represents the d-th cyclotomic polynomial. We let $\mathsf {G}_{p,r} \subseteq {\mathbb {F}}_{p^r}^\times$ denote the cyclic subgroup of order $\varPhi _r(p)$. In [22], Rubin and Silverberg identify $\mathsf {G}_{p,r}$ with the ${\mathbb {F}}_p$-points of an algebraic torus. Namely, they consider

that is, the elements of ${\mathbb {F}}_{p^r}^\times$ whose norm is one down to every intermediate subfield F. Their key observation is that forms a group whose elements can be represented with only $\phi (r)$ elements of ${\mathbb {F}}_p$, where $\phi$ denotes Euler’s totient function. The compression factor is thus of $r/\phi (r)$ over the field representation [15, 22].

4.1 Parametrization of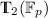

This corresponds to the case $r=2$. We review the explicit representation for presented in [22, Sect. 5.2].

For simplicity, we assume that p is an odd prime. Let $\varDelta = \delta ^2 \in {\mathbb {F}}_p^\times$ with $\delta \notin {\mathbb {F}}_p$. Then is the multiplicative group given by

Define the map . The inverse map is given by . By augmenting ${\mathbb {F}}_p$ with a special symbol $\infty$ and defining $\psi (\infty ) = 1$, maps $\psi$ and $\psi ^{-1}$ extend naturally to give an isomorphism $T_2({\mathbb {F}}_p) \mathop {\rightarrow }\limits ^{\sim } {\mathbb {F}}_p \cup \{\infty \}$.

4.2 An Alternative Representation For $(\mathbb {Z}/N\mathbb {Z})^\times$

One may wonder what happens if $\varDelta$ is chosen as a quadratic residue in the Rubin-Silverberg representation for . As will become apparent in Sect. 4.3, this seemingly useless setting has practical consequences. We start with the multiplicative group ${\mathbb {F}}_p^\times$ and then extend our results to $(\mathbb {Z}/N\mathbb {Z})^\times$ through Chinese remaindering.

The Group $\varvec{\mathcal {F}}_{\!{\varvec{p}},\varvec{\varDelta }}$ . Let p be an odd prime. We henceforth assume that $\delta \in {\mathbb {F}}_p^\times$ and thus that $\varDelta = \delta ^2 \in \mathbb {QR}_p$. In this case, the torus becomes isomorphic to . Note also that map $\psi$ as given in Sect. 4.1 is no longer defined at $u = \delta$. Moreover, when $\delta \in {\mathbb {F}}_p^\times$, $\psi (-\delta ) = 0$ cannot be expressed as $\psi (-\delta ) = x+\delta y$ for some $x,y \in {\mathbb {F}}_p$ with $x^2 - \varDelta y^2 = 1$. So, we define the set

$$\begin{aligned} \mathcal {F}_{\!p,\varDelta } = ({\mathbb {F}}_p \setminus \{\pm \delta \}) \cup \{\infty \} = \{ u \in {\mathbb {F}}_p \mid u^2 \ne \varDelta \} \cup \{\infty \} \end{aligned}$$

and restrict map $\psi$ to $\mathcal {F}_{\!p,\varDelta }$:

$$\begin{aligned} \psi : \mathcal {F}_{\!p,\varDelta } \rightarrow {\mathbb {F}}_p^\times ,\ u \mapsto {\left\{ \begin{array}{ll} \frac{u + \delta }{u - \delta } &{} \text {if }u \ne \infty \,,\\ 1 &{} \text {otherwise}\,. \end{array}\right. } \end{aligned}$$

For completeness, we show that $\mathcal {F}_{\!p,\varDelta }$ equipped with the group law $\circledast$ (defined hereafter) and ${\mathbb {F}}_p^\times$ are isomorphic. Clearly, the map $\psi : \mathcal {F}_{\!p,\varDelta } \rightarrow {\mathbb {F}}_p^\times$ is injective and thus defines a bijection. Indeed, suppose $\psi (u_1) = \psi (u_2)$ for some $u_1, u_2 \in \mathcal {F}_{\!p,\varDelta }$. If $\psi (u_1) \ne 1$, this implies $(u_1 + \delta )(u_2 - \delta ) = (u_2 + \delta )(u_1 - \delta )$ and in turn $u_1 = u_2$; it $\psi (u_1) = 1$ then again this implies $u_1 = u_2$ $(=\infty )$ since $(u+\delta )/(u-\delta ) \ne 1$ for every $u \in \mathcal {F}_{\!p,\varDelta }$. The inverse map is given by

$$\begin{aligned} \psi ^{-1}: {\mathbb {F}}_p^\times \rightarrow \mathcal {F}_{\!p,\varDelta },\ v \mapsto {\left\{ \begin{array}{ll} \frac{\delta (v+1)}{v-1} &{} \text {if }v \ne 1\,,\\ \infty &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

Furthermore, map $\psi$ yields a homomorphism from $\mathcal {F}_{\!p,\varDelta }$ to ${\mathbb {F}}_p^\times$. Let $u_1, u_2 \in \mathcal {F}_{\!p,\varDelta } \setminus \{\infty \}$ with $u_1 \ne -u_2$. Then we have

$$\begin{aligned} \psi (u_1) \cdot \psi (u_2)&= \frac{(u_1 + \delta )(u_2 + \delta )}{(u_1 - \delta )(u_2 - \delta )} = \frac{u_1u_2 + \varDelta + \delta (u_1 + u_2)}{u_1u_2 + \varDelta - \delta (u_1 + u_2)} = \frac{\frac{u_1u_2 + \varDelta }{u_1 + u_2} + \delta }{\frac{u_1u_2 + \varDelta }{u_1 + u_2} - \delta }\\&= \psi (u_3)\quad \text {where }u_3 = \tfrac{u_1u_2 + \varDelta }{u_1 + u_2}. \end{aligned}$$

Note also that $\psi (\infty ) = 1$ and that $\frac{1}{\psi (u_1)} = \frac{u_1 - \delta }{u_1 + \delta } = \frac{-u_1 + \delta }{-u_1 - \delta } = \psi (-u_1)$.

We write $\mathcal {F}_{\!p,\varDelta }$ multiplicatively and use $\circledast$ to denote its group law. In more detail, we have:

• the neutral element is $\infty$: $u \circledast \infty = \infty \circledast u = u$ for all $u \in \mathcal {F}_{\!p,\varDelta }$ ;

• the inverse of $u \in \mathcal {F}_{\!p,\varDelta } \setminus \{\infty \}$ is $-u$: $u \circledast (-u) = (-u) \circledast u = \infty$ ;

• given $u_1, u_2 \in \mathcal {F}_{\!p,\varDelta } \setminus \{\infty \}$, their product is given by:

  $$\begin{aligned} u_1 \circledast u_2 = {\left\{ \begin{array}{ll} \frac{u_1u_2 + \varDelta }{u_1 + u_2}&{} \text {if }u_1 \ne -u_2\,,\\ \infty &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

The Group $\varvec{\mathcal {Z}}_{{\varvec{N,}}\varvec{\varDelta }}$ . The previous setting naturally extends through Chinese remaindering. Let $N = pq$ be an RSA modulus. Then

$$\begin{aligned} \mathcal {Z}_{N,\varDelta } := \mathcal {F}_{\!p,\varDelta } \times \mathcal {F}_{\!q,\varDelta } \cong (\mathbb {Z}/N\mathbb {Z})^\times \end{aligned}$$

(1)

is a group w.r.t. $\circledast$ and has order $\phi (N)$.

For each element $u \in \mathcal {Z}_{N,\varDelta }$, there exists a unique pair of elements $u_{p} \in \mathcal {F}_{\!p,\varDelta }$ and $u_{q} \in \mathcal {F}_{\!q,\varDelta }$ such that $u\,\,\mathrm{{mod}}\,\, p = u_{p}$ and $u\,\,\mathrm{{mod}}\,\,q = u_{q}$. We denote this equivalence by $u = [u_{p}, u_{q}]$ and let $\infty = [\infty _p, \infty _q]$ represent the neutral element. We also define the subset $\widetilde{\mathcal {Z}}_{N,\varDelta } := \bigl ((\mathcal {F}_{\!p,\varDelta }\setminus \{\infty _p\}) \times (\mathcal {F}_{\!q,\varDelta } \setminus \{\infty _q\})\bigr ) \cup \{\infty \}$.

Efficient methods for working in $\mathcal {Z}_{N,\varDelta }$ are discussed in Appendix B.

Remark 5

Please note that 0 is of order 2 as an element of $\mathcal {Z}_{N,\varDelta }$, namely $0 \circledast 0 = \infty$. Note also that for any $u \in \mathcal {Z}_{N,\varDelta }$, $u \ne 0, \infty$, we have $u \circledast 0 = \varDelta /u$.

4.3 The Subset $\mathscr {S}_{N,\varDelta }$ of Squares in $\widetilde{\mathcal {Z}}_{N,\varDelta }$

We now have all ingredients to introduce the useful quasi-group $\mathscr {S}_{N,\delta }$. Let $N = pq$ be an RSA modulus and let $\varDelta = \delta ^2 \in \mathbb {QR}_N$. Consider the set of squares in $\widetilde{\mathcal {Z}}_{N,\varDelta }$, namely $(\widetilde{\mathcal {Z}}_{N,\varDelta })^2 = \{ u \circledast u \mid u \in \widetilde{\mathcal {Z}}_{N,\varDelta } \} \subset (\mathcal {Z}_{N,\varDelta })^2$, or more exactly, the subset

$$\begin{aligned} \mathscr {S}_{N,\varDelta }&\mathop {=}\limits ^{\text {def}} \left\{ \tfrac{u^2 + \varDelta }{2u} \mid u \in (\mathbb {Z}/N\mathbb {Z})^\times \text { and } \gcd (u^2 - \varDelta ,N) = 1\right\} \\&= (\widetilde{\mathcal {Z}}_{N,\varDelta })^2 \setminus \{\infty \}.\nonumber \end{aligned}$$

(2)

The set $\mathscr {S}_{N,\varDelta }$ almost defines a group: it contains all elements s of the group $(\mathcal {Z}_{N,\varDelta })^2 = \{ s = u\circledast u \mid u \in \mathcal {Z}_{N,\varDelta }\}$ minus elements of the form $[s_p, \infty _q]$ or $[\infty _p, s_q]$ (and $\infty = [\infty _p,\infty _q]$). Since it is a subset of $(\mathcal {Z}_{N,\varDelta })^2$, $\mathscr {S}_{N,\varDelta }$ is endowed with the $\circledast$-law. In practice, for cryptographic applications, working in $(\widetilde{\mathcal {Z}}_{N,\varDelta })^2 = {\mathscr {S}}_{N,\varDelta } \cup \{\infty \}$ rather than in $(\mathcal {Z}_{N,\varDelta })^2$ does not really matter since the probability that operation $\circledast$ is not defined on $(\widetilde{\mathcal {Z}}_{N,\varDelta })^2$ is negligible.

What makes the quasi-group $\mathscr {S}_{N,\varDelta }$ special is that, up to a scaling factor of two, it represents the set of all valid [components of] Cocks ciphertexts. Before making this statement clear, we need to explain what is meant by ‘valid component’. This follows from the next lemma, adapted from [12, Sect. 5]. Basically, it shows that, given a (generalized) Cocks ciphertext $C = (c,\bar{c})$, among its two components c and $\bar{c}$, one carries no information whatsoever about the corresponding plaintext. The component that yields the plaintext is called valid component.

Lemma 1

Using the notations of Sect. 3.1, let $C = (c,\bar{c})$ be a (generalized) Cocks ciphertext. If $\mathcal {H}(\mathsf {id}) \notin \mathbb {QR}_N$ then the component c corresponds with the same probability to the encryption of message $m=1$ or $m=-1$. Conversely, if $u\,\mathcal {H}(\mathsf {id}) \notin \mathbb {QR}_N$ then the component $\bar{c}$ corresponds with the same probability to the encryption of message $m=1$ or $m=-1$.

Proof

Suppose that $\mathcal {H}(\mathsf {id}) \notin \mathbb {QR}_N$ (i.e., $\mathcal {H}(\mathsf {id}) \in \mathbb {J}_N \setminus \mathbb {QR}_N$). Let $R_\mathsf {id}= \mathcal {H}(\mathsf {id})$. We have $c = t + \frac{R_\mathsf {id}}{t} \,\,\mathrm {mod}$ N for some random $t \in (\mathbb {Z}/N\mathbb {Z})^\times$ such $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t}}{{N}} \right) \mathclose {}} = m$. Consider also $t_1, t_2, t_3 \in (\mathbb {Z}/N\mathbb {Z})^\times$ such that

• $t_1 \equiv t \,\,(\hbox {mod}\,\,{p})$, $t_1 \equiv R_\mathsf {id}/t \,\,(\hbox {mod}\,\,{q})$;

• $t_2 \equiv R_\mathsf {id}/t \,\,(\hbox {mod}\,\,{p})$, $t_2 \equiv t \,\,(\hbox {mod}\,\,{q})$;

• $t_3 \equiv R_\mathsf {id}/t \,\,(\hbox {mod}\,\,{p})$, $t_3 \equiv R_\mathsf {id}/t \,\,(\hbox {mod}\,\,{q})$.

Note that the condition $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t}}{{N}} \right) \mathclose {}} = m$ implies $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t_1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t_1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t_1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t_1}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t_2}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t_3}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t_3}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t_3}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t_3}}{{N}} \right) \mathclose {}} = m$. The four possible values t, $t_1$, $t_2$, and $t_3$ are equally likely since $c \equiv t + R_\mathsf {id}/t \equiv t_1 + R_\mathsf {id}/t_1 \equiv t_2 + R_\mathsf {id}/t_2 \equiv t_3 + R_\mathsf {id}/t_3 \,\,(\hbox {mod}\,\,{N})$. At the same time, since $R_\mathsf {id}\in \mathbb {J}_N \setminus \mathbb {QR}_N$ we also have $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t_3}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t_3}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t_3}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t_3}}{{N}} \right) \mathclose {}} \ne \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t_1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t_1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t_1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t_1}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t_2}}{{N}} \right) \mathclose {}}$. Hence, component c leaks no information about $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t}}{{N}} \right) \mathclose {}}$; it has the same probability to be 1 or $-1$.

The case $u\,\mathcal {H}(\mathsf {id}) \notin \mathbb {QR}_N$ is proved similarly.   $\square$

With the notations of Sect. 3.1, from a ciphertext $C = (c, \bar{c})$, letting $\varDelta = \mathcal {H}(\mathsf {id}) \in \mathbb {QR}_N$ (resp. $\varDelta = u\,\mathcal {H}(\mathsf {id}) \in \mathbb {QR}_N$) and $\gamma = c$ (resp. $\bar{c}$), we have

$$\begin{aligned} \frac{\gamma }{2} \in \mathscr {S}_{N,\varDelta } \implies \exists \tau \in (\mathbb {Z}/N\mathbb {Z})^\times \text { with }\gcd (\tau ^2 - \varDelta , N) = 1\text { such that }\gamma = \tfrac{\tau ^2 + \varDelta }{\tau }. \end{aligned}$$

In other words, up to a factor of two, the valid component of C is an element of $\mathscr {S}_{N,\varDelta }$; i.e., $\frac{\gamma }{2} \in \mathscr {S}_{N,\varDelta }$. By Lemma 1, the other component does not matter. Note also that the condition $\gcd (\tau ^2 - \varDelta , N) = 1$ is implicit in the (generalized) Cocks encryption since $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\tau }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\tau }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\tau }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\tau }}{{N}} \right) \mathclose {}} = m \in \{\pm 1\}$ where $\tau = t$ (resp. $\tau = \bar{t}$) and decryption is obtained as

$$\begin{aligned} \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\gamma \pm 2\delta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\gamma \pm 2\delta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\gamma \pm 2\delta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\gamma \pm 2\delta }}{{N}} \right) \mathclose {}} \end{aligned}$$

which is 0 when $\gcd (\tau ^2 - \varDelta , N) \ne 1 \iff \tau \equiv \pm \delta (\hbox {mod}\,\{p,q\})$. The condition $\tau \in (\mathbb {Z}/N\mathbb {Z})^\times$ (instead of $t, \bar{t} \in \mathbb {Z}/N\mathbb {Z}$) is trivially satisfied since $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\tau }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\tau }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\tau }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\tau }}{{N}} \right) \mathclose {}} \in \{\pm 1\}$.

5 Computing over Cocks Ciphertexts

Homomorphic encryption is a form of encryption which allows combining two ciphertexts through a non-private operation that results in a third ciphertext which, when decrypted, yields a plaintext that is the combination of the corresponding two plaintexts through a specific operation. Mathematically, for two ciphertexts $C_1 = \mathtt {ENCRYPT}(m_1)$ and $C_2 = \mathtt {ENCRYPT}(m_2)$, there exists a non-private operation $\partial$ such that $C_1 \mathbin {\partial } C_2 = \mathtt {ENCRYPT}(m_1 \star m_2)$ for some specific operation $\star$. Examples of known operations $\star$ include (modular) addition and (modular) multiplication.

5.1 HOM Procedure

Consider the following procedure $\mathbf{HOM}$. It takes as input two elements $x_1, x_2 \in \mathbb {Z}/N\mathbb {Z}$ and an element $\varGamma \in \mathbb {J}_N$, and outputs an element $z \in \mathbb {Z}/N\mathbb {Z}$. We write $z = \mathbf{HOM}(x_1, x_2, \varGamma )$.

Remark 6

Note that when $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{U}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{U}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{U}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{U}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{x_1+x_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{x_1+x_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{x_1+x_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{x_1+x_2}}{{N}} \right) \mathclose {}} = 1$, we can take $t = 0$ (in Procedure $\mathbf{HOM}$, Line 3). This yields $\theta = \varGamma U \,\,\mathrm {mod}$ N ($\in \mathbb {J}_N$) and in turn $z = D/U \,\,\mathrm {mod}$ N.

5.2 Application

The $\mathbf{HOM}$ procedure allows for computing over two Cocks ciphertexts.

Specifically, suppose we are given two ciphertexts $C_1 = \{c_1, \bar{c}_1\}$ and $C_2 = \{c_2, \bar{c}_2\}$ that are the respective encryption of two messages $m_1$ and $m_2$ for a same identity, say $\mathsf {id}$. The system parameters are $\mathsf {mpk}=\{N,u,\mathcal {H}\}$ where $N=pq$ is an RSA modulus, u is a quadratic non-residue in $\mathbb {J}_N$, and $\mathcal {H}$ is a hash function mapping bit-strings to $\mathbb {J}_N$. As in the description given in Sect. 3.1, we assume that the message space is $\mathcal {M}= \{\pm 1\}$.

Let $R_\mathsf {id}= \mathcal {H}(\mathsf {id})$. Two applications of the $\mathbf{HOM}$ procedure yields a third ciphertext $C_3 = (c_3, \bar{c_3})$ obtained as

$$\begin{aligned} c_3 = \mathbf{HOM}(c_1, c_2, R_\mathsf {id}) \quad \text {and}\quad \bar{c}_3 = \mathbf{HOM}(\bar{c}_1, \bar{c}_2, uR_\mathsf {id}). \end{aligned}$$

A simple calculation shows that $C_3$ is the encryption of $m_3 = m_1 \cdot m_2$.

Proof

Suppose first that $R_\mathsf {id}\in \mathbb {QR}_N$. Then, letting $r_\mathsf {id}= {R_\mathsf {id}}^{1/2} \,\,\mathrm {mod}$ N, we have:

$$\begin{aligned} \textstyle \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}&= \textstyle \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\theta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\theta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\theta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\theta }}{{N}} \right) \mathclose {}} \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{(t^2+R_\mathsf {id})D + 4R_\mathsf {id}tU + 2r_\mathsf {id}(tD+(t^2+R_\mathsf {id})U)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{(t^2+R_\mathsf {id})D + 4R_\mathsf {id}tU + 2r_\mathsf {id}(tD+(t^2+R_\mathsf {id})U)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{(t^2+R_\mathsf {id})D + 4R_\mathsf {id}tU + 2r_\mathsf {id}(tD+(t^2+R_\mathsf {id})U)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{(t^2+R_\mathsf {id})D + 4R_\mathsf {id}tU + 2r_\mathsf {id}(tD+(t^2+R_\mathsf {id})U)}}{{N}} \right) \mathclose {}}\\&= \textstyle \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{(t^2+R_\mathsf {id}+2r_\mathsf {id}t)D + (2r_\mathsf {id}t+t^2+R_\mathsf {id})(2r_\mathsf {id}U)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{(t^2+R_\mathsf {id}+2r_\mathsf {id}t)D + (2r_\mathsf {id}t+t^2+R_\mathsf {id})(2r_\mathsf {id}U)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{(t^2+R_\mathsf {id}+2r_\mathsf {id}t)D + (2r_\mathsf {id}t+t^2+R_\mathsf {id})(2r_\mathsf {id}U)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{(t^2+R_\mathsf {id}+2r_\mathsf {id}t)D + (2r_\mathsf {id}t+t^2+R_\mathsf {id})(2r_\mathsf {id}U)}}{{N}} \right) \mathclose {}} = \textstyle \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{(t+r_\mathsf {id})^2(D+2r_\mathsf {id}U)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{(t+r_\mathsf {id})^2(D+2r_\mathsf {id}U)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{(t+r_\mathsf {id})^2(D+2r_\mathsf {id}U)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{(t+r_\mathsf {id})^2(D+2r_\mathsf {id}U)}}{{N}} \right) \mathclose {}}\\&= \textstyle \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{D+2r_\mathsf {id}U}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{D+2r_\mathsf {id}U}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{D+2r_\mathsf {id}U}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{D+2r_\mathsf {id}U}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{(c_1c_2 +4R_\mathsf {id}) +2r_\mathsf {id}(c_1 +c_2)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{(c_1c_2 +4R_\mathsf {id}) +2r_\mathsf {id}(c_1 +c_2)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{(c_1c_2 +4R_\mathsf {id}) +2r_\mathsf {id}(c_1 +c_2)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{(c_1c_2 +4R_\mathsf {id}) +2r_\mathsf {id}(c_1 +c_2)}}{{N}} \right) \mathclose {}}\\&= \textstyle \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c_1+2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c_1+2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c_1+2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c_1+2r_\mathsf {id}}}{{N}} \right) \mathclose {}} \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c_2+2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c_2+2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c_2+2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c_2+2r_\mathsf {id}}}{{N}} \right) \mathclose {}} \end{aligned}$$

as desired.

The case $R_\mathsf {id}\in \mathbb {J}_N \setminus \mathbb {QR}_N$ is similar. Letting $r_\mathsf {id}= (uR_\mathsf {id})^{1/2} \,\,\mathrm {mod}$ N, we then have $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{c}_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{c}_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{c}_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{c}_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{c}_1+2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{c}_1+2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{c}_1+2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{c}_1+2r_\mathsf {id}}}{{N}} \right) \mathclose {}} \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{c}_2+2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{c}_2+2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{c}_2+2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{c}_2+2r_\mathsf {id}}}{{N}} \right) \mathclose {}}$.   $\square$

Why Does It Work? At first sight, the $\mathbf{HOM}$ procedure may appear cumbersome. Actually it is not. Without loss of generality, assume that input $\varGamma \leftarrow R_\mathsf {id}= {r_\mathsf {id}}^2 \in \mathbb {QR}_N$. A straightforward application of the homomorphism induced by the underlying $\circledast$ law will not get the correct result. Clearly, if we call $c_3 = \mathbf{HOM}(c_1, c_2, R_\mathsf {id})$ and let

$$\begin{aligned} \frac{c'_3}{2} = \frac{c_1}{2} \circledast \frac{c_2}{2} \iff c'_3 = \frac{c_1c_2 + 4R_\mathsf {id}}{c_1+c_2} \end{aligned}$$

then $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c'_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c'_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c'_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c'_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}$ if and only if $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c_1+c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c_1+c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c_1+c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c_1+c_2}}{{N}} \right) \mathclose {}} = 1$. Indeed, the above definition of $c'_3$ immediately yields

$$\begin{aligned} \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}} := \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c_1 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c_1 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c_1 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c_1 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}} \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c_2 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c_2 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c_2 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c_2 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c_1+c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c_1+c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c_1+c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c_1+c_2}}{{N}} \right) \mathclose {}} \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c'_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c'_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c'_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c'_3 + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}. \end{aligned}$$

In other words, $c'_3$ is the encryption of $m_1\cdot m_2$ if and only if $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c_1+c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c_1+c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c_1+c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c_1+c_2}}{{N}} \right) \mathclose {}} = 1$. This problem is resolved by randomizing one of the input ciphertexts using the homomorphism. One way to achieve this is to replace ciphertext $c_1$ with an equivalent randomized ciphertext,

until $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c_1+c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c_1+c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c_1+c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c_1+c_2}}{{N}} \right) \mathclose {}} = 1$, where is a random Cocks encryption (w.r.t. $R_\mathsf {id}$) of message $m=1$. Note that no secret is involved in the randomization of $c_1$. This is the design strategy behind the $\mathbf{HOM}$ procedure.

We have seen that the $\mathbf{HOM}$ procedure can be used to randomize ciphertexts. Likewise, it can be used to flip the value of a plaintext message $m_1 \in \{\pm 1\}$ corresponding to a given Cocks ciphertext $C_1 = (c_1, \bar{c}_1)$ by taking the encryption of $m_2 = -1$ for ciphertext $C_2 = (c_2, \bar{c}_2)$.

A variant of Cocks’ scheme that makes easier the computation over ciphertexts can be found in Appendix C.

It is also worth noting that when the message space is $\{0,1\}$ rather than $\{\pm 1\}$ then the scheme is homomorphic with respect the xor operator. Indeed, letting $b_1 = \mu ^{-1}(m_1)$ and $b_2 = \mu ^{-1}(m_2)$, we have $\mu ^{-1}(m_1 \cdot m_2) = b_1 \oplus b_2$, where $\mu ^{-1}(m_i) = (1 - m_i)/2$ —see Sect. 3. We so get $\mu (b_1 \oplus b_2) = (-1)^{b_1 \oplus b_2} = (-1)^{b_1+b_2} = m_1 \cdot m_2$.

6 An Anonymous IBE Scheme

In numerous scenarios, the recipient’s identity in a transmission needs to be kept anonymous. This allows users to maintain some privacy. Protecting communication content may be not enough, as already observed in, e.g., [3, 4, 21]. For example, by analyzing the traffic between an antenna and a mobile device, one can recover some information about [at least] user’s position and some details about the use of her mobile device. This information leaks easily during all day: it is a common habit, indeed, to use a mobile phone every day and to keep it (almost) always switched on.

As pointed out by Galbraith (see [6, Sect. 4], Cocks’ scheme is not anonymous. A detailed discussion on the so-called Galbraith’s test can be found in [2, Sect. 2.3]). In the same paper, Ateniese and Gasti also show that Galbraith’s is the “best test” possible against the anonymity of Cocks’ scheme.

In this section, we rephrase Galbraith’s test using our representation. We then build on an original technique developed in [11] to get anonymized Cocks ciphertexts. However, unlike [11], there is no ciphertext expansion. Anonymized Cocks ciphertexts have the same size as non-anonymized ciphertexts. The decryption algorithm is modified accordingly by first de-anonymizing the ciphertext and then applying the regular decryption process. The resulting scheme is shown to meet the $\mathsf {ANO}$-$\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$ security notion under the $\mathsf {QR}$ assumption in the random oracle model or, equivalently, under the $\mathsf {IQR}$ assumption in the standard model (cf. Remark 2).

6.1 Making Cocks Ciphertexts Anonymous

As Eq. (6) indicates, the subset $\widetilde{\mathcal {Z}}_{N,\varDelta } \subset {\mathcal {Z}}_{N,\varDelta }$ can be defined as

$$\begin{aligned} \widetilde{\mathcal {Z}}_{N,\varDelta } = \{ u \in \mathbb {Z}/N\mathbb {Z} \mid \gcd (u^2 - \varDelta , N) = 1 \} \cup \{\infty \} \end{aligned}$$

where $N=pq$ and $\varDelta \in \mathbb {QR}_N$. The following subsets of $\widetilde{\mathcal {Z}}_{N,\varDelta }$ will be useful:

• $\widehat{\mathcal {Z}}_{N,\varDelta } := \bigl \{ u \in \mathbb {Z}/N\mathbb {Z} \mid \gcd (u^2 - \varDelta , N) = 1 \bigr \} \subset \widetilde{\mathcal {Z}}_{N,\varDelta }$;

• $\widehat{\mathcal {Z}}_{N,\varDelta }^{[-1]} := \bigl \{ u \in \mathbb {Z}/N\mathbb {Z} \mid \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{u^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{u^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{u^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{u^2 - \varDelta }}{{N}} \right) \mathclose {}} = -1\bigr \} \subset \widehat{\mathcal {Z}}_{N,\varDelta }$;

• $\widehat{\mathcal {Z}}_{N,\varDelta }^{[+1]} := \bigl \{ u \in \mathbb {Z}/N\mathbb {Z} \mid \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{u^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{u^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{u^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{u^2 - \varDelta }}{{N}} \right) \mathclose {}} = 1\bigr \} \subset \widehat{\mathcal {Z}}_{N,\varDelta }$;

• $(\widehat{\mathcal {Z}}_{N,\varDelta })^2 := \bigl \{ u \in \mathbb {Z}/N\mathbb {Z} \mid \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{u^2 - \varDelta }}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{u^2 - \varDelta }}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{u^2 - \varDelta }}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{u^2 - \varDelta }}{{p}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{u^2 - \varDelta }}{{q}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{u^2 - \varDelta }}{{q}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{u^2 - \varDelta }}{{q}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{u^2 - \varDelta }}{{q}} \right) \mathclose {}} = 1 \bigr \} \subset \widehat{\mathcal {Z}}_{N,\varDelta }^{[+1]}$.

We have

$$\begin{aligned} \widehat{\mathcal {Z}}_{N,\varDelta } = \widetilde{\mathcal {Z}}_{N,\varDelta } \setminus \{\infty \} = (\mathcal {F}_{\!p,\varDelta } \setminus \{\infty _p\}) \times (\mathcal {F}_{\!q,\varDelta } \setminus \{\infty _q\}) \end{aligned}$$

from Eq. (5). By definition (see Sect. 4.2), for $u \in \mathcal {F}_{\!p,\varDelta } \setminus \{\infty _p\}$, we have $\psi (u) = \frac{u+\delta }{u-\delta }$, and $\psi (\infty _p) =1$. Multiplying both sides by $(u-\delta )^2$, the latter identity yields

$$\begin{aligned} \psi (u) \cdot (u-\delta )^2 = u^2 - \varDelta . \end{aligned}$$

(3)

The group $(\mathcal {F}_{\!p,\varDelta })^2 = \{ u \circledast u \mid u \in \mathcal {F}_{\!p,\varDelta }\}$ is the subgroup of squares in $\mathcal {F}_{\!p,\varDelta }$. Therefore, if $u \in (\mathcal {F}_{\!p,\varDelta })^2$ then $\psi (u)$ is a quadratic residue modulo p; i.e., $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\psi (u)}}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\psi (u)}}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\psi (u)}}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\psi (u)}}{{p}} \right) \mathclose {}} = 1$. Together with Eq. (3) it follows that $u^2 - \varDelta$ is a quadratic residue modulo p when $u \in (\mathcal {F}_{\!p,\varDelta })^2$, $u \ne \infty _p$. This gives an alternative definition for the group $(\mathcal {F}_{\!p,\varDelta })^2$, namely $(\mathcal {F}_{\!p,\varDelta })^2 = \bigl \{ u \in \mathcal {F}_{\!p,\varDelta } \mid \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{u^2 - \varDelta }}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{u^2 - \varDelta }}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{u^2 - \varDelta }}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{u^2 - \varDelta }}{{p}} \right) \mathclose {}} = 1 \bigr \} \cup \{\infty _p\} = \bigl \{ u \in {\mathbb {F}}_p \mid \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{u^2 - \varDelta }}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{u^2 - \varDelta }}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{u^2 - \varDelta }}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{u^2 - \varDelta }}{{p}} \right) \mathclose {}} = 1 \bigr \} \cup \{\infty _p\}$. Hence, using Chinese remaindering, we get

$$\begin{aligned} (\widehat{\mathcal {Z}}_{N,\varDelta })^2 = \bigl ((\mathcal {F}_{\!p,\varDelta })^2 \setminus \{\infty _p\}\bigr ) \times \bigl ((\mathcal {F}_{\!q,\varDelta })^2 \setminus \{\infty _q\}\bigr ). \end{aligned}$$

This means that $(\widehat{\mathcal {Z}}_{N,\varDelta })^2$ is an alternative representation for the subset $\mathscr {S}_{N,\varDelta }$ of squares in $\widetilde{\mathcal {Z}}_{N,\varDelta }$. Likewise, $\widehat{\mathcal {Z}}_{N,\varDelta }^{[-1]}$ denotes the subset of elements that are squares modulo p and non-squares modulo q, or vice-versa; and $\widehat{\mathcal {Z}}_{N,\varDelta }^{[+1]}$ denotes the subset of elements that are either both squares modulo p and modulo q, or both non-squares modulo p and modulo q.

We have shown that:

Proposition 2

Let $N = pq$ be an RSA modulus and let $w \in \widehat{\mathcal {Z}}_{N,\varDelta }$. If

$$\begin{aligned} \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{w^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{w^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{w^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{w^2 - \varDelta }}{{N}} \right) \mathclose {}} = -1 \end{aligned}$$

then $w \notin \mathscr {S}_{N,\varDelta }$.   $\square$

This is nothing but Galbraith’s test. Back to the anonymity problem, letting $u\in \mathbb {J}_N \setminus \mathbb {QR}_N$, it implies that elements of the form $\frac{c}{2} = \frac{t^2+ R_\mathsf {id}}{2t} \,\mathrm{{mod}}\,N$ (respectively, $\frac{\bar{c}}{2} = \frac{\bar{t}^2+ uR_\mathsf {id}}{2\bar{t}} \,\mathrm{{mod}}\,N$) —where $R_\mathsf {id}= \mathcal {H}(\mathsf {id})$ is derived from some user’s identity $\mathsf {id}$— cannot be used as part of a ciphertext for user with identity $\mathsf {id}'$ because if $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{(c/2)^2 - R_{\mathsf {id}'}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{(c/2)^2 - R_{\mathsf {id}'}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{(c/2)^2 - R_{\mathsf {id}'}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{(c/2)^2 - R_{\mathsf {id}'}}}{{N}} \right) \mathclose {}} = -1$ (respectively, if $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{(\bar{c}/2)^2 - uR_{\mathsf {id}'}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{(\bar{c}/2)^2 - uR_{\mathsf {id}'}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{(\bar{c}/2)^2 - uR_{\mathsf {id}'}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{(\bar{c}/2)^2 - uR_{\mathsf {id}'}}}{{N}} \right) \mathclose {}} = -1$) —where $R_{\mathsf {id}'} = \mathcal {H}(\mathsf {id}')$ for some other identity $\mathsf {id}'$— then one can conclude that the identity of the recipient of the ciphertext is not $\mathsf {id}'$. This clearly violates the anonymity requirement.

This issue is easily solved by $\circledast$-multiplying with probability 1/2 the value of $\frac{c}{2}$ (resp. $\frac{\bar{c}}{2}$) by an element $\frac{d}{2}$ satisfying $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{(d/2)^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{(d/2)^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{(d/2)^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{(d/2)^2 - \varDelta }}{{N}} \right) \mathclose {}} = -1$ (resp. $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{(d/2)^2 - u\varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{(d/2)^2 - u\varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{(d/2)^2 - u\varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{(d/2)^2 - u\varDelta }}{{N}} \right) \mathclose {}} = -1$). The decryption algorithm, assuming it is the legitimate recipient of the ciphertext, can then $\circledast$-divide by $\frac{d}{2}$ the ciphertext in the case it were $\circledast$-multiplied by $\frac{d}{2}$; letting $\frac{e}{2}$ (resp. $\frac{\bar{e}}{2}$) the received part of the ciphertext, it is easy for the decryption algorithm to know if $\frac{e}{2}=\frac{c}{2}$ or $\frac{e}{2} = \frac{c}{2} \circledast \frac{d}{2}$ (resp. $\frac{\bar{e}}{2}=\frac{\bar{c}}{2}$ or $\frac{\bar{e}}{2} = \frac{\bar{c}}{2} \circledast \frac{d}{2}$) by checking if $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{(e/2)^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{(e/2)^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{(e/2)^2 - \varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{(e/2)^2 - \varDelta }}{{N}} \right) \mathclose {}} = 1$ or $-1$ (resp. $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{(\bar{e}/2)^2 - u\varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{(\bar{e}/2)^2 - u\varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{(\bar{e}/2)^2 - u\varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{(\bar{e}/2)^2 - u\varDelta }}{{N}} \right) \mathclose {}} = 1$ or $-1$), respectively.

6.2 Anonymous IBE Without Ciphertext Expansion

There is a variety of possible instantiations of the above methodology. An efficient implementation can be achieved by specializing hash function $\mathcal {H}$. Instead of considering a function mapping bit-strings to any element of $\mathbb {J}_N$, we require that, in addition, on input $\mathsf {id}$, the output must satisfy the extra condition $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{{d}^2 - 4R_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{{d}^2 - 4R_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{{d}^2 - 4R_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{{d}^2 - 4R_\mathsf {id}}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{{d}^2 - 4uR_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{{d}^2 - 4uR_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{{d}^2 - 4uR_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{{d}^2 - 4uR_\mathsf {id}}}{{N}} \right) \mathclose {}} =-1$ for some given d:

$$\begin{aligned} \mathcal {H}_d : \{0,1\}^* \rightarrow \mathbb {J}_N,\ \mathsf {id}\mapsto \mathcal {H}_d(\mathsf {id}) \;\text { s.t. } \textstyle \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{{d}^2 - 4\mathcal {H}_d(\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{{d}^2 - 4\mathcal {H}_d(\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{{d}^2 - 4\mathcal {H}_d(\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{{d}^2 - 4\mathcal {H}_d(\mathsf {id})}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{{d}^2 - 4u\mathcal {H}_d(\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{{d}^2 - 4u\mathcal {H}_d(\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{{d}^2 - 4u\mathcal {H}_d(\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{{d}^2 - 4u\mathcal {H}_d(\mathsf {id})}}{{N}} \right) \mathclose {}} =-1. \end{aligned}$$

(4)

Here is the resulting scheme.

• $\mathtt {SETUP}(1^\kappa )$ . Given a security parameter $\kappa$, $\mathtt {SETUP}$ generates an RSA modulus $N = pq$ where p and q are prime. It also selects an element $u \in \mathbb {J}_N\setminus \mathbb {QR}_N$ and a global integer d. The public system parameters are $\mathsf {mpk}= \{N, u, d,\mathcal {H}_d\}$ where $\mathcal {H}_d$ is a cryptographic hash function as per Eq. (4). The master secret key is $\mathsf {msk}= \{p,q\}$.

• $\mathtt {EXTRACT}_\mathsf {msk}(\mathsf {id})$ . Given identity $\mathsf {id}$, algorithm $\mathtt {EXTRACT}$ sets $R_\mathsf {id}= \mathcal {H}_d(\mathsf {id})$. Then if $R_\mathsf {id}\in \mathbb {QR}_N$ it computes $r_\mathsf {id}= {R_\mathsf {id}}^{1/2}\,\mathrm{{mod}}\,N$; otherwise it computes $r_\mathsf {id}= (uR_\mathsf {id})^{1/2} \,\mathrm{{mod}}\,N$. $\mathtt {EXTRACT}$ returns user’s private key $\mathsf {usk}=\{r_\mathsf {id}\}$.

• $\mathtt {ENCRYPT}_{\mathsf {mpk}}(\mathsf {id},m)$ . To encrypt a message $m \in \{\pm 1\}$ for a user with identity $\mathsf {id}$, $\mathtt {ENCRYPT}$ defines $R_\mathsf {id}= \mathcal {H}_d(\mathsf {id})$. It chooses at random $t, \bar{t} \in \mathbb {Z}/N\mathbb {Z}$ such that $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{t}}}{{N}} \right) \mathclose {}} = m$ and lets

  $$\begin{aligned} c^{(0)}= & {} t + \frac{R_\mathsf {id}}{t} \,\mathrm{{mod}}\,N\,,\quad c^{(1)} = \frac{c^{(0)}d + 4R_\mathsf {id}}{c^{(0)}+d} \,\mathrm{{mod}}\, N\,,\\ \bar{c}^{(0)}= & {} \bar{t} + \frac{uR_\mathsf {id}}{\bar{t}} \,\mathrm{{mod}}\, N\,,\quad \bar{c}^{(1)} = \frac{\bar{c}^{(0)}d + 4uR_\mathsf {id}}{\bar{c}^{(0)}+d} \,\mathrm{{mod}}\, N. \end{aligned}$$

  It chooses random bits $\beta _1,\beta _2 \in \{0,1\}$ and sets $c = c^{(\beta _1)}$ and $\bar{c} = \bar{c}^{(\beta _2)}$. The returned ciphertext is $C = (c,\bar{c})$.

• $\mathtt {DECRYPT}_{\mathsf {usk}}(C)$ Let $R_\mathsf {id}= \mathcal {H}_d(\mathsf {id})$ . From $\mathsf {usk}= \{r_\mathsf {id}\}$ and $C = (c,\bar{c})$, if ${r_\mathsf {id}}^2 \equiv R_\mathsf {id}(\hbox {mod}\,N)$, $\mathtt {DECRYPT}$ sets $\gamma = c$ and $\varDelta = R_\mathsf {id}$; otherwise it sets $\gamma = \bar{c}$ and $\varDelta = uR_\mathsf {id}$. Next, it computes $\sigma = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\gamma ^2 -4\varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\gamma ^2 -4\varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\gamma ^2 -4\varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\gamma ^2 -4\varDelta }}{{N}} \right) \mathclose {}}$. Finally, it returns plaintext m as

  $$\begin{aligned} m = {\left\{ \begin{array}{ll} \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\gamma +2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\gamma +2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\gamma +2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\gamma +2r_\mathsf {id}}}{{N}} \right) \mathclose {}} &{} \text {if }\sigma = 1\,,\\ \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{(\gamma +2r_\mathsf {id})(d - 2r_\mathsf {id})(d - \gamma )}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{(\gamma +2r_\mathsf {id})(d - 2r_\mathsf {id})(d - \gamma )}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{(\gamma +2r_\mathsf {id})(d - 2r_\mathsf {id})(d - \gamma )}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{(\gamma +2r_\mathsf {id})(d - 2r_\mathsf {id})(d - \gamma )}}{{N}} \right) \mathclose {}} &{} \text {if }\sigma = -1. \end{array}\right. } \end{aligned}$$

Remark 7

The choice $p \equiv -q\,(\hbox {mod}\,4)$ (or equivalently $N \equiv 3\,(\hbox {mod}\,4)$) simplifies the setting. In this case, we know that $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{-1}}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{-1}}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{-1}}{{p}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{-1}}{{p}} \right) \mathclose {}} = -\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{-1}}{{q}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{-1}}{{q}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{-1}}{{q}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{-1}}{{q}} \right) \mathclose {}}$ and therefore $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{-1}}{{N}} \right) \mathclose {}} = -1$. A nice observation is that $d = 0$ is a valid parameter when $N \equiv 3\,(\hbox {mod}\,4)$ since then $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{{d}^2 - 4\mathcal {H}(\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{{d}^2 - 4\mathcal {H}(\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{{d}^2 - 4\mathcal {H}(\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{{d}^2 - 4\mathcal {H}(\mathsf {id})}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{{d}^2 - 4u\mathcal {H}(\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{{d}^2 - 4u\mathcal {H}(\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{{d}^2 - 4u\mathcal {H}(\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{{d}^2 - 4u\mathcal {H}(\mathsf {id})}}{{N}} \right) \mathclose {}} = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{-1}}{{N}} \right) \mathclose {}} = -1$ as desired. Any cryptographic hash function $\mathcal {H}$ mapping bit-strings to $\mathbb {J}_N$ can be used.

6.3 Security Analysis

The two next propositions assess the security of the scheme under the quadratic residuosity assumption.

Proposition 3

The scheme of Sect. 6.2 is $\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$ under the quadratic residuosity assumption in the random oracle model.

Proof

Assume there exists an $\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$ adversary $\mathcal {A}$ against the previous scheme (Sect. 6.2). We can then use $\mathcal {A}$ to break the semantic security of the generalized Cocks’ scheme (Sect. 3.1), which in turn will contradict the quadratic residuosity assumption. This is readily verified by observing that if $C = (c,\bar{c})$ is a valid ciphertext for the scheme of Sect. 3.1 for some user i with identity $\mathsf {id}$ then $C' = (c',\bar{c}')$ is a valid ciphertext for the scheme of Sect. 6.2, where $c' = c$ with probability 1/2 and $c' = \frac{cd + 4R_\mathsf {id}}{c+d} \,\mathrm{{mod}}\, N$ with probability 1/2 and, likewise, $\bar{c}' = \bar{c}$ with probability 1/2 and $\bar{c}' = \frac{\bar{c}d + 4R_\mathsf {id}}{\bar{c}+d} \,\mathrm{{mod}}\, N$ with probability 1/2.   $\square$

Before proving that the scheme is anonymous, we need the following lemma.

Lemma 2

Let $\mathop {\mathsf {RSAgen}}$ be a probabilistic algorithm which, given a security parameter $\kappa$, outputs primes p and q and their product $N = pq$. Let also $\delta$ be a random element in $(\mathbb {Z}/N\mathbb {Z})^\times$ and $\varDelta = {\delta }^2 \,\mathrm{{mod}}\, N$. Then, under the quadratic residuosity assumption,

$$\begin{aligned} \left| \hbox {Pr}\bigl [\mathcal {D}(x,\varDelta ,N)=1 \mid x \mathop {\leftarrow }\limits ^{R}(\widehat{\mathcal {Z}}_{N,\varDelta })^2\bigr ] - \hbox {Pr}\bigl [\mathcal {D}(x,\varDelta ,N)=1 \mid x \mathop {\leftarrow }\limits ^{R}\widehat{\mathcal {Z}}_{N,\varDelta }^{[+1]}\setminus (\widehat{\mathcal {Z}}_{N,\varDelta })^2\bigr ] \right| \end{aligned}$$

is negligible for any probabilistic polynomial-time distinguisher $\mathcal {D}$; the probabilities are taken over the experiment of running $(N,p,q) \leftarrow \mathop {\mathsf {RSAgen}}(1^\kappa )$, sampling $\delta \mathop {\leftarrow }\limits ^{R}(\mathbb {Z}/N\mathbb {Z})^\times$, and choosing at random $x \in (\widehat{\mathcal {Z}}_{N,\varDelta })^2$ and $x \in \widehat{\mathcal {Z}}_{N,\varDelta }^{[+1]}\setminus (\widehat{\mathcal {Z}}_{N,\varDelta })^2$.

Proof

As previously shown in Sect. 6.1, we have that $(\widehat{\mathcal {Z}}_{N,\varDelta })^2 = \mathscr {S}_{N,\varDelta }$ (i.e., the set of all valid components of Cocks ciphertexts). The lemma now follows as an immediate application of [2, Lemma 2].   $\square$

Proposition 4

The scheme Sect. 6.2 is $\mathsf {ANO}$-$\mathsf {ID}$-$\mathsf {CPA}$ under the quadratic residuosity assumption in the random oracle model.

Proof

As mentioned in Sect. 2.2, since the scheme is already known to be $\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$, it suffices to prove that the statistical distance between the two distributions

$$\begin{aligned} D_0 = \bigl \{ (\mathsf {id}^*_0, \mathsf {id}^*_1, \mathtt {ENCRYPT}_{\mathsf {mpk}}(\mathsf {id}^*_0,m)) \mid m \mathop {\leftarrow }\limits ^{R}\{\pm 1\}\bigr \} \end{aligned}$$

and

$$\begin{aligned} D_1 = \bigl \{ (\mathsf {id}^*_0, \mathsf {id}^*_1, \mathtt {ENCRYPT}_{\mathsf {mpk}}(\mathsf {id}^*_1, m)) \mid m \mathop {\leftarrow }\limits ^{R}\{\pm 1\}\bigr \} \end{aligned}$$

is negligible. In our case, a ciphertext encrypted for identity $\mathsf {id}^*_b$ (with $b \in \{0,1\}$) is of the form $C_b = (c_b, \bar{c}_b)$. From Lemma 1, only the valid component can help in distinguishing $D_0$ from $D_1$. Without loss of generality, we assume that $\mathcal {H}(\mathsf {id}^*_0) = \mathcal {H}(\mathsf {id}^*_1) \in \mathbb {QR}_N$. Letting $\varDelta _b = \mathcal {H}(\mathsf {id}^*_b)$, the valid component is then

$$\begin{aligned} c_b := c_b^{(0)} = t+\frac{\varDelta _b}{t} \,\mathrm{{mod}}\, N \quad \text {or}\quad c_b := c_b^{(1)} = \frac{c_b^{(0)}d + 4\varDelta _b}{c_b^{(0)}+d} \,\mathrm{{mod}}\, N \end{aligned}$$

where $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t}}{{N}} \right) \mathclose {}} = m$.

Omitting $\mathsf {id}^*_0, \mathsf {id}^*_1$ to ease the reading, the above criterion requires that the distributions $D_0 = \{ c_0^{(\beta )} \mid \beta \mathop {\leftarrow }\limits ^{R}\{0,1\}\}$ and $D_1 = \{ c_1^{(\beta )} \mid \beta \mathop {\leftarrow }\limits ^{R}\{0,1\}\}$ —or equivalently rescaling by a factor of two, that the distributions

$$\begin{aligned} D_0^* = \bigl \{ \tfrac{c_0^{(\beta )}}{2} \mid \beta \mathop {\leftarrow }\limits ^{R}\{0,1\}\bigr \} \quad \text {and}\quad D_1^* = \bigl \{ \tfrac{c_1^{(\beta )}}{2} \mid \beta \mathop {\leftarrow }\limits ^{R}\{0,1\}\bigr \} \end{aligned}$$

must be indistinguishable with overwhelming probability. Using the $\circledast$ operator, the elements of $D_b^*$ (for $b \in \{0,1\}$) are

$$\begin{aligned} \tfrac{c_b^{(\beta )}}{2} = {\left\{ \begin{array}{ll} \frac{1}{2}\bigl (t + \frac{\varDelta _b}{t}\bigr ) = \frac{t^2 + \varDelta _b}{2t} = t \circledast t &{} \text {when }\beta = 0\\ \frac{1}{2}\bigl (\frac{c_b^{(0)}d + 4\varDelta _b}{c_b^{(0)}+d}\bigr ) = \frac{\frac{c_b^{(0)}}{2}\frac{d}{2} + \varDelta _b}{\frac{c_b^{(0)}}{2} + \frac{d}{2}} = \tfrac{c_b^{(0)}}{2} \circledast \tfrac{d}{2} = (t \circledast t) \circledast \tfrac{d}{2} &{} \text {when }\beta = 1 \end{array}\right. } \end{aligned}$$

where $t \mathop {\leftarrow }\limits ^{R}\{ t \in (\mathbb {Z}/N\mathbb {Z})^\times \mid \gcd (t^2 - \varDelta _b, N) = 1\}$. Hence, we can see that

$$\begin{aligned} D_b^* = {\left\{ \begin{array}{ll} \, \bigl \{ u \mid u \mathop {\leftarrow }\limits ^{R}(\widehat{\mathcal {Z}}_{N,\varDelta _b})^2 \bigr \} \mathop {\equiv }\limits ^{c}\bigl \{ u \mid u \mathop {\leftarrow }\limits ^{R}\widehat{\mathcal {Z}}_{N,\varDelta _b}^{[+1]} \bigr \}&{} \text {when }\beta = 0\\ \, \bigl \{ u \mid u \mathop {\leftarrow }\limits ^{R}\widehat{\mathcal {Z}}_{N,\varDelta _b}^{[-1]}\bigr \} &{} \text {when }\beta = 1 \end{array}\right. }. \end{aligned}$$

The first assertion (when $\beta = 0$) follows from Lemma 2 (the notation $\mathop {\equiv }\limits ^{c}$ means computationally equivalent —under the $\mathsf {QR}$ assumption in this case). The second assertion (when $\beta =1$) follows by noting that the Jacobi symbol $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{{\frac{{d}^{\!2}}{4}} - {\varDelta _b}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{{\frac{{d}^{\!2}}{4}} - {\varDelta _b}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{{\frac{{d}^{\!2}}{4}} - {\varDelta _b}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{{\frac{{d}^{\!2}}{4}} - {\varDelta _b}}}{{N}} \right) \mathclose {}} = -1$ and thus $\tfrac{d}{2} \in \widehat{\mathcal {Z}}_{N,\varDelta _b}^{[-1]}$.

As a consequence, under the $\mathsf {QR}$ assumption, the distribution $D_b^*$ appears indistinguishable from the uniform distribution over $\widehat{\mathcal {Z}}_{N,\varDelta _b}^{[+1]} \cup \widehat{\mathcal {Z}}_{N,\varDelta _b}^{[-1]} = \widehat{\mathcal {Z}}_{N,\varDelta _b}$. This concludes the proof by noting that $D_0^*$ and $D_1^*$ are essentially the same sets: any random element is $D_0^*$ is also an element in $D_1^*$, and vice-versa.   $\square$

Altogether, this proves that the scheme achieves $\mathsf {ANO}$-$\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$ under the quadratic residuosity assumption in the random oracle model.

7 Conclusion

Somewhat surprisingly, we identified and detailed the algebraic group structure underlying Cocks encryption. The knowledge of this structure gives a better understanding of Cocks’ scheme and allows one to see it differently. In particular, the hidden homomorphism opens the way to applications that were before not readily available or possible with Cocks’ scheme, including homomorphic computations or anonymous encryption.

Appendices

A Proof of Proposition 1

Let $\mathcal {A}=(\mathcal {A}_1,\mathcal {A}_2)$ be adversary that can break the $\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$ security of the generalized scheme described in Sect. 3.1 with probability $\epsilon$. We will use $\mathcal {A}$ to decide whether a random element w in $\mathbb {J}_N$ is quadratic residue modulo N or not.

1.1 A.1 First Case: u Is Universally Fixed

The first case assumes that system parameter u is a universally fixed parameter. It covers the original Cocks’ scheme wherein $p, q \equiv 3 \,(\hbox {mod}\,4)$ and $u = -1 \in \mathbb {J}_N \setminus \mathbb {QR}_N$.

Let $\mathcal {H}:\{0,1\}^* \rightarrow \mathbb {J}_N$ be a hash function viewed as a random oracle. Consider the following distinguisher² $\mathcal {D}(w,u,N)$ for solving the $\mathsf {QR}$ problem. The goal of $\mathcal {D}$ is to distinguish a random element $w \in \mathbb {QR}_N$ from a random element $w \in \mathbb {J}_N\setminus \mathbb {QR}_N$.

• 1. Set $\mathsf {mpk}= \{N,u,\mathcal {H}\}$, and give $\mathsf {mpk}$ to $\mathcal {A}_1^{\mathtt {EXTRACT}_{\mathsf {msk}}(\cdot ), \mathcal {H}(\cdot )}$ —$\mathcal {A}_1$ has oracle access to $\mathtt {EXTRACT}_{\mathsf {msk}}(\cdot )$ and $\mathcal {H}(\cdot )$, it may issue a number of extraction and hash queries, after what it selects a target identity $\mathsf {id}^*$;

• 2. Depending on $\mathsf {id}^*$:

  • (a) If $\mathcal {H}(\mathsf {id}^*) = w$ then

    • i. Choose a random bit $b \in \{0,1\}$, let $R_{\mathsf {id}^*} = \mathcal {H}(\mathsf {id}^*)$, and compute the encryption of $(-1)^b$ as $C_b = (c_b, \bar{c}_b)$ where

      $$\begin{aligned} c_b = t + \frac{R_{\mathsf {id}^*}}{t} \,\mathrm{{mod}}\, N\,,\quad \bar{c}_b = \bar{t} + \frac{uR_{\mathsf {id}^*}}{\bar{t}} \,\mathrm{{mod}}\, N\,, \end{aligned}$$

      for some random elements $t, \bar{t} \in \mathbb {Z}/N\mathbb {Z}$ such that $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t}}{{N}} \right) \mathclose {}} = (-1)^b$ and $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{t}}}{{N}} \right) \mathclose {}} = (-1)^{1-b}$;

    • ii. Give s and $C_b = (c_b,\bar{c}_b)$ to $\mathcal {A}_2^{\mathtt {EXTRACT}_{\mathsf {msk}}(\cdot ),\mathcal {H}(\cdot )}$ —$\mathcal {A}_2$ may issue more extraction and hash queries, after what it returns its guess $b'$;

    • iii. If $b'=b$ return 1; otherwise return 0.

  • (b) If $\mathcal {H}(\mathsf {id}^*) \ne w$ then

    • i. Choose a random bit $b' \in \{0,1\}$;

    • ii. Return $b'$.

It remains to detail how $\mathcal {D}$ simulates answers to oracle queries. $\mathcal {D}$ maintains a history list $\mathsf {Hist}[\mathcal {H}]$ composed of triplets. The list is initialized to $\emptyset$. It also maintains a counter k initialized to 0. Let $q_{H_1}$ denote the number of hash queries that are not followed by extract queries and let $q_{E_1}$ denote the number of extract queries, made by $\mathcal {A}_1$. Without loss of generality, we assume that $\mathcal {A}_1$ issues a hash query on $\mathsf {id}^*$. Finally, we let $k_1$ denote a random integer in $\{1, \cdots , q_{H_1}+q_{E_1}\}$ chosen by $\mathcal {D}$.

• Hash Queries. When $\mathcal {A}$ queries oracle $\mathcal {H}$ on some $\mathsf {id}$, $\mathcal {D}$ checks whether there is an entry of the form $(\mathsf {id}, h, r)$ in $\mathsf {Hist}[\mathcal {H}]$; i.e., a triplet with $\mathsf {id}$ as the first component. If so, it returns h. Otherwise, it does the following:

  • 1. Increment k;

  • 2. Depending on k:

    • (a) If $k = k_1$, define $h = w$ and append $(\mathsf {id},h,\bot )$ to $\mathsf {Hist}[\mathcal {H}]$;

    • (b) Else (if $k \ne k_1$), define $h = u^{-j}\,r^2 \,\mathrm{{mod}}\, N$ with $r \mathop {\leftarrow }\limits ^{R}(\mathbb {Z}/N\mathbb {Z})^\times$ and $j\mathop {\leftarrow }\limits ^{R}\{0,1\}$ and append $(\mathsf {id}, h, r)$ to $\mathsf {Hist}[\mathcal {H}]$;

  • 3. Return h.

• Extraction Queries. When $\mathcal {A}$ queries oracle $\mathtt {EXTRACT}$ on some $\mathsf {id}$, $\mathcal {D}$ checks whether there is an entry of the form $(\mathsf {id}, h, r)$ in $\mathsf {Hist}[\mathcal {H}]$. If not, it calls $\mathcal {H}(\mathsf {id})$ so that there is an entry. Let $(\mathsf {id}, h, r)$ denote the entry in $\mathsf {Hist}[\mathcal {H}]$ corresponding to $\mathsf {id}$. Depending on it, $\mathcal {D}$ does the following:

  • 1. If $r \ne \bot$ then return r;

  • 2. If $r = \bot$ then abort.

We now analyze the success probability of $\mathcal {D}$ in solving the $\mathsf {QR}$ challenge. Since u is an element in $\mathbb {J}_N \setminus \mathbb {QR}_N$, the resulting $\mathsf {mpk}$ appear as valid system parameters. Three subcases can be distinguished.

• Subcase i. The first subcase supposes $w = \mathcal {H}(\mathsf {id}^*) \in \mathbb {QR}_N$. The condition $w = \mathcal {H}(\mathsf {id}^*)$ requires that $\mathsf {id}^*$ is the $k_1$-th query to $\mathcal {H}$. Further, since $\mathcal {H}(\mathsf {id}^*) \in \mathbb {QR}_N$, Lemma 1 teaches that $C_b = (c_b, \bar{c}_b)$ is a valid ciphertext for b. Namely, component $c_b$ correctly decrypts to $(-1)^b$ and component $\bar{c}_b$ is of no use. Hence, $\mathcal {D}$ returns 1 exactly when $\mathcal {A}$ wins in the $\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$ game, provided that there is no abort. But since $\mathcal {A}$ is not allowed to submit $\mathsf {id}^*$ to $\mathtt {EXTRACT}$ (and so there is no abort when $\mathsf {id}^*$ is the $k_1$-th query), we get $\hbox {Pr}[\mathcal {D}(w,u,N) = 1 \mid w \in \mathbb {QR}_N \wedge w = \mathcal {H}(\mathsf {id}^*)] = \epsilon$.

• Subcase ii. The second subcase supposes $w = \mathcal {H}(\mathsf {id}^*) \in \mathbb {J}_N \setminus \mathbb {QR}_N$. Since $\mathcal {H}(\mathsf {id}^*) \in \mathbb {J}_N\setminus \mathbb {QR}_N$, Lemma 1 teaches that $C_b = (c_b, \bar{c}_b)$ is a valid ciphertext for $(-1)^{(1-b)}$ —it is worth noticing that $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{t}}}{{N}} \right) \mathclose {}} = (-1)^{1-b}$. Hence, $\mathcal {D}$ returns 1 exactly when $\mathcal {A}$ looses in the $\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$ game. We therefore get $\hbox {Pr}[\mathcal {D}(w,u,N) = 1 \mid w \in \mathbb {J}_N \setminus \mathbb {QR}_N \wedge w = \mathcal {H}(\mathsf {id}^*)] = 1-\epsilon$.

• Subcase iii. The last subcase supposes $w \ne \mathcal {H}(\mathsf {id}^*)$. In this case $\mathcal {D}$ returns a random bit, regardless of w. Therefore, we have $\hbox {Pr}[\mathcal {D}(w,u,N) = 1 \mid w \in \mathbb {QR}_N \wedge w \ne \mathcal {H}(\mathsf {id}^*)] = \hbox {Pr}[\mathcal {D}(w,u,N) = 1 \mid w \in \mathbb {J}_N \setminus \mathbb {QR}_N \wedge w \ne \mathcal {H}(\mathsf {id}^*)]~=~1/2$.

We so obtain:

$$\begin{aligned} \hbox {Pr}\bigl [\mathcal {D}&(w,u,N) = 1 \mid w \in \mathbb {QR}_N\bigr ]\\&= \hbox {Pr}\bigl [w = \mathcal {H}(\mathsf {id}^*)\bigr ]\cdot \hbox {Pr}\bigl [\mathcal {D}(w,u,N) = 1 \mid w \in \mathbb {QR}_N \wedge w = \mathcal {H}(\mathsf {id}^*)\bigr ]\\&\qquad {}+ \hbox {Pr}\bigl [w \ne \mathcal {H}(\mathsf {id}^*)\bigr ] \cdot \hbox {Pr}\bigl [\mathcal {D}(w,u,N) = 1 \mid w \in \mathbb {QR}_N \wedge w \ne \mathcal {H}(\mathsf {id}^*)\bigr ]\\&= \frac{1}{q_{H_1}}\cdot \epsilon + \left( 1-\frac{1}{q_{H_1}}\right) \cdot \frac{1}{2} = \frac{1}{2} + \frac{\epsilon - \frac{1}{2}}{q_{H_1}} \end{aligned}$$

and similarly,

$$\begin{aligned} \hbox {Pr}\bigl [\mathcal {D}(w,u,N) = 1 \mid w \in \mathbb {J}_N \setminus \mathbb {QR}_N\bigr ]&= \frac{1}{q_{H_1}}\cdot (1-\epsilon ) + \left( 1-\frac{1}{q_{H_1}}\right) \cdot \frac{1}{2}\\&= \frac{1}{2} + \frac{\frac{1}{2} - \epsilon }{q_{H_1}}. \end{aligned}$$

Putting all together, we get:

$$\begin{aligned} \left| \hbox {Pr}\bigl [\mathcal {D}(w,u,N) = 1 \mid w \in \mathbb {QR}_N\bigr ] - \hbox {Pr}\bigl [\mathcal {D}(w,u,N) = 1 \mid w \in \mathbb {J}_N\setminus \mathbb {QR}_N\bigr ]\right| = \frac{2}{q_{H_1}}\left| \epsilon - \frac{1}{2}\right| \end{aligned}$$

which must be negligible by the $\mathsf {QR}$ assumption. As a consequence, $|\epsilon - \tfrac{1}{2}|$ must be negligible, which means that the scheme is $\mathsf {IND}$-$\mathsf {ID}$-$\mathsf {CPA}$ secure under the $\mathsf {QR}$ assumption.

1.2 A.2 Second Case: u Is Random

In this case, the proof can be obtained along the lines of the proof offered in [8, Appendix B.2] for the Boneh-Gentry-Hamburg scheme. The proof features a tight reduction. It however crucially requires that parameter u is defined as a random element in $\mathbb {J}_N\setminus \mathbb {QR}_N$.

B Arithmetic in $\mathcal {Z}_{N,\varDelta }$

As mentioned in Sect. 4.2, each element u of the group $\mathcal {Z}_{N,\varDelta } = \mathcal {F}_{\!p,\varDelta } \times \mathcal {F}_{\!q,\varDelta }$ can be uniquely represented by a pair $[u_p, u_q]$ with $u_p \in \mathcal {F}_{\!p,\varDelta }$ and $u_q \in \mathcal {F}_{\!q,\varDelta }$, and $\infty = [\infty _p, \infty _q]$. There is a slight complication when doing arithmetic in $\mathcal {Z}_{N,\varDelta }$ as we need to deal with the elements of the form $[u_p, \infty _q]$ or $[\infty _p, u_q]$. This can be circumvented by adopting a projective representation. An element $u \in \mathcal {Z}_{N,\varDelta }$ can be written as a pair (U : Z). We say that two elements $u = (U:Z)$ and $u'=(U':Z')$ are equivalent if there exists some $\lambda \in (\mathbb {Z}/N\mathbb {Z})^\times$ such that $U' = \lambda U$ and $Z' = \lambda Z$. Hence, from the definition of $\psi ^{-1}$, we can represent $\mathcal {Z}_{N,\varDelta }$ as

$$\begin{aligned} \mathcal {Z}_{N,\varDelta } = \bigl \{ (\delta (v+1) : v-1) \mid v \in (\mathbb {Z}/N\mathbb {Z})^\times \bigr \}. \end{aligned}$$

The neutral element is $\infty = (1:0)$. The inverse of an element (U : Z) is $(-U:Z)$. The product of two elements $(U_1:Z_1), (U_2,Z_2) \in \mathcal {Z}_{N,\varDelta }$ is given by

$$\begin{aligned} (U_1:Z_1) \circledast (U_2,Z_2) = (U_1 U_2 + \varDelta Z_1Z_2 : U_1Z_2 + U_2Z_1). \end{aligned}$$

Observe that the group law is complete with the projective representation: it works for all inputs.

Another way to deal with the elements of the form $[u_p, \infty _q]$ or $[\infty _p, u_q]$ is simply to ignore them and to work in the subset

$$\begin{aligned} \widetilde{\mathcal {Z}}_{N,\varDelta }&= \bigl ((\mathcal {F}_{\!p,\varDelta } \setminus \{\infty _p\}) \times (\mathcal {F}_{\!q,\varDelta } \setminus \{\infty _q\})\bigr ) \cup \{\infty \}\end{aligned}$$

(5)

$$\begin{aligned}&= \{ u \in \mathbb {Z}/N\mathbb {Z} \mid \gcd (u^2 - \varDelta , N) = 1 \} \cup \{\infty \}. \end{aligned}$$

(6)

wherever it is defined, the $\circledast$-law in $\widetilde{\mathcal {Z}}_{N,\varDelta }$ coincides with the group law on $\mathcal {Z}_{N,\varDelta }$:

$$\begin{aligned} u_1 \circledast u_2 = {\left\{ \begin{array}{ll} \frac{u_1u_2 + \varDelta }{u_1 + u_2} \,(\hbox {mod}\,N) &{} \text {if }u_1 \ne -u_2\\ \infty &{} \text {otherwise} \end{array}\right. }. \end{aligned}$$

(If $u_1 = \infty$ then $u_1 \circledast u_2 = u_2$; if $u_2 = \infty$ then $u_1 \circledast u_2 = u_1$.)

C Some Variants of Cocks’ Scheme

The $\mathbf{HOM}$ is dependent of the cryptosystem. We propose below some variants of Cocks’ scheme that leads to better efficiency. In particular, obtaining the encryption of the complementary value is almost free.

1.1 C.1 Basic Scheme

• $\mathtt {SETUP}(1^\kappa )$ . Given a security parameter $\kappa$, $\mathtt {SETUP}$ generates an RSA modulus $N = pq$ where p and q are prime. It also selects an element $u \in \mathbb {J}_N\setminus \mathbb {QR}_N$. The public system parameters are $\mathsf {mpk}= \{N, u, \mathcal {H}\}$ where $\mathcal {H}$ is a cryptographic hash function mapping bit-strings to $\mathbb {J}_N$; i.e., $\mathcal {H}: \{0,1\}^* \rightarrow \mathbb {J}_N$. The master secret key is $\mathsf {msk}= \{p,q\}$.

• $\mathtt {EXTRACT}_\mathsf {msk}(\mathsf {id})$ . Given identity $\mathsf {id}$, key derivation algorithm $\mathtt {EXTRACT}$ sets $R_\mathsf {id}= \mathcal {H}(\mathsf {id})$. If $R_\mathsf {id}\in \mathbb {QR}_N$ it computes $r_\mathsf {id}= {R_\mathsf {id}}^{1/2} \,\mathrm{{mod}}\,\mathbf N$; otherwise it computes $r_\mathsf {id}= (uR_\mathsf {id})^{1/2} \,\mathrm{{mod}}\, N$. $\mathtt {EXTRACT}$ returns user’s private key $\mathsf {usk}=\{r_\mathsf {id}\}$.

• $\mathtt {ENCRYPT}_{\mathsf {mpk}}(\mathsf {id},m)$ . To encrypt a message $m \in \{\pm 1\}$ for a user with identity $\mathsf {id}$, $\mathtt {ENCRYPT}$ defines $R_\mathsf {id}= \mathcal {H}(\mathsf {id})$. It chooses at random $t, \bar{t} \in \mathbb {Z}/N\mathbb {Z}$ and computes

  $$\begin{aligned} \varepsilon = m \cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t}}{{N}} \right) \mathclose {}}\,,c = t + \frac{R_\mathsf {id}}{t} \,\mathrm{{mod}}\, N\,,\bar{\varepsilon } = m \cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{t}}}{{N}} \right) \mathclose {}}\,,\bar{c} = \bar{t} + \frac{uR_\mathsf {id}}{\bar{t}} \,\mathrm{{mod}}\, N. \end{aligned}$$

  The returned ciphertext is $C = (\varepsilon , c, \bar{\varepsilon }, \bar{c})$.

• $\mathtt {DECRYPT}_{\mathsf {usk}}(C)$ From $\mathsf {usk}= \{r_\mathsf {id}\}$ and $C = (\varepsilon ,c,\bar{\varepsilon },\bar{c})$, if ${r_\mathsf {id}}^2 \equiv \mathcal {H}(\mathsf {id}) \,(\hbox {mod}\,N)$, $\mathtt {DECRYPT}$ sets $\nu = \varepsilon$ and $\gamma = c$; otherwise it sets $\nu = \bar{\varepsilon }$ and $\gamma = \bar{c}$. Next it computes $\tau = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\gamma + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\gamma + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\gamma + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\gamma + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}$ using secret key $r_\mathsf {id}$ and returns plaintext $m = \nu \cdot \tau$.

Homomorphic Computation. Let $C_1 = (\varepsilon _1,c_1,\bar{\varepsilon }_1,\bar{c}_1)$ and $C_2 = (\varepsilon _2, c_2,\bar{\varepsilon }_2,\bar{c}_2)$ be the respective encryption of messages $m_1$ and $m_2$ for a user with identity $\mathsf {id}$. Then, letting $R_\mathsf {id}= \mathcal {H}(\mathsf {id})$ and $\bar{R}_\mathsf {id}= u\cdot \mathcal {H}(\mathsf {id}) \,\mathrm{{mod}}\, N$, we get that $C_3 = (\varepsilon _3, c_3,\bar{\varepsilon }_3,\bar{c}_3)$ with

$$\begin{aligned} \varepsilon _3 = \varepsilon _1 \cdot \varepsilon _2 \cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{c_1 + c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{c_1 + c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{c_1 + c_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{c_1 + c_2}}{{N}} \right) \mathclose {}}\,,\quad c_3 = \frac{c_1 c_2 + 4R_\mathsf {id}}{c_1 + c_2} \,\mathrm{{mod}}\, N\,,\\ \bar{\varepsilon }_3 = \bar{\varepsilon }_1 \cdot \bar{\varepsilon }_2 \cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{c}_1 + \bar{c}_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{c}_1 + \bar{c}_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{c}_1 + \bar{c}_2}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{c}_1 + \bar{c}_2}}{{N}} \right) \mathclose {}}\,,\quad \text {and}\quad \bar{c}_3 = \frac{\bar{c}_1 \bar{c}_2 + 4\bar{R}_\mathsf {id}}{\bar{c}_1 + \bar{c}_2} \,\mathrm{{mod}}\, N \end{aligned}$$

is the encryption of message $m_3 = m_1 \cdot m_2$ (for the user with identity $\mathsf {id}$).

Complementary Encryption. Given the encryption of a message $m \in \{\pm 1\}$, it is easy to get the encryption of the complementary value. If $C = (\varepsilon , c,\bar{\varepsilon },\bar{c})$ is the encryption of $m \in \{\pm 1\}$ then $C' = (-\varepsilon ,c,-\bar{\varepsilon },\bar{c})$ is the encryption of $-m$.

1.2 C.2 Compact Variant

As an illustration, suppose that $R_\mathsf {id}= \mathcal {H}(\mathsf {id}) \in \mathbb {QR}_N$ in the previous scheme. If $C=(\varepsilon ,c)$ with $\varepsilon = m\cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t}}{{N}} \right) \mathclose {}}$ and $c = t + R_\mathsf {id}/t \,\mathrm{{mod}}\, N$ is a valid encryption for message $m \in \{\pm 1\}$ then so is $C' := (\varepsilon ', c')$ where $\varepsilon ' = \varepsilon \cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{-1}}{{N}} \right) \mathclose {}}$ and $c' = N-c$. Indeed, letting $t' = -t \,\mathrm{{mod}}\, N$, we have

$$\begin{aligned}&c' \equiv -c \equiv -\left( t + \frac{R_i}{t}\right) \equiv t' + \frac{R_i}{t'} \,(\hbox {mod}\,N) \quad \text {and}\\&\qquad \qquad \qquad \qquad \qquad \qquad \quad \varepsilon ' = m\cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t'}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t'}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t'}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t'}}{{N}} \right) \mathclose {}} = m\cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{-t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{-t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{-t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{-t}}{{N}} \right) \mathclose {}} = \varepsilon \cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{-1}}{{N}} \right) \mathclose {}}. \end{aligned}$$

One of the two equivalent ciphertexts $C = (\varepsilon ,c)$ and $C' = (\varepsilon ', c')$ is (at least) one bit shorter than the other one.

As a result, if $\ell$ represents the bit-length of RSA modulus N this allows reducing the size a whole ciphertext to at most $2\ell$ bits, as in Cocks’ scheme.

• $\mathtt {SETUP}(1^\kappa )$ . Given a security parameter $\kappa$, $\mathtt {SETUP}$ generates an RSA modulus $N = pq$ where p and q are prime. It also selects an element $u \in \mathbb {J}_N\setminus \mathbb {QR}_N$. The public system parameters are $\mathsf {mpk}= \{N, u, \mathcal {H}\}$ where $\mathcal {H}$ is a cryptographic hash function mapping bit-strings to $\mathbb {J}_N$; i.e., $\mathcal {H}: \{0,1\}^* \rightarrow \mathbb {J}_N$. The master secret key is $\mathsf {msk}= \{p,q\}$.

• $\mathtt {EXTRACT}_\mathsf {msk}(\mathsf {id})$ . Given identity $\mathsf {id}$, key derivation algorithm $\mathtt {EXTRACT}$ sets $R_\mathsf {id}= \mathcal {H}(\mathsf {id})$. If $R_\mathsf {id}\in \mathbb {QR}_N$ it computes $r_\mathsf {id}= {R_\mathsf {id}}^{1/2} \,\mathrm{{mod}}\, N$; otherwise it computes $r_\mathsf {id}= (uR_\mathsf {id})^{1/2} \,\mathrm{{mod}}\, N$. $\mathtt {EXTRACT}$ returns user’s private key $\mathsf {usk}=\{r_\mathsf {id}\}$.

• $\mathtt {ENCRYPT}_{\mathsf {mpk}}(\mathsf {id},m)$ . To encrypt a message $m \in \{\pm 1\}$ for a user with identity $\mathsf {id}$, $\mathtt {ENCRYPT}$ defines $R_\mathsf {id}= \mathcal {H}(\mathsf {id})$. It chooses at random $t, \bar{t} \in \mathbb {Z}/N\mathbb {Z}$ and computes

  $$\begin{aligned} \varepsilon ' = m \cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t}}{{N}} \right) \mathclose {}}\,,c' = t + \frac{R_\mathsf {id}}{t} \,\mathrm{{mod}}\, N\,,\bar{\varepsilon }' = m \cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{t}}}{{N}} \right) \mathclose {}}\,,\bar{c}' = \bar{t} + \frac{uR_\mathsf {id}}{\bar{t}} \,\mathrm{{mod}}\, N. \end{aligned}$$

  Define $c = \min (c', N - c')$ and $\bar{c} = \min (\bar{c}', N - \bar{c}')$. If $c = c'$ then define $\varepsilon = \varepsilon '$; otherwise define $\varepsilon = \varepsilon '\cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{-1}}{{N}} \right) \mathclose {}}$. Similarly, if $\bar{c} = \bar{c}'$ then define $\bar{\varepsilon } = \bar{\varepsilon }'$; otherwise define $\bar{\varepsilon } = \bar{\varepsilon }'\cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{-1}}{{N}} \right) \mathclose {}}$. The returned ciphertext is $C = (\varepsilon , c, \bar{\varepsilon }, \bar{c})$.

• $\mathtt {DECRYPT}_{\mathsf {usk}}(C)$ From $\mathsf {usk}= \{r_\mathsf {id}\}$ and $C = (\varepsilon ,c,\bar{\varepsilon },\bar{c})$, if ${r_\mathsf {id}}^2 \equiv \mathcal {H}(\mathsf {id}) \,(\hbox {mod}\,N)$, $\mathtt {DECRYPT}$ sets $\nu = \varepsilon$ and $\gamma = c$; otherwise it sets $\nu = \bar{\varepsilon }$ and $\gamma = \bar{c}$. Next it computes $\tau = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\gamma + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\gamma + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\gamma + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\gamma + 2r_\mathsf {id}}}{{N}} \right) \mathclose {}}$ using secret key $r_\mathsf {id}$ and returns plaintext $m =\nu \cdot \tau$.

Remark 8

Assuming that primes p and q satisfy the extra condition $p \equiv q \,(\hbox {mod}\,4)$ (for example if $N = pq$ is a Blum integer) —in which case $\mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{-1}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{-1}}{{N}} \right) \mathclose {}} = 1$— the encryption algorithm can then form the ciphertext $C = (\varepsilon , c, \bar{\varepsilon }, \bar{c})$ more simply by defining $\varepsilon = m\cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t}}{{N}} \right) \mathclose {}}$ and $\bar{\varepsilon } = m\cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{t}}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{t}}}{{N}} \right) \mathclose {}}$.

D Public-Key Encryption with Keyword Search

A prominent application of anonymous IBE scheme resides in public-key encryption with keyword search (or PEKS) [6]. Basically, PEKS is a form of encryption that allows searching on data that is encrypted using a public-key system. A typical application is for an email gateway to test whether or not the keyword “urgent” is present in an email. The gateway then routes the email if it is the case. Of course the gateway should only learn whether the word “urgent” is present but nothing else about the email. In the email use-case, another practical application is to test the sender’s name of the email and to route the emails accordingly. Further applications for PEKS can be found in [1, 6]. Of particular interest is the concept of temporarily searchable encryption [1, Sect. 6].

1.1 D.1 Definition

A public-key encryption with keyword search scheme [7] is defined as a tuple of four algorithms :

• Key Generation. The key generation algorithm $\mathtt {KEYGEN}$ is a randomized algorithm that takes as input some security parameter $1^\kappa$ and outputs a matching pair $(\mathsf {upk}, \mathsf {usk})$ of public key and private key: $(\mathsf {upk},\mathsf {usk}) \mathop {\leftarrow }\limits ^{R}\mathtt {KEYGEN}(1^\kappa )$.

• Public-Key Encryption With Keyword Search (PEKS). Let $\mathscr {W}$ denote the keyword space. The PEKS algorithm $\mathtt {PEKS}$ takes as input a public key $\mathsf {upk}$ and a keyword $w \in \mathscr {W}$, and returns a searchable ciphertext S. We write $S \leftarrow \mathtt {PEKS}_\mathsf {upk}(w)$.

• Trapdoor. The trapdoor algorithm $\mathtt {TRAPDOOR}$ takes as input the private key $\mathsf {usk}$ (corresponding to $\mathsf {upk}$) and a keyword w, and returns a trapdoor $T_w$ for keyword w. We write $T_w \leftarrow \mathtt {TRAPDOOR}_\mathsf {usk}(w)$.

• Test. The test algorithm $\mathtt {TEST}$ takes as input a searchable ciphertext S and a trapdoor $T_w$, and returns a bit b. A bit b with 1 means “accept” or “yes”, and a bit b with 0 means “reject” or “no”. We write $b \leftarrow \mathtt {TEST}(S,T_w)$.

It is required that $\mathtt {TEST}(\mathtt {PEKS}_\mathsf {upk}(w), \mathtt {TRAPDOOR}_\mathsf {usk}(w)) = 1$ for all keywords $w \in \mathscr {W}$.

1.2 D.2 Public-Key Encryption with Keyword Search from Quadratic Residuosity

In a PEKS scheme, a sender can send messages in encrypted form to a receiver so that the receiver can allow a designated proxy to search keywords in the encrypted messages without incurring any (additional) loss of privacy. In [6], Boneh et al. suggest the following methodology:

• The sender encrypts the message being sent with a (regular) public-key cryptosystem;

• She appends to the resulting ciphertext a PEKS for each keyword.

In more detail, to encrypt a message m with searchable keywords $w_1, \cdots , w_n$ for the receiver with public key $\mathsf {upk}$, the sender computes and sends

$$\begin{aligned} c = \mathtt {ENCRYPT}_\mathsf {upk}(m)\,,\quad S_1 = \mathtt {PEKS}_\mathsf {upk}(w_1)\,,\quad \dots \,,\quad S_n = \mathtt {PEKS}_\mathsf {upk}(w_n). \end{aligned}$$

The whole ciphertext is $C = \{c, S_1,\cdots , S_n\}$. Now if the receiver has given a proxy a trapdoor $T_{w_j}$ for keyword $w_j$ then this proxy can test whether the corresponding plaintext m contains the keyword $w_j$, but nothing more.

A conversion to turn an anonymous identity-based scheme (under certain conditions) into a PEKS scheme is developed in [6]. Some subsequent refinements are described in [1]. Applied to the scheme of Sect. 6.2 as a building block, we so obtain a PEKS scheme based on the quadratic residuosity. For slightly better efficiency, instead of verifying whether $x_i = \mu ^{-1}(\nu _i \cdot \tau _i)$ ($\in \{0,1\}$), for $0 \le i \le k-1$, the $\mathtt {TEST}$ algorithm equivalently verifies whether $\tau _i = \nu _i \cdot (1 - 2x_i)$. In detail, the scheme is as follows.

• $\mathtt {KEYGEN}(1^\kappa )$ . Given a security parameter $\kappa$, $\mathtt {KEYGEN}$ generates an RSA modulus $N = pq$ where p and q are prime. It defines a security parameter k depending on $\kappa$. It also selects an element $u \in \mathbb {J}_N\setminus \mathbb {QR}_N$ and a global integer d. The user’s public key is $\mathsf {upk}= \{N, k,u, d, \mathcal {H}_d\}$ where $\mathcal {H}_d$ is a cryptographic hash function mapping bit-strings to $\mathbb {J}_N$ as per Eq. (4). The user’s private key is $\mathsf {usk}= \{p,q\}$.

• $\mathtt {PEKS}_\mathsf {upk}(w)$ . To encrypt a keyword $w \in \{0,1\}^*$, $\mathtt {PEKS}$ selects a k-bit integer $x = \sum _{i=0}^{k-1} x_i2^i$ (with $x_i \in \{0,1\}$). It defines $R = \mathcal {H}_d(w)$. For $i = 0, \cdots , k-1$, it does the following:

  • 1. choose at random $t_i, \bar{t}_i \in \mathbb {Z}/N\mathbb {Z}$;

  • 2. let

    $$\begin{aligned}\textstyle \varepsilon _i = (-1)^{x_i} \, \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{t_i}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{t_i}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{t_i}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{t_i}}{{N}} \right) \mathclose {}}\,,{c_i}^{(0)} = t_i + \frac{R}{t_i} \,\mathrm{{mod}}\, N\,,{c_i}^{(1)} = \frac{{c_i}^{(0)}d + 4R}{{c_i}^{(0)}+d} \,\mathrm{{mod}}\, N\,,\\ \textstyle \bar{\varepsilon _i} = (-1)^{x_i} \, \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{t}_i}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{t}_i}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{t}_i}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{t}_i}}{{N}} \right) \mathclose {}}\,,{\bar{c}_i}^{(0)} = \bar{t}_i + \frac{uR}{\bar{t}_i} \,\mathrm{{mod}}\, N\,,{\bar{c}_i}^{(1)} = \frac{{\bar{c}_i}^{(0)}d + 4uR}{{\bar{c}_i}^{(0)}+d} \,\mathrm{{mod}}\, N\,; \end{aligned}$$

  • 3. choose random bits $\beta _{1,i},\beta _{2,i} \in \{0,1\}$ and set $c_i = {c_i}^{(\beta _{1,i})}$ and $\bar{c}_i = {\bar{c}_i}^{(\beta _{2,i})}$.

  $\mathtt {PEKS}$ returns the searchable ciphertext $S = \{x,\varepsilon _0, c_0, \bar{\varepsilon }_0, \bar{c}_0, \cdots , \varepsilon _{k-1}, c_{k-1},\bar{\varepsilon }_{k-1}, \bar{c}_{k-1}\}$.

• $\mathtt {TRAPDOOR}_\mathsf {usk}(w)$ Given keyword w, trapdoor algorithm $\mathtt {TRAPDOOR}$ sets $R = \mathcal {H}(w)$. If $R \in \mathbb {QR}_N$ it computes $T_w = {R}^{1/2}\,\mathrm{{mod}}\,$N; otherwise it computes $T_w = (uR)^{1/2} \,\mathrm{{mod}}\, N$. $\mathtt {TRAPDOOR}$ returns $T_w$.

• $\mathtt {TEST}(S,T_w)$ For keyword w, $\mathtt {TEST}$ uses the trapdoor $T_w$. Let $R = \mathcal {H}_d(w)$. Given a searchable ciphertext $S = \{x,\varepsilon _0, c_0, \bar{\varepsilon }_0, \bar{c}_0, \cdots , \varepsilon _{k-1}, c_{k-1}, \bar{\varepsilon }_{k-1}, \bar{c}_{k-1}\}$, if ${T_w}^2 \equiv R \,(\hbox {mod}\,N)$, $\mathtt {TEST}$ sets $\nu _i = \varepsilon _i$, $\gamma _i = c_i$ for $0\le i\le k-1$, and $\varDelta = R$; otherwise it sets $\nu _i = \bar{\varepsilon }_i$, $\gamma _i = \bar{c}_i$ for $0\le i\le k-1$, and $\varDelta = uR$. Next, for $i = 0, \cdots , k-1$, it does the following:

  • 1. set $\sigma _i = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{{\gamma _i}^2 -4\varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{{\gamma _i}^2 -4\varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{{\gamma _i}^2 -4\varDelta }}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{{\gamma _i}^2 -4\varDelta }}{{N}} \right) \mathclose {}}$;

  • 2. set

    $$\begin{aligned} \tau _i = {\left\{ \begin{array}{ll} \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\gamma _i + 2T_w}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\gamma _i + 2T_w}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\gamma _i + 2T_w}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\gamma _i + 2T_w}}{{N}} \right) \mathclose {}} &{} \text {if }\sigma _i = 1\\ \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{(\gamma _i + 2T_w)(d - 2T_w)(d - \gamma _i)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{(\gamma _i + 2T_w)(d - 2T_w)(d - \gamma _i)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{(\gamma _i + 2T_w)(d - 2T_w)(d - \gamma _i)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{(\gamma _i + 2T_w)(d - 2T_w)(d - \gamma _i)}}{{N}} \right) \mathclose {}} &{} \text {if }\sigma _i = -1 \end{array}\right. }\,; \end{aligned}$$

  • 3. set $b_i = 1$ if $\tau _i = \nu _i \cdot (1-2x_i)$; set $b_i = 0$ otherwise;

  $\mathtt {TEST}$ returns 1 if and only if $b_i = 1$ for all $0 \le i \le k-1$; and 0 otherwise.

E A Remark on Boneh-Gentry-Hamburg Abstract IBE System

Cocks’ scheme was subsequently revisited by Boneh, Gentry, and Hamburg [8]. The advantage of their scheme resides in the length of the ciphertexts. While the encryption of an $\ell$-bit message requires $2\ell \cdot \log _2N$ bits with Cocks’ scheme, ciphertext size in Boneh-Gentry-Hamburg scheme is about $\ell +\log _2N$ bits.

This section simplifies the abstract IBE system with short ciphertexts as presented in [8, Sect. 3].

1.1 E.1 Description

$\mathtt {SETUP}$ and $\mathtt {EXTRACT}$ are similar to Cocks’ scheme. $\mathtt {ENCRYPT}$ and $\mathtt {DECRYPT}$ require a deterministic algorithm $\mathcal {Q}$ taking as input an RSA modulus N and three elements $u, R, S \in \mathbb {Z}/N\mathbb {Z}$ and returning four IBE-compatible polynomials $f, g, \bar{f}, \tau \in \mathbb {Z}/N\mathbb {Z}[X]$. Polynomials $f,\bar{f}, g,\tau$ are said IBE-compatible if and only if the following conditions are met:

• c1. If $R, S \in \mathbb {QR}_N$ then $f(r)g(s) \in \mathbb {QR}_N$ for all square roots r of R and s of S;

• c2. If $R \in \mathbb {QR}_N$ then $f(r)f(-r)S \in \mathbb {QR}_N$ for all square roots r of R;

• c3. If $uR, S \in \mathbb {QR}_N$ then $\bar{f}(\bar{r})g(s)\tau (s) \in \mathbb {QR}_N$ for all square roots $\bar{r}$ of uR and s of S;

• c4. If $uR \in \mathbb {QR}_N$ then $\bar{f}(\bar{r})\bar{f}(-\bar{r})S \in \mathbb {QR}_N$ for all square roots $\bar{r}$ of uR;

• c5. If $S \in \mathbb {QR}_N$ then $\tau (s)\tau (-s)u \in \mathbb {QR}_N$ for all square roots s of S;

• c6. Polynomial $\tau$ is independent of R.

In more detail, the Boneh-Gentry-Hamburg scheme goes as follows.

• $\mathtt {SETUP}(1^\kappa )$ . Given a security parameter $\kappa$, $\mathtt {SETUP}$ generates an RSA modulus $N = pq$ where p and q are prime. It also generates a random element $u \in \mathbb {J}_N\setminus \mathbb {QR}_N$. The public system parameters are $\{N, u, \mathcal {H},\mathcal {Q}\}$ where $\mathcal {H}$ is a cryptographic hash function mapping bitstrings to $\mathbb {J}_N$. The master secret key is $\mathsf {msk}= \{p,q\}$.

• $\mathtt {EXTRACT}_\mathsf {msk}(\mathsf {id})$ . Using hash function $\mathcal {H}$, $\mathtt {EXTRACT}$ sets $R_\mathsf {id}= \mathcal {H}(\mathsf {id})$. If $R_\mathsf {id}\in \mathbb {QR}_N$ it computes $r_\mathsf {id}= {R_\mathsf {id}}^{1/2} \,\mathrm{{mod}}\, N$; otherwise it computes $r_\mathsf {id}= (uR_\mathsf {id})^{1/2} \,\mathrm{{mod}}\, N$. $\mathtt {EXTRACT}$ returns user’s private key $\mathsf {usk}= \{r_\mathsf {id}\}$.

• $\mathtt {ENCRYPT}(\mathsf {id}, m)$ . To encrypt a message $m \in \{\pm 1\}$ for user with identity $\mathsf {id}$, $\mathtt {ENCRYPT}$

• chooses at random $s \in \mathbb {Z}/N\mathbb {Z}$ and computes $S =s^2 \,\mathrm{{mod}}\, N$;

• runs $\mathcal {Q}(N,u,R_\mathsf {id},S)$ where $R_\mathsf {id}= \mathcal {H}(\mathsf {id})$ to obtain g and $\tau$;

• computes $k = \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\tau (s)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\tau (s)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\tau (s)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\tau (s)}}{{N}} \right) \mathclose {}}$;

• forms $w = m\cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{g(s)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{g(s)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{g(s)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{g(s)}}{{N}} \right) \mathclose {}}$;

• returns ciphertext $C = (S,k,w)$.

• $\mathtt {DECRYPT}(\mathsf {usk}, C)$ . To decrypt $C = (S,k,w)$, intended for user with identity $\mathsf {id}$, $\mathtt {DECRYPT}$ runs $\mathcal {Q}(N,u,R_\mathsf {id},S)$ to obtain f and $\bar{f}$. Plaintext m is then recovered as

  $$\begin{aligned} m = {\left\{ \begin{array}{ll} w\cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{f(r_\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{f(r_\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{f(r_\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{f(r_\mathsf {id})}}{{N}} \right) \mathclose {}} &{} \text {if }{r_\mathsf {id}}^2 \equiv R_\mathsf {id}\,(\hbox {mod}\,N)\\ w\cdot k\cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{f}(r_\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{f}(r_\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{f}(r_\mathsf {id})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{f}(r_\mathsf {id})}}{{N}} \right) \mathclose {}} &{} \text {otherwise} \end{array}\right. }, \end{aligned}$$

  using the user’s private key $\mathsf {usk}= \{r_\mathsf {id}\}$.

The correctness of the decryption follows from conditions c1–c6 imposed to polynomials $f,\bar{f},g,\tau$.

The encryption of an $\ell$-bit message $m = (m_1,m_2,\cdots ,m_\ell ) \in \{\pm 1\}^\ell$ proceeds broadly in the same way except that the user’s private key is now $\mathsf {usk}= \{r_{\mathsf {id},1}, r_{\mathsf {id},2}, \cdots , r_{\mathsf {id},\ell }\}$ where ${r_{\mathsf {id},j}}^2 \equiv R_{\mathsf {id},j} \,(\hbox {mod}\,N)$ if $R_{\mathsf {id},j} \in \mathbb {QR}_N$ and ${r_{\mathsf {id},j}}^2 \equiv uR_{\mathsf {id},j} \,(\hbox {mod}\,N)$ if $R_{\mathsf {id},j} \in \mathbb {J}_N\setminus \mathbb {QR}_N$, and where $R_{\mathsf {id},j} = \mathcal {H}(\mathsf {id},j)$ for $1\le j\le \ell$. In other words, identity $\mathsf {id}$ is hashed $\ell$ times so as to produce $\ell$ values $R_{\mathsf {id},j}$ for $1\le j\le \ell$. Now, each pair $(S,R_{\mathsf {id},j})$ (with the same S) is used to encrypt one message bit $m_j$; namely, $w_j = m_j\cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{g_j(s)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{g_j(s)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{g_j(s)}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{g_j(s)}}{{N}} \right) \mathclose {}}$ where $g_j$ is obtained by running $\mathcal {Q}(N,u,R_{\mathsf {id},j},S)$. By the last condition, polynomial $\tau$ is always the same for all values of $R_{\mathsf {id},j}$. The ciphertext corresponding to message $m = (m_1,m_2,\cdots ,m_\ell )$ is therefore given by $C = \{S,k, (w_1, w_2, \cdots , w_\ell )\}$. Plaintext message m is recovered from C bit-by-bit using private key $\mathsf {usk}= \{r_{\mathsf {id},1}, r_{\mathsf {id},2}, \cdots , r_{\mathsf {id},\ell }\}$ as $m_j = w_j\cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{f(r_{\mathsf {id},j})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{f(r_{\mathsf {id},j})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{f(r_{\mathsf {id},j})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{f(r_{\mathsf {id},j})}}{{N}} \right) \mathclose {}}$ if ${r_{\mathsf {id},j}}^2 \equiv R_{\mathsf {id},j} \,(\hbox {mod}\,N)$ and as $m_j = w_j\cdot k \cdot \mathchoice{\mathopen {}\left( \genfrac{}{}{1.0pt}0{{\bar{f}(r_{\mathsf {id},j})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}1{{\bar{f}(r_{\mathsf {id},j})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}2{{\bar{f}(r_{\mathsf {id},j})}}{{N}} \right) \mathclose {}}{\mathopen {}\left( \genfrac{}{}{1.0pt}3{{\bar{f}(r_{\mathsf {id},j})}}{{N}} \right) \mathclose {}}$ otherwise, for $1\le j\le \ell$.

1.2 E.2 A Simplified Abstract IBE

As described in the previous section, the abstract Boneh-Gentry-Hamburg system makes use of polynomials $f, \bar{f}, g, \tau \in \mathbb {Z}/N\mathbb {Z}[X]$. To simplify the notation, we consider one-bit messages but the discussion readily extends to $\ell$-bit messages, $\ell >1$.

We observe that polynomials f and $\bar{f}$ are evaluated at $r_\mathsf {id}$ and that polynomials g and $\tau$ are evaluated at s. Furthermore, we note that the values of $R_\mathsf {id}$ and of S are publicly known. So, letting $\delta$ denote the degree of polynomial f and $f(X) = \sum _{k=0}^\delta f_k \, X^k$ with $f_k \in \mathbb {Z}/N\mathbb {Z}$, we can write

$$\begin{aligned} f(r_\mathsf {id}) = \sum _{k=0}^\delta f_k \, {r_\mathsf {id}}^k = A \, r_\mathsf {id}+ B \,(\hbox {mod}\,N) \end{aligned}$$

(7)

where

$$\begin{aligned} A = \sum _{\begin{array}{c} 0 \le k \le \delta \\ k\text { odd} \end{array}} f_k\, {r_\mathsf {id}}^{(k-1)} = {\left\{ \begin{array}{ll} \displaystyle \sum _{\begin{array}{c} 0 \le k \le \delta \\ k \text { odd} \end{array}} f_k \, {R_\mathsf {id}}^{(k-1)/2} \,(\hbox {mod}\,N)&{} \begin{array}{@{}l@{}}\text {if } {r_\mathsf {id}}^2 \equiv {}\\ \quad R_\mathsf {id}\,(\hbox {mod}\,N)\end{array}\\ \displaystyle \sum _{\begin{array}{c} 0 \le k \le \delta \\ k \text { odd} \end{array}} f_k\, (uR_\mathsf {id})^{(k-1)/2} \,(\hbox {mod}\,N)&\text {otherwise} \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned} B = \sum _{\begin{array}{c} 0 \le k \le \delta \\ k\text { even} \end{array}} f_k\, {r_\mathsf {id}}^{k} = {\left\{ \begin{array}{ll} \displaystyle \sum _{\begin{array}{c} 0 \le k \le \delta \\ k\text { even} \end{array}} f_k\, {R_\mathsf {id}}^{k/2} \,(\hbox {mod}\,N)&{} \text {if }{r_\mathsf {id}}^2 \equiv R_\mathsf {id}\,(\hbox {mod}\,N)\\[2em] \displaystyle \sum _{\begin{array}{c} 0 \le k \le \delta \\ k\text { even} \end{array}} f_k\, (uR_\mathsf {id})^{k/2} \pmod {N}&\text {otherwise} \end{array}\right. }. \end{aligned}$$

There is therefore no loss of generality to consider degree-1 polynomials for f. The same conclusion holds for polynomials $\bar{f}$ (evaluated at $r_\mathsf {id}$), and for polynomials g and $\tau$ (evaluated at s).

As a result, we define $f(X) = f_1\,X+f_0$, $\bar{f}(X) = \bar{f}_1\,X + \bar{f}_0$, $g(X) = g_1\,X + g_0$, and $\tau (X) = \tau _1\,X + \tau _0$. These four polynomials returned by public algorithm $\mathcal {Q}$ must be IBE-compatible.

For example, given $R_\mathsf {id}$ and S, one can select parameters $f_0, f_1, g_0, g_1 \in \mathbb {Z}/N\mathbb {Z}$ such that

$$\begin{aligned} 2f_0g_0 \in \mathbb {QR}(N)\quad \text {and}\quad R_\mathsf {id}\,\bigl (\tfrac{f_1}{f_0}\bigr )^2 + S\,\bigl (\tfrac{g_1}{g_0}\bigr )^2 = 1 \pmod {N}. \end{aligned}$$

(8)

This ensures that compatibility conditions c1 and c2 are satisfied.

Proof

Multiplying the second equation through ${f_0}^2$ yields $S {f_0}^2(\tfrac{g_1}{g_0}\bigr )^2 = {f_0}^2 - R_\mathsf {id}{f_1}^2 = f(r_\mathsf {id})f(-r_\mathsf {id})$ for any square root $r_\mathsf {id}$ of $R_\mathsf {id}$. Consequently, we have $f(r_\mathsf {id})f(-r_\mathsf {id})S = \bigl (Sf_0\,\tfrac{g_1}{g_0}\bigr )^2 \in \mathbb {QR}(N)$. We also have $\bigl (r_\mathsf {id}\,\tfrac{f_1}{f_0} + s\,\tfrac{g_1}{g_0} + 1\bigr )^2 = R_\mathsf {id}\,\bigl (\tfrac{f_1}{f_0}\bigr )^2 + S\,\bigl (\tfrac{g_1}{g_0}\bigr )^2 + 1 + 2r_\mathsf {id}s\,\tfrac{f_1}{f_0}\tfrac{g_1}{g_0} + 2r_\mathsf {id}\,\tfrac{f_1}{f_0} + 2s\,\tfrac{g_1}{g_0} = \tfrac{2}{f_0g_0}(f_0g_0 + r_\mathsf {id}sf_1g_1 + r_\mathsf {id}f_1g_0 + sg_1f_0) = \tfrac{2}{f_0g_0}\,f(r_\mathsf {id})g(s)$ for any square root $r_\mathsf {id}$ of $R_\mathsf {id}$ and any square root s of S. Since $2f_0g_0 \in \mathbb {QR}(N)$, it thus follows that $f(r_\mathsf {id})g(s) = \tfrac{2f_0g_0}{4}\,\bigl (r_\mathsf {id}\,\tfrac{f_1}{f_0} + s\,\tfrac{g_1}{g_0} + 1\bigr )^2 \in \mathbb {QR}(N)$, as required.   $\square$

We also define polynomial $\bar{g} \in \mathbb {Z}/N\mathbb {Z}[X]$ given by $\bar{g}(X) = \bar{g}_1\,X + \bar{g}_0$ where $\bar{g}_1 = g_1\tau _0 + g_0\tau _1 \,\mathrm{{mod}}\, N$ and $\bar{g}_0 = g_1\tau _1S + g_0\tau _0 \,\mathrm{{mod}}\, N$. It is worth noticing that evaluated at s we have $\bar{g}(s) \equiv g(s)\tau (s) \pmod {N}$. Analogously, we require

$$\begin{aligned} 2\bar{f}_0\bar{g_0} \in \mathbb {QR}(N)\quad \text {and}\quad uR_\mathsf {id}\,\bigl (\tfrac{\bar{f}_1}{\bar{f}_0}\bigr )^2 + S\,\left( \tfrac{\bar{g}_1}{\bar{g}_0}\right) ^2 = 1 \pmod {N} \end{aligned}$$

(9)

so as to fulfill compatibility conditions c3 and c4. Compatibility conditions c5 and c6 are automatically satisfied from the product formula in [8, Lemma 5.1]. If $(f_0, f_1, g_0, g_1)$ is a solution to Eq. (8) and if $(\alpha ,\beta )$ is a solution to $u\alpha ^2 + S\beta ^2 = 1$ then $(\bar{f}_0, \bar{f}_1, \bar{g}_0, \bar{g}_1)$ is a solution to Eq. (9) provided that

$$\begin{aligned} \frac{\bar{f}_1}{\bar{f}_0} = \frac{\frac{f_1}{f_0}\alpha }{S\frac{g_1}{g_0}\beta + 1} \pmod {N} \quad \text {and}\quad \frac{\bar{g}_1}{\bar{g}_0} \mathop {\equiv }\limits ^{\text {def}} \frac{g_1\tau _0 + g_0\tau _1}{g_1\tau _1S+g_0\tau _0} \equiv \frac{\frac{g_1}{g_0} + \beta }{S\frac{g_1}{g_0}\beta +1} \pmod {N} \end{aligned}$$

(10)

with $2\bar{f}_0\bar{g_0} \in \mathbb {QR}(N)$.

The instantiation presented in [8, Sect. 4] corresponds to the choice $f_0 = 1$, $f_1 = x$, $g_0 = 2$, $g_1 = 2y$, $\bar{f}_0 = Sy\beta +1$, $\bar{f}_1 = x\alpha$, $\tau _0 = 1$ and $\tau _1 = \beta$, for some (x, y) satisfying $R_\mathsf {id}x^2 + Sy^2 = 1 \pmod {N}$ and $(\alpha ,\beta )$ satisfying $u\alpha ^2 + S\beta ^2=1 \pmod {N}$.