Abstract
Adaptively secure Multi-Party Computation (MPC) is an essential and fundamental notion in cryptography. In this work, we construct Universally Composable (UC) MPC protocols that are adaptively secure against all-but-one corruptions based on LWE. Our protocols have a constant number of rounds and communication complexity dependant only on the length of the inputs and outputs (it is independent of the circuit size).
Such protocols were only known assuming an honest majority. Protocols in the dishonest majority setting, such as the work of Ishai et al. (CRYPTO 2008), require communication complexity proportional to the circuit size. In addition, constant-round adaptively secure protocols assuming dishonest majority are known to be impossible in the stand-alone setting with black-box proofs of security in the plain model. Here, we solve the problem in the UC setting using a set-up assumption which was shown necessary in order to achieve dishonest majority.
The problem of constructing adaptively secure constant-round MPC protocols against arbitrary corruptions is considered a notorious hard problem. A recent line of works based on indistinguishability obfuscation construct such protocols with near-optimal number of rounds against arbitrary corruptions. However, based on standard assumptions, adaptively secure protocols secure against even just all-but-one corruptions with near-optimal number of rounds are not known. However, in this work we provide a three-round solution based only on LWE and NIZK secure against all-but-one corruptions.
In addition, Asharov et al. (EUROCRYPT 2012) and more recently Mukherjee and Wichs (ePrint 2015) presented constant-round protocols based on LWE which are secure only in the presence of static adversaries. Assuming NIZK and LWE their static protocols run in two rounds where the latter one is only based on a common random string. Assuming adaptively secure UC NIZK, proposed by Groth et al. (ACM 2012), and LWE as mentioned above our adaptive protocols run in three rounds.
Our protocols are constructed based on a special type of cryptosystem we call equivocal FHE from LWE. We also build adaptively secure UC commitments and UC zero-knowledge proofs (of knowledge) from LWE. Moreover, in the decryption phase using an AMD code mechanism we avoid the use of ZK and achieve communication complexity that does not scale with the decryption circuit.
This is an extended abstract. Further details can be found in the full version [DPR14].
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Adaptive Security
- Fully Homomorphic Encryption (FHE)
- Dishonest Majority Setting
- Setup Assumptions
- Equivocal Commitment
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Secure multi-party computation is an extremely strong and important tool for making distributed computing more secure. General solutions to the problem allows us to carry out any desired computation among a set of players, without compromising, the privacy of their inputs or the correctness of the outputs. This should even hold if some of the players have been corrupted by an adversary. An important issue in this connection is how the adversary chooses which players to target. In the static model, the adversary must choose who to corrupt before the protocol starts. A more general and also more realistic model is adaptive corruption where the adversary may corrupt new players during the protocol.
Of course efficiency of the protocol is also important, and important measures in this respect are the number of rounds we need to do, as well as the communication complexity (the total number of bits sent). Obviously, achieving a constant number of rounds and small communication complexity, while still getting the best possible security, is an important research goal.
Unconditionally secure protocols such as [BGW88] are typically adaptively secure. But these protocols are not constant round, and it is a major open problem if it is even possible to have unconditional security and constant number of rounds for secure computation of any function, see [DNP15] for a detailed discussion.
If we are willing to make computational assumptions, we can achieve constant round protocols, the first example of this is Yao’s garbled circuits for two players, but on the other hand this does not give us adaptive security. Another class of protocols based on Fully Homomorphic Encryption (FHE) also naturally leads to constant round protocols, where we can tolerate that a majority of players are corrupted. Here we also get low communication complexity, that depends only on the lenght of inputs and outputs. But again, these protocols achieve only static security (see for instance [Gen09, AJLA+12, LTV12]). More recently, the work of Mukherjee and Wichs [MW15] achieve a two-round static protocol assuming LWE and NIZK where additionally the protocol only assumes a random reference string (as opposed to being sampled form a specific distribution).
We can in fact get adaptive security in the computational setting, as shown in [CFGN96] by introducing the notion of Non-Commiting Encryption (NCE). Moreover, in [DN03], adaptive security was obtained as well, but much more efficiently using additively homomorphic encryption. However, neither [CFGN96] nor [DN03] run in a constant number of rounds.
If we assume honest majority we can get both constant round and adaptive security but the communication complexity will be propositional to the size of the evaluated circuit. This was shown in several papers [DI05, DI06, DIK+08, IPS08]. The idea here is to use an unconditionally secure protocol to compute, for instance, a Yao garbled circuit, that is then used to compute the desired function in a constant number of rounds. Since the computation leading to the Yao circuit is easy to parallelise, this can be constant round as well and we inherit adaptive security from the unconditionally secure “preprocessing”. On the other hand, as mentioned this requires communication that is proportional to the size of circuit to be securely evaluated. One may apply the IPS compiler to one of these protocols to get a solution for dishonest majority. This preserves the adaptive security and the constant number of rounds, but unfortunately also preserves the dependence of the communication complexity on the circuit size. Therefore, the question becomes:
Is it possible to construct constant round MPC protocols secure against an adaptive adversary that may corrupt all but one parties with communication complexity independent of the circuit size?
1.1 Contributions
We answer this in the affirmative. More specifically, we achieve an adaptive UC-secure protocol that tolerates corruption of \(n-1\) of the n players with UC secure composition with protocols secure against \(n-1\) corruptions. Our protocol requires a constant number of rounds and its communication complexity depends only on the length of inputs and outputs (and the security parameter), and not on the size of the evaluated circuit and the decryption circuit. The protocol is secure if the LWE problem is hard. Moreover, we do not consider the weaker model of secure erasures.
Theorem 1
(informal). Assuming hardness of LWE, we show that arbitrary functions can be UC-securely computed in the presence of adaptive, active corruption of all-but-one parties within a constant number of rounds.
Assuming adaptively secure UC NIZK, proposed by Groth et al. [GOS12], and LWE our adaptive protocols run in three rounds.
Theorem 2
(informal). Assuming hardness of LWE and the existence of adaptively secure UC NIZK, we show that arbitrary functions can be UC-securely computed in the presence of adaptive, active corruption of all-but-one parties in three rounds of broadcast.
In our construction we assume a broadcast channel where encryption is performed using what we call Equivocal FHE, a notion weaker than non-commiting encryption, presented in Sect. 3 which can be of independent interest. For example, using our equivocal scheme we also build adaptively secure UC commitment and UC zero-knowledge proofs (of knowledge) based on hardness of LWE (see Sect. 4).
Last but not least, in the standard ZK-based decryption used by approaches based on FHE, all the parties need to append a ZK proof, to prove that they decrypted correctly, whose communication complexity grows with the size of the decryption circuit. In this work using an AMD code mechanism [CDF+08] we avoid the use of ZK and achieve communication complexity that does not scale with the decryption circuit. In particular, the total communication complexity of the decryption phase of our concrete protocol is \(\mathcal {O}(n^2 \lambda )\) where \(\lambda \) is the security parameter.
1.2 Technical Difficulties and New Ideas
To construct our adaptively secure protocol, we start from the well known blue-print for FHE-based MPC: players encrypt their inputs under a common public key, evaluate the desired function locally and then jointly decrypt the result. This is possible under an appropriate set-up assumption, which is always needed for UC security and dishonest majority. Namely, we assume that a public key has been distributed, and players have been given shares of the corresponding secret key.
This approach has been used before and usually leads to static security. One reason for this is that encryptions are usually committing, so we are in trouble if the sender of a ciphertext is corrupted later. This can be solved using a cryptosystem with equivocal properties and this would mean that the input and the evaluation phase of the protocol can be simulated, even for adaptive corruptions. Players need, of course, to prove that they know the inputs they contribute, but this can be done once we construct constant round adaptively secure UC commitment and ZK proofs from LWE.
An important tool we would like to get in order to achieve constant-round adaptively secure MPC protocols may be a Fully Homomorphic Encryption (FHE) scheme with equivocal properties.
Starting Point – Fully Homomorphic NCE. It is tempting to consider a generic solution from FHE and Non-Commiting Encryption (NCE). In particular, in such a hypothetical construction, the secret key would be a secret key for an FHE scheme, the public key an FHE encryption of the NCE secret key and the NCE public key. Encryption would be performed using the NCE, and homomorphic evaluation and decryption would be performed as expected. However, there are fundamental caveats with this approach.
It does not seem to buy us any efficiency at all. In particular, NCE schemes are interactive, in that the receiver must send fresh (public-)key material for each new message to be encrypted. There is even a result by Nielsen saying that this is inherent for NCE [Nie02]. It will be hard for an interactive scheme to fit the above suggestion. Indeed, the public key material would run out after encrypting some number of inputs. Therefore, in generic NCE the public-key cannot be reused, and has to be updated for each new message. Moreover, one may go around this issue by having an NCE public-key for each party where the FHE encryption in the public key will include all the public keys. However, such a solution is highly inefficient since it is not the number of parties that matter but the amount of data to be encrypted. The amount of public-key material has to be proportional to size of the plaintext data. For instance, if only a constant number of parties had input, but a lot of, we would have a significant problem.
Another suggestion is to always regenerate this setup afresh using a constant round adaptive protocol prior to each new execution. This might work but unfortunately set-up data are considered reasonable if its size does not depend on the function to be computed (otherwise we are in the preprocessing model which is a completely different ball game). Hence, one would in fact always need this key regeneration step per execution.
It turns out that the motivation of considering NCE in this context is very weak.
Our Approach - Starting Afresh. Towards minimising the above caveat we propose a scheme we call Equivocal FHE. An equivocal FHE scheme is a fully homomorphic encryption scheme with additional properties. Most importantly, it is possible to generate “fake” public keys that look like normal keys but where encryption leads to ciphertexts that contain no information on the plaintext. This is similar to the known notion of meaningful/meaningless keys, but in addition we want that fake public keys come with a trapdoor that allows to “explain” (equivocate) a ciphertext as an encryption of any desired plaintext. This is similar to (but not the same as) what is required for NCE: for NCE one needs to equivocate a ciphertext even if the decryption key is also given (say, by corrupting the receiver), here we only need to give the adversary valid looking randomness for the encryption. In order to achieve such a cryptosystem the main properties we require from an FHE scheme is formula privacy, invertible sampling and homomorphishm over the randomness. Given this, we managed to obtain the required equivocation directly with much less overhead compared to a possible NCE solution.
We give a concrete instantiation of equivocal FHE based on LWE, starting from the FHE scheme by Brakerski et al. [BV11].
Adaptive UC Commitments and ZK from LWE. A second tool we need is constant-round UC-secure commitments and zero-knowledge proofs. For the commitments we start from a basic construction appeared in [CLOS02], which was originally based on claw-free trapdoor permutations (CFTP). We show that it can be instantiated based on LWE (which is not known to imply CFTP). Zero-knowledge then follows quite easily from known techniques.
Achieving a Simulatable Protocol. A harder problem is how to simulate the output phase in which ciphertexts containing the outputs are decrypted. In the simulation we cannot expect that these ciphertexts are correctly formed and hold the actual outputs, so the simulator needs to “cheat”. However, each player holds a share of the secret key which we have to give to the adversary if he is corrupted. If this happens after some executions of the decryption protocol, we (the simulator) may already be committed to this share. It is therefore not clear how the simulator can achieve the desired decryption results by adjusting the shares of the secret key. To get around this, we adapt an idea from Damgård and Nielsen [DN03], who proposed an adaptively secure protocol based on additively homomorphic threshold encryption but in the honest majority scenario. The idea is to add a step to the protocol where each ciphertext is re-randomised just before decryption. This gives the simulator a chance to cheat and turn the ciphertext into one that contains the correct result, and one can therefore simulate the decryption without having to modify the shares of the secret key. The re-randomisation from [DN03] only works for honest majority, we show a different method that works for dishonest majority and augment our Equivocal FHE scheme with the ciphertext randomisation property to achieve our goal.
General Purpose Equivocal FHE. We mention for completeness that there is also a more generic approach which will give us adaptive security based only on our Equivocal FHE: namely, we follow the same blueprint as before, with input, evaluation and output phases. However, we implement the verification of ciphertexts in the input phase and the decryptions in the output phase using generic adaptively secure MPC a la [CLOS02, IPS08]. This way, the communication and the number of rounds do not depend on the size of circuit to be computed securely. However, it would not be genuinely constant round, and the communication complexity would depend on the circuits computing the encryption and decryption functions of the underlying cryptosystem. Hence, unlike our protocol, any such solution would have communication complexity proportional to the Boolean circuit complexity of the decryption function (which seems inherent since one needs Yao garbling underneath). We measure the round and communication complexity of such a possible solution based on the IPS compiler. The bottom line is that using IPS generically would yield a larger (constant) number of rounds (20–30 rounds) and worse dependence on the security parameter. A concise estimate can be found in Appendix A. Clearly the above estimate should be taken with large grains of salt. We have tried to be optimistic on the part of IPS, to not give our concrete protocol an unfair advantage. Thus, actual numbers could be larger. On the other hand, we propose a three-round solution.
AMD Code Solution to Replace ZK. However, contrary to the above generic IPS solution, our approach allows for significant optimization of the decryption as follows. Instead of using ZK proofs to prove that the player’s evaluation shares to the decryption phase are correct, we change the evaluation phase of the protocol. In particular, instead of having ciphertexts containing the desired output z, the evaluation phase computes encryptions containing a codeword \(c=(z,\alpha )\) in an algebraic manipulation detection code, where z is the data and \(\alpha \) is the key/randomness. In the decryption stage, players commit to their decryption shares (recall that we have UC commitment available), and then all shares are opened. If decryption fails, or decoding the codeword fails, we abort, else we output the decoded z. If z and \(\alpha \) are thought of as elements in a (large) finite field, then the codeword can just be \((z, \alpha , \alpha z)\). According to our optimization, the communication complexity of our protocol is not only independent of the size of the evaluated circuit but also independent of the circuit size of the decryption circuit.
Impossibility Results? In the following we mention two impossibility results which apply to adaptively secure MPC and mention why they do not apply in our setting.
Motivated by ruling out one possible approach to achieving adaptive security, Katz et al. [KTZ13] showed that FHE with security against adaptive corruption of the receiver is impossible. In our setting, we distribute the private key of an FHE scheme among n parties; since we allow only \(n-1\) of the parties to be corrupted, the impossibility result from [KTZ13] does not apply. Note that if an FHE scheme is to be of use in MPC, it seems to be necessary that the players are able to decrypt, if not by themselves, then at least by collaborating. But if corruption of all n players was allowed, the adversary would necessarily learn all secret keys, and then the impossibility result from [KTZ13] would apply. This suggests that our result with \(n-1\) corruptions is the best we can achieve based only on FHE.
We note that in [GS12], adaptive security in constant number of rounds in the plain model was obtained using a non-blackbox proof in the stand-alone setting. Also a solution with a blackbox proof was shown to be impossible, but this does not, of course, apply to our case, where we go for UC security, and therefore require a set-up assumption.
Security Against Arbitrary Corruptions: Round complexity of all known adaptively secure protocols secure against n corruptions grows (see, e.g. [CLOS02, KO04, GS12, DMRV13]) linearly in the depth of the evaluated circuit. Recent independent works [GP15, CGP15, DKR15], have been shown that MPC protocols with security against n corruptions in a constant number of rounds can be achieved using indistinguishability obfuscation (IO) [GGH+13].
While the above results on constant round MPC using IO are exciting, the focus of this work is to avoid indistinguishability obfuscation altogether and to achieve adaptive security against corruption of \(n-1\) of the n players, (with communication complexity depended only on the length of inputs and outputs and not on the size of the circuit to be computed securely), using simpler tools with simple standard assumptions involving them. In particular, our construction only requires FHE based on the hardness of LWE and avoids the use of IO which also incurs a cost in efficiency. Also as we have already mentioned, our result with \(n-1\) corruptions is the best we can achieve based only on FHE.
Roadmap. In Sect. 3 we define our Equivocal fully homomorphic encryption scheme and its properties. A concrete instantiation based on the scheme of [BV11] is given in the full version. In Sect. 4 we give our construction for UC commitments and ZKPoK. Next in Sect. 5, we proceed by presenting our MPC protocol. The simulator and the security proof of our protocol can be found in the full version. In Sect. 6 we show how AMD codes can be used in order to avoid the use of ZK.
2 Notation
Throughout the paper \(\lambda \in \mathbb {N}\) will denote the security parameter. We use \(d \leftarrow \mathcal{D}\) to denote the process of sampling d from the distribution \(\mathcal{D}\) or, if \(\mathcal{D}\) is a set, a uniform choice from it. We say that a function \(f: \mathbb {N}\rightarrow \mathbb {R}\) is negligible if \(\forall c~ \exists n_c\) s.t. if \(n>n_c\) then \(f(n)< n^{-c}\). We will use \(\mathrm {negl}(\cdot )\) to denote an unspecified negligible function. We often use [n] to denote the set \(\{1,...,n\}\). We write \(\boxplus \) and \(\boxdot \) to denote operations over encrypted data including multiplication of a ciphertext with a non encrypted string. If \(\mathcal{D}_1\) and \(\mathcal{D}_2\) are two distributions, then we denote that they are statistically close by \(\mathcal{D}_1 \approx _{\mathrm {s}}\mathcal{D}_2\); we denote that they are computationally indistinguishable by \(\mathcal{D}_1 \approx _{\mathrm {c}}\mathcal{D}_2\); and we denote that they are identical by \( \mathcal{D}_1 \equiv \mathcal{D}_2\). For a randomized algorithm A, we use \(a \leftarrow A(x; r)\) to denote running A on input x and uniformly random bits \(r \in \{0, 1\}^*\), producing output a.
Invertible Sampling [OPW11]: We recall the notion of invertible sampling, which is closely connected to adaptive security in simulation models where erasures are not allowed. We say that an algorithm A with input space X has invertible sampling if there exists a PPT inverting algorithm, denoted by \(\mathsf {Inv}_A\), such that for all input \(x \in X\), the outputs of the following two experiments are either computationally, or statistically indistinguishable:

3 Equivocal Fully Homomorphic Encryption Scheme
We start by recalling the notions of (fully) homomorphic encryption. Next we define the new notion of Equivocal FHE and we specify the properties needed for such an instantiation. We give a concrete instantiation of our Equicocal FHE scheme from the LWE assumption, based on Brakerski and Vaikutanathan [BV11] FHE scheme, in the full version.
3.1 Homomorphic Encryption
A homomorphic encryption scheme \(\mathsf {HE}=(\mathsf {KeyGen},\mathsf {Enc},\mathsf {Eval}, \mathsf {Dec})\) is a quadruple of PPT algorithms. In this work, the message space \(M\) of the encryption schemes will be some (modulo 2) ring, and the functions to be evaluated will be represented as arithmetic circuits over this ring, composed of addition and multiplication gates. The syntax of these algorithms is given as follows.
-
Key-Generation. The algorithm \(\mathsf {KeyGen}\), on input the security parameter \(1^\lambda \), outputs \((\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {KeyGen}(1^{\lambda })\), where \(\mathsf {pk}\) is a public encryption key and \(\mathsf {sk}\) is a secret decryption key.
-
Encryption. The algorithm \(\mathsf {Enc}\), on input \(\mathsf {pk}\) and a message \(m \in M\), outputs a ciphertext \(\mathrm {ct}\leftarrow \mathsf {Enc}_{\mathsf {pk}}(m)\).
-
Decryption. The algorithm \(\mathsf {Dec}\) on input \(\mathsf {sk}\) and a ciphertext \(\mathrm {ct}\), outputs a message \(\tilde{m} \leftarrow \mathsf {Dec}_{\mathsf {sk}}(\mathrm {ct})\).
-
Homomorphic-Evaluation. The algorithm \(\mathsf {Eval}\), on input \(\mathsf {pk}\), an arithmetic circuit \(\mathrm {ckt}\), and a tuple of \(\ell \) ciphertexts \((\mathrm {ct}_1, \ldots ,\mathrm {ct}_\ell )\), outputs a ciphertext \(\mathrm {ct}' \leftarrow \mathsf {Eval}_{\mathsf {pk}}\big (\mathrm {ckt}(\mathrm {ct}_1, \ldots ,\mathrm {ct}_\ell )\big )\).
We note that we can treat the evaluation key as a part of the public key. The security notion needed in this work is security against chosen plaintext attacks (IND-CPA security), defined as follows.
Definition 1
(IND-CPA security). A scheme \(\mathsf {HE}\) is IND-CPA secure if for any PPT adversary \(\mathcal {A}\) it holds that:
where, \((\mathsf {pk},\mathsf {sk})\leftarrow \mathsf {KeyGen}(1^{\lambda })\).
3.2 Fully Homomorphic Encryption
A scheme \(\mathsf {HE}\) is fully homomorphic if it is both compact and homomorphic with respect to a class of circuits. More formally:
Definition 2
(Fully homomorphic encryption). A homomorphic encryption scheme \(\mathsf {FHE}=(\mathsf {KeyGen},\mathsf {Enc},\mathsf {Eval}, \mathsf {Dec})\) is fully homomorphic if it satisfies the following properties:
-
1.
Homomorphism: Let \(\mathcal { C}=\{ \mathcal { C}_{\lambda } \}_{\lambda \in \mathbb {N}}\) be the set of all polynomial sized arithmetic circuits. \( (\mathsf {sk},\mathsf {pk}) \leftarrow \mathsf {KeyGen}(1^{\lambda })\), \( \forall \mathrm {ckt}\in { \mathcal { C}}_{\lambda }\), \(\forall (m_1, \ldots , m_{\ell })\in M^\ell \) where \(\ell =\ell (\lambda )\), \(\forall (\mathrm {ct}_1,\dots ,\mathrm {ct}_\ell )\) where \(\mathrm {ct}_i \leftarrow \mathsf {Enc}_{\mathsf {pk}}(m_i)\), it holds that:
$$Pr [\mathsf {Dec}_{\mathsf {sk}}(\mathsf {Eval}_{\mathsf {pk}}(\mathrm {ckt}, \mathrm {ct}_1,\dots ,\mathrm {ct}_\ell )) \ne \mathrm {ckt}(m_1, \ldots , m_{\ell })] = \mathrm {negl}(\lambda )$$ -
2.
Compactness: There exists a polynomial \(\mu =\mu (\lambda )\) such that the output length of \(\mathsf {Eval}\) is at most \(\mu \) bits long regardless of the input circuit \(\mathrm {ckt}\) and the number of its inputs.
3.3 Equivocal Fully Homomorphic Encryption Scheme
Our Equivocal fully homomorphic encryption scheme consists of a tuple \((\mathsf {KeyGen}, \mathsf {KeyGen}^*,\mathsf {QEnc}, \mathsf {Rand}, \mathsf {Eval},\mathsf {Dec}, \mathsf {Equiv})\) of algorithms where the syntax of the procedures \((\mathsf {KeyGen},\mathsf {QEnc}, \mathsf {Eval},\mathsf {Dec})\) is defined as in the above \(\mathsf {FHE}\) scheme. Our scheme is augmented with two algorithms \((\mathsf {KeyGen}^*, \mathsf {Equiv})\) used for equivocation. Jumping ahead, in this paper we are interested in building adaptively secure n-party protocols generically using an equivocal \(\mathsf {QFHE}\) scheme and gain in terms of round and communication efficiency. Two extra properties needed for the MPC purpose, are distributed decryption and ciphertext randomisation where the latter one guarantees simulatable decryptionFootnote 1. If the purpose of our Equivocal scheme is not MPC then these properties are not required, see Sect. 4 for \(\mathsf {QFHE}\) based UC commitment schemes. In the sequel, we will use blue color to stress whether a part is relevant to the ciphertext randomisation property.
Definition 3
(Equivocal fully homomorphic encryption). An Equivocal fully homomorphic encryption scheme  with message space \(M\) is made up of the following PPT algorithms:
with message space \(M\) is made up of the following PPT algorithms:
-
\((\mathsf {KeyGen},\mathsf {QEnc}, \mathsf {Eval},\mathsf {Dec})\) is an FHE scheme with the same syntax as in Sect. 3.1.
-
The Equivocal key generation algorithm \(\mathsf {KeyGen}^*(1^\lambda )\), outputs an equivocal public-key secret-key pair \((\widetilde{\mathsf {PK}},\widetilde{\mathsf {SK}})\).
-
The Equivocation algorithm \(\mathsf {Equiv}(\widetilde{\mathsf {PK}},\widetilde{\mathsf {SK}}, \mathrm {ct},r_\mathrm {ct}, m)\), given \(\widetilde{\mathsf {PK}}\), \(\widetilde{\mathsf {SK}}\), a plaintext m, a ciphertext \(\mathrm {ct}\) and random coins \(r_\mathrm {ct}\), outputs a value e in the randomness space.
-
The Ciphertext Randomisation algorithm
 , given ciphertexts \(\mathrm {ct},\mathrm {ct}'_1,\ldots ,\mathrm {ct}'_n\) generated by the procedure \(\mathsf {QEnc}\) outputs a ciphertext \(\mathrm {CT}\). We require the following properties:
, given ciphertexts \(\mathrm {ct},\mathrm {ct}'_1,\ldots ,\mathrm {ct}'_n\) generated by the procedure \(\mathsf {QEnc}\) outputs a ciphertext \(\mathrm {CT}\). We require the following properties:-
1.
Indistinguishability of equivocal keys. We say that the scheme has indistinguishability of equivocal keys if the distributions of \({\mathsf {PK}}\) and \(\widetilde{\mathsf {PK}}\) are computationally indistinguishable, where \(({\mathsf {PK}},\cdot ) \leftarrow \mathsf {KeyGen}(1^\lambda )\) and \((\widetilde{\mathsf {PK}},\cdot ) \leftarrow \mathsf {KeyGen}^*(1^\lambda ).\)
-
2.
Indistinguishability of equivocation. Let \(\mathcal{D}_{rand}(1^\lambda )\) denote the distribution of randomness used by \(\mathsf {QEnc}\). Let \(\mathcal {O}(\widetilde{\mathsf {PK}}, m)\) and \(\mathcal {O'}(\widetilde{\mathsf {PK}}, \widetilde{\mathsf {SK}},m)\) be the following oracles:
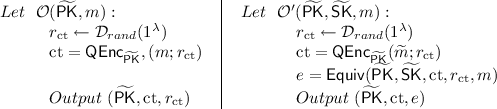
There exists \(\widetilde{m} \in M\) such that for any PPT adversary \(\mathcal {A}\) with oracle access to \(\mathcal {O}(\widetilde{\mathsf {PK}}, \cdot )\) and \(\mathcal {O'}(\widetilde{\mathsf {PK}}, \widetilde{\mathsf {SK}},\cdot )\) the following holds.
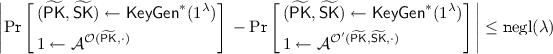
-
3.
 Let \({\mathsf {PK}}\) be the public key used in the procedure \(\mathsf {QEnc}\) for generating ciphertexts \(\mathrm {ct},\mathrm {ct}'_1\ldots \mathrm {ct}_n'\) from the plaintexts \(m,m'_1,\ldots ,m'_n \in M\), respectevely. If \(Pr [\mathsf {Dec}_{\mathsf {sk}}(\mathrm {ct})= m] = 1-\mathrm {negl}(\lambda )\) and for all \(i\in [n]\), \(Pr [\mathsf {Dec}_{\mathsf {sk}}(\mathrm {ct}_i')= m_i'] = 1-\mathrm {negl}(\lambda )\) then it holds that $$Pr [\mathsf {Dec}_{\mathsf {sk}}(\mathsf {Rand}(\mathrm {ct},\mathrm {ct}'_1\ldots \mathrm {ct}_n'))= m] = 1-\mathrm {negl}(\lambda ).$$
Let \({\mathsf {PK}}\) be the public key used in the procedure \(\mathsf {QEnc}\) for generating ciphertexts \(\mathrm {ct},\mathrm {ct}'_1\ldots \mathrm {ct}_n'\) from the plaintexts \(m,m'_1,\ldots ,m'_n \in M\), respectevely. If \(Pr [\mathsf {Dec}_{\mathsf {sk}}(\mathrm {ct})= m] = 1-\mathrm {negl}(\lambda )\) and for all \(i\in [n]\), \(Pr [\mathsf {Dec}_{\mathsf {sk}}(\mathrm {ct}_i')= m_i'] = 1-\mathrm {negl}(\lambda )\) then it holds that $$Pr [\mathsf {Dec}_{\mathsf {sk}}(\mathsf {Rand}(\mathrm {ct},\mathrm {ct}'_1\ldots \mathrm {ct}_n'))= m] = 1-\mathrm {negl}(\lambda ).$$On the other hand, let \(\widetilde{\mathsf {PK}}\) be the public key used in the procedure \(\mathsf {QEnc}\) for generating ciphertexts \(\mathrm {ct},\mathrm {ct}'_1\ldots \mathrm {ct}_n'\), respectevely. If \(Pr [\mathsf {Dec}_{\mathsf {sk}}(\mathrm {ct})= m] =1- \mathrm {negl}(\lambda )\) and for all \(i\in [n]\), \(Pr [\mathsf {Dec}_{\mathsf {sk}}(\mathrm {ct}_i')= m_i'] = 1-\mathrm {negl}(\lambda )\) then it holds that
$$Pr [\mathsf {Dec}_{\mathsf {sk}}(\mathsf {Rand}(\mathrm {ct},\mathrm {ct}'_1\ldots \mathrm {ct}_n'))= m'_1+\ldots +m'_n] = 1-\mathrm {negl}(\lambda ).$$
-
1.
In the sequel for simplicity of exposition, we call the ciphertexts \(\mathrm {ct}'_1\ldots \mathrm {ct}_n'\) \(\mathtt {redundant}\) in case they are generated by \(\mathsf {QEnc}_{\mathsf {PK}}\) and \(\mathtt {non-redundant}\) if they are generated by \(\mathsf {QEnc}_{\widetilde{\mathsf {PK}}}\). Analogously, we call the ciphetext \(\mathrm {ct}\) \(\mathtt {non-redundant}\) or \(\mathtt {redundant}\) if it is generated by \(\mathsf {QEnc}_{\mathsf {PK}}\) or \(\mathsf {QEnc}_{\widetilde{\mathsf {PK}}}\), respectivelyFootnote 2.
In order to construct our equivocal \(\mathsf {QFHE}\) scheme we use the following special \(\mathsf {FHE}\) scheme with some additional properties.
Definition 4
[Special fully homomorphic encryption] We call a fully homomorphic encryption scheme \(\mathsf {FHE}=(\mathsf {KeyGen},\mathsf {Enc}, \mathsf {Eval},\mathsf {Dec})\) a special FHE scheme, if it is IND-CPA secure and satisfies the following properties: Let \(\mathcal{D}_{rand}(1^\lambda )\) denote the distribution of randomness used by \(\mathsf {Enc}\).
-
1.
Additive homomorphism over random coins: \(\forall r_1,r_2 \in \mathsf {Supp}(\mathcal{D}_{rand}(1^\lambda ))\) and \(\forall m\in M\), it holds that \(\big (m \boxdot \mathsf {Enc}_{\mathsf {pk}}(0;r_1)\big )\boxplus \mathsf {Enc}_{\mathsf {pk}}(0;r_2)=\mathsf {Enc}_{\mathsf {pk}}(0;m\cdot r_1+ r_2)\).
-
2.
E-Hiding: There exists \(\mathcal{D}_{rand}'(1^\lambda )\) such that \(\forall m \in M\), if \(r^{blind} \leftarrow \mathcal{D}_{rand}(1^{\lambda })\) and \( r^{K}\leftarrow \mathcal{D}_{rand}'(1^{\lambda })\) then the distribution of \((r^{blind} -m\cdot r^{K})\) is statistically close to \(\mathcal{D}_{rand}(1^\lambda )\).Footnote 3
-
3.
Invertible Sampling: The distribution \(\mathcal{D}_{rand}(1^\lambda )\), has invertible sampling via the algorithm \(\mathsf {Inv}_{\mathcal{D}_{rand}}\).
Recall that we defined an invertible sampler of an algorithm A in Sect. 2 as an algorithm \(\mathsf {Inv}_A\) that takes as inputs the input x and output y with consistent random coins. In our case, \(x = 1^\lambda \) and y is a sample from the range of \(\mathcal{D}_{rand}\). Next, in Fig. 1, we show how to build an equivocal FHE scheme using a special FHE scheme. The high level intuition is as follows. In order to achieve equivocality we modify an FHE scheme satisfying the properties of Definition 4 as follows: The public key contains an encryption of 1 and an encryption of 0. More specifically, \({\mathsf {PK}}= (\mathsf {pk}, K = \mathsf {Enc}_\mathsf {pk}(1), R=\mathsf {Enc}_\mathsf {pk}(0))\) where \(\mathsf {pk}\) is the public key of an FHE scheme. An encryption of a message m in the real world is computed using K as \((m\boxdot K~ \boxplus ~\mathsf {Enc}_\mathsf {pk}(0))\) and encryption for re-randomisation is computed using R as \((z\boxdot R ~\boxplus ~ \mathsf {Enc}_\mathsf {pk}(0))\) for a random value z. In the simulation, the values encrypted in K and R are switched, in particular, \(K = \mathsf {Enc}_\mathsf {pk}(0)\) and \(R=\mathsf {Enc}_\mathsf {pk}(1)\). Therefore, normal encryption leads to encryption of 0 with the guarantee of equivocation. However, encryption for re-randomisation actually encrypts non-zero values i.e., z, in order to force the output.
Theorem 3
Let \(\mathsf {FHE}\) be a special fully homomorphic encryption scheme. Then \(\mathsf {QFHE}=(\mathsf {KeyGen},\mathsf {KeyGen}^*, \mathsf {QEnc}, \mathsf {Rand}, \mathsf {Eval},\mathsf {Dec},\mathsf {Equiv})\) in Fig. 1 is an equivocal \(\mathsf {QFHE}\) scheme.
Proof
-
Indistinguishability of equivocal keys. Let \(({{\mathsf {PK}}}, {\mathsf {SK}}) \leftarrow \mathsf {KeyGen}(1^\lambda )\) and \(({\widetilde{\mathsf {PK}}}, \widetilde{\mathsf {SK}})\leftarrow \mathsf {KeyGen}^*(1^\lambda )\), then the indistinguishability of the two pairs of public keys follows from the IND-CPA security of the \(\mathsf {FHE}\) scheme.
-
Indistinguishability of equivocation. Without loss of generality, we will show that indistinguishability of equivocation holds for \(\widetilde{m}=0\). Let \(\mathcal {A}\) be an adversary that breaks indistinguishability of equivocation; then we construct a PPT algorithm R such that \(R^\mathcal {A}\) breaks E-hiding. R simulates the oracle for every query \(m_i\) as follows. R invokes \(\mathcal {A}\) and receives some message \(m_i\) and forwards it to the E-hiding challenger. Next it receives the challenge \(r_{\mathrm {ct}_i}\) and computes \(\mathrm {ct}_{i}= \mathsf {QEnc}_{\widetilde{\mathsf {PK}}}(0,m_i;r_{\mathrm {ct}_i})\) and forwards \((r_{\mathrm {ct}_i},\mathrm {ct}_{i})\) to \(\mathcal {A}\) and outputs whatever \(\mathcal {A}\) does. Now, if \(r_{\mathrm {ct}_i} \leftarrow \mathcal{D}_{rand}(1^\lambda )\) then \(\mathrm {ct}_i\leftarrow \mathsf {QEnc}_{\widetilde{\mathsf {PK}}}(0,m_i;r_{\mathrm {ct}_i})\), namely, the view of \(\mathcal {A}\) follows the distribution which corresponds to the left game in Definition 3 of indistinguishability of equivocation. On the other hand, if \(r_{\mathrm {ct}_i} = (r^{blind}_i -m_i \cdot r^{\widetilde{K}})\); then \(\mathrm {ct}_i= (m_i\boxdot \widetilde{K}) \boxplus \mathsf {Enc}_{\mathsf {pk}}(0; r^{blind}_i - m_i \cdot r^{\widetilde{K}})=\mathsf {Enc}_{\mathsf {pk}}(0;r^{blind}_i )=\mathsf {QEnc}_{\widetilde{\mathsf {PK}}}(0,0;r^{blind}_i)\) which implies that in this case the view of \(\mathcal {A}\) follows the distribution of the right game in Definition 3 of indistinguishability of equivocation. This means that the distinguishing advantage of R is the same as that of \(\mathcal {A}\) which leads to a contradiction.
-
 The algorithm \(\mathsf {Rand}\) adds the ciphertexts \((\mathrm {ct},\mathrm {ct}'_1,\ldots ,\mathrm {ct}_n')\). If \(\mathrm {ct}\) is a ciphertext generated by \(\mathsf {QEnc}_{{\mathsf {PK}}}\) for \(b=0\) and \((\mathrm {ct}'_1\ldots \mathrm {ct}_n')\) are ciphertexts generated by \(\mathsf {QEnc}_{{\mathsf {PK}}}\) for \(b=1\) then $$Pr [\mathsf {Dec}_{\mathsf {sk}}(\mathsf {Rand}(\mathrm {ct},\mathrm {ct}'_1\ldots \mathrm {ct}_n'))= m] = 1-\mathrm {negl}(\lambda )$$
The algorithm \(\mathsf {Rand}\) adds the ciphertexts \((\mathrm {ct},\mathrm {ct}'_1,\ldots ,\mathrm {ct}_n')\). If \(\mathrm {ct}\) is a ciphertext generated by \(\mathsf {QEnc}_{{\mathsf {PK}}}\) for \(b=0\) and \((\mathrm {ct}'_1\ldots \mathrm {ct}_n')\) are ciphertexts generated by \(\mathsf {QEnc}_{{\mathsf {PK}}}\) for \(b=1\) then $$Pr [\mathsf {Dec}_{\mathsf {sk}}(\mathsf {Rand}(\mathrm {ct},\mathrm {ct}'_1\ldots \mathrm {ct}_n'))= m] = 1-\mathrm {negl}(\lambda )$$since it is easy to see that the ciphertexts \((\mathrm {ct}'_1\ldots \mathrm {ct}_n')\) contain encryptions of zeros due to the fact that \(R=\mathsf {Enc}_{\mathsf {pk}}(0)\). An analogous argument holds for \(\mathrm {ct}\) and \(\mathrm {ct}'_1\ldots \mathrm {ct}_n'\) generated by \(\mathsf {QEnc}_{\widetilde{\mathsf {PK}}}\) for \(b=0\) and \(b=1\), respectively, since in this case the ciphertext \(\mathrm {ct}\) contain an encryption of a zero (because in this case \(\widetilde{K}=\mathsf {Enc}_{\mathsf {pk}}(0)\)) and ciphertexts \((\mathrm {ct}'_1\ldots \mathrm {ct}_n')\) contain encryptions of the corresponding \(m'_i\) since \(\widetilde{R}=\mathsf {Enc}_{\mathsf {pk}}(1)\).
\(\square \)
Distributed Decryption: As we mentioned above, we need distributed decryption to implement our MPC protocol. To this end, we assume that the common public key \(\mathsf {pk}\) has been set up where the secret key \(\mathsf {sk}\) has been secret-shared among the players in such a way that they can collaborate to decrypt. Notice that some setup assumption is always required to show UC security in the dishonest majority setting. Roughly, we assume that a functionality is available which generates a key pair and secret-shares the secret key among the players using a secret-sharing scheme that is assumed to be given as part of the specification of the cryptosystem. Since we allow corruption of all but one player, the maximal unqualified sets must be all sets of \(n - 1\) players. We point out that we could make a weaker set-up assumption, such as a common reference string, and using a general UC secure multiparty computation protocol for the common reference string model to implement the above functionality. While this may not be very efficient, one only needs to run this protocol once in the life-time of the system. The properties needed for the distributed decryption and its protocol are specified later.
4 UC Adaptive Commitments and ZKPoK from LWE
Commitment schemes that satisfy both equivocality and extractability form useful tools in achieving adaptive security. In this section, we show how using a \(\mathsf {QFHE}\) scheme, one can build equivocal and extractable commitments. Having realized a \(\mathsf {QFHE}\) scheme based on the LWE assumption, we consequently get equivocal and extractable commitments assuming the hardness of LWE. Note that such commitments based on LWE can be of independent interest. We remark that any encryption scheme that satisfies the properties specified in Definition 4 would have sufficed for our purposes in this section – the multiplicative homomorphic property of our \(\mathsf {QFHE}\) scheme will not be of use here; however, since we are using our commitment scheme as a tool in our adaptive MPC protocol based on LWE, we use the same \(\mathsf {QFHE}\) scheme in our commitment scheme too.
Since we are interested in UC security against adaptive adversaries, our commitment scheme is in the CRS model. The scheme must satisfy the following two properties, polynomial equivocality and simulation extractability. The former guarantees that the simulator \(\mathcal {S}\) needs to be able to produce polynomially many equivocal commitments using the same CRS. More specifically, \(\mathcal {S}\) can open the equivocal commitments to any value of its choice and give consistent randomness to adversary \(\mathcal {A}\). The latter property says that the simulator \(\mathcal {S}\) needs to be able to extract the contents of any valid commitment generated by adversary \(\mathcal {A}\), even after \(\mathcal {A}\) obtains polynomially many equivocal commitments generated by \(\mathcal {S}\). Note that there is only an apparent conflict between equivocality and the binding property and between the extractability and the hiding property, as the simulator is endowed with additional power (trapdoors) in comparison with the parties in the real world execution. In the following we elaborate how our commitment scheme satisfies the above properties.
Our Construction. Equivocation in our scheme is achieved via \(\mathsf {QFHE}\). In particular, the commitment algorithm is the algorithm \(\mathsf {QEnc}\), defined in Fig. 1. In order to add extractability we must enhance our scheme in such a way that we do not sacrifice equivocality. A failed attempt is to include a public key for an encryption scheme secure against CCA2 attacks in the CRS. In this case, the committer will send an encryption of the decommitment information along with the commitment itself. Then, as the simulator has the associated decryption key, it can decrypt the decommitment information and hence extract the committed value from any adversarially prepared commitment. However, notice that such an encryption is binding even to the simulator, so equivocality cannot be achieved.
The solution to the problem is to send the commitment along with two pseudorandom ciphertexts. One ciphertext is an encryption of the decommitment information and the other ciphertext is a uniformly random string. In this way, the simulator can encrypt both decommitment values and later show that it only knows the decryption to one and that the other was uniformly chosen.
For the security of our construction, the encryption scheme used to encrypt the decommitment information has to be a CCA2-secure encryption scheme with the property that any produced ciphertext is pseudorandom and has deterministic decryption. To this end, the CCA2 encryption scheme of Micciancio and Peikert [MP12] based on LWE satisfies the above properties. They obtain their result via relatively generic assumptions using either strongly unforgeable one-time signatures [DDN00], or a message authentication code and a weak form of commitment [BCHK07]. The first assumption does not yield pseudorandom ciphertexts, thus another encryption producing pseudorandom ciphertexts on top of the scheme of [MP12] could have been used, resulting in a double encryption scheme. However, it turns out that their construction with the latter set of assumptions has pseudorandom ciphertexts.
The reader might have observed that this bears some resemblance with the trick used in the seminal work of [CLOS02], referred to as CLOS hereafter, to achieve extractability. Their scheme is based on enhanced trapdoor permutations, also needed in order to get double encryption CCA2 security. Moreover, in order to build equivocal commitments they need an NP reduction to graph Hamiltonicity since the CRS of their commitment scheme consists of a graph G sampled from a distribution such that it is computationally hard to tell if G has a Hamiltonian cycle. Interestingly, the CLOS commitment scheme does not give an instantiation based on LWE and to begin with, there are no known trapdoor permutations based on LWE. On the other hand, assuming the hardness of LWE, we propose an extractable and equivocal commitment with no need of an NP reduction, leading to a huge improvement in efficiency.
More formally, given a \(\mathsf {QFHE}=(\mathsf {KeyGen},\mathsf {KeyGen}^*,\mathsf {QEnc}, \mathsf {Eval},\mathsf {Dec}, \mathsf {Equiv})\) Footnote 4 scheme, a CCA2-secure scheme \(\mathsf {{E_{CCA}}}\) with encryption algorithm \(\mathsf {ENC_{CCA}}\) based on LWE [MP12], with the property that any ciphertext is pseudorandom and has deterministic decryption, we construct the following equivocal and extractable UC bit-commitment scheme \(\mathrm {\Pi _\textsc {Com}}\). For simplicity of exposition, we will use \(\mathsf {{E_{CCA}}}\) in a black box manner. We note that the scheme naturally extends to a setting where commitments are defined over strings instead of just bits.
-
Common Reference String: The CRS consists of the public key \(({\mathsf {PK}})\) of the \(\mathsf {QFHE}\) scheme and the public key for the encryption scheme \(\mathsf {ENC_{CCA}}\).
-
Commit Phase:
-
1.
On input \((\mathrm {Commit}, sid, ssid, P_i, P_j, b)\) where \(b \in \{0, 1\}\), party \(P_i\) computes \(z = \mathsf {QEnc}_{{\mathsf {PK}}}(b;r)\) where \(r \leftarrow \mathcal{D}_{rand}(1^\lambda )\). Next, \(P_i\) computes \(C_b=\mathsf {ENC_{CCA}}(P_i,P_j,sid,ssid,r;s)\) using random coins s, and sets \(C_{1-b}\) to a random string of length \(|C_b|\). Then, \(P_i\) records \((sid,ssid,P_j,r,s,b)\), and sends \(c = (sid,ssid,P_i,z,C_0,C_1)\) to \(P_j\).
-
2.
\(P_j\) receives and records c, and outputs \((\mathrm {Receipt}, sid, ssid, P_i, P_j)\). \(P_j\) ignores any later commit messages from \(P_i\) with the same (sid, ssid).
-
1.
-
Reveal Phase:
-
1.
On input \((\mathrm {Reveal}, sid, ssid)\), party \(P_i\) retrieves \((sid, ssid, P_j, r, s, b)\) and sends (sid, ssid, r, s, b) to \(P_j\).
-
2.
Upon receiving (sid, ssid, r, s, b) from \(P_i, P_j\) checks that it has a tuple \((sid, ssid, P_i, z, C_0, C_1)\). If yes, then it checks that \(z = \mathsf {QEnc}_{{\mathsf {PK}}}(b;r)\) and that \(C_b = \mathsf {ENC_{CCA}}(P_i,P_j,sid,ssid,r;s)\). If both these checks succeed, then \(P_j\) outputs \((\mathrm {Reveal}, sid, ssid, P_i, P_j, b)\). Otherwise, it ignores the message.
-
1.
Proposition 1
Assuming hardness of LWE, Protocol \(\mathrm {\Pi _\textsc {Com}}\) UC realizes \(\mathcal {F}_\textsc {MCom}\) in the \(\mathcal {F}_\textsc {CRS}\)-hybrid model.
The above commitment scheme UC realizes the multi-session ideal commitment functionality \(\mathcal {F}_\textsc {MCom}\), described in Fig. 2, which reuses the public string for multiple commitments. The proof can be found in the full version. Next, we show how our UC commitment scheme serves towards the realization of a commit-and-prove functionality \(\mathcal {F}_\textsc {Com-ZK}\) based on LWE.
4.1 Adaptive UC ZKPoK from LWE
Our UC commitment scheme serves towards the realization of a commit-and-prove functionality \(\mathcal {F}_\textsc {Com-ZK}\) based on LWE. Such a functionality is generic and hence is quite useful – it allows a party to prove NP statements relative to its commitment value in the setting where parties commit to their inputs but they never decommit. The functionality \(\mathcal {F}_\textsc {Com-ZK}\) is presented in Fig. 3 and is comprised of two phases. In the first phase, a party commits to a specific value. In the second phase, this party proves NP statements in zero-knowledge relative to the committed value. It allows the committer to commit to multiple secret values \(w_i\), and then have the relation \(\mathcal R\) depend on all these values in a single proof. In addition, the committer may ask to prove multiple statements with respect to the same set of secret values. Hence, once a committer gives a new \((\mathrm {Commit}, sid, w)\) command, \(\mathcal {F}_\textsc {Com-ZK}\) adds the current w to the already existing list \(\overline{w}\) of committed values. Then, on receiving a \((\mathrm {Proof}, sid, \mathcal {R}, x)\) request, \(\mathcal {F}_\textsc {Com-ZK}\) evaluates \(\mathcal R\) on x and the current list \(\overline{w}\).
Using the power of the UC commitment scheme we constructed in Sect. 4, we show how it can be used to first construct UC Zero-Knowledge protocols from LWE. Canetti and Fischlin [CF01, Theorem 5], show that in the \(\mathcal {F}_\textsc {Com}\)-hybrid model there exists a 3-round protocol that securely realizes \(\mathcal {F}_\textsc {ZK}\) with respect to any NP relation without any computational assumptions. Using the composition theorem and [CF01, Theorem 5], we can instantate \(\mathcal {F}_\textsc {Com}\) with the UC commitment protocol from LWE (see Sect. 4) in the CRS model and realize \(\mathcal {F}_\textsc {ZK}\) from LWE. Also, as it is noted by [CF01] we can replace \(\mathcal {F}_\textsc {Com}\) by the functionality \(\mathcal {F}_\textsc {MCom}\).
We next obtain a protocol for UC realizing functionality \(\mathcal {F}_\textsc {Com-ZK}\) in the \(\mathcal {F}_\textsc {ZK}\)-hybrid model, in the presence of adaptive adversaries. In [CLOS02, Proposition 7.2], a protocol for UC realizing \(\mathcal {F}_\textsc {Com-ZK}\) in the \(\mathcal {F}_\textsc {ZK}\)-hybrid model, based on any one-way function is proposed. To guarantee security against adaptive adversaries, they need equivocal and extractable commitments which they instantiate assuming the existence of enhanced trapdoor permutations. Using [CLOS02, Proposition 7.2] we can get such an instantiation assuming the hardness of LWE via our extractable and equivocal commitment scheme described above and instantiation of the \(\mathcal {F}_\textsc {ZK}\) functionality from LWE.
5 Our Protocol
Since we established all the primitives needed we are ready to present our MPC protocol. Our protocol is based on any equivocal \(\mathsf {QFHE}\) scheme which comes together with a statistically secure distributed function sharing scheme. In addition, the protocol assumes access to the \(\mathcal {F}_\textsc {Com-ZK}\) functionality which we build from any equivocal \(\mathsf {QFHE}\), see Sect. 4. In Fig. 4 we describe our protocol \(\mathrm {\Pi _\textsc {MPC}}\) realizing the functionality \(\mathcal {F}_\textsc {AMPC}\) in Fig. 6, in the \((\mathcal {F}_\textsc {broadcast}, \mathcal {F}_\textsc {Key-Dist}, \mathcal {F}_\textsc {Com-ZK})\)-hybrid model. The functionality \(\mathcal {F}_\textsc {Key-Dist}\) is described in Fig. 5 and the functionality \(\mathcal {F}_\textsc {Com-ZK}\) is described in Fig. 3.
During the Load phase, players encrypt their inputs \(x_i\) under a common public key \({\mathsf {PK}}\) and give a ZKPoK. In the evaluation phase, players evaluate the desired function locally and obtain the ciphertext \(\mathsf {enc}(z)\). In the output phase they jointly decrypt the result calling the decryption protocol \(\mathrm {\Pi _\textsc {DDec}}\) together with the ciphertext randomisation technique as is abstracted by the algorithm \(\mathsf {Rand}\) of the \(\mathsf {QFHE}\), see Sect. 3.
In the protocol \(\mathrm {\Pi _\textsc {DDec}}\) parties use ZK to prove that their evaluation shares are correct. However, as discussed in the introduction we optimise the output phase avoiding the expensive use of ZK proofs to prove that the player’s evaluation shares to the decryption protocol are correct, changing the evaluation phase of the protocol and avoiding the ZK proofs. For details see Sect. 6.
5.1 Distributed Function Evaluation
In order to achieve distributed decryption, we assume, as a set up assumption, that a common public key \(\mathsf {pk}\) has been set up where the secret key \(\mathsf {sk}\) has been secret-shared between n parties in such a way that they can compute their corresponding decryption evaluation shares and then collaborate to decrypt while the \(\mathsf {sk}\) is kept secret. We also need to enforce honest computation of the evaluation shares of a ciphertext. Commitments to the shares of the secret key are also made public, along with \(\mathsf {pk}\). Using these commitments, when parties are distributedly decrypting a ciphertext, they can then prove (via \(\mathcal {F}_\textsc {Com-ZK}\)) that the evaluation shares were computed honestly using the secret-key shares initially delegated to them.
To this end, the functionality \(\mathcal {F}_\textsc {Key-Dist}\) generates a key pair \((\mathsf {pk}, \mathsf {sk})\) Footnote 5 and secret-shares the secret key \(\mathsf {sk}\) among the players using a secret-sharing scheme that is assumed to be given as part of the specification of the cryptosystem. The validity of the evaluation shares is tested inside the protocol \(\mathrm {\Pi _\textsc {DDec}}\) calling the functionality \(\mathcal {F}_\textsc {Com-ZK}\). In order to describe our protocol \(\mathrm {\Pi _\textsc {DDec}}\), we next define the following distributed sharing scheme.
Definition 5
We call \((\mathsf {ShareSK}, \mathsf {ShareEval}, \mathsf {Combine})\) a distributed function sharing scheme for an encryption scheme \((\mathsf {KeyGen}_\mathsf {FHE}, \mathsf {Enc},\mathsf {Dec})\), with construction threshold \(\textsf {c}\) and privacy threshold \(\textsf {t}\), if for a triple \((\mathsf {ShareSK}, \mathsf {ShareEval},\mathsf {Combine})\) of PPT algorithms the following hold:
-
Key sharing: The algorithm \(\mathsf {ShareSK}\) on input \((\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {KeyGen}_\mathsf {FHE}(1^\lambda )\) and a construction threshold c, outputs a tuple \((\mathsf {sk}_1, \ldots , \mathsf {sk}_n) \leftarrow \mathsf {ShareSK}(\mathsf {sk})\).
-
Evaluation sharing: The evaluation function \(\mathsf {ShareEval}\) on input \((\mathsf {pk},\mathsf {sk}_i)\) and a ciphertext \(\mathsf {Enc}_{\mathsf {pk}}(z)\), outputs an evaluation share
$$ev_i = \mathsf {ShareEval}(\mathsf {pk}, \mathsf {sk}_i,\mathsf {Enc}_{\mathsf {pk}}(z); r_{ev_i})$$for \(i\in [n]\) where \(r_{ev_i}\leftarrow \mathcal{D}_{rand}(1^\lambda )\).
-
Share combining: The algorithm \(\mathsf {Combine}\) on input correctly computed evaluation shares \(\{ev_i\}_{i \in [n]}\) of the same ciphertext \(\mathsf {Enc}_{\mathsf {pk}}(z)\), constructs the output \(\mathsf {Dec}_{\mathsf {sk}}(\mathsf {Enc}_{\mathsf {pk}}(z)) = \mathsf {Combine}(\{ev_i\}_{i \in [n]})\).
For our purposes, the construction threshold \(\textsf {c} = n\) and the corruption threshold \(\textsf {t} = n-1\). In Fig. 7, we describe our protocol \(\mathrm {\Pi _\textsc {DDec}}\), parameterized by \((\mathsf {ShareSK},\mathsf {ShareEval}, \mathsf {Combine})\).
Theorem 4
Let \(\mathsf {QFHE}=(\mathsf {KeyGen},\mathsf {KeyGen}^*, \mathsf {QEnc}, \mathsf {Eval}, \mathsf {Rand}, \mathsf {Dec},\mathsf {Equiv})\) be an equivocal fully homomorphic encryption scheme; let it be associated with a distributed function sharing scheme \((\mathsf {ShareSK},\mathsf {ShareEval},\mathsf {Combine})\). Then the constant-round protocol \(\mathrm {\Pi _\textsc {MPC}}\) UC-securely realises the ideal functionality \(\mathcal {F}_\textsc {AMPC}\) in the \((\mathcal {F}_\textsc {broadcast},\mathcal {F}_\textsc {Key-Dist},\mathcal {F}_\textsc {Com-ZK})\)-hybrid model with computational security against any adaptive, active adversary corrupting at most all-but-one parties.
For the proof of Theorem 4 see the full version. Replacing UC ZK with UC NIZK yields a three-round protocol.
High Level Idea of the Security Proof. Our simulator uses the properties of the \(\mathsf {QFHE}\) scheme such as the indistingusability of equivocation, according to Definition 3. Furthermore, as we discussed in Sect. 1, the simulator will not be able to cheat in the distributed decryption protocol by decrypting a given ciphertext to any desired value. The key setup for the decryption protocol fixes the shares of the private key even in the simulation. Thus, a ciphertext can only be decrypted to the value it actually contains. Of course, when decrypting the outputs, the correct results should be produced both in simulation and real life, and so we have a problem since all ciphertexts in the simulation generated with respect to the honest parties will contain encryptions of 0. For this issue we use the ciphertext randomisation property. Notice that the ciphertext \(\mathrm {ct}\) in the ciphertext randomization property as per Definition 3 corresponds to the real output \(\mathsf {enc}(z)\) of the protocol \(\mathrm {\Pi _\textsc {MPC}}\) and the ciphertexts \(\mathrm {ct}'_1,\ldots ,\mathrm {ct}'_n\) correspond to the ciphertexts \(\{\widetilde{\mathsf {enc}(y_i)}\}_{i\in J}\). In the real-world the ciphertexts \(\{\widetilde{\mathsf {enc}(y_i)}\}_{i\in J}\) are \(\mathtt {redundant}\). On the other hand, in the ideal-world the final ciphertext \(\mathrm {CT}\) decrypts to a value contributed only by the ciphertexts \(\{\widetilde{\mathsf {enc}(y_i)}\}_{i\in J}\). In this case we will call the ciphertexts \(\{\widetilde{\mathsf {enc}(y_i)}\}_{i\in J}\) \(\mathtt {non-redundant}\). This implies that an honest execution of the Output stage is not possible with the ciphertexts of \(\{\widetilde{\mathsf {enc}(y_i)}\}_{i\in J}\) being \(\mathtt {non-redundant}\). Analogously, the ciphertext \(\mathsf {enc}(z)\) can be either \(\mathtt {redundant}\) or \(\mathtt {non-redundant}\). In other words, it is pertinent that before we get to a hybrid where the Output stage is performed honestly, we need a hybrid where \(\{\widetilde{\mathsf {enc}(y_i)}\}_{i\in J}\) turn to \(\mathtt {redundant}\) ciphertexts. However, with both ciphertexts \(\{\widetilde{\mathsf {enc}(y_i)}\}_{i\in J}\) and \(\mathsf {enc}(z)\) \(\mathtt {redundant}\), we can not hope to get the final output \(\mathrm {CT}\) to decrypt to the actual output value. Thus, even before turning \(\{\widetilde{\mathsf {enc}(y_i)}\}_{i\in J}\) to \(\mathtt {redundant}\) ciphertexts, we need a hybrid where we can cheat in the final decryption. That is, we first need to have a hybrid that, instead of running the distributed decryption protocol, runs what we abstract as the simulator for the distributed decryption. Moreover, we also based on the semantic security of the FHE scheme in interchangeably switching the keys K and R to encryptions of 0 and 1, respectively. A full proof is given in the full version.
6 On the Communication Complexity of Distributed Decryption
Our protocol as described in Sect. 5 assumes that the \(\mathsf {QFHE}\) scheme comes with a semi-honest secure distributed decryption protocol: from the ciphertext and shares of the secret key players can compute decryption shares which, if correct, allow the reconstruction of the plaintext. We then augment the distributed decryption with ZK proofs so that players prove that their contributions to the decryption are correct. This solution has communication complexity proportional to the circuit complexity of the decryption function.
However, our approach allows for a significant optimization of the decryption procedure compared to generic solutions. More specifically, we tweak our protocol \(\mathrm {\Pi _\textsc {MPC}}\) such that the communication complexity of the decryption becomes independent of its circuit complexity.
To this end, we modify the evaluation phase of our protocol presented in Sect. 5. Note that our original protocol allows us to securely compute any (randomized) function. In particular, any randomized function allows the parties to encrypt randomized shares and then add up them together. Therefore, instead of computing the original function, we compute a new function, which for each output z of the original function also outputs \(\alpha \) and \(w= \alpha z\) where \(\alpha \) is randomly chosen in some large field, and where the multiplication \(\alpha z\) also takes place in that field. Of course if we can compute this function securely then we can also compute the original function securely. Observe that this new function comes along with an extra property which allows to check if the output is correct or not based on whether \(w= \alpha z\).
In order to incorporate the above, the modification to the protocol is as follows. Instead of having a single ciphertext \(\mathsf {enc}(z)\) containing z, we will have two extra ciphertexts, namely \(\mathsf {enc}(\alpha )\) and \(\mathsf {enc}(w)\). The ciphertext \(\mathsf {enc}(\alpha )\) is computed as follows. Each party randomly selects a one-time \(a_i\) and encrypts it according to the Load phase of our protocol \(\mathrm {\Pi _\textsc {MPC}}\) in Fig. 5. Once each party has loaded and broadcasted \(\mathsf {enc}(a_i)\), each party computes \(\mathsf {enc}(\alpha )= \mathsf {enc}(a_1)\boxplus \ldots \boxplus \ \mathsf {enc}(a_n)\) and \(\mathsf {enc}(w)=\mathsf {enc}(\alpha )\boxdot \mathsf {enc}(z)\). Thus, instead of calling the output phase of our protocol only on input \(\mathsf {enc}(z)\) we call it on three different ciphertexts \(\mathsf {enc}(z),\mathsf {enc}(\alpha ), \mathsf {enc}(w)\). This means that now the decryption protocol will generate three sets of evaluation shares.
The modification in the decryption protocol is as follows. Before we first broadcast the shares and then we prove in ZK that they were correct. Instead, we are not going to broadcast all the evaluation shares immediately due to the adversary who may see the contributions from the honest parties to \(\alpha \) before his broadcast enabling him to forge. We need to guarantee that the adversary cannot forge the output by making sure that he should output his share before he sees \(\alpha \). In order to avoid the above complication, we first commit to the evaluation shares and then we open them. In particular, all players compute their evaluation shares for \(z, \alpha \) and w and commit to them. If opening fails or if the decrypted values do not satisfy \(\alpha z =w\), we abort. This solution avoids the use of ZK proofs yielding a solution which is independent of the circuit complexity of the decryption.
Since there is an encryption of \(\alpha \) available, the new aspect in the proof is to show that this does not help the adversary to learn \(\alpha \) unless he can break CPA security. We can argue this in the proof in the full version where we turn the ciphertext \(\mathsf {enc}(z)\) to \(\mathtt {redundant}\). Therefore, the same proof still applies but instead we will have three \(\mathtt {redundant}\) ciphetexts \(\mathsf {enc}(\alpha z),\mathsf {enc}(\alpha ), \mathsf {enc}(w)\). In this hybrid the outputs cannot be forged since the ciphertext \(\mathsf {enc}(\alpha )\) is \(\mathtt {redundant}\) and it does not contain information about \(\alpha \). Thus, an advesary that he cannot forge he cannot distinguish in the real world and break CPA-security.
Notes
- 1.
Ciphertext randomisation is needed in order to force the output in the simulation.
- 2.
By the ciphertext randomisation property, the reader can think of the \(\mathtt {redundant}\) messages as encryptions of zeros.
- 3.
Intuitively, E-Hiding can be argued in the same way as formula privacy for some FHE schemes. This requires dwarfing in the sense that \(r^{blind}\) should be large enough to dwarf \(mr^K\) where \(\mathcal{D}_{rand}(1^\lambda )\) and \(\mathcal{D}_{rand}'(1^\lambda )\) are Gaussian distributions. Hence, \(r^K\leftarrow \mathcal{D}_{rand}'(1^\lambda )\) and \(r^{blind} \leftarrow \mathcal{D}_{rand}(1^\lambda )\) such that the noise of \(\mathcal{D}_{rand}(1^\lambda )\) is super-polynomially larger than the noise of \(\mathcal{D}_{rand}'(1^\lambda )\).
- 4.
Algorithms \(\mathsf {QEnc'}, \mathsf {Rand}\) are not necessary for the construction of UC Commitments.
- 5.
In the description of our protocol we choose to explicitly refer to the keys \((\mathsf {pk}, \mathsf {sk})\) since it helps in the description of the decryption protocol.
References
Asharov, G., Jain, A., López-Alt, A., Tromer, E., Vaikuntanathan, V., Wichs, D.: Multiparty computation with low communication, computation and interaction via threshold FHE. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 483–501. Springer, Heidelberg (2012)
Boneh, D., Canetti, R., Halevi, S., Katz, J.: Chosen-ciphertext security from identity-based encryption. SIAM J. Comput. 36(5), 1301–1328 (2007)
Ben-Or, M., Goldwasser, S., Wigderson. A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation (extended abstract). In: STOC, pp. 1–10 (1988)
Brakerski, Z., Vaikuntanathan, V.: Fully homomorphic encryption from ring-LWE and security for key dependent messages. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 505–524. Springer, Heidelberg (2011)
Cramer, R., Dodis, Y., Fehr, S., Padró, C., Wichs, D.: Detection of algebraic manipulation with applications to robust secret sharing and fuzzy extractors. In: Smart, N.P. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 471–488. Springer, Heidelberg (2008)
Canetti, R., Fischlin, M.: Universally composable commitments. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 19–40. Springer, Heidelberg (2001)
Canetti, R., Feige, U., Goldreich, O., Naor, M.: Adaptively secure multi-party computation. In: STOC, pp. 639–648 (1996)
Canetti, R., Goldwasser, S., Poburinnaya, O.: Adaptively secure two-party computation from indistinguishability obfuscation. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 557–585. Springer, Heidelberg (2015)
Canetti, R., Lindell, Y., Ostrovsky, R., Sahai, A.: Universally composable two-party and multi-party secure computation. In: Proceedings of the Thiry-fourth Annual ACM Symposium on Theory of Computing, STOC 2002, pp. 494–503 (2002)
Dolev, D., Dwork, C., Naor, M.: Non-malleable cryptography. SIAM J. Comput. 30, 542–552 (2000)
Damgård, I.B., Ishai, Y.: Constant-round multiparty computation using a black-box pseudorandom generator. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 378–394. Springer, Heidelberg (2005)
Damgård, I.B., Ishai, Y.: Scalable secure multiparty computation. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 501–520. Springer, Heidelberg (2006)
Damgård, I., Ishai, Y., Krøigaard, M., Nielsen, J.B., Smith, A.: Scalable multiparty computation with nearly optimal work and resilience. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 241–261. Springer, Heidelberg (2008)
Dachman-Soled, D., Katz, J., Rao, V.: Adaptively secure, universally composable, multiparty computation in constant rounds. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 586–613. Springer, Heidelberg (2015)
Dachman-Soled, D., Malkin, T., Raykova, M., Venkitasubramaniam, M.: Adaptive and concurrent secure computation from new adaptive, non-malleable commitments. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013, Part I. LNCS, vol. 8269, pp. 316–336. Springer, Heidelberg (2013)
Damgård, I.B., Nielsen, J.B.: Universally composable efficient multiparty computation from threshold homomorphic encryption. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 247–264. Springer, Heidelberg (2003)
Damgård, I., Nielsen, J.B., Polychroniadou, A.: On the communication required for unconditionally secure multiplication. Cryptology ePrint Archive, Report 2015/1097 (2015). http://eprint.iacr.org/
Damgård, I., Polychroniadou, A., Rao, V.: Adaptively secure multi-party computation from lwe (via equivocal fhe). Cryptology ePrint Archive, Report 2014/830 (2014). http://eprint.iacr.org/
Damgård, I., Pastro, V., Smart, N., Zakarias, S.: Multiparty computation from somewhat homomorphic encryption. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 643–662. Springer, Heidelberg (2012)
Gentry, C.: A fully homomorphic encryption scheme. Ph.D. thesis, Stanford University (2009). crypto.stanford.edu/craig
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th Annual Symposium on Foundations of Computer Science, Berkeley, CA, USA, IEEE Computer Society Press, 26–29 October, pp. 40–49 (2013)
Groth, J., Ostrovsky, R., Sahai, A.: New techniques for noninteractive zero-knowledge. J. ACM 59(3), 11 (2012)
Garg, S., Polychroniadou, A.: Two-round adaptively secure MPC from indistinguishability obfuscation. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 614–637. Springer, Heidelberg (2015)
Garg, S., Sahai, A.: Adaptively secure multi-party computation with dishonest majority. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 105–123. Springer, Heidelberg (2012)
Ishai, Y., Prabhakaran, M., Sahai, A.: Founding cryptography on oblivious transfer – efficiently. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 572–591. Springer, Heidelberg (2008)
Katz, J., Ostrovsky, R.: Round-optimal secure two-party computation. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 335–354. Springer, Heidelberg (2004)
Katz, J., Thiruvengadam, A., Zhou, H.-S.: Feasibility and infeasibility of adaptively secure fully homomorphic encryption. In: Hanaoka, G., Kurosawa, K. (eds.) PKC 2013. LNCS, vol. 7778, pp. 14–31. Springer, Heidelberg (2013)
López-Alt, A., Tromer, E., Vaikuntanathan, V.: On-the-fly multiparty computation on the cloud via multikey fully homomorphic encryption. In: Proceedings of the 44th Symposium on Theory of Computing Conference, STOC 2012, New York, NY, USA, 19–22 May 2012, pp. 1219–1234 (2012)
Micciancio, D., Peikert, C.: Trapdoors for lattices: simpler, tighter, faster, smaller. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 700–718. Springer, Heidelberg (2012)
Mukherjee, P., Wichs, D.: Two round mutliparty computation via multi-key FHE. Cryptology ePrint Archive, Report 2015/345 (2015). http://eprint.iacr.org/
Nielsen, J.B.: Separating random oracle proofs from complexity theoretic proofs: the non-committing encryption case. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 111–126. Springer, Heidelberg (2002)
O’Neill, A., Peikert, C., Waters, B.: Bi-deniable public-key encryption. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 525–542. Springer, Heidelberg (2011)
Acknowledgements
The authors would like to thank Nico Döttling, Yuval Ishai and Chris Peikert for helpful discussions. We also thank Jonathan Katz for pointing out his result [KTZ13]. Ivan Damgård and Antigoni Polychriniadou acknowledge support from the Danish National Research Foundation and the National Science Foundation of China (under the grant 61361136003) for the Sino-Danish Center for the Theory of Interactive Computation and from the Center for Research in Foundations of Electronic Markets (CFEM), supported by the Danish Strategic Research Council. In addition, the research was supported by the MPCPRO project funded by the ERC.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Performance of General Solution Based on the IPS Compiler
A Performance of General Solution Based on the IPS Compiler
The following should be taken with large grains of salt. We have tried to be optimistic on the part of the IPS compiler, to not give our concrete protocol an unfair advantage. Thus, actual numbers could be larger.
We estimate that using the best known outer and inner protocols in the IPS compiler, one invocation of IPS would require 10–15 rounds. For the generic suggestion one needs two invocations, one to generate key material for NCE (see below) and one for decryption. On top of that one needs a few rounds for distributing inputs and proving knowledge of them in ZK or NIZK. So we estimate at least 30 rounds for the complete protocol.
The computation and communication overhead is even harder to estimate. We looked at communication since that is a lower bound on computation and made a crude estimate that equates statistical and computational security parameters. To do the FHE decryption generically, one needs to write it as a binary circuit, say of size s and then use the IPS compiler. For n players and security parameter \(\lambda \), we get communication \(\varOmega (n^4 \lambda ^2 s)\) where s depends on the FHE scheme but can be expected to be at least quadratic in \(\lambda \). This is based on a very optimistic assumption on what the outer protocol can do while also minimizing the number of rounds. If this is not true, then such a protocol yields an \(\varOmega (n^6 \lambda ^3 s)\) overhead.
In comparison the total communication of the decryption phase of our concrete protocol is \(O(n^2 \lambda )\). We used the IPS paper and there are likely ways to optimize, but it does seem that the difference is very significant nevertheless.
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Damgård, I., Polychroniadou, A., Rao, V. (2016). Adaptively Secure Multi-Party Computation from LWE (via Equivocal FHE). In: Cheng, CM., Chung, KM., Persiano, G., Yang, BY. (eds) Public-Key Cryptography – PKC 2016. PKC 2016. Lecture Notes in Computer Science(), vol 9615. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49387-8_9
Download citation
DOI: https://doi.org/10.1007/978-3-662-49387-8_9
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49386-1
Online ISBN: 978-3-662-49387-8
eBook Packages: Computer ScienceComputer Science (R0)





 , given ciphertexts
, given ciphertexts 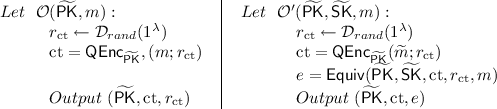
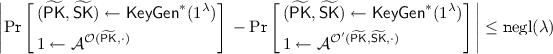
 Let
Let 
 The algorithm
The algorithm 





