Abstract
In the functional programming world, it is common to embed a domain specific language (DSL) in a general purpose language. Unfortunately, the extra abstraction layer provided by the DSL is lost when a type error occurs, and internals leak to users of the DSL.
This paper presents specialized type rules, a way to influence which part of the program is blamed and how the particular error message is worded. These type rules match part of the programming language abstract syntax tree (AST) and guide the type checker in order to provide custom diagnostics. Our goal is to enable DSL writers to keep their high-level abstractions throughout the whole development experience. Specialized type rules have already been considered in the literature: we enhance them by providing a mechanism to allow type rules to depend on partial type information.
The technique presented in this paper can be readily applied to any type engine which uses constraints to perform its duty. We refine the workings of the type engine by including a second gathering pass in case an error is found. In that second pass, partial type information can be used to select a type rule. In particular, we have implemented our techniques in a type engine based on the OutsideIn(X) framework, which underlies the Haskell GHC compiler since version 7.
This work was supported by the Netherlands Organisation for Scientific Research (NWO) project on “DOMain Specific Type Error Diagnosis (DOMSTED)” (612.001.213).
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Domain specific languages (DSLs) are a widely used technique, whose advantages are well-known: they solve a particular problem in an effective way with a language that is close to the domain of the experts, and are thus more likely to be used by experts, even those without prior programming experience. Examples abound, ranging from SQL for database processing to describing drawings [28] and even music harmony analysis [15].
Creating a standalone DSL involves developing a lot of tooling, including a parser, a code generator and static analyzers for the desired domain. Frameworks have been designed to help developers in this task [25]. This approach is called external. Other authors [14] advocate instead embedding DSLs in a general purpose language, in order to reuse part of the machinery which is already implemented, and to allow an easy combination of DSLs. This embedded approach is common in the functional programming world.
Taha [24] describes four characteristics of a good DSL: (1) the domain is well-defined, (2) the notation is clear, (3) the informal meaning is clear, and (4) the formal meaning is clear and implemented. This overlooks one important feature of a good DSL: its implementation should communicate with the user using terms from the specific domain. Otherwise, the encoding into the host language leaks in warnings and type error messages.
Unfortunately, the converse situation is the rule when working with embedded DSLs: error messages are phrased in terms of the underlying general purpose language. The nice abstraction provided by the DSL is broken and the internals of the library are exposed to users of the DSL. As a concrete example, consider a DSL for extensible records in Haskell, similar to Vinyl.Footnote 1 This sort of libraries mandates fields to be declared beforehand, as follows.


Each of the fields has the same representation in memory, but are given different types in the type annotation found after the \(\mathbin {{:}{:}}\) symbol.
Afterwards, it becomes possible to build records with any desired combination of fields. To do so, we use \( RNil \) to represent a record without any field, which we populate by adding new fields and their data using \( RCons \), as in:


The key point of this library is the definition of a strongly-typed get function, which given a field and a record, returns the value associated with such field. By strongly-typed we mean that it should reject code such as get age emily, where a field is requested from a record which does not contain it. This is achieved in the aforementioned library, by leveraging Haskell’s type system.


You can read this signature as ensuring that given a field named f with a type t and a record whose list of fields is fs, the field is an element of the list fs.Footnote 2 This works perfectly for type-correct programs. However, the type error message produced by GHC 7.8 for get age emily is far from perfect:


In order to understand such a message, the user of the DSL needs to know about the internals of the library. Even more problematic, the library uses advanced type-level concepts from Haskell which the user may not know about. The direct consequence is frustration with either the language, the library, or both. In contrast, a good error message would take into account the domain knowledge and be phrased similarly to:


A first advantage of this message is that internals of the library are hidden from the user. The user of the DSL also profits from better guidance to fix the problem.
In order to get domain specific error messages, DSL writers need to be able to hook into the compiler and massage the messages before they are shown to the user. Several approaches are described in the literature, such as the post-processing of messages [2] and inspection of the type engine trace [20]. In our work, we build upon the concept of specialized type rules [11]. In short, a specialized type rule is the description of how to type a concrete piece of syntax, thereby overriding the default behaviour of the type engine for such an expression.
A specialized type rule which improves the message for get age emily is:


The rule consists of four fragments (1)–(4). Fragment (1) is merely an identifier, which is used by the system to provide information about the rule, such as failing the soundness check (Sect. 5). For example, had we mistaken writing \( Recor \) instead of \( Record \), the system would show:


alongside with information to help fixing the problem.
Fragment (2), headed by \(\mathbf {case}\), contains the description of which code pieces are matched by the rule. In this fragment, \(\cdot \) indicates that any expression might be found in that position. Alongisde them, \(\#id\) is used to give a name to a node of the AST, so that we can refer to it in the rest of the rule. This example matches any application of the get function to at least two arguments.
The fragment (4), syntactically indicated between braces, mandates the compiler to produce an error message, built from various literal strings, the type of the field and the expression which encodes the record.
Ingredients comparable to (1), (2) and (4), with a slightly different syntax, were already available in the type rules of [11]. Our contribution is to allow type rules to match and fire only in certain typing contexts. For example, fragment (3) of the previous example, indicates that this specialized type rule shall only be applied when the compiler can prove that the field is not available in the given record (at type-level, this is encoded as \( Elem \, \#\! field \; fs \) being equal to \( False \)).
As described in Sect. 4.1, being able to apply a specialized type rule only when some typing information is known to hold has a number of interesting use cases. For example, a custom error message can be given for a specific instance of a Haskell type class. Also, common failure patterns can be detected and a fix can be suggested to the DSL user.
Being able to use typing information in specialized type rules requires changes to the type engine, as described in Sect. 4. Our approach is to perform type checking in two stages, in which a satisfiable subset of information from the first stage is used to select specialized type rules in the second stage. Furthermore, we want to ensure that the DSL writer does not render the type system unsound with a specialized type rule. Thus, we need to introduce soundness checks (Sect. 5).
A prototype implementation for a type system similar to that in the Haskell GHC compiler (including type classes, type families and higher-rank polymorphism) is available at http://cobalt.herokuapp.com.
2 Constraint-Based Type Inference
An integral part of most compilers involves performing a set of analyses on the input code, in order to detect ill behavior or prepare for optimization and transformation. Many of these analyses are described using a type system, which assigns types to constructs in the programming language. Statically-checked strong type systems, such as that of Haskell or ML, prevent many kinds of errors from arising at run-time. By using the type system, DSL writers can dictate how their DSL should be used.
Throughout this paper, we shall refer to the piece of software dealing with types as the type engine. As a first task, the type engine should be able to check that types match in the correct way: if the programmer has specified that an expression has an integral type, 3.5 should not be a valid value for such an expression. In many cases tagging every expression with a type is not neccessary in a program: the engine is able to reconstruct which types should be given to each expression via a process called inference.
There are several possible ways in which a type engine can be structured. One way is to traverse the Abstract Syntax Tree (AST) of the program, building the corresponding type at each step. This path is taken by the classical \(\mathcal {W}\) and \(\mathcal {M}\) implementations of the Hindley-Milner type system [3, 16]. However, these syntax-directed algorithms are known to introduce some problems related to error reporting, in particular a bias coming from the fixed order in which they traverse the tree [19].
Another approach is to structure the engine around the concept of constraints. Instead of a single pass, the engine operates in two phases: in a first phase, the AST is traversed and all the constraints that types must satisfy are gathered. Afterwards, a solution for those constraints is found. If the set of constraints happens to be inconsistent, we know that a type error exists in the program. This structure is shown in Fig. 1.
A constraint-based approach to typing is shown by Heeren et al. [11, 13] to be a good choice as a basis for domain specific error diagnosis. The main reason is that these systems do not impose a strict order on the whole process. Furthermore, once all constraints are gathered, the solver may have a more holistic view on the structure of the program. For example, it may decide to show a different error for a given identifier based on its use sites. Other advantages of constraint-based type engines are discussed in [21] and include better modularity and a declarative description, instead of an operational one. The main disadvantage of constraint-based approaches to typing is some extra overhead.
2.1 Syntax-Directed Constraint Gathering
We assume constraint gathering to be a syntax-directed process, which traverses the code being analyzed in a top-down fashion, and builds a constraint set bottom-up. The constraint generation judgement
represents that under an environment \(\varGamma \) the expression e is given a type \(\tau \) subject to the constraints C. Note that \(\varGamma \) and e are the inputs in the process, whereas \(\tau \) and C are the outputs.
Figure 2 shows the constraint generation rules for a simply-typed \(\lambda \)-calculus with \(\mathbf {let}\), a subset of the full Haskell language. The details on how to type full Haskell using constraints (which we implement in our prototype) are described in [26] as an instance of the general OutsideIn(X) framework.
As an example of this judgement, consider the following piece of Haskell, which returns the string representation of the successor of a given number n:


In Fig. 3 the full derivation tree of its constraint set is given. We have omitted the \(v : \tau \in \varDelta \) leaves and the name of the rules applied at each step, in order to fit the entire tree on the page.
2.2 Solving Order Matters
Once the constraints are gathered, it is time for the solver to perform its magic. In full generality, a solver is represented by a judgement of the form
which encodes that under some set of axioms \(\mathcal {A}\), the set of constraints Q has a solution given by a substitution \(\theta \) and a set of residual constraints \(Q_r\). It must be the case that the conjunction of the axioms \(\mathcal {A}\) and the residual constraints \(Q_r\) imply an instance of the original constraints \(\theta Q\). We furthermore assume that a special constraint \(\bot \) exists, which is returned when the constraint set Q is found to be inconsistent.
Continuing with the previous example, the type engine needs to solve the constraint set obtained from the gathering process:
In the Haskell Prelude, the Num type class is declared as:


Which means that the set of axioms \(\mathcal {A}\) in which the constraints are to be solved includes, at least, \(\forall a. \, Num \; a \implies Show \; a\), that is, every \( Num \) instance is guaranteed to have a corresponding \( Show \) instance. Under these circumstances, the solver returns the following result:
In particular, for the Haskell program this means that the inferred type is:
But what if solving a set of constraints results in \(\bot \), that is, if the set is found to be inconsistent? In that case, we need to generate an error message to show to the user. This entails pointing at one or several constraints from the original set as responsible for the inconsistency: this process is called blaming. Note that for the same set of constraints, several ways to blame might be possible. For example, take:
It is clear that these constraints form an inconsistent set. If we decide to blame the first two constraints, the error message to show is:


But if we choose the first and the third to blame, we get:


Furthermore, if these constraints come from different expressions, different points in the program would also be blamed for this type violation.
The dependence of error messages on the internal workings is known in the literature as the bias problem. To a certain extent, this problem is unavoidable, since every solver and blamer needs to be implemented in a deterministic way in order to be executed by a computer. Our aim is to look at the reverse side of the coin: how can certain orderings in the solving of constraints help us in giving the desired error message for a given class of expressions?
2.3 Constraint Scripts
In order to be more precise about how blaming needs to be processed in the system, we need to depart from the model in which constraints form an unordered set into one in which they form a partial ordering. Formalizations of this kind have already been considered in [9]. In this paper we use a simplified version of those, consisting of three combinators:
-
\(\cdot ^M\) The label combinator annotates a constraint script with information about the error message to show when the script is found to be unsatisfiable. The exact shape of the labels in implementation-defined: in this paper we use simple strings for ease of presentation.
-
\(\lceil \dots \rfloor \) When several scripts need to be satisfied, the join combinator specifies that at blaming, no preference should be given to any of the contained scripts.
-
\(\lhd \) The ordered combinator introduces asymmetry in blaming. If the combination of the constraints in the two scripts gives rise to an inconsistency, then the second one should be blamed.
If we use a constraint script instead of a simple set for the problem of three different types equated to a variable \(\alpha \), we can be much more precise about the error message. One possibility is to have:
The inconsistency is found then at the stage when the constraints \(\alpha \sim Bool\) and \(\alpha \sim Int\) are merged, and thus the message about not being able to unify \( Bool \) with \( Int \) should be generated. If we want a custom message, we can go one step further and write a constraint script:
One small glitch is that now we need to update the rules from Fig. 2 to produce constraint scripts instead of mere sets. The simplest approach is to change all conjunctions \(\wedge \) into the join \(\lceil \cdot \rfloor \) combinator. However, the implementor of the programming language may want to add some default asymmetries, e.g., giving preference to blaming constraints from e rather than from b in when using the \(\mathbf {let}\; x \mathrel {=} e \;\mathbf {in}\; b \) construct.
3 Specialized Type Rules
Specialized type rules enter the scene in the aforementioned constraint generation phase, by replacing one of the default rules with a DSL-writer-provided one. On the surface they are like any other type rule: each of them matches a syntactic form, and produces a constraints script based on those of its subcomponents.
In many cases, including Fig. 2, the gathering of constraints from an expression is syntax-directed. That is, at most one rule matches a certain set of shapes for expressions. The addition of specialized type rules breaks this property: each of them overlaps with one or more default type rules in a certain context. Thus, at each point of the AST, the type engine needs to decide whether a specialized type rule shall be used instead of the default one.
In our work, each rule defines when to be fired by two elements. The first, encoded in the \(\mathbf {case}\) fragment of the specialized type rule, is a syntactic one: the expression is verified to have a specific shape. After that check, there might be a second check based on typing information, which is given in the \(\mathbf {when}\) fragment of the specialized type rule. Implementation of that second check needs a two-stage type engine; we defer its explanation to Sect. 5.
The way in which a shape is conveyed to the type engine is via an expression matcher. Expression matchers form a subset of the term language, enlarged with metavariables for naming subexpressions. We need these metavariables to refer to the constraints and types of subexpressions of the expression being matched. In our prototype, expression matchers follow this grammar:Footnote 3


The reader may notice that we do not include \(\lambda \)-abstractions and \(\mathbf {let}\) blocks as constructs that a specialized type rule is able to match upon. We have not yet found any use case in which the DSL writer might need to alter the constraint scripts associated to those constructs. Furthermore, matching only on application alleviates us from including special syntax for changing the environment in a type rule: in applications the environment is simply inherited from the parent.
Note also that the system does not consider terms equated under \(\beta \)-reduction or \(\mathbf {let}\)-inlining. For example, the code \(\mathbf {let}\; x \mathrel {=} map \;(\mathbin {+}\mathrm {1})\;\mathbf {in}\; x \;[\mathrm {1},\mathrm {2},\mathrm {3}]\) is not matched by a specialized type rule with a \(\mathbf {case}\) fragment \({map}\;\cdot ^{\# fn }\;\cdot ^{\# lst }\). There are two reasons which incidentally strengthen the decision of taking a completely syntactic approach instead of taking into account some rules of computation:
-
1.
Different modes of use of the same function may correspond to different intentions on the part of the user. Thus, it makes sense to provide different specialized type rules for those different scenarios.
-
2.
A simpler matching procedure is more predictable. If we take \(\beta \)-reduction or \(\mathbf {let}\)-inlining into account, the DSL writer might be surprised that a rule fires (or does not) for a specific expression.
Also, one can always write an extra rule that matches on map with only one parameter.
Once a specialized type rule is found to match an expression, the fragment between braces is executed in order to build a constraint script. We could have used the combinators from last section to define the scripts directly, but they are too low-level to be easily usable by DSL writers. Instead, our prototype defines a higher-level language for constraint scripts which is then translated to the low-level one. The grammar is as follows:


The basic blocks of constraint scripts are, of course, constraints themselves. What distinguishes constraints C from the \(C^*\) mentioned in the grammar above is the ability to refer to the types of subexpressions named by a metavariable in the \(\mathbf {case}\) fragment. For example, when in the introduction we wrote \(\, \# field \sim Field \; f \; t \), the identifier \(\, \# field \) refers to the type that is assigned to the first argument to the get function.
In most cases, a specialized type rule needs to refer to the constraint scripts of one or more subexpressions in order to build the script for the entire expression. The syntax for such a reference is \(\mathbf {constraints}\) followed by the metavariable representing the subexpression in the matcher.Footnote 4 As an example of references, we can reformulate the rule app for application from Fig. 2 as:


But wait a moment, we have three constraint scripts here: \(\mathbf {constraints}\, \# f \), \(\mathbf {constraints}\, \# x \), and \(\, \# f \sim \, \# x \rightarrow alpha \); which combinator is chosen to put them together? By default, \(\lhd \) is chosen; it is the most common choice when providing specialized type rules for DSLs. This choice can be reverted, though, by enclosing a section with a new merger: \(\mathbf {join}\) switches to \(\lceil \cdot \rfloor \), and \(\mathbf {ordered}\) to \(\lhd \) again.
Constraint scripts may also specify a custom error message tied to a combination of constraints. In the high-level syntax \(\mathbf {error}\) is used. As in the case of constraint scripts, the syntax of error messages is defined by the implementation. In our case, the syntax is:


Sometimes, we want a specialized type rule to always generate an error message. One possibility would be to attach the message, using \(\mathbf {error}\), to an inconsistent constraint (such as \( Int \sim Bool \)). Given the usefulness of this scenario, we have included specialized syntax for this task: \(\mathbf {repair}\).
The translation from the high-level constraint script language to the low-level one is unsurprising. The full details of the translation can be found in [22].
3.1 Example DSLs
We have already introduced extensible records à la Vinyl as an example of a DSL which benefits from specialized type rules. In this section we introduce two examples coming from libraries which are commonly used by Haskell programmers: a database mapper called PersistentFootnote 5, and declarative vector graphics from the DiagramsFootnote 6 embedded DSL. Both libraries target a specific domain with their own terms; this makes them a perfect target for specialized type rules.
Note that in the examples we sometimes use type signatures which are simpler than their counterparts in libraries, in order to keep the irrelevant details out and obtain manageable specialized type rules.
Persistent [23]. The designers of this database mapper took a very type-safe approach: each kind of entity in the database is assigned a different Haskell type. Several advanced type-level techniques are used throughout its implementation: the result is a very flexible library, which unfortunately suffers from complicated error messages.
Apart from separating different entities via different types, Persistent imposes a strict distinction between: (1) values which are kept in the database, and which correspond to normal Haskell data types, (2) keys that identify a value in the database (like primary keys in SQL databases), which always have a \( Key \) type tagged with the kind of value it refers to, and (3) entities, which are a combination of key and value.
One important operation in Persistent is updating an entity in the database:


Based on its intended usage, there are two scenarios which benefit from domain specific type rules. One is using a non-\( Key \) value as first argument; based on previous experience with other libraries, the user of the DSL may expect that something like an \( Integer \) is to be given at that position. We can point to information about what a \( Key \) in Persistent represents. Another error which benefits from a domain specific perspective is using a \( Key \; a \) along with a value of a different type b, e.g., using a key for a \( Task \) when you need one for a \( Person \). A specialized type rule encompassing these use cases looks like:


This rule brings to the table an issue which we did not have to deal with before: a specialized type rule needs to ensure that all subexpressions (i.e., all nodes in the AST) are given types. Thus, although our focus is on the first three instructions, we also need to give types to the function replace, to the partially applied replace #key and finally to the whole expression. This is mandated by the soundness check from Sect. 5, although we are currently investigating ways to add these structural constraints automatically.
Diagrams [28]. This library was originally developed by Brent Yorgey, and aims to provide a way to construct pictures in a compositional way, by combining simple pictures into more complex ones. For example, this code taken from the tutorial defines a simple picture as a  image. The result is given in Fig. 4.
image. The result is given in Fig. 4.


The reader may notice that the drawing function has in its type a tag \( PGF \) indicating the back-end used to render it. Other possibilities include SVG, GTK+ or the Cairo graphics library. One invariant of the library is that you can only compose drawings that use the same back-end. This is a sensible use case for a specialized type rule:Footnote 7


In this case, we use \(\mathbf {join}\) and distinct type variables to make the type checking of each argument not influenced by the other. Then, we check that both back-ends coincide, if that fails we give a custom error message. As in the previous example, we need to incorporate types for each subexpression in the AST, something we do in the last \(\mathbf {join}\) section.
4 Two-Stage Specialized Type Rules
The methodology described up to now does not include the \(\mathbf {when}\) mechanism needed to make the extensible records specialized type rule, as described in the introduction, work. Before describing our solution, it is worthwhile to describe the disadvantages of the most obvious technique to reach this goal: when we need to decide whether to apply rule R or not, we look at the constraints gathered prior to that point and check whether those imply the ones in the \(\mathbf {when}\) fragment. The disadvantages can be summarized as:
-
(1)
The traversal of the tree, the process responsible for gathering the constraints for a given expression, becomes very complex: you need to move back and forth between the traversal itself and the constraint solver.
-
(2)
It is not clear how the gathering should proceed if during the process the solver finds an inconsistency, that is, a type error.
-
(3)
The decision of whether to apply a specialized type rule will be biased by the order in which constraints are gathered. If this is done bottom up, then we are constrained to know information only about subexpressions, whereas some more information might come from later use sites. Traversing in a top down fashion only moves the bias on to the other direcion. It might be possible to sketch a bidirectional solution, but this seems both complicated and unpredictable.
Our solution is to use two stages, each of then comprising constraint gathering and solving, instead of a single one in which interleaving is possible. This new architecture for the type engine is depicted in Fig. 5. In the case of successful completion of the type checking and inference procedure, the type engine shall still work as in Fig. 1. However, if an error is found in the process, we prepare for a second stage by pruning the set of constraints \(C_1\) obtained in the first stage until they become a satisfiable set \(S_1\), and then use that set as input to a second gathering from which we obtain a new set of constraints \(C_2\). The new gathering pass uses those pruned constraints to decide whether to apply or not each specialized type rule.
Note that in the second traversal of the AST we still need to call the solver in order to know whether the constraints in a given \(\mathbf {when}\) fragment hold or not. The difference with the alternative described at the beginning of the section is that now the sets of constraints \(S_1\) and \(C_2\) coming from different stages are kept separate: solving is done over \(S_1\), new constraints are gathered in \(C_2\). Furthermore, we know that the constraints \(S_1\) which we query form a satisfiable subset, since we pruned them. This relieves us from dealing with issue (2).
Our two-stage approach still suffers from bias. However, this bias is no longer structural: it is not related to the traversal of the AST, but rather to the operation of a pruner which decides which satisfiable subset of constraints to return, an easily replaceable part of the system. The pruner is now the part of the system which decides, in the presence of a type error, which constraints from the inconsistent set are kept for the second stage.
We think that this is a good choice for two reasons: first, at the stage in which the pruner is executed, it profits from a global view on the solving process, and might decide to select a different set of constraints depending on how many times those constraints were used, in how many inconsistencies they are involved, and similar statistics. A second reason is that the pruner can be easily replaced with another one, maybe one tailored for a specific domain.
Formally, in order to implement two-stage specialized type rules, we replace the constraint generation judgement \(\varGamma \vdash e : \tau \leadsto C\) with a more informed one,
where S is a set of constraints known to be satisfiable. This set S can be used as part of the input for the solver in order to check whether a given constraint set Q from a \(\mathbf {when}\) fragment holds under that assumptions by checking \(\mathcal {A} \, \wedge \, S \vdash Q \twoheadrightarrow \epsilon , \theta \).Footnote 8 That is, to know whether a specialized type rule must be triggered. The complete pipeline has now become:
-
Gather constraints under an empty known satisfiable set of constraints: \(\varGamma , \epsilon \vdash e : \tau _1 \leadsto C_1\). Only specialized type rules without \(\mathbf {when}\) fragments play a role in this first stage.
-
Try to solve the constraints \(\mathcal {A} \vdash C_1 \twoheadrightarrow C'_1, \theta _1\). If \(C'_1\) is empty, then solving was succesful and \(\theta _1\) is the sought-for substitution. We do not need a second stage of typing, and the compiler can proceed with the following stages.
-
Otherwise, there is an error in the expression e, and we need to start the second stage. First, we prune \(C_1\) to a satisfiable subset \(S_1\).
-
Gather constraints under this subset: \(\varGamma , S_1 \vdash e : \tau _2 \leadsto C_2\). At this point, new specialized type rules, those with a \(\mathbf {when}\) fragment, may be triggered.
-
Solve the constraints again \(\mathcal {A} \vdash C_2 \twoheadrightarrow C'_2, \theta _2\). It must still be the case that \(\bot \in C'_2\), but a different set of specialized type rules may now have been used, changing which constraints are blamed for the problem.
-
If the part of the script being blamed contains a custom error message, this message is printed by the compiler. The compiler falls back to the default error message for a given type error when the constraint script did not generate a custom message.
We are now in a position of describing what happens exactly when get age emily from the introduction is type-checked. In the first pass we obtain a set of constraints which include:




As we explained above, before we perform gathering in the second stage, we need to make the set of constraints satisfiable by pruning it. How this is achieved is explained in Sect. 4.2. Here we will take as granted that such a procedure exists. If we take out the last constraint, we can reestablish satisfiability.


The second constraint gathering phase takes this new \(S_1\) as extra input. At some point, we need to decide whether to apply the specialized type rule from the introduction to \( get \; age \; emily \). The particular \(\mathbf {when}\) fragment reads:
The call to the solver returns the following result:
The fact that the residual set is \(\epsilon \) means that \(S_1\) does indeed entail the constraints in the \(\mathbf {when}\) fragment. Thus, that rule will be applied instead of the default one. As a result, the constraint script generated for the expression is:
It is clear that the blame for the inconsistency in this case must go to the explicit \(\bot \) constraints. The message that the user of the DSL sees is the one attached to that constraint, which is the one we desired.
4.1 Improving the Example DSLs
In this section we return back to the Persistent and Diagrams DSLs, enhancing their specialized type rules with \(\mathbf {when}\) fragments. Both examples showcase scenarios where our two-stage approach enables giving a more informative error message than otherwise.
Type Rules for Specific Instances. We have to admit at this point that we made quite a big simplification when explaining the Diagrams \((\mathbin {|||})\) combinator. Its type is not simply


as we implied. Instead, the actual type (in version 1.3) is


This generality allows the same combinator to be used with any type whose values can be put side by side (as witnessed by \( Juxtaposable \)) in a 2-dimensional space (as witnessed by \( InSpace \; V2 \; n \; a \)). \( Diagram \; b \) is an instance of those type classes, as are lists of diagrams, and diagrams with a modified origin.
If we use the specialized type rule given in Sect. 3.1, we get a custom error message for the \( Diagram \; b \) case. But it comes with an undesired side-effect: we can no longer use the \((\mathbin {|||})\) function on other values which are not \( Diagram \)s.Footnote 9 Instead, we want to obtain a custom error message when the arguments are known to be \( Diagram \)s, but not for any other type. We can do so by moving some of the constraints to the \(\mathbf {when}\) fragment:


The \((\mathbin {|||})\) function shows an important trade-off to be made in languages which support a large degree of abstraction, like Haskell. On one side, one would like to make libraries as general as possible, so they can be reused in many different scenarios. On the other hand, this usually implies a more complicated type, which results in more complicated error messages.
Haskell’s libraries and language extensions provide even more compelling examples: we have \( fmap \), which applies to every \( Functor \) and it is thereby very general, and \( map \), which is the restriction of \( fmap \) to lists. One of the reasons why beginners are first introduced to \( map \) is that error messages with \( fmap \) can be quite scary, since they involve type classes, a concept more advanced than lists. With our system in place, a specialized type rule can be defined to regain the error messages of \( map \) when \( fmap \) is used with lists:


In the same way that we declared special type rules for \( fmap \), we can do so for many other \( Applicative \), \( Monad \), \( Foldable \), \( Traversable \) and \( Monoid \)-related functions when they apply to specific types. The functions \( map \) and \( fmap \) can now be merged without compromising the quality of type errors, and the same applies to \( filter \) and \( mfilter \), \( mapM \) in its list-oriented and \( Traversable \)-oriented incarnations, and so on. We think that two-stage specialized type rules may have also eased the transition in the GHC base libraries to \( Foldable \) and \( Traversable \).Footnote 10
The same tension occurs with the reintroduction of monad comprehensions [5, 27]. On the one hand, they generalize a useful construct from lists to other monads. On the other hand, error messages become less clear. As a compromise, GHC includes monad comprehensions, but they must be explicitly turned on.
Suggesting Reparations. As part of its duty as a database library, Persistent includes functionality to query a data source. One of the most common functions to perform queries is \( selectList \), which returns the results of the query as a list of \( Entity \)s (as in our previous usage of Persistent, we assume a simpler type signature in order to focus on the aspects of our specialized type rules):


Values of type \( Filter \; v \) describe those constraints that an entity must satisfy in order to be returned by the call to \( selectList \). For example, one can check that a field in the row has a given value by using:


Values of type \( Filter \; v \) describe those constraints that an entity must satisfy in order to be returned by the call to \( selectList \). For example, one can check that a field in the row has a given value by using:


Unfortunately, the name of \((\equiv \! .)\) is very close to the standard equality operator \((\equiv )\) and it is easy to confuse one for the other. This is a case where, by using our domain knowledge, we can suggest the user of the DSL how to fix the error.
The incorrect expression is of the form \( field \equiv value \), and we write a specialized type rule for this particular kind of expression. In the \(\mathbf {when}\) fragment we check whether the first argument is of type \( EntityField \; v \; t \). If so, it is very likely that the user intented to use \((\equiv \! .)\) instead. This is the specialized type rule:


4.2 Implementing Pruning
Up to now, we have assumed that one can prune any inconsistent set of constraints into a satisfiable subset. This is a fair assumption: many algorithms can be found in the literature to compute them [1, 7]. Even better: many algorithms give us not only any satisfiable subset, but a maximal subset. That is, a subset such that adding any other of the original constraints makes it inconsistent.
The problem with these techniques is that they are non-deterministic: running them over an inconsistent set of constraints returns a maximal satisfiable or minimal unsatisfiable subset, but there is no direct way to influence which. We have discussed the importance of blaming the right constraint in order to obtain the desired diagnosis for a specific scenario, and described constraint script combinators to encode preferences. In this section we describe how to incorporate pruning into the solving phase to obey those preferences.
The solution is to replace the sequential pipeline of solving, and then pruning in case of inconsistency with an interleaving of those two processes. This combined process is defined by a judgement of the form
which, compared with the judgement in Sect. 2.2, has one more input and one more output.Footnote 11 The extra input keeps track of the current error message to be shown in case an inconsistency is found at that point. The extra output is a set of pairs \(Q \mapsto M\) which saves those error messages obtained up to that moment along with the constraints which led to them. Another important difference is that \(Q_r\) is always a satisfiable set of constraints.
The description of the process as implemented in our prototype is given in Fig. 6. For most constraint script combinators, two rules are given: the one suffixed with \({\ }_\textsc {fail}\) corresponds to finding an inconsistency, otherwise the corresponding \({\ }_\textsc {ok}\) rule is applied. The first two rules, single \({\ }_\textsc {ok}\) and single \({\ }_\textsc {fail}\), handle the base case of a single constraint. When the constraint does not lead to an inconsistency (\(\bot \not \in C_r\)), we can return the residual constraints as satisfiable subset, with no errors attached. When the single constraint is inconsistent (like \( Int \sim Bool \)), the only possible pruning is an empty set of constraints. This is exactly what single \({}_\textsc {fail}\) does.
More than one inconsistency may be found in this process, coming from pruning different subsets of constraints from the script. In order to know which error message to associate with each inconsistency, the judgement uses the extra input M. This current message is updated whenever we find an annotation in a script by the message rule. Remember that a reparation instruction such as


leads to a constraint script \(\bot ^\texttt {"my message"}\). Using only these three rules, we can see that the result of combined solving and pruning is:
The last output, the list of errors, contains the message we gave in the type rule.
The case of combining several constraint scripts, either using \(\lceil \cdot \rfloor \) or \(\lhd \) is a bit more involved. In both cases, we start by considering the solving and pruning of the constraint scripts being combined. Each of those executions will return a satisfiable residual subset, a substitution and a list of errors. We need to put together all those residual subsets, but we also need to ensure that substitution are compatible among themselves. In order to do so we ask the constraint system to include a \(\mathsf {intern}\) operation which internalizes a substitution as a set of constraints (in our case, each \(\alpha \mapsto \tau \) is translated into \(\alpha \sim \tau \)). At the end, we might end up being consistent or inconsistent. In the first case, we just pop the errors found in the children; but when an inconsistency is found, we need to first perform pruning.
Pruning is the point where the difference between \(\lceil \cdot \rfloor \) and \(\lhd \) needs to manifest itself. In the first case, the pruner should treat all constraints equally, without any specific preference for blaming. On the other hand, \(\lhd \) imposes such a preference, which the pruner should take into account when performing its task. In the rules in Fig. 6, we encode these two modes of operation as two operations that the pruner needs to define: \(\mathsf {prune}\) for no preference, \(\mathsf {aprune}\) to blame constraints from its second argument preferably than from the first one.
In both operations, the result is a triple \(\langle Q_\uparrow , \theta _\uparrow , Q_\bot \rangle \). The first two elements are the pruned set of constraints and the pruned substitution, which are now known to be satisfiable. The last element is composed of those constraints which are blamed for the error. The set \(Q_\bot \) is saved along with the current error message in order to be shown to the user once the solving is finished.
At the end of Sect. 2.3 we looked at the following constraint script:
Using the rules from Fig. 6, we arrive to the point of applying the \(\lhd \) case:
Both branches are consistent, with the residual satisfiable subset being equal to the original set. Thus, we need to check what is the result of the solver for the combined set:
It is inconsistent, so we need to prune the set:
The corresponding operator from the pruner preferred the second constraint to the first, as the semantics of \(\lhd \) mandate. The blamed constraint is put into the error list along with the current message:
There are benefits to making the pruner a parameter of the solver. First of all, we can reuse work on maximal satisfiable subsets, improving the pruning as the state of the art advances in this respect. Furthermore, it opens the door to using heuristics for blaming [8] and even to use domain-specific pruners which understand the most common source of errors for a given domain.
5 Soundness and Completeness
Specialized type rules are intended to offer guidance to the type engine in order to provide better error diagnosis. However, a DSL writer should not be able to subvert the type system using this kind of rule, especially if this happens inadvertedly. For that reason, type rules are checked for soundness by the checker prior to the AST traversal, as Fig. 5 shows. A nice feature of our design is that we do not need to change the solver in order to make this soundness check.
Consider first those specialized type rules without a \(\mathbf {when}\) fragment. Given such a rule, the initial step is to generate an expression which represents all the possible instances of the rule. This is achieved by building an expression e equal to the one in the \(\mathbf {case}\) fragment, but where unconstrained subexpressions are replaced by fresh metavariables with fresh types assigned to them. Then, we generate two constraint scripts:
-
\(S_{with}\), by traversing e taking into account the specialized type rule we are checking at that moment,
-
\(S_{none}\), by traversing e using only the default type rules.
One small detail is needed to make this process work: we need to ensure that type variables assigned to each subexpression in the AST are stable under different traversals. This is not hard to accomplish, but deviates from the standard approach of generating completely fresh variables in every traversal.
Intuitively, we want to check whether the constraints in the set gathered using the specialized type rule, \(S_{with}\), imply the conjunction of the constraint in the set obtained using only the default rules, \(S_{none}\). However, our constraint solving judgement cannot use a constraint script as part of the set of assumptions (the argument at the left of the \(\vdash \) symbol). Thus, we need to flatten the script back to a set, via the following auxiliary operation:
In this form, if we want to check whether \(S_{with}\) entails \(S_{none}\) given some axioms \(\mathcal {A}\), we can use \(\mathcal {A} \wedge \mathsf {flatten}(S_{with}) \vdash S_{none} \twoheadrightarrow S', \theta \). In particular, we must verify that \(S'\) is empty. This approach does not work in the extreme case of \(\bot \in \mathsf {flatten}(S_{with})\). In that case, it is automatically the case that \(S_{none}\) is implied (“ex falso quodlibet”). This is summarized in a new judgement \(\mathcal {A} \vdash S_1 \Rightarrow S_2\):


By using \(\mathcal {A} \vdash S_{with} \Rightarrow S_{none}\) we check for soundness. This means that type rules which are stricter than the defaults are allowed. One example is a type rule which restricts the type of \( fmap \) from \( Functor \; f \Rightarrow ( a \rightarrow b )\rightarrow f \; a \rightarrow f \; b \) to \(( a \rightarrow b )\rightarrow [ a ]\rightarrow [ b ]\). If we want to keep the type exactly the same, the domain specific type rules must also be checked for completeness: this can be done easily by using the converse implication: \(\mathcal {A} \vdash S_{none} \Rightarrow S_{with}\).
The definition of \(\Rightarrow \) explains why we need to type every node in the AST when developing a specialized type rule. In the default gathering scheme, \(S_{none}\) contains typing information for all those nodes. Had we not included those in \(S_{with}\), some leftover constraints remain in the residual set, which we need to be empty in order to check the implication.
The novel feature of our specialized type rules is the dependence on a typing context. When a specialized type rule includes a \(\mathbf {when}\) fragment, the previous direct approach is not enough. First of all, since the soundness check has no associated context, such specialized type rules would never be applied if \(\mathbf {when}\) fragments are taken into account during traversal. Thus, when gathering constraints for the soundness check we refrain from looking at \(\mathbf {when}\) fragments. However, checking the implication \(\mathcal {A} \vdash S_{with} \Rightarrow S_{none}\) is not correct in this scenario, since the constraints in \(S_{with}\) are only valid in a specific context. The solution is to take the constraints as additional axioms.
To illustrate, consider our running example, a specialized type rule for extensible records. This rule only fires in a specific typing context:


The expression which is generated in this case is \(get \; x_1 \; x_2\), where the \(x_i\) are fresh metavariables. In addition, two scripts \(S_{with}\) and \(S_{none}\) are generated by traversing the expression with and without the specialized type rule in place. But it is not correct to check whether \(\mathcal {A} \vdash S_{with} \Rightarrow S_{none}\), since the type rule is only supposed to be valid when the field cannot be found in the record. The correct property to check is \(\mathcal {A} \, \wedge \, \tau _2 \sim Record \; fs \, \wedge \, Elem \; \tau _1 \; fs \sim False \vdash S_{with} \Rightarrow S_{none}\), where \(\tau _1\) and \(\tau _2\) are the types assigned to the \(\, \# field \) and \(\, \# record \) subexpressions, respectively.
More generally, let \(S_{with}\) be the script obtained from the application of the domain specific type rules, \(Q_{with}\) the checks that would have been made in order to apply those rules, and \(S_{none}\) the script obtained by the default traversal. Previously, we ensured that the following relations held between those scripts:
The change is to add \(Q_{with}\) to the list of axioms:
In that way, we ensure that the check is performed only for the cases in which the type rule can be applied.
6 Related Work
The system presented in this paper has a unique feature compared to other approaches to domain specific error diagnosis: using a satisfiable subset of constraints obtained from solving to trigger (more) specialized to type rules.
Helium. Our domain specific type rules were directly inspired by those found in the Helium compiler [10–13]. There are however several differences between their work and ours.
First of all, Helium focuses on the problem of providing good error messages. Apart from domain specific type rules, Helium uses heuristics to guide the blaming process and try to ensure that the messages shown to the user are the most helpful to fix errors. Our work focuses instead on giving DSL writers the tools to tailor error messages to the needs of the particular specific domain. For that reason, our focus is only on enhancing type rules.
Some of Helium heuristics involve reparation. A siblings heuristics is described in [13], which suggests replacing a function call with another function if the first one cannot be correctly type but it is possible in the second case. One example is replacing \((\mathbin {+\!\!\!+})\) by \((\mathbin {:})\) or vice versa, a common error for beginner programmers. As seen in Sect. 4.1, our specialized type rules can handle this case using a different approach. The main disadvantage of our system is that type rule descriptions are much longer than siblings enumeration.
Another important difference lies in the source language that is addressed. Whereas Helium supports only Haskell 98 constructs, we support a wider range of Haskell features such as type families and multiparameter type classes within the same framework. This implies that the constraints involved in our type rules are more complicated than those in Helium. Furthermore, Helium heuristics are tied to a representation of the constraint solving process using type graphs. Our system, being based on OutsideIn(X) is extensible, and could be used to accomodate type system enhancements such as units of measure [6].
GHC. From version 8 on, GHC supports custom type errors for instance and type family resolution [4]. For example, you can define:


Then, when a constraint like \( Show \;( Int \rightarrow Bool )\) is found by the solver, it is rewritten to \( TypeError \;( Text \mathbin {...})\). The compiler knows that when such a constraint is in the set, it should produce an error message with the given text.
The main advantage of this approach is that it reuses type-level techniques, leveraging the abstraction facilities that Haskell provides for type programming. However, these combinators cannot influence the ordering of constraint solving, which is an important feature for precise error messages, as explained in Sect. 2.2.
Idris. The support for custom error messages in Idris [2], a dependently typed language with a syntax similar to Haskell’s, is based on post-processing the errors generated by the compiler prior to showing them to the user. There is no way to influence the actual type inference and checking process. We discussed in this paper the importance of this influence: our \( get \; age \; emily \) example cannot be expressed using only post-processing. As future work we want to experiment with adding a post-processing stage to our own type engine, and see how it interacts with the rest of the system.
Scala. An instrumented version of the Scala compiler geared towards type feedback is described in [20]. Starting with low-level type checker events, a derivation tree is built on demand. Custom compiler plug-ins are able to inspect this tree and generate domain specific error messages. This approach is strictly more powerful than Idris’, but still cannot influence the way in which the type engine performs inference.
SoundExt. Language extensions are defined in SoundExt [17] by rewriting to a core language plus specific type rules for the new construct. As in our work, the system checks for the soundness of the new type rules before they can be applied. However, the authors mention that two sound language extensions might result in an unsound combination, thus requiring extra checks when put together. In our case, the way the soundness check is performed ensures that if all specialized type rules pass the test, they can be freely combined
Racket. The programming environment offered by Racket is well-known for its focus on students [18]. Their notion of language levels, where only some constructs of the full Racket language are available, could be simulated using purposefully incomplete type rules.
7 Conclusion and Future Work
We have shown how a second stage in the type checking and inference process can be used in a constraint-based type engine to introduce custom error messages for DSLs. The way in which that information is conveyed to the compiler is via specialized type rules. The ability to depend on partial type information is provided in a dedicated fragment of the type rule.
Right now, our prototype only compiles programs for a specific subset of Haskell. We aim to implement our ideas in an actual Haskell compiler, and evaluate the power of specialized type rules for realistic libraries and programs.
In the future, we want to ease the description of specialized type rules in several ways. Right now there is no way to abstract common type rule patterns, although one may expect very similar looking rules for a big library. We aim to introduce parametrized type rules, which can be reused in different contexts by providing the missing moving parts. Another possibility is to help the DSL writer by giving a way to obtain the default type rule for a given expression. That type rule can later be refined by changing the priorities for blaming and adding custom error messages.
Another area which we aim to research is how tools can aid in the process of writing and understanding specialized type rules. For example, a graphical user interface might help when writing complicated expression matchers. Another interesting tool is a type rule debugger, which shows which rule has been applied at each point in the tree, in order to diagnose problems when a rule is applied unexpectedly more or less often than expected.
Notes
- 1.
- 2.
\( Elem \) is a so called “type family”, a restricted version of a type-level function, and the relation \( \sim \) means “equality on types”. In Haskell, Booleans are available at the type level via a technique called data type promotion.
- 3.
In the implementation,
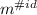 is written as \(\# id@(m)\), with the special case \(\cdot ^{\# id}\) being written simply as \(\# id\).
is written as \(\# id@(m)\), with the special case \(\cdot ^{\# id}\) being written simply as \(\# id\). - 4.
Thus, metavariables introduced in the matcher can refer inside a constraint script to types or other scripts depending on the context in which they occur.
- 5.
- 6.
- 7.
The actual type of \((\mathbin {|||})\) is more general than shown in this example. We take care of this fact in Sect. 4.1.
- 8.
It is important that the obtained residual set of constraints is empty and not simply different from \(\bot \), because in other case we would be checking only the compatibility of Q with S instead of its entailment.
- 9.
The type rule is sound but not complete. Sect. 5 explains how completeness is automatically checked by our system.
- 10.
Arguments for and against generalizing list functions in Haskell’s Prelude have been given at https://ghc.haskell.org/trac/ghc/wiki/Prelude710.
- 11.
A summary of all the judgements used for gathering and solving throughout this paper is given in Fig. 7.
References
Bailey, J., Stuckey, P.J.: Discovery of minimal unsatisfiable subsets of constraints using hitting set dualization. In: Hermenegildo, M.V., Cabeza, D. (eds.) PADL 2004. LNCS, vol. 3350, pp. 174–186. Springer, Heidelberg (2005)
Christiansen, D.R.: Reflect on Your Mistakes!. Lightweight Domain-Specific Error Messages, Presented at TFP (2014)
Damas, L., Milner, R.: Principal type-schemes for functional programs. In: Proceedings of the 9th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 1982, NY, USA, pp. 207–212. ACM, New York (1982)
Diatchki, I.: Custom type errors. https://ghc.haskell.org/trac/ghc/wiki/Proposal/CustomTypeErrors
Giorgidze, G., Grust, T., Schweinsberg, N., Weijers, J.: Bringing back monad comprehensions. In: Proceedings of the 4th ACM Symposium on Haskell, Haskell 2011, NY, USA, pp. 13–22. ACM, New York (2011)
Gundry, A.: A typechecker plugin for units of measure: domain-specific constraint solving in GHC haskell. In: Proceedings of the 8th ACM SIGPLAN Symposium on Haskell, Haskell 2015, NY, USA, pp. 11–22. ACM, New York (2015)
Haack, C., Wells, J.B.: Type error slicing in implicitly typed higher-order languages. Sci. Comput. Program. 50(1–3), 189–224 (2004)
Hage, J., Heeren, B.: Heuristics for type error discovery and recovery. In: Horváth, Z., Zsók, V., Butterfield, A. (eds.) IFL 2006. LNCS, vol. 4449, pp. 199–216. Springer, Heidelberg (2007)
Hage, J., Heeren, B.: Strategies for solving constraints in type and effect systems. Electron. Notes Theor. Comput. Sci. 236, 163–183 (2009)
Heeren, B., Hage, J.: Type class directives. In: Hermenegildo, M.V., Cabeza, D. (eds.) PADL 2004. LNCS, vol. 3350, pp. 253–267. Springer, Heidelberg (2005)
Heeren, B., Hage, J., Swierstra, S.D.: Scripting the type inference process. In: Proceedings of the Eighth ACM SIGPLAN International Conference on Functional Programming, ICFP 2003, NY, USA, pp. 3–13. ACM, New York (2003)
Heeren, B., Leijen, D., van IJzendoorn, A.: Helium, for learning Haskell. In: Proceedings of the 2003 ACM SIGPLAN Workshop on Haskell, Haskell 2003, NY, USA, pp. 62–71. ACM, New York (2003)
Heeren, B.J.: Top Quality Type Error Messages. Ph.D. thesis, Universiteit Utrecht, The Netherlands, September 2005
Hudak, P.: Building domain-specific embedded languages. ACM Comput. Surv. 28(4es), Article No. 196 (1996). http://dl.acm.org/citation.cfm?id=242477
Koops, H.V., Magalhães, J.P., De Haas, W.B.: A functional approach to automatic melody harmonisation. In: Proceedings of the First ACM SIGPLAN Workshop on Functional Art, Music, Modeling & Design, FARM 2013, pp. 47–58. ACM (2013)
Lee, O., Yi, K.: Proofs about a folklore let-polymorphic type inference algorithm. ACM Trans. Program. Lang. Syst. 20(4), 707–723 (1998)
Lorenzen, F., Erdweg, S.: Modular and automated type-soundness verification for language extensions. In: Proceedings of the 18th ACM SIGPLAN International Conference on Functional Programming, ICFP 2013, NY, USA, pp. 331–342. ACM, New York (2013)
Marceau, G., Fisler, K., Krishnamurthi, S.: Mind your language: on novices’ interactions with error messages. In: Proceedings of the 10th SIGPLAN Symposium on New Ideas, New Paradigms, and Reflections on Programming and Software, Onward! 2011, NY, USA, pp. 3–18. ACM, New York (2011)
McAdam, B.J.: On the unification of substitutions in type inference. In: Hammond, K., Davie, T., Clack, C. (eds.) IFL 1998. LNCS, vol. 1595, pp. 137–152. Springer, Heidelberg (1999)
Plociniczak, H., Miller, H., Odersky, M.: Improving human-compiler interaction through customizable type feedback (2014)
Pottier, F., Rémy, D.: The essence of ML type inference. In: Pierce, B.C. (ed.) Advanced Topics in Types and Programming Languages, chapter 10, pp. 389–489. MIT Press, Cambridge (2004). http://dl.acm.org/citation.cfm?id=1076265
Serrano, A., Hage, J.: Specialized type rules in Cobalt. Technical report, Department of Information and Computing Sciences, Utrecht University (2015)
Snoyman, M.: Developing Web Applications with Haskell and Yesod. O’Reilly Media Inc, USA (2012)
Taha, W.: Plenary talk III domain-specific languages. In: ICCES 2008, International Conference on Computer Engineering Systems, 2008, pp. xxiii–xxviii. November 2008
Voelter, M.: DSL Engineering - Designing, Implementing and Using Domain-Specific Languages. CreateSpace Independent Publishing Platform, Hamburg (2013)
Vytiniotis, D., Peyton Jones, S., Schrijvers, T., Sulzmann, M.: OutsideIn(X): modular type inference with local assumptions. J. Funct. Program. 21(4–5), 333–412 (2011)
Wadler, P.: Comprehending monads. In: Proceedings of the 1990 ACM Conference on LISP and Functional Programming, LFP 1990, NY, USA, pp. 61–78. ACM, New York (1990)
Yorgey, B.A.: Monoids: Theme and variations. In: Proceedings of the 2012 Haskell Symposium, Haskell 2012, NY, USA, pp. 105–116. ACM, New York (2012)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 Springer-Verlag Berlin Heidelberg
About this paper
Cite this paper
Serrano, A., Hage, J. (2016). Type Error Diagnosis for Embedded DSLs by Two-Stage Specialized Type Rules. In: Thiemann, P. (eds) Programming Languages and Systems. ESOP 2016. Lecture Notes in Computer Science(), vol 9632. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-49498-1_26
Download citation
DOI: https://doi.org/10.1007/978-3-662-49498-1_26
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-49497-4
Online ISBN: 978-3-662-49498-1
eBook Packages: Computer ScienceComputer Science (R0)
















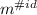 is written as
is written as 